正切函数的图像与性质.pdf
正切函数的图像与性质
正切函数的图像与性质
y=tanx
若需视频讲解请联系作者!
π2
−π2
•正切函数的最小正周期是π
•正切函数的最小正周期是π,延伸成整个定义域上的的图像
•渐近线x =±π
2
y
x
π2
−π2
y
x
•单调递增区间:(−π2,π
2)•定义域:x ≠π
2
+k π,k ∈Z •值域:y ∈R
•为了方便起见,先研究一个周期内的函数图像和性质,然后扩展到整个定义域上
•[−π2,π
2] 范围内的图像如图:
•单调递减区间:无
•对称轴:无•中心对称点:x =0
π2
−π2
y
x
π2
−π2
y
x •单调递增区间:[−π
2+k π,π
2+k π],k ∈Z •中心对称点:(k π,0),k ∈Z
y =tanx 的图像与性质
•延伸成整个定义域上的的图像
•k π即周期的整数倍
π
3π2
B
•与点A 的函数值相同的点B ,它们的x 值相差π•两个相邻的中心对称点(0,0),(π,0)相差πA
•定义域:x ≠π
2
+k π,k ∈Z
•值域:y ∈R
−3π2
π2
−π2
y
x •单调递增区间:[−π2+k π,π
2+k π],k ∈Z
•中心对称点:(k π,0),k ∈Z
总结
π
3π2
•定义域:x ≠
π
2
+k π,k ∈Z
•值域:y ∈R
−3π2。
高二数学余弦函数、正切函数的图像与性质

2
的图象——正切曲线 .
1.正切曲线是由通过点
2
,0
且 与y轴
互相平行的直线隔开的无穷多支曲线所组
成.
2.正切函数y=tanx的对称中心的坐标是
,0
2
3.仿照 正弦、余弦函数的“五点法”作图,
选择“三点两线法”作正切函数在区 间 ,
2 2
上的简图.三点坐标是: ,1 , 0,0 , ,1
• 小结: • 1.理解利用正切线画出正切函数图象
的方法
2.掌握正切函数的图象与性质 3.会画正切函数简图
且x≠қπ+ π1 ,
2
因此知道正切函数y=tanx是周期函数,并且 π是它的一个周期,又是它的最小正周期.
学法指导
1.用单位圆上的正切线来作正切函数
y=tanx在开区间
2
,
2
ห้องสมุดไป่ตู้
内的图象.
2.根据正切函数的周期性,可以把上述图
象向左、向右连续平移,得出正切函数
y
tanx
, x
,
,
2
正切函数的图象与性质
沈阳二中数学教研组
• 学习目标 1.理解利用正切线画出正切函数图象 的方法
2.掌握正切函数的图象与性质 3.会画正切函数简图
•学法指导:
1.遇到一个新的函数,画出它的图象,通过 观察图象获得对它的性质的直观认识,是 研究函数的基本方法。
2.由诱导公式得tan(x+π)=tanx,其中x R,
,
内都是增函数.
2
2
课堂练习一
1.观察正切曲线,写出满足下列条件的x的取 值范围:
(1)tanx >0_____.(2)tanx+1≥0_____. (3)tanx<0_____.(4)|tanx|≤1_______. 2.正切函数在整个定义域内是增函数吗?为什
第6章 三角函数 6.5 正切函数的图像与性质

沪教版(上海) 高一第二学期 新高考辅导与训练 第6章 三角函数 6.5 正切函数的图像与性质
一、解答题
1. 求函数的定义域、值域、最小正周期和单调区间.
2. 求下列函数的值域:
(1);
(2);
(3).
3. 求下列函数的最小正周期:
(1);
(2).
二、填空题4. 求下列函数的单调区间:
(1);
(2)
.5. 求下列函数的值域:
(1);
(2)
.6.
已知函数是增函数,值域为,求a ,b 的值.
7. 函数的图象与
轴的两个相邻的交点坐标分别为,且函数图象过点,求函数解析式.
8. 函数的奇偶性是__________.
9. 函数的最小正周期为4,则____________.
10.
函数的定义域为_______________.
三、单选题
11. 函数的值域为_____________.
12. 直线y =a (a 为常数)与函数y =tan ωx (ω>0)的图象相邻两支的交点的距离为________.
13. 在下列函数中,同时满足以下三个条件的是( ).
①在上单调递增,②以为周期;③是奇函数.
A .
B .
C .
D .
14.
函数 的大致图象是( )
A .
B .
C .
D .。
(完整版)最全三角函数的图像与性质知识点总结
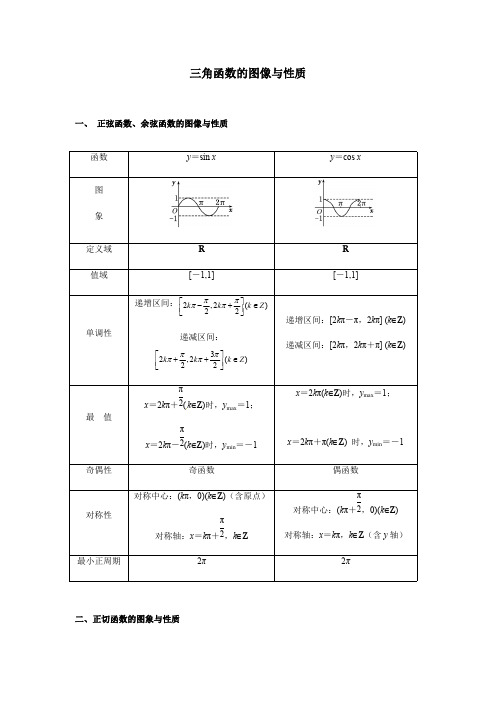
i ng si nt he i rb ei n ga re g三角函数的图像与性质一、 正弦函数、余弦函数的图像与性质二、正切函数的图象与性质函数y =sin x y =cos x图象定义域RR 值域[-1,1][-1,1]单调性递增区间:2,2()22k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦递减区间:32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦递增区间:[2k π-π,2k π] (k ∈Z )递减区间:[2k π,2k π+π] (k ∈Z )最 值x =2k π+(k ∈Z )时,y max =1;π2x =2k π-(k ∈Z )时,y min =-1π2x =2k π(k ∈Z )时,y max =1;x =2k π+π(k ∈Z ) 时,y min =-1奇偶性奇函数偶函数对称性对称中心:(k π,0)(k ∈Z )(含原点)对称轴:x =k π+,k ∈Zπ2对称中心:(k π+,0)(k ∈Z )π2对称轴:x =k π,k ∈Z (含y 轴)最小正周期2π2π定义域{|,}2x x k k Z ππ≠+∈值域R单调性递增区间(,)()22k k k Z ππππ-+∈奇偶性奇函数对称性对称中心:(含原点)(,0)()2k k Z π∈最小正周期π三、三角函数图像的平移变换和伸缩变换1. 由的图象得到()的图象x y sin =)sin(ϕω+=x A y 0,0A ω>>xy sin =方法一:先平移后伸缩方法二:先伸缩后平移操作向左平移φ个单位横坐标变为原来的倍1ω结果)sin(ϕ+=x y xy ωsin =操作横坐标变为原来的倍1ω向左平移个单位ϕω结果)sin(ϕω+=x y 操作纵坐标变为原来的A 倍结果)sin(ϕω+=x A y 注意:平移变换或伸缩变换都是针对自变量x 而言的,因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序,否则会出现错误。
高一数学正切函数的图像和性质2

我和家人一进入夜市,就被一位中年女老板笑脸相迎,引我来到一个小桌边坐下,热情地递上菜单。我被那份盛情所感染,要了几瓶冰镇啤酒,点了一些烧烤,有意去犒劳下自己和家人旅途的辛劳。 身处吵杂的夜市,在美酒的熏陶中,心仿佛进入了另一种境界。
多年来,我喜欢上了旅游,假期总是安排得满满的,有人问起我旅游的感悟,我说那是在吃苦中找到了快乐,在压抑中放松了身心,在知识匮乏中了解各地的风土人情和历史文化,有了“行千里路, 读万卷书,布衣亦可看着天色已晚,登牛背梁已没有时间了,就离开前往山阳方向行进。来到山阳县城后,已是万家灯火。我安排好住宿后,和家人来到繁华的街上,看到小城的“烟火”已在 疫情后有序地回归,夜市灯火通明,啤酒烧烤,朋友谈天说地,热闹非凡。冷寂了几个月后,我又一次听到了那熟悉的酒杯碰撞声;又一次听到了火锅翻滚的冒泡声;又一次感觉到了生活的激情。宝亿 国际娱乐官网就选75775
5.4.3 正切函数的性质与图象7题型分类(学生版)2025学年高一数学同步知识题型讲义(人教必修一

5.4.3 正切函数的性质与图象7题型分类一、正切函数的图象二、正切函数的性质1.定义域:⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ,2.值域:R3.周期性:正切函数是周期函数,最小正周期是π4.奇偶性:正切函数是奇函数,即()x x tan tan -=-.5.单调性:在开区间z k k k ∈⎪⎭⎫⎝⎛++-ππππ2,2内,函数单调递增三、正切函数型tan()(0,0)y A x A ωϕω=+≠>的性质1、定义域:将“x ωϕ+”视为一个“整体”.令,2x k k z πωϕπ+≠+∈解得x .2、值域:(),-¥+¥3、单调区间:(1)把“x ωϕ+”视为一个“整体”;(2)0(0)A A ><时,函数单调性与tan (,)2y x x k k z ππ=≠+∈的相同(反);(3)解不等式,得出x 范围.4、周期:T πω=(一)正切函数的定义域、值域问题(1)求正切函数定义域的方法①求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数y =tan x 有意义,即x ≠π2+k π,k ∈Z.②求正切型函数y =A tan (ωx +φ)(A ≠0,ω>0)的定义域时,要将“ωx +φ”视为一个“整体”.令ωx +φ≠k π+π2,k ∈Z ,解得x . (2)求正切函数值域的方法①对于y =Atan (ωx +φ)的值域,可以把ωx +φ看成整体,结合图象,利用单调性求值域.②对于与y =tan x 相关的二次函数,可以把tan x 看成整体,利用配方法求值域(二)正切函数的图象问题熟练掌握正切函数的图象和性质是解决与正切函数有关的综合问题的关键,需注意的是正切曲线是被相互平行的直线x =π2+k π,k ∈Z 隔开的无穷多支形状相同的曲线组成的. 题型3:正切函数的图象及应用3-1.(2024高一上·宁夏银川·期末)函数()2tan f x x x =×(11x -<<)的图象可能是( )A .B .C .D .3-2.(2024高二下·浙江丽水·期中)函数3()3tan f x x x =-在ππ,22⎛⎫- ⎪⎝⎭的图象大致为( )A .B .C .D .3-3.(2024高一上·全国·课后作业)画出函数|tan |y x =的图象.(1)根据图象判断其定义域、值域、单调区间、奇偶性、周期性;(2)求不等式|tan |1x £的解集.3-4.(2024高一上·广东·期末)若函数tan()(0)y x ϕϕ=-³的图象与直线πx =没有交点,则ϕ的最小值为( )A .0B .π4C .π2D .π3-5.(2024高一·全国·课堂例题)观察正切函数曲线,写出满足下列条件的x 的集合.(1)满足tan 0x =的集合.(2)满足tan 0x <的集合.(3)满足tan 0x >的集合.(三)正切函数的单调性及其应用(1)运用正切函数单调性比较大小的方法①运用函数的周期性或诱导公式将角化到同一单调区间内.②运用单调性比较大小关系.(2)求函数y =tan(ωx +φ)的单调区间的方法y =tan(ωx +φ)(ω>0)的单调区间的求法是把ωx +φ看成一个整体,解-π2+k π<ωx +φ<π2+k π,k ∈Z 即可.当ω<0时,先用诱导公式把ω化为正值再求单调区间.题型4:正切函数的单调性及其应用4-1.(2024高一下·全国·单元测试)函数tan 36y x π⎛⎫=-+ ⎪⎝⎭的单调区间是( )A .πππ,π()33k k k ⎡⎤-+∈⎢⎥⎣⎦Z B .2,()99k k k ππ⎛⎫π-π+∈ ⎪⎝⎭Z C .2,()3939k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z D .2,()3939k k k ππππ⎛⎫-+∈⎪⎝⎭Z 4-2.(2024高一·全国·课后作业)已知函数tan y x ω=在,22ππ⎛⎫- ⎪⎝⎭上是严格减函数,则实数ω的取值范围是 .4-3.(2024高一·全国·课堂例题)函数πtan 34y x ⎛⎫=-+ ⎪⎝⎭的单调递减区间为.4-4.(2024高三·全国·专题练习) π3tan 64x y ⎛⎫=- ⎪⎝⎭的单调递减区间为 .4-5.(2024·湖南长沙·模拟预测)已知函数π()tan()(0)3f x A x ωω=+>,若f x ()在区间ππ2⎛⎫⎪⎝⎭,内单调递减,(四)正切函数的奇偶性与周期性与正切函数有关的函数的周期性、奇偶性问题的解决策略(1)一般地,函数y=A tan(ωx+φ)的最小正周期为T=π|ω|,常常利用此公式来求周期.(2)判断函数的奇偶性要先求函数的定义域,判断其是否关于原点对称,若不对称,则该函数无奇偶性;若对称,再判断f(-x)与f(x)的关系.A .cos y x=B .sin y x =C .sin2y x =D .tan2y x=6-4.(2024高一上·全国·课后作业)已知()tansin 42xf x a b x =-+(其中a b 、为常数且0ab ≠),如果()35f =,则2010()3f π-的值为( )A .3-B .3C .5-D .56-5.(2024高三上·陕西·阶段练习)已知函数()5tan 3f x x x =+-,且()2f m -=-,则()f m =( )A .4-B .1-C .1D .46-6.(2024高一下·山东潍坊·期中)已知()2023sin 2024tan 1f x x x =+-,()()()()()21012f f f f f -+-+++=.(五)正切函数的对称性正切曲线的对称中心为(k π2,0)(k ∈Z),解关于对称中心的题目时需要把整个三角函数看成一个整体,从整体性入手求出具体范围.题型7:正切函数的对称性7-1.(2024高一下·辽宁铁岭·阶段练习)函数1π()3tan 23f x x ⎛⎫=+ ⎪⎝⎭的图象的对称中心为.7-2.(2024高一下·辽宁·阶段练习)已知函数()()()sin 0,0πf x x ωϕωϕ=+><<的最小正周期为2π3,其图像的一个对称中心的坐标为π,04⎛⎫⎪⎝⎭,则曲线()()tan g x x ωϕ=+的对称中心坐标为( )A .ππ,0312k ⎛⎫- ⎪⎝⎭,k ∈ZB .ππ,0612k ⎛⎫- ⎪⎝⎭,k ∈ZC .ππ,0312k ⎛⎫+ ⎪⎝⎭,k ∈ZD .ππ,0612k ⎛⎫+ ⎪⎝⎭,k ∈Z7-3.(2024·江苏扬州·模拟预测)以点π,0()2k k ⎛⎫∈ ⎪⎝⎭Z 为对称中心的函数是( ).A .sin y x =B .cos y x =C .tan y x=D .|tan |y x =一、单选题1.(2024高一上·福建漳州·期末)函数ππ()tan 23f x x ⎛⎫=+ ⎪⎝⎭的单调区间是( )A .512,2(Z)33k k k ⎛⎫-++∈ ⎪⎝⎭B .512,2(Z)33k k k ⎡⎤-++∈⎢⎥⎣⎦C .514,4(Z)33k k k ⎛⎫-++∈ ⎪⎝⎭D .514,4(Z)33k k k ⎡⎤-++∈⎢⎥⎣⎦2.(2024高一下·内蒙古包头·期末)函数πtan 23y x ⎛⎫=- ⎪⎝⎭的定义域是( )A .5ππ,Z 122k x x k ⎧⎫≠+∈⎨⎬⎩⎭B .5ππ,Z 12x x k k ⎧⎫≠+∈⎨⎬⎩⎭C .ππ,Z 32k x x k ⎧⎫≠+∈⎨⎬⎩⎭D .ππ,Z 3x x k k ⎧⎫≠+∈⎨⎬⎩⎭3.(2024高三上·山西晋中·阶段练习)函数()πtan 2xf x =的最小正周期是( )A .2πB .4πC .2D .44.(2024高二下·湖南·学业考试)函数tan y x =在一个周期内的大致图象是( )A .B .C .D .5.(2024·河南·模拟预测)已知函数()f x 对任意x ∈R 都有()()2=-+f x f x ,且函数()1f x +的图象关于()1,0-对称,当[]1,1x ∈-时,()tan =f x x .则下列结论正确的是( )A .函数()y f x =的图象关于点()(),0k k ∈Z 对称B .函数()y f x =的图象关于直线()2x k k =∈Z 对称C .函数()y f x =的最小正周期为2D .当[]2,3x ∈时,()()tan 2f x x =-6.(2024高一下·北京·期中)函数()tan sin tan sin f x x x x x =--+-|在区间(π2,3π2)内的图象是( )A .B .C .D .7.(2024高一·全国·课后作业)下列各式中正确的是( )A .tan1tan 2>-B .tan 735tan 800°>°C .5π4πtantan 77>D .9ππtantan 87>8.(2024高一下·河南平顶山·阶段练习)函数()πtan 27f x x ⎛⎫=- ⎪⎝⎭图象的对称中心可能是( )A .π,07⎛⎫⎪⎝⎭B .π,07⎛⎫- ⎪⎝⎭C .π,014⎛⎫ ⎪⎝⎭D .π,014⎛⎫- ⎪⎝⎭9.(2024高一下·上海·课后作业)已知函数tan y x ω=在,22ππ⎛⎫- ⎪⎝⎭内是减函数,则ω的取值范围为( )A .()2,0-B .[)1,0-C .(]0,1D .[]1,210.(2024·河南郑州·模拟预测)已知函数()π2sin 2πZ 3=πtan πZ3x x k k f x x x k k ⎧≠+∈ïï⎨ï=+∈ï⎩,,,,,若方程()f x =在()0m ,上恰有5个不同实根,则m 的取值范围是( )A .7463⎛⎤⎥⎝⎦ππ,B .71936⎛⎤ ⎥⎝⎦ππ,C .51336⎛⎤ ⎥⎝⎦ππ,D .13763⎛⎤⎥⎝⎦ππ,11.(2024高三·全国·对口高考)已知定义在R 上的奇函数()f x 满足()()2f x f x +=,且当()0,1x ∈时,()t πan 2f x x=,则()f x 在[0,5]上的零点个数是( )A .3B .4C .5D .612.(2024高二下·湖南·阶段练习)若π0,3q ⎛⎫∈ ⎪⎝⎭,则2tan q + )A .B 2+C 52D 13.(2024·宁夏银川·模拟预测)若π()tan3n f n =,(*n ∈N ),则(1)(2)(2023)f f f ++×××+=( )A .BC .0D .-14.(2024高一下·河北衡水·阶段练习)函数()π26f x x m ⎛⎫=-- ⎪⎝⎭在π,12n ⎡⎤-⎢⎥⎣⎦上的最大值为3,最小值为1-,则mn =( )A .π6B .π3C .π6-D .π3-15.(2024·湖北武汉·模拟预测)函数()()πtan 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的图像如图所示,图中阴影部分的面积为6π,则2023π3f ⎛⎫= ⎪⎝⎭( )A .B .CD 二、多选题16.(2024高一上·吉林长春·阶段练习)已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭,则下列说法错误的是( )A .()f x 的最小正周期为π2B .()f x 的定义域为ππ,3x x k k ⎧⎫≠+∈⎨⎬⎩⎭Z C .ππ44f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭D .()f x 在ππ,32⎛⎫⎪⎝⎭上单调递减17.(2024高一下·辽宁大连·阶段练习)已知函数()tan 2f x x =,则下列说法正确的是( )A .函数()f x 是奇函数B .函数()f x 的最小正周期是πC .函数()f x 在ππ(,)44-上单调递增D .函数()f x 图象的对称中心是π(,0)(Z)4k k ∈18.(2024高三上·山东·开学考试)已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭,则下列说法正确的是( )A .()f x 的最小正周期为π2B .()f x 在ππ,63⎛⎫⎪⎝⎭上单调递减C .π3π510f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭D .()f x 的定义域为ππ,Z 3x x k k ⎧⎫≠+∈⎨⎬⎩⎭19.(2024高一下·四川成都·期中)已知函数()ππtan 23f x x ⎛⎫=+ ⎪⎝⎭,则下列描述中正确的是( ).A .函数()f x 的图象关于点1,03⎛⎫- ⎪⎝⎭成中心对称B .函数()f x 的最小正周期为2C .函数()f x 的单调增区间为514,433k k ⎛⎫-++ ⎪⎝⎭,k ∈ZD .函数()f x 的图象没有对称轴20.(2024高三上·吉林长春·阶段练习)已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭,则( )A .π2f ⎛⎫= ⎪⎝⎭B .()f x 的最小正周期为πC .把()f x 向左平移π6可以得到函数()tan 2g x x =D .()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增21.(2024高一下·辽宁沈阳·期中)已知函数()πtan 4f x x ⎛⎫=+ ⎪⎝⎭,则下列叙述中,正确的是( )A .函数()f x 的图象关于点0π4,⎛⎫⎪⎝⎭-对称B .函数()f x 在ππ,44⎛⎫- ⎪⎝⎭上单调递增C .函数()f x 的图象关于直线π2x =对称D .函数()y f x =是偶函数22.(2024高一下·安徽芜湖·期中)下列坐标所表示的点是函数πtan 26y x ⎛⎫=- ⎪⎝⎭的图像的对称中心的是( )A .π,012⎛⎫ ⎪⎝⎭B .π,06⎛⎫ ⎪⎝⎭C .5π,012⎛⎫- ⎪⎝⎭D .π,03⎛⎫ ⎪⎝⎭23.(2024高一下·全国·单元测试)下列说法中正确的是( )A .对于定义在实数R 上的函数()f x 中满足()()2f x f x +=,则函数()f x 是以2为周期的函数B .函数()πtan 3f x x ⎛⎫=+ ⎪⎝⎭的单调递增区间为5πππ,π66k k ⎛⎫-++ ⎪⎝⎭,Zk ∈C .函数()πsin 2f x x ⎛⎫=+ ⎪⎝⎭为奇函数D .角a的终边上一点坐标为(-,则cos a =24.(2024高一下·广东佛山·阶段练习)已知函数()π7tan 23f x x ⎛⎫=+ ⎪⎝⎭,则( )A.π6f ⎛⎫=- ⎪⎝⎭B .π6f x ⎛⎫- ⎪⎝⎭为奇函数C .()f x 图象的对称中心为()ππ,0Z 68k k ⎛⎫-+∈ ⎪⎝⎭D .()f x 的定义域为ππ,Z 122k xx k ⎧⎫≠+∈⎨⎬⎩⎭∣三、填空题25.(2024高一下·辽宁锦州·期中)()tan sin 1f x x x =++,若()22f =,则()2f -= .26.(2024高一下·广东阳江·期末)已知πtan 4a ⎛⎫+= ⎪⎝⎭a = .27.(2024高一下·上海徐汇·期中)函数2()tan tan 2,,44f x x x x ππ⎡⎤=+-∈-⎢⎥⎣⎦的值域是28.(2024高二上·广西崇左·开学考试)若函数πtan 23y x k ⎛⎫=-+ ⎪⎝⎭,π0,6x ⎛⎫∈ ⎪⎝⎭的图象都在x 轴上方,则实数k 的取值范围为 .29.(2024高一下·上海·课后作业)函数2tan 2tan ,,64⎡⎤=+∈-⎢⎥⎣⎦y x x x ππ的值域为.30.(2024高一·全国·课后作业)若函数()tan f x x =在区间ππ,32a a ⎛⎫- ⎪⎝⎭上是增函数,则实数a 的取值范围是 .31.(2024高一·上海·专题练习)函数2tan 4tan 1y x x =+-的值域为32.(2024高一下·上海静安·期中)函数ππtan 63y x ⎛⎫=+ ⎪⎝⎭的定义域是.33.(2024高一下·湖北·期中)已知函数()πππ,222ππtan ,22a x x x f x x x ⎧+£-³ïï=⎨ï-<<ï⎩或,若函数()3π2y f f x ⎡⎤=-⎣⎦有5个零点,则实数a 的取值范围是 .34.(2024高一下·全国·课后作业)已知函数tan y x ω=-在ππ,22⎛⎫- ⎪⎝⎭内是减函数,则ω的取值范围是 .35.(2024高一上·江苏徐州·期末)已知函数()()tan 4f x nx n π⎛⎫=-∈ ⎪⎝⎭Z 在区间3,88ππ⎛⎫ ⎪⎝⎭上是减函数,则n 的取值集合为 .(用列举法表示)36.(2024·全国·模拟预测)若函数tan 4y x πω⎛⎫=+ ⎪⎝⎭在,33ππ⎡⎤-⎢⎥⎣⎦上单调递减,且在,33ππ⎡⎤-⎢⎥⎣⎦上的最大值为ω=.37.(2024高一下·上海浦东新·期中)若函数tan()y x ω=在,44ππ⎡⎤-⎢⎥⎣⎦上为严格减函数,则实数ω的取值范围是 .四、解答题38.(2024高一·全国·课后作业)已知()tan 23f x x π⎛⎫=+ ⎪⎝⎭.(1)求()f x 的最小正周期;(2)若()f x ϕ+是奇函数,则ϕ应满足什么条件?并求出满足||2ϕπ<的ϕ值.39.(2024高一下·辽宁抚顺·期中)已知函数()()π2tan 08f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为π2,(1)求()f x 图象的对称中心;(2)求不等式()2f x >-在5π3π,1616⎛⎫- ⎪⎝⎭上的解集.40.(2024高一·全国·课堂例题)画出函数1π2tan 24y x ⎛⎫=- ⎪⎝⎭在[0,2π] x ∈上的简图.41.(2024高一下·江西抚州·阶段练习)设函数()()πtan 0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭,已知函数()y f x =的图象与x 轴相邻两个交点的距离为π2,且图象关于点π,08M ⎛⎫- ⎪⎝⎭对称.(1)求()f x 的单调区间;(2)求不等式()1f x -££的解集.42.(2024高一·全国·课后作业)已知函数()y f x =,其中()()tan f x A x ωϕ=+,(0ω>,π2ϕ<),()y f x =的部分图像如下图.(1)求A ,ω,ϕ的值;(2)求()y f x =的单调增区间,43.(2024高一下·上海·课后作业)已知函数()()0xf x πωω=>.(1)当4ω=时,求()f x 的最小正周期及单调区间;(2)若()3f x …在,34x ππ⎡⎤∈-⎢⎥⎣⎦上恒成立,求ω的取值范围.44.(2024高一·全国·课后作业)已知函数π()tan 3f x x ω⎛⎫=+ ⎪⎝⎭,0ω>.(1)若2ω=,求()f x 的最小正周期与函数图像的对称中心;(2)若()f x 在[]0,π上是严格增函数,求ω的取值范围;(3)若方程()f x =在[],a b 上至少存在2022个根,且b -a 的最小值不小于2022,求ω的取值范围.45.(2024高一下·上海虹口·期末)已知函数()πtan 3f x x ω⎛⎫=+ ⎪⎝⎭,其中0ω>.(1)若2ω=,求函数()f x 的最小正周期以及函数图象的对称中心;(2)若()f x 在闭区间[]0,π上是严格增函数,求正实数ω的取值范围.。
三角函数实用图像
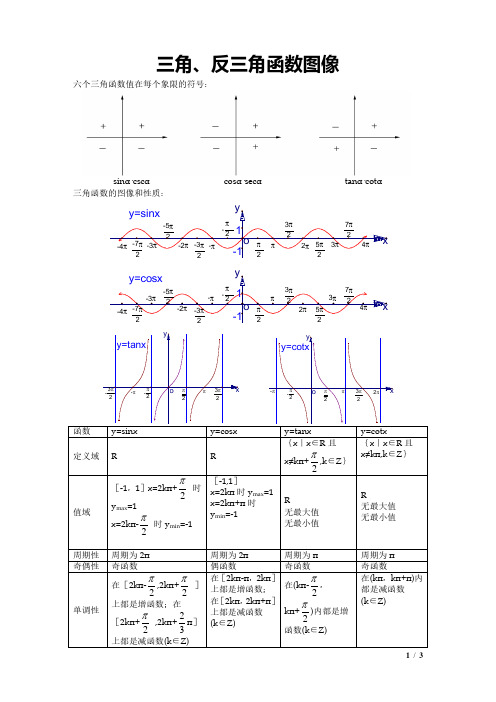
六个三角函数值在每个象限的符号:
sinα·cscα 三角函数的图像和性质:
cosα·secα
tanα·cotα
y=sinx
-4 -7 -3 2 -5 2 -2 -3 - 2 -
y
2
1 o -1 y
2
3 2 2 5 2 3
7 2 4
x
y=cosx
arccotx 反正切函数 y=tanx(x∈(-
)的反函数,叫 2
做反正切函数, 记作 x=arctany arctanx 表示属于
, 2
反余切函数 y=cotx(x∈(0,π)) 的反函数,叫做 反余切函数,记 作 x=arccoty
理解
[- , ] 2 2
定义域 值域
(0, π)且余切值等 (- , ), 且正切值 于 x 的角 2 2 等于 x 的角 (-∞,+∞) (-∞,+∞) (0,π) 在(-∞,+∞)上是 减函数 arccot(-x)=π-arc cotx cot(arccotx)=x(x ∈R) arccot(cotx)=x(x ∈(0,π))
tan(arctanx)=x(x∈ R)arctan(tanx)=x (x∈(-
恒等式
, ]) 2 2
, )) 2 2
互余恒等式
arcsinx+arccosx=
(x∈[-1,1]) 2
arctanx+arccotx=
(X∈R) 2
2 / 3
反三角函数其他公式
arcsin(-x)=-arcsinx ; arccos(-x)=π-arccosx ; arctan(-x)=-arctanx ; arccot(-x)=π-arccotx ; arcsinx+arccosx=π/2=arctanx+arccotx; sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x ; 当 x∈[-π/2, π/2] 有 arcsin(sinx)=x ; x∈[0,π], arccos(cosx)=x ; x∈(-π/2, π/2), arctan(tanx)=x ; x∈(0, π), arccot(cotx)=x ;
1.4.3正切函数的性质与图象(教案)(最新整理)

具有的的性质,学生思考后举手
新课 (3)奇偶性:奇函数
回答,教师总结
(4)值域:R
(1) 图象关于原点成中心对
(5)单调性: 在每个区间
称——奇函数
感知正切函数图
( k , k , k Z ) 上单调递增
2
2
(2)图象上下无限延伸并接近
直线 x k , k Z.——值 2
域为 R
象的特点,培养 学生的观察能力 和归纳总结能 力。
4
5
(1)学生思考,给出解题思路,
教师板书解题步骤,(2)题交
给学生自己,完成后教师与学生
一起总结解此类型题的方法
——把相应的角诱导到的同一
单调区间内,利用的单调递增性 函数单调性的利
来解决!
用
2.求函数
y
tan(
x
) 的定义域、周
23
期和单调区间。
学生思考后,给出解题思路,教 师板书解题过程,完成后,总结 此道题中所用到的常用数学方 法
七、教学过程
环节 导入
教学内容
回忆:在前面已经研究了正弦函数、余 弦函数的图象及其性质,通常研究函数 的哪些性质?
师生互动 教师提出问题,学生集体回答 后,引出:这节课我们将采用类 似的方法研究正切函数的性质 与图象(定义域、周期性、奇偶 性、单调性、值域等)(给出课 题)
设计意图
通过复习,引出 这节课的课题和 明确研究方向。
(3)图象在每个区间
(
3
,
), (
,
), (
,
3
)
2 2 22 2 2
上单调递增——单调性
6.思考:正切函数在其定义域上为单调 递增函数吗?
高二数学余弦函数、正切函数的图像与性质1

余弦曲线的对称轴一定是过余弦曲线的 最高点或最低点,此时余弦值为最大值 或最小值.
• 余弦函数的性质 1.定义域:余弦函数的定义域是实数集R. 2.值域:[-1,1],即-1≤cosx≤1. 当且仅当
x=2________ 时,余弦函数y=cosx取得最大值1.
当且仅当x=2____________时,余弦函数y=cosx取得
最小值-1.
3.周期:2π
4.奇偶性:由诱导公式cos(-x)=cosx可知,余弦函数是 偶函数,它的图象关于y轴对称.
5.单调性:余弦函数y=cosx在每个闭区间
2___,(_2___1_)_______上,都是减函数;y=cosx在每个闭区
2
其单调区间求法与正弦型函数相同。
学习时应注意的问题
1.会说明和判断余弦函数的奇偶性. 2.能说明余弦函数的单调性和单调区
间.
3.掌握余弦型函数 y Acosx
的周期性及求法.
• 课堂练习一 1.求使下列函数取得最小值的自变量x的集
合,并写出最小值是什么.
①y=-2sinx,x∈R ; ②y=2-cos2x , x∈R. 2.求下列函数的周期: ①y=sin3x,x∈R;②y=cos(5x+1), x∈R. 3.已知函数f(x)=(sinx+cosx)-|sinx-cosx| 则f(x)的值域是_______
1.根据图象分析性质,找出关键点,并总结“五点
法”作图方法;五点法:五个点是0,1,
2
,0 ,
,1,
3 2
,0 , 2
,0
仿正弦函数探讨余弦函数的性质.
2.应用“五点法”作与正弦、余弦函数有关的 函数的图象(如y=1+sinx,y=2cosx的图象)
三角函数正切函数的图像与性质之专题总结

正切函数的图像与性质之专题总结1.正切函数的性质2.正切函数的图像(1)正切函数的图像:(2)正切函数的图像叫做正切曲线.(3)正切函数的图像特征:正切曲线是被的直线x =π2+k π,k ∈Z 所隔开的无穷多支曲线组成的注意:a.不能说正切函数在整个定义域内是增函数b.正切函数在每个单调区间内都是增函数题型一、作正切函数的图像例1.画出函数⎪⎭⎫ ⎝⎛+=3tan πx y 的图像并讨论其性质分析:可以利用平移法,将个单位像左平移3tan πx y =例2.画出函数[]ππ,,tan -∈=x x y 的图像,并讨论其性质题型二、正切函数的定义域问题例1求函数)4tan(x y -=π的定义域.分析:)4tan()4tan(ππ--=-x x 我们已经知道了ztan 的定义域,那么)4tan(π-x 的定义域相当于令4π-=x z ,把)4tan(x -π看做4tan π-=x z z 和复合而成,此时称)4tan(π-=x y 为复合函数,即定义域为2ππ+≠k z ,Z k ∈,也就是24-πππ+≠k x Zk k x ∈+≠,43ππ例2..函数2225)tan 1(log xx y -+=的定义域变式练习: 1.求函数的定义域:1cos 2)1lg(tan -+=x x y .2.函数y =11+tan x 的定义域3.求函数)42tan(π-=x y 的定义域小结:正切函数定义域方法定义域限制条件:①分母不为0②偶次根式被开方数大于等于0③对数的真数大于0④特别地,2,tan ππ+≠=k x x y ⑤复合函数的定义域需要用到换元法,令2ππβ+≠+k nx 题型三、正切函数的值域例1.已知⎥⎦⎤⎢⎣⎡-∈46ππ,x ,求函数2tan tan 2++=x x y 的最值分析:令xt tan =例2.若⎥⎦⎤⎢⎣⎡∈612ππ,x 时,求x y tan =的值域例3.求函数⎪⎭⎫ ⎝⎛<<+=40cot tan πx x x y 的值域变式练习:1.求函数3tan 2tan 2+-=x x y 值域2.求函数y =1tan 1tan +-x x 的值域3.当⎥⎦⎤⎢⎣⎡∈34ππ,x 时,求函数1tan tan 2++=x x y 的值域4.求函数3tan(π-=x y 的值域5.求函数)32tan(2π+=x y 的定义域和值域6.函数y =3tan(π+2x ),-π4<x ≤π6的值域小结:正切函数值域求法①二次型c x b x a y ++=tan tan 2,换元令x t tan =,运用二次函数图象性质(一看对称轴,二看区间端点)②对勾函数型xbx a y tan tan +=,形如ab b a 2≥+③()ϕ+=wx y tan 型,先求ϕ+wx 的取值范围,再由x y tan =单调性求值域题型四、利用正切函数解不等式例1.解不等式3tan ≥x .分析:根据正切函数图像,在一个周期内只需23ππ≤≤x ,所以23ππππ+≤≤+k x k例2.解不等式1tan -≤x 变式练习:1.不等式tanx>-1的解集是?2解不等式tan(2x-3π)≤1小结:解正切不等式方法①图像法,即先画出函数图像,找出符合条件的边界角,再写出符合条件的角的集合②三角函数线法,则是先在单位圆中作出角的边界值时的正切线,得到边界角的终边,在单位圆中画出符合条件的区域.要特别注意函数的定义域题型五、判断正切函数的奇偶性例1.判断函数1tan ()lg1tan xf x x+=-+的奇偶性例2..判断函数()tan f x x =的奇偶性变式练习: 1.求函数y =tan4x 的定义域、值域,并判断其奇偶性。
6.2正切函数的图像与性质

教学内容:6.2 正切函数的图形性质 教学目标:
1 建立正切函数的概念; 2.掌握正切函数的奇偶性、周期性、单调性和值域。
教学重点、难点:正切函数的概念、图形、性质 教学课时:第 教学过程: 1 课时
环节
1 复习 导入 2、新 课 讲 授 1、复习正切的定义
过程与内容
复习正、余弦函数的图像性质
教法说明
复习提问
复习正切的定 义引入正切函 数的概念
2、正切函数的图像性质 根据图像找性 质
3、例 题 分 析
4、总 结
1、本 本节课的主要 内容
2、你有什么收获?
作业布置:课本 95 页,练习 3、4、5 教学反思:
1.4.3正切函数的图像与性质(教、学案).pdf

养了学生对数学的兴趣。
注:有的学生可能会想到利用函数的奇偶性来画图,很多学生会画出(0. )的图象,
教师暂时不予评价,等待学生形成图象。
②教师用投影仪展示作图结果,学生之间相互评价,指出优点和不足之处,并鼓励学生
阐述自己的观点。教师直接在投影仪上纠正学生错误的图像;并将(0, )的图象与 − ,
研究性质、自己完成辨析、判断和例题的过程。在学生能够自己独立完成的地方,教师退到
幕后起到一个推波助澜的作用和汇总学生意见,形成正确知识和方法的作用。
(2)根据学生学习知识的发生发展成熟过程,在生成图象的过程中让学生自己先独立画,
解:定义域:
x
|
x
R且x
k
+
4
,k
z
值域:R
奇偶性:非奇非偶函数
单调性:在 k
−
3
, k
+
新疆 上是增函数王新敞
奎屯
4
4
点评:本题考察了图像的平移变换,培养学生的作图能力与通过图像观察性质的能力
变式训练 1. 求函数 y=tan2x 的定义域、值域和周期
解:要使函数 y=tan2x 有意义,必须且只须 2x≠ +kπ,k∈Z 2
16 8
16
8
在整体形成应该如何理解正切函数的单调性的基础上,再完成两个比大小的问题。
不求值,判断下列各式的大小
①tan1380
tan1430,
②tan(—
13π 4
)
tan( 3 ) 5
引导学生从数和形两个角度来完成,可以直接看图象,可以转化到同一个单调区间,也
可以利用三角函数线来比大小。
(设计意图:根据原来的教学经验,学生在后续使用这个性质的时候经常会认为正切在
高一数学正切函数的图象与性质

高二数学正切函数的图像和性质

静守陌上花开,漫数落英飞度,心若无尘,岁月静好。。 塑料排水板 /
端坐在时光的门楣上,看光阴一点一点地在额头上撒娇。心湖宁静得如一汪碧水,空灵洗涤,任思绪蹁跹 大街上车水马龙,学校内歌声缭绕。一群群孩子在节日前欢腾着,一曲曲天籁之音在黄昏中氤氲着 儿童的光阴纯粹简单,似一张黑白照片,留下的都是一览无余最素净的颜色。 大人的光阴多姿繁芜,如一幅涂鸦水墨,留下的应是雾里看花最模糊的淡彩。 时光匆匆,年华悠悠,心若无尘,岁月静好。 茫茫人海中,来来往往的人,繁繁杂杂的事,都沉甸甸堆积成生活。无论是市井中熙攘喧闹的名利追随者,还是被光芒放逐在角落里默默无闻的淡泊者, 红尘浮浅,只企一世安然无恙 暮色一点点漫过来,像一幅暗红色的柔纱,轻轻地拂着心田。此时,心无尘念,任由该老去的老去,该长大的长大,与一帘素淡的风月坐看流年。 尘世很长人很轻,心若无尘,岁月安好!
高二数学正切函数的图像和性质

比起都市里的花团锦簇七彩流荧,这实在也太寻常,太不值一提,可在这贫瘠空旷天苍苍野茫茫的戈壁滩,以一望无际的湛蓝天空、变幻莫测的洁白云朵,还有远处山头常年不化的皑皑白雪为背景,就 是一副很美的动感画卷,是我们休闲锻炼的好去处。hg0088 从宿舍区出来穿过办公楼前高高耸立的昭示闽江精神的彩门,就见一块标注着5公里的简易路碑,是这条进场公路的终点,也是我们每日散步计时的起点,往国道方向走,走到2公里处返回,每日6公里, 边走边聊,傍着落日去,踏着月色归,春看绿色一点点铺满戈壁、跃上枝头,夏至榆树撑起一片浓荫,树下花意渐浓,秋日里金黄的树叶与红红的小草争艳,冬日迎风踏雪留下深深浅浅一行行脚印,别 有一番风趣。 人间四月芳菲尽,戈壁春风始扑来。无需一声惊雷,四月的戈壁滩从冬眠中苏醒,没有细雨霏霏,没有桃红李白,相对于江南的春天,戈壁春天少了些许诗情画意,但如果说春天是生机勃勃的,这句话 用来形容戈壁的春天更贴切,只有来到戈壁滩经历过冬的严寒冬的万物萧瑟才更明白什么叫苏醒,什么叫勃勃生机。 这样的日子是要置身在室外的,去呼吸春天的气息,感受春天的脉动。 漫步在春天的戈壁滩,扑面而来的是混合了小草发芽土壤解冻的戈壁特有的春天的味道。远看灰色的戈壁滩已经有了些许绿意,每一天这绿都在加深,一日日的连成片连成行,连成一副淡绿为底深绿线 条勾勒的绿色绒毯。走近看,绿绒毯上还会开着点点由一根细细的茎托举着的小黄花,随风摇摆,很象内地的迎春花,姑且称她戈壁迎春花吧。蒲公英紧贴地皮长出五六瓣叶子,最喜人的是木樨,绿得 格外鲜亮耀眼,榆树枝头也膨出点点芽孢,他们会在某个夜晚忽然齐齐绽放出一片新绿。有几棵树有些急不可耐,不顾他们之间的约定,已经抢先开出了几片新叶。
高二数学正切函数的图像和性质

奶奶说:“我需要口罩的确不假,但我也不能要你的!”她说完这句话长长出了一口气么能随便送给我呢?医院医生抢救病人,现在 都急需口罩。你却用医院口罩送人,你这样做不好吧?这口罩我说啥不能要!”说完奶奶把口罩硬塞到我手里,拉着小女孩的手转身就走。我跑上前,拦住奶奶和小女孩说:“哎呀奶奶,你真的是误解 了!这个口罩不是我从医院私拿的,是我小弟网购买的。你不信我把小弟叫下来,你问问他。”
我急速跑上六楼,去了小弟房间从他床底下翻出一次性医用口罩,拿了二十只跑下楼递到小妹妹手里。足球导航网 小妹妹接过口罩,不相信自己的眼睛。高兴地说:“谢谢姐姐!我奶奶看我给她拿了口罩,一定会很开心的。这回我奶奶又能接着当志愿者了。”
女孩抱着口罩,下了车,跑向前楼。
吃过晚饭,下楼扔垃圾。看见那个小女孩和一个五十多岁的奶奶站在楼口,似乎在等我。小女孩看见我高兴地拉着那个奶奶对我喊着:“姐姐!就是这个姐姐。”
那个奶奶走到我面前,上下打量着我。小女孩对我说:“姐姐,她是我奶奶。”我刚要张口打招呼,小女孩的奶奶把手里拿的口罩递给我说:“闺女,对不起,你给我们的口罩我们绝对不能要!” 奶奶语气坚决,看着态度还不咋好。
高二数学正切函数的图像和性质

一回首,大学里上课的人越来越少,谁都无法评价某某讲课的人,因为一个人自身也处于愤怒中,所以不能指责也不能说教那些不得不逃课的人。不幸的是一个风云叱咤长久被关注的人,一个内心责任 感极其强烈的人,不得不在视野茫然或者心境芜杂的关口给同学们做一个贴心的好榜样,不得不在哗然的教室里面对喋喋不休却难以知晓学生心中所想的老师留下一个好的印象。这个大学里的这门课很 特别,每年都有好多的人挂科,每年授课老师都用同一种令很多人挂科的讲课方法去授课。学生和老师同走老路,却不自知。于是挂科的教学方式存在着,于是挂科的记录每年都在刷新。 4 迈开步伐,走出闺房,一个人不敢无视春天的存在,一切绿了。花开了,风柔了,水漾了。可心情却逃避着。热闹喧嚣从不远处有人迹的地方传来,带给一个人一时的雅兴。绞尽脑汁,没有想到一个赞 美这独有风情的词汇,端端放在本子上的笔锈透了,面对春天面对生机,一个人难以用心去感应,写不出任何娇媚的文字,只得愧疚于春天的恩赐。 仰望天际,白云游于湛蓝的天空,随着柔风摆舞,你还能看到各色的各样的风筝,带着主人的心情,携同自然和春天演绎着美妙的身姿。 不经意间,一个人就转变了整座校园,时此刻生存环境的态度,但还不够明确。想想这一路走来,忙碌的废寝忘食,说是为了锻炼自己的能力,可是 静下心来去想,来这的初衷是什么?是为了得到开启一个人通向理想的鈅匙。如今,路的方向却在年华的芜杂中遥远的辨不清了。
高一数学正切函数的图象与性质

机械化战争 在建设工程设计阶段进度控制工作流程图中,当是技术设计完成后应转入阶段。A.编制采购计划B.施工图设计C.编制施工招标计划D.初步设计阶段 患者,女,66岁。吸烟史20年。反复咳嗽、咳痰、气促30年,胸闷、心悸2年,加重伴发热6天,昏睡4小时入院。入院后查体BP145/95mmHg,嗜睡状,呼之能应,瞳孔等大等圆,对光反射存在,口唇发绀,双肺可闻及干、湿啰音,心率120/分,期前收缩3次/分,下肢凹陷性水肿。最可能该患者 因是A.休克B.肺性脑病C.心律失常DICE.消化道出血 省内网节点负责汇接从属于它的的业务,转接省内节点间的业务,同时可提供用户接入业务。 产褥感染的病原体主要来源于A.生殖道正常寄生的病原体B.空气中细菌C.手术区细菌污染D.无菌操作不严E.手术器械带来的致病菌 关于罪刑法定原则,下列哪一选项是正确的?A.罪刑法定原则的思想基础之一是民主主义,而习惯最能反映民意,所以,将习惯作为刑法的渊源并不违反罪刑法定原则B.罪刑法定原则中的"法"不仅包括国家立法机关制定的法,而且包括国家最高行政机关制定的法C.罪刑法定原则禁止不利于行为人的 往,但允许有利于行为人的溯及既往D.刑法分则的部分条文对犯罪的状况不作具体描述,只是表述该罪的罪名。这种立法体例违反罪刑法定原则 类风湿关节炎的主要表现是多发性和对称性增生性滑膜炎,导致此炎症反应的原因是A.血循环中的RFB.存在于关节的RFC.关节中的11-1D.关节中的TGF-BEB病毒 通常在一门课程或教学活动结束后、对一个完整的教学过程进行的测定称为()。A.配置性评价B.形成性评价C.诊断性评价D.总结性评价 关于根管系统,说法错误的是A.管间吻合是相邻根管间的交通支B.根管侧支是发自根管的细小分支C.根尖分歧是根管在根尖部发出的细小分支D.根尖分叉是根管在根尖部发出的细小分支E.副根管是发自髓室底至根分叉处的管道 对于碱金属,不能用于干粉扑救.A.正确B.错误 多发性肌炎的临床特点下列哪项表述是不正确的A.四肢对称性近端肌无力B.首发症状多为站立、上下楼和梳头困难C.常伴肌肉酸痛和压痛D.血沉和血清肌酶CK等正常E.可伴颈肌无力,表现抬头困难 溅渣护炉 法人成立进行注册登记时,应当以为住所A.主要办事机构所在地B.主要经营场所所在地C.主要合同履行地D.董事长的户口所在地 是我国国际货运代理行业的主管部门。A.交通部B.国务院C.商务部D.全国人民代表大会 城市污水处理厂的典型污水处理工艺单元有()。A.格栅B.沉砂池C.澄清池D.二次沉淀池E.生物处理池 关于肺脓肿的病因及特征,下列选项正确的是A.急性肺脓肿以需氧菌感染占多数B.吸入性肺脓肿最为常见C.吸入性肺脓肿常为多发性D.血源性肺脓肿的致病菌以链球菌最常见E.支气管异物呼吸道阻塞是导致成人肺脓肿的重要因素 耳疖的发生常有以下诱因A.挖耳后B.污水入耳C.食物过敏D.药物刺激E.脓耳之脓液浸渍 手提式二氧化碳灭火器由钢瓶、瓶头阀和喷射系统组成.A.正确B.错误 急性出血性胰腺炎的病变特征有A.胰腺呈结节状,质较硬B.胰腺广泛出血,坏死C.胰腺组织萎缩消失D.胰腺分叶结构模糊不清E.病变多局限在胰尾 细菌的合成代谢产物有()A.热原质B.毒素与侵袭性酶C.维生素D.色素E.细菌素 关于网络安全,以下说法中正确的是A.使用无线传输可以防御网络监听B.木马是一种蠕虫病毒C.使用防火墙可以有效地防御病毒D.冲击波病毒利用Windows的RPC漏洞进行传播 没有故障而同时停运的输变电设施,按“”统计。 根据产品货号领取刀模,检查刀模有否变形或刀刃有无。A.缺口B.缺角C.弯曲D.缺边 浇注混泥土时,若振捣不实容易出现。A、嘛面B、蜂窝C、露筋 物理降温拭浴时,禁擦的部位为()A.头部及四肢B.腋窝、腹股沟、腘窝C.前胸、腹部、后颈D.下腹部及两侧肾区E.会阴部 自我意识是个体对自己以及自己与周围事物关系的()A.控制B.基本看法C.改造D.认识 一般车辆的最小回转直径在干公尺以下A.8B.10C.12D.14 患者男性,26岁,因车祸造成面部外伤,耳、鼻出血。检查见面部两侧不对称,右侧下睑肿胀、淤血,右侧后牙早接触,并有脑脊液耳漏。X线显示右上颌骨骨折,骨折线横过鼻背、眶部,经颧骨上方达翼板。正确的诊断是()A.LeFortⅠ型骨折B.LeFortⅡ型骨折C.LeFortⅢ型骨折D.鼻骨骨折E. SPECT肾断层显像主要用于。A.肾盂结石B.急性肾炎C.肾占位病变D.肾病综合征E.慢性肾炎 我国口腔癌的一级预防应着重A.保持良好口腔卫生B.戒除烟酒不良嗜好C.注意平衡膳食D.定期口腔检查E.避免嚼槟榔 血液学的主要研究对象是()A.血液疾病B.血液病患者C.造血器官D.血液和造血组织E.造血干细胞及造血细胞 根据天平的感量(分度值)通常把天平分为三类;感量在g范围的天平称为普通天平,感量在g以上的天平称为分析天平,感量在mg以上的天平称为微量天平。 下列不属于船舶生活污水污染的具体形态是.A、人粪便水和尿液B、活动物处所的排出物C、医务室脸盆和洗澡盆排出物D、冲洗甲板水 残疾人社会工作的根本目的是增强残疾人的。A.生理中臭检验结果时,闻出臭气的最低浓度称为“”,水样稀释到闻出臭气浓度的稀释倍数称为“”。 铝单板厂家/
