第五章-传热学数值计算资料
数值传热_南昌大学传热学复习资料(计算题)

12.“善于发射的物体必善于吸收” ,即物体辐射力越大,其吸收比也越大。你认为对吗?
解:基尔霍夫定律对实际物体成立必须满足两个条件:物体与辐射源处于热平衡,辐射源为黑体。 也即物体辐射力越大,其对同样温度的黑体辐射吸收比也越大,善于发射的物体,必善于吸收同温 度下的黑体辐射。所以上述说法不正确。
13.在波长 λ <2 µ m 的短波范围内,木板的光谱吸收比小于铝板,而在长波( λ >2 µ m )范围内则
即方腔内自然对流完全忽略时,依靠纯导热的 Nu 数将等于 1,即 Nu 数的最小值为 1,不会小于 1, 所以上述结果是不正确的。
10.一般情况下粘度大的流体其 Pr 数也较大。 由对流换热的实验关联式 Nu = C Rem Pr n 可知 ( m >0, n >0) , Pr 数越大, Nu 数也越大,从而 h 也越大。即粘度大的流体其表面传热系数也越高。这与 经验得出的结论相反,为什么? 解:粘度越高时, Pr 数越大,但 Re 数越小。由 ud ν Nu = C Re Pr = C e ∝ ν n − m 。一般情况下,对流换热 m > n ,即 n − m <0,所以粘 ν a
相反。在木板和铝板同时长时间放在太阳光下时,哪个温度高?为什么?
解:波长小于 2 µ m 时,太阳光的辐射能量主要集中在此波段,而对常温下的物体,其辐射波长一 般大于 2 µ m 。在同样的太阳条件下,铝板吸收的太阳能多,而在此同时,其向外辐射的能量却少 于木板(在长波范围内,铝板吸收比小于木板,由基尔霍夫定律,其发射率亦小于木板) 。因此, 铝板温度高。
15.试解释下列名词 (1)有效辐射; (2)表面辐射热阻; (3)重辐射面; (4)遮热板。
解: (1) 有效辐射——包括辐射表面的自身辐射 E 和该表面对投入辐射 G 的反射辐射 ρ G , 记为 J , 即 J = E + ρG 。 (2)表面辐射热阻——当物体表面不是黑体表面时,该表面不能全部吸收外来投射辐射能量, 这相当于表面存在热阻。该热阻称为表面辐射热阻。以 1− ε 表示,它取决于表面的辐射特性。 εA
哈尔滨工业大学 计算传热学 第五章 对流-扩散方程的离散格式-2013

aPP aEE aWW
Fe Fw exp( Pw ) aE , aW exp( Pe ) 1 exp( Pw ) 1
(D)
aP aE aW (Fe Fw )
区别就在函数 aE和aW
aE De
Pe aE De exp( Pe ) 1
aE Pe De
该格式计算量比指数小,且指数格式的解差别很小。
§ 5-3
为了在讨论中引入 PE 记
通用表达式
x
i
J*
i+1 i+1/2
x
1 界面i+ 上的值可以用界面两侧节点值表示 2
J * Bi Ai 1 (y)
系数A和B的性质的讨论 (1)当 i i 1 时,扩散量=0, J *完全由对流造成,即
即
aPP aEE aW W
显然不论那种格式,仅仅是 A(| P |) 表达式的区别。
A( P )
A(|P |)
中心 1 0.5 | P | 迎风 1 混合 [| 0,1 0.5 | P | |] 指数 | P | [exp(| P |) 1]
1.0
迎风
指数 乘方
乘方 | 0, (1 0.1| P |)5 |
中心
混合
P
§ 5-4
原始的假扩散概念
关于假扩散的讨论
一维非稳态对流方程(纯对流,没有扩散)
u t x
显示迎风差分格式
in1 in
t
u
in in 1
x
, o(x, t )
将上式在(i,n)点做Taylar级数展开,保留二阶。
上述若对任何成立,必得
B( P ) A( P ) A( P ) B( P )
传热学-第五章1-2

假设边界层内的速度分布和温度分布,解积分方程 c)数值解法:近年来发展迅速 可求解很复杂问题:三维、紊流、变物性、超音速 (2)动量传递和热量传递的类比法 利用湍流时动量传递和热量传递的类似规律,由湍流 时的局部表面摩擦系数推知局部表面传热系数 (3)实验法 用相似理论指导
五、
对流换热过程的单值性条件
c [J (kg C) ]
[N s m2 ]
[1 K ]
运动粘度 [m 2 s]
1 v 1 v T p T p
h (流体内部和流体与壁 面间导热热阻小)
、c h (单位体积流体能携带更多能量)
流动引起的对流相项 非稳态项
导热引起的扩散项
1)如u=0、v=0上式即为二维导热微分方程。 2)如控制体内有内热源,在其右端加上
1 ( x, y) c
3)由能量方程说明,运动的流体除了依靠流体的 宏观位移传递热量,还依靠导热传递热量。
归纳对流换热微分方程组:(常物性、无内热源、 二维、不可压缩牛顿流体)
前面4个方程求出温度场之后,可以利用牛顿冷 却微分方程: t
hx t y w, x
计算当地对流换热系数 hx
四、表面传热系数的确定方法 (1)微分方程式的数学解法 a)精确解法(分析解):根据边界层理论,得到 边界层微分方程组 常微分方程 求解
b)近似积分法:
单值性条件:能单值地反映对流换热过程特点的条件 完整数学描述:对流换热微分方程组 + 单值性条件 单值性条件包括四项:几何、物理、时间、边界 (1) 几何条件 说明对流换热过程中的几何形状和大小 平板、圆管;竖直圆管、水平圆管;长度、 直径等 (2) 物理条件 说明对流换热过程的物理特征
传热学数值计算

Fe aE De 2
Thermal
Fw Fe aP Dw De aW aE Fe Fw 2 2
2、对方程的几点说明 由于连续性,Fe=Fw, aP aW aE(只是在流 场满足连续性条件时才具有这一性质); 方程 aP P aE E aW W 隐含着分段线性分布的含
讨论只有对流项和扩散项存在时的一维稳态问题,控 制方程为:
u j ( ) S x j x j x j
d d d u ( ) dx dx dx
d 连续方程: u 0 dx
u const
任务:导出相应方程的离散化形式
义,也是熟知的中心差分格式(用左右节点值表示
界面上的值以及界面上的导数值); 方程必须遵守四项基本法则,否则会产生灾难性的 结果。
2018-11-24
太 原 理 工 大 学
7 /70
Thermal
例如:设 De Dw 1, Fe Fw 4 若E、W给定,即可由离散方程求得P 。
即, F 2D时,有可能使 aE 或aW 为负 产生不切实际的结果
2018-11-24
太 原 理 工 大 学
8 /70
Thermal
这就是中心差分格式求解对流换热问题时仅限于低
Fw Fe Re(低的F/D)的原因 . aP Dw De aW aE Fe Fw 2 2
原通用方程可改写为
u j ( )S x j x j x j
对于已知的ρ、uj、Γ及S(常量)的分布,任何解及
+c 将同时满足方程,故系数和的法则仍然适用。
2018-11-24
太 原 理 工 大 学
传热学计算公式范文

传热学计算公式范文传热学是物理学的一个分支,研究能量在物体之间的传递过程。
在传热学中,有许多重要的计算公式可以用于解决热传导、对流和辐射等传热现象。
下面将介绍一些常见的传热学计算公式。
热传导是物质内部由高温区向低温区传递热量的过程。
热传导热量的大小与物体的温度差、物体的热导率以及物体的尺寸等因素有关。
下面是一些常用的热传导计算公式:1.热流密度公式:热流密度(q)是单位时间内通过单位面积的热量传递量,可以由下式计算:q = -k * (dT/dx)其中,k是物体的热导率,dT/dx是温度梯度。
2.热传导率(k):物体的热传导率是描述物质导热能力的物理量,可以用以下公式计算:k=Q*L/(A*ΔT)其中,Q是通过物体的热量,L是物体的长度,A是传热的横截面积,ΔT是温度差。
3.热阻(R):热阻是描述物质阻碍热传导的程度的物理量,可以用以下公式计算:R=L/(k*A)其中,L是物体的长度,k是物体的热导率,A是传热的横截面积。
对流是物体表面与流体之间的热传递方式,流体通过对流来接触物体表面并将热量带走。
对于对流传热的计算,常用的公式有:1.流体的对流换热公式:流体通过对流来接触物体表面并带走热量,可以由下式计算:q = h * A * (T - Tfluid)其中,h是对流换热系数,A是物体表面积,T是物体表面的温度,Tfluid是流体的温度。
2.对流换热系数(h):对流换热系数描述了流体的传热能力,它可以由以下公式计算:h=(Nu*k__)/L其中,Nu是Nusselt数,k__是流体的导热系数,L是流体经过的长度。
3. Nusselt数(Nu):Nusselt数描述了流动体系中传热性能的参数,可以通过以下公式计算:Nu=(h*L)/k__其中,h是对流换热系数,L是流体经过的长度,k__是流体的导热系数。
辐射传热是物体通过辐射来传递能量的过程,对于辐射传热的计算,常用的公式有:1.斯特藩-玻尔兹曼定律:斯特藩-玻尔兹曼定律描述了黑体辐射能量的传递率,可以用下式表示:q=σ*ε*A*(T1^4-T2^4)其中,σ是斯特藩-玻尔兹曼常数,ε是物体的辐射率,A是物体的面积,T1和T2是物体的温度。
大学课件_计算传热学_第五章非稳态问题的求解方法

第5章 非稳态问题的求解方法1.1 通用输运方程()()()()()t t f q Γv tφφρφρφφ,grad div div =++-=∂∂ ( 5-1 )5.1 显式Euler 方法考虑1D, 定速度,常物性,无源项的特例22xx u t ∂∂Γ+∂∂-=∂∂φρφφ ( 5-2 ) 时间向前,空间中心差分,得FD 与FV 相同形式代数方程()t x x u nin i n i n i n i nin i∆⎥⎦⎤⎢⎣⎡∆-+Γ+∆--+=-+-++21111122φφφρφφφφ( 5-3 ) 可写成()ni n i n i n i c d c d d 1112221-++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-+-=φφφφ ( 5-4 ) 其中()xtu c and x t d ∆∆=∆Γ∆=2ρ ( 5-5 ) d 表示时间步长与特征扩散时间()Γ∆/2ξρ的比。
后者代表一个扰动由于扩散通过∆x 一段距离所需时间。
c 表示时间步长与特性对流传递时间x u ∆/的比。
后者代表一个扰动由于对流通过∆x 一段距离所需时间。
c 成为Courant number, 为CFD 中一个关键的参数。
此格式为时间为1阶精度,空间为2阶精度。
方程(4)内的系数在某些条件下,可能会是负值。
用矩阵表示:n n A φφ=+1 ( 5-6 )观察函数:()∑---=-=in i ni n n 211φφφφε( 5-7 )如果系数矩阵A 的本征值中有大于1,则ε随着n 的增加而增加。
如果本征值全部小于1,则ε是递减的。
一般本征值很难求得,对于本特例,它的解可用复数形式表示ji n n j e ασφ= ( 5-8 )其中,α为波数,可取任意值。
∙ 无条件发散:φn 无条件随n 增加→|σ|>1 ∙无条件稳定:φn 无条件随n 降低→|σ|<1代入差分方程,得到本征值为:()αασsin 2cos 21c i d +1-+= ( 5-9 )考虑特殊情况,∙ 无扩散:d=0, →σ >0, 无条件发散,充分条件∙无对流:c=0, →当cos α= -1时,σ最大,→d<1/2,无条件收敛,充分条件从另一个稳定条件考虑,要求系数矩阵A 的所有系数为正,可得到类似稳定性条件:(充分条件)d c d 2and 5.0<<( 5-10 )第一个条件要求()Γ∆<∆22x t ρ ( 5-11 )表示,每当∆x 减少一半,时间步长需减少到1/4. 第二个条件要求2Pe or2<<Γ∆cell xu ρ ( 5-12 )这同前述的用1D 稳态对流/扩散问题的CDS 要求是一致的。
传热学5

分析 解法
采用数学分析求解的方法。
传热学 Heat Transfer
2.如何从获得的温度场来计算h 无论是分析解法还是数值法首先获得都是温度场, 如何由T→h? t q 由傅里叶定律 w y
y 0
牛顿冷却公式
q w qc
qc h t w t
y
主流区
u∞
d 5 .0 离开前缘x处的边界层厚度 x Re x
局部表面传热系数
1/ 2 1/ 3 hx 0.332 Re x Pr x hx x 0.332 Re x1/ 2 Pr 1/ 3 Nu x 努塞尔数
(特征数方程,关联式)
u x 雷诺数: Re x 5 Re Re 5 10 关联式适用范围: c
25/42
传热学 Heat Transfer
1.数量级分析方法的基本思想 分析比较方程中等号两侧各项的数量级大小,在 同一侧内保留数量级大的项而舍去数量级小的项 2.实施方法 ①列出所研究问题中几何变量及物理变量的数量 级的大小,一般以1表示数量级大的物理量的量级。 以Δ表示小的数量级 ②导数中导数的数量级由自变量及因变量的数量 级代入获得
2t t t 2t c p u x v y x 2 y 2
28/42
传热学 Heat Transfer
5.4流体外掠平板传热层流 分析解及比拟理论
29/42
传热学 Heat Transfer
一、外掠等温平板层流流动下对流换热问 题的分析解
u v 0 x y
u u u p 2u 2u ( u v ) Fx ( 2 2 ) x y x x y v v v p 2v 2v ( u v ) Fy ( 2 2 ) x y y x y
第五章-传热学
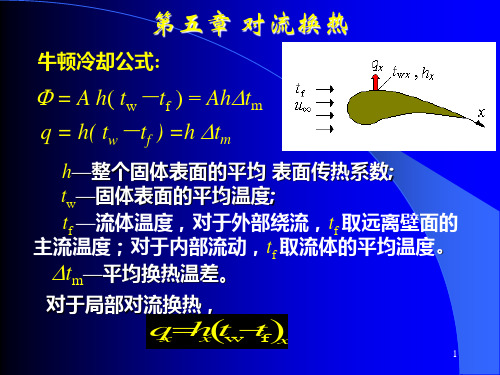
h
' h,x
' h,y
cpuxtvytdxdy
8
单位时间内微元体热力学能的增加为
dU
d
cp
t
dxdy
于是根据微元体的能量守恒
h
dU
d
可得
2t x2
2t y2
dxdy
cpuxtvytdxdy
cp
t
dxdy
cptux tvy ttu xv y
2t x2
2t y2
2
20
cp
uxt
v t y
=
2t x2
2t y2
1
11 1
1
2
1 1
1
2
对流换热微分方程组简化为
h t tw tf y w
u v 0 x y
简化方程组只有4个方
程,但仍含有h、u、v、 p、t 等5个未知量,方
程组不封闭。如何求解?
uuxvuy1ddpxy2u2
u t x
v t y
26
第六节 相似理论基础
相似原理指导下的实验研究仍然是解决复杂对流换 热问题的可靠方法。
相似原理回答三个问题: (1)如何安排实验? (2)如何整理实验数据? (3)如何推广应用实验研究结果?
一、 相似原理的主要内容
1.物理现象相似的定义 2.物理现象相似的性质 3.相似特征数之间的关系 4.物理现象相似的条件
三、解的函数形式——特征数关联式
特征数是由一些物理量组成的无量纲数,例如毕 渥数Bi和付里叶数Fo。对流换热的解也可以表示成 特征数函数的形式,称为特征数关联式。
通过对流换热微分方程的无量纲化可以导出与对 流换热有关的特征数。
传热学 数值计算

数值计算
4、一无限大平壁厚度为 0.3m,其导热系数为λ =36.4 W/ (m·K)。平壁两侧表面均给定 为第三类边界条件,即 h 1 =60W/ (m 2 ·K),t f 1 =25℃;h 2 =300W/ (m 2 ·K),t f 2 =215℃。 当平壁中具有均匀的内热源 q v =2 10 W / m 时,试计算沿平壁厚度的稳态温度分布。
k
0
k k 1
11
k 2Fo (t 10 t f Bi ) (1 2Fo 2Bi Fo) t11 t11
0
四、
计算过程
⑴ 设定初值:
t (1~11) 35 ℃;
36W / m k ;
Bi h / ;
根据不同的 Fo 计算Δ τ :
qv x 2
)/2
h2 x
h2 x TRB
qv x 2
) /(1
)
|T[i]-t[i]|<=EPS
NO
IT=IT+1
YES
打印“t[i]” , “IT”
YES
IT>K
NO
停止
⑷ 程序与计算结果 #include"iostream.h" #include"iomanip.h" #include"math.h" #include"stdio.h" #define N 16 void main() { int M,i,IT,flag; //定义节点个数
计算结果:
各节点温度: 节点 1 2 411.24 10 422.65 3 420.33 11 414.23 4 427.22 12 403.62 5
传热学第五章

h Atw t
以后除非特殊声明外,我们所说的对流换热系数皆指平均对流换
热系数,以 h 表示.
h(x)规律说明
Laminar region
x (x) h (x) 导热
Transition region
扰动
h(x)
Turbulent region
湍流部分的热阻很小,热阻主要集中在
粘性底层中.
2.按有无相变分
单相介质传热:对流换热时只有一种流体.
相变换热:传热过程中有相变发生.
物质有三态,固态,液态,气态或称三相.
相变换热有分为:
沸腾换热:(boiling heat transfer)物质由液态变为气态时发生 的换热.
凝结换热:(condensation heat transfer)物质由气态变为 液态时发生的换热. 熔化换热(melting heat transfer) 凝固换热(solidification heat transfer) 升华换热(sublimation heat transfer) 凝华换热(sublimation heat transfer )
由上述分析可见,边界层控制着传热过程,故一些研究人员试图通过
破坏粘性底层来达到强化传热的目的,并取得了一些成果.
二、边界层微分方程组.
牛顿流体(Newtonian fluid),常物性,无内热源,耗散不计,稳态,
二维,略去重力.
完性分析已知:u,t,l 的量级为0(1) , t 的量级为0()
以此五个量为分析基础。
2.动量方程(momentum equation)
u v 0 x y
u
u
u x
v
u y
Fx
p x
第5章 化工原理 传热学

(2)传热的三种基本方式
热的传递是由于物体内部或物体之间的温度不同而引起的。
根据热力学第二定律,热量总是自动地从温度较高的物体传给温度较的物体;
传热的推动力 传热的方向
温度差
高温向低温
化工生产中对传热过程的要求 一是强化传热过程,如各种换热设备中的传热。 二是削弱传热过程,如对设备或管道的保温,以减少热损失。
(2) 本章应掌握的内容 ① 三种传热方式的基本概念与基本方程式的应用; ② 单壁、多层壁热传导计算; ③ 牛顿定律、常用准数及对流传热系数关联式应用; ④ 热辐射斯蒂芬玻尔兹曼定律、两固体间的相互辐射; ⑤ 填料床层内热流量计算与热平衡分析。
5.1 概述
(1)传热在工业中的应用
5.2 热传导
5.2.1 傅里叶定律 5.2.2 热导率 5.2.3 平壁的稳定热传导 5.2.4 圆筒壁的稳定热传导
5.2.1傅里叶定律
温度场
温度的分布状况。
等温面和等温线 温度梯度 沿等温面法线方向的温度的变化率。
gradt lim
第五章 传热学
5.1 概述 5.2 热传导 5.3 两流体间的热量传递 5.4 给热系数 5.5 辐射传热 5.6 传热设备 5.7 填料床层的传热分析
--内容提要--
第五章
( 1) . 本章学习目的
传热学 .学习要求
通过本章学习,重点掌握传热学基本原理,并运用这些原理和规律去分析和 解决冶金和化工生产中传热过程的有关问题: ① 热传导基本原理,掌握傅立叶定律及平壁、圆筒壁的热传导计算; ② 对流传热的基本原理、牛顿冷却定律及影响对流传热的因素;掌握对流传热系 数的物理意义和经验关联式的用法、使用条件; ③ 辐射传热的基本概念及基本定律; ④ 熟练掌握传热过程的计算,传热基本方程式、热流量、平均传热温度差、总传 热系数的计算;了解强化传热过程的途径; ⑤ 填料床层的传热过程分析与计算 此外,工业生产中常用的换热器类型、结构、特点;掌握列管式换热器的设 计、选型。
传热学的数值解法

导热问题的数值求解方法数值解法的基本思想是用空间和时间区域内有限个离散点(称为节点)上温度的近似值,代替物体内实际的连续温度分布,然后由导热方程和边界条件推导出各节点温度间的相互关系的代数方程组(称为离散方程),求解此方程组,得到节点上的温度值,此即物体中温度场的解。
只要节点分布的足够稠密,数值解就有足够的精度。
求解导热问题的数值方法有有限差分法及有限元法,近几年又发展了边界元法和有限分析法。
数值方法适用于求解各种导热问题,不管物体的几何形状有多复杂,不管线性或非线性问题,都能使用。
由于计算机的飞速发展,计算技术软件发展也很快,数值方法的的地位越来越重要。
1 数值求解的基本思路及稳态导热内节点离散方程的建立一、 解法的基本思路1、基本思路:数值解法的求解过程可用框图4-1表示。
由此可见:1)物理模型简化成数学模型是基础;2)建立节点离散方程是关键;3)一般情况微分方程中,某一变量在某一坐标方向所需边界条件的个数等于该变量在该坐标方向最高阶导数的阶数。
二、稳态导热中位于计算区域内部的节点离散方程的建立方法1、基本方法方法:①泰勒级数展开法;②热平衡法。
1)泰勒级数展开法如图4-3所示,以节点(m,n)处的二阶偏导数为例,对节点(m+1,n)及(m-1,n)分别写出函数t 对(m,n)点的泰勒级数展开式:对(m+1,n):+∂∂∆+∂∂∆+∂∂∆+∂∂∆+=+444333,222,,,12462x t x x t x x t x x t x t t n m n m n m n m (a )对(m-1,n ):+∂∂∆+∂∂∆-∂∂∆+∂∂∆-=-444333,222,,,12462x t x x t x x t x x t xt t n m n m n m n m (b )(a )+(b )得: +∂∂∆+∂∂∆+=+-+444,222,,1,1122x t x x t x t t t n m n m n m n m 变形为n m x t,22∂∂的表示式得:n m x t,22∂∂)(0222,1,,1x x t t t nm n m n m ∆+∆+-=-+ 上式是用三个离散点上的值计算二阶导数n m x t ,22∂∂的严格表达式,其中:)(02x ∆―― 称截断误差,误差量级为2x ∆在数值计算时,用三个相邻节点上的值近似表示二阶导数的表达式即可,则相应的略去)(02x ∆。
传热流体数值计算

1 傅立叶定律傅立叶定律是导热理论的基础。
其向量表达式为:q g r a d T λ=-⋅ (2-1)式中:q —热流密度,是向量,2/()Kcal m h ;gradT —温度梯度,是向量,℃/m ;λ—导热系数,又称热导率,/()Kcal mh C ; 式中的负号表示q 的方向始终与gradT 相反。
2 导热系数(thermal conductivity )及其影响因素导热系数λ(/()Kcal mh C )是一个比例常数,在数值上等于每小时每平方米面积上,当物体内温度梯度为1℃/m 时的导热量。
导热系数是指在稳定传热条件下,1m 厚的材料,两侧表面的温差为1度(K ,°C ),在1秒内,通过1平方米面积传递的热量,用λ表示,单位为瓦/米·度,w/m·k (W/m·K,此处的K 可用℃代替)。
导热系数为温度梯度1℃/m ,单位时间通过每平方米等温面的热传导热流量。
单位是:W/(m·K)。
3.热传导微分方程推导 ♥ 在t 时刻w 界面的温度梯度为xT∂∂在t 时刻e 界面的温度梯度为dx x T x T dx x x Tx T 22∂∂+∂∂=∂∂∂∂+∂∂ 单位时间内六面体在x 方向流入的热流量为:dydz xT∂∂-λ; 单位时间内六面体在x 方向流出的热流量为:dydz dx x T x T ⎥⎦⎤⎢⎣⎡∂∂+∂∂-22λ;单位时间内六面体在x 方向流入的净热量为:dxdydz xT22∂∂λ 图3-1 微分单元体各面上进出流量示意图同理,单位时间内六面体在y 方向流入的净热量为:dxdydz yT22∂∂λ; 单位时间内六面体在y 方向流入的净热量为:dxdydz z T 22∂∂λ; 单位时间内流入六面体的总热量为:dxdydz z T y T xT ⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂222222λ (3-1) 六面体内介质的质量为:dxdydz ρ。
数值传热第五章课件2陶文铨

主讲陶文铨西安交通大学能源与动力工程学院热流中心CFD-NHT-EHT CENTER2010年10月18日, 西安数值传热学第五章对流扩散方程的离散格式(2)对流项离散格式的重要性及两种离散方式5.5.1假扩散的含义与成因5.5.2一阶截差格式引起严重假扩散举例1.本来的含义2.扩充的含义3.Taylor 展开法的分析5.5关于假扩散的讨论5.5.3网格倾斜交叉引起的计算误差5.5.4 非常数源项引起的假扩散5.5.5 两个名例以一维非稳态纯对流过程为例俩分析,其中有两n nφφ2(,O x φΔΔ其中关于时间的二阶导数项可做如下变化:时才没有这部分的计算误差。
2. 扩充的含义现有文献中常常将较大的计算误差都称为假扩散,大致有以下几项原因:(1) 一阶导数的一阶截差格式;(2) 流动方向与网格线呈倾斜交叉;(3) 离散格式未计及非常数源项的影响。
5.5.2一阶截差格式引起严重假扩散举例1.一维稳态对流扩散问题对流项用FUD,扩散项用CD,当Pe较大时,数值计算结果严重偏离精确解。
Physically plausible solution纯对流传递纯对流传递由离散方程:1n−1此时只有对流,没有扩散!时则有严重假扩散!0.8C =0.8C =当时,产生了严重的扩散作此种误差称为流向假扩散Γ≠Γ气流01. 设UE对P 控制容积,有2. 设控制容积,此时:计算误差纯对流传递三个对流问题的归纳这就是假扩散纯对流传递3)网格倾斜交叉引起的计算误差E冷热流体之间产生了温度均匀化的过程,即交叉5.5.5 已知流场计算温度场232(1),2(1)u y x v x y =−=−−参考解xT严重假扩散2) Leonard细高方腔中的自然对流换热5.6.1采用高阶格式克服流向假扩散5.6可以克服或减轻假扩散的格式与方法5.2.2 克服、减轻交叉假扩散的方法1. 采用二阶迎风2.采用三阶迎风3. 采用QUICK 格式1. 采用有效扩散系数2.采用自适应网格4. 采用SGSD 格式可以克服或减轻假扩散的格式与方法相当于界面上的中心差分)W WWxφ+Δ如型线上凹,则(2) FVM向上游取两点定义界面插值2.采用三阶迎风展开定义-一阶导数的三阶偏差分格式3. 采用定义-界面的插值在中心差分基础上考虑曲中心差分插值率修正?需要满足两个条件:插值的正确修正:相邻(2)0W PE φφφ−+<型线下凹8Cur −对e-界面u e 小于零时,取,,W P φφφu e 大于零时,取怎样相邻的三点?QUICK(2)e φφ=1/2w i φφ−=有:4. 采用CD条件稳定,但没有二阶假扩散;二阶迎风绝对稳定,组合起来,但是:如何确定值,特别是如何由计算结果来5. 高阶格式实施中的问题f u f计算边界:固o2) 代数方程的求解:等时,5.6.2用减小扩散系采用自适应网格(以减轻流5.7 对流-扩散方程离散形式稳定性分析5.7.1 数值计算中常见的三种不稳定性5.7.2 分析对流项格式不稳定性的“符号不变原则”5.7.3 稳定性分析结果讨论5.7.4 对流项格式问题讨论小结2.“符号不变”原则的基本思想3. “符号不变”原则的实施步骤4. “符号不变”原则的实施例子1. 研究背景扩散方程离散形式稳定性分析也会产生振荡的解,称为对流项离散格式的不稳态定性,研究目的是,找出产生振荡的临界Peclet 数。
传热学-导热数值计算

对物理问题进行数值解法的基本思路可以概括 为:把原来在时间、空间坐标系中连续的物理量的 场,如导热物体的温度场等,用有限个离散点上的 值的集合来代替,通过求解按一定方法建立起来的 关于这些值的代数方程,来获得离散点上被求物理 量的值,该方法称为数值解法。 这些离散点上被求物理量值的集合称为该物理 量的数值解。
1 (tm 1,n tm 1,n tm ,n 1 tm,n 1 ) 4
一阶
4.2.2 控制容积平衡法(热平衡法)
基本思想:对每个有限大小的控制容积应用能量守
恒,从而获得温度场的代数方程组,它从基本物理
现象和基本定律出发,不必事先建立控制方程,依 据能量守恒和Fourier导热定律即可。 能量守恒: 流入控制体的总热流量+控制体内热源生成热 = 流出控制体的总热流量+控制体内能的增量
x y
tm , n
y
2x 2 qw x 1 3x 2 (2tm 1,n 2tm ,n 1 tm ,n 1 tm 1,n ) 6 2
讨论关于边界热流密度的三种情况: (1)绝热边界
即令上式 qw 0 即可。
(2)qw 值不为零
流入元体,qw 取正,流出元体,qw 取负 (3)对流边界 此时 qw h(t f tm,n ) ,将此表达式代入上述方程,并 将此项中的
tm , n 1 (tm 1,n tm 1,n tm ,n 1 tm ,n 1 ) 4
(4) 设立迭代初场
代数方程组的求解方法有直接解法与迭
代解法,传热问题的有限差分法中主要采用
迭代法。采用迭代法求解时,需对被求的温
度场预先设定一个解,这个解称为初场,并
在求解过程中不断改进。
4.1.2 物理问题的数值求解过程
传热学基本定律和计算

2 、换热特征-沿圆管局部表面传热系数的变化
边界层的成长和脱体决定了外掠圆管换热的特征。
湍流 层流
一个实际问题:内部均匀加热的圆柱放在空气中风机吹 风冷却,圆柱表面何处温度最高?
温度最高点
层流: 80 85度
ห้องสมุดไป่ตู้
湍流:
85 90度
虽然局部表面传热系数变化比较复杂,但从平均表面换热系数看,渐变规 律性很明显。
温差修正系数 ct :
它是考虑到流体与壁面间存在较大温差 时,对关联式作的修正。
对气体被加热时
ct Tf Tw 0.5
当气体被冷却时
ct 1
对液体 ct f w m 液体受热时 m=0.11 液体受冷时 m=0.25
管长修正系数 cl :
当 L / d 60 时,称之为长管,虽然进口处 的 h 较大,但管较长,可忽略进口段的影响,而
们推荐的准则关联式中都应该有所反映。
准则关联式: Nu f
C
Re
f
m max
Prf
n
Prf Pr w
k
s1 s2
p
C Cz
适用条件:
0.7 Prf 500
定型尺寸:管外径do
定性温度:流体的算术平均温度 ;
tm
tf1
tf 2
2
计算流速:管间最大流速umax
3 、圆管表面传热系数的关联式
分段幂次关联式: Nu C Ren Pr1/3 (6-28)
式中:定性温度为 (tw t ) / 2; 特征长度为管外径;
Re数的特征速度为来流速度 u。
实验验证范围: t 15.5 ~ 982 C tw 21 ~ 1046 C
工程传热学第五章对流换热计算

大温差情况下计算换热时准则式右边要 乘以物性修正项 。 对于液体乘以 f w n
液 体 被 加 热 n=0.11 , 液 体 被 冷 却 n=0.25( 物性量的下标表示取值的定性温 度) 对于气体则乘以: T f Tw
n
气 体 被 加 热 n=0.55 , 气 体 被 冷 却 n=0.0 (此处温度用大写字符是表示取绝对温 标下的数值)。
qw w LT L 层流: t 0.055 Re Pr; t 0.07 Re Pr 热进口段长度: d d
L 紊流 : 50 d
热边界条件有均匀壁温和均匀热流两种。 对于管壁热流为常数时,流体温度随流动方 向线性变化,且与管壁之间的温差保持不变, 有
t f ( x) t 'f 4qw x cpumd
n m
准则的特征流速为流体最小截面处的最大流 速 umax ;特征尺寸为圆柱体外直径 d ;定性温 度除 Prw 按壁面温 tw 取值之外,皆用流体的主 流温度tf ;
Pr f Pr w
0.25
是在选用 tf 为定性温度时考虑热流方 向不同对换热性能产生影响的一个修 正系数。
如果流体流动方向与圆 柱体轴线的夹角(亦称 冲击角)在 30°- 90° 的范围内时,平均表面 传热系数可按下式计算
如果边界层在管中心处 汇合时流体已经从层流 流动完全转变为紊流流 动,那么进入充分发展 区后就会维持紊流流动 状态,从而构成流体管 内紊流流动过程。
如果出现紊流,紊流的扰动与混合作用又会 使表面传热系数有所提高,再逐渐趋向一个 定值。
Re
um04) — — 过渡区 Re 10
层流流动
紊流流动
0
传热学 数值计算

综合计算报告( 2011- 2012 年度第 1 学期)名称:传热学题目:肋片温度和效率数值计算院系:能源动力与机械工程学院班级:热能0906班学号:1091170611学生姓名:宋伟指导教师:周乐平成绩:日期:2011年10月28日一.综合计算的目的与要求1.根据数值分析计算的方法求出其温度分布。
2.根据计算出的温度分布计算肋效率。
3.根据计算结果讨论对流传热系数、材料导热系数和翅片厚度等数值对翅片效率的影响。
二. 综合计算的正文1.数值计算的基本思想对物理问题进行数值求解的基本思想可以概括为:把原来在时间、空间坐标系中连续的物理量的场,如导热物体的温度场,用有限个离散的点上的值的集合来代替,通过求解按一定方法建立起来关于这些值的代数方程,来获得离散点上被求物理量的值。
这些离散点上被求物理量值的集合称为该物理量的数值解。
if i==1&j==1rt(i,j)=(2*db*rt(i,j+1)+2*db*rt(i+1,j)+2*hb*tf/1000)/(4*db+2*hb/1000); elseif i==1&j>1&j<13rt(i,j)=(db*(rt(i,j-1)+rt(i,j+1))+2*db*rt(i+1,j+1)+2*hb*tf/1000)/(4*db+2*hb/1000); elseif i==1&j==13rt(i,j)=(db*(rt(i,j-1)+rt(i+1,j))+2*hb*tf/1000)/(2*db+2*hb/1000); elseif i>=2&i<=8&j==1rt(i,j)=(2*rt(i,j+1)+rt(i-1,j)+rt(i+1,j))/4; elseif rt(i,j)==10^9 continue; elseif rt(i,j)==50 continue;elseif i>=2&i<=28&j==13rt(i,j)=(db*(rt(i-1,j)+rt(i+1,j))+2*db*rt(i,j-1)+2*hb*tf/1000)/(4*db+2*hb/1000); elseif i==29&j==13rt(i,j)=(2*db*rt(i-1,j)+2*db*rt(i,j-1)+2*hb*tf/1000)/(4*db+2*hb/1000); elseif i==29&j>9&j<13rt(i,j)=(rt(i,j-1)+rt(i,j+1)+2*rt(i-1,j))/4; elsert(i,j)=(rt(i-1,j)+rt(i+1,j)+rt(i,j-1)+rt(i,j+1))/4;对于第一类点:首先根据热平衡有:22,,1,1,,1,=⨯∆⨯+⨯∆⨯∆-+⨯∆⨯∆-⨯+⨯∆⨯∆-⨯++-δδδλδλx q x yt t y xt t y xt t w nm n m nm n m nm n m由于其满足第三类边界条件,故:)(q ,n m f w t t h -⨯= 带入数据得:6.18116.190)(45,11,1,,fn m n m n m n m t t t t t +⨯++⨯=+++对于第二类点: 同理16.9116.1)(45t ,11,,fn m n m n m t t t ++⨯=+-对于第三类点: 6.18116.190)(45t 1,,1,1,fn m n m n m n m t t t t +++⨯=-+-对于第四类点: 6.18116.1)(901,,1,fn m n m n m t t t t ++⨯=--对于第五类点: )2(411,1,,1,+--++⨯⨯=n m n m n m n m t t t t对于第六类点: )(41t 1,11,1,,+-+-+++⨯=m n m n m n m n m t t t t对于第七类点: )2(41,1,11,,n m n m n m n m t t t t +-+++⨯⨯=对于第八类点: 16.18116.1)(90,11,,fn m n m n m t t t t ⨯++⨯=++根据此时得出的八类点的迭代关系式得出温度分布,然后利用∑∑∆Θ∆=iiiiA A iη算出其肋片效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢ 上风方案充分考虑了流动方向对导数差分计算式及 界面上函数取值方法的影响。
2020-9-23
太原理工大学
11 /70
1、上(迎)风格式两种离散方式的定义
①. 泰勒级数展开法定义(第
ui 0
若E 200, W 1P 250 符合实际
aE De Fe 2 1 2 1 违 背 了 正 系 数 规 则
aW Dw Fw 2 1 2 3
aP aE aW 1 3 2, 而 anb 1 3 4
这样,aP anb , 违反了斯卡巴勒准则(主对角占优)
( u j
x j
)
u j
x j
u j
x j
原通用方程可改写为
u j
x j
x j
( ) S
x j
对于已知的ρ、uj、Γ及S(常量)的分布,任何解及 +c 将同时满足方程,故系数和的法则仍然适用。
2020-9-23
太原理工大学
4 /70
Thermal
§5.2 一维稳态对流与扩散
讨论只有对流项和扩散项存在时的一维稳态问题,控
Thermal
一类迎风格式)
i-1
i
i+1
以流动方向而言,P 点的
W
P
E
一阶导数是该方向的向后差
分,即永远是从上游获得构
(a)
ui 0
造一阶导数的信息,公式表
示:
d
dx
i
i i1
x w
ui 0
i-1 w W
(b)
ui 0
i
e i+1
P
E
ui 0
d i1 i
dx i
x e
ui 0
一阶上(迎)风的构造方式
x
x x
3、通用方程的改写形式
x j
u j
( ) S
xj xj
x j
u j
(u j )
x j
u j
x j
2020-9-23
太原理工大学
3 /70
Thermal
两式相加得
x j
u j
(u j )
x j
u j
x j
x j
u j
Thermal
第五章 对流与扩散
主要内容: • §5.1 任务 • §5.2 一维稳态对流与扩散 • §5.3 二维问题的离散化方程 • §5.4 三维问题的离散化方程 • §5.5 单向空间坐标 • §5.6 假扩散
2020-9-23
太原理工大学
1 /70
§5.1 任 务
1、上章内容总结
Thermal
即,F 2D时,有可能使aE或aW为负 产生不切实际的结果
2020-9-23
太原理工大学
9 /70
Thermal
这就是中心差分格式求解对流换热问题时仅限于低
Re(低的F/D)的原因aP .
Dw
Fw 2
De
Fe 2
aW
aE
Fe
Fw
➢ 扩散项为零(Γ=0),中心差分格式导致 aP 0
于是方程 aPTP anbTnb 不适用于逐点迭代法求解
x
F u 对流或流动强度,可正、可负,由流动方向定
整理后的离散化方程
apP aEE aWW
其中:
aE
De
Fe 2
aW
Dw
Fw 2
2020-9-23
太原理工大学
7 /70
aP
Dw
Fw 2
De
Fe 2
aW
aE
Fe
Fw
2、对方程的几点说明
Thermal
➢ 由于连续性,Fe=Fw, aP aW aE(只是在流
2020-9-23
太原理工大学
2 /70
Thermal
① 获得流场的方法:可以得知于实验;也可以由一个解
析解给定;或通过流动的数值计算获得;或干脆由猜
测估计得知。
② “扩散”的广义解释:不仅限于表示由浓度梯度引起
的一种化学组分的扩散,由的梯度引起的扩散流是
,即方程中的 二阶导数项为扩散项。
场满足连续性条件时才具有这一性质);
➢ 方程 aPP aEE aWW 隐含着分段线性分布的含 义,也是熟知的中心差分格式(用左右节点值表示 界面上的值以及界面上的导数值);
➢ 方程必须遵守四项基本法则,否则会产生灾难性的 结果。
2020-9-23
太原理工大学
8 /70
Thermal
例如:设 De Dw 1, Fe Fw 4 若E、W给定,即可由离散方程求得P 。
Thermal
e
1 2
E
P
w
1 2
W
P
(e、w位于节点中间)
对于不同的界面位置,则需要采用其它的内插因子。
式
u e
u w
d
dx
e
d
dx
w
可写成
1 2
u e E
P
1 2
u w W
P
e E P xe
w P W xw
Γe、Γw可以用算术平均法或调和平均法求得。
定义: D 扩散传导性.
在通用微分方程中忽略了对流项,给出了非稳态项、 扩散项及源项的离散化方法,阐述了求解代数方程 组的方法。只要对流项的加入不改变离散化方程的 形式,方程组的求解方法仍然适用。
2、本章任务
在已知流场(V分量及ρ)的情况下,求解分布。对 流项与扩散项之间有不可分割的关系,因此需要把
这两项处理成一个单位,其它项可以作为陪衬.
制方程为:
x j
u j
( ) S
xj xj
d u d ( d )
dx
dx dx
连续方程: d u 0 u const
dx
任务:导出相应方程的离散化形式
2020-9-23
太原理工大学
5 /70
Thermal
§5.2-1 预备性的推导 (中心差分格式)
1、离散化方程的导出 选三点网格群见右图。控制
2020-9-23
太原理工大学
12 /70
② 控制容积积分法定义(第
二类迎风格式)
i-1 w
控制容积界面上值的规定: W
界面上的值等于界面上风侧
了,也不适用于采用其它的迭代解法了。
aE
De
Fe 2
aW
Dw
Fw 2
TP anbTnb aP
aP
Dw
Fw 2
De
Fe 2
aW
aE
Fe
Fw
2020-9-23
太原理工大学
10 /70
§5.2-2 上风方案
Thermal
➢ 为解决中心差分在 F 2D 之后产生解失去物理上 真实性的问题,提出了上风方案。
(x)w
(x)e
容积界面e、w的实际位置 不会影响最终的公式。在此
W w PP
x
eE x
设定其位于节点中间,这样还是比较方便的。
在控制容积内对微分方程积分
u
e
u w
d
dx
e
d
dx
w
d dx
u
d dx
d
dx
对流项及扩散项中的均采用分段线性的函数表示
2020-9-23
太原理工大学
6 /70
