实验六Matlab频域分析
matlab频域分析
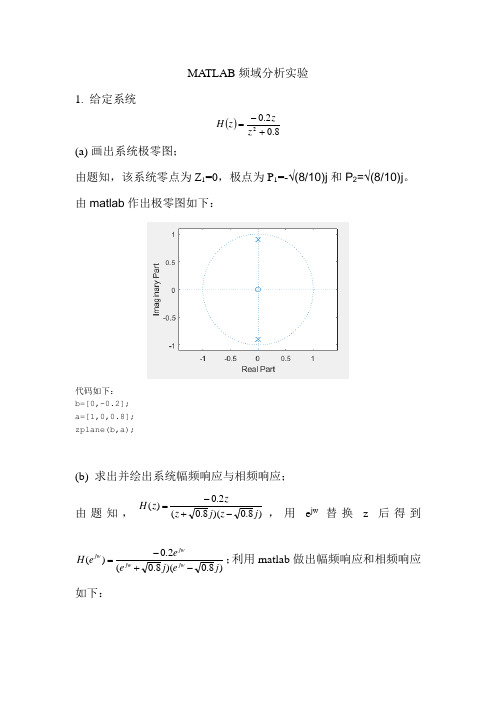
MATLAB 频域分析实验1. 给定系统()8.02.02+-=z zz H (a) 画出系统极零图;由题知,该系统零点为Z 1=0,极点为P 1=-√(8/10)j 和P 2=√(8/10)j 。
由matlab 作出极零图如下:代码如下:b=[0,-0.2]; a=[1,0,0.8]; zplane(b,a);(b) 求出并绘出系统幅频响应与相频响应; 由题知,)8.0)(8.0(2.0)(j z j z zz H -+-=,用e jw替换z 后得到)8.0)(8.0(2.0)(j e j e e e H jwjw jwjw-+-=;利用matlab 做出幅频响应和相频响应如下:代码如下:clear all ; b=[0,-0.2]; a=[1,0,0.8];[H,w]=freqz(b,a,512,1); Hr=abs(H);Hphase=angle(H)*180/3.1415;Hphase=unwrap(Hphase); subplot(221);plot(2*w,Hr);grid on ; xlabel( '\omega/\pi');ylabel('幅频响应 '); subplot(222);plot(w,Hphase);grid on ; xlabel( '\omega/\pi');ylabel('相频响应/°');(c) 求出并绘出系统的单位样值响应; 由(b) 中结果,利用matlab中的iztrans命令求得)()21sin(8.08.041-)(n u n n h n π=,在matlab 中做出单位样值响应如下:代码如下:clear all ; b=[0,-0.2]; a=[1,0,0.8]; N=50;[h,t]=impz(b,a,N);subplot(223);stem(t,h,'.');grid; xlabel( 'n');ylabel('单位样值响应 h(n) ');(d) 令x (n ) = u (n ), 求出并绘出系统的单位阶跃响应.由题知,)()()(n h n x n g ⊗=,由卷积定理得G(z)=X(z)*H(z),则)8.0)(1(2.08.02.0*1)(*)()(222+--=+--==z z z z z z z z H z X z G ,利用matlab 进行逆变换后得)(91)()21c o s (8.091)()21s i n (0.8452)(n u n u n n u n n g n n -+-=ππ,利用matlab 做出图形如下:代码如下:clear all ;b=[0,-0.2]; a=[1,0,0.8];x=ones(100);t=1:100; y=filter(b,a,x);subplot(224);plot(t,y);grid on ; xlabel( 'n');ylabel('阶跃响应 ');2. 某离散系统用以下差分方程表示()()()()()1224.012.0-+=---+n x n x n y n y n y .(a) 画出系统极零图; 将原式两边进行z 变换得)1()()())2()1()((24.0))1()((2.0)(1122-++=-+-+--++--x z X z z X z y z zy z Y zzy z Y z z Y ,由于初始状态为零状态,将上式整理后得)(2)(24.0)(2.0)(1-2z X z z Y zz Y z z Y =-+,则可得系统函数 24.02.02)()()(2-+==z z zz X z Y z H ,极点为P 1=0.4,P 2=-0.6,零点为Z 1=0。
《自动控制原理》MATLAB用于频域分析实验

[mag,phase,w]=bode(num,den,w)
四、实验内容及步骤
1、曲线1
k = 500;
num = [1,10];
den = conv([1,0],conv([1,1],conv([1,20],[1,50])));
《自动控制原理》MATLAB用于频域分析实验
一、实验目的
1、加深了解系统频率特性的概念。
2、学习使用Matlab软件绘制Nyquist图、
Matlab2014b版
三、实验原理
1、奈奎斯特图(幅相频率特性图)
MATLAB为用户提供了专门用于绘制奈奎斯特图的函数nyquist
五、实验原始数据记录与数据处理
六、实验结果与分析讨论
通过使用Matlab2014b版,加深了解系统频率特性的概念以及典型环节的频率特性。
七、结论
本实验验证的典型环节的频率特性。
八、实验心得体会(可略)
常用格式:
nyquist (num,den)
或nyquist (num,den,w) 表示频率范围0~w。
或nyquist (num,den,w1:p:w2) 绘出在w1~w2频率范围内,且以频率间隔p均匀取样的波形。
举例:
2、对数频率特性图(波特图)
MATLAB为用户提供了专门用于绘制波特图的函数bode
常用格式:
bode (num,den)
或bode (num,den,w) 表示频率范围0~w。
或bode (num,den,w1:p:w2) 绘出在w1~w2频率范围内,且以频率间隔p均匀取样的波形。
举例:系统开环传函为 绘制波特图。
基于Matlab对信号进行频域分析的方法

基于Matlab对信号进行频域分析的方法Matlab可以说是一个非常有用且功能齐全的工具,在通信、自控、金融等方面有广泛的应用。
本文讨论使用Matlab对信号进行频域分析的方法。
说到频域,不可避免的会提到傅里叶变换,傅里叶变换提供了一个将信号从时域转变到频域的方法。
之所以要有信号的频域分析,是因为很多信号在时域不明显的特征可以在频域下得到很好的展现,可以更加容易的进行分析和处理。
FFTMatlab提供的傅里叶变换的函数是FFT,中文名叫做快速傅里叶变换。
快速傅里叶变换的提出是伟大的,使得处理器处理数字信号的能力大大提升,也使我们生活向数字化迈了一大步。
接下来就谈谈如何使用这个函数。
fft使用很简单,但是一般信号都有x和y两个向量,而fft只会处理y向量,所以想让频域分析变得有意义,那么就需要用户自己处理x向量一个简单的例子从一个简单正弦信号开始吧,正弦信号定义为:我们现在通过以下代码在Matlab中画出这个正弦曲线fo = 4; %frequency of the sine waveFs = 100; %sampling rateTs = 1/Fs; %sampling time intervalt = 0:Ts:1-Ts; %sampling periodn = length(t); %number of samplesy = 2*sin(2*pi*fo*t); %the sine curve%plot the cosine curve in the TIme domainsinePlot = figure;plot(t,y)xlabel(‘TIme (seconds)’)ylabel(‘y(t)’)TItle(‘Sample Sine Wave’)grid这就是我们得到的:当我们对这条曲线fft时,我们希望在频域得到以下频谱(基于傅里叶变换理论,我们希望看见一个幅值为1的峰值在-4Hz处,另一个在+4Hz处)使用FFT命令我们知道目标是什么了,那么现在使用Matlab的内建的FFT函数来重新生成频谱%plot the frequency spectrum using the MATLAB fft commandmatlabFFT = figure; %create a new figureYfreqDomain = fft(y); %take the fft of our sin wave,y (t)stem(abs(YfreqDomain)); %use abs command to get the magnitude%similary,we would use angle command to get the phase plot!%we‘ll discuss phase in another post though!xlabel(’Sample Number‘)ylabel(’Amplitude‘)TItle(’Using the Matlab fft command‘)gridaxis([0,100,0,120])效果如下:但是注意一下,这并不是我们真正想要的,有一些信息是缺失的x轴本来应该给我们提供频率信息,但是你能读出频率吗?幅度都是100没有让频谱中心为为FFT定义一个函数来获取双边频谱以下代码可以简化获取双边频谱的过程,复制并保存到你的.m文件中function [X,freq]=centeredFFT(x,Fs)%this is a custom function that helps in plotting the two-sided spectrum%x is the signal that is to be transformed%Fs is the sampling rateN=length(x);%this part of the code generates that frequency axisif mod(N,2)==0k=-N/2:N/2-1; % N evenelsek=-(N-1)/2:(N-1)/2; % N oddendT=N/Fs;freq=k/T; %the frequency axis%takes the fft of the signal,and adjusts the amplitude accordinglyX=fft(x)/N; % normalize the dataX=fftshift(X); %shifts the fft data so that it is centered这个函数输出正确的频域范围和变换后的信号,它需要输入需要变换的信号和采样率。
第六章 利用Matlab对信号进行频域分析

练习 1连续求以下信号的DTFS的系数 连续求以下信号的DTFS的系数
x[n] = cos(nπ / 30) + 2sin(nπ / 90)
2已知一个信号在一个周期内的DTFS系数由下式给 已知一个信号在一个周期内的DTFS系数由下式给 出X[k]=(1/2)k,假设N=10,求出时域信号x[n]. 假设N=10,求出时域信号x[n].
Example T0=1;N=19;T=T0/N; t=0:T:T0; x=cos(2*pi*5*t)+2*sin(2*pi*9*t); Xm=fft(x,N)/N; f=(-(N-1)/2:(N-1)/2)/N/T;%% f=(-(N-1)/2:(Nfigure; stem(t,xlabel('f(Hz)');ylabel('Magnitude');title('幅度谱'); xlabel('f(Hz)');ylabel('Magnitude');title('幅度谱');
例题2 例题2 π π 7π x[n] = cos( n + ) + 0.5cos( n) 已知一个周期序列, 8 3 8 利用FFT计算它的离散时间傅里叶级数 利用FFT计算它的离散时间傅里叶级数 理论计算可得
7π x[n] = cos( n + ) + 0.5cos( n) 8 3 8 = e
∞
∫
相比离散时间非周期信号的DTFT分析方法,连续非周期信号的 相比离散时间非周期信号的DTFT分析方法,连续非周期信号的 DFT分析方法增加了时域抽样环节.如果不满足抽样定理,会出 DFT分析方法增加了时域抽样环节.如果不满足抽样定理,会出 现混叠误差.如果信号在时域加窗截断过程中,窗口宽度(截断 长度)或窗口类型不合适,则会产生较大的频率泄露而影响频谱 分辨率.因此确定抽样间隔T和相应的截断长度是决定DTFT能否 分辨率.因此确定抽样间隔T和相应的截断长度是决定DTFT能否 正确分析信号频谱的关键.
matlab频域分析实验报告

Matlab频域分析实验报告引言频域分析是一种常用的信号处理技术,可以帮助我们理解信号的频率特性和频率成分。
在本实验中,我们将使用Matlab进行频域分析,并通过实际的信号示例来说明其应用。
实验目标本实验的目标是通过Matlab进行频域分析,了解信号的频率特性,并能够对信号进行频域滤波、谱估计和频域增强。
实验步骤步骤一:加载信号数据首先,我们需要加载信号数据。
在Matlab中,我们可以使用load()函数来加载数据文件。
假设我们的信号数据文件名为signal.mat,则可以使用以下代码进行加载:load('signal.mat');步骤二:绘制时域波形图加载信号数据后,我们可以通过绘制时域波形图来观察信号的时域特性。
可以使用plot()函数来绘制信号的时域波形图。
以下是示例代码:plot(signal);xlabel('时间');ylabel('信号幅度');title('信号的时域波形图');步骤三:进行傅里叶变换为了将信号转换到频域,我们需要进行傅里叶变换。
在Matlab中,可以使用fft()函数对信号进行傅里叶变换。
以下是示例代码:signal_freq = fft(signal);步骤四:绘制频域幅度谱进行傅里叶变换后,我们可以绘制信号的频域幅度谱来观察信号的频率特性。
可以使用abs()函数来计算频域幅度,并使用plot()函数来绘制频域幅度谱图。
以下是示例代码:signal_freq_amp = abs(signal_freq);plot(signal_freq_amp);xlabel('频率');ylabel('幅度');title('信号的频域幅度谱');步骤五:频域滤波频域分析不仅可以帮助我们观察信号的频率特性,还可以进行频域滤波。
例如,我们可以通过在频域中将低幅度的频率成分设置为0来实现低通滤波。
《MATLAB》连续时间信号的频域分析和连续时间系统的时域分析实验报告
《MATLAB 》连续时间信号的频域分析和连续时间系统的时域分析实验报告1、编写程序Q3_1,绘制下面的信号的波形图:其中,ω0 = 0.5π,要求将一个图形窗口分割成四个子图,分别绘制cos(ω0t)、cos(3ω0t)、cos(5ω0t) 和x(t) 的波形图,给图形加title ,网格线和x 坐标标签,并且程序能够接受从键盘输入式中的项数n。
2、给程序例3_1增加适当的语句,并以Q3_2存盘,使之能够计算例题3-1中的周期方波信号的傅里叶级数的系数,并绘制出信号的幅度谱和相位谱的谱线图。
-+-=)5cos(51)3cos(31)cos()(000t t t t x ωωω∑∞==10)cos()2sin(1n t n n nωπ3.3反复执行程序例3_2,每次执行该程序时,输入不同的N值,并观察所合成的周期方波信号。
通过观察,你了解的吉布斯现象的特点是什么?3.4分别手工计算x1(t) 和x2(t) 的傅里叶级数的系数。
1.利用MATLAB 求齐次微分方程,,起始条件为,,时系统的零输入响应、零状态响应和全响应。
2. 已知某LTI 系统的方程为:其中,。
利用MATLAB 绘出范围内系统零状态响应的波形图。
3.已知系统的微分方程如下,利用MATLAB 求系统冲激响应和阶跃响应的数值解,并绘出其时域波形图。
(1)'''()2''()'()'()y t y t y t x t ++=()()t x t e u t -=(0)1y -='(0)1y -=''(0)2y -=''()5'()6()6()y t y t y t x t ++=()10sin(2)()x t t u t π=05t ≤≤''()3'()2()()y t y t y t x t ++=(2)''()2'()2()'()y t y t y t x t ++=。
matlab信号频域分析实验报告

matlab信号频域分析实验报告《Matlab信号频域分析实验报告》摘要:本实验通过Matlab软件对信号进行频域分析,探究信号在频域中的特性。
首先,我们使用Matlab生成了不同频率和幅度的正弦信号,并对其进行了傅里叶变换。
然后,我们利用频谱分析工具对信号进行了频谱分析,观察了信号在频域中的频率成分和能量分布。
最后,我们对信号进行了滤波处理,观察了滤波后信号在频域中的变化。
引言:信号的频域分析是数字信号处理中的重要内容,通过频域分析可以了解信号的频率成分和能量分布情况,对信号的特性有着重要的指导意义。
Matlab作为一种强大的数学计算软件,提供了丰富的信号处理工具,能够方便快捷地进行信号的频域分析。
本实验旨在通过Matlab软件进行信号频域分析,探究信号在频域中的特性。
实验过程:1. 生成不同频率和幅度的正弦信号首先,我们使用Matlab生成了不同频率和幅度的正弦信号,分别代表不同的信号特性。
通过绘制时域波形图,我们可以直观地观察到信号的波形特点。
2. 进行傅里叶变换接下来,我们对生成的正弦信号进行了傅里叶变换,得到了信号在频域中的频率成分和能量分布情况。
通过绘制频谱图,我们可以清晰地观察到信号的频率成分和能量分布情况。
3. 频谱分析利用Matlab提供的频谱分析工具,我们对信号进行了频谱分析,进一步观察了信号在频域中的特性。
通过频谱分析,我们可以了解信号的频率成分和能量分布情况,为后续的信号处理提供了重要参考。
4. 滤波处理最后,我们对信号进行了滤波处理,观察了滤波后信号在频域中的变化。
通过比较滤波前后的频谱图,我们可以了解滤波对信号频域特性的影响,进一步认识信号在频域中的变化情况。
实验结论:通过本次实验,我们对信号在频域中的特性有了更深入的了解。
通过Matlab软件进行信号频域分析,我们可以清晰地观察到信号的频率成分和能量分布情况,为信号处理和分析提供了重要参考。
同时,我们也了解到了滤波对信号在频域中的影响,为信号处理提供了重要指导。
在MATLAB中使用频域方法进行信号分析

在MATLAB中使用频域方法进行信号分析信号分析是一种用于探索信号特征、提取有用信息以及解决实际问题的方法。
在信号分析中,频域方法是一种常用且有效的工具。
频域方法通过将信号从时域转换为频域,可以更好地理解信号的频率特征和谱密度。
MATLAB是一款功能强大的数学计算和数据分析软件,在信号处理领域广泛应用。
通过其丰富的函数库和强大的计算能力,我们可以使用多种频域方法进行信号分析。
本文将介绍一些MATLAB中常用的频域方法,并展示如何使用这些方法进行信号分析。
第一部分:频域变换频域变换是将时域信号转换为频域信号的过程。
在MATLAB中,常用的频域变换方法包括傅里叶变换、快速傅里叶变换等。
下面我们将详细介绍这些方法的原理和使用。
1. 傅里叶变换傅里叶变换是频域分析的基础。
它将信号表示为一组正弦和余弦波的和,可以将信号的时域特征转化为频域特征。
在MATLAB中,可以使用fft函数进行傅里叶变换。
例如,我们有一段包含正弦信号的时域数据,可以使用fft函数计算其频域表示。
代码如下:```MATLABt = 0:0.01:1; % 时间范围f = 10; % 信号频率x = sin(2*pi*f*t);X = fft(x);```通过上述代码,我们可以得到信号x的频谱表示X。
可以使用plot函数绘制频谱图,代码如下:```MATLABf = (0:length(X)-1)/length(X)*Fs; % 频率范围plot(f, abs(X))```上述代码中,我们计算了频率范围f,并使用abs函数计算频域信号的模。
绘制得到的图形可以直观地显示信号的频率成分。
2. 快速傅里叶变换(FFT)傅里叶变换是一种高效的频域变换方法,但是当信号长度较大时,计算复杂度较高。
为了解决这个问题,快速傅里叶变换(FFT)被广泛应用。
FFT算法通过分治策略将傅里叶变换的复杂度从O(n^2)降低到O(nlogn),大大提高了计算效率。
信号_频域分析实验报告(3篇)

第1篇一、实验目的1. 理解信号的频域分析方法及其在信号处理中的应用。
2. 掌握傅里叶变换的基本原理和计算方法。
3. 学习使用MATLAB进行信号的频域分析。
4. 分析不同信号在频域中的特性,理解频域分析在实际问题中的应用。
二、实验原理频域分析是信号处理中一种重要的分析方法,它将信号从时域转换到频域,从而揭示信号的频率结构。
傅里叶变换是频域分析的核心工具,它可以将任何信号分解为不同频率的正弦波和余弦波的线性组合。
三、实验内容及步骤1. 信号生成与傅里叶变换- 使用MATLAB生成一个简单的正弦波信号,频率为50Hz,采样频率为1000Hz。
- 对生成的正弦波信号进行傅里叶变换,得到其频谱图。
2. 频谱分析- 分析正弦波信号的频谱图,观察其频率成分和幅度分布。
- 改变正弦波信号的频率和幅度,观察频谱图的变化,验证傅里叶变换的性质。
3. 信号叠加- 将两个不同频率的正弦波信号叠加,生成一个复合信号。
- 对复合信号进行傅里叶变换,分析其频谱图,验证频谱叠加原理。
4. 窗函数- 使用不同类型的窗函数(如矩形窗、汉宁窗、汉明窗等)对信号进行截取,观察窗函数对频谱的影响。
- 分析不同窗函数的频率分辨率和旁瓣抑制能力。
5. 信号滤波- 设计一个低通滤波器,对信号进行滤波处理,观察滤波器对信号频谱的影响。
- 分析滤波器对信号时域和频域特性的影响。
6. MATLAB工具箱- 使用MATLAB信号处理工具箱中的函数,如`fft`、`ifft`、`filter`等,进行信号的频域分析。
- 学习MATLAB工具箱中的函数调用方法和参数设置。
四、实验结果与分析1. 正弦波信号的频谱分析实验结果显示,正弦波信号的频谱图只有一个峰值,位于50Hz处,说明信号只包含一个频率成分。
2. 信号叠加的频谱分析实验结果显示,复合信号的频谱图包含两个峰值,分别对应两个正弦波信号的频率。
验证了频谱叠加原理。
3. 窗函数对频谱的影响实验结果显示,不同类型的窗函数对频谱的影响不同。
实验六-信号与系统复频域分析

实验六 信号与系统复频域分析一、实验目的1.学会用MATLAB 进行部分分式展开;2.学会用MATLAB 分析LTI 系统的特性;3.学会用MATLAB 进行Laplace 正、反变换。
4.学会用MATLAB 画离散系统零极点图;5.学会用MATLAB 分析离散系统的频率特性;二、实验原理及内容1.用MATLAB 进行部分分式展开用MATLAB 函数residue 可以得到复杂有理分式F(s)的部分分式展开式,其调用格式为[],,(,)r p k residue num den =其中,num,den 分别为F(s)的分子和分母多项式的系数向量,r 为部分分式的系数,p 为极点,k 为F(s)中整式部分的系数,假设F(s)为有理真分式,则k 为零。
例6-1 用部分分式展开法求F(s)的反变换 322()43s F s s s s+=++解:其MATLAB 程序为format rat; num=[1,2]; den=[1,4,3,0]; [r,p]=residue(num,den)程序中format rat 是将结果数据以分数形式显示 F(s)可展开为210.536()13F s s s s --=++++ 所以,F(s)的反变换为3211()()326t t f t e e u t --⎡⎤=--⎢⎥⎣⎦2.用MATLAB 分析LTI 系统的特性系统函数H 〔s 〕通常是一个有理分式,其分子和分母均为多项式。
计算H 〔s 〕的零极点可以应用MATLAB 中的roots 函数,求出分子和分母多项式的根,然后用plot 命令画图。
在MATLAB 中还有一种更简便的方法画系统函数H 〔s 〕的零极点分布图,即用pzmap 函数画图。
其调用格式为pzmap(sys)sys 表示LTI 系统的模型,要借助tf 函数获得,其调用格式为sys=tf(b,a)式中,b 和a 分别为系统函数H 〔s 〕的分子和分母多项式的系数向量。
MATLAB进行控制系统频域分析报告

一、基于MATLAB 的线性系统的频域分析基本知识(1)频率特性函数)(ωj G 。
设线性系统传递函数为:nn n n m m m m a s a s a s a b s b s b s b s G ++⋅⋅⋅++++⋅⋅⋅++=---1101110)( 则频率特性函数为:nn n n m m m m a j a j a j a b j b j b j b jw G ++⋅⋅⋅++++⋅⋅⋅++=---)()()()()()()(1101110ωωωωωω 由下面的MATLAB 语句可直接求出G(jw)。
i=sqrt(-1) % 求取-1的平方根GW=polyval(num ,i*w)./polyval(den ,i*w)其中(num ,den )为系统的传递函数模型。
而w 为频率点构成的向量,点右除(./)运算符表示操作元素点对点的运算。
从数值运算的角度来看,上述算法在系统的极点附近精度不会很理想,甚至出现无穷大值,运算结果是一系列复数返回到变量GW 中。
(2)用MATLAB 作奈魁斯特图。
控制系统工具箱中提供了一个MATLAB 函数nyquist( ),该函数可以用来直接求解Nyquist 阵列或绘制奈氏图。
当命令中不包含左端返回变量时,nyquist ()函数仅在屏幕上产生奈氏图,命令调用格式为:nyquist(num,den)nyquist(num,den,w)或者nyquist(G) nyquist(G,w)该命令将画出下列开环系统传递函数的奈氏曲线: )()()(s den s num s G = 如果用户给出频率向量w,则w 包含了要分析的以弧度/秒表示的诸频率点。
在这些频率点上,将对系统的频率响应进行计算,若没有指定的w 向量,则该函数自动选择频率向量进行计算。
w 包含了用户要分析的以弧度/秒表示的诸频率点,MATLAB 会自动计算这些点的频率响应。
当命令中包含了左端的返回变量时,即:[re,im,w]=nyquist(G)或[re,im,w]=nyquist(G,w)函数运行后不在屏幕上产生图形,而是将计算结果返回到矩阵re 、im 和w 中。
MATLAB课程设计报告--信号的频域分析及MATLAB实现

MATLAB电子信息应用课程设计设计五信号的频域分析及MA TLAB实现学院:信息学院专业班级:电信1201学号:201姓名:一、 设计目的通过该设计,理解傅里叶变换的定义及含义,掌握对信号进行频域分析 的方法。
二、 设计内容相关的信号知识:信号的离散傅里叶变换 从连续到离散:连续时间信号)(t x 以及对应的连续傅里叶变换)(ˆωx 都是连续函数。
将x和xˆ都离散化,并且建立对应的傅里叶变换。
假设x(t)时限于[0, L],再通过时域采样将)(t x 离散化,就可以得到有限长离散信号,记为)(t x discrete。
设采样周期为T ,则时域采样点数N=L/T 。
)()()()()(11nT t nT x nT t t x t x N n N n discrete-=-=∑∑-=-=δδ它的傅里叶变换为∑∑-=--==-=11)(1)()()(ˆN n Tin N n discrete enT x TnT t F nT x xωδω这就是)(t x 在时域采样后的连续傅里叶变换,也就是离散时间傅里叶变换,它在频域依然是连续的。
下面将频域信号转化为有限长离散信号。
与对时域信号的处理类似,假设频域信号是带限的,再经过离散化,即可得到有限长离散信号。
依据采样定理,时域采样若要能完全重建原信号,频域信号)(ˆωx应当带限于(0,1/T)。
由于时域信号时限于[0, L],由采样定理以及时频对偶的关系,频域的采样间隔应为1/L 。
故,频域采样点数为:NLT =11即频域采样的点数和时域采样同为N ,频域采样点为Nk kNT k <≤=0}/2{πω在DTFT 频域上采样:=][ˆk x∑-=-=12)(1)(ˆN n nkNik discrete enT x Tx πω令T=1,将其归一化,就得到离散傅里叶变换。
因此,DFT 就是先将信号在时域离散化,求其连续傅里叶变换后,再在频域离散化的结果。
离散傅里叶变换:1、有限长序列的离散傅里叶变换公式⎪⎪⎩⎪⎪⎨⎧==∑∑-=-=-10)/2(10)/2()(1)()()(N n knN j N n kn N j e k X N n x e n x k X ππMATLAB 函数:fft 功能是实现快速傅里叶变换,fft 函数的格式为: y=fft (x ),返回向量x 的不连续fourier 变化。
基于matlab的控制系统频域分析实验

基于matlab 的控制系统频域分析实验1. 已知系统开环传递函数)1()3()()(-+=s s s K s H s G用两种以上的方法,研究闭环系统稳定时K 的取值范围; 解:法一:闭环特征方程:s^2+(K-1)*s+3*K=0 列劳斯表: s^2 1 3 s^1 K-1 0 s 3*K系统稳定时:K-1>0 3*k>0所以:K>1 此时,系统稳定法二:由闭环特征方程得特征根:S=(-(K-1) + sprt((K-1)^2-12*K))/2由系统稳定的充要条件:所有特征根具有负实部,于是有:K-1>0得K>1法三:闭环传递函数为:由系统稳定的充要条件:闭环传递函数的极点均位于S 左半平面,于是有:K-1>0得K>1法四:令K=1,做Nyquist 图:曲线过(-1,j0)点,说明K=1时,系统临界稳定。
又令K=2,做Nyquist图:此时,系统稳定。
综上述,当K>1时,系统稳定。
2. 用MATLAB 绘制系统传递函数为2525)(2++=s s s G的Bode 图,并求取谐振频率和谐振峰值,相角裕度及幅值裕度。
G=tf([25],[1 1 25]) margin(G);幅值裕度:Gm=Inf dB 相角裕度:Pm=16.3 deg 谐振频率:10^0.845谐振峰值:14.02353. 单位反馈系统,开环传递函数为12.012)(232+++++=s s s s s s G用MATLAB 绘制系统的Nyquist 图及Bode 图,并求幅值裕量和相角裕量,在图中判断系统的稳定性。
G=tf([1 2 1],[1 0.2 1 1]) figure(1)margin(G); figure(2) nyquist(G); axis equalTransfer function: s^2 + 2 s + 1 --------------------- s^3 + 0.2 s^2 + s + 1由bode 图可知,相角裕度为Pm=26.8deg;幅值裕度为Gm=-5.35dB 。
用MATLAB实现连续系统的频域分析

用MATLAB实现连续系统的频域分析
MATLAB是一款具有强大功能的科学数学软件,它用于数值计算、算法设计、函数图形化等,也可以用于连续系统的频域分析。
下面介绍一般的频域分析的基本步骤,并用MATLAB编程实现,从而实现连续系统的频域分析。
首先,将连续时间信号转换为数字,并计算出相应的变换系数。
一般情况下,可以使
用MATLAB中的函数“fft”和“ifft”根据时域输入信号进行傅里叶变换。
具体过程,可
以按照以下步骤逐步实现:
1. 首先,将函数转换成实数集合并将它们用MATLAB以连续信号的形式写出。
2. 接着,遵循N分频原则,解决连续信号的采样问题,然后对其进行频谱分析。
3. 然后,在实际计算中,根据采样时间及相关的参数计算频率及其带宽,并将每个
离散频率的相应信号分量分开。
4. 接着,使用MATLAB的fft()函数进行正变换处理,得到实现的频域模型。
5. 最后,使用disp()或plot()函数,将计算出的频谱信号以可视化的方式展现出来,方便观察和分析。
MATLAB中,提供了多种用于傅里叶变换的函数,可用于连续系统的频域分析,比如
fft()函数和ifft()函数,等等。
使用这些函数,可以在MATLAB中实现连续系统的频域分析,帮助用户轻松地进行频域分析,并展示出可视化的结果,提高效率。
如何使用Matlab进行频域分析和滤波处理

如何使用Matlab进行频域分析和滤波处理频域分析和滤波处理在信号处理领域中具有重要的地位。
Matlab是一种专业的数学软件,在频域分析和滤波处理方面提供了丰富的工具和函数。
本文将介绍如何使用Matlab进行频域分析和滤波处理,包括频谱分析、滤波器设计和滤波器应用等方面的内容。
一、频域分析的基本原理频域分析是将时域信号转换为频域表示的过程。
在频域中,信号的特征通过频谱来描述,频谱展示了信号中各个频率分量的强度和相位信息。
常用的频域分析方法有傅里叶变换、快速傅里叶变换(FFT)等。
1. 傅里叶变换傅里叶变换是将一个信号从时域转换到频域的数学工具。
在Matlab中,可以使用fft函数进行傅里叶变换。
例如,对于一个长度为N的时域信号x,在Matlab中可以使用X = fft(x)来计算其频域表示。
得到的频域信号X是一个复数数组,包含了信号在各个频率上的幅度和相位信息。
2. FFT算法快速傅里叶变换(FFT)是一种快速计算傅里叶变换的算法。
相较于传统的傅里叶变换,FFT算法具有计算效率高的优势,在信号处理中得到广泛应用。
在Matlab中,可以使用fft函数进行FFT计算。
例如,对于一个长度为N的时域信号x,在Matlab中可以使用X = fft(x, N)来进行FFT计算。
其中N是指定的变换点数,通常选择2的幂次作为变换点数,以提高计算效率。
二、频谱分析的应用频谱分析可以用来探索信号中各个频率分量的特点和相互关系。
常用的频谱分析方法有功率谱密度估计、谱系分析、半对数谱等。
1. 功率谱密度估计功率谱密度估计是分析信号的功率在不同频率上的分布情况。
在Matlab中,可以使用pwelch函数进行功率谱密度估计。
例如,对于一个长度为N的时域信号x,在Matlab中可以使用[Pxx, f] = pwelch(x)来计算其功率谱密度。
得到的Pxx是功率谱密度估计结果,f是对应的频率向量。
2. 谱系分析谱系分析是研究信号频谱在时间和频率上的变化规律。
如何利用Matlab技术进行频域分析

如何利用Matlab技术进行频域分析MATLAB是一种功能强大的数学软件,被广泛应用于科学研究和工程领域。
其中的频域分析功能被广泛用于信号处理、图像处理、音频处理等领域。
本文将介绍如何利用MATLAB技术进行频域分析,以及常用的频域分析方法和技巧。
一、频域分析的基本概念在开始介绍如何利用MATLAB进行频域分析之前,我们先来了解一下频域分析的基本概念。
频域分析是指将信号从时域(时间域)转换到频域(频率域),以便更好地理解信号的频谱特性。
频域分析的基本原理是傅里叶变换。
傅里叶变换是将一个信号分解成一系列正弦函数和余弦函数的和,通过这种方式可以清晰地看到信号的频谱成分。
MATLAB中提供了多种傅里叶变换的函数,比如fft、ifft等,可以快速、方便地进行频域分析。
二、MATLAB中的频域分析函数MATLAB中提供了多种用于频域分析的函数,包括快速傅里叶变换(FFT)、离散傅里叶变换(DFT)、傅里叶逆变换(IFFT)等。
1. 快速傅里叶变换(FFT)快速傅里叶变换是一种将离散信号转换为频域表示的快速方法。
在MATLAB 中,可以使用fft函数进行快速傅里叶变换,如下所示:```MATLABX = fft(x);```其中,x为输入信号,X为傅里叶变换后的结果。
通过快速傅里叶变换,可以将信号从时域转换到频域,得到信号的频谱信息。
2. 离散傅里叶变换(DFT)离散傅里叶变换是一种将离散信号转换为频域表示的方法。
在MATLAB中,可以使用dft函数进行离散傅里叶变换,如下所示:```MATLABX = dft(x);```其中,x为输入信号,X为傅里叶变换后的结果。
3. 傅里叶逆变换(IFFT)傅里叶逆变换是一种将频域信号转换回时域信号的方法。
在MATLAB中,可以使用ifft函数进行傅里叶逆变换,如下所示:```MATLABx = ifft(X);```其中,X为输入的频域信号,x为傅里叶逆变换后的结果。
实验六Matlab频域分析
实验六 MATLAB 频域分析5.1 频率特性的概念系统的频率响应是在正弦信号作用下系统的稳态输出响应。
对于线性定常系统,在正弦信号作用下,稳态输出是与输入同频率的正弦信号,仅是幅值和相位不同。
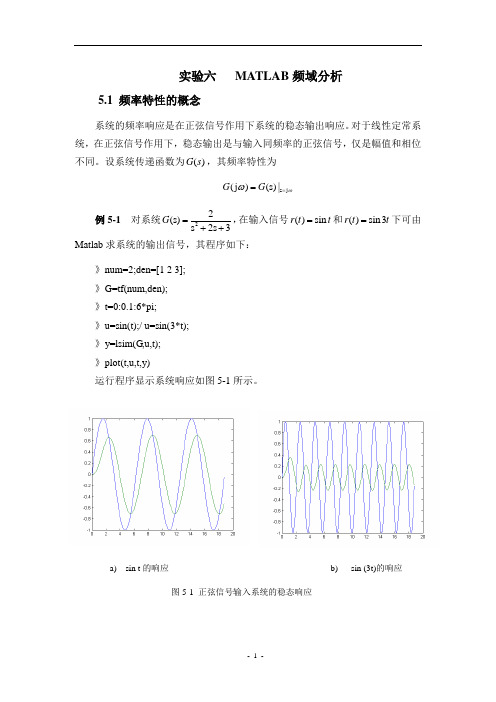
设系统传递函数为()G s ,其频率特性为s j (j )(s)|G G ωω==例5-1 对系统22(s)s 2s 3G =++,在输入信号()sin r t t =和()sin3r t t =下可由Matlab 求系统的输出信号,其程序如下:》num=2;den=[1 2 3]; 》G=tf(num,den); 》t=0:0.1:6*pi; 》u=sin(t);/ u=sin(3*t); 》y=lsim(G ,u,t); 》plot(t,u,t,y)运行程序显示系统响应如图5-1所示。
a) sin t 的响应 b) sin (3t)的响应 图5-1 正弦信号输入系统的稳态响应5.2用()nyquist sys 绘制极坐标图频率特性中的奈奎斯特图是奈奎斯特(Nyquist )稳定性判据的基础。
反馈控制系统稳定的充分必要条件为:奈奎斯特曲线逆时针包围(1,0)j -点的次数等于系统开环右极点个数。
调用Matlab 中nyquist() 函数可绘出奈奎斯特图,其调用格式为:,,[re im ω]=nyquist(num,den,ω)或sys =tf(num,den);nyquist(sys)式中,()/G s num den =;ω为用户提供的频率范围;re 为极坐标的实部;im 为极坐标的虚部。
若不指定频率范围,则为nyquist(num,den)。
在输入指令中,如果缺省了左边的参数说明,奈奎斯特函数将直接生成奈奎斯特图;当命令包含左端变量时,即[re,im,ω]=nyquist(num,den)时,则奈奎斯特函数将只计算频率响应的实部和虚部,并将计算结果放在数据向量re 和im 中。
在此情况下,只有调用plot 函数和向量re 、im ,才能生成奈奎斯特图。
如何使用Matlab进行频域分析与滤波处理

如何使用Matlab进行频域分析与滤波处理引言:MATLAB是一种功能强大的数值计算和数据分析工具,广泛应用于各个领域,包括信号处理。
频域分析和滤波处理是信号处理中重要的内容之一,本文将介绍如何使用MATLAB进行频域分析和滤波处理。
一、频域分析的基本概念频域分析是将信号从时域转换到频域的过程,通过分析信号在频率上的分布情况,可以获取信号的频谱信息。
常用的频域分析方法有傅里叶变换和功率谱分析。
1.1 傅里叶变换傅里叶变换是时域信号与频域信号之间的转换关系,将一个信号表示为振幅和相位的频谱形式。
在MATLAB中,可以使用fft函数进行傅里叶变换。
例如,对一个时域信号x进行傅里叶变换,可以使用以下代码:```matlabX = fft(x);```1.2 功率谱分析功率谱分析是对信号在频域上能量分布的分析,通过计算信号的功率谱密度,可以了解信号在不同频率下的能量分布情况。
在MATLAB中,可以使用pwelch函数进行功率谱分析。
例如,对一个时域信号x进行功率谱分析,可以使用以下代码:```matlab[P,F] = pwelch(x,[],[],[],Fs);```二、频域滤波的基本原理频域滤波是通过改变信号在频域上的能量分布情况,来实现对信号的滤波处理。
常用的频域滤波方法包括低通滤波、高通滤波、带通滤波和带阻滤波。
2.1 低通滤波低通滤波是用来去除信号中高频成分,只保留低频成分的滤波方法。
在MATLAB中,可以使用fir1函数设计一个低通滤波器,并使用filter函数进行滤波处理。
例如,设计一个截止频率为100Hz的低通滤波器对信号x进行滤波:```matlabFs = 1000; % 采样率Fc = 100; % 截止频率order = 50; % 滤波器阶数b = fir1(order,Fc/(Fs/2),'low');y = filter(b,1,x);```2.2 高通滤波高通滤波是用来去除信号中低频成分,只保留高频成分的滤波方法。
实验六连续信号与系统的复频域分析及matlab实现

实验六连续信号与系统的复频域分析及matlab实现实验目的:(1)掌握连续系统及信号拉普拉斯变换概念(2)掌握利用MATLAB绘制系统三维曲面图的方法(3)掌握利用MATLAB求解拉普拉斯逆变换的方法实验内容:12.1程序:(1):f1=(1-exp(-2.5*t))*heaviside(t)syms tf1=(1-exp(-2.5*t))*heaviside(t);F1=laplace(f1);F1F1 =1/s - 1/(s + 5/2)(2): f2=t^2*exp(-2*t)*heaviside(t)syms tf2=t^2*exp(-2*t)*heaviside(t);F2=laplace(f2);F2F2 =2/(s + 2)^3(3): f3=(3*sin((pi/2)*t-(pi/4)))*heaviside(t)syms tf3=(3*sin((pi/2)*t-(pi/4)))*heaviside(t);F3=laplace(f3);F3F3 =(3*2^(1/2)*pi)/(4*(s^2 + pi^2/4)) - (3*2^(1/2)*s)/(2*(s^2 + pi^2/4))12.2程序:(1):F=(s+2)/(s^2+6*s+8)sym s;L=sym('(s+2)/(s^2+6*s+8)');F=ilaplace(L)F =exp(-4*t)(2):F=1/(s^2*(s+1))sym s;L=sym('1/(s^2*(s+1))');F=ilaplace(L)F =t + exp(-t) - 112.4程序:(2):a=-5:0.1:5;b=-4:0.08:4;[a,b]=meshgrid(a,b);t=a+i*b;F=abs(cos(pi*t)*(heaviside(t)-heaviside(t-2))); mesh(a,b,F);surf(a,b,F);colormap(hsv);title('cos(pi*t)[u(t)-u(t-2)]的拉氏变换曲面图');实验小结:通过实验我掌握了利用MATLAB绘制系统三维曲面图的方法,掌握了利用MATLAB求解拉普拉斯逆变换的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六 MATLAB 频域分析5.1 频率特性的概念系统的频率响应是在正弦信号作用下系统的稳态输出响应。
对于线性定常系统,在正弦信号作用下,稳态输出是与输入同频率的正弦信号,仅是幅值和相位不同。
设系统传递函数为()G s ,其频率特性为s j (j )(s)|G G ωω==例5-1 对系统22(s)s 2s 3G =++,在输入信号()sin r t t =和()sin3r t t =下可由Matlab 求系统的输出信号,其程序如下:》num=2;den=[1 2 3]; 》G=tf(num,den); 》t=0:0.1:6*pi; 》u=sin(t);/ u=sin(3*t); 》y=lsim(G ,u,t); 》plot(t,u,t,y)运行程序显示系统响应如图5-1所示。
a) sin t 的响应 b) sin (3t)的响应 图5-1 正弦信号输入系统的稳态响应5.2用()nyquist sys 绘制极坐标图频率特性中的奈奎斯特图是奈奎斯特(Nyquist )稳定性判据的基础。
反馈控制系统稳定的充分必要条件为:奈奎斯特曲线逆时针包围(1,0)j -点的次数等于系统开环右极点个数。
调用Matlab 中nyquist() 函数可绘出奈奎斯特图,其调用格式为:,,[re im ω]=nyquist(num,den,ω)或sys =tf(num,den);nyquist(sys)式中,()/G s num den =;ω为用户提供的频率范围;re 为极坐标的实部;im 为极坐标的虚部。
若不指定频率范围,则为nyquist(num,den)。
在输入指令中,如果缺省了左边的参数说明,奈奎斯特函数将直接生成奈奎斯特图;当命令包含左端变量时,即[re,im,ω]=nyquist(num,den)时,则奈奎斯特函数将只计算频率响应的实部和虚部,并将计算结果放在数据向量re 和im 中。
在此情况下,只有调用plot 函数和向量re 、im ,才能生成奈奎斯特图。
例5-2 设系统的传递函数为21G(s)s 2s 2=++,绘制其奈奎斯特图。
解 程序如下: 》num=[1];den=[1,2,2]; 》nyquist(num,den)运行程序,显示奈奎斯特曲线如图5-2所示。
图5-2 奈奎斯特曲线值得注意的是,由于nyquist ()函数自动生成的坐标尺度固定不变,nyquist ()函数可能会生成异常的奈奎斯特图,也可能会丢失一些重要的信息。
在这种情况下,为了重点关注奈奎斯特图在点(-1,j0)附近的形状,着重分析系统的稳定性,需要首先调用轴函数axis(),自行定义坐标轴的显示尺度,以提高图形的分辨率;或用放大镜工具放大,以便进行稳定性分析。
例5-3 设某系统的传递函数为321000G(s)s 8s 17s 10=+++,则绘制其奈奎斯特图的程序如下:》num=[1000];den=[1,8,17,10]; 》nyquist (num,den);grid 或num=[1000];den=[1,8,17,10]; sys=tf(num,den); nyquist (sys); grid运行程序,显示奈奎斯特曲线如图5-3 a)所示。
可以看出在点(-1,j0)附近,奈奎斯特图很不清楚,可利用放大镜对得出的奈奎斯特图进行局部放大,或利用如下Matlab 命令》v=[-10,0,-1.5,1.5];》axis(v)a) b)图5-3 奈奎斯特局部图例5-4 设某系统的开环传递函数为2210(s 2)(s)(s 1)(s 2s 9)G +=+-+则绘制其奈奎斯特图的程序如下:》num=10*[1, 4, 4]; 》den=conv([1, 1],[1, -2,9]); 》nyquist (num,den); 》grid 或num=10*[1,4,4];》den=conv([1,1],[1,-2,9]); sys=tf(num,den); nyquist (sys); grid运行程序,显示得图5-4 a)。
若规定实轴、虚轴范围(10,10),(-10,10),则绘制其奈奎斯特图的程序如下: 》num=10*[1 4 4]; den=conv([1 1],[1 -2 9]); 》nyquist (num,den); 》axis([-10,10,-10,10]) 运行程序,显示得图5-4 b)。
a )b )图 5-4 奈奎斯特曲线5.3 用bode(sys)画对数坐标图伯德图由对数幅频和对数相频两张图构成,ω轴采用对数分度,幅值为对数增益即分贝(dB ),相位()ϕω为线性分度。
Matlab 中绘制伯德图的函数为bode( ),其调用格式为[mag,phase,w]=bode(num,den,w) 或 sys=tf(num,den); bode(sys)式中,G(s)=num/den ,频率ω自动选择范围从0.11000/rad s ωω==到,若自行选择频率范围,可应用logspace()函数,其格式为ω=logspace(a,b,n)式中,a 表示最小频率10a ,b 表示最大频率10b ,n 表示10a ~10b 之间频率点数。
例5-5 设某系统的传递函数为225(0.1s 1)(s)10.6s(0.5s 1)(s s 1)5050G +=+++,则绘制其伯德图的Matlab 程序如下:>> num=5*[0.1 1];>> den=conv([1 0],conv([0.5 1],[1/2500 0.6/50 1])); >> bode(num,den)-150-100-50M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/sec)函数log (,,)space a b n ω= 的应用。
程序如下:>> w=logspace(-1,4,300); %确定频率范围及点数 >> [mag,phase,w]=bode(num,den,w);>> semilogx(w,20*log(mag));grid %绘图坐标及大小 >> xlabel('Frequency[rad/s]'),ylabel('20*log(mag)')101010101010-400-350-300-250-200-150-100-50050100Frequency[rad/s]20*l o g (m a g )图5-6 伯德图5.4 用margin (sys )计算增益裕量和相位裕量Matlab 中采用裕量函数 margin ()来确定相对稳定性,其调用格式为 [Gm,Pm, Wcg, Wcp]=margin(sys) 或 margin(sys)式中,Gm 为增益裕量;Pm 为相为裕量;Wcg 为相角穿越频率;Wcp 为幅值穿越频率。
在输入指令中,如果缺省了左边的参数说明,margin ()函数将在伯德图上自动标注系统的增益裕量和相位裕量.例5-7 设某系统的传递函数为 0.5s 2s s 0.8s)G 23+++=(,则计算其增益裕量和相位裕量的程序如下:>> num=[0.8];den=[1 2 1 0.5]; >> sys=tf(num,den);>> margin(sys)执行程序,显示该系统的伯德图及相对稳定裕度如图5-7所示。
M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramGm = 5.47 dB (at 1 rad/sec) , P m = 21.9 deg (at 0.788 rad/sec)Frequency (rad/sec)图5-7 例5-7中系统的伯德图及相对稳定裕度若执行[Gm,Pm, Wcg, Wcp]=margin(sys)则可得Gm = 1.8772,Pm = 21.9176,Wcg = 1.0004,Wcp = 0.7881 纯滞后环节的表示 Sys.iodelay=0.1; Margin(sys);闭环系统带宽、谐振峰值、谐振频率 >> BW=bandwidth(sys) 作业:MP8.1 用MATLAB 绘制()22525T s s s =++的Bode 图,并验证其谐振频率为5/rad s ,谐振峰值为14dB 。
>> num=[25];den=[1 1 25]; sys=tf(num,den); bode(sys) >> BW=bandwidth(sys),运行结果 BW = 7.711210101010-180-135-90-450P h a s e (d e g )Frequency (rad/sec)-60-40-2020M a g n i t u d e (d B )MP8.2先手工绘制下列传递函数的Bode 图,然后用MATLAB 加以验证。
(a) ()()()1110G s s s =++(b) ()()()10120s G s s s +=++(c) ()21250G s s s =++ (d) ()()()2511250s G s s s s +=+++MP8.3某单位负反馈系统的开环传递函数为:()()252G s s s =+用MATLAB 绘制闭环系统的Bode 图,根据Bode 图估计闭环带宽,并在图上标注所得结果。
MP8.4某2阶系统框图如图MP8.4所示,图MP8.4 2阶反馈控制系统(a) 在0.1ω=到1000/rad s ω=之间,用logspace 函数生成系统闭环Bode 图。
根据该Bode 图,估计系统的谐振峰值M p M 、谐振频率r ω、和带宽B ω;(b) 用图8.11估算系统的阻尼系数ζ和固有频率n ω;(c) 根据闭环传递函数计算ζ和n ω的精确值,并与(b)的结果作比较。
MP8. 5考虑图MP8.5给出的闭环反馈系统,用MATLAB 绘制系统的开环和闭环Bode 图。
图MP8.5 闭环反馈系统MP9.1某单位负反馈系统的开环传递函数为()()2100/410G s s s =++,试用MATLAB 程序验证:该系统的增益裕度为∞,相角裕度为24o。
MP9.2 用nyquist 函数绘制下列传递函数的Nyquist 。
(a) ()11G s s =+ (b) ()21585G s s s =++(c) ()3210331G s s s s =+++MP9.4 考虑某单位负反馈控制系统,其开环传递函数为:()1TsKe G s s -=+ (a)当T=0.1s 时,利用margin 函数,确定使相角裕度为45o的K 的取值; (b)利用所得的增益K ,在00.2T s ≤≤的范围内,画出相角裕度与T 的关系曲线。
