五年级数学寒假讲义
【寒假讲义】温故知新篇03《倍数与因数》—2020-2021学年五年级数学上册寒假学习精编讲义

2020-2021学年北师大版五年级数学上册寒假学习精编讲义温故知新篇03 倍数与因数一.选择题1.(2020秋•南丹县期中)一个数是9的倍数,这个数一定是( )的倍数.A .3B .5C .62.(2018秋•深圳期末)一个数,它既是12的倍数,又是12的因数,这个数是( )A .6B .12C .24D .1443.(2019•连江县)和奇数K 相邻的两个奇数是( )A .1K -和1K +B .1K -和3K +C .2K -和2K +D .3K -和3K +4.自然数按是不是2的倍数来分,可以分为( )A .奇数和偶数B .素数和合数C .素数、合数、0和15.(2018春•漳平市校级期末)从0、1、4、5这四个数字中选择三个不同的数字,组成既是3的倍数,又是2的倍数的三位教,有( )种不同的组法.A .2B .3C .4D .5 6.(2015春•昭通月考)自然数(0除外)按因数的个数分,可以分为( )A .奇数和偶数B .质数和合数C .质数、合数和1二.填空题7.(2020秋•临漳县期中)一个数的最大因数是56,这个数是 ;一个数的最小倍数是18,这个数是 。
8.(2020•石阡县)用1,0,8三个数字组成三位数,其中能被2整除的最大数是 ;能被3整除的最小数是 ;能被2,3,5整除的数是 .9.(2019•长沙)一个分数,分子是最小的质数,分母是20以内的最大的奇数,这个分数是 .10.(2020•长沙)我是一个两位数,十位数字是最小的合数,个位数字是最小的质数,我是 .11.(2016•长沙模拟)自然数1~9中,最小的质数、最小的合数、最大的质数、最大的合数这四个数的和是.12.(2014秋•温江区期中)两个质数相加的和为49,这两个数的积是.13.(2015春•东胜区期中)猜猜我是谁.(1)我是6的倍数,又是4的倍数,别忘了我还是12的因数.(2)我们两个的和是6,积是8,质数是,合数是.(3)我们两个的和是18,积是77,这两个质数分别是和.(4)我们两个的和是20,差是6,这两个质数分别是和.14.(2013秋•射洪县校级期中)在乘法运算中积是100,如果一个因数扩大20倍,另一个因数缩小10倍,积是.三.判断题15.(2019秋•高平市期末)自然数中,最小的质数与最小的合数相差2..(判断对错)16.(2020秋•高台县期中)偶数都是合数,奇数都是质数(判断对错)17.(2020•洛阳)两个质数相乘的积一定是偶数.(判断对错)18.(2016春•未央区期末)相邻的两个自然数的积一定是偶数..(判断对错)19.一个数既是12的因数,又是12的倍数,那么这个数一定是12.(判断对错)四.计算题20.写出下面各数的因数.25 12 49 36.五.应用题21.(2020秋•新丰县期中)幼儿园大班有一些小朋友(多于10人,且少于40人),李老师拿了48颗糖平均分给他们,正好分完,小朋友的人数可能是多少?22.龙一鸣和壮壮玩抽数字卡片游戏,有意思的是,一次两人抽出卡片上的数都是质数,且两个数的和是奇数,还是小于50的7的倍数.这两个质数的积可能是多少?23.某电影院的座位号码是单号与单号相邻,双号与双号相邻.(1)一个人拿了三张座位相邻的电影票,这三个座位号码相加之和等于15,这三个座位分别是多少号?(2)若三张座位相邻的电影票的座位号码相加之和等于36,这三个座位分别是多少号?六.解答题24.(2020秋•成都期中)小明、小红、小刚三人的年龄正好是三个连续的偶数,他们的年龄总和是48岁,他们中最小的是多少岁?最大的是多少岁?25.(2019春•罗平县校级期中)两个质数的和是18,积是65,这两个质数分别是多少?26.(2019春•兴仁市月考)五(1)班6名同学去给小树苗浇水,小树苗不到30棵,他们发现每人浇水棵数相同,这批小树苗可能有多少棵?27.(2019春•洪泽区校级期中)三个连续偶数的和是72,这三个数分别是多少?28.(2019秋•惠城区校级期中)按要求写数.24的因数有:50以内6的倍数有:29.(2016秋•惠济区校级期中)三个相邻偶数的和是84,这三个偶数分别是多少?30.(2019秋•定西期中)小明家有三种塑料桶,分别是5千克装,10千克装,2千克装.小明妈妈买回75千克豆油,选哪种塑料桶装能正好把豆油装完?需这样的桶多少个?31.(2016春•克州校级期中)一个人说大于2的偶数,另一个人说两个质数,这两个质数的和等于第一个人说的偶数,你能写这样的三组吗?如:偶数10;两个质数3和7;3710+=写三组:参考答案与试题解析一.选择题1.【解答】解:因为9是3倍数,所以一个数是9的倍数,这个数一定是3的倍数。
五年级奥数寒假讲义
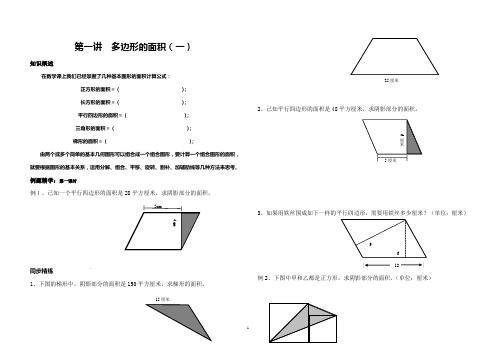
第一讲多边形的面积(一)知识概述在数学课上我们已经掌握了几种基本图形的面积计算公式:正方形的面积=();长方形的面积=();平行四边形的面积=();三角形的面积=();梯形的面积=();由两个或多个简单的基本几何图形可以组合成一个组合图形,要计算一个组合图形的面积,就要根据图形的基本关系,运用分解、组合、平移、旋转、割补、加辅助线等几种方法来思考。
例题精学:第一课时例1、已知一个平行四边形的面积是28平方厘米,求阴影部分的面积。
同步精练1、下图的梯形中,阴影部分的面积是150平方厘米,求梯形的面积。
2、已知平行四边形的面积是48平方厘米,求阴影部分的面积。
3、如果用铁丝围成如下一样的平行四边形,需要用铁丝多少厘米?(单位:厘米)| 12|例2、下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)5cm4cm 15厘米25厘米5厘米6厘米96 6 4甲乙同步精练1、求右图中阴影部分的面积。
(单位:厘米)2、求右图中的阴影部分的面积。
(单位:厘米)3、如图所示,四边形ABCD 是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
例题精学 第二课时:例3、如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
同步精练1、四边形ABCD 是一个长为10厘米,宽为6厘米的长方形,三角形ADE 的面积比三角形CEF 的面积大10平方厘米。
求CF 的长是多少厘米?4厘米3厘米DCAB8厘米5厘米甲A 乙 CB EDF4 厘米 4厘米FEADC B2、平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长为8厘米,已知阴影部分三角形ABG 和三角形CDF 的面积和比三角形EFG 的面积大10平方厘米。
求CF 的长。
3、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,求: (1)三角形DEF 的面积; (2)CF 的长。
例4、两条对角线把梯形ABCD 分割成四个三角形。
小学数学五年级思维奥数寒假讲义-第8讲 牛吃草问题进阶(学生版)

第8讲牛吃草问题进阶【知识梳理】1、英国科学家牛顿在他的《普通算术》一书中,有一道关于牛在牧场上吃草的问题,即牛在牧场上吃草,牧场上的草在不断的、均匀的生长。
后人把这类问题称为牛吃草问题或叫做“牛顿问题”。
2、“牛吃草”问题主要涉及三个量:草的数量、牛的头数、时间.难点在于随着时间的增长,草也在按不变的速度均匀生长,所以草的总量不定。
“牛吃草”问题是小学应用题中的难点。
3、解“牛吃草”问题的主要依据:草的每天生长量不变每头牛每天的食草量不变草的总量=草场原有的草量+新生的草量,其中草场原有的草量是一个固定值新生的草量=每天生长量⨯天数4、同一片牧场中的“牛吃草”问题,一般的解法可总结为:⑴设定1头牛1天吃草量为“1”⑵草的生长速度=(对应牛的头数⨯较多天数-对应牛的头数⨯较少天数)÷(较多天数-较少天数)⑶原来的草量=对应牛的头数⨯吃的天数-草的生长速度⨯吃的天数⑷吃的天数=原来的草量÷(牛的头数-草的生长速度)⑸牛的头数=原来的草量÷吃的天数+草的生长速度5、“牛吃草”问题有很多的变例,像抽水问题、检票口检票问题等等,只有理解了“牛吃草”问题的本质和解题思路,才能以不变应万变,轻松解决此类问题。
【典例精讲】一牧场长满青草,27头牛6个星期可以吃完,或者23头牛9个星期可以吃完。
若是21头牛,要几个星期才可以吃完?(注:牧场的草每天都在生长)牧场上长满牧草,每天牧草都匀速生长.这片牧场可供10头牛吃20天,可供15头牛吃10天.供25头牛可吃几天?由于天气逐渐变冷,牧场上的草每天以均匀的速度减少.经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天.那么,可供11头牛吃几天?由于天气逐渐冷起来,牧场上的草不仅不长,反而以固定的速度在减少。
如果某块草地上的草可供25头牛吃4天,或可供16头牛吃6天,那么可供10头牛吃多少天?一水库原有存水量一定,河水每天均匀入库.5台抽水机连续20天可抽干;6台同样的抽水机连续15天可抽干.若要求6天抽干,需要多少台同样的抽水机?北京密云水库建有10个泄洪洞,现在水库的水位已经超过安全线,并且水量还在以一个不变的速度增加,为了防洪,需要调节泄洪的速度,假设每个闸门泄洪的速度相同,经测算,若打开一个泄洪闸,30个小时以后水位降至安全线;若同时打开两个泄洪闸,10个小时后水位降至安全线.根据抗洪形势,需要用2个小时使水位降至安全线以下,则至少需要同时打开泄洪闸的数目为多少个?画展8:30开门,但早有人来排队入场,从第一个观众来到时起,若每分钟来的观众一样多,如果开3个入场口,9点就不再有人排队;如果开5个入场口,8点45分就没有人排队。
小学五年级基础寒假班教案(整理18讲)

目录第一讲:数的认识(一) (2)第二讲:数的认识(二) (5)第三讲:三角形和四边形的面积 (9)第四讲:组合图形的面积(一) (14)第五讲:组合图形的面积(二) (19)第六讲:混合面积计算(一) (24)第七讲:混合面积计算(二) (29)第八讲一般应用题(一) (33)第九讲:小数的巧算 (36)第十讲:周期问题(一) (44)第十一讲:周期问题(二) (48)第十二讲:质数与合数 (51)第十五讲:单位换算 (51)第十六讲:数学与交通(一)(旅游费用) (55)第十七讲:数学与交通(二)(相遇) (60)第十八讲:一般应用题(二) (63)第一讲:数的认识(一)【专题分析】整数:象–3、–2、–1、0、1、2、3,……这样的数都是整数 自然数:象0、1,2,3……这样的数都是自然数。
倍数与因数:如果数a 能被数b (b ≠0)整除,a 就叫做b 的倍数,b 就叫做a 的约数(或a 的因数)。
倍数和约数是相互依存的。
因为35能被7整除,所以35是7的倍数,7是35的约数。
一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
偶数与奇数:2的倍数的数叫偶数,不是2的倍数的数叫奇数。
自然数按能否被2 整除的特征可分为奇数和偶数。
2、3、5、9的倍数特征 :个位上是0、2、4、6、8的数,都能被2整除。
个位上是0或5的数,都能被5整除。
一个数的各位上的数的和能被3整除,这个数就能被3整除。
一个数各位数上的和能被9整除,这个数就能被9整除。
能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除。
【典型例题】一、填空题:1、把下面各数填入合适的圈里。
-4 11 360 32 0 7.3 1998 -213 自然数:( )整数: ( )2、25⨯3=75。
( )是( )和( )的倍数,( )和( )是( )的因数。
寒假衔接五年级数学讲义

第一讲小数乘法一、教学目标(1)复习小数乘整数,掌握小数乘整数的竖式计算要点,能正确地进行笔算。
(2)复习小数乘小数,掌握小数乘法中积的小数点位置的确定方法。
(3)会用“四舍五入”法截取积是小数的近似值。
(4)掌握连乘、乘加、乘减的运算顺序,提高小数混合运算能力。
二、例题探究例1计算:0.47×9 = 4.230. 4 7――――〉扩大到它的100倍――――――〉 4 7×9 ×9------------------------------4. 2 3〈――――缩小到它的100倍〈――――――4 2 3在乘法算式中,因数扩大多少倍,积缩小相同的倍数,等于不扩大不缩小。
对比观察发现0. 4 7…………………………两位小数×9 积中的小数位数和因数中的小数位-----------数相同4. 2 3………………………….两位小数方法总结:计算小数乘整数时,先按照整数乘法的计算法则算出积,然后看因数中有几位小数,就从积的右边起数出几位,点上小数点。
例2计算:3.35×18 =60.33. 3 5× 1 8----------------2 6 8 03 3 5-------------------计算后要先点上小数点,再将小数末尾的0用斜线划去。
6 0. 3 0方法总结:在计算出小数乘整数的乘积后,如果积的末尾有0,应先点上小数点,然后根据小数的基本性质把小数末尾的0去掉,切不可先去掉末尾的0,再点小数点。
例3计算4.7×2.8 0.38×0.084.7………………一位小数0.38…………….两位小数×2.8………………一位小数×0.08…………….两位小数--------------------------3 7 6 0.03 0 4…………….四位小数9 4-------------13.16…………….两位小数方法总结:小数乘小数先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
五年级数学 寒假讲义(7讲)

目录第1讲多边形的面积 (2)第2讲因数与倍数 (9)第3讲质数与合数 (16)第4讲分数的认识 (23)第5讲2、3、5的倍数特征 (29)第6讲流水行船 (35)第7讲期末闯关 (41)第1讲多边形的面积1. 复习平行四边形、三角形、梯形面积公式.2. 选用合理灵活的计算方法,简便运算过程,化繁为简,化难为易,使计算又快又准确.21. 割补法:将不规则的组合图形经过分割(用连线分割)、切拼、拼合后,转化成一个规则的几何图形,从而交易求得面积的方法,就是割补法求面积.2.图形变换:图形变换指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),利用模型,构成新的图形.例题1: 如图,平行四边形ABCD中,AD的长度为20厘米,高CH的长度为9厘米,.那么两个阴影三角形面积之和为多少平方厘米?H B DAE CF练习1: 如图,平行四边形ABCD中,AD的长度为30厘米,高CE的长度为8厘米,.那么阴影三角形面积为多少平方厘米?例题2: 如图,用两块长方形和一块正方形拼成了一个大正方形,其中一块小正方形的面积是36平方厘米,一块长方形的面积是48平方厘米,那么最后拼成的大正方形的面积是多少平方厘米?练习2: 如图,一个大正方形被分割成4份,其中左上和右下两个正方形的面积分别为9平方厘米和36平方厘米,求大正方形的面积..例题3:如图,ABCD 是边长为 4 厘米的正方形,CGFE 是长方形,CE 等于7 厘米.已知BCFH是平行四边形,则BCFH 的面积是________平方厘米.练习3: 如图,BCDG 是边长为 5 厘米的正方形,AGFE 是长方形,AE 等于9 厘米.已知DCFE是平行四边形,则DCFE 的面积是________平方厘米.4例题4: 如图,三角形ABC中,DC=2BD,CE=3AE,三角形ADE的面积是20平方厘米,三角形ABC的面积是多少?练习4: 三角形ABC中,BD=3DC,且三角形ABC的面积为48平方厘米,求三角形ABD的面积.例题5: 如图,已知平行四边形ABCD 的面积为36,三角形AOD 面积为8.求三角形BOC 面积.思考: 如图,有大中小三个正方形,边长分别为3、2、1 厘米,求阴影三角形的面积.61.如图,ABCD 和BEFC 都是长方形,AE=4 厘米,EF=3 厘米,问图中阴影面积是多少.2. 如图,三角形ABC 中,BD=6,DC=3,AE=4,EC=2,若三角形DEC 的面积是3,那么三角形ABC 的面积是多少?6.07-1.69= 8.2+1.8= 100-35.22= 12.6-0.9= 2.5×0.4= 48+1.6= 2.4×5= 1.1×40=0.22×4= 2.2×6=0.9-0.52= 138-8.9= 3.99×1= 0.35÷0.1=0×3.52= 75.35-23.04= 2.5÷5= 4.007-0.09= 8.4÷7= 8.2+1.8= 0.34÷17= 100-35.22= 2.5÷0.5= 2.5×0.4= 5.00+6.13= 2.4×5=8.24-7.63= 0.22×4=5.21+5.49= 0.9-0.52= 40×0.25= 3.99×1=4×0.4= 0×3.52=7.5÷0.25= 2.5÷5=4.2÷0.7= 8.4÷7=4.5×2= 0.34÷17= 7.8+0.22= 2.5÷0.5=8第2讲因数与倍数1. 学生掌握找一个数的因数和一个数的倍数的方法.2. 学生能了解一个数的因数是有限的,倍数是无限的;能熟练的找一个数的因数和倍数.1. 因数与倍数的意义:在整数除法的算式中,如果商是整数并且没有余数,则被除数是除数的和商的倍数,除数和商是被除数的因数.2. 因数与倍数的依存性: 因数与倍数不能单独存在,不能说谁是倍数,谁是因数,应该说谁是谁的倍数,谁是谁的因数.3.倍数与几倍的关系:例题1: 判断题.(1) 42÷6=7,所以42是6的倍数,6是42的因数. ( )(2)42÷6=7,所以42是倍数,6是因数. ( )(3)42÷9=4``````6,所以42是9的倍数,9是42的因数. ( )(4) 4.2÷0.6=7,所以4.2是0.6的倍数,0.6是4.2的因数. ( )(5) 4.2÷0.6=7,所以4.2是0.6的7倍. ( )练习1: 填空.(1) 根据12 ÷ 3 = 4请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(2) 根据6 × 4 = 24请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(3) 如果一个数的最小倍数和最小因数的差是10,那么这个数的最大因数是( ).例题2: 18的因数有哪些?练习2: 请找出30和36的因数.10例题3: 五年级(1)班的36名同学进行文艺汇演,表演的时候全班排成长方形方阵(包括正方形)如果规定每行每列不得少于3人,那么一共有几种排法?练习3: 大熊家有一盒糖果,共56颗糖,熊妈妈规定,大熊每天可以吃相同数量的糖果,但是不允许一天吃完,那么大熊一共有多少种吃法?每种吃法对应吃多少天?每天吃多少个?例题4: 小雅妈妈买来一些苹果,小雅发现,无论自己是2个2个数、3个3个数、4个4个数、5个5个数,都恰好数完,如果苹果的数量在55~65之间,那么妈妈一共买回来多少个苹果?练习4: 呆呆熊买了糖果若干,呆呆熊发现如果每天吃5颗糖,恰好可以整数天吃完,如果每天吃7颗糖,也恰好可以整数天吃完,如果糖果的数量不超过50颗,那么呆呆熊买了多少颗糖?例题5: 小聪练习俯卧撑,如果小聪做俯卧撑的总数是100以内9的倍数,并且它还有因数5,那么小聪可能做了多少个俯卧撑?练习5: 呆呆熊去采野花,采的野花数是50以内7的倍数,并且它还有因数4,那么呆呆熊采了多少朵野花?121. 根据100 ÷ 20 = 5回答,20和5都是( )的因数.2. 根据5 ×8 = 40回答,5和( )是40的因数.3. 如果一个数的最大因数和最小倍数都是27,那么这个数是( ).4. 顽皮猴家有一盒糖果,共28颗糖,熊妈妈规定,大熊每天可以吃相同数量的糖果,但是不允许一天吃完,那么大熊一共有多少种吃法?2.6×3= 48+1.6= 4.1×2= 80×25=0.35×0.2= 1-0.93=0.25÷40= 1.25×100= 50÷1000= 5.6+99= 45.03+0.52= 40100÷25= 14.1-10.02= 90-0.9=5.6÷0.8= 51÷0.001= 5.6÷1.4= 35×0.001= 0.48÷0.8= 54÷0.1=4.4÷0.11= 54×0.1=1.1×40= 8.2+1.8=2.2×6= 100-35.22= 138-8.9= 2.5×0.4= 0.35÷0.1= 2.4×5=0.36×0.01= 0.22×4= 75.35-23.04= 0.9-0.52= 4.007-0.09= 3.99×1=17÷1000= 0×3.52=0.56+0.4= 20÷0.1=14第3讲质数与合数1. 使学生理解质数合数的意义,会判断一个数是质数还是合数.2. 能够熟练判断质数合数,能够找到100以内的质数.一、定义质数:一个数,如果只有1和它本身两个因数,这个数叫做质数(或素数). 合数:一个数,如果除了1和它本身以外还有别的因数,这个数叫做合数. 1既不是质数,也不是合数.二、100以内的质数例题1: 填空.(1)自然数1~20中,最小的合数是_____ ,最小奇数是_____ ,是偶数又是质数的是_____ ,是奇数又是合数的是_____.(2)用排除法找出20以内的质数: _____ .练习1:判断.(1)3的倍数一定是合数_____(2)所有的偶数一定是合数_____(3)所有的奇数都是质数_____(4)有的质数都是奇数_____(5)11的因数都是质数_____例题2: 填空.(1) 在1、2、3、13、27、53、49、80这八个数中,_____是质数,_____是合数.(2) 在自然数中,最小的质数是_____ ,最小的合数是_____.(3) 掌小萌有三张卡片,上面各印有一个数字7、8、9、从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?练习2: 自然数N是一个两位数,它是一个质数,而且N的个位数字与十位数字都是质数,这样的自然数有多少个?16例题3:(1)如果两个不同的质数相加等于26,那么这两个质数的乘积可能是多少?请全部写出.(2)如果两个不同的质数相加等于25,那么这两个质数的乘积可能是多少?请全部写出.(3)三个互不相同的质数相加,和为40,这三个质数的乘积可能是多少?请全部写出. 练习3: 如果三个互不相同的质数相加,和为52,这三个质数可能是多少?例题4: 请把下面的数分解质因数:(1)360; (2) 539 (3) 999 (4) 10101练习4: 请把下面的数分解质因数: (1) 373; (2) 12660.思考: 三个连续自然数的乘积等于39270,那么这三个数的和等于多少?181. 如果两个不同的质数相加等于19,那么这两个质数的乘积是多少?2. 请把下面的数分解质因数.260 99 873. 在自然数49,57,87,101,103,121中,质数有多少个?20÷0.1= 1×0.001=1÷20= 1÷0.001= 0.1÷20= 0.001÷1= 54÷1000= 0.001÷0.1= 25.23+0.77= 3.4-1.4= 98.54-63.45= 7.82-7.2= 30÷0.003= 2.19+9.1= 612÷6= 10.1-0.89= 12×80= 0.68+0.42= 1.5×100= 8.1-5.1= 840÷40= 0.728-0.24= 8.94-6.73= 0.8+0.18= 8.95-0.73= 0.89-0.25= 3.61-0.30= 1-0.98=7.78-5.15= 0.048+0.52= 4.68+7.10= 5×400=9.63+6.28= 19.9+11.1= 7.71-2.69= 187÷1000= 9.91-8.74= 1+3.89= 3.6÷0.3= 0.75÷0.25= 0.96÷2= 0.64÷0.8=20第4讲分数的认识1. 在学生原有分数知识基础上,使学生知道分数的产生,.理解分数的意义,知道分子、分母和分数单位的含义2. 经历认识分数意义的过程,培养学生的抽象、概括能力.一、分数的意义1. 单位1: 一个物体、一些物体等都可以看作一个整体,这个整体可以用自然数1来表示,通常把它叫做单位1.2. 分数的意义: 把一个整体(单位1)平均分成若干份,这样的一份或者几份都可以用分数表示.二、分数单位: 把单位1平均分成若干份,表示其中的1份数的数叫做分数单位.三、分数与除法的关系:(1) 当用分数表示整数除法的商时,要用除数作分母,被除数作分子;(2) 一个分数可以看作两个数相除,分子相当于除法算式中的被除数,分母相当于除数,分数线相当于除号.四、求一个数是另一个数的几分之几用除法:通常两个数相除,如果商是整数,则两数的关系用几倍来表示;如果商是小数,则两个数的关系就用几分之几表示.例题1: 根据分数的意义填一填.(1) 婴儿每天的睡眠时间约占全天的5 8把_____看作单位“1”,平均分成_____份,睡眠时间是这样的_____份.(2) 五(1)班喜欢跳绳的人数占全班人数的2 9把_____ 看作单位“1”,平均分成_____ 份,喜欢跳绳的人数是这样的_____份.练习1: 一张正方形纸,连续对折两次后展开,每份是这张纸的_____ ;如果连续对折三次之后展开,将其中的2份涂上颜色,那么未涂色部分是这张纸的_____.例题2: 填空.(1)1里面有_____ 个15,1里面有_____ 个17;(2) 59的分数单位是_____,有_____个这样的分数单位,再添上_____个这样的分数单位就刚好是1.(3) 13个115是_____,38里有_____ 个_____.练习2: 填空.(1)1116的分数单位是_____,它减去6个这样的单位,结果是_____.(2)57的分数单位是______,它加上_____个这样的分数单位就成为最小的质数.例题3: 把6米长的彩带平均分给5个小朋友,每个小朋友分到_____米,占全部彩带的_____.22练习3: 把4米长的绳子平均分成5段,每段占这根绳子的_____,每段长______米;把3千克苹果平均分成10份,每份占这些苹果的_____,每份重______千克.例题4: 五年级(1)班举行绘画比赛,一共有30人参赛,其中女生有13人,且有5名女生、7名男生获奖:(1)男生参赛人数是女生参赛人数的几倍?女生参赛人数占总参赛人数的几分之几?(2)男生获奖人数占五年级(1)班总获奖人数的几分之几?练习4: 小学举行运动,五年级(2)班一共有53人参赛,其中有30人是女生.比赛结束后,统计发现,女生有13人获奖,男生有11人获奖:(1) 女生参赛人数是男生参赛人数的几倍?男生参赛人数是总参赛人数的几分之几?(2) 女生获奖人数占五年级(2)班总获奖人数的几分之几?例题5: 小心陷阱.(1)如果把1 袋米当成一个整体的话,就是单位“1”;如果把2 袋米当成一个整体的话,就是单位“2”. ( )(2)把1块蛋糕分成5份,每份占15. ( )(3)不同分数的分数单位一定不一样. ( )例题6: 思考.有同样大小的红、黑、白三种颜色的珠子共89颗,按1颗红珠、3颗白珠、2颗黑珠的顺序排列在一起.那么三种珠子各占总数的几分之几?1.919的分数单位是( ),它至少再添上( )个这样的分数单位就是一个质数.2. 呆呆熊买了20个苹果、23个梨,苹果的数量是梨的几分之几?3. 一个蛋糕平均分给7个小朋友,每个小朋友分得这块蛋糕的几分之几?240.081×10= 430-250= 75÷10= 0.17+0.06= 0.96÷0.8= 1.02-0.09=0.8×7= 7200÷800=1.5×7= 0.17+0.6= 1.32×8= 0.83-0.6= 0.7×8= 17×300= 10.3×2= 0.98-0.09= 5×0.6= 0.2+0.78= 0.9×0.3= 600×700= 3.5×0.2= 10.2+0.02=2.01×0= 0.15+0.7= 10×0.05= 670+250= 0.13×7= 10.2+0.2= 0.21×100= 9.2-6=0.7×4= 8500÷500= 0.05×4= 3.2-3.2=4×0.3= 3.7+2.3= 6.3÷7= 0.125×8= 0.56÷28= 0.72÷3.6= 5.6÷100= 4.8÷0.3=26第5讲2、3、5的倍数特征1. 结合具体实例,了解2、3、5的倍数特征,能找出100以内的了解2、3、5的倍数.2. 在探索新知识的过程中,初步了解观察、类比、猜测和归纳等探索规律的基本方法.一、2,3,5的倍数特征(1)5的倍数特征: 个位上是0或5的数都是5的倍数;(2) 2的倍数特征: 个位上是0、2、4、6、8的数都是2的倍数;(3) 2和5共同的倍数特征: 个位上是0的数是2和5共同的倍数的特征;(4) 3的倍数的特征: 一个数各个位上数字的和是3的倍数,这个数就是3的倍数.例题1: 练一练.6、18、27、40、215、179、800、1000、873(1)2的倍数有______________________(2)5的倍数有______________________(3)既是2的倍数,又是5的倍数有________________________练习1: 练一练.(1) 既是2的倍数,又是5的倍数的最大两位数是_____;(2)要使12□是5的倍数,□里可以填______;(3)如果35□既是5的倍数,也是2的倍数,□里可以填_____;例题2: 173□是一个四位数,先后依次在方框中填入3个数字,使得分别是2,3,5的倍数,那么填入的三个数之和最大是多少?练习2: 23□是一个三位数,先后依次在方框中填入3个数字,使得分别是2,3,5的倍数,那么填入的三个数之和最大是多少?例题3: 四位数3AA1能被3整除,求A是多少?28练习3: 五位数51A8A能被3整除,求A是多少?例题4: 在□内填上适当的数字,使五位数23□6□既能被3整除又能被5整除. 练习4: 若四位数9a8a能被15整除,则a代表的数字是多少?例题5: 从0,3,5,7四个数字中任选三个,排成能同时被2、3、5整除的三位数,你能找出多少个这样的三位数呢?练习5: 在865后面补上3个数字,组成一个六位数,使它能分别被3、2、5整除,且使这个数值尽可能的小.301. 有5个自然数:48、124、7836、4105、89765,其中能被2整除的有哪几个?2. 从2、5、7、三张卡片中任意抽取两张卡片,组成既有因数5的数是_____.3. 要使四位数514□是3的倍数,□里可以填_____ ;要使514□有因数5,□里可以填_____.25×100= 9.5-0.5=3.2-0.32= 3.5+2.4=2+2.8= 1-0.95=380-290= 0.3+0.27= 0.35+0.5= 0.47+0.13= 0.35+0.63= 4.5+4= 3500÷70= 4-0.6=3.1+3= 0.95+0.05= 3.8+0.38= 2.5+3.2= 7500÷250= 0.74+0.16= 3.8+1= 23×100=0.95-0.05= 9.8-4.8=450+780= 480÷40=3.1+0.3= 0.53÷100=3+0.3= 5.1+2.3= 630÷9= 125×80=4.5-0.4= 0.078÷10= 9.5-5= 70×12=330×9= 0.25×100= 9.53-1.53= 3.4-2.8=0.36÷0.4= 3.6÷24=第6讲流水行船321. 掌握行船流水问题的基本规律,能理清水速、船速之间的关系.2. 经历应用问题的解决,掌握流水行船问题的基本解决方法和步骤,学会用画图等方法解决问题.一、流水行船问题:船在江河里航行时,除了本身的前进速度外,还受到流水的推送或顶逆,在这种情况下计算船只的航行速度、时间和所行的路程,叫做流水行船问题.二、四个速度:船速:船在静水中航行的速度,即船本身的速度.水速:水流动的速度,即没有外力的作用水中漂浮的速度.顺水速度:当船航行方向与水流方向一致时的速度,即顺水行船的速度.逆水速度:当船航行方向与水流方向相反时的速度,即逆水行船的速度.三、四个公式:顺水速度=静水速度+水速逆水速度=静水速度-水速水速=(顺水速度-逆水速度)÷2 船速=(顺水速度+逆水速度)÷2例题1: 甲乙两港间的水路长100千米,一只船顺流而下从甲港开往乙港,已知船的静水速度40千米/时,水流速度是10千米/时,请问:这艘船多长时间才能到达乙港?练习1: 甲乙两港间的水路长100千米,一只船逆流而上从甲港开往乙港,已知船的静水速度30千米/时,水流速度是5千米/时,请问:这艘船多长时间才能到达乙港?例题2: 甲乙两港间的水路长100千米,一只船顺流而下从甲港开往乙港用了5小时,已知水流速度是2千米/时,请问:这艘船的静水速度是多少?练习2: 甲乙两港间的水路长200千米,一只船逆流而上从甲港开往乙港用了10小时,已知水流速度是2千米/时,请问:这艘船的静水速度是多少?例题3: 甲乙两港间的水路长100千米,一只船顺流而下从甲港开往乙港用了5小时,逆流而上从乙港开往甲港用了10小时,请问:这艘船的静水速度和水速分别是多少?34练习3: 甲、乙之间的水路是234千米,一只船从甲港到乙港顺水需9小时,从乙港返回甲港逆水需13小时,问船速和水速各为每小时多少千米?例题4: 某船在静水中每小时行18千米,水流速度是每小时2千米.此船从甲地逆水航行到乙地需要15小时.求甲、乙两地的路程是多少千米?此船从乙地回到甲地需要多少小时?练习4: 某船在静水中的速度是每小时15千米,它从上游甲港开往乙港共用8小时.已知水速为每小时3千米.此船从乙港返回甲港需要多少小时?例题5: A、B两码头间河流长为200千米,甲、乙两船分别从A、B两码头同时相向航行,甲的静水速度是30千米每小时,乙的静水速度是20千米每小时,水流速度为5千米每小时,请问:出发后多长时间两船相遇?练习5: A、B两码头间河流长为100千米,甲、乙两船分别从A、B两码头同时起航.如果相向而行5小时相遇,如果同向而行10小时甲船追上乙船,求两船在静水中的速度.1. 一只渔船顺水行25千米,用了5小时,水流的速度是每小时1千米.此船逆水航行30千米需要多少小时?362. 一只船,顺水每小时行30千米,逆水每小时行20千米.这只船在静水中的速度和水流的速度各是多少?3. 某船在静水中的速度是每小时18千米,它从上游甲港开往乙港共用10小时.已知水速为每小时3千米.此船从乙港返回甲港需要多少小时?0.6-0.37= 3.5+2.4=0.052×10= 5+0.07=10+0.08= 1-0.61=1-0.75= 0.47+0.23=0.5×1000= 0.25+0.75=0.82+0.3= 3.7+0.33=13.5+6.5= 0.51+0.33=3.05×100= 1-0.6=1.2-0.8= 8-4.6=21.6-12.6= 5.8-3.6=63÷100= 0.52+0.4=0.83-0.5= 6.45+5.5=5.6÷100= 4.5-1.3=0.76+0.14= 3.4-2.8=80÷1000= 9.53-1.53=2.7+0.4= 8.8-6.7= 0.72-0.43= 10+0.08= 30×100= 9.5-7.3= 0.92-0.2= 8.8-6.7=3.5+4.8= 3.4-2.8=38第7讲期末闯关1. 复习前六讲内容,联系相关知识点形成知识网,查漏补缺.2. 通过复习,使学生对寒假所学的概念、计算法则、应用题知识得到进一步巩固.1: 如图,平行四边形ABCD中,AD的长度为20厘米,高CH的长度为9厘米,.那么两个阴影三角形面积之和为多少平方厘米?H B DAE CF2: 如图,三角形ABC 中,BD=6,DC=3,AE=4,EC=2,若三角形ABD 的面积是12,那么三角形DEC 的面积是多少?3: 填空.(1) 根据12 ÷ 3 = 4请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(2) 根据6 × 4 = 24请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(3) 如果一个数的最小倍数和最小因数的差是10,那么这个数的最大因数是( ).4: 请写出42的所有因数.5: 掌小萌有三张卡片,上面各印有一个数字7、8、9从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?40例题6: 填空.(1)1116的分数单位是_____,它减去6个这样的单位,结果是_____.(2)57的分数单位是______,它加上_____个这样的分数单位就成为最小的质数.例题7: 把6米长的彩带平均分给5个小朋友,每个小朋友分到_____米,占全部彩带的_____.例题8: 练一练.(1)既是2的倍数,又是5的倍数的最大两位数是_____;(2)要使12□是5的倍数,□里可以填______;(3)如果35□既是5的倍数,也是2的倍数,□里可以填_____;例题9: 173□是一个四位数,先后依次在方框中填入3个数字,使得分别是2,3,5的倍数,那么填入的三个数之和是多少?例题10: 甲、乙之间的水路是234千米,一只船从甲港到乙港顺水需9小时,从乙港返回甲港逆水需13小时,问船速和水速各为每小时多少千米?例题11: 某船在静水中每小时行18千米,水流速度是每小时2千米.此船从甲地逆水航行到乙地需要15小时.求甲、乙两地的路程是多少千米?此船从乙地回到甲地需要多少小时?421. 如图,已知平行四边形ABCD 的面积为36,三角形AOD 面积为8.求三角形BOC 面积.2.五年级(1)班的36名同学进行文艺汇演,表演的时候全班排成长方形方阵(包括正方形)如果规定每行每列不得少于3人,那么一共有几种排法?442.7+0= 0.75×100= 12.5×8= 0.02×0.5=2.3×4=3.6×0.3=3.25×0= 5.6×100= 0.4×50= 0.75÷0.25= 30×0.1= 0.125×8= 2.6×3= 0.86÷2=4.1×2= 0.56÷28= 0.35×0.2= 0.36÷0.4= 7.5×0.1= 0.7×9= 2.5×2= 3.6÷24= 0.5×10= 0.8×1.1= 0.6×8= 46.7-3.8= 2.8×10= 12.8÷4= 0.7×0.8=5.2÷13= 5.6+0.4= 1.64+4.1= 4.7+2.3= 10÷20= 4.5×2= 24÷15= 7.2×0.8= 0.35×0.6= 6×3.4= 4.7+2.3= 0.62-0.32= 4.5×2=。
五年级奥数寒假讲义

第一讲多边形的面积(一)知识概述在数学课上我们已经掌握了几种基本图形的面积计算公式:正方形的面积=();长方形的面积=();平行四边形的面积=();三角形的面积=();梯形的面积=();由两个或多个简单的基本几何图形可以组合成一个组合图形,要计算一个组合图形的面积,就要根据图形的基本关系,运用分解、组合、平移、旋转、割补、加辅助线等几种方法来思考。
例题精学:第一课时例1、已知一个平行四边形的面积是28平方厘米,求阴影部分的面积。
同步精练1、下图的梯形中,阴影部分的面积是150平方厘米,求梯形的面积。
2、已知平行四边形的面积是48平方厘米,求阴影部分的面积。
3、如果用铁丝围成如下一样的平行四边形,需要用铁丝多少厘米?(单位:厘米)| 12|例2、下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)5cm4cm 15厘米25厘米5厘米6厘米96 6 4甲乙同步精练1、求右图中阴影部分的面积。
(单位:厘米)2、求右图中的阴影部分的面积。
(单位:厘米)3、如图所示,四边形ABCD 是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
例题精学 第二课时:例3、如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
同步精练1、四边形ABCD 是一个长为10厘米,宽为6厘米的长方形,三角形ADE 的面积比三角形CEF 的面积大10平方厘米。
求CF 的长是多少厘米?4厘米3厘米DCAB8厘米5厘米甲A 乙 CB EDF4 厘米 4厘米FEADC B2、平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长为8厘米,已知阴影部分三角形ABG 和三角形CDF 的面积和比三角形EFG 的面积大10平方厘米。
求CF 的长。
3、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,求: (1)三角形DEF 的面积; (2)CF 的长。
例4、两条对角线把梯形ABCD 分割成四个三角形。
五年级奥数能力提升寒假讲义

第一节定义新运算【知识要点】说起运算,同学们马上就会想到我们课堂上学过的加、减、乘、除四则运算,并且还能熟练地说出这些运算的一些运算性质和运算定律。
当然,对于什么样的问题该用加法或减法、乘法还是除法计算更是烂熟于胸。
其实,在加、减、乘、除四则运算之外,还有其他多种法则的运算。
我们这一讲里将要学习的“新运算”,就是用*、△、☆、⊙等多种符号,按照一定的关系,临时规定的一种新的运算程序(新运算)。
学习“定义新运算”,关键是要深刻理解运算符号的新规定,严格按照规定的法则运算,最后达到解决问题的目的。
【典型例题】例1 设a,b都表示数,规定是a△b表示a的3倍减去b的2倍,a△b=a×3-b×2。
试计算:5△6;(7△6)△4的值。
例2 有两个数是A 、B ,A △B 表A 与B 的平均数。
、(1)已知A △6=17,求A 。
(2)如果已知4△B=2,求B 。
例3 规定△=x+,那么3△4= 。
例4 如果2*3=2+3+4,5*4=5+6+7+8,按此规律计算:3*5;5*3x y 32y x yx ⨯+【小试锋芒】1.设a,b都表示数,规定a△b=6×a-2×b。
试计算3△42.设a,b都表示数,规定a△b=3×a+2×b 试计算:(5△6)△7;5△(6△7)3. 规定:6*2=6+66=72,2*3=2+22+222=246,1*4=1+11+111+1111=1234。
求:7*54.如果2*4=24÷(2+4),按此规律计算3*6;6*3;历届竞赛中的定义新运算:1.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是?(第一届小学“希望杯”全国数学邀请赛五年级 第1试)2.规定:A*B=3A+2B,如4*5=3×4+2×5,那么,B*A=________。
(第四届小学“希望杯”全国数学邀请赛五年级 第1试)3.“△”是一种新运算,规定:a△b=a×c+b×d(其中c,d为常数),如5△7=5×c+7×d。
五年级数学寒假讲义

橡树初春,大地从沉睡中苏醒。
田野里飘来一阵阵泥土的清香,草儿吐露出娇嫩的幼芽,好奇地窥视着人间;姑娘们穿着艳丽的衣裳,在碧绿色的草地上欢快地歌唱。
万木争春,小溪哗哗作响,两岸铺上翡翠般的地毯。
举目眺望,大自然一片生机,令人陶醉,使人神往。
只有一棵橡树默默地站在一旁。
它没有穿上新装,它那饱经沧桑、满是皱纹的老皮一丝不挂地袒露着;它雄伟、挺拔、巍然屹立,干枯的树枝直指天穹,犹如高举双臂,祈求上帝的怜悯。
可是它的血液已经凝滞,生命的火花已经消失,严酷的寒冬结束了它的残生。
不久前,它还神采奕奕,英姿勃勃。
然而,自它睡下去,就再也没有醒来。
几天之后,来了几个人,七手八脚把它锯断,又把它连根刨出,装车运走。
在生长过它的地方,只剩下一堆黄土。
橡树啊,我童年的伙伴和朋友,你曾赋予我多少甜蜜的幻想!我喜欢在你高大的躯干上攀登,在你坚韧而富有弹性的树枝上尽情地悠荡。
多少次,我在你那幽静、凉爽的浓荫下悠闲地歇息,自由地畅想。
如今,那些甜蜜的时光同你一起离开了我们可爱的故乡。
幼小的橡树长出第一批嫩叶,又把枝条向四处伸延,转眼之间填补了你留下的空间。
茁壮的幼苗变成参天大树,孩子们又会在它的树荫下嬉笑、玩耍,成年人又会在那里歇息、畅想。
第1讲方阵问题1.认识方阵,掌握方阵的基本结构;2.探索方阵每边数量、每层数量、总数之间的关系。
一.方阵问题1.定义把若干人或物排列成正方形队列的形式,根据排列规律,引出的计算问题就叫做方阵问题。
2.方阵问题的特点方阵每边的实物数量相等,相邻两边的实物数量相差2,相邻两层的实物数量相差8。
棋子若干粒,恰好可排成每边8粒的正方形,棋子的总数是多少?棋子最外层有多少粒?1.同学们排队,要排成每行10人,共10行的方阵,共需要多少人?2.同学们排成十行十列的方阵,如果去掉一行一列,要去掉多少人?3.小明用棋子摆了一个实心方阵,后来他又加上15个棋子,使横竖各增加一排,成为一个大的实心方阵,原来的实心方阵每排有几个棋子?4.一个围棋爱好者,用围棋子组成一个正方形实心阵,最外层用白子,共92颗,里面全部用黑子,共多少颗?5.某校学生刚好排成一个方阵,最外层的人数是96人,问这个学校共有学生?二.方阵问题解题思路1.实心方阵每边数×每边数=总数(每边数-1)×4=每层数每层数÷4+1=每边数2. 空心方阵大实心方阵-小实心方阵=总数(每边数-层数)×层数×4=总数一个正方形池塘四周栽满了树,已知每边栽了9棵,并且四个角上都有一棵,这个池塘四周一共栽了多少棵树?1.沿一个正方形水池的四周栽树一行,四角都要栽1棵,共载树152棵。
寒假衔接五年级数学讲义

寒假衔接五年级数学讲义一、教学目标(1)复习小数乘整数;掌握小数乘整数的竖式计算要点;能正确地进行笔算。
(2)复习小数乘小数;掌握小数乘法中积的小数点位置的确定方法。
(3)会用“四舍五入”法截取积是小数的近似值。
(4)掌握连乘、乘加、乘减的运算顺序;提高小数混合运算能力。
二、例题探究例1计算:0.47×9 = 4.230. 4 7――――〉扩大到它的100倍――――――〉 4 7×9 ×9------------ ------------------4. 2 3〈――――缩小到它的100倍〈――――――4 2 3在乘法算式中;因数扩大多少倍;积缩小相同的倍数;等于不扩大不缩小。
对比观察发现0. 4 7…………………………两位小数×9 积中的小数位数和因数中的小数位----------- 数相同4. 2 3………………………….两位小数方法总结:计算小数乘整数时;先按照整数乘法的计算法则算出积;然后看因数中有几位小数;就从积的右边起数出几位;点上小数点。
例2计算:3.35×18 =60.33. 3 5× 1 8----------------2 6 8 03 3 5------------------- 计算后要先点上小数点;再将小数末尾的0用斜线划去。
6 0. 3 0方法总结:在计算出小数乘整数的乘积后;如果积的末尾有0;应先点上小数点;然后根据小数的基本性质把小数末尾的0去掉;切不可先去掉末尾的0;再点小数点。
例3计算4.7×2.8 0.38×0.084.7………………一位小数0.38…………….两位小数×2.8………………一位小数×0.08…………….两位小数------------- -------------3 7 6 0.03 0 4…………….四位小数9 4-------------13.16…………….两位小数方法总结:小数乘小数先按整数乘法算出积;再看因数中一共有几位小数;就从积的右边起数出几位点上小数点。
(讲义)温故知新篇05简易方程2021-2022学年五年级数学寒假学习精编讲义(人教版含解析)

20212022学年人教版五年级数学寒假学习精编讲义温故知新篇05 简易方程知识点一:用字母表示数1. 用字母表示数量关系(1)可以用字母或含有字母的式子来表示一个数或表示数量关系;(2)字母与数字相乘时,把乘号省略。
省略乘号时,一般把数字写在字母前面。
含有字母的式子中的加、减、除号不能省略。
2. 用字母表示运算定律和计算公式(1)在含有字母的式子里,只有字母与字母、数字与字母之间的“×”才能简写成“.”或者省略不写。
注意:省略乘号后,数字必须写在字母的前边。
(2)应用公式求值解决问题的步骤:第一步:写出字母公式第二步:把字母表示的数值代入公式第三步:计算出结果,记住写单位3. 用字母表示复杂的数量关系(1)不同的式子可以表示相同的数量关系。
(2)将字母的具体数值代入含有字母的式子中,即可求得相应式子的值。
4. 化简含有字母的式子并代入数据求值计算含有字母的式子的时候,可以先运用运算定律将含有字母的式子进行化简,再求值。
知识点二:解简易方程1.方程的意义(1)方程的意义:含有未知数的等式是方程。
(2)方程必须具备的两个条件:一是等式;二含有未知数。
2.方程一定是等式;但等式不一定是方程。
3. 所有的方程都是等式,但等式不一定都是方程。
4.等式的性质等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
5.方程的解使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
一.选择题1.(2021秋•沈河区期末)a﹣b﹣c=()A.a﹣b+d B.a+(b﹣c)C.a﹣(b﹣c)D.a﹣(b+c)2.(2021秋•永吉县期末)当x等于()时,18x﹣16与6x+56这两个式子的结果相等。
A.6 B.5 C.43.(2021秋•土默特左旗校级期末)一个两位数,个位上的数字是x,十位上的数字是y,这个两位数是()A.xy B.10x+y C.10y+x4.(2021秋•永吉县期末)下面算式中,m表示大于0的数,商最大的算式是()A.m÷2.3 B.m÷0.8 C.m÷0.25.(2020秋•通州区期末)动物园里有猴子22只,猴子的只数是老虎只数的5倍还少3只。
【知识点归纳】五年级下册数学寒假预习衔接讲义-第一单元 观察物体(三)(知识梳理 同步测试) 人教新课标

2019-2020学年人教版小学五年级数学下册寒假预习与检测专题讲义运算定律一.知识点归纳1. 作简单图形的三视图在画组合体三视图之前,首先运用形体分析法把组合体分解为若干个形体,确定它们的组合形式,判断形体间邻接表面是否处于共面、相切和相交的特殊位置;然后逐个画出形体的三视图;最后对组合体中的垂直面、一般位置面、邻接表面处于共面、相切或相交位置的面、线进行投影分析.当组合体中出现不完整形体、组合柱或复合形体相贯时,可用恢复原形法进行分析.画哪个方向上的三视图就想象哪个方向上有光照到物体上,画出投影即可.【经典例题】例:如图立体图形,从正面、上面、侧面看到的形状分别是什么?在方格纸上画一画.分析:观察图形可知,从正面看到的图形是2层:下层3个正方形,上层1个正方形靠左边;从上面看到的图形是一行3个正方形;从侧面看到的图形是一列2个正方形,据此即可解答问题.解:根据题干分析画图如下:点评:此题考查从不同方向观察物体,意在培养学生观察物体的空间思维能力.2. 三视图与展开图三视图怎么看:1.从正面看,为主视图2.从侧面看,为左视图3.从上面看,为俯视图展开图为空间形体的表面在平面上摊平后得到的图形.二.同步测试同步测试题一.选择题(共6小题)1.观察三视图,要摆成下面的情况,需要用()块正方体.A.9B.10C.11D.122.用同样大小的正方体摆成的物体,从正面看到,从上面看到,从右面看到()A.B.C.D.3.如图是由4个完全相同的小正方体堆成的一个立体图形,从上面看这个图形,可以看到这个立体图形的()个面.A.2B.3C.4D.以上答案都不正确4.根据所给的三视图,摆出立体图形,并数出组成立体图形的小正方体个数是()A.3B.4C.5D.65.观察三视图,要摆成下面的情况,最少用()块.A.9块B.10块C.11块D.12块6.如图是由一些相同的小正方形构成的几何体的三视图.有几个正方体()A.4B.5C.6D.7二.填空题(共10小题)7.如图两个图,从面看到的形状是一样的,并在下面方格纸上画出这个面的形状.8.观察物体,从右面观察,画出你看到的图形.9.如图从前面看到的图形是,从右面看到的图形是.10.小泉同学到学校领来n盒粉笔,整齐地摞在讲桌上,其三视图如图,则n的值是.11.如图,桌上放着等底等高的圆柱和圆锥各一个,请画出从前面看到的图形.12.下面的物体分别从前面、左面、上面看到的形状分别是什么?请你在方格纸上画出来.13.从正面看到的是图形,从上面看到的是图形,从左侧面看到的是,从右侧面看到的是图形.14.用三个同样大小的正方体拼成一个长方体,从正面看,看到的是;从侧面看到的是.15.从前面看如图,看到的是.(画出你看到的形状)16.画出如图的立体图形从正面看到的图形,从上面看到的图形,从右面看到的图形.三.操作题(共4小题)17.看左图立体图形,在方格纸上分别画出从正面、上面、右面看到的形状.18.一个立体图形如图所示,分别画出从正面、上面、左面看到的形状.19.看一看,把你从正面、上面和右面看到的形状分别在方格纸上画出来.20.下面立体图形从正面和左面看到的形状分别是什么图形?请动手画一画.四.解答题(共4小题)21.在下面的方格图中分别画出从不同方向观察左边物体所看到的图形.(从正面看)(从左面看)(从上面看)22.画出下图分别从正面、左面、上面看到的形状.23.分别画出从正面、上面、左面看到的形状.24.作图题:分别画出从正面、上面、左面看到的形状.参考答案与试题解析一.选择题(共6小题)1.【分析】观察三视图可知,这个几何体共有2层,由俯视图可得第一层小正方体的块数,由正视图和左视图可得第二层最少有小正方体的块数,相加即可.【解答】解:由俯视图可得最底层有8块小正方体,由正视图和左视图可得第二层最少有2块小正方体,最少共有8+2=10(块).故选:B.【点评】此题主要考查了由三视图判断几何体,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.2.【分析】根据从正面看到,从上面看到,可知该物体有前后两排,都只有一层高,依此即可得到从右面看到的图形.【解答】解:由主视图和俯视图可知该物体有前后两排,有一层高,则从右面看到.故选:A.【点评】考查了三视图与展开图,得到该物体的排数和每排的层高是解题的关键.3.【分析】从上面看所得到的图形是俯视图,根据图中正方体摆放的位置判定即可.【解答】解:从上面看下来,左面一行是2个正方体,右面一行是1个正方体.可以看到这个立体图形的2+1=3个面.故选:B.【点评】此题主要考查了三种视图中的俯视图,比较简单.4.【分析】根据从上面看的图形可得最下面一层5个小正方形,根据从正面看的图形和从左面看的图形可得第二层应有1个小正方形.【解答】解:由图可知,这个立体图形的底层应该有3+2=5个,第二层应该有1个小正方体,因此构成这个立体图形的小正方体的个数是5+1=6个.如图:故选:D.【点评】本题考查从不同方向观察物体和几何体,本题解题的关键是利用上面、左面、正面图看出下层和上层共有多少个小正方形,加起来得到结果.5.【分析】观察三视图可知,这个几何体共有2层,由俯视图可得第一层小正方体的块数,由正视图和左视图可得第二层最少有小正方体的块数,相加即可.【解答】解:由俯视图可得最底层有8块小正方体,由正视图和左视图可得第二层最少有2块小正方体,最少共有8+2=10(块).故选:B.【点评】此题主要考查了由三视图判断几何体,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.6.【分析】由俯视图可得最底层几何体的个数,由主视图和左视图可得几何体第二层正方体的个数,相加即可.【解答】解:俯视图中有4个正方形,那么最底层有4个正方体,由主视图可得第二层最多有2个正方体,有左视图可得第二层只有1个正方体,所以共有4+1=5个正方体.故选:B.【点评】考查对三视图的理解应用及空间想象能力.只要掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就很容易得到答案.注意俯视图中正方形的个数即为最底层正方体的个数.二.填空题(共10小题)7.【分析】左图:从正面能看到4个正方形,分两行,下行3个,上行1个居中;从左面能看到3个正方形,分两行,上行1个,下行2个,左齐;从上面能看到4个正方形,分两行,上行3个,下行1个,左齐;从右面能看到3个正方形,分两行,上行1个,下行2个,右齐’.右图:从正面看到3个正方形,分两行,上行1个,下行2个,左齐;从左面能看到3个正方形,分两行,上行1个,下行2个,左齐;从上面能看到3个正方形,分两行,上行1个,下行2个,左齐;从右面能看到3个正方形,分两行,上行1个,下行2个,右齐’.由此可见,这两个图形从左面、右面,即侧看到的形状是一样的.【解答】解:如图两个图,从侧面看到的形状是一样的,在方格纸上画出这个面的形状如下:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.8.【分析】这个立体图形由4个相同的小正方体构成,从右面观察,能看到一行2个正方形.【解答】解:如图从右面观察,画出我看到的图形:.故答案为:.【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.9.【分析】这个立体图形由6个相同的小正方体组成,从前面能看到6个正方形,分两行,下行4个,上行2个,左齐;从面只看到一列2个长方形.【解答】解:如图,故答案为:,.【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.10.【分析】观察主视图和左视图可知粉笔盒共放了三层,由俯视图可知第一层的盒数为4,结合主视图和俯视图可知第二层共2盒,放置在左边;第三层1盒,放置在左上方,由此把各层的盒数相加即可.【解答】解:由分析知,粉笔盒放置如下图所示:所以n=4+2+1=7,答:n的值是7.故答案为:7.【点评】本题考查了学生对三视图的掌握程度和灵活运用能力,训练了学生的空间想象能力.11.【分析】从正面看,左边的圆柱看到的图形是长方形,右面的圆锥看到的图形是一个三角形;据此画图即可.【解答】解:画图如下:故答案为:.【点评】本题考查了几何体的三视图,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.12.【分析】此立体图形由8个相同的小正方体组成,从前面能看到4个正方形,分两行,下行3个,上行1个居中;从右面看到的形状与从前面看到的形状相同;从上能看到7个正方形,分三行,上、中行各3个,下行1个居中.【解答】解:下面的物体分别从前面、左面、上面看到的形状分别是什么?请你在方格纸上画出来(下图):【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.13.【分析】观察图形可知,从正面看到的图形是3层:最下层是3个小正方形,上两层都是1个小正方形居中;从上面看到的图形是两行,上面1行3个正方形,下面1行1个小正方形居中;从左侧面看到的图形是3层:最下层是2个小正方形,上两层都是1个小正方形靠左;右侧面看到的图形是3层:最下层是2个小正方形,上两层都是1个小正方形靠右,据此即可解答问题.【解答】解:从正面看到的是图形,从上面看到的是图形,从左侧面看到的是,从右侧面看到的是图形.故答案为:,,,.【点评】此题主要考查从不同方向观察物体的能力,意在培养学生的观察能力和空间思维能力.14.【分析】观察图形可知,从正面看到的图形是一行3个正方形;从侧面看到的图形是一个正方形,据此即可解答问题.【解答】解:根据题干分析可得:从正面看,看到的是;从侧面看到的是.故答案为:;.【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.15.【分析】此立体图形由5个相同的小正方体组成,从正面只能看到一排三个正方形,每个正方形只能看到一个面,即从正面能看到一排三个正方形.【解答】解:如图,从正看到的是:故答案为:.【点评】此题是考查作简单图形的三视图,要注意观察的方向与角度.16.【分析】观察图形可知,从正面看到的图形是两列:左边一列3个正方形,右边一列1个正方形靠下边;从上面看到的图形是两行:后面一行2个正方形,前面一行1个正方形靠左边;从右面看到的图形是两列:右边一列3个正方形,左边一列1个正方形靠下边,据此即可画图.【解答】解:根据题干分析可得:立体图形从正面看到的图形,从上面看到的图形,从右面看到的图形.故答案为:;;.【点评】此题考查了从不同方向观察问题和几何体,锻炼了学生的空间想象力和抽象思维能力.三.操作题(共4小题)17.【分析】这个立体图形由5个相同的小正方体组成.从正面能看到4个正方形,分两行,上行1个,下行3个,右齐;从上面能看到4个正方形,分两行,上行3个,下居中1个;从右面能看到3个正方形,分两行,上行1个,下行2个,右齐.【解答】解:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.18.【分析】这个立体图形由6个相同的小正方体组成.从正面能看到5个正方形,分两层,下层4个,上层1个与下层左数第二个齐;从上面能看到45个正方形,分下、下两层,上层4个,下层1个,左齐;从左面能看到3个正方形,分上、下两层,上层1个,下层2个,左齐.【解答】解:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.19.【分析】(1)从正面能看到4个正方形,分两行,下行3个,上行1个居中;从上面能看到一行3个正方形;从右面能看到一列2个正方形.(2)从正面能看到3个正方形,分两行,上行1个,下行2个,右齐;从上面能看到3个正方形,分两行,上行2个,下行1个,左齐;从右面与从前面看到的相同.【解答】解:看一看,把正面、上面和右面看到的形状分别在方格纸上画出来.【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.20.【分析】这个立体图形由9个相同的小正方体构成,从正面能看到6个正方形,分两行,上行2个,下行4个,左齐;从左面能看到3个正方形,分两行,上1个,下行2个,左齐.【解答】解:下面立体图形从正面和左面看到的形状分别是什么图形?请动手画一画.【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.四.解答题(共4小题)21.【分析】观察图形可知,从正面看到的是3层:下层4个正方形,上两层都是1个正方形在从左数第二的位置;从左面看到的图形是2层:下层3个正方形,上两层都是1个正方形靠右边;从上面看到的图形是3行上面一行3个正方形,第二行1个正方形在第一行的最左边的正方形下面,第三行1个正方形在第二行的正方形左边,据此画图即可.【解答】解:根据题干分析可得:【点评】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.22.【分析】此立体图形是由5个相同的小正方体组成的,从正面能看到4个正方形,分二行,下行3个,上行1个居中;从在能看到3个正方形,分两行,下行2个,上行1个,左对齐;从上面能看到4个正方形,分两行,上行3个,下行1个居中.【解答】解:画出下图分别从正面、左面、上面看到的形状:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.23.【分析】观察图形可得,从正面看是2层:下层3个正方形,上层1格正方形靠左边;从上面看是三行:中间一行是3个正方形,前面一行1个正方形靠左边,后面一行1个正方形靠右边;从左面看是2层:下层3个正方形,上层1个正方形靠中间;据此即可画图.【解答】解:根据题干分析可得:【点评】此题考查了从不同的方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.24.【分析】此立体图形由5个相同的正方体组成,从正面能看到3个正方体,每个正方体能看到1个面,即能看到3个正方形,分两行,下行2个,上行一个居左;从上面能看到4个正方形,分两行,第行2个;从左面能看到3个正方形,分两行,下行2个,上行一个居右.【解答】解:分别画出从正面、上面、左面看到的形状:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.。
【寒假讲义】温故知新篇05《分数的意义》—2020-2021学年五年级数学上册寒假学习精编讲义

2020-2021学年北师大版五年级数学上册寒假学习精编讲义温故知新篇05 分数的意义一.选择题1.(2020秋•历城区校级期中)下面各题中,应把“男生人数”看做单位“1”的是()A.男生人数是女生人数的3 4B.男生人数的113倍相当于女生人数C.女生人数与男生人数相差10人D.男生比女生多1 52.(2020•马鞍山)如果56的分子加上10,要使分数的大小不变,分母应()A.加上10 B.乘10 C.加上12 D.乘2 3.(2019秋•合肥期末)如图中,涂色部分占整个图形的()A.13B.14C.154.(2013春•榕江县校级期中)237A=⨯⨯,253B=⨯⨯,那么A和B的最大公因数是() A.2 B.6 C.7 D.255.27的分子增加6,要使分数的大小不变,分母应该()A.增加6 B.扩大3倍C.扩大4倍6.一个真分数,把它的分子、分母同时加上一个相同的自然数(0除外),所得的新分数() A.比原分数小B.与原分数相等C.比原分数大二.填空题7.(2020春•昆山市校级期中)二月份,食堂吃了大米总数的47,把看做单位“1”,平均分成份,吃了的占这样的份.小红走了45千米,把看做单位“1”,平均分成份,已走的有份.8.(2020•大同)3米长的木材,锯成每段一样长的小段,共锯了7次,每段占全长的,每段长米.9.(2020春•石阡县期末)118的分数单位是,它有个这样的分数单位.10.(2020春•萍乡期末)一个分数,分子比分母少10,约分后等于35,这个分数是.23加上等于最小的质数.11.(2020•长沙)一个最简分数,分子、分母的和是86,如果分子、分母都减去9,得到的分数是89,则原分数是.12.(2019•岳麓区)一个分数,分子减1可以化简为13,分子加1可以化简为37,则这个分数为。
三.判断题13.(2019秋•雅安期末)把一个圆分成5份,每份是它的15..(判断对错)14.(2020春•临朐县期末)约分时,每个分数值越来越小;通分时,每个分数的值越来越大..(判断对错)15.(2020春•随州期末)把一个苹果分成4块,其中一块占这个苹果的14.(判断对错)16.(2019春•西塞山区期末)任何两个自然数都有无数个公倍数.(判断对错)17.(2019春•邓州市期末)一根电线用去56,还剩下16米.(判断对错)18.两个自然数的乘积一定是它们的公倍数.(判断对错)四.计算题19.(2019春•吴忠期中)写出每组数的最小公倍数.20和304和981和2720.(2016春•清城区期中)先约分,再比较两个分数的大小.24 32和31216 24和1230.五.应用题21.一个分数,它的分子比分母小48,并且约分后是23,约分前这个分数是多少?22.化简一个分数时,用2、3、5分别约分一次,得57.原来的分数是多少?23.如果一个自然数除以7余3,除以5也余3,那么这个自然数最小是多少?24.化简一个分数时,用2约了三次,用3约了一次,结果是14,原来的分数是多少?25.化简一个分数时,用2约了一次,用3约了两次,这时得到一个最简分数是25,原来这个分数是几分之几?六.解答题26.(2021•宁波模拟)甲数比乙数多25,乙数比甲数少几分之几?27.(2020秋•滨湖区期中)把25克盐放在100克水中溶成盐水,那么盐占盐水的() ().28.(2018春•简阳市期中)求下面每组数的最大公因数和最小公倍数.6和1818和2435和84.29.(2018秋•天长市校级期中)把假分数化成整数或带分数,把带分数化成假分数.144 125468531782915415a46530.(2019春•卢龙县期末)五年级(1)班学生进行队列表演,每行12人或16人都正好整行,已知这个班的学生不到50人,这个班有多少人?31.(2018春•淮北期末)有一块长24分米,宽16分米的布,把它平均剪成大小一样的正方形布料,从不浪费的角度考虑,小正方形布料的边长最大为多少分米?能剪下这样的布料多少块?32.(2019春•梁子湖区期末)一个带分数的分子是3,化成假分数后分子是13.这个带分数可能是多少?33.(2019春•成武县期末)有一张长方形纸,长24厘米,宽16厘米,如果要剪成若干个同样大小的正方形纸而没有剩余,剪出的小正方形的边长最大是几厘米?一共可以剪多少个这样大小的正方形纸?参考答案与试题解析 一.选择题1.【解答】解:男生人数的113倍相当于女生人数,是把男生人数看作单位“1”。
五年级数学 寒假讲义(7讲)

目录第1讲多边形的面积 (2)第2讲因数与倍数 (9)第3讲质数与合数 (16)第4讲分数的认识 (23)第5讲2、3、5的倍数特征 (29)第6讲流水行船 (35)第7讲期末闯关 (41)第1讲多边形的面积1. 复习平行四边形、三角形、梯形面积公式.2. 选用合理灵活的计算方法,简便运算过程,化繁为简,化难为易,使计算又快又准确.21. 割补法:将不规则的组合图形经过分割(用连线分割)、切拼、拼合后,转化成一个规则的几何图形,从而交易求得面积的方法,就是割补法求面积.2.图形变换:图形变换指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),利用模型,构成新的图形.例题1: 如图,平行四边形ABCD中,AD的长度为20厘米,高CH的长度为9厘米,.那么两个阴影三角形面积之和为多少平方厘米?H B DAE CF练习1: 如图,平行四边形ABCD中,AD的长度为30厘米,高CE的长度为8厘米,.那么阴影三角形面积为多少平方厘米?例题2: 如图,用两块长方形和一块正方形拼成了一个大正方形,其中一块小正方形的面积是36平方厘米,一块长方形的面积是48平方厘米,那么最后拼成的大正方形的面积是多少平方厘米?练习2: 如图,一个大正方形被分割成4份,其中左上和右下两个正方形的面积分别为9平方厘米和36平方厘米,求大正方形的面积..例题3:如图,ABCD 是边长为 4 厘米的正方形,CGFE 是长方形,CE 等于7 厘米.已知BCFH是平行四边形,则BCFH 的面积是________平方厘米.练习3: 如图,BCDG 是边长为 5 厘米的正方形,AGFE 是长方形,AE 等于9 厘米.已知DCFE是平行四边形,则DCFE 的面积是________平方厘米.4例题4: 如图,三角形ABC中,DC=2BD,CE=3AE,三角形ADE的面积是20平方厘米,三角形ABC的面积是多少?练习4: 三角形ABC中,BD=3DC,且三角形ABC的面积为48平方厘米,求三角形ABD的面积.例题5: 如图,已知平行四边形ABCD 的面积为36,三角形AOD 面积为8.求三角形BOC 面积.思考: 如图,有大中小三个正方形,边长分别为3、2、1 厘米,求阴影三角形的面积.61.如图,ABCD 和BEFC 都是长方形,AE=4 厘米,EF=3 厘米,问图中阴影面积是多少.2. 如图,三角形ABC 中,BD=6,DC=3,AE=4,EC=2,若三角形DEC 的面积是3,那么三角形ABC 的面积是多少?6.07-1.69= 8.2+1.8= 100-35.22= 12.6-0.9= 2.5×0.4= 48+1.6= 2.4×5= 1.1×40=0.22×4= 2.2×6=0.9-0.52= 138-8.9= 3.99×1= 0.35÷0.1=0×3.52= 75.35-23.04= 2.5÷5= 4.007-0.09= 8.4÷7= 8.2+1.8= 0.34÷17= 100-35.22= 2.5÷0.5= 2.5×0.4= 5.00+6.13= 2.4×5=8.24-7.63= 0.22×4=5.21+5.49= 0.9-0.52= 40×0.25= 3.99×1=4×0.4= 0×3.52=7.5÷0.25= 2.5÷5=4.2÷0.7= 8.4÷7=4.5×2= 0.34÷17= 7.8+0.22= 2.5÷0.5=8第2讲因数与倍数1. 学生掌握找一个数的因数和一个数的倍数的方法.2. 学生能了解一个数的因数是有限的,倍数是无限的;能熟练的找一个数的因数和倍数.1. 因数与倍数的意义:在整数除法的算式中,如果商是整数并且没有余数,则被除数是除数的和商的倍数,除数和商是被除数的因数.2. 因数与倍数的依存性: 因数与倍数不能单独存在,不能说谁是倍数,谁是因数,应该说谁是谁的倍数,谁是谁的因数.3.倍数与几倍的关系:例题1: 判断题.(1) 42÷6=7,所以42是6的倍数,6是42的因数. ( )(2)42÷6=7,所以42是倍数,6是因数. ( )(3)42÷9=4``````6,所以42是9的倍数,9是42的因数. ( )(4) 4.2÷0.6=7,所以4.2是0.6的倍数,0.6是4.2的因数. ( )(5) 4.2÷0.6=7,所以4.2是0.6的7倍. ( )练习1: 填空.(1) 根据12 ÷ 3 = 4请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(2) 根据6 × 4 = 24请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(3) 如果一个数的最小倍数和最小因数的差是10,那么这个数的最大因数是( ).例题2: 18的因数有哪些?练习2: 请找出30和36的因数.10例题3: 五年级(1)班的36名同学进行文艺汇演,表演的时候全班排成长方形方阵(包括正方形)如果规定每行每列不得少于3人,那么一共有几种排法?练习3: 大熊家有一盒糖果,共56颗糖,熊妈妈规定,大熊每天可以吃相同数量的糖果,但是不允许一天吃完,那么大熊一共有多少种吃法?每种吃法对应吃多少天?每天吃多少个?例题4: 小雅妈妈买来一些苹果,小雅发现,无论自己是2个2个数、3个3个数、4个4个数、5个5个数,都恰好数完,如果苹果的数量在55~65之间,那么妈妈一共买回来多少个苹果?练习4: 呆呆熊买了糖果若干,呆呆熊发现如果每天吃5颗糖,恰好可以整数天吃完,如果每天吃7颗糖,也恰好可以整数天吃完,如果糖果的数量不超过50颗,那么呆呆熊买了多少颗糖?例题5: 小聪练习俯卧撑,如果小聪做俯卧撑的总数是100以内9的倍数,并且它还有因数5,那么小聪可能做了多少个俯卧撑?练习5: 呆呆熊去采野花,采的野花数是50以内7的倍数,并且它还有因数4,那么呆呆熊采了多少朵野花?121. 根据100 ÷ 20 = 5回答,20和5都是( )的因数.2. 根据5 ×8 = 40回答,5和( )是40的因数.3. 如果一个数的最大因数和最小倍数都是27,那么这个数是( ).4. 顽皮猴家有一盒糖果,共28颗糖,熊妈妈规定,大熊每天可以吃相同数量的糖果,但是不允许一天吃完,那么大熊一共有多少种吃法?2.6×3= 48+1.6= 4.1×2= 80×25=0.35×0.2= 1-0.93=0.25÷40= 1.25×100= 50÷1000= 5.6+99= 45.03+0.52= 40100÷25= 14.1-10.02= 90-0.9=5.6÷0.8= 51÷0.001= 5.6÷1.4= 35×0.001= 0.48÷0.8= 54÷0.1=4.4÷0.11= 54×0.1=1.1×40= 8.2+1.8=2.2×6= 100-35.22= 138-8.9= 2.5×0.4= 0.35÷0.1= 2.4×5=0.36×0.01= 0.22×4= 75.35-23.04= 0.9-0.52= 4.007-0.09= 3.99×1=17÷1000= 0×3.52=0.56+0.4= 20÷0.1=14第3讲质数与合数1. 使学生理解质数合数的意义,会判断一个数是质数还是合数.2. 能够熟练判断质数合数,能够找到100以内的质数.一、定义质数:一个数,如果只有1和它本身两个因数,这个数叫做质数(或素数). 合数:一个数,如果除了1和它本身以外还有别的因数,这个数叫做合数. 1既不是质数,也不是合数.二、100以内的质数例题1: 填空.(1)自然数1~20中,最小的合数是_____ ,最小奇数是_____ ,是偶数又是质数的是_____ ,是奇数又是合数的是_____.(2)用排除法找出20以内的质数: _____ .练习1:判断.(1)3的倍数一定是合数_____(2)所有的偶数一定是合数_____(3)所有的奇数都是质数_____(4)有的质数都是奇数_____(5)11的因数都是质数_____例题2: 填空.(1) 在1、2、3、13、27、53、49、80这八个数中,_____是质数,_____是合数.(2) 在自然数中,最小的质数是_____ ,最小的合数是_____.(3) 掌小萌有三张卡片,上面各印有一个数字7、8、9、从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?练习2: 自然数N是一个两位数,它是一个质数,而且N的个位数字与十位数字都是质数,这样的自然数有多少个?16例题3:(1)如果两个不同的质数相加等于26,那么这两个质数的乘积可能是多少?请全部写出.(2)如果两个不同的质数相加等于25,那么这两个质数的乘积可能是多少?请全部写出.(3)三个互不相同的质数相加,和为40,这三个质数的乘积可能是多少?请全部写出. 练习3: 如果三个互不相同的质数相加,和为52,这三个质数可能是多少?例题4: 请把下面的数分解质因数:(1)360; (2) 539 (3) 999 (4) 10101练习4: 请把下面的数分解质因数: (1) 373; (2) 12660.思考: 三个连续自然数的乘积等于39270,那么这三个数的和等于多少?181. 如果两个不同的质数相加等于19,那么这两个质数的乘积是多少?2. 请把下面的数分解质因数.260 99 873. 在自然数49,57,87,101,103,121中,质数有多少个?20÷0.1= 1×0.001=1÷20= 1÷0.001= 0.1÷20= 0.001÷1= 54÷1000= 0.001÷0.1= 25.23+0.77= 3.4-1.4= 98.54-63.45= 7.82-7.2= 30÷0.003= 2.19+9.1= 612÷6= 10.1-0.89= 12×80= 0.68+0.42= 1.5×100= 8.1-5.1= 840÷40= 0.728-0.24= 8.94-6.73= 0.8+0.18= 8.95-0.73= 0.89-0.25= 3.61-0.30= 1-0.98=7.78-5.15= 0.048+0.52= 4.68+7.10= 5×400=9.63+6.28= 19.9+11.1= 7.71-2.69= 187÷1000= 9.91-8.74= 1+3.89= 3.6÷0.3= 0.75÷0.25= 0.96÷2= 0.64÷0.8=20第4讲分数的认识1. 在学生原有分数知识基础上,使学生知道分数的产生,.理解分数的意义,知道分子、分母和分数单位的含义2. 经历认识分数意义的过程,培养学生的抽象、概括能力.一、分数的意义1. 单位1: 一个物体、一些物体等都可以看作一个整体,这个整体可以用自然数1来表示,通常把它叫做单位1.2. 分数的意义: 把一个整体(单位1)平均分成若干份,这样的一份或者几份都可以用分数表示.二、分数单位: 把单位1平均分成若干份,表示其中的1份数的数叫做分数单位.三、分数与除法的关系:(1) 当用分数表示整数除法的商时,要用除数作分母,被除数作分子;(2) 一个分数可以看作两个数相除,分子相当于除法算式中的被除数,分母相当于除数,分数线相当于除号.四、求一个数是另一个数的几分之几用除法:通常两个数相除,如果商是整数,则两数的关系用几倍来表示;如果商是小数,则两个数的关系就用几分之几表示.例题1: 根据分数的意义填一填.(1) 婴儿每天的睡眠时间约占全天的5 8把_____看作单位“1”,平均分成_____份,睡眠时间是这样的_____份.(2) 五(1)班喜欢跳绳的人数占全班人数的2 9把_____ 看作单位“1”,平均分成_____ 份,喜欢跳绳的人数是这样的_____份.练习1: 一张正方形纸,连续对折两次后展开,每份是这张纸的_____ ;如果连续对折三次之后展开,将其中的2份涂上颜色,那么未涂色部分是这张纸的_____.例题2: 填空.(1)1里面有_____ 个15,1里面有_____ 个17;(2) 59的分数单位是_____,有_____个这样的分数单位,再添上_____个这样的分数单位就刚好是1.(3) 13个115是_____,38里有_____ 个_____.练习2: 填空.(1)1116的分数单位是_____,它减去6个这样的单位,结果是_____.(2)57的分数单位是______,它加上_____个这样的分数单位就成为最小的质数.例题3: 把6米长的彩带平均分给5个小朋友,每个小朋友分到_____米,占全部彩带的_____.22练习3: 把4米长的绳子平均分成5段,每段占这根绳子的_____,每段长______米;把3千克苹果平均分成10份,每份占这些苹果的_____,每份重______千克.例题4: 五年级(1)班举行绘画比赛,一共有30人参赛,其中女生有13人,且有5名女生、7名男生获奖:(1)男生参赛人数是女生参赛人数的几倍?女生参赛人数占总参赛人数的几分之几?(2)男生获奖人数占五年级(1)班总获奖人数的几分之几?练习4: 小学举行运动,五年级(2)班一共有53人参赛,其中有30人是女生.比赛结束后,统计发现,女生有13人获奖,男生有11人获奖:(1) 女生参赛人数是男生参赛人数的几倍?男生参赛人数是总参赛人数的几分之几?(2) 女生获奖人数占五年级(2)班总获奖人数的几分之几?例题5: 小心陷阱.(1)如果把1 袋米当成一个整体的话,就是单位“1”;如果把2 袋米当成一个整体的话,就是单位“2”. ( )(2)把1块蛋糕分成5份,每份占15. ( )(3)不同分数的分数单位一定不一样. ( )例题6: 思考.有同样大小的红、黑、白三种颜色的珠子共89颗,按1颗红珠、3颗白珠、2颗黑珠的顺序排列在一起.那么三种珠子各占总数的几分之几?1.919的分数单位是( ),它至少再添上( )个这样的分数单位就是一个质数.2. 呆呆熊买了20个苹果、23个梨,苹果的数量是梨的几分之几?3. 一个蛋糕平均分给7个小朋友,每个小朋友分得这块蛋糕的几分之几?240.081×10= 430-250= 75÷10= 0.17+0.06= 0.96÷0.8= 1.02-0.09=0.8×7= 7200÷800=1.5×7= 0.17+0.6= 1.32×8= 0.83-0.6= 0.7×8= 17×300= 10.3×2= 0.98-0.09= 5×0.6= 0.2+0.78= 0.9×0.3= 600×700= 3.5×0.2= 10.2+0.02=2.01×0= 0.15+0.7= 10×0.05= 670+250= 0.13×7= 10.2+0.2= 0.21×100= 9.2-6=0.7×4= 8500÷500= 0.05×4= 3.2-3.2=4×0.3= 3.7+2.3= 6.3÷7= 0.125×8= 0.56÷28= 0.72÷3.6= 5.6÷100= 4.8÷0.3=26第5讲2、3、5的倍数特征1. 结合具体实例,了解2、3、5的倍数特征,能找出100以内的了解2、3、5的倍数.2. 在探索新知识的过程中,初步了解观察、类比、猜测和归纳等探索规律的基本方法.一、2,3,5的倍数特征(1)5的倍数特征: 个位上是0或5的数都是5的倍数;(2) 2的倍数特征: 个位上是0、2、4、6、8的数都是2的倍数;(3) 2和5共同的倍数特征: 个位上是0的数是2和5共同的倍数的特征;(4) 3的倍数的特征: 一个数各个位上数字的和是3的倍数,这个数就是3的倍数.例题1: 练一练.6、18、27、40、215、179、800、1000、873(1)2的倍数有______________________(2)5的倍数有______________________(3)既是2的倍数,又是5的倍数有________________________练习1: 练一练.(1) 既是2的倍数,又是5的倍数的最大两位数是_____;(2)要使12□是5的倍数,□里可以填______;(3)如果35□既是5的倍数,也是2的倍数,□里可以填_____;例题2: 173□是一个四位数,先后依次在方框中填入3个数字,使得分别是2,3,5的倍数,那么填入的三个数之和最大是多少?练习2: 23□是一个三位数,先后依次在方框中填入3个数字,使得分别是2,3,5的倍数,那么填入的三个数之和最大是多少?例题3: 四位数3AA1能被3整除,求A是多少?28练习3: 五位数51A8A能被3整除,求A是多少?例题4: 在□内填上适当的数字,使五位数23□6□既能被3整除又能被5整除. 练习4: 若四位数9a8a能被15整除,则a代表的数字是多少?例题5: 从0,3,5,7四个数字中任选三个,排成能同时被2、3、5整除的三位数,你能找出多少个这样的三位数呢?练习5: 在865后面补上3个数字,组成一个六位数,使它能分别被3、2、5整除,且使这个数值尽可能的小.301. 有5个自然数:48、124、7836、4105、89765,其中能被2整除的有哪几个?2. 从2、5、7、三张卡片中任意抽取两张卡片,组成既有因数5的数是_____.3. 要使四位数514□是3的倍数,□里可以填_____ ;要使514□有因数5,□里可以填_____.25×100= 9.5-0.5=3.2-0.32= 3.5+2.4=2+2.8= 1-0.95=380-290= 0.3+0.27= 0.35+0.5= 0.47+0.13= 0.35+0.63= 4.5+4= 3500÷70= 4-0.6=3.1+3= 0.95+0.05= 3.8+0.38= 2.5+3.2= 7500÷250= 0.74+0.16= 3.8+1= 23×100=0.95-0.05= 9.8-4.8=450+780= 480÷40=3.1+0.3= 0.53÷100=3+0.3= 5.1+2.3= 630÷9= 125×80=4.5-0.4= 0.078÷10= 9.5-5= 70×12=330×9= 0.25×100= 9.53-1.53= 3.4-2.8=0.36÷0.4= 3.6÷24=第6讲流水行船321. 掌握行船流水问题的基本规律,能理清水速、船速之间的关系.2. 经历应用问题的解决,掌握流水行船问题的基本解决方法和步骤,学会用画图等方法解决问题.一、流水行船问题:船在江河里航行时,除了本身的前进速度外,还受到流水的推送或顶逆,在这种情况下计算船只的航行速度、时间和所行的路程,叫做流水行船问题.二、四个速度:船速:船在静水中航行的速度,即船本身的速度.水速:水流动的速度,即没有外力的作用水中漂浮的速度.顺水速度:当船航行方向与水流方向一致时的速度,即顺水行船的速度.逆水速度:当船航行方向与水流方向相反时的速度,即逆水行船的速度.三、四个公式:顺水速度=静水速度+水速逆水速度=静水速度-水速水速=(顺水速度-逆水速度)÷2 船速=(顺水速度+逆水速度)÷2例题1: 甲乙两港间的水路长100千米,一只船顺流而下从甲港开往乙港,已知船的静水速度40千米/时,水流速度是10千米/时,请问:这艘船多长时间才能到达乙港?练习1: 甲乙两港间的水路长100千米,一只船逆流而上从甲港开往乙港,已知船的静水速度30千米/时,水流速度是5千米/时,请问:这艘船多长时间才能到达乙港?例题2: 甲乙两港间的水路长100千米,一只船顺流而下从甲港开往乙港用了5小时,已知水流速度是2千米/时,请问:这艘船的静水速度是多少?练习2: 甲乙两港间的水路长200千米,一只船逆流而上从甲港开往乙港用了10小时,已知水流速度是2千米/时,请问:这艘船的静水速度是多少?例题3: 甲乙两港间的水路长100千米,一只船顺流而下从甲港开往乙港用了5小时,逆流而上从乙港开往甲港用了10小时,请问:这艘船的静水速度和水速分别是多少?34练习3: 甲、乙之间的水路是234千米,一只船从甲港到乙港顺水需9小时,从乙港返回甲港逆水需13小时,问船速和水速各为每小时多少千米?例题4: 某船在静水中每小时行18千米,水流速度是每小时2千米.此船从甲地逆水航行到乙地需要15小时.求甲、乙两地的路程是多少千米?此船从乙地回到甲地需要多少小时?练习4: 某船在静水中的速度是每小时15千米,它从上游甲港开往乙港共用8小时.已知水速为每小时3千米.此船从乙港返回甲港需要多少小时?例题5: A、B两码头间河流长为200千米,甲、乙两船分别从A、B两码头同时相向航行,甲的静水速度是30千米每小时,乙的静水速度是20千米每小时,水流速度为5千米每小时,请问:出发后多长时间两船相遇?练习5: A、B两码头间河流长为100千米,甲、乙两船分别从A、B两码头同时起航.如果相向而行5小时相遇,如果同向而行10小时甲船追上乙船,求两船在静水中的速度.1. 一只渔船顺水行25千米,用了5小时,水流的速度是每小时1千米.此船逆水航行30千米需要多少小时?362. 一只船,顺水每小时行30千米,逆水每小时行20千米.这只船在静水中的速度和水流的速度各是多少?3. 某船在静水中的速度是每小时18千米,它从上游甲港开往乙港共用10小时.已知水速为每小时3千米.此船从乙港返回甲港需要多少小时?0.6-0.37= 3.5+2.4=0.052×10= 5+0.07=10+0.08= 1-0.61=1-0.75= 0.47+0.23=0.5×1000= 0.25+0.75=0.82+0.3= 3.7+0.33=13.5+6.5= 0.51+0.33=3.05×100= 1-0.6=1.2-0.8= 8-4.6=21.6-12.6= 5.8-3.6=63÷100= 0.52+0.4=0.83-0.5= 6.45+5.5=5.6÷100= 4.5-1.3=0.76+0.14= 3.4-2.8=80÷1000= 9.53-1.53=2.7+0.4= 8.8-6.7= 0.72-0.43= 10+0.08= 30×100= 9.5-7.3= 0.92-0.2= 8.8-6.7=3.5+4.8= 3.4-2.8=38第7讲期末闯关1. 复习前六讲内容,联系相关知识点形成知识网,查漏补缺.2. 通过复习,使学生对寒假所学的概念、计算法则、应用题知识得到进一步巩固.1: 如图,平行四边形ABCD中,AD的长度为20厘米,高CH的长度为9厘米,.那么两个阴影三角形面积之和为多少平方厘米?H B DAE CF2: 如图,三角形ABC 中,BD=6,DC=3,AE=4,EC=2,若三角形ABD 的面积是12,那么三角形DEC 的面积是多少?3: 填空.(1) 根据12 ÷ 3 = 4请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(2) 根据6 × 4 = 24请回答,( )和( )是( )的因数,( )是( )和( )的倍数;(3) 如果一个数的最小倍数和最小因数的差是10,那么这个数的最大因数是( ).4: 请写出42的所有因数.5: 掌小萌有三张卡片,上面各印有一个数字7、8、9从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?40例题6: 填空.(1)1116的分数单位是_____,它减去6个这样的单位,结果是_____.(2)57的分数单位是______,它加上_____个这样的分数单位就成为最小的质数.例题7: 把6米长的彩带平均分给5个小朋友,每个小朋友分到_____米,占全部彩带的_____.例题8: 练一练.(1)既是2的倍数,又是5的倍数的最大两位数是_____;(2)要使12□是5的倍数,□里可以填______;(3)如果35□既是5的倍数,也是2的倍数,□里可以填_____;例题9: 173□是一个四位数,先后依次在方框中填入3个数字,使得分别是2,3,5的倍数,那么填入的三个数之和是多少?例题10: 甲、乙之间的水路是234千米,一只船从甲港到乙港顺水需9小时,从乙港返回甲港逆水需13小时,问船速和水速各为每小时多少千米?例题11: 某船在静水中每小时行18千米,水流速度是每小时2千米.此船从甲地逆水航行到乙地需要15小时.求甲、乙两地的路程是多少千米?此船从乙地回到甲地需要多少小时?421. 如图,已知平行四边形ABCD 的面积为36,三角形AOD 面积为8.求三角形BOC 面积.2.五年级(1)班的36名同学进行文艺汇演,表演的时候全班排成长方形方阵(包括正方形)如果规定每行每列不得少于3人,那么一共有几种排法?442.7+0= 0.75×100= 12.5×8= 0.02×0.5=2.3×4=3.6×0.3=3.25×0= 5.6×100= 0.4×50= 0.75÷0.25= 30×0.1= 0.125×8= 2.6×3= 0.86÷2=4.1×2= 0.56÷28= 0.35×0.2= 0.36÷0.4= 7.5×0.1= 0.7×9= 2.5×2= 3.6÷24= 0.5×10= 0.8×1.1= 0.6×8= 46.7-3.8= 2.8×10= 12.8÷4= 0.7×0.8=5.2÷13= 5.6+0.4= 1.64+4.1= 4.7+2.3= 10÷20= 4.5×2= 24÷15= 7.2×0.8= 0.35×0.6= 6×3.4= 4.7+2.3= 0.62-0.32= 4.5×2=。
五年级寒假班讲义第1讲定义新运算

第一讲定义新运算数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的极深。
——高斯(德国数学家)【知识对对碰】基本概念:定义新运算通常是用特殊的符号表示特定的运算意义。
在每一道题中都会有它自己规定的新的运算规则,这个新的运算符号包含有多种基本(混合)运算。
通常这种新的运算规则会和加减乘除四则运算相关联。
基本思路:严格按照新定义的运算规则,把已知的数代入,转化为加减乘除的运算,然后按照基本运算过程、规律进行运算。
如果没有给出用字母表示的规则,则应通过给出的具体的数字表达式,先求出表示定义规则的一般表达式,方可进行运算。
关键问题:正确理解定义的运算符号的意义。
注意事项:1.新定义运算中,括号的作用不变。
2.新的定义运算都有自己的特点,不一定符合四则运算规律,特别注意运算顺序。
3.每个新定义的运算符号只能在本次定义中使用。
分类:1.直接运算型2.反解未知数型3.观察规律型4.其他类型综合【名题典中典】模块一、直接运算型【例1】对于任意数a,b,定义运算“*”:a*b=a×b-a-b。
求12*4的值。
思路导航:根据题目定义的运算要求,直接代入后用四则运算即可。
12*4=12×4-12-4=48-12-4=32。
【我能行】1、设a,b表示整数,规定“※”的运算为:a※b=a÷b×2+3×a-b。
计算169※13.2、对于任意整数A、B规定:A¤B=3A+2B-2。
求:10¤113、设ab都表示数,规定a△b表示a的4倍减去b的3倍,计算5△6,6△5。
(思考:这个新运算“△”有交换律吗?)【例2】对于两个数a、b,规定a☆b表示3×a+2×b,试计算(5☆6)☆7,5☆(6☆7)。
思路导航:把括号内的部分看成一个整体,先做括号内的运算。
(5☆6)☆7=(5×3+6×2)☆7=27☆7=27×3+7×2=955☆(6☆7)=5☆(6×3+7×2)=5☆32=5×3+32×2=79说明:本题定义的运算不满足结合律。
