数字设计——原理与实践第四版习题答案第3章
数字设计原理与实践 第四版

数字设计原理与实践第四版
数字设计原理与实践第四版是一本介绍数字电路设计基础知识和实践的教材。
本书主要分为五个部分,分别是数字系统基础、组合逻辑设计、时序逻辑设计、专用逻辑器件与PLD设备以及数字系统的设计示例。
在数字系统基础部分,本书首先介绍了数字系统的基本概念和表示方法,包括二进制数表示、布尔代数和逻辑运算。
接着讲解了数字电路的基本组成部分,如逻辑门、多路选择器、译码器等,并介绍了常用的编码方式如BCD码和格雷码。
在组合逻辑设计部分,本书详细介绍了基本的组合电路设计方法,包括真值表、卡诺图和最小化布尔函数等。
同时还介绍了常见的组合逻辑器件和集成电路,如多输入AND、OR和XOR门等。
在时序逻辑设计部分,本书介绍了时钟信号的基本概念和使用方法,同时还详细讲解了触发器、计数器、移位寄存器等时序电路的设计和应用。
在专用逻辑器件与PLD设备部分,本书介绍了常见的专用逻辑器件如加法器、比较器和MUX等,并详细介绍了可编程逻辑器件(PLD)的原理和应用,包括可编程逻辑阵列(PLA)和可编程逻辑芯片(CPLD)等。
在数字系统的设计示例部分,本书通过实际案例分析和设计实例,将前面所学的知识应用到具体的数字系统设计中,如计算
机CPU设计、外设接口设计等。
综上所述,数字设计原理与实践第四版是一本全面介绍数字电路设计原理和实践的教材,内容丰富、结构清晰,适合作为数字电路设计和相关专业学生的教材和参考书。
数字设计原理与实践 第四版 (john F.Wakerly ) 课后答案

3.65 在图 3-32(b)中,有多少电流与功率被浪费了。 解:浪费的电流为流过 4kΩ电阻的电流:
I=(5-0.24)/4=1.19 mA 浪费的功率为上述电流经过两个电阻产生的功率: P = RI2 = 4.2 x (1.19)2 = 5.95 mW
解:由图中可以看到,输出 3.5V 对应的输入为 2.4V,输出 1.5V 对应 的输入为 2.5V; 所以,高态噪声容限为:3.5-2.5=1 V ;低态噪声 容限为:2.4-1.5=0.9 V。
3.26 利用表 3-3 计算 74HC00 的 p 通道和 n 通道的导通电阻。 解:采用极端值计算(对商用芯片,最低电源电压设为 4.75V) 表中所列输出电压与电流关系如图所示:
=157255.5756748 2.5 将下面的数转换成十进制数。
(a) 11010112=107 (b) 1740038=63491 (c) 101101112=183
(d) 67.248=55.3125 (e)10100.11012=20.8125 (f)F3A516=
62373
(g) 120103=138
(h) AB3D16=43837
(i) 71568=3694
(j) 15C.3816=348.21875
2.6 完成下面的数制转换。
(a) 125= 1 111 1012 (b) 3489= 66418 (c) 209= 11 010 0012
(d) 9714= 227628
(e) 132= 10 000 1002 (f) 23851= 5D2B16
(g) 727= 104025
(h) 57190=DF6616 (i) 1435=26338
数字电子技术基础(第四版)课后习题答案_第三章
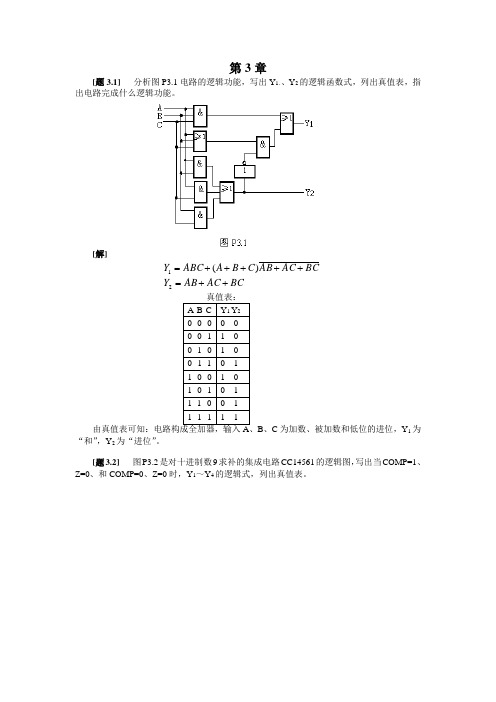
第3章[题3.1] 分析图P3.1电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式,列出真值表,指出电路完成什么逻辑功能。
[解]BCAC AB Y BCAC AB C B A ABC Y ++=+++++=21)(B 、C 为加数、被加数和低位的进位,Y 1为“和”,Y 2为“进位”。
[题3.2] 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1、Z=0、和COMP=0、Z=0时,Y 1~Y 4的逻辑式,列出真值表。
[解](1)COMP=1、Z=0时,TG 1、TG 3、TG 5导通,TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===, 4324A A A Y ++=(2)COMP=0、Z=0时,Y 1=A 1, Y 2=A 2, Y 3=A 3, Y 4=A 4。
COMP =0、Z=0的真值表从略。
[题3.3] 用与非门设计四变量的多数表决电路。
当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1,输入为其他状态时输出为0。
[解] 题3.3的真值表如表A3.3所示,逻辑图如图A3.3所示。
ABCD D ABC D C AB CD B A BCD A Y ++++= BCD ACD ABC ABC +++=B C D A C D A B D A B C ⋅⋅⋅=[题3.4] 有一水箱由大、小两台泵M L 和M S 供水,如图P3.4所示。
水箱中设置了3个水位检测元件A 、B 、C 。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作;水位低于C 点而高于B 点时M S 单独工作;水位低于B 点而高于A 点时M L 单独工作;水位低于A 点时M L 和M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
[解] 题3.4的真值表如表A3.4所示。
数字设计-原理与实践(第四版)课后习题答案

第1 章习题参考答案:1-6 一个电路含有一个2 输入与门(AND2),其每个输入/输出端上都连接了一个反相器;画出该电路的逻辑图,写出其真值表;能否将该电路简化解:电路图和真值表如下:由真值表可以看出,该电路与一个2 输入或门(OR2)相同。
第2 章习题参考答案:将下面的八进制数转换成二进制数和十六进制数。
(a) 12348=1 010 011 1002=29C16(b) 1746378=1 111 100 110 011 1112=F99F16(c) 3655178=11 110 101 101 001 1112=1EB4F16(d) =10 101 011 101 011 010 0012=ABAD116(e) =111 100 011 0012=(f) =100 101 011 001 100 111 12=将下面的十六进制数转换为二进制数和八进制数。
(a) 102316=1 0000 0010 00112=100438(b) 7E6A16=111 1110 0110 10102=771528(c) ABCD16=1010 1011 1100 11012=1257158(d) C35016=1100 0011 0101 00002=1415208(e)=1001 1110 10102=(f)=1101 1110 1010 1110 1110 11112=将下面的数转换成十进制数。
(a) =107 (b) 1740038=63491 (c) 2=183(d) = (e)= (f)F3A516=62373(g) 120103=138 (h) AB3D16=43837 (i) 71568=3694(j) =完成下面的数制转换。
(a) 125= 1 111 1012 (b) 3489= 66418 (c) 209= 11 010 0012(d) 9714= 227628 (e) 132= 10 000 1002 (f) 23851= 5D2B16(g) 727= 104025 (h) 57190=DF6616 (i) 1435=26338(j) 65113=FE5916将下面的二进制数相加,指出所有的进位:(a) S:1001101 C:100100(b) S: 1010001 C: 1011100(c) S: 0 C: 0(d) S: C:利用减法而不是加法重复训练题,指出所有的借位而不是进位:(a) D:011 001 B:110000 (b) D:111 101 B:1110000(c) D: B:00111000 (d) D:1101101 B:写出下面每个十进制数的8 位符号-数值,二进制补码,二进制反码表示。
数字设计原理与实践复习总资料

能按选定的方向传输数据.
多路复用器
74x151
8输入1位多路复用器,选择输入为C、B、A,其中C是最高 有效位;使能输入EN_L低电平有效;输出为Y及Y_L。
74x153
4输入2位多路复用器,具有分开的1位使能输入(1G、2G).
多路分配器
多路分配器的功能恰好与多路复用器的功
能相反。 b位、n输出的多路分配器,其有b个
A B C
A B C
i
2 1
n
A B C
如:
4. 且有
Mi m
或
M
i
mi
m 4 = ( A B C ) = A B C = M 4
竞争-冒险产生的原因:电路延时
如何判断与消除冒险。
1、如采用卡诺图法,则判断:观察是否存在 “相切”的卡诺圈, 若存在则可能产生冒险。 2、如采用卡诺图法,则消除:在卡诺图中增 加卡诺圈以消除“相切”现象。
数据输入、s个选择输入选择n=2s个b位数据输
出集合之一。在正常操作中,被选中的输出等
于数据输入,其它输出均为0。
奇偶校验电路
异或(XOR)门: Y X Y X Y X 异或非(XNOR)门: Y X Y X Y X
0 A的个数为偶数 A的个数为奇数 A的个数为偶数 A的个数为奇数
5 1 0 1 0 1 0
6 1 0 1 0 1 0
7 0 0 1 1 0 0
8 1 1 0 0 1 1
CP: x: y2: y1: y2*: y1*: z:
1 0 0 0 0 0 0
2 1 0 0 0 1 0
3 0 0 1 1 0 0
数字设计原理与实践 第四版 (john F.Wakerly ) 课后答案

第1章习题参考答案:1-6 一个电路含有一个2输入与门(AND2),其每个输入/输出端上都连接了一个反相器;画出该电路的逻辑图,写出其真值表;能否将该电路简化? 解:电路图和真值表如下:由真值表可以看出,该电路与一个2输入或门(OR2)相同。
第2章习题参考答案:2.2将下面的八进制数转换成二进制数和十六进制数。
(a) 12348=1 010 011 1002=29C 16(b) 1746378=1 111 100 110 011 1112=F99F 16(c) 3655178=11 110 101 101 001 1112=1EB4F 16(d) 25353218=10 101 011 101 011 010 0012=ABAD116(e) 7436.118=111 100 011 110.001 0012=F1E.2416(f) 45316.74748=100 101 011 001 110.111 100 111 12=4ACE.F2C 162.3将下面的十六进制数转换为二进制数和八进制数。
(a) 102316=1 0000 0010 00112=100438(b) 7E6A 16=111 1110 0110 10102=771528(c) ABCD 16=1010 1011 1100 11012=1257158(d) C35016=1100 0011 0101 00002=1415208(e)9E36.7A 16=1001 1110 00110110.0111 10102=117066.3648 (f)DEAD.BEEF 16=1101 1110 1010 1101.1011 1110 1110 11112 =157255.57567482.5将下面的数转换成十进制数。
(a) 11010112=107 (b) 1740038=63491 (c) 101101112=183 (d) 67.248=55.3125 (e)10100.11012=20.8125 (f)F3A516= 62373(g) 120103=138 (h) AB3D 16=43837 (i) 71568=3694 (j) 15C.3816=348.218752.6 完成下面的数制转换。
精品文档-数字电子技术(第四版)(江晓安)-第三章

第三章 布尔代数与逻辑函数化简
15
其对偶式为
_
AB AC
_
( A B) ( A C)
如不加括号,就变成
_
A B A C
这显然是错误的。
第三章 布尔代数与逻辑函数化简
16
3.
由原函数求反函数,称为反演或求反。摩根定律是
进行反演的重要工具。 多次应用摩根定律,可以求出一个函
数的反函数。
例
2求
F
第三章 布尔代数与逻辑函数化简
9
第三章 布尔代数与逻辑函数化简
10
多余项定律可推广为
_
_
AB AC AB AC BC(A A)
_
AB AC ABC ABC
AB(1 C) AC(1• B)
_
AB AC
(证毕)
第三章 布尔代数与逻辑函数化简
11
注意, 上述我们讲的均是公式的基本形式, 在应用时要 注意推广。 例如多余项定律可推广为
8
吸收律在逻辑函数化简中十分有用, 吸收律(1)可将两 项合并为一项, 并消去一个变量; 吸收律(2)可消去相应的 逻辑项; 吸收律(3)可将某些项中的部分因子消去。 特别是 吸收律(1)是卡诺图化简的基础。
求反律又称摩根定律, 它在逻辑代数中十分重要, 它解 决逻辑函数的求反问题和逻辑函数的变换问题。 它的正确性 可用真值表3-3证明。
37
_
_
例 12 F AC ABC D(E F)
_
解 令AC G
,则
F G GBD(E F )
_
G AC
第三章 布尔代数与逻辑函数化简
38
__
__
例 13 F AB AB ABCD ABCD
数字电路逻辑设计课后习题答案第三章

3-1 分析题图3-1所示电路,写出电路输出Y 1和Y 2的逻辑函数表达式,列出真值表,说明它的逻辑功能。
解:由题图3-1从输入信号出发,写出输出Y 1和Y 2的逻辑函数表达式为1Y A B C =⊕⊕ ; 2()()Y A B C AB A B C A =⊕⋅⋅=⊕⋅+B将上式中的A 、 B 、C 取值000~111,分别求出Y 1和Y 2,可得出真值表如题解 表3-1所示。
题解 表3-1ABCA B ⊕()A B C ⊕⋅AB1Y2Y0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 1 0 0 0 1 0 1 111111综上,由题解 表3-1可以看出,该电路实现了一位全加器的功能。
其中,A 和B 分别是被加数及加数,C 为相邻低位来的进位数;Y1为本位和数,Y 2为相邻高位的进位数。
3-2 分析题图3-2所示电路,要求:写出输出逻辑函数表达式,列出真值表,画出卡诺图,并总结电路功能。
解:由题图3-2从输入信号出发,写出输出F 的逻辑函数表达式为()()F A B C D =:::将上式中的A 、 B 、C 、D 取值0000~1111,求出F ,可得真值表和卡诺图分别如题解 表3-2和题解 图3-1所示。
题解 表3-2A B C DA B : C D :F0 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 0 11 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1综上,由题解 表3-2可以看出,当输入A 、 B 、C 、D 中含有偶数个“1”时,输出;否则,当输入A 、 B 、C 、D 中含有奇数个“1”时,输出。
数字设计原理与实践 第四版 (john F.Wakerly ) 课后答案

按照一阶电路三要素法的分析方法,对于电容上的电压分析如下:
初态:VL=0.2V
终态:VH=4.45V
换路后的等效电阻:R=164Ω
电路时间常数: τ = RC = 16.4ns
输出电压随时间变化关系为:
( ) VOUT = VL + VH − VL (1 − e−t /τ )
由上式可以得出从 1.5V 到 3.5V 的上升时间为:
10010
00101 00110 01001 01010 01100 01110
数字逻辑第 3 章参考解答:
3.11 对图 X3.11(a)所示的 AOI 电路图,采用 AND,OR,INV 画出对 应的逻辑图。
解: Z = (A ⋅ B + C + D)'
3.12 对图 X3.11(b)所示的 OAI 电路图,采用 AND,OR,INV 画出对 应的逻辑图。
解: Z = ((A + B)⋅ C ⋅ D)'
3.68 分析图 3-37 所示反相器的下降时间,设 RL=900Ω,VL=2V。 解:该电路图可以等效为下列带开关的一阶电路图。当输出从高态转 为低态时,可以等效为开关 K 从位置 1 转到位置 2。
按照一阶电路三要素法的分析方法,对于电容上的电压分析如下:
初态:VH=4.45V
终态:VL=0.2V
I=(3.84-2.03)/0.487 = 3.72 < 4mA 可以驱动。
3.40 一个发光二极管导通时的电压降约为 2.0V,正常发光时需要约 5mA 的电流。当发光二极管如图 3-54(a)那样连接时,确定上拉电 阻的适当值。 解:根据 3.7.5 所给的条件,低态输出电平 VOLmax=0.37V。 对应等效 电路如下:
数字设计原理与实践第四版中文答案

。动驱以可
Am 4 < 27. 3 = 7 84.0/ � 30.2- 48.3 �= I
�下如 路电效等出输态 高 。动驱以可 Am 4 < 94. 3 = 7 84.0/ � 33.0- 30.2 �= I
�下如 路电效等出输态低 。出 输 态 高 和 出 输 态 低 虑 考 别 分 要 需 � 地 接 Ω 0 2 8 , c c V 接 Ω k 2 . 1 ) f 。动驱能不 Am4 > 7 6.4=1 / �33. 0-5 �=I
') D + C + B ⋅ A ( = Z �解
。图辑逻的应 对出画 VNI,RO�DNA 用采�图路电 IOA 的示所�a�11.3X 图对 11.3
�答解考参章 3 第辑逻字数
。 2�界边坏为界边的半一有�解
1-n
�界边”坏“个 少 多 有 中 盘 码 编 械 机 的 码 编 制 进 二 位 n 用 使 在 � 数 函 的 n 为 作 63.2 0 0 0 / 1 1 1、 0 1 1 / 1 0 1 、 0 0 1 / 1 1 0 、 0 1 0 / 1 0 0 �解 。界边 ”坏“ 有 所 的 置 位 确 正 不 生 产 会能 可 中 盘 码 编 械 机的 5 - 2 图 出 列 5 3 . 2 0 4 0 5 = 2 x 3 x 4 x 5 x 6 x 7 = N � 为 量 数 式 方 � 列排 行进个 6 取选中从�码制进二位 3 的用可种 7 有只�下件条此在�解 �式方码编制进二位 3 的同不种少多有�器 制 控 灯 通 交 的 21-2 表 于 对 � 0 个一 有 含 要 少 至 中 字 码 编 个 每 若 4 3 . 2 。同相时态状 7 与量数类种�态状 8 于对 02304 =2x3x4x5x6x7x8=N�列排的 7 取中 8 个一是这�态状 7 于对
数字设计基础与运用第3章习题解答
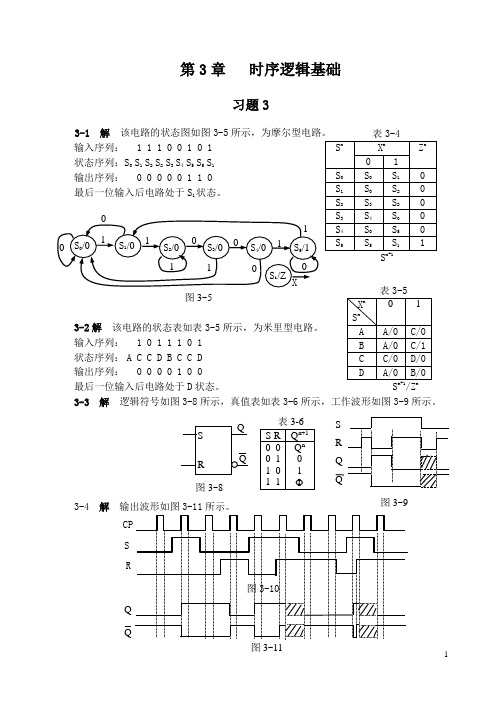
1第3章 时序逻辑基础习题33-1 解 该电路的状态图如图3-5输入序列: 1 1 1 0 0 1 0 1 状态序列:S 0 S 1 S 2 S 2 S 3 S 4 S 5 S 5 S 1输出序列: 0 0 0 0 0 1 1 0最后一位输入后电路处于S 1状态。
3-2解 该电路的状态表如表3-5所示,为米里型电路。
输入序列: 1 0 1 1 1 0 1 状态序列: A C C D B C C D 输出序列:0 0 0 0 1 0 0 最后一位输入后电路处于D 状态。
3-3 解 逻辑符号如图3-8所示,真值表如表3-6所示,工作波形如图3-9所示。
3-4 解 输出波形如图3-11所示。
3-5 解 Q端波形如图3-13所示。
3-19(a)、(b)、(c)所示。
3-9 解 Q3-10 解 Q1、Q0的输出波形如图3-23图3-22X图3-161J1KC1QQCPJKRSCLRPR图3-20233-11 解 8进制异步行波加法计数器电路如图3-24所示。
3-12解 4进制异步行波可逆计数器电路如图3-25所示。
3-13 解 5进制异步加法计数器电路如图3-26所示。
3-14 解 8进制同步减法计数器电路如图3-27所示。
3-15 解 4图3-24CLK 1D Q 0 Q 0 C1 1D Q 1 Q 1C1 1DQ 2Q 2C143-16 解 用7493构成的13进制和172进制计数器电路分别如图3-29和图3-30所示,因为13=(1101)2,172=16⨯10+12。
3-17 分别用74163构成8421BCD 和5421BCD 加法计数器,并画出全状态图。
解 8421BCD 加法计数器及全状态图如图3-31所示,采用同步清0方式变模。
5421BCD 加法计数器及全状态图如图3-32所示,采用预置方式变模。
根据5421BCD 码的编码规律,当Q D Q C Q B Q A =0100时,下一个CP 脉冲应置入1000;当Q D Q C Q B Q A =1100时,下一个CP 脉冲应置入0000。
数字设计原理与实践第四版习题答案

04
第三章习题答案
习题一答案
要点一
答案
这道题考查的是二进制数的加法运算,根据二进制数的加 法规则,当两个二进制数的某一位相加和大于等于2时,需 要向高位进位,因此,二进制数10100101与10110000相 加的结果是10110101。
要点二
答案解释
这道题要求计算二进制数10100101与10110000的和。首先, 从最低位开始逐位相加,当某一位的和大于等于2时,需要向 高位进位。具体来说,第一位相加得0,不进位;第二位相加 得0,不进位;第三位相加得1,不进位;第四位相加得1, 进位;第五位相加得0,不进位;第六位相加得1,进位;第 七位相加得1,不进位;第八位相加得1,不进位。因此,最 终结果是10110101。
03
04
05
1.0 互补性:对于任何逻 辑门,其互补门的输出 与原门的输入反相。例 如,AND门的互补是 OR门,OR门的互补是 AND门。
2.0 消抖动性:在输入信 号的上升沿或下降沿, 逻辑门电路的输出不会 发生多次跳变,而是保 持稳定状态。
3.0 扇入扇出系数:一个 逻辑门可以驱动的最大 逻辑门数称为扇出系数; 一个逻辑门可以接收的 最大逻辑门数称为扇入 系数。
习题三答案
•· 数字逻辑门电路的应用
1.0 AND门在数据传输中的应用: 用于控制信号的传输,确保只有 在两个控制信号都有效时,数据 信号才会被传输。
2.0 OR门在报警系统中的应用: 当任何传感器触发时,OR门将输 出高电平,触发报警系统。
3.0 NOT门在时钟信号中的应用: 用于产生与主时钟信号反相的时 钟信号,用于触发边沿触发的数 字逻辑门电路。
THANKS
感谢观看
05
