电学计算题专题训练(包含答案)
中考物理必做10道经典电学计算题(附答案)

1.饮水机是一种常见的家用电器,其工作电路可简化为如图1所示的电路,其中S是一个温控开关,当开关S接a时,饮水机正常工作,将水迅速加热;当水达到一定温度时,开关S 自动换到b,饮水机处于保温状态,若饮水机正常工作时发热板的电功率为550 W,而保温时的发热板的功率是正常工作时电热板功率的0.1倍,求电阻R1的阻值.【答案】190Ω图12.在如图2的电路中,已知滑动变阻器的最大阻值为18Ω,电流电压恒为6 V,灯泡上有“6 V3 W”的字样.图2(1)闭合S1、S2滑片P滑到b端时,电流表示数为1 A,求电阻R1的值.(2)闭合S1断开S2,滑片P滑到a端时,电压表的示数为多少?电阻R上消耗的电功率是多大?【答案】(1)12Ω(2)2.4 V,0.48 W3.如图3所示的电路中,滑动变阻器R3的最大阻值是20Ω,电源电压为8 V且保持不变,当滑动变阻器的滑片P移至a端时,将S1闭合,S2断开,电流表的示数为0.8 A,当滑动变阻器滑片P移至b端时,将S1、S2都闭合,电流表的示数为2A,求:R1、R2的阻值.图3ΩΩ.I U R 108082===则解:(1)当滑片P 移至a 端,闭合S1,断开S2时,R3连入电路的阻值为0,R1短路,只有R2连入电路,其等效电路为图4(a)所示(2)当滑片P 移至b 端,闭合S1、S2时,R2短路,R1与R3并联,且R3=20Ω,其等效电路如图4(b)所示I3=8/20 A=0.4 AI2=2A-0.4 A=1.6 AR3=U/I3=8/1.6Ω=5Ω图44.如图5所示电路,电源电压U=4.5 V 且保持不变,R 1=5Ω,变阻器R2的最大阻值为20Ω,电流表量程为0~0.6 A ,电压表量程为0~3 V ,通过分析计算:说明变阻器R2允许的取值范围图5解:(1)当滑片P 向左端移动时,R2减小,电路中电流增大,R2两端的电压减小,电流表的量程为0~0.6 A ,即电路中的电流最大值为0.6 A ,那么此时R2接入电路中的值为最小值、R2minU1=I1·R1=0.6×5 V=3 VU2=4.5 V-3V=1.5 V∴R2min=U2/I2=1.5/0.6Ω=2.5Ω(2)当滑片P 向右端移动时,R2增大,R2两端的电压增大,电压表的量程为0~3 V ,即R2两端的电压最大值为3 V ,此时R2接入电路中的阻值为最大值R2maxU ′1=4.5 V-3 V=1.5 VI ′1=1.5/5 A=0.3 A∴R2max=U ′/I ′2=3/0.3Ω=10Ω综上所述R2的取值范围为2.5Ω≤R2≤10Ω.2020.R U L =+∴⎩⎨⎧==⎩⎨⎧==Ω1063010L L R V U ΩR V U (舍去)或W .W R U P P L 6310622====额额实t 0020R U R =V V t QR U 22604846000=⨯==∴ΩΩ43562219848400=⨯=⨯=∴U U R R R 5.如图6所示电路,电源电压U 恒定且小于10 V ,R1=1 5Ω,滑动变阻器的最大阻值为20Ω,小灯泡L 的电阻小于15Ω,当开关S 断开,滑动变阻器的滑片位于b 端时,○A 表示数为0.2 A ,当开关S 闭合,滑动变阻器的滑片位于a 端时,○A 表示数为1 A ,且小灯泡正常发光,求小灯泡的额定功率(忽略温度对灯丝电阻的影响).图6解:(1)当开关S 断开,滑动变阻器置于b 端时,灯泡与RL 串联①(2)当开关S 闭合,滑动变阻器置于a 端时,灯泡与R1并联115=+U R U L ②解①②式方程组得 此时灯泡正常发光则U 额=6 V6.如图7所示是一个电热毯示意图,R0是电热毯中的电阻丝,R 是与电阻丝串联的电阻,电热毯上标有“220V100W ”字样,S 是控制电热毯处于加热状态或保温状态的开关.(1)用学过的公式推理说明开关S 断开时,电热毯是处于加热状态还是保温状态?(2)若要求在保温时电流通过电阻丝R0每1分钟有60 J 的电能转化为内能,电阻R 的阻值为多大?【解析】(1)当S 闭合时,R0的功率,P0=U2/R0当S 断开时,R0的功率,P ′0=U20/R0 图7∵U0<U ∴P ′0<P0即S 断开时,电热毯处于保温状态.(2)电阻丝的电阻R0=U2额/P 额=2202/100Ω=484Ω保温状态时,电阻丝两端的电压为U0R 两端电压 UR=220 V-22 V=198 V492112221222=⋅⎪⎪⎭⎫ ⎝⎛==∴P P R R U R I P 222122*********⎪⎪⎭⎫ ⎝⎛=∴=⎪⎪⎭⎫ ⎝⎛∴R U I R U R I ΩΩ332632332122221=⨯⨯==∴=I U R R U I 即A A R U I 236222===ΩΩ6233221221=-⨯=-⋅=∴I I R I R 7.如图8所示的电路中,电源电压保持不变,闭合开关S ,已知当滑片P 分别滑至a 端和b 端时,电阻R1消耗的电功率之比为P1∶P2=9∶4,当滑片在a 端时,电流表示数为3 A ,滑片P 在b 端时电压表示数为6 V ,求:(1)R1的阻值和滑动变阻器的最大阻值R2;(2)电源电压是多少伏?图8【解析】(1)当滑片P 在a 端时P1=I21R1当滑片P 在b 端时I2=U2/R2滑片在a 端时U=I1·R1滑片在b 端时U=I2(R1+R2)I1·R1=I2(R1+R2)(2)由I=U/R 得U=I1·R1=3×6 V=18 V8.如图9所示的电路中,电源电压为12 V 且保持不变,滑动变阻器最大值为R2,闭合开关S 后,当滑动变阻器的滑片P 由a 端向b 端滑动时,○A 表示数由1.5A 变为0.5 A.求:图9(1)滑动变阻器的最大阻值.(2)电压表的示数的变化范围.(3)滑动变阻器的滑片P滑到b端时,通电2minR1产生的热量.【答案】(1)16Ω(2)0~8 V(3)240 J9.如图10所示,灯L1标有“6V3W”灯L2标有“12V4W”,将开关闭合后L1恰好正常发光,求:(1)电压表示数.(2)电流表A2的示数. 图10(3)灯L2的实际功率和L2通电1min产生的热量.【答案】(1)6 V(2)0.17 A(3)60 J10.如图11所示,电源电压为6 V且保持不变;灯L1上标有“8V8W”字样,滑动变阻器的最大阻值为20Ω.图11(1)当滑片P移到b端,开关S1闭合,S2断开时,○A示数为0.2 A,求电压表的示数和L2的电阻.(2)当滑片P移到a端,开关S1、S2均闭合时,求灯L1消耗的实际功率和电流表的示数. 【答案】(1)4 V,10Ω(2)4.5 W,0.6 A。
(中考物理)电学综合计算 提分专题(解析版)

专题十二 电学综合计算题题型一:电学基础计算1.(2021·广东中考真题)如图甲电路,电源电压不变,闭合开关S ,将滑动变阻器R 的滑片P 由a 移动到b 时,R 0的电功率和电流的P-I 关系图像如图乙所示,求: (1)电源电压;(2)滑动变阻器的最大阻值。
【答案】(1)9V ;(2)72欧 【详解】解:(1)当滑片P 在b 端时,只有R 0工作,电流最大为b 0.5A I =电源电压为b 4.5W =9V 0.5A P U I == (2)R 0的阻值为0b 9V 18Ω0.5AU R I === 当滑片P 在a 端时,电阻最大,电流最小,此时a 0.1A I =总电阻为a 9V 90Ω0.1AU R I ===总 滑动变阻器最大电阻为0=90Ω18 Ω72ΩR R R -=-=总滑答:(1)电源电压为9V ;(2)滑动变阻器的最大阻值为72Ω。
2.(2021·江苏扬州市·中考真题)如图所示为模拟调光灯电路,电源电压恒为6V ,灯泡标有“2.5V0.5A”字样(灯阻值不变),滑动变阻器标有“20Ω1A ”字样, (1)求灯泡正常发光时的电功率;(2)求灯泡正常发光时滑动变阻器接入电路的阻值; (3)该电路设计是否有缺陷?如有,请给出解决办法。
【答案】(1)1.25W ;(2)7Ω;(3)见解析 【详解】解:(1)灯泡正常发光时的电功率P L =U L I L =2.5V×0.5A=1.25W(2)灯泡正常发光时通过电路的电流是0.5A ,滑动变阻器接入电路的阻值L 6V V=0.5AU U U R I I -==滑滑-2.5=7Ω (3)因为当灯泡正常发光时,滑动变阻器接入电路中的电阻不为零,所以不足是:再移动滑动变阻器的滑动片时,可能会使灯泡烧坏;改进的措施:串联一个保护电阻。
答:(1)灯泡正常发光时的电功率是1.25W ;(2)灯泡正常发光时滑动变阻器接入电路的阻值是7Ω; (3)见解析。
2023年物理中考真题分类---电学计算题(含解析)

2023年中考题分类---电学计算1、(2023湖南常德)在图甲所示电路中,电源电压保持不变,电阻R1的阻值为30Ω,闭合开关S,两电流表的指针均指在表盘正中位置如图乙所示。
(1)求电源电压U;(2)求电阻R2的功率;(3)现用电阻R替换原来的两个电阻中的一个,发现替换前后只有一个电流表的示数发生了变化,且电路的总功率变化了1.2W。
求电阻R的阻值(结果保留1位小数)。
答案:(1)9V;(2)10.8W;(3)6.8Ω或8.4Ω解析:解:由图甲可知,两电阻并联,电流表A1测通过R1的电流,电流表A2测干路电流;(1)由并联电路的电流特点可知,干路电流大于支路电流,A2的示数应大于A1的示数,因此A2选用大量程,A1选用小量程,由图乙可知,A1的分度值为0.02A,示数为0.3A,A2的分度值为0.1A,示数为1.5A,由并联电路的电压特点和欧姆定律可知,电源电压U=U2=U1=I1R1=0.3A×30Ω=9V(2)由并联的电流特点可知,通过R2的电流I2=I﹣I1=1.5A﹣0.3A=1.2A则电阻R2的功率P2=U2I2=9V×1.2A=10.8W(3)由于替换前后只有一个电流表的示数发生了变化,由并联电路的特点可知,此时无论更换哪个电阻,干路电流一定会发生变化,则A1的示数不能发生变化,因此被替换的电阻为R2,通过R1的电流不变;原来电路的总功率P=UI=9V×1.5A=13.5W则更换后电路的总功率P'=P+ΔP=13.5W+1.2W=14.7W或P″=P﹣ΔP=13.5W﹣1.2W=12.3W当P'=14.7W时,由P=UI可知,干路电流'14.7W 49'A 9V 30P I U ===由并联电路的电流特点可知,此时通过R 的电流R 1494'A 0.3A A 303I I I =-=-=由欧姆定律可知,电阻R 的阻值R 9V 6.8Ω4A 3U R I ==≈当P″=12.3W 时,干路电流''12.3W 41''A 9V 30P I U ===此时通过R 的电流R 14116'''A 0.3A A 3015I I I =-=-=电阻R 的阻值R 9V '8.4Ω16'A 15U R I ==≈因此电阻R 的阻值为6.8Ω或8.4Ω。
初三物理—电学计算专题(附答案)

电功与电功率计算专题1、如图所示电路,电源电压不变,R 1的电阻为20Ω。
只闭合开关S 1时,电流表的读数为0.3A;S 1、S 2都闭合时,电流表的读数为0.5A。
求:(1)电源电压;(2)S 1、S 2都闭合时R 2的电功率。
解:(1)1110.3A 20Ω6V U U I R ===⨯=(2)210.5A 0.3A 0.2AI I I =-=-=226V 0.2A 1.2WP UI ==⨯=2、如图甲电路所示,电源电压为9V 且保持不变,小灯炮标有“6V6W”的字样,小灯泡的电流随电压的变化曲线如图乙。
求:(1)小灯炮正常发光时电阻为多少欧?(2)当电流表的示数为0.7A 时,小灯泡的电功率为多少瓦?(3)当电压表的示数为2V 时,整个电路10s 内消耗的电能是多少焦?甲乙解:1)R L =U L 2/P L =(6V)2/6W=6Ω2)P 实=U 实×I 实=3V×0.7A=2.1W3)电压表示数为2V 时,由图可知此时电路中的电流为0.5A,则:W=UTt=9V×0.5A×10s=45W3、如图13所示电路图,电源电压U=6V 且保持不变,闭合开关后,电流表A 1的示数为0.2A,A 的示数为0.5A。
求:(1)电阻R1的阻值。
(2)电阻R 2的电功率。
解:(1)U 1=U 2=U=6VR 1=AVI U 2.0611==30Ω(2)I 2=I-I 1=0.5A-0.2A=0.3AP 2=U 2I 2=6V×0.3A=1.8W4、某校师生自制了一台电烘箱.电烘箱的电阻丝通过5A 的电流时,每分钟可产生6.6×104J 的热量。
求:(1)此时电阻丝的电功率;(2)此时电阻丝的电阻;(3)此时电阻丝的工作电压。
解:(1)1100W(2)44Ω(3)220V5、如图所示的电路中,当ab 两点间接入4Ω的电阻时,其消耗的功率为16W。
电学计算题及标准答案

电学计算题249.把R 1和R 2串联后接到电压为12V的电路中,通过R 1的电流为0.2A,加在R 2两端的电压是4V.试求:(1)R 1和R 2的电阻各是多少?(2)如果把R 1和R 2并联后接入同一电路(电源电压不变),通过干路的电流是多少?250.如图132所示电源电压不变,闭合开关后,用电器R 1、R 2均正常工作.已知R 1的额定功率为1.5瓦,电流表A1的示数为0.5A,电流表A2的示数为1.5A.根据以上所给的条件,你最多可以求出几个与该电路有关的物理量?并逐一列式计算出这些物理量.图132图133图134251.如图133所示电路中,电源电压为10V,R 1=40Ω,开关闭合后,电流表的示数为0.75A.求:(1)通过电阻R 2的电流强度;(2)电阻R 2的阻值.252.如图134中,电源电压为10V,灯L 1、L 2上分别标有“12V36W”、“12V24W”字样.求:(1)当开关S 1、S 2均闭合时,电流表、电压表的示数分别为多少?(2)当开关S 1断开时,电流表、电压表的示数又是多少?253.组成串联电路和并联电路,所给器材有:定值电阻R 1、R 2、R 3,电源(电压不变)和开关各一个,导线若干.每次组成电路时,可以三个电阻都用或任意选用两个.对符合以上要求的所有的各种电路,用电流表来测量通过各个电阻的电流和干路电流,用电压表来测量各个电阻两端的电压,结果发现:(1)电流表最小的示数为0.5A;(2)R 1消耗的电功率的最大值为某一值P m;(3)在组成的图135甲所示的电路中,R 1消耗的电功率为P m/9,电压表的示数为4V;(4)在组成的图135乙图所示的电路中,a、b两处的电流强度之比等于1∶4.求:定值电阻R 1的阻值为多少?图135254.如图136所示,已知R 1=20Ω,把电阻R 1和R 2并联后接到电源上,已知电路总电阻是12Ω,电流表示数为0.3A,求:(1)电阻R 2的阻值;(2)电源电压;(3)通过R 2的电流.255.如图137所示,有两个阻值分别为20Ω、30Ω的电阻串联在电路中.请你任意补充一个条件,提出问题,然后解答.(至少选择两种做法,但要求每次补充不同类型的条件,提出不同的问题)256.如图138所示,R 1和R 2为两个定值电阻,R 2是R 1的n倍,小灯泡L 上标有“6V3W”的字样,S 为单刀双掷开关.当S 与点a接通时,小灯泡正常发光;当S 与点b接通时,小灯泡消耗的功率为额定功率的四分之一.(1)若n为小于5的正整数,试通过计算说明n的可能值.(2)试求n取以上可能值时,R 1和R 2相应的阻值.图136图137图138图139257.如图139所示,R 1=10Ω,R 2=20Ω,电源电压U=6V.(1)当S 1、S 2都断开、S 3闭合时,求电流表的示数和R 1的电压.(2)当S 1、S 2都闭合、S 3断开时,求电流表的示数.(3)开关处于何种情况下,电流表会烧坏?258.如图140所示,R 1=20Ω,R 2=40Ω,电源电压保持不变.(1)当开关S 1、S 2都闭合时,电流表A1的示数是0.6A,小灯泡L 恰好正常发光,求电源电压和小灯泡的额定电压;(2)当开关S 1、S 2都断开时,电流表A2的示数是0.2A,求小灯泡的实际功率;(3)小灯泡的额定功率是多少?259.一只标有“6V3W”的小灯泡(电阻不变)与R 1=12Ω的电阻串联后,接在电源上恰能正常发光;若灯与R 2串联后接在原电路中,用电流表测得通过小灯泡的电流为0.6A;若R 1与R 2串联后接在原电路中,试求出与R 2有关系的电学物理量.260.如图141所示电路,电源电压U恒定且小于10V,R 1=15Ω,滑动变阻器的最大阻值为20Ω,小灯泡的电阻小于15Ω.当开关S 断开,滑动变阻器的滑片位于b端时,电流表的示数为0.2A;当开关S 闭合,滑动变阻器的滑片位于a端时,电流表的示数为1A,且小灯泡正常发光.求小灯泡的额定功率(温度对灯丝电阻的影响忽略不计).图141图142261.如图142所示,设电源由1.5V干电池4节串联而成,并保持电压不变.滑动变阻器固定端A、B之间电阻值R 0=18Ω,灯泡L 上有“6V?2W”字样.当开关S 闭合后,求:(1)当变阻器滑片P 在A端时,电流表的读数和灯泡L 消耗的功率.(2)当变阻器滑片P 在B端时,电流表的读数和灯泡L 消耗的功率.262.如图143所示的电路中,R 0=30Ω.当闭合开关S 后,滑动变阻器的滑片P 移动到a端时,电流表的示数I1=0.2A;当滑片P 移动到b点时,电流表的示数I2=0.1A.求:(1)电源的电压是多少?(2)滑片P 分别移到a端和b点时,电阻R 0的电功率各是多少?(3)滑动变阻器ab之间的阻值R ab是多少?图143图144263.如图144所示,电源电压不变,开关S 闭合后,移动滑动变阻器的滑片,使它连入电路的电阻为滑动变阻器最大电阻R ′的1/4,此时电压表的示数为10V,变阻器上消耗的功率为10瓦;当滑动变阻器的滑片移到最右端时,电压表的示数为5V,电流表的示数为0.5A,求:(1)定值电阻R 的阻值及滑动变阻器的最大阻值R ′的大小;(2)电源电压.264.如图145所示电路中,电源电压为16V,R 1为滑动变阻器,电流表的量程为0~0.6A,定值电阻R 2为18Ω,灯泡L 上标有“12V8W”字样.设灯泡电阻为恒定值.(1)当开关S 1闭合、开关S 2断开时,电流表的读数为0.4A,求此时滑动变阻器接入电路的电阻值.(2)当开关S 1、S 2都闭合后,若整个电路处在A全工作状态,求灯泡L 上消耗的最大功率.图145图146265.在如图146所示的电路中,电源电压不变.当开关S 闭合,滑片P 置于滑动变阻器的b端时,电压表V1的示数为12V,电流表A的示数为0.4A;当滑片P 移至滑动变阻器的中点时,电压表V2的示数恰等于V1示数的一半.(滑片处于任何位置灯泡均可发光)求:(1)画出P 在中点时的简化电路图.(2)滑动变阻器的最大阻值为多少Ω?(3)滑片P 的由变阻器的b端移至中点过程中,灯泡E消耗的电功率变化了多少瓦?266.王明同学家的电炉铭牌模糊不清了,为了测出电炉的额定功率,他让家里所有的用电器都停止工作,只接入电炉让其正常工作,然后观察家里配电盘上正在运行的电能表,电能表上标有“3000R /kWh”,利用手表计时,发现1分钟电表盘转了50转,那么:图140(1)电炉的额定功率是多少?(2)王明同学觉得电炉使用不方便,想对电炉进行改装:使电炉的功率可以为额定功率,也可以为额定功率的1/4.请你利用一个开关和一个定值电阻帮助他设计一个电路,画出电路图,并计算出定值电阻的大小.267.如图147所示,定值电阻R 0=10Ω,当S 1和S 2均闭合且滑动变阻器的滑片P 滑到b端时,电流表A1、A2示数的比值为4∶5;当S 1和S 2均断开且滑片P 置于滑动变阻器的中点时,小灯泡的功率为5W.已知灯泡发光时的电阻为5Ω,求电源电压及滑动变阻器的最大阻值为多少(设电源电压不变)?图147268.如图148所示,R 0为3Ω,R 为滑动变阻器.当滑动变阻器的滑片P 滑到M点时,电压表读数为9V;当滑动变阻器滑片P 滑到N点时,变阻器连入电路的阻值为滑片P 滑到M点时变阻器连入电路的阻值的5倍,此时电压表读数为4.5V.已知电源电压保持不变,求:(1)电源电压;(2)滑动变阻器滑片P 到N点时滑动变阻器的电功率.图148图149269.如图149所示,电源电压保持不变,小灯泡L 标有“2.5V 1.25W”字样,滑动变阻器R 的最大阻值是40Ω.闭合开关后,当滑动变阻器接入电路的阻值为4Ω时,小灯泡L 恰好正常发光,求:(1)电源电压;(2)小灯泡在此电路中的最小功率.270.如图150所示,电源电压保持不变,电阻R 2=4Ω,滑动变阻器的总电阻R 0=20Ω.当开关与触点1连接,滑动变阻器的滑片P 滑到b端时,电流表示数为0.2A;当滑片P 滑到a端时电流表示数为0.6A.求:(1)电阻R 1的阻值;(2)当开关S 与触点2连接,调整滑动变阻器的阻值时,电阻R 2上消耗电功率的最大值和最小值.图150图151271.如图151所示,一只标有“8V4W”的灯泡L 与一只滑动变阻器R 串联.当开关S 闭合后,已知滑动片P 在b点时,电压表V的示数为12V;当滑动片P 从b点滑到a点时,电路中电阻值增大了6Ω.求:(1)滑动片P 在b点时,灯泡的电阻值及通电3分钟灯泡消耗的电能.(2)滑动片P 在a点时,灯泡的实际功率多大?(灯泡灯丝电阻保持不变)272.如图152所示电路,电源两端电压保持不变,L 是“6V3W”的小灯泡,滑动变阻R ′的最大阻值是20Ω.当开关S 2断开,S 1闭合时,调节滑动变阻器的滑片P 处于某一位置时,灯L 刚好正常发光.问:(1)灯L 的电阻是多少?(2)电源的电压是多少?(3)再将开关S 2闭合,电压表、电流表的读数各是多少?图152图153273.如图153所示电路的电源电压保持恒定,滑动变阻器R 的最大阻值为20Ω,灯泡L 1、L 2上分别标有“6V6W”、“12V6W”字样.当闭合开关S 、S 1、S 2,滑动变阻器的滑片P 处于某一位置时,灯L 1正常发光,电流表的示数为1.5A.(设两灯的电阻均为恒定值)求:(1)灯L 1的电阻是多大?(2)此时滑动变阻器接入电路的阻值是多少?(3)当开关S 闭合,S 1、S 2断开时,调节滑动变阻器滑片的位置,使灯L 2消耗的最小功率为多少?274.如图154所示,小灯泡L 标有“6V1.5W”字样,滑动变阻器R 2的最大阻值为24Ω,电压表的量程为0~3V,电源电压保持不变.(1)当开关S 1、S 2都闭合时,小灯泡恰能正常发光,电流表示数为0.55A,求电阻R 1的阻值和电流通过小灯泡在1分钟内做的功.(2)当开关S 1、S 2都断开时,整个电路消耗的最小功率是多少?图154图155275.在图155所示的电路中,开关S 1、S 2是两只能同时断开或同时闭合的联动开关,R 1=10Ω,灯泡L 上标有“6V3.6W”的字样,滑动变阻器R 2的滑片置于中点,电源电压恒定.闭合开关S ,当两开关S 1、S 2处于某一状态时,用电流表测量得电流为1.2A;当两开关S 1、S 2处于另一状态时,用电流表测得电流为0.3A.(1)求电源的电压及R 2的最大阻值.(2)当灯泡上有电流通过时,移动变阻器滑片,求灯泡L 实际功率的变化范围.276.如图156所示,电源电压恒定不变,R 1=6Ω,R 2=24Ω,滑动变阻器R 3的最大阻值为20Ω,电流表量程为0~0.6A,电压表量程为0~3V.(1)断开开关S 1、闭合开关S 2,10秒钟内电流通过R 1产生的热量为60焦,求电源电压;(2)闭合开关S 1、S 2,求这时电路的总电阻及电压表的示数;(3)断开开关S 1、S 2,求当电路处于A全工作状态时,电路消耗功率的实际范围.277.家用简易调光台灯实际上是将白炽灯与变阻器串联后,再接入220V电路中.若某调光台灯的灯泡上标有“P Z220-40”字样.求:(1)该灯泡正常工作时的电流;(2)该灯泡正常工作时的电阻;(3)当该灯泡的实际功率约为额定功率的50%时,变阻器连入电路的电阻约为多少Ω?(假设灯丝的电阻不变)278.如图157所示的电路中,电源电压不变,R 1、R 2是定值电阻.若开关S 闭合,电流表示数为1.8A,电阻R 2消耗的电功率为3.6瓦;若开关S 断开,电流表的示数为1.2A.求:电阻R 1和R 2的阻值各为多少?图157图158279.在温度为20℃、质量2400克的水里有一根阻值为10Ω的电阻丝,若通过此电阻丝的电流是10A,需要多少时间才能把水加热到95℃?(假设电阻丝放出的热量全部被水吸收)?280.有一电热毯,附有如图158所示的电路图,说明书上标明所用的电压为220V,电热毯电阻R 为1210Ω.现利用开关S 的通断可以使电热毯的发热功率分为两档,Ⅰ挡为功率最大档,Ⅱ挡功率为Ⅰ挡的1/4.试问:(1)开关处于什么状态时,电热毯的功率最大?它的值为多少?(2)电阻R ′应为多大?281.小明家的一电热水壶,铭牌如下表所示.现他在壶中装上3升20℃的水[c水=4.2×103焦耳/(千克·℃)].求:(1)壶中所装水的质量是多少?(2)在额定电压下烧开这些水需要多少分钟?(假设壶内气压等于1个标准大气压且不计热损失)(3)若在用电高峰,电热水壶的实际电压为额定电压的90%,则此时该水壶的实际电功率是多少?282.一台电动机,线圈的电阻为40Ω,接在220V的电路中使用,正常工作时通过的电流为0.5A.(电动机的转轴与轴承间的摩擦忽略不计)求:(1)这部电动机转变为机械能的功率是多少?(2)用此电动机匀速竖直向上提起质量为20千克的物体,10秒钟能使物体升高多少米?283.有两根电阻丝,其阻值R 1=2R 2,分别用并联和串联两种方式接在同一电源上使用.问:(1)在相等的时间内,哪一种接法产生的热量比较多?写出你判断时所根据的公式和理由.(2)并联时产生的热量与串联时产生的热量之比是多少?284.某工地的电压为220V,且保持不变.因工作需要,用较长的导线A装了一只“220V100W”的白炽电灯.通电后发现灯泡亮度比正常工作时暗一些,用电压表测得灯泡两端的电压为200V.现用一只“220V200W”的灯泡替换“220V100W”的灯泡接在电路中,达到了工地照明要求.求:(1)电路中导线的阻值.(2)“220V200W”的灯泡在电路中消耗的实际功率.(温度变化对电阻的影响不计)285.一般情况下,用电器的实际工作电压并不完全等于它的额定电压.家庭里通常不备电压表,但借助电能表可以近似测出用电器的实际工作电压.如果在家庭电路中只接入一个电饭锅,测得电能表转过100转的时间为121秒,求此时电饭锅的工作电压.(设电饭锅的电热图156丝电阻不变,电饭锅的铭牌和电能表的盘面如下表所示)286.家用电熨斗为满足不同布料的整烫需要,通常设计成三档不同的温度档.图159甲是它的工作原理图,其中R 1、R 2为电热丝,且R 1=R 2=R ,图159乙是电熨斗旋转开关在不同温度档时的连接情况.图159(1)若电熨斗处于“低温档”,正常工作时消耗的电功率约为220瓦,求每根电热丝的阻值.(2)电熨斗处于“高温档”时,求工作1分钟所产生的热量.287.李华同学准备自制一个亮度可调的玩具台灯,他选用了下列器材:一个电压为6V的电源,标有“10Ω1A”的小滑动变阻器,一只标有“2.5V0.5A”的灯泡,一个开关和若干导线等.李华用这些器材组成一个串联电路.请问:(1)李华同学选用的这些器材的规格合适吗?为什么?(2)现有一段电阻丝(其电阻丝的电阻为每厘米1Ω),将这段电阻丝接入李华设计的上述串联电路后,无论怎样移动滑动变阻器,灯泡的亮度都不会超过正常发光时的亮度.那么电阻丝是怎样接入电路的?其长度为多少?(3)电阻丝接入电路后,电阻丝消耗的最大功率是多少?288.下表所示为国产某型号全自动洗衣机说明书中所列的主要技术数据,根据表格,回答:(1)这台洗衣机在额定电压下洗衣时,通过洗衣机的电流是多大?(2)若洗衣的累计时间为20分钟,则洗衣机消耗的电能为多少千瓦时?289.张明得到一个旧电热暖手器,铭牌上表示额定值的字样中,能看清的只有“24W”这几个字,为了能正确地使用这只电器,他找来一只标有“600Ω0.4A”字样的电阻.他将电阻、电热暖手器和开关串联起来接到家庭电路中,然后进行如下的实验和观察:将开关接通后,电能表在5分钟内恰好转动411转;断开开关后,电能表在3分钟内恰好转动240转.已知他家电能表上标着3000R /kWh(表示每消耗1千瓦时的电能,电能表的转盘转3000转),家庭电路的电压为220V,在张明做实验的时间内,家中其他用电器用电情况没有变化,假定电热暖手器和电阻的阻值都不随温度变化.求:(1)电热暖手器的额定功率是多少?(2)除做实验的支路外,张明家3分钟用电多少千瓦时?(3)电热暖手器和电阻支路的电功率是多少?(4)电热暖手器的额定电压是多少?(此项结果四舍五入到整数)电学计算题答案249.R 1=40ΩR 2=20ΩI=0.9A250.U1=3VU2=3VU=3VI2=1A R 2=3ΩR 1=6ΩR 总=2ΩP 2=3瓦P 总=4.5瓦251.(1)I2=0.5A(2)R 2=20Ω252.(1)I=2.5AU=10V(2)I=1AU1=4V253.R 1=2Ω254(1)R 2=30Ω(2)U=6V(3)I2=0.2A255.(1)补充条件:电源电压为12V求:电路中的电流强度I=0.24A(2)补充条件:20Ω电阻的功率是3.2瓦求:30Ω电阻的功率是多少P 2=4.8瓦256.(1)n=3n′=4(2)R 1=12ΩR 1′=6ΩR 2=36ΩR 2′=24Ω257.(1)2V(2)0.9A(3)S 1、S 3闭合258.(1)U=U额=12V(2)P L 实=0.8瓦(3)P L 额=7.2瓦259.R 2=8ΩI2=0.6AU2=4.8V P 2=2.88瓦260.P =3.6瓦261.(1)I1≈0.67A P 1=2瓦(2)I2=0.33A P 2=0262.(1)U=6V(2)P 1=1.2瓦P 2=0.3瓦(3)R ab=30Ω263.(1)R =10ΩR ′=40Ω(2)U=20V264.(1)R 1=22Ω(2)P 2=1.07瓦265.(1)如图27所示(2)R P =20Ω(3)ΔP E=2瓦266.(1)P =1千瓦(2)R =48.4Ω如图28所示267.U=25V R =40Ω268.(1)U=12V(2)P L =11.25瓦269.(1)U=4.5V(2)P L =0.05瓦270.(1)R 1=10ΩP 大=9瓦(2)P 小=0.25瓦271.(1)R L =16ΩW=720焦P 实=2.56瓦272.(1)R L =12Ω(2)U=12V(3)U=0I=1.0A273.(1)R L 1=6Ω(2)R =12Ω(3)P 最小≈0.45瓦274.(1)R 1=20ΩW=90焦(2)P 最小=0.75瓦275.U=60V R 2=20Ω(2)0.4~3.6瓦276.(1)U=6V(2)R 总=4.8ΩU1=0(3)3.6瓦~3瓦277.(1)I=0.18A(2)R L =1210Ω(3)R =496Ω278.R 1=5ΩR 2=10Ω279.t=756秒280.(1)闭合状态P 大=40瓦(2)R ′=1210Ω281.(1)m=3千克(2)t=20分种(3)P 实=680.4瓦282.(1)100瓦(2)h≈5.1米283.(1)并联(2)Q并/Q串=9/2284.(1)R 线=48.4Ω(2)P L ′=140瓦285.U=200V286.(1)R =110Ω(2)Q=5.28×104焦287.(1)不合适.因为当滑动变阻器接入电路中的电阻逐渐减小时,灯泡两端的电压会逐渐增加并大大超过其额定电压,这样会烧坏灯泡.(2)串联接入电路长度=7厘米(3)P 大=1.75瓦288.(1)I=1.64A (2)W=0.12千瓦时289.(1)P 额=24瓦(2)W1=0.08千瓦时(3)P =44瓦(4)U1=110V.。
电学计算试题及答案

电学计算试题及答案1. 题目:计算电阻R1和R2串联后的总电阻值。
答案:当两个电阻R1和R2串联时,总电阻R等于R1和R2的和,即R = R1 + R2。
2. 题目:已知电路中电流I=2A,电阻R=10Ω,求通过电阻的电压U。
答案:根据欧姆定律,电压U等于电流I乘以电阻R,即U = I * R = 2A * 10Ω = 20V。
3. 题目:计算并联电路中总电流I。
假设电路中有两个并联电阻R1和R2,电流分别为I1和I2,已知I1=3A,I2=4A。
答案:并联电路的总电流I等于各支路电流之和,即I = I1 + I2 = 3A + 4A = 7A。
4. 题目:计算电容器C在电压U=12V下储存的电荷Q。
假设电容C=2μF。
答案:电荷Q等于电压U乘以电容C,即Q = U * C = 12V * 2μF = 24μC。
5. 题目:已知电感L=0.5H,电流I=5A,求电感L储存的能量W。
答案:电感储存的能量W等于0.5乘以电流I的平方乘以电感L,即W = 0.5 * I^2 * L = 0.5 * (5A)^2 * 0.5H = 6.25J。
6. 题目:计算直流电路中电阻R=20Ω的功率P。
假设电流I=0.5A。
答案:功率P等于电流I的平方乘以电阻R,即P = I^2 * R = (0.5A)^2 * 20Ω = 5W。
7. 题目:已知交流电路中电压有效值U=120V,频率f=50Hz,求电感L 的感抗XL。
假设电感L=0.02H。
答案:感抗XL等于2π乘以频率f乘以电感L,即XL = 2π * f* L = 2π * 50Hz * 0.02H = 6.28Ω。
8. 题目:计算交流电路中电容C=0.00001F的容抗XC。
假设频率f=60Hz。
答案:容抗XC等于1除以2π乘以频率f乘以电容C,即XC = 1/ (2π * f * C) = 1 / (2π * 60Hz * 0.00001F) = 1.41kΩ。
初三电学计算测试题及答案

初三电学计算测试题及答案一、选择题(每题2分,共10分)1. 一个电阻为10欧姆的电阻器,通过它的电流为0.2安培,根据欧姆定律,该电阻两端的电压是多少伏特?A. 0.2伏特B. 2伏特C. 20伏特D. 200伏特2. 两个电阻分别为R1=20欧姆和R2=30欧姆,串联后接入电路中,总电阻是多少?A. 40欧姆B. 50欧姆C. 100欧姆D. 120欧姆3. 一个电路中,电源电压为12伏特,串联电路的总电阻为6欧姆,通过电路的电流是多少?A. 1安培B. 2安培C. 3安培D. 4安培4. 一个电容器的电容为4微法拉,当它被充电到6伏特时,储存的电荷量是多少?A. 12微库仑B. 24微库仑C. 36微库仑D. 48微库仑5. 一个电感器的自感系数为0.5亨利,当通过它的电流以每秒0.1安培的速率变化时,产生的感应电动势是多少?A. 0.05伏特B. 0.5伏特C. 5伏特D. 50伏特二、填空题(每空1分,共10分)6. 欧姆定律的公式是:_________________。
7. 串联电路中,总电阻等于各个电阻之_______。
8. 并联电路中,总电阻的倒数等于各个电阻倒数之_______。
9. 电容器的电容公式是:C=_______/Q。
10. 电感器的感应电动势公式是:E=_______。
三、计算题(每题10分,共30分)11. 一个电路中,电源电压为24伏特,串联电路的总电阻为12欧姆,求通过电路的电流。
12. 一个电容器的电容为5微法拉,当它被充电到10伏特时,储存的电荷量是多少?13. 一个电感器的自感系数为0.2亨利,当通过它的电流以每秒0.2安培的速率变化时,产生的感应电动势是多少?四、简答题(每题5分,共10分)14. 解释什么是串联电路和并联电路,并说明它们的特点。
15. 简述电容器和电感器在电路中的作用。
答案:一、选择题1. B2. C3. B4. B5. B二、填空题6. V=IR7. 和8. 和9. Q/U10. L*ΔI/Δt三、计算题11. 电流I=V/R=24V/12Ω=2A12. 电荷量Q=C*U=5*10^-6 F*10V=50*10^-6 C=50μC13. 感应电动势E=L*ΔI/Δt=0.2H*0.2A/s=0.04V四、简答题14. 串联电路是指电路元件首尾相连的电路,其特点是电流在各个元件中相同,总电阻等于各个电阻之和。
中考物理总复习《电学计算题》专题训练(带有答案)

中考物理总复习《电学计算题》专题训练(带有答案)学校:___________班级:___________姓名:___________考号:___________典例精讲例 如图甲所示电路,小灯泡L 上标有“2.5 V 1.25 W”字样,滑动变阻器R 2上标有“10 Ω 1 A”字样.闭合开关S 、S 1,移动滑动变阻器滑片使小灯泡正常发光,此时电压表示数为2 V ,求:(1)小灯泡L 正常发光时的电阻;(2)若电流表选用0~0.6 A 量程,电压表选用0~3 V 量程,在确保电路各元件安全的情况下,求电路消耗的最大电功率(假定灯丝电阻保持不变);(3)若更换电源,只闭合开关S 、S 2,移动滑片到某一个位置,电流表和电压表指针位置如图乙所示(可能与之前相比更换了量程但在后续操作中量程不变),当向某个方向移动变阻器的滑片到某位置时,其中一个表指针达到满偏,另一个表指针在刻度盘23处.求定值电阻R 1的可能值.实战演练1.(2022河北18题)如图所示,电源电压为18 V,R0为定值电阻,R为滑动变阻器,电流表量程为“0~0.6 A”,电压表量程为“0~15 V”.闭合开关S,移动滑片,当滑片移至滑动变阻器中点时,电流表的示数为0.36 A,电压表的示数为3.6 V.(1)求R0的阻值;(2)求滑动变阻器的最大阻值;(3)在保证电路安全的情况下,电路消耗的最大功率为P1;将电压表改接在R两端,电路消耗的最小功率为P2.求P1∶P2.2.(2022河北预测卷)如图所示,电源电压为12 V且保持不变,小灯泡L标有“6 V 3 W”字样,滑动变阻器的规格为“20 Ω 1 A”,电压表的量程为0~15 V,电流表的量程为0~0.6 A.求:(1)小灯泡正常发光时的电阻;(2)为了保证电路安全,滑动变阻器接入电路的阻值范围;(3)调节滑片,当小灯泡正常发光时,保持滑片的位置不变,用定值电阻R0替换小灯泡L,替换前后,电路的总功率变化了1.2 W.求R0可能的电阻值.参考答案典例精讲例 解:(1)根据电功率的变形式P =U 2R 可知,小灯泡L 正常发光时的电阻R 灯=U 灯2P 灯=(2.5V )21.25W =5 Ω (2)闭合开关S 、S 1,小灯泡L 和滑动变阻器R 2串联,电压表测量滑动变阻器R 2两端的电压.移动滑片使小灯泡正常发光,此时小灯泡两端的电压为2.5 V ,滑动变阻器R 2两端的电压为2 V ,故电源电压U 电=U 灯+U 滑=2.5 V +2 V =4.5 V由I =U R 可知,小灯泡正常发光时的电流I 灯=U 灯R 灯=2.5V 5Ω =0.5 A 为了保证电路各元件安全,通过电路的最大电流为0.5 A ,则电路消耗的最大电功率P max =U 电I max =U 电I 灯=4.5 V×0.5 A =2.25 W(3)只闭合开关S 、S 2,电阻R 1和滑动变阻器R 2串联.因滑动变阻器允许通过的最大电流为1 A ,所以由图乙可知,电流表选择的量程为0~0.6 A ,此时电路中的电流为0.5 A.若电压表的量程为0~15 V ,则其示数为12 V ,滑动变阻器的阻值为R 滑=U 1I´ =12V 0.5A=24 Ω>10 Ω,滑动变阻器R 2上标有“10 Ω 1 A”,故不符合题意;若电压表的量程为0~3 V ,则其示数为2.4 V ,滑动变阻器接入电路的阻值为R 滑′=U 2I´ =2.4V 0.5A=4.8 Ω<10 Ω,符合题意;若电流表达到满偏0.6 A ,则电流表示数增大了ΔI =0.6 A -0.5 A =0.1 A电压表则减小了ΔU =2.4 V -23×3 V =0.4 V 因串联电路总电压等于各分压之和,所以R 1两端电压变化量和电压表示数变化量相等,则由I =U R可知,定值电阻R 1=ΔU ΔI =0.4V 0.1A=4 Ω 若电压表示数达到满偏3 V ,则电压表的示数增大了ΔU ′=3 V -2.4 V =0.6 V根据串联电路电压规律可知,R 1两端电压变化量也为0.6 V ,电流表示数减小了ΔI ′=0.5 A -23×0.6 A =0.1 A 由I =U R 可知,定值电阻R 1=ΔU ′ΔI ′ =0.6V 0.1A=6 Ω 所以,定值电阻R 1的阻值可能为4 Ω或6 Ω.实战演练1.解:(1)由题图可知,定值电阻R 0与滑动变阻器串联,电流表测电路中的电流,电压表测定值电阻两端的电压根据题意及欧姆定律得,定值电阻R 0的阻值R 0=U 0I =3.6 V 0.36 A=10 Ω (2)根据题意,当滑动变阻器滑片移至中点时滑动变阻器两端的电压U 滑=U -U 0=18 V -3.6 V =14.4 V通过滑动变阻器的电流即电路中的电流I =0.36 A所以滑动变阻器一半的阻值R 滑2=U 滑I =14.4 V 0.36 A=40 Ω 则滑动变阻器的最大阻值R 滑=2×40 Ω=80 Ω(3)当电流表示数最大为0.6 A 时定值电阻R 0两端的电压U 0′=I max R 0=0.6 A×10 Ω=6 V <15 V电压表可以正常工作所以电路消耗的最大功率P 1=UI max =18 V×0.6 A =10.8 W当电压表改接在R 两端,R 两端的电压最大为15 V 时,R 接入电路的电阻最大,此时电路中的功率最小R 0两端的电压U 0″=U -U 滑′=18 V -15 V =3 V此时电路中的电流I min =U 0″R 0=3 V 10 Ω=0.3 A R 接入电路的电阻R 滑′=U 滑′I min =15 V 0.3 A=50 Ω<R 滑 所以电路中的最小功率P 2=UI min =18 V×0.3 A =5.4 WP 1∶P 2=10.8 W ∶5.4 W =2∶12.解:(1)小灯泡正常发光时的电阻R L =U 额2P 额=(6 V )23 W =12 Ω (2)电流表的量程为0~0.6 A ,小灯泡规格为“6 V 3 W”,所以,电路中的最大电流:I 大=I L =P 额U 额 =3 W 6 V =0.5 A此时电路中的总电阻:R 总=U I 大 =12 V 0.5 A=24 Ω 滑动变阻器接入电路中的最小阻值R 小=R 总-R L =24 Ω-12 Ω=12 Ω电压表的量程为0~15 V ,电源电压为12 V ,所以滑动变阻器接入电路的阻值可以达到最大值,即为20 Ω故滑动变阻器R 接入电路的阻值范围为12~20 Ω(3)用定值电阻R 0替换小灯泡L ,替换之前,小灯泡正常发光通过电路的电流:I =0.5 A由串联电路中各部分两端电压之和等于总电压可得:U 滑=U -U 额=12 V -6 V =6 V所以R 滑=R L =12 Ω由题知,用电阻R 0替换L ,R 滑保持不变,总功率的变化量为1.2 W则由P =UI 可得串联电路电流的变化量:ΔI =ΔP U =1.2 W 12 V=0.1 A 若电流减小0.1 A ,则此时通过电路的电流:I 0=I -ΔI =0.5 A -0.1 A =0.4 A则电路中的总电阻为:R 总′=U I 0 =12 V 0.4 A=30 ΩR0=R总′-R滑=30 Ω-12 Ω=18 Ω若电流增大0.1 A,则此时通过电路的电流:I0′=I+ΔI=0.5 A+0.1 A=0.6 A 则电路中的总电阻为:R总″=UI0′=12 V0.6 A=20 ΩR0′=R总″-R滑=20 Ω-12 Ω=8 Ω综上所述:电阻R0可能的电阻值为18 Ω或8 Ω.。
九年级物理电学计算题专题(含参考答案)

交乐学校九年级物理电学计算题专题1.如图23甲所示电路,滑动变阻器的最大阻值为Ω=401R ,电源电压及灯L 的电阻保持不变。
当1S 、2S 均闭合且滑片滑到b 端时,电流表1A 、2A 的示数分别为如图23乙、丙所示;当1S 、2S 均断开且滑片P 置于变阻器的中点时,电流表1A 的示数为0.4A ,求:(1)电源的电压; (2)2R 的电阻; (3)灯L 的电阻; (4)整个电路消耗的最小电功率;(提示:电路的总电阻最大时消耗的电功率最小)。
2.如图同学们常见的家用饮水机,它的铭牌上标有:额定电压220V ,频率50Hz ,加热功率350W 。
将它接在220V 的电压下, (1) 当它处于保温状态时,饮水机中的电流为0.1A ,这时饮水机消耗的电功率是多大? (2)当它处于加热状态时,如果消耗的电能全部用来加热水,它能使热水罐中0.5kg ,20℃的水的温度升高到90℃要多少时间? (3) 它的工作原理比较简单:整个电路由一个电热元件R 1、一个限流电阻R 2和一个温控开关S 组成(如图13)。
当S 接a 时,电热元件R 1被接入电路中,饮水机开始将水加热;当水温达到一定温度时,温控开关自动切换到b 处,饮水机处于保温状态。
请你按上述原理完成图13中的电路图。
3.如图是一条电热毯电路的示意图,R 0是发热电阻丝,R 是串联在电路中的电阻,S 是控温开关。
电热毯标牌上标有“220V 40W ”字样。
问(不考虑温度对电阻值的影响): ⑴、要使电热毯处于低温挡时,开关S 应处于什么状态? ⑵、发热电阻丝R 0的阻值是多大?⑶、当电热毯处于低温挡时,电路中的电流为0.1A ,则在10s内电阻丝R 0产生的热量是多少?S220V4.如图10所示电路中,小灯泡L标有“6V 6W”字样,R2=3Ω,当S1、S2都闭合时,电流表示数为1.2A,这时小灯泡L正常发光,求:(1)电源电压U(2)电阻R1的阻值(3)当S1、S2都断开时,小灯泡L消耗的功率5.如图所示的电路中,电源电压恒定为4.5V 。
中考物理《电学》计算题专项练习题(含答案)

中考物理《电学》计算题专项练习题(含答案)1.某品牌的电热水器,有加热和保温两种挡位,它的工作电路如图所示。
已知R2=176Ω,当S1、S2均闭合时,电热水器处于加热挡,此时消耗的功率为1100W。
求:(1)电阻R1的阻值;(2)当只闭合S1时,电热水器处于保温挡,求保温档的功率;(3)已知电热水器电热转化效率为80%,求用加热档将1.1kg水从18℃加热到98℃所需的时间。
(水的比热容为4.2×103J/(kg·℃))2.如图甲是小明家豆浆机的工作原理图,在接入220V电压工作时,电动机带动刀头将黄豆进行粉碎打浆,额定功率是200W;R是加热电热管,额定功率是1000W。
小明记录了豆浆机正常制作一次豆浆过程中电热管和电动机交替工作的“P﹣t”图象如图乙。
请计算:(1)电动机正常工作时的电流(结果保留两位小数);(2)豆浆机正常制作一次豆浆,消耗的总电能。
3.小新喜欢吃爆米花,学习电加热原理后自己制作了一个简易的爆米花机,图甲是爆米花机的简易电路图.开关S接a时,1R加热同时电动机搅拌;开关S接b时,2R单独工作并处于保温状态。
图乙是小新设计的相关参数。
小新将100g的玉米粒放入制好的爆米花机中,玉米粒初温为20℃,加热5min后玉米粒温度升高到300℃并爆成了玉米花,此后小新将爆米花机调至保温状态。
求:(()31.210J /kg =⨯⋅玉米℃c )(1)保温状态时电路中的电流;(2)电阻1R 的阻值;(3)加热过程电路消耗的电能;(4)电阻1R 给玉米加热的效率。
4.如图所示电路中,电源电压保持不变,灯泡L 标有“8V 4W ”字样,当开关S 闭合时,灯泡L 正常发光,电流表的示数为0.7A .求:(1)此时通过灯泡L 的电流;(2)定值电阻R 的阻值。
5.图甲是小明家安装的即热式热水器,其具有高、低温两挡加热功能,低温挡功率为5500W ,内部等效电路如图乙所示,R 1和R 2是两个电热丝.某次小明用高温挡淋浴时,水的初温是20℃,淋浴头的出水温度为40℃,淋浴20min 共用水100kg .假设热水器电热丝正常工作且产生的热量全部被水吸收[c 水=4.2×103J/(kg·℃)],求: (1)电热丝R 1的阻值。
中考物理必做10道经典电学计算题(附答案)

中考物理必做10道经典电学计算题(附答案)嗨,同学们,今天咱们来聊聊中考物理电学计算题。
这可是咱们物理考试的重头戏,搞定了这些题,电学部分基本就稳了。
我呢,就给大家整理了10道必做的经典电学计算题,保证让你一看就会,一做就对!**第一题:**小明家中的电灯功率是60瓦,电压是220伏,问电灯正常工作时的电流是多少安培?(答案:0.27安培)**第二题:**一个电阻器的电阻值是100欧姆,通过的电流是2安培,问电阻器两端的电压是多少伏特?(答案:200伏特)**第三题:**小华用电池组给一个电路供电,电池组电压是3伏特,电路中有一个电阻值是10欧姆的电阻器,问电路中的电流是多少安培?(答案:0.3安培)**第四题:**一个电路中有两个电阻器,一个电阻值是4欧姆,另一个电阻值是6欧姆,它们是串联连接的,求整个电路的总电阻是多少欧姆?(答案:10欧姆)**第五题:**两个电阻器并联连接,一个电阻值是8欧姆,另一个电阻值是12欧姆,求并联电路的总电阻是多少欧姆?(答案:3.2欧姆)**第六题:**一个电路中有两个电阻器,一个电阻值是5欧姆,另一个电阻值是15欧姆,它们是串联连接的,电路中的电流是5安培,求电路中的总电压是多少伏特?(答案:100伏特)**第七题:**一个电路中有两个电阻器并联连接,一个电阻值是10欧姆,另一个电阻值是20欧姆,电路中的电压是12伏特,求电路中的电流是多少安培?(答案:1安培)**第八题:**一个电路中有三个电阻器,两个电阻值是相同的,都是20欧姆,它们是串联连接的,第三个电阻值是30欧姆,电路中的电流是3安培,求电路中的总电压是多少伏特?(答案:90伏特)**第九题:**一个电路中有两个电阻器并联连接,一个电阻值是15欧姆,另一个电阻值是30欧姆,电路中的电压是24伏特,求电路中的电流是多少安培?(答案:1.2安培)**第十题:**一个电路中有三个电阻器,一个电阻值是10欧姆,一个电阻值是20欧姆,它们是串联连接的,第三个电阻值是30欧姆,电路中的电压是50伏特,求电路中的电流是多少安培?(答案:1安培)怎么样,这些题目是不是很简单?其实电学计算题的关键就是公式要记牢,然后代入数值,算一算就出来了。
(完整版)电学综合计算题(包含答案)30道题

电学综合计算题(含答案) 30道题1、研究表明,有些金属电阻的阻值会随温度的变化而变化,物理学中利用这类金属的特性可以制成金属电阻温度计,它可以用来测量很高的温度,其原理如图所示.图中电流表量程为0~15mA(不计其电阻),电源的电压恒为3V,R′为滑动变阻器,金属电阻作为温度计的测温探头,在t≥0℃时其阻值R t随温度t的变化关系为R t=100+0.5t(单位为Ω).(1)若要把R t放入温度为0℃处进行测量,使电流表恰好达到满量程,既电流为15mA,则这时滑动变阻器R′接入电路的阻值为多大?(2)保持(1)中滑动变阻器R′接入电路的阻值不变,当被测温度为600℃时,电路消耗的电功率为多大?(3)若把电流表的电流刻度盘换为对应的温度刻度盘,则温度刻度的特点是什么?2、小红学了电学知识后画出了家里的电吹风的电路图(甲图),她认识只闭合开关S1时,电吹风吹冷风,当S1和S2同时闭合时,电吹风吹热风,小芬同学看了她的电路图觉得有问题:如果只闭合S2,会出现电热丝R工作时而电动机不工作的现象,从而使电吹风的塑料外壳过热造成损坏,小芬认为只要把其中一个开关移到干路上,就能做到电热丝R工作时,电动机就一定在工作,从而使塑料外壳不会因操作失误而损坏.乙图为电吹风机的铭牌.请分析回答下列问题:(1)你认为小芬应该把那个开关移到干路上,才能符合安全要求?为什么?(2)电吹风正常工作且吹热风时,流过电热丝的电流多大?(3)电热丝R的阻值多大(电热丝的阻值随温度变化不计)?3、某学校生物小组的同学为了探索一项技术,使一种名贵的花在寒冷的冬季也能正常生长,决定搭建一个微型温室,温室内需要安装一个电发热体.根据设计,该发热体用36V电压供电,发热功率为200W(设电能全部转化为内能).(1)电发热体不采用220V电压而用36V电压供电的考虑是什么?(2)采用36V电压供电,电发热体需要自制,现决定用镍铬合金丝绕制,则绕制成的电发热体正常工作时的电阻应为多大?(3)同学们在实验室里用2节干电池、电流表、电压表等器材,测出一段镍铬合金丝的阻值等于计算结果,用它制成发热体后,实际功率却小于设计的要求.经检查,电压正常,请你猜想产生这种情况的原因可能是什么?4、如图所示,电源电压U=12V,R1为定值电阻,阻值为100Ω,R为滑动变阻器,R的最大阻值为50Ω,电流表量程为“0~0.6A”, 电压表量程为“0~15V”,小灯泡上标有“6V 3W”字样,小灯泡的U —I关系如右图所示,求:(1)灯泡正常工作时通过灯丝的电流是多少?(2)S闭合,S1、S2都断开时调节滑动变阻器,当小灯泡两端的电压为4V时,滑动变阻器接入电路中的阻值为多大?(3)S、S1、S2都闭合时,移动滑片P,当滑动变阻器接入电路的阻值为多少时,整个电路消耗的总功率最大?最大总功率是多少?5、保温箱的简化电路如图所示,A为温度传感器,它的作用相当于开关,达到设定温度时自动断开电路;低于设定温度时,自动接通电路。
中考物理电学计算经典练习及答案40题

中考物理电学计算经典练习(括号里为参考答案)1.如图1所示,已知R1=2Ω, R2=4Ω,U=12V;求:1)通过电阻R1的电流I1;2)电阻R2两端的电压U2。
(2A,8V)2.如图2所示,电流表示数为0.5A, R2=20Ω,通过R2的电流是0.3A,求:1)电压表的示数;2)电阻R1=?(6V30Ω)3. 如图3所示,电源电压为8V,R1=4R2,电流表A的示数为0.2A;求:电阻R1, R2各为多少欧?(200Ω50Ω)4. 如图4所示,电源电压U不变,当开关S闭合时,通过电阻R1的电流为3A。
当电路中开关S断开时,R1两端电压为5V,R2的电功率为10W.求:电源电压U及电阻R1和R2的阻值。
(15V 5Ω 10Ω)5.把阻值为300Ω的电阻R1接入电路中后,通过电阻R1的电流为40mA;把阻值为200Ω的电阻R2和R1串联接入同一电路中时;求:1)通过电阻R2的电流为多少?2)R2两端的电压为多少?3)5min内电流通过R2做功多少?(0.25A 0.75A)6. 如图5所示,电源电压恒为3V,知R1=12Ω, R2=6Ω。
求:1)当开关S断开时电流表A的读数2)当开关S闭合时电流表A的读数7. 如图6所示,电源电压U不变,R1=6Ω.1)当开关S断开时电流表A的示数为1A,求R1两端的电压;2)当开关S闭合时电流表A的示数为1.2A,求R2的电阻值。
(6V 30Ω)8.如图7所示,定值电阻R1和R2串联,电源电压为7V,电流表的示数为0.5A, R2的电功率为2.5W。
求:电阻R2两端电压和电阻R1的电功率。
(5V 1W)9.如图8所示,电源电压为8V,且保持不变。
R1=4R2。
当开关S断开时,电流表的示数为2A。
求:1)电阻R1和R2的阻值各为多少欧?(4Ω 1Ω)2)当开关S闭合时电阻R1和R2的电功率各为多大?(16W 64W)10.如图9所示,已知R1=6Ω,通过电阻R2的电流I2=0.5A, 通过电阻R1和R2的电流之比为I1: I2=2:3。
初中物理电学计算题(含答案)

初中电学计算题1、如图所示的电路中,电阻R1的阻值为10Ω。
闭合电键S,电流表A1的示数为0.3A,电流表A的示数为0.5A.求(1)通过电阻R2的电流.(2)电源电压.(3)电阻R2的阻值2、如图所示,小灯泡标有“2.5V”字样,闭合开关S后,灯泡L正常发光,电流表、电压表的示数分别为0.14A和6V.试求(1)电阻R的阻值是多少?(2)灯泡L消耗的电功率是多少?3、把一个标有“220V 40W”灯泡接在电压为110V电源上使用,该灯泡的额定状态下的电阻、额定电流、额定功率、实际状态下的电阻、电流、实际功率分别是多少?4、标有“6V,6W”和“3V,6W”的两只灯泡串联接在电源上,有一只灯泡正常发光,而另一只较暗,分析:(1)电源电压(2)两灯泡消耗的实际功率分别是多少?(3)两灯泡哪只较亮?5、两电阻串联在电路中,其R1=4Ω,R2=6Ω,电源电压10V,那么在1min时间内电流通过各电阻产生的热量是多少?总共产生了多少热量?6、一台电动机线圈电阻0.3Ω,接在12V的电路上时,通过电动机的电流为0.5A,在5min内电流做功及电流产生的热量分别多大?7、一台接在220V电压的电路中正常工作的电风扇,通过风扇电动机的电流为0.455A,测得风扇电动机线圈电阻为5Ω,试求(1)电风扇的输入功率多大?(2)电风扇每分钟消耗电能多少?(3)风扇的电动机每分钟产生的电热多少?产生机械能多少?8、小欣家的电冰箱功率是0.2kW。
双休日全家外出的两整天里,只有电冰箱在自动间歇工作。
这两天前后,电能表示数如图所示。
则这两天时间内,电冰箱消耗的电能是多少?实际工作时间是多长?9、如图所示,已知电阻R1=10Ω,R2=20Ω,电源电压U=6V.试根据下列要求进行求解:(1)当开关S1、S2都断开,S3闭合时,求电流表的示数和R1的电压;(2)当S1、S2都闭合,S3断开时,求电流表示数;(3)开关处于何种情况下,电流表会烧坏?10、在伏安法测电阻的实验中,电压表的示数为4.8V,电流表的示数为0.5A。
初中物理专题复习——电学计算题(含答案)

中考专题复习——电学计算题1. 如图10所示电路中,小灯泡L 标有“6V 6W ”字样,R 2=3Ω,当S 1、S 2都闭合时,电流表示数为1.2A ,这时小灯泡L 正常发光,求: (1)电源电压U (2)电阻R 1的阻值(3)当S 1、S 2都断开时,小灯泡L 消耗的功率.解:(1)当S 1、S 2都闭合时,R 2短路,R 1与L 并联接入电源两端 ∵L 正常发光 ∴电源电压U =U L =6V (2) ∵P L =I L U L 。
∴I L =L L U P =VW 66=1A R 1=11I U =L I I U -1=A A V 12.16-=30Ω (3)当S 1、S 2都断开时,R 2与L 串联在此电路中R L =LLP U 2=W V 6)6(2=6Ω I L =I =R U =L R R U +2=Ω+Ω636V =32AP L =I L 2R L =2)32(A ×6Ω=2.67W2.如图19甲所示的电路中,电源电压为3Ⅴ,小灯泡上标有“2.5Ⅴ 0.25A”字样。
当滑动变阻器的滑片P 从最右端移到a 点时,小灯泡正常发光;再移动滑片到某点b 时,电压表的读数如图19乙所示(电源电压和小灯泡的电阻保持不变).请回答:(1)当滑片P 移到b 点时,电压表的读数为__ 2 V 。
小灯泡的电阻为 10 Ω。
b 点在a 点的__右____边(选填“左”或“右”)。
(2)滑片在b 处时,求滑动变阻器接人电路的阻值是多少? R =U/I=5Ω(3)滑片在b 处时,求滑动变阻器消耗的功率是多少? P=I 2R=0.2W3.某保温电热水壶电路如图21,S 是温控开关,R 1为加热器。
当开关S 接到a 时,电热水壶处于加热状态,此时通过电热水壶的电流是5A ;当水烧开时,开关S 自动切换到b ,电热水壶处于保温状态,此时电热水壶的电功率为165W 。
(不考虑温度对电阻阻值的影响),求: 图21 (1)加热电阻R 1的阻值是多大?(2)在保温状态下,通过电阻R 2的电流是多少?4.小明学习了电功率的知识后,想利用家里的电能表(如图21)和手表,测出一些家用电器的有关数据。
初中物理九年级电学经典计算题(含答案)
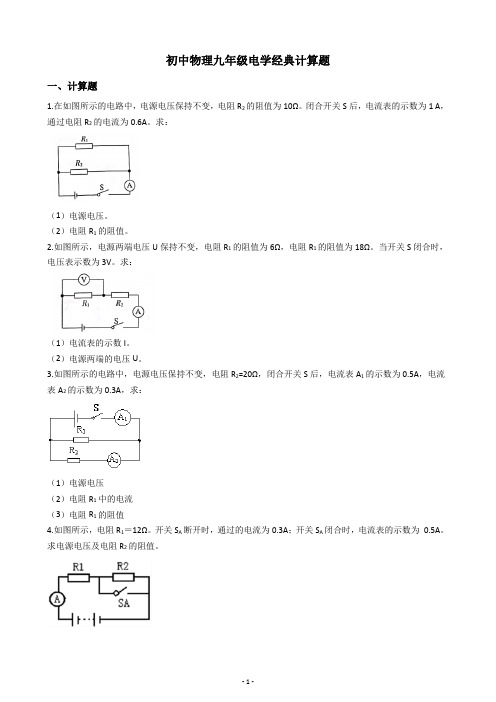
初中物理九年级电学经典计算题一、计算题1.在如图所示的电路中,电源电压保持不变,电阻R2的阻值为10Ω。
闭合开关S后,电流表的示数为1 A,通过电阻R2的电流为0.6A。
求:(1)电源电压。
(2)电阻R1的阻值。
2.如图所示,电源两端电压U保持不变,电阻R1的阻值为6Ω,电阻R1的阻值为18Ω。
当开关S闭合时,电压表示数为3V。
求:(1)电流表的示数I。
(2)电源两端的电压U。
3.如图所示的电路中,电源电压保持不变,电阻R2=20Ω,闭合开关S后,电流表A1的示数为0.5A,电流表A2的示数为0.3A,求:(1)电源电压(2)电阻R1中的电流(3)电阻R1的阻值4.如图所示,电阻R1=12Ω。
开关S A断开时,通过的电流为0.3A;开关S A闭合时,电流表的示数为0.5A。
求电源电压及电阻R2的阻值。
5.多功能养生壶(如图甲)具有精细烹饪、营养量化等功能,深受市场认可和欢迎,图乙是某品牌养生壶的简化电路图,当养生壶正常工作时,它的加热功率为880W,保温总功率为242W。
求:(1)该养生壶高温挡加热时的电流。
(2)电阻R2的阻值。
(3)某一天,小明断开家中其他用电器,只接通养生壶在高温挡烧水发现家中标着“3000r/(kw·h)”字样的电能表转盘在2min内转了80转,求此养生壶的实际功率。
6.某一家用两档可控的恒温餐盘,其高温档电功率为880W,简化电路如图甲所示,R1、R2均是发热电阻,R2的阻值是R1的3 倍。
求:(1)餐盘处于低温档时,电路中电流是多少?(2)1kg 米饭温度升高40℃,吸收的热量是多少?[米饭的比热容取2.5×10 3J /(kg•℃)](3)若电路中只使用该恒温餐盘,同样加热1kg的米饭,电能表的脉冲指示灯闪烁了125 次,如图乙所示,这个恒温餐盘的效率是多少?7.如图的电路中,R1为10Ω,R2为30Ω。
闭合开关S后,电流表的示数为1A,电源电压保持不变。
中考电学综合计算题专题 (带答案)
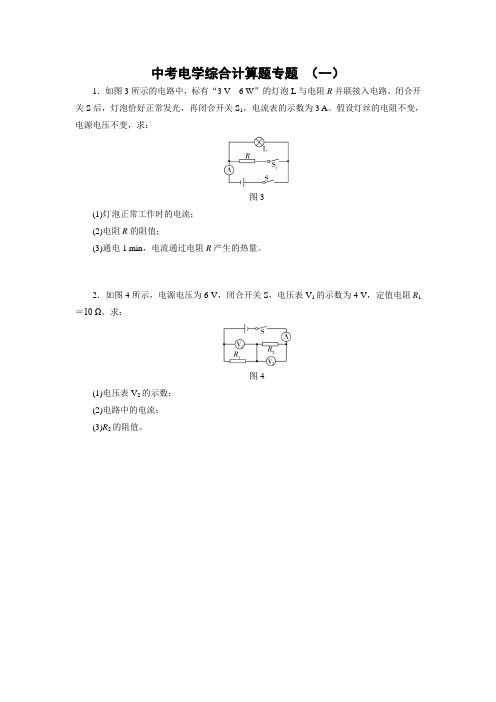
中考电学综合计算题专题(一)1.如图3所示的电路中,标有“3 V 6 W”的灯泡L与电阻R并联接入电路。
闭合开关S后,灯泡恰好正常发光,再闭合开关S1,电流表的示数为3 A。
假设灯丝的电阻不变,电源电压不变,求:图3(1)灯泡正常工作时的电流;(2)电阻R的阻值;(3)通电1 min,电流通过电阻R产生的热量。
2.如图4所示,电源电压为6 V,闭合开关S,电压表V1的示数为4 V,定值电阻R1=10 Ω。
求:图4(1)电压表V2的示数;(2)电路中的电流;(3)R2的阻值。
3.如图5所示,电源电压不变,小灯泡标有“6 V 3 W”字样,滑动变阻器的最大阻值为24 Ω。
则:图5(1)小灯泡正常工作时的电阻是多大?(2)小灯泡正常工作10 min将消耗多少电能?(3)当滑片P在中点时,小灯泡恰好正常发光,则电源电压为多大?4.在如图6所示的电路中,电源电压保持不变,灯泡L2标有“24 V12 W”。
开关S1闭合、S2断开时,电流表的示数为1 A,电压表的示数为12 V,灯泡L1正常发光,不考虑温度对灯泡灯丝电阻的影响。
求:图6(1)灯泡L1的电阻;(2)在10 s内,灯泡L1正常发光时消耗的电能;(3)灯泡L2的电阻;(4)当开关S1、S2都闭合时,电流表的示数和灯泡L2的实际功率。
5.(2017广东模拟)如图7所示,是某课外活动小组设计的小台灯的电路图。
S 为单刀双掷开关,电源电压为12 V ,且保持不变,小灯泡的额定功率是6 W ,灯丝的电阻不变,电阻R 的阻值为6 Ω。
当开关S 接“2”时,小灯泡恰好正常发光。
则:图7(1)小灯泡正常发光5 min ,电流通过小灯泡做的功是多少? (2)小灯泡的额定电流是多少?灯丝的电阻是多少? (3)开关S 接“1”时,电阻R 的功率是多少?参考答案1.解:(1)闭合开关S 后,电路为L 的简单电路,因为额定电压下灯泡正常发光,所以,电源电压U =U L =3 V由P =UI 可得,灯泡正常工作时的电流:I L =P L U L =6 W 3 V=2 A (2)闭合开关S 、S 1时,灯泡L 与电阻R 并联,电流表测干路电流,因为并联电路中干路电流等于各支路电流之和,所以,通过R 的电流:I R =I -I L =3 A -2 A =1 A因为并联电路中各支路两端的电压相等,所以,由I =U R 可得,电阻R 的阻值:R =UI R=3 V1A=3 Ω (3)通电1 min 内电流通过电阻R 产生的热量: Q R =W R =UI R t =3 V ×1 A ×60 s =180 J2.解:(1)电源电压U =6 V ,闭合开关S ,电阻R 1、R 2串联,电压表V 1测R 1两端的电压,电压表V 1的示数U 1=4 V ,根据串联电路的电压规律知,R 2两端的电压,即电压表V 2的示数:U 2=U -U 1=6 V -4 V =2 V(2)根据欧姆定律I =UR知,通过R 1的电流:I 1=U 1R 1=4 V 10 Ω=0.4 A 由串联电路的电流特点知,电路中的电流大小为0.4 A (3)由串联电路的电流特点得,通过R 2的电流I 2=I 1=0.4 A 由欧姆定律I =U R 得,R 2=U 2I 2=2 V0.4 A=5 Ω3.解:(1)小灯泡正常工作时的电压U L =U 额=6 V ,其功率P L =P 额=3 W ,由P =U 2R 可得小灯泡正常工作时的电阻:R L =U 2LP L =(6 V )23 W=12 Ω(2)由P =Wt 可得小灯泡正常工作10 min 消耗的电能:W =P L t =3 W ×10×60 s =1 800 J(3)由题图可知,小灯泡与滑动变阻器串联,当滑片P 在中点时,小灯泡恰好正常发光,由P =UI 可得,此时电路中的电流:I =I L =P L U L =3 W 6 V=0.5 A 由欧姆定律I =UR 可得滑动变阻器两端的电压:U 滑=I ×12R =0.5 A ×12×24 Ω=6 V电源电压:U =U L +U 滑=6 V +6 V =12 V4.解:(1)当开关S 1闭合、S 2断开时,电路为L 1的简单电路,电流表测电路中的电流,电压表测电源两端的电压,则电源的电压U =12 V ,此时电路中的电流为I 1=1 A ,由I =UR 可得,灯泡L 1的电阻:R 1=U I 1=12 V1 A=12 Ω(2)在10 s 内灯泡L 1正常发光时消耗的电能: W 1=UI 1t =12 V ×1 A ×10 s =120 J (3)由P =UI =U 2R 可得,灯泡L 2的电阻:R 2=U 22P 2=(24 V )212 W=48 Ω(4)当开关S 1、S 2都闭合时,两灯泡并联,电流表测干路电流,电路中的总电阻: R =R 1R 2R 1+R 2=12 Ω×48 Ω12 Ω+48 Ω=9.6 Ω电流表的示数:I =U R =12 V9.6 Ω=1.25 A因为并联电路中各支路两端的电压相等,所以,灯泡L 2的实际功率:P 2实=U 2R 2=(12 V )248 Ω=3 W5.解:(1)小灯泡正常发光5 min ,电流通过小灯泡做的功: W =P 额t =6 W ×5×60 s =1 800 J(2)开关S 接“2”时,小灯泡正常发光,小灯泡的额定电压: U 额=U =12 V小灯泡的额定电流:I 额=P 额U 额=6 W12 V =0.5 A灯丝的电阻:R 灯=U 额I 额=12 V0.5 A=24 Ω(3)开关S 接“1”时,电路总电阻:R 总=R 灯+R =24 Ω+6 Ω=30 Ω 电路中的电流 I =U R 总=12 V30 Ω=0.4 A电阻R 的功率P R =I 2R =(0.4 A)2×6 Ω=0.96 W电学综合计算题 (二)1.如图2-甲所示的电路中,R 1为定值电阻,R 2为滑动变阻器,电源电压保持不变。
中考物理《电学》计算题专项练习题(含答案)

中考物理《电学》计算题专项练习题(含答案)1. 如图, 电流表量程为0~0.6A, 电压表量程为0~15V, 电阻R0=30Ω, 电源电压恒为24V, 滑动变阻器最大阻值为100Ω, 求:(1)当电流表示数为0.4A时, R0两端电压是多少V?此时滑动变阻器连入电路的阻值是多少Ω?(2)当滑动变阻器连入电路的电阻太小时, 电路中的电流会超过电流表量程, 当滑动变阻器连入电路的电阻太大时, 变阻器两端电压会超过电压表量程, 求:在不超过电表量程的情况下, 滑动变阻器连入电路的电阻范围。
2. 如图所示, 电流表A1.A2和A3的示数分别为1.2A.0.8A和0.3A, 那么:(1)通过L1的电流是?(2)通过L2的电流是?(3)通过L3的电流是?3. 汽车尾气是造成雾霾指数PM2.5升高的原因之一, 某物理实验小组的同学们设计了如图所示的有害尾气排放检测电路。
在一项针对某种有害尾气浓度进行的测试中, 气敏电阻的阻值随有害尾气浓度变化的部分数据如下表所示。
已知电源电压18V恒定不变, R0为定值电阻, R为气敏电阻。
有害尾气浓度/%V ol … 2.5 5 7.5 10 15 …R/Ω…8 5.2 3.9 3 2 …(1)测试过程中, 闭合开关S, 当电压表读数为13V时, 电流表的读数为0.5A, 求电阻R0的阻值是多大?(2)闭合开关S, 当这种有害尾气浓度增大到15%Vol时, 则在1min内定值电阻R0产生的热量是多大?(3)当电路消耗的总功率为18W时, 有害尾气的浓度是多少?4. 图所示, 电源两端电压保持不变, 电阻R1的阻值为10Ω, 电阻R2的阻值为20Ω, 当只闭合开关S1时, 电流表的示数为1.2A。
求:(1)电源电压U;(2)开关S1.S2都闭合时, 电路消耗的总功率P。
5. 实验室使用的电压表是由小量程的电流表G改装而成的, 图乙是小量程电流表G改装成电压表的原理图, 当将“﹣”和“3”接线柱接入电路时, 表示电压表的量程为3V;当将“﹣”和“15”接线柱接入电路时, 表示电压表时量程为15V, 已知小量程电流表G的满偏电流为3mA, 内阻为10Ω, 试求:(1)将小量程电流表G直接接入电路中, 当指针满偏时其两端的电压为多少?(2)改装后的电压表内部电阻R1.R2的阻值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电学计算题——带电粒子在复合场中运动
35.如图9所示,在坐标平面的第Ⅰ象限内有水平向左的匀强电场E =1.0×103
V/m ,第Ⅱ象限内有垂直纸面向外的匀强磁场B =0.4T ,一荷质比为
51.010/q
C Kg m
=⨯的带正电粒子,从x 轴上的P 点以初速度v 0垂直x 轴进入磁场,已知P 与原点O 之间的距离为L =0.1m ,粒子恰好到达O 点而不进入电场,不计重力。
求: (1)带电粒子的初速度v 0 (2)若带电粒子的初速度方向不变,大小为原来的2倍,粒子第三次到达y 轴的位置为N ,求粒子从P 到N 的时间t 和总路程S 。
(结果取两位有效数)
35.(18分)如图,相距为R 的两块平行金属板M 、N 正对放置,s 1、s 2分别为M 、N 板上 的小孔,s 1、s 2、O 三点共线且水平,且s 2O =R 。
以O 为圆心、R 为半径的圆形区域内存在 大小为B 、方向垂直纸面向外的匀强磁场。
收集板D 上各点到O 点的距离以及板两端点的 距离都为2R ,板两端点的连线垂直M 、N 板。
质量为m 、带电量为+q 的粒子,经s 1无初速 进入M 、N 间的电场后,通过s 2进入磁场。
粒子重力不计。
(1)若粒子恰好打在收集板D 的中点上,求M 、N 间的电压值U ; (2)求粒子从s 1到打在D 的最右端经历的时间t 。
图9
M N
s
35.(18分)如图所示,水平放置的两块长直平行金属板a 、b 相距m d 10.0=,a 、b 间的电场强度为C N E /100.55⨯=,b 板下方整个空间存在着磁感应强度大小为
T B 6.0=、方向垂直纸面向里的匀强磁场。
今有一质量为kg m 25
10
8.4-⨯=、电荷量为
C q 18106.1-⨯=的带正电的粒子(不计重
力),从贴近a 板的左端以
s m v /100.160⨯=的初速度水平射入匀强
电场,刚好从狭缝P 处穿过b 板而垂直进入匀强磁场,最后粒子回到b 板的Q 处(图中未画出)。
(1)判断a 、b 两板间电场强度的方向;
(2)求粒子到达P 处的速度与水平方向的夹角θ; (3)求P 、Q 之间的距离L (结果可保留根号)。
36.(18分)如图,POy 区域内有沿y 轴正方向的匀强电场,POx 区域内有垂直纸面向里
的匀强磁场,OP 与x 轴成θ角.不计重力的负电荷,质量为m 、电量为q ,从y 轴上某点以初速度v 0垂直电场方向进入,经电场偏转后垂直OP 进入磁场,又垂直x 轴离开磁场.求:
(1)电荷进入磁场时的速度大小
(2)电场力对电荷做的功
(不作要求)(3)电场强度E 与磁感应强度B 的比值
36.(18分)如图所示,在一底边长为2L ,θ=45°的等腰三角形区域内(O 为底边中点)有垂直纸面向外的匀强磁场. 现有一质量为m ,电量为q 的带正电粒子从静止开始经过电势差为U 的电场加速后,从O 点垂直于AB 进入磁场,不计重力与空气阻力的影响. (1)粒子经电场加速射入磁场时的速度?
(2)磁感应强度B 为多少时,粒子能以最大的圆周半径偏转后打到OA 板?
(不作要求) (3)增加磁感应强度的大小,可以再延长粒子在磁场中的运动时间,求粒
子在磁场中运动的极限时间.(不计粒子与AB 板碰撞的作用时间,设粒子与AB 板碰撞前后,电量保持不变并以相同的速率反弹)
36.(18分)如图所示装置由加速电场、偏转电场和偏转磁场组成,偏转电场处在加有电
压的相距为d 的两块水平平行放置的导体板之间,匀强磁场水平宽度为l ,竖直宽度足够大,大量电子(其重力不计)由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间射入偏转电场。
当两板没有加电压时,这些电子通过两板之间的时间为2t 0,当在两板间加上如图乙所示的周期为2t 0,幅值恒为U 0的电压时,所有电子均能通过电场,穿过磁场,最后打在竖直放置的荧光屏上(已知电子的质量为m 、电荷量为e ),求:
(1)如果电子在t=0时刻进入偏转电场,求它离开偏转电场时的侧向位移大小; (2)通过计算说明,所有通过偏转电场的电子的偏向角(电子离开偏转电场的速度方
向与进入电场速度方向的夹角)都相同。
(不作要求)(3)要使电子能垂直打在荧光屏上,匀强磁场的磁感应强度为多少?
C
电学计算题——电磁感应综合应用
36.(18分)两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间距为l .导轨上面横放着两根导体棒PQ 和MN ,构成矩形回路,如图所示.导体棒PQ 的质量为m 、MN 的质量为2m ,两者的电阻皆为R ,回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B .设两导体棒均可沿导轨无摩擦地滑行.开始时,棒MN 静止处于距导轨右端为d 处,PQ 棒以大小为v 0的初速度从导轨左端开始运动(如图).忽略回路的电流对磁场产生的影响. (1)求PQ 棒刚开始运动时,回路产生的电流大小. (2)若棒MN 脱离导轨时的速度大小为
4
v ,则回路中产生的焦耳热是多少? (不作要求)(3)若原来回路中靠近MN 棒一侧的导轨中串联接有一个恒流电源,该电
源使回路中的电流大小始终保持为I 0(沿PMNQP 方向),试讨论MN 棒脱离导轨时速度v 的大小与d 的关系.
35.如图所示,串联阻值为R 的闭合电路中,面积为S 的正方形区域abcd 存在一个方向垂直纸面向外、磁感应强度均匀增加且变化率为k 的匀强磁场t B ,abcd 的电阻值也为R ,其他电阻不计.电阻两端又向右并联一个平行板电容器.在靠近M 板处由静止释放一质量为m 、电量为q +的带电粒子(不计重力),经过N 板的小孔P 进入一个垂直纸面向内、磁感应强度为B的圆形匀强磁场,已知该圆形匀强磁场的半径为q
mSk
B r 1=。
求:
(1)电容器获得的电压;
(2)带电粒子从小孔P 射入匀强磁场时的速度;
(3)带电粒子在圆形磁场运动时的轨道半径及它离开磁场时的偏转角.
35.(18分)
如图所示,两根半径为光滑的
圆弧轨道间距为L ,电阻不计,在其上端连有一阻值为R 0的电阻,整个
装置处于竖直向上的匀强磁场中,磁感应强度为B .现有一根度稍大于L、质量为m 、电阻为R 的金属棒轨 道的顶端PQ 处开始下滑,到达轨道底端MN 时对轨道的压力为2mg,求: (1 )棒到达最低点时电阻R 0两端的电压; (2)棒下滑过程中产生R 0的热量; (3)棒下滑过程中通过R 0的电量.
35.如图甲所示,在水平面上固定有宽为m L 0.1=足够长的金属平行导轨,导轨左端接有的Ω=5.0R 的电阻, 垂直于导轨平面有一磁场,且磁感应强度随时间变化规律如图乙所示。
在
0=t 时刻,在距导轨左端d=5m 处有一阻值Ω
=5.0r 光滑导体棒,放置在导轨上,第1S 内导体棒在一变力作用下始终处于静止状态,不计导体棒与导轨之间的接触电阻。
求 ⑴ 第1s 内的感应电动势大小; ⑵ 第1s 末拉力的大小及方向;
⑶若1s 后拉力保持与第1s 末相同,求导体棒的最终速度。
图甲
图乙
36.(18分)
如图甲所示,圆形导线框中磁场B 1 的大小随时间t 周期性变化,使平行金属板M 、N 间获得如图乙的周期性变化的电压。
M 、N 中心的小孔P 、Q 的连线与金属板垂直,N 板右侧匀强磁场(磁感应强度为B 2)的区域足够大。
绝缘档板C 垂直N 板放置,距小孔Q 点的距离为h 。
现使置于P 处的粒子源持续不断地沿PQ 方向释放出质量为m 、电量为q 的带正电粒子(其重力、初速度、相互间作用力忽略不计)。
(1)在0~
2
T
时间内,B 1大小按1B kt =的规律增大,此时M 板电势比N 板高,请判断此时B 1的方向。
试求,圆形导线框的面积S 多大才能使M 、N 间电压大小为U ?
(2)若其中某一带电粒子从Q 孔射入磁场B 2后打到C 板上,测得其落点距N 板距离为2h ,
则该粒子从Q 孔射入磁场B 2时的速度多大?
(不作要求)(3)若M 、N 两板间距d 满足以下关系式:22
25qUT md =,则在什么时刻
由P 处释放的粒子恰能到达Q 孔但不会从Q 孔射入磁场?结果用周期T 的函数表示。
36、如图a ,间距为d 的平行金属板MN 与一对光滑的平行导轨相连,平行导轨间距L =
2
d
,一根导体棒ab 以一定的初速度向右匀速运动,棒的右端存在一个垂直纸面向里,磁感应强度大小为B 的匀强磁场。
棒进入磁场的同时,粒子源P 释放一个初速度为零的带电粒子,已知带电粒子质量为m ,电荷量为q ,粒子能从N 板加速到M 板,并从M 板上的一个小孔穿出。
在板的上方,有一个环形区域内存在磁感应强度大小也为B ,垂直纸面向外的匀强磁场。
已知外圆半径为2d ,内圆半径为d ,两圆的圆心与小孔重合(粒子重力不计)。
(1)判断带电粒子的正负,并求当ab 棒的速度为v o 时,粒子到达M 板的速度v ; (2)若要求粒子不能从外圆边界飞出,则ab 棒运动速度v 0的取值范围是多少? (不作要求)(3)若棒ab 的速度'
0qBd
v m
=
,为使粒子不从外圆飞出,可通过控制导轨区域磁场的宽度S (如图b ),则该磁场宽度S 应控制在多少范围内?
U -。
