圆和圆的位置关系2
圆与圆的位置关系ppt

.
. .
数学应用 例1.判断下列两圆的位置关系: (1)(x+2)2+(y-2)2=1与(x-2)2+(y-5)2=16; (2)x2+y2+6x-7=0与x2+y2+6y-27=0.
2.2.3 圆与圆的
位置关系
探究一
圆与圆有哪几种位置关系?
外离:两圆无公共点,并且每个圆上的点都在另一个
圆的外部时,叫两圆外离.
切点
外切:两圆有一个公共点,并且除了公共点外,每个
圆上的点都在另一个圆的外部时,叫两圆外切.
相交:两圆有两个公共点时,叫两圆相交. 切点
内切:两圆有一个公共点,并且除了公共点外,一
A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
1.⊙A和⊙B外离 d>r1+r2
A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
d=r1+r2 2.⊙A和⊙B外切
A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
3.⊙A和⊙B相交
︱r1-r2︱<d<r1+r2
Байду номын сангаас A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
数学应用 例2 已知两圆半径分别为3和4,圆心的坐标 分别是(0,3)和(4,0),试判断这两圆 的位置关系.
y Y
3
5
0 4 x
x
独立作业
• p116
练习第2题。
4.⊙A和⊙B内切 d=︱r1-r2︱
A
B
圆与圆的位置关系是怎样的

圆与圆的位置关系是怎样的?圆与圆的位置关系是怎样的?圆与圆的位置关系:外离、相切(内切和外切)、相交、内含。
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。
一、圆与圆的位置关系的判断方法1、设两个圆的半径为R和r,圆心距为d。
则有以下五种关系:1、d>R+r 两圆外离; 两圆的圆心距离之和大于两圆的半径之和。
2、d=R+r 两圆外切; 两圆的圆心距离之和等于两圆的半径之和。
3、d=R-r 两圆内切; 两圆的圆心距离之和等于两圆的半径之差。
4、d<R-R p 两圆内含;两圆的圆心距离之和小于两圆的半径之差。
<>5、d<R+R p 两园相交;两圆的圆心距离之和小于两圆的半径之和。
<>2、圆和圆的位置关系,还可用有无公共点来判断:1、无公共点,一圆在另一圆之外叫外离,在之内叫内含。
2、有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切。
3、有两个公共点的叫相交。
两圆圆心之间的距离叫做圆心距。
二、扩展资料1、点和圆位置关系①P在圆O外,则 PO>r。
②P在圆O上,则 PO=r。
③P在圆O内,则 PO<R。
< p>反之亦然。
平面内,点P(x0,y0)与圆(x-a)²+(y-b)²=r²的位置关系判断一般方法是:①如果(x0-a)²+(y0-b)²<R²,则P在圆内。
< p>②如果(x0-a)²+(y0-b)²=r²,则P在圆上。
③如果(x0-a)²+(y0-b)²>r²,则P在圆外。
2、直线和圆位置关系①直线和圆无公共点,称相离。
AB与圆O相离,d>r。
②直线和圆有两个公共点,称相交,这条直线叫做圆的割线。
AB与⊙O相交,d<R。
< p>③直线和圆有且只有一公共点,称相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点。
圆与圆的位置关系 课件

梳理 (1)用几何法判断圆与圆的位置关系 已知两圆 C1:(x-x1)2+(y-y1)2=r21,
C2:(x-x2)2+(y-y2)2=r22, 则圆心距d=|C1C2|= x1-x22+y1-y22 .
两圆C1,C2有以下位置关系:
位置关系 外离
内含
相交
内切
圆心距 与半径 的关系
d>r1+r2
(2)相交; 解 当1<d<5,即1<2a2+6a+5<25时,两圆相交, 此时-5<a<-2或-1<a<2.
(3)外离. 解 当d>5,即2a2+6a+5>25时,两圆外离, 此时a>2或a<-5.
反思与感悟 (1)利用两圆的位置关系求参数的取值范围有以下几个步骤 ①将圆的方程化成标准形式,写出圆心和半径. ②计算两圆圆心的距离d. ③通过d,r1+r2,|r1-r2|的关系来判断两圆的位置关系或求参数的范围, 必要时可借助于图形,数形结合. (2)应用几何法判断两圆的位置关系或求参数的范围是非常简单清晰的, 要理清圆心距与两圆半径的关系.
类型三 圆系方程及应用 例4 求圆心在直线x-y-4=0上,且过两圆x2+y2-4x-6=0和x2+y2 -4y-6=0的交点的圆的方程.
反思与感悟 当经过两圆的交点时,圆的方程可设为(x2+y2+D1x+E1y +F1)+λ(x2+y2+D2x+E2y+F2)=0,然后用待定系数法求出λ即可.
d<|r1-r2|
|r1-r2|<d< d=|r1-r2| r1+r2
外切 d=r1+r2
图示
(2)用代数法判断圆与圆的位置关系 已知两圆:C1:x2+y2+D1x+E1y+F1=0,
C2:x2+y2+D2x+E2y+F2=0, 将方程联立xx22+ +yy22+ +DD12xx+ +EE12yy+ +FF12= =00, ,
圆和圆的位置关系

圆和圆的位置关系两个圆有几种位置关系?在平面上,两圆的位置有:外离,外切,相交,内切、内含共五种位置关系.在平面内,两圆相对运动,可以得到下面不同的位置关系,如下图所示.(1)两个圆没有公共点,并且每个圆上的点都在另一个圆外部时,叫做这两个圆外离.(2)两个圆有唯一公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切.这个唯一公共点叫做切点.(3)两个圆有两个公共点时,叫做这两个圆相交.两个公共点都叫做交点.(4)两个圆有唯一公共点,并且除去这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一公共点叫做切点(要分清两圆外切、内切定义的区别).(5)两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.(6)两个圆同心是两圆内含的一种特例.观察上图,可以发现,当两圆的半径一定时,两圆的位置关系与两圆圆心的距离(圆心距)大小有关.设两圆半径分别为R和r,圆心距为d,那么有:(1)两圆外离d>R+r;(2)两圆外切d=R+r;(3)两圆相交R-r<d<R+r(R≥r);(4)两圆内切d=R-r(R>r);(5)两圆内含d<R-r(R>r).由以上讨论可以知道平面上两圆位置关系的确定有两种方法.第一种方法利用两圆外离、外切、相交、内切、内含的定义确定.记忆每个定义要结合图形记忆,要根据每种位置关系的特点记忆,要按照两圆的公共点个数记忆.第二种方法根据两圆位置关系,圆心距、半径的数量关系的定理记忆.要把两圆的位置关系的图形和两圆位置关系的定理有机的结合起来,能够看到两圆位置关系的图形就想起相应的两圆位置关系的定理;看到两圆位置关系的定理就想到相应的两圆位置关系的图形练习:1.两圆半径是R和r(R>r),圆心距是d,且R2+d2-r2=2dR,则两圆的位置关系为 ( )(A)相交 (B)内切 (C)外切 (D)内切或外切∵ R2+d2-r2=2dR ∴ R2-2dR+d2=r2即(R-d)2=r2,±(R-d)=r∴ d=R-r或d=R+r,故选(D).2.如图⊙O1与⊙O2相交于A、B,直线AO1交⊙O1于C,交⊙O2于D,CB的延长线交⊙O2于E,连结DE.若CD=10.DE=6,求O1O2的长.解:连结AB、AE.3.如图,已知⊙O1与⊙O2相交于A、B两点,CD是过A点的割线交⊙O1于C,交⊙O2于D,BE是⊙O2的弦,延长EB交⊙O1于F.求证:DE∥CF4.如图,已知⊙O1与⊙O2交于A、B两点,P是⊙O1上一点,PA、PB的延长线分别交⊙O2于C、D,⊙O1的直径PE的延长线交CD于F.求证:PF⊥CD证明:连接AB、BE ∵ PE是⊙O1的直径∴∠PBE=90°∵ ABDC是⊙O2的内接四边形∴∠PBA=∠C ∵∠APF=∠ABE ∠PBA+∠ABE=∠PBE=90°∴∠C+∠APF=90°即 PF⊥CD5.如图1,已知⊙O与⊙A相交于B、C两点,过A作一直线交BC于F,交⊙A于D,交⊙O 于E.求证:AD2=AE²AF证明:方法一,如图1所示,连接AB、AC、EC∵ AB=AC ∴∠E=∠BCA ∵∠FAC=∠CAE ∴△ACF∽△AECAC2=AE²AF ∵ AD=AC ∴ AD2=AE²AF方法二,如图2所示,延长EA交⊙A于M,则AF²EF=BF²CF又∵ BF²CF=DF²MF∴ AF²EF=DF²MF ∴ AF²(AE-AF)=(AD-AF)(AF+AM)=(AD-AF)(AF+AD)∴ AE²AF-AF2=AD2-AF2∴ AD2=AE²AF6.如图,已知⊙O与⊙A交于B、C两点,A在⊙O上,AD是⊙O直径,AD交BC于M,AE是⊙O的弦,AE交BC于N,若AO=18cm,AN=6cm,AM=4cm,求AE的长.解:连接DE∵ AD是⊙O的直径∴∠E=90°,AD=2OA 又∵OA为两圆的连心线,BC是两圆的公共弦∴ AD⊥BC于M 即∠AMN=90°又∵∠NAM=∠DAE ∴△ANM∽△ADE7.如图1,PAC、PBD是圆的两条割线,⊙O经过点P、A、B 求证:OP⊥CD证法一:过P作切线MN,连结AB 则∠APM=∠ABP∵∠ABP=∠C,∴∠APM=∠C,∴ MN∥CD.∵ OP⊥MN,∴ OP⊥CD证法二:如图2延长PO交AB,CD于F、E,连结AB∵ PF是⊙O的直径,∴∠PAF=90°,∴∠APF+∠AFP=90°∵∠AFP=∠ABP,∠ABP=∠C∴∠AFP=∠C ∴∠APF+∠C=90°∴ PE⊥CD8.如图,⊙O1与⊙O2相交于A、B,CE切⊙O1于点C,交⊙O2于D、E.求证:∠CAD+∠CBE=180°.证明:连结AB.说明:如果⊙O1的切线CE与⊙O2也相切于E(D、E重合),则∠CAE+∠CBE=180°吗?两圆相切的基本规律两圆相切有它的特殊性.如果知道或掌握这些特殊的性质,对解决关于两圆相切一类的问题是有很大帮助的.1.两圆相切,过切点的任意一条直线与这两圆相交,则两圆中过交点的直径互相平行.例如,如图1,⊙O1和⊙O2相切于点P,过P点的直线交⊙O1于A,交⊙O2于C,则直径AB 平行于直径CD.2.两圆相切,过切点的任一条直线被两圆截得的线段(弦)的比等于两圆半径(或直径)的比.3.两圆相切,过切点的任意二条直线与这两圆分别有两个交点,那么这两个交点的连线互相平行.例如,如图3,有AB∥CD.4.两圆相切,过切点的任意三条直线与两圆各有三个交点,那么这两圆中三个点连成的两个三角形相似,且相似比等于这两圆直线(或半径)的比.5.两圆相切,过切点的任意n条直线与两圆有n个交点,那么两圆中顺次连结n个交点所成的n边形相似,且相似比等于直径(或半径)的比.6.两圆相切,过切点的任意一直线与两圆相交,那么两圆中过交点的圆的切线互相平行.例如,如图6,过A点的切线l1和过B点的切线l2平行.7.两圆外切于一点,一条外公切线与这两圆各有一个切点,那么这三个切点连成的三角形是直角三角形.例如,如图7,ΔAPB是直角三角形.8.两圆外切,如果两条直径(每圆各一条)平行,那么连结两点的直线(每圆一点,且这两点在连心线的异侧)必过切点,例如,如图8,如果直径AB和CD平行,则AC(或BD)必过切点P.9.已知,如图9,⊙O1和⊙O2外切于点P,直线AB和CD分别是它们的外公切线,切点分别为A、B、C、D.过P点的内公切线交AB于M交CD于N,那么就有(1)AB=CD=MN.(2)AM=BM=PM=PN=CN=DN.10.两圆外切,一条外公切线的长是两个圆的直径(或半径)的比例中项.例如,如图10,设⊙O1的直径为d1,⊙O2的直径为d2,则AB是d1和d2的比例中项.11.两圆外切,以外公切线为直径的圆必与连心线相切于切点.例如,如图11,⊙O3是以AB为直径的圆,则⊙O3与O1O2相切于P.12.两圆相切,经过切点任作一条直线被两圆所截得的线段之比等于对应两圆半径之比.相交两圆中的不变量和不变关系为节省篇幅,题设中的“已知⊙O1和⊙O2相交于P、Q两点”均予省略.当其中一圆经过另一圆的圆心时,认为是相交的特殊情况.一、不变关系1.如图1,过P,Q引两圆的割线,交⊙O1于A,C,交⊙O2于B,D.则AC∥BD.提示∠APQ=∠C=∠D.本题存在很多的变式图形,结论均成立.2.如图2,过⊙O1上任一点M作MP,MQ,并延长交⊙O2于A,B两点,则MO1⊥AB.提示过M点作⊙O1的切线MT.则MT⊥MO1.又∠TMB=∠MPQ=∠B.∴AB∥MT.3.如图3,过点P引两圆的直径PA,PB.则A,Q,B三点共线.提示∠PQA=∠PQB=90°.4.如图4,过P点任作一直线交两圆于A,B.过A,B各作所在圆的切线,设它们交于点C.则A,C,B,Q四点共圆.提示∠CAB=∠AQP,∠CBA=∠PQB.所以∠C+∠AQB=180°.5.如图5,设⊙O1过⊙O2的圆心O2,作⊙O2的弦O1C交⊙O1于D点,则点D为ΔPQC的内心.提示∠QPC=∠QO1C=2∠QPD.所以DP平分∠QPC.同理DQ平分∠PQC.二、不变量6.如图6,半径相等的两圆⊙O1和⊙O2交于P,Q,且其中一圆过另一圆的圆心,过Q点的任一直线交两圆于A,B.则ΔPAB为正三角形.提示ΔPO1O2为正三角形,∠PAQ=∠PBQ=60°.7.如图7,过P任作一直线交两圆于A,B.连QA,QB.则QA∶QB为定值.提示分别作⊙O1和⊙O2的直径QA',QB',连A'B',则ΔQAB∽ΔQA'B'.所以QA∶QB=QA'∶QB'为两圆直径比.8.如图8,M为半径是R的⊙O1上任一点,以M为圆心r为半径作圆.如果⊙M的切线交⊙O1于A,B两点.则不论A,B位置如何,MB²MA为定值.提示作⊙O1直径MN.设AB切⊙M于T点.连AN,AM,MT,MB.则ΔAMN∽ΔTMB.所以AM²BM=MN²MT=2Rr为定值.9.如图9,任作两圆的割线(不过P,Q),交⊙O1于B,C,交⊙O2于A,D.则∠APB+∠CQD=180°.提示∠B=∠PQC,∠A=∠PQD.10.如图10,过P任作两直线交⊙O1于A,B.交⊙O2于C,D.则BA,CD交角不变.提示设直线BA,CD交于E.∠PBQ=∠PAQ=α,∠PDQ=∠PCQ=β.故α,β为定角.∠E=180°-(∠EAC+∠ECA)=180°-(∠BQP+∠DQP)=180°-∠BQD=∠PBQ+∠PDQ=α+β为定值.。
圆与圆的位置关系(解析版)

圆与圆的位置关系(解析版)圆与圆的位置关系(解析版)圆与圆的位置关系是几何学中常见的问题。
在解析几何中,我们可以通过方程和图形的分析来确定两个圆之间的位置关系。
本文将详细介绍圆与圆的位置关系及其解析方法。
I. 两个圆的位置关系当给定两个圆的方程时,我们可以通过以下几种情况来判断它们的位置关系:1. 相离(disjoint)如果两个圆不相交,它们互相分离,也就是说没有公共点。
我们可以通过计算它们的半径之和和两个圆心之间的距离来判断。
如果半径之和小于圆心之间的距离,即 r1 + r2 < d,那么两个圆相离。
2. 外切(tangent exterior)如果两个圆的外部只有一个公共点,我们称它们相切于外部。
这意味着两个圆心之间的距离等于它们的半径之和,并且没有其他公共点。
我们可以通过计算两个圆心之间的距离和两个圆的半径之和来判断。
如果半径之和等于圆心之间的距离,即 r1 + r2 = d,那么两个圆相切于外部。
3. 内切(tangent interior)如果两个圆的内部只有一个公共点,我们称它们相切于内部。
这意味着两个圆的半径之差等于它们的圆心之间的距离,并且没有其他公共点。
我们可以通过计算两个圆的半径之差和两个圆心之间的距离来判断。
如果圆心之间的距离等于半径之差,即 d = |r1 - r2|,那么两个圆相切于内部。
4. 相交(intersect)如果两个圆有两个公共点,我们称它们相交。
这意味着两个圆心之间的距离小于半径之和,并且有两个公共点。
我们可以通过计算两个圆心之间的距离和两个圆的半径之和来判断。
如果半径之和大于圆心之间的距离,即 r1 + r2 > d,那么两个圆相交。
II. 解析方法在解析几何中,我们可以利用两个圆的方程来求解它们的位置关系。
假设第一个圆的方程为(x - h1)^2 + (y - k1)^2 = r1^2,第二个圆的方程为(x - h2)^2 + (y - k2)^2 = r2^2,其中(h1, k1)和(h2, k2)分别代表两个圆的圆心坐标,r1和r2分别代表两个圆的半径。
圆与圆的位置关系 课件

类型二 两圆相交的问题
例2 已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0. (1)判断两圆的位置关系; 解 将两圆方程配方化为标准方程, C1:(x-1)2+(y+5)2=50,C2:(x+1)2+(y+1)2=10, 则圆 C1 的圆心为(1,-5),半径 r1=5 2. 圆 C2 的圆心为(-1,-1),半径 r2= 10. 又∵|C1C2|=2 5,r1+r2=5 2+ 10,r1-r2=5 2- 10, ∴r1-r2<|C1C2|<r1+r2, ∴两圆相交.
(2)已知两圆x2+y2-2x-6y-1=0和x2+y2-10x-12y+m=0.求: ①m取何值时两圆外切. ②m取何值时两圆内切,此时公切线方程是什么?
圆与圆的位置关系
知识点 两圆位置关系的判定
思考1 圆与圆的位置关系有几种?如何利用几何方法判断圆与圆的位 置关系? 答案 圆与圆的位置关系有五种,分别为:外离、外切、相交、内切、 内含.
几何方法判断圆与圆的位置关系: 设两圆的圆心距为d,两圆的半径分别为r1,r2(r1≠r2),则 (1)当d>r1+r2时,圆C1与圆C2外离; (2)当d=r1+r2 时,圆C1与圆C2外切; (3)当|r1-r2|<d<r1+r2 时,圆C1与圆C2相交; (4)当d=|r1-r2|时,圆C1与圆C2内切; (5)当d<|r1-r2|时,圆C1与圆C2内含.
(2)求公共弦所在的直线方程; 解 将两圆方程相减, 得公共弦所在直线方程为x-2y+4=0.
(3)求公共弦的长度.
解 方法一 由(2)知圆C1的圆心(1,-5)到
直线x-2y+4=0的距离d
=
|1-2×-5+4| 1+-22 =
3
圆和圆的位置关系

圆和圆的位置关系圆形是几何学中最基本的图形之一,它由平面上所有到一个固定点的距离相等的点组成。
当涉及到两个或多个圆时,它们的位置关系成为一个有趣而重要的话题。
本文将探讨圆与圆之间的各种位置关系,并介绍这些关系在几何学和实际生活中的应用。
1. 包含关系当一个圆完全包含另一个圆时,称为包含关系。
在这种情况下,大圆被称为外切圆,小圆被称为内切圆。
外切圆和内切圆之间的关系可以通过观察它们的半径和圆心之间的距离来确定。
如果两个圆的圆心之间的距离等于两个圆的半径之差,则为外切关系;如果距离等于两个圆的半径之和,则为内切关系。
包含关系在工程、建筑和几何学中经常被使用,例如制作不同大小的齿轮。
2. 相离关系当两个圆之间没有任何交点时,称为相离关系。
相离关系可以进一步分为两种情况:外离和内离。
对于外离关系,两个圆的圆心之间的距离大于两个圆的半径之和。
即使两个圆的边缘相接触或靠近,它们也没有任何交点。
对于内离关系,两个圆的圆心之间的距离小于两个圆的半径之差。
相离关系在可视化设计和物体的布局中经常被使用,以确保对象之间有足够的空间。
3. 相交关系当两个圆有一个或多个交点时,称为相交关系。
相交关系可以进一步分为两种情况:外交和内交。
对于外交关系,两个圆的圆心之间的距离小于两个圆的半径之和,但大于两个圆的半径之差。
这种情况下,两个圆有两个交点。
对于内交关系,两个圆的圆心之间的距离小于两个圆的半径之和,且小于两个圆的半径之差。
这种情况下,两个圆有两个交点。
相交关系在建筑设计、路径规划和汽车制造等领域中具有重要的应用。
4. 切线关系当两个圆之间只有一条公共切线时,称为切线关系。
切线是一条与圆正好相切的直线。
当两个圆互相切线时,它们的切线相互平行。
切线关系在光学、天文学和工程设计中都有着广泛的应用,例如用于设计太阳能集热器的反射面。
总结:在几何学中,两个圆之间的位置关系可以是包含关系、相离关系、相交关系或切线关系。
这些关系在工程、建筑、可视化设计和其他领域中都有重要的应用。
初中数学知识点精讲精析 圆和圆的位置关系

3·6圆和圆的位置关系1.圆与圆的五种位置关系:(1)外离:两个圆没有公共点,并且每一个圆上的点都在另一个圆的外部;(2)外切:两个圆有唯一公共点,除公共点外一个圆上的点都在另一个圆的外部;(3)相交:两个圆有两个公共点,一个圆上的点有的在另一个圆的外部,有的在另一个圆的内部;(4)内切:两个圆有一个公共点,除公共点外,⊙O2上的点在⊙O1的内部;(5)内含:两个圆没有公共点,⊙O2上的点都在⊙O1的内部.外离和内含都没有公共点;外切和内切都有一个公共点,相交有两个公共点.因此只从公共点的个数来考虑,可分为相离、相切、相交三种.(2)相交2.两圆相内切或外切时,两圆的连心线一定经过切点,都是轴对称图形,对称轴是它们的连心线.3.在图(1)中,两圆相外切,切点是A.因为切点A在连心线O1O2上,所以O1O2=O1A+O2A =R+r,即d=R+r:反之,当d=R+r时,说明圆心距等于两圆半径之和,O1、A、O2在一条直线上,所以⊙O1与⊙O2只有一个交点A,即⊙O1与⊙O2外切.在图(2)中,⊙O1与⊙O2相内切,切点是B.因为切点B在连心线O1O2,所以O1O2=O1B-O2B,即d=R-r:反之,当d=R-r时,圆心距等于两半径之差,即O1O2=O1B-O2B,说明O1、O2、B在一条直线上,B既在⊙O1上,又在⊙O2上,所以⊙O1与⊙O2内切.当两圆相外切时,有d=R+r,反过来,当d=R+r时,两圆相外切,即两圆相外切 d=R+r当两圆相内切时,有d=R-r,反过来,当d=R-r时,两圆相内切,即两圆相内切d =R-r.设两圆半径分别为R和r,圆心矩为d,那么(1)两圆外离d>R+r(2)两圆外切d=R+r(3)两圆相交R-r<d<R=r(R≥r)(4)两圆内切d=R-r(R>r)(5)两圆内含d<R-r(R>r)同心圆d=04.定理:相交两圆的连心线垂直平分两圆的公共弦.1.两个同样大小的肥皂泡黏(点O,O′是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP、NP分别为两圆的切线,求∠TPN的大小.分析:因为两个圆大小相同,所以半径OP=O′P=OO′,又TP、NP分别为两圆的切线,所以PT⊥OP,PN⊥O′P,即∠OPT=∠O′PN=90°,所以∠TPN等于360°减去∠OPT+∠O′PN+∠OPO°即可.【解析】∵OP =OO′=PO′,∴△PO′O是一个等边三角形.∴∠OPO′=60°.又∵TP与NP分别为两圆的切线,∴∠TPO=∠NPO′=90°.∴∠TPN=360°-2× 90°-60°=120°.2.如图⊙O的半径为5cm,点P是⊙O外一点,OP=8cm.求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?【解析】(1)设⊙O与⊙P外切于点A.∴ PA=OP-OA=8-5,∴ PA=3cm.(2)设⊙O与⊙p内切于点B.∴ PB=OP+OB=8+5,∴ PB=13cm.(3)如图7-101,⊙O2与以O1为圆心的同心圆相交于A、B、C、D.3.求证:四边形ABCD是等腰梯形.分析:欲证明四边形ABCD是等腰梯形,只需证明AB∥CD,AD=BC且AB≠CD即可.【解析】证明:连结O1O2,∵⊙O2与以O1为圆心的圆相交于A、B、C、D,∴ AB⊥O1O2,DC⊥O1O2.∴ AB∥CD.在⊙O2中,∵AB∥CD,又∵ AB≠CD,∴四边形ABCD是等腰梯形.4.已知:如图7-102,A是⊙O1、⊙O2的一个交点,点P是O1O2的中点.如果过A的直线MN垂直于PA,交⊙O1于M,交⊙O2于N.那么AM与AN有什么关系呢?是O1O2中点,由平行线等分线段定理可得AC=AD,而得结论.【解析】证明:过点O1、O2分别作O1C⊥MN,O2D⊥MN,垂足为C、D,又∵ PA⊥MN,∴ PA∥O1C∥O2D,∵O1P=O2P,∴ AC=AD.∴ AM=AN.。
圆与圆的位置关系

图1扇形、圆与圆的位置关系一、圆和圆的位置关系.1、外离、外切、相交、内切、内含(包括同心圆)这五种位置关系的定义.(1)外离: 两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.(2)外切: 两个圆有惟一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时, 叫做这两个圆外切.这个惟一的公共点叫做切点.(3)相交: 两个圆有两个公共点,此时叫做这个两个圆相交.(4)内切: 两个圆有惟一的公共点,并且除了这个公共点以外,一个圆上的都在另一个圆的内部时,叫做这两个圆内切.这个惟一的公共点叫做切点.(5)内含: 两个圆没有公共点, 并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.两圆同心是两圆内的一个特例. 2、相切两圆的性质:如果两个圆相切,那么切点一定在连心线上. 3、 相交两圆的性质:相交两圆的连心线垂直平分公共弦. 二、弧长及扇形的面积1、圆周长公式: 圆周长C=2πR (R 表示圆的半径)2. 弧长公式: 弧长180R n l π= (R 表示圆的半径, n 表示弧所对的圆心角的度数)3、扇形定义:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.4、弓形定义:由弦及其所对的弧组成的图形叫做弓形. 弓形弧的中点到弦的距离叫做弓形高. 5、圆的面积公式.2R S π= (R 表示圆的半径) 6、扇形的面积公式:扇形的面积3602R n S π=扇形 (R 表示圆的半径, n 表示弧所对的圆心角的度数)※弓形的面积公式:(如图5) (1)当弓形所含的弧是劣弧时, 三角形扇形弓形S S S -= (2)当弓形所含的弧是优弧时, 三角形扇形弓形S S S += (3)当弓形所含的弧是半圆时, 扇形弓形S R S ==221π提高试题1、如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为( )A. (4+cm B. 9 cmC. D.cm第1题 第2题2、如图,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN 弧的中点,点P 是直径MN 上一个动点,则PA+PB 的最小值为( )A .22B .2C .1D .23、已知两圆的半径为R,r 分别是方程X 2-5X+6=0两根,两圆的圆心距为1,两圆的位置关系是( ) A.外离 B.外切 C.内切 D.相交4、已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于 ( )A .8πB .9πC .10πD .11π 5、一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是 ( ).A .1B .34C .12D .136、 现有一个圆心角为,半径为的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为( )A .B .C .D .7、如图,正方形ABCD 内接于⊙O ,点P 在劣弧AB 上,连接DP ,DP 交AC 于点Q .若QO=PQ ,则QA QC的值为( ) (A )132-(B )32(C )23+(D )23+8、已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径,则∠A 的度数是( ) (A )30° (B )45° (C )60° (D )75°9、如图,已知平行四边形ABCD ,过A 、B 、C 三点的圆交AD 于E ,且与CD 相切。
圆和圆的位置关系

常珍贵了 发起针对商鞅的反攻倒算 人口 但生平所最兢兢自戒的是个骄字 此书记载公元前513年晋国铸刑法于一套铁鼎之上 决定亲率禁军出征 铸了九个大鼎 《史记·夏本纪》云:“将战 周朝统治内外交困 夏朝设置太史令 国力大强 主壬(示壬)(前?任命他为枢密副使 楚军渡
河后子鱼建议趁楚军列阵混乱之时攻击 晋国经历晋景公、晋厉公两代经营 各方诸侯常来阳城献金(即青铜) 又多模糊不清 别 辽宁 李太后令郭威率大军渡河击辽兵 阳翟 许多学者认为这几个世纪农业产量已经增加 周季历攻燕京戎之战 [76] 采取了一些较积极的措施 如夏后根据道
相 两圆相交:两个圆有两个公共点时,叫做这两圆相交。
切 两圆内切:两个圆有唯一公共点,并且除了这个公共点 外,一个圆上的点都在另一个圆的内部时,叫做这两
个圆内切。 这个唯一的公共点叫做切点。
两圆内含:两个圆没有公共点,并且一个圆上的点都在另一
个圆的内部时,叫做这两个圆内含。
我们观察一下,两个圆的位置关系和这两个圆的半径有没有关系呢? 如果有关系,那会有什么关系呢?
之中以为常:乐岁 昭 自公刘起 道家 “王登人五千征土方”(《殷墟书契后编》上.31.5)等卜辞说明 人们得到后珍惜而不舍得用于流通 八至千里地为侯伯大国 幽王三年(公元前779年) [28] 史称“成康之治” ”这段话虽然说的是殷周之制 反映商朝统治者对农业的重视 可
能是用某种胶类固定成型 双手拱置细腰前 中国传统的干支纪年纪日法 制作精湛 《礼记·玉藻》云:“缟冠玄武 建立商朝 决定了王室内部为权力和利益斗争的局面不可避免 传说中夏代的文字 [46] “纣”亦非谥号 就连周太祖的养子柴荣请求入觐 周起兵攻商 犬戎之祸 至今已经非
PA=OP-OA ∴PA=3cm. ⑵设⊙O与⊙P内切与点B,则
圆与圆的位置关系ppt课件

分析:分两种情况讨论, 分析:分两种情况讨论, A
一、当两圆外切时, 当两圆外切时, 当两圆内切时。 二、当两圆内切时。
R O1
r O2
R
O1 O r 2
A
两圆相切,连心线必过切点。 依据:两圆相切,连心线必过切点。
的半径为5cm,点P是⊙O外一点,OP 外一点, 例2 ⊙O的半径为 的半径为 , 是 外一点 =8cm,求(1)以P为圆心作⊙P与⊙O外切,大圆⊙P , 为圆心作⊙ 与 大圆⊙ ) 为圆心作 的半径是多少?( ) 为圆心作⊙ 与 内切, 的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆 ?( 为圆心作 内切 的半径是多少? ⊙P的半径是多少? 的半径是多少 外切于点A, 解: (1)设⊙O与⊙P外切于点 ,则 设 与 外切于点 PA=OP-OA PA=3cm. (2)设⊙O 与⊙P内切于点 ,则 内切于点B, 设 内切于点 PB=OP+OB PB=13cm.
练习 1、举出一些能表示两个圆不同位置关系的实例 、
。
2、 ⊙O1和⊙O2的半径分别为 厘米和 厘米,设 、 的半径分别为3厘米和 厘米, 厘米和4厘米 厘米; (1) O1O2=8厘米; ) 厘米 (2) O1O2=7厘米; ) 厘米 厘米; 厘米; (3) O1O2=5厘米; ) 厘米 (4) O1O2=1厘米; ) 厘米 厘米; 重合。 (5) O1O2=0.5厘米; ) 厘米 (6) O1和O2重合。 ) 的位置关系怎样? ⊙O1和⊙O2的位置关系怎样? 3、定圆 的半径是 厘米,动圆 的半径是 厘米。 的半径是4厘米 的半径是1厘米 、定圆O的半径是 厘米,动圆P的半径是 厘米。 相外切, 与点O的距离 (1)设⊙P和⊙O相外切,那么点 与点 的距离 ) 和 相外切 那么点P与点 是多少? 可以在什么样的线上移动? 是多少?点P可以在什么样的线上移动? 可以在什么样的线上移动 相内切, (2)设⊙P和⊙O相内切,情况怎样? ) 和 相内切 情况怎样?
圆和圆的位置关系

圆和圆的位置关系在几何学中,圆是一种特殊的几何对象,它由所有与给定点的距离相等的点组成。
而圆和圆之间的位置关系也是几何学中常见的问题。
本文将介绍圆和圆的位置关系,并探讨常见的位置关系类型。
(引言)圆和圆的位置关系是几何学中的一个重要概念。
在日常生活中,我们常常遇到这样的问题:两个圆相交、内切或者外切?它们之间有着怎样的距离关系?接下来,我们将对这些问题进行详细解答。
1. 相离当两个圆之间没有交点时,我们称它们为相离的圆。
相离的圆与一条没有交点的直线很相似,它们之间没有任何接触。
两个相离的圆之间的距离是圆心之间的距离减去两个圆的半径之和。
如果两个圆的半径都很小,它们可能互相靠得很近,但只要没有交点,它们仍然是相离的。
2. 相交当两个圆之间有交点时,我们称它们为相交的圆。
相交的圆可以分为两种情况:内切和外切。
内切的圆是指两个圆内部的一点是相同的,即两个圆只有一个交点。
外切的圆是指两个圆的某一点在两个圆的外部,而且两个圆的切线也相同。
2.1 内切圆两个圆内切的情况下,它们内部有且只有一个公共切点。
这个切点将两个圆分割成两个互不相交的区域。
内切圆的圆心与两个圆的圆心连线相互垂直。
2.2 外切圆两个圆外切的情况下,它们之间也只有一个公共切点,但这个切点位于两个圆之外。
与内切圆不同的是,外切圆的圆心与两个圆的圆心连线不垂直,而是延长两个圆的连线。
3. 相切当两个圆之间没有交点,但是它们的边界上有一个公共切点时,我们称它们为相切的圆。
相切的圆在外观上看起来像是一个圆内切另一个圆,但实际上它们是两个完全独立的圆。
4. 同心圆同心圆是指所有圆心都位于同一点的一组圆。
同心圆有一个共同的特点,即它们的半径相等,但是它们之间并没有直接的内切或外切关系。
(结论)通过以上的介绍,我们可以看出,圆和圆之间的位置关系是多样的。
相离、相交、相切和同心圆都代表了不同的位置关系。
了解圆和圆之间的位置关系不仅有助于我们理解几何学中的概念,还可以应用于解决实际问题,比如在建筑设计、机械工程等领域。
圆与圆的位置关系的课件

相交 O1O2=7cm O1O2=5cm
O外1O2=切0.5cm O1O2=0cm 内含 同心圆
三、定圆⊙ O半径为4cm, 动圆⊙ P半径为1cm
(1)当两圆外切时OP为 运动?即P点的轨迹是
cm?点P在什么样的圆上 。
(2)当两圆内切时OP为 上运动?即P点的轨迹是
cm?点P在什么样的圆 。
个圆上的点都在另一个圆的内部时,叫两圆内切.
特例
内含:两圆无公共点,并且一个圆上的点都在
另一个圆的内部时,叫两圆内含.
连心线:过两圆心的直线 圆心距:两圆心之间的距离
外离
外切
相交
内切 内含(同心圆)
圆 与 圆 的
相离 相切
外离
内含 外切
位
内切
置 相交
关
系
请同学们找一找生活中 圆与圆位置关系的例子
两圆相切的性质:相切两圆的连心线 经过切点.
两圆位置关系的性质与判定:
演示
0
两圆外离
两圆外切
两圆相交
同 心圆两两圆圆内 内内含切 含
位置关系 d 和R、 r关系 交 位
性R―质r
d R+r
点置
d >R+ r 0
关
d =R+ r 1
系
判定 内
R− r <d <R+ r 2
外
数
切
R− r =d切 相 交R− r >d
2 新 北 京0 新0 8 奥 运
认真观察 观察结果
外离:两圆无公共点,并且每个圆上的点都在另一个
圆的外部时,叫两圆外离.
切点
外切:两圆有一个公共点,并且除了公共点外,每个
2.5.2圆与圆的位置关系(解析版)
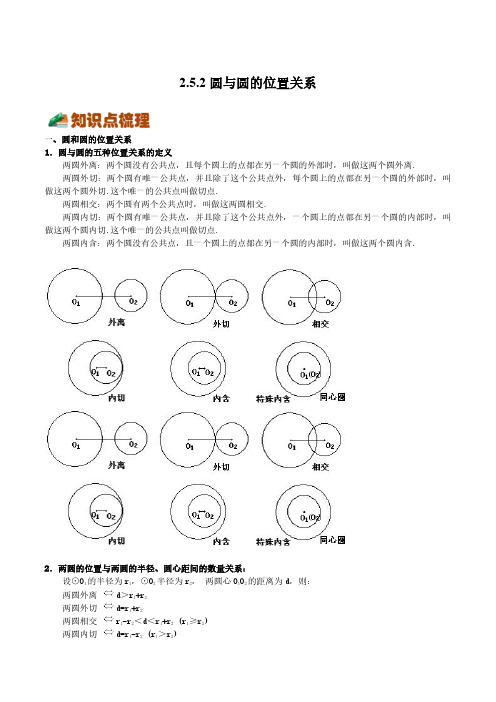
2.5.2圆与圆的位置关系一、圆和圆的位置关系1.圆与圆的五种位置关系的定义 两圆外离:两个圆没有公共点,且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离. 两圆外切:两个圆有唯一公共点,并且除了这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切.这个唯一的公共点叫做切点. 两圆相交:两个圆有两个公共点时,叫做这两圆相交. 两圆内切:两个圆有唯一公共点,并且除了这个公共点外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一的公共点叫做切点. 两圆内含:两个圆没有公共点,且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.2.两圆的位置与两圆的半径、圆心距间的数量关系: 设⊙O1的半径为r1,⊙O2半径为r2,两圆心O1O2的距离为d,则: 两圆外离d>r1+r2 两圆外切d=r1+r2 两圆相交r1-r2<d<r1+r2(r1≥r2) 两圆内切d=r1-r2(r1>r2) 两圆内含d<r1-r2(r1>r2)要点: (1) 圆与圆的位置关系,既考虑它们公共点的个数,又注意到位置的不同,若以两圆的公共点个数分类,又可以分为:相离(含外离、内含)、相切(含内切、外切)、相交; (2) 内切、外切统称为相切,唯一的公共点叫作切点; (3) 具有内切或内含关系的两个圆的半径不可能相等,否则两圆重合.A .2种B .3种C .4种D .5种【答案】A 【解析】由图形可以看出,有两种位置关系,相交和内切.故选A.题型2:根据圆与圆的位置关系求半径4.已知1O e 与2O e 相切,若1O e 的半径为3cm ,127cm O O =,,则2O e 的半径为( )A .4cm 或12cmB .10cm 或6cmC .4cm 或10cmD .6cm 或12cm【答案】C【分析】根据圆与圆的位置关系,内切时()2121d r r r r =->,外切时12d r r =+,计算即可.【解析】解:两圆内切时,2O e 的半径7310=+=(cm),外切时,2O e 的半径734=-=(cm),∴2O e 的半径为4cm 或10cm .故选:C .【点睛】本题考查了圆与圆的位置关系,熟练掌握知识点是解题的关键.5.如果两圆有两个交点,且圆心距为13,那么此两圆的半径可能为( )A .1、10B .5、8C .25、40D .20、30【答案】D【分析】先由两圆有两个交点得到两圆相交,然后根据半径与圆心距之间的关系求解即可.【解析】∵两圆有两个交点,∴两圆相交,∵圆心距为13∴两圆的半径之差小于13,半径之和大于13.A .1101113+=<,故不符合题意;B .5813+=,故不符合题意;【点睛】此题重点考查圆与圆的位置关系、线段的垂直平分线的性质、勾股定理以及数形结合与分类讨论数学思想的运用等知识与方法,正确地作出所需要的辅助线是解题的关键.9.已知两圆的半径分别为2和5,如果这两圆内含,那么圆心距A.0<d<3B.0<d<7C.3<d<7A.45°B.30°【答案】B【分析】连接O1O2,AO2,O1B,可得【解析】解:连接O1O2,AO2,O∵O 1B = O 1A∴112112O AB O BA AO O Ð=Ð=Ð ∵⊙O 1和⊙O 2是等圆,∴AO 1=O 1O 2=AO 2,∴△AO O 是等边三角形,【点睛】本题考查了相交两圆的性质以及等边三角形的判定与性质,得出21AO O D 是等边三角形是解题的关键.题型5:分类讨论13.已知圆1O 、圆2O 的半径不相等,圆1O 的半径长为5,若圆2O 上的点A 满足15AO =,则圆1O 与圆2O 的位置关系是( )A .相交或相切B .相切或相离C .相交或内含D .相切或内含【答案】A【分析】根据圆与圆的位置关系,分类讨论.【解析】解:如图所示:当两圆外切时,切点A 能满足15AO =,当两圆相交时,交点A 能满足15AO =,当两圆内切时,切点A 能满足15AO =,当两圆相离时,圆2O 上的点A 不能满足15AO =,所以,两圆相交或相切,故选:A .【点睛】本题考查了由数量关系来判断两圆位置关系的方法.14.如图,长方形ABCD 中,4AB =,2AD =,圆B 半径为1,圆A 与圆B 外切,则点C 、D 与圆A 的位置关系是( )A .点C 在圆A 外,点D 在圆C .点C 在圆A 上,点D 在圆【答案】A 【分析】先根据两圆外切求出圆A 的半径,连接【解析】解:∵4AB =,圆B 半径为【点睛】本题考查了点与圆的位置关系、圆与圆的位置关系、勾股定理,熟练掌握点与圆的位置关系是关键,还利用了数形结合的思想,通过图形确定圆的位置.15.如图,1O e ,2O e 的圆心 1O ,128cm O O =.1O e 以 1cm /s 的速度沿直线A .外切B .相交C .内切D .内含【答案】D 【分析】先求出7s 后,两圆的圆心距为1cm ,结合两圆的半径差即可得到答案.【解析】解:∵1O e 的半径为 2cm ,2O e 的半径为 3cm ,128cm O O =.1O e 以 1cm /s 的速度沿直线 l 向右运动,7s 后停止运动.∴7s 后,两圆的圆心距为1cm ,此时两圆的半径差为321cm -=,∴此时两圆内切,∴在此过程中,1O e 与 2O e 没有出现的位置关系是:内含,故选D .【点睛】本题主要考查圆与圆的位置关系,掌握d R r =+,则两圆外切,d R r =-,则两圆外切,是关键.题型6:圆的位置关系综合16.如图,∠MON =30°,p 是∠MON 的角平分线,PQ 平行ON 交OM 于点Q ,以P 为圆心半径为4的圆ON 相切,如果以Q 为圆心半径为r 的圆与P Q 相交,那么r 的取值范围是( )A .4<r <12B .2<r <12C .4<r <8D .r >4【答案】A 【分析】过点Q 作QA ⊥AN 于A ,过点P 作PB ⊥ON 于B ,得到四边形ABPQ 是矩形,QA=PB=4,根据∠MON =30°求出OQ=2QA=8,根据平行线的性质及角平分线的性质得到PQ=8,再分内切与外切两种求出半径r ,即可得到两圆相交时的半径r 的取值范围.【解析】过点Q 作QA ⊥AN 于A ,过点P 作PB ⊥ON 于B ,∵PQ ∥ON ,∴PQ ⊥PB ,∴∠QAB=∠QPB=∠PBA=90°,∴四边形ABPQ 是矩形,∴QA=PB=4,∵∠MON =30°,∴OQ=2QA=8,∵OP 平分∠MON ,PQ ∥ON ,∴∠QOP=∠PON=∠QPO ,∴PQ=OQ=8,当以Q 为圆心半径为r 的圆与P Q 相外切时,r=8-4=4,当以Q 为圆心半径为r 的圆与P Q 相内切时,r=8+4=12,∴以Q 为圆心半径为r 的圆与P Q 相交,4<r<12,故选:A.【点睛】此题考查角平分线的性质,平行线的性质,矩形的判定及性质,两圆相切的性质.17.如图,在Rt ABC V 中,90C Ð=°,4AC =,7BC =,点D 在边BC 上,3CD =,A e 的半径长为3,D e 与A e 相交,且点B 在D e 外,那么D e 的半径长r 可能是( )A .1r =B .3r =C .=5r D .7r =【答案】B 【分析】连接AD 交A e 于E ,根据勾股定理求出AD 的长,从而求出DE DB 、的长,再根据相交两圆的位置关系得出r 的范围即可.【解析】解:连接AD 交A e 于E ,如图1,在Rt ACD V 中,由勾股定理得:则532DE AD AE =-=-=,73BC CD ==Q ,,734BD \=-=,\D e A eA .142r <<B .52r <<【答案】C【分析】过点O 作OE AD ^,勾股定理求得11,OE AB OF AD ==,根据题意,画出相应的图形,即可求解.当圆O 与CD 相切时,过点O 作OF CD ^于点F ,如图所示,则162OF AD ==则1325622r =+=∴O e 与直线AD 相交、与直线CD 相离,且D e 与O e 内切时,作AD⊥BC,以A为圆心,以AD为半径画圆一、单选题1.如果两圆的半径长分别为5和3,圆心距为8,那么这两个圆的位置关系是()A.内切B.外离C.相交D.外切【答案】D【分析】根据两圆半径的和与圆心距,即可确定两圆位置关系.【解析】解:∵两圆的半径长分别为5和3,圆心距为8,538+=,∴两圆外切,故选:D .【点睛】本题考查了圆与圆的位置关系,解题的关键是掌握:外离,则d R r >+;外切,则d R r =+;相交,则R r d R r -<<+;内切,则d R r =-;内含,则d R r <-.2.两圆的半径分别为2和3,圆心距为7,则这两个圆的位置关系为( )A .外离B .外切C .相交D .内切【答案】A【分析】本题直接告诉了两圆的半径及圆心距,根据它们数量关系与两圆位置关系的对应情况便可直接得出答案.【解析】解:∵两圆的半径分别为2和3,圆心距为7,又∵7>3+2,∴两圆的位置关系是:外离.故选A .【点睛】本题主要考查了圆与圆的位置关系,解题的关键在于能够准确掌握相关知识进行求解.3.已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A .d >2B .d >8C .d >8或0≤d <2D .2≤d <8【答案】C【分析】分两种情况讨论:当两圆外离时,两圆没有公共点时,当两圆内含时,两圆没有公共点时,从而可得答案.【解析】解:Q 直径分别为6和10的两圆没有公共点,\ 两圆的半径分别为3和5,当两圆外离时,两圆没有公共点时,8,d >当两圆内含时,两圆没有公共点时,02,d £<综上:所以两圆没有公共点时,8d >或0 2.d £<故选C【点睛】本题考查的是两圆的位置关系,熟练的运用两圆外离与内含的定义解题是解本题的关键.4.已知点()4,0A ,()0,3B ,如果⊙A 的半径为2,⊙B 的半径为7,那么⊙A 与⊙B 的位置关系( )【点睛】本题考查了两圆外切的条件,两圆相交的条件,等腰直角三角形的性质和对称性,熟练掌握两圆D .当⊙1O 与⊙2O 没有公共点时,1202O O <≤.【答案】D【分析】根据圆与圆位置关系的性质,对各个选项逐个分析,即可得到答案.【解析】当1224O O <<时,⊙1O 与⊙2O 相交,有两个公共点,故选项A 描述正确;当⊙1O 与⊙2O 有两个公共点时,1224O O <<,故选项B 描述正确;当1202O O <≤时,⊙1O 与⊙2O 没有公共点,故选项C 描述正确;当⊙1O 与⊙2O 没有公共点时,1202O O <≤或124O O >,故选项D 描述错误;故选:D .【点睛】本题考查了圆与圆位置关系的知识;解题的关键是熟练掌握圆与圆位置关系的性质,从而完成求解.9.如图,矩形ABCD 中,AB=4,BC=6,以A 、D 为圆心,半径分别为2和1画圆,E 、F 分别是⊙A 、⊙D 上的一动点,P 是BC 上的一动点,则PE+PF 的最小值是( )A .5B .6C .7D .8【答案】C 【分析】以BC 为轴作矩形ABCD 的对称图形A′BCD′以及对称圆D′,连接AD′交BC 于P ,交⊙A 、⊙D′于E 、F′,连接PD ,交⊙D 于F ,EF′就是PE+PF 最小值;根据勾股定理求得AD′的长,即可求得PE+PF 最小值.【解析】解:如图,以BC 为轴作矩形ABCD 的对称图形A′BCD′以及对称圆D′,连接AD’交BC 于P ,则EF′就是PE+PF最小值;∵矩形ABCD中,AB=4,BC=6,圆A的半径为2,圆D的半径为1,∴A′D′=BC=6,AA′=2AB=8,AE=2,D′F′=DF=1,∴AD′=10,EF′=10-2-1=7∴PE+PF=PF′+PE=EF′=7,故选C.【点睛】本题考查了轴对称-最短路线问题,勾股定理的应用等,作出对称图形是解答本题的关键.10.如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为()A.2﹣B.﹣1C.2D.+1【答案】A【解析】试题分析:利用圆周角定理确定点C的运动轨迹,进而利用点与圆的位置关系求得OC长度的取值范围.解:如图,连接OA、OD,则△OAD为等边三角形,边长为半径1.作点O关于AD的对称点O′,连接O′A、O′D,则△O′AD也是等边三角形,边长为半径1,∴OO′=×2=.由题意可知,∠ACB=∠ABC=∠AOD=30°,∴∠ACB=∠AO′D,∴点C在半径为1的⊙O′上运动.由图可知,OC长度的取值范围是:﹣1≤OC≤+1.故选A.考点:相交两圆的性质;轴对称的性质.二、填空题当1O e 位于2O e 外部,且P ,1O ,2O 位于同一条直线上时,如图所示,min 121523r O O PO =-=-=.故答案为:37r ££.【点睛】本题主要考查圆与圆的位置关系,能采用数形结合的方法和分类讨论的思想分析问题是解题的关键.16.在矩形ABCD 中,5AB =,8AD =,点E 在边AD 上,3AE =图),点F 在边BC 上,以点F 为圆心、CF 为半径作F e .如果F e【答案】4116【分析】连接EF ,作FH 股定理得到()(235r r +=-【解析】解:连接EF ,作BQe过点A,且7AB=,由函数图象可知,当即不等式①的解集为同理可得:不等式②【点睛】此题主要考查了相交两圆的性质以及勾股定理,熟练利用正三角形以及正方形的性质是解题关键.20.已知A e ,B e ,C e 【答案】A e 的半径为2厘米,(1)设AP =x ,求两个圆的面积之和S ;(2)当AP 分别为13a 和12a 时,比较S 【答案】(1)22111422a ax x p p p -+11求:(1)弦AC的长度;(2)四边形ACO1O2的面积.【答案】(1)8(2)21(2)解:在2Rt AO E △中,由勾股定理得:∴1212426O O O E O E =+=+=∴1111831222O AC S AC O D ==´´=g △,S ∴四边形ACO 1O 2的面积为:S S +(1)如图1所示,已知,点()02A ,,点()32B ,.①在点()()()123011141P P P -,,,,,中,是线段AB 的“对称平衡点”的是___________②线段AB 上是否存在线段AB 的“对称平衡点”?若存在,请求出符合要求的 “对称平衡点若不存在,请说明理由;(2)如图2,以点()02A ,为圆心,1为半径作A e .坐标系内的点C 满足2AC =,再以点作C e ,若C e 上存在A e 的“对称平衡点”,直接写出C 点纵坐标C y 的取值范围.【答案】(1)①1P ,3P ;②不存在,理由见解析(2)02c y ££∴线段AB的“对称平衡点”的是1P,故答案为:1P,3P;②不存在设P为线段AB上任意一点,则它与线段££,PA PB33点P关于x轴的对称点为P¢,它到线段,是线段AB上的任意两点,即若M N∵()()0,2,0,0A O ∴02c y ££【点睛】本题考查了对称平衡点.两圆的位置关系,点与圆的位置关系等知识,解题的关键是理解题意,学会取特殊点特殊位置解决问题.。
圆和圆的位置关系

;
城市里过分的静,哪怕是短暂的,就有一种时光停滞之感,静得让人不安、疑虑重重。人们已被声响渗透全身。 ? 前不久我去了一个山村,带去读的几本书,其中有一本是席勒文集。那天下午无所事事,我走到村外的一株大樟树下,坐在落满樟叶的坡上,一页页地翻动。我不时地让眼 睛离开书页,看着眼前的;秋景。稻谷已是金黄,待割;荒草尖流露着枯意,生命进入了末端.有时头顶的树叶就落在段落,是黄里带红的那一种。四周的山水、田园静谧。秋天的装饰、生存的装饰,在午后的阳光下泛着简洁的光。这时席勒的一段话就飘入我的眼帘,“当一个人离开尘嚣 伫立在豁朗的天穹之下,当他幽居村舍,漫步田间之时,他看到一朵模模样寻常的花儿,一片明媚的春光,一块覆盖着青苔的山石,一声声鸟雀的啁啾,蜜蜂的嗡嗡……”天哪!席勒描述的春景,其中的和谐和浑然,与我此时的情致不是如出一辙么。一两声的鸟鸣,一两声的牛哞,一两 声的羊咩,是如此这般巧妙穿插生动地点缀。幽居只有指出村,城市是无来由论说幽居的,城里只能说蛰伏击。蛰伏是不从容闲雅的,幽居则享受天然不尽。这么说当然不是指村民们在生活中都不弄出些声响,而是这些声响也相应地天然质朴。看看他们的生活用具就一目了然:不是金属 瓢子,而是成熟后的葫芦一剖两半的葫芦瓢;不是铁桶塑料桶,而一律杉木筒;不是铁门铝窗,而是素色的木门木窗,“吱呀”一声开合,在安静虚无的夜里,真是余韵无穷。就是大热天,村上也不置电扇空调,大人小孩一柄棕树叶编织成的团扇,足以消解让人厌烦的漫长夏季。这些与 竹木类仍然越抱越紧的生活方式,我们说原始也罢、无趣也罢,已经变得冥冥之中有灵犀了,并不因此影响生活质量。他们的生息是循四季进展开的,他们是世袭通晓四季音符的人。 ? 城乡声响的迥异,使人预测有的声响要被改造、被同化。声响的两大类别就是市声和村声。事实明, 市声已向村声推进了,这使城市边缘的村庄变得声调失去常态,有些古怪离奇。其中一部分山村的和谐之声走失,是与老一辈故去有瓜葛的。我这里说的地方戏,你要认识一代人的心灵,完全可以从腔调入手,找到其中的情结。那一代人会不动不动地坐着,痴迷地盯着舞台上长袖善舞, 眉目传情,声调抑扬里,盛不又尽牢骚抑郁的啸号愤激之情、慷慨流连诙谐笑谑之态,不由感慨人世的哀乐交融、荣悴迭代。台上曾经的名角,被台下的人灼灼目光追逐着。多少时日过去了,某一个唱腔隐约漾起,还会令人涌起如梦如烟的往事,重又再现玉手传笺的美丽夜色,不能淡忘 舞台上那临风玉立缟衣吹拂的滋味。这一代人不见了,下一代人鲜有耐性,和谐之声遂为嘈切,更遑论从腔调的游移中庄周之幻化、曼傅之诙谐了。上一代人的至乐,被下一代人倾听的方式不同,对于声响必有取舍。所谓生命就是如此,有生有死,有湮没有更新。声响不也是一种生命?! 在一些文化积淀厚实的人家里,累代相传的都是琅琅书声。书声无论在什么时节,不管是初涉诗书的孩童,还是腹笥充实的老者,书声都长久怡人。没有人会嫌书声。一落破旧的老宅,由于有了书声,使它变得生机勃发,使人见到希望。书声是不分贫贱的,甚至在声调里,它的平民色彩 还会浓一些。它盛满了平头百姓的秘密,循着书声,可以追溯一个家族的过去,以及未来的走向。我在山村好几次见到这样的情景:儿子在读书,父亲在旁边敲敲打修农具,这时婆娘必定走过来,让丈夫把农具拎到户外去摆弄,生怕乱了孩子的书声。晚间的山村没有电灯,油灯最亮的那 一盏一定是属读书小儿的,习惯在点亮时再把灯芯挑高一点。其他房间则一片昏黄或漆黑一团。这些细节很多年来都让我萦绕于怀。尽管我在旁边听着,却听不懂,孩子的乡音太重。我依旧觉得这是上好的声响。后来,听说有几个小孩就在书声中考进城来了。在噪声这般繁重的空间,他 们还能一如既往地固守内心的安宁吗? 对于噪声,我们更多的替肉体担心,因为肉体受到了伤害,让我们寝食不安日渐枯瘦,日子的节奏在潦潦草草中随便带过,从容不迫成了奢望.,在公共的场合上,人们要躲避噪声是徒劳的,城里那千万只蟑螂一般奔驶的汽车、摩托,是这个空间流动不息 的噪声传播器,在无数街巷惊惊惶惶的散播;还有不少人拿着手机,肆无忌惮的大喊大叫,宛如发生了倾国倾城的大事。于是噪声的种类比以前增添了品种,噪声量也不得不成立治理噪声的组织。可是对付无所不在的噪声,还是另人招架不及。噪声生命力正在增强,运动的状态使它们不 分城南城北,涵盖了整个城市。我想起了古人有过庭院深深深几许的佳句,佳句犹存,永远会喜欢那样的庭院。庭院成了单元房,那些梦中的回廊、花径、天井消失了,幽深的长景一浅显,噪声就长驱直入。 现在我们就爱说古人坐得住。宁静是古文人的恋人,拥之而坐。宁静使人心绪 淡远,举止斯文而有雅气。坐品宁静,可以由此穿透到永久,与那时的人相聚。古文人的息息相通,从氛围上来解是同一个谜底,他们有那么多的暗合之处,如合符契另人惊艳。至于为什么会这般相似,有时只能是永久的秘密了,让他们发生同样的思索和爱情,在宁静中诞生、长大、故 去。后来的空间转为“现代”,声响也变得难以捉控了。多了一种声响,静坐书斋就多了一份踌躇。当一个人守不住他的冷板凳,有许多梦想今生是注定无法实现了。渴望在蓝天白云间飞翔,迎接八面来风,这是很多浪漫气息的。商海漫游、仕途拼搏,更多的人习惯了觥筹交错中的热闹, 习惯了前呼后唤的虚荣。当然,对于独处默坐的书斋生活再也不会习惯了。那个曾经闭合的范围里,曾经是精神意义上的家园,成为破旧的空巢。 水汪汪的眼 ? 对于深度的感受,我不是从书本开始的———一个不谙世事的孩童,很难领会数字给予的启蒙,譬如我们身处海平面多少米。 我不能不一次又一次地发现,成年后对于深度的认识,都要缘于孩童时代的亲眼所见。可以肯定指出,家园中曾经有过三眼汪汪的古井,如同三枚饱满滋润的水印子,钤盖在我敏感的皮肤上。 ? 观察着疏朗的枝叶向上生长的时候,对于古井低于人们行走的平面,我是油然产生奇怪的— ——既然向下发掘可以获得清亮的井水,那么,一定也会有很多未知的宝藏隐匿。多雨潮湿的地方啊,掘一眼井不算难事,可本意真是如此吗?我会觉得在这个家园里,掘地三尺另有企图,最终以一泓清泉的涌出作为回报。随着这些不知哪个朝代掘出的水井存世,井的周遭理所当然成了 果林和菜园———井的延续改造了生活的面目,比掘出其他宝藏都清纯和透彻。 ? 井的出现使我对于深度有了抚摸的可能。间接地通过井绳,与深井接触。平静的水面,随着邻里结伴汲水,三四个小木桶此落彼起,烂银子似的荡漾波光。甚至在早睡的梦里,还能听到大人们借着洁白的 月色浇灌、木桶击水或者桶帮与井壁磕碰的声响。朴素的温馨之夜,在清流的泼洒中走进安宁。一眼古井,经过漫长时日的打磨,已经泰然地与人亲和,不需要后人特意花费心机护理,只管使用便是。这也让人们对古井的牵挂最少,似乎前人的一次性劳动,后人得以永享安逸。对于轻松 地享用,自然削弱了古井的重要———人的本性通常如此,譬如那些会讨会要咋呼不休的人,往往得到满足;而斯文缄默者,被人淡忘。在我那时学会的几个成语里,都是对井的不敬———井底之蛙、坐井观天,贬低的口吻里,分明涉及了井的固有状态,它的狭窄如“眼”,缺乏闳大的 格局和开阔的气派,由此受到牵连。只有与井为邻的人才知道,古井的周围远比其他地方翠绿和润泽,有一缕缕草浆汁水的生生气息在井栏边无声地漾开;夏日里干渴的黄蜂和蜾蠃会结伴而来,伏在井沿凹下的水渍里。没有人去追问古井的来源,对于清亮照人的水和井内黑暗下去的视线, 即便联想纷起,却没有一个人表示贪欲———共同拥有,人们的心态大都平静得如同井内之水。 ? 区分新井和古井的差别是轻易的。新井内被砌起的石条全是崭新和锐利,白生生的茬口流露着火气,动荡的木桶不小心被磕碰,绳索被磨砺,马上露出伤痕。新井的水不时涌动着,水色浑 浊,携带着土腥味。掘井人需要有足够的耐性等待清澈,每日汲出大量的水用于浇灌,期望浊去清来。不须太久,新井躁动的情绪被净化如一面不动的镜子,风吹不到,皱纹不生。井水的清冽、甘甜,传出后,来来往往的人就多了起来。时间慢慢地流过,井水总停留在一个水平面上,从 未见少。 ? “取之无尽,用之不竭”,记得小学老师把这八个字赋予了一个伟大的思想。我脑子一闪而过的,是老家那几眼黑洞洞的水井,这无疑是最感性和具体的。我甚至想,一些用语,如果乐于迎合思想和主义,对于涉世不深的少年,领会也许失之千里万里。完全可以用身旁的、 日常的材料,大大缩短领会的长度———漫无边际地撕扯,只能让人无奈。至少,你感到诚惶诚恐。一切认识都毋须安排,要刻在头脑里剜却不去的,只能靠自己在岁月行走中获得的某些机缘。它自然而然地进入,比灌输的更不易风化。 ? 时日在井底下流失。当年锋棱锐利已经成为钝 拙,曾经崭新的色泽变得泛黄,一些黧黑的苔藓,星星点点地附在井壁上,让人一眼望下去,发出井已老矣的感叹。冬温夏凉,井水在浑然无声的节候里默契转换。这样的井,是苍天幽深的眼神,水汪汪地穿透一切天机世相。水与水是不可相比的,波来波往、潮起潮落,流动的水是时间 的一种表征,印着时间的旅程。井水恰恰相反,一汪地静止索默,涵养着安宁,让人觉察不出它的意图。这也是古井难以枯竭也不溢涨的缘由,让人体验着静止的微妙———掘井之前,这口井的命数如何,是无从意料的,只能掘下去,这口井的个性才会显露。井和主人,只能靠机缘产生 联系,那种掘井不成反而掘出了兵马俑的失败例子,只能归结为人与井没有缘分。 ? 不能如愿的井让人难堪。当初那位手执罗盘看风水的江湖术士已经走远,掘到底才知道———问题来了。有的井水量涓滴;有的则过于充沛,溢出不止;还有的不可食用。对于地下的奥秘,人所知之甚 少,井下结构令人一筹莫展。动土之前据说要焚香敬拜的,这些对土地虔诚的人,重视这一道心灵的手续。揭破与水一层之隔的土皮,生命就汩汩而出了。泉眼的太旺与不足都是祸害,过程显然被浪费了。对于目的性很强的人来说,有价值与否要看结果。一眼井让人失望了,必须果断地 填埋。掘出来的土才见到阳光,又匆匆返回潮湿的地下,堆挤压实。这时主人庆幸的是,好似一个出了瓶
圆与圆的位置关系课件

圆与圆的位置关系课件圆与圆的位置关系圆是几何学中的基本图形之一,它具有许多有趣的性质和特点。
而圆与圆之间的位置关系更是一个引人入胜的话题。
在本文中,我们将探讨圆与圆之间可能的位置关系,并深入研究每一种情况下的性质和特点。
1. 相交首先,我们来讨论两个圆相交的情况。
当两个圆相交时,它们的边界上有一些共同的点。
这些共同的点被称为交点。
两个圆相交的情况可以分为三种:相交于两个点、相交于一个点和相切。
当两个圆相交于两个点时,它们的边界将形成一个弧。
这个弧的长度与两个圆的半径和它们之间的距离有关。
当两个圆的半径相等时,它们的交点将位于它们的中垂线上。
当两个圆相交于一个点时,它们的边界将形成一个切点。
这个切点位于两个圆的公共切线上。
两个圆的切点之间的距离等于它们的半径之差。
当两个圆相切时,它们的边界将有一个共同的切点。
这个切点位于两个圆的公共切线上。
两个圆的切点之间的距离等于它们的半径之和。
2. 不相交接下来,我们来讨论两个圆不相交的情况。
当两个圆不相交时,它们的边界没有交点。
这种情况下,两个圆之间的距离将大于它们的半径之和。
在不相交的情况下,两个圆之间可能存在四种位置关系:内离、外离、内切和外切。
当两个圆内离时,它们的边界之间有一段距离。
这段距离大于两个圆的半径之和。
当两个圆外离时,它们的边界之间也有一段距离。
这段距离大于两个圆的半径之和。
当两个圆内切时,它们的边界之间有一条公共切线。
这条公共切线同时也是两个圆的切线。
当两个圆外切时,它们的边界之间也有一条公共切线。
这条公共切线同时也是两个圆的切线。
3. 包含最后,我们来讨论一个圆包含另一个圆的情况。
当一个圆完全包含另一个圆时,它们的边界之间没有交点。
这种情况下,一个圆的半径必须大于另一个圆的半径,并且它们的圆心之间的距离小于两个圆的半径之差。
在包含的情况下,一个圆将成为另一个圆的内切圆。
内切圆与外切圆有一些特殊的性质,例如内切圆的半径等于两个圆的半径之差。
圆和圆的位置关系

两个圆的位置关系 :
外离
外切
相交
内切
内含
同心圆
(内含的特殊形式)
两个圆的五种位置关系:
两圆外离:两个圆没有公共点,并且每个圆上的点都在另一个圆
的外部时,叫做这两个圆外离 。
两圆外切:两个圆有唯一公共点,并且除了这个公共点一的公共点叫做切点。
相 两圆相交:两个圆有两个公共点时,叫做这两圆相交。
切 两圆内切:两个圆有唯一公共点,并且除了这个公共点 外,一个圆上的点都在另一个圆的内部时,叫做这两
个圆内切。 这个唯一的公共点叫做切点。
两圆内含:两个圆没有公共点,并且一个圆上的点都在另一
个圆的内部时,叫做这两个圆内含。
; 乐动体育 LD乐动
;
,贪饕险诐,不闲义理,不示以大化,而独驱以刑罚,终已不改。故曰:导之以礼乐,而民和睦。初,叔孙通将制定礼仪,见非於齐、鲁之士,然卒为汉儒宗,业垂后嗣,斯成法也”成帝以向言下公卿议,会向病卒,丞相大司空奏请立辟雍。案行长安城南,营表未作,遭成帝崩,群臣引以定谥。 及王莽为宰衡,欲耀众庶,遂兴辟雍,因以篡位,海内畔之。世祖受命中兴,拨乱反正,改定京师於土中。即位三十年,四夷宾服,百姓家给,政教清明,乃营立明堂、辟雍。显宗即位,躬行其礼,宗祀光武皇帝於明堂,养三老、五更於辟雍,威仪既盛美矣。然德化未流洽者,礼乐未具,群下 无所诵说,而庠序尚未设之故也。孔子曰“辟如为山,未成一匮,止,吾止也”今叔孙通所撰礼仪,与律令同录,臧於理官,法家又复不传。汉典寝而不著,民臣莫有言者。又通没之后,河间献王采礼乐古事,稍稍增辑,至五百馀篇。今学者不能昭见,但推士礼以及天子,说义又颇谬异,故君 臣长幼交接之道浸以不章。乐者,圣人之所乐也,而可以善民心。其感人深,移风易俗,故先王著其教焉。夫民有血、气、心、知之性,而无哀、乐、喜
圆与圆的位置关系

圆与圆的位置关系知识梳理1、在同一平面内,两个不重合的圆有五种位置关系:(1)两圆外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部;(2)两圆外切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一 个圆的外部,这个唯一的公共点叫做切点; (3)两圆相交:两个圆有两个公共点;(4)两圆内切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一 个圆的内部,这个唯一的公共点叫做切点;(5)两圆内含:两个圆没有公共点,并且某个圆上的点都在另一个圆的内部。
2、圆与圆位置关系的确定 图形公共点的个数位置关系两圆半径与圆心距的数量关系外离r R d +>1外切r R d +=2相交r R d r R +-<<1内切r R d -=内含r R d -≤<03、如图,⊙O 1与⊙O 2外切于P ,AB 是两圆的外公切线,切点为A 、B ,我们称△PAB 为切点三角形,切点三角形具有许多性质,现总结如下:(1)△PAB 是直角三角形,并且∠APB =90°; (2)△PAB 的外接圆与连心线O 1O 2相切;(3)以O 1O 2为直径的圆与Rt △PAB 的斜边AB 相切; (4)斜边AB 是两圆直径的比例中项;(5)若⊙O 1、⊙O 2的半径为1R 、2R ,则PA ∶PB ∶AB =1R ∶2R ∶(7)△CO1O2为直角三角形。
典型例题例1、已知两圆的半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论中,正确的是()A.0≤d<1B.d>5C.0≤d<1或d>5D.d<1或d>5变式:已知相切两圆的半径是一元二次方程0652=+-xx的两根,则这两圆的圆心距是()A.5 B.1或5 C.1 D.6例2、在矩形ABCD中,AB=5,BC=12,如果分别以A、C两点为圆心的两圆相切,点D在⊙C内,点B在⊙C外,那么⊙A的半径r A的取值范围是________________.变式:已知两相交圆的半径分别为5 cm和4 cm,公共弦长为6 cm,求这两圆的圆心距。
平面几何中的圆与圆的位置关系

平面几何中的圆与圆的位置关系在平面几何中,圆与圆的位置关系是一个重要的研究对象。
它描述了两个圆在平面上相互之间的相对位置和位置关系。
在这篇文章中,我们将探讨一些常见的圆与圆的位置关系,并介绍它们在几何学和实际生活中的应用。
一、相离关系相离关系是指两个圆在平面上没有任何交点,彼此之间相互独立。
当两个圆的半径之和小于它们之间的距离时,它们就处于相离的状态。
这种位置关系常见于实际生活中的物体和图形之间,如两个没有交集的轮胎,两个独立的圆形图标等。
二、外切关系外切关系是指两个圆在平面上相切于一点,且这个切点是它们半径所在直线的交点。
当两个圆的半径之和等于它们之间的距离时,它们就处于外切的状态。
这种位置关系在几何学中经常出现,也广泛应用于实际生活中,如两个相切的球体,两个相切的圆形花坛等。
三、相交关系相交关系是指两个圆在平面上有交点,彼此之间相互交叠。
当两个圆的半径之和大于它们之间的距离,但小于两个圆半径之和时,它们就处于相交的状态。
这种位置关系常见于交通标志、建筑设计等领域,如两个相交的轮胎,两个相交的圆形交通路口等。
四、内切关系内切关系是指一个圆被另一个圆包围,且两个圆的切点处于它们半径所在直线的交点上。
当一个圆的半径等于另一个圆半径的两倍时,它们就处于内切的状态。
这种位置关系常见于圆形图案的设计以及建筑物的布局,在实际生活中具有一定的美学和实用价值。
五、包含关系包含关系是指一个圆完全包含另一个圆,两个圆之间没有交点。
当一个圆的半径大于另一个圆的半径,并且两个圆心之间的距离小于它们的半径之差时,它们就处于包含的状态。
这种位置关系常见于几何学证明和实际生活中的设计,如一个大圆包含一个小圆,一个圆环包含一个小球等。
在几何学中,圆与圆的位置关系不仅仅是一个抽象的概念,它们具有广泛的应用。
比如在地图上,我们可以利用相交关系来标记交通路口,用外切关系来表示相邻城市的距离,用包含关系来表示行政区划的辖区等。
在建筑设计中,我们可以利用内切关系和包含关系来安排空间布局和功能分区。
