数学建模 课件 自定义函数
合集下载
函数y=Asin(ωx+φ)的图象课件

1 2
参数ω对周期的影响 随着ω的增大,函数y=asin(ωx+φ)的周期会减 小;反之,随着ω的减小,函数的周期会增大。
参数φ对相位的影响 当φ增加时,函数图像会沿x轴向右移动;反之, 当φ减小时,图像会向左移动。
3
参数a对振幅的影响
a的大小决定了函数图像的振幅。当a增大时,图 像的振幅增大;反之,当a减小时,振幅减小。
使用数学软件绘制图像
MATLAB
MATLAB是一款强大的数学软件,可以用来绘制各种复杂的函数图像,包括函数 y=asin(ωx+φ)。使用MATLAB,用户可以自定义ω和φ的值,观察图像的变化。
Python (Matplotlib)
Matplotlib是Python的一个绘图库,也可以用来绘制函数y=asin(ωx+φ)。通过 Matplotlib,用户可以轻松地定制图像的样式和颜色。
在通信系统中,信号的传输通常会受到噪声和其他干扰的影响。利用函数 y=asin(ωx+φ)进行信号调制可以提高信号的抗干扰能力和传输质量。例如,在调 频(FM)通信中,调制信号的频率会随着声音信号的变化而变化,解调后可以得到 还原的声音信号。
04 函数y=asin(ωx+φ)的变 种形式
多参数变化的影响
函数图像的基本特征
周期性
极值点
由于正弦函数的周期性,函数 y=asin(ωx+φ)的图像也具有周期性, 周期取决于ω的取值。
函数图像在每个周期内有两个极值点, 极值点的位置和高度取决于参数ω、 φ的取值。
对称性
函数图像具有对称性,包括轴对称和 中心对称,具体对称轴和对称中心取 决于参数φ的取值。
02 函数y=asin(ωx+φ)的图 像绘制
《数学建模》PPT课件

( x2
x1)
f
f (x2 ) (x2 ) f
2 1 ( x1) 22
1
f
( x1 )
f
(x2 )
3
f
( x1 ) x1
f (x2 ) x2
2 (12 f (x1)f (x2 ))1/2
如函数的导数容易求得,一般首先考虑使用三次插值
法,因为它具有较高效率。对于只需要计算函数值的方
法中,二次插值法是一个很好的方法,它的收敛速度较
优化模型
(2)多项式近似法 该法用于目标函数比较复杂的情 况。此时寻找一个与它近似的函数代替目标函数,并用 近似函数的极小点作为原函数极小点的近似。常用的近 似函数为二次和三次多项式。
二次内插涉及到形如下式的二次函数数据拟合问题:
mq() a2 b c
其中步长极值为:
b
2a
完整版课件ppt
求解单变量最优化问题的方法有很多种,根据目标函 数是否需要求导,可以分为两类,即直接法和间接法。 直接法不需要对目标函数进行求导,而间接法则需要用 到目标函数的导数。
完整版课件ppt
4
优化模型
1、直接法 常用的一维直接法主要有消去法和近似法两种: (1)消去法 该法利用单峰函数具有的消去性质进行
反复迭代,逐渐消去不包含极小点的区间,缩小搜索区 间,直到搜索区间缩小到给定允许精度为止。一种典型 的消去法为黄金分割法(Golden Section Search)。黄金 分割法的基本思想是在单峰区间内适当插入两点,将区 间分为三段,然后通过比较这两点函数值的大小来确定 是删去最左段还是最右段,或同时删去左右两段保留中 间段。重复该过程使区间无限缩小。插入点的位置放在 区间的黄金分割点及其对称点上,所以该法称为黄金分 割法。该法的优点是完整算版课法件p简pt 单,效率较高,稳定性好5 。
高中数学 第四章 函数应用 2 实际问题的函数建模课件 北师大版必修1.pptx

14 解答
反思与感悟
在实际问题中,有很多问题的两变量之间的关系是已知函数模型,如 一次、二次函数、反比例函数、幂函数、指数函数、对数函数,这时 可借助待定系数法求出函数解析式,再根据解题需要研究函数性质.
16
跟踪训练1 如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面 宽4米.则水位下降1米后,水面宽__2__6____米.
8
可将这些步骤用框图表示如下:
9
知识点三 数据拟合
思考
自由落体速度公式v=gt是一种函数模型.类比这个公式的发现过 程,简述什么是数据拟合? 答案 函数模型来源于现实(伽利略斜塔抛球),通过收集数据 (打点计时器测量),画散点图分析数据(增长速度、单位时间内 的增长量等),寻找或选择函数(假说)来作为函数模型,再检验 这个函数模型是否符合实际,这就是数据拟合.
25 解答
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最
多为多少元?
解 当3≤x≤6,且x∈N时,
因为y=50x-115是增函数,
所以当x=6时,ymax=185元. 当6<x≤20,且x∈N时,
y=-3x2+68x-115=-3x-3342+8311, 所以当x=11时,ymax=270元. 综上所述,当每辆自行车日租金定为11元时才能使日净收入最多,为
28
跟踪训练3 学校某研究性学习小组在对学生上课注 意力集中情况的调查研究中,发现其在40 min的一节 课中,注意力指数y与听课时间x(单位:min)之间的关 系满足如图的图像.当x∈(0,12]时,图像是二次函数图 像 的 一 部 分 , 其 中 顶 点 A(10,80) , 过 点 B(12,78) ; 当 x∈[12,40]时,图像是线段BC,其中C(40,50).根据专 家研究,当注意力指数大于62时,学习效果最佳. (1)试求y=f(x)的函数关系式;
反思与感悟
在实际问题中,有很多问题的两变量之间的关系是已知函数模型,如 一次、二次函数、反比例函数、幂函数、指数函数、对数函数,这时 可借助待定系数法求出函数解析式,再根据解题需要研究函数性质.
16
跟踪训练1 如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面 宽4米.则水位下降1米后,水面宽__2__6____米.
8
可将这些步骤用框图表示如下:
9
知识点三 数据拟合
思考
自由落体速度公式v=gt是一种函数模型.类比这个公式的发现过 程,简述什么是数据拟合? 答案 函数模型来源于现实(伽利略斜塔抛球),通过收集数据 (打点计时器测量),画散点图分析数据(增长速度、单位时间内 的增长量等),寻找或选择函数(假说)来作为函数模型,再检验 这个函数模型是否符合实际,这就是数据拟合.
25 解答
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最
多为多少元?
解 当3≤x≤6,且x∈N时,
因为y=50x-115是增函数,
所以当x=6时,ymax=185元. 当6<x≤20,且x∈N时,
y=-3x2+68x-115=-3x-3342+8311, 所以当x=11时,ymax=270元. 综上所述,当每辆自行车日租金定为11元时才能使日净收入最多,为
28
跟踪训练3 学校某研究性学习小组在对学生上课注 意力集中情况的调查研究中,发现其在40 min的一节 课中,注意力指数y与听课时间x(单位:min)之间的关 系满足如图的图像.当x∈(0,12]时,图像是二次函数图 像 的 一 部 分 , 其 中 顶 点 A(10,80) , 过 点 B(12,78) ; 当 x∈[12,40]时,图像是线段BC,其中C(40,50).根据专 家研究,当注意力指数大于62时,学习效果最佳. (1)试求y=f(x)的函数关系式;
用户自定义函数素材课件

面组 • 节点线索(node thread) 节点组 • 区域(domain) 由网格定义的所有节点、面和单元线索的组合
Fluent数据类型
• cell_t cell_t是线索(thread)内单元标识符的数据类
• face_t
型。它是一个识别给定线索内单元的整数索引。 face_t是线索内面标识符的数据类型。它是一
• 判断单元是否在多孔区域, 给多孔介质区域定义反应 速率;
• real 指 针 变 量 rr 是一 个 传 递给函数的自变量。UDF 使用废弃操作符* 分配反 应 速 率 值 给 废 弃 指 针 * rr 。 指针rr指向的目标是设置 反应速率。通过这个操作, 存储在内存中这个指针上 的字符的地址被改变了, 不再是指针地址本身
个识别给定线索内面的整数索引。
• Thread Thread数据类型是FLUENT中的数据结构。它
充当了一个与它描述的单元或面的组合相关的
数据容器。
• Node Node数据类型也是FLUENT中的数据结构。它
充当了一个与单元或面的拐角相关的数据容器。
•
Domain
Domain数据类型代表了FLUENT中最高水平的 数据结构。它充当了一个与网格中所有节点、
UDF分类与区别
• UDFs 使用时可以被当作解释函数或编译函数 • 解释函数在运行时读入并解释 • 编译UDFs 则在编译时被嵌入共享库中并与
Fluent 连接
• 解释UDFs 用起来简单但是有源代码和速度方 面的限制不足。编译型UDFs 执行起来较快也
没有源代码限制但设置和使用较为麻烦
UDF的用途-满足用户个性化需求
UDF处理温度
#include "udf.h"
Fluent数据类型
• cell_t cell_t是线索(thread)内单元标识符的数据类
• face_t
型。它是一个识别给定线索内单元的整数索引。 face_t是线索内面标识符的数据类型。它是一
• 判断单元是否在多孔区域, 给多孔介质区域定义反应 速率;
• real 指 针 变 量 rr 是一 个 传 递给函数的自变量。UDF 使用废弃操作符* 分配反 应 速 率 值 给 废 弃 指 针 * rr 。 指针rr指向的目标是设置 反应速率。通过这个操作, 存储在内存中这个指针上 的字符的地址被改变了, 不再是指针地址本身
个识别给定线索内面的整数索引。
• Thread Thread数据类型是FLUENT中的数据结构。它
充当了一个与它描述的单元或面的组合相关的
数据容器。
• Node Node数据类型也是FLUENT中的数据结构。它
充当了一个与单元或面的拐角相关的数据容器。
•
Domain
Domain数据类型代表了FLUENT中最高水平的 数据结构。它充当了一个与网格中所有节点、
UDF分类与区别
• UDFs 使用时可以被当作解释函数或编译函数 • 解释函数在运行时读入并解释 • 编译UDFs 则在编译时被嵌入共享库中并与
Fluent 连接
• 解释UDFs 用起来简单但是有源代码和速度方 面的限制不足。编译型UDFs 执行起来较快也
没有源代码限制但设置和使用较为麻烦
UDF的用途-满足用户个性化需求
UDF处理温度
#include "udf.h"
人教A版高中数学必修第一册数学建模 建立函数模型解决实际问题【课件】

收集数据.
上述过程可以概括为:
3.数学建模活动的要求
(1)组建合作团队:数学建模活动需要团队协作.首先在班级中
组成3~5人的研究小组,每位同学参加其中一个小组.在小组
内,要确定一个课题负责人,使每位成员都有明确的分工;然后
拟定研究课题、确定研究方案、规划研究步骤、编制研究手
册,最后在班里进行一次开题报告.
算得y≈63.98,因为78÷63.98≈1.22>1.2,所以这个男性体型偏胖.
【典例2】 个体经营者把开始六个月试销A,B两种商品的逐
月投资与所获纯利润列成下表:
投资 A 种商品金额/万元
获纯利润/万元
投资 B 种商品金额/万元
获纯利润/万元
1
0.65
1
0.25
2
1.39
2
0.49
3
1.85
3
(2)开展研究活动:根据开题报告所规划的研究步骤,通过背景
分析、收集数据、数据分析、数学建模、获得结论等过程,
完成课题研究.在研究过程中,可以借助信息技术解决问题.
(3)撰写研究报告:以小组为单位,撰写一份研究报告.
(4)交流展示:①对同一个课题,先由3~4个小组进行小组交流,
每个小组都展示自己的研究成果,相互借鉴、取长补短.在小
们选择函数模型.
以身高x为横坐标,体重y为纵坐标,
画出用y=a·bx作为刻画这个地
区未成年男性的体重与身高关系的函数模型.
建立模型 设函数的解析式为 y=a·bx(a>0,b>0,b≠1).
不妨取其中的两组数据(70,7.90),(160,47.25)代入 y=a·bx,
气最少,最少是多少?
分析数据 烧开一壶水所需的燃气量与燃气灶旋钮角度有关,
上述过程可以概括为:
3.数学建模活动的要求
(1)组建合作团队:数学建模活动需要团队协作.首先在班级中
组成3~5人的研究小组,每位同学参加其中一个小组.在小组
内,要确定一个课题负责人,使每位成员都有明确的分工;然后
拟定研究课题、确定研究方案、规划研究步骤、编制研究手
册,最后在班里进行一次开题报告.
算得y≈63.98,因为78÷63.98≈1.22>1.2,所以这个男性体型偏胖.
【典例2】 个体经营者把开始六个月试销A,B两种商品的逐
月投资与所获纯利润列成下表:
投资 A 种商品金额/万元
获纯利润/万元
投资 B 种商品金额/万元
获纯利润/万元
1
0.65
1
0.25
2
1.39
2
0.49
3
1.85
3
(2)开展研究活动:根据开题报告所规划的研究步骤,通过背景
分析、收集数据、数据分析、数学建模、获得结论等过程,
完成课题研究.在研究过程中,可以借助信息技术解决问题.
(3)撰写研究报告:以小组为单位,撰写一份研究报告.
(4)交流展示:①对同一个课题,先由3~4个小组进行小组交流,
每个小组都展示自己的研究成果,相互借鉴、取长补短.在小
们选择函数模型.
以身高x为横坐标,体重y为纵坐标,
画出用y=a·bx作为刻画这个地
区未成年男性的体重与身高关系的函数模型.
建立模型 设函数的解析式为 y=a·bx(a>0,b>0,b≠1).
不妨取其中的两组数据(70,7.90),(160,47.25)代入 y=a·bx,
气最少,最少是多少?
分析数据 烧开一壶水所需的燃气量与燃气灶旋钮角度有关,
数学建模——建立函数模型解决实际问题课件--2024学年高一上学期数学人教A版(2019)必修第一册

2.收集数据
我们可以利用秒表、温度计等工具(若用计算机、数据采集器、
温度传感器等信息技术更好),收集茶水温度随时间变化的数据.
请同学们课后按照实验流程进行实验,获取并记录一组数据.
某研究人员每隔1 min测量一次茶水温度,得到表1的一组数据.
新 知 探 究 一、数学建模活动的实例—茶水的口感何时最佳
1.观察实际情景,发现提出问题
我国是茶的故乡,是世界上最早发现茶树、利用茶叶和栽培茶叶
的国家,也是茶文化的发源地.
泡茶和饮茶都有很多讲究.其中,
很重要.
中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关,
经验表明,某种绿茶用85℃的水泡制,再等到茶水温度降至60℃时饮
用,可以产生最佳口感,那么在25℃室温下,刚泡好的茶水大约需要
新 知 探 究 一、数学建模活动的实例—茶水的口感何时最佳
6.求解问题
将y=60代入y=60×0.9227x+25,得
60×0.9227x+25=60
解得
=
7
log 0.9227
12
由信息技术得
x≈6.6997
观察实际情景
发现和提出问题
上述过程
可概括为
收集数据
选择函数模型
求解函数模型
检验
符合实际
④当时间不断延长,最终茶水能降到什么温度?
90
80
70
x
O
1
2
3
图1
4
5
新 知 探 究 一、数学建模活动的实例—茶水的口感何时最佳
请同学们在前期学习的函数中找到符合趋势的函数模型.
y
观察散点图的分布状况,并考虑到
茶水温度降至室温就不能再降的事实,
我们可以利用秒表、温度计等工具(若用计算机、数据采集器、
温度传感器等信息技术更好),收集茶水温度随时间变化的数据.
请同学们课后按照实验流程进行实验,获取并记录一组数据.
某研究人员每隔1 min测量一次茶水温度,得到表1的一组数据.
新 知 探 究 一、数学建模活动的实例—茶水的口感何时最佳
1.观察实际情景,发现提出问题
我国是茶的故乡,是世界上最早发现茶树、利用茶叶和栽培茶叶
的国家,也是茶文化的发源地.
泡茶和饮茶都有很多讲究.其中,
很重要.
中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关,
经验表明,某种绿茶用85℃的水泡制,再等到茶水温度降至60℃时饮
用,可以产生最佳口感,那么在25℃室温下,刚泡好的茶水大约需要
新 知 探 究 一、数学建模活动的实例—茶水的口感何时最佳
6.求解问题
将y=60代入y=60×0.9227x+25,得
60×0.9227x+25=60
解得
=
7
log 0.9227
12
由信息技术得
x≈6.6997
观察实际情景
发现和提出问题
上述过程
可概括为
收集数据
选择函数模型
求解函数模型
检验
符合实际
④当时间不断延长,最终茶水能降到什么温度?
90
80
70
x
O
1
2
3
图1
4
5
新 知 探 究 一、数学建模活动的实例—茶水的口感何时最佳
请同学们在前期学习的函数中找到符合趋势的函数模型.
y
观察散点图的分布状况,并考虑到
茶水温度降至室温就不能再降的事实,
第14讲数学建模函数的模型及其应用2023高三数学一轮复习提高版课件共32张PPT

是均匀的,故为一次函数模型.
目标 2 已知函数模型求解实际问题
已知某物体的温度 θ(单位:℃)随时间 t(单位:min)的变化规律为 θ=m·2t+
21-t(t≥0,且 m>0).
(1) 如果 m=2,求经过多长时间,物体的温度为 5 ℃; 【解答】 若 m=2,则 θ=2·2t+21-t=22t+21t, 当 θ=5 时,2t+21t=52, 令 2t=x≥1,则 x+1x=52, 即 2x2-5x+2=0,解得 x=2 或 x=12(舍去),此时 t=1. 所以经过 1 min,物体的温度为 5 ℃.
时,P(x)max=P(300)=25 000.
当 x>400 时,函数 P(x)=60 000-100x 是减函数,没有最大值,且 p(x)<20 000.
综上,总利润最大时,该网店经营的天数为 300.
实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系 式构成,如出租车计价与路程之间的关系,应构建分段函数模型求解.但应关注以下 两点:①分段要简洁合理,不重不漏;②分段函数的最值是各段的最大(或最小)值中的 最大(或最小)值.
一片森林原来面积为 a,计划每年砍伐一些树,且每年砍伐面积的百分比相
等,当砍伐到原面积的一半时,所用时间是 10 年,为保护生态环境,森林面积至少要
保留原面积的14.已知到
2019
年为止,森林剩余面积为原来的
2 2.
(1) 求每年砍伐面积的百分比; 【解答】 设每年砍伐面积的百分比为 x(0<x<1),则 a(1-x)10=12a,即(1-x)10=
(2) 若物体的温度总不低于 2 ℃,求 m 的取值范围.
【解答】 物体的温度总不低于 2 ℃,即 θ≥2 恒成立,
初中数学建模(第一课) PPT课件 图文

二、解答数学模型问题的一般步骤
(1)明确实际问题,并熟悉问题的背景; (2)构建数学模型(例如:方程模型、不等式模型、函数模
型、几何模型、概率模型、统计模型等); (3)求解数学问题,获得数学模型的解答; (4)回到实际问题,检验模型,解释结果。
三、初中数学建模的几种题型
1、建立“方程(组)”模型 2、建立“不等式(组)”模型 3、建立“函数”模型 4、建立“几何”模型 5、建立“概率”与“统计”模型
数学建模(第一课)
一、数学模型思想在初中数学中的意义
所谓数学模型,是指通过抽象和模拟,利用数学语言和方 法对所要解决的实际问题进行的一种刻画 。一般地,通过建立 数学模型来解决实际问题的过程称为数学建模。
数学教学要让学生亲身经历将实际问题抽象成数学模型并 进行解释与应用的过程,进而使学生获得对数学理解的同时, 在思维能力、情感态度与价值观等多方面得到进步和发展。
现实生活中同样也广泛存在着数量之间的 不等关系。如市场营销、生产决策、统筹 安排、核定价格范围等问题,可以通过给出 的一些数据进行分析,将实际问题转化成 相应的不等式问题,利用不等式的有关性 质加以解决。
例9、小明准备用50元钱买甲、乙两种饮料 共10瓶。已知甲饮料每瓶7元,乙饮料每瓶 4元,则小明最多能买多少瓶甲饮料?
所以,放入一个小球水面升高2cm,放入一个大球水面升 高3cm;
(2)设应放入大球m个,小球n个.由题意,
得:
解得: m 4
n
6
答:如果要使水面上升到50cm,应放入大球4个,小球6
个.
方法归纳:本题考查了列一元一次方程和列二元 一次方程组解实际问题的运用,二元一次方程组
三角函数数学建模课件PPT

7
例2
方案2:若P处也是一可攀登建筑物(如楼房),则可在同一垂线上选两个 测量点(见图3—113),被测数据为PC和CD的长度,仰角α和β.
设AB=x,PA=y,则计算公式为
说明:无论哪个方案都至少要测4个数据.
8
例3
房间的门宽为0.9米, 墙厚为0.28米.今有一家具其水平截面如图, 问能否把此家具水平地移入房间内(说明理由).
5
例2
如图所示,有一条河MN,河岸的一侧有一很高建筑物AB.一人位于河 岸另一侧P处,手中有一个测角器(可以测仰角)和一个可以测量长度 的皮尺(测量长度不超过5米)。
请你设计一种测量方案(不允许过河),并给出计算建筑物的高度AB及距 离PA的公式.希望在你的方案中被测量数据的个数尽量少.
6
例2
常见有两种测量方案。 方案1: P位于开阔地域,则测量方案如下图所示,被测量的数据 为PC(测角器的高)和PQ(Q为在PA水平直线上选取的另一测量点)的长度, 仰角α和β。 设AB为x,PA为y,则计算公式为
9
例3
解法一 如图,墙厚CD=0.28米,家具的一边AB
只要h不超过门宽0.9米,则家具可水平地搬入屋内. 从图中可见h=AEsinθ,又AE=AG+GF+FE,其中AG=0.48,GF =CDcosθ=0.28cosθ,FE=FCctgθ=0.48ctgθ.因此 h=AEsinθ=(0.48+0.28cosθ+0.48ctgθ)sinθ =0.48(sinθ+cosθ)+0.28cosθsinθ
12
再见!
13
例3
14
cos 2α = 2 cos 2 α − 1 = 1 − 2 sin 2 α sin 2α = 2sin α cos α
讲函数模型及其应用课件

在生物学中,一次函数模型可以用来描述 物种数量与时间的关系、生长曲线等。
一次函数模型在社会科学中的应 用
在社会科学中,一次函数模型可以用来描 述人口增长、城市化率等社会现象。
二次函数模型的应用
二次函数模型在经济学中的应用
通过建立二次函数模型,可以描述和分析经济现象,例如需求与价格 的关系、供给与价格的关系等。
总结词
生物学中,函数模型被用来描述和分析生物体的生理特征和行为,如种群动态、基因表 达等。
详细描述
在生物学中,函数模型被用来描述和分析生物体的生理特征和行为,例如种群动态、基 因表达等。通过建立函数模型,生物学家可以对生物数据进行数学分析和预测,从而更
好地理解生物系统的运行规律和演化趋势。
计算机科学中的函数模型应用
三角函数模型在社会科学 中的应用
在社会科学中,三角函数模型 可以用来描述社会现象的周期 性变化,例如人口普查、就业 率变化等。
指数函数与对数函数模型的应用
指数函数与对数函数在经济学中的应用
在经济学中,指数函数和对数函数被广泛应用于描述增长和衰减过程 ,例如复利计算、人口增长预测等。
指数函数与对数函数在物理学中的应用
总结词
计算机科学中,函数模型被用来描述和 分析计算机系统和算法的性能和行为。
VS
详细描述
在计算机科学中,函数模型被用来描述和 分析计算机系统和算法的性能和行为。通 过建立函数模型,计算机科学家可以对计 算机系统和算法进行数学分析和优化,从 而提高计算机系统的效率和性能。
THANKS
感谢观看
三角函数模型在物理学中 的应用
在物理学中,三角函数模型可 以用来描述周期性运动,例如 简谐振动、交流电等。
三角函数模型在工程学中 的应用
一次函数模型在社会科学中的应 用
在社会科学中,一次函数模型可以用来描 述人口增长、城市化率等社会现象。
二次函数模型的应用
二次函数模型在经济学中的应用
通过建立二次函数模型,可以描述和分析经济现象,例如需求与价格 的关系、供给与价格的关系等。
总结词
生物学中,函数模型被用来描述和分析生物体的生理特征和行为,如种群动态、基因表 达等。
详细描述
在生物学中,函数模型被用来描述和分析生物体的生理特征和行为,例如种群动态、基 因表达等。通过建立函数模型,生物学家可以对生物数据进行数学分析和预测,从而更
好地理解生物系统的运行规律和演化趋势。
计算机科学中的函数模型应用
三角函数模型在社会科学 中的应用
在社会科学中,三角函数模型 可以用来描述社会现象的周期 性变化,例如人口普查、就业 率变化等。
指数函数与对数函数模型的应用
指数函数与对数函数在经济学中的应用
在经济学中,指数函数和对数函数被广泛应用于描述增长和衰减过程 ,例如复利计算、人口增长预测等。
指数函数与对数函数在物理学中的应用
总结词
计算机科学中,函数模型被用来描述和 分析计算机系统和算法的性能和行为。
VS
详细描述
在计算机科学中,函数模型被用来描述和 分析计算机系统和算法的性能和行为。通 过建立函数模型,计算机科学家可以对计 算机系统和算法进行数学分析和优化,从 而提高计算机系统的效率和性能。
THANKS
感谢观看
三角函数模型在物理学中 的应用
在物理学中,三角函数模型可 以用来描述周期性运动,例如 简谐振动、交流电等。
三角函数模型在工程学中 的应用
函数建模 北师大版(PPT)2-2
•
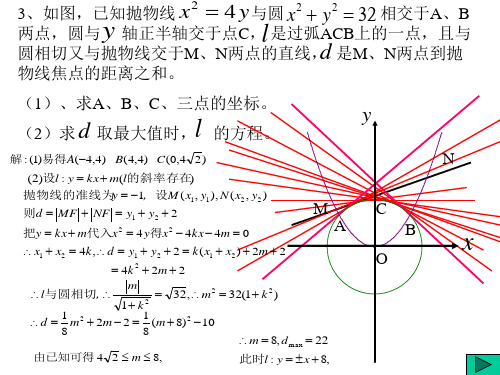
又 4 y0 4
2 , 1 1 1
42Biblioteka y04当 1 y0
1 4
时
即y0
4时
d m ax 22此时, l : y x 8
•
;股票入门基础知识 股票入门基础知识
•
•
今日本色在此癫,无人过眼无人厌。 我笑他人伤醉酒,何不学我来发癫。 一笑无人回我语,二笑我心已癫狂。 今夜寒风呼啸,北国风雪飘飘。 顿时举国上下,美梦睡中突醒。 风呼啸,鸡飞狗跳。 一曲清幽,一夜无眠。 万里山水,数亿生灵,尽皆殆灭。 一夜癫狂后清醒,人生能得几回癫。 今朝痛楚随疯去,明日依旧笑人生。 三笑放下心中事,四笑心静如止水。 天降倾盆大雨,地落涛涛江水。 我独一人望月 雨嚎嚎,乱水成荒。 天初晓,鸡鸣不在;日初升,生机不存。 此世独我存!心孤寥,人已亡。
M A
x1 x2 4k, d y1 y2 2 k (x1 x2 ) 2m 2 4k 2 2m 2
l与圆相切, m 32,m2 32(1 k 2 )
1 k2
d 1 m2 2m 2 1 (m 8)2 10
8
8
解 : (1)易得A(4,4) B(4,4) C(0,4 2)
(2)设l : y kx m(l的斜率存在)
抛物线的准线为y 1, 设M (x1, y1), N (x2 , y2 )
则d MF NF y1 y2 2
把y kx m代入x2 4 y得x2 4kx 4m 0
m 8, dmax 22
由已知可得 4 2 m 8,
此时l : y x 8,
C B
O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自定义函数方式(五)
关于 subs 的一个注解
subs 命令的一种比较方便的调用方法:
当所要替代的符号在调用前都已经有了数值定义,则 可以直接调用:subs(f)
例:
自定义函数方式(三)
自定义函数方式(三)
%函数文件:function []=funtry3() lfg=inline('x.^(1/3)'); %表达式两端的单引号不可缺少 fid=fopen('myfile3.txt','w'); for t=1:50; y=lfg(t); fprintf(fid,'%4d^(1/3) = %6.4f\n',t,y); end fclose(fid); ezplot(lfg,[0,50])
例:Βιβλιοθήκη 自定义函数方式(三) 这种函数定义方式是将 f 作为一个内部函数调用。其特 点是:调用方式最接近于我们平时对函数的定义,使程序 更具可读性。同时由于它是基于 Matlab 的数值计算内核 的,所以它的运算速度较快,程序更有效率。 这种定义方式的缺点: 定义一个内联函数用去的内存空间比相同条件下其他 的方法要大得多。 该方法只能对数值进行代入,不支持符号代入,并且 对于定义后的函数不能进行求导等符号运算。
函数文件中可以定义一个或多个子函数,此时我们称该函 数为主函数,子函数只能被主函数或同一个函数文件中的 其它子函数调用!
自定义函数方式(三)
方式(3):inline + 命令/函数文件
inline 命令可以用来定义一个内联函数 f=inline('函数表达式','变量1','变量2',...) 调用方式: y=f(数值列表) 代入的数值列表顺序应与定义时的变量名顺序一致
diff(lfg,'x')
X
自定义函数方式(四)
方式(4): syms + subs
syms 定义一个符号表达式,用 subs 命令调用
syms f x %定义符号 f=1/(1+x^2); %定义符号表达式
subs(f,'x',代替 x 的数值或符号)
注:对于在 syms 中已经定义过符号变量,在 subs 中进行
直接定义一个字符串,用 subs 命令完成调用。
例: f='1/(1+x^2)'
% 定义字符串
z=subs(f,'x',2) g=subs(f,'x','y^2')
注:此处 x 的单引号不可省略。本函数方式可以代入字符,
但字符不能参与运算,否则将自行转化成该字符的 ASCII 码运算,这与我们想要的结果可能会大相径庭。 优点:占内存最少,定义格式方便自由。 缺点:是无法对字符进行符号转化。
数学实验
Matlab 自定义函数
自定义函数的五种方式
Matlab 自定义函数的五种方式
命令文件/函数文件+ 函数文件 - 多个 M 文件 函数文件 + 子函数 - 一个 M 文件 inline - 无需 M 文件 syms + subs 方式 - 无需 M 文件 字符串 + subs 方式 - 无需 M 文件
function y = mylfg(x) y=x^(1/3);
函数名与文件名必须一致!
函数必须单独写一个文件! 不能与命令文件写在同一个文件中!
自定义函数方式(二)
方式(2):函数文件 + 子函数
%函数文件:funtry2.m function []=funtry2() for t=1:10 y=lfg2(t); fprintf('%4d^(1/3) = %6.4f\n',t,y); end function y=lfg2(x) y=x^(1/3); %%子函数
替代时,单引号可以省略。但如果在 syms 后又被重新 定义为其它类型,则必须加单引号,否则不可替换。
自定义函数方式(四)
这种函数定义方法的一个特点是可以用符号进行替换
该方法的缺点也是明显的:由于使用符号运算内 核,运算速度会大大降低。
自定义函数方式(五)
方式(5):字符串 + subs
自定义函数方式(一)
方式(1):命令文件/函数文件 + 函数文件
%命令/函数文件:myfile1.m clear for t=1:10; y=mylfg(t); fprintf('%4d^(1/3) = %6.4f\n',t,y); end
调用函数时要注意实参与形参的匹配!
%函数文件:mylfg.m
