高三第一次月考试卷数学 及答案
高三第一次月考(数学)试卷含答案

高三第一次月考(数学)(考试总分:150 分)一、 单选题 (本题共计12小题,总分60分)1.(5分)1.若{}{}2|22,|log (1)M x x N x y x =-≤≤==-,则M N =( )A.{}|20x x -≤<B. ﹛x| -1<x<0﹜C.{}2,0-D.{}21|≤<x x 2.(5分)2.复数imi212+-=A+B i (m 、A 、B ∈R),且A+B=0,则m 的值是 ( ) A. 32- B. 32 C.2 D.23.(5分)3.下列命题中,真命题是 ( )A .,00≤∈∃x e R x B .22,x R x x >∈∀C .0=+b a 的充要条件是1-=baD .1,1>>b a 是1>ab 的充分条件 4.(5分)4.函数212log 4f xx 的单调递增区间是( )A.(0,+∞)B. (-∞,0)C. (2,+∞)D. (-∞,-2)5.(5分)5.函数f(x)=-1x+log 2x 的一个零点落在下列哪个区间( ) A.(0,1)B.(1,2)C.(2,3)D.(3,4)6.(5分)6.如果函数f(x)=x 2+bx+c 对任意实数t 都有f(2+t)=f(2-t),那么( )A.f(2)<f(1)<f(4)B.f(1)<f(2)<f(4)C.f(2)<f(4)<f(1)D.f(4)<f(2)<f(1) 7.(5分)7.函数()3cos 2xxf x x⋅=的部分图象大致是( )A .B .C .D .8.(5分)8.曲线y =e x +1在x =1处的切线与坐标轴所围成的三角形的面积为( )A.12e B .e 2 C .2e 2D .94e 2 9.(5分)9.已知函数f(x)是定义在R 上的偶函数,且对任意的x ∈R ,都有f(x +2)=f(x).当0≤x≤1时,2()f x x =.若直线y =x +a 与函数y =f(x)的图像在[0,2]内恰有两个不同的公共点,则实数a 的值是 ( ) A .0 B .0或-14 C .-14或-12 D.0或-1210.(5分)10.若函数x x f xx2sin 3)(1212++=+-在区间[-k,k](k>0)上的值域为[m,n],则m+n 等于( )A.0B.2C.4D.611.(5分)11.已知函数f(x)在R 上满足f(x)=2f(2-x)-x 2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是 ( )A.y=-2x+3B.y=xC. y=2x-1D.y=3x-212.(5分)12.设定义域为R 的函数2lg (>0)()-2(0)x x f x x x x ⎧=⎨-≤⎩ 则关于x 的函数1)(3-)(2y 2+=x f x f 的零点的个数为( )A .3B .7C .5D .6二、 填空题 (本题共计4小题,总分20分)13.(5分)13.函数24ln(1)x y x -=+的定义域为_______________14.(5分)14.函数y =log a (2x -3)+8的图象恒过定点A ,且点A 在幂函数f(x)的图象上,则f (3)=________.15.(5分)15.若函数1,0()1(),03x x xf x x ⎧<⎪⎪=⎨⎪≥⎪⎩ 则不等式1|()|3f x ≥的解集为________16.(5分)16.已知定义域为R 的函数f (x )满足f (4)=-3,且对任意x ∈R 总有)('x f <3,则不等式 f (x)<3x -15的解集为________.三、 解答题 (本题共计7小题,总分80分) 17.(12分)17.(本大题满分12分)设p :函数y =log a (x +1)(a >0且a≠1)在(0,+∞)上单调递减;q :曲线y =x 2+(2a -3)x +1与x 轴交于不同的两点.如果p∧q 为假,p∨q 为真,求实数a 的取值范围.18.(12分)18.(本大题满分12分)已知函数f (x )=x 2-2x +2.(1)求f (x )在区间[12,3]上的最大值和最小值;(2)若g (x )=f (x )-mx 在[2,4]上是单调函数,求m 的取值范围.19.(12分)19.(本大题满分12分)为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中微量元素x ,y 的含量(单位:毫克).下表是乙厂的5件产品的测量数据: 编号 1 2 3 4 5 x 169 178 166 175 180 y7580777081(1)已知甲厂生产的产品共98件,求乙厂生产的产品数量;(2)当产品中的微量元素x ,y 满足x≥175且y≥75时,该产品为优等品,用上述样本数据估计乙厂生产的优等品的数量;(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列.20.(12分)20. (本大题满分12分)设函数3()f x ax bx c =++(0)a ≠为奇函数,其图象在点(1,(1))f 处的切线与直线670x y --=垂直,导函数'()f x 的最小值为12-.(1)求a ,b ,c 的值;(2)求函数()f x 的单调递增区间,并求函数()f x 在[1,3]-上的最大值和最小值.21.(12分)21. (本大题满分12分)已知函数f(x)=ax -ln x ,a ∈R.(1)求函数f(x)的单调区间; (2)当x ∈(0,e]时,求g (x )=e 2x -ln x 的最小值; (3)当x ∈(0,e]时,证明:e 2x -ln x -x x ln >52.22.(10分)22.(本大题满分10分)选修4-4:坐标系与参数方程已知直线l :⎪⎪⎩⎪⎪⎨⎧+=+=t y t x 213235 (t 为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=2cos θ. (1)将曲线C 的极坐标方程化为直角坐标方程;(2)设点M 的直角坐标为(5,3),直线l 与曲线C 的交点为A ,B ,求|MA|·|MB|的值.23.(10分)23. (本大题满分10分) 选修4-5:不等式选讲已知关于x 的不等式|ax -1|+|ax -a |≥1(a >0). (1)当a =1时,求此不等式的解集;(2)若此不等式的解集为R ,求实数a 的取值范围答案一、单选题(本题共计12小题,总分60分)1.(5分)D2.(5分)A3.(5分)D4.(5分)D5.(5分)B6.(5分)A7.(5分)D8.(5分)A9.(5分)B10.(5分)D11.(5分)C12.(5分)B二、填空题(本题共计4小题,总分20分)13.(5分)13.(-1,0)∪(0,2]14.(5分) 14. 2715.(5分) 15.[-3,1]16.(5分) 16.(4,+∞)三、解答题(本题共计7小题,总分80分)17.(12分)17.1/2≤a<1或a>5/218.(12分)18.(1)f(x)最大值为5,最小值为1;(2)m的取值范围为(-∞,2]∪[6,+∞)19.(12分)19.(1)35件;(2)35×2/5=14件;(3)由题意,ξ的取值有0,1,2,P(ξ=0)=3/10,P(ξ=1)=3/5,P(ξ=2)=1/10,分布列为(2)f(x)的最大值为18,最小值为-8221.(12分)21.(1)综上,a≤0时,f(x)的单调递减区间是(0,+∞),无单调增区间;a>0时,f(x)的单调递减区间是(0,1/a),单调增区间是(1/a,+∞);(2)g(x)最小值为3;(3)略22.(10分)22.(1)x2+y2=2x;(2)|MA|·|MB|=1823.(10分)23.(1)(-∞,1/2]∪[5/2.+∞); (2)[4,+∞)。
2024-2025学年安徽省芜湖市无为中学高三(上)第一次月考数学试卷(含答案)
2024-2025学年安徽省芜湖市无为中学高三(上)第一次月考数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
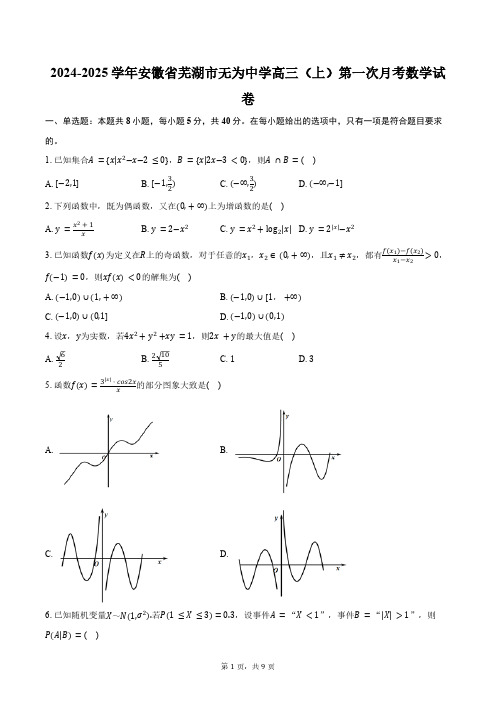
1.已知集合A ={x|x 2−x−2≤0},B ={x|2x−3<0},则A ∩B =( )A. [−2,1]B. [−1,32)C. (−∞,32)D. (−∞,−1]2.下列函数中,既为偶函数,又在(0,+∞)上为增函数的是( )A. y =x 2+1xB. y =2−x 2C. y =x 2+log 2|x|D. y =2|x|−x 23.已知函数f(x)为定义在R 上的奇函数,对于任意的x 1,x 2∈(0,+∞),且x 1≠x 2,都有f(x 1)−f(x 2)x 1−x 2>0,f(−1)=0,则xf(x)<0的解集为( )A. (−1,0)∪(1,+∞)B. (−1,0)∪[1,+∞)C. (−1,0)∪(0,1]D. (−1,0)∪(0,1)4.设x ,y 为实数,若4x 2+y 2+xy =1,则2x +y 的最大值是( )A. 62 B. 2 105 C. 1 D. 35.函数f(x)=3|x|⋅cos2x x的部分图象大致是( )A. B.C. D.6.已知随机变量X ~N(1,σ2).若P(1≤X ≤3)=0.3,设事件A =“X <1”,事件B =“|X|>1”,则P(A|B)=( )A. 38B. 35C. 58D. 277.已知函数f(x)={|log 3x|,x >03x ,x ≤0,若函数g(x)=[f(x)]2−(m +2)f(x)+2m 恰好有5个不同的零点,则实数m 的取值范围是( )A. (0,1]B. (0,1)C. [1,+∞)D. (1,+∞)8.已知f(x)是定义在R 上的函数,且满足f(3x−2)为偶函数,f(2x−1)为奇函数,则下列说法正确的( )①函数f(x)的图象关于直线x =1对称;②函数f(x)的图象关于点(−1,0)中心对称;③函数f(x)的周期为4;④f(2023)=0.A. ①②③B. ①②④C. ②③④D. ①③④二、多选题:本题共3小题,共18分。
2024-2025学年上海华二附中高三上学期数学月考试卷及答案(2024.09)

1华二附中2024学年第一学期高三年级数学月考2024.09一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分) 1.已知i 为虚数单位,复数12iz i+=,则z 的实部为________. 2.若函数()133x xf x a =⋅+为偶函数,则实a =________. 3.若事件A 、B 发生的概率分别为1()2P A =,2()3P B =,且相互独立,则()P A B =________.4.已知集合(){}2|log 1A y y x ==−,{}3|27B x x =≤,则A B =________.5.设{}n a 是等比数列,且13a =,2318a a +=,则n a =________.6.现有一球形气球,在吹气球时,气球的体积V 与直径d 的关系式为36d V π=,当2d =时,气球体积的瞬时变化率为________. 7.已知随机变量X 的分布为123111236⎛⎫⎪ ⎪ ⎪⎝⎭,且3Y aX =+,若[]2E Y =−,则实数a =________. 8.记函数()()()cos 0,0f x x =ω+ϕω><ϕ<π的最小正周期为T ,若()f T =,9x π=为()f x 的零点,则ω的最小值为________.9.若6(0)b ⎛> ⎝的展开式中含x 项的系数为60,则2a b +的最小值为________.10.顶点为S 的圆锥的母线长为60cm ,底面半径为25cm ,A ,B 是底面圆周上的两点,O 为底面中心,且35AOB π∠=,则在圆锥侧面上由点A 到点B 的最短路线长为____cm .(精确到0.1cm )11.已知△ABC 中,22AB BC ==,AB 边上的高与AC 边上的中线相等,则tan B =2________.12.给定公差为d 的无穷等差数列{}n a ,若存在无穷数列{}n b 满足: ①对任意正整数n ,都有1n n b a −≤②在21b b −,32b b −,…,20252024b b −中至少有1012个为正数,则d 的取值范围是________. 二、单选题(本大题共4小题,共18.0分.在每小题列出的选项中,选出符合题目的一项) 13.“1a b +>”是“33a b >”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件14.如果两种证券在一段时间内收益数据的相关系数为正数,那么表明( ) A .两种证券的收益之间存在完全同向的联动关系,即同时涨或同时跌 B .两种证券的收益之间存在完全反向的联动关系,即涨或跌是相反的 C .两种证券的收益有同向变动的倾向 D .两种证券的收益有反向变动的倾向15.设0k >,若向量a 、b 、c 满足::1::3a b c k =,且2()b a c b −=−,则满足条件的k 的取值可以是( )A .1B .2C .3D .416.设1A ,1B ,1C ,1D 分别是四棱锥P ABCD −侧棱PA ,PB ,PC ,PD 上的点.给出以下两个命题,①若ABCD 是平行四边形,但不是菱形,则1111A B C D 可能是菱形;②若ABCD 不是平行四边形,则1111A B C D 可能是平行四边形.( ) A .①真②真 B .①真②假 C .①假②真 D .①假②假三、解答题(本大题共5小题,共78.0分.)17.(本小题14.0分)如图,在圆柱中,底面直径AB等于母线AD,点E在底面的圆周⊥,F是垂足.(1)求证:AF DB⊥;(2)若圆柱与三棱锥D ABE−的体积的比等于3π,求直线DE与平面ABD所成角的大小.3418.(本小题14.0分)李先生是一名上班旋,为了比较上下班的通勤时间,记录了20天个工作日内,家里到单位的上班时间以及同路线返程的下班时间(单位:分钟),如下茎叶图显示两类时间的共40个记录:(1)求出这40个通勤记录的中们数M ,并完成下列22⨯列联表:(2)根据列联表中的数据,请问上下班的通勤时间是否有显著差异?并说明理由. 附:()()()()()22n ad bc a b c d a c b d −χ=++++,()2 3.8410.05P χ≥≈.519.(本小题14.0分)如图,某城市小区有一个矩形休闲广场,20AB =米,广场的一角是半径为16米的扇形BCE 绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN (宽度不计),点M 在线段AD 上,并且与曲线CE 相切;另一排为单人弧形椅沿曲线CN (宽度不计)摆放,已知双人靠背直排椅的造价每米为2a 元,单人弧形椅的造价每米为a 元,记锐角NBE ∠=θ,总造价为W 元。
高三数学上学期第一次月考试题含解析

一中2021-2021学年第一学期高三年级阶段性检测〔一〕创作人:历恰面日期:2020年1月1日数学学科一、填空题:本大题一一共14小题,每一小题5分,一共70分.,,那么___________.【答案】【解析】【分析】此题是集合A与集合B取交集。
【详解】因为,所以【点睛】交集是取两集合都有的元素。
是虚数单位)是纯虚数,那么实数的值是___________.【答案】-2【解析】【分析】此题考察的是复数的运算,可以先将复数化简,在通过复数是纯虚数得出结果。
【详解】,因为是纯虚数,所以。
【点睛】假如复数是纯虚数,那么。
3.“〞是“直线与直线互相垂直〞的___________条件〔填“必要不充分〞“充分不必要〞“充要〞或者“既不充分又不必要〞〕.【答案】充分不必要【解析】【分析】可以先通过“直线与直线互相垂直〞解得的取值范围,再通过与“〞进展比照得出结论。
【详解】因为直线与直线互相垂直,所以两直线斜率乘积为或者者一条直线与轴平行、一条与轴平行,所以或者者,解得或者者,由“〞可以推出“或者者〞,但是由“或者者〞推不出“〞,所以为充分不必要条件。
【点睛】在判断充要条件的时候,可以先将“假设A那么B〞中的A和B化为最简单的数集形式,在进展判断。
的递增区间是___________.【答案】【解析】【分析】此题可以先通过的取值范围来将函数分为两段函数,再依次进展讨论。
【详解】当时,,开口向下,对称轴为,所以递增区间是,当时,,开口向上,对称轴是,所以在定义域内无递增区间。
综上所述,递增区间是。
【点睛】在遇到带有绝对值的函数的时候,可以根据的取值范围来将函数分为数段函数,在依次求解。
5.按如下图的程序框图运行后,输出的结果是63,那么判断框中的整数的值是___________.【答案】5【解析】【分析】此题中,,可根据这几个式子依次推导出每一个A所对应的S的值,最后得出结果。
【详解】因为当时输出结果,所以【点睛】在计算程序框图时,理清每一个字母之间的关系,假如次数较少的话可以依次罗列出每一步的运算结果,最后得出答案。
雅礼中学高三月考试卷(一)数学及答案

雅礼中学高三月考试卷(一)数学一、单项选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合A =-2,0 ,B =x x 2-2x =0 ,则以下结论正确的是()A.A =BB.A ∩B =0C.A ∪B =AD.A ⊆B2.已知等比数列a n 满足a 1=1,a 3⋅a 5=4a 4-1 ,则a 7的值为()A.2B.4C.92D.63.已知复数z =a +1 -ai a ∈R ,则a =-1是z =1的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知向量a =cos θ,sin θ ,b =2,-1 ,若a ⊥b ,则cos 2θ+12sin2θ的值为()A.13B.35C.45D.235.如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是棱AA 1,CC 1的中点,过BE 的平面α与直线A 1F 平行,则平面α截该正方体所得截面的面积为()A.5B.25C.4D.56.某工厂有A ,B 两个生产车间,所生产的同一批产品合格率分别是99%和98%,已知某批产品的60%和40%分别是A ,B 两个车间生产,质量跟踪小组从中随机抽取一件,发现不合格,则该产品是由A 车间生产的概率为()A.34B.47C.12D.377.已知椭圆C :x 2a2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,P 为椭圆上一点,且∠F 1PF 2=π3,若F 1关于∠F 1PF 2平分线的对称点在椭圆C 上,则该椭圆的离心率为()A.22B.33C.12D.138.△ABC 中,角A ,B ,C 所对的三边分别为a ,b ,c ,c =2b ,若△ABC 的面积为1,则BC 的最小值是()A.2B.3C.3D.33二、多项选择题:本大题共4个小题,每小题5分,共20分。
高三月考数学试卷含解析

一、选择题(每题5分,共50分)1. 已知函数$f(x) = x^3 - 3x^2 + 4$,则$f(x)$的对称中心为()。
A. $(0, 4)$B. $(1, 2)$C. $(2, 0)$D. $(3, 1)$2. 在等差数列$\{a_n\}$中,$a_1 + a_5 = 10$,$a_3 + a_4 = 12$,则$a_1$的值为()。
A. 1B. 2C. 3D. 43. 已知圆$x^2 + y^2 - 4x - 6y + 9 = 0$的半径为()。
A. 1B. 2C. 3D. 44. 函数$y = \log_2(x - 1)$的图象与直线$y = 3x - 1$的交点个数为()。
A. 1B. 2C. 3D. 45. 若复数$z = a + bi$($a, b \in \mathbb{R}$)满足$|z - 3i| = |z + 2|$,则$z$在复平面内的轨迹是()。
B. 圆C. 直线D. 双曲线6. 在三角形ABC中,$AB = 4$,$AC = 6$,$BC = 8$,则$\cos A$的值为()。
A. $\frac{1}{4}$B. $\frac{1}{2}$C. $\frac{3}{4}$D. $\frac{5}{8}$7. 已知函数$f(x) = ax^2 + bx + c$($a \neq 0$),若$f(-1) = 0$,$f(1) = 0$,则$f(0)$的值为()。
A. $-a$B. $-b$C. $-c$D. $a$8. 若$|x - 1| + |x + 2| = 3$,则$x$的取值范围是()。
A. $-2 \leq x \leq 1$B. $-2 < x < 1$C. $x \leq -2$ 或 $x \geq 1$D. $x > -2$ 且 $x < 1$9. 已知数列$\{a_n\}$的前$n$项和为$S_n$,若$S_n = 3n^2 - 2n$,则$a_5$的值为()。
2024-2025学年海南省北京师大万宁附中高三(上)第一次月考数学试卷(含答案)

2024-2025学年海南省北京师大万宁附中高三(上)第一次月考数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合M ={x|x 2+x−2≤0},Q ={x ∈N||x|≤2},则M ∩Q =( )A. {0,1}B. {−2,−1,0,1}C. [−2,1]D. [0,1]2.设{a n }是首项大于零的等比数列,则“a 1<a 2”是“数列{a n }是递增数列”的( )A. 充要条件B. 充分而不必要条件C. 必要而不充分条件D. 既不充分也不必要条件3.设a ,b ,c 为实数,且a <b <0,则下列不等式正确的是( )A. 1a <1bB. ac 2<bc 2C. b a >a bD. a 2>ab >b 24.已知函数f(x)=e x (2x−1)x−1,则f(x)的大致图象为( )A. B.C. D.5.若正实数x ,y 满足xy +3x =3,则12x +y 的最小值为( )A. 7B. 8C. 9D. 106.设函数f(x)=log 2|x|−x −2,则不等式f(x−2)≥f(2x +2)的解集为( )A. [−4,0]B. [−4,0)C. [−4,−1)∪(−1,0]D. [−4,−1)∪(−1,0)7.已知函数f(x)={x 2−ax +5,(x ≤1)a x ,(x >1)满足对任意实数x 1≠x 2,都有f(x 2)−f(x 1)x 2−x 1<0成立,则a 的取值范围是( )A. 0<a ≤3B. a ≥2C. a >0D. 2≤a ≤38.如图,圆锥的高SO = 3,底面直径AB =2,C 是圆O 上一点,且AC =1,若SA 与BC 所成角为θ,则sin 2θ2−cos 2θ2=( )A. 134B. −34C. 58D. − 134二、多选题:本题共3小题,共18分。
高三第一次月考试卷数学及答案

高三第一次月考试卷数学及答案一、选择题(共15题,每小题4分,共60分)1. 一幢大厦的边长为6米,高度为20米。
一个人从这座大厦的一侧往上望去,他的目视线与大厦顶端连线与大厦相交的角的大小为()。
A. 30°B. 45°C. 60°D. 90°2. 若函数 f(x) 在区间 (-∞, a) 上是增函数,在区间(a, +∞) 上为减函数,则 a 的值为()。
A. 0B. 1C. 2D. 33. 已知集合 A = {2, 4, 6, 8},集合 B = {3, 6, 9, 12},则A ∩ B 的元素个数为()。
A. 0B. 1C. 2D. 34. 若等差数列 {a_n} 的前 5 项和为 15,且公差为 2,则 a_5 等于()。
A. -1B. 0C. 1D. 25. 已知正整数 n 的个位数是 5,十位数是 3,百位数是 1,其千位数是()。
A. 0B. 1C. 3D. 56. 设甲, 乙两车同时从 A, B 两地相向而行,两车相遇后又同时返回原地,已知甲车以每小时 60 公里的速度行驶,求相对速度小的车(乙车)的速度是几公里每小时。
7. 已知等比数列 {a_n} 的前 3 项分别是 1, 2, 4,若 a_4 = 16,则 a_5 = ()。
A. 16B. 20C. 24D. 328. 已知函数 f(x) 关于 y 轴对称,且图像经过点 (1, 1),则函数图像在点 (-1, -1) 是否对称?()A. 是B. 否9. 在直角坐标系中,已知点 A(-1, 3)、B(4, -2),则 AB 的中点坐标为()。
A. (0.5, 0.5)B. (1.5, 0.5)C. (1.5, 2.5)D. (2.5, 0.5)10. 设函数 f(x) = x^2 - 2x - 3,则过点 (1, -4) 的切线方程为()。
A. y = -2x - 6B. y = 2x + 6C. y = 2x - 6D. y = -2x + 611. 已知向量 a = <2, -3>,向量 b = <6, -1>,则 |a + b| = ()。
高三上学期第一次月考数学试卷(带答案)

高三上学期第一次月考数学试卷(带答案)时量:120分钟 满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数z =11+i 的虚部是A .1B .12C .-12D .-12.已知a 是单位向量,向量b 满足||a -b =3,则||b 的最大值为 A .2 B .4 C .3 D .13.已知角θ的终边在直线y =2x 上,则cos θsin θ+cos θ的值为A .-23B .-13C .23D .134.已知函数f (x )=⎩⎪⎨⎪⎧e x +3-3a ,x <0,x 2+a ,x ≥0,对任意的x 1,x 2∈R ,且x 1≠x 2,总满足以下不等关系:f (x 1)-f (x 2)x 1-x 2>0,则实数a 的取值范围为A .a ≤34B .a ≥34C .a ≤1D .a ≥15.如图,圆柱的母线长为4,AB ,CD 分别为该圆柱的上底面和下底面直径,且AB ⊥CD ,三棱锥ABCD 的体积为83,则圆柱的表面积为A .10πB .92πC .4πD .8π6.已知抛物线C :y 2=2px (p >0)的焦点F 到准线的距离为2,过焦点F 的直线l 与抛物线交于A ,B 两点,则2|AF |+3|BF |的最小值为 A .6+52B .26+5C .46+10D .117.设函数f (x )=cos(x +φ),其中|φ|<π2.若x ∈R ,都有f ⎝⎛⎭⎫π4+x =f ⎝⎛⎭⎫π4-x .则y =f (x )的图象与直线y =14x -1的交点个数为A .1B .2C .3D .48.已知定义域为R 的函数f (x ),g (x )满足:g (0)≠0,f (x )g (y )-f (y )·g (x )=f (x -y ),且g (x )g (y )-f (x )f (y )=g (x -y ),则下列说法正确的是 A .f (0)=1B .f (x )是偶函数C .若f (1)+g (1)=12,则f (2024)-g (2024)=-22024D .若g (1)-f (1)=1,则f (2024)+g (2024)=2二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分. 9.下列说法中正确的是A .一个样本的方差s 2=120[(x 1-3)2+(x 2-3)2+…+(x 20-3)2],则这组样本数据的总和等于60B .若样本数据x 1,x 2,…,x 10的标准差为8,则数据2x 1-1,2x 2-1,…,2x 10-1的标准差为16C .数据13,27,24,12,14,30,15,17,19,23的第70百分位数是23D .若一个样本容量为8的样本的平均数为5,方差为2.现样本中又加入一个新数据5,此时样本容量为9,平均数不变,方差变小 10.已知函数f (x )=ax 3-bx +2,则A .f (x )的值域为RB .f (x )图象的对称中心为(0,2)C .当b -3a >0时,f (x )在区间(-1,1)内单调递减D .当ab >0时,f (x )有两个极值点11.我国古代太极图是一种优美的对称图.定义:能够将圆O 的周长和面积同时等分成两个部分的函数称为圆O 的一个“太极函数”,则 下列命题中正确的是A .函数f (x )=sin x +1是圆O :x 2+(y -1)2=1的一个太极函数B .对于圆O :x 2+y 2=1的所有非常数函数的太极函数中,都不能 为偶函数C .对于圆O :x 2+y 2=1的所有非常数函数的太极函数中,均为中心对称图形D .若函数f (x )=kx 3-kx (k ∈R )是圆O :x 2+y 2=1的太极函数,则k ∈(-2,2)三、填空题:本题共3小题,每小题5分,共15分.12.曲线y =2x -ln x 在点(1,2)处的切线与抛物线y =ax 2-ax +2相切,则a = .13.已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1,F 2,若P 为椭圆C 上一点,PF 1⊥F 1F 2,△PF 1F 2的内切圆的半径为c3,则椭圆C 的离心率为 .14.设函数f (x )=ax +xx -4(x >4),若a 是从1,2,3,4四个数中任取一个,b 是从4,8,12,16,20,24六个数中任取一个,则f (x )>b 恒成立的概率为 .四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分13分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知(b +c )(sin B -sin C )=(a -c )sin A . (1)求B ;(2)若△ABC 的面积为334,且AD →=2DC →,求BD 的最小值.16.(本小题满分15分)已知双曲线E 的焦点在x 轴上,离心率为233,点(3,2)在双曲线E 上,点F 1,F 2分别为双曲线的左、右焦点.(1)求E 的方程;(2)过F 2作两条相互垂直的直线l 1和l 2,与双曲线的右支分别交于A ,C 两点和B ,D 两点,求四边形ABCD 面积的最小值.17.(本小题满分15分)如图,侧面BCC 1B 1水平放置的正三棱台ABCA 1B 1C 1,AB =2A 1B 1=4,侧棱长为2,P 为棱A 1B 1上的动点.(1)求证:AA 1⊥平面BCC 1B 1;(2)是否存在点P ,使得平面APC 与平面A 1B 1C 1的夹角的余弦值为53333若存在,求出点P ;若不存在,请说明理由.18.(本小题满分17分)若无穷正项数列{a n }同时满足下列两个性质:①存在M >0,使得a n <M ,n ∈N *;②{a n }为单调数列,则称数列{a n }具有性质P .(1)若a n =2n -1,b n =⎝⎛⎭⎫13n(ⅰ)判断数列{a n },{b n }是否具有性质P ,并说明理由;(ⅱ)记S n =a 1b 1+a 2b 2+…+a n b n ,判断数列{S n }是否具有性质P ,并说明理由;(2)已知离散型随机变量X 服从二项分布B (n ,p ),0<p <12,记X 为奇数的概率为c n .证明:数列{c n }具有性质P .19.(本小题满分17分)已知函数f (x )=4e x -2x -2x ,g (x )=-x 2+3ax -a 2-3a (a ∈R 且a <2).(1)令φ(x )=f (x )-g (x ),h (x )是φ(x )的导函数,判断h (x )的单调性; (2)若f (x )≥g (x )对任意的x ∈(1,+∞)恒成立,求a 的取值范围.参考答案题号 1 2 3 4 5 6 7 8 9 10 11 答案CBDDABCCABDBDAD一、选择题:本题共8小题,每小题5分,共40分。
2024-2025学年福建省福州市高新一中高三(上)第一次月考数学试卷(含答案)

2024-2025学年福建省福州市高新一中高三(上)第一次月考数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={x ∈Z|x(x−3)<0},B ={−1,2,3},则A ∩B =( )A. {2}B. {2,3}C. {−1,1,2,3}D. ⌀2.已知α∈(π2,π),sinα=35,则tan (α+π4)=( )A. −17B. 7C. 17D. −73.“lna >lnb ”是“ a >b ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.函数f(x)=xcosxe |x|−1的图象大致为( )A. B.C. D.5.实数x ,y 满足2x +y =−1,x >0,则x−yx 的最小值为( )A. 1B. 2C. 3D. 46.已知函数f(x)=log 0.5(x 2−ax +3a)在(2,+∞)上单调递减,则实数a 的取值范围( )A. (−∞,4]B. [4,+∞)C. [−4,4]D. (−4,4]7.已知定义域为R 的函数f(x),其导函数为f′(x),且满足f′(x)−f(x)<0,f(0)=1,则( )A. ef(−1)<1B. f(1)>eC. f(12)<eD. f(1)>e f(12)8.已知f(x)={|ln (−x)|,x <0x 2−4x +5,x ≥1,若方程f(x)=m(m ∈R)有四个不同的实数根x 1,x 2,x 3,x 4,则x 1⋅x 2⋅x 3⋅x 4的取值范围是( )A. (3,4)B. (2,4)C. [0,4)D. [3,4)二、多选题:本题共3小题,共18分。
在每小题给出的选项中,有多项符合题目要求。
9.下列选项中,与sin5π6的值相等的是( )A. cos2π3B. cos18°cos42°−sin18°sin42°C. 2sin15°sin75°D. tan30°+tan15°1−tan30∘tan15∘10.已知a>0,b>0,a+2b=1,下列结论正确的是( )A. 1a +2b的最小值为9 B. a2+b2的最小值为15C. log2a+log2b的最小值为−3D. 2a+4b的最小值为2211.设函数f(x)与其导函数f′(x)的定义域均为R,且f′(x+2)为偶函数,f(1+x)−f(1−x)=0,则( )A. f′(1+x)=f′(1−x)B. f′(3)=0C. f′(2025)=0D. f(2+x)+f(2−x)=2f(2)三、填空题:本题共3小题,每小题5分,共15分。
2024-2025学年上海同一附中高三上学期数学月考试卷及答案(2024.10)

1同一附中2024学年第一学期高三年级数学月考2024.09一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分) 1.集合{}1,3,M t =,{}21P t t =−+,若MP M =,则t =________.2.关于x 的一元二次不等式20ax bx c ++<的解集为空集的充要条件为________. 3.集合{}|3,x S y y x R ==∈,{}2|1,T y y x x R ==−∈,则ST =________.4.周长为20的扇形的面积取到最大值时,扇形圆心角的大小是________. 5.若函数1,0()1(),03x x x f x x ⎧<⎪⎪=⎨⎪≥⎪⎩则不等式1()3f x ≥的解集为________. 6.对于实数x ,y ,“221x y +<”是“1x <且1y <”的________条件.7.()f x 为定义在R 上的奇函数,当0x >时,()22x f x x =+,则0x <时,()f x =________. 8.设(72)n x −的展开式中,各项系数之和为625,则展开式中各项系数的绝对值之和 是________.9.已知等比数列{}n a 满足22a =,31a =,则()12231lim n n n a a a a a a +→+∞+++=________.10.对于定义在集合D 上的函数()f x ,若存在实数0x 满足00()f x x =,则把0x 叫做()f x 的一个不动点,已知()224f x x mx =++,[]1,2D =没有不动点,则实数m 的取值范围 是________.11.当1,33x ⎛⎫∈ ⎪⎝⎭时,不等式log 1a x <恒成立,则实数a 的取值范围为________.12.记()22ln 2f x x x kx k =+−+,若存在实数a 、b ,满足122a b ≤<≤,使得函数()y f x =在区间[],a b 上是严格增函数,则实数k 的取值范围是________.2二、选择题(本大题满分445518+++=分)13.某班有50名学生,期末考试数学成绩服从正态分布()2120,N σ,已知(140)0.2P X >=,则[]100,140X ∈的学生人数为( ) A .5B .10C .20D .3014.若偶函数()f x 在区间[)0,+∞上严格增加,则1(21)3f x f ⎛⎫−< ⎪⎝⎭的x 取值范围是( )A .12,33⎛⎫ ⎪⎝⎭B .1,323⎡⎫⎪⎢⎣⎭C .12,23⎛⎫ ⎪⎝⎭D .12,23⎡⎫⎪⎢⎣⎭15.若函数()()20.5log 3f x x ax a =−+在[)2,+∞上是严格减函数,则实数a 的取值范围( ) A .(),4−∞B .(]4,4−C .()[),42,−∞−+∞ D .[]4,2−16.已知函数()ln f x x x =,若120x x <<,则下列结论正确的个数是( ) (1)2112()()x f x x f x <; (2)()()1122x f x x f x +<+ (3)()()12120f x f x x x −<−; (4)当ln 1x >−时,112221()()2()x f x x f x x f x +>A .1B .2C .3D .4三、解答题(本大题满分78分)17.(本题8614+=分)如图,在棱长为2的正方体1111ABCD A B C D −中,E ,F 分别为线段1DD ,BD 的中点.(1)求点D 到平面AEF 的距离; (2)求异面直线EF 与BC 所成的角.18.(本题6814+=分)已知△ABC中,三个内角A,B,C的对边分别为a,b,c,22sin)()sin A C a b B−=−,外接圆半径R=.(1)求C∠的度数;(2)求△ABC面积S的最大值.19.(本题26614++=分)疫情期间居家学习,某校随机抽取了100名居家学习的高二学生进行问卷调查,得到学生每天学习时间(单位:h)的频率分布直方图如下,若被抽取的这100名学生中,每天学习时间不低于8小时有30人.(1)求频率分布直方图中实数a,b的值;(2)每天学习时间在[)6.0,6.5的7名学生中,有4名男生,3名女生,现从中抽2人进行电话访谈,已知抽取的学生有男生,求抽取的2人恰好为一男一女的概率;(3)依据所抽取的样本,从每天学习时间在[)6.0,6.5和[)7.0,7.5的学生中按比例分层抽样抽取8人,再从这8人中选3人进行电话访谈,求抽取的3人中每天学习时间在[)6.0,6.5的人数X的分布和数学期望.320.(本题46818++=分)若椭圆22:143x yΓ+=的右焦点为F,过F的直线l交Γ于A,B两点.(1)若直线l垂直于x轴,求线段AB的长;(2)若直线l与x轴不重合,O为坐标原点,求△AOB面积的最大值;(3)若椭圆Γ上存在点C使得AC BC=,且△ABC的重心G在y轴上,求此时直线l的方程.4521.(本题46818++=分)设()y f x =、()y g x =是定义域为R 的函数,当12()()g x g x ≠时,记121212()()(,)()()f x f x x xg x g x −δ=−.(1)已知()y g x =在区间I 上严格增,且对任意1x ,2x I ∈,12x x ≠,有12(,)0x x δ>,证明:函数()y f x =在区间I 上严格增; (2)已知()32133g x x ax x =+−,且对任意1x ,2x R ∈,当12()()g x g x ≠时,有12(,)0x x δ>,若当1x =时,函数()y f x =取得极值,求实数a 的值; (3)已知()sin g x x =,12πf ⎛⎫= ⎪⎝⎭,1πf2⎛⎫−=− ⎪⎝⎭,且对任意1x ,2x R ∈,当12()()g x g x ≠时,有12(,)1x x δ≤,证明:()sin f x x =.6参考答案一、填空题1.1,0,2−;2.20,40a b ac >−≤;3.(]0,1;4.2;5.[]3,1−;6.充分不必要;7.22x x −+;8.6561;9.323; 10.()3,2,2⎛⎫−∞−⋃−+∞ ⎪⎝⎭; 11.[)10,3,3⎛⎤⋃+∞ ⎥⎝⎦ 12.9{|}4k k <12.记()22ln 2f x x x kx k =+−+,若存在实数a 、b ,满足122a b ≤<≤,使得函数()y f x =在区间[],a b 上是严格增函数,则实数k 的取值范围是________. 【答案】9{|}4k k <【解析】()222f x lnx x kx k =+−+在区间[]a,b 上是严格增函数, ()1'220f x x k x ∴=+−…在[]a,b 上恒成立,可得1122k x x ⎛⎫+ ⎪⎝⎭…成立,又()1122g x x x ⎛⎫=+ ⎪⎝⎭在02⎛⎝⎭上递减,在(2,⎫+∞⎪⎪⎭上单调递增, 122a b ≤<≤,()139,2224g g ⎛⎫== ⎪⎝⎭,故94k <.故答案为:9{|}4k k <.二、选择题13.D 14.A 15. 16.B16.已知函数()ln f x x x =,若120x x <<,则下列结论正确的个数是( ) (1)2112()()x f x x f x <; (2)()()1122x f x x f x +<+ (3)()()12120f x f x x x −<−; (4)当ln 1x >−时,112221()()2()x f x x f x x f x +>A .1B .2C .3D .4【答案】B7【解析】(1)正确;因为令()()f x g x lnx x==, 在()0,+∞上是增函数,∴当120x x <<时,()()12g x g x <,()()1212f x f x x x ∴<即()()2112x f x x f x <.(2)错误;因为令()()g x f x x xlnx x =+=+()'2,g x lnx ∴=+()2x e ,−∴∈+∞时,()()'0,g x g x >单调递增,()20x ,e −∈时,()()'0,g x g x <单调递减.()11x f x ∴+与()22x f x +无法比较大小.(3)错误;因为令()()g x f x x xlnx x =−=−,()'g x lnx =()01x ,∴∈时,()()'0,g x g x <在()01,单调递减,()1x ,∈+∞时,()()'0,g x g x >在()1,+∞单调递增,()()()()1212112201,,,x x g x g x f x x f x x ∴<<−><∴−>当时()()()()12121212,0f x f x f x f x x x x x −∴−>−∴<−当121x x <<时,()()12g x g x <()()()()()()121122121212,,0.f x f x f x x f x x f x f x x x x x −∴−<−∴−<−∴>−(4)正确;因为1lnx >−时,()f x 单调递增, 又(1)正确,()()()()()()()1122211122212x f x x f x x f x x f x f x x f x f x ⎡⎤⎡⎤∴⋅+⋅−>−+−⎣⎦⎣⎦()()()12120x x f x f x ⎡⎤=−−>⎣⎦,故选B.三.解答题17.(1) (2)18.(1)3π(219.(1)0.26,0.38a b == (2)23(3)()34E X =820.(本题46818++=分)若椭圆22:143x y Γ+=的右焦点为F ,过F 的直线l 交Γ于A ,B 两点.(1)若直线l 垂直于x 轴,求线段AB 的长;(2)若直线l 与x 轴不重合,O 为坐标原点,求△AOB 面积的最大值; (3)若椭圆Γ上存在点C 使得AC BC =,且△ABC 的重心G 在y 轴上,求此时直线l 的方程. 【答案】(1)3AB =(2)32(3) 直线;1l x =或0y =或1x y =+. 【解析】(1)()10F ,,令1x =, 则21143y +=,3,32y AB ∴=±∴=(2) 设直线()()11:10,l x my m A x ,y =+≠,()22B x ,y 联立得221431x y x my ⎧+=⎪⎨⎪=+⎩, 则()2234690,m y my ++−=则()212261441,,34mm y y m −∆=++=+12122293434y y y y m m −⋅=∴−=++121122AOBS OF y y ∆∴=⋅−=令,1t t …, 则2661313AOB tS t t t ∆==++,13y t t=+在[)1,+∞上为增函数,926663142313AOB tS t t t∆∴===++…, 当且仅当1t =, 即0m =时取等号, AOB ∴∆面积的最大值为32. (3)当直线l 不与x 轴重合时,设直线()()(112:10,,l x my m A x ,y B x =+≠,)2,y AB 的中点为M ,联立得221431x y x my ⎧+=⎪⎨⎪=+⎩, 则()2234690m y my ++−= ()212261441,34mm y y m −∆=++=+122934y y m −⋅=+ ABC ∆的重心G 在y 轴上,120C x x x ∴++=()()12122C x x x m y y ∴=−+=−+−=28,34m −+()12122242234M m y y x x x m +++===+1223234M y y my m +−==+,AC BC CM AB=∴⊥∴直线():M M CM y y m x x −=−−,()2934C M C M my y m x x m ∴=−−=+22893434m C ,m m −⎛⎫∴ ⎪++⎝⎭, 代入椭圆得,()22310m m −=,0m∴=或m =, ∴直线:1lx =或1x y =+, 当直线 与x 轴重合时,C 点在椭圆的上,下顶点,满足题意,此时:0l y =, 综上, 直线;1l x =或0y =或1x y =+. 21.(本题46818++=分)设()y f x =、()y g x =是定义域为R 的函数,当12()()g x g x ≠时,记121212()()(,)()()f x f x x xg x g x −δ=−.(1)已知()y g x =在区间I 上严格增,且对任意1x ,2x I ∈,12x x ≠,有12(,)0x x δ>,证明:函数()y f x =在区间I 上严格增;10(2)已知()32133g x x ax x =+−,且对任意1x ,2x R ∈,当12()()g x g x ≠时,有12(,)0x x δ>,若当1x =时,函数()y f x =取得极值,求实数a 的值; (3)已知()sin g x x =,12πf ⎛⎫= ⎪⎝⎭,1πf2⎛⎫−=− ⎪⎝⎭,且对任意1x ,2x R ∈,当12()()g x g x ≠时,有12(,)1x x δ≤,证明:()sin f x x =.【答案】(1)见解析 (2)1a =(3)见解析【解析】(1) 证明: 不妨设12x x <,因为()y g x =在I 上严格增,所以对任意1212,,x x I x x ∈<, 有()()120g x g x −<, 又()()()()()121212,0,f x f x x x g x g x −δ=>−所以()()120f x f x −<,所以()y f x =在区间I 上严格增.(2)由(1)可知:当()y g x =在区间I 上严格增时,()y f x =在I 上严格增, 当()y g x =在区间I 上严格减时,()y f x =在I 上严格减,又当1x =时,()y f x =取得极值,所以当1x =时,()y g x =也取得极值,()()2'23,'1220g x x ax g a =+−=−=, 可得1a =,当1a =时,()()()'31g x x x =+−, 所以在()3,−∞−上,()()'0,g x g x >单调递增,在()31,−上,()()'0,g x g x <单调递减, 在()1,+∞上,()()'0,g x g x >单调递增,所以()g x 在1x =处取得极值,所以1a =. (3)证明: 当()2x k k Z π≠+π∈时, 由条件知()1121f x x,sinx +π⎛⎫δ−=≤ ⎪+⎝⎭ 所以()()1,121f x f x sinx ,x sinx −π⎛⎫δ=≤ ⎪−⎝⎭…,所以()f x sinx …,所以()f x sinx =, 当()202x k k Z ,k π=+π∈≠时, 对任意22t ,ππ⎛⎫∈− ⎪⎝⎭, 有()()11f x sint x,t sint −δ=≤− 所以()211sint f x −剟,又因为21sint −的值域为()31,−,所以()1f x =,11 当()202x k k Z ,k π=−+π∈≠时, 对任意22t ,ππ⎛⎫∈− ⎪⎝⎭, 有()()11f x sint x,t sint −δ=≤−−, 所以()112f x sint −+剟,又因为12sint +值域为()13,,所以()1f x =−, 综上可知, 对任意(),x R f x sinx ∈=.。
2024-2025学年高三上学期第一次联考(9月月考) 数学试题[含答案]
![2024-2025学年高三上学期第一次联考(9月月考) 数学试题[含答案]](https://img.taocdn.com/s3/m/4ca444db8662caaedd3383c4bb4cf7ec4afeb6db.png)
2024~2025学年高三第一次联考(月考)试卷数学考生注意:1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.4.本卷命题范围:集合、常用逻辑用语、不等式、函数、导数及其应用.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则集合的真子集的个数为(){}4,3,2,0,2,3,4A =---{}2290B x x =-≤A B ⋂A.7B.8C.31D.322.已知,,则“,”是“”的( )0x >0y >4x ≥6y ≥24xy ≥A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件3.国家速滑馆又称“冰丝带”,是北京冬奥会的标志性场馆,拥有亚洲最大的全冰面设计,但整个系统的碳排放接近于零,做到了真正的智慧场馆、绿色场馆,并且为了倡导绿色可循环的理念,场馆还配备了先进的污水、雨水过滤系统,已知过滤过程中废水的污染物数量与时间(小时)的关系为()mg /L N t (为最初污染物数量,且).如果前4个小时消除了的污染物,那么污染物消0e kt N N -=0N 00N >20%除至最初的还需要( )64%A.3.8小时 B.4小时C.4.4小时D.5小时4.若函数的值域为,则的取值范围是()()()2ln 22f x x mx m =-++R m A.B.()1,2-[]1,2-C.D.()(),12,-∞-⋃+∞(][),12,-∞-⋃+∞5.已知点在幂函数的图象上,设,(),27m ()()2n f x m x =-(4log a f =,,则,,的大小关系为( )()ln 3b f =123c f -⎛⎫= ⎪⎝⎭a b c A.B.c a b <<b a c<<C. D.a c b <<a b c<<6.已知函数若关于的不等式的解集为,则的()()2e ,0,44,0,x ax xf x x a x a x ⎧->⎪=⎨-+-+≤⎪⎩x ()0f x ≥[)4,-+∞a 取值范围为( )A.B. C. D.(2,e ⎤-∞⎦(],e -∞20,e ⎡⎤⎣⎦[]0,e 7.已知函数,的零点分别为,,则( )()41log 4xf x x ⎛⎫=- ⎪⎝⎭()141log 4xg x x ⎛⎫=- ⎪⎝⎭a b A. B.01ab <<1ab =C.D.12ab <<2ab ≥8.已知,,,且,则的最小值为( )0a >0b >0c >30a b c +-≥6b a a b c ++A. B. C. D.29495989二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列说法正确的是( )A.函数是相同的函数()f x =()g x =B.函数6()f x =C.若函数在定义域上为奇函数,则()313xx k f x k -=+⋅1k =D.已知函数的定义域为,则函数的定义域为()21f x +[]1,1-()f x []1,3-10.若,且,则下列说法正确的是()0a b <<0a b +>A. B.1a b >-110a b+>C. D.22a b <()()110a b --<11.已知函数,则下列说法正确的是( )()()3233f x x x a x b=-+--A.若在上单调递增,则的取值范围是()f x ()0,+∞a (),0-∞B.点为曲线的对称中心()()1,1f ()y f x =C.若过点可作出曲线的三条切线,则的取值范围是()2,m ()()3y f x a x b =+-+m ()5,4--D.若存在极值点,且,其中,则()f x 0x ()()01f x f x =01x x ≠1023x x +=三、填空题:本题共3小题,每小题5分,共15分.12.__________.22lg 2lg3381527log 5log 210--+⋅+=13.已知函数称为高斯函数,表示不超过的最大整数,如,,则不等式[]y x =x []3.43=[]1.62-=-的解集为__________;当时,的最大值为__________.[][]06x x <-0x >[][]29x x +14.设函数,若,则的最小值为__________.()()()ln ln f x x a x b =++()0f x ≥ab 四、解答题:本题共5小题、共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)已知全集,集合,.U =R {}231030A x x x =-+≤{}220B x xa =+<(1)若,求和;8a =-A B ⋂A B ⋃(2)若,求的取值范围.()UA B B ⋂= a 16.(本小题满分15分)已知关于的不等式的解集为.x 2280ax x --<{}2x x b-<<(1)求,的值;a b (2)若,,且,求的最小值.0x >2y >-42a bx y +=+2x y +17.(本小题满分15分)已知函数.()()()211e 2x f x x ax a =--∈R (1)讨论的单调性;()f x (2)若对任意的恒成立,求的取值范围.()e x f x x ≥-[)0,x ∈+∞a 18.(本小题满分17分)已知函数是定义在上的奇函数.()22x xf x a -=⋅-R(1)求的值,并证明:在上单调递增;a ()f x R (2)求不等式的解集;()()23540f x x f x -+->(3)若在区间上的最小值为,求的值.()()442x x g x mf x -=+-[)1,-+∞2-m 19.(本小题满分17分)已知函数.()()214ln 32f x x a x x a =---∈R (1)若,求的图像在处的切线方程;1a =()f x 1x =(2)若恰有两个极值点,.()f x 1x ()212x x x <(i )求的取值范围;a (ii )证明:.()()124ln f x f x a+<-数学一参考答案、提示及评分细则1.A 由题意知,又,所以{}2290B x x ⎡=-=⎢⎣∣ {}4,3,2,0,2,3,4A =---,所以的元素个数为3,真子集的个数为.故选.{}2,0,2A B ⋂=-A B ⋂3217-=A 2.A 若,则,所以“”是“”的充分条件;若,满足4,6x y 24xy 4,6x y 24xy 1,25x y ==,但是,所以“”不是“”的必要条件,所以“”是24xy 4x <4,6x y 24xy 4,6x y “”的充分不必要条件.故选A.24xy 3.B 由题意可得,解得,令,可得4004e 5N N -=44e 5k -=20004e 0.645t N N N -⎛⎫== ⎪⎝⎭,解得,所以污染物消除至最初的还需要4小时.故选B.()248e e ek kk---==8t =64%4.D 依题意,函数的值域为,所以,解得()()2ln 22f x x mx m =-++R ()2Δ(2)420m m =--+ 或,即的取值范围是.故选D.2m 1m - m ][(),12,∞∞--⋃+5.C 因为是軍函数,所以,解得,又点在函数的图()()2nf x m x =-21m -=3m =()3,27()n f x x =象上,所以,解得,所以,易得函数在上单调递增,又273n=3n =()3f x x =()f x (),∞∞-+,所以.故选C.1241ln3lne 133log 2log 2->==>=>=>a c b <<6.D 由题意知,当时,;当时,;当时,(),4x ∞∈--()0f x <[]4,0x ∈-()0f x ()0,x ∞∈+.当时,,结合图象知;当时,,当()0f x 0x ()()()4f x x x a =-+-0a 0x >()e 0x f x ax =- 时,显然成立;当时,,令,所以,令,解0a =0a >1e x x a (),0e x x g x x =>()1e xxg x -='()0g x '>得,令0,解得,所以在上单调递增,在上单调递减,所以01x <<()g x '<1x >()g x ()0,1()1,∞+,所以,解得综上,的取值范围为.故选D.()max 1()1e g x g ==11e a0e a < a []0,e 7.A 依题意得,即两式相减得4141log ,41log ,4a b a b ⎧⎛⎫=⎪ ⎪⎝⎭⎪⎨⎛⎫⎪= ⎪⎪⎝⎭⎩441log ,41log ,4a ba b ⎧⎛⎫=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪-= ⎪⎪⎝⎭⎩.在同一直角坐标系中作出的图()44411log log log 44a ba b ab ⎛⎫⎛⎫+==- ⎪ ⎪⎝⎭⎝⎭4141log ,log ,4xy x y x y ⎛⎫=== ⎪⎝⎭象,如图所示:由图象可知,所以,即,所以.故选A.a b >1144ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭()4log 0ab <01ab <<8.C 因为,所以,所以30a b c +- 30a b c +> 11911121519966399939911b a b a b b b b a b c a b a b a a a a ⎛⎫++=+=++--=-= ⎪+++⎝⎭++ ,当且仅当,即时等号成立,所以的最小值为.故选C.1911991b b a a ⎛⎫+= ⎪⎝⎭+29b a =6b aa b c ++599.AD 由解得,所以,由,解得10,10x x +⎧⎨-⎩ 11x - ()f x =[]1,1-210x -,所以的定义域为,又,故函数11x - ()g x =[]1,1-()()f x g x ===与是相同的函数,故A 正确;,()f x ()g x ()6f x ==当且仅当方程无解,等号不成立,故B 错误;函数=2169x +=在定义域上为奇函数,则,即,即()313x x k f x k -=+⋅()()f x f x -=-331313x xx x k k k k ----=-+⋅+⋅,即,整理得,即,()()33313313x x xxxxk k k k ----=-+⋅+⋅313313x x x x k kk k ⋅--=++⋅22919x x k k ⋅-=-()()21910x k -+=所以,解得.当时,,该函数定义域为,满足,210k -=1k =±1k =()1313xx f x -=+R ()()f x f x -=-符合题意;当时,,由可得,此时函数定义域为1k =-()13311331x x xxf x --+==--310x -≠0x ≠,满足,符合题意.综上,,故C 错误;由,得{}0x x ≠∣()()f x f x -=-1k =±[]1,1x ∈-,所以的定义域为,故D 正确.故选AD.[]211,3x +∈-()f x []1,3-10.AC 因为,且,所以,所以,即,故A 正确;0a b <<0a b +>0b a >->01a b <-<10ab -<<因为,所以,故В错误;因为,所以,0,0b a a b >->+>110a ba b ab ++=<0a b <<,a a b b =-=由可得,所以,故C 正确;因为当,此时,故0a b +>b a >22a b <11,32a b =-=()()110a b -->D 错误.故选AC.11.BCD 若在上单调递增,则在上佰成立,所以()f x ()0,∞+()23630f x x x a '=-+- ()0,x ∞∈+,解得,即的取值范围是,故A 错误;因为()min ()13630f x f a '==--'+ 0a a (],0∞-,所以,又()()32333(1)1f x x x a x b x ax b =-+--=---+()11f a b =--+,所以点()()()332(21)21(1)1222f x f x x a x b x ax b a b -+=-----++---+=--+为曲线的对称中心,故B 正确;由题意知,所以()()1,1f ()y f x =()()3233y f x a x b xx =+-+=-,设切点为,所以切线的斜率,所以切线的方程为236y x x =-'()32000,3x x x -20036k x x =-,所以,整理得()()()3220000336y x x x x x x --=--()()()322000003362m xx x x x --=--.记,所以3200029120x x x m -++=()322912h x x x x m =-++()26h x x '=-,令,解得或,当时,取得极大值,当时,1812x +()0h x '=1x =2x =1x =()h x ()15h m =+2x =取得极小值,因为过点可作出曲线的三条切线,所以()h x ()24h m=+()2,m ()()3y f x a x b =+-+解得,即的取值范围是,故C 正确;由题意知()()150,240,h m h m ⎧=+>⎪⎨=+<⎪⎩54m -<<-m ()5,4--,当在上单调递增,不符合题意;当,()223633(1)f x x x a x a =-+-=--'()0,a f x (),∞∞-+0a >令,解得,令,解得在()0f x '>1x <-1x >+()0f x '<11x -<<+()f x 上单调递增,在上单调递堿,在上单调递增,因为,1∞⎛- ⎝1⎛+ ⎝1∞⎛⎫+ ⎪ ⎪⎝⎭存在极值点,所以.由,得,令,所以,()f x 0x 0a >()00f x '=()2031x a-=102x x t+=102x t x =-又,所以,又,()()01f x f x =()()002f x f t x =-()()32333(1)1f x x x a x b x ax b =-+--=---+所以,又,所以()()()330000112121x ax b t x a t x b ---+=-----+()2031x a-=,化简得()()()()()()()322320000000013112121312x x x b x x b t x x t x b----=----=------,又,所以,故D 正确.故选BCD.()()20330t x t --=010,30x x x t ≠-≠103,23t x x =+=12. 由题意知10932232862log 184163381255127log 5log 210log 5log 121027---⎛⎫+⋅+=+⋅-+ ⎪⎝⎭62511411410log 5log 2109339339=-⋅+=-+=13.(2分)(3分) 因为,所以,解得,又函数[)1,616[][]06x x <-[][]()60x x -<[]06x <<称为高斯函数,表示不超过的最大整数,所以,即不等式的解集为.当[]y x =x 16x < [][]06x x <-[)1,6时,,此时;当时,,此时01x <<[]0x =[]2[]9x x =+1x []1x ,当且仅当3时等号成立.综上可得,当时,的[][][]2119[]96x x x x ==++[]x =0x >[]2[]9x x +最大值为.1614. 由题意可知:的定义域为,令,解得令,解21e -()f x (),b ∞-+ln 0x a +=ln ;x a =-()ln 0x b +=得.若,当时,可知,此时,不合题1x b =-ln a b -- (),1x b b ∈--()ln 0,ln 0x a x b +>+<()0f x <意;若,当时,可知,此时,不合ln 1b a b -<-<-()ln ,1x a b ∈--()ln 0,ln 0x a x b +>+<()0f x <题意;若,当时,可知,此时;当ln 1a b -=-(),1x b b ∈--()ln 0,ln 0x a x b +<+<()0f x >时,可知,此时,可知若,符合题意;若[)1,x b ∞∈-+()ln 0,ln 0x a x b ++ ()0f x ln 1a b -=-,当时,可知,此时,不合题意.综上所ln 1a b ->-()1,ln x b a ∈--()ln 0,ln 0x a x b +<+>()0f x <述:,即.所以,令,所以ln 1a b -=-ln 1b a =+()ln 1ab a a =+()()ln 1h x x x =+,令,然得,令,解得,所以在()ln 11ln 2h x x x '=++=+()0h x '<210e x <<()0h x '>21e x >()h x 上单调递堿,在上单调递增,所以,所以的最小值为.210,e ⎛⎫ ⎪⎝⎭21,e ∞⎛⎫+ ⎪⎝⎭min 2211()e e h x h ⎛⎫==- ⎪⎝⎭ab 21e -15.解:(1)由题意知,{}2131030,33A x x x ⎡⎤=-+=⎢⎥⎣⎦∣ 若,则,8a =-{}()22802,2B x x =-<=-∣所以.(]1,2,2,33A B A B ⎡⎫⋂=⋃=-⎪⎢⎣⎭(2)因为,所以,()UA B B ⋂= ()UB A ⊆ 当时,此时,符合题意;B =∅0a 当时,此时,所以,B ≠∅0a <{}220Bx x a ⎛=+<= ⎝∣又,U A ()1,3,3∞∞⎛⎫=-⋃+ ⎪⎝⎭13解得.209a -< 综上,的取值范围是.a 2,9∞⎡⎫-+⎪⎢⎣⎭16.解:(1)因为关于的不等式的解集为,x 2280ax x --<{2}xx b -<<∣所以和是关于的方程的两个实数根,且,所以2-b x 2280ax x --=0a >22,82,b a b a⎧=-⎪⎪⎨⎪-=-⎪⎩解得.1,4a b ==(2)由(1)知,所以1442x y +=+()()()221141422242241844242y xx y x y x y x y y x ⎡⎤+⎛⎫⎡⎤+=++-=+++-=+++-⎢⎥ ⎪⎣⎦++⎝⎭⎣⎦,179444⎡⎢+-=⎢⎣ 当且仅当,即时等号成立,所以.()2242y x y x +=+x y ==2x y +74-17.解:(1)由题意知,()()e e x x f x x ax x a=-=-'若,令.解得,令,解得,所以在上单调递琙,在0a ()0f x '<0x <()0f x '>0x >()f x (),0∞-上单调递增.()0,∞+若,当,即时,,所以在上单调递增;0a >ln 0a =1a =()0f x ' ()f x (),∞∞-+当,即时,令,解得或,令,解得,ln 0a >1a >()0f x '>0x <ln x a >()0f x '<0ln x a <<所以在上单调递增,在上单调递减,在上单调递增;()f x (),0∞-()0,ln a ()ln ,a ∞+当,即时,令,解得或,令,解得,ln 0a <01a <<()0f x '>ln x a <0x >()0f x '<ln 0a x <<所以在上单调递增,在上单调递减,在上单调递增.()f x (),ln a ∞-()ln ,0a ()0,∞+综上,当时,在上单调递减,在上单调递增;当时,在0a ()f x (),0∞-()0,∞+01a <<()f x 上单调递增,在上单调递减,在上单调递增当时,在上(,ln )a ∞-()ln ,0a ()0,∞+1a =()f x (),∞∞-+单调递增;当时,在上单调递增,在上单调递减,在上单调递增.1a >()f x (),0∞-()0,ln a ()ln ,a ∞+(2)若对任意的恒成立,即对任意的恒成立,()e xf x x - [)0,x ∞∈+21e 02xx ax x -- [)0,x ∞∈+即对任意的恒成立.1e 102x ax -- [)0,x ∞∈+令,所以,所以在上单调递增,当()1e 12x g x ax =--()1e 2x g x a=-'()g x '[)0,∞+,即时,,所以在上单调递增,所以()10102g a =-' 2a ()()00g x g '' ()g x [)0,∞+,符合题意;()()00g x g = 当,即时,令,解得,令,解得,所()10102g a =-<'2a >()0g x '>ln 2a x >()0g x '<0ln 2a x < 以在上单调递减,()g x 0,ln 2a ⎡⎫⎪⎢⎣⎭所以当时,,不符合题意.0,ln 2a x ⎛⎫∈ ⎪⎝⎭()()00g x g <=综上,的取值范围是.a (],2∞-18.(1)证明:因为是定义在上的奇函数,所以,()f x R ()010f a =-=解得,所以,1a =()22x xf x -=-此时,满足题意,所以.()()22x x f x f x --=-=-1a =任取,所以12x x <,()()()()211122121211122222122222222122x x x x x x x x x x x x f x f x x x --⎛⎫--=---=--=-+ ⎪++⎝⎭又,所以,即,又,12x x <1222x x <12220x x -<121102x x ++>所以,即,所以在上单调递增.()()120f x f x -<()()12f x f x <()f x R (2)解:因为,所以,()()23540f x x f x -+->()()2354f x x f x ->--又是定义在上的奇函数,所以,()f x R ()()2354f x x f x ->-+又在上单调递增,所以,()f x R 2354x x x ->-+解得或,即不等式的解集为.2x >23x <-()()23540f x x f x -+->()2,2,3∞∞⎛⎫--⋃+ ⎪⎝⎭(3)解:由题意知,令,()()()44244222xxxxxxg x mf x m ---=+-=+--322,,2x x t t ∞-⎡⎫=-∈-+⎪⎢⎣⎭所以,所以.()2222442x xxxt --=-=+-()2322,,2y g x t mt t ∞⎡⎫==-+∈-+⎪⎢⎣⎭当时,在上单调递增,所以32m -222y t mt =-+3,2∞⎡⎫-+⎪⎢⎣⎭,解得,符合题意;2min317()323224g x m m ⎛⎫=-++=+=- ⎪⎝⎭2512m =-当时,在上单调递减,在上单调递增,32m >-222y t mt =-+3,2m ⎛⎫- ⎪⎝⎭(),m ∞+所以,解得或(舍).222min ()2222g x m m m =-+=-=-2m =2m =-综上,的值为或2.m 2512-19.(1)解:若,则,所以,1a =()214ln 32f x x x x =---()14f x x x =--'所以,又,()14112f =--='()1114322f =--=所以的图象在处的切线方程为,即.()f x 1x =()1212y x -=-4230x y --=(2)(i )解:由题意知,()22444a x a x x x af x x x x x '---+=--==-又函数恰有两个极值点,所以在上有两个不等实根,()f x ()1212,x x x x <240x x a -+=()0,∞+令,所以()24h x x x a =-+()()00,240,h a h a ⎧=>⎪⎨=-<⎪⎩解得,即的取值范围是.04a <<a ()0,4(ii )证明:由(i )知,,且,12124,x x x x a +==04a <<所以()()2212111222114ln 34ln 322f x f x x a x x x a x x ⎛⎫⎛⎫+=---+--- ⎪ ⎪⎝⎭⎝⎭()()()2212121214ln ln 62x x a x x x x =+-+-+-,()()()21212121214ln 262x x a x x x x x x ⎡⎤=+--+--⎣⎦()116ln 1626ln 22a a a a a a =----=-+要证,即证,只需证.()()124ln f x f x a+<-ln 24ln a a a a -+<-()1ln 20a a a -+-<令,所以,()()()1ln 2,0,4m a a a a a =-+-∈()11ln 1ln a m a a a a a -=-++=-'令,所以,所以即在上单调递减,()()h a m a ='()2110h a a a =--<'()h a ()m a '()0,4又,所以,使得,即,()()1110,2ln202m m '-'=>=<()01,2a ∃∈()00m a '=001ln a a =所以当时,,当时,,所以在上单调递增,在()00,a a ∈()0m a '>()0,4a a ∈()0m a '<()m a ()00,a 上单调递减,所以.()0,4a ()()()max 00000000011()1ln 2123m a m a a a a a a a a a ==-+-=-+-=+-令,所以,所以在上单调递增,所以()()13,1,2u x x x x =+-∈()2110u x x =->'()u x ()1,2,所以,即,得证.()000111323022u a a a =+-<+-=-<()0m a <()()124ln f x f x a +<-。
2023-2024学年福建省龙岩市第一中学高三上学期第一次月考数学试题及答案

龙岩一中2024届高三上学期第一次月考数学试题(考试时间:120分钟 满分:150分)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一一次可使杂质含量减少1/4,要使产品达到市场要求,则至少应过滤的次数为(已知:lg2=0.3010,lg3=0.4771)( )目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知A B 、为实数集R 的非空集合,则A B ≠⊂的必要不充分条件可以是( )A .AB A ⋂=B .A ∩C R B =C .C R B ≠⊂C R AD .B ∪C R A=R三、填空题:本题共4小题,每小题5分,共20分.13.已知实数集R ,集合A ={x|log 2x<1},B ={x ∈Z |x 2+4≤5x},则(C R A)∩B = 15. 已知()24,1,log ,2,ax x f x x x +≤⎧=⎨≥⎩则()()0f f =______;若函数()f x 的值域为[)1,+∞,则a 的最小值为______.17.(本题满分10分)已知集合{}2680A x x x =-+<,{}22430B x x ax a =-+<.(1)若a =1,求(C R B )∩A ;(2)若a >0,设命题:p x A ∈,命题:q x B ∈,已知命题p 是命题q 的充分不必要条件,求实数a 的取值围.18. (本题满分12分)已知函数1(=21xf x a +-)是奇函数.(1)求a ;(2)若[](1ln 0f x x -⋅<),求x 的范围.19.(本题满分12分)已知函数232)1(31)(x k x x f +-=,kx x g -=31)(,且)(x f 在区间),2(+∞上为增函数.(1)求实数k 的取值范围;(2)若函数)(x f 与)(x g 的图象有三个不同的交点,求实数k 的取值范围.20. (本题满分12分)某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出()*x x N∈名员工从事第三产业,调整后他们平均每人每年创造利润为310500x a ⎛⎫- ⎪⎝⎭万元()0a >,剩下的员工平均每人每年创造的利润可以提高0.2%x .(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a 的取值范围是多少?21. (本题满分12分)已知函数())2log f x x =-是R 上的奇函数,()2g x t x a =--.(1)若函数()f x 与()g x 有相同的零点,求t 的值;(2)若123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x g x ≤,求t 的取值范围.22. (本题满分12分)已知函数()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦,a ∈R .(1)讨论函数()f x 单调性;(2)当0a =时,若函数()()()11g x f x m x =---在[)0,∞+有两个不同零点,求实数m 的取值范围.龙岩一中2024届高三上学期第一次月考数学参考答案题号123456789101112答案BBCDDDABABDCDBCDABD13.{2,3,4}143-15.2, -316.-1两个函数图象如下图所示:121,ln ln e 1x x <<=,又当1x <时,()f x 单调递增,所以又由{}2680(2,4)A x x x =-+<=,所以()[)3,4B A ⋂=R ð.. ........5分(2)当0a >时,可得(),3B a a =.因为命题p 是命题q 的充分不必要条件,则A ≠⊂B ,可得243a a≤⎧⎨≤⎩,等号不能同时成立,解得423a ≤≤,所以实数a 的取值范围为4,23⎡⎤⎢⎥⎣⎦ ......10分18. .......1分.....................6分 (用特殊值没检验的,扣2分)................8分.....................12分19.解:(1)由题意xk x xf )1()(2+-=' ∵)(x f 在区间),2(+∞上为增函数,≥0在区间(2,+∞)上恒成立..........2分即k+1≤x 恒成立,又2>x ,∴21≤+k ,故1≤k ∴k 的取值范围为1≤k ..........4分 ( 没有等号扣2分)(2)设312)1(3)()()(23-++-=-=kx x k x x g x f x h ,)1)(()1()(2--=++-='x k x k x k x x h ...........6分令0)(='x h 得k x =或1=x 由(1)知1≤k ,①当1=k 时,0)1()(2≥-='x x h ,)(x h 在R 上递增,显然不合题意...........7分②当1<k 时,)(x h ,)(x h '随x 的变化情况如下表:x ),(k -∞k )1,(k 1),1(+∞)(x h '+0—0+)(x h ↗极大值312623-+-k k ↘极小值21-k ↗由于021<-k ,欲使)(x f 与)(x g 的图象有三个不同的交点,即方程0)(=x h 有三个不同的实根,故需0312623>-+-k k ,即0)22)(1(2<---k k k ...........10分∴⎩⎨⎧>--<02212k k k ,解得31-<k ,综上,所求k 的取值范围为31-<k ...........12分20. 解:(1)由题意,得()()10100010.2%101000x x -+≥⨯,..................3分即25000x x -≤,又0x >,所以0500x <≤.即最多调整500名员工从事第三产业. ..........5分(2)从事第三产业的员工创造的年总利润为310500⎛⎫- ⎪⎝⎭x a x 万元,从事原来产业的员工的年总利润为110(1000)1500⎛⎫-+⎪⎝⎭x x 万元,..............7分21. 解:(1)因为())2log f x x =-是R 上的奇函数,所以()00f =,即log 0=解得1a =..................2分因为0x =是函数()f x 的零点,所以()010g t =-=,则1t =....................4分(2)由(1)可得())2log f x x =-,()121,221121,2x t x g x t x x t x ⎧-++≥⎪⎪=--=⎨⎪+-<⎪⎩, (6)分因为奇函数())2log log f x x ==()f x 在3,24⎡⎤-⎢⎥⎣⎦上是减函数,则()f x 在3,24⎡⎤-⎢⎥⎣⎦上的最大值为()2max 33log 144f x f ⎫⎛⎫⎛⎫⎪=-=-= ⎪ ⎪⎪⎝⎭⎝⎭⎭.......8分因为()121,2121,2x t x g x x t x ⎧-++≥⎪⎪=⎨⎪+-<⎪⎩,所以()gx 在31,42⎡⎤-⎢⎥⎣⎦上是增函数,在1,22⎡⎤⎢⎥⎣⎦上是减函数.则()g x 的最小值为34g ⎛⎫-⎪⎝⎭和()2g 中的较小的一个.因为33521442g t t ⎛⎫⎛⎫-=⨯-+-=- ⎪ ⎪⎝⎭⎝⎭,()22213g t t =-⨯++=-.所以()()min 23g x g t ==-.............10分因为123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x f x ≤,所以13t ≤-.解得4t ≥.故t 的取值范围为[)4,+∞.....................12分22. 解(1):因为()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦定义域为R ,所以()()()211e e x xf x x ax x x a --'=+=+,..........1分当0a >时,令()0f x ¢>,解得0x >或x a <-,令()0f x '<,解得0a x -<<,所以()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增,..........2分当0a =时()21e 0xf x x -'=≥恒成立,所以()f x 在R 上单调递增, ..........3分当a<0时,令()0f x ¢>,解得x a >-或0x <,令()0f x '<,解得0x a <<-,所以()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增,..........4分综上可得,当0a >时,()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增;当0a =时,()f x 在R 上单调递增;当a<0时,()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增;..........5分解(2):当0a =时,()()()()()211122e 11x g x f x m x x x m x -=---=-+---,所以()21e x g x x m -'=-,令()()21e x P x g x x m -'==-,则()()212e 0x P x x x -'=+>,所以()21e x g x x m -'=-在[)0,∞+上单调递增,所以()()0g x g m ''≥=-,①当0m -≥,即0m ≤时()()00g x g m ''≥=-≥,所以()g x 在[)0,∞+上单调递增,又()10g =,所以函数()g x 只有一个零点,不符合题意,舍去;..........6分②当0m -<,即0m >时()()00g x g m ''≥=-<,又()()211e 0m g m m m '+=+->,所以存在唯一的()00,1x m ∈+,使得()00g x '=,当()00,x x ∈时,'()0g x <,当()0,x x ∈+∞时,'()0g x >所以()g x 在()00,x 上单调递减,在()0,x +∞上单调递增,又()11g m '=-,当1m =时()10g '=,此时01x =,所以()()10g x g ≥=,函数()g x 只有一个零点,不符合题意,舍去;当1m ≠时()110g m '=-≠,01x ≠,此时有两个零点时,应满足()()0000g g x ⎧≥⎪⎨<⎪⎩,..........8分即()()()011200002e 1022e 110x m g x x x m x --⎧+-≥⎪⎨=-+---<⎪⎩,其中()()()()()0001112220000000022e 1122e e 11x x x g x x x m x x x x x ---=-+---=-+---()0132000222e 1x x x x -=-+-+-,..........9分设()()321222e 1x h x x x x -=-+-+-,()0,1x m ∈+,则()()()121e x h x x x x -'=+-,令()()()121e 0x h x x x x -'=+-=,解得1x =,所以当01x <<时()0h x '>,当11x m <<+时()0h x '<,所以()h x 在()0,1上单调递增,在()1,1m +上单调递减,所以()()10h x h ≤=,..........11分即()()()012000022e 110x g x x x m x -=-+---<恒成立,所以112e m -≥-且1m ≠...........12分【方法点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.龙岩一中2024届高三上学期第一次月考数学试题一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一故选:D5.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量减少1/4,要使产品达到市场要求,则至少应过滤的次数为(已知:lg2=0.3010,lg3=0.4771)( )A.8B.9C.10D.11【答案】D【详解】设至少需要过滤n次,则10.0210.0014n⎛⎫⨯-≤⎪⎝⎭,即31420n⎛⎫≤⎪⎝⎭,所以3lg204nlg≤-,即lg2010.301010.42lg4lg320.30100.4471n+≥=≈-⨯-,又n N∈,所以11n≥,所以至少过滤11次才能使产品达到市场要求,故选D.【点睛】本题主要考查指数与对数的运算,考查学生的阅读能力,考查学生的建模能力,属于中档题.与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际【点睛】本题考查了比较大小的问题,考查了同构的思想,考查了利用导数求函数的单调区ln二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知A B 、为实数集R 的非空集合,则A B ≠⊂的必要不充分条件可以是( )⊂-x 121,ln ln e 1x x <<=,又当1x <时,()f x 单调递增,所以()()3233223ln 3ln ln ln e ex x x x x f x f x x ==⇒=,又2x 所以23ln x x =,332222ln 1ln ln x x x x x x m ===,21ln x x =确,故选:ABD三、填空题:本题共4小题,每小题5分,共20分.13.已知实数集R ,集合A ={x|log 2x<1},B ={x ∈Z |x 2+4≤5x},则(C R A)∩B = 【答案】{2,3,4}解析 由log 2x<1,解得0<x<2,故A =(0,2),故C R A =(-∞,0]∪[2,+∞),由x 2+4≤5x ,即x 2-5x +4≤0,解得1≤x ≤4,又x ∈Z ,所以B ={1,2,3,4}.15. 已知()24,1,log ,2,ax x f x x x +≤⎧=⎨≥⎩则()()0f f =______;若函数()f x 的值域为[)1,+∞,则a 的最小值为______.【答案】23- 【详解】()()()204log 42f f f ===,要使得函数()f x 的值域为[)1,+∞,则满足041a a ≤⎧⎨+≥,解得30a -≤≤,所以实数a 的最小值为3-.出文字说明、证明过程和演算步骤.17.(本题满分10分)已知集合{}2680A x x x =-+<,{}22430B x x ax a =-+<.(1)若a =1,求(C R B )∩A ;(2)若a >0,设命题:p x A ∈,命题:q x B ∈,已知命题p 是命题q 的充分不必要条件,求实数a 的取值围.17解:(1)当1a =时,{}2430(1,3)B x x x =-+<=,可得][(),13,=-∞⋃+∞R B ð,又由{}2680(2,4)A x x x =-+<=,所以()[)3,4B A ⋂=R ð.. ........5分(2)当0a >时,可得(),3B a a =.因为命题p 是命题q 的充分不必要条件,则A ≠⊂B ,可得243a a≤⎧⎨≤⎩,等号不能同时成立,解得423a ≤≤,所以实数a 的取值范围为4,23⎡⎤⎢⎥⎣⎦ (10)分18. (本题满分12分)已知函数1(=21x f x a +-)是奇函数.(1)求a ;(2)若[](1ln 0f x x -⋅<),求x 的范围........1分.....................6分 (用特殊值没检验的,扣2分).....................8分.....................12分19.(本题满分12分)已知函数232)1(31)(x k x x f +-=,kx x g -=31)(,且)(x f 在区间),2(+∞上为增函数.(1)求实数k 的取值范围;(2)若函数)(x f 与)(x g 的图象有三个不同的交点,求实数k 的取值范围.解:(1)由题意x k x x f )1()(2+-=' ∵)(x f 在区间),2(+∞上为增函数,≥0在区间(2,+∞)上恒成立..........2分即k+1≤x 恒成立,又2>x ,∴21≤+k ,故1≤k ∴k 的取值范围为1≤k ..........4分 ( 没有等号扣2分)(2)设312)1(3)()()(23-++-=-=kx x k x x g x f x h ,)1)(()1()(2--=++-='x k x k x k x x h ...........6分令0)(='x h 得k x =或1=x 由(1)知1≤k ,②当1=k 时,0)1()(2≥-='x x h ,)(x h 在R 上递增,显然不合题意...........7分②当1<k 时,)(x h ,)(x h '随x 的变化情况如下表:x ),(k -∞k )1,(k 1),1(+∞)(x h '+0—0+)(x h ↗极大值312623-+-k k ↘极小值21-k ↗由于021<-k ,欲使)(x f 与)(x g 的图象有三个不同的交点,即方程0)(=x h 有三个不同的实根,故需0312623>-+-k k ,即0)22)(1(2<---k k k ...........10分∴⎩⎨⎧>--<02212k k k ,解得31-<k ,综上,所求k 的取值范围为31-<k ...........12分20. (本题满分12分)某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出()*x x N∈名员工从事第三产业,调整后他们平均每人每年创造利润为310500x a ⎛⎫- ⎪⎝⎭万元()0a >,剩下的员工平均每人每年创造的利润可以提高0.2%x .(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a 的取值范围是多少?解:(1)由题意,得()()10100010.2%101000x x -+≥⨯,..................3分即25000x x -≤,又0x >,所以0500x <≤.即最多调整500名员工从事第三产业. ..........5分(2)从事第三产业的员工创造的年总利润为310500⎛⎫-⎪⎝⎭x a x 万元,从事原来产业的员工的年总利润为110(1000)1500⎛⎫-+ ⎪⎝⎭x x 万元,..............7分21. (本题满分12分)已知函数())2log f x x =是R 上的奇函数,()2g x t x a =--.(1)若函数()f x 与()g x 有相同的零点,求t 的值;(2)若123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x g x ≤,求t 的取值范围.解:(1)因为())2log f x x =是R 上的奇函数,所以()00f =,即log 0=解得1a =..................2分因为0x =是函数()f x 的零点,所以()010g t =-=,则1t =....................4分(2)由(1)可得())2log f x x =-,()121,221121,2x t x g x t x x t x ⎧-++≥⎪⎪=--=⎨⎪+-<⎪⎩,............6分因为奇函数())22log log f x x =-=()f x 在3,24⎡⎤-⎢⎥⎣⎦上是减函数,则()f x 在3,24⎡⎤-⎢⎥⎣⎦上的最大值为()2max 33log 144f x f ⎫⎛⎫⎛⎫⎪=-=-= ⎪ ⎪⎪⎝⎭⎝⎭⎭.......8分因为()121,2121,2x t x g x x t x ⎧-++≥⎪⎪=⎨⎪+-<⎪⎩,所以()g x 在31,42⎡⎤-⎢⎥⎣⎦上是增函数,在1,22⎡⎤⎢⎥⎣⎦上是减函数.则()g x 的最小值为34g ⎛⎫- ⎪⎝⎭和()2g 中的较小的一个.因为33521442g t t ⎛⎫⎛⎫-=⨯-+-=-⎪ ⎪⎝⎭⎝⎭,()22213g t t =-⨯++=-.所以()()min 23g x g t ==-.............10分因为123,,24x x ⎡⎤∀∈-⎢⎥⎣⎦,()()12f x x ,所以13t ≤-.解得4t ≥.故t 的取值范围为[)4,+∞.....................12分22. (本题满分12分)已知函数()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦,a ∈R .(1)讨论函数()f x 单调性;(2)当0a =时,若函数()()()11g x f x m x =---在[)0,∞+有两个不同零点,求实数m 的取值范围.解(1):因为()()2122e x f x x a x a -⎡⎤=+-+-⎣⎦定义域为R ,所以()()()211e e x xf x x ax x x a --'=+=+,..........1分当0a >时,令()0f x ¢>,解得0x >或x a <-,令()0f x '<,解得0a x -<<,所以()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增,..........2分当0a =时()21e 0xf x x -'=≥恒成立,所以()f x 在R 上单调递增, ..........3分当a<0时,令()0f x ¢>,解得x a >-或0x <,令()0f x '<,解得0x a <<-,所以()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增,..........4分综上可得,当0a >时,()f x 在(),0a -上单调递减,在(),a -∞-和()0,∞+上单调递增;当0a =时,()f x 在R 上单调递增;当a<0时,()f x 在()0,a -上单调递减,在(),0∞-和(),a -+∞上单调递增;..........5分解(2):当0a =时,()()()()()211122e 11x g x f x m x x x m x -=---=-+---,所以()21e x g x x m -'=-,令()()21e x P x g x x m -'==-,则()()212e 0x P x x x -'=+>,所以()21e x g x x m -'=-在[)0,∞+上单调递增,所以()()0g x g m ''≥=-,①当0m -≥,即0m ≤时()()00g x g m ''≥=-≥,所以()g x 在[)0,∞+上单调递增,又()10g =,所以函数()g x 只有一个零点,不符合题意,舍去;..........6分②当0m -<,即0m >时()()00g x g m ''≥=-<,又()()211e 0m g m m m '+=+->,所以存在唯一的()00,1x m ∈+,使得()00g x '=,当()00,x x ∈时,'()0g x <,当()0,x x ∈+∞时,'()0g x >所以()g x 在()00,x 上单调递减,在()0,x +∞上单调递增,又()11g m '=-,当1m =时()10g '=,此时01x =,所以()()10g x g ≥=,函数()g x 只有一个零点,不符合题意,舍去;当1m ≠时()110g m '=-≠,01x ≠,此时有两个零点时,应满足()()0000g g x ⎧≥⎪⎨<⎪⎩,..........8分即()()()011200002e 1022e 110x m g x x x m x --⎧+-≥⎪⎨=-+---<⎪⎩,其中()()()()()0001112220000000022e 1122e e 11x x x g x x x m x x x x x ---=-+---=-+---()0132000222e 1x x x x -=-+-+-,..........9分设()()321222e 1x h x x x x -=-+-+-,()0,1x m ∈+,则()()()121ex h x x x x -'=+-,令()()()121e0x h x x x x -'=+-=,解得1x =,所以当01x <<时()0h x '>,当11x m <<+时()0h x '<,所以()h x 在()0,1上单调递增,在()1,1m +上单调递减,所以()()10h x h ≤=,..........11分即()()()012000022e 110x g x x x m x -=-+---<恒成立,所以112e m -≥-且1m ≠...........12分【方法点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.。
2024-2025学年河北省省级联测高三(上)月考数学试卷(含答案)

2024-2025学年河北省省级联测高三(上)月考数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={−1,2,3,4},B ={x ∈Z|y =ln (9−x 2)},则A ∩B =( )A. {1,2,3}B. {−1,2}C. {2,3}D. {0,1,2,3,4}2.已知复数z 1=a 2−3a +3i ,z 2=2+(a 2−4a)i ,a ∈R ,若z 1+z 2为纯虚数,则a =( )A. 1或2B. 1C. 2D. 33.已知向量a ,b 满足|a |=2,b =(2,0),且|a +b |=2,则a 在b 上的投影向量的坐标为( )A. (−1,0)B. (1,0)C. (−2,0)D. (2,0)4.已知cos (α+π2)=2cos(α+3π),则sin 2α+12sin2αcos 2α=( )A. −14 B. 34 C. 2D. 65.某中学开展劳动实习,学习制作模具,有一个模具的毛坏直观图如图所示,它是由一个圆柱体与一个半球对接而成的组合体,已知该几何体的下半部分圆柱的轴截面(过圆柱上、下底面圆的圆心连线的平面)ABCD 是面积为16的正方形,则该几何体的体积为( )A. 16π3B. 16πC. 64π3D. 72π6.设S n 为正项等比数列{a n }的前n 项和,3S 2=a 1+2a 3,a 3=8,则数列{a n +2n−1}的前5项和为( )A. 55B. 57C. 87D. 897.已知函数f(x)=Asin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示,将函数f(x)的图象先向右平移π4个单位长度,再将所有点的横坐标缩短为原来的12(纵坐标不变),得到函数g(x)的图象,若关于x 的方程g(x)−m =0在x ∈[−π12,π6]上有两个不等实根,则实数m 的取值范围为( )A. (−2,2]B. (−2,− 3]C. [ 3,2]D. (− 3, 3]8.已知定义域为R的函数f(x)不是常函数,且满足f(x+y)+f(x−y)=f(x)f(y),f(1)=0,则∑2026i=1f (i)=( )A. −2B. 2C. −2026D. 2026二、多选题:本题共3小题,共18分。
2024-2025学年湖南师范大学附属中学高三上学期月考(一)数学试题及答案

大联考湖南师大附中2025届高三月考试卷(一)数学命题人:高三数学备课组 审题人:高三数学备课组时量:120分钟 满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,1. 已知{}()260,{lg 10}A x x xB x x =+-≤=-<∣∣,则A B = ( )A. {}32x x -≤≤∣ B. {32}xx -≤<∣C. {12}xx <≤∣ D. {12}xx <<∣2. 若复数z 满足()1i 3i z +=-+(i 是虚数单位),则z 等于( )A.B.54C.D.3. 已知平面向量()()5,0,2,1a b ==- ,则向量a b + 在向量b 上投影向量为( )A. ()6,3- B. ()4,2- C. ()2,1- D. ()5,04. 记n S 为等差数列{}n a 的前n 项和,若396714,63a a a a +==,则7S =( )A. 21B. 19C. 12D. 425. 某校高二年级下学期期末考试数学试卷满分为150分,90分以上(含90分)为及格.阅卷结果显示,全年级1200名学生的数学成绩近似服从正态分布,试卷的难度系数(难度系数=平均分/满分)为0.49,标准差为22,则该次数学考试及格的人数约为( )附:若()2,X Nμσ~,记()()p k P k X k μσμσ=-≤≤+,则()()0.750.547,10.683p p ≈≈.A 136人B. 272人C. 328人D. 820人6. 已知()π5,0,,cos ,tan tan 426αβαβαβ⎛⎫∈-=⋅= ⎪⎝⎭,则αβ+=( )A.π6 B.π4C.π3D.2π37. 已知12,F F 是双曲线22221(0)x y a b a b-=>>的左、右焦点,以2F 为圆心,a 为半径的圆与双曲线的一条的.渐近线交于,A B 两点,若123AB F F >,则双曲线的离心率的取值范围是( )A. ⎛ ⎝B. ⎛ ⎝C. (D. (8. 已知函数()220log 0x a x f x x x ⎧⋅≤=⎨>⎩,,,,若关于x 的方程()()0f f x =有且仅有两个实数根,则实数a 的取值范围是( )A. ()0,1 B. ()(),00,1-∞⋃ C. [)1,+∞ D. ()()0,11,+∞ 二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分9. 如图,在正方体111ABCD A B C D -中,E F M N ,,,分别为棱111AA A D AB DC ,,,的中点,点P 是面1B C 的中心,则下列结论正确的是( )A. E F M P ,,,四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN10. 已知函数()5π24f x x ⎛⎫=+ ⎪⎝⎭,则( )A. ()f x 的一个对称中心为3π,08⎛⎫ ⎪⎝⎭B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象C. ()f x 在区间5π7π,88⎡⎤⎢⎥⎣⎦上单调递增D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点,则5π13π,24m ⎛⎤∈⎥⎝⎦11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++-=,则()A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =-=∑三、填空题:本题共3小题,每小题5分,共15分.12. 6(31)x y +-的展开式中2x y 的系数为______.13. 已知函数()f x 是定义域为R 的奇函数,当0x >时,()()2f x f x '->,且()10f =,则不等式()0f x >的解集为__________.14. 已知点C 为扇形AOB 弧AB 上任意一点,且60AOB ∠=,若(),R OC OA OB λμλμ=+∈,则λμ+的取值范围是__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ,已知22cos a b c B +=.(1)求角C ;(2)若角C 的平分线CD 交AB于点,D AD DB ==CD 的长.16. 已知1ex =为函数()ln af x x x =的极值点.(1)求a 的值;(2)设函数()ex kxg x =,若对()120,,x x ∀∈+∞∃∈R ,使得()()120f x g x -≥,求k 的取值范围.17. 已知四棱锥P ABCD -中,平面PAB ⊥底面,ABCD AD∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥====为AB 的中点,F 为棱PC 上异于,P C 的点.的(1)证明:BD EF ⊥;(2)试确定点F 的位置,使EF 与平面PCD18. 在平面直角坐标系xOy 中,抛物线21:2(0)C y px p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长,点P 在抛物线1C 上,圆222:(2)E x y r -+=(其中01r <<).(1)若1,2r Q =为圆E 上的动点,求线段PQ 长度的最小值;(2)设()1,D t 是抛物线1C 上位于第一象限的一点,过D 作圆E 的两条切线,分别交抛物线1C 于点,M N .证明:直线MN 经过定点.19. 龙泉游泳馆为给顾客更好的体验,推出了A 和B 两个套餐服务,顾客可选择A 和B 两个套餐之一,并在App 平台上推出了优惠券活动,下表是该游泳馆在App 平台10天销售优惠券情况.销售量千张经计算可得:10101021111 2.2,118.73,38510i i i i i i i y y t y t =======∑∑∑(1)因为优惠券购买火爆,App 平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,已知销售量y 和日期t 呈线性关系,现剔除第10天数据,求y 关于t 的经验回归方程结果中的数值用分数表示;(2)若购买优惠券的顾客选择A 套餐的概率为14,选择B 套餐的概率为34,并且A 套餐可以用一张优惠券,B 套餐可以用两张优惠券,记App 平台累计销售优惠券为n 张的概率为n P ,求n P ;(3)记(2)中所得概率n P 的值构成数列{}()N n P n *∈.①求n P 的最值;②数列收敛的定义:已知数列{}n a ,若对于任意给定的正数ε,总存在正整数0N ,使得当0n N >时,n a a ε-<,(a 是一个确定的实数),则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛..参考公式:()()()1122211ˆˆ,n ni i i ii in ni ii ix x y y x y nx ya y bxx x x nx====---==---∑∑∑∑.大联考湖南师大附中2025届高三月考试卷(一)数学命题人:高三数学备课组 审题人:高三数学备课组时量:120分钟 满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,1. 已知{}()260,{lg 10}A x x xB x x =+-≤=-<∣∣,则A B = ( )A. {}32x x -≤≤∣ B. {32}xx -≤<∣C. {12}xx <≤∣ D. {12}xx <<∣【答案】D 【解析】【分析】通过解一元二次不等式和对数函数的定义域,求出集合,A B ,再求交集.【详解】集合{}()32,{lg 10}{12}A x x B x x x x =-≤≤=-<=<<∣∣∣,则{12}A B xx ⋂=<<∣,故选:D .2. 若复数z 满足()1i 3i z +=-+(i 是虚数单位),则z 等于( )A.B.54C.D.【答案】C 【解析】【分析】由复数的除法运算计算可得12i z =-+,再由模长公式即可得出结果.【详解】依题意()1i 3i z +=-+可得()()()()3i 1i 3i 24i12i 1i 1i 1i 2z -+--+-+====-+++-,所以z ==.故选:C3. 已知平面向量()()5,0,2,1a b ==- ,则向量a b +在向量b 上的投影向量为( )A. ()6,3- B. ()4,2- C. ()2,1- D. ()5,0【答案】A 【解析】【分析】根据投影向量的计算公式即可求解.【详解】()()7,1,15,a b a b b b +=-+⋅=== 所以向量a b +在向量b 上的投影向量为()()236,3||a b b b b b +⋅==- .故选:A4. 记n S 为等差数列{}n a 的前n 项和,若396714,63a a a a +==,则7S =( )A. 21 B. 19C. 12D. 42【答案】A 【解析】【分析】根据等差数列的性质,即可求解公差和首项,进而由求和公式求解.【详解】{}n a 是等差数列,396214a a a ∴+==,即67a =,所以67769,a a a a ==故公差76162,53d a a a a d =-=∴=-=-,()767732212S ⨯∴=⨯-+⨯=,故选:A5. 某校高二年级下学期期末考试数学试卷满分为150分,90分以上(含90分)为及格.阅卷结果显示,全年级1200名学生的数学成绩近似服从正态分布,试卷的难度系数(难度系数=平均分/满分)为0.49,标准差为22,则该次数学考试及格的人数约为( )附:若()2,X Nμσ~,记()()p k P k X k μσμσ=-≤≤+,则()()0.750.547,10.683p p ≈≈.A. 136人B. 272人C. 328人D. 820人【答案】B 【解析】【分析】首先求出平均数,即可得到学生的数学成绩2~(73.5,22)X N ,再根据所给条件求出(5790)P X ≤≤,即可求出(90)P X ≥,即可估计人数.【详解】由题得0.4915073.5,22μσ=⨯==,()()(),0.750.547p k P k X k p μσμσ=-≤≤+≈ ,()5790P X ∴≤≤()0.750.547p =≈,()()900.510.5470.2265P X ≥=⨯-=,∴该校及格人数为0.22651200272⨯≈(人),故选:B .6. 已知()π5,0,,cos ,tan tan 426αβαβαβ⎛⎫∈-=⋅= ⎪⎝⎭,则αβ+=( )A.π6 B.π4C.π3D.2π3【答案】D 【解析】【分析】利用两角差的余弦定理和同角三角函数的基本关系建立等式求解,再由两角和的余弦公式求解即可.【详解】由已知可得5cos cos sin sin 6sin sin 4cos cos αβαβαβαβ⎧⋅+⋅=⎪⎪⎨⋅⎪=⋅⎪⎩,解得1cos cos 62sin sin 3αβαβ⎧⋅=⎪⎪⎨⎪⋅=⎪⎩,,()1cos cos cos sin sin 2αβαβαβ∴+=⋅-⋅=-,π,0,2αβ⎛⎫∈ ⎪⎝⎭,()0,παβ∴+∈,2π,3αβ∴+=,故选:D .7. 已知12,F F 是双曲线22221(0)x y a b a b-=>>的左、右焦点,以2F 为圆心,a 为半径的圆与双曲线的一条渐近线交于,A B 两点,若123AB F F >,则双曲线的离心率的取值范围是( )A. ⎛ ⎝B. ⎛ ⎝C. (D. (【答案】B 【解析】【分析】根据双曲线以及圆的方程可求得弦长AB =,再根据不等式123AB F F >整理可得2259c a <,即可求得双曲线的离心率的取值范围.【详解】设以()2,0F c 为圆心,a 为半径的圆与双曲线的一条渐近线0bx ay -=交于,A B 两点,则2F 到渐近线0bx ay -=的距离d b ==,所以AB =,因为123AB F F >,所以32c ⨯>,可得2222299a b c a b ->=+,即22224555a b c a >=-,可得2259c a <,所以2295c a <,所以e <,又1e >,所以双曲线的离心率的取值范围是⎛ ⎝.故选:B8. 已知函数()220log 0x a x f x x x ⎧⋅≤=⎨>⎩,,,,若关于x 的方程()()0f f x =有且仅有两个实数根,则实数a 的取值范围是( )A. ()0,1 B. ()(),00,1-∞⋃ C. [)1,+∞ D. ()()0,11,+∞ 【答案】C 【解析】【分析】利用换元法设()u f x =,则方程等价为()0f u =,根据指数函数和对数函数图象和性质求出1u =,利用数形结合进行求解即可.【详解】令()u f x =,则()0f u =.①当0a =时,若()0,0u f u ≤=;若0u >,由()2log 0f u u ==,得1u =.所以由()()0ff x =可得()0f x ≤或()1f x =.如图所示,满足()0f x ≤的x 有无数个,方程()1f x =只有一个解,不满足题意;②当0a ≠时,若0≤u ,则()20uf u a =⋅≠;若0u >,由()2log 0f u u ==,得1u =.所以由()()0ff x =可得()1f x =,当0x >时,由()2log 1f x x ==,可得2x =,因为关于x 的方程()()0f f x =有且仅有两个实数根,则方程()1f x =在(,0∞-]上有且仅有一个实数根,若0a >且()(]0,20,xx f x a a ≤=⋅∈,故1a ≥;若0a <且()0,20xx f x a ≤=⋅<,不满足题意.综上所述,实数a 的取值范围是[)1,+∞,故选:C .二、多选题:本题共36分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分9. 如图,在正方体111ABCD A B C D -中,E F M N ,,,分别为棱111AA A D AB DC ,,,的中点,点P 是面1B C 的中心,则下列结论正确的是( )A. E F M P ,,,四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN【答案】BD 【解析】【分析】可得过,,E F M 三点的平面为一个正六边形,判断A ;分别连接,E F 和1,B C ,截面1C BEF 是等腰梯形,判断B ;分别取11,BB CC 的中点,G Q ,易证EF 显然不平行平面QGMN ,可判断C ;EM ⊥平面PMN ,可判断D.【详解】对于A :如图经过,,E F M 三点的平面为一个正六边形EFMHQK ,点P 在平面外,,,,E F M P ∴四点不共面,∴选项A 错误;对于B :分别连接,E F 和1,B C ,则平面PEF 即平面1C BEF ,截面1C BEF 是等腰梯形,∴选项B 正确;对于C :分别取11,BB CC 的中点,G Q ,则平面PMN 即为平面QGMN ,由正六边形EFMHQK ,可知HQ EF ,所以MQ 不平行于EF ,又,EF MQ ⊂平面EFMHQK ,所以EF MQ W = ,所以EF I 平面QGMN W =,所以EF 不平行于平面PMN ,故选项C 错误;对于D :因为,AEM BMG 是等腰三角形,45AME BMG ∴∠=∠=︒,90EMG ∴∠=︒,EMMG ∴⊥,,M N 是,AB CD 的中点,易证MN AD ∥,由正方体可得AD ⊥平面11ABB A ,MN ∴⊥平面11ABB A ,又ME ⊂平面11ABB A ,EM MN ∴⊥,,MG MN ⊂ 平面PMN ,EM ∴⊥平面GMN ,EM ⊂ 平面MEF ,∴平面MEF ⊥平面,PMN 故选项D 正确.故选:BD .10. 已知函数()5π24f x x ⎛⎫=+ ⎪⎝⎭,则( )A. ()f x 的一个对称中心为3π,08⎛⎫ ⎪⎝⎭B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象C. ()f x 在区间5π7π,88⎡⎤⎢⎥⎣⎦上单调递增D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点,则5π13π,24m ⎛⎤∈ ⎥⎝⎦【答案】BD 【解析】【分析】代入即可验证A ,根据平移可得函数图象,即可由正弦型函数的奇偶性求解B ,利用整体法即可判断C ,由5πcos 24x ⎛⎫+= ⎪⎝⎭求解所以根,即可求解D.【详解】对于A ,由35π3π2π0848f ⎛⎫⎛⎫=+⨯=≠⎪ ⎪⎝⎭⎝⎭,故A 错误;对于B ,()f x 的图象向右平移3π8个单位长度后得:3π3π5ππ228842y f x x x x ⎡⎤⎛⎫⎛⎫⎛⎫=-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,为奇函数,故B 正确;对于C ,当5π7π,88x ⎡⎤∈⎢⎥⎣⎦时,则5π5π2,3π42x ⎡⎤+∈⎢⎥⎣⎦,由余弦函数单调性知,()f x 在区间5π7π,88⎡⎤⎢⎥⎣⎦上单调递减,故C 错误;对于D ,由()1f x =,得5πcos 24x ⎛⎫+= ⎪⎝⎭ππ4x k =+或ππ,2k k +∈Z ,()y f x =在区间()0,m 上与1y =有且只有6个交点,其横坐标从小到大依次为:ππ5π3π9π5π,,,,,424242,而第7个交点的横坐标为13π4,5π13π24m ∴<≤,故D 正确.故选:BD11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++-=,则( )A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =-=∑【答案】ABC 【解析】【分析】根据函数奇偶性以及所满足的表达式构造方程组可得()()222f x f x ++-=,即可判断A 正确;利用对称中心表达式进行化简计算可得B 正确,可判断()g x 也是以8为周期的周期函数,即C 正确;根据周期性以及()()42f x f x ++=计算可得20241(42)2024k f k =-=∑,可得D 错误.【详解】由题意()()()(),f x f x g x g x -=-=-,且()()()00,21g f x g x =++-=,即()()21f x g x +-=①,用x -替换()()21f x g x ++-=中的x ,得()()21f x g x -+=②,由①+②得()()222f x f x ++-=所以()f x 的图象关于点(2,1)对称,且()21f =,故A 正确;由()()222f x f x ++-=,可得()()()()()42,422f x f x f x f x f x ++-=+=--=-,所以()()()()82422f x f x f x f x ⎡⎤+=-+=--=⎣⎦,所以()f x 是以8为周期的周期函数,故B 正确;由①知()()21g x f x =+-,则()()()()882121g x f x f x g x +=++-=+-=,故()()8g x g x +=,因此()g x 也是以8为周期的周期函数,所以()()202400g g ==,C 正确;又因为()()42f x f x ++-=,所以()()42f x f x ++=,令2x =,则有()()262f f +=,令10x =,则有()()10142,f f +=…,令8090x =,则有()()809080942f f +=,所以1012(2)(6)(10)(14)(8090)(8094)2222024f f f f f f ++++++=+++=个所以20241(42)(2)(6)(10)(14)(8090)(8094)2024k f k f f f f f f =-=++++++=∑ ,故D 错误.故选:ABC【点睛】方法点睛:求解函数奇偶性、对称性、周期性等函数性质综合问题时,经常利用其中两个性质推得第三个性质特征,再进行相关计算.三、填空题:本题共3小题,每小题5分,共15分.12. 6(31)x y +-的展开式中2x y 的系数为______.【答案】180-【解析】【分析】根据题意,由条件可得展开式中2x y 的系数为213643C C (1)⋅-,化简即可得到结果.【详解】在6(31)x y +-的展开式中,由()2213264C C 3(1)180x y x y ⋅⋅-=-,得2x y 的系数为180-.故答案为:180-.13. 已知函数()f x 是定义域为R 的奇函数,当0x >时,()()2f x f x '->,且()10f =,则不等式()0f x >的解集为__________.【答案】()()1,01,-⋃+∞【解析】【分析】根据函数奇偶性并求导可得()()f x f x ''-=,因此可得()()2f x f x '>,可构造函数()()2xf x h x =e并求得其单调性即可得()f x 在()1,+∞上大于零,在()0,1上小于零,即可得出结论.【详解】因为()f x 为奇函数,定义域为R ,所以()()f x f x -=-,两边同时求导可得()()f x f x ''--=-,即()()f x f x ''-=且()00f =,又因为当0x >时,()()2f x f x '->,所以()()2f x f x '>.构造函数()()2x f x h x =e ,则()()()22xf x f x h x '-'=e,所以当0x >时,()()0,h x h x '>在()0,∞+上单调递增,又因为()10f =,所以()()10,h h x =在()1,+∞上大于零,在()0,1上小于零,又因为2e 0x >,所以()f x 在()1,+∞上大于零,在()0,1上小于零,因为()f x 为奇函数,所以()f x 在(),1∞--上小于零,在()1,0-上大于零,综上所述,()0f x >的解集为()()1,01,-⋃+∞.故答案为:()()1,01,-⋃+∞14. 已知点C 为扇形AOB 的弧AB 上任意一点,且60AOB ∠=,若(),R OC OA OB λμλμ=+∈,则λμ+的取值范围是__________.【答案】⎡⎢⎣【解析】【分析】建系设点的坐标,再结合向量关系表示λμ+,最后应用三角恒等变换及三角函数值域求范围即可.【详解】方法一:设圆O 的半径为1,由已知可设OB 为x 轴的正半轴,O 为坐标原点,过O 点作x 轴垂线为y 轴建立直角坐标系,其中()()1,1,0,cos ,sin 2A B C θθ⎛ ⎝,其中π,0,3BOC θθ⎡⎤∠=∈⎢⎥⎣⎦,由(),R OC OA OB λμλμ=+∈,即()()1cos ,sin 1,02θθλμ⎛=+⎝,整理得1cos sin 2λμθθ+==,解得cos λμθ==,则ππcos cos ,0,33λμθθθθθ⎛⎫⎡⎤+==+=+∈ ⎪⎢⎥⎝⎭⎣⎦,ππ2ππ,,sin 3333θθ⎤⎡⎤⎛⎫+∈+∈⎥⎪⎢⎥⎣⎦⎝⎭⎦所以λμ⎡+∈⎢⎣.方法二:设k λμ+=,如图,当C 位于点A 或点B 时,,,A B C 三点共线,所以1k λμ=+=;当点C 运动到AB的中点时,k λμ=+==,所以λμ⎡+∈⎢⎣故答案为:⎡⎢⎣四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ,已知22cos a b c B +=.(1)求角C ;(2)若角C 的平分线CD 交AB于点,D AD DB ==CD 的长.【答案】(1)2π3C = (2)3CD =【解析】【分析】(1)利用正弦定理及两角和的正弦定理整理得到()2cos 1sin 0C B +=,再利用三角形的内角及正弦函数的性质即可求解;(2)利用正弦定理得出3b a =,再由余弦定理求出4a =,12b =,再根据三角形的面积建立等式求解.【小问1详解】由22cos a b c B +=,根据正弦定理可得2sin sin 2sin cos A B C B +=,则()2sin sin 2sin cos B C B C B ++=,所以2sin cos 2cos sin sin 2sin cos B C B C B C B ++=,整理得()2cos 1sin 0C B +=,因为,B C 均为三角形内角,所以(),0,π,sin 0B C B ∈≠,因此1cos 2C =-,所以2π3C =.【小问2详解】因为CD 是角C的平分线,AD DB ==所以在ACD 和BCD △中,由正弦定理可得,,ππsin sin sin sin 33AD CD BD CDA B ==,因此sin 3sin B ADA BD==,即sin 3sin B A =,所以3b a =,又由余弦定理可得2222cos c a b ab C =+-,即222293a a a =++,解得4a =,所以12b =.又ABC ACD BCD S S S =+△△△,即111sin sin sin 222ab ACB b CD ACD a CD BCD ∠∠∠=⋅⋅+⋅⋅,即4816CD =,所以3CD =.16. 已知1ex =为函数()ln af x x x =的极值点.(1)求a 的值;(2)设函数()ex kxg x =,若对()120,,x x ∀∈+∞∃∈R ,使得()()120f x g x -≥,求k 的取值范围.【答案】(1)1a = (2)(]()10,-∞-+∞ ,【解析】【分析】(1)直接根据极值点求出a 的值;(2)先由(1)求出()f x 的最小值,由题意可得是求()g x 的最小值,小于等于()f x 的最小值,对()g x 求导,判断由最小值时的k 的范围,再求出最小值与()f x 最小值的关系式,进而求出k 的范围.【小问1详解】()()111ln ln 1a a f x ax x x x a x xα--=='+⋅+,由1111ln 10e e e a f a -⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪⎪⎝⎭⎝⎭'⎭⎝,得1a =,当1a =时,()ln 1f x x ='+,函数()f x 在10,e ⎛⎫ ⎪⎝⎭上单调递减,在1,e∞⎛⎫+ ⎪⎝⎭上单调递增,所以1ex =为函数()ln af x x x =的极小值点,所以1a =.【小问2详解】由(1)知min 11()e e f x f ⎛⎫==- ⎪⎝⎭.函数()g x 的导函数()()1exg x k x -=-'①若0k >,对()1210,,x x k ∞∀∈+∃=-,使得()()12111e 1e k g x g f x k ⎛⎫=-=-<-<-≤ ⎪⎝⎭,即()()120f x g x -≥,符合题意.②若()0,0k g x ==,取11ex =,对2x ∀∈R ,有()()120f x g x -<,不符合题意.③若0k <,当1x <时,()()0,g x g x '<在(),1∞-上单调递减;当1x >时,()()0,g x g x '>在(1,+∞)上单调递增,所以()min ()1ek g x g ==,若对()120,,x x ∞∀∈+∃∈R ,使得()()120f x g x -≥,只需min min ()()g x f x ≤,即1e ek ≤-,解得1k ≤-.综上所述,k 的取值范围为(](),10,∞∞--⋃+.17. 已知四棱锥P ABCD -中,平面PAB ⊥底面,ABCD AD ∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥====为AB 的中点,F 为棱PC 上异于,P C 的点.(1)证明:BD EF ⊥;(2)试确定点F 的位置,使EF 与平面PCD【答案】(1)证明见解析(2)F 位于棱PC 靠近P 的三等分点【解析】【分析】(1)连接,,PE EC EC 交BD 于点G ,利用面面垂直的性质定理和三角形全等,即可得证;(2)取DC 的中点H ,以E 为坐标原点,分别以,,EB EH EP 所在直线为,,x y z 轴建立,利用线面角公式代入即可求解.小问1详解】如图,连接,,PE EC EC 交BD 于点G .因为E 为AB 的中点,PA PB =,所以PE AB ⊥.因为平面PAB ⊥平面ABCD ,平面PAB ⋂平面,ABCD AB PE =⊂平面PAB ,所以PE ⊥平面ABCD ,因为BD ⊂平面ABCD ,所以BD ⊥.因为ABD BCE ≅ ,所以CEB BDA ∠∠=,所以90CEB ABD ∠∠+= ,所以BD EC ⊥,因为,,PE EC E PE EC ⋂=⊂平面PEC ,所以BD ⊥平面PEC .因为EF ⊂平面PEC ,所以BD EF ⊥.【小问2详解】如图,取DC 的中点H ,以E 为坐标原点,分别以,,EB EH EP 所在直线为,,x y z 轴建立空间直角坐标系,【设2AB =,则2,1,BC AD PA PB ====则()()()()0,0,1,1,2,0,1,1,0,0,0,0P C D E -,设(),,,(01)F x y z PF PC λλ=<<,所以()(),,11,2,1x y z λ-=-,所以,2,1x y z λλλ===-,即(),2,1F λλλ-.则()()()2,1,0,1,2,1,,2,1DC PC EF λλλ==-=-,设平面PCD 的法向量为(),,m a b c =,则00DC m PC m ⎧⋅=⎪⎨⋅=⎪⎩,,即2020a b a b c +=⎧⎨+-=⎩,,取()1,2,3m =--,设EF 与平面PCD 所成的角为θ,由cos θ=sin θ=.所以sin cos ,m EF m EF m EF θ⋅====整理得2620λλ-=,因为01λ<<,所以13λ=,即13PF PC = ,故当F 位于棱PC 靠近P 的三等分点时,EF 与平面PCD18. 在平面直角坐标系xOy 中,抛物线21:2(0)C y px p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长,点P 在抛物线1C 上,圆222:(2)E x y r -+=(其中01r <<).(1)若1,2r Q =为圆E 上的动点,求线段PQ长度的最小值;(2)设()1,D t 是抛物线1C 上位于第一象限的一点,过D 作圆E 的两条切线,分别交抛物线1C 于点,M N .证明:直线MN 经过定点.【答案】(1(2)证明见解析【解析】【分析】(1)根据椭圆的短轴可得抛物线方程2y x =,进而根据两点斜率公式,结合三角形的三边关系,即可由二次函数的性质求解,(2)根据两点坐标可得直线,MN DM 的直线方程,由直线与圆相切可得,a b 是方程()()()2222124240r x r x r -+-+-=的两个解,即可利用韦达定理代入化简求解定点.【小问1详解】由题意得椭圆的方程:221116y x +=,所以短半轴14b =所以112242p b ==⨯=,所以抛物线1C 的方程是2y x =.设点()2,P t t ,则111222PQ PE ≥-=-=≥,所以当232ι=时,线段PQ.【小问2详解】()1,D t 是抛物线1C 上位于第一象限的点,21t ∴=,且()0,1,1t D >∴设()()22,,,M a a N b b ,则:直线()222:b a MN y a x a b a --=--,即()21y a x a a b-=-+,即()0x a b y ab -++=.直线()21:111a DM y x a --=--,即()10x a y a -++=.由直线DMr =,即()()()2222124240r a r a r -+-+-=..同理,由直线DN 与圆相切得()()()2222124240r b r b r -+-+-=.所以,a b 是方程()()()2222124240r x r x r -+-+-=的两个解,22224224,11r r a b ab r r --∴+==--代入方程()0x a b y ab -++=得()()222440x y r x y +++---=,220,440,x y x y ++=⎧∴⎨++=⎩解得0,1.x y =⎧⎨=-⎩∴直线MN 恒过定点()0,1-.【点睛】圆锥曲线中定点问题的两种解法(1)引进参数法:先引进动点的坐标或动线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点.(2)特殊到一般法:先根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关.技巧:若直线方程为()00y y k x x -=-,则直线过定点()00,x y ;若直线方程为y kx b =+ (b 为定值),则直线过定点()0,.b 19. 龙泉游泳馆为给顾客更好的体验,推出了A 和B 两个套餐服务,顾客可选择A 和B 两个套餐之一,并在App 平台上推出了优惠券活动,下表是该游泳馆在App 平台10天销售优惠券情况.日期t 12345678910销售量千张 1.9 1.98 2.2 2.36 2.43259 2.682.76 2.70.4经计算可得:10101021111 2.2,118.73,38510i i i i i i i y y t y t =======∑∑∑.(1)因为优惠券购买火爆,App 平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,已知销售量y 和日期t 呈线性关系,现剔除第10天数据,求y 关于t 的经验回归方程结果中的数值用分数表示;..(2)若购买优惠券的顾客选择A 套餐的概率为14,选择B 套餐的概率为34,并且A 套餐可以用一张优惠券,B 套餐可以用两张优惠券,记App 平台累计销售优惠券为n 张的概率为n P ,求n P ;(3)记(2)中所得概率n P 的值构成数列{}()Nn P n *∈.①求n P 的最值;②数列收敛的定义:已知数列{}n a ,若对于任意给定的正数ε,总存在正整数0N ,使得当0n N >时,n a a ε-<,(a 是一个确定的实数),则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛.参考公式: ()()()1122211ˆˆ,n ni i i i i i n n ii i i x x y y x y nx y ay bx x x x nx ====---==---∑∑∑∑.【答案】(1)673220710001200y t =+ (2)433774n n P ⎛⎫=+⋅- ⎪⎝⎭(3)①最大值为1316,最小值为14;②证明见解析【解析】【分析】(1)计算出新数据的相关数值,代入公式求出 ,ab 的值,进而得到y 关于t 的回归方程;(2)由题意可知1213,(3)44n n n P P P n --=+≥,其中12113,416P P ==,构造等比数列,再利用等比数列的通项公式求解;(3)①分n 为偶数和n 为奇数两种情况讨论,结合指数函数的单调性求解;②利用数列收敛的定义,准确推理、运算,即可得证.【小问1详解】解:剔除第10天的数据,可得 2.2100.4 2.49y ⨯-==新,12345678959t ++++++++==新,则9922111119.73100.4114,73,38510285i i i i t y t ==⎛⎫⎛⎫=-⨯==-= ⎪ ⎪⎝⎭⎝⎭∑∑新新,所以912922119114,7395 2.4673ˆ2859560009i i i i t y t y b t t ==⎛⎫- ⎪-⨯⨯⎝⎭===-⨯⎛⎫- ⎪⎝⎭∑∑新新新新新,可得6732207ˆ 2.4560001200a =-⨯=,所以6732207ˆ60001200y t =+.【小问2详解】解:由题意知1213,(3)44n n n P P P n --=+≥,其中12111313,444416P P ==⨯+=,所以11233,(3)44n n n n P P P P n ---+=+≥,又由2131331141644P P +=+⨯=,所以134n n P P -⎧⎫+⎨⎬⎩⎭是首项为1的常数列,所以131,(2)4n n P P n -+=≥所以1434(2)747n n P P n --=--≥,又因为1414974728P -=-=-,所以数列47n P ⎧⎫-⎨⎬⎩⎭是首项为928-,公比为34-的等比数列,故143)74n n P --=-,所以1934433(()2847774n n n P -=--+=+-.【小问3详解】解:①当n 为偶数时,19344334()(28477747n n n P -=--+=+⋅>单调递减,最大值为21316P =;当n 为奇数时,19344334()(28477747n n n P -=--+=-⋅<单调递增,最小值为114P =,综上可得,数列{}n P 的最大值为1316,最小值为14.②证明:对任意0ε>总存在正整数0347[log ()]13N ε=+,其中 []x 表示取整函数,当 347[log ()]13n ε>+时,347log ()34333333()()()7747474n n n P εε-=⋅-=⋅<⋅=,所以数列{}n P 收敛.【点睛】知识方法点拨:与新定义有关的问题的求解策略:1、通过给出一个新的定义,或约定一种新的运算,或给出几个新模型来创设新问题的情景,要求在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实心信息的迁移,达到灵活解题的目的;2、遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使得问题得以解决.方法点拨:与数列有关的问题的求解策略:3、若新定义与数列有关,可得利用数列的递推关系式,结合数列的相关知识进行求解,多通过构造的分法转化为等差、等比数列问题求解,求解过程灵活运用数列的性质,准确应用相关的数列知识.。
2023-2024学年天津市耀华中学高三上学期第一次月考数学试题及答案

天津市耀华中学2024届高三年级第一次月考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟.第Ⅰ卷(选择题 共45分)一、选择题:本大题共9小题,每小题5分,共45分,在每小题给出的四个选项中,有且只有一项是符合题目要求的,请把正确答案填涂在答题卡上.1 已知集合{}220A x x x =+-<,{}lg 1B x x =<,A B = ( )A. ()2,10-B. ()0,1C. ()2,1-D. (),10-∞2. 设x ∈R ,则“11||22x -<”是“31x <”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件3. 函数()3ln xf x x=的部分图象是A. B.C. D.4. 5G 技术在我国已经进入调整发展的阶段,5G 手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:.时间x12345销售量y (千只)0.50.81.01.21.5若x 与y 线性相关,且线性回归方程为 0.24y x a=+,则下列说法不正确的是( )A. 由题中数据可知,变量y 与x 正相关,且相关系数1r <B. 线性回归方程 0.24y x a=+中 0.26a =C. 当解释变量x 每增加1个单位时,预报变量 y 平均增加0.24个单位D. 可以预测6x =时,该商场5G 手机销量约为1.72(千只)5. 已知0.20.212log 0.5,0.5,log 0.4a b c ===,则a ,b ,c 的大小关系为( )A. a b c <<B. a c b<< C. b<c<a D. c<a<b6. 已知4log a a =,则2log a a +=( )A 11或238-B. 11或218-C. 12或238-D. 10或218-7. “送出一本书,共圆读书梦”,某校组织为偏远乡村小学送书籍的志愿活动,运送的卡车共装有10个纸箱,其中5箱英语书、2箱数学书、3箱语文书.到目的地时发现丢失一箱,但不知丢失哪一箱.现从剩下9箱中任意打开2箱都是英语书的概率为( )A.29B.18C.112D.588. 将函数()π2sin 23f x x ⎛⎫=- ⎪⎝⎭的图像上所有点横坐标变为原来的2倍,纵坐标不变,得到函数()g x 的图像,有下述四个结论:①()π2sin 6g x x ⎛⎫=-⎪⎝⎭②函数()g x 在π0,2⎛⎫⎪⎝⎭上单调递增③点4π,03⎛⎫⎪⎝⎭是函数()g x 图像的一个对称中心④当ππ,2x ⎡⎤∈-⎢⎥⎣⎦时,函数()g x 的最大值为2其中所有正确结论的编号是( )A. ①②③B. ②③C. ①③④D. ②④.9. 已知函数()()()()()()22121,1,11,1,1a x a x x f x a x ax x x ⎧-++-∈-⎪=⎨-++∉-⎪⎩有且只有3个零点,则实数a 的取值范围是( )A. ()0,1 B. ()(),80,1-∞- C. [)0,1 D. (][),80,1-∞- 第Ⅱ卷(非选择题 共105分)二、填空题:本大题共6小题,每小题5分,共30分,请将答案填写在答题卡上.10. 复数()21i 1iz -=+(i 为虚数单位),则z =______.11.在6的二项展开式中,2x 的系数为___________.12.若2sin sin αβ+=3π2αβ+=,则sin α=________;cos 2β=________.13. 某专业资格考试包含甲、乙、丙3个科目,假设小张甲科目合格的概率为34,乙、丙科目合格的概率均为23,且3个科目是否合格相互独立.设小张3科中合格的科目数为X ,则(2)P X ==___________;()E X =___________.14. 已知0a >,0b >的最大值为________.15. 设R ω∈,函数()2π2sin ,0,6314,0,22x x f x x x x ωω⎧⎛⎫+≥ ⎪⎪⎪⎝⎭=⎨⎪++<⎪⎩()g x x ω=.若()f x 在1π,32⎛⎫- ⎪⎝⎭上单调递增,且函数()f x 与()g x 图象有三个交点,则ω的取值范围是________.三、解答题:本大题共5小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答案卡上.16. 已知ABC 的内角A ,B ,C 的对边分别为a,b ,c ,满足22cos c b A =+.(1)求角B ;(2)若1cos 4A =,求sin(2)A B +的值;(3)若7c =,sin b A =b 的值.的17. 已知底面ABCD 是正方形,PA ⊥平面ABCD ,//PA DQ ,33PA AD DQ ===,点E 、F 分别为线段PB 、CQ 的中点.(1)求证://EF 平面PADQ ;(2)求平面PCQ 与平面CDQ 夹角的余弦值;(3)线段PC 上是否存在点M ,使得直线AM 与平面PCQ,若存在求出PM MC 的值,若不存在,说明理由.18. 已知{}n a 为等差数列,6,2,n n n a n b a n -⎧=⎨⎩为奇数为偶数,记n S ,n T 分别为数列{}n a ,{}n b 的前n 项和,432S =,316T =.(1)求{}n a 通项公式;(2)证明:当5n >时,n n T S >.19. 如图,已知椭圆E :22221(0)x y a b a b +=>>()F 且斜率为k 的直线交椭圆E 于,A B 两点,线段AB 的中点为M ,直线l :40x ky +=交椭圆E 于,C D 两点.(1)求椭圆E 的方程;(2)求证:点M 在直线l上;的(3)是否存在实数k ,使得3BDM ACM S S ∆∆=?若存在,求出k 的值,若不存在,说明理由.20 已知函数()()1211222x f x x ex x -=--++,()()24cos ln 1g x ax x a x x =-+++,其中a ∈R .(1)讨论函数()f x 的单调性,并求不等式()0f x >的解集;(2)用{}max ,m n 表示m ,n 的最大值,记()()(){}max ,F x f x g x =,讨论函数()F x 的零点个数..天津市耀华中学2024届高三年级第一次月考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟.第Ⅰ卷(选择题 共45分)一、选择题:本大题共9小题,每小题5分,共45分,在每小题给出的四个选项中,有且只有一项是符合题目要求的,请把正确答案填涂在答题卡上.1. 已知集合{}220A x x x =+-<,{}lg 1B x x =<,A B = ( )A. ()2,10-B. ()0,1C. ()2,1-D. (),10-∞【答案】B 【解析】【分析】根据解一元二次不等式的解法,结合对数函数的单调性、集合交集的定义进行求解即可.【详解】因为{}()2202,1A x x x =+-<=-,{}()lg 10,10B x x =<=,所以A B = ()0,1,故选:B2. 设x ∈R ,则“11||22x -<”是“31x <”的A. 充分而不必要条件B 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A 【解析】【详解】分析:首先求解绝对值不等式,然后求解三次不等式即可确定两者之间的关系.详解:绝对值不等式1122x -<⇔111222x -<-<⇔01x <<,由31x <⇔1x <..据此可知1122x -<是31x <的充分而不必要条件.本题选择A 选项.点睛:本题主要考查绝对值不等式的解法,充分不必要条件的判断等知识,意在考查学生的转化能力和计算求解能力.3. 函数()3ln xf x x =的部分图象是A. B.C. D.【答案】A 【解析】【分析】根据奇偶性排除B ,当1x >时,()3ln 0xf x x =>,排除CD ,得到答案.【详解】()()()33ln ln ,x xf x f x f x x x =-==--, ()f x 为奇函数,排除B 当1x >时,()3ln 0xf x x=>恒成立,排除CD 故答案选A【点睛】本题考查了函数图像的判断,通过奇偶性,特殊值法排除选项是解题的关键.4. 5G 技术在我国已经进入调整发展的阶段,5G 手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:时间x12345销售量y (千只)0.50.8 1.0 1.2 1.5若x 与y 线性相关,且线性回归方程为 0.24y x a=+,则下列说法不正确的是( )A. 由题中数据可知,变量y 与x 正相关,且相关系数1r <B. 线性回归方程 0.24y x a=+中 0.26a =C. 当解释变量x 每增加1个单位时,预报变量 y 平均增加0.24个单位D. 可以预测6x =时,该商场5G 手机销量约为1.72(千只)【答案】ACD 【解析】【分析】根据已知数据,分析总体单调性,结合增量的变化判断A 选项;根据已知数据得到样本中心点,代入回归方程求解即可判断B 选项;根据回归方程判断CD 选项.【详解】从数据看y 随x 的增加而增加,故变量y 与x 正相关,由于各增量并不相等,故相关系数1r <,故A 正确;由已知数据得()11234535=++++=,()10.50.8 1.0 1.2 1.515y =++++=,代入ˆˆ0.24yx a =+中得到ˆ130.240.28a =-⨯=,故B 错;根据线性回归方程ˆ0.240.28yx =+可得x 每增加一个单位时,预报变量ˆy 平均增加0.24个单位,故C 正确.将6x =代入ˆ0.240.28yx =+中得到ˆ0.2460.28 1.72y =⨯+=,故D 正确.故选:ACD.5. 已知0.20.212log 0.5,0.5,log 0.4a b c ===,则a ,b ,c 的大小关系为( )A. a b c << B. a c b<< C. b<c<a D. c<a<b【答案】A 【解析】【分析】由指数函数与对数函数的单调性求解即可【详解】因为0.20.20.21log 0.5log log 2a ==<=,而150.2110.522b ⎛⎫==> ⎪⎝⎭,且0.20.51<,所以a b <.又12225log 0.4log log 212c ==>>,所以a b c <<,故选:A.6. 已知4log a a =,则2log a a +=( )A. 11或238-B. 11或218-C. 12或238-D. 10或218-【答案】A 【解析】【分析】对4log a a =43log 2a =或32-,讨论43log 2a =或32-时2log a a+的值,即可得出答案.【详解】由4log aa =()(4log 44log log aa=()49249log log4a ==,所以43log 2a =或32-.当43log 2a =时,33242a ===8,所以22log 8log 811a a +=+=;当43log 2a =-时,32148a -==,所以221123log log 888a a +=+=-,综上,a +2log 11a =或238-,故选:A.7. “送出一本书,共圆读书梦”,某校组织为偏远乡村小学送书籍的志愿活动,运送的卡车共装有10个纸箱,其中5箱英语书、2箱数学书、3箱语文书.到目的地时发现丢失一箱,但不知丢失哪一箱.现从剩下9箱中任意打开2箱都是英语书的概率为( )A.29B.18C.112D.58【答案】A 【解析】【分析】剩下9箱中任意打开2箱都是英语书的情况整体分为三种情况:丢失的英语书、数学书和语文书,计算出每种情况的概率即可.【详解】设事件A 表示丢失一箱后任取两箱是英语书,事件k B 表示丢失的一箱为,1,2,3k k =分别表示英语书、数学书、语文书.由全概率公式得()()()2223554222219999C C C 11382|2C 5C 10C C 9k k k P A P B P A B ===⨯+⨯+⨯==∑.故选:A8. 将函数()π2sin 23f x x ⎛⎫=- ⎪⎝⎭的图像上所有点横坐标变为原来的2倍,纵坐标不变,得到函数()g x 的图像,有下述四个结论:①()π2sin 6g x x ⎛⎫=-⎪⎝⎭②函数()g x 在π0,2⎛⎫⎪⎝⎭上单调递增③点4π,03⎛⎫⎪⎝⎭是函数()g x 图像的一个对称中心④当ππ,2x ⎡⎤∈-⎢⎥⎣⎦时,函数()g x 的最大值为2其中所有正确结论的编号是( )A. ①②③ B. ②③C. ①③④D. ②④【答案】B 【解析】【分析】根据图象变换可得()π2sin 3g x x ⎛⎫=-⎪⎝⎭,结合正弦函数的性质逐项分析判断.【详解】由题意可得:()π2sin 3g x x ⎛⎫=-⎪⎝⎭,故①错误;因为π0,2x ⎛⎫∈ ⎪⎝⎭,则πππ,336x ⎛⎫-∈- ⎪⎝⎭,且sin y x =在ππ,36⎛⎫- ⎪⎝⎭上单调递增,所以函数()g x 在π0,2⎛⎫⎪⎝⎭上单调递增,故②正确;因为4π4ππ2sin 2sin π0333g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,所以点4π,03⎛⎫⎪⎝⎭是函数()g x 图像的一个对称中心,故③正确;因为ππ,2x ⎡⎤∈-⎢⎥⎣⎦,则π4ππ,336x ⎡⎤∈-⎢⎥⎣⎦-,所以当π4π33x -=-,即πx =-时,函数()g x 的最大值为()4ππ2sin 3g ⎛⎫-=-= ⎪⎝⎭,故④错误;故选:B.9. 已知函数()()()()()()22121,1,11,1,1a x a x x f x a x ax x x ⎧-++-∈-⎪=⎨-++∉-⎪⎩有且只有3个零点,则实数a 的取值范围是( )A. ()0,1 B. ()(),80,1-∞- C. [)0,1 D. (][),80,1-∞- 【答案】B【解析】【分析】先求1a =时函数()f x 的零点,再考虑1a ≠时,函数()f x 在(][),11,-∞+∞ 的零点,由此确定函数()f x 在()1,1-上的零点个数,结合二次函数性质求a 的取值范围.【详解】当1a =时,()()[)(]31,1,1,1,0,,1x x f x x x x x ∞∞⎧-∈-⎪=+∈+⎨⎪∈--⎩,所以区间(],1-∞-内的任意实数和13都为函数()f x 的零点,不满足要求;当1a ≠时,若(],1x ∈-∞-,则()()21f x a x ax x =-+-,令()0f x =,可得0x =(舍去),或=1x -,所以=1x -为函数()f x 的一个零点;若[)1,x ∞∈+,则()()21f x a x ax x =-++,令()0f x =,则()210a x ax x -++=,所以11a x a +=-,若111a a+≥-,即01a ≤<,则函数()f x 在[)1,+∞上有一个零点;若1a >或a<0时,则函数()f x 在[)1,+∞上没有零点;当01a ≤<时,函数()f x 在(][),11,-∞-⋃+∞上有两个零点;当1a >或a<0时,函数()f x 在(][),11,-∞-⋃+∞上有一个零点,因为当01a ≤<时,函数()f x 在(][),11,-∞-⋃+∞上有两个零点;又函数()f x 在R 上有3个零点,所以函数()f x 在()1,1-上有且只有一个零点,即方程()()21210a x a x -++-=在()1,1-上有一个根,由()()()22418a a a a ∆=++-=+,当0a =时,方程()()21210a x a x -++-=的根为1x =(舍去),故0a =时,方程()()21210a x a x -++-=在()1,1-上没有根,矛盾当01a <<时,0∆>,设()()()[]2121,1,1g x a x a x x =-++-∈-,函数()()()2121g x a x a x =-++-的对称轴为2122a x a+=>-,函数()g x 的图象为开口向下的抛物线,由方程()()21210a x a x -++-=在()1,1-上有一个根可得()()10,10g g >-<,所以()()()()1210,1210a a a a -++->--+-<,所以01a <<,当1a >时,则函数()f x 在(][),11,-∞-⋃+∞上有一个零点;又函数()f x 在R 上有3个零点,所以函数()f x 在()1,1-上有且只有两个零点,即方程()()21210a x a x -++-=在()1,1-上有两个根,由()()()[]2121,1,1g x a x a x x =-++-∈-可得函数()g x 的图象为开口向上的抛物线,函数()()()2121g x a x a x =-++-的对称轴为222a x a+=-,则()()()224180a a a a ∆=++-=+>,21122a a+-<<-, ()()10,10g g >->,所以4a >,()()()()1210,1210a a a a -++->--+->,满足条件的a 不存在,当a<0时,则函数()f x 在(][),11,-∞-⋃+∞上有一个零点;又函数()f x 在R 上有3个零点,所以函数()f x 在()1,1-上有且只有两个零点,即方程()()21210a x a x -++-=在()1,1-上有两个根,由()()()[]2121,1,1g x a x a x x =-++-∈-可得函数()g x 的图象为开口向下的抛物线,函数()()()2121g x a x a x =-++-的对称轴为222a x a+=-,则()()()224180a a a a ∆=++-=+>,21122a a +-<<-, ()()10,10g g <-<,所以8a <-,a<0,()()()()1210,1210a a a a -++-<--+-<,所以8a <-,故实数a 的取值范围是()(),80,1-∞- .故选:B【点睛】关键点睛:含绝对值函数的相关问题的解决的关键在于去绝对值,将其转化为不含绝对值的函数,分段函数的性质的研究可以分段研究.第Ⅱ卷(非选择题 共105分)二、填空题:本大题共6小题,每小题5分,共30分,请将答案填写在答题卡上.10. 复数()21i 1iz -=+(i 为虚数单位),则z =______.【解析】【分析】先利用复数的运算化简复数,再利用模长的公式求解模长.【详解】()()()()()21i 2i 1i 2i i 1i 1i 1i 1i 1i 1i z ----====--=--+++-.所以z ==.11. 在6的二项展开式中,2x 的系数为___________.【答案】38-【解析】【详解】试题分析:因为6263166((1)2r r r r r r r r T C C x ---+==-,所以由32r -=得1r =,因此2x 的系数为1463(1)28C --=-考点:二项式定理【方法点睛】1.求特定项系数问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件,即n ,r 均为非负整数,且n≥r );第二步是根据所求的指数,再求所求解的项的系数.2.有理项是字母指数为整数的项.解此类问题必须合并通项公式中同一字母的指数,根据具体要求,令其为整数,再根据数的整除性来求解.12. 若2sin sin αβ+=3π2αβ+=,则sin α=________;cos 2β=________.【答案】 ①. ②. 35##0.6【解析】【分析】由2sin sin αβ+=3π2αβ+=,可得出2sin cos αα-=,再结合同角平方关系即可求出sin α=,从而算出sin β=3cos 25β=.【详解】 2sin sin αβ+=3π2αβ+=,3π2sin sin()2αα∴+-=2sin cos αα-=,cos 2sin αα∴=-,又22sin cos 1αα+= ,∴(22sin 2sin 1,αα+=解得sin α=∴2sin β+=,解得sin β=,23cos 212sin 5ββ∴=-=.综上,sin α=3cos 25β=.,35.13. 某专业资格考试包含甲、乙、丙3个科目,假设小张甲科目合格的概率为34,乙、丙科目合格的概率均为23,且3个科目是否合格相互独立.设小张3科中合格的科目数为X ,则(2)P X ==___________;()E X =___________.【答案】①. 49; ②. 2512##1212.【解析】【分析】根据独立事件概率的公式,结合数学期望的公式进行求解即可.【详解】3223223224(2)(1(1(1)4334334339P X ==-⨯⨯+⨯-⨯+⨯⨯-=;3221(0)(1)(1(1)43336P X ==-⨯-⨯-=,3223223227(1)(1(1)(1)(1)(1)(143343343336P X ==⨯-⨯-+-⨯⨯-+-⨯-⨯=,3221(3)4333P X ==⨯⨯=,所以174125()012336369312E X =⨯+⨯+⨯+⨯=,故答案为:49;251214. 已知0a >,0b >的最大值为________.【解析】【分析】利用基本不等式可得答案.【详解】因为0a >,0b >,所以=≤==,当且仅当2a a b=+即a b=等号成立..15. 设Rω∈,函数()2π2sin,0,6314,0,22x xf xx x xωω⎧⎛⎫+≥⎪⎪⎪⎝⎭=⎨⎪++<⎪⎩()g x xω=.若()f x在1π,32⎛⎫- ⎪⎝⎭上单调递增,且函数()f x与()g x的图象有三个交点,则ω的取值范围是________.【答案】23⎤⎥⎦.【解析】【分析】利用()f x在1π,32⎛⎫- ⎪⎝⎭上单调递增可得1243ω≤≤,函数()f x与()g x的图象有三个交点,可转化为方程23610x xω++=在(),0x∈-∞上有两个不同的实数根可得答案.【详解】当π0,2x⎡⎫∈⎪⎢⎣⎭时,πππ,626ωω⎡⎫++⎪⎢⎣⎭x,因为()f x在1π,32⎛⎫- ⎪⎝⎭上单调递增,所以()π0ππ2624133π12sin62ω⎧+≤⎪⎪⎪-≤-⎨⎪⎪≥⎪⎩,解得1243ω≤≤,又函数()f x与()g x图象有三个交点,所以在(),0x∈-∞上函数()f x与()g x的图象有两个交点,即方程231422x x xωω++=在(),0x∈-∞上有两个不同的实数根,即方程23610x xω++=在(),0x∈-∞上有两个不同的实数根,的所以22Δ3612003060102ωωω⎧=->⎪⎪-<⎨⎪⨯+⨯+>⎪⎩,解得ω>当0x ≥时,令()()π2sin 6ωω⎛⎫-=+- ⎪⎝⎭f xg x x x ,由0x =时,()()10f x g x -=>,当π5π66ω+=x 时,7π3ω=x ,此时,()()7π203-=-<f x g x ,结合图象,所以0x ≥时,函数()f x 与()g x 的图象只有一个交点,综上所述,23ω⎤∈⎥⎦.故答案为:233⎤⎥⎦.【点睛】关键点点睛:解题的关键点是转化为方程23610x x ω++=在(),0x ∈-∞上有两个不同的实数根.三、解答题:本大题共5小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答案卡上.16. 已知ABC 的内角A ,B ,C 的对边分别为a ,b ,c,满足22cos c b A =+.(1)求角B ;(2)若1cos 4A =,求sin(2)AB +的值;(3)若7c =,sin b A =b 的值.【答案】(1)6π.(2.(3【解析】【分析】(1)由正弦定理化边为角后,由诱导公式和两角和的正弦公式化简后可求得B ;(2)由二倍角公式求得sin 2,cos 2A A 后再由两角和的正弦公式可求值;(3)由正弦定理求得a ,再由余弦定理求得b .【详解】(1)∵22cos c b A =+,由正弦定理得,2sin 2sin cos C A B A=+∴2(sin cos cos sin )2sin cos A B+A B A B A =+,即2sin cos A B A =.∵sin 0A ≠,∴cos B =又0B π<<,∴6B π=(2)由已知得,sin A ==∴sin 22sin cos A A A ==,27cos 22cos 18A A =-=-∴sin(2)sin(2sin 2cos cos 2sin 666A B A A A πππ+++==.(3)由正弦定理sin sin a b A B =,得sin sin b A a B =.由(1)知,6B π=,∴a =由余弦定理得,2222cos 19b a c ac B =+-=.∴b =【点睛】本题考查正弦定理、余弦定理、考查两角和的正弦公式、二倍角公式、诱导公式,同角间的三角函数关系,考查公式较多,解题关键是正确选择应用公式的顺序.在三角形中出现边角关系时,常常用正弦定理进行边角转换.17. 已知底面ABCD 是正方形,PA ⊥平面ABCD ,//PA DQ ,33PA AD DQ ===,点E 、F 分别为线段PB 、CQ 中点.(1)求证://EF 平面PADQ ;(2)求平面PCQ 与平面CDQ 夹角的余弦值;(3)线段PC 上是否存在点M ,使得直线AM 与平面PCQ,若存在求出PM MC 的值,若不存在,说明理由.【答案】(1)证明见解析(2(3)存在;1PM MC =或15PM MC =【解析】【分析】(1)法一:分别取AB 、CD 的中点G 、H ,连接EG 、GH 、FH ,证明出平面//EGHF 平面ADQP ,利用面面平行的性质可证得结论成立;法二:以点A 为坐标原点,以AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法可证得结论成立;(2)利用空间向量法可求得平面PCQ 与平面CDQ 夹角的余弦值;(3)假设存在点M ,使得PM PC λ= ,其中[]0,1λ∈,求出向量AM 的坐标,利用空间向量法可得出关于λ的方程,解之即可.【小问1详解】的证明:法一:分别取AB 、CD 的中点G 、H ,连接EG 、GH 、FH ,由题意可知点E 、F 分别为线段PB 、CQ 的中点.所以//EG PA ,//FH QD ,因为//PA DQ ,所以//EG FH ,所以点E 、G 、H 、F 四点共面,因为G 、H 分别为AB 、CD 的中点,所以//GH AD ,因为AD ⊂平面ADQP ,GH ⊄平面ADQP ,所以//GH 平面ADQP ,又因为//FH QD ,QD ⊂平面ADQP ,FH ⊄平面ADQP ,所以//FH 平面ADQP ,又因为FH GH H = ,FH 、GH Ì平面EGHF ,所以平面//EGHF 平面ADQP ,因为EF ⊂平面EGHF ,所以//EF 平面ADQP ;法二:因为ABCD 为正方形,且PA ⊥平面ABCD ,所以AP 、AB 、AD 两两互相垂直,以点A 为坐标原点,以AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()0,0,3P 、()3,3,0C 、()0,3,1Q 、()3,0,0B 、33,0,22E ⎛⎫⎪⎝⎭、31,3,22F ⎛⎫ ⎪⎝⎭,所以()0,3,1EF =- ,易知平面PADQ 的一个法向量()1,0,0a = ,所以0a EF ⋅= ,所以E F a ⊥ ,又因为EF ⊄平面ADQP ,所以//EF 平面ADQP .【小问2详解】解:设平面PCQ 的法向量(),,m x y z = ,()3,3,3PC =- ,()3,0,1CQ =- ,则333030m PC x y z m CQ x z ⎧⋅=+-=⎪⎨⋅=-+=⎪⎩ ,取1x =,可得()1,2,3m = ,所以平面PCQ 的一个法向量为()1,2,3m = ,易知平面CQD 的一个法向量()0,1,0n = ,设平面PCQ 与平面CQD 夹角为θ,则cos cos ,m n m n m n θ⋅=====⋅ ,所以平面PCQ 与平面CQD【小问3详解】解:假设存在点M ,使得()3,3,3PM PC λλλλ==- ,其中[]0,1λ∈,则()()()0,0,33,3,33,3,33AM AP PM λλλλλλ=+=+-=- ,由(2)得平面PCQ 的一个法向量为()1,2,3m = ,由题意可得c os ,AM = ,整理可得212810λλ-+=.即()()21610λλ--=,因为01λ≤≤,解得16λ=或12,所以,15PM MC =或1PM MC=.18. 已知{}n a 为等差数列,6,2,n n na nb a n -⎧=⎨⎩为奇数为偶数,记n S ,n T 分别为数列{}n a ,{}n b 的前n 项和,432S =,316T =.(1)求{}n a 的通项公式;(2)证明:当5n >时,n n T S >.【答案】(1)23n a n =+;(2)证明见解析.【解析】【分析】(1)设等差数列{}n a 的公差为d ,用1,a d 表示n S 及n T ,即可求解作答.(2)方法1,利用(1)的结论求出n S ,n b ,再分奇偶结合分组求和法求出n T ,并与n S 作差比较作答;方法2,利用(1)的结论求出n S ,n b ,再分奇偶借助等差数列前n 项和公式求出n T ,并与n S 作差比较作答.【小问1详解】设等差数列{}n a 的公差为d ,而6,21,N 2,2n n n a n k b k a n k*-=-⎧=∈⎨=⎩,则112213316,222,626b a b a a d b a a d =-==+=-=+-,于是41314632441216S a d T a d =+=⎧⎨=+-=⎩,解得15,2a d ==,1(1)23n a a n d n =+-=+,所以数列{}n a 的通项公式是23n a n =+.【小问2详解】方法1:由(1)知,2(523)42n n n S n n ++==+,23,21,N 46,2n n n k b k n n k*-=-⎧=∈⎨+=⎩,当n 为偶数时,12(1)34661n n b b n n n -+=--++=+,213(61)372222n n n T n n ++=⋅=+,当5n >时,22371()(4)(1)0222n n T S n n n n n n -=+-+=->,因此n n T S >,当n 奇数时,22113735(1)(1)[4(1)6]52222n n n T T b n n n n n ++=-=+++-++=+-,当5n >时,22351(5)(4)(2)(5)0222n n T S n n n n n n -=+--+=+->,因此n n T S >,所以当5n >时,n n T S >.方法2:由(1)知,2(523)42n n n S n n ++==+,23,21,N 46,2n n n k b k n n k*-=-⎧=∈⎨+=⎩,当n 为偶数时,21312412(1)3144637()()222222n n n n n n n T b b b b b b n n --+--++=+++++++=⋅+⋅=+ ,当5n >时,22371()(4)(1)0222n n T S n n n n n n -=+-+=->,因此n n T S >,当n 为奇数时,若3n ≥,则为132411231144(1)61()()2222n n n n n n n T b b b b b b --+-++-+-=+++++++=⋅+⋅ 235522n n =+-,显然111T b ==-满足上式,因此当n 为奇数时,235522n T n n =+-,当5n >时,22351(5)(4)(2)(5)0222n n T S n n n n n n -=+--+=+->,因此n n T S >,所以当5n >时,n n T S >.19. 如图,已知椭圆E :22221(0)x y a b a b +=>>()F 且斜率为k 的直线交椭圆E 于,A B 两点,线段AB 的中点为M ,直线l :40x ky +=交椭圆E 于,C D 两点.(1)求椭圆E 的方程;(2)求证:点M 在直线l 上;(3)是否存在实数k ,使得3BDM ACM S S ∆∆?若存在,求出k 的值,若不存在,说明理由.【答案】(1)22141x y +=(2)详见解析(3)存在,且k =【解析】【分析】(1)根据离心率和焦点坐标列方程组,解方程组求得,a b 的值,进而求得椭圆E 的方程.(2)写出直线AB 的方程,联立直线的方程和椭圆的方程,求得中点M 的坐标,将坐标代入直线l 的方程,满足方程,由此证得点M 在直线l 上.(3)由(2)知,A B 到l 的距离相等,根据两个三角形面积的关系,得到M 是OC 的中点,设出C 点的坐标,联立直线l 的方程和椭圆的方程,求得C 点的坐标,并由此求得k 的值.【详解】解:(1)解:由c a c ⎧=⎪⎨⎪=⎩,解得2a =,1b =所以所求椭圆的标准方程为22141x y +=(2)设()11,A x y ,()22,B x y ,()00,M x y,(2244y k x x y ⎧=+⎪⎨+=⎪⎩,消x 得,()2222411240k x x k +-+-=,解得12012022x x x y y y ⎧+==⎪⎪⎨+⎪==⎪⎩将()00,M x y 代入到40x ky +=中,满足方程所以点M 在直线l 上.(3)由(2)知,A B 到l 的距离相等,若BDM ∆的面积是ACM ∆面积的3倍,得3DM CM =,有DO CO =,∴M 是OC 的中点,设()33,C x y ,则302y y =,联立224044x ky x y +=⎧⎨+=⎩,解得3y =,=解得218k =,所以k =.【点睛】本小题主要考查椭圆标准方程的求法,考查直线和椭圆的位置关系,考查根与系数关系,考查方程的思想,属于中档题.要证明一个点在某条直线上,那么先求得这个点的坐标,然后将点的坐标代入直线方程,如果方程成立,则这个点在直线上,否则不在这条直线上.20. 已知函数()()1211222x f x x e x x -=--++,()()24cos ln 1g x ax x a x x =-+++,其中a ∈R .(1)讨论函数()f x 的单调性,并求不等式()0f x >的解集;(2)用{}max ,m n 表示m ,n 的最大值,记()()(){}max ,F x f x g x =,讨论函数()F x 的零点个数.【答案】(1)增函数;()1,+∞;(2)答案见解析.【解析】【分析】(1)先对函数求导,得到()()()111x f x x e-'=--,根据导数的方法,即可判定其单调性,进而可求出不等式的解集.(2)1x >时,()0F x >恒成立,当11x -<<时,()0f x <恒成立,故()F x 的零点即为函数()g x 的零点,讨论()g x 在11x -<<的零点个数得到答案.【详解】(1)()()()()111111x x f x x e x x e --'=--+=--,当1x >时,10x ->,110x e -->,∴()0f x ¢>,当1x <时,10x -<,110x e --<,∴()0f x ¢>,当1x =时,()0f x '=,所以当x ∈R 时,()0f x '≥,即()f x 在R 上是增函数;又()10f =,所以()0f x >的解集为()1,+∞.(2))函数()F x 的定义域为(1,)-+∞由(1)得,函数()f x 在x ∈R 单调递增,()10f =当1x >时,()0f x >,又()max{(),()}F x f xg x =,所以1x >时,()0F x >恒成立,即1x >时,()0F x =无零点.当11x -<<时,()0f x <恒成立,所以()F x 零点即为函数()g x 的零点下面讨论函数()g x 在11x -<<的零点个数:1()214sin 1g x ax a x x '=--++,所以21()24cos (11)(1)g x a a x x x ''=---<<+①当0a >时,因为11x -<<,cos (cos1,1)x ∈又函数cos y x =在区间π0,2⎛⎫ ⎪⎝⎭递减,所以π1cos1cos 32>=即当11x -<<时,12cos 0x -<,21()2(12cos )0(1)g x a x x ''=--<+所以()g x '单调递减,由()00g '=得:当10x -<<时()0g x '>,()g x 递增的当01x <<时()0g x '<,()g x 递减当1x →-时ln(1)x +→-∞,()g x ∴→-∞,当0x =时(0)40g a =>又(1)14cos1ln 2g a a =-++,()10f =当1ln 2(1)014cos1g a ->⇒>+时,函数()F x 有1个零点;当1ln 2(1)014cos1g a -=⇒=+时,函数()F x 有2个零点;当1ln 2(1)0014cos1g a -<⇒<<+时,函数()F x 有3个零点;②当0a =时,()ln(1)g x x x =+-,由①得:当10x -<<时,()0g x '>,()g x 递增,当01x <<时,()0g x '<,()g x 递减,所以max ()(0)0g x g ==,(1)ln 210g =-<,所以当0a =时函数()F x 有2个零点③当a<0时,()2()4cos ln(1)g x a x x x x =+-++()24cos 0a x x +<,ln(1)0x x -++≤,即()0g x <成立,由()10f =,所以当a<0时函数()F x 有1个零点综上所述:当1ln 214cos1a ->+或a<0时,函数()F x 有1个零点;当1ln 214cos1a -=+或0a =时,函数()F x 有2个零点;当1ln 2014cos1a -<<+时,函数()F x 有3个零点.【点睛】思路点睛:导数的方法研究函数的零点时,通常需要对函数求导,根据导数的方法研究函数单调性,极值或最值等,有时需要借助数形结合的方法求解.。
宁夏银川一中2024届高三上学期第一次月考数学理科试题及参考答案

银川一中2024届高三年级第一次月考理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}1A x x =≤,{}20B x x a =-<,若A B ⊆,则实数a 的取值范围是A .()2,+∞B .[)2,+∞C .(),2-∞D .(],2-∞2.已知复数z 满足i zz =+-112,则复数z 的虚部是A.-1B.iC.1D.-i3.如图,可以表示函数()f x 的图象的是A .B .C .D .4.已知a ,b 为实数,则使得“0a b >>”成立的一个充分不必要条件为A .11a b>B .ln(1)ln(1)a b +>+C .33a b >D 11a b ->-5.函数()214log 2y x x =--的单调递增区间为A .1,2⎛⎫-∞ ⎪⎝⎭B .(),1-∞-C .1,2⎛⎫+∞ ⎪⎝⎭D .()2,+∞6.的大小关系为则,,设c b a c b a ,,,21(31log 2log 3.02131===A .b c a <<B .cb a <<C .ca b <<D .ac b <<7.已知函数ay x=,xy b=,log cy x=的图象如图所示,则A.e e ea c b<<B.e e eb a c<<C.e e ea b c<<D.e e eb c a<<8.若命题“[]()21,3,2130a ax a x a∃∈---+-<”为假命题,则实数x的取值范围为A.[]1,4-B.50,3⎡⎤⎢⎥⎣⎦C.[]51,0,43⎡⎤⎢⎥⎣-⎦D.[)51,0,43⎛⎤- ⎥⎝⎦9.已知函数则函数2,0,()()()1,0,x xf xg x f xxx⎧≥⎪==-⎨<⎪⎩,则函数()g x的图象大致是A.B.C.D.10.已知函数()()()314(1)1a x a xf x axx⎧-+<⎪=⎨≥⎪⎩,满足对任意的实数1x,2x且12x x≠,都有[]1212()()()0f x f x x x--<,则实数a的取值范围为A.1,17⎡⎫⎪⎢⎣⎭B.10,3⎡⎫⎪⎢⎣⎭C.11,63⎡⎫⎪⎢⎣⎭D.1,16⎡⎫⎪⎢⎣⎭11.已知定义在R上的函数()f x在(],2-∞上单调递减,且()2f x+为偶函数,则不等式()()12f x f x->的解集为A.()5,6,3⎛⎫-∞-+∞⎪⎝⎭B.()5,1,3⎛⎫-∞-+∞⎪⎝⎭C.5,13⎛⎫- ⎪⎝⎭D.51,3⎛⎫- ⎪⎝⎭12.已知函数()ln1af x xx=++.若对任意1x,(]20,2x∈,且12x x≠,都有()()21211f x f xx x->--,则实数a的取值范围是A.27,4⎛⎤-∞⎥⎝⎦B.(],2-∞C.27,2⎛⎫-∞⎪⎝⎭D.(],8∞-二、填空题(本大题共4小题,每小题5分.共20分)13.已知lg 2a b +=-,10b a =,则=a ______.14.已知()222,02,0x x x f x x x x ⎧-+≥=⎨+<⎩,满足()()f a f a <-,则a 的取值范围是.15.若函数()21x mf x x +=+在区间[]0,1上的最大值为3,则实数=m _______.16.已知函数()e e 21x x f x x -=--+,则不等式(23)()2f x f x -+>的解集为____________.三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答。
2024-2025学年渭南市蒲城县高三数学上学期10月第一次月考卷及答案解析

蒲城中学2024—2025学年上学期高三第一次月考数学注意事项:1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.3.本试卷命题范围:集合与逻辑、不等式、函数.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1. 已知集合{}13,5A =,,{}1,2,3B =,则A B = ( )A. {}3 B. {}1,2,5 C. {}1,2,3,5 D. {}1,2,3,4,5【答案】C【解析】【分析】根据并集的知识求得正确答案.【详解】依题意,A B = {}1,2,3,5.故选:C2. 已知命题2024:R,20230x p x x ∀∈+>,则p 的否定是( )A. 2024R,20230x x x ∀∈+≤ B. 2024R,20230x x x ∃∈+<C. 2024R,20230x x x ∃∈+≤ D. 2024R,20230x x x ∃∈+≠【答案】C【解析】【分析】根据全称命题的否定即可得到结果.【详解】先变量词,再否结论,而“202420230x x +>”的否定是“202420230x x +≤”,故p 的否定是:2024R,20230x x x ∃∈+≤.故选:C.3. 不等式304x x+≥-的解集为( )A. []3,4- B. [)3,4-C. ()(),33,∞∞--⋃+ D. (](),34,-∞-+∞ 【答案】B【解析】【分析】转化为一元二次不等式,求出解集.【详解】304x x +≥-等价于()()34040x x x ⎧+-≥⎨-≠⎩,解得[)3,4x ∈-.故选:B4. 函数211x y x -=+-的定义域是( )A. [)4,-+∞ B. ()4,-+∞C. [)()4,00,-+∞ D. [)()4,11,-+∞ 【答案】D【解析】【分析】根据给定条件,利用函数有意义列出不等式组求解即得.【详解】函数211x y x -=-有意义,则4010x x +≥⎧⎨-≠⎩,解得4x ≥-且1x ≠,所以所求定义域为[)()4,11,-+∞ .故选:D5. 函数()21ex x f x +=的大致图象为( )A. B.C. D.【答案】A【解析】【分析】利用导数研究函数的单调性,即可确定.【详解】()()()2222212e (1)e 21210e e e e x xx x x x x x x x x x x f x --+-+--+'===-=-≤恒成立,所以函数()21ex x f x +=在定义域R 上单调递减,且对任意R x ∈,都有210,e 0x x +>>,所以对任意R x ∈,都有()0f x >,所以结合选项可知A 满足,故选:A.6. 已知120232023202212024,log 2022,log 2023a b c ===,则,,a b c 的大小关系是( )A. a b c>> B. b a c >>C. c a b>> D. a c b>>【答案】A【解析】【分析】根据指数函数、对数函数的单调性确定范围即可比较大小.【详解】依题意102023202420241a =>=,2023202320230log 1log 2022log 20231<<<=,202220221log log 102023c =<=,所以a b c >>.故选:A7. 函数()f x =[]1,1-上单调递减,则a 的取值范围为( )A. 1a ≤- B. 1a <- C. 31a -≤≤- D. 31a -<<-【答案】C【解析】【分析】令()272t x ax x =+-,由题意可得()t x 需满足在区间[]1,1-上单调递减,且()min 0t x ≥,由此列出不等式,求得答案.【详解】令()272t x ax x =+-,则()f t =由题意可得()272t x ax x =+-需满足在区间[]1,1-上单调递减,且()min 0t x ≥,而()272t x ax x =+-图象开口向下,对称轴为t a =,故1a ≤-且()1620t a =+≥,即31a -≤≤-,故选:C8. 设0a >,0b >,则下列不等式中不恒成立的是( ).A. 12a a +≥ B. 222(1)a b a b +≥+-C. ≥D. 3322a b ab +≥【答案】D【解析】【详解】分析:根据基本不等式、作差法、分析法论证A,B,C 正确,举反例得D 错误.详解:332222()()a b ab a b a ab b +-=-+-,a b <<有3322a b ab <+,故D项错误,其余恒成立:1122,a a a a+≥=⇒+≥2222222(1)(1)(1)02(1),a b a b a b a b a b +-+-=-+-≥⇒+≥+-当a b ≥时0a b a b a b a b ---+≥---+=⇒-当a b <0>D .点睛:本题考查根据基本不等式、作差法、分析法论证等知识点,考查推理论证能力.二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 下列函数在其定义域上既是奇函数又是增函数的是( )A. 1y x = B. e e x xy -=-的C. 3y x = D. 2log y x=【答案】BC【解析】【分析】根据解析式直接判断奇偶性与单调性即可求解.【详解】选项A :1y x =为奇函数不是增函数,选项B :e e x x y -=-,为奇函数和增函数,选项C :3y x =为奇函数和增函数,选项D :2log y x =不是奇函数.故选:BC.10. 下列四个命题中正确的是( )A. 若,a b c d >>,则a d b c->- B. 若22a m a n >,则m n >C. 若110a b <<,则2b ab > D. 若a b >,则11a b a>-【答案】ABC【解析】【分析】根据不等式的性质判断ABC ,举反例排除D ,从而得解.【详解】A.由条件可知,a b >,d c ->-,所以a d b c ->-,故A 正确;B.因为22a m a n >,所以20a >,所以m n >,故B 正确;C.因为110a b<<,所以0b a <<,所以2b ab >,故C 正确;D.因为a b >,取1,0a b ==,则111a b a ==-,故D 错误.故选:ABC11. 下列说法正确的是( )A. “万事俱备,只欠东风”,则“东风”是“赤壁之战东吴打败曹操”的必要不充分条件B. 若p 是q 的必要不充分条件,p 是r 的充要条件,则q 是r 的充分不必要条件C. 方程20ax x a ++=有唯一解的充要条件是12a =±D. []x 表示不超过x 的最大整数,x 表示不小于x 的最小整数,则“[]ab =”是“a b ≥”的充要条件【答案】AB【解析】【分析】根据充分条件和必要条件的定义依次判断各选项即可.【详解】对于A ,“东风”是“赤壁之战东吴打败曹操”的必要条件,但不是充分条件,故A 正确;对于B ,若p 是q 的必要不充分条件,则q p ⇒,p q ¿;若p 是r 充要条件,则p r ⇒,r p ⇒;则有q r ⇒,r q ¿,即q 是r 的充分不必要条件,故B 正确;对于C ,当0a =时,方程20ax x a ++=可化为0x =,也满足唯一解的条件,故C 错误;对于D ,依题意,得[]a a ≥,b b ≥,所以“[]a b =”⇒“a b ≥”,即充分性成立;反之不成立,如3.1 1.5≥,[3.1]3=,1.52=,不能推出“[3.1] 1.5=”,即必要性不成立,故D 错误.故选:AB .三、填空题:本大题共3小题,每小题5分,共15分.12. 已知函数()()16log ,2,21,2x x f x f x x ≤⎧=⎨->⎩则(4)f =______.【答案】1【解析】【分析】根据自变量确定代入哪段,结合对数性质计算即可.【详解】因为()()()42342f f f ==,()1612log 24f ==,所以()()4421f f ==.故答案为:113. 若“x ∃∈R ,使得2210x mx -+<”是假命题,则实数m 的取值范围是______.【答案】⎡⎣-【解析】【分析】根据特称命题的定义和一元二次不等式的恒成立问题求解.【详解】因为“x ∃∈R ,使得2210x mx -+<”是假命题,所以“x ∀∈R ,使得2210x mx -+≥”是真命题,所以280m ∆=-≤,解得m ⎡∈-⎣,故答案为: ⎡⎣-.14. 已知函数e ()1x mx f x x =+-是偶函数,则m =__________.【答案】2【解析】【分析】求出f(x)定义域,根据f(x)是偶函数,可取定义域内任意x ,根据f(-x)=f(x)即可求得m 的值.【详解】由e 10x -≠得e ()1x mx f x x =+-的定义域为{}|0x x ≠,则∵e ()1x mx f x x =+-是偶函数,故f(-1)=f(1),即111e 1e 1m m ---+=+--,解得m=2.此时()1(e )e 1e 21x x x x x f x x +=+=--,而()()e (1e 1)x x xf x f x ---+-==-,故()f x 确为偶函数,故m=2.故答案为:2.四、解答题:本大题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15. 设集合{}52A x x =-<.{}121B x x m =<<+.(1)若A B =∅ ,求实数m 的取值范围;(2)若“x A ∈”是“x B ∈”的充分不必要条件,求实数m 的取值范围.【答案】(1)1m ≤;(2)[)3,+∞.【解析】【分析】(1)分B =∅和B ≠∅两种情况讨论即可;(2)由题得A 是B 的真子集,根据集合间的基本关系求解即可.【小问1详解】{}{}{}5225237A x x x x x x =-<=-<-<=<<,当B =∅时,121m ≥+,解得0m ≤当B ≠∅时,由A B =∅ 得:0213m m >⎧⎨+≤⎩,解得01m <≤;综上,1m ≤;【小问2详解】由题得,A 是B 的真子集,所以31721m ≥⎧⎨≤+⎩,且等号不同时成立,解得3m ≥,所以实数m 的取值范围为[)3,+∞.16. 已知函数()21x b f x ax +=+,点()1,5A ,()2,4B 是()f x 图象上的两点.(1)求a ,b 的值;(2)求函数()f x 在[]1,3上的最大值和最小值.【答案】(1)18a b =⎧⎨=⎩(2)max ()5f x =,min 7()2f x =【解析】【分析】(1)把图象上的两点代入函数解析式,由方程组求a ,b 的值;(2)定义法求函数单调性,由单调性求最值.【小问1详解】因为点()1,5A ,()2,4B 是()f x 图象上的两点,所以2514421b a b a +⎧=⎪⎪+⎨+⎪=⎪+⎩,解得18a b =⎧⎨=⎩.【小问2详解】设1213x x ≤<≤,则()()()()()2112121212628281111x x x x f x f x x x x x -++-=-=++++,因为1213x x ≤<≤,所以210x x ->,()()12110x x ++>,则()()120f x f x ->,即()()12f x f x >,所以函数()281x f x x +=+在[]1,3上单调递减.故()max ()15f x f ==,()min 7()32f x f ==.17. 已知函数()2109f x x x =-+.(1)求不等式()0f x >的解集;(2)若0x >,不等式()f x ax ≥恒成立,求a 的取值范围.【答案】(1){1x x <或}9x >;(2)(],4-∞-【解析】【分析】(1)直接解不等式21090x x -+>即可;(2)转化问题转化为()9100x a x x +-≥>恒成立,然后利用基本不等式求出910x x +-的最小值即可.【小问1详解】不等式()0f x >,即为21090x x -+>,则有()()190x x -->,解得1x <或9x >,所以不等式()0f x >的解集为{1x x <或}9x >.【小问2详解】不等式()()0f x ax x ≥>,即为2109x x ax -+≥,所以()9100x a x x +-≥>,只需910x x+-的最小值大于或等于a 即可,因为910104x x +-≥-=-,当且仅当9x x =即3x =时取等号.所以910x x+-的最小值为4-,所以4a ≤-,故a 的取值范围是(],4-∞-18. 若定义在R 上的奇函数()f x 满足()()2=f x f x -,当[]0,1x ∈时,()22f x x x =-.(1)求()2024f 值;(2)当[]3,4x ∈时,求函数()f x 的解析式.【答案】(1)0 (2)()268x x f x =-+-的【解析】【分析】(1)根据函数的奇偶性、周期性等知识求得正确答案.(2)根据函数解析式的求法求得正确答案.小问1详解】定义在R 上的奇函数()f x 满足()()2=f x f x -,()()f x f x ∴-=-,()()()2+==f x f x f x --,()()4f x f x ∴+=,即函数()f x 是以4为周期的周期函数()()()2024450600f f f ∴=⨯==.【小问2详解】当[]0,1x ∈时,()22f x x x =-,∴当[]1,0x ∈-时,[]0,1x -∈,()()()22()22f x f x x x x x ⎡⎤=--=----=--⎣⎦,又当[]3,4x ∈时,[]41,0x -∈-,()()()224(4)2468f x f x x x x x ∴=-=----=-+-.19. 已知()f x 为偶函数、()g x 为奇函数,且满足1()()2x f x g x --=.(1)求()f x ,()g x ;(2)若方程2()[()]29mf x g x m =++有解,求实数m 的取值范围.【答案】(1)()()22,22x x x xf xg x --=+=- (2)10m ≥【解析】【分析】(1)根据函数的奇偶性列方程组来求得()(),f x g x .(2)利用分离常数法、构造函数法,结合基本不等式求得正确答案【小问1详解】依题意,()f x 为偶函数、()g x 为奇函数,且满足1()()2x f x g x --=,所以11()()2()()2x x f x g x f x g x -+⎧-=⎨---=⎩,则11()()2()()2xx f x g x f x g x -+⎧-=⎨+=⎩,解得()()22,22x x x x f x g x --=+=-.【.【小问2详解】若方程2()[()]29mf x g x m =++有解,即()()2222229x x x xm m --+-=++有解,即()()222222722225x x x x x x m ---⎡⎤-=++=++⎣⎦+,对于方程()()2222522x x x x m --⎡⎤-=++⎣⎦+①,当0x =时,方程左边为0,右边为9,所以0x =不是①的解.当0x ≠时,令22x x t -=+,由于222x x -+>=,所以2t >,20t ->,则方程①可化()()()2222429525,22t t t t m t m t t -+-++-=+==--9244102t t =-++≥+=-,当且仅当92,52t t t -==-时等号成立,所以10m ≥.【点睛】方法点睛:对于奇函数,有()()f x f x -=-,对于偶函数,有()()f x f x -=.当题目所给条件中包括奇函数或偶函数时,首先应想到运用上述两个式子来对问题进行求解.求方程有解的问题,可以考虑利用分离参数法来进行求解.为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三第一次月考试卷数学(理科) 及答案一、选择题(每小题5分,共60分) 1、设集合},33|{Z x x x I ∈<<-=,}2,1,2{},2,1{--==B A ,则=)(B C A I I ( )A .}1{B .}2,1{C . }2,1,0{D . }2,1,0,1{-2、函数y=)1(log 221-x 的定义域是()A.[-2,-1)∪(1,2]B.(-3,-1)∪(1,2)C.[-2,-1)∪(1,2]D.(-2,-1)∪(1,2) 3、已知函数f (x )=lg xx +-11,若f (a )=b ,则f (-a )等于( )B.-bC.b1D.-b14、函数()27log f x x x=-的零点包含于区间( ) A .()1,2B .(2,3)C .(3,4)D .()4,+∞5、函数4)3(42-+=x y 的图像可由函数4)3(42+-=x y 的图像经过下列平移得到( ) A .向右平移6,再向下平移8 B .向左平移6,再向下平移8 C .向右平移6,再向上平移8 D .向左平移6,再向上平移8 6、曲线xy e =在点2(2)e ,处的切线与坐标轴所围三角形的面积为( )A.294eB.22eC.2eD.22e7、下列命题正确的个数是( )(1)命题“若0m >则方程20x x m +-=有实根”的逆否命题为:“若方程20x x m +-=无实根则0m ≤” (2)对于命题:p “R x ∈∃使得210x x ++<”,则:p ⌝“,R ∀∈均有210x x ++≥”(3)“1x =”是 “2320x x -+=”的充分不必要条件 (4)若p q ∧为假命题,则,p q 均为假命题A 、4B 、3C 、2D 、18、设111()()1222b a <<<,那么 ( ) A.abab a a << B. ba a ab a <<C. aa b b a a <<D. aa b a b a <<9、已知函数()()32120f x x ax x a a=++>,则()2f 的最小值为( )A .32 B .16 C .288a a++D .1128a a++10、设2()lg()1f x a x=+-是奇函数,则使()f x <0的x 的取值范围是( )A 、(-1,0)B 、(0,1)C 、(-∞,0)D 、(,0)(1,)-∞+∞U11、函数/()f x 是函数y=()f x 的导函数,且函数y=()f x 在点P00(,())x f x 处的切线 方程为/000:()()()(),()()()l y g x f x x x f x F x f x g x ==-+=-如果y=()f x 在区间[],a b 上的图像如图所示,且0a x b <<那么( ) A ./00()0,F x x x ==是F(x) 的极大值点 B ./00()0,F x x x ==是F(x) 的极小值点 C ./00()0,F x x x ≠=不是F(x)的极值点 D ./00()0,F x x x ≠=是F(x)极值点 12、已知1212,()x x x x <是方程24410,()x kx k R --=∈的两个不等实根,函数22()1x kf x x -=+的定义域为[]12,x x ,max min ()()()g k f x f x =-,若对任意k R ∈,恒有2()1g k a k ≤+成立,则实数a 的取值范围是( )A. 8,5⎡⎫+∞⎪⎢⎣⎭B.8,5⎛⎤-∞ ⎥⎝⎦C.3,5⎡⎫+∞⎪⎢⎣⎭.D.38,55⎡⎤⎢⎥⎣⎦二、填空题(每小题5分,共20分)13、设函数()211log (2)23222x x x f x x ---<⎧⎪=⎨+≥⎪⎩,则((3))f f =14、一元二次不等式20x ax b ++>的解集为()(),31,x ∈-∞-+∞U ,则一元一次不等式0ax b +<的解集为15、已知偶函数()f x 在[]0,2内单调递减,若()()0.511,(log ),lg 0.54a fb fc f =-==,则,,a b c 从小到大的顺序为 。
16、已知函数f (x )=ln x1-x,若f (a )+f (b )=0,且0<a <b <1,则ab 的取值范围是______三、解答题(共6个小题,共70分)17、已知a ,b 为常数,且a ≠0,f (x )=ax 2+bx ,f (2)=0,方程f (x )=x 有两个相等实根.(12分)(1)求函数f (x )的解析式;(2)当x ∈(-1,2]时,求函数f (x )的值域; 18、1{24}32x A x-=≤≤,{}012322<--+-=m m mx x x B . (12分)(1)当时,列举法表示集合A 且求其非空真子集的个数; (2)若B A ⊇,求实数m 的取值范围.P N MDCBA 19、(12分)设p :函数f(x)=a x x --33在x ?[21-,3]内有零点;q :,0>a 函数g(x)=x a x ln 2-在区间)2,0(a 内是减函数.若p 和q 有且只有一个为真命题,求实数a 的取值范围.20、如图所示,将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ,要求B 点在AM 上,D 点在AN 上,且对角线MN 过C 点,已知AB=3米,AD=2米. (12分)(1)要使矩形AMPN 的面积大于32平方米,则AN 的长度应在什么范围?(2)当AN 的长度是多少时,矩形AMPN 的面积最小?并求最小值21、已知函数x axx x f -++=2)1(n 1)( (∈a R ).(12分)(Ⅰ)当14a =时,求函数()y f x =的单调区间和极值; (Ⅱ)若对任意实数(1,2)b ∈,当(1,]x b ∈-时,函数()f x 的最大值为()f b ,求实数a 的取值范围.请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。
做答时用2B 铅笔在答题卡上把所选题目的题号涂黑。
(22)(本小题满分10分)选修4-1:几何证明讲已知∆ABC 中,AB=AC, D 是 ∆ABC 外接圆劣弧»AC 上的点(不与点A,C 重合),延长BD 至E 。
(1) 求证:AD 的延长线平分∠CDE ;(2) 若∠BAC=30,∆ABC 中BC 边上的高为2+3,求∆ABC 外接圆的面积。
(23)(本小题满分10分)选修4-4 :坐标系与参数方程在直角坐标系xOy 中,以O 为极点,x 正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρcos (3πθ-)=1,M,N 分别为C 与x 轴,y轴的交点。
(1)写出C 的直角坐标方程,并求M,N 的极坐标; (2)设MN 的中点为P ,求直线OP 的极坐标方程。
(24)(本小题满分10分)选修4-5:不等式选讲已知,m n +∈R ,()f x =||+|2|x m x n +-.(10分)(1)求()f x 的最小值;(2)若()f x 的最小值为2,求422n m +的最小值.参考答案1-5 AABCB ,6-10 DBCBA ,11-12 BA 13、3;14、3,2⎛⎫-∞ ⎪⎝⎭ ,15、c a b << ,16、)41,0( 17、解析: (1)f (x )=-12x 2+x . (6分)(2)由(1)知函数的值域是]21,23(-.(12分) 18、(1){}5,4,3,2,1,0,=∴∈A N x Θ,即A 中含有6个元素,∴A 的非空真子集数为62226=-个.(2).综上所述,m 的取值范围是:m=-2或.21≤≤-m19、函数f(x)=a x x --33在x ?[0,3]内有零点等价于a 在函数y =x x 33- (x ?[3,21-])的值域内.∴p :]811,2[-∈a . 函数g(x)=x a x ln 2-在区间(0,)2a内是减函数.∴q :]2,0(∈a ) 当p 真q 假时,a ?[-2,0],当p 假q 真时,]2,811(∈a .综上,a 的取值范围为[-2,0]⋃]2,811(。
20、 21、解:(Ⅰ)当14a =时,21()ln(1)4f x x x x =++-,则11(1)()1(1)122(1)x x f x x x x x -'=+-=>-++,令()0f x '>,得10x -<<或1x >;令()0f x '<,得01x <<,∴函数()f x 的单调递增区间为(1,0)-和(1,)+∞,单调递减区间为(0,1).极大值0,极小值432ln -。
(Ⅱ)由题意[2(12)]()(1)(1)x ax a f x x x --'=>-+, (1)当0a ≤时,函数()f x 在(1,0)-上单调递增,在(0,)+∞上单调递减,此时,不存在实数(1,2)b ∈,使得当(1,]x b ∈-时,函数()f x 的最大值为()f b 。
(2)当0a >时,令()0f x '=,有10x =,2112x a=-, ①当12a =时,函数()f x 在(1,)-+∞上单调递增,显然符合题意,②当1102a ->即102a <<时,函数()f x 在(1,0)-和1(1,)2a-+∞上单调递增, 在1(0,1)2a-上单调递减,()f x 在0x =处取得极大值,且(0)0f =, 要使对任意实数(1,2)b ∈,当(1,]x b ∈-时,函数()f x 的最大值为()f b ,只需(1)0f ≥,解得1ln 2a ≥-,又102a <<,所以此时实数a 的取值范围是11ln 22a -≤<.③当1102a-<即12a >时,函数()f x 在1(1,1)2a --和(0,)+∞上单调递增,在1(1,0)2a-上单调递减,要存在实数(1,2)b ∈,使得当(1,]x b ∈-时,函数()f x 的最大值为()f b ,需1(1)(1)2f f a -≤,代入化简得1ln 2ln 2104a a++-≥,①令11()ln 2ln 21()42g a a a a =++->,因为11()(1)04g a a a '=->恒成立,故恒有11()()ln 2022g a g >=->,所以12a >时,①式恒成立, 实数a 的取值范围是[1ln 2,)-+∞. (12分)(22)解:(Ⅰ)如图,设F 为AD 延长线上一点 ∵A ,B ,C ,D 四点共圆, ∴∠CDF =∠ABC又AB=AC ∴∠ABC=∠ACB, 且∠ADB=∠ACB, ∴∠ADB=∠CDF, 对顶角∠EDF=∠ADB, 故∠EDF=∠CDF, 即AD 的延长线平分∠CDE.(Ⅱ)设O 为外接圆圆心,连接AO 交BC 于H,则AH ⊥BC.连接OC,A 由题意∠OAC=∠OCA=150, ∠ACB=750,∴∠OCH=600. 设圆半径为r,则r+23r=2+3,a 得r=2,外接圆的面积为4π。
