全等三角形专题三角形的旋转翻折与线段的截长补短

合集下载

人教版数学八年级上册第12章全等三角形专题课截长补短法教学设计

-组织小组合作学习，让学生在讨论和互助中共同探究截长补短法的应用。
-通过小组间的交流，分享解题思路和经验，提高学生之间的相互学习和借鉴。
4.实践操作，加深理解：
-安排尺规作图实践，让学生动手操作，加深对截长补短法的理解和记忆。
-教师巡回指导，及时纠正学生在作图和证明过程中的错误，确保学习效果。
5.反思评价，促进成长：
-在复杂问题中识别应用截长补短法的时机，并能够结合全等三角形的判定定理进行有效证明。
-对于一些非标准图形，能够创造性地运用截长补短法，培养学生的创新思维和解决问题的能力。
（二）教学设想
1.创设情境，引入新课：
-通过展示一些生活中的实际例子，如建筑设计中的几何图形，引出全等三角形的应用。
-设计问题，让学生在实际情境中发现全等三角形，并感受到截长补短法在解决问题时的便捷性。
2.教学实施：
-分组讨论：将学生分成小组，每组分配一个或多个问题，要求运用截长补短法解决。
-教师巡回指导：观察学生的讨论过程，适时给予提示和指导，引导学生深入思考。
-小组分享：鼓励各小组展示解题过程和结果，其他小组给予评价和反馈。
（四）课堂练习
1.教学设计：设计具有梯度性的练习题，让学生独立完成，巩固所学知识。
-鼓励学生在课后进行反思，总结截长补短法在解决问题时的优势和局限。
-通过自我评价和同伴评价，帮助学生认识自身的进步和需要提升的地方，促进他们的个性化发展。
四、教学内容与过程
（一）导入新课
1.教学设计：通过生活实例和问题情境，自然导入新课——截长补短法在全等三角形中的应用。
-展示图片：呈现一些包含全等三角形的生活场景，如建筑物的立面图、拼图游戏等。
人教版数学八年级上册第12章全等三角形专题课截长补短法教学设计

华师大版全等三角形辅助线做法之截长补短

1 全等三角形问题中常见的辅助线的作法常见辅助线的作法有以下几种：1) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”．2) 遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”．3) 遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．4) 过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”5) 截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答．三角形辅助线做法图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

一、倍长中线（线段）造全等1、（“希望杯”试题）已知，如图△ABC 中，AB=5，AC=3，则中线AD 的取值范围是_________.2、如图，△ABC 中，BD=DC=AC ，E 是DC 的中点，求证：AD 平分∠BAE.3、（09崇文二模）以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆，90,BAD CAE ∠=∠=︒连接DE ，M 、N 分别是BC 、DE 的中点．探究：AM 与DE 的位置关系及数量关系．（1）如图① 当ABC ∆为直角三角形时，AM 与DE 的位置关系是，线段AM 与DE 的数量关系是；（2）将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ(0<θ<90)后，如图②所示，（1）问中得到的两个结论是否发生改变？并说明理由．4、已知：AB=4，AC=2，D是BC中点，AD是整数，求AD。

三角形全等(旋转与截长补短专题)

向量与矩阵
向量与矩阵是高等数学中的重要概念，它们在解决几何问题，特别是涉及旋转、平移等变换的问题时具有广泛的应用。
THANKS FOR WATCHING
感谢您的观看
全等三角形的性质
对应边相等
对应角相等面积相等
周长相等
判定三角形全等条件
01
02
03
04
SSS（边边边）
三边分别相等的两个三角形全等。
SAS（边角边）
两边和它们之间的夹角分别相等的两个三角形全等。
ASA（角边角）
两角和它们之间的夹边分别相等的两个三角形全等。
AAS（角角边）
两角和一角的对边分别相等的两个三角形全等。
04 复杂图形中三角形全等问题解决方法
分析复杂图形中隐藏信息
观察图形特点
挖掘隐藏条件
注意图形的对称性、角的度数、边的长度等，这些可能是解决问题的关键。
根据已知信息和图形特点，挖掘出可能对解决问题有帮助的隐藏条件。
寻找潜在的全等三角形
通过观察和分析，尝试找出可能的全等三角形，以便利用全等三角形的性质解决问题。
应注意准确理解和运用各种判定定理。
02
旋转操作中的误区
在运用旋转证明三角形全等时，学生可能忽略旋转前后的图形关系，导
致证明失败。应注意保持旋转前后的图形对应关系。
03
截长补短法的使用不当
学生可能在不适当的场合使用截长补短法，或者在使用时未能正确构造
出全等三角形。应注意分析问题的具体条件，合理运用截长补短法。
截取法
通过截取线段，使得两个三角形在对应边上相等。例如，在证明两三角形全等时，可以截取其中一个三角形的一条边，使得这条边与另一个三角形的一条边相等。

初中数学全全等三角形截长补短知识点-+典型题及答案

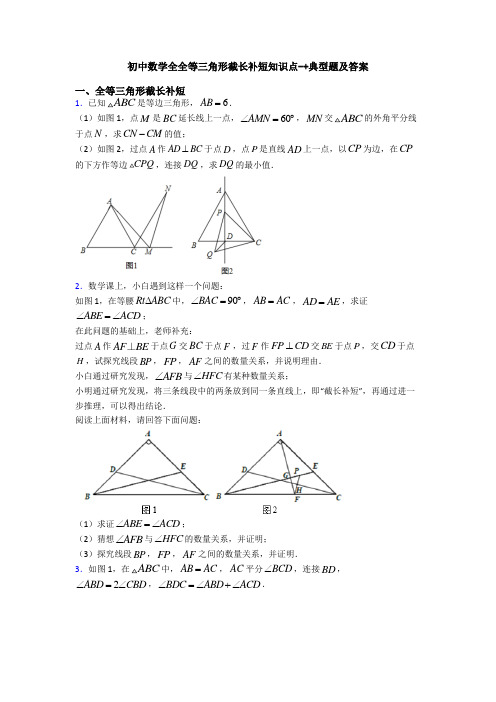
初中数学全全等三角形截长补短知识点-+典型题及答案一、全等三角形截长补短1．已知ABC 是等边三角形，6AB =．（1）如图1，点M 是BC 延长线上一点，60AMN ∠=︒，MN 交ABC 的外角平分线于点N ，求CN CM -的值；（2）如图2，过点A 作AD BC ⊥于点D ，点P 是直线AD 上一点，以CP 为边，在CP 的下方作等边CPQ ，连接DQ ，求DQ 的最小值．2．数学课上，小白遇到这样一个问题：如图1，在等腰Rt ABC ∆中，90BAC ∠=︒，AB AC =，AD AE =，求证ABE ACD ∠=∠；在此问题的基础上，老师补充：过点A 作AF BE ⊥于点G 交BC 于点F ，过F 作FP CD ⊥交BE 于点P ，交CD 于点H ，试探究线段BP ，FP ，AF 之间的数量关系，并说明理由．小白通过研究发现，AFB ∠与HFC ∠有某种数量关系；小明通过研究发现，将三条线段中的两条放到同一条直线上，即“截长补短”，再通过进一步推理，可以得出结论．阅读上面材料，请回答下面问题：（1）求证ABE ACD ∠=∠；（2）猜想AFB ∠与HFC ∠的数量关系，并证明；（3）探究线段BP ，FP ，AF 之间的数量关系，并证明．3．如图1，在ABC 中，AB AC =，AC 平分BCD ∠，连接BD ，2ABD CBD ∠=∠，BDC ABD ACD ∠=∠+∠．（1）求A ∠的度数：（2）如图2，连接AD ，AE AD ⊥交BC 于E ，连接DE ，求证：DEC BAE ∠=∠；（3）如图3，在（2）的条件下，点G 为CE 的中点，连接AG 交BD 于点F ，若32ABC S =△，求线段AF 的长．4．阅读题：如图1，OM 平分AOB ∠，以O 为圆心任意长为半径画弧，交射线OA ，OB 于C ，D 两点，在射线OM 上任取一点E （点O 除外），连接CE ，DE ，可证OCE ODE △△≌，请你参考这个作全等的方法，解答下列问题：（1）如图2，在ABC 中，2A B ∠=∠，CD 平分ACB ∠交AB 于点D ，试判断BC 与AC 、AD 之间的数量关系；（2）如图3，在四边形ABCD 中，AC 平分BAD ∠，10BC CD ==，20AB =，8AD =，求ABC 的面积．5．在△ABC 中，AB =AC ，点D 与点E 分别在AB 、AC 边上，DE //BC ，且DE =DB ，点F 与点G 分别在BC 、AC 边上，∠FDG 12=∠BDE ．（1）如图1，若∠BDE =120°，DF ⊥BC ，点G 与点C 重合，BF =1，直接写出BC = ；（2）如图2，当G 在线段EC 上时，探究线段BF 、EG 、FG 的数量关系，并给予证明；（3）如图3，当G 在线段AE 上时，直接写出线段BF 、EG 、FG 的数量关系：_____________．6．已知等边三角形ABC ，D 为△ABC 外一点，BDC 120∠=︒，BD=DC ，MDN 60∠=︒，射线DM 与直线AB 相交于点M ，射线DN 与直线AC 相交于点N ．（1）当点M 、N 在边AB 、AC 上，且DM=DN 时，直接写出BM 、NC 、MN 之间的数量关系；（2）当点M 、N 在边AB 、AC 上，且DM ≠DN 时，猜想①中的结论还成立吗？若成立，请证明；（3）当点M 、N 在边AB 、CA 的延长线上时，请画出图形，并求出BM 、NC 、MN 之间的数量关系．7．把两个全等的直角三角板的斜边重合，组成一个四边形ACBD ，以D 为顶点作MDN ∠，交边AC ，BC 于点M ，N ．（1）如图（1），若30ACD ∠=︒，60MDN ∠=︒，当MDN ∠绕点D 旋转时，AM ，MN ，BN 三条线段之间有何种数量关系？证明你的结论；（2）如图（2），当90ACD MDN ∠+∠=︒时，AM ，MN ，BN 三条线段之间有何数量关系？证明你的结论；（3）如图（3），在（2）的条件下，若将M ，N 分别改在CA ，BC 的延长线上，完成图（3），其余条件不变，则AM ，MN ，BN 之间有何数量关系（直接写出结论，不必证明）．8．在菱形ABCD 中，射线BM 从对角线BD 所在的位置开始绕着点B 逆时针旋转，旋转角为()0180αα︒<<︒，点E 在射线BM 上，DEB DAB ∠=∠．（1）当60DAB ∠=︒时，BM 旋转到图①的位置，线段BE ，DE ，AE 之间的数量关系是______；（2）在（1）的基础上，当BM 旋转到图②的位置时，探究线段BE ，DE ，AE 之间的数量关系，并证明；（3）将图②中的60DAB ∠=︒改为90DAB ∠=︒，如图③，其他条件不变，请直接写出线段BE ，DE ，AE 之间的数量关系．9．如图，在四边形ABCD 中，AB =AD ，∠B =∠D =90°，E 、F 分别是边BC 、CD 上的点，且∠EAF =12∠BAD ．求证：EF =BE +FD ．10．如图所示，平行四边形ABCD 和平行四边形CDEF 有公共边CD ，边AB 和EF 在同一条直线上，AC ⊥CD 且AC=AF ，过点A 作AH ⊥BC 交CF 于点G ，交BC 于点H ，连接EG ．（1）若AE=2，CD=5，则△BCF 的面积为；△BCF 的周长为；（2）求证：BC=AG+EG ．【参考答案】***试卷处理标记，请不要删除一、全等三角形截长补短1．（1）6；（2）32【分析】（1）在CN 上截取点H ，使CH=CM ，先证出△CMH 为等边三角形，然后利用ASA 证出△AMC ≌△NMH ，从而得出AC=NH ，从而求出结论；（2）连接BQ ，利用SAS 证出△QCB ≌△PCA ，从而得出∠CBQ=∠CAP ，然后根据三线合一和等量代换即可求出∠CBQ=30°、∠ABQ =90°，从而判断出点Q 的运动轨迹，然后根据垂线段最短即可得出当DQ ⊥BQ 时，DQ 最短，然后利用30°所对的直角边是斜边的一半即可得出结论．【详解】解：（1）在CN 上截取点H ，使CH=CM ，连接MH∵△ABC 为等边三角形∴∠ACB=60°，AC=AB=6∴∠ACM=180°－∠ACB=120°∵CN 平分∠ACM∴∠MCN=12∠ACM=60° ∴△CMH 为等边三角形 ∴CM=HM ，∠CMH=∠CHM=60°∴∠NHM=180°－∠CHM=120°，∠AMC ＋∠AMH=60°∴∠ACM=∠NHM∵60AMN ∠=︒∴∠NMH ＋∠AMH=60°∴∠AMC=∠NMH在△AMC 和△NMH 中AMC NMH CM HMACM NHM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AMC ≌△NMH∴AC=NH∴CN CM -=CN －CH=NH=AC=6（2）连接BQ∵△ABC 和△CPQ 都是等边三角形∴BC=AC ，QC=PC ，∠PCQ =∠ACB=∠ABC=∠BAC =60°∴∠PCQ －∠PCB=∠ACB －∠PCB∴∠QCB=∠PCA在△QCB 和△PCA 中BC AC QCB PCA QC PC =⎧⎪∠=∠⎨⎪=⎩∴△QCB ≌△PCA∴∠CBQ=∠CAP∵AD BC ⊥∴∠CAP=12∠BAC=30°，BD=12BC=3 ∴∠CBQ=30°∴∠ABQ=∠ABC ＋∠CBQ=90°∴点Q 在过点B 作AB 的垂线上运动根据垂线段最短可得：当DQ ⊥BQ 时，DQ 最短此时在Rt △BDQ 中，∠QBD=30°∴DQ=12BD=32即DQ 的最小值为32．【点睛】此题考查的是全等三角形的判定及性质、等边三角形的判定及性质、直角三角形的性质和垂线段最短的应用，掌握构造全等三角形的方法、全等三角形的判定及性质、等边三角形的判定及性质、30°所对的直角边是斜边的一半和垂线段最短是解决此题的关键． 2．（1）见解析；（2）HFC BFA ∠=∠，证明见解析；（3）BP AF PF =+，证明见解析【分析】（1）利用SAS 证明ABE ACD ≅可得结论；（2）设ABE ACD x ∠=∠=，推出=45BFA x ∠︒+，=45HFC x ∠︒+，即可证明HFC BFA ∠=∠；（3）过点C 作CM AC ⊥交AF 延长线于点M ，延长FP 交AC 于点N ，证明△ABE ≌△CAM ，得出BE AM =和M BEA ∠=∠，从而证明△NFC ≌△MFC ，得到FM FN =和M FNC ∠=∠，可得PN=PE ，从而得出BP=AF+PF.【详解】解：（1）∵在△ABE 和△ACD 中，==AB AC A A AE AD ⎧⎪∠=∠⎨⎪⎩，ABE ACD ∴∆≅∆（SAS ），ABE ACD ∴∠=∠；（2）设ABE ACD x ∠=∠=，AF BE ⊥，90BAF x ∴∠=︒-，()=9045=45BFA x x ∴∠︒-︒-︒+，ACD x ∠=，45HCF x ∴∠=︒-，FP CD ⊥，()9045=45HFC x x ∴∠=︒-︒-︒+，HFC BFA ∴∠=∠；（3）过点C 作CM AC ⊥交AF 延长线于点M ，延长FP 交AC 于点N ，90BAF FAC ∠+∠=︒，90BAF ABG ∠+∠=︒，FAC ABG ∴∠=∠，在△ABE 和△CAM 中，===BAE ACM AB AC ABE CAM ∠∠⎧⎪⎨⎪∠∠⎩， ABE CAM ∴∆≅∆（ASA ），BE AM ∴=，M BEA ∠=∠，BFA MFC NFC ∠=∠=∠，FC FC =，45ACB BCM ∠=∠=︒，NFC MFC ∴∆≅∆（ASA ），FM FN ∴=，M FNC ∠=∠，FNC BEA ∴∠=∠，PN PE ∴=，∴BP BE PE AM PE AF FM PE =-=-=+-AF FN PN AF PF =+-=+.【点睛】本题考查了全等三角形的判定和性质、等腰直角三角形的性质以及等角对等边等知识点，解题的关键是根据截长补短法添加适当的辅助线，构造全等三角形证明结论，有一定难度. 3．（1）90A ∠=︒；（2）见解析；（3）4【分析】（1）设.DBC x ∠=推出2ABC x ∠=，3ABC ACB ACD x ∠=∠=∠=，5D x ∠=，利用三角形内角和定理构建方程求出x 即可；（2）先依据ASA 证明BEA CDA △≌△，再依据全等三角形的性质得到AE AD =，结合AE AD ⊥，依据三角形内角和求出45AED ∠=︒,再依据三角形外角的性质及等式的基本性质即可求证；（3）根据直角三角形的面积公式求出AB ，延长AG 至K ，使GK AG =，连接CK ，先依据SAS 证明AEG KCG △≌△，结合等量代换得到AE KC AD ==，ACK BAD ∠=∠，再依据SAS 证明AKC BDA △≌△，依据全等的性质求得CAG ABD ∠=∠215=⨯︒30=︒，从而得到60BAF ∠=︒，继而得到90AFB ∠=︒，最后依据直角三角形30度角的性质解决问题．【详解】()1解：如图1中，设DBC x ∠=．2ABD DBC ∠=∠，AB AC =，2ABD x ∴∠=，3ABD ACB x ∠=∠=， AC 平分BCD ∠，3ACD ACB x ∴∠=∠=，26DCB ACB x ∠=∠=,5D ABD ACD x ∠=+∠=，又∵在BCD ∆中，180D DBC DCB ∠+∠+∠=︒，56180x x x ∴++=︒，15x ∴=︒，45ABC ACB ∴∠=∠=︒，30ABD ∠=︒，180454590A ∴∠=︒-︒-︒=︒；（2）AE AD ⊥,90EAD ∴∠=︒,90BAC EAD ∠=∠=︒,BAC EAC EAD EAC ∴∠-∠=∠-∠,BAE CAD ∴∠=∠,=345ABE x ACD ∠=︒=∠，AB AC =()BEA CDA ASA ∴△≌△AE AD ∴=，又∵90EAD ∠=︒,∴45AED ADE ∠=∠=︒又AEC ABE BAE AED DEC ∠=∠+∠=∠+∠，DEC BAE ∴∠=∠；（3）延长AG 至K ，使GK AG =，连接CK点G 为CE 的中点，EG CG ∴=，AGE KGC ∠=∠，()AEG KCG SAS ∴△≌△，AE KC ∴=，AEG KCG ∠=∠，AE KC AD ∴==，45ACK ACB KCG AEC ∠=∠+∠=︒+∠4590ABE BAE BAE BAD =︒+∠+∠=︒+∠=∠AB AC =()AKC BDA SAS ∴△≌△21530CAG ABD ∠=∠=⨯︒=︒60BAF ∴∠=︒90AFB ∴∠=︒32ABC S =211=3222AB AC AB ∴⨯= 8AB ∴=142AF AB ∴==．【点睛】本题属于三角形综合题，考查了三角形内角和定理，三角形外角的性质，三角形全等的判定和性质，含30度的直角三角形的性质，第（1）问的关键在于设未知数，列方程；第（2）问的关键得到了等腰直角三角形和利用三角形的外角性质建立起了两个待证量之间的等式；第（3）问的关键在于作辅助线证明了30CAG ∠=︒.4．（1）BC=AC+AD ；（2）△ABC 的面积为80．【分析】（1）在CB 上截取CE=CA ，则由题意可得AD=DE ，∠CED=∠A ，再结合∠A=2∠B 可得DE=BE ，从而得到BC=AD+AC ；（2）在AB 上截取AE=AD ，连结CE ，过C 作CF ⊥AB 于F 点，由题意可得EC=BC ，从而得到EF 的长度，再由勾股定理根据EC 、EF 的长度求得CF 的长度，最后根据面积公式可以得到解答．【详解】解：（1）如图，在CB 上截取CE=CA ，则由题意得：△CAD ≌△CED ，∴AD=DE ，∠CED=∠A ，∵∠A=2∠B ，∴∠CED=2∠B ，又∠CED=∠B+∠EDB ，∴∠B+∠EDB=2∠B ，∴∠EDB=∠B ，∴DE=BE ，∴BC=BE+CE=DE+CE=AD+AC ；（2）如图，在AB 上截取AE=AD ，连结CE ，过C 作CF ⊥AB 于F 点，∴由题意可得：△CDA ≌△CEA ，∴EC=CD=BC=10，AE=AD=8，∵CF ⊥AB ，∴EF=FB=208622AB AE --==， ∴22221068CF EC EF =--=， ∴112088022ABC S AB CF =⨯=⨯⨯=．【点睛】本题考查三角形全等的综合运用，熟练掌握三角形全等的判定和性质、等腰三角形的判定和性质、勾股定理是解题关键．5．（1）4；（2）FG=BF+EG ，见解析；（3）FG=BF-EG【分析】（1）解直角三角形分别求出DF，CF即可解决问题．（2）如图2中，结论：FG=BF+EG．在EA上截取EH，使得EH=BF．利用两次全等，证明FG=GH即可解决问题．（3）如图3中，结论：FG=BF-EG．在射线EA上截取EH，使得EH=BF．利用两次全等，证明FG=GH即可解决问题．【详解】（1）∵DE∥BC，∴∠BDE+∠ABC=180°，∵∠BDE=120°，∴∠ABC=60°，∵DF⊥BF，∴∠BFD=90°，∴DF=BF•tan60°133=⨯=，∵∠CDF1=∠BDE=60°，∠DFC=90°，2∴CF=DF•tan60°333=⨯=，∴BC=BF+CF=1+3=4；（2）如图2中，结论：FG=BF+EG．理由：在EA上截取EH，使得EH=BF．∵AB=AC，∠B=∠C，∵DE∥BC，∴∠ADE=∠B，∠AED=∠C，∴∠ADE=∠AED，∴∠DEH=∠B，在△DBF和△DEH中，B DEH BD DE ⎪∠=∠⎨⎪=⎩，∴△DBF ≌△DEH （SAS ），∴DF=DH ，∠BDF=∠EDH ，∵∠FDG 12=∠BDE ， ∴∠BDF+∠EDG=∠EDH+∠EDG=∠GDH 12=∠BDE ， ∴∠GDF=∠GDH ，在△DGF 和△DGH 中，DF DH GDF GDH DG DG =⎧⎪∠=∠⎨⎪=⎩，∴△DGF ≌△DGH （SAS ），∴FG=HG ，∵HG=EG+HE=EG+BF ，∴FG=BF+EG ；（3）如图3中，结论：FG=BF-EG ．理由：在射线EA 上截取EH ，使得EH=BF ．∵AB=AC ，∠B=∠C ，∵DE ∥BC ，∴∠ADE=∠B ，∠AED=∠C ，∴∠ADE=∠AED ，∴∠DEH=∠B ，在△DBF 和△DEH 中，B DEH BD DE ⎪∠=∠⎨⎪=⎩，∴△DBF ≌△DEH （SAS ），∴DF=DH ，∠BDF=∠EDH ，∴∠BDE=∠FDH ，∵∠FDG 12=∠BDE 12=∠FDH ， ∴∠GDF=∠GDH ，在△DGF 和△DGH 中，DF DH GDF GDH DG DG =⎧⎪∠=∠⎨⎪=⎩，∴△DGF ≌△DGH （SAS ），∴FG=HG ，∵HG=HE-GE=BF-EG ，∴FG=BF=-EG ．【点睛】本题考查了等腰三角形的性质，全等三角形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．6．（1）BM+NC=MN ，证明见解析；（2）成立，证明见解析；（3）NC-BM=MN ，证明见解析．【分析】（1）由DM=DN ，∠MDN=60°，可证得△MDN 是等边三角形，又由△ABC 是等边三角形，CD=BD ，易证得Rt △BDM ≌Rt △CDN ，然后由直角三角形的性质，即可求得BM 、NC 、MN 之间的数量关系 BM+NC=MN ；（2）在CN 的延长线上截取CM 1=BM ，连接DM 1．可证△DBM ≌△DCM 1，即可得DM=DM 1，易证得∠CDN=∠MDN=60°，则可证得△MDN ≌△M 1DN ，然后由全等三角形的性质，即可得结论仍然成立；（3）首先在CN 上截取CM 1=BM ，连接DM 1，可证△DBM ≌△DCM 1，即可得DM=DM 1，然后证得∠CDN=∠MDN=60°，易证得△MDN ≌△M 1DN ，则可得NC-BM=MN ．【详解】解（1）BM 、NC 、MN 之间的数量关系：BM+NC=MN ．证明如下：∵BD=DC ，DM=DN ，MDN 60∠=︒∴∠BDC=∠DCB=180302BDC ，△MDN 为等边三角形，∴MN=MD=DN ，∵△ABC 是等边三角形，∴∠ABC=∠ACB=60°，∴∠ABD=∠ACD=90°，∴Rt △BDM ≌Rt △CDN （HL ），∴∠BDM =∠CDN=302BDC MDN ， ∴11,22BM DM NC DN , ∴BM+NC=MN ．（2）猜想：结论仍然成立．证明：在CN 的反向延长线上截取CM 1=BM ，连接DM 1．∵∠MBD=∠M 1CD=90°，BD=CD ，∴△DBM ≌△DCM 1，∴DM=DM 1，∠MBD=∠M 1CD ，∵∠MDN=60°，∠BDC=120°，∴∠M 1DN=∠MDN=60°，∴△MDN ≌△M 1DN ，∴MN=M1N=M 1C+NC=BM+NC ，（3）证明：在CN 上截取CM 1=BM ，连接DM 1．与（2）同理可证△DBM ≌△DCM 1，∴DM=DM 1，与（2）同理可证∠CDN=∠MDN=60°，∴△MDN ≌△M 1DN ，∴MN=M 1N ，∴NC-BM=MN ．【点睛】本题考查了等边三角形，直角三角形，等腰三角形的性质以及全等三角形的判定与性质等知识．此题综合性很强，难度较大，解题的关键是注意数形结合思想的应用与辅助线的作法．7．（1）AM BN MN +=；证明见解析；（2）AM BN MN +=；证明见解析；（3）补图见解析；BN AM MN -=；证明见解析．【分析】（1）延长CB 到E ，使BE=AM ，证△DAM ≌△DBE ，推出∠BDE=∠MDA ，DM=DE ，证△MDN ≌△EDN ，推出MN=NE 即可；（2）延长CB 到E ，使BE=AM ，证△DAM ≌△DBE ，推出∠BDE=∠MDA ，DM=DE ，证△MDN ≌△EDN ，推出MN=NE 即可；（3）在CB 截取BE=AM ，连接DE ，证△DAM ≌△DBE ，推出∠BDE=∠MDA ，DM=DE ，证△MDN ≌△EDN ，推出MN=NE 即可．【详解】（1）AM BN MN +=．证明如下：如图，延长CB 到E ，使BE AM =，连接DE ．90A CBD ∠=∠=︒，90A EBD ∴∠=∠=︒．ADC BDC ≌，AD BD ∴=．在DAM △和DBE 中，AM BE A DBE AD BD =⎧⎪∠=∠⎨⎪=⎩，()DAM DBE SAS ∴≌，BDE MDA ∴∠=∠，DM DE =．MDN ADC BDC ∠=∠=∠，ADM NDC BDE ∴∠=∠=∠，MDC NDB ∠=∠，MDN NDE ∴∠=∠．在MDN △和EDN △中，DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩，()MDN EDN SAS ∴△≌△，MN NE ∴=．NE BE BN AM BN =+=+，AM BN MN ∴+=；（2）AM BN MN +=．证明如下：如图，延长CB 到E ，使BE AM =，连接DE ．90A CBD ∠=∠=︒，90A DBE ∴∠=∠=︒．ADC BDC ≌，AD BD ∴=，ADC CDB ∠=∠．在DAM △和DBE 中，AM BE A DBE AD BD =⎧⎪∠=∠⎨⎪=⎩，()DAM DBE SAS ∴≌，BDE MDA ∴∠=∠，DM DE =．90MDN ACD ∠+∠=︒，90ACD ADC ∠+∠=︒，ADC CDB ∠=∠，NDM ADC CDB ∴∠=∠=∠，ADM CDN BDE ∴∠=∠=∠，CDM NDB ∠=∠，MDN NDE ∴∠=∠．在MDN △和EDN △中，DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩，()MDN EDN SAS ∴△≌△，MN NE ∴=．NE BE BN AM BN =+=+，AM BN MN ∴+=；（3）补充完成题图，如图所示．BN AM MN -=．证明如下：如上图，在CB 上截取BE=AM ，连接DE ．90CDA ACD ∠+∠=︒，90MDN ACD ∠+∠=︒，MDN CDA ∴∠=∠，MDA CDN ∴∠=∠．90B CAD ∠=∠=︒，90B DAM ∴∠=∠=︒．在DAM △和DBE 中，AM BE DAM DBE AD BD =⎧⎪∠=∠⎨⎪=⎩，()DAM DBE SAS ∴≌，BDE ADM CDN ∴∠=∠=∠，DM DE =．ADC BDC MDN ∠=∠=∠，ADN CDE ∴∠=∠，MDN EDN ∴∠=∠．在MDN △和EDN △中，DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩，()MDN EDN SAS ∴△≌△，MN NE ∴=．NE BN BE BN AM =-=-，BN AM MN ∴-=．【点睛】本题考查了全等三角形的性质和判定的应用，作出辅助线构造全等三角形是解题的关键． 8．（1）BE DE AE =+；（2）BE DE AE =-，证明见解析；（3）2BE DE AE =-【分析】（1）在射线BM 上截取BF DE =，连接AF ，首先利用菱形的性质证明ADE ABF ≌，然后利用全等三角形的性质及等边三角形的性质得出EF AE =，从而可得出结论BE DE AE =+；（2）在DE 上截取DG BE =，连接AG ，首先利用菱形的性质证明ADG ABE ≌，然后利用全等三角形的性质及等边三角形的性质得出EG AE =，从而可得出结论BE DE AE =-；（3）在DE 上截取DH BE =，连接AH ，首先利用正方形的性质证明ADH ABE △≌，然后利用全等三角形的性质及等腰直角三角形的性质得出2EH AE =，从而可得出结论2BE DE AE =-．【详解】（1）解：BE DE AE =+；如图①，在射线BM 上截取BF DE =，连接AF ，60DEB DAB ∠=∠=︒，EDA ABE ∴∠=∠．四边形ABCD 是菱形，AB AD ∴=．()ADE ABF SAS ∴△≌△，AE AF ∴=，EAD BAF ∠=∠．60DAB DAF BAF DAF EAD EAF ∴∠=∠+∠=∠+∠=∠=︒．AEF ∴是等边三角形，EF AE ∴=．BE BF EF =+，BE DE AE ∴=+．图①（2）BE DE AE =-．证明：如图②，在DE 上截取DG BE =，连接AG ，60DEB DAB ∠=∠=︒，EDA ABE ∴∠=∠．四边形ABCD 是菱形，AB AD ∴=．()ADG SAS ∴△≌△ABE ．AE AG ∴=，DAG BAE ∠∠=．60DAB DAG BAG BAE BAG EAG ∴∠=∠+∠=∠+∠=∠=︒． ∴AEG 是等边三角形．EG AE ∴=．DG DE EG =-，BE DE AE ∴=-；图②（3）2BE DE AE =-．如图③，在DE 上截取DH BE =，连接AH ，90DEB DAB ∠=∠=︒，EDA ABE ∴∠=∠．四边形ABCD 是正方形，AB AD ∴=．()ADH ABE SAS ∴△≌△．AE AH ∴=，HAD BAE ∠=∠．90DAB DAH BAH BAE BAH EAH ∴∠=∠+∠=∠+∠=∠=︒．AEH ∴是等腰直角三角形．2EH AE ∴=．DH DE EH =-，2BE DE AE ∴=-．图③【点睛】本题主要考查全等三角形的判定及性质，等腰直角三角形和等边三角形的性质，正方形和菱形的性质，合理的作出辅助线是解题的关键．9．证明见解析．【分析】延长EB到G，使BG=DF，连接AG．先说明△ABG≌△ADF，然后利用全等三角形的性质和已知条件证得△AEG≌△AEF，最后再运用全等三角形的性质和线段的和差即可解答．【详解】延长EB到G，使BG=DF，连接AG．∵∠ABG=∠ABC=∠D=90°，AB=AD，∴△ABG≌△ADF．∴AG=AF，∠1=∠2．∠BAD．∴∠1+∠3=∠2+∠3=∠EAF=12∴∠GAE=∠EAF．又∵AE=AE，∴△AEG≌△AEF．∴EG=EF．∵EG=BE+BG．∴EF=BE+FD【点睛】本题考查了全等三角形的判定与性质，做出辅助线构造全等三角形是解答本题的关键．10．（1）3，23234+2）见解析【分析】（1）根据平行和垂直的特点求出BF，AF，再根据勾股定理求出CD，根据FP与BA的比值求出面积，再根据勾股定理求CF，BC即可得到周长．（2）在AD上截取AM=AG，连接CM，证△FAG≌△CAM；证△EFG≌△DCM．【详解】+解：（1）面积为3；周长为23234∵四边形ABCD和四边形CDEF都是平行四边形，∴EF=CD，AB=CD，AB∥CD∴EF=AB=CD=5∴AE=EF-AE=5-2=3∴BF=5-3=2过F作FP⊥BC则FP ：AH=BF ：AB=2：5， ∴::2:5BCF BCA S S FP AH == , ∵AC ⊥CD ，AB ∥CD,∴AB ⊥AC ，即∠BAC=90°， ∵AC=AF=3,∴CF=223332+= ，BC=223534+= ， ∴2213552BCF BCA S S CD AC ==⨯⨯= ∴△BCF 的面积为3，△BCF 周长为23234++ （2）在AD 上截取AM=AG ，连接CM ，∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AD=BC∵AH ⊥BC∴AD ⊥AH∴∠DAH=90°∵∠BAC=90°∴∠DAH=∠BAC∴∠DAH-∠CAH =∠BAC-∠CAH ∴∠BAH=∠CAD∵AF=AC∴△FAG ≌△CAM∴FG=CM ，∠ACM=∠AFG∵四边形CDEF 是平行四边形， ∴EF ∥CD ，EF=CD ，∴∠DCF+∠AFC=180°，∵AF=AC ， ∠BAC=90°，∴∠AFC=∠ACF=45°，∴∠DCF=180°-∠AFC=135°，∴∠ACM=∠AFG=45°，∴∠DCM=∠FCD-∠ACF-∠ACM=45°，∴∠AFG=∠DCM，∴△EFG≌△DCM，∴EG=DM，∵AD=AM+DM，∴AD=AG+EG，∵AD=BC，∴BC=AG+EG．【点睛】此题考查平行四边形的性质，平行线分线段成比例和勾股定理的应用．。

三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结

i n ga re与，连结与，证BCE ∆AE CDosrofdoogeragnii rb ei n ga re go od fo r二、倍长与中点有关的线段考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

．1()2AB AC <+Aean dAl l t h i ng si nt he i rb ei n ga re go 三、截长补短问题1：垂直平分线（性质）定理是_______________________________________________________问题2：角平分线（性质）定理是__________________________________________________________问题3：等腰三角形的两个底角________，简称______________；如果一个三角形有两个角相等，那么它们所对的边也______，简称____________．问题4：当见到线段的______________考虑截长补短，构造全等或等腰转移____、转移____，然后和_________重新组合解决问题．三角形全等之截长补短（一）一、单选题(共4道，每道25分)1.已知，如图，BM 平分∠ABC，P 为BM 上一点，PD⊥BC 于点D ，BD=AB+CD ．求证：∠BAP+∠BCP=180°．请你仔细观察下列序号所代表的内容：①；②∵∠1=∠2；③∠A=∠BEP；④AP=PE；⑤；⑥；⑦；⑧．以上空缺处依次所填最恰当的是( )A.①③⑥⑦B.①③⑤⑧C.②③⑥⑦D.②④⑤⑧2.已知，如图，BM 平分∠ABC，点P 为BM 上一点，PD⊥BC 于点D ，BD=AB+DC ．求证：∠BAP+∠BCP=180°．e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 请你仔细观察下列序号所代表的内容：①延长BA ，过点P 作PE⊥BA 于点E ；②延长BA 到E ，使AE=DC ，连接PE ；③延长BA 到E ，使DC=AE ；④；⑤；⑥；⑦．以上空缺处依次所填最恰当的是( )A.②④⑦B.①⑤⑥C.③④⑥D.①⑤⑦3.已知，如图，在五边形ABCDE 中，AB=AE ，AD 平分∠CDE，∠BAE=2∠CAD，求证：BC+DE=CD ．e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 请你仔细观察下列序号所代表的内容：①在CD 上截取CF=CB ，连接AF ；②在DC 上截取DF=DE ，连接AF ；③在DC 上截取DF=DE ；④AE=AF；⑤AF=AE，∠4=∠3；⑥∠4=∠3；⑦；⑧；⑨．以上空缺处依次所填最恰当的是( )A.①④⑨ B.③⑤⑧ C.①⑥⑦ D.②⑤⑨4.已知，如图，在五边形ABCDE 中，AB=AE ，∠BAE=2∠CAD，∠ABC+∠AED=180°，求证：BC+DE=CD ．请你仔细观察下列序号所代表的内容：①延长DE 到F ，使EF=BC ，连接AF ；②延长DE 到F ，使BC=EF ；e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o ③延长DE 到F ，连接AF ；④；⑤；⑥；⑦；⑧；⑨．以上空缺处依次所填最恰当的是( )A.③⑤⑥⑧B.①④⑥⑨C.①⑤⑥⑨D.②④⑦⑧r四、三角形全等旋转与截长补短专题问题一：题中出现什么的时候，我们应该想到旋转？(构造旋转的条件)问题二：旋转都有哪些模型？【例1】如图，P 是正△ABC 内的一点，若将△PBC 绕点B 旋转到△P ＇BA ，则∠PBP ＇的度数是( ) A ．45°B ．60° C ．90° D ．120°【例2】如图，正方形BAFE 与正方形ACGD 共点于A ，连接BD 、CF ，求证：BD ＝CF 并求出∠DOH 的度数。

三角形全等之截长补短 (整理)

三角形全等之截长补短 (整理)三角形全等之截长补短一、知识点概述截长补短是指在几何题目中，当出现线段和的情况时，可以考虑通过截取一段线段并加上一段等于原线段的线段，将原问题转化为线段等量的问题。

二、例题讲解1.已知：如图，在△ABC中，∠1=∠2，∠B=2∠C．求证：AC=AB+BD．证明：可以通过截长法和补短法两种方法证明。

截长法：在AC上截取AF=AB，连接DF。

在△ABD和△AFD中，根据SAS准则可以得到△ABD≌△AFD，进而得到∠B=∠AFD，BD=FD。

又因为∠B=2∠C，所以∠AFD=2∠C。

因为∠AFD是△DFC的一个外角，所以∠AFD=∠C+∠XXX。

因为∠1=∠2，所以∠XXX∠C，进而得到∠AFD=2∠C=∠B。

因此，根据三角形内角和定理，可以得到∠A=180°-∠B-∠C=∠AFD+∠XXX∠C=2∠C+∠C+∠C=4∠C。

在△ABC中，∠B=2∠C，所以∠A=60°。

在△ADE和△ADC中，因为∠E=∠C，∠1=∠2，AD=AD，所以△ADE≌△ADC （AAS），进而得到AE=AC。

因此，AC=AB+BD。

补短法：延长AB到E，使BE=BD，连接DE。

因为BE=BD，所以∠XXX∠BDE。

因为∠ABD是△XXX的一个外角，所以∠ABD=∠E+∠BDE=2∠E。

因为∠ABD=2∠C，所以∠XXX∠C。

在△ADE和△ADC中，因为∠E=∠C，∠1=∠2，AD=AD，所以△ADE≌△ADC（AAS），进而得到AE=AC。

因此，XXX。

2.如图，在四边形ABCD中，∠A=∠B=90°，点E为AB边上一点，且DE平分∠ADC，CE平分∠BCD．求证：XXX．证明：在△ADE和△BCE中，因为∠A=∠B=90°，所以AD=BC。

因为DE平分∠ADC，CE平分∠BCD，所以∠AED=∠DEC，∠XXX∠XXX。

因为∠AED+∠BCE=180°，所以∠DEC+∠CDE=180°。

全等三角形截长补短法的经典例题

全等三角形截长补短法的经典例题（最新版）目录1.截长补短法的概念2.截长补短法的两种方法：截长法和补短法3.截长补短法在全等三角形中的应用4.经典例题解析4.1 例题一4.2 例题二4.3 例题三5.截长补短法的优点和意义正文一、截长补短法的概念截长补短法是一种在几何问题中添加辅助线的方法，主要用于解决全等三角形的问题。

截长指的是在较长的线段上截取一段较短的线段，补短则是在较短线段上补一段线段，使其和较长的线段相等。

截长补短法的目的是将问题合理地转化为更容易解决的形式，从而简化结论。

二、截长补短法的两种方法截长补短法包括两种方法：截长法和补短法。

1.截长法：在较长的线段上截取与较短线段相等的线段。

2.补短法：在较短线段上补一段线段，使其和较长的线段相等。

三、截长补短法在全等三角形中的应用在全等三角形的证明中，截长补短法是非常常用的一种方法。

通过添加适当的辅助线，可以将问题转化为更容易证明的形式，从而得出结论。

下面通过几个经典例题来具体讲解截长补短法在全等三角形中的应用。

四、经典例题解析1.例题一已知三角形 ABC 和三角形 DEF 满足条件：AB=DE，BC=EF，∠ABC=∠DEF，求证三角形 ABC 与三角形 DEF 全等。

解：通过截长补短法，我们可以在 BC 上截取 BE=CF，连接 AD 和 CE。

由于 AB=DE，BC=EF，且∠ABC=∠DEF，根据三角形全等的 SAS 条件，可得三角形 ABC≌三角形 DEF。

2.例题二已知三角形 ABC 和三角形 DEF 满足条件：AB=DE，BC=EF，∠ABC=∠DEF，求证三角形 ABC 与三角形 DEF 全等。

解：这次我们可以在 AB 上截取 AD=DF，连接 CE 和 BD。

同样地，由于 AB=DE，BC=EF，且∠ABC=∠DEF，根据三角形全等的 SAS 条件，可得三角形 ABC≌三角形 DEF。

3.例题三已知三角形 ABC 和三角形 DEF 满足条件：AB=DE，BC=EF，∠ABC=∠DEF，求证三角形 ABC 与三角形 DEF 全等。

三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结

一、手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA平分∠BOC变形：例 1.如图在直线ABC的同一侧作两个等边三角形ABD∆，连∆与BCE结AE与CD，证明（1）DBC≅∆ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)DFBAGB∆∆≅(5)CFB∆EGB∆≅(6)BH平分AHC∠(7)ACGF//变式精练1：如图两个等边三角形ABD∆，连∆与BCE结AE与CD，证明（1）DBCABE∆∆≅（2）DCAE=（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠ 例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ∠？二、倍长与中点有关的线段倍长中线类?考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

第08讲全等三角形中“截长补短”模型

第08讲全等三角形中“截长补短”模型（核心考点讲与练）【基础知识】1、补短法：通过添加辅助线“构造”一条线段使其为求证中的两条线段之和，在证所构造的线段和求证中那一条线段相等；2、截长法：通过添加辅助线先在求证中长线段上截取与线段中的某一段相等的线段，在证明截剩部分与线段中的另一段相等。

3、截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明，这种做法一般遇到证明三条线段之间关系是常用.如图1，若证明线段AB,CD,EF之间存在EF=AB+CD,可以考虑截长补短法.截长法：如图2，在EF上截取EG=AB,在证明GF=CD即可；补短法：如图3，延长AB至H点，使BH=CD,再证明AH=EF即可.【考点剖析】1、如图，已知在△ABC中，∠C=2∠B,∠1=∠2，求证：AB=AC+CD解析：在AB上取一点E,使AE=AC,连接DE,∵AE=AC,∠1=∠2，AD=AD∴△ACD≌△AED∴CD=DE,∠C=∠3∵∠C=2∠B∴∠3=2∠B=∠4+∠B∴∠4=∠B，∴DE=BE,CD=BE∵AB=AE+BE∴AB=AC+CD2、如图，AC平分∠BAD，CE⊥AB于点E，∠B+∠D=180°，求证：AE=AD+BE.解析：如图，在EA上取点F,使EF=BE,连接CF,∵CE⊥AB∴CF=CB∠CFB=∠B∵∠AFC+∠C FB=180°，∠D+∠B=180°∴∠D=∠AFC∵AC平分∠BAD即∠DAC=∠FAC在△ACD和△ACF中∠D=∠AFC∠DAC=∠FACAC=AC∴ACD≌△ACF（AAS）∴AD=AF∴AE=AF+EF=AD+BE3．如图，在△ABC 中，∠A ＝60°，BD ，CE 分别平分∠ABC 和∠ACB ，BD ，CE 交于点O ，试判断BE ，CD ，BC 的数量关系，并加以证明．证明：在BC 上截取BF ＝BE ，连接OF .∵BD 平分∠ABC ，∴∠EBO ＝∠FBO .∴△EBO ≌△FBO .∴∠EOB ＝∠FOB .∵∠A ＝60°，BD ，CE 分别平分∠ABC 和∠ACB ，∴∠BOC ＝180°－∠OBC －∠OCB ＝180°－12∠ABC －12∠ACB ＝180°－12(180°－∠A )＝120°.∴∠EOB ＝∠DOC ＝60°.∴∠BOF ＝60°，∠FOC ＝∠DOC ＝60°.∵CE 平分∠DCB ，∴∠DCO ＝∠FCO .∴△DCO ≌△FCO .∴CD ＝CF .∴BC ＝BF ＋CF ＝BE ＋CD .4．如图，AD //BC ，DC ⊥AD ，AE 平分∠BAD ，E 是DC 的中点．问：AD ，BC ，AB 之间有何关系？并说明理由．解：AB ＝AD ＋BC .理由：作EF ⊥AB 于F ，连接BE .∵AE 平分∠BAD ，DC ⊥AD ，EF ⊥AB ，∴EF ＝DE .∵DE ＝CE ，∴EC ＝EF .∴Rt △BFE ≌Rt △BCE (HL)．∴BF ＝BC同理可证：AF ＝AD .∴AD ＋BC ＝AF ＋BF ＝AB ，即AB ＝AD ＋BC .　5．如图，已知DE ＝AE ，点E 在BC 上，AE ⊥DE ，AB ⊥BC ，DC ⊥BC ，请问线段AB ，CD 和线段BC 有何大小关系？并说明理由．解：线段AB ，CD 和线段BC 的关系是：BC ＝AB ＋CD .理由：在△DCE 中，∠EDC ＋∠DEC ＝90°，∵∠AEB ＋∠DEC ＝90°，∴∠AEB ＝∠EDC ，又∵ED ＝AE ，∠ABE ＝∠ECD ＝90°，∴△ABE ≌△ECD (AAS)，∴AB ＝EC ，BE ＝CD ，∴BC ＝BE ＋EC ＝CD ＋AB .【过关检测】1．（2021·辽宁大连·八年级期中）如图，ABC V 为等边三角形，若()060DBC DAC a a Ð=Ð=°<<°，则BCD Ð=__________（用含a 的式子表示）．【答案】120a°-【分析】在BD 上截取BE =AD ，连结CE ，可证得BEC ADC @△△ ，从而得到CE =CD ，∠DCE =∠ACB =60°，从而得到DCE V 是等边三角形，进而得到∠BDC =60°，则有60B CE a Ð=°-，即可求解．【详解】解：如图，在BD 上截取BE =AD ，连结CE ，∵ABC V 为等边三角形，∴BC =AC ，∠BAC =∠ABC =∠ACB =60°，∵a Ð=Ð=DBC DAC ，BE =AD ，∴BEC ADC @△△ ，∴CE =CD ，∠BCE =∠ACD ，∴∠BCE +∠ACE =∠ACD +∠ACE ，∴∠DCE =∠ACB =60°，∵CE =CD ，∴DCE V 是等边三角形，∴∠BDC =60°，∴18060120BCD a a Ð=°-°-=°-．故答案为：120a°-【点睛】本题主要考查了等边三角形判定和性质，全等三角形的判定和性质，解题的关键是做出辅助线构造全等三角形是解题的关键．2.（2019·浙江嘉兴市·八年级期中）（1）问题背景：如图1，在四边形ABCD 中，AB ＝AD ，∠BAD ＝120°，∠B ＝∠ADC ＝90°．E ，F 分别是BC ，CD 上的点，且∠EAF ＝60°，请探究图中线段BE ，EF ，FD 之间的数量关系是什么？小明探究此问题的方法是：延长FD 到点G ，使DG ＝BE ，连结AG ．先证明△ABE ≌△ADG ，得AE ＝AG ；再由条件可得∠EAF ＝∠GAF ，证明△AEF ≌△AGF ，进而可得线段BE ，EF ，FD 之间的数量关系是．（2）拓展应用：如图2，在四边形ABCD 中，AB ＝AD ，∠B +∠D ＝180°．E ，F 分别是BC ，CD 上的点，且∠EAF ＝12∠BAD ．问（1）中的线段BE ，EF ，FD 之间的数量关系是否还成立？若成立，请给出证明；若不成立，请说明理由．【答案】（1）EF ＝BE +DF ；（2）结论EF ＝BE +DF 仍然成立；证明见解析．【分析】（1）延长FD 到点G ．使DG=BE ．连结AG ，即可证明△ABE ≌△ADG ，可得AE=AG ，再证明△AEF ≌△AGF ，可得EF=FG ，即可解题；（2）延长FD 到点G ．使DG=BE ．连结AG ，即可证明△ABE ≌△ADG ，可得AE=AG ，再证明△AEF ≌△AGF ，可得EF=FG ，即可解题．解答：（1）EF ＝BE +DF ，理由如下：在△ABE 和△ADG 中，90DG BE B ADG AB AD °=ìïÐ=Ð=íï=î，∴△ABE ≌△ADG （SAS ），∴AE ＝AG ，∠BAE ＝∠DAG ，∵∠EAF ＝12∠BAD ，∴∠GAF ＝∠DAG +∠DAF ＝∠BAE +∠DAF ＝∠BAD ﹣∠EAF ＝∠EAF ，∴∠EAF ＝∠GAF ，在△AEF 和△GAF 中，AE AG EAF GAF AF AF =ìïÐ=Ðíï=î，∴△AEF ≌△AGF （SAS ），∴EF ＝FG ，∵FG ＝DG +DF ＝BE +DF ，∴EF ＝BE +DF ；故答案为：EF ＝BE +DF ．（2）结论EF ＝BE +DF 仍然成立；理由如下：延长FD 到点G ．使DG ＝BE ．连结AG ，如图2，∵∠B +∠ADC ＝180°，∠ADC +∠ADG ＝180°，∴∠B ＝∠ADG ，在△ABE 和△ADG 中，DG BE B ADG AB AD =ìïÐ=Ðíï=î，∴△ABE ≌△ADG （SAS ），∴AE ＝AG ，∠BAE ＝∠DAG ，∵∠EAF ＝12∠BAD ，∴∠GAF ＝∠DAG +∠DAF ＝∠BAE +∠DAF ＝∠BAD ﹣∠EAF ＝∠EAF ，∴∠EAF ＝∠GAF ，在△AEF 和△GAF中，AE AG EAF GAF AF AF =ìïÐ=Ðíï=î，∴△AEF ≌△AGF （SAS ），∴EF ＝FG ，∵FG ＝DG +DF ＝BE +DF ，∴EF ＝BE +DF ．【点拨】本题是四边形综合题，考查了全等三角形的判定和性质，直角三角形的性质，添加恰当辅助线构造全等三角形是解题的关键．3.（2020·全国八年级单元测试）在△ABC 中，∠ACB=2∠B ，（1）如图①，当∠C=90°，AD 为∠ABC 的角平分线时，在AB 上截取AE=AC ，连接DE ，易证AB=AC+CD ．请证明AB=AC+CD ；（2）①如图②，当∠C ≠90°，AD 为∠BAC 的角平分线时，线段AB 、AC 、CD 又有怎样的数量关系？请直接写出你的结论，不要求证明；②如图③，当∠C ≠90°，AD 为△ABC 的外角平分线时，线段AB 、AC 、CD 又有怎样的数量关系？请写出你的猜想并证明．【答案】（1）证明见解析；（2）①AB=AC+CD ；②AC+AB=CD ，证明见解析．【分析】（1）首先得出△AED ≌△ACD （SAS ），即可得出∠B=∠BDE=45°，求出BE=DE=CD ，进而得出答案；（2）①首先得出△AED ≌△ACD （SAS ），即可得出∠B=∠BDE ，求出BE=DE=CD ，进而得出答案；②首先得出△AED ≌△ACD （SAS ），即可得出∠B=∠EDC ，求出BE=DE=CD ，进而得出答案．（1）证明：∵AD 为∠ABC 的角平分线，∴∠EAD=∠CAD ，在△AED 和△ACD 中，∵AE=AC ，∠EAD=∠CAD ，AD=AD ，∴△AED ≌△ACD （SAS ），∴ED=CD ，∠C=∠AED=90°，∵∠ACB=2∠B，∠C=90°，∴∠B=45°，∴∠BDE=45°，∴BE=ED=CD，∴AB=AE+BE=AC+CD；（3）①AB=AC+CD．理由如下：在AB上截取AE=AC，连接DE，∵AD为∠ABC的角平分线，∴∠EAD=∠CAD，在△AED和△ACD中，∵AE=AC，∠EAD=∠CAD，AD=AD，∴△AED≌△ACD（SAS），∴ED=CD，∠C=∠AED，∵∠ACB=2∠B，∴∠AED=2∠B，∵∠B+∠BDE=∠AED，∴∠B=∠BDE，∴BE=ED=CD，∴AB=AE+BE=AC+CD；②AC+AB=CD．理由如下：在射线BA上截取AE=AC，连接DE，∵AD为∠EAC的角平分线，∴∠EAD=∠CAD，在△AED和△ACD中，∵AE=AC，∠EAD=∠CAD，AD=AD，∴△AED≌△ACD（SAS），∴ED=CD，∠ACD=∠AED，∵∠ACB=2∠B，∴设∠B=x，则∠ACB=2x，∴∠EAC=3x，∴∠EAD=∠CAD=1.5x，∵∠ADC+∠CAD=∠ACB=2x，∴∠ADC=0.5x，∴∠EDC=x，∴∠B=∠EDC，∴BE=ED=CD，∴AB+AE=BE=AC+AB=CD．【点拨】此题主要考查了全等三角形的判定与性质以及三角形外角的性质等知识，利用已知得出△AED≌△ACD是解题关键．4．（2020·山东青岛·八年级单元测试）如图，在△ABC中，AB＝BC，∠ABC＝60°，线段AC与AD关于直线AP对称，E是线段BD与直线AP的交点．（1）若∠DAE＝15°，求证：△ABD是等腰直角三角形；（2）连CE，求证：BE＝AE+CE．【分析】（1）首先根据题意确定出△ABC是等边三角形，然后根据等边三角形的性质推出∠BAC＝60°，再根据线段AC与AD关于直线AP对称，以及∠DAE＝15°，推出∠BAD＝90°，即可得出结论；（2）利用“截长补短”的方法在BE上取点F，使BF＝CE，连接AF，根据题目条件推出△ABF≌△ACE，得出AF＝AE，再进一步推出∠AEF＝60°，可得到△AFE是等边三角形，则得到AF＝FE，从而推出结论即可．【详解】证明：（1）∵在△ABC中，AB＝BC，∠ABC＝60°，∴△ABC是等边三角形，∴AC＝AB＝BC，∠BAC＝∠ABC＝∠ACB＝60°，∵线段AC与AD关于直线AP对称，∴∠CAE＝∠DAE＝15°，AD＝AC，∴∠BAE＝∠BAC+∠CAE＝75°，∴∠BAD＝90°，∵AB ＝AC ＝AD ，∴△ABD 是等腰直角三角形；（2）在BE 上取点F ，使BF ＝CE ，连接AF ，∵线段AC 与AD 关于直线AP 对称，∴∠ACE ＝∠ADE ，AD ＝AC ，∵AD ＝AC ＝AB ，∴∠ADB ＝∠ABD=∠ACE ，在△ABF 与△ACE 中，AC AB ACE ABFCE BF =ìïÐ=Ðíï=î∴△ABF ≌△ACE （SAS ），∴AF ＝AE ，∵AD ＝AB ，∴∠D ＝∠ABD ，又∠CAE ＝∠DAE ，∴()()111806022AEB D DAE D ABD DAC BAC Ð=Ð+Ð=Ð+Ð+Ð=°-Ð=°，∴在△AFE 中，AF ＝AE ，∠AEF ＝60°，∴△AFE 是等边三角形，∴AF ＝FE ，∴BE ＝BF +FE ＝CE +AE ．【点睛】本题考查全等三角形的判定与性质，以及等边三角形的判定与性质等，掌握等边三角形的判定与性质，以及全等三角形的常见辅助线的构造方法是解题关键．5．（2021·广东·珠海市九洲中学八年级期中）如图，在△ABC 中，∠C ＝90°，AD 是∠BAC的角平分线，交BC 于点D ，过D 作DE ⊥BA 于点E ，点F 在AC 上，且BD ＝DF ．（1）求证：AC ＝AE ；（2）若AB ＝7.4，AF ＝1.4，求线段BE 的长．【答案】（1）见解析；（2）3【分析】（1）证明△ACD ≌△AED （AAS ），即可得出结论；（2）在AB 上截取AM =AF ，连接MD ，证△FAD ≌△MAD （SAS ），得FD =MD ，∠ADF =∠ADM ，再证Rt △MDE ≌Rt △BDE （HL ），得ME =BE ，求出MB =AB -AM =6，即可求解．【详解】解：（1）证明：∵AD 平分∠BAC ，∴∠DAC =∠DAE ，∵DE ⊥BA ，∴∠DEA =∠DEB =90°，∵∠C =90°，∴∠C =∠DEA =90°，在△ACD 和△AED 中，C DEA DAC DAE AD AD Ð=ÐìïÐ=Ðíï=î，∴△ACD ≌△AED （AAS ），∴AC =AE ；（2）在AB 上截取AM =AF ，连接MD ，在△FAD 和△MAD 中，AF AM DAF DAM AD AD =ìïÐ=Ðíï=î，∴△FAD ≌△MAD （SAS ），∴FD =MD ，∠ADF =∠ADM，∵BD =DF ，∴BD =MD ，在Rt △MDE 和Rt △BDE 中，MD BD DE DE=ìí=î，∴Rt △MDE ≌Rt △BDE （HL ），∴ME =BE ，∵AF =AM ，且AF =1.4，∴AM =1.4，∵AB =7.4，∴MB =AB -AM =7.4-1.4=6，∴BE ＝12BM ＝3，即BE 的长为3．【点睛】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识；证明△FAD ≌△MAD 和Rt △MDE ≌Rt △BDE 是解题的关键．6．（2021·贵州·铜仁市第十一中学八年级期中）如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．【分析】如图，在AB 上截取,AH AD =证明,ADE AHE V V ≌再证明,HBE CBE V V ≌可得,BC BH = 从而可得结论.【详解】证明：如图，在AB 上截取,AH AD =AE ∵平分,DAB Ð,DAE HAE \Ð=Ð,AE AE =Q,ADE AHE \V V ≌,ADE AHE \Ð=Ð//,AD BC Q180,ADE BCE \Ð+Ð=°180,AHE BHE Ð+Ð=°Q,BCE BHE \Ð=ÐBE Q 平分,ABC Ð,ABE CBE \Ð=Ð,BE BE =Q,HBE CBE \V V ≌,BC BH \=,AB AH HB =+Q.AB AD BC \=+【点睛】本题考查的是全等三角形的判定与性质，掌握“利用截长补短的方法证明两条线段的和等于另一条线段”是解题的关键.7．（2021·湖北·武汉外国语学校（武汉实验外国语学校）八年级期中）在ABC V 中，BE ，CD 为ABC V 的角平分线，BE ，CD 交于点F ．（1）求证：1902BFC A Ð=°+Ð；（2）已知60A Ð=°．①如图1，若4BD =， 6.5BC =，求CE 的长；②如图2，若BF AC =，求AEB Ð的大小．【答案】（1）证明见解析；（2）2.5；（3）100°．【分析】（1）由三角形内角和定理和角平分线得出1902FBC FCB A Ð+Ð=°-Ð的度数，再由三角形内角和定理可求出BFC Ð的度数，（2）在BC 上取一点G 使BG=BD ，构造BFG BFD @V △（SAS ），再证明()FEC FGC ASA @V V ，即可得BC BD CE =+，由此求出答案；（3）延长BA 到P ，使AP=FC ，构造BFC CAP @V △（SAS ），得PC=BC ，12P BCF ACB Ð=Ð=Ð，再由三角形内角和可求40ABC Ð=°，80ACB Ð=°，进而可得180()100AEB ABE A Ð=°-Ð+Ð=°．【详解】解：（1）BE Q 、CD 分别是ABC Ð与ACB Ð的角平分线，11(180)9022FBC FCB A A \Ð+Ð=°-Ð=°-Ð，1180()180(90)2BFC FBC FCB A \Ð=°-Ð+Ð=°-°-Ð，1902BFC A \Ð=°+Ð，（2）如解（2）图，在BC 上取一点G 使BG=BD ，由（1）得1902BFC A Ð=°+Ð，60BAC Ð=°Q ，120BFC \Ð=°，∴18060BFD EFC BFC Ð=Ð=°-Ð=°，在BFG V 与BFD △中，BF BF FBG FBD BD BG =ìïÐ=Ðíï=î，∴BFG BFD @V △（SAS ）∴BFD BFG Ð=Ð，∴60BFD BFG Ð=Ð=°，∴12060CFG BFG Ð=°-Ð=°，∴60CFG CFE Ð=Ð=°在FEC V 与FGC △中，CFE CFG CF CFECF GCF Ð=Ðìï=íïÐ=Ðî，()FEC FGC ASA \@V V ，CE CG \=，BC BG CG =+Q ，BC BD CE \=+；∵4BD =， 6.5BC =，∴ 2.5CE =（3）如解（3）图，延长BA 到P ，使AP=FC ，60BAC Ð=°Q，∴180120PAC BAC Ð=°-Ð=°，在BFC △与CAP V 中，120BF AC BFC CAP CF PA =ìïÐ=Ð=°íï=î，∴BFC CAP @V △（SAS ）∴P BCF Ð=Ð，BC PC =，∴P ABC Ð=Ð，又∵12P BCF ACB Ð=Ð=Ð，∴2ACB ABC Ð=Ð，又∵180ACB ABC A Ð+Ð+Ð=°，∴360180ABC Ð+°=°，∴40ABC Ð=°，80ACB Ð=°，∴1202ABE ABC Ð=Ð=°，180()180(2060)100AEB ABE A Ð=°-Ð+Ð=°-°+°=°【点睛】本题考查的是角平分线的性质、全等三角形的判定与性质，根据题意作出辅助线，构造出全等三角形是解答此题的关键．8．（2021·福建省福州第十六中学八年级期中）如图，△ABC 为等边三角形，直线l 过点C ，在l 上位于C 点右侧的点D 满足∠BDC ＝60°（1）如图1，在l 上位于C 点左侧取一点E ，使∠AEC ＝60°，求证：△AEC ≌△CDB ；（2）如图2，点F 、G 在直线l 上，连AF ，在l 上方作∠AFH ＝120°，且AF ＝HF ，∠HGF ＝120°，求证：HG +BD ＝CF ；（3）在（2）的条件下，当A 、B 位于直线l 两侧，其余条件不变时（如图3），线段HG 、CF 、BD 的数量关系为．【答案】（1）见解析；（2）见解析；（3）CF =EF -BD ．【分析】（1）先证明∠ACE =∠CBD ，即可利用AAS 证明△AEC ≌△CDB ；（2）在直线l 上位于C 点左侧去一点E ，使得∠AEC =60°，连接AE ，由（1）可知△AEC ≌△CDB ，CE =BD ，然后证明△FAE ≌△HFG 得到GH =EF ，则CF =EF +CE =GH +BD 即HG +BD =CF ；（3）在直线l 上位于C 点右侧取一点E 使得∠AED =60°，连接AE ，在直线l 上位于D 点左侧取一点M 使得BM =BD ，设AB 与直线l 交于N ，先证明△BDM 是等边三角形，得到∠DBM =∠DMB =60°，然后证明∠ACE =∠ABD =∠CBM ，即可利用AAS 证明△AEC ≌△CMB 得到CE =BM =BD ；最后证明△AEF ≌△FGH 得到HG =EF ，则EF =CE +CF =CF +BD 即CF =EF -BD ．【详解】解：（1）∵△ABC 是等边三角形，∴AC =BC ，∠ACB =60°，∴∠ACE +∠BCD =180°-∠ACB =120°，∵∠BDC =60°，∴∠BCD +∠CBD =180°-∠BDC =120°，∴∠ACE =∠CBD ，在△AEC 和△CDB 中，===60ACE CBD AEC CDB AC CB ÐÐìïÐÐíï=îo ，∴△AEC ≌△CDB （AAS）（2）如图所示，在直线l 上位于C 点左侧取一点E ，使得∠AEC =60°，连接AE ，由（1）可知△AEC ≌△CDB ，∴CE =BD ，∵∠ACE =60°，∴∠AEF =120°，∴∠AEF =∠AFH =120°，∴∠AFE +∠FAE =180°-∠AEF =60°，∠AFE +∠HFG =180°-∠AFH =60°，∴∠FAE =∠HFG ，在△FAE 和△HFG 中，120FAE HFG AEF FGH AF FH Ð=ÐìïÐ=Ð=íï=îo ，∴△FAE ≌△HFG （AAS ），∴GH =EF ，∴CF =EF +CE =GH +BD 即HG +BD =CF ；（3）如图所示，在直线l 上位于C 点右侧取一点E 使得∠AED =60°，连接AE ，在直线l 上位于D 点左侧取一点M 使得BM =BD ，设AB 与直线l 交于N∵∠BDC =60°，BM =BD ，∴△BDM 是等边三角形，∴∠DBM =∠DMB =60°，∵三角形ABC 是等边三角形，∴∠ABC =∠BAC =60°，AC =BC∴∠ABM +∠CBM =∠ABM +∠ABD，∴∠ABD =∠CBM ，∵∠BAC =∠BDC =60°，∠ANE =∠DNB ，∴∠ACE =∠ABD =∠CBM ，∵∠CMB =180°-∠DMB =120°，∠AEC =180°-∠AED =120°，∴∠CMB =∠AEC ，在△AEC 和△CMB 中，120ACE CBM AEC CMB AC CB Ð=ÐìïÐ=Ð=íï=îo ，∴△AEC ≌△CMB （AAS ），∴CE =BM =BD ；∵∠AFH =120°，∴∠AFC +∠GFH =60°，∵∠GFH +∠FHG =180°-∠HGF =60°，∴∠AFC =∠FHG ，在△AEF 和△FGH 中，120AFE FHG AEF FGH AF FH Ð=ÐìïÐ=Ð=íï=îo ，∴△AEF ≌△FGH （AAS ），∴HG =EF ，∴EF =CE +CF =CF +BD 即CF =EF -BD ．故答案为：CF =EF -BD ．【点睛】本题主要考查了全等三角形的性质与判定，等边三角形的性质与判定，三角形内角和定理，解题的关键在于能够熟练掌握全等三角形的性质与判定条件．9.（2021·云南昆明·八年级期中）阅读下面材料：【原题呈现】如图1，在V ABC 中，∠A ＝2∠B ，CD 平分∠ACB ，AD ＝2.2，AC ＝3.6，求BC 的长．【思考引导】因为CD 平分∠ACB ，所以可在BC 边上取点E ，使EC ＝AC ，连接DE ．这样很容易得到V DEC ≌V DAC ，经过推理能使问题得到解决（如图2）．【问题解答】（1）参考提示的方法，解答原题呈现中的问题；（2）拓展提升：如图3，已知V ABC 中，AB ＝AC ，∠A ＝20°，BD 平分∠ABC ，BD ＝2.3，BC ＝2．求AD 的长．【答案】（1）5.8；（2）4.3【分析】（1）由已知条件和辅助线的作法，证得△ACD ≌△ECD ，得到AD ＝DE ，∠A ＝∠DEC ，由于∠A ＝2∠B ，推出∠DEC ＝2∠B ，等量代换得到∠B ＝∠EDB ，得到△BDE 是等腰三角形，得出AC ＝CE ＝3.6，DE ＝BE ＝2.2，相加可得BC 的长；（2）在BA 边上取点E ，使BE ＝BC ＝2，连接DE ，得到△DEB ≌△DBC （SAS ），在DA 边上取点F ，使DF ＝DB ，连接FE ，得到△BDE ≌△FDE ，即可推出结论．【详解】解：（1）如图2，在BC 边上取点E ，使EC ＝AC ，连接DE ．在△ACD 与△ECD 中，AC CE ACD ECD CD CD =ìïÐ=Ðíï=î，∴△ACD ≌△ECD （SAS ），∴AD ＝DE ，∠A ＝∠DEC ，∵∠A ＝2∠B ，∴∠DEC ＝2∠B ，∴∠B ＝∠EDB ，∴△BDE 是等腰三角形；∴BE ＝DE ＝AD ＝2.2，AC ＝EC ＝3.6，∴BC 的长为5.8；（2）∵△ABC 中，AB ＝AC ，∠A ＝20°，∴∠ABC ＝∠C ＝80°，∵BD 平分∠B ，∴∠1＝∠2＝40°，∠BDC ＝60°，在BA 边上取点E ，使BE ＝BC ＝2，连接DE ，在△DEB 和△DBC 中，12BE BC BD BD =ìïÐ=Ðíï=î，∴△DEB ≌△DBC （SAS ），∴∠BED ＝∠C ＝80°，∴∠4＝60°，∴∠3＝60°，在DA 边上取点F ，使DF ＝DB ，连接FE ，同理可得△BDE ≌△FDE ，∴∠5＝∠1＝40°，BE ＝EF ＝2，∵∠A ＝20°，∴∠6＝20°，∴AF ＝EF ＝2，∵BD ＝DF ＝2.3，∴AD ＝BD +BC ＝4.3．【点睛】本题考查了全等三角形的性质与判定，等腰三角形的性质，熟悉这些定理是解决本题的关键．10．（2022·广东东莞·八年级期末）（1）如图1，在四边形ABCD 中，AB ＝AD ，∠B ＝∠D ＝90°，E 、F分∠BAD，线段EF、BE、FD之间的关系是；（不需要证明）别是边BC、CD上的点，且∠EAF＝12（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝1∠BAD，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证2明．（3）如图3，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF ∠BAD，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并＝12证明．【答案】（1）EF＝BE+FD；（2）（1）中的结论仍然成立，见解析；（3）结论不成立，EF＝BE﹣FD，见解析【分析】（1）延长CB至G，使BG＝DF，连接AG，证明△ABG≌△ADF，根据全等三角形的性质得到AG ＝AF，∠BAG＝∠DAF，再证明△GAE≌△FAE，根据全等三角形的性质得出EF＝EG，结合图形计算，证明结论；（2）延长CB至M，使BM＝DF，连接AM，仿照（1）的证明方法解答；（3）在EB上截取BH＝DF，连接AH，仿照（1）的证明方法解答．【详解】解：（1）EF＝BE+FD，理由如下：如图1，延长CB至G，使BG＝DF，连接AG，在△ABG 和△ADF 中，90AB AD ABG D BG DF °=ìïÐ=Ð=íï=î，∴△ABG ≌△ADF （SAS ），∴AG ＝AF ，∠BAG ＝∠DAF ，∵∠EAF ＝12∠BAD ，∴∠DAF +∠BAE ＝∠EAF ，∴∠GAE ＝∠BAG +∠BAE ＝∠DAF +∠BAE ＝∠EAF ，在△GAE 和△FAE 中，AG AF GAE FAE AE AE =ìïÐ=Ðíï=î，∴△GAE ≌△FAE （SAS ），∴EF ＝EG ，∵EG ＝BG +BE ＝BE +DF ，∴EF ＝BE +FD ，故答案为：EF ＝BE +FD ；（2）（1）中的结论仍然成立，理由如下：如图2，延长CB 至M ，使BM ＝DF ，连接AM ，∵∠ABC +∠D ＝180°，∠ABC +∠1＝180°，∴∠1＝∠D ，在△ABM 和△ADF 中，1AB AD D BM DF =ìïÐ=Ðíï=î，∴△ABM ≌△ADF （SAS ），∴AM ＝AF ，∠3＝∠2，∵∠EAF ＝12∠BAD ，∴∠2+∠4＝∠EAF ，∴∠EAM ＝∠3+∠4＝∠2+∠4＝∠EAF ，在△MAE 和△FAE 中，AM AF MAE FAE AE AE =ìïÐ=Ðíï=î，∴△MAE ≌△FAE （SAS ），∴EF ＝EM ，∵EM ＝BM +BE ＝BE +DF ，∴EF ＝BE +FD ；（3）（1）中的结论不成立，EF ＝BE ﹣FD ，理由如下：如图3，在EB 上截取BH ＝DF ，连接AH ，同（2）中证法可得，△ABH ≌△ADF ，∴AH ＝AF ，∠BAH ＝∠DAF ，∴∠HAE ＝∠FAE ，在△HAE 和△FAE 中，AH AF HAE FAE AE AE =ìïÐ=Ðíï=î，∴△HAE ≌△FAE （SAS），EF EH\=∵EH ＝BE ﹣BH ＝BE ﹣DF ，∴EF ＝BE ﹣FD ．【点睛】本题考查了三角形全等的性质与判定，掌握三角形全等的性质与判定是解题的关键．11．（2022·四川南充·八年级期末）（1）阅读理解：问题：如图1，在四边形ABCD 中，对角线BD 平分ABC Ð，180A C Ð+Ð=°．求证：DA DC =．思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题．方法1：在BC 上截取BM BA =，连接DM ，得到全等三角形，进而解决问题；方法2：延长BA 到点N ，使得BN BC =，连接DN ，得到全等三角形，进而解决问题．结合图1，在方法1和方法2中任选一种，添加辅助线并完成证明．（2）问题解决：如图2，在（1）的条件下，连接AC ，当60DAC Ð=°时，探究线段AB ，BC ，BD 之间的数量关系，并说明理由；（3）问题拓展：如图3，在四边形ABCD 中，180A C Ð+Ð=°，DA DC =，过点D 作DE BC ^，垂足为点E ，请直接写出线段AB 、CE 、BC 之间的数量关系．【答案】（1）证明见解析；（2）AB BC BD +=；理由见解析；（3）2BC AB CE -=．【分析】（1）方法1：在BC 上截取BM BA =，连接DM ，得到全等三角形，进而解决问题；方法2：延长BA 到点N ，使得BN BC =，连接DN ，得到全等三角形，进而解决问题；（2）延长CB 到点P ，使BP BA =，连接AP ，证明ΔΔPAC BAD ≌，可得PC BD =，即PC BP BC AB BC=+=+（3）连接BD ，过点D 作DF AC ^于F ，证明ΔΔDFA DEC ≌，RtΔRtΔBDF BDE ≌，进而根据2BC BE CE BA AF CE BA CE =+=++=+即可得出结论．【详解】解：（1）方法1：在BC 上截BM BA =，连接DM ，如图．BD Q 平分ABC Ð，ABD CBD \Ð=Ð．在ΔABD 和ΔMBD 中，BD BD ABD MBD BA BM =ìïÐ=Ðíï=î，ΔΔABD MBD \≌，A BMD \Ð=Ð，AD MD =．180BMD CMD °Ð+Ð=Q ，180C A °Ð+Ð=．C CMD \Ð=Ð．DM DC \=，DA DC \=．方法2：延长BA 到点N ，使得BN BC =，连接DN ，如图．BD Q 平分ABC Ð，NBD CBD \Ð=Ð．在ΔNBD 和ΔCBD 中，BD BD NBD CBD BN BC =ìïÐ=Ðíï=î，ΔΔNBD CBD \≌．BND C \Ð=Ð，ND CD =．180NAD BAD °Ð+Ð=Q ，180C BAD °Ð+Ð=．BND NAD \Ð=Ð，DN DA \=，DA DC \=．（2）AB 、BC 、BD 之间的数量关系为：AB BC BD +=．（或者：BD CB AB -=，BD AB CB -=）．延长CB 到点P ，使BP BA =，连接AP ，如图2所示．由（1）可知AD CD =，60DAC °Ð=Q ．ΔADC \为等边三角形．AC AD \=，60ADC °Ð=．180BCD BAD °Ð+Ð=Q ，36018060120ABC °°°°\Ð=--=．18060PBA ABC °°\Ð=-Ð=．BP BA =Q ，ΔABP \为等边三角形．60PAB °\Ð=，AB AP =．60DAC °Ð=Q ，PAB BAC DAC BAC \Ð+Ð=Ð+Ð，即PAC BAD Ð=Ð．在ΔPAC 和ΔBAD 中，PA BA PAC BAD AC AD =ìïÐ=Ðíï=î，ΔΔPAC BAD \≌．PC BD \=，PC BP BC AB BC =+=+Q ，AB BC BD \+=．（3）AB ，CE ，BC 之间的数量关系为：2BC AB CE -=．（或者：2BC CE AB -=，2AB CE BC +=）解：连接BD ，过点D 作DF AC ^于F ，如图3所示．180BAD C °Ð+Ð=Q ，180BAD FAD °Ð+Ð=．FAD C \Ð=Ð．在ΔDFA 和ΔDEC 中，DFA DEC FAD C DA DC Ð=ÐìïÐ=Ðíï=î，ΔΔDFA DEC \≌，DF DE \=，AF CE =．在RtΔBDF 和RtΔBDE 中，BD BD DF DE =ìí=î，RtΔRtΔ\≌．BDF BDE\=，BF BE\=+=++=+，2BC BE CE BA AF CE BA CE\-=．BC BA CE2【点睛】本题考查了三角形全等的性质与判定，正确的添加辅助线是解题的关键．。

三角形全等之手拉手模型-倍长中线-截长补短法-旋转-寻找三角形全等与方法归纳总结

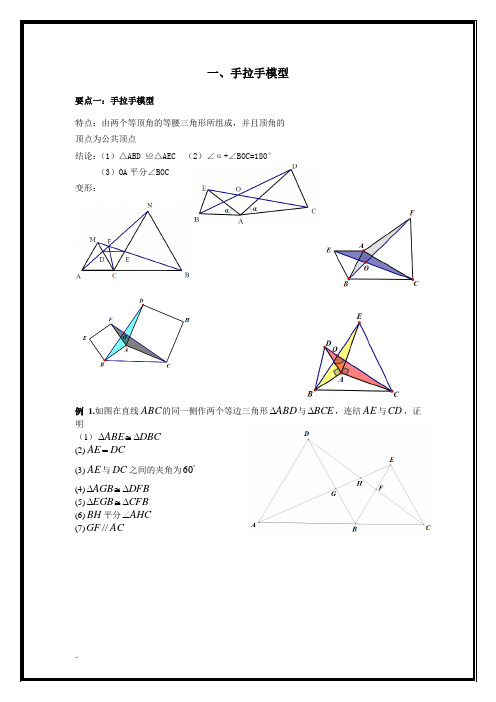
一、手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180° （3）OA 平分∠BOC 变形：例 1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ∠？二、倍长与中点有关的线段倍长中线类☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

八年级数学全等三角形专题-三角形的旋转、翻折与线段的截长补短

全等三角形专题 - 三角形的旋转、翻折与线段的截长补短经典例题透析类型一：由角平分线想到构造全等不管轴对称图形还是两个图形轴对称，我们不难发现对应点与轴上一点（此点作为顶点）组成的角被轴平分，根据这一特点，在做题中如果遇到角平分线我们就会联想到，以角平分线为轴构造对称（全等），从而把角、线段转移达到解题目的．．如图 1，等腰梯形 ABCD 中， AD ∥BC ，∠ DBC=45 °，翻折梯形 ABCD ，使点 B 与点 D 重合，折痕分别交 AB 、BC 于点 F 、E ．若 AD=2 ，BC=8 ．求 BE 的长．解析：由题意得△BFE ≌△ DFE ，∴ BE=DE ，在△ BDE 中， ED=BE ，∠ DBE=45 °，∴ ∠BDE= ∠DBE=45 °，∴ ∠DEB=90 °，即 DE ⊥BC ，在等腰梯形中， AD=2 ， BC=8 ，过 A 作 AG ⊥ BC ，交 BC 于 G ，如图 2，∴ △EDG ≌△ AGD ，∴GE=AD=2 ，在 Rt △ABG 和Rt △DCE 中， AB=DC ，AG=DE ， ∴ Rt △ABG ≌Rt △DCE ，∴ BG=CE ，∴ ，∴ BE=5 ．图3 解析：如图 4，作∠ B 的平分线交 AC 于D ，则∠ A= ∠ABD ，∠ BDC=2∠A=∠C ∴AD=BD=BC作 BM ⊥AC 于 M ，则 CM=DM．图2 图43．如图 5，已知梯形 ABCD 中，AB∥CD，AD>BC，求证： AC>BD图 5 图 6 解析：如图 6，作DE∥AC，DF∥BC，交 BA 或延长线于点 E、F，四边形 ACDE 和四边形 BCDF 都是平行四边形．∴ DE=AC ， DF=BC ， AE=CD=BF作 DH ⊥ AB 于 H，根据勾股定理，，∵ AD > BC ，AD >DF∴ AH > FH，EH >BH，∴ DE>BD ，即 AC > BD.4．如图 7，已知△ ABC 中， AD ⊥ BC，AB+CD=AC+BD ．求证： AB=AC ．图7解析：设 AB 、AC 、BD 、，CD 分别为 b、c、m、n，则 c+n=b+m ，c-b=m-n ，∵ AD ⊥ BC，根据勾股定理，得， ∵ c+b> m+n ，∴ c-b=0 即 c=b ，∴ AB=AC ．类型二：勾股定理的逆定理的运用5．如图 8，P 是正△ ABC 内的一点，且 PA=6，PB=8，PC=10，若将△ PAC 绕点A 旋转后，得到，则点 P 与点之间的距离为解析：如图 9，连结，是由旋转得到的，所以 ≌所以 . .所以三角形是等边三角形，．则在三角形中．所以是直角，．，∠ APB= 6．如图 10，已知∠ ABC=30 °，∠ ADC=60 °，AD=DC ．求证：．根据勾股定理有，即．7．如图 12， D 为等腰△ ABC 的腰 AB 上的一点， E 为另一腰 AC 延长线上的一点，且 BD=CE ，则 A．DE=BC C．DE<BCB．DE>BC解析：如图 13，分别过 D 和E点作到BC 边的垂线，交 BC 及其延长线于 G和H．则根据，可得到△ BDG≌△ ECH. 所以 BG=CH ．所以 BC=GH ．显然 DE >GH. 所以 DE>BC.．如图 14，已知等边△ ABC 内有一点 N，ND⊥BC，NE⊥AB ，NF⊥AC，D、E、F 都是垂足，M 是△ABC 中异于 N 的另一点，若，图 15 解析：如图15，作 M 到正三角形的各边上的高，根据面积相等的关系，有，分别化简为所以．而根据直角三角形斜边与直角边的关系有，，．所以有． 9．如图 16，梯形 ABCD 中，AD ∥BC ，E 是 AB 的中点， CE 恰好是平分∠BCD ，若 AD=3 ， BC=4，则 CD 的长是A ．5B ．6C ． 7D ．8图 18 解析：作△ ABC 的高 h ，那么 BC=2h ．而 BE=2h ．所以 BE=BC ．解析：根据三角形的面积公式，可知，而根据，可得到解析：如图 17，延长 CE 交 DA 的延长线于 F ，则容易证明△ BEC ≌△AEF ，于是可得到 ∠ DCE= ∠ BCE= ∠ AFE ，所以 △ FCD 是等腰三角形，CD=AD+AF=710 ．如图 18，在等腰直角△ ABC 中，∠BAC=90 E ，使∠ EBC=30 °，则 BE 和 BC 的大小关系是（）， AD ∥ BC ，在 AD 上取一点11．已知三角形的两条边长分别为 a=5， b=4 ，它们的高分别为，若那么该三角形的面积是 _______图 17/ + 2ah l L+方：=⅛a ÷ 2bh^+ 方;,所以a3 - 2∣a⅛α+-I^- 2地+⅛J 所以α-⅛fl= ⅛-¼或Q■忙二备".如杲a-h a = b-hb则结合β+⅝≡⅛i+A可得到a=b,矛盾.所以fl"⅛ = ⅛∙i,结合α+∕⅛=⅛+⅛,得到Λ=⅛,所以Aj = 5, 所以三角形的面积为5x4÷2 = 10.。

全等三角形专题三角形的旋转翻折与线段的截长补短

人教版数学八年级上册第12章全等三角形专题课截长补短法教学设计

华师大版 全等三角形辅助线做法之截长补短

三角形全等(旋转与截长补短专题)

初中数学全全等三角形截长补短知识点-+典型题及答案

三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结

三角形全等之截长补短 (整理)

全等三角形截长补短法的经典例题

三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结

第08讲全等三角形中“截长补短”模型

三角形全等之手拉手模型-倍长中线-截长补短法-旋转-寻找三角形全等与方法归纳总结

八年级数学全等三角形专题-三角形的旋转、翻折与线段的截长补短

华师大版全等三角形辅助线做法之截长补短