-河南城建学院高等数学下期末考试题
高数下册期末试题及答案

高数下册期末试题及答案第一部分:选择题(共50题,每题2分,共100分)1. 某函数的导函数为f(x)=3x^2+2x-1,则该函数f(x)在x=1处的导数值为多少?A. 6B. 7C. 8D. 92. 下列哪个极限是不存在的?A. lim(x→∞) 1/(1+x)B. lim(x→0) sin(1/x)C. lim(x→1) (x-1)/(x-1)D. lim(x→∞) e^(-x)3. 物体在空气中自由下落的速度v(t)与时间t之间的关系可以用下列哪个微分方程描述?A. v'(t) = g - kv(t)B. v'(t) = g - ktC. v'(t) = g - kv(t)^2D. v'(t) = g - k/v(t)...第二部分:填空题(共30题,每题3分,共90分)31. 若a=3,b=-2,则方程组3x+ay=1,bx-2y=5的解为x=___,y=___。
32. 设函数f(x)=sin(x),则f''(x) = ___。
33. 若函数f(x)在区间[a,b]上连续,则必在该区间上有___。
...第三部分:解答题(共4题,每题15分,共60分)问题一:已知函数f(x) = x^3 - 3x^2 + 1,求f(x)的极值及对应的取值范围。
解答:首先求导数f'(x) = 3x^2 - 6x,令其等于零,得到极值点x=0和x=2。
将这两个极值点代入原函数f(x),可以求得f(0) = 1和f(2) = -1。
因此,函数f(x)的极值为1和-1,取值范围为[-1, 1]。
问题二:已知函数y = e^x / (1 + e^x),求该函数的反函数及其定义域。
解答:为求反函数,首先将y = e^x / (1 + e^x)改写为x = ln(y / (1-y))。
然后交换x和y,得到y = ln(x / (1-x))。
因此,函数y = ln(x / (1-x))为原函数的反函数。
大学高等数学下考试题库(附答案)

大学高等数学下考试题库(附答案)一、填空题(每题2分,共20分)1. 设函数f(x)在区间I上单调递增,若a < b,则必有__________。
【答案】f(a) < f(b)2. 函数y = e^x在区间(-∞,+∞)上的最小值为__________。
【答案】03. 设函数f(x) = x^3 - 6x + 9,则f'(x) =__________。
【答案】3x^2 - 64. 设矩阵A = [a_{ij}],则矩阵A的行列式det(A) = __________。
【答案】a_{11}a_{22}...a_{nn} -a_{11}a_{23}...a_{n2} + a_{12}a_{21}...a_{n3} - ... + (-1)^(n+1)a_{1n}a_{21}...a_{n1}5. 向量组α = (α1, α2, α3)和β = (β1, β2, β3)垂直的条件是__________。
【答案】α1β1 + α2β2 + α3β3 = 06. 设线性方程组Ax = b的解集为N,则N是__________。
【答案】向量空间7. 若函数f(x)在区间(a,b)上连续,且f(a) = f(b),则函数f(x)在区间(a,b)上必有零点,此结论称为__________。
【答案】零点定理8. 设函数f(x)在区间I上单调递减,若a < b,则必有__________。
【答案】f(a) > f(b)9. 设函数f(x) = ln(x),则f''(x) =__________。
【答案】1/x10. 设矩阵A = [a_{ij}],则矩阵A的逆矩阵A^-1 = __________。
【答案】(1/det(A))[c_{ij}],其中c_{ij} = (-1)^(i+j)det(A)/a_{ii}a_{jj}二、选择题(每题2分,共20分)1. 下列函数在区间(0,1)上单调递增的是__________。
高等数学下考试题库(附答案)

高等数学下考试题库(附答案)一、选择题(每题5分,共25分)1. 设函数f(x)在区间[a, b]上单调递增,且f(a) = 1,f(b) = 2,则下列不等式成立的是:A. f(x) ≥ 1,a ≤ x ≤ bB. f(x) ≤ 2,a ≤ x ≤ bC. f(x) ≥ f(a),a ≤ x ≤ bD. f(x) ≤ f(b),a ≤ x ≤ b答案:C2. 设函数f(x) = x^3 - 3x,其导函数f'(x) =3x^2 - 3,则f'(x)的符号变化点为:A. x = -1 和 x = 1B. x = 0 和 x = 2C. x = -1 和 x = 1D. x = 0 和 x = 1答案:A3. 下列关于极限的叙述正确的是:A. 当x → 0时,sinx → 0B. 当x → ∞时,e^x → ∞C. 当x → -∞时,|x| → ∞D. 当x → a时,x^2 → a^2答案:B4. 设函数f(x) = (x - 1)^2,则f(x)的极值点为:A. x = 1B. x = -1C. x = 0D. x = 2答案:A5. 下列关于积分计算的叙述正确的是:A. 定积分与不定积分具有相同的计算法则B. 定积分的计算结果为数值,不定积分的计算结果为函数C. 被积函数为偶函数时,定积分的计算结果为非负数D. 被积函数为奇函数时,定积分的计算结果为0答案:D二、填空题(每题5分,共25分)1. 设函数f(x) = x^3 - 3x,其导函数为f'(x) = ______。
答案:3x^2 - 32. 函数y = e^x的导数为y' = ______。
答案:e^x3. 定积分$$ ∫_{ a }^{ b }$$f(x)dx的定义为f(x)在[a, b]上的______。
答案:面积4. 设函数f(x) = x^2,则f(x)的极值点为______。
答案:x = 05. 设函数f(x) = sinx,则f(x)的周期为______。
23高数 期末考试试卷(河南城建学院南阳函授站)
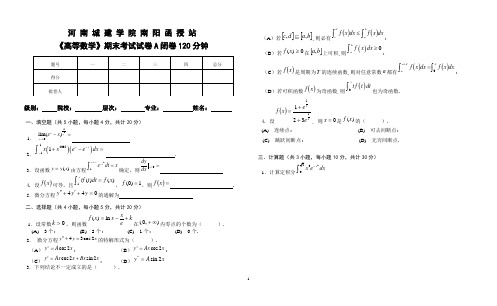
河 南 城 建 学 院 南 阳 函 授 站 《高等数学》期末考试试卷A 闭卷120分钟级别: 院校: 层次: 专业: 姓名:一、填空题(共5小题,每小题4分,共计20分)1. 21lim()x x x e x →-=.2.()()1200511x x x x e e dx --+-=⎰. 3.设函数()y y x =由方程21x y t e dt x +-=⎰确定,则0x dy dx == .4. 设()x f 可导,且1()()x tf t dt f x =⎰,1)0(=f ,则()=x f .5.微分方程044=+'+''y y y 的通解为 .二、选择题(共4小题,每小题5分,共计20分)1.设常数0>k ,则函数k e x x x f +-=ln )(在),0(∞+内零点的个数为( ).(A) 3个; (B) 2个; (C) 1个; (D) 0个. 2. 微分方程43cos 2y y x ''+=的特解形式为( ).(A )cos2y A x *=; (B )cos 2y Ax x *=;(C )cos2sin 2y Ax x Bx x *=+; (D )x A y 2sin *=. 3.下列结论不一定成立的是( ).(A )若[][]b a d c ,,⊆,则必有()()⎰⎰≤bad cdxx f dx x f ;(B )若0)(≥x f 在[]b a ,上可积,则()0b af x dx ≥⎰;(C )若()x f 是周期为T 的连续函数,则对任意常数a 都有()()⎰⎰+=TT a adxx f dx x f 0;(D )若可积函数()x f 为奇函数,则()0x t f t dt⎰也为奇函数.4. 设()xx e ex f 11321++=, 则0=x 是)(x f 的( ).(A) 连续点; (B) 可去间断点;(C) 跳跃间断点; (D) 无穷间断点.三.计算题(共3小题,每小题10分,共计30分) 1.计算定积分230x x e dx-.2.计算不定积分dx x xx ⎰5cos sin .3.求摆线⎩⎨⎧-=-=),cos 1(),sin (t a y t t a x 在2π=t 处的切线的方程.四.应用题(共3小题,每小题10分,共计30分) 1.求由曲线2-=x y 与该曲线过坐标原点的切线及x 轴所围图形的面积.2.设平面图形D 由222x y x +≤与y x ≥所确定,试求D 绕直线2=x 旋转一周所生成的旋转体的体积.3. 设1,a >at a t f t-=)(在(,)-∞+∞内的驻点为 (). t a 问a 为何值时)(a t 最小? 并求最小值.高等数学试题答案一.填空题:1. 21lim()xx x e x →-=21e .2.()()1200511x x x x e e dx --+-=⎰e 4.3.设函数()y y x =由方程21x yt e dt x +-=⎰确定,则0x dydx==1-e .4. 设()x f 可导,且1()()x tf t dt f x =⎰,1)0(=f ,则()=x f 221x e.5.微分方程044=+'+''y y y 的通解为xe x C C y 221)(-+=.二.选择题:1.设常数0>k ,则函数ke x x xf +-=ln )( 在),0(∞+内零点的个数为( B ). (A) 3个; (B) 2个; (C) 1个; (D) 0个. 2. 微分方程x y y 2cos 34=+''的特解形式为 ( C )(A )cos2y A x *=; (B )cos2y Ax x *=; (C )cos2sin2y Ax x Bx x *=+; (D )x A y 2sin *= 3.下列结论不一定成立的是 ( A )(A) (A) 若[][]b a d c ,,⊆,则必有()()⎰⎰≤badcdxx f dx x f ;(B) (B) 若0)(≥x f 在[]b a ,上可积,则()0baf x dx ≥⎰;(C) (C) 若()x f 是周期为T 的连续函数,则对任意常数a 都有()()⎰⎰+=TT a adxx f dx x f 0;(D) (D) 若可积函数()x f 为奇函数,则()0x t f t dt⎰也为奇函数.4. 设()xx e ex f 11321++=, 则0=x 是)(x f 的( C ). (A) 连续点; (B) 可去间断点;(C) 跳跃间断点; (D) 无穷间断点. 三.计算题: 1.计算定积分⎰-2032dxe x x .解:⎰⎰⎰----===202020322121,2t t x tde dt te dx e x t x 则设 -------2⎥⎦⎤⎢⎣⎡--=⎰--200221dt e te t t -------2 2223210221----=--=e e e t --------22.计算不定积分dx x x x ⎰5cos sin .解:⎥⎦⎤⎢⎣⎡-==⎰⎰⎰x dx x x x xd dx x x x 4445cos cos 41)cos 1(41cos sin --------3C x x x x x d x x x +--=+-=⎰tan 41tan 121cos 4tan )1(tan 41cos 43424 -----------3 3.求摆线⎩⎨⎧-=-=),cos 1(),sin (t a y t t a x 在2π=t 处的切线的方程. 解:切点为)),12((a a -π-------22π==t dx dy k 2)c o s 1(s i n π=-=t ta ta 1= -------2切线方程为 )12(--=-πa x a y 即ax y )22(π-+=. -------2四.应用题(每小题9分,3题共27分)1.求由曲线2-=x y 与该曲线过坐标原点的切线及x 轴所围图形的面积.解:设切点为),00y x (,则过原点的切线方程为xx y 2210-=, 由于点),00y x (在切线上,带入切线方程,解得切点为2,400==y x .-----3 过原点和点)2,4(的切线方程为22xy =-----------------------------3面积dyy y s )222(22⎰-+==322-------------------3或 322)2221(2212042=--+=⎰⎰dx x x xdx s2.设平面图形D 由222x y x +≤与y x ≥所确定,试求D 绕直线2=x 旋转一周所生成的旋转体的体积.解: 法一:21V V V -=[][]⎰⎰⎰---=-----=1022121022)1(12)2()11(2dyy ydy y dy y πππ -------6)314(201)1(31423-=⎥⎦⎤⎢⎣⎡--=ππππy --------3 法二:V =⎰---12)2)(2(2dxx x x x π⎰⎰----=101022)2(22)2(2dxx x dx x x x ππ ------------------ 5[]⎰--+--=102234222)22(ππdx x x x x x ππππππππ322134213234141201)2(3222232-=-+=-⎥⎦⎤⎢⎣⎡⨯⨯+-=x x------------- 43. 设1,a >at a t f t-=)(在(,)-∞+∞内的驻点为 (). t a 问a 为何值时)(a t 最小? 并求最小值.解:.ln ln ln 1)(0ln )(a aa t a a a t f t -==-='得由 --------------- 30)(l n 1ln ln )(2ee a a a a a t ==-='得唯一驻点又由------------3.)(,0)(,;0)(,的极小值点为于是时当时当a t e a a t e a a t e a e e e =<'<>'>-----2故.11ln 1)(,)(e e e e t a t e a e e -=-==最小值为的最小值点为--------------1。
高数期末下册考试题及答案

高数期末下册考试题及答案序章数学是一门科学,也是一门工具学科,对于不少学子而言,高等数学一直是一门令人头疼的学科,尤其是对于高数期末考试而言,更是充满了挑战。
本文将提供高数期末下册考试题及答案,以帮助读者更好地准备并且顺利通过这一考试。
第一章:导数与微分题目一:计算以下函数的导数并求出导函数1. $f(x)=3x^2+2x+1$2. $g(x)=\sin(x)-\cos(x)$3. $h(x)=e^x\cdot\ln(x)$题目二:应用题一天中,某商品的销售量随时间变化的规律如下:$Q(t) = 100e^{-0.02t}$,其中时间$t$以小时为单位。
求在第3小时以内的销售量的平均增长速度。
第二章:积分学题目三:求下列不定积分1. $\int (2x^2+3x-1)dx$2. $\int \frac{1}{x}dx$3. $\int \frac{2x+3}{x^2+3x+2}dx$题目四:计算定积分已知函数$f(x)=x^2-3x+2$,计算$\int_0^3 f(x)dx$的值。
第三章:微分方程题目五:求解下列微分方程1. $\frac{dy}{dx}=2x+1$2. $\frac{d^2y}{dx^2}+4\frac{dy}{dx}+4y=0$3. $\frac{d^2y}{dx^2}+9y=\sin(x)$题目六:应用题一个满足空气阻力的物体由高空自由落下,求解物体落地时的速度和位移。
第四章:无穷级数题目七:判断级数是否收敛1. $\sum_{n=1}^\infty \frac{1}{2^n}$2. $\sum_{n=1}^\infty \frac{n}{n^2+1}$3. $\sum_{n=1}^\infty \frac{2^n}{n!}$题目八:计算级数的和计算级数$\sum_{n=1}^\infty \frac{1}{2^n}$的和。
结语通过以上的考题,相信读者们对于高数期末下册考试的复习有了更明确的目标和方向。
高数下册期末考试题及答案

高数下册期末考试题及答案一、选择题(每题2分,共10分)1. 函数 \( f(x) = \ln(x^2 + 1) \) 的导数是:A. \( 2x/(x^2 + 1) \)B. \( 2x/x^2 + 1 \)C. \( 2x/(x^2 - 1) \)D. \( 2x/(x^2 + 1)^2 \)答案:A2. 已知 \( e^x \) 的泰勒展开式为 \( 1 + x + x^2/2! + x^3/3! + \cdots \),那么 \( e^{-x} \) 的泰勒展开式是:A. \( 1 - x + x^2/2! - x^3/3! + \cdots \)B. \( 1 + x - x^2/2! + x^3/3! - \cdots \)C. \( 1 - x - x^2/2! + x^3/3! - \cdots \)D. \( 1 + x + x^2/2! - x^3/3! + \cdots \)答案:A3. 若 \( \int_0^1 x^2 dx = \frac{1}{3} \),则 \( \int_0^1 x^3 dx \) 的值是:A. \( \frac{1}{4} \)B. \( \frac{1}{5} \)C. \( \frac{1}{6} \)D. \( \frac{1}{7} \)答案:A4. 曲线 \( y = x^3 - 3x^2 + 2x \) 在 \( x = 2 \) 处的切线斜率是:A. 0B. 1C. 2D. -1答案:B5. 若 \( \lim_{x \to 0} \frac{\sin x}{x} = 1 \),则\( \lim_{x \to 0} \frac{\sin 2x}{x} \) 等于:A. 1B. 2C. 4D. 8答案:B二、填空题(每题3分,共15分)6. 若 \( f(x) = x^3 - 2x^2 + x \),则 \( f'(x) = \) ________。
高数期末考试题及答案下册

高数期末考试题及答案下册一、选择题(每题2分,共20分)1. 若函数f(x)在点x=a处连续,则下列说法正确的是:A. f(a)存在B. 左极限lim(x→a-) f(x)存在C. 右极限lim(x→a+) f(x)存在D. 所有选项都正确答案:D2. 函数f(x)=x^2在区间[-1,1]上是:A. 单调递增函数B. 单调递减函数C. 有增有减函数D. 常数函数答案:C3. 若f(x)=sin(x),则f'(x)是:A. cos(x)B. -sin(x)C. x*cos(x)D. x*sin(x)答案:A4. 函数f(x)=x^3-6x^2+11x-6的零点个数为:A. 0B. 1C. 2D. 3答案:D5. 曲线y=x^2与直线y=4x在第一象限的交点坐标为:A. (1,1)B. (2,8)C. (4,16)D. (0,0)答案:B6. 若∫(0,1) f(x)dx = 2,则∫(0,1) x*f(x)dx的值为:A. 0B. 1C. 2D. 无法确定答案:B7. 函数f(x)=ln(x)的泰勒展开式在x=0处的前两项为:A. 1-xB. x-x^2/2C. -x^2/2D. -1-x答案:D8. 若函数f(x)在区间(a,b)内可导,且f'(x)>0,则f(x)在该区间内是:A. 单调递减函数B. 单调递增函数C. 有增有减函数D. 常数函数答案:B9. 函数f(x)=e^x的无穷级数展开式为:A. 1+x+x^2/2!+x^3/3!+...B. 1-x+x^2-x^3+...C. 1+x-x^2+x^3-...D. 1-x-x^2+x^3-...答案:A10. 若函数f(x)在区间[a,b]上连续,则∫(a,b) f(x)dx:A. 一定存在B. 可能不存在C. 等于0D. 等于f(a)-f(b)答案:A二、填空题(每题2分,共20分)1. 若函数f(x)在点x=a处可导,则f'(a)表示______。
高等数学期末考试试题及解答

高等数学(下)期末试题(2)二、填空题(每题3分,总计15分)。
1、函数22(,)22f x y x ax xy y =+++在点(1,1)-处取得极值,则常数a =______。
2、若曲面2222321x y z ++=的切平面平行于平面46250x y z -++=,则切点坐标为______________________。
3、二重积分3110x ydyye dx -蝌的值为______________。
5、微分方程2yy x y ¢=+的通解为_____________________。
三、计算题(每题7分,总计35分)。
2、设(,)z f x y xy =-具有连续的二阶偏导数,求2z x y¶抖。
3、将函数23()2f x x x=--展开成x 的幂级数,并指出收敛域。
4、设)(x y y 满足方程322x y y y e ⅱ?-+=,且其图形在点)1,0(与曲线21y x x =-+相切,求函数)(x y 。
5、计算222Ldsx y z++ò,其中L 是螺旋线8cos ,8sin ,x t y t z t ===对应02t p#的弧段。
四、计算题(每题7分,总计35分)。
1、设0a >,计算极限23123lim ()n n na a a a??++++的值。
2、计算z dv W蝌?,其中W 由不等式z ?22214x y z ?+?所确定。
4、将函数()(11)f x x x =-#展开成以2为周期的傅立叶级数。
5、设函数)(x f 具有连续导数并且满足(1)3f =,计算曲线积分22(())(())Ly f x x dx x f x y dy +++ò的值,假定此积分在右半平面内与路径无关,曲线L 是由)2,1(到)1,2(的任一条逐段光滑曲线。
五、本题5分。
对0p >,讨论级数11(1)nn n n p¥+=-å的敛散性。
24、固体废物处置-期末考试试卷——答案(河南城建学院南阳函授站)

河南城建学院南阳函授站《高等数学》期末考试试卷A闭卷120分钟级别:院校:层次:专业:姓名:一、填空题(25分)1.固体废物污染控制的“3R”原则指的是减少产生Reduce、再利用Reuse、再循环Recycle。
2.生活垃圾的收集、运输分为搬运与贮存(运贮)、清除与收集(清运)、转运三个阶段。
3.固体废物进行燃烧必须具备的三个基本条件是:可燃物质、助燃物质和引燃火源,并在着火条件下才会着火燃烧。
4.目前在垃圾焚烧中应用最广的生活垃圾焚烧炉,主要有流化床焚烧炉、机械炉排焚烧炉、旋转窑焚烧炉3种类型。
5.根据固化剂及固化过程的不同,目前常用的固化技术主要包括水泥固化、沥青固化、塑料固化、熔融固化、石灰固化。
6.固体废弃物的水分存在形式有间隙水,毛细管水,表面吸附水和内部水。
7.浮选所需药剂有捕收剂、起泡剂、调整剂。
8.厌氧消化分为水解,产酸和产甲烷三个阶段。
二、选择题(20分)1.城市生活垃圾的产污系数一般用每人每天的垃圾产量来表示,下面给出的数据,哪一个更接近我国目前大中城市的实际垃圾产污系数 B kg/人.天A. 0.5-0.7B. 0.7-1.5C. 1.5-2.0D.2.0-2.52.重介质分选时,下列物质中常用来作为重介质的为 B 。
A.粉煤灰 D. 硅铁 C. 粘土 D.炉渣3.通常采用浓缩法去除的是污泥中的 A 。
A.间隙水B.毛细水C. 表面吸附水D.内部结合水4.生活垃圾焚烧过程中,停留时间最长的阶段是 C 。
A. 干燥段B. 燃烧段C. 燃烬段5.我国“城市生活垃圾堆肥处理厂技术评价指标”中规定:堆肥产品的含水率必须小于 C 。
A. 20%B. 30%C.35%D. 40%6.根据世界各国垃圾焚烧炉的使用情况, A 焚烧炉应用最广且技术比较成熟,其单台日处理量的范围也最大。
A.机械炉排式B. 流化床C. 回转窑式D. 熔融气化7.对于高放射性的固体废物,主要采用 B 法进行固化处理。
河南城建学院--高数期末08-09

a
0
4.积分
2
1 cos 2xdx ___2___2___ .
2
5.方程y y 2x满足条件y(0) 2的特解为_y___4_e_x __2_x___2.
二、单项选择题(每小题3分,共15分)
1. f ( x) x 2 在点x 2处的导数是( D ) ( A). 1; (B). 0; (C). 1; (D) .不存在
)2
(dy dt
)2
a2(1 cos t)2
a2 sin2 t
P283例12
a 1 2cos t cos2 t sin2 t
a 2(1 cos t) y
x a (t sin t)
y
a
(1
cos
t)
(a
0)
2π
s 0 a 2(1 cos t) d t
2π
t
2a sin d t
dt
11 dt
0 1t
0 1
1
et 1
et
e
t
dt
[
ln(1
t
)]10
[t ln(1 et )]01 ln 2 ln(1 e).
P270T13.
求
2
0
解:令x 1 t,
f (x
则x
1)dx , 其中f
1 t,dx
(x)
dt,
1 1
1, x 1 ex
x0 ,x0
t
)]10
[t ln(1 et )]01 ln 2 ln(1 e).
六、解答题(每题6分,共12分)
1.求曲线 y lnsec x 在点( x, y) 处的曲率及曲率半径.
解:y tan x; y sec2 x;
2020-2021大学《高等数学》(下)期末课程考试试卷A4(含答案)

2020-2021《高等数学》(下)期末课程考试试卷A4适用专业: 考试日期:试卷类型:闭卷 考试时间:120分钟 试卷总分:100分一. 填空题:(共5小题,每小题3分,共15分)1. 方程7100y y y '''++=的通解为2. 求Lds ⎰= 其中22:9L x y +=3.改变积分顺序220(,)xxdx f x y dy ⎰⎰= .4.级数013nn ∞=⎛⎫⎪⎝⎭∑的和为5.()()(),0,0sin lim→=x y xy xy. 二.单项选择. (共5小题,每小题3分,共15分)1. 设D 为圆域: 224x y +≤,曲面1D 是D 在第一象限中的部分.则有( ). (A) 14DD xd xd σσ=⎰⎰⎰⎰ (B) 14DD yd yd σσ=⎰⎰⎰⎰(C) 14DD xyd xyd σσ=⎰⎰⎰⎰ (D) 122224DD x y d x y d σσ=⎰⎰⎰⎰.2. lim 0n n u →∞=是级数∑∞=1n n u 收敛的( )(A)充分条件 (B)必要条件 (C)充要条件 (D)无关条件. 3.积分 ()(),,LP x y dx Q x y dy +⎰与路径无关的充要条件是( )(A)P Q y x ∂∂=∂∂ (B) P Q y x∂∂=-∂∂ (C) P Q x y ∂∂=∂∂ (D)P Q y y ∂∂=∂∂ 4. 函数223246ux y y x z 在原点沿(2,3,1)l 方向的方向导数u l( )(A).(B).(C).(D). 5. 级数111(1)n n n ∞-=-∑为( )级数(A).收敛 (B). 发散 (C).既不收敛也不发散 (D)既收敛也发散 三、解下列各题。
(共4小题,每小题10分,共40分)1. 设2sin =z x y ,求全微分dz 。
2.证明曲线积分()()()()2,02,0sin cos xx ey y dx e y x dy -+++⎰在整个平面内与路径无关,并计算积分值3.求过点12,1,3⎛⎫ ⎪⎝⎭的平面,使它与三个坐标面在第一象限内所围成的立体体积最小。
高等数学(下)试卷

高等数学(下册)考试试卷(一)一、填空题(每小题3分,共计24分)1、 z =)0()(log 22>+a y x a 的定义域为D= 。
2、二重积分⎰⎰≤++1||||22)ln(y x dxdy y x 的符号为 。
3、由曲线x y ln =及直线1+=+e y x ,1=y 所围图形的面积用二重积分表示为 ,其值为 。
4、设曲线L 的参数方程表示为),()()(βαψϕ≤≤⎩⎨⎧==x t y t x 则弧长元素=ds 。
5、设曲面∑为922=+y x 介于0=z 及3=z 间的部分的外侧,则=++⎰⎰∑ds y x )122( 。
6、微分方程xyx y dx dy tan +=的通解为 。
7、方程04)4(=-y y 的通解为 。
8、级数∑∞=+1)1(1n n n 的和为 。
二、选择题(每小题2分,共计16分)1、二元函数),(y x f z =在),(00y x 处可微的充分条件是( ) (A )),(y x f 在),(00y x 处连续;(B )),(y x f x ',),(y x f y '在),(00y x 的某邻域内存在;(C ) y y x f x y x f z y x ∆'-∆'-∆),(),(0000当0)()(22→∆+∆y x 时,是无穷小;(D )0)()(),(),(lim2200000=∆+∆∆'-∆'-∆→∆→∆y x yy x f x y x f z y x y x 。
2、设),()(x y xf y x yf u +=其中f 具有二阶连续导数,则2222yuy x u x ∂∂+∂∂等于( )(A )y x +; (B )x ; (C)y ; (D)0 。
3、设Ω:,0,1222≥≤++z z y x 则三重积分⎰⎰⎰Ω=zdV I 等于( )(A )4⎰⎰⎰20213cos sin ππϕϕϕθdr r d d ;(B )⎰⎰⎰2012sin ππϕϕθdr r d d ;(C )⎰⎰⎰ππϕϕϕθ202013cos sin dr r d d ;(D )⎰⎰⎰ππϕϕϕθ2013cos sin dr r d d 。
高数下期末基础试题及答案

高数下期末基础试题及答案一、选择题(每题5分,共20分)1. 以下哪个选项是洛必达法则的适用条件?A. 0/0型未定式B. ∞/∞型未定式C. 0×∞型未定式D. ∞-∞型未定式答案:A2. 函数f(x)=x^3-3x在x=0处的导数是:A. -3B. 0C. 3D. 1答案:B3. 以下哪个选项是定积分的几何意义?A. 曲线下的面积B. 曲线上的长度C. 曲线的斜率D. 曲线的曲率答案:A4. 以下哪个选项是泰勒级数展开的一般形式?A. f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + ...B. f(x) = f(a) - f'(a)(x-a) + f''(a)(x-a)^2/2! + ...C. f(x) = f(a) + f'(a)(x-a) - f''(a)(x-a)^2/2! + ...D. f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! - ...答案:A二、填空题(每题5分,共20分)1. 函数f(x)=x^2-4x+4在x=2处的极值是________。
答案:02. 曲线y=x^3-3x^2+2在点(1,0)处的切线斜率是________。
答案:-23. 定积分∫<sub>0</sub><sup>1</sup>x^2dx的值是________。
答案:1/34. 函数f(x)=e^x的泰勒级数展开式在x=0处的前三项是________。
答案:1+x+x^2/2!三、解答题(每题10分,共20分)1. 求函数f(x)=x^3-6x^2+11x-6在区间[1,3]上的最大值和最小值。
答案:首先求导数f'(x)=3x^2-12x+11。
令f'(x)=0,解得x=1或x=11/3。
河南城建学院--线性代数

线内不要答题☆河南城建学院2学年第二学期期末考试《线性代数》试题(A卷)本套试卷共3 页一.选择题(每小题3分,共15分)1、设A、B均为n阶方阵,且满足等式0AB=,则必有()(A)0A=或0B=;(B)0A B+=;(C)||0A=或||0B=;(D)||||0A B+=.2、设12,x xηη==都是方程Ax b=的解,则()(A)12ηη+也是Ax b=的解;(B)12ηη-也是0Ax=的解;(C)12ηη-是Ax b=的解;(D)12ηη+是0Ax=的解;3、设))2(3(,3241321EF⎪⎪⎪⎭⎫⎝⎛=是3阶单位矩阵的第3行(列)乘以2所得的初等方阵,则FE))2(3(等于()(A)⎪⎪⎪⎭⎫⎝⎛3281621(B)⎪⎪⎪⎭⎫⎝⎛4132321(C)⎪⎪⎪⎭⎫⎝⎛3214231(D)⎪⎪⎪⎭⎫⎝⎛64413214.下列选项中,两向量组是等价关系的为()(A)⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫⎝⎛=611433:112521:2121bbBaaA(B)⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=251453:11112:2121bbBaaA(C)⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=1224:1121:2121bbBaaA(D)⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=251453:111:2121bbBaaA5.下列说法错误的为()(A)n阶方阵A满足||0A=,则nAR<)(。
(B)4个三维列向量组成的向量组一定线性相关。
(C)若向量组12,,ma a aL线性相关,则1a可由2,ma aL线性表示。
(D)若向量组12,,,ma a aL线性相关,则向量组121,,,,m ma a a a+L必线性相关。
二.填空题(每小题3分,共15分)1.五阶行列式中,1425324351a a a a a 前符号为 . 2.设⎪⎪⎪⎭⎫ ⎝⎛=032810621A ,则32a代数余子式为 .3. 设A 是3阶方阵,且5=A ,则行列式=-A 2 .4.已知:01101,10211A B -⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭,则T TB A = .5.设1122233123,2,3,βααβααβααα=+=-=+-则123,,βββ线性 . (相关、无关)三.计算题(本题共6小题,每题10分,共60分)1.计算行列式2726222001435430---2. 设B A AB A 2,321011330+=⎪⎪⎪⎭⎫⎝⎛-=,求B3.设有线性方程组123123123(1)0(1)3(1)x x x x x x x x x λλλλ+++=⎧⎪+++=⎨⎪+++=⎩, 问λ取何值时,此方程组(1)有唯一解; (2)无解; (3)有无穷多解. (10分)4.求下列矩阵的列向量组的一个最大无关组,并把其余列向量用最大无关组线性表示。
河南城建下终考试题usr

(B)绝对收敛;
(D)敛散性不能确定.
4、 与向量a=(1,0,- 1) 垂直的单位向量是(D)
(A)(- 1,0,1)
5、级
(A)条件收敛;
(C)绝对收敛;
(B)发散;
(D)敛散性无法确定.
三、 计算下列各题(共38分)
1、设 z= f(x,y)由方程z=e 2x-32+2y 确定,求dz. 解:令F(x,y,z)=z-e 2x-3z-2y 则
08-- 09( 下)终考试题
1
一、填空题(每小题3分,共15分)
1、若直线L: 平行,则m= -4
与平面x-2y+3z- 1=0,
2、 曲线积分fe' x²+y²ds = 6πe 3 .其中L 为x²+y²=9 一 周
L
3、 函数z=xe² 在点P(1,0) 处沿着从点P(1,0)到点Q(2,- 1) 的 方向的方向导数是
1.将函数 域
开为(x+2)的幂级数并给出收敛
<1
2.确定级数
解:∵
的收敛域及和函数.
对端点x=1, 级数为交错级数
对端点x=- 1, 级数为
发散.
?
所以,级数的收敛域为(一1,1)
收敛;
当x∈[-1,1],设 .
,显然 s(0)=0,
两边积分得
解方程组
得唯一驻点:(0,e⁻')
第二步判别.求二阶偏导数
B
在点(0,e⁻') 处A=2(2+e⁻²),B-O,
C=e,
A
AC-B²>0
-1
A>0,
∴ f(0,e )=-e
为板小值
5、 计算曲面积分 其中 ∑是抛物面
高等数学(下)期末复习题(附答案)

《高等数学〔二〕》期末复习题一、选择题1、假设向量b 与向量)2,1,2(-=a 平行,且满足18-=⋅b a ,则=b 〔 〕 〔A 〕 )4,2,4(-- 〔B 〕(24,4)--, 〔C 〕 (4,2,4)- 〔D 〕(4,4,2)--.2、在空间直角坐标系中,方程组2201x y z z ⎧+-=⎨=⎩代表的图形为 ( )〔A 〕直线 (B) 抛物线 〔C 〕 圆 (D)圆柱面 3、设22()DI x y dxdy =+⎰⎰,其中区域D 由222x y a +=所围成,则I =〔 〕 (A)2240a d a rdr a πθπ=⎰⎰ (B) 22402ad a adr a πθπ=⎰⎰(C)223023ad r dr a πθπ=⎰⎰(D) 2240012a d r rdr a πθπ=⎰⎰4、 设的弧段为:230,1≤≤=y x L ,则=⎰L ds 6 〔 〕 〔A 〕9 (B) 6 〔C 〕3 (D)23 5、级数∑∞=-11)1(n nn的敛散性为 〔 〕 〔A 〕 发散 (B) 条件收敛 (C) 绝对收敛 (D) 敛散性不确定 6、二重积分定义式∑⎰⎰=→∆=ni i i i Df d y x f 10),(lim),(σηξσλ中的λ代表的是〔 〕〔A 〕小区间的长度 (B)小区域的面积 (C)小区域的半径 (D)以上结果都不对 7、设),(y x f 为连续函数,则二次积分⎰⎰-1010d ),(d x y y x f x 等于 ( )〔A 〕⎰⎰-1010d ),(d xx y x f y (B) ⎰⎰-1010d ),(d yx y x f y(C)⎰⎰-x x y x f y 1010d ),(d(D)⎰⎰11d ),(d x y x f y8、方程222z x y =+表示的二次曲面是 ( )〔A 〕抛物面 〔B 〕柱面 〔C 〕圆锥面 〔D 〕 椭球面 9、二元函数),(y x f z =在点),(00y x 可微是其在该点偏导数存在的〔 〕. 〔A 〕 必要条件 〔B 〕 充分条件 〔C 〕 充要条件 〔D 〕 无关条件10、设平面曲线L 为下半圆周 21,y x =--则曲线积分22()Lx y ds +=⎰( )(A) 0 (B) 2π (C) π (D) 4π 11、假设级数1nn a∞=∑收敛,则以下结论错误的选项是 〔 〕(A)12nn a∞=∑收敛 (B)1(2)nn a∞=+∑收敛 (C)100nn a∞=∑收敛 (D)13nn a∞=∑收敛12、二重积分的值与 〔 〕〔A 〕函数f 及变量x,y 有关; (B) 区域D 及变量x,y 无关; 〔C 〕函数f 及区域D 有关; (D) 函数f 无关,区域D 有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.函数z xe2y在点P(1,0)的梯度 (1 , 2 ) .
grad u( x, y) (ux , uy )
2
4.设f
(
x)
1,
1
x2
x 0 ,0 x
,
则其以2为周期的傅里叶
级数在点x 2处收敛于 0 .
5.若级数 un绝对收敛,则级数 un必定 收敛 .
n1
n1
6.若级数 un条件收敛,则级数 un 必定 发散 .
n1
n1
(填收敛或发散)
3
二、单项选择题(每小题 3分,共18分)
1.设f
( x,
y)
xy x2 y2
,
x2 y2 0,则f ( x, y)在点(0, 0)处( B )
0,
x2 y2 =0
( A)连续 (B)可导 (C)可微 (D)有极限
4.若幂级数 an xn在x 1处收敛,则该级数在x
n1
1 处( 2
B
)
( A)发散 (B)绝对收敛 (C)条件收敛 (D)敛散性无法确定
5.级数
n1
an
x
n收敛是
lim
n
an
0(
A
)条件
( A)充分 (B)充分必要 (C)必要 (D)非充分也非必要
6.下列级数中收敛的是( C ).
3n
( A) n1 n
(B) n1
1
1
n2 1 (C )n1 nsin n3
1
(D) n1 (1 1 )n n
5
三、计算题(每题10分,共40分)
1.设函数z z( x, y)由方程 x ln z 确定,求dz. zy
解:方程 x ln z 两边微分: zy
d( x ) z
y d( z ) zy
zdx xdz z2
12
练习:求f ( x, y) x2 y2 2在椭圆域D {( x, y) x2 y2 1}
上的最大值和最小值. (05研)
4
解:(1)解方程组
f f
x y
( (
x, x,
y) y)
2x 2
0 得区域内部的驻点(0, y0
0)
(2)求边界上的可能极值点
令F ( x, y, ) x2 y2 2 ( x2 y2 1)
解:原式= 3xdxdy y2dxdy 6 ydxdy 9 dxdy
D
D
D
D
=0 y2dxdy 0 9 12 D
=9 1 ( x2 y2 )dxdy
2D
(提示:用对称性)
=9 1
2
d
1 2 d
20
0
= 37
4
7
3.计算线积分I ( x2 y)dx ( x sin2 y)dy,其中L是在 L 圆周y 2x x2上点(0,0)到点(1,1)的有向弧.
S( x) (1)n1 x2n x (1)n1 x2n1dx
n1 2n
0 n1
x
(
(1)n1 x2n1 )dx
0 n1
x1 0 1 x2dx arctan x.
11
五、应用题(本题8分)
求f ( x, y) x2 y2 1在椭圆域D {( x, y) x2 y2 1} 4
n 1
n3
n1
n3
p 3 1 所以级数 1 收敛,
2
n3
n1
所以,原级数收敛, 是绝对收敛.
10
(1)n x2n2
解: lim n
2n+2 (1)n1 x2n
x2
2n
x2 1,即 1 x 1时,级数绝对收敛,
x2 1,即x 1, x 1时,级数发散,
所以级数的收敛半径为1,收敛区间为:(1,1)
y z
ydz zdy y2
1 x 11 z dx z2 dz z dz y dy
1x 11
z
dz
z2
dz
z
dx
dy y
z
z2
dz dx
dy
z x y(z x)
6
2.计算二重积分 (3x y2 6 y 9)dxdy, D
其中D {( x, y) x2 y2 1} .
解: P x2 y,Q ( x sin2 y)
y
P 1, Q 1
y
x
o
故所积分与路径无关.
B(1,1)
A
x
设L1 : y 0, x : 0 1; L2 : x 1, y : 0 1
则 原式 ( )( x2 y)dx ( x sin2 y)dy
L1
L2
1 x2dx 1(1 sin2 y)dy sin 2 7 .
0
0
46
8
4.设为圆柱面x2 y2 9介于z 0和z 3之间的部分的外侧,
计算曲面积分 xdydz ydzdx zdxdy .
解:补充曲面:1:z 3,上侧, n (0,0,1)
2:z 0,下侧, n (0,0,1)
( x, y) D {( x, y) x2 y2 9},
2013—2014学年《高等数学》 第二学期期末考试试题及答案
1
一、填空题(每小题3分, 共18分)
1.若直线L:x 1 y 3 z 5 与平面:x 2 y 3z 1 0平行,
m1 2
则m ___4_ .
2.z f ( x, y)在点( x, y)的偏导数 z ,z 存在是z f ( x, y)在 x y
上的最大值和最小值.
解: 设F ( x, y, ) x2 y2 1 ( x2 y2 1),则
4
Fx ( x, y, ) 2x 2 x 0,
解方程组
Fy ( x, F ( x,
y, ) y, )
2
x2Байду номын сангаас
y
y2
4
y
2 1,
0,
得:(0, 2); (1, 0).
f (0, 2) 3; f (1, 0)) 2; 所求的最大值为2,最大值为 3.
原式
3 dv
1 +2
1
2
1
2
3 dv 3 dxdy 0
D
3 32 3 3 32
54
9
四、解答题(每题8分,共16分)
1.级数 (1)n1
2
收敛吗?若收敛, 是绝对收敛
n1
n3
还是条件收敛 ?
解: 首先,考察级数
2
n3
n1
2
lim n3 2 且级数 1 为p 级数,
2.设区域D为x2 y2 1在第一象限的部分,则二重积分
xydxdy ( B )
D
1 y2
1 x2
( A)0 dx0 xydy;
1
1 y2
(C)0 dx0 xydy;
1
1 y2
(B)0 dy0 xydx;
(D) 1
2 d
1 r 2 sin 2dr.
20
0
4
3.设是曲面x2 y2 z2 R2,则 ( x2 y2 z2 )dS ( D ) ( A)2 R2 (B)2 R4 (C )4 R2 ( D)4 R4
