2013年华二冬令营数学试卷答案
2013华二附中自主招生数学试题与答案

已知:2222411b a b a +=+D 'A 'EADCB7.1,2,2,3,3,3,4,4,4,4,7.1,2,2,3,3,3,4,4,4,4,……..,第2013个数是_____________. 2013华二附中华二附中自主招生自主招生数学试题与参考答案(部分)数学试题与参考答案(部分)1.在,,90b AC a AB A ABC Rt ==°=ÐD ,中,在AC 上有一点E ,在BC 上有一点F ,x AE EF BE =^,, ,y SEFC =D 求x y 与的函数关系。
关系。
2.定义○1111=*,○2()1111+=+**n n ,求=*1n3.()()()()41128231)(22-+++--++++=a x a x a a x a x a x f 定义域为D,0)(>x f 在定义域D 内恒成立,求a 的取值范围?的取值范围?4.,求20132012÷øöçèæ+÷øöçèæb a a b =__________. 5.如图,有如图,有棋子棋子摆成这样,求第n 幅图有_________颗棋子。
颗棋子。
∙∙∙∙∙∙(3)(2)(1)6.如图,在矩形ABCD 中,2AE=BE,将=а=ÐD D ECB EA D EC BE DEC ABE ,求翻折,、分别沿、15''____. 8.已知:y x 、4B10室,室,详细答案咨询上海牛人数学工作室,有偿提供详细答案咨询上海牛人数学工作室,有偿提供1. 2.n 3. .7216157216151-<+>=a a a 或或4.2,0 5.)2(+n n6.37.5°7.63 8.(3/2,3) 为有理数,且满足,33421y x +=+求._________),(=y x上海牛人数学工作室主要从事“新知杯”“初“初高中数学高中数学联赛”“美国数学竞赛AMC8/10/12,AIME ,PUMAC(普林斯顿数学竞赛)”名校”名校自主招生自主招生考试,“大同杯”“大同杯”物理物理竞赛研究和辅导,提供疑难问题解答,各种竞赛资料,各种竞赛资料详细解答,疑难问题致电135********刘老师,****************,QQ2640199717,福州路567号。
华师大二附中自主招生2013真题及答案解析

2013华二自主招生试卷1、在,,90b AC a AB A ABC Rt ==︒=∠∆,中,在AC 上有一点E ,在BC 上有一点F ,x AE EF BE =⊥,,,y S EFC =∆求x y 与的函数关系。
2、定义○1111=*,○2()1111+=+**n n ,求=*1n ;3、()()()()41128231)(22-+++--++++=a x a x a a x a x a x f 定义域为D,0)(>x f 在定义域D 内恒成立,求a 的取值范围?4、已知:2222411b a b a +=+,求20132012⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛b a a b =__________.5、如图,有棋子摆成这样,求第n 幅图有_________颗棋子。
∙∙∙∙∙∙(3)(2)(1)冲刺2019年华师大二附中自主招生真题及答案解析6、如图,在矩形ABCD 中,2AE=BE,将=∠︒=∠∆∆ECB EA D EC BE DEC ABE ,求翻折,、分别沿、15''____.7.1,2,2,3,3,3,4,4,4,4,…..,第2013个数是_____________.8.已知:y x 、为有理数,且满足,33421y x +=+求._________),(=y xADCB-2-121Oyx2013华二自主招生数学试题B1.寒山寺每隔9秒敲一此钟,第一次敲钟时,甲乙两船分别向上、下游驶去,速度分别为3m/s ,9m/s ,当甲船听到第108声时,乙船只能听见第_______声.(V 声=300m/s) 2.9名同学分别投票给“杨坤组”5票,“那英组”4票,问“杨坤组”的票数始终压过“那英组”的概率为__________.3.(x-3)2+(y-3)2=6的所有实数对(x ,y) 使yx 最大,则这个最大值为______.4.a x 12有三个整数解,则a =______.5.若方程x 2+2(a+1)x+2a+1=0有个小于1的正数根,a 的范围_______6.n 为正整数,S=1+2+3+,+n 为一个由同一数字组成的三位数,则n =______.7.在一个8×8的正方形格子中,一角剪去一个2×2的小正方形,问其余部分可否剪成15块“L ” 型纸片?若能剪,给出剪切方法,若不能剪,请说明理由.8.正方形ABCD 中有一点E ,使E 到A 、B 、C 的距离之和最小为62,求正方形边长.9.“帽子函数”(1)求函数解析式(2)若有抛物线y=-x 2+a(a<43),求它与“帽子函数”交点个数;(3)请试写一个抛物线,使它与“帽子函数”有且只有2个交点,横坐标分别为27,25.答案十。
上海中考自招真题26套及其答案

四校八大历年自招真题答案目录2013年上中自招试卷2014年上中自招试卷2015年上中自招试卷2011年华二自招试卷2012年华二自招试卷2014年华二自招试卷2013年华二冬令营数学试卷2015年年华二自招试卷2017年年华二自招试卷2013年复附自招试题2014年复附自招试题一2014年复附自招试题二2015年复附自招试题一2015年复附自招试题二2012年交附自招试题2013年交附自招试题2014年交附自招试题2015年交附自招试题2016年交附自招试题2014年七宝自招试题2016年七宝自招试题2016年南模自招试题2016年建平自招试题2017年建平自招试题建平数学培训资料试卷2015年控江自招试题2013年华二冬令营数学试卷1、“帽子函数”的图像如图所示:(1)求此函数的解析式;(2)若有抛物线23(),4y x a a =-+<求它与“帽子函数”图像的交点个数; (3)请试写出一个抛物线解析式,使它与“帽子函数”图像有且只有2个交点,横坐标分别为5722,.【解析】:⑴1,211,12x k x k y x k k x k ⎧≤<+⎪⎪=⎨⎪-+++≤<+⎪⎩⑵0a <时,无交点0a =时,一个交点304a <<时,两个交点 ⑶考虑到34a =时,抛物线234y x =-+与帽子函数交于11,22⎛⎫- ⎪⎝⎭、11,22⎛⎫ ⎪⎝⎭两点, 所以可以将234y x =-+向右平移3个单位,即满足条件 该抛物线解析式为()2334y x =--+2、在一个8×8的正方形方格纸中,一个角剪去一个2×2的小正方形,问其余部分可否剪成15块“L ”型(如图)纸片,若能剪,给出剪切方法,若不能剪,请说明理由。
【解析】(一道基础的染色问题)如图进行黑白相间染色,那么L 型放入方格纸中,必定可以盖住1个黑格子和3个白格子,或者3个黑格子和1个白格子。
2010~2013年考研数学二真题及答案

2010~2013年考研数学二真题及答案2010考研数学二真题及答案一、填空题(本题共 6 小题,请将答案写在题中横线上.)(1)三阶常系数线性齐次微分方程的通解为 y= .(2)曲线的渐近线方程为.(3)函数 y=ln(1-2x)在 x=0 处的 n 阶导数.(4)当 0≤θ≤π时,对数螺线 r=eθ的弧长为.(5)已知一个长方形的长 l 以 2cm/s 的速率增加,宽w 以 3cm/s 的速率增加,则当 l=12cm,w=5cm 时,它的对角线增加的速率为.(6)设 A,B 为 3 阶矩阵,且|A|=3,|B|=2,|A-1+B|=2,则|A+B-1|= .二、选择题(本题共 8 小题,每小题给出的四个选项中,只有一项符合题目要求,请将所选项前的字母填在题后括号内.)(7)函数的无穷间断点数为(A) 0. (B) 1. (C) 2. (D) 3.(8)设y1,y2 是一阶线性非齐次微分方程的两个特解.若常数λ,μ使该方程的解是对应的齐次方程的解,则(9)曲线y=x2 与曲线y=aln x(a≠O)相切,则 a= (A)4e. (B) 3e. (C) 2e. (D) e.(10)设m,n 是正整数,则反常积分的收敛性(A) 仅与 m 值有关. (B) 仅与 n 值有关.(C) 与 m,n 值都有关. (D) 与 m,n 值都无关.(11)设函数z=z(x,y)由方程确定,其中F为可微函数,且(A) x (B) z. (C) -x. (D)-z. (12)(C) (D)三、解答题(本题共 9 小题,解答应写出文字说明、证明过程或演算步骤.)(15) 求函数的单调区间与极值.(16) (Ⅰ) 比较的大小,说明理由; (Ⅱ) 记,求极限(17) 设函数 y =f(x)由参数方程所确定,其中φ(t)具有二阶导数,且φ(1)=(18) 一个高为 j 的柱体形贮油罐,底面是长轴为 2a ,短轴为 2b 的椭圆,现将贮油罐平放,当油罐中油面高度为时(如图 2),计算油的质量.(长度单位为m ,质量单位为 kg ,油的密度为常数 ρkg/m 3)(14) 设 A 为 4 阶实对称矩阵,且A 2+A=0,若 A 的秩为 3,则 A 与相似于(19)设函数u=(x,y)具有二阶连续偏导数,且满足等式,确定a,b 的值,使等式在变换(20)计算二重积分(21)设函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,且。
七年级试卷-2013年冬令营初一年级测试(二)2013年“华杯赛”

2013年冬令营初一年级测试(二)一、填空题1、多项式9x 2+1加上一个单项式后,使它们等于一个整式的平方,那么所有满足条件的单项式可以为_____________________。
2、令a=1-221+231-241+……+2991-21001 ,则a 化为小数后的十分位的数字是_________。
3、a 是自然数,且17a=1n 111111个⋯⋯ ,那么a 的最小值是______。
4、奇数数独:在空格内填入数字1-9,使得每行、每列和每个3*3的宫内数字都不重复。
灰色的单元格内只能填入奇数,那么,A+B=___。
5、如图,多边形ABCFDE 中,已知AB=8,BC=12,ED+DF=13,AE=CF ,那么多边形ABCFDE 的面积是_________。
6、使表达式3-m 2m6+之值为整数的所有整数m 之和等于_____。
7、如图,已知梯形ABCD 的面积为2013,。
AD ∥BC ,AE=BF 。
△COD 面积为618,那么△COD 与△EOD 面积之和是__。
8、计算:=⎥⎦⎤⎢⎣⎡⨯+÷⎥⎦⎤⎢⎣⎡÷⨯)()()()()(32-3-152-2-52--12--32-2-22243__________.9、现有棋子100颗,甲先乙后轮流取走棋子,如果每人每次可以取1颗或5颗或6颗,并规定谁无法按规定取走棋子谁就败。
那么甲要保证必胜,第一次该取走___颗棋子。
二、解答题10、方程4x-15+5×⎥⎦⎤⎢⎣⎡+9x 92=0 ,(这里[x]表示不超过x 的最大整数)的正数解释多少?11、如图,在一个凸四边形ABCD 中,如果AB+AC+CD=14,那么四边形ABCD面积最大值是多少?12、满足方程组⎩⎨⎧=++=++abc z y x xyzc b a 的所有正整数数组(a ,b ,c ,x ,y ,z )有多少组?。
(完整word版)2013年华杯赛初二试题(B)卷解析word版

第十八届华罗庚金杯少年邀请赛初赛试题B (初二组)(时间2013年3月23日10:00~11:00) 一、选择题(每题10分,满分60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1.下列三个命题中, 正确的命题有( )个:① 两个不同的无理数的和可以是有理数;② 两个不同的无理数的积可以是整数;③ 有理数除以无理数的商一定是无理数.A.0B.1C.2D.3 解析:22-112=++)()(,①对;1222=⨯,②对;0除以任意无理数都得0(0是有理数)③错,所以选C 。
2.以 O (0,0), B (40, 20) ,C (60, 0), 为顶点的三角形的三边上, 整点(横坐标和纵坐标都是整数的点)的个数是( ).A.81B.90C.100D.103解析:如右图,在边OC 上整点个数为61个(看横坐标变化0~60);在边OB 上整点的横坐标与纵坐标的比值为2,所以有21个;在边CB 上整点的横坐标与纵坐标的比值为1,所以有11个;由于三角形三个顶点重复计算,所以整点的个数为61+21+11-3=100个,选C 。
3. 如果关于x , y的方程组 3x+4y=2m+n-4的解满足0y x =+, 那么m-n 的值等于( ).x-2y= m-2n+3A.-1B.1C.3D.5解析:根据根式的意义,可知道x=y=0,可将有关x , y 的方程组转化为m ,n 的方程,解得m=1,n=2,m-n 的值等于-1,选A 。
4.圣诞老人有44个礼物, 分别装在8个袋子中, 袋子中礼物的个数各不相同, 最多的有9个. 现要从中选出一些袋子, 将其中的所有礼物恰好平均分给8个同学(每个同学至少分得一个礼物), 那么共有( )种不同的选择.A.20B.25C.27D.31解析:8个不同数相加等于44,最大的数是9,1~9相加等于45,所以这8个袋子里分别装有2~9个礼物。
2013年考研数学真题及参考答案(数学二)

π
2
, 则当 x → 0 时, α ( x ) 是
【 】 .
(A) 比 x 高阶的无穷小 (C) 与 x 同阶但不等价的无穷小 【答案】 答案】C.
(B) 比 x 低阶的无穷小 (D) 与 x 等价的无穷小
【考点】 考点】计算极限的方法:常用的等价无穷小.
【解析】 解析】 x sin α ( x) = cos x − 1 ~ −
(D) I 4 > 0
【解析】 解析】在第 II 象限除原点外被积函数 y − x > 0 ,因此 I 2 > 0 . 【评注】 评注】在第 IV 象限除原点外被积函数 y − x < 0 ,因此 I 4 < 0 ; 在第 I 象限和第 III 象限,根据轮换对称性得
I1 = I 3 = 0 .
(7)设 A, B, C 均为 n 阶矩阵,若 AB = C ,且 B 可逆,则 (A) 矩阵 C 的行向量组与矩阵 A 的行向量组等价 (C) 矩阵 C 的行向量组与矩阵 B 的行向量组等价 【答案】 答案】B. 【考点】 考点】向量组的线性表示方法. 【解析】 解析】将矩阵 A 和 C 按列分块,设 A = (α1 , α 2 ,⋯ , α n ) , B = (bij ) , C = (γ 1 , γ 2 ,⋯ , γ n ) . ①由 AB = C 组线性表示; 【 】 . (B) 矩阵 C 的列向量组与矩阵 A 的列向量组等价 (D) 矩阵 C 的列向量组与矩阵 B 的列向量组等价
π
6
≤θ ≤
π
6
),则 L 所围平面图形的面积为
.
【答案】 答案】
π
12
.
【考点】 考点】计算极坐标曲线所围图形的面积.
2013年数二-真题+答案

1 E A a
1
2
a
1 a (2 (b 2) 2b 2a 2 )
b
a
1
从而可知 2b 2a 2b ,即 a 0 , b 为任意常数,故选择(B) .
二、填空题(本题共 6 小题,每小题 4 分,满分 24 分. 把答案填在题中横线上)
(A) a 0, b 2 (C) a 2, b 0 (B) a 0 , b 为任意常数 (D) a 2 , b 为任意常数
二、填空题(本题共 6 小题,每小题 4 分,满分 24 分. 把答案填在题中横线上)
ln(1 x) x 9. lim 2 x 0 x
该选(A) . 6. 【详解】由极坐标系下二重积分的计算可知
4
考研专业课咨询 QQ:197—567—2201 考研专业课真题资料淘宝网址:/
2
I k ( y x)dxdy
Dk
k
( k 1) k
2 d (sin cos ) r dr 2 0
10 . 设 函 数 f ( x)
1
.
1
x 1
1 e t dt , 则 y f ( x) 的 反 函 数 x f
( y) 在 y 0.
11.设封闭曲线 L 的极坐标方程为 r cos 3 图形的面积为 12.曲线上 .
n
16. (本题满分 10 分) 设 D 是由曲线 y
3
x, 直线 x a ( a 0) 及 x 轴所转成的平面图形, V x ,V y 分别是 D 绕 x
轴和 y 轴旋转一周所形成的立体的体积,若 10V x V y ,求 a 的值. 17. (本题满分 10 分)
2013年试卷及答案
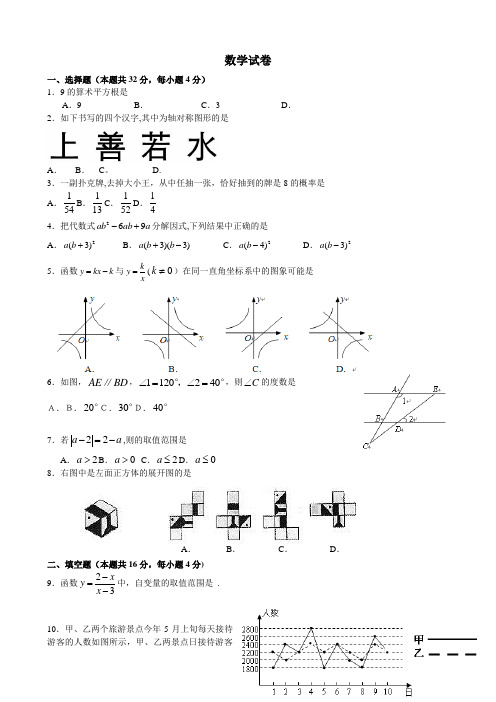
数学试卷一、选择题(本题共32分,每小题4分) 1.9的算术平方根是A .9B .C .3D . 2.如下书写的四个汉字,其中为轴对称图形的是A .B .C 。
D.3.一副扑克牌,去掉大小王,从中任抽一张,恰好抽到的牌是8的概率是 A .154B .113C .152D .144.把代数式269ab ab a -+分解因式,下列结果中正确的是A .2(3)a b +B .(3)(3)a b b +-C .2(4)a b -D .2(3)a b - 5.函数y kx k =-与ky x=(0k ≠)在同一直角坐标系中的图象可能是6.如图,AE BD ∥,1120240∠=∠=°,°,则C ∠的度数是A.B.20°C.30°D.40°7.若22a a -=-,则的取值范围是A .2a >B .0a >C .2a ≤D .0a ≤ 8.右图中是左面正方体的展开图的是二、填空题(本题共16分,每小题4分) 9.函数23xy x -=-中,自变量的取值范围是 .10.甲、乙两个旅游景点今年5月上旬每天接待游客的人数如图所示,甲、乙两景点日接待游客A .B .C .D .人数的方差大小关系为:2S 甲2S 乙.11.若把代数式257x x ++化为2()x m k -+的形式,其中、为常数,则k m -= .12.正方形111A B C O , 2221A B C C ,,3332A B C C , …按如图所示的方式放置.点 ,,,…和点,,…分别在直线(0)y kx b k =+>和轴上,已知点1(1,1)B ,2(3,2)B ,则点的坐标是 , 点的坐标是 .三、解答题(本题共30分,每小题5分)132013tan 30()2)2-︒+-.14.解方程:21133x x x-+=--。
15.已知220x x +-=,求代数式2(2)(3)(3)(1)x x x x x -++--+的值.16.已知:如图,在ABC ∆中,AC BC =,90ACB ∠=︒,MN 是过点的一条直线,AM MN ⊥于,BN MN ⊥于。
2013年华约自主招生数学试题解析

21.设},10|{Z x x x A ∈≥=,A B ⊆,且B 中元素满足:任意一个元素各数位的数字互不相同;任意一个元素的任意两个数字之和不等于9. (1)求B 中的两位数和三位数的个数; (2)是否存在五位数,六位数?(3)将B 中的元素从小到大排列,求第1081个元素.解析(1)所有的两位数共90个,其中数字相同的有9个,两数字之和为9的有9个, 所以B 中的两位数有90―9―9=72个;所有的各数位的数字互不相同三位数共9×9×8=648个,其中含有数字0和9的有4×8=32个,含有数字1和8,2和7,3和6,4和5的各有4×8+2×7=46个, 所以B 中的三位数有648―32―46×4=432个;另解(1)将10个数字分为5组:(0,9),(1,8),(2,7),(3,6),(4,5),每组中的两数不能同时出现在一个元素中.对于两位数,若最高位为9,则共有2×4=8个,若最高位不为9,则共有2×4×4×2=64个,所以B 中的两位数有72个; 对于三位数,若最高位为9,则共有24A ×2×2=48个, 若最高位不为9,则共有14A ×2×24A ×2×2=384个, 所以B 中的三位数有48+384=432个;(2)对于五位数,若最高位为9,则共有44A ×2×2×2×2=384个, 若最高位不为9,则共有14A ×2×44A ×2×2×2×2=3072个, 所以B 中的五位数有3072+384=3456个; 显然B 中不存在六位数.(3)B 中的两位数和三位数共有72+432=504个, 在B 中的四位数中,千位上为1,2,3的各有192个,而504+192×3=1080个,所以第1081个元素应为四位数中,千位上为4的最小数,即4012.2.已知31sin sin =+y x ,51cos cos =-y x ,求)cos(y x +,)sin(y x -. 解析 由31sin sin =+y x ,得91=sin sin 2+sin +sin 22y x y x ……①由51cos cos =-y x ,得251=2cosxcosy cos +cos 22-y x ……②两式相加,得22534=251+91=)+cos(22y x -, 所以 225208=225171=)+cos(-y x . 又由31sin sin =+y x ,得31=2cos 2+sin 2y x y x - ……③ 由51cos cos =-y x ,得51=2sin 2+sin 2y x y x --……④ 两式相除,得53=2tan --y x , 所以 1715=259+153×2=2tan +12tan2=)sin(2-----y x yx y x .3.点A 在kx y =上,点B 在kx y -=上,其中0>k ,12+=k OB OA ,且A ,B 在y轴同侧.(1)求AB 中点M 的轨迹C 的方程;(2)曲线C 与抛物线)0(22>=p py x 相切,求证:切点分别在两定直线上,并求切线方程.解析 (1)设),(11kx x A ,),(22kx x B -,021>x x , 由 12+=k OB OA ,得222222221221)1+(=)+)(+(k x k x x k x ,所以1=21x x .设点M 的坐标为),(y x M ,则2+=21x x x ,2=2=2121x x k kx kx y --所以 1==)y (2122x x k x -,即点M 的轨迹C 的方程为 1=222ky x -. (2)因为曲线C 与抛物线)0(22>=p py x 相切,得 222=2k y y pk -, 由 0=4)2(=222k pk --∆,得pk 1=,此时p y 1=,两切点坐标为)1,2(p ,)1,2(p- ,即切点分别在两定直线2±=x 上.切线方程分别为0=12--py x 和0=1++2py x .4.7个红球,8个黑球,任取4个. (1)求恰有1个红球的概率;(2)记取黑球个数为x ,求其分布列和期望; (3)取出4球同色,求全为黑球的概率. 解析 (1)恰有1个红球的概率为4153817C C C 13×15×756×7=19556=;(2)黑球个数为4,3,2,1,0=x ,黑球数为0的概率为4150847C C C 13×15×735=1955=;黑球数为1的概率为4151837C C C 13×15×78×35=19540=;黑球数为2的概率为4152827C C C 13×15×728×21=19584=;黑球数为3的概率为4153817C C C 13×15×756×7=19556=;黑球数为4的概率为4154807C C C 13×15×710×7=19510=;其分布列为x 的数学期望为0×1955+1×19540+2×19584+3×19556+4×19510=1532.(3)由(2)知4球同色的概率为 195519510+19515=, 所以,取出4球同色,全为黑球的概率为 32=1951519510.5.已知21++=n n n ca a a , ,3,2,1=n ,0>1a ,0>c .(1)证明对任意的0>M ,存在正整数N ,使得对于N n >,M a n > (2)设1+1=n n ca b ,记n s 为n b 前项和,证明n s 有界,且0>d 时,存在正整数k ,kn >时d ca s n <1<01-. 解析 (1)由0>1a ,0>c ,知0=21+>-n n n ca a a ,于是11121121+++1=+=------))>()(-(---n n n n n n n n n n n n a a a a c a a ca a ca a a a122111+a a a a a a a a n n n n n n ->>->->----所以2112112211)1(n =))(1(n ++++=ca a a a a a a a a a a n n n n n --->------对任意的0>M ,要使M a n >,只需M ca n >)1(21-,1+>21ca Mn , 取]2+[=21ca MN ,于是N n >,M a n >.(2)1+1=n n ca b n n na ca a +=21+=n n a a 1+2=n n n a ca ca 1+1+=n n n n a ca a a -n ca 1=1+1n ca -, 所以 n s 11=ca 1+1n ca -,1+11=1n n ca ca s ->0, 由(1)知211+nca a n >,所以2121+1<1a nc ca n ,即1+11=1n n ca ca s -2121<a nc , 所以n s 有界; 令d 2121=a nc ,得 n 2121=a dc , 取k ]1+1[=212a dc ,则k n >时d ca s n<1<01-.6.设z y x ,,是两两不等且大于1的正整数,求所有使得xyz 整除)1)(1z (1)(---zx y xy 的z y x ,,.解析 因为)1)(1z (1)(---zx y xy =z)+y +z(x z)(2xy xy -+zx y xy +z +-1, 而z)+y +z(x z)(2xy xy -能被xyz 整除, 于是只需zx y xy +z +-1能被xyz 整除即可.又z y x ,,是两两不等且大于1的正整数,不妨设z >>y x∴ ≤xyz zx y xy +z +-1xy 3<,即3<z ,∴2=z . 于是只需x y xy 2+2+-1能被xy 2整除,当然 12+2+≤2-x y xy xy ,即12+2-x y xy ≤,∴x x y xy 4<2+2<. 于是4<y ,∴ 3=y ,进而5≤x ,∴ 5=x ,4. 检验知2、3、5能使zx y xy +z +-1能被xyz 整除,∴ ),,(z y x )5,3,2(=)3,5,2(=)5,2,3(=)2,5,3(=)3,2,5(=)2,3,5(=.7.设1e )1(=)(--xx x f . (1)证明当0>x 时,0<)(x f ;(2)令1e =1+-n n x x n ex ,1=1x ,证明n x 递减且nn x 21>. 解析 (1)因为0=1e )01(=)0(0--f ,又当0>x 时,x x e x e x f )1(+=)('--x xe -=0<, 所以当0>x 时,0<)(x f ;(2)由1e =1+-n n x x n ex ,得nx x x e n n 1e =1+-,又x e x+1>,可得0>n x . 由(1)知0>x 时,0<)(x f ,0<1e )1(=)(--n xn n x x f ,1+e =1>e n n n x n x x n x e x -,∴1+e >e n n x x ,即n n x x <1+,n x 递减.下面用数学归纳法证明 n n x 21>.1=n 时显然成立,假设k n =(*∈N k )时,k k x 21>, 构造函数x1=)(-x e x g ,当0>x 时,)(x g 为增函数,∴)21(>)(k k g x g .又当0>x 时,2+1>2xe x,再设函数))((=)(2xe x g x x h -,则0))2+1(=2+1=)(222'>-()-(x e e e x e x h xx x x ,)(x h 在)÷∞,0(上是增函数, 0>)21(k h ,∴1+21>)21(k e g k , ∴121+>k e e x, 1121++>k k x , 由数学归纳法知,对于正整数n ,有n n x 21>.唤醒了夕阳 惆怅又向东流 月下琴音畅饮醉英雄 看战火重现 结义乱世流年 望落叶飘零 荒凉染遍诸侯裂B :W.K. 英雄 叹千古恨 巨澜 触动天河泪 看不凡少年 天涯结豪杰 铮铮铁骨 气宇千年传C :W.K. 痴狂一生一世任逍遥 智取江东少年出英豪 若饮醇醪忠诚万人仰 群英会唱剑舞荡气浩D :W.K.笑叹鸿儒吴蜀战一场 羽扇纶巾笑谈赤壁烧 三足鼎立一战千古扬 伊人相望把琴吟沧桑 间奏诗(Rap):苍狼 群雄逐鹿天下争江山 战场狼烟四起春秋乱 三国饥荒饮遍冷月光 红颜秋风断箫愁断肠英雄久经沙场定江山天下谁怜伊人多情泪美人挥泪提笔千古伤岁月只剩传奇来绝唱A1:W.K.吹断了秋风思念憔悴红颜月下风霜画满诗两行燃烽火岁月相约乱世流年叹饥饿兵荒血染君王风云变B1:W.K.对酒当歌论英雄沙场兵如千机变看不凡少年战场称豪杰铮铮铁骨气宇千年传C:W.K.痴狂一生一世任逍遥智取江东少年出英豪若饮醇醪忠诚万人仰群英会唱剑舞荡气浩D:W.K.笑叹鸿儒吴蜀战一场羽扇纶巾笑谈赤壁烧三足鼎立一战千古扬伊人相望把琴吟沧桑C:W.K.痴狂一生一世任逍遥智取江东少年出英豪若饮醇醪忠诚万人仰群英会唱剑舞荡气浩D:W.K.笑叹鸿儒吴蜀战一场羽扇纶巾笑谈赤壁烧三足鼎立一战千古扬伊人相望把琴吟沧桑。
2013华约、北约自主招生数学、物理试题和答案详解

2013“华约”自主招生试题2013-03-16(时间90分钟,满分100分)1.(10分)集合{|10,}A x x x N *=≥∈,B 为A 的子集,若集合B 中元素满足以下条件:①任意数字都不相等;②任意两个数之和不为9(1)B 中两位数有多少?三位数有多少? (2)B 中是否有五位数?六位数?(3)若将集合B 的元素按从小到大的顺序排列,第1081个数为多少?【解】将0,1,2,…,9这10个数字按照和为9进行配对,考虑(0,9),(1,8),(2,7),(3,6), (4,5),B 中元素的每个数位只能从上面五对数中每对至多取一个数构成.(1)两位数有22215242272C A C ⨯⨯-⨯=个; 三位数有333222534222432C A C A ⨯⨯-⨯⨯=个;(2)存在五位数,只需从上述五个数对中每对取一个数即可构成符合条件的五位数;不存在六位数,由抽屉原理易知,若存在,则至少要从一个数对中取出两个数,则该两个数字之和为9,与B 中任意一个元素的任意两个数位的数字之和不等于矛盾,因此不存在六位数;(3)四位数共有4443335443221728C A C A ⨯⨯-⨯⨯=个,因此第1081个元素是四位数,且是第577个四位数,我们考虑千位,千位为1,2,3的四位数有3334332576C A ⨯⨯⨯=个,因此第1081个元素是4012.2.(15分)1sin sin 3x y +=,1cos cos 5x y -=,求sin()x y -与cos()x y +的值 【解】由1sin sin 3x y +=……①,1cos cos 5x y -=……②,平方相加得208cos()225x y +=;另一方面由①可得12sincos 223x y x y +-=……③ 由②式可得12sin sin 225x y x y +--=……④,由③/④式得3tan 25x y -=-,也所以22tan152sin()171tan 2x y x y x y --==--+即求.3.点A 在y kx =上,点B 在y kx =-上,其中0k >,2||||1OA OB k ⋅=+,且A B 、在y 轴同侧. (1)求AB 中点M 的轨迹C ;(2)曲线C 与22(0)x py p =>相切,求证:切点分别在两条定直线上,并求切线方程. 【解】(1)设1122(,),(,)A x y B x y ,(,)M x y ,则1212121122(),,,222x x y y k x x y kx y kx x y ++-==-===, 由2||||1OA OB k ⋅=+得,121x x =,显然22121212()()44x x x x x x +--==,于是得2221(0)y x k k-=>,于是AB 中点M 的轨迹C是焦点为(,实轴长为2的双曲线.(2)将22(0)x py p =>与2221(0)y x k k-=>联立得22220y pk y k -+=,由曲线C 与抛物线相切,故242440p k k ∆=-=,即1pk =,所以方程可化为2220y ky k -+=,即切点的纵从标均为y k =,代入曲线C 得横坐标为.因此切点分别在定直线x x ==,两切点为),()D k E k ,又因为xy p'=,于是在)D k处的切线方程为y k x -=,即1y x p=-;同理在()E k处的切线方程为1y x p p=--. 4. (15分)7个红球,8个黑球,从中任取4个球.(1)求取出的球中恰有1个是红球的概率;(2)求所取出球中黑球个数X 的分布列及期望()E X ; (3)若所取出的4个球颜色相同,求恰好全黑的概率;【解】(1)由题知恰有一个红球的概率为137841556195C C C =; (2)易知X 的所有可能取值为0,1,2,3,4,则由古典概型知,474155(0)195C P X C ===,137841540(1)195C C P X C ===,227841584(2)195C C P X C ===,137841556(3)195C C P X C ===, 4841510(4)195C P X C ===,即X 的分布列为:所以其数学期望为 540845610320123419519519519519515EX =⨯+⨯+⨯+⨯+⨯=(事实上由超几何分布期望公式可以直接得出期望为83241515EX =⨯=,无须繁杂计算) (3)取出四个球同色,全为黑色的概率为48447823C C C =+即求. 5. (15分)数列{}n a 均为正数,且对任意*n N ∈满足21(0n nn a ca a c +=+>为常数).(1) 求证:对任意正数M ,存在N *N ∈,当n N >时有n a M >; (2)设11n n b ca =+,n S 是数列{}n b 的前n 项和,求证:对任意0d >,存在*N N ∈,当n N >时,110||n S d ca <-<. 【证明】:(1)因为对任意的*n N ∈满足0n a >,所以21n n n n a ca a a +=+>,又因为0c >, 所以22111121()n n n n n n n n a a c a a a a a a a a +----=-+->->>-,所以2112211211()(1)()(1)n n n n n a a a a a a a a n a a n a ---=-+-++-+>--=-故对任意的正整数M ,存在*21{1,[]2}MN N a =+∈,当n N >时有n a M >; (注:21M a ⎡⎤⎢⎥⎣⎦表示不超过21Ma 的最大正整数.)(2)由21(1)n n n n n a ca a a ca +=+=+可得,111n n n a ca a +=+,所以211111111n n n n n n n n n n ca a a ca ca a ca a ca ca ++++-===-+; 也所以11111nn i i n S b ca ca =+==-∑,即11110n n S ca ca +-=> 且由(1)知211n a na +>,所以21111n ca nca +<, 即对任意0d >,存在211max 1,N dca ⎧⎫⎡⎤⎪⎪=⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭,当n N >时,有110||n S d ca <-<. 6. (15分)已知,,x y z 是互不相等的正整数,|(1)(1)(1)xyz xy xz yz ---,求,,x y z . 【解】本题等价于求使(1)(1)(1)1()xy xz yz xy yz zx xyz x y z xyz xyz---++-=-+++为整数的正整数,,x y z ,由于,,x y z 是互不相等的正整数,因此|1xyz xy yz zx ++-,不失一般性不妨设x y z >>,则13xyz xy yz zx yx ≤++-<,于是3z <,结合z 为正整数,故1,2z =,当1z =时,|1xy xy y x ++-,即|1xy y x +-,于是12xy xy y x x ≤++-<,所以2y <, 但另一方面y z >,且为正整数,所以2y ≥矛盾,不合题意.所以2z =,此时2|221xy xy y x ++-,于是2221xy xy y x ≤++-,即221xy y x ≤+-,也所以224xy y x x <+<,所以4y <,又因为2y z >=,所以3y =; 于是6|55x x +,所以655x x ≤+,即5x ≤,又因为3x y >=,所以4,5x =, 经检验5x =符合题意,于是符合题意的正整数,,x y z 有(,,)x y z =(2,3,5)、(2,5,3)、(3,2,5)、(3,5,2)、(5,2,3)、(5,3,2)注:该题与2011年福建省高一数学竞赛试题雷同. 7. (15分)已知()(1)1x f x x e =-- 求证:(1)当0x >,()0f x <;(2)数列{}n x 满足111,1n n x x n x e e x +=-=,求证:数列{}n x 单调递减且12n nx >. 【解】(1)当0x >时,()0xf x xe '=-<,所以()f x 在(0,)+∞上递减,所以()(0)0f x f <=. (2)由11n nx x n x ee +=-得11n n x x ne ex +-=,结合11x =,及对任意0,1xx e x >>+,利用数学归纳法易得0n x >对任意正整数n 成立,由(1)知()0n f x <,即1n n xxn e x e -<, 即1n n x x n n x ex e +<,因为0n x >,所以1n n x x e e +<,即1n n x x +>,所以数列{}n x 递减,下面证明12n n x >,用数学归纳法证,设1()x e g x x -=,则221()()x x xe e f x g x x x -+'==-,由(1)知当0x >时,()0f x <,即()0g x '>,故()g x 在(0,)+∞递增,由归纳假设12n n x >得1()()2n n g x g >,要证明1112n n x ++>只需证明1112n n xe e ++>,即112()n n g x e +>,故只需证明1121()2n n g e +>,考虑函数2()()x h x xg x xe =-,因为当0x >时212x x e >+,所以222()(1)[(1)]022x x xxx x h x e e e e =-+=-+>,故()h x 在(0,)+∞上递增,又102n >,所以1()02n h >,即1121()2n n g e +>,由归纳法知,12n n x >对任意正整数n 成立.注:此题的函数模型与2012年清华大学保送生考试试题的函数模型相似.2013“北约”自主招生试题2013-03-16(时间90分钟,满分120分)一、选择题(每题8分,共48分)1.和1( ) A. 2 B. 3 C. 5 D. 6【解】由1x =可知22x =,同理由1x 可知3(1)2x -=; 所以方程23(2)[(1)2]0x x ---=的次数最小,其次数为5,故选C.2.在66⨯的表中停放3辆完全相同的红色和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车只占一格,共有 种停放方法.A. 720B. 20C. 518400D. 14400 【解】红色车选3列有3620C =种方法,再从这三列中选三行有3620C =种方法,另外将红色车放在已选好的三列三行中有326⨯=种方法,同理黑色车只能从剩下的三行三列九个格中选,也有326⨯=种方法,因此方法数有(20206)614400⨯⨯⨯=种.故选D.3.已知225x y =+,225y x =+(x y ≠),则32232x x y y -+值为( ) A. 10- B. 12- C. 14- D. 16-【解】由225x y =+与225y x =+两式作差得2()x y x y +=-≠,代入两式中分别化出 2210x x +-=、2210y y +-=,所以,x y 是方程2210t t +-=的两个不等实根,于是 2,1x y x y +=-=-,也所以 3223222()[()3]2()(2)7216x x y y x y x y x y x y -+=++--=-⨯-=-.故选D. 4.在数列{}n a 中,11a =,142n n S a +=+(1n ≥),则2013a 值为( )A. 201230192⨯B. 201330192⨯C. 201230182⨯D. 无法确定 【解】由11a =,142n n S a +=+(1n ≥)……①可知,当1n =时,2142S a =+,所以25a =;当2n ≥时,有142(2)n n S a n -=+≥……②,由①-②式得,1144(2)n n n a a a n +-=-≥,即1122()(2)n n n n a a a a n +--=-≥,且2123a a -=所以11232n n n a a -+-=⨯(*n N ∈),同除以2n 得,113222n n n n a a +--=,且1012a =;所以13122n n a n +=+,故令2012n =时,得2012201323019a =⨯,故选A. 5.在ABC ∆中,D 为BC 中点,DM 平分ADB ∠交AB 于点M ,DN 平分ADC ∠交AC 于N ,则BM CN +与MN 的关系为( ) A.BM CN MN +> B.MN CN MN +< C.BM CN MN +=D.无法确定【解】如图,在DA 取DE DB =,连接,,ME NE MN则显然可证,ME MB EN NC ==,且有ME NE MN +≥,即BM CN MN +≥, 上述不等式当且仅当180MED DEN ∠+∠=, 也即180B C ∠+∠=,这显然与三角形内角和定理矛盾,故等号取不到, 也即选A.6.模长都为1的复数,,A B C 满足0A B C ++≠,则BC AC ABA B C++++的模长为( )A. 12- B. 1 C. 2 D. 无法确定 【解】由题知1AA BB CC ===,所以2BC AC AB BC AC AB BC AC ABA B C A B C A B C ++++++=⨯++++++,也即2BC AC AB BC AC AB BC AC ABA B C A B C A B C++++++=⨯++++++313BA C A AB CB AC BCAB AC BA BC C A CB++++++==++++++,故选B.二、解答题(每题18分,共72分)7.最多能找多少个两两不相等的正整数使其任意三个数之和为质数,并证明你的结论.【解】:至多有4个.首先可以取1,3,7,9这四个数,它们任意三个数之和分别为11,13,17,19符合质数定义.下面再证明5个正整数是不符合题意的.若有5个正整数,则考虑质数被3除的余数,如果有一个数的余数为0,那么考虑余下的4个数被3除的余数,如果余数既有1也有2,那么这两个数与前面余数为0的数的和刚好为3的倍数,故不符合题意,如果余下四个数的余数均相等,显然取余下四个数中的三个数,则这三个数的和为3的倍数不是质数,也不符合题意,如果这5个数被3除的余数都不等于3,则由抽屉原理,至少有3个数被3除的余数相同,这三个数的和是3的倍数不是质数,也不符合题意.综上可知,不存在5个正整数符合题意,即至多有4个正整数符合题意. 8.已知12320130a a a a ++++=,且122320131|2||2||2|a a a a a a -=-==-证明:12320130a a a a =====.【证明】:观察可知12320130a a a a ++++=,即21322013201212013(2)(2)(2)(2)0a a a a a a a a -+-++-+-=……① 又122320131|2||2||2|a a a a a a -=-==-,不妨设12|2|a a t -=,M ACDBE则①可写为(2013)0(02013,)kt k t k k N --=≤≤∈,即(22013)0k t -=, 又显然220130k -≠,则有0t =,于是有122320122013201312,2,,2,2a a a a a a a a ====,所以2013112a a =,即10a =.也所以12320130a a a a =====,即证.9.对于任意θ,求632cos cos66cos415cos2θθθθ---的值. 【解】632cos cos66cos415cos2θθθθ--- 31c o s 232()c o s 66c o s 415c o s 22θθθθ+=--- 3234(1c o s 23c o s 23c o s 2)(3c o s 24c o s 2)6c o s 415c o s2θθθθθθθ=+++---- 2412c o s 26c o s 446(1c o s 4)6c o s 410θθθθ=+-=++-=即求. 10.有一个m n ⨯的数表,已知每一行的数均是由小到大排列.现在将每一列的数由小到大重新排列,则新的数表中每一行的数满足什么样的关系?请证明你的结论.〖原题叙述〗:已知有m n ⋅个实数,排列成m n ⨯阶数阵,记作{}ij m n a ⨯,使得数阵中的每一行从左到右都是递增的,即对意的1,2,3,,i m =,当12j j <时,都有12ij ij a a <.现将{}ij m n a ⨯的每一列原有的各数按照从上到下递增的顺序排列,形成一个新的m n ⨯阶数阵,记作{}ijm n a ⨯',即对任意的1,2,3,,i n =,当12i i <时,都有12i ji j a a ''<.试判断{}ijm n a ⨯'中每一行的n 个数的大小关系,并说明理由. 【解】:数阵{}ijm n a ⨯'中每一行的n 个数从左到右都是递增的,理由如下: 显然,我们要证明数阵{}ijm n a ⨯'中每一行的n 个数从左到右都是递增的,我们只需证明, 对于任意1,2,3,,i m =,都有(1)iji j a a +''<,其中1,2,3,,(1)j n =-. 若存在一组(1)pq p q a a +''>,令(1)(1)k k q i q a a ++'=,其中121,2,3,,,{,,,}{1,2,,}k k m i i i m ==,则当t p ≤时,都有(1)(1)(1)t t i q i q t q p q pq a a a a a +++'''≤=≤<.也即在(1,2,,)iq a i m =中,至少有p 个数小于pq a ',也即pq a '在数阵{}ij m n a ⨯'中的第q 列中,至少排在第1p +行,与pq a '排在第p 行矛盾.所以对于任意的1,2,,i m =,都有(1)iji j a a +''<,即数阵{}ij m n a ⨯'中每一行的n 个数从左到右都是递增的.2013年高水平大学(华约)自主选拔学业能力测试物理探究注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
华师大附中2012-2013学年度第二学期高三测试(二)数学(理)及答案

华师大附中2012-2013学年度第二学期高三测试(二)数学(理)本试卷分选择题和非选择题两部分,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的班别、姓名、考号填写在答题卡的密封线内。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上 3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷 各题目指定区域内的相应位置上;如需改动,选划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要求作答的答案无效. 4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回.第一部分选择题一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设集合A 、B 均为数集,且{}{}12123,,,,A a a B b b b ==,则集合A Y B 中元素的个数至 多( )A .2个B .3个C .4个D .5个2.已知 5.10.90.90.9, 5.1,log 5.1,m n p ===则这三个数的大小关系是( )A .m n p <<B .m p n <<C .p m n <<D .p n m << 3.已知直线3443x ty t=+⎧⎨=-+⎩(t 为参数),则下列说法错误的是( )A .直线的倾斜角为3arctan 4B .直线必经过点11(1,)2-C .直线不经过第二象限D .当t=1时,直线上对应点到点(1,2)的距离为4.已知函数232,()3 2.x f x x a a ⎧⎪=⎨+-+⎪⎩[0,)(,0)x x ∈+∞∈-∞在区间(,-∞+∞)是增函数,则常数a 的取值范围是 ( )A .12a ≤≤B .1,2a a ≤≥或C .12a <<D .1,2a a <>或5.若奇函数()()(2)1,(2)()(2),(1)f x x R f f x f x f f ∈=+=+满足则等于( )A .0B .1C .12-D .126.已知1x y +=,那么2223x y +的最小值是( )A .56B .65C .2536D .36257.函数ln 1xy e x =--的图象大致是( )8.定义在R 上的偶函数()f x 满足[](1)(),()0f x f x f x +=-且在-1,上是增函数,下列五个关于()f x 的命题中①()f x 是周期函数;②()f x 的图象关于1x =对称; ③()f x 在[0,1]上是增函数 ④()f x 在[1,2]上是减函数;⑤(2)(0)f f = 正确命题的个数是 ( )A .1个B .2个C .3个D .4个第二部分非选择题(110分)二、填空题(本大题共6小题,每小题5分,共30分) 9.函数()1f x x =-的定义域为 .21,(0)x x -⎧-≤⎪11.在极坐标系中,若过点(4,0)且与极轴垂直的直线交曲线6cos ρθ=于A 、B 两点,则AB = .12.如下图,在直角梯形ABCD 中,AB//CD ,AB ⊥BC,AB=1,CD=3,6BC D S ∆=,则梯形ABCD 的面积为 ,点A 到BD 的距离AH= .13.设()f x 是定义在R 上的奇函数,且()y f x =的图象关于直线12x =对称,则(2)(4)f f +=14.已知函数2()24(3)5f x ax a x =+-+是在区间(,3)-∞上的减函数,则a 的取值范围是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤. 15.(本题满分12分)设集合{}212,12x A x x a B xx -⎧⎫=-<=<⎨⎬+⎩⎭,若A ⋂B=A ,求实数a 的取值范围.16.(本题满分12分)计算222lg 5lg 8lg 5lg 20lg 2.3++⋅+17.(本题满分14分)已知2(),x f x ax b=+且方程()120f x x -+=有两个实根为13x =, 24x =(这里a 、b 为常数). (1)求函数()f x 的解析式 (2)求函数()f x 的值域.18.(本题满分14分)某宾馆有相同标准的床位100米,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床位高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;② 该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用x 表示床价,用y 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)(1)把y 表示成x 的函数,并求出其定义域;(2)试确定该宾馆将床位定价为多少时既符合上面的两个条件,又能使净收入最多?19.(本题满分14分)已知函数()f x 的定义域为{},0x x R x ∈≠且对定义域内的任意1x 、2x ,都有1212()()(),1()0,(2) 1.f x x f x f x x f x f ⋅=+>>=且当时(1)求证:()f x 是偶函数;(2)求证:()f x 在(0,)+∞上是增函数; (3)解不等式2(21) 2.f x -<20.(本题满分14分)设函数321()(),3f x ax bx cx a b c =++<<其图象在点(1,(1)),A f(,()B m f m 处的切线的斜率分别为0,a - (1)求证:01;b a ≤<(2)若函数()f x 的递增区间为[],,s t 求s t -的取值范围.参考答案第一部分 选择题(40分) 1-5DCDAD 6-8ADC第二部分 非选择题(110分)二、填空题(本大题共6小题,每小题5分,共30分) 9.{}4,1x x x ≤≠且. 10.(,1)(1,),-∞-⋃+∞11. 12.8;4.513.0. 14.30,4⎡⎤⎢⎥⎣⎦三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤. 15.(本题满分12分).解:{}{}222.x x a x a x a -<=-<<+ …………3分 2112 3.2x B xx x x -⎧⎫=<=-><⎨⎬+⎩⎭………3分 因为,A B A A B ⋂=⊆即, ……………2分所以23.22a a +≤⎧⎨-≥-⎩ …………2分解得01a ≤≤,故实数a 的取值范围为[0,1] ………2分16.(本题满分12分) 解:原式22(lg 5lg 2)lg 5(1lg 2)lg 2=++⋅++ 2l g 5(l g 5l g=+++⋅ 2l g 5l g 2=++=………3分 17.(本题满分14分)解:(1)依已知条件可知方程()120f x x -+=即为2120,xx ax b-+=+…1分因为123,4x x ==是上述方程的解,所以931203,1641204a ba b⎧-+=⎪⎪+⎨⎪-+=⎪+⎩解得12a b =-⎧⎨=⎩ …………4分 所以函数的解析式为2()2xf x x =--; ………1分(2)因为24()(2)422xf x x x x ⎡⎤=-=--++⎢⎥--⎣⎦, ………2分 当42,(2)42x x x >-+≥-时,当且仅当4x =时取等号,所以8y ≤-,…2分 当42,(2)42x x x <-+≤--时,当且仅当0x =时取等号,所以0y ≥,…3分所以函数][()0,)f x ∞⋃+∞的值域为(-,-8. …………1分 18.(本题满分14分).解:(1)依题意有[]100575100(10)3575x y x x -⎧⎪=⎨--⨯-⎪⎩(10)(10)x x ≤>,且*x N ∈,……3分因为*0,y x N >∈,由*1005750,610,.10x x x N x ->⎧≤≤∈⎨≤⎩得 ……2分由[]10,100(10)35750x x >⎧⎪⎨--⨯->⎪⎩得*1038,,x x N <≤∈ ………2分所以函数为21005753130575x y x x -⎧=⎨-+-⎩(,610(,1038)x N a n d x x N a n d x ∈≤≤∈<≤, ……1分定义域为{}638,;x x x N ≤≤∈ ………1分(2)当10x =时,*100575(610,)y x x x N =-≤≤∈取得最大值425元,1分当10x >时,23130575y x x =-+-,仅当130652(3)3x =-=⨯-时,y 取最大值,但*2*223130575(1038,)x N x y x x x x N ∈==-+-<≤∈,所以当时,取得最大值833元, ……3分比较两种情况,可知当床位定价为22元时净收入最多.………1分 19.(本题满分14分).解;(1)证明 因对定义域内的任意1x 、2x 都有121212()()(),,1f x x f x f x x x x ⋅=+==-令,则有()()(f x f x f -=+- ……2分 又令121,2(1)(1)x x f f ==--=得 ……1分 再令121,(1)0,(1)0,x x f f ===-=得从而 ……1分 于是有()(),()f x f x f x -=所以是偶函数. ……1分(2)设212121110()()()(.)x x x f x f x f x f x x <<-=-,则 ……1分221111()()()(),x xf x f x f f x x ⎡⎤=-+=-⎢⎥⎣⎦ ………3分由于21210,1,x x x x ><>所以从而21()0x f x >, ………1分故1212()()0()(),()(0,)f x f x f x f x f x -<<+∞,即所以在上是增函数. (3)由于(2)1,211(2)(2)(4),f f f f ==+=+=所以 ……1分 于是待解不等式可化为2(21)(4)f x f -<, ………1分 结合(1)(2)已证结论,可得上式等价于 2214x -<………1分解得022x x x ⎧⎫⎪⎪-<<≠⎨⎬⎪⎪⎩⎭且. ………1分 20.(本题满分14分).解(1)因为2()2f x ax bx c '=++ ………1分于是依题意有(1)20,f a b c '=++= ① ……1分2()2,f m a m b m c a '=++=- ② ……1分又由,a b c <<可得424a a b c c <++<,即404a c <<,所以0,0,a c <> 由①得2,c a b a b c =--<<代入再由10,1,3b a a<-<<得③ ……2分将2c a b =--代入②得2220,am bm b +-=即方程2220ax bx b +-=有实根,故其判别式2480,b ab ∆=+≥由此可得2()2()0,bbaa+≥解得2,0,b b aa≤-≥或④ ……2分由③、④即可得01b a≤<; ………1分(2)由于2()2f x ax bx c '=++的判别式2440b ac '∆=->, ……1分 所以方程220()a bx c ++=*有两个不相等的实数根,设为12,x x , 又由(1)201f a b c '=++=1知是(*)的一个根,记x =1, ……1分 则由根与系数的关系得221b x a+=-,即21210,b x x a=--<<当2,1x x x <>或时,()0;f x '>当21x x <<时,()0f x '>, ……1分 所以函数()f x 的单调递增区间为[]2,1x 由题设[][]2,1,,x s t =……1分 因此2212,b s t x a-=-=+由(1)知01b a≤<,所以[2,4).s t -∈…1分。
2013华杯赛北京数学冬令营小中组

2013年“华杯赛”北京数学冬令营测试二(小学中年级组)1.计算:(25-1)×(25-1×2)×(25-1×2×3)×(25-1×2×3×4)=2.有两盒巧克力,如果从甲盒拿出8块放入乙盒后,两盒巧克力的块数就同样多;如果从乙盒拿出13块放入甲盒后,甲盒巧克力的块数是乙盒的2倍。
那么甲盒原来有块巧克力。
3.由正方形的六个面构成的其平面展开图是一个n边形,那么n的最小值是4.有一串连续的奇数:1,3,5,7,...,2009,2011,2013,用7分别除这1007个整数,得到1007个算式,那么,其中余数等于2的算式有个。
5.某牌子的汽车有四缸发动机和六缸发动机两种,其发动机的每个缸都配有一个火花塞。
如果15辆这种牌子的汽车共有78个火花塞i,那么,其中四缸发动机的汽车有辆。
6.有大小两个正方形,如果它们的周长相差16厘米,面积相差88平方厘米,那么小正方形的面积是平方厘米。
7.足球世界杯小组赛,每组四个队进行单循环比赛。
每场比赛胜队得3分,败对得0分,平局时两队各记1分。
小组比赛全赛完以后,最后积分最高的两个队出线进入下轮比赛。
如果积分相同,还要算小分。
在所有可能出线的情况下,出线的队的最小得分为分。
8.如右图所示,在三角形的每条边上各取4个点,那么以这12个点中的3为顶点可以画出个三角形。
9.有10名学生,每人参加两个课外小组,而且只参加两个课外小组。
如果共有5个课外小组,并且没有2名学生参加的课外小组完全相同,那么成员最多的课外小组有名成员。
10.从自然数1~20中取三个数,将它们两两相乘得到三个积,再将三个积相加得到一个和。
那么这样得到的和为奇数的取法有种。
2013年“华杯赛”北京数学冬令营测试一(小学中年级组)1.从1986至2012之间的偶数之和:1986+1988+1990+...+2010+2012=如果要拼成10×n的方格,使得每一列和每一行中0的小数都是偶数,那么非零自然数n的最小值是3.已知三角形ABC中:BE=1,EF=3,FC=2,BD=AD,三角形AHG的面积是2.61,三角形GFC的面积是 1.08 ,那么四边形BEHD的面积为4.里山镇到省城的高速路全长千米,途径县城。
156:2013年华二附中冬令营数学试题

4 寒山 隔 9 秒敲一次钟,第一次敲钟时, 乙两船 别向
游驶去,速度 别
为 3m / s,9m / s ,当 船听到第 108 声时,乙船只能听见第_______声.(V声 =300m / s )
5 于满足 (x − 3)2 + ( y − 3)2 = 6的所有实数 (x, y),使 x 最大,这个最大值为________. y
6 方程 x − 2 −1 = a 有 个整数解,求 a 的值. 7 若方程 x2 + 2(a +1)x + 2a +1 = 0 有一个小于 1 的 数根,那么实数 a 的取值范围______.
微信公众号上海中高考提供,仅限学习使用,严禁商用
8 方程 x2 + y2 + z2 + w2 = u2 共有_____组整数解.
帽子函数 图 的交点个数, 帽子函数 图 有且只有 2 个交点,
2 在一个 8×8 的 方形方格纸中,一个角剪去一个 2×2 的小 方形,问其余部 可否剪成 15 块 L 型(如图)纸片,若能剪,给出剪 方法,若 能剪,请说明理
微信公众号上海中高考提供,仅限学习使用,严禁商用
3 n 为 整数, S = 1+ 2 + 3 +⋯+ n, S为一个 一个数字组成的 位数,求n的值.
9 方形 ABCD 中有一点 E ,使 E 到 A B C 的距离之和最小为 2+ 6, 求 方形的边长.
10 9 学 别投票给 杨坤组
那英组 ,最终 杨坤组 5 票,
那英组 4 票,问 杨坤组 的票数始终压过 那英组 的概率为____________.
微信公众号上海中高考提供,仅限学习使用,严禁商图所示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
300 9
97 97
则有 900k 900 972 8 ,解得 k 105.8
97 97
11
所以乙只能听到第 105 声
5、对于满足 (x 3)2 ( y 3)2 6的所有实数对(x, y), 使 x 最大,这个最大值为________. y
【解析】设 x k ,则 x ky y
解得 a 6 ,∴边长 AB 6a 2 3
10、9 名同学分别投票给“杨坤组”与“那英组”,最终“杨坤组”5 票,“那英组”4
票,问“杨坤组”的票数始终压过“那英组”的概率为____________.
【解析】满足条件 的情况数为
C84 5
14 ,总情况数为 C94
126
所以概率 P 14 1 126 9
代入原式,得 ky 32 y 32 6
化为 k2 1 y2 6k 6 y 12 0 要使 y 有实数解,则 6k 62 48 k2 1 0
解得 3 2 2 k 3 2 2
所以最大值为 3 2 2
所以 a 1 (当然也可以用分类讨论的方法做)
7、若方程 x2 2(a 1)x 2a 1 0 有一个小于 1 的正数根,那么实数 a 的取值范围
__________.
【解析】对原式进行十字相乘可得 x 1 x 2a 1 0
所以 x 1或 2a 1 ∵方程有一个小于 1 的正数根 ∴ 0 2a 11,解得 1 a 1
为 5 ,7 . 22
【解析】:⑴ y x,xkkx1,kk1212 x k 1 ⑵ a 0 时,无交点 a 0 时,一个交点 0 a 3 时,两个交点
4
⑶考虑到
a
3 4
时,抛物 线
y
x2
3 4
与帽,
1 2
形的边长.
【解析】费马点问 题:是指位于三角形内且到三角形三 个顶点距离之和最短的点。 简证:将 ABP 绕点 A 旋转 60 至 AB ' P ' ,则 APP ' 为正三角形 距离之和 PA PB PC PP' P'B' PC B'C , 当 B ', P ', P,C 四点共线时“=”成立,此时 APB BPC CPA 120 所以费马点该点所 对三角形三边的张角相等,均为 120
卡产品部
【解析】设该三位数为 aaa ,则 S nn 1 111 a
2
变形为 n n 1 2 3 37 a ,
考虑到 a 为整数,且1 a 9 只能 a 6 , n 36
学而思上海分校九年 级产品部
4、寒山寺每隔 9 秒敲一次钟,第一次敲钟时,甲、乙两船分别向上、下游驶去,速度分别
2
8、方程 x2 y2 z2 w2 u2 共有_____组整数解.
【解析】无数组整数解,取 x, y, z, w,u (0,0,0, k, k) ,其中 k 为任意整数
学而思上海分校九年 级产品部
9、正方形 ABCD 中有一点 E ,使 E 到 A、B、C 的距离之和最小为 2+ 6,求此正方
注:本试卷为冬令营考卷,主要目的为筛选竞赛考生,所以难度较高,2,8,9,10 等题均需 要一定的竞赛背景,难度超出一般自招难度,不必过于较真
学而思上海分校九年 级产品部
6、方程 x 2 1 a 有三个整数解,求 a 的值.
【解析】 f x x 2 1 的图像如图所示,只有 y 1 与 f x 有三个整数解,
【解析】(一道基础的染色问题)如图进行黑白相间染色,那么 L 型放入方格纸中,必定可 以盖住 1 个黑格子和 3 个白格子,或者 3 个黑格子和 1 个白格子。L 形格子盖住的黑格子数 都是奇数个,所以 15 个 L 形盖住的黑格子也还是奇数个,而方格纸中有偶数个黑格子,矛 盾。所以不能。
3、n 为正整数,S 1 2 3 n, S为一个由同一个数字组成的三位数,求n的值.
冲刺 17 年自主招生之 2013 年华二冬令营数学试卷
1、“帽子函数”的图像如图所示:
y
1
••••••
2
-2
-1
0
1
••••••
2
x
(1)求此函数的解析式;
(2)若有抛物线 y x2 a(a 3), 求它与“帽子函数”图像的交点个数; 4
(3)请试写出一个抛物线解析式,使它与“帽子函数”图像有且只有 2 个交点,横坐标分别
C
B' A
P' P
H
a
3a
E
2a
B
CB
A
对于此题,点 E 应满足 AEB BEC CEA 120
设 EH a ,则 AE 2a , AH BH 3a , BE 3 1 a
EA EB EC 2a 3 1 a 2a 3 3 a 2 6
为 3m / s,9m / s ,当甲船听到第 108 声时,乙船只能听见第_______声.( V声 =300m / s )
【解析】设第一次敲钟时的时刻为 0 秒,
则甲听到第 108 声的时刻为 107 9 107 9 3 972 8 秒
300 3
11
设乙只能听到第 k 声,则乙听到第 k 声的时刻为 k 1 9 k 1 9 9 900k 900
、
1 2
,
1 2
两点,
所以可以将 y x2 3 向右平移 3 个单位,即满足条件 4
该抛物线解析式为 y x 32 3
4
学而思上海分校九年 级产品部
2、在一个 8×8 的正方形方格纸中,一个角剪去一个 2×2 的小正方形,问其余部分可否剪 成 15 块“L”型(如图)纸片,若能剪,给出剪切方法,若不能剪,请说明理由。
