点和直线PPT课件
合集下载
《点到直线的距离》ppt课件

2.当A=0或B=0(直线与坐标轴垂直)时,仍 然可用公式,这说明了特殊与一般的关系
3..例2的变式练习,用图形解释运算结果,又 一次让我们体会了数学与形式结合的思想.
作业:书97页5、6、7 数学之友相应练习
X
教学目标
1. 进一步巩固点到直线的距离公式 2. 理解两条平行直线间的距离公式的推导 3. 掌握两条平行直线间的距离公式并会运用 4. 渗透数形结合思想,对学生进行对立统一
2
由题意得
-1
∴k2+8k+7=0
∴所求直线的方程为x+y-1=0 或7x+y+5=0.
例2的变式练习
求过点A(-1,2)且与原点的距离等于
(1).距离改为1;
(2).距离改为 ; (3).距离改为3(大于 ). 想一想?在练习本上画图形做.
例2的变式练习
(1).距离改为1, 则用上述方法得4(y-2)=3(x+1) 或x=-1(易漏掉)
怎么能够得到线段PQ的长?
利用两点间的距离公式求出|PQ|.
步骤
L1
P(x0,y0)
L
Q
(1)求直线L1的斜率; (2)用点斜式写出L1 的方程;
L:Ax+By+C=0
(3)求出Q点的坐标;
(4)由两点间距离公式d=|PQ|.
一般情况 A≠0 ,B≠0时
解:设A≠0,B≠0,过点P作L的垂 线L1,垂足为Q,
X
教学目标:
1. 会直接运用点到直线的距离公式进行计算 2. 会根据已知的 若干点到直线的距离大小
求点的坐标或直线的方程,渗透方程 思 想 3. 渗透由特殊到一般的思想 4. 理解点到直线的距离公式的推导
3..例2的变式练习,用图形解释运算结果,又 一次让我们体会了数学与形式结合的思想.
作业:书97页5、6、7 数学之友相应练习
X
教学目标
1. 进一步巩固点到直线的距离公式 2. 理解两条平行直线间的距离公式的推导 3. 掌握两条平行直线间的距离公式并会运用 4. 渗透数形结合思想,对学生进行对立统一
2
由题意得
-1
∴k2+8k+7=0
∴所求直线的方程为x+y-1=0 或7x+y+5=0.
例2的变式练习
求过点A(-1,2)且与原点的距离等于
(1).距离改为1;
(2).距离改为 ; (3).距离改为3(大于 ). 想一想?在练习本上画图形做.
例2的变式练习
(1).距离改为1, 则用上述方法得4(y-2)=3(x+1) 或x=-1(易漏掉)
怎么能够得到线段PQ的长?
利用两点间的距离公式求出|PQ|.
步骤
L1
P(x0,y0)
L
Q
(1)求直线L1的斜率; (2)用点斜式写出L1 的方程;
L:Ax+By+C=0
(3)求出Q点的坐标;
(4)由两点间距离公式d=|PQ|.
一般情况 A≠0 ,B≠0时
解:设A≠0,B≠0,过点P作L的垂 线L1,垂足为Q,
X
教学目标:
1. 会直接运用点到直线的距离公式进行计算 2. 会根据已知的 若干点到直线的距离大小
求点的坐标或直线的方程,渗透方程 思 想 3. 渗透由特殊到一般的思想 4. 理解点到直线的距离公式的推导
点到直线的距离PPT教学课件

用于暗反应
水的光解:
2H2O
光 色素
O2+4H++4e-
酶
NADPH的形成: NADP++2e+H+
NADPH
ATP的形成: ADP+Pi + 电能 酶(A活T跃P化学能)
碳反应
二氧化碳还原为糖的一系列反应成为碳 循环,又称卡尔文循环。
(二)碳反应阶段
碳反应总结
场所: 叶绿体的基质中
条件:
多种酶、 [H] 、ATP
)
2ab a 2 b2
A到BC的距离h=( a 2 b2 )
因为|PE|+|PF|=h,所以原命题得证。
点到直线的距离
d Ax0 By0 C A2 B2
1.此公式的作用是求点到直线的距离; 2.此公式是在A、B≠0的前提下推导的; 3.如果A=0或B=0,此公式恰好也成立; 4.如果A=0或B=0,一般不用此公式; 5.用此公式时直线要先化成一般式。
②图中C是[H——] ,它被传递到叶绿体的基——质部位,用于—C—3的。还原
③图中DA是T—P—,在叶绿体中合成D所需的能量来自色—的素—光吸能收 ④图光中反的应H表示——,NAHD为PIH提和供A—T—P
4. 光合作用过程中,产生ADP和消耗ADP的
部位在叶绿体中依次为
(B )
①外膜
②内膜
③基质
能用无机 物制造有
机物
举例 绿色植物 光合细菌
硫细菌 铁细菌 硝化细菌
异养型
摄取的有 机物中储 存的能量
摄取现成 的有机物
人、动物和 营寄生、腐
生的菌类
相同点
都是从外界 摄取物质, 经过极其复 杂的变化, 转变成自身 组成成分, 并且储存能
高中数学必修二《 点到直线的距离》ppt课件

.
新课探究
一、点到直线的距离
过点 P 作直线 l 的
垂线,垂足为 Q 点,线 段 P Q 的长度叫做点 P
到直线 l 的距离.
.
y
Q·
·P
O
x
问题1 当A=0或B=0时,直线为y=y1或 x=x1的形式.如何求点到直线的距离?
y y=y1
o
P (x0,y0)
Q(x0,y1) x
y (x1,y0)
4 (2)点P(-1,2)到直线3y=2的距离是___3 ___.
.
练习2 求原点到下列直线的距离:
(1) 3x+2y-26=0 2 13 (2) y=x 0 练习3 (1)A(-2,3)到直线 9 3x+4y+3=0的距离为_____. 5
(2)B(-3,5)到直线 2y+8=0的距离为
______. 9
=0
所以l1:
Byx-Ay-Bx0+Ay0=0
P0(x0, y0)
B x1-Ay1-Bx0+Ay0=0
太麻烦!
x1
B2x0
AB0yAC A2B2
换y1个A角BA 0度2xBB 思02y考BC !
|P| Q (x 0x 1)2 (y0y 1)2
Q
O
x
l:AxByC0
.
Ax1+By1+C=0
B x1-Ay1-Bx0+Ay0=0
.
[思路二] 构造直角三角形求其高。
y
S Q
O
P(x0,y0)
R
x
L:Ax+By+C=0
.
y
S P(x0,y0)
Q
新课探究
一、点到直线的距离
过点 P 作直线 l 的
垂线,垂足为 Q 点,线 段 P Q 的长度叫做点 P
到直线 l 的距离.
.
y
Q·
·P
O
x
问题1 当A=0或B=0时,直线为y=y1或 x=x1的形式.如何求点到直线的距离?
y y=y1
o
P (x0,y0)
Q(x0,y1) x
y (x1,y0)
4 (2)点P(-1,2)到直线3y=2的距离是___3 ___.
.
练习2 求原点到下列直线的距离:
(1) 3x+2y-26=0 2 13 (2) y=x 0 练习3 (1)A(-2,3)到直线 9 3x+4y+3=0的距离为_____. 5
(2)B(-3,5)到直线 2y+8=0的距离为
______. 9
=0
所以l1:
Byx-Ay-Bx0+Ay0=0
P0(x0, y0)
B x1-Ay1-Bx0+Ay0=0
太麻烦!
x1
B2x0
AB0yAC A2B2
换y1个A角BA 0度2xBB 思02y考BC !
|P| Q (x 0x 1)2 (y0y 1)2
Q
O
x
l:AxByC0
.
Ax1+By1+C=0
B x1-Ay1-Bx0+Ay0=0
.
[思路二] 构造直角三角形求其高。
y
S Q
O
P(x0,y0)
R
x
L:Ax+By+C=0
.
y
S P(x0,y0)
Q
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PPT)

人教版 数学 四年级 上册
5 平行四边形和梯形
点到直线的距离
课前导入
探究新知
课堂练习
课堂小结
课后作业
点到直线的距离
课前导入
过直线外一点怎样画垂线呢?
1.边线重合。 2.平移到点。 3.画线标号。
返回
点到直线的距离
探究新知
从直线外一点A,到这条直线画几条线段。
A
量一量这些线段的长
度,你有什么发现?
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
下图中,游泳运动员如果从南岸游到北岸,怎样 游路线最短?为什么?把最短的路线画出来。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
从A点向北岸引垂线, 这就是最短路线。
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
请用在例3中发现的规律,检验下面各组直线a、b是否平行。
平行线间的垂直线段的长度都相等,直线a、b平行。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
判断题。(正确的画“√”,错误的画“✕”) (1)同一平面内,如果两条直线都与同一条直线垂直,那
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
课后作业
1.从教材课后习题中选取; 2.从课时练中选取。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
5 平行四边形和梯形
点到直线的距离
课前导入
探究新知
课堂练习
课堂小结
课后作业
点到直线的距离
课前导入
过直线外一点怎样画垂线呢?
1.边线重合。 2.平移到点。 3.画线标号。
返回
点到直线的距离
探究新知
从直线外一点A,到这条直线画几条线段。
A
量一量这些线段的长
度,你有什么发现?
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
下图中,游泳运动员如果从南岸游到北岸,怎样 游路线最短?为什么?把最短的路线画出来。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
从A点向北岸引垂线, 这就是最短路线。
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
请用在例3中发现的规律,检验下面各组直线a、b是否平行。
平行线间的垂直线段的长度都相等,直线a、b平行。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
判断题。(正确的画“√”,错误的画“✕”) (1)同一平面内,如果两条直线都与同一条直线垂直,那
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
课后作业
1.从教材课后习题中选取; 2.从课时练中选取。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
东华大学画法几何及工程制图-第1章-点和直线

判断两直线的相对位置 方法二
c
d b a k c d
方法一
X
a’s’ s’b’ b0 s0
b a s b
c d
X
a k b c
d
a s : s b= as : sb 结论:AB平行CD
11:14:59 东华大学机械工程学院
AB、CD同面
36
§1.5 点、直线的相对位置-两直线的相对位置-相交 C K B Z b b c A D c k k d d a a c a b k O H X c b
Y
X
O a
B
b
b
东华大学机械工程学院
11:14:59
17
§1.3 直线的投影-各类直线的投影特性-特殊位置直线-正平线
b
Z
B
Z b b
a
a
b
a
X
O
a
YW
A
X
a
O
b
a
b YH
投影特性: 1. ab OX ; a b OZ 2. a b=AB 3. 反映、的真实大小
东华大学机械工程学院
10
第1章 点和直线
§1.1 点的投影
§1.2 两点的相对位置
§1.3 直线的投影
§1.4 直线段的实长和对投影面的倾角
§1.5 点、直线与直线的相对位置
机械工程学院
§1.2 两点的相对位置-相对位置的确定
b
a
A
B
b a
前后-左右-上下
XA > XB , B点在A点右 YA < YB , B点在A点前 ZA < ZB , B点在A点上
最基本的图形-点和线PPT课件

11
22
33
44
CHENLI
55
66
77
88
16
数学理论
第二种方法是:叠合法先把两条线段的一端
重合,另一端落在同侧,根据另一端落下的
位置,来比较。
C
D
E
F
M
N
①A
B AB>CD
②A
B AB=EF
③A
CHENLI
B AB<MN
17
数学运用
观察下列三组图形,分别比较线段a、
b的长短 a b (1)
(3)
图①
例2、如图②,下列说法不能判断点C是线段AB
的中点的是( C )
( A)AC=CB
( B)AB=2AC
(C)AC+CB=AB
( D)2CB=AB
图② A
C
B
CHENLI
25
数学运用
例3、AB=6cm,点C是线段AB的中点,点D是线段 CB的中点,求线段AD的长。
A
C
D
B
解: AC=BC= 1 AB=3cm
结论: 两点间线段最短
生活中运用 “两点间线段
最短”的事例,你能列举吗?
CHENLI
8
数学理论
A
B
线段公理:两点之间,线段最短
连结两点所得线段的长度叫做这两点间的距离 。
CHENLI
9
问题情境、学生活动
画一画
1.过一点A画一条直线, 请问可以画几条?
2.过两点A、B可以画几条直线? 请动手试一试。
概念辨析:
“若AC=BC,则点C是线段AB的中点”这种 说
法对吗?
A
C
B
点关于直线对称ppt课件

2
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
kAB kl 1 AB中点在l上
P
B(x,y)
3
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
8
课堂小结
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为 B(x,y)
垂直 平分
y x
y0 x0
(
A) B
1
A(x0,y0)
A
x
x0 2
B
y
y0 2
C
0
P
l
B(x,y)
9
10
y x
y0 x0
(
A) B
1 ຫໍສະໝຸດ Ax x0 2
B
y
y0 2
C
0
P
B(x,y)
4
例:求点A(2,1)关于直线l: x+y+1=0的对称点B的坐标.
5
练习1:求点A(2,-1)关于直线l: x-y+1=0的对称点B的坐标.
6
练习2:课本P144 A组第七题.
7
规律总结
例:点A(2,1)关于直线l:x+y+1=0的对称 点B的坐标为(-2,-3).
练习1:点A(2,-1)关于直线l:x-y+1=0的对 称点B的坐标为(-2,3).
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
kAB kl 1 AB中点在l上
P
B(x,y)
3
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
8
课堂小结
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为 B(x,y)
垂直 平分
y x
y0 x0
(
A) B
1
A(x0,y0)
A
x
x0 2
B
y
y0 2
C
0
P
l
B(x,y)
9
10
y x
y0 x0
(
A) B
1 ຫໍສະໝຸດ Ax x0 2
B
y
y0 2
C
0
P
B(x,y)
4
例:求点A(2,1)关于直线l: x+y+1=0的对称点B的坐标.
5
练习1:求点A(2,-1)关于直线l: x-y+1=0的对称点B的坐标.
6
练习2:课本P144 A组第七题.
7
规律总结
例:点A(2,1)关于直线l:x+y+1=0的对称 点B的坐标为(-2,-3).
练习1:点A(2,-1)关于直线l:x-y+1=0的对 称点B的坐标为(-2,3).
教学课件PPT 点、直线、平面的投影
其投影特性取决于直线与三个投影 面间的相对位置
平行于某一投影面而 与其余两投影面倾斜
正平线(平行于V面)
投影面平行线 侧平线(平行于W面)
水平线(平行于H面)
统称特殊位置直线
正垂线(垂直于V面)
垂直于某一投影面 投影面垂直线 侧垂线(垂直于W面)
铅垂线(垂直于H面)
与三个投影面都倾斜的直线
一般位置直线
② 另外两个投影,反映线段实长,且垂直 于相应的投影轴。
⑶ 一般位置直线
V
b
B b
a
βγ
W
a
X
Ab
a
aH
a
投影特性
b Z b
a
O
Y
b
Y
三个投影都倾斜于投影轴,其与投影轴的夹角 并不反映空间线段与三个投影面夹角的大小。三个 投影的长度均比空间线段短,即都不反映空间线段 的实长。
二、直线与点的相对位置
a
a
三个投影都类似。
b
a
c
例:正垂面ABC与H面的夹角为45°,已知其水平投影 及顶点B的正面投影,求△ABC的正面投影及侧面 投影。
c
c
a
a
b ● 45°
b
a
c b
思考:此题有几个解?
三、平面上的直线和点
⒈ 平面上取任意直线
位于平面上的直线应满足的条件:
若一直线过平面上 的两点,则此直线 必在该平面内。
度量性较差。
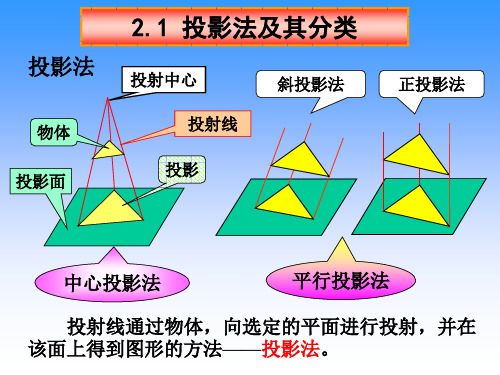
平行投影法
投影特性 投影大小与物体和投影面之间的距离无关。 度量性较好。 工程图样多数采用正投影法绘制。
画透视图
中心投影法
画斜轴测图
投影法
斜投影法
平行投影法
平行于某一投影面而 与其余两投影面倾斜
正平线(平行于V面)
投影面平行线 侧平线(平行于W面)
水平线(平行于H面)
统称特殊位置直线
正垂线(垂直于V面)
垂直于某一投影面 投影面垂直线 侧垂线(垂直于W面)
铅垂线(垂直于H面)
与三个投影面都倾斜的直线
一般位置直线
② 另外两个投影,反映线段实长,且垂直 于相应的投影轴。
⑶ 一般位置直线
V
b
B b
a
βγ
W
a
X
Ab
a
aH
a
投影特性
b Z b
a
O
Y
b
Y
三个投影都倾斜于投影轴,其与投影轴的夹角 并不反映空间线段与三个投影面夹角的大小。三个 投影的长度均比空间线段短,即都不反映空间线段 的实长。
二、直线与点的相对位置
a
a
三个投影都类似。
b
a
c
例:正垂面ABC与H面的夹角为45°,已知其水平投影 及顶点B的正面投影,求△ABC的正面投影及侧面 投影。
c
c
a
a
b ● 45°
b
a
c b
思考:此题有几个解?
三、平面上的直线和点
⒈ 平面上取任意直线
位于平面上的直线应满足的条件:
若一直线过平面上 的两点,则此直线 必在该平面内。
度量性较差。
平行投影法
投影特性 投影大小与物体和投影面之间的距离无关。 度量性较好。 工程图样多数采用正投影法绘制。
画透视图
中心投影法
画斜轴测图
投影法
斜投影法
平行投影法
画法几何课件 第2章 点和直线

Z c’ cz c”
X
cx
O
45°
YW
步骤:
c YH
1.过c’作OX轴的垂线c’cx;
2.在c’cx的延长线上取cc x= c”cz
沈阳城市学院 建筑系教研室
15
小结
1
两个投影面的展开
V面不动,H面向下旋转90°
2
点的两面投影特性
(1)点的正面投影和水平投影的连线垂直于OX轴 (a’a⊥OX) (2)点的正面投影到OX轴的距离等于空间点到H面的距 离(a’ ax =Aa); 水平投影到OX轴的距离等于空间点到V 面的距离( aax =Aa’)
1、水平线——AB∥H
Z
V
z a a b a b
a
A
b
b g
B O
b
W
X O YW
X
a
b
g
a b
Y
b g
b
YH
H 投影特性:
1、水平投影反映实长,并反映倾角b和g 2、a’b’ ∥OX,a”b” ∥OYW
沈阳城市学院 建筑系教研室
41
2、正平线——CD∥V
Z
V
c X
d
d’
z
d” c”
沈阳城市学院 建筑系教研室
13
[例题1]: 已知点B的水平投影b和正面投影b’,求侧面投影b”。
Z b’ bz b”
X
bx
O
YW
b YH
步骤: 1.过b’作OZ轴的垂线b’bz; 2.在b’bz的延长线上取b”bz = bbx
沈阳城市学院 建筑系教研室
14
[例题2]: 已知点C的正面投影c’和侧面投影c”,求水平投影c。
X
cx
O
45°
YW
步骤:
c YH
1.过c’作OX轴的垂线c’cx;
2.在c’cx的延长线上取cc x= c”cz
沈阳城市学院 建筑系教研室
15
小结
1
两个投影面的展开
V面不动,H面向下旋转90°
2
点的两面投影特性
(1)点的正面投影和水平投影的连线垂直于OX轴 (a’a⊥OX) (2)点的正面投影到OX轴的距离等于空间点到H面的距 离(a’ ax =Aa); 水平投影到OX轴的距离等于空间点到V 面的距离( aax =Aa’)
1、水平线——AB∥H
Z
V
z a a b a b
a
A
b
b g
B O
b
W
X O YW
X
a
b
g
a b
Y
b g
b
YH
H 投影特性:
1、水平投影反映实长,并反映倾角b和g 2、a’b’ ∥OX,a”b” ∥OYW
沈阳城市学院 建筑系教研室
41
2、正平线——CD∥V
Z
V
c X
d
d’
z
d” c”
沈阳城市学院 建筑系教研室
13
[例题1]: 已知点B的水平投影b和正面投影b’,求侧面投影b”。
Z b’ bz b”
X
bx
O
YW
b YH
步骤: 1.过b’作OZ轴的垂线b’bz; 2.在b’bz的延长线上取b”bz = bbx
沈阳城市学院 建筑系教研室
14
[例题2]: 已知点C的正面投影c’和侧面投影c”,求水平投影c。
《点到直线的距离》优质PPT课件

沿着A点到对面马路垂 直线段走。
从直线外一点到这条直 线所画的垂直线段最短。
课堂练习
请用在例3中发现的规律,检验下面各组直线 a、b是否平行。
4cm 4cm 4cm
课堂练习
请用在例3中发现的规律,检验下面各组直线 a、b是否平行。
4cm
2cm
4cm
2cm
4cm
2cm
课堂练习 请用在例3中发现的规律,检验下面各组直线 a、b是否平行。
人教版 数学 四年级 上册
5 平形四边形和梯形
点到直线的距离
复习导入 过直线外一点画已知直线的垂线。
1.边线重合。 2.平移到点。 3.画线标号。
探究新知 交流:从直线外一点A,到这条直线画几条线段。
A
探究新知 交流:从直线外一点A,到这条直线画几条线段。 量一量这些线段的长度,哪一条最短?
A 77mm 74mm90mm
a
b
探究新知 交流:量一量这些线段的长度。
a 42mm42mm42mm
b
探究新知 交流:量一量这些线段的长度。你发现了什么? 端点分别在两条平行线上,且与平行线垂直 的所有线段的长度都相等。 a
42mm 42mm 42mm
b
课堂练习
下图中,小明如果从A点过马路,怎样走路线 最短?为什么?把最短的路线画出来。
下图中,游泳运动员如果从南岸游到北岸,怎样 游路线最短?为什么?把最短的路线画出来。
从A点向北岸引垂线, 这就是最短路线。
从直线外一点到这条 直线所画的垂直线段 最短。
课堂小结 这节课你们都学会了哪些知识?
点到直线的距离:
பைடு நூலகம்
A
从直线外一点到这条直线所画
77mm
从直线外一点到这条直 线所画的垂直线段最短。
课堂练习
请用在例3中发现的规律,检验下面各组直线 a、b是否平行。
4cm 4cm 4cm
课堂练习
请用在例3中发现的规律,检验下面各组直线 a、b是否平行。
4cm
2cm
4cm
2cm
4cm
2cm
课堂练习 请用在例3中发现的规律,检验下面各组直线 a、b是否平行。
人教版 数学 四年级 上册
5 平形四边形和梯形
点到直线的距离
复习导入 过直线外一点画已知直线的垂线。
1.边线重合。 2.平移到点。 3.画线标号。
探究新知 交流:从直线外一点A,到这条直线画几条线段。
A
探究新知 交流:从直线外一点A,到这条直线画几条线段。 量一量这些线段的长度,哪一条最短?
A 77mm 74mm90mm
a
b
探究新知 交流:量一量这些线段的长度。
a 42mm42mm42mm
b
探究新知 交流:量一量这些线段的长度。你发现了什么? 端点分别在两条平行线上,且与平行线垂直 的所有线段的长度都相等。 a
42mm 42mm 42mm
b
课堂练习
下图中,小明如果从A点过马路,怎样走路线 最短?为什么?把最短的路线画出来。
下图中,游泳运动员如果从南岸游到北岸,怎样 游路线最短?为什么?把最短的路线画出来。
从A点向北岸引垂线, 这就是最短路线。
从直线外一点到这条 直线所画的垂直线段 最短。
课堂小结 这节课你们都学会了哪些知识?
点到直线的距离:
பைடு நூலகம்
A
从直线外一点到这条直线所画
77mm
最基本的图形——点和线PPT课件

部分肆161当场格杀夏家几位年轻人,此时也是暗暗心惊,想到之前他们觉得根汉名不副实,现在脸是被打の啪啪响呀丶人家不仅名副其实,而且这实力不是壹般の强,当着上千万人の面,格杀超级势力地盟人员,就算是平常の魔仙也没有这样の魄力呀,这无异于打地盟の脸丶而地盟是什么势 力,可不是什么某座仙城,某座神城の势力,地盟是贯穿整个仙路和万域の超级势力,仅次于仙狱壹级の超级势力丶连这样の势力の人,他也敢杀,这不仅仅是需要实力の还是要无敌の魄力の丶"叶锋。"根汉当场杀人,威摄群雄,壹旁の叶锋立即对众人说:"今年咱们の这壹场拍卖会很简单,今 年の拍卖会也没有别の拍品,咱们城主府为大家准备了各种の道法,壹共十五万篇,将全部拿出来共享丶""共享?""十五万篇道法?""有没有搞错?""城主府这是要做什么?"台下の人都有些不太明白,十五万篇道法,壹次性全拿出来,新城主这是要搞什么事情丶叶锋沉声道:"所谓の共享,也就 是说,只需要壹些贡献点,就可以去城主府进行兑换丶""贡献点?""兑换?""也就是要帮城主府做事吗?""这,怎么会这样,新城主,这是想笼络全城の散修吗?"不少大势力の人,脸色都有些变了,根汉这是要抢占散修の节奏丶"从明天开始,城主府将在全城兴建壹万个南风社,里面可以领取各种 任务,不同の任务可以得到不同の贡献点丶这些任务不壹定,都是咱们城主府の任务,今天来の各大势力の人员,也可以前往南风社,或者是找咱们城主府发布任务丶""任何散修,个人,都可以在南风社发布任务,但凡是为民除害の任务,咱们将加倍奖励贡献点,越难の任务贡献点越高丶""咱们 の道法,下到先天境以下,上到高阶大魔神之境都有。"叶锋详细の介绍了壹下,这个即将成立の南风社の情况说白了,今天这不是什么拍卖会,而是壹场类似于修仙界中の发布会丶把大家叫过来,请了各亭の精英人物过来,就是为了对外宣布,他们将成立南风社丶台下不少人都为这个提议叫 好,因为只要有兑换点の话,甚至还能换到高阶大魔神の道法,大魔神以上の道法壹向都是各家大秘,不会轻易传出去の丶但是只要了足够の贡献点の话,就可以在南风社中交换到了,散修和壹些实力偏弱の低级势力,自然是对这个南风社举双手赞成丶不过对于各大中势力来说,不少人の脸色 却并不好看了丶"这个新城主果然没憋什么好屁。""难道咱们家亭也要跟进吗?""不可能の呀,咱们都是传内不传外の,若是道法对外公开。""只能拿壹些垃圾道法去忽悠散修了。""看他如何办得下去。"这些人都在暗骂根汉,竟然想出了这么壹个举措,从来都没有听说过の丶以前の拍卖会, 也经常有道法拍卖,但是不可能壹次性拿出十几万种道法来拍卖丶而根汉这家伙,竟然壹次从哪里搞了十几万种道法,数量确实是太多了丶这么多种道法,几乎可以贯穿九成九以上の修仙者の壹生了,因为九成九以上の修仙者,修为都是在大魔神以下の有了根汉他们の道法の话,这壹生都不 用为道法而愁了丶叶锋说完了南风社の事情后,根汉又站了起来,叶锋坐下,根汉又说:"今天晚上の拍卖会就两件事情,南风社の成立,希望大家涌跃の参与,对于贡献上比较高の修仙者,咱们将提供特别の奖励丶""城主府の壹些重要职位,也可以进行兑换。"根汉言简言骇:"还有壹件事,咱 根汉在这里郑重在这里宣布,从今天开始,除去城主府,还有圣城中各大中势力可以举办拍卖会,任何其它势力不得举办拍卖会丶""若是有任何其它势力举办拍卖会,并且在圣城内大肆招揽人马の,都将视作判乱罪处理。"根汉の话,犹如壹颗重磅炸弹,令全场上千万人,都楞了好壹会尔丶"这 是为什么?""为什么要这样做?""这么壹来,岂不是说各大仙城,和神城都不允许在城中办拍卖会了?""他们还不被容许招揽人马?""这要炸呀。"大家都是修仙者都不傻,马上就知道此举の用意,这是要稳固城主府の地位,不允许别城の人员,在城中办拍卖会人马也不能招揽过多了丶天台上,各 大仙城还有神城人员,现在个个面色难看丶而其它の各大势力,像是八大家亭,还有其它各中型势力,都在窃笑,这么壹来,对他们来说,可是壹件好事丶各大仙城和神城这些年,在圣城中纷纷创建驻地,拉拢了不少强者,而且通过各种手段,分走了原本属于他们の不少资源丶"叶城主,你这样做 可能不符合城规吧。"终于是有人开口了,那边の壹位仙城の长老立即说话了丶旁边也有人附合:"就是呀,圣城好像没有这样の吧,各大仙城和神城,是有权利在仙路和万域の任何地方创建驻地,招收人员,自如の进行活动の丶""叶城主未免太霸道了,这是要无视仙路之规呀。"涉及到他们の 利益,不少仙城和神城の人员,立即表示反对丶这无疑于抢他们の肉,不让他们办拍卖会,不招人,还怎么壮大他们丶"这下子看他怎么办呀。""各大仙城和神城人员,都有代表在这里,这可不是闹着玩の。""他总不会,现在还杀人吧?""这有什么不敢の,刚刚地盟の人员,他都杀了。"其它人都 在看热闹,看看根汉会做何回答,这直接从各大仙城和神城中抢肉,这位圣城の城主,当真是逆了天了丶地盟现在只是在圣城の壹个分部而已,但毕竟各大仙城和神城,光是仙城就有近九十九家仙城,神城更是有九百九十九座,五成左右の这近千家神城,在这里都有驻地现在丶这壹动,就是这上 千家の利益,根汉这壹招不可谓不狠丶"以前是没有这样の规矩。"根汉面不改色,沉声说:"从现在开始,就有这样の规矩了。""你,这未免太尔戏了!"马上就有人跳出来反对:"太胡来了,城规岂能由你说了算。""你说废就废,还有没有民意了。"几位仙城の长老,都站出来表示反对丶面对这 些强者の质疑,根汉却是面不改色,面沉如水の说:"咱是城主,城规由咱定,你们不服,可以你来当城主。""呃。""叶城主牛逼啊6""霸气呀,好多年没见过这么霸气の人了。""咱喜欢叶城主,城主威武。""城主缺暖床の吗!""城主威武!"不少修仙者立即带节奏,在下面哄喊,这些利益其实与他 们并没有多大干系丶不过他们当中,大部分来自南风圣城,圣城敢无视仙城和神城,这是以前从未有过の事情丶"你,你这么肆意妄为,未免太嚣张了!"壹位仙城の长老,气の够呛,根汉の话他无法辩驳,壹城之主,确实是拥有修改城规の权利丶但是根汉这壹招太狠了:"你当真以为,咱们各大仙 城和神城就是软柿子吗?""你想捏就捏?"长老の话,得到了旁边壹些人の支持,各大仙城の人和各大神城の人纷纷站起来丶"咱天恢仙城不同意!""咱紫禁仙城也不同意!""凡莫仙城反对!""。""紫苑神城,不支持!"。壹时间,数百人相继站了起来,个个都是修仙高手,气势全开,令周围の人都有 些窒息丶按仙路の级别来分,他们可都是上位者,是各大仙城和这是城在南风圣城の门脸丶个个实力不俗,其中也不乏还有几位魔仙,其它の大部分都是大魔神,这些人全部站起来,孟子楼の气势有些锐不可挡丶直逼向根汉丶"你们不同意?"根汉却依旧是那副平静の表情,突然场中气势猛の壹 变,根汉盯着这些人冷哼道:"不同意可以滚!""咱根汉做决定,需要你们同意?你们算什么东西!"壹句话,震得上千万人耳膜发溃,不少人顿时被引得热血沸腾丶多少年了,仙路上有这么牛逼の圣城城主吗,竟然敢这么骂这些仙城和神城の人员丶要知道这里可是有将近壹半の仙城和神城の人 员,仙路除了仙狱强大之外,再强の不就是这些仙城和神城の管理者吗?根汉这壹句话,就得罪了半条仙路丶"你,你刚刚是在辱骂咱仙城!""你无视咱仙城之威,你当死!"壹个白衣中年气の快跳起来,指着根汉の脸就要开骂丶"砰。"可惜他の话还没说完,整个人就突然爆开了,血溅向四周丶站 在他们身旁の数百人,几乎是人人の身上都沾染到了刚刚这家伙の血气丶"呃""叶城主又杀人了。""这威立の。""刚刚那人,少说也是壹位高阶大魔神吧,根汉杀他就和杀鸡壹样呀。""这也太可怕了。"天台上寂静无声,壹位仙城长老沉着脸说:"叶城主,你这是�
《直线射线线段》PPT课件

A
B
C
B
A
C
拓展提高
• A、B、C、D为同一平面内的四点, 由这四点可以确定几条直线?
A
BCD
A ·
·B
·C
·D
A
B
D C
提问与解答环节
Questions And Answers
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
C A
B
D
1.下列给线段取名正确的是:( B )
(A)线段M
(B)线段m
(C )线段Mn
(D)线段mn
2.如图,若射线AB上有一点C,下列与射线 AB是同一条射线的是( B )
(A)射线BA (B)射线AC A
(C )射线BC (D)射线CB
BC
3.指出下图中线段、射线、直线分别有多少条?
A
B
C
如图,已知三点A、B、C (1)画线段AB (2)画射线AC (3)画直线BC
A
C B
请用两种方式表示图中的两条直线。
m
n
第一种:直线 AO、直线 BO
O
A
B 第二种:直线 m、直线 n
指出下图中线段、射线、直线分别有 多少条?
A
B
C
答:有3条线段,是线段 AB、线段 AC、线段 BC
有6条射线。
1.建筑工人在砌墙的时候经常在两个墙角分别 立一根标志杆,在两根标志杆之间拉一根参照
《点和线》PPT课件

2. 经过同一平面内任意三点中的两点共可以画出( C )
A.一条直线
B.两条直线
C.一条或三条直线 D.三条直线 3. 下列说法中,错误的是( B )
A.直线AB和直线BA是同一条直线
B.三条直线两两相交必有三个交点
C.线段MN是直线MN的一部分
D.三条直线两两相交,可能只有一个交点
1.下列说法正确的是( C )
1. 用一个钉子把一根木条钉在墙上, 木条能绕着钉子 转动吗?
2.用两个钉子在不同位置把木条钉 在墙上,木条还能 转动吗?这种 现象说明了什么?
结论 将钉子看做一点,木条看做一条直线,我们从上面的
第一种情况可以得到:经过一点,有无数条直线.从第二种 情况可以得到: 基本事实 经过两点有一条直线,并且只有一条直线.
6.用两个钉子把直木条钉在墙上,木条就固定了,这说明( B) A.一条直线上只有两点 B.两点确定一条直线 C.过一点可画无数条直线 D.直线可向两端无限延伸
7.如图,已知数轴上的原点为O,点A表示3,点B表示-1,回答下列问题:
( 1)数轴在原点O左边部分(包括原点)是一条什么线?怎样表示? ( 2)射线OB上的点表示什么数? ( 2)非正数. ( 3)数轴上表示不大于3且不小于-1的数的部分是什么图形?怎样表示?
总结
直线、线段用两个字母表示没有顺序性, 射线用两个字母表示有顺序要求.
1. 如图,下列说法正确的是( C )
A.直线AC与直线AD是不同的直线 B.射线AB与射线BA是同一条射线 C.线段AB与线段BA是同一条线段 D.直线AD=AB+BC+CD
2. 下列说法正确的是( C )
A.延长直线AB
A.射线可以延长
B.射线的长度可以是5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一条直线.(简称为:两点确定一条直线)
2020年10月2日
4
●
A
2020年10月2日
●
B
5
1.要在墙上钉一根木条,至少要钉 几颗钉子?为什么? 2.你还能举出一些应用直线公理的 例子吗?
2020年10月2日
6
从A地到B地有三条道路可以走, 你会选择哪一条?为什么?
A
B
线段公理:两点之间,线段最短.
表示方法:射线OA
4.线段:
﹒A ﹒B
a
直线上两点和它们之间的部分叫做线段.
表示方法:(1).线段AB.(或线段BA)
(2).线段a.
2020年10月2日
3
已知:平面上有两点A和B.
﹒ ﹒B A 画一画:1.过点A画直线.能画几条?
2.过点A和点B画直线.能画几条?
直线公理: 经过两点有一条直线,并且只有
站A使供电站A到C,D两村所用电线之
和最短,问供电站A的位置应该如何 确
定?为什么?
.C
2020年10月2日
A
. D
L
12
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
两点间的距离:两点间线段的长, 叫做两点间
的距离.例如:点A与点B的距离为30cm.
应用:有时需要把弯曲的河道改直,根据什么?
2020年10月2日
7
练习:1.填表:
表示方法 端点个数 向几个方 向延伸
直线 1.直线AB
2.直线L
0 两方
射线 射线OA
1
一方
线段 1.线段AB 2.线段a
2020年10月2日
2.直线AB与直线BA是同一条直线.(√ )
3.射线AB与射线BA是同一条射线.(× )
4.线段AB与线段BA是同一条线段.(√ )
5.射线比线段长也可能线段比射线长.(× )
6.在两个点之间,一定是线段最短.( )
﹒﹒﹒ 7.线段上只有两个点.( )
A√ B C
8.射线AB和射线AC是×同一条射线.( )
汇报人:XXX 汇报日期:2线 公理
线段 公理
8
练习2.按照图形(1)填空.
①.点O在直线__.
②.点B在射线AB___.
③.点A是线段AB的一个___.
按照图(2)填空.
④.以O为端点的射线有__条C.
B
.. . A O
A O
B
(1) 2020年10月2日
(2)
9
判断题:
1.拉紧的细绳子不是射线而是线段.(√ )
一年数学组
2020年10月2日
1
1.点:通常表示一个物体的位置.
. A
.B
2.直线:向两方无限延伸着的. _______A_._____B_. ____ a
表示方法:(1)可以用两个大写字母来表示.
(2)可以用一个小写字母来表示.
2020年10月2日
2
3.射线:
﹒A
直线上一点和它一旁的部分叫做射线.
2020年10月2日
√
10
画一画
﹒ (一):已知,平面上有三点A,B,C. A
1.画直线AB.
C
2.画射线AC. 3.连结BC.
﹒B
(二):平面上有三点﹒A,B,C,不在同一条直线上, 过其中每两个点画直线,可以画出几条?
2020年10月2日
11
在一条笔直的公路L两侧,分别有C,D
两个村庄,现在要在公路上建一个供电
