湖南师大高三数学第五讲函数的单调性与最值课件新人教A版

合集下载

函数的单调性和最值PPT精品课件

函数单调性的定义可以通过函数的导数来判断。如果函数的导数大于0，则函数在该区间内单调递增；如果函数的导数小于0，则函数在该区间内单调递减。
函数单调性的性质
函数单调性具有传递性，即如果函数在区间I上单调递增，且在区间J上单调递增，则函数在区间I和J的交集上也是单调递增的。
函数单调性具有相对性，即如果函数在区间I上单调递增，且另一个函数在区间J上单调递增，则这两个函数在区间I和J的交集上也是单调递增的。
求函数最值的方法
配方法：将函数进行配方，利用二次函数的性质求最值。
导数法：求出函数的导数，令导数为 0，解出极值点，再比较区间端点和
极值点的函数值，得到最值。
判别式法：对于一些特殊的分式函数，通过判别式法求最值。
实际问题的解决
利用函数的单调性和最值解决实际问题，如最大利润、最小成本等问题。
通过建立数学模型，将实际问题转化为数学问题，利用函数的单调性和最值求解。
函数的拐点
定义
函数图像上凹凸性发生变化的点，即二阶导数由正变负或由负变正的点。
判断方法
求函数二阶导数，令其等于0，然后检查三阶导数在该点的符号，以确定函数在拐点左侧是凹还是凸。
极值和拐点的应用
优化问题
通过找到函数的极值点，可以确定使目标函数取得最大或最小值的自变量取值。
动态分析
拐点可以用于分析经济、物理等系统的变化趋势和稳定性。
单调性在生活中的应用
单调性在经济学中有着广泛的应用，例如在股票价格、商品价格和供需关系等方面的分析中，可以利用单调性来判断市场的变化趋势。
单调性在物理学中也有着重要的应用，例如在研究物体的运动规律、热量传递和电磁场等方面，可以利用单调性来分析物理现象的变化趋势。

函数的单调性极值与最值课件

2) 对常见函数, 极值可能出现在导数为 0 或
y
不存在的点.
x1 , x4 为极大点
x 2 , x5 为极小点
x3 不是极值点
o a x1 x2 x3 x4 x5 b x
机动目录上页下页返回结束
定理 1 (极值第一判别法)
设函数 f (x)在 x0 的某邻域内连续, 且在空心邻域内有导数, 当x由小到大通过 x0 时,
x2
2
x1
)2
[
f
(1)
f (2 )]
当 f (x) 0时,
f
( x1
) 2
f
(
x2
)
f (x1 x2 ),
2
说明 (1) 成立; (2) 证毕
机动目录上页下页返回结束
推论
如果在区间(a,b)内恒有f ''(x) 0(或f ''(x) 0). 且使得f ''(x) 0的点只是一些离散的点，则函数曲线y f (x)在区间(a,b)内上凹（或下凹）
综上,f (x)在(0,1)内只有一个零点，即方程f (x)=0,亦即xex 2在(0,1)内仅有一个实根.
例6 设f (x)在[a, b]上连续，且在(a, b)内f ''(x) 0,
证明 f (x) f (a) 在(a, b)内单调增加. xa
证明设F (x) f (x) f (a) , x (a,b) xa
而F ' (x)
f ' (x)(x a) f ' ( )(x a)
(x a)2
f ' (x) f ' ( ) 0,
xa F (x) f (x) f (a) 在(a,b)内单调递增.

湖南师大高三数学第五讲函数的单调性与最值课件新人教A版

求y f (x)单调区间.
h
13
例3 确定下列函数的单调区间：（1）f (x) x2 1 ；
（2）f(x)log1(2x25x3)；
（3）f(x)|lg(x21)| .
h
14
规律总结
确定函数的单调区间的方法有： (1)定义法 (2)导数法 (3)利用复合函数的单调性求解 (4)利用单调性的性质求解 (5)利用函数的图像求解
h
3
第五讲函数的单调性与最值
h
4
知识回顾
1.增函数与减函数：
对于函数f(x)定义域I内某个区间D上的
任意两个自变量的值x1，x2，若当x1＜x2 时，都有
（1）f(x1)＜f(x2)，则称函数f(x)在区间D上是增函数.
（2）f(x1)＞f(x2)，则称函数f(x)在区间D上是减函数.
h
5
2.单调性与单调区间：
如果函数y＝f(x)在区间D上是增函数或减函数，则称函数f(x)在这一区间具有（严格的）单调性，区间D叫做函数f(x) 的单调区间.
3.复合函数的单调性：
若函数f(x)和g(x)的单调性相同，则
f[g(x)]为增函数；若函数f(x)和g(x)的
单调性相反，则f[g(x)h ]为减函数.
（1） f(x1)f(x2) 0f(x)在区间D上
x1x2
是增函数；
（2） f(x1)f(x2) 0f(x)在区间D上
x1 x2
是减函数；
h
8
7.若函数f(x)在区间A，B上都是增函数，则 f(x)在区间A∪B上不一定是增函数，对减函数也如此.
h
9
8.设函数yf(x)的定义域为I，如果存在
实数M满足：对任意的xI,都有f(x)M；存在x0I,使得f(x0)M,那么，称M是函数 yf(x)的最大值.

5.3.2函数的极值课件2024-2025学年人教A版必修第一册

x0 f′(x) =0 极大值
x0 f′(x) =0 极小值
x0右侧 f′(x) <0 减
x0右侧 f′(x) >0 增
练习：(多选)定义在 R 上的可导函数 y＝f(x)的导函数的图象如图所示，以下结论正
确的是
()
A．－3 是 f(x)的一个极小值点
B．－2 和－1 都是 f(x)的极大值点
C．f(x)的单调递增区间是(－3，＋∞)
x3
a x1 O x2
x4 x5
x6
bx
x4为极小值点，f (x4 )为极小值.
练1.下图是导函数y f '(x) 的图象，试找出函数y f (x) 的极值点. 并且指出哪些是极大值点，哪些是极小值点.
y
x
(x4 , x6 )
x6
(x6 , b)
y f ( x)
f '(x) +
0
+
x3
f (x) 单调递增
O
b
x
(2)
注意：
(1) 极值是某一点附近的小区间而言的，是函数的局部性质，不是整体的最值； (2) 函数的极值不一定唯一，在整个定义区间内可能有多个极大值和极小值；
(3) 极大值与极小值没有必然关系，极大值可能比极小值还小. (4) 对于可导函数，若x0是极值点，则 f '(x0)=0;反之，若f '(x0)=0，则x0不一定是极值点.
单调递增
a x1 O x2
x4 x5
x6
bx
f (x6 )既不是极大值也不是极小值.
问题3：导数值为0的点一定是函数的极值点吗？
f ′(x0)=0 ⇏ x0是函数 f(x) 的极值点

新教材高中数学5-3-1函数的单调性课件新人教A版选择性必修第二册

[方法技巧] 1．利用导数判断或证明函数单调性的思路
2．含有参数的函数单调性的解题技巧讨论含有参数的函数的单调性，通常归结为求含参不等式的解集问题，而对含有参数的不等式要针对具体情况进行分类讨论，但要始终注意定义域以及分类讨论的标准．含参数的二次不等式问题，一般从最高次项的系数、判别式Δ及根的大小关系等方面进行讨论．
[解] (1)函数 f(x)的定义域为(0，＋∞)，f′(x)＝2x－1x＝2x2x－1. 令 f′(x)>0，得 x> 22，令 f′(x)<0，得 0<x< 22， ∴f(x)在0， 22上单调递减，在 22，＋∞上单调递增，∴函数 f(x)的单调递增区间为 22，＋∞，单调递减区间为0， 22.
法二：数形结合法 f′(x)＝(x－1)[x－(a－1)]． ∵在(1,4)内 f′(x)≤0，在(6，＋∞)内 f′(x)≥0，且 f′(x)＝0 有一根为 1，作出 y＝f′(x)的示意图如图所示，则 f′(x)＝0 的另一根在[4,6]上． ∴ff′′64≥≤00，，即53××75－－aa≥≤00，， ∴5≤a≤7. 故实数 a 的取值范围为[5,7]．
在某个区间(a，b)上，如果f′(x)>0，那么函数y＝f(x)在区间(a，b)上单调递增；在某个区间(a，b)上，如果f′(x)<0，那么函数y＝f(x)在区间(a，b)上单调递减；如果在区间(a，b)上恒有f′(x)＝0，那么函数y＝f(x)在区间(a，b)上是常数函数．
2．函数图象的变化趋势与导数值大小的关系
[对点练清]
1．若函数 f(x)＝ex(sin x＋a)在区间－π2，π2上单调递增，则实数 a 的取值范围是
()
A．[ 2，＋∞)

高中数学人教新课标A版：导数与函数的单调性、极值与最值课件

2．利用导数判断函数单调性的一般步骤 (1)求 f′(x) ； (2)在定义域内解不等式 f′(x)>0 或 f′(x)<0 ； (3)根据结果确定 f(x)的单调性及单调区间． 3．用充分必要条件诠释导数与函数单调性的关系 (1)f′(x)>0(<0)是 f(x)在区间(a，b)内单调递增(减)的充分不必要条件． (2)f′(x)≥0(≤0)是 f(x)在区间(a，b)内单调递增(减)的必要不充分条件． (3)若 f′(x)在区间(a，b)的任意子区间内都不恒等于零，则 f′(x)≥0(≤0)是 f(x)
3．(多选)如果函数 y＝f(x)的导函数 y＝f′(x)的图象如图所示，则以下关于函
数 y＝f(x)的判断正确的是
()
A．在区间(2,4)内单调递减 B．在区间(2,3)内单调递增 C．x＝－3 是极小值点 D．x＝4 是极大值点
解析： A 项，函数 y＝f(x)在区间(2,4)内 f′(x)＞0，则函数 f(x)在区间(2,4)上单调递增，故 A 不正确； B 项，函数 y＝f(x)在区间(2,3)内的导数 f′(x)＞0，则函数 f(x)在区间(2,3)上单调递增，故 B 正确； C 项，由图象知当 x＝－3 时，函数 f′(x)取得极小值，但是函数 y＝f(x)没有取得极小值，故 C 错误； D 项，当 x＝4 时，f′(x)＝0，当 2＜x＜4 时，f′(x)＞0，函数 y＝f(x)为增函数，当 x>4 时，f′(x)＜0，函数 y＝f(x)为减函数，则 x＝4 是函数 f(x)的极大值点，故 D 正确．答案：BD
[题组练透]
1．函数 f(x)＝cos x－x 在(0，π)上的单调性是
A．先增后减
B．先减后增

函数的单调性与最值课件(共20张PPT)

最值. 三．对于较复杂函数，可用换元法化归为简单函数、或者运用导数，
求出在给定区间上的极值，最后结合端点值，求出最值.
课堂小结
单调性
定义
图象特征判断方法
应用
定义法图象变换求导法求最值求参数范围解不等式
祝同学们前程似锦！
专题一：判断、证明函数的单调性
例 1：(3)已知 f x 2x , x 2,6. (1)判断 f x 的单调性，并加以证明；(2)求 f x 的最值.
x 1
专题一：判断、证明函数的单调性
变式 3：讨论 f x ax a 0, 的单调性.
x 1
小结：确定函数单调性的四种方法 (1)定义法；(2)导数法；(3)图象法；(4)性质法．
【学习目标】
01
理解函数的单调性、最大值、最小值及其几何意义；
02
会运用函数图象理解和研究函数的单调性，并利用单调性求最值或者求参数范围；
03
培养抽象概括、逻辑推理、运算求解等能力．
复习回顾 1.函数的单调性 (1)单调函数的定义
增函数
减函数
一般地，设函数f(x)的定义域为I，区间D⊆I，如果∀x1，x2∈D 定义当x1<x2时，都有__f_(x_1_)_<_f(_x_2)_，当x1<x2时，都有_f_(_x_1)_>_f_(x_2_)，
自左向右看图象是下降的
复习回顾
(2)单调区间的定义如果函数y＝f(x)在区间D上_单__调__递__增__或_单__调__递__减__，那么就说函数y＝f(x) 在这一区间具有(严格的)单调性，区间D叫做y＝f(x)的单调区间.
复习回顾 2.函数的最值
前提
设函数y＝f(x)的定义域为I，如果存在实数M满足

高中数学必修第一册人教A版5.4《正弦函数、余弦函数的性质---单调性和最值》名师课件

典例讲授
例2、利用三角函数的单调性,比较下列各组数的大小.
() , , ; ∘ , ∘ .
思路 (1)利用诱导公式化到同一单调区间,再根据单调性比较大小;
解析 2 第一化成同名三角函数,再把角化到同一单调区间,然后比较大小.
解析

(1) ∵ 1 < < 2 < 3 < , sin − 2 = sin 2, sin − 3 = sin 3,
当x 2k , k Z时，ymin 1
小组讨论：余
x) cos x
奇偶性：偶函数 cos(
Z
对称轴：x k , k 弦函数的性质

对称中心：( k ,0) , k Z
2
余
弦
函
数
性
质
的
研
究
典例讲授
例1、下列函数有最大值、最小值吗？如果有,请写出取最大值、最小值时自变量的
数学学科素养
1.数学抽象：理解周期函数、周期、最小正周期等的含义；
2.逻辑推理：求正弦、余弦形函数的单调区间；
3.数学运算：利用性质求周期、比较大小、最值、值域及判断奇偶性.
4.数学建模：让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.
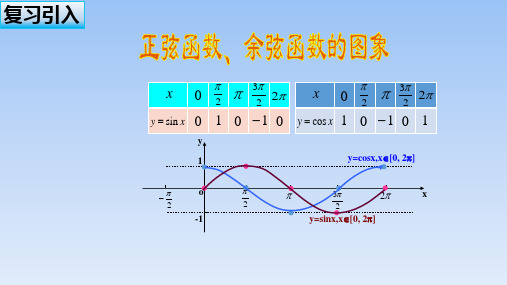
探究新知
正弦函数性质的研究
y
y sin x
1
-3
-2
-
o

2
3
4
5
6
x
6
x
-1
y cos x
y
1
-4
-3
-2
-
o
-1

2
3
4
5

函数的单调性与最值课件理新人教A版课件

(2)复合函数单调性的判断法则：“同增异减”，即对于 y＝ f[g(x)]型的复合函数，我们令 t＝g(x)，则可以把它看成由 y＝f(t) 和 t＝g(x)复合而成的，若它们的单调性相同，则复合后的函数为增函数；若它们的单调性相反，则复合后的函数为减函数．
(3)利用函数的运算性质：若 f(x)，g(x)为增函数，则 ①f(x)＋g(x)为增函数； ②f1x为减函数(f(x)＞0)； ③ fx为增函数(f(x)≥0)； ④f(x)·g(x)为增函数(f(x)＞0，g(x)＞0)； ⑤－f(x)为减函数． (4)图象法：根据图象上升或下降来确定函数的单调性． (5)导数法：利用导数研究函数的单调性．
(2)∵y＝log2(x2－1)， ∴该函数的定义域为(－∞，－1)∪(1，＋∞)．又∵y＝log2(x2－1)可看作由 y＝log2μ 和 μ＝x2－1 两个函数复合而成的，且 y＝log2μ 在 μ∈(0，＋∞)上为增函数，而 μ＝x2 －1 在(－∞，－1)上为减函数且 μ>0，在(1，＋∞)上为增函数且 μ>0. ∴当 x∈(－∞，－1)时，y＝log2(x2－1)为减函数，当 x∈(1，＋∞)时，y＝log2(x2－1)为增函数．
[解] 解法一：由解析式可知，函数的定义域是(－∞，0) ∪(0，＋∞)．在(0，＋∞)内任取 x1，x2，令 x1＜x2，那么 f(x2) －f(x1)＝(x2＋xk2)－(x1＋xk1)＝(x2－x1)＋k(x12－x11)＝(x2－x1)x1xx12x－2 k.
因为 0＜x1＜x2，所以 x2－x1＞0，x1x2＞0.
第二节函数的单调性与最值
1.理解函数的单调性，会讨论和证明一些简单的函数的单调性．
2．理解函数的最大(小)值及其几何意义，并能求出一些简单的函数的最大(小)值．

人教A版高中数必修一PPT-函数的单调性与最值PPT课件

所以，函数 f ( x ) 2 是区间 [ 2 , 6 ]上的减函数。 x 1
因此，函数 f ( x ) 2 在区间 [ 2 , 6 ]的两个断点上 x 1
分别取得最大值与最小值，即在 x 2时取得最大
值，最大值为 2 ，在 x 6 时取得最小值，最小值是 0 .4
(1)x∈[2, 3]；(2)x∈[0, 3] ;(3)x∈[-3, 0]
1 2 3 4 5 6x
且 x1 x2,则
y
［名师课堂教学］人教A 版高中数必修一PPT- 函数的单调性与最值 PPT课件（完整版PPT )
［名师课堂教学］人教A 版高中数必修一PPT- 函数的单调性与最值 PPT课件（完整版PPT )
f ( x1)
f (x2)
(1)对于任意x∈I，都有f(x)≤M.
(2)存在x0∈I，使得f(x0)＝M. 那么，称M是函数y＝f(x)的
如果存在实数M，同时满足： (1)对于任意x∈I，都有f (x)≥M. (2)存在x0∈I，使得f (x0)＝M. 那么，称M是函数y＝f (x)的最小值.
最大值.
二.有关函数最值的几点说明：
［名师课堂教学］人教A 版高中数必修一PPT- 函数的单调性与最值 PPT课件（完整版PPT )
讲授新课
一.函数最大值概念：
一般地，设函数y＝f(x)的定义域为I. 如果存在实数M，
？
你能类比函数最大值的研究方法来定义函数最小值吗？
函数最小值概念：
同时满足：
一般地，设函数y＝f (x)的定义域为I.

新教材高中数学第5章第2课时单调性与最值课件新人教A版必修第一册ppt

(3)cos－253π＝cos253π＝cos4π＋35π＝cos35π， cos－147π＝cos147π＝cos4π＋π4＝cosπ4. ∵0＜π4＜35π＜π，且 y＝cos x 在[0，π]上是单调递减的， ∴cos35π＜cosπ4，即 cos－253π＜cos－147π.
三角函数值大小比较的策略 (1)利用诱导公式，对于正弦函数来说，一般将两个角转化到－π2，π2或2π，32π内；对于余弦函数来说，一般将两个角转化到[－π， 0]或[0，π]内． (2)不同名的函数化为同名的函数． (3)自变量不在同一单调区间化至同一单调区间内，借助正弦、余弦函数的单调性来比较大小．
∴函数 y＝sin3π－x的单调递增区间为56π＋2kπ，116π＋2kπ，k∈Z.
1．求形如 y＝Asin(ωx＋φ)＋b 或形如 y＝Acos(ωx＋φ)＋b(其中 A≠0，ω>0，b 为常数)的函数的单调区间，可以借助于正弦函数、余弦函数的单调区间，通过解不等式求得．
2．具体求解时注意两点：①要把 ωx＋φ 看作一个整体，若 ω<0，先用诱导公式将式子变形，将 x 的系数化为正；②在 A>0，ω>0 时，将“ωx＋φ”代入正弦(或余弦)函数的单调区间，可以解得与之单调性一致的单调区间；当 A<0，ω>0 时同样方法可以求得与正弦(余弦)函数单调性相反的单调区间．
类型 1 求正弦函数、余弦函数的单调区间
【例 1】求函数 y＝2sinx－π3的单调区间． [解] 令 z＝x－π3，则 y＝2sin z. ∵z＝x－π3是增函数， ∴y＝2sin z 单调递增时，
函数 y＝2sinx－π3也单调递增．
由 z∈2kπ－π2，2kπ＋π2(k∈Z)，得 x－π3∈2kπ－π2，2kπ＋π2(k∈Z)，即 x∈2kπ－π6，2kπ＋56π(k∈Z)，故函数 y＝2sinx－π3的单调递增区间为2kπ－π6，2kπ＋56π(k∈Z)．同理可求函数 y ＝ 2sin x－π3 的单调递减区间为

湖南师大 高三数学 第五讲 函数的单调性与最值课件 新人教A版

函数的单调性和最值PPT精品课件

函数的单调性极值与最值课件

湖南师大 高三数学 第五讲 函数的单调性与最值课件 新人教A版

5.3.2函数的极值课件2024-2025学年人教A版必修第一册

新教材高中数学5-3-1函数的单调性课件新人教A版选择性必修第二册

高中数学人教新课标A版：导数与函数的单调性、极值与最值 课件

函数的单调性与最值 课件(共20张PPT)

高中数学必修第一册人教A版5.4《正弦函数、余弦函数的性质---单调性和最值》名师课件

函数的单调性与最值课件理 新人教A版课件

人教A版高中数必修一PPT-函数的单调性与最值PPT课件

新教材高中数学第5章第2课时单调性与最值课件新人教A版必修第一册ppt

湖南师大高三数学第五讲函数的单调性与最值课件新人教A版

湖南师大高三数学第五讲函数的单调性与最值课件新人教A版

高中数学人教新课标A版：导数与函数的单调性、极值与最值课件

函数的单调性与最值课件(共20张PPT)

函数的单调性与最值课件理新人教A版课件