弦切角定理[下学期] 浙教版ppt课件
《弦切角定理 》

∴ ∠ACD +∠DAC=900.
又∵AC是弦,且直线CE和⊙O切于点 C, ∴ ∠ACD =∠B.
∴ ∠DAC=∠CAB,即AC平分∠BAD.
练习:
1.如图,AC是⊙O的弦,BD切⊙O于C, O 4 则图中弦切角有 个. 若∠AOC=1200,则∠ ACD = 600 . B C ∠ACD, ∠ACB, ∠OCD, ∠OCB. 2.如图,直线MN切⊙O于C,AB是⊙O的直 径,若∠ BCM=400,则∠ ABC等于( B ) A.400 B. 500 C. 450 D.600
D 几何语言:
BA切⊙O于A
C
O A
B
AC是圆O的弦
∠BAC= ∠ADC
例1:如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点 C,AD⊥CE垂足为D.求证:AC平分∠BAD. 证明:连接BC. ∵AB是⊙O的直径, ∴ ∠ACB=900. ∴ ∠B +∠CAB=900. ∵AD⊥CE, ∴ ∠ADC=900.
E B
O
F D C
小结:
1.弦切角的概念。 2.弦切角定理及其简单应用。
作业:
p16 1,2题
O
A
D O B C F C N A
E
A
例2: 如图,AD是△ABC中 ∠BAC的平分线,经过点A 的⊙O与BC切于点D,与AB、 AC分别相交于E、F. 求证: EF∥BC. 证明:连结DF. ∵AD是∠BAC的角平分线, ∴∠BAD=∠DAC. 又∵∠EFD=∠BAD, ∴∠EFD=∠DAC. 又∵⊙O切BC于D, ∴∠FDC= ∠DAC. ∴∠FDC= ∠EFD ∴ EF∥BC
C
C C
. O
弦切角定理 (2)

例3、如图,割线PAB、PCD分别交⊙O于A、B 和C、D。若PC=2,CD=16,PA∶AB=1∶2。 求AB的长
C
P
D
。A O
B
例4、如图,已知 PAB、PCD是⊙O的割线,PE 切⊙O于点E,PE=6cm,PC=3cm,PA=4cm, AC=2cm求BD的长
E
P
C
D
A O·
B
例5、已知AB是⊙O的直径,AC是弦,CD⊥AB,D 为垂足,AE是⊙O的切线,A为切点且AE=AC, 求证:EF·EB=AD·AB
C
A DO
B
EF
例6、已知:⊙O的两弦AB、CD的延长线 交圆外一点E,EF∥DA交CB的延长线于F, FG切⊙O于G,求证:FG=FE
AG
F
O
B
C
D
E
例7、已知:ΔABC内接于⊙O,AB的延长线与 过点C的切线GC相交于D,BE与AC相交于点F, 且CB=CE, 求证:(1)BE∥DG (2)CB2-CF2=BF·FE
A
相交弦定理:PA·PB=PC·PD
D
P B
C
探索:如果把什么
比例关系?
A
O
P
B
C
切割线定理:从圆外一点引圆的切线和割线, 切线长是这点到割线与圆交点的两条线段长 的比例中项。
A
O
P
B
C
PA2=PB·PC
推论:从圆外一点引圆的两条割线,这点到每 条割线与圆的交点的两条线段长的积相等。
A
B
O
P
C
D
PA·PB=PC·PD
例1、已知:如图,⊙O的割线PAB交⊙O于点A 和B,PA=6,AB=8,PO=10.9,求⊙O的半径。
弦切角定理及其逆定理PPT课件

2020年9月28日
9
2020年9月28O于A、B两点,AE是⊙O的
直径,点C为⊙O上一点,且AC平分∠PAE,过C作 CD⊥PA于D. (1)求证:CD为⊙O的切线; (2)若DC+DA=6,⊙O的直径为10,求AB的长.
2020年9月28日
4
提高练习
练3.已知直线l切△ABC外接圆于点C, AD⊥BC于点D,BE⊥AC于点E,EG⊥l于点G ,DF⊥l于点F. 求证:EG=DF.
回味无穷
2020年9月28日
7
课后作业
《优等生数学》九年级 P66-67 T1、 T2 、T3、T4 写在作业本上. 预习《优等生数学》九年级的第29、30节
2020年9月28日
8
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
XUSUHUA
第二十七章 圆
27.16 弦切角定理及其逆定理
2020年9月28日
1
经典例题
例. 如图,从圆上一点A作直径BC的垂线AD,
过A作圆的切线MN. 证明:AB、AC分别平分
MN与AD的夹角.
2020年9月28日
2
巩固练习
练1. 如图,四边形ABCD内接于圆O,AD是圆O 的直径,直线MN切圆O于B点,∠MBA=40°, 求∠BCD.
浙教版九年级下册数学《6.6弦切角》PPT课件

⊙O于C 、AD⊥CD,延长AD
交BC延长线于E。
求证:
B O
1.AB=AE
A
2.BC=CE
1
C2
D
E
变式已3、知:AB是直径、E是 ⊙O外一点,ED⊥AB于D, EC切⊙O于C,连结BC交DE 于F。
求证:
B
D
CE=E F
3
O
F
1
A
2
E
C
思考题:、如图;已知BE、CF
是△ABC两条高,O是外心,
90° 120° 270°
180°
猜想:弦切角的度数等于它所夹的弧度 数的__一_半_____
证明:分三种情况
(1)圆心O在∠BAC的边AC上
∵AB切圆O于A ,AC是直径 ∴ ∠BAC=90 °
∵ AmC是半圆
∴ AmC= 180°
1 ∴ ∠BAC= AmCm 2
C
m O
A
B
(2)圆心0在∠BAC的内部
A
E B
O F
D
C
顶点在圆上,一边与圆相交,另一边与圆相切的角叫做弦切角。
弦切角定理: 弦切角的度数等于它所
夹的弧度数的一半
推论: 弦切角等于它所夹的弧对的圆周角
一般情况下,弦切角、圆周角、圆心角都是通过它们夹的(或对的)
小 时常添线 同一条弧(或等弧)联系起来,因此,当已知有切线 结 构建弦切角或添切点处的半径应用切线的性质
圆中的∠BAC和∠BOC分别是 什么角?与所对弧有何关系?
A
O
B C
∠CAB的顶点及两边与圆 的位置关系是什么?
C
B
A
∠CAB的顶点及两边与圆 的位置关系是什么?
弦切角定理

弦切角定理顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
(弦切角就是切线与弦所夹的角)如图所示,线段PT所在的直线切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半.如上图,已知:直线PT切圆O于点C,BC、AC为圆O的弦。
求证:∠TCB=1/2∠BOC=∠BAC证明:设圆心为O,连接OC,OB,。
∵PT为圆O的切线∴OC⊥PT∴∠TCB=90°-∠OCB∵∠BOC=180°-2∠OCB∴,∠BOC=2∠TCB∵∠BOC=2∠BAC∴∠TCB=∠BAC综上所述:∠TCB=1/2∠BOC=∠BAC已知:AC是⊙O的弦,AB是⊙O的切线,A为切点,弧CmA是弦切角∠BAC所夹的弧.求证:弦切角∠BAC的度数等于它所夹的弧的度数的一半证明:分三种情况:(1)圆心O在∠BAC的一边AC上∵AC为直径∴弧CmA=弧CA ∵弧CA为半圆,∴弧CmA的度数为180°∵AB为圆的切线∴∠CAB=90°∴弦切角∠BAC的度数等于它所夹的弧的度数的一半(2)圆心O在∠BAC的内部.过A作直径AD交⊙O于D,在优弧m所对的劣弧上取一点E,连接EC、ED、EA。
则∵弧CD=弧CD∴∠CED=∠CAD∵AD是圆O的直径∴∠DEA=90°∵AB为圆的切线∴∠BAD=90°∴∠DEA=∠BAD∴∠CEA=∠CED+∠DEA=∠CAD+∠BAD=∠BAC又∠CEA的度数等于弧CmA的度数的一半∴弦切角∠BAC的度数等于它所夹的弧的度数的一半(3)圆心O在∠BAC的外部过A作直径AD交⊙O于D,连接CD∵AD是圆的直径∴∠ACD=90°∴∠CDA+∠CAD=90°∵AB是圆O的切线∴∠DAB=90°∴∠BAC+∠CAD=90°∴∠BAC=∠CDA∵∠CDA的度数等于弧CmA的度数的一半∴弦切角∠BAC的度数等于它所夹的弧的度数的一半推论内容若两弦切角所夹的弧相等,则这两个弦切角也相等应用举例例1:如图,在⊙O中,⊙O的切线AC、BC交于点C,求证:∠CAB=∠CBA。
九年级数学弦切角定理、相交弦定理浙江版知识精讲

九年级数学弦切角定理、相交弦定理某某版【本讲教育信息】一. 教学内容:弦切角定理、相交弦定理二. 教学重、难点:重点:正确理解弦切角定理与相交弦定理难点:弦切角定理以及相交弦定理的应用三. 补充:弦切角定理与相交弦定理的知识要点:1. 学习和识别弦切角需注意两个方面(1)顶点在圆上(2)一边与圆相交成弦,另一边与圆相切于顶点.2. 弦切角定理:弦切角的度数等于它所夹弧的度数的一半.推论:弦切角等于它所夹弧所对的圆周角.3. 相交弦定理:圆内的两条弦相交,则被交点分成的两条线段长的积相等.如图,弦AB、CD相交于P,则PA·PB=PC·PD.【典型例题】例1. 如图,AB是圆O的弦,P在AB上,AB=10cm,PA=4cm,OP=5cm,求圆O的半径.解析:由P为AB上一点且已知PA、PB,可联想到相交弦定理,不妨向两方延长OP,分别交圆O于C、D.由相交弦定理:BP·AP=CP·DP又CP=CO+OP ,DP=OD -OP 且CO=DO .∴BP ·AP=(CO+OP )(CO -OP )=CO 2-PO 2 ∴当AB=10,PA=4时,BP=6 又OP=5∴解得CO=7即圆O 的半径为7cm .例2. 如图,圆内接四边形ABCD 的对角线AC 平分∠C ,BD 交AC 于点F ,过A 作圆O 的切线AE 交CB 的延长线于点E 。
求证:①AE//DB ②AE DF AD 2⋅=E解析:AE 切圆O ,ACB EAB ∠=∠∴(弦切角定理) 又ABD DCA ∠=∠A ∠∴是DCB ∠的平分线。
DB //AE ,ABD EAB ∴∠=∠∴ AEDF AD AD AB BCA DCA AD AEDF AB ,DFA ~ABE )(ADB BAE DACDBC E 2⋅=∴=∠=∠=∴∆∆∴∠=∠∠=∠=∠∴ 又弦切角定理例3. 如图,已知圆O 中,AB//CD ,BG 切圆O 于B ,P 为⋂CD 上一点,PA 、PB 交CD 于E 、F 。
弦切角PPT课件

2
教学重点、难点
重
1、弦切角的概念和定理的证明。
点
2、弦切角定理的运用。
难 点
3、通过作辅助线把“一般情况”
转化为“特殊情况”。
2020年10月2日
3
教学方法
在复习圆心角、圆周角的概念的 基础上,通过几何画板的动画演 示,由学生通过观察动画,抽象 总结出弦切角的定义,并揭示出 弦切角与圆周角的关系,然后引 导学生观察思考、阅读教材、分 析议论得到弦切角定理。
2020年10月2日
4
教学过程
复习引入 探求新知 例题选讲
课堂练习 小结
2020年10月2日
5ห้องสมุดไป่ตู้
复习引入
复习 1、在贺 1、
我们已学过了两个与圆有
关的角,即圆心角和圆周角,那么怎样的角 是圆心角、圆周角?
2. 引入
2020年10月2日
6
弦切角定理教学
探求定理
演示及证明过程
2020年10月2日
7
演讲完毕,谢谢观看!
汇报人:XXX 汇报日期:20XX年10月10日
8
教学目的 教学重点、难点
教学方法 教学过程
2020年10月2日
1
教学目的
1、使学生理解弦切角的定义,掌握弦切角定理 并能初步加以运用。
2、运用运动的观点进行概念教学,逐步培养学 生探讨问题从感性认识上升到理性认识的抽 象思维能力求。
3、通过对定理的证明,训练学生认识事物由特 殊到一般的思想方法。
2020年10月2日
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
弦切角精品PPT教学课件

教学方法 教学过程
2020/12/6
1
教学目的
1、使学生理解弦切角的定义,掌握弦切角定理 并能初步加以运用。
2、运用运动的观点进行概念教学,逐步培养学 生探讨问题从感性认识上升到理性认识的抽 象思维能力求。
3、通过对定理的证明,训练学生认识事物由特 殊到一般的思想方法。
2020/12/6
2020/12/6
4
教学过程
复习引入 探求新知 例题选讲
课堂练习 小结
2020/12/6
5
复习引入
复习 1、在贺 1、
我们已学过了两个与圆有
关的角,即圆心角和圆周角,那么怎样的角 是圆心角、圆周角?
2. 引入
2020/12/6
6
弦切角定理教学
探求定理
2020/12/6
演示及证明过程
7
感谢你的阅览
Thank you for reading
温馨提示:本文内容皆为可修改式文档,下载后,可根据读者的需求 作修改、删除以及打印,感谢各位小主的阅览和下载
日期:
演讲者:蒝味的薇笑巨蟹
2
教学重点、难点
重
1、弦切角的概念和定理的证明。
点
2、过作辅助线把“一般情况”
转化为“特殊情况”。
2020/12/6
3
教学方法
在复习圆心角、圆周角的概念的 基础上,通过几何画板的动画演 示,由学生通过观察动画,抽象 总结出弦切角的定义,并揭示出 弦切角与圆周角的关系,然后引 导学生观察思考、阅读教材、分 析议论得到弦切角定理。
《弦切角定理》课件
m
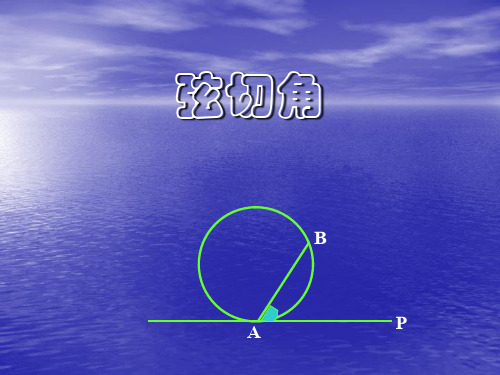
的角叫做弦切角
A
P
AmB 是弦切角∠PAB所夹的弧。
顶点在圆上,一边与圆相交,另一边
与圆相切的角叫做弦切角。
下面五个图中的∠BAC是不是弦切角?
C
B
A×
B
× C A
B C
×B
A C
C
×
√
A
A
B
从数学的角度看,弦切角能分成几大类?
C C
C
.O P
P D AB
.O AB
.O
P DA B
BAC为直角, 圆心在 AC上。
C
B O
E
A
D
例题解析
例1:如图:已知AB是⊙O的直
径,AC是弦,直线CE和⊙O切于
点C,AD⊥CE于D。
B
O
求证:(1)AC平分∠BAD
(2)AC2=2AD·AO
A
你还能用其他方法解答 吗?试试看!
E
C
D
有弦切角,常连结弦切角 所夹弧所对的圆周角。
例题解析(思路2)
例1: 如图,已知AB是⊙O的直径,AC是弦,直 线CE和⊙O切于点C,AD⊥CE,垂足是D,求证: AC平分∠BAD.
C
10.9
·
O
B D
故 (10.9-r ) (10.9+r)=6×14
取正数解,得r=5.9(cm)
答: ⊙O的半径为5.9cm
另解
• 利用垂径定理
B 8 6A
P
10.9
·
O
法三:
• 利用切割线定理
B 8 6A
P
10.9
·
O
T
练习三:如图,圆o1和圆o2都经过点A和 B,点P在BA
新浙教版九年级数学下册第一章《 有关三角函数的计算》课件

ห้องสมุดไป่ตู้太阳光
25° A
住
宅
新
楼
楼
B
C
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是 高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的 新楼.当冬季正午的阳光与水平线的夹角为25°时.
问:若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
D
太阳光
25° A
F
住 宅
新
楼
w如图,在Rt△ABC中,∠C=90°, BC=ABsin16° .
w你知道sin16°等于多少吗?
对于不是30°,45°,60°这些特殊角的三角函 数值,可以利用计算器来求
w怎样用科学计算器求锐角的三角函数值呢?
动手实践
知识在于积累
驶向胜利 的彼岸
w用科学计算器求锐角的三角函数值,要用到三个键: w例如,求sin16°、cos42°、tan85° 和sin72°38′25″的按键盘顺序如下: sin cos tan
A
B
变式:在△ABC中,已知AB=12cm,AC=10cm
∠ A=35 °,求△ABC 的周长和面积(周长精确到 0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC・AB ・sin ∠ A
随堂练习
行家看“门道”
驶向胜利 的彼岸
w1 用计算器求下列各式的值: w(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°, w(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
按键的顺序
显示结果
sin16° sin 1 6 °′″ =
弦切角定理

学习目标
1、 理解弦切角的概念,掌握弦切角定理及 、 理解弦切角的概念, 其推论,能运用它们解决有关问题。 其推论,能运用它们解决有关问题。 2、 通过弦切角定理的证明,了解分情况证 、 通过弦切角定理的证明, 明数学命题的思想和方法。 明数学命题的思想和方法。 3、 体会分类、转化的思想方法。 、 体会分类、转化的思想方法。
1.先组内 强帮弱” 最后集体讨论争取解决基本问 为展示点评做好准备; 1.先组内 “ 强帮弱” 、最后集体讨论争取解决基本问 题, 为展示点评做好准备;同 时用红色笔记住疑惑。 时用红色笔记住疑惑。 2.力争全部达成目标 力争全部达成目标, 层多拓展, B层注重总结 层注重总结, 层力争全部掌握。 2.力争全部达成目标,且A层多拓展, B层注重总结,C层力争全部掌握。
在交流中融情 在讨论中提升
认 真 思
非 展 示 同 学 浏 览 展 示 内 容 ,
规 范 , 步 骤 清 晰 简 洁 ;
黑 板 展 示 , 上 台 迅 速 , 书 写 认 真
大 声 , 富 有 激 情 ;
口 头 展 示 , 面 向 同 学 , 大 胆 大
要 求 : 通 过 你 的 展 示 让 同 学 们 思 路 更 加 清 晰
探究
画一个圆O和一条切线 画一个圆 和一条切线L, 切点为A, 是圆的一条弦 是圆的一条弦, 切点为 ,AE是圆的一条弦,直线L上有一点 上有一点 D,如图
L F A D
角 弦切角是: 弦切角是: EAD, 角EAF
O E
·
弦切角的定义是
新知: 新知:
弦切角定理: 弦切角定理:
弦切角等于它所夹弧所对的圆周角, 弦切角等于它所夹弧所对的圆周角, 等于它所夹弧的度数的一半. 等于它所夹弧的度数的一半
浙教版九年级下册数学《相交弦定理》PPT课件

小结: 2、本节课我们学习了哪些
▪ 学习了由一般到特殊的数数学学思想? (由定理直接得到
推论)
▪ 相交弦定理及推论在证明等积式及圆中相 关线段的求值问题中有着广泛的运用。
AB是过点P的一条弦。设圆的半径为r,OP=d
r d 求证: PA• PB 2 2
B
C
D
O
P
A
例 3 、 如 图 : 在 ⊙ O 中 , P 是 弦 AB 上 一 点 , OP⊥PC,PC 交⊙O于C.
求证:PC2=PA·PB
C
A
P
B
O
D
课堂练习(口答)
1.填空题 (1) 如图,弦AB和CD相交于
口答:
1、如右图,由射影定理可以得 出什么关系式?
A
2、根据垂径定理,改写上式
:
A
CP×PD=AP ×PB
C
O
PB
C
O
PB
D
将AC、BE改为两条对一般情形
的相交弦,上式还会成立吗?
C
A
D
A
O
PBO PBD来自C? AP×PB==CP ×PD
A
D
O PB
C
D
A
P
O
B
C
D
A
P
O
B
C
同学们,你们现在可以证明 AP×PB=CP ×PD吗?
MN⊥CD于N,以下式子B 成立的是(
). a2 bc
b2 ac
M b
(A)c2 a(bB) a c 2b C a N c D
(C)
(D)
小结: 1、本节课我们学习了哪些
主要内容?
相交弦定理: 圆内的两条相交弦,被交
浙教版九年级下册 1.3 解直角三角形 课件(共42张PPT)

3.5 5
=0.7,
∴α≈350.
答:斜面钢条a的长度约为6.1米,坡角约为350.
特别强调:
在解直角三角形的过程中,常会遇到近似计
算,本书除特别说明外,边长保留四个有效数 字,角度精确到1′.
解直角三角形,只有下面两种情况: (1)已知两条边; (2)已知一条边和一个锐角 (必须有一个条件是边)
钢条的长度a和倾角a 吗?
L
变化:已知平顶屋面的宽度
L和坡顶的设计倾角α(如
述例题中,我们都是利用直角三角 形中的已知边、角来求出另外一些的边角. 像这样,
******************************** 在直角三角形中,由已知的一些
因此 AB=AE+EF+BF
≈6.72+12.51+7.90 ≈27.13(米).
图 19.4.6
答:路基下底的宽约为27.13米.
如图,沿水库拦水坝的背水坡将坝面加宽两 米,坡度由原来的1:2改成1:2.5,已知原背水坡 长BD=13.4米,
求: (1)原背水坡的坡角 和加宽后的背水
坡的坡角
(1)c=10,∠A=30°
B
(2)b=4,∠B=72°
(3)a=5, c=7
C
A
(4)a=20,sinA= 1
2
应用练习
如图东西两炮台A、B相距2000米,同时发现入侵敌 舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B 测得敌舰C在它的正南方,试求敌舰与两炮台的距离.
(精确到1米)
本题是已知
面的夹角叫做坡角,记作a,有i= h = tan a. l
显然,坡度越大,坡角a就越大,坡面就越陡.
试一试
1、如图
1)若h=2cm, l=5cm,则i= 2 ; 5
切线长与弦切角PPT教学课件

D P
N C
O
M
L
B
圆的外切四边形的两组对边的和相等 AB+CD=AD+BC
2021/01/21
8
弦切角
2021/01/21
9
弦切角的定义
弦切角:顶点在圆上,
一边和圆相交、另一 D 边和圆相切的角叫做
弦切角。
A
要点:
➢ 顶点在圆上
➢ 一边和圆相交
➢ 一边和圆相切
E O
C
B
2021/01/21
10
三角形的外接圆: 三角形的内切圆:
A
A
O
B
C
B
I C
2021/01/21
1
特殊三角形外接圆、内切圆半径的求法:
直角三角形外接圆、
B
内切圆半径的求法
R= —c2
r = —a—+b—-c— 2
等边三角形外接圆、
内切圆半径的求法 A
c
O a
I
A
b
C
基本思路:
RO
r
B 2021/01/21D
C
构造三角形BOD,BO为外
2021/01/21
18
如图,⊙O和⊙O′都经过A、B两点,AC是 ⊙O ′的切线,交⊙O于C,AD是⊙O的切线, 交⊙O ′于D,求证:AB2=BC·BD。
A
B
C
D
2021/01/21
A O
B C
19
O' D
如图:AE、BF分别切⊙O于A、 B,且AE∥BF,EF切⊙O于C。 y 试证:⑴ AB是⊙O的直径;⑵ OE⊥OF;⑶ OC是AE、BF的 A 比例中项
演变1:在△ABC中,过点A和BC切于D的⊙O和
弦切角的性质 课件

证明:如图,连接 BC. MN CD MAC ACD, MN切 O于点A MAC B CAAECDCABB, ⇒△ACE∽△ABC ⇒ AC = AE ⇒AC2=ABAE.
AB AC
点评:此题主要是利用弦切角的性质去证明两个角相等, 再利用三角形相似证比例中项,这样的类型题较常见.
已知四边形ABCD内接于⊙O,点D是 AC 的 中,BC和AD的延长线相交于点E,DH切⊙O于点D,求证: DH平分∠CDE.
证明:如图,连接BD. ∵D是 AC 的中点, ∴∠ABD=∠CBD. ∵DH切⊙O于点D, ∴∠CDH=∠CBD=∠ABD. 又∠CDE=∠ABC, ∴∠HDE=∠ABD, ∴∠CDH=∠HDE, ∴DH平分切线和弦BC的延长 线相交于点P,若∠CAP=40°,∠ACP=100°,则 ∠BAC所对的弧的度数为( C )
A.40° B.100° C.120° D.30°
3.如图所示,AB是⊙O的直径,EF切⊙O于点C, AD⊥EF于点D,AD=2,AB=6,则AC的长为( C )
A.2 B.3 C.2 3 D.4
又∵∠BAD=∠ACB,且∠CAE=∠ABC,
∴∠BAD=∠CAE.
1.如图所示,AB为⊙O直径,CD切⊙O于点D,AB 的延长线交CD于点C.若∠CAD=25°,则∠C为( )
A.45° B.40° C.35° D.30°
解析:连接BD,∵AB为直径, ∴∠BDA=90°. 又∵CD为⊙O的切线,切点为D,由弦切角定理可知 ∠BDC=∠CAD=25°, ∴∠CDA=90°+25°=115°. 在△ACD中, ∠C=180°-∠A-∠CDA=180°-25°-115°=40°. 答案:B
弦切角的性质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AB = 度,∠AOB= 度,∠ABD= 度;
(2)若已知⊙O的半径为3cm,AB长⌒为 cm,求弦切角∠BAC的度数。
(3)若AC⊥BC,垂足为C ,AC=
,
BC= , 求扇形OAB的面积。
D
A
O
C
B
图3
提掌高握学基习本积技极能性 常培用养辅发助散线思维
;.
7
例2 如图,AD是△ABC中 ∠BAC的平分线,经过点A的⊙O 与BC切于点D,与AB、AC分别 相交于E、F。 求证:EF∥BC。
A
O
D
C
E
图一
;.
12
A
B
乙
270º
C O
A
B
丙
90º
弦切角 的度数
90º
135º
猜想: 弦切角的度数等于它所夹的弧的度数的一半。
;.
45º
5
圆心在弦切角的一边上 C
m O
A
B
甲
圆心在弦切角的内部
D
C
m O
圆心在弦切角的外部
D C m
O
A
B
乙
A
B
丙
证明: ∵ AC是直径, AB是切线
∴ ∠BAC=900
证明:作直径AD,则
问:弦切角与所 夹的弧、及所夹 的弧所对的圆心 角、圆周角有何 关系?
C
B
o
P A
弦切角及其性质是证明相等的重要依据,它常常与圆周角、圆心角 等性质联合应用来进行证明、计算。圆心角、圆周角、弦切角是与 圆有关的三种角,三者之间关系如图,PA切⊙O于A,则有: ∠PAB= ∠ ACB= 1/2∠ BOA= AB
E B
A
O F
D
C
证明:连结DF. ∵AD是∠BAC的角平分线 ∴∠BAD=∠DAC 又∵∠EFD=∠BAD
∴∠EFD=∠DAC 又∵⊙O切BC于D ∴∠FDC=∠DAC ∴∠FDC=∠DAC
∴ EF∥BC
变式练习1 如图4,连结DE、DF, 你能找出图中有哪些相等的角, 哪些相似三角形。
;.
8
动动脑筋
初中数学第六册
;.
1
C
. O
A
B
C C
.O
B A
.O
A
B
顶点在圆上,并且一边和圆相交、另一边和圆相切的角 叫做弦切角。
已知:如图,AB切⊙O于点A,AC与⊙O相交, 即: ∠CAB是弦切角。
;.
2
观察辨析 B
A
DC
(切点)
B
A
C
B
m
A
(切点)
C
(切点)
B
BA
D
A
A (切点)
C
m
B
C
;.
3
概念应用
证明:作直径AD,则∠BAC= ∠∠BACD= ∠ BAD - ∠DAC
+ ∠DAC
= 1/2 AmD-1/2CD
又∵ AmC是半圆,
∴AmC=1800 ∴ ∠BAC=1/2m
=m1/2 AmD+ 1/2CD
AmC
;.
m
⌒
⌒
6
例1 如图3,AC与△ABD的外接圆⊙O 相切于A.
⌒
(1)若弦切角∠BAC=30º,则
B A
O E
C 图一
O
1、 这是一个定滑轮装置示意图,指出图中有哪 几个弦切角。 D (口答)
2、 AB与⊙O切于A ,请同学们画出三个以 A为顶点的弦切角,使它们所夹的弧分别为 180º、270º、90º。
A
B
图二
;.
4
动手实验,猜想命题
通过测量得到弦切角度数。
CCOO来自所夹弧 的度数A
B
甲
180º
m⌒
;.
9
圆周角
直线和 圆相切
应用
圆心角
弦切角
圆周角
弧
;.
10
1.如图,AC是⊙O的弦,BD切⊙O于C,则图中弦切角有
个
4
。 若上题, ∠ AOC=120,则
∠ ACD = 12.0度
2.如图,直线MN切⊙O于C,AB是⊙O的直径,若∠ BCM=40度,则∠ ABC等于( )
A: 40度B B: 50度 C: 45度 D:60度
3.已知⊙O是△ABC的内切圆,D,E,F为切点,
若∠ A: ∠ B: ∠ C=4:3:2,则∠DEF = 度, 50 ∠FBC= 度。
70
OA
B
CD
A
.O
B
D
MC
N
;.
11
1、作业本6.6节
2、思考:设滑轮的半径为3㎝,那么拉力与竖直成 60º角时绕滑轮的绳子长度比拉力为水平方向时绕滑
B
轮的绳子多多少?
