积分的对称性问题
微积分III对称性的应用

z
ln( x2 x2
y
y2 2
z2 z2
1
1)
dxdydz
0.
轮换对称性 定义1 设对任意的点P1(x1, x2 ,L xn-1, xn ) Rn, P2 (x2 , x3,L xn , x1) Rn ,L L Pn (xn , x1,L xn-2 , xn1) Rn成立,则称区域关于变量x1, x2 ,L xn-1, xn具有 轮换对称性.
对称性在积分中的应用
使用对称性时应注意: 1、积分区域关于坐标面的对称性; 2、被积函数在积分区域上的关于三个坐标轴的
奇偶性.
定理1
若积分区域D关于y轴(x 0)对称,则
(i) 若f (x, y) f (x, y),即f (x, y)关于x为奇函数,
则 f (x, y)d 0. D
(ii) 若f (x, y) f (x, y),即f (x, y)关于x为偶函数,
例如;u x2 y2 z2关于x, y, z具有轮换对称性.
定理3 (1)设积分区域D关于x, y具有轮换对称性,则有
D
f
(x,
y)d
D
f
( y,
x)d
1 2
D
f
(x,
y)
f
( y,
x)d .
(2)设积分区域关于x, y, z具有轮换对称性,则有
f (x, y, z)dv f ( y, z, x)dv f (z, x, y)dv
则 f (x, y)d 2 f (x, y)d,
D
D右
其中D右为区域D的右半部分.
若积分区域D关于x轴( y 0)对称,则
(i) 若f (x, y) f (x, y),即f (x, y)关于y为奇函数,
关于曲线、曲面积分对称性的几个结论

关于曲线、曲面积分对称性的几个结论
曲线和曲面积分的对称性是数学中一个重要的概念,它提供了一种有效的方法来计算复杂的函数的积分。
曲线和曲面积分的对称性可以用来求解复杂的函数的积分,从而节省大量的计算时间。
首先,曲线和曲面积分的对称性可以用来求解复杂的函数的积分。
例如,如果一个函数具有对称性,那么可以将函数分成两部分,分别求解,然后将两部分的结果相加,从而节省大量的计算时间。
其次,曲线和曲面积分的对称性可以用来求解复杂的函数的积分。
例如,如果一个函数具有对称性,那么可以将函数分成两部分,分别求解,然后将两部分的结果相加,从而节省大量的计算时间。
最后,曲线和曲面积分的对称性可以用来求解复杂的函数的积分。
例如,如果一个函数具有对称性,那么可以将函数分成两部分,分别求解,然后将两部分的结果相加,从而节省大量的计算时间。
总之,曲线和曲面积分的对称性是一个重要的概念,它可以用来求解复杂的函数的积分,从而节省大量的计算时间。
它的应用范围很广,可以用来解决各种复杂的数学问题,为我们的研究提供了很大的帮助。
对称性解决积分问题方法

利用对称性、奇偶性求积分
有关对称性的结论
(1 )对于对称区间上的积分,有
(a )当在区间上为奇函数[ 即] 时
(b )当在区间上为偶函数[ 即] 时
(2 )对于平面区域D 上的二重积分,有
1 )设D 关于y 轴对称,则
(a )当为的奇函数[ 即] 时,得
(b )当为的偶函数[ 即] 时,得
其中是的右半部分:
2) 设D 关于x 轴对称,则
(a )当为的奇函数[ 即] 时,得
(b )当为的偶函数[ 即] 时,得
其中是的上半部分:
3) 设D 关于原点对称,则
(a )当时,得
(b )当时,得
其中,。
4 )设D 关于x 轴和y 轴均对称,且关于变量和均为偶函数,则
其中是在第一象限的部分:
5 )设D 关于直线对称,则
(3 )积分区域上的三重积分有类似于二重积分的性质。
例如,
设关于坐标面对称,则
(a )当是关于变量为奇函数[ 即] 时,得
(b )当是关于变量为偶函数[ 即] 时,得
其中是的前半部分:
如果积分区域关于坐标面(或)对称,而被积函数
是(或)的奇函数或偶函数时,有类似的结论。
(4 )第一型曲线积分和曲面积分也有类似的结论。
例如
1 )设平面分段段线关于轴对称,则
(a )当为的奇函数[ 即] 时,得
(b )当为的偶函数[ 即] 时,得
其中是的右半段:
2 )设分片光滑曲面关于坐标面对称,则
(a )当是关于变量为奇函数[ 即] 时,得
(b )当是关于变量为偶函数[ 即] 时,得
其中是的前半部分:
说明:以上结论不适用于第二型曲线积分和第二型曲面积分。
对称性求解积分

(x y z)2dV
x2dV y2dV z2dV xydV yzdV xzdV
3
z2dV 3
2
d
sin d
R r4 cos2 dr 6
sin cos2 d
R r4dr
0
0
0
0
0
4 R5.
5
D
解:如图所示,积分区域D关于x轴对称,且f(x,-y)=-(xy+y3 )=-f(xy)
即f (x, y)是关于y的奇函数,由定理知, (xy y3)dxdy=0. D
计算 (x+y+z)2dV ,其中是x2 y2 z2 R2的球体.
解由对称性知
xydV yzdV xzdV, x2dV y2dV z2dV,
D
答案:1. ln 2 2.- 2 3. a b
2Hale Waihona Puke 52利用对称性简化二重积分计算
1、I=
z ln(x2 1 x2
y2 y2
zz22)dxdydz,
其中为x2
y2
z2
1.
解:由被积函数可以看出,此函数是关于z的奇函数,因为关于坐标轴 、坐标原点都对称,则:I=0
2、计算I = (xy y3)dxdy,其中D为由y2 2x与x 2围成的区域
f (x, y)dxdy f (y, x)dxdy
D1
D2
f (x, y)dxdy f (y, x)dxdy
D
D
对称性的应用
例1:设区域D={(x,y)|x2 y2 1, x 0},计算二重积分I = 1 xy dxdy
D 1 x2 y2
例2:计算 x[1 yf (x2 y2 )]dxdy,其中D是由y=x3, y 1, x 1围成的区域,f
对称性在积分中应用

对称性在积分中的应用摘要:对称性是宇宙中许多事物都具有的性质,大到银河星系, 小到分子原子.根据对称性, 我们就可以把复杂的东西简单化,把整体的东西部分化. 本文介绍运用数学中的对称性来解决积分中的计算问题, 主要介绍了几种常见的对称性在积分计算过程中的一些结论及其应用,并通过实例讨论了利用积分区间、积分区域、被积函数的奇偶性, 从而简化定积分、重积分、曲线积分、曲面积分的计算方法. 另外对于曲面积分的计算,本文还给出了利用轮换对称性简化积分的计算. 积分的计算是高等数学教学的难点, 在积分计算时, 许多问题用“正规” 的方法解决,反而把计算复杂化, 而善于运用积分中的对称性,往往能使计算简捷, 达到事半功倍的效果.关键词:积分对称定积分重积分曲线积分曲面积分区域对称轮换对称目录一、引言二、相关对称的定义(一)区域对称的定义(二)函数对称性定义(三)轮换对称的定义三、重积分的对称性(一)定积分中的对称性定理及应用(二)二重积分中的对称性定理及应用(三)三重积分中的对称性定理及应用四、曲线积分的对称性(一)第一曲线积分的对称性定理及应用(二)第二曲线积分的对称性定理及应用五、曲线积分的对称性(一)第一曲面积分的对称性定理及应用(二)第二曲面积分的对称性定理及应用六、小结参考文献引言积分的对称性包括重积分、曲线积分、曲面积分的对称性•在积分计算中,根据题目的条件,充分利用积分区域的对称性及被积函数的奇偶性,往往可以达到事半功倍的效果•下面我将从积分对称性的定理及结论,再结合相关的实例进行具体探讨•本文从积分区域平行于坐标轴、对角线的直线的对称性,平行于坐标面的平面等的对称性定义•二、相关的定义定义1:设平面区域为D ,若点(x, y) • D= (2a-x,y),则D关于直线x = a对称,对称点(x,y)与(2a - x,y)是关于x = a的对称点•若点(x, y) € D = (x,2b-y)-D(x, y),则D关于直线y二b对称,称点(x, y)与(x,2b - y)是关于y = b的对称(显然当a =0,b = 0对D关于y , x轴对称).定义2:设平面区域为D ,若点(x, y) • D = (y—a,x-a),则D y二x,a对称,称点(x, y)与(y - a, x - a)是关于y 二x • a 的对称点.若点(x, y) • D = (a - y,a - x)-D,贝U D关于直线y 对称.注释:空间区域关于平行于坐标面的平面对称;平面曲线关于平行于坐标轴的直线对称;平面曲面以平行于坐标面对称,也有以上类似的定义.空间对称区域.定义3: (1)若对-(x, y, z^ 1,点(x,y,-z)・1 ,则称空间区域门关于xoy面对称;利用相同的方法,可以定义关于另外两个坐标面的对称性.⑵ 若对P(x, y, z)匕0 ,二点(x, y,—z)匕O ,则称空间区域0关于z轴对称;利用相同的方法,可以定义关于另外两个坐标轴的对称性.(3)若对_(x, y, z^ 1 1, -J点(-x,-y,-z) • 11,则称空间区域门关于坐标原点对称.⑷ 若对一(x, y,z) •门,T点(y,乙x),(z, x, 1 1 ,则称空间区域门关于x, y, z具有轮换对称性.定义4:若函数f(x)在区间- a,a上连续且有f(x-a) = f(x • a),则f(x)关于x二a对称当且仅当a = 0时f (-x)二f (x),则f (x)为偶函数.若f (a - x) =-f (a x),则f(x)为关于a,0中心对称.当且仅当a=0时有f(_x)-_f(x)则f(x)为奇函数.若f (x -a) = f (x • a)且f (a -x) = - f (a x)则f (x)既关于x = a对称,又关于a,0 中心对称.定义5 若n元函数f(X i,X2,…,X n)三f (X i,X i 1,…,X n,X i,…,x:丄),(i =1,2,…,n ), 则称n元函数f (X i,X2,…,X n)关于X i,X2,…,X n具有轮换对称性•定义6:若- p(X i,X2, ,X n) D n R n( n N)有P i(X i,X i 1, ,X n,X i,厶J D n(i =1,2,…,n)成立,则称D n关于p(X i,X2,…,X n)具有轮换对称性.三、重积分的对称性(一)对称性在定积分中的应用利用函数图形的对称性可简化定积分的计算■在特殊情况下,甚至可以求出原函数不是初等函数的定积分■因此掌握对称性在积分中的方法是必要的■下面首先给出一个引理,由此得出一系列的结论,并通过实例说明这是结论的应用■引理设函数f (x)在a - h, a h上连续,则有f (x)dx = f (a x) f (a - x) dx (1)证令x二a t,有a h h hf(x)dx f(a t)dt f(a t)dta -h ' -h 0令t u,则0 0 hf (a t)dt = f (a -u)du = i f (a - u)du•山h 0将( 3)式带入(2)式,并将积分变量统一成x ,则(x)dx = ° f (a x) f (a - x)dx dx特别地,令a =0,就得公式:f(x)dx= :〔f(x) f (-x)d x由函数奇偶性的定义及上式,易知定理1设函数f (x)在[- h, h上连续,那么h h2)若 f(x)为偶函数,则f(x)dx=2 f(x)dx■_hoh3)若f(x)为奇函数,则 』f(x)dx=O次结论有广泛的应用,如能恰当地使用,对简化定积分的计算有很大的帮助,是奇函数,后一部分是偶函数,运用定理1的结论简化其计算.2一 : cosxdx 2_ cosxdx匕x 21 2 2cosxdx=2注:而对于任 意区间上的定积分问题,可以平移 到对称区间Lh,h 1上求解。
2类曲面积分对称性的问题的理解

2类曲⾯积分对称性的问题的理解
若曲⾯∑关于x=0对称,∑1是∑⼤于等于部分,正侧不变,则当f(-x,y,z)=-f(x,y,z)时
∫∫(∑)f(x,y,z)dxdz=∫∫(∑)f(x,y,z)dxdy=0;∫∫(∑)f(x,y,z)dydz=2∫∫(∑1)f(x,y,z)dydz
f(-x,y,z)=f(x,y,z)时
∫∫(∑)f(x,y,z)dydz=0
∫∫(∑)f(x,y,z)dxdz=2∫∫(∑1)f(x,y,z)dxdz
∫∫(∑)f(x,y,z)dxdy=2∫∫(∑1)f(x,y,z)dxdy
若关于y=0(z=0)对称,则有类似结论。
对亏了他⼈为我指点迷津,我才真正的理解了这个结论。
先整理如下
曲⾯关于x=0对称就是说关于yoz⾯对称,xy⾯这边有⼀个微元,那边也有⼀个微元,投影到xy⾯或xz⾯上时,投影域⼤⼩、形状、⽅向都相同;⽽投影到yz⾯时⼤⼩形状相同,但是⽅向相反。
f(-x,y,z)=f(x,y,z)就是说函数f在上述两个微元处函数值相等,对dydz积分时,因为两个微元的投影域反向,积分值为零。
对dxdy或dxdz积分时是单侧积分的2倍。
f(-x,y,z)=-f(x,y,z)的情况正好相反,在投影域⼤⼩、形状、⽅向都相同是由于f(-x,y,z)=-f(x,y,z)所以导致⽅向前加个负号,也就是与f(-x,y,z)=f(x,y,z)时的情况完全相对。
这类问题由于区⾯是可以分解投影到3个坐标平⾯,所以要结合空间想象能⼒,弄清楚投影区域与⽅向的关系。
同时本题也可以从物理流量的⾓度来考虑!。
对称性在积分计算中的应用

对称性在积分计算中的应用摘要:在积分计算中,运用积分区域的对称性和被积函数的奇偶性,以及轮换对称性可以简化计算.本文总结了对称性在定积分、重积分、曲线积分以及曲面积分计算中的应用.对于积分区域不具有对称性的情形,文中总结了几种方法来创造对称性,如平移变换、伸缩变换、区域划分等.关键词:对称性;奇偶性;积分计算;轮换对称引言数学是一个充满了美的世界,对称性不仅是数学美的重要特征,也是一个非常重要的艺术要素,因此很有必要去探讨一下对称性在解题这门艺术中的应用.在学习的过程中,常常发现自己在计算积分时,把简单的问题复杂化而增加了计算的难度,若在积分的计算中能充分利用积分区域的对称性和被积函数的奇偶性以及轮换对称性,就能简化计算.很多文献讨论了对称性在积分计算中的应用这个问题.如文献[3]和文献[4]主要讨论了二重积分的对称性定理及其应用,得出了当积分区域关于x轴(或y轴、或原点)对称且被积函数关于变量x(或y)为奇函数或偶函数时的对称性定理.文献[5]讨论了轮换对称性在各类积分计算中的应用.文献[6]讨论了对称性在三重积分计算中的应用,得出了当积分区域关于某个坐标面对称且被积函数是关于某变量的奇函数或偶函数时的对称性定理.文献[7]给出了积分区域关于变量x,y,z的轮换对称性定义.文献[13]将定积分、重积分、第一型曲线积分和第一型曲面积分的对称性定理写成统一的形式.当积分区域不具有对称性时,不能直接利用对称性来简化计算,但有时可以通过适当的变换化积分区域为对称区域.本文总结了几种创造对称性的方法,如伸缩变换、平移变换、区域划分等,有时候可以将两种变换结合起来使用.1.对称性在定积分计算中的应用在定积分的计算中,根据积分区间的对称性和被积函数的奇偶性,可以简化计算.定理1.1[1] 设f(x)在[?a,a]上连续,则当f(x)是奇函数时,?当f(x)是偶函数时,?a?aa?af(x)dx?0;f(x)dx?2?f(x)dx.a1周口师范本科毕业论文(设计)证明?a?af(x)dx??af(x)dx?0?a?0?af(x)dx.令x??t,有dx??dt.则?当f(x)为偶函数时,当f(x)为奇函数时,f(x)dx???f(?t)dt?a0f(?t)dt.a?a0f(?t)dt??a0f(t)dt,则?aa?aaf(x)dx?2?f(x)dx.?af(?t)dt???f(t)dt,则??af(x)dx?0.下面我们来看一个例题.例1?x3sin2x2?计算定积分I???6?x2?x???dx.2?2?x?3x?5? 2解3I??2?2xsinxx?3x?56232??2?2x(2?x)dx.2由于xsinxx?3x?5622是变量x的奇函数,由定理1.1知?2?2xsinxx?3x?56232由于x(2?x2)是变量x的偶函数,由定理1.1知?则I?0?16?16.2?2x(2?x)dx?2?x(2?x)dx?16,2202在定积分的计算中,当积分区间关于原点对称时,我们容易想到用对称性,而当积分区间为任意有限区间?a,b?时,我们往往想不到去利用对称性.实际上,积分区间?a,b?一定关于直线x?12bbaa(a?b)对称,由此我们可以得出如下定理.定理1.2[2]设f(x)在?a,b?上连续,则?f(x)dx??f(a?b?x)dx.只需令x?a?b?t即可证明此定理.这一公式对于积分的计算并没有多少的帮助,但从该公式易得如下推论.推论1设f(x)在?a,b?上连续,则? baf(x)dx??ba12[f(x)?f(a?b?x)]dx.对于有些计算起来非常困难甚至无法计算的积分,我们只需将被积函数换成[f(x)?f(a?b?x)]就能简化运算.21例2计算定积分?4ln(9?x)ln(9?x)?ln(3?x).22周口师范本科毕业论文(设计)解记f(x)?442,则f(6?x)?,由推论1知?f(x)dx??212f(x)?f(6?x)]dx?4212dx?1.我们已经总结了对称性在定积分计算中的应用,从上面的讨论中我们可以看出根据对称性确实可以简化计算,下面来讨论对称性在重积分计算中的应用.2.对称性在重积分计算中的应用2.1对称性在二重积分计算中的应用我们已经讨论了对称性在定积分计算中的应用,得出了相应的结论.对于二重积分,我们主要讨论积分区域关于x轴(或y轴)对称、关于原点对称以及轮换对称性.定理2.1.1[3]x设函数f(x,y)在xoy平面上的有界区域D上连续,且D关于轴对称.如果函数f(x,y)是关于y的奇函数,即f(x,?y)??f(x,y),(x,y)?D,则??f(x,y)d??0;如果f(x,y)是关于y的偶函数,即f(x,?y)?f(x,y),D(x,y)?D,则??f(x,y)d??2??f(x,y)d?.DD1其中D1是D在x轴上方的平面区域.同理可写出积分区域关于y轴对称的情形.证明根据二重积分的性质得??Df(x,y)d????f(x,y)d??D1??D2f(x,y)d?,其中D1??(x,y)?D|y?0?,D2??(x,y)?D|y?0?.作变量替换x?x,y??t,(x,t)?D1.则J??(x,y)?(x,t)?100?1??1.若f(x,y)为关于y的奇函数,则??D2f(x,y)d????D1f(x,?t)J?????f(x,t)d?????f(x,y)d?D1D1,3周口师范本科毕业论文(设计)??Df(x,y)d????f(x,y)d??D1D1f(x,y)d??0,若f(x,y)为关于y的偶函数,则??D2f(x,y)d????f(x,?t)Jd??D1??D1f(x,t)d????D1f(x,y)d?,??Df(x,y)d????f(x,y)d??D1??D1f(x,y)d??2??f(x,y)d?D1.综合以上可知结论成立.例3计算二重积分??y3sin2xd?,其中D是由x?y?1,x?y?1和x?0围D成的平面闭区域.解由于区域D关于x轴对称,且f(x,y)?y3sin2x是关于变量y的奇函数,则由定理2.1.1知??y3sin2xd??0.D由定理2.1.1可得如下推论.推论2设函数f(x,y)在xoy平面上的有界区域D上连续,若积分区域D既关于x轴对称,又关于y轴对称,则⑴若函数f(x,y)关于变量x,y均为偶函数,则??f(x,y)d??4??f(x,y)d?.DD1其中D1是区域D在第一象限的部分,D1??(x,y)?D|x?0,y?0?.⑵若函数f(x,y)关于变量x或变量y为奇函数,则??f(x,y)d??0.D当积分区域关于原点对称时,我们可以得到如下的定理.定理2.1.2?4?设函数f(x,y)在xoy平面上的有界区域D上连续,且D关于原点对称.如果f(?x,?y)??f(x,y),(x,y)?D,则??Df(x,y)d??0;如果f(?x,?y)?f(x,y),(x,y)?D,则??f(x,y)d??2??f(x,y)d??2??f(x,y)d?,DD1D2其中D1??(x,y)?D|x?0?,D2??(x,y)?D|y?0?.为了叙述的方便,我们给出区域关于x,y的轮换对称性的定义.定义2.1.1设D为一有界可度量平面区域(或光滑平面曲线段),如果对于任意(x,y)?D,存在(y,x)?D,则称区域D(或光滑平面曲线段)关于x,y具4周口师范本科毕业论文(设计)有轮换对称性.关于区域的轮换对称性,有如下定理.定理2.1.3[5]x,y设函数f(x,y)在xoy平面上的有界区域D上连续,且D关于具有轮换对称性,则??f(x,y)d??D??Df(y,x)d?.上面所列推论及定理的证明方法均与定理2.1.1类似,此处不再赘述,下面给出相应的例题.例4解计算二重积分I?I???(xD2?5x?3y?2)d?,其中D:x2?y2?1.??(5x?3y)d??D??Dxd??2由于D关于原点对称,且5x?3y是??2d?,D(x,y)的奇函数,则由定理2.1.2知??(5x?3y)d??0.故D2?01I???Dxd??2??2d???Dd??(rcos?)rdr?2??2094?.例5计算二重积分I???其中f(x)是区间??1,1?上的?,正值连续函数,D??(x,y)|x2?y2?1,x?0,y?0?.解由于积极分区域D关于x,y具有轮换对称性,则由定理2.1.3得I?所以I???2D1??D?????D?,a?bd??2??d??D?2(a?b).2.2对称性在三重积分计算中的应用经过分析,我们可以很容易地看到对称性在三重积分计算中的应用与二重积分非常类似,根据对称性在二重积分计算中的结论可以得到下面的定理.定理2.2.1[6]设函数f(x,y,z)是定义在空间有界区域?上的连续函数,且?关于坐标平面x?0对称,则(1)若f(x,y,z)是关于变量x的奇函数,则???f(x,y,z)dV?0;?(2)若f(x,y,z)是关于变量x的偶函数,则?1是?的前半部分,?1??(x,y,z)??|x?0?.同理可写出?关于坐标平面y?0(或z?0)对称时的情形.证明由三重积分的性质得????f(x,y,z)dV?????1f(x,y,z)dV?????2f(x,y,z)dV,其中?1??(x,y,z)??|x?0?,?2??(x,y,z)??|x?0?.作变量替换x??t,y?y,z?z,(t,y,z)??1,则?(x,y,z)?(t,y,z)?1?0001000??1.1J?(1)当f(x,y,z)为关于变量x的奇函数时,有????2f(x,y,z)dV????f(?t,y,z)JdV?????f(t,y,z)dV?????f(x,y,z)dV?1?1?1????f(x,y,z)dV?????1f(x,y,z)dV?????1f(x,y,z)dV?0.(2)当f(x,y,z)为关于变量x的偶函数时,有????2f(x,y,z)dV????f(?t,y,z)JdV??1????1?1f(t,y,z)dV?????1f(x,y,z)dV,????f(x,y,z)dV?2???f(x,y,z)dV.综合(1)和(2)可知结论成立.例6z?计算三重积分I?????(x?z)dV,其中?是由曲面z?与.解I?????xdV?????zdV,由于?关于坐标面x?0对称,且x为关于变量x的奇函数,则由定理2.2.1知???xdV?0.则?I?????zdV??2?0?40d??d??rcos?rsin?dr?201?8.与二重积分类似,我们也可得到如下结论.6周口师范本科毕业论文(设计)定理2.2.2设函数f(x,y,z)是定义在空间有界区域?上的连续函数,且?关于原点对称,则(1)若f(?x,?y,?z)??f(x,y,z),(x,y,z)??,则???f(x,y,z)dV?0;?(2)若f(?x,?y,?z)?f(x,y,z),(x,y,z)??,则????f(x,y,z)dV?2???f(x,y,z)dV?2???f(x,y,z)dV?2???f(x,y,z)dV?1?2?3.其中?1??(x,y,z)??|x?0?,?2??(x,y,z)??|y?0?,?3??(x,y,z)??|z?0?为了方便叙述,我们先给出一个空间几何体关于x,y,z的轮换对称性定义.定义2.2.1[7]设?是一有界可度量的集几何体(?可为空间区域、空间曲线或曲面块),且它的边界光滑,若对任意的(x,y,z)??,都存在(y,z,x)??,存在(z,x,y)??,则称?关于x,y,z具有轮换对称性.关于空间区域的轮换对称性,我们有如下的定理.定理2.2.3设函数f(x,y,z)是定义在空间有界区域?上的连续函数,且?关于x,y,z具有轮换对称性,则???f(x,y,z)dV????f(y,z,x)dV???????f(z,x,y)dV.例7解计算三重积分???xyzdV,其中?:x2?y2?z2?4.?由于?关于原点对称,且xyz是关于(x,y,z)奇函数,由定理2.2.2知???xyzdV??0.例8[8]解计算???(x?y?z)2d?.其中?为正方体0?x?1,0?y?1,0?z?1.<B< body>。
对称性在定积分中的-应用

对称性在定积分中的应用a定积分的计算中,对称性也简称“偶倍奇零”性质。
恰当地运用对称性能够大大地简化计算步骤,得到事半功倍的效果。
还可以根据问题的特点发现潜在的对称关系或构造某种对称性,使问题得到巧妙的解决。
一、对称性适用的条件对称性包括积分区间的对称性和被积函数的奇偶性,两个条件缺一不可。
当然很多情况下,我们可以挖掘潜在的对称性和奇偶性。
二、对称性解决的题型1. 积分区间对称且被积函数具有奇偶性时,直接利用“偶倍奇零”性质。
定理:例题:2. 积分区间对称的前提下,被积函数非奇非偶利用任一函数可写成一奇函数和一偶函数的和,把积分改写成0()()()()()[][()()]22aa a a a f x f x f x f x f x dx dx f x f x dx --+---=+=+-⎰⎰⎰ 例题:例2 计算积分44cos .1x x dx e ππ-+⎰ 解:原式40cos cos()[]11x xx x dx e e π--=+++⎰ 40cos xdx π=⎰2= 例3 计算积分()121ln 1.x x e dx -+⎰ 解:原式()()1220[ln 1()ln 1]x x x e x e dx -=++-+⎰ ()21201[ln 1ln ]x x x e x e x dx e ⎛⎫+=+- ⎪⎝⎭⎰ ()()12220[ln 1ln 1ln ]x x x x e x e x e dx =+-++⎰1202x dx =⎰ 23=a)b) 充分利用被积函数某一项的奇偶性进行简化积分的运算例1 计算积分(121arctan .x x dx -⎰解:原式121arctan x xdx -=⎰11x -+⎰1002x =+⎰令sin x t = 原式2202sin cos cos t t tdt π=⋅⋅⎰ 22402(sin sin )t t dt π=-⎰ 1312()2422π=-8π=c)3. 积分区间不对称的情况a) 作变量代换使变换后的积分区间对称。
对称性在积分计算中的应用

对称性在积分计算中的应用对称性在积分计算中的应用对称性是数学中重要的概念之一,它的应用涉及到各个数学领域中。
在积分计算中,对称性也是一个非常重要的工具和思想,能够帮助我们简化、优化和解决复杂的积分问题。
本文将介绍对称性在积分计算中的应用,以及如何利用对称性求解各类复杂积分。
一、对称性概述对称性是指物体或者数学对象的部分或整体运动具有某种规则性的现象。
常见的对称性包括轴对称、中心对称、对角线、对边对称、等等。
对称性是自然界现象和数学理论中广泛存在的一种现象,也是数学中强有力的工具和思想。
二、对称性在积分计算中的基本应用对称性在积分计算中的使用具有以下优点:1.减少计算量:使用对称性可以将积分的计算范围缩小为对称区间内的一半,从而大大减少了计算量,简化了计算过程。
2.避免重复计算:利用对称性可以避免重复计算某些部分,减少了计算量和出错的概率。
3.提高准确度和精度:对称性具有非常清晰的数学定义和可操作性,使用对称性可以提高准确度和精度,更好地描述数学对象的性质和特征。
下面分别对轴对称、中心对称、对角线对称、对边对称等对称性进行介绍,并说明其在积分计算中的具体应用。
1.轴对称轴对称是指数学对象在某个轴线旋转180度以后不改变其形状和大小。
在数学中,轴对称包括平面上的x轴、y轴和45度斜线轴等。
轴对称在积分计算中的应用非常广泛,常见的应用包括:(1)基本函数关于坐标轴对称的性质:例如正弦函数和余弦函数关于y轴对称,正切函数和余切函数关于x轴对称。
利用这些对称性质可以简化复杂函数的积分。
(2)轮换对称性:对于一类具有一定规则性的函数,可以通过对其进行轮换得到新的函数,这样可以将原函数分成几个对称的部分,从而提高计算效率。
例如,对于函数f(x,y) = x + y的积分计算,因为其具有xy的轮换对称性,可以将其分解成两部分f1(x,y) = x和f2(x,y) = y,从而使积分计算简化。
(3)利用轴对称性质求偶函数和奇函数的积分:如果f(x)是关于y轴对称的偶函数,则∫f(x)dx从-x到x之间的积分等于2∫f(x)dx从0到x之间的积分,即∫-xf(x)dx = 2∫0f(x)dx如果f(x)是关于y轴对称的奇函数,则∫f(x)dx从-x到x之间的积分等于0。
对称性在多元函数积分中的应用

对称性在多元函数积分中的应用1.引言多元函数积分计算是微积分中的一个重点和难点,很多初学者对此是望而却步。
但被积函数和积分区域的某些特殊结构特征常常会对问题的求解带来便捷,对于被积函数存在奇偶性、积分区域具有对称性的重积分、第一类曲线积分、第一类曲面积分的计算问题,巧妙利用对称性,能使复杂的计算变得简单易行。
2.主要结论定理1:(1)如果积分区域D关于y轴对称,则:(ⅰ)当时,有;(ⅱ)当时,有其中.(2)如果积分区域D关于x轴对称,则:(ⅰ)当时,有;(ⅱ)当时,有,其中.证明:(1)如果积分区域D关于y轴对称,按y型积分区域顺序计算二重积分有,其中为D在y轴上的投影,为任意平行于x轴的且穿越区域内部的直线与区域边界交点的横坐标。
由于积分区域D关于y轴对称,故在平行于x轴的直线上关于点对称,由定积分对称性结论[1],[3]可得:当时,,所以;当时,,所以,其中同理可证结论(2)。
以上结论可进一步推广到积分区域关于原点和关于直线对称的情况。
推论1(1)如果积分区域D关于原点对称,则:(ⅰ)当时,有;(ⅱ)当时,有,其中D1为D的右半平面.(2)如果积分区域D关于对称,则,其中,分别为在的上方与下方部分。
将二重积分积分区域定义的平面直角坐标系推广到空间直角坐标系,将平面直角坐标系中关于坐标轴的对称推广到空间直角坐标系中关于坐标面的对称即可得到三重积分的相关结论。
定理2:设在有界闭区域连续,若关于平面对称,则:(1),若关于为奇函数;(2),若关于为偶函数,其中.类似可得到关于平面对称的情况下的结论。
另外,由二重积分的结论可直接推广得到第一类曲线积分的结论,由三重积分的结论可直接推广得到第一类曲面积分的结论。
定理3:设在分段光滑的曲线L上连续.若L关于x轴(或y轴)对称,则:(1),若关于y(或x)为奇函数;(2),若关于y(或x)为偶函数,其中L1为L的右半平面或上半平面。
定理4:设在分块光滑曲面S上连续,若S关于平面对称,则:(1),若关于x为奇函数;(2),若关于x为偶函数,其中.类似可得到关于平面对称的情况下的结论。
对称性在积分中的应用

第20卷第4期2000年10月 数学理论与应用MA THEMA TICAL THEOR Y AND APPL ICA TIONSVol.20No.4Oct.2000对称性在积分中的应用Ξ陈云新(中南工学院基础部,衡阳市421001)摘 要 本文讨论了在各类积分中利用对称性解题的技巧和使用方法.关键词 积分,对称在积分中的计算中,经常遇到积分区域具备对称性的题型.如果能利用其对称性的性质,则可以简化其计算过程,特别是有些题不用计算可以直接判断出其结果.本文讨论了利用积分区域的对称性配合被积函数的奇,偶性简化定积分,重积分,第一类曲线,曲面积分计算过程的使用方法.(以下都在积分存在的前提下予以讨论)一、定积分的对称性若积分区间为[-a,a],则(1)当f(-X)=f(X)时∫a-a f(x)dx=2∫a0f(x)dx(2)当f(-X)=-f(X)时,∫a-a f(x)dx=0二、二重积分的对称性在二重积分κDf(x,y)dσ的计算过程中;11若积分区域D关于X轴对称,记位于X轴上半部分区域为D1,则(1)当f(x,-y)=f(x,y)时,κD f(x,y)dσ=2κD1f(x,y)dσ(2)当f(x,-y)=-f(x,y)时,κDf(x,y)dσ=021若积分区域D关于Y轴对称,记位于Y轴右半部分区域为D1,则;(1)当f(-x,y)=f(x,y)时κD f(x,y)dσ=2κD1f(x,y)dσ(2)当f(-x,y)=-f(x,y)时,κDf(x,y)dσ=0三、三重积分的对称性在三重积分µΩf(x,y,z)dv的计算过程中;Ξ收稿日期:2000年4月11若积分区域Ω关于XO Y面对称,记Ω位于XO Y面上半部分为Ω1,则:(1)当f(x,y,-z)=f(x,y,z)时,µΩf(x,y,z)dv=2µΩ1f(x,y,z)dv(2)当f(x,y,-z)=-f(x,y,z)时µΩf(x,y,z)dv=021若积分区域#W关于YOZ面对称,记Ω位于YOZ面前冲击2部分为Ω1,则(1)当f(-x,y,z)=f(x,y,z)时,µΩf(x,y,z)dv=2µΩ1f(x,y,z)dv(2)当f(x,-y,z)=-f(x,y,z)时,µΩf(x,y,z)dv=031若积分区域Ω关于ZO Y面对称,记Ω位于ZOX面右半部分为Ω1,则:(1)当f(x,-y,z)=f(x,y,z)时,µΩf(x,y,z)dv=2µΩ1f(x,y,z)dv(2)当f(x,-y,z)=-f(x,y,z)时,µΩf(x,y,z)dv=0四、第一类曲线积分的对称性A1平面曲线积分∫L f(x,y)ds的计算过程11若曲线L关于X轴对称,记L位于X轴上半部分为L1:则:(1):当f(x,-y)=f(x,y)时∫L f(x,y)ds=2∫L1f(x,y)ds(2):当f(x,-y)=-f(x,y)时,∫L f(x,y)ds=021若曲线L关于Y轴对称,记L位于Y轴右半部分为L1:则:(1):当f(-x,y)=f(x,y)时,∫L f(x,y)ds=∫L1f(x,y)ds(2):当f(-x,y)=-f(x,y)时,∫L f(x,y)ds=0B:空间曲线积分∫ΓF(x,y,z)ds的计算过程11若积分曲线Γ关于XO Y面对称,记Γ位于XO Y面上半部分为Γ1,则:(1)当F(x,y,-z)=f(x,y,z)时,∫ΓF(x,y,z)ds=2∫Γ1F(x,y,z)ds (2):当F(x,y,-z)=-F(x,y,z)时,∫ΓF(x,y,z)ds=021若积分曲线Γ关于YOZ面对称,记Γ位于YOZ面前半部分为Γ1,则:(1)当F(-x,y,z)=F(x,y,z)时,∫ΓF(x,y,z)ds=2∫Γ1F(x,y,z)ds (2)当F(-x,y,z)=-F(x,y,)时,∫ΓF(x,y,z)ds=031若积分曲线Γ关于ZOX面对称,记Γ位于ZOX面右半部分为Γ1,则:(1)当F(x,-y,z)=F(x,y,z)时,∫ΓF(x,y,z)=2∫Γ1F(x,y,z)ds (2):当F(x,-y,z)=-F(x,y,z)时,∫ΓF(x,y,z)=014第4期陈云新:对称性在积分中的应用五、第一类曲面积分的对称性在第一类曲面积分κ∑F(x,y,z)ds的计算过程中.11若积分曲面∑关于XO Y面对称,记∑位于XO Y面上半部分为∑1;则:(1):当F(x,y,-z)=F(x,y,z)时,κ∑F(x,y,z)ds=2κ∑1F(x,y,z)ds(2)当F(x,y,-z)=-F(x,y,z)时,κ∑F(x,y,z)ds=021若积分曲面∑关于YOZ面对称,记∑位于YOZ面前半部分为∑1;则:(1)当F(-x,y,z)=F(x,y,z)时,κ∑F(x,y,z)ds=2κ∑1F(x,y,z)ds(2)当F(-x,y,z)=-F(x,y,z)时,κ∑F(x,y,z)ds=031若积分曲面∑关于ZOX面对称,记∑位于ZOX面右半部分为∑1;则:(1)当F(x,-y,z)=F(x,y,z)时,κ∑F(x,y,z)ds=2κ∑1F(x,y,z)ds(2)当F(x,-y,z)=-F(x,y,z)时,κ∑F(x,y,z)ds=0六、应用举例例1:求µΩzln(x2+y2+z2+1)x2+y2+z2+1dv,其中Ω:x2+y2+z2Φ1.解:∵积分区域Ω关于XO Y面对称而被积函数f(x,y,z)=zln (x2+y2+z2+1)x2+y2+z2+1满足:f(x,y,-z)=-f(x,y,z)∴µΩzln(x2+y2+z2+1)x2+y2+z2+1dv=0例2:求∮L x2+y2ds,其中L为圆周x2+y2=ax.解:因为曲线L关于X轴对称,记位于X轴上方部分为L1而被积函数f(x,y)=x2+y2满足:f(x,-y)=f(x,y)所以∮L x2+y2ds=2∮L1x2+y2ds=2a2例3:计算λ∑xyzds,其中∑是球面x2+y2+z2=1.解:此题中积分区域∑具有多重对称性,任选其中一种都可以得出本题的结果.所以24数学理论与应用第20卷λ∑xyzds =0参考文献[1] 同济大学编《高等数学》第四版下期,高等教育出版社,1996,12(上接39页)而求得所求积分值为π24.从以上的分析讨论可以看到,分解变形这一技巧在积分运算中是一种用途广泛的方法,应用得恰当,不但可以将复杂问题简单化,而且有时还可以起到提示解题思路的作用.附:主要参考资料[1]同济大学数学教研室编.高等数学1高教出版社[2]西安交通大学高等数学教研室编.复变函数论1高等教育出版社出版34第4期陈云新:对称性在积分中的应用。
积分对称性解答

问题 1、为什么说设 f (x, y) 在区域 D ⊂ R2 上可积,若 D 的的形状关于 x 轴
对称,当 f (x, − y) = − f (x, y) 时, ∫∫ f (x, y)dxdy = 0 ;当 f (x, − y) = f (x, y) 时,
D
∫∫ f (x, y)dxdy = 2∫∫ f (x, y)dxdy ,其中 D1 为 D 中位于 x 轴上方的部分?
D(2) k
,
D(1) k
与
D(2) k
关于
x
轴对称.
∀(ξk ,ηk
)∈
D(1) k
(ηk
≥
0)
,则 ∃(ξk , −ηk
)∈
Dk(2) ,记 λ
=
max{Dk(1)
的直径},则
n2
∫∫ ∑ D1
f (x, y)dxdy = lim λ →0 k =1
f (ξk ,ηk )Δσ k
,
n2
∫∫ ∑ D2
Σ
Σ1
于 xz 面右边的部分。
(3) 设 Σ 的形状关于 yz 面对称,若在 Σ 上,有 f (−x, y, z) = − f (x, y, z) ,则
∫∫ f (x, y, z)dS = 0
Σ
若 f (−x, y, z) = f (x, y, z) ,则 ∫∫ f (x, y, z)dS = 2∫∫ f (x, y, z)dS ,其中 Σ1 是 Σ
D
D1
1
问题 2、若区域 D ⊂ R2 关于直线 y = x (或 y = −x )对称,且
f (x, y) = − f ( y, x) (或 f (− y, −x) = − f (x, y) ),是否有 ∫∫ f (x, y)dxdy = 0 ? D
积分区域的对称性和被积函数的奇偶性在积分计算中的应用

积分区域的对称性和被积函数的奇偶性在积分计算中的应用在积分计算中,积分区域的对称性和被积函数的奇偶性是非常有用的工具。
它们可以简化积分计算的过程,减少计算的复杂性。
本文将详细介绍积分区域的对称性和被积函数的奇偶性在积分计算中的应用。
一、积分区域的对称性1.轴对称性当被积函数在积分区域上关于一个轴对称,可以利用轴对称性将积分区域的整个积分化简为积分区域的一半。
具体来说,对于轴对称的积分区域,可以通过在轴上取等于0的新变量,达到积分区域的简化。
例如,对于关于x轴对称的积分区域,可以将原来的积分区域分成上下两个相等的部分,只需计算其中一个部分的积分,再乘以2即可得到整个积分的结果。
2.点对称性当被积函数在积分区域上关于一个点对称,可以利用点对称性将积分区域的整个积分化简为积分区域的一部分。
具体来说,对于关于原点对称的积分区域,可以将原来的积分区域分成两个对称的部分,只需计算其中一个部分的积分,再乘以2即可得到整个积分的结果。
3.面对称性当被积函数在积分区域上关于一个平面对称,可以利用面对称性将积分区域的整个积分化简为积分区域的一部分。
具体来说,对于关于xy平面对称的积分区域,可以将原来的积分区域分成上下两个对称的部分,只需计算其中一个部分的积分,再乘以2即可得到整个积分的结果。
利用积分区域的对称性可以有效地简化积分计算的过程,减少计算量,提高计算效率。
同时,对称性还可以帮助我们更好地理解被积函数在不同区域上的行为,为进一步的积分分析提供指导。
二、被积函数的奇偶性被积函数的奇偶性是指被积函数在积分区域上的对称性质。
被积函数的奇偶性可以决定积分的结果,从而简化积分计算的过程。
下面,我们将介绍两种常见的被积函数的奇偶性。
1.奇函数如果被积函数f(x)满足f(-x) = -f(x),则被积函数f(x)是奇函数。
奇函数具有以下特点:在关于原点对称的积分区域上,奇函数的积分结果为0,即∫[-a, a] f(x) dx = 0。
重积分积分区域的对称性

重积分积分区域的对称性公司内部编号:(GOOD-TMMT-MMUT-UUPTY-UUYY-DTTI-情形一:积分区域D 关于坐标轴对称定理4 设二元函数(,)f x y 在平面区域D 连续,且D 关于x 轴对称,则 1)当(,)(,)f x y f x y -=-(即(,)f x y 是关于y 的奇函数)时,有 (,)0Df x y dxdy =⎰⎰ .2)当(,)(,)f x y f x y -=(即(,)f x y 是关于y 的偶函数)时,有1(,)2(,)DD f x y dxdy f x y dxdy =⎰⎰⎰⎰ .其中1D 是由x 轴分割D 所得到的一半区域。
例5 计算3()DI xy y dxdy =+⎰⎰,其中D 为由22y x =与2x =围成的区域。
解:如图所示,积分区域D 关于x 轴对称,且3(,)()(,)f x y xy y f x y -=-+=- 有即(,)f x y 是关于y 的奇函数,由定理13()0Df xy y dxdy +=⎰⎰.类似地,有:定理5 设二元函数(,)f x y 在平面区域D 连续,且D 关于y 轴对称,则 其中2D 是由y 轴分割D 所得到的一半区域。
例6 计算2,DI x ydxdy =⎰⎰其中D 为由22;-220y x y x y =+=+=及所围。
解:如图所示,D 关于y 轴对称,并且2(,)(,)f x y x y f x y -==,即被积分函数是关于x 轴的偶函数,由对称性定理结论有:11222220022215x DD I x ydxdy x ydxdy dx x ydxdy -+====⎰⎰⎰⎰⎰⎰.定理6 设二元函数(,)f x y 在平面区域D 连续,且D 关于x 轴和y 轴都对称,则 (1)当(,)(,)f x y f x y -=-或(,)(,)f x y f x y -=-时,有(,)0Df x y dxdy =⎰⎰.(2)当(,)(,)(,)f x y f x y f x y -=-=时,有 其中1D 为由x 轴和y 轴分割D 所的到的1/4区域。
对称性在积分计算中的应用

对称摘 要 对称性是解决数学问题的重要方法之一.在积分学中充分利用积分区域的对称性和被积函数的奇偶性,使得数学积分的计算过程得到简化.本文通过总结定理和性质并借助实例说明对称性在定积分、重积分、曲线积分、曲面积分计算中的应用.关键词 对称性 定积分 重积分 曲线积分 曲面积分1. 前言在许多人眼里,数学是抽象和复杂的,但在此背后,也有着它和谐的旋律.如果我们能够更多的理解和掌握数学中的很多规律,就会对数学有更深的认识和感受.目前人们普遍认识到的数学美的基本内容有:统一美、对称美、简洁美、奇异美.它们各有内涵,各有吸引人之处,而对称美是指数学内容中的部分与部分、部分与整体之间和谐一致,以及各种数学概念和理论之间所存在的“对等美”.关于对称性在积分计算中的应用,首先明确以下问题:(1)关于对称性的了解,以简单点为例:点),(y x 关于x 轴的对称点为),(y x -;点),(y x 关于y 轴的对称点为),(y x -;点),(y x 关于原点对称的对称点为),(y x --;点),(y x 关于x y =对称的对称点为),(x y .(2)函数的奇偶性判断,以及两个函数和差积运算后的奇偶性.(3)本文所涉及内容都是R —可积函数.(],[b a 上的连续函数在],[b a 上必可积;只有有限个第一类不连续点的函数是可积的,即分段函数是可积的;单调有界函数必定可积.)(4)清楚的区分各种积分的表达式.(5)用极坐标将二、三重积分化为累次积分时应该注意的地方.(6)数学分析就是用极限的思想来研究函数的一门学科,需对研究内容的产生和如何解决的方式有一定的了解.(7)基本积分公式、倍角公式的熟悉应用.2. 对称性在定积分计算中的应用定理1[4] 设函数)(x f 在],[a a -上连续,那么⎪⎩⎪⎨⎧=--=-=⎰⎰-aaax f x f x x f x f x f x x f 0)()(,d )(2)()(,0d )( 2.1 计算.d 11lnI 442⎰-+-=ππx xxx分析:定积分在研究区间]4,4[ππ-是关于原点对称的, 又因为2x 为偶函数,xx+-11ln是奇函数,故由定理1可知,0=I . 2.2 计算.d cos21)arctan 1(I 22⎰-++=ππx x x分析:定积分在研究区间是关于原点对称的,又因为⎰-++=22d cos21)arctan 1(I ππx x x⎰-+++=22d )2cos 1arctan 2cos 1(ππx x x x因为x 2cos 1+为偶函数,x x2cos 1arctan +为奇函数,故由定理1知 ,0d 2cos 1220++=⎰πx x⎰=202d cos 22πx x⎰=20d cos 22πx x22 =2.3[8] 计算.d 4cos I 224⎰-=ππx x 分析:定积分研究区间]4,4[ππ-是关于原点对称的, 因为x 4cos 4为偶函数,故由定理1知,23d cos 8d cos 42I 204204πππ===⎰⎰x x x x (进行积分计算时,有x x x x n nn d cos d sin 2020⎰⎰==I ππ,且有递推公式21-I -=I n n nn 成立.) 2.4 计算.d 1)(arcsin I 232322x xx ⎰--=分析:先用凑分法,再做代换,最后利用对称性,则有 x xx d 1)(arcsin I 232322⎰--=x x darcsin )(arcsin 23232⎰-=⎰=33-2d ππt t27d 330-2ππ==⎰t t2.5 计算.d )1ln(I 22⎰-+=x e x x分析:显然积分区间关于原点对称,但)1ln(x e +既不是奇函数也不是偶函数,我们可以利用2)()(2)()()(x f x f x f x f x f --+-+=,其中2)()(x f x f -+为偶函数, 2)()(x f x f --为奇函数,把它分解成为一个奇函数和一个偶函数的和. 令)1ln()(xe xf +=,则)2ln(212)()(x x e e x f x f -++=-+,22)()(x x f x f =--所以有, ⎰-+=22d )1ln(I xe x x⎰--+++=22d )]2ln([21xe e x x x x 然而)2ln(xxe e x -++是关于x 的奇函数,2x 是关于x 的偶函数,由定理1知,⎰⎰-==202222d d 21x x x x 38= 2.6 计算.d 1I 112⎰-=x x分析:定积分在研究区间]1,1[-是关于原点对称的,又因为21x 是偶函数,由定理1知, ⎰-=112d 1I x x⎰=102d 12x x2-=然而这个答案是不正确的,事实上,由于被积函数012>x ,所以当积分存在时,其值必大于零,原因在于在区间]1,1[-上有第二类间断点0=x ,因而不能用对称性或者莱布尼茨公式计算. 小结 在定积分对称性的应用中,我们看到,这里所指的对称性是区间是否关于原点对称,而与被积函数的图像是否关于对称轴或者原点对称无关,但是与被积函数的奇偶性密切相关;另外经过奇偶函数的和差积得到的新函数的奇偶性,倍角公式,特殊公式的熟练掌握和应用也是非常重要的;最重要的是无论用公式还是用对称性来解题都要首先确定被积函数是R —可积函数.3. 对称性在二重积分计算中的应用定理2 [5][7][9] 设函数),(y x f 在D 上连续,且⎰⎰=I Dy x y x f d d ),(存在,记}0,),(|),{(1≥∈=x D y x y x D }0,),(|),{(2≥∈=y D y x y x D}0,0,),(|),{(3≥≥∈=y x D y x y x D }0,),(|),{(4≥∈=y D y x y x D(1)设D 关于轴x 对称,D y x ∈∀),(,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰2),(),(,d d ),(2),(),(,0d d ),(D Dy x f y x f y x y x f y x f y x f y x y x f(2)设D 关于y 轴对称,D y x ∈∀),(,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰1),(),(,d d ),(2),(),(,0d d ),(D Dy x f y x f y x y x f y x f y x f y x y x f(3)设D 关于原点对称,D y x ∈∀),(,()⎪⎩⎪⎨⎧=---=--=⎰⎰⎰⎰3),(),(,d d ,2),(),(,0d d ),(D Dy x f y x f y x y x f y x f y x f y x y x f(4)设D 关于直线x y =对称,D y x ∈∀),(,⎪⎩⎪⎨⎧=-==⎰⎰⎰⎰4),(),(,d d ),(2),(),(,0d d ),(D Dy x f x y f y x y x f y x f x y f y x y x f(5)设D 关于x 轴和y 轴均对称,D y x ∈∀),(⎪⎩⎪⎨⎧=-=--=--=-=⎰⎰⎰⎰3),(),(),(),(,d d ),(4),(),(),(),(,0d d ),(D Dy x f y x f y x f y x f y x y x f y x f y x f y x f y x f y x y x f 或者或者(6)(变量可轮换性)若积分区域关于z y x ,,具有轮换对称性,则[]⎰⎰⎰⎰⎰⎰⎰⎰++===DDDDy x x z f z y f y x f yx x z f y x z y f y x y x f d d ),(),(),(31d d ),(d d ),(d d ),(3.1 计算⎰⎰=I Dy x y x d d sin 其中D 由双纽线)()(222222y x a y x -=+围成. 分析:已知D 关于y 轴对称,且是关于x 的奇函数,所以0=I . 3.2[8] 计算⎰⎰++-=I Dy x zy x x y d d 22222,其中}1|),{(≤+=y x y x D分析:由于D 关于直线y x =对称,且被积函数具有性质),(),(y x f z y f -=,所以0=I . 3.3[5] 计算()⎰⎰+=I Dy x y x d d 22,其中D :122≤+y x 分析:()⎰⎰+=I Dy x y x d d 22⎰⎰++=Dy x xy y x d d 4422积分区域D 关于x 轴对称,且被积函数xy 4为y 的奇函数,所以,0d d 4=⎰⎰Dy x xy又因为在积分区域D 中y x ,的地位相同,则有⎰⎰⎰⎰=DDy x y y x x d d d d 22,所以, ⎰⎰=I Dy x y d d 52⎰⎰+=Dy x y x d )d (2522 ⎰⎰=10320d d 25r r πθ45π=3.4 计算⎰⎰+=I Dy x y x d )d (,其中D :1y x22≤+.分析:积分区域D :1y x 22≤+关于x 轴,y 轴均对称,而且被积函数关于y 和x 是偶函数, 固有 ⎰⎰+=I 3d )d (4D y x y x⎰⎰+=120d )d sin cos (4r r r r πθθθ⎰⎰+=12220)d sin cos (d 4r r r θθθπ38=3.5[5] 设D 是()()()1-1-1,1-1,1,、、为顶点的三角形区域,1D 为D 在第一象限的部分,则) (d d )sin (22=+⎰⎰--Dy x y x ye xy分析:如图4321D D D D D =,由对称性可知0d d 21=⎰⎰D D y x xy ,0d d 43=⎰⎰D D y x xy 所以0d d =⎰⎰Dy x xy .在43D D 上,22--sinye y x 是关于y 的奇函数,故有,0d d esin 4322-=⎰⎰D D -y xy x y在21D D 上 是关于x 的偶函数,所以,⎰⎰⎰⎰=+12222d d sinye 2d )d sinye (--D -y xD-y xy x y x xy3.6 计算⎰⎰++=I Dy x y x yf x d d ])(1[22,其中D 由1,1,3-===x y x y 围成. 分析:如图所示,做辅助线3x y -=的左半部分,则积分区域被分为21D D 和,其中21D 表示1D 位于x 轴上方的部分,1D 关于x 对称,2D 关于y 轴对称,由于被积函数是关于x 的奇函数,故有,0d d ])(1[222=++=I ⎰⎰D y x y x yf x 又由于)(22y x xyf +是关于y 的奇函数,故有,⎰⎰++=I 1d d ])(1[22D y x y xyf x0d d 21+=⎰⎰D y x x⎰⎰-=2001d d 2x y x x⎰--=014d 2x x52-= 小结 )(x,y f 关于x,y 的奇偶性,只能分别对一个变量来考虑,而不能将两个变量混在一起来考虑,即若区域关于x 轴对称,就要考虑)(x,y f 关于y 的奇偶性,若区域关于y 轴对称,就要考虑)(x,y f 关于x 的奇偶性,且容易看出对称性应用过程中被积函数一般比较复杂和抽象.4.对称性在三重积计算分中的应用定理3 设函数)(x,y,z f 在空间区域Ω上连续,且⎰⎰⎰Ω=I z y x x,y,z f d d d )(存在,记}0,)(|){(1≥Ω∈=Ωz x,y,z x,y,z }0,)(|){(2≥Ω∈=Ωx x,y,z x,y,z{}0)(|)(3≥Ω∈=Ωy x,y,z x,y,z ,(1)设Ω关于xoy 面对称,Ω∈∀)(x,y,z ,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰⎰⎰ΩΩ1)(),,(,d d d )(2)(),,(,0d d d )(x,y,z f z y x f z y x x,y,z f x,y,z f z y x f z y x x,y,z f(2)设Ω关于yoz 面对称,Ω∈∀)(x,y,z ,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰⎰⎰ΩΩ2)(),,(,d d d )(2)(),,(,0d d d )(x,y,z f z y x f z y x x,y,z f x,y,z f z y x f z y x x,y,z f (3)设Ω关于xoz 面对称,Ω∈∀)(x,y,z ,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰⎰⎰ΩΩ3)(),,(,d d d )(2)(),,(,0d d d )(x,y,z f z y x f z y x x,y,z f x,y,z f z y x f z y x x,y,z f (4)(变量可轮换性)若积分区域Ω关于z y x ,,具有轮换对称性,则[]⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩΩ++===z y x z,x,y f y,z,x f x,y,z f zy x z,x,y f z y x y,z,x f z y x x,y,z f d d d )()()(31d d d )(d d d )(d d d )(4.1 计算z y x z y x z y x z d d d 1)1ln(222222⎰⎰⎰Ω++++++=I ,其中Ω是球体1222≤++z y x . 分析:被积函数是z 的奇函数,而积分区域Ω关于平面xoy 对称,故有,0d d d 1)1ln(222222=++++++=I ⎰⎰⎰Ωz y x z y x z y x z 4.2 计算z y x e xd d d ⎰⎰⎰Ω=I ,其中Ω是球体1222≤++z y x . 分析:被积函数是x 的偶函数,而积分区域Ω关于平面yoz 对称, 故z y x e z y x e xxd d d 2d d d 1⎰⎰⎰⎰⎰⎰ΩΩ==I ,其中1Ω是半球体:0,1222≥≤++x z y x . 从而 , z y x e z y x e xx d d d 2d d d 1⎰⎰⎰⎰⎰⎰ΩΩ==I⎰⎰⎰=xD 1d de d 2z y x x⎰=102d )z -1(e2x xππ2=4.3 计算z y x z y x d d d )(⎰⎰⎰Ω++=I ,其中Ω是球体)0,0,0(2222≥≥≥≤++z y x R z y x . 分析:由变量的轮换性可知,z y x z z y x y z y x x d d d d d d d d d ⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ==,设)0,0(:2222≥≥-≤+y x z R y x D Z .则有,z y x z d d d 3⎰⎰⎰Ω=I⎰⎰⎰=RD Zy x z z 0d d d 3 ( 4.3.1 )z z R Rd )(3022⎰-=π443R π= 此题容易在(4.3.1)式中将z 判断为奇函数,则积分为零,但是在条件0,0,0≥≥≥z y x 下,区域不是关于平面0=z 对称的,故有以上做法,这也充分说明了,区域的对称性和被积函数的奇偶性必须同时满足才能进行积分计算.4.4 计算z y x z y x d d d )532(222⎰⎰⎰Ω++=I ,其中Ω是球体)0(2222≥≤++R R z y x . 分析:由变量的轮换性可得,z y x z z y x y z y x x d d d d d d d d d 222⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ==,设)0,0(:2222≥≥-≤+y x z R y x D Z .则有,z y x z z y x y z y x x d d d 5d d d 3d d d 2222⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ++=Iz y x z d d d 102⎰⎰⎰Ω= ⎰⎰⎰=RD Zy x z z 02d d d 20⎰-=Rz z z 0222d )R (20π385R π=4.5 计算z y x z x d d d )(2⎰⎰⎰Ω+=I ,其中Ω是球体)0(,1222≥≤++z z y x . 分析:z y x xz z x d d d )2(22⎰⎰⎰Ω++=I (xz 2关于yoz 平面对称,又是关于x 的奇函数) z y x z x d d d )(22⎰⎰⎰Ω+=(根据Ω具有轮换性,z y x z z y x x d d d d d d 22⎰⎰⎰⎰⎰⎰ΩΩ=) z y x z d d d 22⎰⎰⎰Ω=(由于条件0≥z ,2z 关于xoy 面不对称,所以不能用其偶函数的性质) =⎰⎰⎰102d d d 2ZD y x zz⎰-=1022)d (12z z zπ154π=小结 4.3和4.5充分说明当且仅当积分区域的对称性与被积函数),,(z y x f 奇偶性同时具备才能使用定理3.5.对称性在第一类曲线积分计算中的应用第一型曲线积分的奇偶性与二重积分类似. 定理4 函数),(y x f 在曲线L 上连续,s y x f Ld ),(⎰=I 存在,记}{0,),(|),(1≥∈=y L y x y x L }{0,),(|),(2≥∈=x L y x y x L}{0,0,),(|),(3≥≥∈=y x L y x y x L }{y x L y x y x L ≥∈=,),(|),(4(1)设积分曲线L 关于x 轴对称,则⎪⎩⎪⎨⎧=--=-=⎰⎰),(),(,d ),(2),(),(,0d ),(1y x f y x f s y x f y x f y x f s y x f L L(2)设积分曲线L 关于y 轴对称,则⎪⎩⎪⎨⎧=--=-=⎰⎰),(),(,d ),(2),(),(,0d ),(2y x f y x f s y x f y x f y x f s y x f L L(3)设积分曲线L 关于原点对称,则⎪⎩⎪⎨⎧=---=--=⎰⎰),(),(,d ),(2),(),(,0d ),(3y x f y x f s y x f y x f y x f s y x f L L(4)设积分曲线L 关于x y =对称,则⎪⎩⎪⎨⎧=-==⎰⎰),(),(,d ),(2),(),(,0d ),(4y x f x y f s y x f y x f x y f s y x f L L(5)设积分曲线L 关于x 轴, y 轴均对称,则⎪⎩⎪⎨⎧=-=--=--=-=⎰⎰),(),(),().(,d ),(4),(),(),(),(,0d ),(3y x f y x f y x f y x f s y x f y x f y x f y x f y x f s y x f L L或者或者5.1[4] 计算s x Ld ⎰=I ,其中L 是双纽线:)()(22222y x y x -=+.分析: 被积函数x 为偶函数,双纽线关于x 轴、y 轴均对称, 故s x s x L Ld 4d 1⎰⎰==I ,其中1L 是L 在第一象限的部分,将双纽线化为极坐标表示:θ2cos 2=r ,则1L :40,2cos πθθ≤≤=r ,θθθd 2cos 1d 'd 22=+=r r s则 22d 2cos 1cos 2cos 4d 4401===I ⎰⎰πθθθθs x L5.2 计算⎰++=I s y x xy )d 23(22,设L 为椭圆13222=+y x ,其周长为a . 分析:由于L 关于x 轴(或y 轴)对称, 且xy 是关于y (或x )的奇函数, 故有, 0xyd =⎰s ,那么 , ⎰+=I s y x )d 23(22a s 66d ==⎰5.3 计算s z y x Ld )573(⎰++=I ,已知积分曲线L :⎩⎨⎧=+=++1122y x z y x ,其周长为a . 分析:已知积分曲线L 中y x ,的位置对称,可得⎰⎰=LLs s x yd d ,所以, s z y x Ld )573(⎰++=Is z y x Ld )(5⎰++=a s L5d 5==⎰5.4 计算s x Ld 2⎰=I ,其中L 为圆周2222a z y x =++,0=++z y x .分析:由对称性知,s z s y s x LLLd d d 222⎰⎰⎰==.于是,s z y x s x LLd )(31d 2222⎰⎰++= ⎰=Ls a d 32 332a π= 5.5 计算s xy Ld ⎰=I ,其中L :2y x =上从)1,1(A -到)1,1(B 的一段弧.分析:由于L 关于x 轴对称,被积函数xy 是关于y 的奇函数,所以, 0d ==I ⎰s xy L6.[10]对称性在第二类曲线积分计算中的应用定理15[10] 设L 为xoy 平面上关于x 轴对称的一条光滑曲线弧,其方程是一双值函数,设为)(),(b x a x y y ≤≤±=.记21,L L 分别为L 位于x 轴的上半部分和下半部分,21,L L 分别在x 轴上的投影方向相反,函数()y x f ,在L 上连续,那么⎪⎩⎪⎨⎧-=-=-=⎰⎰),(),(,d ),(2),(),(,0d ),(1y x f y x f x y x f y x f y x f x y x f L L同理:设L 为xoy 平面上关于y 轴对称的一条光滑曲线弧,其方程是一双值函数,设21,L L 为分别为L 位于y 轴的左半部分和右半部分,21,L L 分别在y 轴上的投影方向相反,函数),(y x f 在L 上连续,那么⎪⎩⎪⎨⎧-=-=-=⎰⎰),(),(,d ),(2),(),(,0d ),(1y x f y x f y y x f y x f y x f y y x f L L应用口诀:“反对偶零,反对奇倍”,其中“反”指21,L L 在x (或y )轴上的投影方向相反;“对”指L 关于x (或y )轴对称;“偶”指被积函数在L 上关于y (或x )为偶函数;“零”指曲线积分的结果等于零.反对奇倍的含义类似解释.定理25[10] 设L 为xoy 平面上关于x 轴对称的一条光滑曲线弧,其方程是一双值函数,设21,L L 为分别为L 位于x 轴的上半部分和下半部分,21,L L 分别在y 轴上的投影方向相同,函数),(y x f 在L 上连续,那么⎪⎩⎪⎨⎧=--=-=⎰⎰),(),(,d ),(2),(),(,0d ),(1y x f y x f x y x f y x f y x f x y x f L L同理:设L 为xoy 平面上关于y 轴对称的一条光滑曲线弧,其方程是一双值函数,设21,L L 为分别为L 位于y 轴的右半部分和左半部分,21,L L 分别在x 轴上的投影方向相同,函数),(y x f 在L 上连续,那么⎪⎩⎪⎨⎧-=-=-=⎰⎰),(),(,d ),(2),(),(,0d ),(1y x f y x f y y x f y x f y x f y y x f L L应用口诀:“同对奇零 ,同对偶倍”,其中“同”指21,L L 在x 轴上的投影方向相同;“对”指L 关于y 轴对称;“奇”指被积函数在L 上关于x 为奇函数;“零”指曲线积分的结果等于零.同对偶倍的含义类似解释.6.1 计算x xy Ld ⎰=I ,其中L :2y x =上从A(1,-1)到B(1,1)的一段弧.分析:满足“反对奇倍”,故有 , x xy Ld ⎰=Idx 21⎰=L xy⎰=1d 2x x x54=其中,x 从点0变化到点1.小结 6.1和 5.5很相似,它们唯一的区别在于积分式子x xy Ld ⎰=I ,s xy Ld ⎰=I 的不同,其根本原因是第二类曲线积分具有方向性.6.2 计算x y x Ld ⎰=I 其中L :2y x =上从A(1,-1)到B(1,1)的一段弧.分析:满足“反对偶零”.故有0d ==I ⎰x xy L6.3 计算y y y x x y x Ld )sin (d )(222+-+=I ⎰,其中L :)0(222>=+a a y x 按逆时针方向从)0,A(a ,)0,(B a -的上半圆周.分析:y y y x x xy x y x LL Ld )sin (d 2d )(222⎰⎰⎰+-++=I(三个积分分别适合“同对偶倍”、“同对奇零”、“反对偶零”) ⎰+=I 1d )(22L x y x⎰+=02d )(2a x y x32a -= 其中, x 从点a 变化到点0.6.4[4] 计算⎰++=I ABCDAy x yx d d ,其中ABCDA 是以A(1,0)、B(0,1)、C(-1,0)、D(0,-1)为顶点的正方形正向边界线.分析:⎰++=I ABCDA y x y x d d ⎰⎰+++=ABCDAABCDA y x yy x x d d 对于第一个积分,因为曲线关于x 轴对称,且在x 轴上的投影方向相反,被积函数yx +1是y 的偶函数,所以积分为零.对于第二个积分,因为曲线关于y 轴对称,且方y 轴上的投影方向相反,被积函数yx +1是x 的偶函数,所以积分为零.7.对称性在第一类曲面积分计算中的应用第一类曲面积分的奇偶性与三重积分相似. 定理6 设函数),,(z y x f 在曲面S 中连续,⎰⎰=I Ss z y x f d ),,(存在,记{}0,),,(|),,(1≥∈=z S z y x z y x S{}0,),,(|),,(2≥∈=x S z y x z y x S{}0,),,(|),,(3≥∈=y S z y x z y x S(1)设积分曲面关于xoy 面对称,S z y x ∈∀),,(,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰),,(),,(,d ),,(2),,(),,(,0d ),,(1z y x f z y x f s z y x f z y x f z y x f s z y x f S S(2)设积分曲面关于yoz 面对称,S z y x ∈∀),,(,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰),,(),,(,d ),,(2),,(),,(,0d ),,(2z y x f z y x f s z y x f z y x f z y x f s z y x f S S(3)设积分曲面关于xoz 面对称, S z y x ∈∀),,( ,⎪⎩⎪⎨⎧=--=-=⎰⎰⎰⎰),,(),,(,d ),,(2),,(),,(,0d ),,(3z y x f z y x f s z y x f z y x f z y x f s z y x f S S(4)(变量可轮换性)若积分曲面关于z y x ,,具有轮换对称性,则[]⎰⎰⎰⎰⎰⎰⎰⎰++-===-SSSSs y x z f x z y f z y fx sy x fz s x z y f s z y fx d ),,(),,(,,31d ,,d ),,(d ,,7.1 计算⎰⎰=I Ss z d 2,其中S :2222R z y x=++.分析:由S 的轮换对称性知,⎰⎰⎰⎰⎰⎰==SSSs z s y s x d d d 222,故有,⎰⎰=I Ss z d 2⎰⎰++=Ss z y x )d (31222 ⎰⎰=Ss R d 312 434R π=7.2 计算⎰⎰++=I Ss z y x )d (,其中S 为球面2222a z y x =++上满足)0(a h h z <<≥的部分.分析:由S 的对称性知,0d d ==⎰⎰⎰⎰SSs y s x ,那么,⎰⎰++=I Ss z y x )d (⎰⎰=Ss z d⎰⎰++--=xyD y x s z z y x a d ''1222⎰⎰=xyD s a d)(22h a a -=π7.3 计算⎰⎰+=I Ss z y x )d 2(224,其中S 是闭曲面:2222=++z y x . 分析:由S 的轮换对称性知, ⎰⎰+=I Ss z y x )d 2(224 ⎰⎰+++++=Ss y x z z x y z y x]d )2()2()2([224224224⎰⎰++=Ss z y x d )(312222 ⎰⎰=Ss 4d 31ο332=7.4 计算⎰⎰=I Ss x d 2,其中S 为圆柱面:222a y x =+,介于平面0=z 和h z =之间的部分.分析:由于在S 中,x 与y 的地位是等价的,所以, ⎰⎰⎰⎰==I SSs y s x d d 22,于是, ⎰⎰⎰⎰+==I SSs y x s x )d (21d 222 ⎰⎰=Ss a d 212h a a ⋅⋅=π2212h a 3π=8. 对称性在第二类曲面积分计算中的应用定理7[10] 设∑为关于xoy 面对称的有向光滑曲面,其方程是一双值函数,设为xy D y x y x z z ∈±=),(),,((其中xy D 为∑在xoy 平面上的投影),记21,∑∑分别为位于xoy 平面的上半部分和下半部分,21,∑∑的侧关于xoy 平面相反,函数),,(z y x f 在∑上连续,那么⎪⎩⎪⎨⎧-=-=-=⎰⎰⎰⎰∑∑),,(),,(,d d ),,(2),,(),,(,0),,(1z y x f z y x f y x z y x f z y x f z y x f ds z y x f同理有:(1)设积分曲面关于xoz 面对称,∑∈∀),,(z y x ,⎪⎩⎪⎨⎧-=-=-=⎰⎰⎰⎰∑∑),,(),,(,d d ),,(2),,(),,(,0),,(1z y x f z y x f z x z y x f z y x f z y x f ds z y x f(2)设积分曲面关于yoz 面对称,∑∈∀),,(z y x ,⎪⎩⎪⎨⎧-=-=-=⎰⎰⎰⎰∑∑),,(),,(,d d ),,(2),,(),,(,0),,(1z y x f z y x f z y z y x f z y x f z y x f ds z y x f8.1 计算()⎰⎰∑++++=I 23222d d d d d d z y xyx z z x y z y x ,其中∑是球面:2222a z y x =++的外侧.分析:由∑的轮换对称性知,⎰⎰∑++=I y x z z x y z y x a d d d d d d 13⎰⎰∑=z y x a d d 33]d )d y -x -a (d d y -x -a [32222223⎰⎰⎰⎰--=xy xyD D y x y x a ⎰⎰=xyD y x a d d y -x -a 6222333326a a π⋅=π4=8.2 计算⎰⎰∑=I y x xyz d d ,其中∑是球面:1222=++z y x的外侧,位于0,0≥≥y x 的部分.分析:∑关于xoy 面对称,而xyz 是关于z 的奇函数,满足“反对奇倍”, 故有, ⎰⎰∑=I 1d d 2y x xyz⎰⎰=xyD y x xy d d y -x -1222 ⎰⎰=13320d r -1d sin r r πθθ152=其中1∑: 22y -x -1=z , }0,0,1|),{(),(22≥≥=+=∈y x y x y x D y x xy8.3[10] 计算y x z z x z y yz x d d 2d d )xz -y (d )d (22++-=I ⎰⎰∑,其中∑是锥面:221y x z +-=被平面0=z 所截得的部分,取上侧.分析:y x z z x z y yz xd d 2d d )xz -y (d )d (22++-=I ⎰⎰∑⎰⎰⎰⎰⎰⎰∑∑∑++-=y x z z x z y yz x d d 2d xz)d -(y d )d (22 ⎰⎰∑++=y x z d d 200⎰⎰+-=xyD y x y x d d )1(222 ⎰⎰-=120d )1(d 2r r r πθπ32=其中}1|),{(22≤+=y x y x D xy8.4[10] 计算⎰⎰∑++=I y x r z z x r y z y r x d d d d d d 333,其中222z y x r ++=, ∑是球面:)0(2222>=++a a z y x 的外侧.分析:根据∑的轮换对称性,可知, ⎰⎰∑=I z y zd d r33⎰⎰∑=1d d r63z y z(反对奇倍) ⎰⎰--=xyD y x a y x a d d 63222π4=8.5 设∑是球面:2222R z y x =++,在下面四组积分中,同一组的两个积分均为0的是:(C )A . ⎰⎰∑=I s x d 2, ⎰⎰∑=I z y x d d 2B . ⎰⎰∑=I s x d , ⎰⎰∑=I z y x d dC . ⎰⎰∑=I s x d , ⎰⎰∑=I z y x d d 2D . ⎰⎰∑=I s xy d , ⎰⎰∑=I z y y d d分析:由于曲面∑关于yoz 平面对称,被积函数 xy x ,关于x 为奇函数,被积函数2x 关于x 为偶函数.故有, 第一型曲面积分 0d ==I ⎰⎰∑s x , 0d ==I ⎰⎰∑s xy ,⎰⎰⎰⎰∑∑++==I s z y x s x )d (31d 22224234d 31R s R π==⎰⎰∑第二型曲面积分 0d d 2==I ⎰⎰∑z y x0d d 2d d 222222>--==I ⎰⎰⎰⎰≤+∑R z y z y z y R z y x0d d 2d d 222222>--==I ⎰⎰⎰⎰≤+∑R x y z x z x R z y y8.6 [6] 设∑是球面:1222=++z y x 的上半部分,则下列错误的是:(B )A . 0d d 2==I ⎰⎰∑z y x B . 0d d ==I ⎰⎰∑z y xC . 0d d 2==I ⎰⎰∑z y y D . 0d d ==I ⎰⎰∑z y y分析:由于曲面∑关于yoz 面对称,被积函数x 关于x 为奇函数,被积函数22,,y y x 关于x 为偶函数.0d d 2==I ⎰⎰∑z y x ,0d d ==I ⎰⎰∑z y y ,0d d 2==I ⎰⎰∑z y y0d d 2d d 222222>--==I ⎰⎰⎰⎰≤+∑R z y z y z y R z y x9.总结(1)对称的对象:积分区间对称,积分区域对称.(2)关于对称性,除关于原点和x y =对称外,都遵循关于谁对称谁不变的原则. (3)变量的轮换性是指对称的对象∑由0),,(≤z y x f 表示,若将z y x ,,的位置变换后,0),,(≤z y x f 仍然表示∑.在其他书籍和相关资料中提及的y x ,具有相同的地位,y x ,具有循环性都是这里所指的轮换性.(4)当且仅当积分区域对称性与被积函数),(y x f 奇偶性同时具备才能使用本文中提及的定理.(5)),(y x f 关于y x ,的奇偶性,只能分别对一个变量来考虑,而不能将两个变量混在一起来考虑.若关于x 轴对称,就要考虑关于y 的奇偶性,若关于y 轴对称,就要考虑关于x 的奇偶性. 若关于xoy 面对称,就要考虑被积函数关于z 的奇偶性依次类推.(6)第二类曲线积分和第二类曲面积分如果关于对称对象方向相反,那么它们的积分结论刚好与第一类曲线积分和第一类曲面积分结论相反.根据以上总结,对称性的问题便能很好的被应用,使数学积分的计算过程得到简化.参考文献:[1] 明清河著.数学分析的思想与方法[M].济南:山东大学出版社,2004.7(2006.9重印) [2] 殷锡鸣等编著.高等数学(下册)[M].上海:华东理工大学出版社,2005.2(2007.6重印)[3] 吴良森等编著.数学分析学习指导书(下册)[M].北京:高等教育出版社,2004.8[4] 费定辉,周学圣编演.吉米多维奇数学分析习题集题解(第三版)[M].济南:山东科学技术出版社,2005.1(2005.3重印)[5] 顾庆凤.关于重积分、曲线积分、曲面积分的对称性定理的应用[J].中国教育研究论丛,2006[6] 苏海军.对称性在定积分中的应用[J].四川文理学院学报(自然科学),2007.9,17(5)[7] 赵云梅,李薇. 对称性在积分中的妙用[J].红河学院学报,2005.6,3(3)[8] 常浩.对称性在积分学中的应用[J].高等数学研究,2011.3,14(2)[9] 于宁丽,王静.利用对称性计算两类区面积分时的差异问题[J].专题研究,2009.7[10] 刘福贵,鲁凯生.利用对称性计算第二类曲线积分与曲面积分的方法[J].武汉理工大学学报,2006,30(6):1069-1072[11] 西北工业大学高等数学教研室编.高等数学学习辅导:问题、解法、常见错误剖析[M].北京:科学出版社,2007[12] 魏平等编著.高等数学复习指导[M].西安:西安交通大学出版社,1999.11[13] 华罗庚著.高等数学引论[M].沈阳:科学出版社.2003[14] 朱学炎等编著.数学分析[M].北京:高等教育出版社,2007.4[15] 裴礼文.数学分析中的典型问题与方法[M].高等教育出版社,2006.4[16]邹本腾等编著.高等数学辅导[M].北京:科学技术文献出版社,1999.6数学系数学与应用数学2009级本科毕业论文Application of symmetry in the integral calculation Abstract The s ymmetry is one of the important methods to solve mathematical problems. In integral calculus, it can make the integral calculation process simplified to make full use of symmetry of integral region and the parity of integrand. This paper illustrates the application of symmetry in definite integral, multiple integrals, curve integrals, and surface integrals in the calculation through summary theorem and its nature and with the aid of examples.Key words definite integral multiple integrals curve integrals surface integrals第21页共22页。
对称性在积分计算中的应用

引言对称性是在生产、科学研究和日常生活中常会遇到的一类特殊的数学问题,它涉及到初高等数学知识的各个方面,解决这类问题往往需要综合运用各种技巧,灵活选用合理的解题途径和方法。
解决积分问题的方法多种多样,若仅限定于初等数学方法,解题往往需要较强的技巧,因此高等数学又从对称性的角度找到了便利,它是讨论积分问题的有力武器。
对称性的作用在许多工程,经济等方面也非同小可。
因此无论从考试角度及能力方面都需要对对称性进行系统的总结。
1 对称性在积分计算中的应用1.1 对称性在计算区间[],a a -上的定积分的应用性质1 对于对称区间[],a a -上的定积分,有:0()()2()()aaaf x x f x dx f x dx f x x -⎧⎪=⎨⎪⎩⎰⎰如果关于变量为奇函数如果关于变量为偶函数证明:①设()f x 为奇函数,则()f x =()f x --,故:()()()aa aaf x dx f x dx f x dx --=+⎰⎰⎰在第二个式子中令x t =-,则(1)dx dt =-,所以:原式0()(1)()aaf t dt f x dx -=--+⎰⎰()()a af t dt f x dx =-+⎰⎰0=②如果()f x 为偶函数,证明方法类似于①。
例1.1 已知()f x =36x x +为定义于闭区间[]1,1-上的函数。
求:11()f x dx -⎰。
解:因为3()6f x x x =+为定义于定义域上的奇函数,故由上面的性质可得:11()0f x dx -=⎰例1.2 设2242sin cos 1x x M dx xππ-=+⎰,2234(sin cos )N x x dx ππ-=+⎰,22234(sin cos )P x x x dx ππ-=-⎰。
则有______()A N P M << ()B M P N << ()C N M P << ()D P M N <<解:在M 中,因为被积分函数42sin cos 1x x x +是奇函数且积分区域为,22ππ⎡⎤-⎢⎥⎣⎦,因此 0M =。
积分对称性定理

曲面 1取前侧,在 yoz后半空间的部分曲面 2 取后侧,则
P x, y, z dxdy
0,
P x, y, z 关于x是偶函数,
2 P x, y, z dydz, P x, y, z 关于x是奇函数.
1
(3)设分片光滑的曲面 关于 xoz 坐标面对称,且 在 xoz 右半空间的部分 曲面 1取右侧,在 xoz 左半空间的部分曲面 2 取左侧,则
f x, y ds
L
0,
f x, y 为x的奇函数,
2 f x, y ds, f x, y 为x的偶函数. L1
(2)若分段光滑平面曲线 L 关于 x 轴对称,且 f x, y 在 L 上为连续函
数, L1 为 L 位于 x 轴上侧的弧段,则
欢迎下载
3
—
f x, y ds
L
0,
f x, y 为y的奇函数,
4
—
位于 xoy上侧 z 0的部分曲面,则
f x, y, z dS
0,
f x, y, z 为z的奇函数,
2 f x, y, z dS, f x, y, z 为z的偶函数.
1
曲面关于 yoz, xoz坐标平面对称也有类似的性质。
7、第二类曲面积分的对称性
设函数 P( x, y, z) , Q (x, y, z) , R( x, y, z) 在分片光滑的曲面 上连续,
—
f x, y dxdy
D
0,
f x, y 为x的奇函数 ,
2 f x, y dxdy, f x, y 为x的偶函数 .
D2
其中: D2 为 D 满足 x 0 的右半平面区域。 (3) 如果积分区域 D 关于原点对称, f ( x, y) 为 x, y 的奇(或偶)函
二重积分积分区域的对称性

二重积分积分区域的对称性Company number:【0089WT-8898YT-W8CCB-BUUT-202108】情形一:积分区域D 关于坐标轴对称定理4 设二元函数(,)f x y 在平面区域D 连续,且D 关于x 轴对称,则1)当(,)(,)f x y f x y -=-(即(,)f x y 是关于y 的奇函数)时,有(,)0Df x y dxdy =⎰⎰ .2)当(,)(,)f x y f x y -=(即(,)f x y 是关于y 的偶函数)时,有1(,)2(,)D D f x y dxdy f x y dxdy =⎰⎰⎰⎰ . 其中1D 是由x 轴分割D 所得到的一半区域。
例5 计算3()DI xy y dxdy =+⎰⎰,其中D 为由22y x =与2x =围成的区域。
解:如图所示,积分区域D 关于x 轴对称,且3(,)()(,)f x y xy y f x y -=-+=- 即(,)f x y 是关于y 的奇函数,由定理1有3()0D f xy y dxdy +=⎰⎰.类似地,有:定理5 设二元函数(,)f x y 在平面区域D 连续,且D 关于y 轴对称,则其中2D 是由y 轴分割D 所得到的一半区域。
例6 计算2,DI x ydxdy =⎰⎰其中D 为由22;-220y x y x y =+=+=及所围。
解:如图所示,D 关于y 轴对称,并且2(,)(,)f x y x y f x y -==,即被积分函数是关于x 轴的偶函数,由对称性定理结论有:11222220022215x D D I x ydxdy x ydxdy dx x ydxdy -+====⎰⎰⎰⎰⎰⎰. 定理6 设二元函数(,)f x y 在平面区域D 连续,且D 关于x 轴和y 轴都对称,则(1)当(,)(,)f x y f x y -=-或(,)(,)f x y f x y -=-时,有(,)0D f x y dxdy =⎰⎰ .(2)当(,)(,)(,)f x y f x y f x y -=-=时,有其中1D 为由x 轴和y 轴分割D 所的到的1/4区域。
关于利用对称性积分的问题
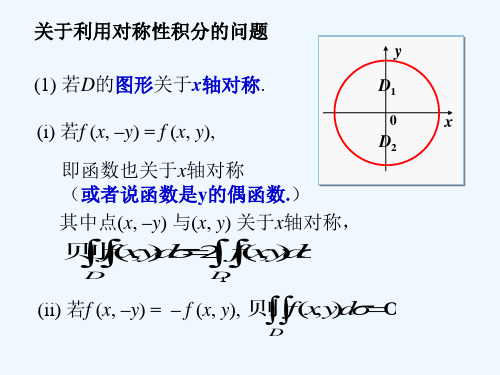
y
D2
0
x
则 f( x ,y ) d 2 f( x ,y ) d
D D 1
(ii) f (– x, y) = – f( x, y),则
f (x, y)d0
D
(3) 一般,若D关于平面上某直线l对称.
对(x, y)D1,有关于l的对称点(x1, y1)D2.
D D 1
,y ) d 0 (ii) 若f (x, –y) = – f (x, y), 则 f(x
D
(2) 若D的图形关于y轴对称. (i) 若f (– x, y) = f ( x, y). 即函数也关于y轴对称 (或者说函数是x的偶函数.) 其中点(– x, y)和 (x, y)关于y轴对称.
z为偶函数时 (ii ):当 f(x ,y ,z)关于 ____ ,
f(x ,y ,z) dv ___ f(x ,y ,z) dv 2
其中 为 在 xy 面上方的部分 . 1
1
( i ) : 当 f ( x , y , z ) 关 ____ 于 为奇 , 函 f ( x , y , z 数 ) dv 0 ; 时
z
3, 界 上述结论该怎 ? 么样呢
若f (x, y) = f (x1, y1).
则 f ( x , y ) d 2 f ( x , y ) d .
D D 1
y y=x D1 D2
0
若f (x, y)= – f (x1, y1),则
0 . f (x,y)d
D
x
3 ( 4 )若 为 R 中关 xy 于 面对称的有界 f(x , 闭 y ,z ) 区 为 上的连续 ,则 函数
关于利用对称性积分的问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 1:求积分 ∫(∫ 2x + y)2dxdy x2 + y 2 ≤1
分析: ∫(∫ 2x + y)2dxdy = ∫∫ (4x2 + y2 + 4xy)dxdy = 4 ∫∫ x2 + ∫∫ y2 + 4 ∫∫ xy 。
x2 + y 2 ≤1
x2 + y 2 ≤1
x2 + y 2 ≤1
x2 + y2 ≤1
43
L
分析:xy 关于 x 为奇函数,曲线 L 关于 Oyz 面对称。
∫ ∫ ∫ ∴ 2xyds = 0 ,原积分 = 12 ( x2 + y2 )ds = 12 ds = 12a。
L
L4 3
L
上面的结论还可推广到第二型曲面积分,但第二型曲面积分的奇偶对称性定理与第一型积分及重积分的奇偶对称性定理
相反。
D1UD2
D3UD4
D
∫∫ 而在 D3∪D4 上, f (x, y) = sin ye−x2 −y2 是关于 y 的奇函数,所以 sin ye−x2−y2dxdy = 0 。
D3UD4
∫∫ ∫∫ 在 D1∪D2 上, f (x, y) = sin ye−x2 −y2 是关于 x 的偶函数,所以 sin ye−x2−y2 dxdy = 2 sin ye−x2−y2dxdy 。因此选 A。
x2+ y2≤1
x2 + y2≤1
(-1,1)
y
∫∫ ∫∫ ∫ ∫ 所以:原积分 = 5 y2dσ = 5 (x2 + y2)dσ = 5 2π dθ 1r3dr = 5π 。
D
2D
20
0
4
D2 D1
(1,1)
例 2:设 D 是以(1,1),(-1,1)和(-1,-1)为顶点的三角形域,D1
∫∫ 为 D 在第一象限的部分。则 (xy + sin ye−x2−y2)dxdy =( )。
⎪⎩ S
S1
f (−x, y, z) = − f (x, பைடு நூலகம், z) f (−x, y, z) = f (x, y, z)
(6)
类似地,可写出关于 y 和关于 z 为奇偶函数的结果(略)。 2.轮换对称性:若积分区域 L 和 S 中 x,y,z 的地位对称,则在被积函数中互换 x,y,z,结果不变。
D3 o
x
∫∫ A.2 sin ye−x2−y2 dxdy D
B.2∫∫ xydxdy
D4
D1
D1
∫∫ C.4 (xy + sin ye−x2−y2)dxdy
D1
D.0
(-1,-1)
图1
·154·
CHINA EDUCATION RESEARCH ANALECTS
高等教育研究 — 学科探讨
分析:这里应选 A。事实上,如图 1,D=D1∪D2∪D3∪D4,由对称性知 ∫∫ xydxdy = 0, ∫∫ xydxdy = 0。∴ ∫∫ xydxdy = 0。
f (−x, y, z) = − f (x, y, z)
∫ ∫ ⎨
⎪⎩
f (x, y, z)ds = 2 f (x, y, z)ds,
L
L1
f (−x, y, z) = f (x, y, z)
(5)
对第一型曲面积分有(S1 为 S 的一半):
⎧⎪⎪∫S∫ f (x, y, z)ds = 0,
⎨
⎪∫∫ f (x, y, z)ds = 2∫∫ f (x, y, z)ds,
L
:
⎧x +
⎨ ⎩
x2
y +
+ z =1 y2 =1
中
x,y
位置对称,得
xds =
L
yds,所以 (3x + y + 2z)ds = 2 (x + y + z)ds = 2 ds = 2a。
L
L
L
L
∫ 例 4:已知曲线 L : x2 + y2 = 1,其周长为 a,求积分 (2xy + 3x2 + 4y2)ds 。
例数 35
46
18
11
16
26
10
16
4
8
4
194
%
18.0 23.7 9.3
5.7
8.2 13.4 5.1
8.2
2.1
4.1
2.1
100
2.在受伤性质和受伤部位调查中,各项运动受伤部位主要集中在踝、膝、腰、腕、指关节。四个部位占总调查量的 79.3%。
二、调查结果与分析
1.在各项运动项目损伤的发生率调查中,足球、篮球、排球、体操、田径在学生中受伤率较高。因为在部分成人高校
里,由于受场地和器材等条件限制,一般球类和田径项目开展的相对多一些,所以受伤面要广一些,其次为体操、武术、健
美操见表 1。
表 1 各项运动项目运动损伤发生率
项目 篮球 足球 排球 跳高 跳远 短跑 单杠 双杠 支撑跳跃 武术 健美操 合计
=
2∫∫
f
(x,
y,
z), (S关于Oxy对称,f
(x,
y,
−z)
=
−
f
(x,
y,
z)
⎪⎩ S
S1
类似地,可写出关于 x 和关于 y 为奇偶函数的结果(略)。(用法见例 5、例 6) 注意点:①第二型曲面积分的奇偶对称性定理与第一型积分及重积分的奇偶对称性定理相反。②第二型曲面积分的奇偶 性只能一项一项地用,即 dydz 项用曲面 S 关于 Oyz 面对称;dzdx 项用曲面 S 关于 Ozx 面对称;dxdy 项用曲面 S 关于 Oxy 面对称。不能三项一起用,而且 dydz 项只能用曲面 S 关于 Oyz 面对称,不能用关于 Ozx,Oxy 面对称。 针对这两点,下面给出两个例子加以说明。 例 5:设 S 为球面:x2+y2+z2 = R2 在下列四组积分中,同一组的两个积分均为 0 的是( )。
(4)
D
D
常用方式为
∫∫
D
f
(x)dσ
=
∫∫
D
f
( y)dσ
=
1 2
∫(∫ f
D
(x) +
f
( y))dσ
。
∫∫ ∫∫ 例如,
x2dσ = 1 (x2 + y2)dσ
x2 + y2≤1
2 x2+ y2≤1
其中(1)(2)(3)为二重积分的奇偶对称性定理,(4)称为二重积分的轮换对称性定理。对于三重积分也有类似情形。
常用方式为: ∫L f (x)ds = ∫L f ( y)ds = ∫L f (z)ds ;∫∫ f (x)ds = ∫∫ f ( y)ds = ∫∫ f (z)ds 。
S
S
S
∫ 例
3:已知积分曲线
L
:
⎧x +
⎨ ⎩
x2
y +
+ z =1 y2 =1
,其周长为
a,求积分
(3x
L
+
y
+
2z)ds 。
∫ ∫ ∫ ∫ ∫ 分析:由曲线
决此类问题。
定理一:二重积分的对称性定理
1.如果积分域 D 关于 x 轴对称,f(x,y)为 y 的奇(或偶)函数,D1 为 D 中 y ≥ 0 的部分,则:
⎧0,
f (x, − y) = − f (x, y)
∫∫
D
f (x, y)dσ
=
⎪
∫∫ ⎨ 2
⎪⎩ D1
f (x, y)dσ ,
f (x, − y) = f (x, y)
D
D1
在第一型曲线、曲面积分中,也有与重积分完全类似的对称性定理。
定理二:第一型曲线积分、曲面积分的对称性定理
1.奇偶对称性:若 f(x,y,z)关于 x 为奇函数(或偶函数),积分区域 L 或 S 关于 oyz 面对称,则对第一型曲线积分有
(L1 为 L 的一半):
⎧⎪∫L f (x, y, z)ds = 0,
x2 + y 2 ≤1
∫∫ 积分区域 D: x2 + y2 ≤ 1关于 x 轴对称,而被积函数 f ( x, y ) = xy 为 y 的奇函数,由定理 1(1)知: xydσ = 0 。
x2+ y2≤1
∫∫ ∫∫ 又积分区域 D: x2 + y2 ≤ 1关于 y = x 对称,由定理 1(4)知: x2dσ = y2dσ。
定理三:第二型曲面积分的对称性定理
若 f(x,y,z)关 z 为偶函数(或奇函数),积分区域 S 关于 Oxy 面对称,则对第二型曲面积分有:
⎧⎪⎪∫S∫ f (x, y, z)dxdy = 0, (S关于Oxy对称,f (x, y, −z) = f (x, y, z))
⎨
⎪∫∫
f
(x,
y,
z)dxdy
y2 +z2 ≤R2
1
+
⎛ ⎜ ⎝
∂x ∂y
⎞2 ⎟ ⎠
+
⎛ ⎜⎝
∂x ∂z
⎞2 ⎟⎠
dydz
>0
又曲面 S 关于 Oyz,Ozx,Oxy 面都对称,
∴ ∫∫ x2ds = 0 ,S 关于 Oyz 对称,f(x,y,z)= x2 关于 x 为偶函数。
S
∫∫ xdydz = 2 ∫∫ xdydz = 2 ∫∫ R2 − y2 − z 2 dydz > 0,S 关于 Oyz 面对称,f(x,y,z)= x 关于 x 为奇函数。
(1)
2.如果积分域 D 关于 y 轴对称,f(x,y)为 x 的奇(或偶)函数,D2 为 D 中 x ≥ 0 的部分,则:
