各类梁的弯矩剪力计算汇总表
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =m ,每跨各有一集中荷载F =,求中间支座的最大弯矩和剪力。
[解] M B 支=(-××52)+(-××5)=(-)+()=-·mV B 左=(-××5)+(-×)=(-)+(-)=-[例2] 已知三跨等跨梁l =6m ,均布荷载q =m ,求边跨最大跨中弯矩。
[解] M1=××62=·m 。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
3)四跨等跨连续梁内力和挠度系数表2-13注:同三跨等跨连续梁。
4)五跨等跨连续梁内力和挠度系数表2-14注:同三跨等跨连续梁。
各种梁的弯矩剪力计算(大全)表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5 .......资料.注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
各类梁弯矩剪力计算汇总表

12(26] + *)
学号截面简圏
截面积
A
戴面抵抗矩
W
回转半轻
W=^(RH3'bfi2)
Drl
序号戡面简图
A=Ki+
旳=
1
2
J;-H■yx
"十如十E屛e(e-历
x3-J)']
H
■粗BHUM"诂吹心讪牛心的厝疙豁
A
rfiH®+(Bib}ti
X■■-|-
'L日注l+6A十
(Bl-占M2円二
表
某一段梁上的外力情况
剪力图的特征
弯矩图的特征
无载荷11
水平直线
斜直线、^或
集中力1F
突变
r
F
转折\或\/或
Me
集中力偶’门、
突变]M e
无变化
q
均布载荷]]]][
斜直线
抛物线—或
零点
极值厂
表Байду номын сангаас
约束类型
位移边界条件
力边界条件
(约束端无集中载荷)
固定端y”
w0,0
一
简支端垢JT3
w0
M0
自由端=
一
M O'Fs0
注:力边界条件即剪力图、弯矩图在该约束处的特征。
蔽面积
常用截面几何与力学特征表
主轴的距离予
对主轴的情性矩鬣面抵抗幫
Lw
回转半程
■b
i =O.2t59ft
*=0.236A
A=-y (fr+t>i)h
(bi+2b)h
X1=
(b + 2t|)h
各类梁的弯矩剪力计算归纳表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
各类梁的弯矩剪力计算汇总表

各类梁的弯矩剪力计算汇总表表1 简单载荷下基本梁的剪力图与弯矩图lF l a -l eMsF lM e +M+laeMsF lM e +Me M lal -e M la +-lqsF +-2ql 2qlM82ql +2l lqasF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+l a l qa 2)(2-la l a 2)2(-sF 30l q 2l q注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件约束类型位移边界条件力边界条件(约束端无集中载荷)固定端=w,0=θ—简支端=w0=M自由端—=M,0=S F注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=AdA y I 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y I W = 3.i 称截面回转半径(mm ),其基本计算公式如下:A Ii =4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
各类梁的弯矩剪力计算汇总表
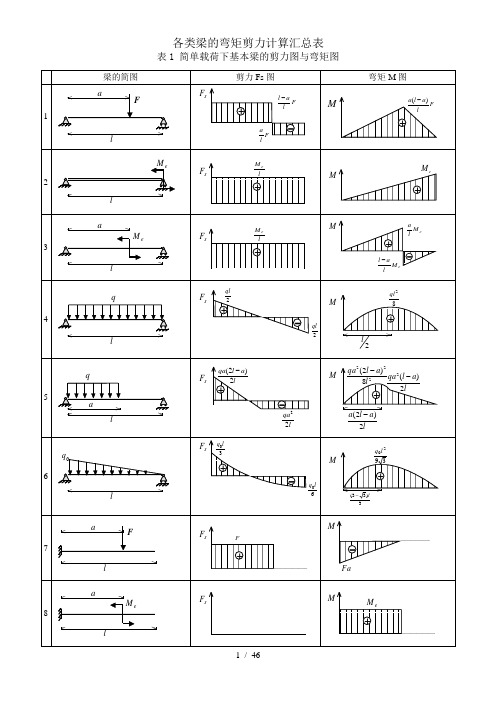
表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-53 / 464 /465 /466 /467 /468 /469 /4610 /46注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA y I 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:m axy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =m ,每跨各有一集中荷载F =,求中间支座的最大弯矩和剪力。
[解] M B 支=(-××52)+(-××5)=(-)+()=-·m V B 左=(-××5)+(-×)=(-)+(-)=-[例2] 已知三跨等跨梁l =6m ,均布荷载q =m ,求边跨最大跨中弯矩。
各类梁的弯矩剪力计算汇总表
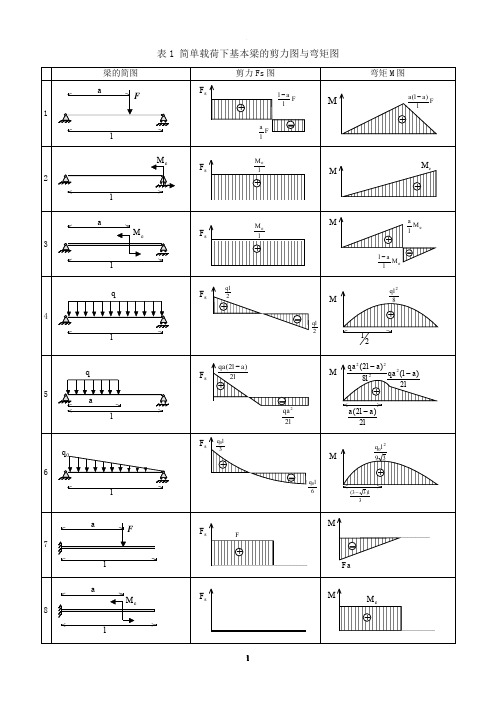
表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F l a F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lq asF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折 或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线 或零点极值表3 各种约束类型对应的边界条件约束类型 位移边界条件力边界条件(约束端无集中载荷)固定端0=w ,0=θ—简支端 0=w0=M 自由端—0=M ,0=S F注:力边界条件即剪力图、弯矩图在该约束处的特征。
3常用截面几何与力学特征表 表2-5。
4。
5。
6。
7。
8。
9注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
各类梁的弯矩剪力计算汇总表
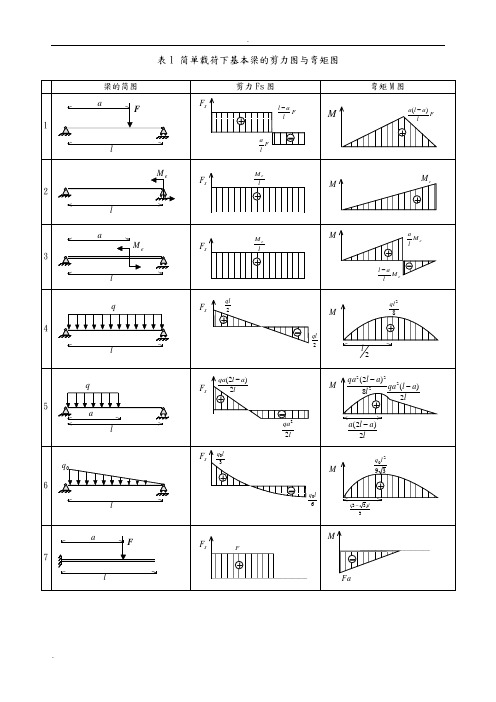
表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5 .........注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =m ,每跨各有一集中荷载F =,求中间支座的最大弯矩和剪力。
[解] M B 支=(-××52)+(-××5)=(-)+()=-·m V B 左=(-××5)+(-×)=(-)+(-)=-[例2] 已知三跨等跨梁l =6m ,均布荷载q =m ,求边跨最大跨中弯矩。
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F la F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lq asF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线 或零点极值表3 各种约束类型对应的边界条件约束类型 位移边界条件力边界条件(约束端无集中载荷)固定端0=w ,0=θ —简支端0=w0=M自由端 —0=M ,0=S F常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA y I 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW =3.i 称截面回转半径(mm ),其基本计算公式如下:AI i = 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
各类梁支反力剪力弯矩挠度计算公式一览表

各类梁支反力剪力弯矩挠度计算公式一览表一、简支梁1、支反力对于均布荷载 q 作用下的简支梁,两端支反力大小相等,均为 R = qL / 2 ,其中 L 为梁的跨度。
2、剪力距离左端为 x 处的剪力 V = qx qL / 2 (0 < x < L )3、弯矩距离左端为 x 处的弯矩 M = qx^2 / 2 qLx / 2 (0 < x < L )最大弯矩发生在跨中,Mmax = qL^2 / 84、挠度均布荷载下的挠度ω = 5qL^4 / 384EI ,其中 E 为材料的弹性模量,I 为梁截面的惯性矩。
二、悬臂梁1、支反力固定端支反力 R = qL ,支反力矩 M = qL^2 / 22、剪力距离固定端为 x 处的剪力 V = qL + qx (0 < x < L )3、弯矩距离固定端为 x 处的弯矩 M = qLx + qx^2 / 2 (0 < x < L )最大弯矩发生在固定端,Mmax = qL^2 / 24、挠度均布荷载下的挠度ω = qL^4 / 8EI三、外伸梁外伸梁的计算较为复杂,需要根据具体的荷载分布和外伸长度进行分析。
1、支反力一般通过对梁的整体受力平衡和力矩平衡方程求解得出。
2、剪力分别计算各段的剪力表达式。
3、弯矩同样分段计算弯矩表达式。
4、挠度利用叠加原理,将各段的挠度贡献相加。
四、连续梁连续梁由多个跨度组成,各跨之间通过中间支座相连。
1、支反力通过结构力学的方法,如力法、位移法等求解。
2、剪力和弯矩根据求得的支反力,计算各跨的剪力和弯矩。
3、挠度通常采用结构力学的方法或有限元分析软件进行计算。
五、变截面梁对于变截面梁,其截面特性(惯性矩I 等)沿梁长度方向发生变化。
1、支反力计算方法与等截面梁类似,但需考虑截面变化的影响。
2、剪力和弯矩采用积分的方法求解。
3、挠度计算过程较为复杂,可能需要借助数值方法或专业软件。
在实际工程中,梁的受力情况往往较为复杂,可能同时受到多种荷载的作用,如集中力、集中力偶、分布荷载等。
各类梁的弯矩剪力计算汇总表
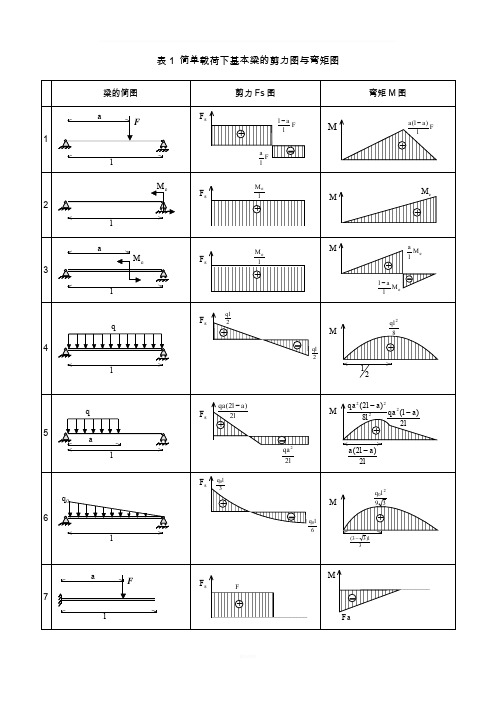
精品资料表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F l a F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lqasF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M精品资料8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线或零点极值表3 各种约束类型对应的边界条件约束类型位移边界条件力边界条件精品资料(约束端无集中载荷)固定端0=w ,0=θ —简支端0=w0=M 自由端—0=M ,0=S F注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5精品资料精品资料精品资料精品资料精品资料精品资料精品资料______________________________________________________________________________________________________________精品资料注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=A dA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW =3.i 称截面回转半径(mm ),其基本计算公式如下:AI i = 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
各类梁的弯矩剪力计算汇总表-剪力计算公式一览表

表 1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)1)简支梁的反力、剪力、弯矩、挠度表2-62)悬臂梁的反力、剪力、弯矩和挠度表2-73)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-84)两端固定梁的反力、剪力、弯矩和挠度表2-95 )外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14 )1)二跨等跨梁的内力和挠度系数表2-11均布荷载 q =11.76kN/m ,每跨各有一集中荷载 F =29.4kN ,求中间支座的最大弯矩和剪力。
M B 支=(-0.125×11.76×52)+(- 0.188×29.4×5)=(- 36.75)+( -27.64)=- 64.39kN ·mV B 左=(-0.625×11.76×5)+(- 0.688×29.4)=(- 36.75)+(- 20.23)=- 56.98kN[例 2] 已知三跨等跨梁 l = 6m ,均布荷载 q =11.76kN/m ,求边跨最大跨中弯矩 [解 ] M1 = 0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表 2-12注: 1.在均布荷载作用下: M =表中系数×4ql 2;V =表中系数× ql ; w 表中系数ql。
100EI Fl 3Fl ;V =表中系数× F ; w 表中系数 Fl。
100EI2.在集中荷载作用下: M =表中系数×[例 1] 已知二跨等跨梁 l =5m ,[解]f ⅜ 跨内帰大 支座弯矩 弯矩荷載图VCXAflM 2-0.5500 -O I OSo-O (O 5Q0.4500.550(Jf≡¾-0,050 -0.500 D.0751-0.050 -0.050 -0,0500,5000.050UHiD跨度中点挠度-0.45(J 0,990 -0.625 0.990L A 4-L073L054-0÷117-0.033 0.383D-0.C67 0.0170.433f t J÷175 -0.150一(L 1500.350-0,075 -0.0750.425ΓJ⅛3.175 -0.075-0.075-0,07S0.050-0.3131 0,677 -0.313λ1620.1370 + 175-o r osα 0,325-0.617-0.4170*033 0.5β3 0.033-0.5670.0830.5730.365 -0.208-O.on-0,017 0.885 -0.313 0.104-0.650 0.500"-W0.650-0,5750 0.575-0.425E146 1.6150.208 1.146- 0,075- 0,50C 0.5000.0750.075-0Λ69-0.9371U46L 615-0.469-0,675-0.375 0,6250.0500.0500.9900.677 L 0.3124 注:1.在均布荷载作用下:M =表中系数× ql2;V=表中系数× ql;w表中系数ql 100EI2.在集中荷载作用下:M =表中系数× Fl;V=表中系数× F;w 表中系数Fl。
各类梁弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图1d注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件2d注:力边界条件即剪力图、弯矩图在该约束处的特征。
3d常用截面几何与力学特征表表2-54d5d6d7d8d9d10d注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
各类梁的弯矩剪力计算汇总表

在此输入你的公司名称LOGO各类梁的弯矩剪力计算汇总表表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=A dA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW =3.i 称截面回转半径(mm ),其基本计算公式如下:AI i = 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表1 简单载荷下基本梁的剪力图与弯矩图
梁的简图
剪力Fs 图
弯矩M 图
1
l
a
F
s
F F l a F l a
l -+
-
F l
a l a )
(-+
M
2
l e
M
s
F l
M e +
M
e
M +
3
l
a
e
M
s
F l
M e +
M
e M l
a
l -e M l
a +
-
4
l
q
s
F +
-2
ql 2
ql
M
8
2ql +
2
l
5
l
q a
s
F +
-l
a l qa 2)
2(-l
qa 22
M
2
228)2(l a l qa -+
l
a l qa 2)
(2
-l
a l a 2)2(-
6
l
q
s
F +
-3
0l q 6
0l q
M
3
920l q +
3
)33(l
-
7
a
F
l
s
F F
+
Fa
-M
8
a
l
e
M
s
F
+
e
M M
9
l
q
s F ql
+
M
2
2ql -
10
l
q
s
F 2
l q +
M
6
20l q -
注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁
表2 各种载荷下剪力图与弯矩图的特征
某一段梁上的外力情况 剪力图的特征
弯矩图的特征
无载荷
水平直线
斜直线
或
集中力 F
突变 F 转折
或
或
集中力偶
e
M 无变化 突变
e M
均布载荷
q
斜直线
抛物线 或
零点
极值
表3 各种约束类型对应的边界条件
约束类型 位移边界条件
力边界条件
(约束端无集中载荷)
固定端
0=w ,0=θ
—
简支端
0=w
0=M 自由端
—
0=M ,0=S F
注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5
注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=
A
dA y I 2
2.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max
y I W =
3.i 称截面回转半径(mm ),其基本计算公式如下:A
I
i =
4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)
(1)简支梁的反力、剪力、弯矩、挠度表2-6
(2)悬臂梁的反力、剪力、弯矩和挠度表2-7
(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8
(4)两端固定梁的反力、剪力、弯矩和挠度表2-9
(5)外伸梁的反力、剪力、弯矩和挠度表2-10
3.等截面连续梁的内力及变形表
(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)
1)二跨等跨梁的内力和挠度系数表2-11
注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI
w 100ql 表中系数4
⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EI
w 100Fl 表中系数3
⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)
=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)
=(-36.75)+(-20.23)=-56.98kN
[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表2-12
注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI
w 100ql 表中系数4
⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EI
w 100Fl 表中系数3⨯=。
3)四跨等跨连续梁内力和挠度系数 表2-13
注:同三跨等跨连续梁。
4)五跨等跨连续梁内力和挠度系数表2-14
注:同三跨等跨连续梁。
(2)不等跨连续梁的内力系数(表2-15、表2-16)
1)二不等跨梁的内力系数表2-15
注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max)、(V max)表示它为相应跨内的最大内力。
2)三不等跨梁内力系数表2-16
注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max)、(V max)为荷载在最不利布置时的最大内力。
4.双向板在均布荷载作用下的内力及变形系数表(表2-17~表2-22) 符号说明如下:
刚度 )1(1223
υ-=Eh K
式中 E ——弹性模量;
h ——板厚; ν——泊松比;
ω、ωmax ——分别为板中心点的挠度和最大挠度;
M x ——为平行于l x 方向板中心点的弯矩; M y ——为平行于l y 方向板中心点的弯矩; M x 0——固定边中点沿l x 方向的弯矩; M y 0——固定边中点沿l y 方向的弯矩。
正负号的规定:
弯矩——使板的受荷面受压者为正; 挠度——变位方向与荷载方向相同者为正。
四边简支 表2-17
三边简支,一边固定 表2-18
两边简支,两边固定表2-19
一边简支,三边固定表2-20
四边固定表2-21
两边简支,两边固定表2-22
5.拱的内力计算表(表2-23)
各种荷载作用下双铰抛物线拱计算公式表2-23
注:表中的K为轴向力变形影响的修正系数。
(1)无拉杆双铰拱
1)在竖向荷载作用下的轴向力变形修正系数
式中I c——拱顶截面惯性矩;
A c——拱顶截面面积;
A——拱上任意点截面面积。
当为矩形等宽度实腹式变截面拱时,公式I=I c/cosθ所代表的截面惯性矩变化规律相当于下列的截面面积变化公式:
此时,上式中的n可表达成如下形式:
下表中列出了矩形等宽度实腹式变截面拱的n值。
f/l 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 n 1.67 1.59 1.51 1.43 1.36 1.29 1.23 1.17 1.12 2)在水平荷载作用下的轴向力变形修正系数,近似取
K=1
(2)带拉杆双铰拱
1)在竖向荷载作用下的轴向力变形修正系数
式中E——拱圈材料的弹性模量;
E1——拉杆材料的弹性模量;
A1——拉杆的截面积。
2)在水平荷载作用下的轴向力变形修正系数(略去拱圈轴向力变形影响)
式中f——为矢高;
l——为拱的跨度。
6.刚架内力计算表
内力的正负号规定如下:
V——向上者为正;
H——向内者为正;
M——刚架中虚线的一面受拉为正。
(1)“┌┐”形刚架内力计算(表2-24、表2-25)
“┌┐”形刚架内力计算表(一)表2-34
“┌┐”形刚架内力计算表(二)表2-35
(2)“”形刚架的内力计算(表2-26)“”形刚架的内力计算表表2-26。
