(完整版)2020年高考理科数学《圆锥曲线》题型归纳与训练,推荐文档
2020高考—圆锥曲线(解答+答案)

2020年高考——圆锥曲线1.(20全国Ⅰ文21)(12分)已知A 、B 分别为椭圆E :2221x y a+=(a >1)的左、右顶点,G 为E 的上顶点,8AG GB ⋅=,P 为直线x =6上的动点,PA 与E 的另一交点为C ,PB 与E 的另一交点为D . (1)求E 的方程; (2)证明:直线CD 过定点.2.(20全国Ⅰ理20)(12分)已知A 、B 分别为椭圆E :2221x y a+=(a >1)的左、右顶点,G 为E 的上顶点,8AG GB ⋅=,P 为直线x =6上的动点,PA 与E 的另一交点为C ,PB 与E 的另一交点为D . (1)求E 的方程; (2)证明:直线CD 过定点.3.(20全国Ⅱ文19)(12 分)已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴重直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |.(1)求C 1的离心率;(2)若C 1的四个顶点到C 2的准线距离之和为12,求C 1与C 2的标准方程.4.(20全国Ⅱ理19)(12分)已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |. (1)求C 1的离心率;(2)设M 是C 1与C 2的公共点,若|MF |=5,求C 1与C 2的标准方程.5.(20全国Ⅲ文21)(12分)已知椭圆222:1(05)25x y C m m +=<<,A ,B 分别为C 的左、右顶点. (1)求C 的方程;(2)若点P 在C 上,点Q 在直线6x =上,且||||BP BQ =,BP BQ ⊥,求APQ △的面积.6.(20全国Ⅲ理20)(12分)已知椭圆222:1(05)25x y C m m+=<<,A ,B 分别为C 的左、右顶点. (1)求C 的方程;(2)若点P 在C 上,点Q 在直线6x =上,且||||BP BQ =,BP BQ ⊥,求APQ △的面积.7.(20新高考Ⅰ22)(12分)已知椭圆C :22221(0)x y a b a b +=>>的离心率为2,且过点A (2,1).(1)求C 的方程:(2)点M ,N 在C 上,且AM ⊥AN ,AD ⊥MN ,D 为垂足.证明:存在定点Q ,使得|DQ |为定值.8.(20天津18)(本小题满分15分)已知椭圆22221(0)x y a b a b+=>>的一个顶点为(0,3)A -,右焦点为F ,且||||OA OF =,其中O 为原点.(Ⅰ)求椭圆的方程;(Ⅱ)已知点C 满足3OC OF =,点B 在椭圆上(B 异于椭圆的顶点),直线AB 与以C 为圆心的圆相切于点P ,且P 为线段AB 的中点.求直线AB 的方程.9.(20浙江21)(本题满分15分)如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C 与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于点M (B ,M 不同于A ). (Ⅰ)若116p =,求抛物线2C 的焦点坐标; (Ⅱ)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值.10.(20江苏18)(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B .(1)求12AF F △的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ⋅的最小值;(3)设点M 在椭圆E 上,记OAB △与MAB △的面积分别为S 1,S 2,若213S S =,求点M 的坐标.11.(20北京20)(本小题15分)已知椭圆2222:1x y C a b+=过点(2,1)A --,且2a b =.(Ⅰ)求椭圆C 的方程:(Ⅱ)过点(4,0)B -的直线l 交椭圆C 于点,M N ,直线,MA NA 分别交直线4x =-于点,P Q .求||||PB BQ 的值.参考答案:1.解:(1)由题设得(,0),(,0),(0,1)A a B a G -.则(,1)AG a =,(,1)GB a =-.由8AG GB ⋅=得218a -=,即3a =.所以E 的方程为2219x y +=.(2)设1122(,),(,),(6,)C x y D x y P t .若0t ≠,设直线CD 的方程为x my n =+,由题意可知33n -<<. 由于直线PA 的方程为(3)9t y x =+,所以11(3)9ty x =+.直线PB 的方程为(3)3t y x =-,所以22(3)3ty x =-.可得12213(3)(3)y x y x -=+.由于222219x y +=,故2222(3)(3)9x x y +-=-,可得121227(3)(3)y y x x =-++, 即221212(27)(3)()(3)0m y y m n y y n ++++++=.①将x my n =+代入2219xy +=得222(9)290m y mny n +++-=.所以212122229,99mn n y y y y m m -+=-=-++. 代入①式得2222(27)(9)2(3)(3)(9)0m n m n mn n m +--++++=. 解得3n =-(舍去),32n =. 故直线CD 的方程为32x my =+,即直线CD 过定点3(,0)2. 若0t =,则直线CD 的方程为0y =,过点3(,0)2.综上,直线CD 过定点3(,0)2.2.解:(1)由题设得A (–a ,0),B (a ,0),G (0,1).则(,1)AG a =,GB =(a ,–1).由AG GB ⋅=8得a 2–1=8,即a =3.所以E 的方程为29x +y 2=1.(2)设C (x 1,y 1),D (x 2,y 2),P (6,t ).若t ≠0,设直线CD 的方程为x =my +n ,由题意可知–3<n <3. 由于直线PA 的方程为y =9t (x +3),所以y 1=9t (x 1+3).直线PB 的方程为y =3t (x –3),所以y 2=3t(x 2–3).可得3y 1(x 2–3)=y 2(x 1+3).由于222219x y +=,故2222(3)(3)9x x y +-=-,可得121227(3)(3)y y x x =-++, 即221212(27)(3)()(3)0.m y y m n y y n ++++++=①将x my n =+代入2219xy +=得222(9)290.m y mny n +++-=所以12229mn y y m +=-+,212299n y y m -=+.代入①式得2222(27)(9)2(3)(3)(9)0.m n m n mn n m +--++++= 解得n =–3(含去),n =32.故直线CD 的方程为3=2x my +,即直线CD 过定点(32,0). 若t =0,则直线CD 的方程为y =0,过点(32,0).综上,直线CD 过定点(32,0).3.解:(1)由已知可设2C 的方程为24y cx =,其中c =不妨设,A C 在第一象限,由题设得,A B 的纵坐标分别为2b a ,2b a -;,C D 的纵坐标分别为2c ,2c -,故22||b AB a=,||4CD c =.由4||||3CD AB =得2843b c a=,即2322()c c a a ⨯=-,解得2c a =-(舍去),12c a =.所以1C 的离心率为12.(2)由(1)知2a c =,b =,故22122:143x y C c c+=,所以1C 的四个顶点坐标分别为(2,0)c ,(2,0)c -,),(0,),2C 的准线为x c =-. 由已知得312c c c c +++=,即2c =.所以1C 的标准方程为2211612x y +=,2C 的标准方程为28y x =.4.解:(1)由已知可设2C 的方程为24y cx =,其中c =不妨设,A C 在第一象限,由题设得,A B 的纵坐标分别为2b a ,2b a -;,C D 的纵坐标分别为2c ,2c -,故22||b AB a=,||4CD c =.由4||||3CD AB =得2843b c a=,即2322()c c a a ⨯=-,解得2c a =-(舍去),12c a =.所以1C 的离心率为12.(2)由(1)知2a c =,b =,故22122:143x y C c c+=,设00(,)M x y ,则220022143x y c c +=,2004y cx =,故20024143x x c c+=.①由于2C 的准线为x c =-,所以0||MF x c =+,而||5MF =,故05x c =-,代入①得22(5)4(5)143c c c c --+=,即2230c c --=,解得1c =-(舍去),3c =. 所以1C 的标准方程为2213627x y +=,2C 的标准方程为212y x =.5.解:(1)由题设可得54=,得22516m =,所以C 的方程为221252516x y +=. (2)设(,),(6,)P P Q P x y Q y ,根据对称性可设0Q y >,由题意知0P y >, 由已知可得(5,0)B ,直线BP 的方程为1(5)Qy x y =--,所以||BP y =,||BQ =, 因为||||BP BQ =,所以1P y =,将1P y =代入C 的方程,解得3P x =或3-. 由直线BP 的方程得2Q y =或8.所以点,P Q 的坐标分别为1122(3,1),(6,2);(3,1),(6,8)P Q P Q -.11||PQ 11PQ 的方程为13y x =,点(5,0)A -到直线11PQ,故11APQ △的面积为1522=. 22||PQ =22P Q 的方程为71093y x =+,点A 到直线22P Q的距离为26,故22AP Q △的面积为152262⨯=. 综上,APQ △的面积为52.6.解:(1)由题设可得54=,得22516m =, 所以C 的方程为221252516x y +=. (2)设(,),(6,)P P Q P x y Q y ,根据对称性可设0Q y >,由题意知0P y >,由已知可得(5,0)B ,直线BP 的方程为1(5)Qy x y =--,所以||BP y =,||BQ =, 因为||||BP BQ =,所以1P y =,将1P y =代入C 的方程,解得3P x =或3-. 由直线BP 的方程得2Q y =或8.所以点,P Q 的坐标分别为1122(3,1),(6,2);(3,1),(6,8)P Q P Q -.11||PQ 11PQ 的方程为13y x =,点(5,0)A -到直线11PQ 的距离为2,故11APQ △的面积为1522=.22||PQ =22P Q 的方程为71093y x =+,点A 到直线22P Q故22AP Q △的面积为1522=. 综上,APQ △的面积为52.7.解:(1)由题设得22411a b +=,22212a b a -=,解得26a =,23b =. 所以C 的方程为22163x y +=. (2)设11(,)M x y ,22(,)N x y .若直线MN 与x 轴不垂直,设直线MN 的方程为y kx m =+,代入22163x y +=得222(12)4260k x kmx m +++-=. 于是2121222426,1212km m x x x x k k -+=-=++.①由AM AN ⊥知0AM AN ⋅=,故1212(2)(2)(1)(1)0x x y y --+--=, 可得221212(1)(2)()(1)40k x x km k x x m ++--++-+=.将①代入上式可得22222264(1)(2)(1)401212m kmk km k m k k-+---+-+=++.整理得(231)(21)0k m k m +++-=.因为(2,1)A 不在直线MN 上,所以210k m +-≠,故2310k m ++=,1k ≠.于是MN 的方程为21()(1)33y k x k =--≠. 所以直线MN 过点21(,)33P -. 若直线MN 与x 轴垂直,可得11(,)N x y -.由0AM AN ⋅=得1111(2)(2)(1)(1)0x x y y --+---=. 又2211163x y +=,可得2113840x x -+=.解得12x =(舍去),123x =. 此时直线MN 过点21(,)33P -. 令Q 为AP 的中点,即41(,)33Q . 若D 与P 不重合,则由题设知AP 是Rt ADP △的斜边,故1||||2DQ AP ==. 若D 与P 重合,则1||||2DQ AP =. 综上,存在点41(,)33Q ,使得||DQ 为定值.8.(Ⅰ)解:由已知可得3b =.记半焦距为c ,由||||OF OA =可得3c b ==.又由222a b c =+,可得218a =.所以,椭圆的方程为221189x y +=. (Ⅱ)解:因为直线AB 与以C 为圆心的圆相切于点P ,所以AB CP ⊥.依题意,直线AB 和直线CP 的斜率均存在.设直线AB 的方程为3y kx =-.由方程组223,1,189y kx x y =-⎧⎪⎨+=⎪⎩消去y ,可得()2221120k x kx +-=,解得0x =,或21221k x k =+.依题意,可得点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭.因为P 为线段AB 的中点,点A 的坐标为(0,3)-,所以点P 的坐标为2263,2121k k k -⎛⎫ ⎪++⎝⎭.由3OC OF =,得点C 的坐标为(1,0),故直线CP 的斜率为2230216121k k k --+-+,即23261k k -+.又因为AB CP ⊥,所以231261k k k ⋅=--+,整理得22310k k -+=,解得12k =,或1k =. 所以,直线AB 的方程为132y x =-,或3y x =-.9.(Ⅰ)由116p =得2C 的焦点坐标是1(,0)32. (Ⅱ)由题意可设直线:(0,0)l x my t m t =+≠≠,点00(,)A x y .将直线l 的方程代入椭圆221:12x C y +=得222(2)220m y mty t +++-=, 所以点M 的纵坐标22M mt y m =-+. 将直线l 的方程代入抛物线22:2C y px =得2220y pmy pt --=,所以02M y y pt =-,解得202(2)p m y m+=, 因此22022(2)p m x m+=. 由220012x y +=得2421224()2()160m m p m m =+++≥,所以当m,t =时,p.10.解:(1)椭圆22:143x y E +=的长轴长为2a ,短轴长为2b ,焦距为2c , 则2224,3,1a b c ===.所以12AF F △的周长为226a c +=.(2)椭圆E 的右准线为4x =.设(,0),(4,)P x Q y ,则(,0),(4,)OP x QP x y ==--,2(4)(2)44,OP QP x x x ⋅=-=--≥-在2x =时取等号.所以OP QP ⋅的最小值为4-.(3)因为椭圆22:143x y E +=的左、右焦点分别为12,F F ,点A 在椭圆E 上且在第一象限内,212AF F F ⊥, 则123(1,0),(1,0),(1,)2F F A -. 所以直线:3430.AB x y -+= 设(,)M x y ,因为213S S =,所以点M 到直线AB 距离等于点O 到直线AB 距离的3倍. 由此得|343||30403|355x y -+⨯-⨯+=⨯, 则34120x y -+=或3460x y --=. 由2234120,143x y x y -+=⎧⎪⎨+=⎪⎩得2724320x x ++=,此方程无解; 由223460,143x y x y --=⎧⎪⎨+=⎪⎩得271240x x --=,所以2x =或27x =-. 代入直线:3460l x y --=,对应分别得0y =或127y =-. 因此点M 的坐标为(2,0)或212(,)77--.11.。
圆锥曲线十大题型全归纳

目录圆锥曲线十大题型全归纳题型一弦的垂直平分线问题 (2)题型二动弦过定点的问题 (3)题型三过已知曲线上定点的弦的问题 (4)题型四共线向量问题 (5)题型五面积问题 (7)题型六弦或弦长为定值、最值问题 (10)题型七直线问题 (14)题型八轨迹问题 (16)题型九对称问题 (19)题型十存在性问题 (21)圆锥曲线题型全归纳题型一:弦的垂直平分线问题例题1、过点T(-1,0)作直线l 与曲线N :2y x =交于A 、B 两点,在x 轴上是否存在一点E(0x ,0),使得ABE ∆是等边三角形,若存在,求出0x ;若不存在,请说明理由。
题型二:动弦过定点的问题例题2、已知椭圆C :22221(0)x y a b a b+=>>的离心率为32,且在x 轴上的顶点分别为A 1(-2,0),A 2(2,0)。
(I )求椭圆的方程;(II )若直线:(2)l x t t =>与x 轴交于点T,点P 为直线l 上异于点T 的任一点,直线PA 1,PA 2分别与椭圆交于M 、N 点,试问直线MN 是否通过椭圆的焦点?并证明你的结论题型三:过已知曲线上定点的弦的问题例题4、已知点A 、B 、C 是椭圆E :22221x y a b+= (0)a b >>上的三点,其中点A (23,0)是椭圆的右顶点,直线BC 过椭圆的中心O ,且0AC BC =,2BC AC =,如图。
(I)求点C 的坐标及椭圆E 的方程;(II)若椭圆E 上存在两点P 、Q ,使得直线PC 与直线QC 关于直线3x =对称,求直线PQ 的斜率。
题型四:共线向量问题1:如图所示,已知圆M A y x C ),0,1(,8)1(:22定点=++为圆上一动点,点P 在AM 上,点N 在CM 上,且满足N AM NP AP AM 点,0,2=⋅=的轨迹为曲线E.I )求曲线E 的方程;II )若过定点F (0,2)的直线交曲线E 于不同的两点G 、H (点G 在点F 、H 之间),且满足FH FG λ=,求λ的取值范围.2:已知椭圆C 的中心在坐标原点,焦点在x 轴上,它的一个顶点恰好是抛物线214y x =的焦点,离心率为5.(1)求椭圆C 的标准方程;(2)过椭圆C 的右焦点作直线l 交椭圆C 于A 、B 两点,交y 轴于M 点,若1MA AF λ=,2MB BF λ= ,求证:1210λλ+=-.题型五:面积问题例题1、已知椭圆C :12222=+by a x (a >b >0)的离心率为,36短轴一个端点到右焦点的距离为3。
2020年高考数学真题汇编10 圆锥曲线 理( 解析版)

2020高考真题分类汇编:圆锥曲线一、选择题1.【2020高考真题浙江理8】如图,F 1,F 2分别是双曲线C :22221x y a b-=(a,b >0)的左、右焦点,B 是虚轴的端点,直线F 1B 与C 的两条渐近线分别交于P,Q 两点,线段PQ 的垂直平分线与x 轴交与点M ,若|MF 2|=|F 1F 2|,则C 的离心率是A.33 B 。
6223【答案】B【解析】由题意知直线B F 1的方程为:b x c b y +=,联立方程组⎪⎪⎩⎪⎪⎨⎧=-+=0,b y a x b x cb y 得点Q ),(a c bc a c ac --,联立方程组⎪⎪⎩⎪⎪⎨⎧=++=0,b y a x b x cb y 得点P ),(ac bc a c ac ++-,所以PQ 的中点坐标为),(222b c b c a ,所以PQ 的垂直平分线方程为:)(222bca xbc b c y --=-,令0=y ,得)1(22b a c x +=,所以c ba c 3)1(22=+,所以2222222a cb a -==,即2223c a =,所以26=e 。
故选B2.【2020高考真题新课标理8】等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B 两点,43AB =;则C 的实轴长为( )()A 2 ()B 22()C 4 ()D 8【答案】C【解析】设等轴双曲线方程为)0(22>=-m m y x ,抛物线的准线为4-=x ,由34=AB ,则32=A y ,把坐标)32,4(-代入双曲线方程得4121622=-=-=y x m ,所以双曲线方程为422=-y x ,即14422=-y x ,所以2,42==a a ,所以实轴长42=a ,选C. 3.【2020高考真题新课标理4】设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32ax =上一点,12PF F ∆是底角为30o 的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34 ()D 45【答案】C【解析】因为12PF F ∆是底角为30o 的等腰三角形,则有PF F F 212=,,因为2130=∠F PF ,所以0260=∠D PF ,0230=∠DPF ,所以21222121F F PF D F ==,即c c c a =⨯=-22123,所以c a 223=,即43=a c ,所以椭圆的离心率为43=e ,选C.4.【2020高考真题四川理8】已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点0(2,)M y 。
(精校版)高考圆锥曲线题型归类总结

(直打版)高考圆锥曲线题型归类总结(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)高考圆锥曲线题型归类总结(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)高考圆锥曲线题型归类总结(word版可编辑修改)的全部内容。
)直接法:直接利用条件建立之间的关系;和直线的距离之和等于),向圆作两条切线的距离比它到直线的距离小于M:和⊙:都外切,则动圆圆心的轨迹为动点依赖于另一动点的变化而变化,并且又在某已知曲线上,则可先用的代数式表示,再将代入已知曲线得要求的轨迹方程是抛物线上任一点,定点为,分所成的比为参数法:当动点坐标之间的关系不易直接找到,也没有相关动点可用时均用一中间变量过抛物线的焦点作直线交抛物线于题型七:(直线与圆锥曲线常规解题方法)一、设直线与方程;(提醒:①设直线时分斜率存在与不存在;②设为y=kx+b 与x=my+n 的区别)二、设交点坐标;(提醒:之所以要设是因为不去求出它,即“设而不求”)三、联立方程组;四、消元韦达定理;(提醒:抛物线时经常是把抛物线方程代入直线方程反而简单)五、根据条件重转化;常有以下类型:①“以弦AB 为直径的圆过点0”(提醒:需讨论K 是否存在)⇔OA OB ⊥⇔121K K ∙=-⇔0OA OB ∙=⇔12120x x y y += ②“点在圆内、圆上、圆外问题”“直角、锐角、钝角问题” “向量的数量积大于、等于、小于0问题”⇔⇔ >0;⇔1212x x y y + ③“等角、角平分、角互补问题” 斜率关系(或);⇔120K K +=12K K = ④“共线问题”(如: 数的角度:坐标表示法;形的角度:距离转化法);AQ QB λ=⇔(如:A 、O 、B 三点共线直线OA 与OB 斜率相等);⇔ ⑤“点、线对称问题” 坐标与斜率关系;⇔ ⑥“弦长、面积问题”转化为坐标与弦长公式问题(提醒:注意两个面积公式的合理选择);⇔六、化简与计算;七、细节问题不忽略;①判别式是否已经考虑;②抛物线问题中二次项系数是否会出现0。
2020年高考理科数学一轮复习题型(4份+大题+详细答案)圆锥曲线及其性质

2020年高考理科数学一轮复习题型归纳与变式演练《抛物线及其性质》【题型一】:抛物线的标准方程 【题型二】:抛物线定义的理解 【题型三】:抛物线定义的应用 【题型四】:与抛物线有关的综合问题 【题型一】:抛物线的标准方程例1.求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程: (1)过点(3,2)-;(2)焦点在直线l :240x y --=上【思路点拨】从方程形式看,求抛物线的标准方程仅需确定一次项系数;从实际分析,一般需结合图形确定开口方向和一次项系数两个条件,否则,应展开相应的讨论【解析】(1)∵点(3,2)-在第二象限,∴抛物线开口方向上或者向左当抛物线开口方向左时,设所求的抛物线方程为22y px =-(0p >), ∵过点(3,2)-,∴222(3)p =-⋅-,∴23p =,∴243y x =-,当抛物线开口方向上时,设所求的抛物线方程为22x py =(0p >), ∵过点(3,2)-,∴2322p =⨯,∴94p =,∴292x y =,∴所求的抛物线的方程为243y x =-或292x y =,对应的准线方程分别是13x =,98y =-.(2)令0x =得2y =-,令0y =得4x =,∴抛物线的焦点为(4,0)或(0,2)- 当焦点为(4,0)时,42p=,∴8p =, 此时抛物线方程216y x =;焦点为(0,2)-时,22p=,∴4p =, 此时抛物线方程为28x y =-∴所求的抛物线的方程为216y x =或28x y =-, 对应的准线方程分别是4x =-,2y =.【总结升华】这里易犯的错误就是缺少对开口方向的讨论,先入为主,设定一种形式的标准方程后求解,以致失去一解.求抛物线的标准方程关键是根据图象确定抛物线开口方向,选择适当的方程形式,准确求出焦参数P.举一反三:【变式1】分别求满足下列条件的抛物线的标准方程. (1)焦点为F(4,0);(2)准线为1y 2=- ;(3)焦点到原点的距离为1; (4)过点(1,-2); (5)焦点在直线x-3y+6=0上.【解析】(1)所求抛物线的方程为y 2=16x ; (2)所求抛物线的标准方程为x 2=2y ; (3)所求抛物线的方程y 2=±4x 或x 2=±4y ; (4)所求抛物线的方程为24y x =或212x y =-; (5)所求抛物线的标准方程为y 2=-24x 或x 2=8y.【变式2】已知抛物线的顶点在原点,焦点在x 轴负半轴上,过顶点且倾角为43π的弦长为22,求抛物线的方程.【解析】设抛物线方程为22y px =-(0p >),又弦所在直线方程为y x =-由⎩⎨⎧-=-=x y px y 22,解得两交点坐标(0,0), (2,2)p p - ∴22(2)(2)22p p -+=,解得1p =. ∴抛物线方程为22y x =-. 【题型二】:抛物线定义的理解【例2】已知点(),P x y 在以原点为圆心的单位圆上运动,则点(),Q x y xy +的轨迹是( ) A .圆 B.抛物线 C.椭圆 D.双曲线 【答案】B【解析】设(),Q u v ,则u x yv xy=+⎧⎨=⎩221x y +=22221u v x y ∴-=+=∴点Q 的轨迹为抛物线.故选B.【变式训练】:【变式1】动圆C 经过点F(1,0),并且与直线x=-1相切,若动圆C 与直线221y x =++总有公共点,则圆C 的面积( )A.有最大值8πB.有最小值2πC.有最小值3πD.有最小值4π 【答案】D【解析】由题意可得:动圆圆心C(a,b)的方程为24y x =.即24b a = 动圆C 与直线221y x =++总有公共点,∴圆心C 到此直线的距离11d r a a ≤=+=+即22112a b a -++≤+又24b a = 化简整理得()()22144210b b -+-+≥解得2b ≥或()642b ≤-+当2b =时,a 取得最小值1,此时圆C 由最小面积4π.故选D.【变式2】抛物线y=4x 2上的一点M 到焦点的距离为1,则点M 的纵坐标是( ) A .1716 B .1516 C .78D .0 【答案】B方法一:由题意抛物线为214x y =,则焦点为1(0,)16F ,准线为:116y =-; 由抛物线上的点M (x 0,y 0)到焦点的距离与到准线的距离相等,得01516y =, 即M 点的纵坐标为1516,故选择B 。
人教A版 高中数学2020届 高考复习专题--圆锥曲线(含解析)

第 1 页 共 65 页圆锥曲线一、知识结构 1.方程的曲线在平面直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹 )上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:(1)曲线上的点的坐标都是这个方程的解;(2)以这个方程的解为坐标的点都是曲线上的点.那么这个方程叫做曲线的方程;这条曲线叫 做方程的曲线.点与曲线的关系 若曲线C 的方程是f(x,y)=0,则点P 0(x 0,y 0)在曲线C 上⇔f(x 0,y 0)=0;点P 0(x 0,y 0)不在曲线C 上⇔f(x 0,y 0)≠0两条曲线的交点 若曲线C 1,C 2的方程分别为f 1(x,y)=0,f 2(x,y)=0,则 f 1(x 0,y 0)=0 点P 0(x 0,y 0)是C 1,C 2的交点⇔f 2(x 0,y 0) =0方程组有n 个不同的实数解,两条曲线就有n 个不同的交点;方程组没有实数解,曲线就没有 交点.2.圆 圆的定义 点集:{M ||OM |=r },其中定点O 为圆心,定长r 为半径. 圆的方程 (1)标准方程圆心在c(a,b),半径为r 的圆方程是(x-a)2+(y-b)2=r 2圆心在坐标原点,半径为r 的圆方程是x 2+y 2=r 2(2)一般方程当D 2+E 2-4F >0时,一元二次方程x 2+y 2+Dx+Ey+F=0叫做圆的一般方程,圆心为(-2D ,-2E,半径是24F-E D 22+.配方,将方程x 2+y 2+Dx+Ey+F=0化为(x+2D )2+(y+2E )2=44F -E D 22+当D 2+E 2-4F=0时,方程表示一个点(-2D ,-2E); 当D 2+E 2-4F <0时,方程不表示任何图形.点与圆的位置关系 已知圆心C(a,b),半径为r,点M 的坐标为(x 0,y 0),则|MC |<r ⇔点M 在圆C 内,第 2 页 共 65 页|MC |=r ⇔点M 在圆C 上, |MC |>r ⇔点M 在圆C 内,其中|MC |=2020b)-(y a)-(x +.(3)直线和圆的位置关系①直线和圆有相交、相切、相离三种位置关系 直线与圆相交⇔有两个公共点 直线与圆相切⇔有一个公共点 直线与圆相离⇔没有公共点 ②直线和圆的位置关系的判定 (i)判别式法(ii)利用圆心C(a,b)到直线Ax+By+C=0的距离d=22C Bb Aa BA +++与半径r 的大小关系来判定.3.椭圆、双曲线和抛物线椭 圆 双曲线抛物线轨迹条件 点集:({M ||MF 1+|MF 2|=2a,|F 1F 2|<2a = 点集:{M ||MF 1|-|MF 2|.=±2a,|F 2F 2|>2a}. 点集{M | |MF |=点M 到直线l 的距离}. 圆 形标准方程 22a x +22b y =1(a >b >0)22a x -22by =1(a >0,b >0)y 2=2px(p >0)顶 点 A 1(-a,0),A 2(a,0); B 1(0,-b),B 2(0,b)A 1(0,-a),A 2(0,a) O(0,0) 轴对称轴x=0,y=0 长轴长:2a 短轴长:2b 对称轴x=0,y=0 实轴长:2a 虚轴长:2b 对称轴y= 焦 点F 1(-c,0),F 2(c,0) 焦点在长轴上 F 1(-c,0),F 2(c,0) 焦点在实轴上 F(2P,0) 焦点对称轴上焦 距|F 1F 2|=2c , c=b2-a2|F 1F 2|=2c, c=b2a2+准 线x=±c a 2x=±ca 2x=-2p 准线与焦点位于顶点曲 线 性 质第 3 页 共 65 页准线垂直于长轴,且在椭圆外.准线垂直于实轴,且在两顶点的内侧.两侧,且到顶点的距离相等.离心率e=a c,0<e <1 e=ac,e >1 e=14.圆锥曲线的统一定义平面内的动点P(x,y)到一个定点F(c,0)的距离与到不通过这个定点的一条定直线l 的距离之 比是一个常数e(e >0),则动点的轨迹叫做圆锥曲线.其中定点F(c,0)称为焦点,定直线l 称为准线,正常数e 称为离心率. 当0<e <1时,轨迹为椭圆 当e=1时,轨迹为抛物线 当e >1时,轨迹为双曲线 5.坐标变换坐标变换 在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做 坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点 的坐标与曲线的方程.坐标轴的平移 坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫 做坐标轴的平移,简称移轴.坐标轴的平移公式 设平面内任意一点M ,它在原坐标系xOy 中的坐标是9x,y),在新坐标系x ′O ′y ′中的坐标是(x ′,y ′).设新坐标系的原点O ′在原坐标系xOy 中的坐标是(h,k),则x=x ′+h x ′=x-h (1) 或(2)y=y ′+k y ′=y-k 公式(1)或(2)叫做平移(或移轴)公式. 中心或顶点在(h,k)的圆锥曲线方程中心或顶点在(h,k)的圆锥曲线方程见下表.方 程 焦 点 焦 线 对称轴椭圆22h)-(x a +22k)-(y b =1 (±c+h,k)x=±c a 2+hx=h y=k 22h)-(x b +22k)-(y a =1 (h,±c+k) y=±c a 2+kx=h y=k 双曲线22h)-(x a -22k)-(y b =1 (±c+h,k) =±c a 2+kx=h y=k 22k)-(y a -22h)-(x b =1(h,±c+h)y=±c a 2+kx=h y=k 抛物线 (y-k)2=2p(x-h)(2p+h,k) x=-2p +hy=k (y-k)2=-2p(x-h)(-2p+h,k) x=2p +h y=k (x-h)2=2p(y-k)(h, 2p+k)y=-2p +kx=h二、知识点、能力点提示(一)曲线和方程,由已知条件列出曲线的方程,曲线的交点说明在求曲线方程之前必须建立坐标系,然后根据条件列出等式进行化简 .特别是在求出方程后要考虑化简的过程是否是同解变形,是否满足已知条件,只有这样求出的曲线方程才能准确无误.另外,要求会判断曲线间有无交点,会求曲线的交点坐标.三、考纲中对圆锥曲线的要求:考试内容:. 椭圆及其标准方程.椭圆的简单几何性质.椭圆的参数方程;. 双曲线及其标准方程.双曲线的简单几何性质;. 抛物线及其标准方程.抛物线的简单几何性质;考试要求:. (1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程;. (2)掌握双曲线的定义、标准方程和双曲线的简单几何性质;. (3)掌握抛物线的定义、标准方程和抛物线的简单几何性质;. (4)了解圆锥曲线的初步应用。
【2020届】高考数学圆锥曲线专题复习:圆锥曲线常用解法、常规题型与性质

圆锥曲线八种解题方法、七种常规题型和性质(有相应例题详解) 总论:常用的八种方法1、定义法2、韦达定理法3、设而不求点差法4、弦长公式法5、数形结合法6、参数法(点参数、K 参数、角参数)7、代入法中的顺序8、充分利用曲线系方程法七种常规题型(1)中点弦问题(2)焦点三角形问题(3)直线与圆锥曲线位置关系问题(4)圆锥曲线的有关最值(范围)问题 (5)求曲线的方程问题1.曲线的形状已知--------这类问题一般可用待定系数法解决。
2.曲线的形状未知-----求轨迹方程(6) 存在两点关于直线对称问题 (7)两线段垂直问题常用的八种方法1、定义法(1)椭圆有两种定义。
第一定义中,r 1+r 2=2a 。
第二定义中,r 1=ed 1 r 2=ed 2。
(2)双曲线有两种定义。
第一定义中,a r r 221=-,当r 1>r 2时,注意r 2的最小值为c-a :第二定义中,r 1=ed 1,r 2=ed 2,尤其应注意第二定义的应用,常常将 半径与“点到准线距离”互相转化。
(3)抛物线只有一种定义,而此定义的作用较椭圆、双曲线更大,很多抛物线问题用定义解决更直接简明。
2、韦达定理法因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用。
3、设而不求法解析几何的运算中,常设一些量而并不解解出这些量,利用这些量过渡使问题得以解决,这种方法称为“设而不求法”。
设而不求法对于直线与圆锥曲线相交而产生的弦中点问题,常用“点差法”,即设弦的两个端点A(x 1,y 1),B(x 2,y 2),弦AB 中点为M(x 0,y 0),将点A 、B 坐标代入圆锥曲线方程,作差后,产生弦中点与弦斜率的关系,这是一种常见的“设而不求”法,具体有:(1))0(12222>>=+b a b y a x 与直线相交于A 、B ,设弦AB 中点为M(x 0,y 0),则有02020=+k b y a x 。
【2020届】高考数学圆锥曲线专题复习:圆锥曲线解答题12大题型解题套路归纳

【高考数学中最具震撼力的一个解答题!】注:【求解完第一问以后,】→WILL COME ACROSS圆锥曲线题10大题型:(1)弦长问题(2)中点问题(3)垂直问题(4)斜率问题(5)对称问题(6)向量问题(7)切线问题(8)面积问题(9)最值问题(10)焦点三角形问题。
中的2-----4类;分门别类按套路求解;1.考(总与三个问题有关):(1)———————;(2)——————————;(3)—————————;2.圆锥曲线题,直线代入圆锥曲线的“:---------------------------------------------------; ——————————————————————————————————————;3.圆锥曲线题-------------------;---------------------------------------------;————————————;—————————;——————————;—————————————————;———————————;——————————————;4.STEP1:首先看是否属于3种特殊弦长:(1)圆的弦长问题;(2)中点弦长问题(3)焦点弦长问题;→(1)圆的弦长问题:(2法)首选方法:垂径定理+勾股定理:图示:--------------------------------;公式为:-------------------------;其中求“点线距”的方法:———————;次选:弦长公式;→(2)中点弦长问题:(2法)首选方法:“点差法”椭圆:(公式一)--------------------------------;(公式二)--------------------------------;副产品:两直线永远不可能垂直!原因:___________;【两直线夹角的求法:(夹角公式)___________;】双曲线(公式一)--------------------------------;(公式二)--------------------------------;抛物线:形式一:___________;(公式一)--------------------------------;(公式二)--------------------------------;形式2:___________;(公式一)--------------------------------;(公式二)--------------------------------;附:“点差法”步骤:椭圆:“点”_______________________;___________________________;“差”__________________________________;“设而不求法”_______________________________;“斜率公式”+“中点公式”_____________________;___________;___________;→得公式:(公式一)-------------------;(公式二)---------------------;附:“点差法”步骤:抛物线;形式一___________;:“点”_______________________;_____________________;“差”_________________________;“设而不求法”___________________;“斜率公式”+“中点公式”_____________;___________;___________;→得公式:(公式一)---------------------;(公式二)--------------------;附:“点差法”步骤:抛物线:形式二:____________;“点”_______________________;_________________;“差”__________________________________;“设而不求法”______________________;“斜率公式”+“中点公式”_____________;___________;___________;→得公式:(公式一)-------------------;(公式二)--------------------------------;法二次选:中点公式;→(2)焦点弦长问题:(2(公式一)左焦点弦长:--------------------------------;图示:__________________;右焦点弦长:--------------------------------;图示:__________________;公式一适用于:__________________________;(公式二)--------------------------------;其中:________________;适用于:__________________________; ________;公式一:__________________;图示:_____________________;公式一适用于:__________________________;焦点弦公式二:____________________;公式2适用于:__________________________;→ STEP2:除了这三种特殊弦长以外,其余弦长求解都用【弦长公式】(保底方法);【弦长公式】3类型:【类1】___________;___________;_______________;适用于:__________________________;【类2】___________;____________;_______________;适用于:__________________________;【类3】___________;____________;_______________;适用于:__________________________;5.【2次选-------------------------;--------------------------;--------------------------;---------;6. 2种特殊的垂直问题:(1【2法】:法一:“圆的直径式方程”____________________________________;法二:向量垂直法:____________________;____________________________________; (2)“原点张角垂直问题”首选方法:向量垂直法+韦达定理【最快!】图示:_____________________;套路:___________________;_______________________________;7.“结论法+代入法最快!”【2题型】(1)结论一:【原点对称】_______________________________;结论二:【任意点对称】_______________________________;(2【x 轴对称】_______________________________;结论二:【y轴对称】_______________________________;结论三【x=a对称】------------------------------------------;结论四【y=b对称】:______________________;结论5【y=x对称】:__________________________;结论6【y=-x对称】:_______________________________;结论7【y=x+c对称】:___________________;结论8【y=-x+c对称】:_____________________;结论9【任意直线Ax+By+C=0对称】:_______________________________;8.【大纲内2题型】(1)题:【3套路8结论】(1)“点线距等于半径”________________________;(2)斜率乘积等于-1;______________;(3)勾股定理:__________________;结论:(1)【切线长公式】_______________________;(2)【圆心在原点时】_______________________;(3)【切点弦直线方程】_______________________;(4)_______________________;(5)_______________________;(6)_______________________;(7)________________________;(2【导数法】(2形式)【形式一】________;____________________;【形式二】_________;__________________________;9.圆锥曲线题题型六:固定套路:_________+___________+_____________+___________+__________ ___+___________+_____________;【相关结论】:【两焦半径】左焦半径_____________;右焦半径_____________;特别的,通径:______________;半通径:______________;【三边长】_____________;_____________;_____________;【周长】_____________;【两焦半径乘积】_____________;【焦点三角形面积】_____________;_____________;作用:_____________;_____________;【余弦定理式】_____________;_____________;_____________;【正弦定理式】________;【求解离心率】__________;_________;________;__________;_____;【焦点三角形中内心公式】_____________________;10.“向量法最快”!平解几中,向量问题均采用“坐标运算”最佳!】首先:坐标化→→【平面向量10公式】【向量平行】_____________________;【向量垂直】_____________________;【向量夹角公式】_____________________;【加减式】_____________________;【数乘式】_____________________;【向量数量积公式】_____________________;【向量模的公式】_____________________;【量模转化公式】_____________________;【向量平方差公式】_____________________;【向量完全平方公式】_____________________;11.【2类】(1】→→“成锐角时《=》向量数量积>0;”“成钝角时《=》向量数量积<0;”“成直角时《=》向量数量积=0;”(2)【2法】(1)向量数量积公式_____________________;(2)两直线夹角公式_____________________;12.圆锥曲线题题型9_____________________;_____________________;_____________________;【凡与垂直相关的斜率问题】首选:斜率乘积等于-1。
(完整版)圆锥曲线常见题型及答案

圆锥曲线常见题型归纳一、基础题涉及圆锥曲线的基本概念、几何性质,如求圆锥曲线的标准方程,求准线或渐近线方程,求顶点或焦点坐标,求与有关的值,求与焦半径或长(短)轴或实(虚)轴有关的角和三角形面积。
此类题在考试中最常见,解此类题应注意:(1)熟练掌握圆锥曲线的图形结构,充分利用图形来解题;注意离心率与曲线形状的关系; (2)如未指明焦点位置,应考虑焦点在x 轴和y 轴的两种(或四种)情况;(3)注意2,2,a a a ,2,2,b b b ,2,2,c c c ,2,,2p p p 的区别及其几何背景、出现位置的不同,椭圆中222b a c -=,双曲线中222b a c +=,离心率a c e =,准线方程a x 2±=;例题:(1)已知定点)0,3(),0,3(21F F -,在满足下列条件的平面上动点P 的轨迹中是椭圆的是 ( )A .421=+PF PFB .621=+PF PF C .1021=+PF PF D .122221=+PF PF (答:C );(2)方程8=表示的曲线是_____ (答:双曲线的左支)(3)已知点)0,22(Q 及抛物线42x y =上一动点P (x ,y ),则y+|PQ|的最小值是_____ (答:2)(4)已知方程12322=-++k y k x 表示椭圆,则k 的取值范围为____ (答:11(3,)(,2)22---); (5)双曲线的离心率等于25,且与椭圆14922=+y x 有公共焦点,则该双曲线的方程_______(答:2214x y -=);(6)设中心在坐标原点O ,焦点1F 、2F 在坐标轴上,离心率2=e 的双曲线C 过点)10,4(-P ,则C 的方程为_______(答:226x y -=)二、定义题对圆锥曲线的两个定义的考查,与动点到定点的距离(焦半径)和动点到定直线(准线)的距离有关,有时要用到圆的几何性质。
此类题常用平面几何的方法来解决,需要对圆锥曲线的(两个)定义有深入、细致、全面的理解和掌握。
高三高考数学总复习《圆锥曲线》题型归纳与汇总

高考数学总复习题型分类汇《圆锥曲线》篇经典试题大汇总目录【题型归纳】题型一求曲线的方程 (3)题型二最值(范围)问题 (4)题型三定点定值与存在性 (6)【巩固训练】题型一求曲线的方程 (8)题型二最值(范围)问题 (9)题型三定点定值与存在性 (11)高考数学《圆锥曲线》题型归纳与训练【题型归纳】题型一 求曲线的方程例1 已知定点()0,3-G ,S 是圆()723:22=+-y x C (C 为圆心)上的动点,SG 的垂直平分线与SC 交于点E ,设点E 的轨迹为M . 求M 的方程. 【答案】见解析【解析】由题意知ES EG =,所以26=+=+EC ESEC EG ,又因为266<=GC .所以点E 的轨迹是以G ,C 为焦点,长轴长为26的椭圆,动点E 的轨迹方程为191822=+y x . 例2 设O 为坐标原点,动点M 在椭圆22:12x C y +=上,过点M 作x 轴的垂线,垂足为N , 点P 满足2NP NM =.求点P 的轨迹方程.【答案】见解析【解析】如图所示,设(),P x y ,(),0N x ,()1,M x y . 由2NP NM =知,12y y =,即12y =.又点M 在椭圆2212x y +=上,则有22122x y +=,即222x y +=.例3 如图,矩形ABCD 中, ()()()()2,0,2,0,2,2,2,2A B C D -- 且,AM AD DN DC λλ==,[]0,1,AN λ∈交BM 于点Q .若点Q 的轨迹是曲线P 的一部分,曲线P 关于x 轴、y 轴、原点都对称,求曲线P 的轨迹方程.【答案】Q 的轨迹为第二象限的14椭圆,由对称性可知曲线P 的轨迹方程为2214x y +=. 【解析】设(),Q x y ,由,AM AD DN DC λλ==,求得()()2,2,42,2M N λλ--, ∵1,22QA AN QB BM k k k k λλ====-,∴11224QA QB k k λλ⎛⎫⋅=⋅-=- ⎪⎝⎭, P x,y ()NM Oxy∴1224y y x x ⋅=-+-,整理得()22120,014x y x y +=-≤≤≤≤.可知点Q 的轨迹为第二象限的14椭圆,由对称性可知曲线P 的轨迹方程为2214x y +=. 【易错点】求轨迹问题学生容易忽视范围 【思维点拨】高考中常见的求轨迹方程的方法有:1.直译法与定义法:直译法求轨迹方程:题目给出的条件可以直接得到一个关于动点坐标的关系式,化简; 定义法求轨迹方程:轨迹方程问题中,若能得到与所学过的圆锥曲线定义相符的结论,可以根据相应圆锥曲线的定义求出相关的参数,从而得到方程.2.相关点法:找动点之间的转化关系(平移,伸缩,中点,垂直等),用要求的代替已知轨迹的,代入化简3.参数法:可用联立求得参数方程,消参.注意此种问题通常范围有限制.4.交轨法:联立求交点,变形的轨迹. 题型二 最值(范围)问题例1 已知F 为抛物线C :x y 42=的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则DE AB +的最小值为( )A. 16B. 14C. 12D. 10 【答案】A【解析】设()()()()11223344,,,,,,,A x y B x y D x y E x y ,直线1l 的方程为()11y k x =-,联立方程()214 1y xy k x ==-⎧⎪⎨⎪⎩,得2222111240k x k x x k --+=,∴21122124k x x k --+=- 212124k k +=, 同理直线2l 与抛物线的交点满足:22342224k x x k ++=, 由抛物线定义可知12342AB DE x x x x p +=++++=22122222121224244448816k k k k k k ++++=++≥=, 当且仅当121k k =-=(或1-)时,取等号.【易错点】本题考查抛物线的焦点弦长,利用抛物线的焦点弦长公式,表示出DE AB +,然后利用基本不等式求最值.对相关流程应有所熟练例2 已知点A (0,2)-,椭圆E :22221(0)x y a b a b+=>>的离心率为2,F 是椭圆E 的右焦点,直线AF,O 为坐标原点. (1)求E 的方程;(2)设过点A 的动直线l 与E 相交于,P Q 两点,当OPQ ∆的面积最大时,求l 的方程. 【答案】见解析【解析】(1)2(c,0)F c c 设,由条件知,222=2, 1.c a b a c a ==-=又所以 22 1.4x E y +=故的方程为 (2)1122:=2,(,),(,).l x l y kx P x y Q x y ⊥-当轴时不合题意,故设22214x y kx y =-+=将代入得22(14)16120.k x kx +-+=221,23=16(43)0,4k k x ∆->>=当即时,12PQ x =-=从而O PQ d OPQ =∆又点到直线的距离所以的面积21=241OPQ S d PQ k ∆⋅=+244,0,.44OPQ t t t S t t t∆=>==++则44,20.2t t k t +≥==±∆>因为当且仅当,即OPQ ∆所以,当的面积最大时,l 的方程为2222y x y x =-=--或. 【思维点拨】 圆锥曲线中的取值范围问题常用的方法有以下几个:(1)利用已知参数的范围,求新参数的范围,解这类问题的关键是在两个参数之间建立等量关系;(2)利用基本不等式求出参数的取值范围;(3)利用函数的值域的求法(甚至求导),确定参数的取值范围. 题型三 定点定值与存在性问题例1 已知椭圆C :()222210x y a b a b +=>>上.(1)求C 的方程.(2)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .直线OM 的斜率与直线l 的斜率的乘积为定值. 【答案】见解析【解析】 (1=22421a b+=,解得28a =,24b =. 所以C 的方程为22184x y +=. (2)设直线l :()00y kx b kb =+≠≠,,()11A x y ,, ()22B x y ,,()M M M x y ,.将 y kx b =+代入22184x y +=得()22221+4280k x kbx b ++-=. 故1222221M x x kb x k +-==+,221M M by kx b k =+=+ . 于是直线OM 的斜率12M OM M y k x k ==-,即12OM k k ⋅=-. 所以直线OM 的斜率与直线l 的斜率的乘积为定值.【思维点拨】解析几何是高考必考内容之一,在命题时多从考查各种圆锥曲线方程中的基本量关系及运算,在直线与圆锥曲线关系中.一般用方程的思想和函数的观点来解决问题,并会结合中点坐标,方程根与函数关系来求解.例2 已知抛物线2:4C y x =,点()0,m M 在x 轴的正半轴上,过M 点的直线l 与抛物线C 相交于A ,B 两点,O 为坐标原点.(1) 若1=m ,且直线l 的斜率为1,求以AB 为直径的圆的方程;(2) 是否存在定点M ,使得不论直线:l x ky m =+绕点M 如何转动,2211AMBM+恒为定值?【答案】(1)()()223216x y -+-=. (2)存在定点M (2, 0). 【解析】(1)当1=m 时,()0,1M ,此时,点M 为抛物线C 的焦点,直线l 的方程为1-=x y ,设()()1122,,A x y B x y ,,联立24{ 1y xy x ==-,消去y 得, 2610x x -+=,∴126x x +=, 121224y y x x +=+-=,∴圆心坐标为(3, 2).又1228AB x x =++=,∴圆的半径为4,∴圆的方程为()()223216x y -+-=. (2)由题意可设直线l 的方程为x ky m =+,则直线l 的方程与抛物线2:4C y x =联立,消去x 得: 2440y ky m --=,则124y y m =-, 124y y k +=,()()22222211221111AMBMx m y x m y +=+-+-+()()()22122222222121211111y y k y k y k y y +=+=+++ ()()()()222121222222221221682111621y y y y k m k mky y k m m k +-++===+++ 对任意k R ∈恒为定值, 于是2=m ,此时221114AMBM+=. ∴存在定点()0,2M ,满足题意. 【易错点】定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果(取特殊位置或特殊值),因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.【思维点拨】定点、定值问题通常先假设存在,推证满足条件的结论,若结论正确,则存在;若结论不正确,则不存在.在求解中通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的.【巩固训练】题型一 求曲线的方程1.设圆222150x y x ++-=的圆心为A ,直线l 过点()0,1B 且与x 轴不重合,l 交圆A 于C ,D 两点,过B 作AC的平行线交AD 于点E .证明EA EB +为定值,并写出点E 的轨迹方程.【答案】13422=+y x (0≠y ) 【解析】因为||||AC AD =,AC EB //,故ADC ACD EBD ∠=∠=∠, 所以||||ED EB =,故||||||||||AD ED EA EB EA =+=+.又圆A 的标准方程为16)1(22=++y x ,从而4||=AD ,所以4||||=+EB EA .由题设得)0,1(-A ,)0,1(B ,2||=AB ,由椭圆定义可得点E 的轨迹方程为13422=+y x (0≠y ).2.已知动圆G 过定点()4,0F ,且在y 轴上截得的弦长为8.求动圆G 的圆心点G 的轨迹方程; 【答案】28y x =【解析】设动圆圆心(),G x y ,设圆交y 轴于,M N 两点,连接,GF GM , 则GF GM =,过点G 作GH MN ⊥,则点H 是MN 的中点, 显然()22224,4GM x GF x y =+=-+,于是()222244x y x -+=+,化简整理得28y x =,故的轨迹方程为28y x =.3.已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于A B ,两点,交C 的准线于P Q ,两点.(1)若F 在线段AB 上,R 是PQ 的中点,证明AR FQ ∥;(2)若PQF △的面积是ABF △的面积的两倍,求AB 中点的轨迹方程.【答案】(1)见解析; (2)12-=x y .【解析】由题设)0,21(F .设b y l a y l ==:,:21,则0≠ab ,且记过B A ,两点的直线为l ,则l 的方程为0)(2=++-ab y b a x .(1)由于F 在线段AB 上,故01=+ab .记AR 的斜率为1k ,FQ 的斜率为2k ,则222111k b aaba ab a b a a b a k =-=-==--=+-=.所以FQ AR ∥. (2)设l 与x 轴的交点为)0,(1x D , 则1111,2222ABF PQF a b S b a FD b a x S -=-=--=△△. 由题设可得221211b a x a b -=--,所以01=x (舍去),11=x . 设满足条件的AB 的中点为),(y x E . 当AB 与x 轴不垂直时,由DE AB k k =可得)1(12≠-=+x x yb a . 而y b a =+2,所以)1(12≠-=x x y . 当AB 与x 轴垂直时,E 与D 重合.所以,所求轨迹方程为12-=x y .题型二 最值(范围)问题1.已知动点E 到点A ()2,0与点B ()2,0-的直线斜率之积为14-,点E 的轨迹为曲线C . (1)求C 的方程;(2)过点D ()1,0作直线l 与曲线C 交于P , Q 两点,求OP OQ ⋅的最大值.【答案】(1)()22124x y x +=≠±(2)14 【解析】(1)设(),E x y ,则2x ≠±.因为E 到点A ()2,0,与点B ()2,0-的斜率之积为14-,所以122y yx x ⋅=-+-,整理得C 的方程为()22124x y x +=≠±. (2)当l 垂直于轴时,l 的方程为1x =,代入2214x y +=得P ⎛ ⎝⎭,1,Q ⎛ ⎝⎭.11,4OP OQ ⎛⎛⋅=⋅= ⎝⎭⎝⎭. 当l 不垂直于x 轴时,依题意可设()()10y k x k =-≠,代入2214x y +=得 ()2222148440k xk x k +-+-=.因为()216130k ∆=+>,设()11,P x y , ()22,Q x y .则2122814k x x k +=+, 21224414k x x k -=+.()()21212121211OP OQ x x y y x x k x x ⋅=+=+-- ()()22212121k x x k x x k =+-++14+21174416k =-+ 14< 综上OP OQ ⋅ 14≤,当l 垂直于x 轴时等号成立,故OP OQ ⋅的最大值是14.2.设椭圆()2222:10x y M a b a b +=>>经过点12,,P F F ⎭是椭圆M 的左、右焦点,且12PF F ∆的面积为2. (1)求椭圆M 的方程;(2)设O 为坐标原点,过椭圆M 内的一点()0,t 作斜率为k 的直线l 与椭圆M 交于,A B 两点,直线,OA OB 的斜率分别为12,k k ,若对任意实数k ,存在实数m ,使得12k k mk +=,求实数m 的取值范围.【答案】(1)22143x y +=;(2)[)2,m ∈+∞. 【解析】(1)略(2)设直线l 的方程为y kx t =+,由221{ 43x y y kx t+==+,得()2223484120k x ktx t +++-=,设()()1122,,,A x y B x y ,则21212228412,3434kt t x x x x k k -+=-=++,()212121221212122223t x x y y t t kt k k k k k k x x x x x x t ++=+=+++=+=--, 由12k k mk +=对任意k 成立,得22223t m t =--,∴()232m t m-=,又()0,t 在椭圆内部中,∴203t ≤<,∴2m ≥,即[)2,m ∈+∞.题型三 定点定值与存在性问题1.已知12,F F 分别是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,离心率为12, ,M N 分别是椭圆的上、下顶点,22•2MF NF =-.(1)求椭圆E 的方程;(2)若直线y kx m =+与椭圆E 交于相异两点,A B ,且满足直线,MA MB 的斜率之积为14,证明:直线AB 恒过定点,并求定点的坐标.【答案】(1)22143x y +=(2)直线AB恒过定点(0,.【解析】(1)由题知()0,2c F ,()b M ,0,()b N -,0,22222-=-=⋅∴b c NF MF ①由21==a c e ,得c a 2= ② 又222cb a =- ③ 由①②③联立解得:42=a ,32=b ∴椭圆E 的方程为13422=+y x . (2)证明:由椭圆E 的方程得,上顶点()3,0M ,设()11,y x A ,()22,y x B ,由题意知,01≠x ,02≠x由⎪⎩⎪⎨⎧=++=13422y x m kx y 得:()()034843222=-+++m kmx x k∴221438kkmx x +-=+,()22214334k m x x +-=, 又111133x m kx x y k MA -+=-=,222233x m kx x y k MB -+=-=, 由41=⋅NB MA k k ,得()()2121334x x m kx m kx =-+-+, ()()()()()()0433483414342222=+-+--+--k m km m k k m ,化简得:06332=+-m m 解得:3=m 或32=m ,结合01≠x ,02≠x 知32=m ,即直线AB 恒过定点()32,0.2.已知椭圆C :22221(0)x y a b a b+=>>的离心率为2,(,0)A a ,(0,)B b ,(0,0)O ,ΔOAB 的面积为1.(1)求椭圆C 的方程;(2)设P 是椭圆C 上一点,直线PA 与y 轴交于点M ,直线PB 与x 轴交于点N .求证:||||AN BM ⋅为定值.【答案】(1) 1422=+y x (2)见解析. 【解析】(1)由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧+===,,121,23222c b a ab a c 解得1,2==b a . 所以椭圆C 的方程为1422=+y x . (2)由(1)知,)1,0(),0,2(B A ,设),(00y x P ,则442020=+y x .当00≠x 时,直线PA 的方程为)2(200--=x x y y .令0=x ,得2200--=x y y M .从而221100-+=-=x y y BM M . 直线PB 的方程为110+-=x x y y . 令0=y ,得100--=y x x N .从而12200-+=-=y x x AN N . 所以221120000-+⋅-+=⋅x y y x BM AN 228844224844400000000000000002020+--+--=+--+--++=y x y x y x y x y x y x y x y x y x 4=.当00=x 时,10-=y ,,2,2==AN BM 所以4=⋅BM AN .综上,BM AN ⋅为定值.3. 在平面直角坐标系xOy 中,已知椭圆C :22221(0)x y a b a b+=>>的离心率e =C 上的点 到(0,2)Q 的距离的最大值为3. (1)求椭圆C 的方程;(2)在椭圆C 上,是否存在点(,)M m n 使得直线l :1mx ny +=与圆O :221x y += 相交于不同的两点,A B ,且OAB ∆的面积最大?若存在,求出点M 的坐标及相对应的OAB ∆的面积;若不存在,请说明理由.【答案】(1) 2213x y += (2)见解析【解析】(1)由2223c e c a a ==⇒=,所以222213b ac a =-= 设(,)P x y 是椭圆C 上任意一点,则22221x y a b+=,所以222222(1)3y x a a y b =-=-||PQ ===所以,当1y =-时,||PQ 3=,可得a =1,b c ==故椭圆C 的方程为:2213x y += (2)存在点M 满足要求,使OAB ∆得面积最大.假设直线:1l mx ny +=与圆22:1O x y +=相交于不同两点,A B , 则圆心O 到l的距离1d =<,∴221m n +> ①因为(,)M m n 在椭圆C 上,所以2213m n +=②,由①②得:203m <∵||AB ==所以1||2OABSAB d =⋅=2213m n =-代入上式得213221213OABmS m m ∆==+⋅,当且仅当22231(0,3]32m m =⇒=∈,∴2231,22m n ==,此时满足要求的点(M 有四个. 此时对应的OAB ∆的面积为12. 4.已知过抛物线()022>=p px y 的焦点F 的直线交抛物线于()()()112212,,,A x y B x y x x < 两点,且6AB =.(1)求该抛物线E 的方程;(2)过点F 任意作互相垂直的两条直线12,l l ,分别交曲线E 于点,C D 和,M N .设线段,CD MN 的中点分别为,P Q ,求证:直线PQ 恒过一个定点.【答案】(1)24y x = (2)直线PQ 恒过定点()3,0.【解析】(1)抛物线的焦点,02p F ⎛⎫⎪⎝⎭,∴直线AB 的方程为:2p y x ⎫=-⎪⎭联立方程组22{ 2y pxp y x =⎫=-⎪⎭,消元得: 22204p x px -+=, ∴212122,4px x p xx +==∴6AB ===,解得2p =±.∵0p >,∴抛物线E 的方程为:24y x =.(2)设,C D 两点坐标分别为()()1122,,,x y x y ,则点P 的坐标为1212,22x x y y ++⎛⎫⎪⎝⎭..由题意可设直线1l 的方程为()()10y k x k =-≠. 由()24{1y x y k x ==-,得()2222240k x k x k -++=.()24224416160k k k ∆=+-=+>因为直线1l 与曲线E 于,C D 两点,所以()1212122442,2x x y y k x x k k+=++=+-=. 所以点P 的坐标为2221,k k ⎛⎫+⎪⎝⎭. 由题知,直线2l 的斜率为1k-,同理可得点Q 的坐标为()212,2k k +-. 当1k ≠±时,有222112k k+≠+,此时直线PQ 的斜率2222221112PQ kk k k k k k+==-+--. 所以,直线PQ 的方程为()222121k y k x k k+=---,整理得()230yk x k y +--=. 于是,直线PQ 恒过定点()3,0; 当1k=±时,直线PQ 的方程为3x =,也过点()3,0.综上所述,直线PQ 恒过定点()3,0.新课程标准的内容与现形课标内容的对比如下表:与现形课标对比,必修3中的“算法初步”删掉了;删掉了必修5中的解三角形,不等式的大部分内容。
2020年高考山东版高考理科数学 10.4 圆锥曲线的综合问题
- 8������2
4������2 - 12
则
x1+x2=
3
+
4������2,x1x2=3
+
4������2,
所以|AC|= 1 + ������2|x1-x2|=123(+������24+������21),
1 3 + 4������2
从而|������������|=12(������2
+
考题示例 2017 课标Ⅰ,20
5 年考情
考向
关联考点
定点问题 直线与椭圆的位置关系
2017 课标 Ⅰ,10 最值问题
直线与抛物线的位置关 系
2016 课标Ⅰ,20 2015 山东,20
弦长问题 面积问题
2018 北京,19 定值问题
直线与椭圆的位置关系 直线与椭圆的位置关系 直线与抛物线的位置关
系
10.4 圆锥曲线的综合问题
备战 2020 高考
挖命题 【考情探究】
考点 1.定值、定 点、最值及范 围问题
2.存在性问题
内容解读
①了解圆锥曲线的简单应用; ②了解参变量的意义; ③理解函数思想和方程思想在 圆锥曲线中的应用 ①理解圆锥曲线中存在性问题 的基本解法; ②理解转化思想在圆锥曲线中 的应用
,
1)
1 4 + 3������2
同理可得|������������|=12(������2
+
,
1)
1 1 7(������2 + 1) 7
7
7
所以|������������|+|������������|=12(������2 + 1)=12,令12=2λ,得 λ=24.
2020学年度普通高等学校招生全国统一考试知识汇编(圆锥曲线方程)新课标 人教版

2020年普通高等学校招生全国统一考试知识汇编圆锥曲线方程一、选择题:1. (2020浙江)函数y =ax 2+1的图象与直线y =x 相切,则a =( B )(A)18 (B)41 (C) 21(D)1 2.( 2020年浙江卷)若双曲线221x y m -=上的点到左准线的距离是到左焦点距离的13,则m = ( C)(A)21 (B)23 (C)81 (D)893. (2020天津卷)设双曲线以椭圆192522=+y x 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( C )A .2±B .34±C .21±D .43±4.(2020天津卷)从集合{1,2,3…,11}中任选两个元素作为椭圆方程12222=+ny m x 中的m和n,则能组成落在矩形区域B={(x ,y)| |x |<11且|y|<9}内的椭圆个数为(B )A .43B . 72C . 86D . 905.(2020年天津卷)如果双曲线的两个焦点分别为)0,3(1-F 、)0,3(2F ,一条渐近线方程为x y 2=,那么它的两条准线间的距离是( C )A .36B .4C .2D .16. (2020上海)过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点,它们的横坐标之和等于5,则这样的直线( B )A .有且仅有一条B .有且仅有两条C .有无穷多条D .不存在 7.(2020年上海春卷)抛物线x y 42=的焦点坐标为( B )(A ))1,0(. (B ))0,1(. (C ))2,0(. (D ))0,2(.8.(2020年上海春卷)若R ∈k ,则“3>k ”是“方程13322=+--k y k x 表示双曲线”的( A ) (A )充分不必要条件. (B )必要不充分条件.(C )充要条件. (D )既不充分也不必要条件.9. (2020山东卷)设直线:220l x y ++=关于原点对称的直线为l ',若l '与椭圆2214y x +=的交点为A 、B 、,点P 为椭圆上的动点,则使PAB ∆的面积为12的点P 的个数为( B )(A )1 (B )2 (C )3 (D )4 10.(2020年山东卷)在给定椭圆中,过焦点且垂直于长轴的弦长为2,焦点到相应准线的距离为1,则该椭圆的离心率为 (B)(A)2 (B)22 (C) 21(D)42 11.(2020年山东卷)某公司招收男职员x 名,女职员y 名,x 和y 须满足约束条件⎪⎩⎪⎨⎧≤≥+-≥-.112,932,22115x y x y x 则z =10x +10y 的最大值是 (C) (A)80 (B) 85 (C) 90 (D)9512 (2020全国卷Ⅰ)已知双曲线)0( 1222>=-a y ax 的一条准线为23=x ,则该双曲线的离心率为(A)(A )23(B )23 (C )26 (D )332A .)22,22(-B .)2,2(-C .)42,42(D .)81,81(-13.(2020年全国卷I )双曲线221mx y +=的虚轴长是实轴长的2倍,则m =A .14-B .4-C .4D .1414.(2020年全国卷I )抛物线2y x =-上的点到直线4380x y +-=距离的最小值是A .43B .75C .85D .315.(2020年全国卷I )用长度分别为2、3、4、5、6(单位:cm )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为A.2B.2C.2D .220cm16.( 2020全国卷II) 双曲线22149x y -=的渐近线方程是( C)(A) 23y x =± (B) 49y x =± (C) 32y x =± (D) 94y x =±17. (2020全国卷II)已知双曲线22163x y-=的焦点为1F 、2F ,点M 在双曲线上且1MF x ⊥轴,则1F 到直线2F M 的距离为(C )(A)(B) (C) 65 (D) 5618. (2020全国卷III)设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是(D )(A)2 (B)12(C)2 (D1- 19.(2020年全国卷II )已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是 (C )(A )2 3 (B )6 (C )4 3 (D )1220.(2020年全国卷II )已知双曲线x 2a 2-y 2b2=1的一条渐近线方程为y =43x ,则双曲线的离心率为 (A )(A )53 (B )43 (C )54 (D )3221. (2020辽宁卷)已知双曲线的中心在原点,离心率为3.若它的一条准线与抛物线x y 42=的准线重合,则该双曲线与抛物线x y 42=的交点到原点的距离是( B )A .23+6B .21C .21218+D .2122.(2020年辽宁卷)曲线221(6)106x y m m m +=<--与曲线221(59)59x y m m m+=<<--的 (A)焦距相等 (B) 离心率相等 (C)焦点相同 (D)准线相同【解析】由221(6)106x y m m m+=<--知该方程表示焦点在x 轴上的椭圆,由221(59)59x y m m m+=<<--知该方程表示焦点在y 轴上的双曲线,故只能选择答案A 。
专题20 圆锥曲线的综合问题(解析版)

专题20 圆锥曲线的综合问题命题规律内 容典 型1 圆锥曲线中的弦长(面积)问题 2020年高考全国Ⅲ卷理数20 2圆锥曲线中的定点问题 2020年高考全国Ⅲ卷理数20 3 圆锥曲线中的最值问题 2020年高考浙江卷21 4 圆锥曲线中的定值问题 2020•山东高考,22 5 圆锥曲线中的取值范围问题 2020•上海高考,20 6圆锥曲线中的证明问题2018年高考全国Ⅲ理数命题规律一 圆锥曲线中的弦长(面积)问题【解决之道】圆锥曲线中的弦长(面积)问题,一般利用根与系数的关系采用“设而不求”“整体代入”等解法. 【三年高考】1.【2020年高考全国Ⅲ卷理数20】已知椭圆()222:10525x y C m m +=<<,,A B 分别为C 的左、右顶点. (1)求C 的方程;(2)若点P 在C 上,点Q 在直线6x =上,且,BP BQ BP BQ =⊥,求△APQ 的面积.【解析】解法一:(1)由c e a =,得2221b e a =-,即21511625m =-,∴22516m =,故C 的方程为221612525x y +=. (2)设点P 的坐标为(,)s t ,点Q 的坐标为(6,)n ,根据对称性,只需考虑0n >的情形,此时55s -<<,504t<. ∵||||BP BQ =,∴有222(5)1s t n -+=+ ①. 又∵BP BQ ⊥,∴50s nt -+= ②.又221612525s t +=③. 联立①、②、③,可得,312s t n =⎧⎪=⎨⎪=⎩或318s t n =-⎧⎪=⎨⎪=⎩.当312s t n =⎧⎪=⎨⎪=⎩时,(8,1)AP =,(11,2)AQ =,∴22215()|82111|22APQ S AP AQ AP AQ =⋅-⋅=⨯-⨯=△.同理可得,当318s t n =-⎧⎪=⎨⎪=⎩时,52APQ S =△.综上所述,可得APQ △的面积为52.解法二:(1)222:1(05)25x y C m m +=<<,∴5a =,b m =,根据离心率4c e a ====,解得54m =或54m =-(舍), ∴C 的方程为:22214255x y ⎛⎫ ⎪⎝⎭+=,即221612525x y +=.(2)点P 在C 上,点Q 在直线6x =上,且||||BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N ,根据题意画出图形,如图,||||BP BQ =,BP BQ ⊥,90PMB QNB ∠=∠=︒,又90PBM QBN ∠+∠=︒,90BQN QBN ∠+∠=︒,∴PBM BQN ∠=∠,根据三角形全等条件“AAS ”,可得:PMB BNQ ≅△△,221612525x y +=,∴(5,0)B ,∴651PM BN ==-=. 设P 点为(,)P P x y ,可得P 点纵坐标为1P y =,将其代入221612525x y +=,可得:21612525P x +=,解得:3P x =或3P x =-,∴P 点为(3,1)或(3,1)-, ①当P 点为(3,1)时,故532MB =-=,PMB BNQ ≅△△,∴||||2MB NQ ==,可得:Q 点为(6,2),画出图象,如图,(5,0)A-,(6,2)Q,可求得直线AQ的直线方程为:211100x y-+=,根据点到直线距离公式可得P到直线AQ的距离为:5d===,根据两点间距离公式可得:AQ ==∴APQ面积为:1522⨯=.②当P点为(3,1)-时,故5+38MB==,PMB BNQ≅△△,∴||||8MB NQ==,可得:Q点为(6,8),画出图象,如图,(5,0)A-,(6,8)Q,可求得直线AQ的直线方程为:811400x y-+=,根据点到直线距离公式可得P 到直线AQ的距离为:d===,根据两点间距离公式可得:AQ==∴APQ面积为:1522=.综上所述,APQ面积为:52.2.【2020年高考天津卷18】已知椭圆22221(0)x ya ba b+=>>的一个顶点为(0,3)A-,右焦点为F,且||||OA OF=,其中O为原点.(Ⅲ)求椭圆的方程;(Ⅲ)已知点C 满足3OC OF =,点B 在椭圆上(B 异于椭圆的顶点),直线AB 与以C 为圆心的圆相切于点P ,且P 为线段AB 的中点.求直线AB 的方程.【解析】(Ⅲ)椭圆()222210x y a b a b+=>>的一个顶点为()0,3A -,∴3b =,由OA OF =,得3c b ==,又由222a b c =+,得2228313a =+=,所以椭圆的方程为221189x y +=.(Ⅲ)直线AB 与以C 为圆心的圆相切于点P ,所以CP AB ⊥,根据题意可知,直线AB 和直线CP 的斜率均存在, 设直线AB 的斜率为k ,则直线AB 的方程为3y kx ,即3y kx =-,2231189y kx x y =-⎧⎪⎨+=⎪⎩,消去y ,可得()2221120k x kx +-=,解得0x =或21221k x k =+. 将21221k x k =+代入3y kx =-,得222126321213k y k k k k =⋅--=++,所以点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭, 因为P 为线段AB 的中点,点A 的坐标为()0,3-,所以点P 的坐标为2263,2121kk k -⎛⎫ ⎪++⎝⎭,由3OC OF =,得点C 的坐标为()1,0,所以直线CP 的斜率为222303216261121CP k kk k k k --+=-+-+=, 又因为CP AB ⊥,所以231261k k k ⋅=--+,整理得22310k k -+=,解得12k =或1k =. 所以,直线AB 的方程为132y x =-或3y x =-.3.【2019年高考全国Ⅰ卷理数】已知抛物线C :y 2=3x 的焦点为F ,斜率为的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程; (2)若,求|AB |. 【解析】设直线()()11223:,,,,2l y x t A x y B x y =+. 323AP PB =(1)由题设得3,04F ⎛⎫⎪⎝⎭,故123||||2AF BF x x +=++,由题设可得1252x x +=.由2323y x t y x⎧=+⎪⎨⎪=⎩,可得22912(1)40x t x t +-+=,则1212(1)9t x x -+=-. 从而12(1)592t --=,得78t =-. 所以l 的方程为3728y x =-.(2)由3AP PB =可得123y y =-.由2323y x t y x⎧=+⎪⎨⎪=⎩,可得2220y y t -+=. 所以122y y +=.从而2232y y -+=,故211,3y y =-=. 代入C 的方程得1213,3x x ==.故||AB =. 4.【2019年高考天津卷理数】设椭圆22221(0)x y a b a b+=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4(1)求椭圆的方程;(2)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||ON OF =(O 为原点),且OP MN ⊥,求直线PB 的斜率.【答案】(1)22154x y +=;(2或. 【解析】(1)设椭圆的半焦距为c ,依题意,24,5c b a ==,又222a b c =+,可得a =2,b =1c =.所以,椭圆的方程为22154x y +=.(2)由题意,设()()()0,,0P P p M P x y x M x ≠,.设直线PB 的斜率为()0k k ≠, 又()0,2B ,则直线PB 的方程为2y kx =+,与椭圆方程联立222,1,54y kx x y =+⎧⎪⎨+=⎪⎩整理得()2245200k x kx ++=,可得22045P k x k =-+,代入2y kx =+得2281045P k y k-=+, 进而直线OP 的斜率24510P p y k x k-=-. 在2y kx =+中,令0y =,得2M x k=-. 由题意得()0,1N -,所以直线MN 的斜率为2k -. 由OP MN ⊥,得2451102k k k-⎛⎫⋅-=- ⎪-⎝⎭,化简得2245k =,从而k =±所以,直线PB的斜率为5或5-. 5.【2019年高考江苏卷】如图,在平面直角坐标系xOy 中,椭圆C :22221(0)x y a b a b+=>>的焦点为F 1(–1、0),F 2(1,0).过F 2作x 轴的垂线l ,在x 轴的上方,l 与圆F 2:222(1)4x y a -+=交于点A ,与椭圆C 交于点D .连结AF 1并延长交圆F 2于点B ,连结BF 2交椭圆C 于点E ,连结DF 1. 已知DF 1=52. (1)求椭圆C 的标准方程; (2)求点E 的坐标.【答案】(1)22143x y +=;(2)3(1,)2E --. 【解析】(1)设椭圆C 的焦距为2c .因为F 1(−1,0),F 2(1,0),所以F 1F 2=2,c =1. 又因为DF 1=52,AF 2⊥x 轴,所以DF 232==, 因此2a =DF 1+DF 2=4,从而a =2. 由b 2=a 2−c 2,得b 2=3.因此,椭圆C 的标准方程为22143x y +=.(2)解法一:由(1)知,椭圆C :22143x y +=,a =2,因为AF 2⊥x 轴,所以点A 的横坐标为1. 将x =1代入圆F 2的方程(x −1) 2+y 2=16,解得y =±4. 因为点A 在x 轴上方,所以A (1,4). 又F 1(−1,0),所以直线AF 1:y =2x +2.由22()22116y x x y =+-+=⎧⎨⎩,得256110x x +-=,解得1x =或115x =-. 将115x =-代入22y x =+,得 125y =-, 因此1112(,)55B --.又F 2(1,0),所以直线BF 2:3(1)4y x =-.由221433(1)4x y x y ⎧⎪⎪⎨⎪+=-⎩=⎪,得276130x x --=,解得1x =-或137x =.又因为E 是线段BF 2与椭圆的交点,所以1x =-. 将1x =-代入3(1)4y x =-,得32y =-. 因此3(1,)2E --.解法二:由(1)知,椭圆C :22143x y +=.如图,连结EF 1.因为BF 2=2a ,EF 1+EF 2=2a ,所以EF 1=EB , 从而∠BF 1E =∠B .因为F 2A =F 2B ,所以∠A =∠B , 所以∠A =∠BF 1E ,从而EF 1∥F 2A . 因为AF 2⊥x 轴,所以EF 1⊥x 轴.因为F 1(−1,0),由221431x x y ⎧⎪⎨+==-⎪⎩,得32y =±.又因为E 是线段BF 2与椭圆的交点,所以32y =-. 因此3(1,)2E --.6.【2018年高考全国Ⅱ卷理数】设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =.(1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.【答案】(1)1y x =-;(2)22(3)(2)16x y -+-=或22(11)(6)144x y -++=. 【解析】(1)由题意得(1,0)F ,l 的方程为(1)(0)y k x k =->. 设1221(,),(,)A y x y x B ,由2(1),4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=. 216160k ∆=+>,故122224kx k x ++=. 所以122244||||||(1)(1)x k AB AF BF k x +=+=+++=.由题设知22448k k +=,解得1k =-(舍去),1k =. 因此l 的方程为1y x =-.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为2(3)y x -=--,即5y x =-+. 设所求圆的圆心坐标为00(,)x y ,则00220005,(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩解得003,2x y =⎧⎨=⎩或0011,6.x y =⎧⎨=-⎩ 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.7..【2018年高考江苏卷】如图,在平面直角坐标系xOy 中,椭圆C过点1)2,焦点12(F F ,圆O 的直径为12F F .(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标; ②直线l 与椭圆C 交于,A B 两点.若OAB △,求直线l 的方程.【答案】(1)椭圆C 的方程为2214x y +=,圆O 的方程为223x y +=;(2)①;②y =+. 【解析】(1)因为椭圆C的焦点为12(),F F -,可设椭圆C 的方程为22221(0)x y a b a b+=>>.又点1)2在椭圆C 上,所以2222311,43,a b a b ⎧+=⎪⎨⎪-=⎩,解得224,1,a b ⎧=⎪⎨=⎪⎩ 因此椭圆C 的方程为2214x y +=.因为圆O 的直径为12F F ,所以其方程为223x y +=.(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>,则22003x y +=,所以直线l 的方程为0000()x y x x y y =--+,即0003x y x y y =-+. 由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩消去y ,得222200004243640()x y x x x y +-+-=.(*)因为直线l 与椭圆C 有且只有一个公共点,所以222222000000()()(24)(44364820)4x x y y y x ∆=--+-=-=. 因为00,0x y >,所以001x y ==.因此点P的坐标为.②因为三角形OAB,所以1 2AB OP ⋅=,从而AB =. 设1122,,()(),A x y B x y ,由(*)得001,2x =,所以2222121()()x B y y x A =-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+.因为22003x y +=,所以22022016(2)32(1)49x AB x -==+,即42002451000x x -+=, 解得22005(202x x ==舍去),则2012y =,因此P的坐标为. 综上,直线l的方程为y =+.8.【2018年高考天津卷理数】设椭圆22221x y a b+=(a >b >0)的左焦点为F ,上顶点为B.已知椭圆的离心率为A 的坐标为(,0)b,且FB AB ⋅= (1)求椭圆的方程;(2)设直线l :(0)y kx k =>与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q .若4AQ AOQ PQ=∠(O 为原点),求k 的值. 【答案】(1)22194x y +=;(2)111228或. 【解析】(1)设椭圆的焦距为2c ,由已知有2259c a =,又由a 2=b 2+c 2,可得2a =3b .由已知可得,FB a =,AB =,由FB AB ⋅=ab =6, 从而a =3,b =2,所以椭圆的方程为22194x y +=.(2)设点P 的坐标为(x 1,y 1),点Q 的坐标为(x 2,y 2). 由已知有y 1>y 2>0,故12sin PQ AOQ y y ∠=-. 又因为2sin y AQ OAB =∠,而∠OAB =π4,故2AQ =.由AQ AOQ PQ=∠,可得5y 1=9y 2. 由方程组22194y kx x y =⎧⎪⎨+=⎪⎩,,消去x,可得1y =. 易知直线AB 的方程为x +y –2=0,由方程组20y kx x y =⎧⎨+-=⎩,,消去x ,可得221ky k =+.由5y 1=9y 2,可得5(k +1)=两边平方,整理得25650110k k -+=,解得12k =,或1128k =. 所以k 的值为111228或. 命题规律二 圆锥曲线中定点问题【解决之道】圆锥曲线中定点问题的两种解法(1)引进参数法:引进动点的坐标或动线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点.(2)特殊到一般法,根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关. 【三年高考】1.【2020年高考全国Ⅰ卷理数20】已知,A B 分别为椭圆()222:11x E y a a+=>的左、右顶点,G 为E 的上顶点,8AG GB ⋅=,P 为直线6x =上的动点,PA 与E 的另一交点为,C PB 与E 的另一交点为D . (1)求E 的方程;(2)证明:直线CD 过定点. 【解析】(1)依据题意作出如下图像:由椭圆方程222:1(1)x E y a a+=>可得:(),0A a -, (),0B a ,()0,1G ,∴(),1AG a =,(),1GB a =-,∴218AG GB a ⋅=-=,∴29a =,∴椭圆方程为:2219x y +=. (2)证明:设()06,P y ,则直线AP 的方程为:()()00363y y x -=+--,即:()039y y x =+,联立直线AP 的方程与椭圆方程可得:()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩,整理得:()2222000969810y x y x y +++-=,解得:3x =-或20203279y x y -+=+,将20203279y x y -+=+代入直线()039y y x =+可得:02069y y y =+,∴点C 的坐标为20022003276,99y y y y ⎛⎫-+ ⎪++⎝⎭,同理可得:点D 的坐标为2002200332,11y y y y ⎛⎫-- ⎪++⎝⎭, ∴直线CD 的方程为:0022********2000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=-⎪ ⎪-+-++⎝⎭⎝⎭-++, 整理可得:()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭,整理得:()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭,故直线CD 过定点3,02⎛⎫ ⎪⎝⎭.2.【2019年高考全国Ⅲ卷理数】已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点: (2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积. 【答案】(1)见详解;(2)3或 【解析】(1)设()111,,,2D t A x y ⎛⎫-⎪⎝⎭,则2112x y =.由于y'x =,所以切线DA 的斜率为1x ,故11112y x x t+=- .整理得112 2 +1=0. tx y -设()22,B x y ,同理可得222 2 +1=0tx y -. 故直线AB 的方程为2210tx y -+=. 所以直线AB 过定点1(0,)2.(2)由(1)得直线AB 的方程为12y tx =+. 由2122y tx x y ⎧=+⎪⎪⎨⎪=⎪⎩,可得2210x tx --=. 于是()2121212122,1,121x x t x x y y t x x t +==-+=++=+,()212||21AB x t =-==+.设12,d d 分别为点D ,E到直线AB的距离,则12d d ==因此,四边形ADBE 的面积()(2121||32S AB d d t =+=+设M 为线段AB 的中点,则21,2M t t ⎛⎫+⎪⎝⎭. 由于EM AB ⊥,而()2,2EM t t =-,AB 与向量(1, )t 平行,所以()220t t t +-=.解得t =0或1t =±. 当t =0时,S =3;当1t =±时,S =因此,四边形ADBE 的面积为3或3.【2019年高考北京卷理数】已知抛物线C :x 2=−2py 经过点(2,−1).(1)求抛物线C 的方程及其准线方程;(2)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线y =−1分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点. 【答案】(1)抛物线C 的方程为24x y =-,准线方程为1y =;(2)见解析.【解析】(1)由抛物线2:2C x py =-经过点(2,1)-,得2p =.所以抛物线C 的方程为24x y =-,其准线方程为1y =. (2)抛物线C 的焦点为(0,1)F -. 设直线l 的方程为1(0)y kx k =-≠. 由21,4y kx x y=-⎧⎨=-⎩得2440x kx +-=. 设()()1122,,,M x y N x y ,则124x x =-. 直线OM 的方程为11y y x x =. 令1y =-,得点A 的横坐标11A x x y =-. 同理得点B 的横坐标22B x x y =-. 设点(0, )D n ,则1212,1,,1x x DA n DB n y y ⎛⎫⎛⎫=---=--- ⎪ ⎪⎝⎭⎝⎭,21212(1)x x DA DB n y y ⋅=++ 2122212(1)44x x n x x =++⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭ 21216(1)n x x =++ 24(1)n =-++.令0DA DB ⋅=,即24(1)0n -++=,则1n =或3n =-. 综上,以AB 为直径的圆经过y 轴上的定点(0,1)和(0,3)-.命题规律三 圆锥曲线中的最值问题【解决之道】圆锥曲线中的最值问题类型较多,解法灵活多变,但总体上主要有两种方法:一是利用几何法,即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解;二是利用代数法,即把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式),然后利用函数方法、不等式方法等进行求解. 【三年高考】1.【2020年高考江苏卷18】在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为1F 、2F ,点A 在椭圆E 上且在第一象限内,212AF F F ⊥,直线1AF 与椭圆E 相交于另一点B .(1)求12AF F ∆的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ⋅的最小值; (3)设点M 在椭圆E 上,记OAB ∆与MAB ∆的面积分别为12,S S ,若213S S =,求点M 的坐标.【解析】(1)12AF F ∆的周长226l a c =+=.(2)由椭圆方程得3(1,)2A ,设点(,0)P t ,则直线AP 方程为32()1y x t t =--,令24a x c ==得361232 12(1)Q t t y t t --==--,即123(4,)22t Q t --,123(4,)22t QP t t -=--, 224(2)44OP QP t t t ⋅=-=--≥-,即OP QP ⋅的最小值为4-.(3)设 O 到直线AB 的距离为1d ,M 到直线AB 的距离为2d ,若213S S =,则2111||||322AB d AB d ⨯⨯=⨯⨯⨯,即213d d =, 由(1)可得直线AB 方程为3(1)4y x =+,即3430x y -+=,∴135d =,295d =.由题意得,M 点应为与直线AB 平行且距离为95的直线与椭圆的交点,设平行于AB 的直线l 为340x y m -+=,与直线AB 的距离为95,95=,即6m =-或12.当6m =-时,直线l 为3460x y --=,即3(2)4y x =-, 联立223(2)4143y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩可得(2)(72)0x x -+=,即20M N x y =⎧⎨=⎩或27127M Nx y =⎧⎪-=⎨-⎪⎪⎪⎩, ∴(2,0)M 或212(,)77--. 当12m =时,直线l 为34120x y -+=,即3(4)4y x =+, 联立223(4)4143y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩可得221182404x x ++=,9(3656)0∆=⨯-<,∴无解. 综上所述,M 点坐标为(2,0)或212(,)77--. 2.【2020年高考浙江卷21】如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于M (B ,M 不同于A ).(Ⅲ)若116=p ,求抛物线2C 的焦点坐标; (Ⅲ)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值. 【解析】(Ⅲ)当116=p 时,2C 的方程为218y x =,故抛物线2C 的焦点坐标为1(,0)32;(Ⅲ)设()()()112200,,,,,,:A x y B x y M m l x y x y λ=+由()22222222220x y y my m x y mλλλ⎧+=⇒+++-=⎨=+⎩ 1200022222,,222m m my y y x y m λλλλλλ--∴+===+=+++ 由M 在抛物线上,∴()222222244222m pm mp λλλλλ=⇒=+++ 22222()220y pxy p y m y p y pm x y mλλλ⎧=⇒=+⇒--=⎨=+⎩ 12101021202222222y y p x x y m y m p mmx p m λλλλλλ∴+=∴+=+++=+∴=+-+由22221{42,22x y x px y px+=⇒+==即2420x px +-=12x p ⇒==-222221822228162p p p m p p p λλλλλ+⇒-=+⋅=++≥+18p ≥,21160p ≤,p ≤ ∴p的最大值为40,此时(55A .3.【2019年高考全国Ⅱ卷理数】已知点A (−2,0),B (2,0),动点M (x ,y )满足直线AM 与BM 的斜率之积为−12.记M 的轨迹为曲线C .(1)求C 的方程,并说明C 是什么曲线;(2)过坐标原点的直线交C 于P ,Q 两点,点P 在第一象限,PE ⊥x 轴,垂足为E ,连结QE 并延长交C 于点G .(i )证明:PQG △是直角三角形; (ii )求PQG △面积的最大值.【解析】(1)由题设得1222y y x x ⋅=-+-,化简得221(||2)42x y x +=≠,所以C 为中心在坐标原点,焦点在x 轴上的椭圆,不含左右顶点.(2)(i )设直线PQ 的斜率为k ,则其方程为(0)y kx k =>.由22142y kxx y =⎧⎪⎨+=⎪⎩得x =.记u =,则(,),(,),(,0)P u uk Q u uk E u --.于是直线QG 的斜率为2k ,方程为()2ky x u =-. 由22(),2142k y x u x y ⎧=-⎪⎪⎨⎪+=⎪⎩得 22222(2)280k x uk x k u +-+-=.①设(,)G G G x y ,则u -和G x 是方程①的解,故22(32)2G u k x k +=+,由此得322G uky k=+.从而直线PG 的斜率为322212(32)2uk uk k u k kuk -+=-+-+. 所以PQ PG ⊥,即PQG △是直角三角形.(ii )由(i)得||2PQ =||PG =△PQG 的面积222218()18(1)||12(12)(2)12()k k k k S PQ PG k k k k++===++++‖. 设t =k +1k ,则由k >0得t ≥2,当且仅当k =1时取等号.因为2812t S t =+在[2,+∞)单调递减,所以当t =2,即k =1时,S 取得最大值,最大值为169.因此,△PQG 面积的最大值为169.4.【2019年高考浙江卷】如图,已知点(10)F ,为抛物线22(0)y px p =>的焦点,过点F 的直线交抛物线于A 、B 两点,点C 在抛物线上,使得ABC △的重心G 在x 轴上,直线AC 交x 轴于点Q ,且Q 在点F 的右侧.记,AFG CQG △△的面积分别为12,S S . (1)求p 的值及抛物线的准线方程; (2)求12S S 的最小值及此时点G 的坐标.【答案】(1)p =2,准线方程为x =−1;(2)最小值为1+G (2,0).【解析】(1)由题意得12p=,即p =2. 所以,抛物线的准线方程为x =−1.(2)设()()(),,,,,A A B B c c A x y B x y C x y ,重心(),G G G x y .令2,0A y t t =≠,则2A x t =.由于直线AB 过F ,故直线AB 方程为2112t x y t-=+,代入24y x =,得()222140t y y t---=,故24B ty =-,即2B y t =-,所以212,B tt ⎛⎫- ⎪⎝⎭.又由于()()11,33G A B c G A B c x x x x y y y y =++=++及重心G 在x 轴上,故220c t y t-+=,得242211222,2,,03t t C t t G t t t ⎛⎫⎛⎫-+⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 所以,直线AC 方程为()222y t t x t-=-,得()21,0Q t-.由于Q 在焦点F 的右侧,故22t >.从而4224221244242222211|2|||322221222211|||1||2|23Ac t t t FG y t S t t t t t S t t QG y t t t t-+-⋅⋅--====--+--⋅--⋅-.令22m t =-,则m >0,12212221343242S m S m m m m m =-=--=+++++. 当m =时,12S S 取得最小值1+G (2,0). 命题规律四 圆锥曲线中的定值问题【解决之道】圆锥曲线中定值问题的特点及两大解法(1)特点:待证几何量不受动点或动线的影响而有固定的值. (2)两大解法:①从特殊入手,求出定值,再证明这个值与变量无关;②引起变量法:其解题流程为【三年高考】1.(2020•山东高考,22)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为2,且过点(2,1)A .(1)求C 的方程;(2)点M ,N 在C 上,且AM AN ⊥,AD MN ⊥,D 为垂足.证明:存在定点Q ,使得||DQ 为定值. 【解析】(1)离心率c e a ==a ∴=,又222a b c =+, b c ∴=,a =,把点(2,1)A 代入椭圆方程得,224112b b+=,解得23b =, 故椭圆C 的方程为22163x y +=.(2)①当直线MN 的斜率存在时,设其方程为y kx m =+,联立22163y kx mx y =+⎧⎪⎨+=⎪⎩,得222(21)4260k x kmx m +++-=,由△222(4)4(21)(26)0km k m =-+->,知2263m k <+,设1(M x ,1)y ,2(N x ,2)y ,则122421kmx x k +=-+,21222621m x x k -=+,AM AN⊥,∴1(2AM AN x =-,121)(2y x --,21)0y -=,即221212(1)(2)()250k x x km k x x m m ++--++-+=,22222264(1)(2)()2502121m kmk km k m m k k -∴++---+-+=++,化简整理得,2248321(21)(231)0k km m m k m k m ++--=+-++=, 12m k ∴=-或213k m +=-, 当12m k =-时,21y kx k =-+,过定点(2,1)A ,不符合题意,舍去; 当213k m +=-时,213k y kx +=-,过定点21(,)33-. 设0(D x ,0)y ,则00y kx m =+, ()i 若0k ≠,AD MN ⊥,∴00112kx m k x +-=--,解得20224633k k x k ++=+,20234133k k y k +-=+, ∴22422222002222412422428(21)8()()()()3333339(1)9k k k k k k x y kk k -+++-++-+-=+==+++,∴点D 在以4(3,1)3为半径的圆上, 故存在4(3Q ,1)3,使得||DQ =,为定值.()ii 若0k =,则直线MN 的方程为13y =-,AD MN ⊥,1(2,)3D ∴-,||DQ ∴=,为定值.②当直线MN 的斜率不存在时,设其方程为x t =,(,)M t s ,(,)N t s -,且22163t s +=,AM AN ⊥,∴(2AM AN t =-,1)(2s t --,22231)454202s t t s tt --=--+=-+=,解得23t =或2(舍2),2(3D ∴,1),此时||DQ ==,为定值. 综上所述,存在定点4(3Q ,1)3,使得||DQ .2.【2018年高考北京卷理数】已知抛物线C :2y =2px 经过点P (1,2).过点Q (0,1)的直线l 与抛物线C 有两个不同的交点A ,B ,且直线P A 交y 轴于M ,直线PB 交y 轴于N . (1)求直线l 的斜率的取值范围;(2)设O 为原点,QM QO λ=,QN QO μ=,求证:11λμ+为定值.【答案】(1)(-∞,-3)∪(-3,0)∪(0,1);(2)见解析.【解析】(1)因为抛物线y 2=2px 经过点P (1,2), 所以4=2p ,解得p =2,所以抛物线的方程为y 2=4x . 由题意可知直线l 的斜率存在且不为0, 设直线l 的方程为y =kx +1(k ≠0). 由241y x y kx ⎧=⎨=+⎩得22(24)10k x k x +-+=. 依题意22(24)410k k ∆=--⨯⨯>,解得k <0或0<k <1. 又P A ,PB 与y 轴相交,故直线l 不过点(1,-2).从而k ≠-3. 所以直线l 斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1). (2)设A (x 1,y 1),B (x 2,y 2). 由(1)知12224k x x k -+=-,1221x x k =. 直线P A 的方程为1122(1)1y y x x --=--. 令x =0,得点M 的纵坐标为1111212211M y kx y x x -+-+=+=+--. 同理得点N 的纵坐标为22121N kx y x -+=+-. 由=QM QO λ,=QN QO μ得=1M y λ-,1N y μ=-.所以2212121212122224112()111111=2111(1)(1)11M N k x x x x x x k k y y k x k x k x x k k λμ-+---++=+=+=⋅=⋅------.所以11λμ+为定值.命题规律五 圆锥曲线中的取值范围问题【解决之道】解决圆锥曲线中的取值范围问题应考虑的五个方面(1)利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围;(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是建立两个参数之间的等量关系; (3)利用隐含的不等关系建立不等式,从而求出参数的取值范围; (4)利用已知的不等关系构造不等式,从而求出参数的取值范围;(5)利用求函数的值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围. 【三年高考】1.(2020•上海,20)已知双曲线2212:14x y bΓ-=与圆2222:4(0)x y b b Γ+=+>交于点(A A x ,)A y (第一象限),曲线Γ为1Γ、2Γ上取满足||A x x >的部分. (1)若A x =b 的值;(2)当b 2Γ与x 轴交点记作点1F 、2F ,P 是曲线Γ上一点,且在第一象限,且1||8PF =,求12F PF ∠;(3)过点2(0,2)2b D +斜率为2b-的直线l 与曲线Γ只有两个交点,记为M 、N ,用b 表示OM ON ,并求OM ON 的取值范围.【解析】(1)由A x =,点A 为曲线1Γ与曲线2Γ的交点,联立222222144A A A Ax y bx y b ⎧-=⎪⎨⎪+=+⎩,解得A y =,2b =; (2)由题意可得1F ,2F 为曲线1Γ的两个焦点,由双曲线的定义可得12||||2PF PF a -=,又1||8PF =,24a =, 所以2||844PF =-=,因为b =3c =, 所以12||6F F =,在△12PF F 中,由余弦定理可得22212121212||||||cos 2||||PF PF F F F PF PF PF +-∠=6416361128416+-==⨯⨯,由120F PF π<∠<,可得1211arccos16F PF ∠=;(3)设直线24:22b b l y x +=-+,可得原点O 到直线l 的距离24||b d +== 所以直线l 是圆的切线,设切点为M , 所以2OM k b =,并设2:OM y x b =与圆2224x y b +=+联立,可得222244x x b b+=+, 可得x b =,2y =,即(,2)M b ,注意直线l 与双曲线的斜率为负的渐近线平行, 所以只有当2A y >时,直线l 才能与曲线Γ有两个交点, 由222222144A A A Ax y b x y b⎧-=⎪⎨⎪+=+⎩,可得422A b y a b =+,所以有4244b b<+,解得22b >+22b <-, 因为OM 为ON 在OM 上的投影可得,24OM ON b =+,所以246OM ON b =+>+,则(6OM ON ∈+)+∞.2.【2018年高考浙江卷】如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线C :y 2=4x 上存在不同的两点A ,B 满足P A ,PB 的中点均在C 上.(1)设AB 中点为M ,证明:PM 垂直于y 轴;(2)若P 是半椭圆x 2+24y =1(x <0)上的动点,求△P AB 面积的取值范围.【答案】(1)见解析;(2)]4. 【解析】本题主要考查椭圆、抛物线的几何性质,直线与抛物线的位置关系等基础知识,同时考查运算求解能力和综合应用能力.满分15分. (1)设00(,)P x y ,2111(,)4A y y ,2221(,)4B y y . 因为PA ,PB 的中点在抛物线上,所以1y ,2y 为方程202014()422y x y y ++=⋅即22000280y y y x y -+-=的两个不同的实数根. 所以1202y y y +=. 因此,PM 垂直于y 轴.(2)由(1)可知120212002,8,y y y y y x y +=⎧⎪⎨=-⎪⎩所以2221200013||()384PM y y x y x =+-=-,12||y y -=因此,PAB △的面积32212001||||4)24PABS PM y y y x =⋅-=-△. 因为220001(0)4y x x +=<,所以2200004444[4,5]y x x x -=--+∈.因此,PAB △面积的取值范围是. 命题规律六 圆锥曲线中的证明问题【解决之道】圆锥曲线中证明问题,常见位置关系方面的,如证明相切、垂直、过定点等;数量关系方面的,如存在定值、恒成立等.在熟悉圆锥曲线的定义和性质的前提下,要多采用直接法证明,但有时也会用到反证法. 【三年高考】1.【2018年高考全国Ⅲ卷理数】设椭圆22:12x C y +=的右焦点为F ,过F 的直线l 与C 交于,A B 两点,点M 的坐标为(2,0).(1)当l 与x 轴垂直时,求直线AM 的方程; (2)设O 为坐标原点,证明:OMA OMB ∠=∠.【答案】(1)y x =或y x =;(2)见解析. 【解析】(1)由已知得(1,0)F ,l 的方程为x =1.由已知可得,点A 的坐标为(1,2或(1,2-,所以AM 的方程为2y x =-2y x =. (2)当l 与x 轴重合时,0OMA OMB ∠=∠=︒.当l 与x 轴垂直时,OM 为AB 的垂直平分线,所以OMA OMB ∠=∠.当l 与x 轴不重合也不垂直时,设l 的方程为(1)(0)y k x k =-≠,1221(,),(,)A y x y x B ,则12x x <<MA ,MB 的斜率之和为212122MA MB x x y yk k +=+--. 由1122,y k k x y k x k =-=-得121212(23()42)(2)MA MB x x x x k k x x kk k -+++=--.将(1)y k x =-代入2212x y +=得2222(21)4220k x k x k +-+-=.所以21221222422,2121x x x k k k x k -+==++, 则3131322244128423()4021k k k k kk k k k x x x x --++-++==+. 从而0MA MB k k +=,故MA ,MB 的倾斜角互补,所以OMA OMB ∠=∠. 综上,OMA OMB ∠=∠.2.【2018年高考全国Ⅲ卷理数】已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点,线段AB 的中点为()()10M m m >,. (1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且FP FA FB ++=0.证明:FA ,FP ,FB 成等差数列,并求该数列的公差.【答案】(1)见解析;(2)见解析.【解析】(1)设1221(,),(,)A y x y x B ,则222212121,14343y x y x +=+=.两式相减,并由1221y x y k x -=-得1122043y x y k x +++⋅=.由题设知12121,22x y x y m ++==,于是34k m=-. 由题设得302m <<,故12k <-.(2)由题意得(1,0)F ,设33(,)P x y ,则331122(1,)(1,)(1,)(0,0)y x x y x y -+-+-=. 由(1)及题设得3321213()1,()20y y x x y x m =-+==-+=-<.又点P 在C 上,所以34m =,从而3(1,)2P -,3||2FP =.于是1||(22x FA x ===-,同理2||22x FB =-, 所以121||||4()32FA FB x x +=-+=,故2||||||FP FA FB =+,即||,||,||FA FP FB 成等差数列.设该数列的公差为d ,则1212||||||||||2FB FA x x d =-=-=.① 将34m =代入34k m =-得1k =-,所以l 的方程为74y x =-+,代入C 的方程,并整理得2171404x x -+=,故121212,28x x x x +==,代入①解得||d =或。
(晨鸟)2020年高考理科数学《圆锥曲线》题型归纳与训练

2020年高考理科数学《圆锥曲线》题型归纳与训练【题型归纳】题型一求曲线的方程例1已知1(2,0)F ,2(2,0)F ,点P 满足12||||2PF PF ,记点P 的轨迹为E .求轨迹E 的方程.【答案】1322yx【解析】由1212||||24||PF PF F F 可知:点P 的轨迹E 是以12,F F 为焦点的双曲线的右支,由2,22c a ,∴222213b,故轨迹E 的方程为)(01322xyx.【易错点】(1)对于双曲线的定义理解片面;(2)如果动点P 满足)(212122F F aa PF PF ,则点P 的轨迹是双曲线。
但该题已知条件中给出的是“12||||2PF PF ”只能表示点P 的轨迹是双曲线的右支,而不是双曲线的全部。
【思维点拨】利用双曲线解题时,一定要观察是双曲线的全部还是部分。
题型二定值、定点问题例2已知椭圆C :x 2a 2+y2b 2=1过A(2,0),B(0,1)两点.(1)求椭圆C 的方程及离心率;(2)设P 为第三象限内一点且在椭圆C 上,直线PA 与y 轴交于点M ,直线PB 与x 轴交于点N ,求证:四边形ABNM 的面积为定值.【答案】(1)x 24+y 2=1,e =32(2)2.【解析】(1)由题意得a=2,b=1,所以椭圆C的方程为x24+y2=1.又c=a2-b2=3,所以离心率e=ca=32.(2)证明:设P(x0,y0)(x0<0,y0<0),则x20+4y20=4. 又A(2,0),B(0,1),所以直线P A的方程为y=y0x0-2(x-2).令x=0,得y M=-2y0x0-2,从而|BM|=1-y M=1+2y0x0-2.直线PB的方程为y=y0-1x0x+1.令y=0,得x N=-x0y0-1,从而|AN|=2-x N=2+x0y0-1.所以四边形ABNM的面积S=12|AN|·|BM|=122+x0y0-11+2y0x0-2=x20+4y20+4x0y0-4x0-8y0+42x0y0-x0-2y0+2=2x0y0-2x0-4y0+4x0y0-x0-2y0+2=2.从而四边形ABNM的面积为定值.【易错点】(1).想不到设出P(x0,y0)后,利用点斜式写出直线P A,PB的方程.不会由直线P A,PB的方程求解|BM|,|AN|;(2).不知道四边形的面积可用S=12| AN|·|BM|表示;(3).四边形ABNM的面积用x0,y0表示后,不会变形、化简,用整体消参来求值.【思维点拨】第(1)问由a=2,b=1,c=3,解第一问;第(2)问画草图可知AN ⊥BM ,四边形ABNM 的面积为12|AN|·|BM|,设点P(x 0,y 0),得出P A ,PB 的方程,进而得出M ,N 的坐标,得出|AN|,|BM|,只需证明12|AN|·|BM|是一个与点P 的坐标无关的量即可.例3已知椭圆C :x 2a 2+y2b 2=1(a>b>0),四点P 1(1,1),P 2(0,1),P 3231,,P 423,1,中恰有三点在椭圆C 上.(1)求C 的方程;(2)设直线l 不经过P 2点且与C 相交于A ,B 两点.若直线P 2A 与直线P 2B 的斜率的和为-1,证明:l 过定点.【答案】(1)x 24+y 2=1(2)(2,-1)【解析】(1)因为P 3231,,P 423,1,,所以P 3,P 4两点关于y 轴对称,故由题设知椭圆C 经过P 3,P 4两点.又由1a 2+1b 2>1a 2+34b 2知,椭圆C 不经过点P 1,所以点P 2在椭圆C 上.因此1b2=1,1a 2+34b2=1,解得a 2=4,b 2=1.故椭圆C 的方程为x 24+y 2=1.(2)证明:设直线P 2A 与直线P 2B 的斜率分别为k 1,k 2. 如果l 与x 轴垂直,设l :x =t ,由题设知t ≠0,且|t|<2,可得A ,B 的坐标分别为242t t ,,242t t ,.则k 1+k 2=4-t 2-22t -4-t 2+22t =-1,得t =2,不符合题设.从而可设l :y =kx +m(m ≠1).将y =kx +m 代入x 24+y 2=1得(4k 2+1)x 2+8kmx +4m 2-4=0. 由题设可知Δ=16(4k 2-m 2+1)>0. 设A(x 1,y 1),B(x 2,y 2),x 1+x 2=-8km4k 2+1,x 1x 2=4m 2-44k 2+1.而k 1+k 2=y 1-1x 1+y 2-1x 2=kx 1+m -1x 1+kx 2+m -1x 2=12121221kx x m x x x x .由题设k 1+k 2=-1,故(2k +1)x 1x 2+(m -1)(x 1+x 2)=0. 即(2k +1)·4m 2-44k 2+1+(m -1)·-8km 4k 2+1=0.解得k =-m +12.当且仅当m>-1时,Δ>0,于是l :y =-m +12x +m ,即y +1=-m +12(x -2),所以l 过定点(2,-1).【易错点】(1)观察不出P 3,P 4对称,忽视对称性导致判断失误;(2)不会用点的坐标代入方程判断P 1,P 2是否在椭圆上而滞做;(3)联立直线l 与椭圆C 的方程,计算化简失误而滞做; (4)利用k 1+k 2=-1运算变形不明确变形目标,导致化简不出k ,m 的关系.【思维点拨】第(1)问利用椭圆的性质,易排除点P 1(1,1)不在椭圆上,从而求椭圆方程;第(2)问分类讨论斜率是否存在,若存在,设l :y =kx +m ,利用条件建立k ,m的等量关系,消参后再表示出直线l 的方程可证明.题型三最值(范围)问题例4已知椭圆C :x 2a 2+y 2=1(a >0),F 1,F 2分别是其左、右焦点,以F 1F 2为直径的圆与椭圆C 有且仅有两个交点.(1)求椭圆C 的方程;(2)设过点F 1且不与坐标轴垂直的直线l 交椭圆于A ,B 两点,线段AB 的垂直平分线与x 轴交于点P ,点P 横坐标的取值范围是-14,0,求线段AB 长的取值范围.【答案】(1)x 22+y 2=1(2)322,22【解析】(1)因为以F 1F 2为直径的圆与椭圆C 有且仅有两个交点,所以b =c =1,a =2,所以椭圆C 的方程为x 22+y 2=1.(2)根据题意,直线A ,B 的斜率存在且不为0,设直线AB 的方程为y =k(x +1),与x 22+y 2=1联立,消去y 并整理得(1+2k 2)x 2+4k 2x +2k 2-2=0,设A(x 1,y 1),B(x 2,y 2),AB 的中点为M(x 0,y 0),则x 1+x 2=-4k21+2k 2,x 1·x 2=2k 2-21+2k2,y 1+y 2=k(x 1+1)+k(x 2+1)=k(x 1+x 2+2)=2k1+2k 2,即M -2k 21+2k 2,k 1+2k 2. 则直线AB 的垂直平分线为y -k 1+2k 2=-1k x +2k 21+2k 2,令y =0,得x P =-k 21+2k2,因为x P ∈-14,0,即-14<-k 21+2k2<0,所以0<k 2<12,22121214AB kx x x x =222222422142121k k kkk=2212221k k=21+11+2k 2.∵12<12k 2+1<1,∴|AB|∈322,22.【易错点】运算错误,由于运算方法、运算技巧以及自身运算能力差,都是出错原因。
2020年全国高考数学·第46讲 圆锥曲线综合

2020年全国高考数学第46讲圆锥曲线综合考纲解读1.掌握与圆锥曲线有关的最值、定值和参数范围问题.2.会处理动曲线(含直线)过定点的问题.3.会证明与曲线上的动点有关的定值问题.4.会按条件建立目标函数,研究变量的最值及取值范围问题,注意运用数形结合法和几何法求某些量的最值.命题趋势研究从内容上看,高考主要考查两大类问题:一是根据条件,求出表示平面曲线的方程;二是通过方程,研究平面曲线的性质,其热点有:①以客观题的形式考查圆锥曲线的基本概念和性质;②求平面曲线的方程和轨迹;③圆锥曲线的有关元素计算、关系证明或范围确定;④涉及圆锥曲线对称变换、最值或位置关系的有关问题.从形式上看,以解答题为主,难度较大.从能力要求上看,要求学生具备一定的数形结合、分析问题和解决问题及运算能力.知识点精讲一、定值问题解析几何中定值问题的证明可运用函数的思想方法来解决.证明过程可总结为“变量—函数—定值”,具体操作程序如下:(1)变量----选择适当的量为变量.(2)函数----把要证明为定值的量表示成变量的函数.(3)定值----化简得到的函数解析式,消去变量得到定值.求定值问题常见的方法有两种:(1)从特殊情况入手,求出定值,再证明该定值与变量无关;(2)直接推理、计算,并在计算推理过程中消去变量,从而得到定值.二、求最值问题常用的两种方法(1)几何法:题中给出的条件有明显的几何特征,则考虑用几何图形性质来解决,这是几何法.(2)代数法:题中给出的条件和结论的几何特征不明显,则可以建立目标函数,再求该函数的最值.求函数的最值常见的方法有基本不等式法、单调性法、导数法和三角换元法等,这就是代数法.三、求定值、最值等圆锥曲线综合问题的“三重视”(1)重视定义在解题中的作用(把定义作为解题的着眼点).(2)重视曲线的几何特征特别是平面几何性质与方程的代数特征在解题中的作用.(3)重视根与系数的关系在解题中的作用(涉及弦长、中点要用根与系数的关系).四、求参数的取值范围据已知条件及题目要求等量或不等量关系,再求参数的范围.题型归纳及思路提示题型150 平面向量在解析几何中的应用思路提示解决平面向量在解析几何中的应用要把几何特征转化为向量关系,并把向量用坐标表示.常见的应用有如下两个方面.(1)用向量的数量积解决有关角的问题.直角⇔0a b =r r g ,钝角⇔0a b <r r g (且,a b r r 不反向), 锐角⇔0a b >r r g (且,a b r r不同向).(2)利用向量的坐标表示解决共线问题.一、利用向量的数量积解决有关夹角(锐角、直角、钝角)的问题 其步骤是:先写出向量坐标式,再用向量数量积的坐标公式121222221122cos ,a b x yx y<>=++r r例10.44 过抛物线22(0)x py p =>的焦点F 作直线交抛物线于A ,B 两点,O 为坐标原点.求证:△ABO 的是钝角三角形.变式1 如图10-34所示,设椭圆的中心为原点O ,长轴在x 轴上,上顶点为A ,左右焦点分别为F 1,F 2,线段OF 1,OF 2的中点分别为B 1,B 2,且△AB 1B 2是面积为4的直角三角形. (1)求该椭圆的离心率和标准方程;(2)过B 1作直线l 交椭圆于P ,Q 两点,使PB 2⊥QB 2,求直线l 的方程.变式2 设A ,B 分别为椭圆22143x y +=的左右顶点,P 为直线4x =上不同于(4,0)的任意一点,若直线AP ,BP 分别与椭圆交于异于A ,B 的点M ,N ,证明:点B 在以MN 为直径的圆内.变式3已知1m >,直线2:02m l x my --=,椭圆222:1x C y m+=,F 1,F 2分别为椭圆C 的左右焦点. (1)当直线l 过右焦点F 2时,求直线l 的方程;(2)设直线l 与椭圆C 交于A ,B 两点,△AF 1F 2和△BF 1F 2和的重心分别是G ,H ;若原点O 在以线段GH 为直径的圆内,求实数m 的取值范围.例10.45 在直角坐标系xOy 中,点P 到两点(0,3)-,(0,3)的距离之和等于4,设点P 的轨迹为C ,直线1y kx =+与C 交于A ,B 两点.(1)写出C 的方程; (2)若OA u u u r ⊥OB uuu r,求k 的值.变式1如图10-35所示,椭圆2222:1(0)x y C a b a b+=>>的顶点为A 1,A 2,B 1,B 2,焦点为F 1,F 2,117A B =,112211222B A B A B F B F S S =Y Y .(1)求椭圆C 的方程; (2)设n 为过原点的直线,l 是与n 垂直相交于P 点,与椭圆相交于A ,B 两点的直线,1OP =u u u r,是否存在上述直线l 使0OA OB =u u u r u u u rg成立?若存在求出直线l 的方程;若不存在,请说明理由.变式2如图10-36所示,椭圆2222:1(0)x y C a b a b+=>>的一个焦点是(1,0)F ,O 为坐标原点,设过点F 的直线l交椭圆于A ,B 两点.若直线l 绕点F 任意转动,恒有222OA OB AB +<,求a 的取值范围.二、利用向量的坐标表示解决共线问题向量,a b r r共线的条件是a b λ=r r 或1221x y x y =.例10.46在平面直角坐标系xOy 中,经过点(0,2)且斜率为k 的直线l 与椭圆2212x y +=有两个不同的交点P ,Q . (1)求k 的取值范围;(2)设椭圆与x 轴正半轴、y 轴正半轴的交点分别为A ,B ,是否存在常数k ,使得向量OP uuu r +OQ uuu r 与AB u u u r共线?若存在,求k 的值;若不存在,请说明理由.变式1设椭圆22221(0)x y a b a b+=>>的左右焦点分别为F 1,F 2,离心率22e =,直线2:a l x c =,如图10-37所示,M ,N 是l 上的两个动点,120F M F N =u u u u r u u u u rg. (1)若1225F M F N ==u u u u r u u u u r,求,a b 的值;(2)证明:当MN u u u u r 取最小值时,12F M F N +u u u u r u u u u r 与12F F u u u u r共线.例10.47设A ,B 是椭圆2212x y +=上的两点,并且点(2,0)N -满足NA NB λ=u u u r u u u r ,当11[,]53λ∈时,求直线AB 斜率的取值范围.变式1已知F 1,F 2分别为椭圆22132x y +=的左右焦点,直线1l 过点F 1且垂直于椭圆的长轴,动直线2l 垂直于直线1l ,垂足为D ,线段DF 2的垂直平分线交2l 于点M . (1)求动点M 的轨迹C 的方程;(2)过点F 1作直线交曲线C 于两个不同的点P 和Q ,设11F P FQ λ=u u u r u u u r ,若[2,3]λ∈,求22F P F Q u u u u r u u u u rg的取值范围.变式2过点(1,0)F 的直线交抛物线24y x =于A ,B 两点,交直线:1l x =-于点M ,已知1MA AF λ=u u u r u u u r ,2MB BF λ=u u u r u u u r,求12λλ+的值.题型151 定点问题思路提示(1)直线过定点,由对称性知定点一般在坐标轴上,如直线y kx b =+,若b 为常量,则直线恒过(0,)b 点;若bk为常量,则直线恒过(,0)b k -.(2)一般曲线过定点,把曲线方程变为12(,)(,)0f x y f x y λ+=(λ为参数),解方程组12(,)0(,)0f x y f x y =⎧⎨=⎩即得定点.模型一:三大圆锥曲线(椭圆、双曲线、抛物线)中的顶点直角三角形的斜边所在的直线过定点.例10.48 已知椭圆22143x y +=,直线:l y kx m =+与椭圆交于A ,B 两点(A ,B 不是原点),且以AB 为直径的圆过椭圆的右顶点.求证:直线l 过定点,并求出该定点的坐标.变式1已知椭圆2214x y +=的左顶点为A ,不过点A 的直线:l y kx b =+与椭圆交于不同的两点P ,Q ,当0AP AQ =u u u r u u u rg ,求k 与b 的关系,并证明直线l 过定点.变式2 已知焦点在x 轴上的椭圆C 过点(0,1)Q 为椭圆C 的左顶点. (1)求椭圆C 的标准方程;(2)已知过点6(,0)5-的直线l 与椭圆C 交与A ,B 两点.(Ⅰ)若直线l 垂直于x 轴,求∠AQB 的大小;(Ⅱ)若直线l 与x 轴不垂直,是否存在直线l 使得△QAB 为等腰三角形?如果存在,求出直线l 的方程;如果不存在,请说明理由.例10.49已知抛物线22(0)y px p =>上异于顶点的两动点A ,B 满足以AB 为直径的圆过顶点. 求证:AB 所在的直线过定点,并求出该定点的坐标.变式1 如图10-39所示,已知定点00(,)P x y 在抛物线22y px = (0)p >上,过点P 作两直线12,l l 分别交抛物线于A,B ,且以AB 为直径的圆过点P ,证明:直线AB 过定点,并求出此定点的坐标.图10-39变式2 已知抛物线24y x =,过点(1,2)M 作两直线12,l l 分别与抛物线交于,A B 两点,且12,l l 的斜率12,k k 满足122k k =.求证:直线AB 过定点,并求出此定点的坐标.模型二:三大圆锥曲线(椭圆,双曲线,抛物线)中,若过焦点的弦为AB ,则焦点所在坐标轴上存在唯一定点N ,使得NA NB ⋅u u u r u u u r为定值.例10.50 已知椭圆2222:1(0)x y C ab a b+=>>的右焦点为(1,0)F ,且点(1,2-在椭圆C 上. (1)求椭圆C 的标准方程;(2)已知动直线l 过点F ,且与椭圆C 交于,A B 两点,试问x 轴上是否存在定点Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.变式1 已知双曲线222x y -=的左、右焦点分别为12,F F ,过点2F 的动直线与双曲线相交于,A B 两点.在x 轴上是否存在定点C ,使得CA CB ⋅u u u r u u u r为常数?若存在,求出点C 的坐标;若不存在,请说明理由。
2020高考数学分项汇编专项09圆锥曲线(含解析)理

得 OQM ONQ ?假设存在,求点 Q 的坐标;假设 不存在,说明理由.
x2
【答案】 (1)
y2
m
1, M(
,0) ,(2) 存在点 Q(0, 2)
2
1n
考点: 1. 求椭圆方程; 2. 求直线方程及与坐标轴的交点; 3. 存在性问题 .
椭圆上,假设 | PF1 | 4 ,那么 | PF2 | _________; F1PF2 的小大为 __________.
【答案】 2, 120
考点:圆的定义、焦点、长轴、短轴、焦距之间的关系以及余弦定理
.
4. 【 2018 高考北京理第 13 题】双曲线 x 2 a2
y2 b2
x2 1 的离心率为 2,焦点与椭圆
16. 【 2019 高考北京理第 19 题】〔本小题总分值 14〕
椭圆 C : x2 2 y2 4 . 〔 1〕求椭圆 C 的离心率; 〔 2〕设 O 为原点,假设点 A 在椭圆 C 上,点 B 在直线 y 2 上,且 OA OB ,试判断直线 AB 与圆 x2 y 2 2 的位置关系,并证明你的结论 .
14. 【 2019 高考北京理第 19 题】〔本小题共 14 分〕
曲线 C : 5 m x2 m 2 y2 8 m R . 〔 1〕假设曲线 C 是焦点在 x 轴上的椭圆,求 m 的取值范围; 〔 2〕设 m 4 ,曲线 C 与 y 轴的交点为 A , B 〔点 A 位于点 B 的上方〕,直线 y kx 4 与 曲线 C 交于不 同的两点 M , N ,直线 y 1与直线 BM 交于点 G ,求证: A , G , N
10. 【 2018 高考北京理第 19 题】〔本小题共 14 分〕
菱形 ABCD 的顶点 A,C 在椭圆 x2 3y2 4 上,对角线 BD 所在直线的斜率为 1. 〔Ⅰ〕当直线 BD 过点 (0,1) 时,求直线 AC 的方程; 〔Ⅱ〕当 ABC 60 时,求菱形 ABCD 面积的最大值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2y0
2y0
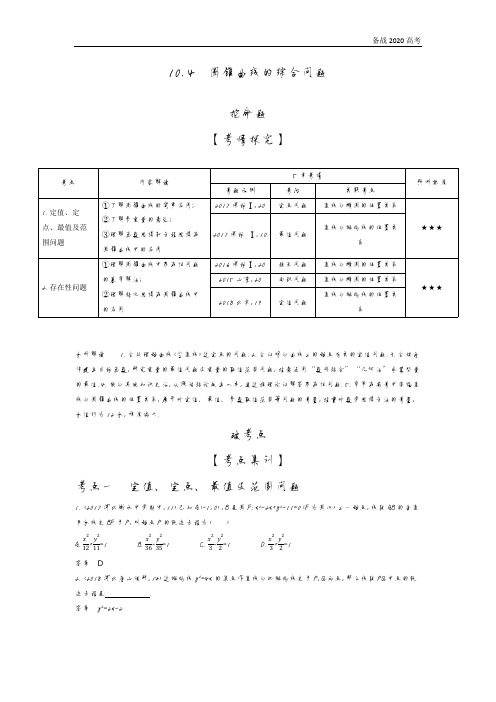
令 x=0,得 yM=-x0-2,从而|BM|=1-yM=1+x0-2.
y0-1 直线 PB 的方程为 y= x0 x+1.
x0
x0
令 y=0,得 xN=-y0-1,从而|AN|=2-xN=2+y0-1.
1 所以四边形 ABNM 的面积 S=2|AN|·|BM|
1 =2
( )2y0 x20+4y20+4x0y0-4x0-8y0+4 2x0y0-2x0-4y0+4
2020 年高考理科数学《圆锥曲线》题型归纳与训练 【题型归纳】
题型一 求曲线的方程
例 1 已知 F1(2, 0) , F2 (2, 0) ,点 P 满足| PF1 | | PF2 | 2 ,记点 P 的轨迹为 E .求轨迹 E 的方程. 【答案】 x2 y2 1
3
【解析】由| PF1 | | PF2 | 2 4 | F1F2 | 可知:点 P 的轨迹 E 是以 F1, F2 为焦点的双曲 线的右支,
x2 y2 例 2 已知椭圆 C:a2+b2=1 过 A(2,0),B(0,1)两点. (1)求椭圆 C 的方程及离心率;
1
(2)设 P 为第三象限内一点且在椭圆 C 上,直线 PA 与 y 轴交于点 M,直线 PB 与 x 轴交于点 N,求证:四边形 ABNM 的面积为定值.
x2
3
【答案】(1) 4 +y2=1,e= 2 (2)2.
1+
=2.
x0-2 = 2x0y0-x0-2y0+2 = x0y0-x0-2y0+2
2
从而四边形 ABNM 的面积为定值.
【易错点】(1).想不到设出 P(x0,y0)后,利用点斜式写出直线 PA,PB 的方 程.不会由直线 PA,PB 的方程求解|BM|,|AN|;
1 (2).不知道四边形的面积可用 S=2| AN|·|BM|表示;
m+1 l:y=- 2 x+m,
m+1 即 y+1=- 2 (x-2), 所以 l 过定点(2,-1).
【易错点】(1)观察不出 P3,P4 对称,忽视对称性导致判断失误; (2)不会用点的坐标代入方程判断 P1,P2 是否在椭圆上而滞做;
5
(3)联立直线 l 与椭圆 C 的方程,计算化简失误而滞做; (4)利用 k1+k2=-1 运算变形不明确变形目标,导致化简不出 k,m 的关系.
【解析】(1)由题意得a=2,b=1,
x2 所以椭圆 C 的方程为 4 +y2=1.
c3 又 c= a2-b2= 3,所以离心率 e=a=(x0<0,y0<0),则 x20+4y20=4. 又 A(2,0),B(0,1),
y0 所以直线 PA 的方程为 y=x0-2(x-2).
x2 故椭圆 C 的方程为 4 +y2=1. (2)证明:设直线 P2A 与直线 P2B 的斜率分别为 k1,k2.
如果l与x轴垂直,设l:x=t,
由题设知
t≠0,且|t|<2,可得
A,B
的坐标分别为
t,
4
2
t
2
,
t,
4t2 2
.
4-t2-2 4-t2+2 则 k1+k2= 2t - 2t =-1, 得 t=2,不符合题设.从而可设 l:y=kx+m(m≠1).
(3).四边形 ABNM 的面积用 x0,y0 表示后,不会变形、化简,用整体消参来求 值.
【思维点拨】第(1)问由 a=2,b=1,c= 3,解第一问;
1 第(2)问画草图可知 AN⊥BM,四边形 ABNM 的面积为2|AN|·|BM|,设点 P(x0,y0), 得出 PA,PB 的方程,进而得出 M,N 的坐标,得出|AN|,|BM|,只需证明
kx1+m-1 kx2+m-1 = x1 + x2
= 2kx1x2 m 1x1 x2 .
x1x2
由题设 k1+k2=-1,故(2k+1)x1x2+(m-1)(x1+x2)=0.
4m2-4
-8km
即(2k+1)· 4k2+1 +(m-1)·4k2+1=0.
m+1 解得k=- .
2
当且仅当 m>-1 时,Δ>0,于是
【思维点拨】第(1)问利用椭圆的性质,易排除点 P1(1,1)不在椭圆上,从而求椭 圆方程;
第(2)问分类讨论斜率是否存在,若存在,设 l:y=kx+m,利用条件建立 k,m 的等量关系,消参后再表示出直线 l 的方程可证明.
题型三最值(范围)问题
x2 例 4 已知椭圆 C:a2+y2=1(a>0),F1,F2 分别是其左、右焦点,以 F1F2 为直
x2 【答案】(1) 4 +y2=1(2)(2,-1)
3
【解析】(1)因为
P3
1, 3 2
,P4
1,2,3
,所以
P3,P4
两点关于
y
轴对称,
故由题设知椭圆 C 经过 P3,P4 两点.
1 11 3 又由a2+b2>a2+4b2知,椭圆 C 不经过点 P1,
所以点 P2 在椭圆 C 上.
Error!
x2 将 y=kx+m 代入 4 +y2=1 得
(4k2+1)x2+8kmx+4m2-4=0.
由题设可知 Δ=16(4k2-m2+1)>0.
4
设 A(x1,y1),B(x2,y2),
8km
4m2-4
x1+x2=-
,x1x2=
.
4k2+1
4k2+1
y1-1 y2-1 而 k1+k2= x1 + x2
由 c 2, 2a 2 ,∴ b2 22 12 3 ,故轨迹 E 的方程为 x2 y2 (1 x 0).
3
【易错点】(1)对于双曲线的定义理解片面;(2)如果动点 P 满足 PF1 PF2 2a(2a F1F2 ), 则点 P 的轨迹是双曲线。但该题已知条件中给出的是“| PF1 | | PF2 | 2 ”只能表示点 P 的轨迹是双曲线的右支,而不是双曲线的全部。 【思维点拨】利用双曲线解题时,一定要观察是双曲线的全部还是部分。 题型二 定值、定点问题
1 2|AN|·|BM|是一个与点 P 的坐标无关的量即可.
x2 y2
例
3
已知椭圆
C:a2+b2=1(a>b>0),四点
P1(1,1),P2(0,1),P3
1, 3 2
,P4
1,2,3 中恰有三点在椭圆 C 上.
(1)求 C 的方程;
(2)设直线 l 不经过 P2 点且与 C 相交于 A,B 两点.若直线 P2A 与直线 P2B 的斜 率的和为-1,证明:l 过定点.
