逻辑代数的基本定理_基本规则_逻辑函数简化(18)
逻辑代数的基本定律及规则2010.9.23

_ _ _
_
_ _
_
三变量最小项的编号
长春理工大学软件学院
最大项
最大项标准式是以“或与”形式出现的标准式。 最大项: 对于一个给定变量数目的逻辑函数, 所有变 量参加相“或”的项叫做最大项。 在一个最大项中, 每个 变量只能以原变量或反变量出现一次。 例如, 一个变量A有二个最大项: (2 ) A, A。
例题:化简函数
AB + AC + BC = AB + AC
F = ABC + AD + C D + BD
F = ABC + AD + C D + BD
= ABC + ( A + C ) D + BD
= AC ⋅ B + AC ⋅ D + BD
= AC ⋅ B + AC ⋅ D
= ABC + AD + C D
最小项
2 n 个最小项。最小项通 以此类推,n变量共有
常用 mi 表示。 最小项标准式:全是由最小项组成的“与或” 式,便是最小项标准式(不一定由全部最小项 组成)。 例如:
F ( ABC ) = A B C + BC + A C = A B C + ABC + A BC + AB C + AB C = ∑ m(0,3,4,6,7)
长春理工大学软件学院
逻辑代数的基本定律及规则
对合律: A = A
冗余律: AB + A C + BC = AB + A C
长春理工大学软件学院
逻辑代数的基本定律及规则
3 基本规则
代入规则:任何一个含有变量A的等式,如果将所有 出现A的位置都用同一个逻辑函数代替,则等式仍然 成立。这个规则称为代入规则。 反演规则:对于任何一个逻辑函数F,想要得到F的反 函数,只需要将F中的所有“·”换成“+”,“+”换 成“·”,“0”换成“1”,“1”换成“0”,原变量换成反 变量,反变量换成原变量。 长春理工大学软件学院
逻辑代数的基本定律

逻辑代数的基本定律逻辑代数的基本定律是指逻辑代数中的基础规则和定理,这些定理是逻辑代数中最基本的概念和方法。
逻辑代数是用数学方法来处理逻辑问题的一种方法,它将逻辑问题转化为数学问题,从而可以用数学方法来解决。
逻辑代数的基本定律主要包括以下几个方面:1. 同一律同一律是指一个逻辑表达式和它自身相与(或相或)的结果不变。
即A ∧ T = A,A ∨ F = A。
这个定律的意思是,当逻辑表达式与真值或假值相与(或相或)时,结果不变。
例如,如果有一个逻辑表达式A ∧ T,它与真值T 相与的结果仍然是A。
同样地,如果有一个逻辑表达式A ∨ F,它与假值 F 相或的结果仍然是 A。
2. 恒等律恒等律是指一个逻辑表达式与一个恒等式相与(或相或)的结果相等。
即A ∧ A = A,A ∨ A = A。
这个定律的意思是,当逻辑表达式与一个恒等式相与(或相或)时,结果相等。
例如,如果有一个逻辑表达式A ∧ A,它与恒等式 A 相与的结果仍然是A。
同样地,如果有一个逻辑表达式A ∨ A,它与恒等式 A 相或的结果仍然是 A。
3. 交换律交换律是指一个逻辑表达式中的两个变量相与(或相或)的顺序可以交换。
即A ∧ B = B ∧ A,A ∨ B = B ∨ A。
这个定律的意思是,当逻辑表达式中的两个变量相与(或相或)时,它们的顺序可以交换。
例如,如果有一个逻辑表达式A ∧ B,它与表达式B ∧ A 相与的结果是相等的。
同样地,如果有一个逻辑表达式A ∨ B,它与表达式B ∨ A 相或的结果是相等的。
4. 结合律结合律是指一个逻辑表达式中的多个变量相与(或相或)时,可以任意加括号,而结果不变。
即A ∧ (B ∧ C) = (A ∧ B) ∧ C,A ∨ (B ∨ C) = (A ∨ B) ∨ C。
这个定律的意思是,当逻辑表达式中有多个变量相与(或相或)时,可以任意加括号,而结果不变。
例如,如果有一个逻辑表达式A ∧ (B ∧ C),它与表达式(A ∧ B) ∧ C 相与的结果是相等的。
逻辑代数

1.逻辑函数的变换 1.逻辑函数的变换
3.1.3 逻辑函数的代数变换与化简
L = AC + C D = AC + C D = AC • C • D = ( A + C ) • (c + D ) = AC + AD + C D = AC + C D = AC + C D = A + C + C + D
在逻辑代数中, 在逻辑代数中,逻辑函数的变量只能取两个 二值变量), ),即 和 。 值(二值变量),即0和1。
基本运算规则
, 加运算规则: 加运算规则: 0+0=0 ,0+1=1 ,1+0=1,1+1=1 A+0 =A,A+1 =1,A+A =A, , , , A+A =1 乘运算规则: 0•0=0 乘运算规则: A•0 =0 非运算规则: 非运算规则: 0=1
根据逻辑表达式,可以画出相应的逻辑图, 根据逻辑表达式,可以画出相应的逻辑图,表 达式的形式决定门电路的个数和种类, 达式的形式决定门电路的个数和种类,因此实际中 需要对表达式进行变换。 需要对表达式进行变换。 例如L=A⊕B ⊕ 例如 1.用与非门实现:与或表达式→摩根定律 用与非门实现:与或表达式 摩根定律 用与非门实现 有反变量输入、 有反变量输入、无反变量输入 2.用或非门实现:或与表达式→摩根定律 用或非门实现:或与表达式 摩根定律 用或非门实现 有反变量输入、 有反变量输入、无反变量输入 3.用最少门实现 用最少门实现 化简;选用异( 化简;选用异(同)或门
(完整版)逻辑代数的基本公式和运算规则
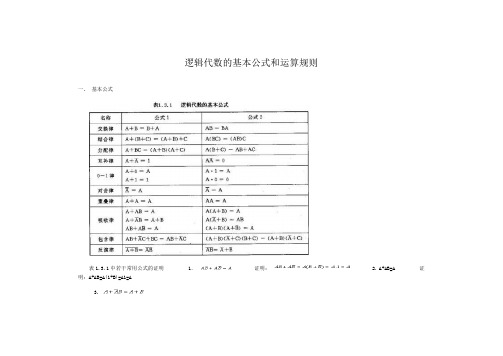
逻辑代数的基本公式和运算规则
一、基本公式
表1.3.1中若干常用公式的证明1.证明: 2. A+AB=A 证明:A+AB=A(1+B)=A1=A
3.
证明:
4.
证明:
推论:
二、运算规则
1.代入定理任何一个含有某变量的等式,如果等式中所有出现此变量的位置均代之以一个逻辑函数式,则此等式依然成立,这称为代入规则。
利用代入规则,反演律能推广到n个变量,即:
2.反演定理对于任意一个逻辑函数式F,若把式中的运算符“.”换成“+”, “+” 换成“.”,常量“0”换成“1”,“1”换成“0”,原变量换成反变量,反变量换成原变量,则得到的结果为。
这个规则叫反演定理运用反演定理时注意两点:① 必须保持原函数的运算次序。
② 不属于单个变量上的非号保留,而非号下面的函数式按反演规则变换。
例如:
其反函数:
3.对偶定理对于任意一个逻辑函数F,若把式中的运算符“.”换成“+”,“+”换成“.”,常量“0”换成“1”,“1”换成“0”,则得到F的对偶式F′。
例如:
其对偶式:
对偶定理:如果两个函数式相等,则它们对应的对偶式也相等。
逻辑代数的运算法则

逻辑代数的运算法则逻辑代数又称布尔代数。
逻辑代数与普通代数有着不同概念,逻辑代数表示的不是数的大小之间的关系,而是逻辑的关系,它仅有0、1两种状态。
逻辑代数有哪些基本公式和常用公式呢?1.变量与常量的关系与运算公式 一、基本公式A·1=AA·0=0或运算公式A+0=A A+1=101律2.与普通代数相似的定律与运算公式A·B=B·A 或运算公式A+B=B+A交换律A·(B·C)=(A·B)·C A+(B+C)=(A+B)+C 结合律A·(B+C)=A·B+A·C A+(B·C)=(A+B)(A+C)分配律3.逻辑代数特有的定律与运算公式或运算公式互补律重叠律(同一律) 反演律(摩根定律)0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+ 非非律(还原律)AA =A A A =⋅A A A =+真值表证明摩根定律0001101111111100结论:BA B A +=⋅ 以上定律的证明,最直接的办法就是通过真值表证明。
若等式两边逻辑函数的真值表相同,则等式成立。
【证明】公式1AB A AB =+B A AB +)(B B A += 互补律1⋅=A 01律A= 合并互为反变量的因子【证明】公式2AAB A =+AB A +)(B A +=1 01律A= 吸收多余项【证明】公式3BA B A A +=+B A A +BA AB A ++=B A A A )(++= 互补律BA += 消去含有另一项的反变量的因子【证明】CA AB BC C A AB +=++BC A A C A AB )(+++=BC C A AB ++ 分配律BC A ABC C A AB +++= 吸收多余项公式2互补律CA AB += 公式2逻辑代数的运算法则一、基本公式二、常用公式A·1=AA·0=0A+0=A A+1=1 1.变量与常量的关系01律2.与普通代数相似的定律交换律A·B=B·A A+B=B+A结合律 分配律3.逻辑代数特有的定律互补律A·A=A A+A=A 重叠律(同一律)反演律(摩根定律)0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+非非律(还原律)AA =AB A AB =+.1AAB A =+.2BA B A A +=+.3CA AB BC C A AB +=++.4A·(B·C )=(A·B )·C A+(B+C )=(A+B )+C A·(B+C )=A·B+A·CA +(B·C )=(A+B )(A+C )谢谢!。
逻辑代数基本定律规则及常用公式

逻辑代数基本定律规则及常⽤公式在四则运算中,我们知道有交换律、结合律以及分配律等。
那么在逻辑运算中,也有它⾃⼰的基本定律,下⾯将介绍逻辑代数运算中的基本定理。
逻辑代数基本定理1.0、1定律0、1定律描述的是单个变量A和0、1之间的运算规则。
其中有以下四条定律:(1)A·0=0,即A和0相与始终为0;(2)A·1=A,即A与1相与结果为A;(3)A+0=A,即A和0相或结果为A;(4)A+1=1,即A和1相或始终为1。
2.重叠律重叠率描述逻辑变量A和其⾃⾝的运算。
(1)A·A=A,即A和⾃⼰相与等于它本⾝;(2)A+A=A,即A和⾃⼰相或亦等于它本⾝。
3.互补律互补律描述A和⾃⾝的反变量¬A之间的关系。
(1)A·¬A=0,即A和⾃⾝反变量相与始终为0;(2)A+¬A=1,即A和⾃⾝反变量相或始终为1。
证明:由于A和¬A之间⾄少有⼀个为0,即⼆者不可能全为1,所以相与得0;同时,A和¬A之间⾄少有⼀个为1,满⾜或运算的“有1出1”,所以相或得0。
4.还原律A的反变量再取反,等于本⾝,即¬(¬A)=A。
5.交换律在此定律及之后的定律中,都将会涉及到两个及以上的逻辑变量。
交换律即两个逻辑变量运算时交换位置,结果不变。
(1)A·B=B·A,即A 与B等于B与A;(2)A+B=B+A,即A或B等于B或A。
6.结合律结合律指三个及以上变量相与或相或时,可以使任意两个变量先进⾏运算,再去和别的变量进⾏运算。
(1)(A·B)·C=A·(B·C),即A与B后再与C,等于B与C后再与A。
(2)(A+B)+C=A+(B+C),即A或B后再或C,等于B或C后再或A。
7.分配律逻辑代数的分配律和四则运算的分配律很类似,但是有⼀些不同。
(1)A·(B+C)=A·B+A·C,即A和B或C相与,等于A和B、C分别相与,然后进⾏或运算;(2)(A+B)·(A+C)=A+B·C,这⼀条定律显得有⼀些特殊,它的结果并不像四则运算中展开后有四项的形式,实际上,我们可以这样的得到:(A+B)·(A+C)=A·A+A·C+A·B+B·C=A+AC+AB+BC=A(1+B+C)+BC=A·1+BC=A+BC。
逻辑代数的基本知识

逻辑代数的基本知识 1. 逻辑代数的基本定律根据逻辑变量和逻辑运算的基本定义,可得出逻辑代数的基本定律。
①交换律: A+B = B+A , A • B = B • A;②结合律: A+(B+C) = (A+B)+ C , A • (B • C) = (A • B) • C;③分配律: A •(B+C) = A • B+A • C , A+B • C=(A+B) • (A+C);④互非定律: A+A = l ,A • A = 0 ;1=+A A ,0=•A A ; ⑤重叠定律(同一定律):A • A=A, A+A=A ;⑥反演定律(摩根定律):A • B=A+B 9 A+B=A • B B A B A •=+,B A B A +=•;⑦还原定律: A A = 2. 逻辑代数的基本运算规则 (1)代入规则在逻辑函数表达式中凡是出现某变量的地方都用另一个逻辑函数代替,则等式仍然成立,这个规则称为代入规则。
例如,已知A+AB=A ,将等式中所有出现A 的地方都以函数(C+D)代替则等式仍然成立,即(C+D) + (C+D)B = C+D 。
(2)反演规则对于任意的Y 逻辑式,若将其中所有的“ • ”换成“ + ”换成“ • ”,0换成1,1换成0,原变量换成反变量,反变量换成原变量,则得到原函数Y 的反函数,运用它可以简便地求出一个函数的反函数。
运用反演规则时应注意两点: ① 要注意运算符号的优先顺序,不应改变原式的运算顺序。
例:CD B A Y +=应写为))((D C B A Y ++= 证: ))((D C B A CD B A CD B A Y ++=•=+=② 不属于单变量上的非号应保留不变。
例:)(E D C C B A Y•+•= 则[])()(E D C C B A Y ++•++=D C B A Y +•= 则 D C B A Y •++=(3)对偶规则对于任何一个逻辑函数,如果将其表达式Y 中所有的算符“ • ”换成“ + ”换成“ •”,常量 “0”换成换成“0”,而变量保持不变,则得出的逻辑函数式就是Y 的对偶式,记为Y’。
逻辑代数的基本定理基本规则逻辑函数简化(18)

A B ,用函数Y=AC代 例如,已知等式 AB 替等式中的A,根据代入规则,等式仍然成立,即有:
( AC ) B AC B A B C
5
例、证明:A+C+D=A • C • D
证明: A+C+D=A • C+D 求反律A+B=A•B 用Y=C+D代替B
=A • C • D
它们的变量都是A、B、C、…,如果对应于变量A、B、 C、…的任何一组变量取值,Y1和Y2的值都相同,则称Y1和 Y2是相等的,记为Y1=Y2。
若两个逻辑函数相等,则它们的真值表一定相同;反之, 若两个函数的真值表完全相同,则这两个函数一定相等。因此 ,要证明两个逻辑函数是否相等,只要分别列出它们的真值表 ,看看它们的真值表是否相同即可。
Y A B C D E
Y ( A B )( C D E )
对偶规则的意义在于:如果两个函数相等,则它们的对偶函 数也相等。利用对偶规则 , 可以使要证明及要记忆的公式数目减 少一半。例如:
A B A B A
即就是摩根定理,可以推广到多个变量
6
( 2 )反演 ( 求反 ) 规则:对于任何一个逻辑表达式 Y ,如果将 表达式中的所有“ ·” 换成“+”,“+”换成“ ·” ,“ 0” 换成 “ 1” ,“ 1” 换成“ 0”,原变量换成反变量,反变量换成原变量 ,那么所得到的表达式就是函数 Y的反函数Y(或称补函数)。 这个规则称为反演规则,亦称求反规则。例如:
F与/或
与非/与
反演规则
两次求反 一次摩根定律
再用 一次摩根定律
再用 一次摩根定律
18
非 运 算 : 1 0
逻辑代数的基本定律和规则.ppt

则逻。辑函数作为一个逻辑变量对待。
推广 2020/10/8 利用代入规则可以扩大公式的应用范围。 12
(2)反演规则
对任何一个逻辑表达式Y 作反演变换,可得Y 的 反函数 Y 。这个规则叫做反演规则。
17
2020/10/8
14
对偶定理: 若等式Y=G成立,则等式Y ˊ=Gˊ也成立。 利用对偶定理,可以使要证明和记忆的公式数目 减少一半。
2020/10/8
互为对偶式
15
小结: 1、基本定律和公式; 2、三大规则的运用。
作业: 2-2; 2-4
2020/10/8
16
再 见!
2020/10/8
返回首页
反演变换: “﹒”→“﹢” “﹢”→“﹒”
“0” → “1” “1” →“0”, 原变量→反变量 反变量→原变量
Y A B CD 0 Y A B (C D) 1
Y ABC DE Y ABC DE Y A(B C D E)
运用反演规则时,要注意运算的优先顺序(先
括号、再相与,最后或) ,必要时可加或减扩号。
2020/10/8
2
2.3.1 逻辑代数的基本公式
已知逻辑函数Y = F1 (A、B、C……)和 G= F2 (A、B、C……)
问:逻辑函数Y = G相等的条件?
仅当A、B、C……的任一组取值所对应的Y和G 都相同,具体表现为二者的真值表完全相同时, Y = G。
等号“=”不表示两边数值相等,仅表示一种 等价、等效的逻辑关系。因为逻辑变量和逻辑函数 的取值0和1是不能比较大小的,仅表示一种状态。
逻辑代数的基本定律及规则

逻辑代数的基本定律及规则文章来源:互联网作者:佚名发布时间:2012年05月26日浏览次数: 1 次评论:[已关闭] 功能:打印本文一、逻辑代数相等:假定F、G都具有n个相同变量的逻辑函数,对于这n个变量中的任意一组输入,如F和G都有相同的输出值,则称这两个函数相等。
在实际中,可以通过列真值表来判断。
二、逻辑代数的基本定律:在逻辑代数中,三个基本运算符的运算优先级别依次为:非、与、或。
由此推出10个基本定律如下:1.交换律A+B=B+A;A·B=B·A2.结合律A+(B+C)=(A+B)+C;A·(BC)=(AB)·C3.分配律A·(B+C)=AB+AC;A+BC=(A+B)·(A+C)4.0-1律A+0=A;A·1=AA+1=1 ;A·0=05.互补律A+=1 ;A·=06.重叠律A·A=A;A+A=A7.对合律=A8.吸收律A+AB=A;A·(A+B)=AA+B=A+B;A·(+B)=ABAB+B=B;(A+B)·(+B)=B9.反演律=·;=+10.多余项律AB+C+BC=AB+C;(A+B)·(+C)·(B+C)=(A+B)·(+C)上述的定律都可用真值表加以证明,它们都可以用在后面的代数化简中。
三、逻辑代数的基本规则:逻辑代数中有三个基本规则:代入规则、反演规则和对偶规则。
1.代入规则:在任何逻辑代数等式中,如果等式两边所有出现某一变量(如A)的位置都代以一个逻辑函数(如F),则等式仍成立。
利用代入规则可以扩大定理的应用范围。
例:=+,若用F=AC代替A,可得=++2.反演规则:已知函数F,欲求其反函数时,只要将F式中所有的“·”换成“+”,“+”换成“·”;“0”换成“1”,“1”换成“0”时,原变量变成反变量,反变量变成原变量,便得到。
逻辑代数的基本定理和规则

2、基本公式的证明 (真值表证明法)
例 证明 A A B=A B
列出等式、右边的函数值的真值表
AB A
00 1 01 1 10 0 11 0
A· B A+AB A+B
0 0+0=0 0 1 0+1=1 1 0 1+0=1 1 0 1+0=1 1
例:试化简下列逻辑函数L=(A + B)(A + B)
解:按照反演规则,得
L (A B) (C D) 1 ( A B)(C D)
3. 对偶规则:
对于任何逻辑函数式,若将其中的与(• )换成或(+),或(+) 换成与(•);并将1换成0,0换成1;那么,所得的新的函数式就 是L的对偶式,记作 。 L
例: 逻辑函数 L (A B)(A C)的对偶式为
2.1.1 逻辑代数的基本定律和恒等式
1、基本公式 0、1律:A + 0 = A A + 1 = 1 A ·1 = A A ·0 = 0 互补律:A + A = 1 A ·A = 0 交换律:A + B = B + A A ·B = B ·A 结合律:A + B + C = (A + B) + C A ·B ·C = (A ·B) ·C 分配律:A ( B + C ) = AB + AC A + BC = ( A + B )( A + C )
2.1 逻辑代数的基本定理和规则
逻辑代数又称布尔代数。它是分析和设计现代数字逻辑电路不 可缺少的数学工具。逻辑代数有一系列的定律、定理和规则, 用于对表达式进行处理,以完成对逻辑电路的化简、变换、分 析和设计。 逻辑关系指的是事件产生的条件和结果之间的因果关系。在数字 电路中往往是将事情的条件作为输入信号,而结果用输出信号表 示。条件和结果的两种对立状态分别用逻辑“1” 和“0”表示。
数电-第二章 逻辑代数

= AB AC
=右式
如果两个乘积项中,一项包括了原变量,另一项包括反变量, 次吸收律消 而这两项剩余因子都是第三个乘积项的因子,则第三个乘积 除C和B 项是多余的。
分别应用两
2.1 逻辑代数
• For example: a) AB AB AB AB b)AB AC AB AC
2.1 逻辑代数
• For example: 化简函数
Y AB C ABC AB Y AB C ABC AB
AB(C C) AB
B(A A)
B
• For example: 化简函数
Y AB C ABC B D
Y AB C ABC B D
(A B)(A C)
AB 证明: B AB A B AB 证明: AC AB AC A
(A B)(A B) A A A B AB BB A B AB
AA AC AB BC AB AC BC A B AC
2.1 逻辑代数
• B、异或运算的一些公式 异或的定义:在变量A、B取值相异时其值为1, 相同时其值为0。即: B AB AB A 根据相似道理,我们把异或的非(反)称为同或, 记为:A⊙B= A B
1、交换律:
A B BA
2、结合律: (A B) C A (B C)
第二章 逻辑代数
本章重点内容 逻辑函数的化简
2.1 逻辑代数
逻辑代数是英国数学家乔治· 布尔(George Boole)于1849年提出的,所以逻辑代数又称 布尔代数。直到1938年美国人香农在开关 电路中才用到它,现在它已经成为分析和 设计现代数字逻辑电路不可缺少的数学工 具。 •A、逻辑代数的基本定律和恒等式
逻辑代数基础

Y AC AB
AC( B B) AB(C C)
ABC ABC ABC ABC ABC ABC ABC m5 m6 m7
例1:画出 Y AC AB 的卡诺图
Y ABC ABC ABC m5 m6 m7
输入变量 BC 00 A 0 0 1 00 01 11 10 m0 m1 m3 m2 m4 m5 m7 m6 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
② 最小项的性质 对于任意一个最小项,只有一组变量取值使 它的值为1,而在变量取其它各值时,这个 最小项的值都是零; 不同的最小项,使它的值为1的那组变量取 值也不同; 对于变量的同一组取值,任意两个最小项 的乘积为零; 对于变量的同一组取值,所有最小项的逻辑 或为1。
第2章 逻辑代数基础
§2.1 逻辑代数 § 2.2 逻辑函数表达式的形式与变换 §2.3逻辑函数的化简
§2.1逻辑代数的基本规则和定理
逻辑代数(又称布尔代数),它是分析和 设计逻辑电路的数学工具。虽然它和普通代 数一样也用字母表示变量,但变量的取值只 有“0”,“1”两种,分别称为逻辑“0”和逻 辑 “1”。这里“0”和“1”并不表示数量的大小, 而是表示两种相互对立的逻辑状态。
③最小项的编号
注:下标与编码所对应的十进制数值相同
④函数的最小项表达式
将逻辑函数表达式化成一组最小项之和,称为 最小项表达式。任何一个函数均可表达成 唯一的 最小项之和。 如:
L( A, B, C ) ( AB AB C ) AB
( AB A B C ) AB AB ABC AB ABC A BC ABC ABC m3 m5 m 6 m 7 m(3,5,6,7)
2-逻辑代数基本定律

2、基本公式
A 0 A 0-1 律: A 1 A
互补律: A A 1
A 1 1 A 0 0
A A 0
等幂律: A A A
A A A
双重否定律: A A
分别令A=0及 A=1代入这些 公式,即可证 明它们的正确 性。
3、基本定律
Y ABC AD C D BD
ABC D( A C ) BD
ACB AC D BD ACB AC D ABC AD C D
消去法 运用吸收律 A AB A B ,消去多余因子。
Y AB AC BC
AB ( A B )C AB ABC AB C
=A+BC
4、常用公式
A B A B A 还原律: ( A B ) ( A B ) A
A A B A 吸收律: A ( A B) A A ( A B) A B A A B A B
高电平为逻辑 0。未加说明则默认为正逻辑 体制。
化简逻辑函数的目的是为了获得最简逻辑式, 从而使逻辑电路简单,成本低、可靠性高。 不同形式的逻辑式有不同的最简式,求 最简式的一般方法是:先求最简与或式,然 后变换成所需的最简形式。
最简与或式标准 最简与非式标准 (1)与项的个数最少 (2)每个与项中的变量数最少 (1)非号个数最少 (2)每个非号中的变量数最少
一、逻辑函数式的几种常见形式和变换
例如 Y AB BC 与或表达式 ( A B )( B C ) 或与表达式 逻辑式有多种形式,采用何种形式视 与非 - 与非表达式 A B BC 需要而定。各种形式间可以相互变换。 A B B C 或非 - 或非表达式 与或非表达式 AB BC 转换方法举例 与或式 与非式 或与式 或非式 Y ( A B )( B C )
逻辑代数的公式与基本定理

逻辑代数的公式与基本定理逻辑代数是一门研究命题和命题逻辑关系的数学分支。
它通过符号表示和操作来研究命题的逻辑结构。
在逻辑代数中,有一些重要的公式和基本定理,它们对于理解和应用逻辑代数具有重要的意义。
一、公式1. 吸收律(Absorption Law):a∨(a∧b)=aa∧(a∨b)=a这个定律表明,当两个命题中一个包含另一个时,可以通过去除其中一个命题来简化表达式。
2. 结合律(Associative Law):(a∨b)∨c=a∨(b∨c)(a∧b)∧c=a∧(b∧c)这个定律表明,当有多个命题连接在一起时,可以改变它们的组合方式而不改变逻辑等价关系。
3. 分配律(Distributive Law):a∨(b∧c)=(a∨b)∧(a∨c)a∧(b∨c)=(a∧b)∨(a∧c)这个定律表明,当一个命题与两个命题的逻辑运算混合时,可以通过改变运算的顺序来简化表达式。
4. 归纳法则(Inductive Law):a∨¬a=1a∧¬a=0这个定律表明,任何命题与其否定的逻辑运算结果为真或假。
二、基本定理1. 双重否定定理(Double Negation Theorem):¬(¬a)=a这个定理表明,一个命题的否定再次否定后与原命题等价。
2. 德·摩根定理(De Morgan's Theorem):¬(a∨b)=¬a∧¬b¬(a∧b)=¬a∨¬b这个定理表明,一个命题的合取或析取的否定可以分别表示为各个命题的否定的合取或析取。
3.等幂律(Law of Identity):a∧1=aa∨0=a这个定理表明,一个命题与恒等元素进行合取或析取运算后仍等于原命题。
4. 否定消除律(Law of Noncontradiction):a∨¬a=1a∧¬a=0这个定理表明,一个命题与其否定进行合取或析取运算后结果为真或假。
卡诺图化简

(一)最小项的概念与性质
1. 最小项的定义和编号 n 个变量有 2n 种组合,可对应写出 2n 个乘积
项,这些乘积项均具有下列特点:包含全部变量, 且每个变量在该乘积项中 (以原变量或反变量)只 出现一次。这样的乘积项称为这 n 个变量的最小 项,也称为 n 变量逻辑函数的最小项。
简为 2 个相同变量相与。
圈 2 个可消去 1 个变量,化 简为 3 个相同变量相与。
10
m1a9
Yc = AB
孤立项 Ya=ABCD Yb = BCD (5)将各图化简结果逻辑加,得最简与或式
Y ABCD BCD AB AD
EXIT
逻辑代数基础
[例] 用卡诺图化简逻辑函数 Y(A,B,C,D)=∑m (0,2,5,7,8,10,12,14,15)
(1)任何两个(21个)标1的相邻最小项,可以合并为一项, 并消去一个变量(消去互为反变量的因子,保留公因子)。
AB C
0 1
AB CD
00 01 11 10
00
01
11
10
1
0
0
1
0
1
1
0
ABC ABC BC
ABC ABC BC
ห้องสมุดไป่ตู้
00
01
11
10
0
1
0
0
0
0
0
1 ABCD ABCD
B10
0 量卡0 0 00 1 0m000 0mA0111 AmB33 AmB22
1 诺1 0 图
11 1 m44
mA55 Am7B7 AmB66
以循环变码量排取列0 的以代保以证反相变邻量性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y AB AC
①求出反函数的最简 与或表达式
Y AB AC (A B)(A C) AB AC BC AB AC
②利用反演规则写出函数的最 简或与表达式
Y ( A B)( A C )
15
4、最简或非-或非表达式
非号最少、并且每个非号下面相加的变量也最少的或非-或非表达式。
则可得到的一个新的函数表达式Y',Y'称为函Y的对
偶函数。这个规则称为对偶规则。例如:
Y AB CDE
Y (A B)(C D E)
Y ABC DE
Y ABC DE
8
P21 表2.3.4
对偶规则的意义在于:如果两个函数相等,则它们的对偶函数也相等。利用对偶 规则,可以使要证明及要记忆的公式数目减少一半。例如:
0
00
1 11
0
101 101源自001 011
11
0 00
A B A+B A+B A B
0
00
1 11
0
11
0 10
1
01
0 01
1
11
0 00
A+B
1 1 1 0
A·B 1 0 0 0
2
2.3.2 逻辑代数的基本定 律
(1)常量之间的关系
与运算:0 0 0 0 1 0 1 0 0 111
或运算:0 0 0 0 11 1 0 1 111
10
本节小结
逻辑代数是分析和设计数字电路的重 要工具。利用逻辑代数,可以把实际逻 辑问题抽象为逻辑函数来描述,并且可 以用逻辑运算的方法,解决逻辑电路的 分析和设计问题。
与、或、非是3种基本逻辑关系,也 是3种基本逻辑运算。与非、或非、与或 非、异或则是由与、或、非3种基本逻辑 运算复合而成的4种常用逻辑运算。
AB AB A
(A B) (A B) A
A(B C) AB AC
A BC (A B)(A C)
注意:1、在运用反演规则和对偶规则时,必须按照逻辑运算的优先顺序进行: 先算括号,接着与运算,然后或运算,最后非运算,否则容易出错。
2、F的对偶式F’与反函数F不同,在求F’时不要求将原变量 和反变量互换,所以一般情况下,F’ ≠ F,只有在特殊情况下才相等。
Y (A B)(C D E)
注意:
1、变换时要保持原式中的运算顺序。
2、不是在“单个”变量上面的“非”号应保持不
变Y 。A B C D E
Y AB CD E
Y ABC DE
Y=A•B •C •D •E
7
(3)对偶规则:对于任何一个逻辑表达式Y,如果将 表达式中的所有“·”换成“+”,“+”换成“·”, “0”换成“1”,“1”换成“0”,而变量保持不变,
12
一个逻辑函数的表达式可以 有与或表达式、或与表达式、与 非-与非表达式、或非-或非表达 式、与或非表达式5种基本表示形 式。对应的门为与或门、或与门、 与非门、或非门、与或非门。
13
1、化简为最简与或表达式
乘积项最少、并且每个乘积项中的变量也最少的与或表达式。
Y ABE AB AC ACE BC BCD
非运算: 1 0 0 1
3
(2)逻辑代数的基本定律 P21 表2.3.4
重点强调
A B A B A
8、吸收律
1:
( A
B)
(A
B)
A
4
2.3.3 逻辑代数运算的基本规 则
(1)代入规则:任何一个含有变量A的等式,如果 将所有出现A的位置都用同一个逻辑函数代替,则等式 仍然成立。这个规则称为代入规则。
例如,已知等式 AB A B ,用函数Y=AC代
替等式中的A,根据代入规则,等式仍然成立,即有:
( AC)B AC B A B C
5
例、证明:A+C+D=A • C • D
证明: A+C+D=A • C+D =A • C • D
求反律A+B=A•B 用Y=C+D代替B
即就是摩根定理,可以推广到多个变量
2.3 逻辑代数的基本定理和基本规则
2.3.1 逻辑函数的相等
逻辑函数相等的概念:设有两个逻辑函数
Y1 f ( A, B,C,) Y2 g( A, B,C,)
它们的变量都是A、B、C、…,如果对应于变量A、B、C、…的任何一组变量 取值,Y1和Y2的值都相同,则称Y1和Y2是相等的,记为Y1=Y2。
6
(2)反演(求反)规则:对于任何一个逻辑表达式Y,如果将表达式中的所有“·” 换成“+”,“+”换成“·”,“0”换成“1”,“1”换成“0”,原变量换成反 变量,反变量换成原变量,那么所得到的表达式就是函数Y的反函数Y(或称补函数)。 这个规则称为反演规则,亦称求反规则。例如:
Y AB CDE
AB AC BC AB AC
最简与或表达式
14
2、最简与非-与非表达式
非号最少、并且每个非号下面乘积项中的变量也最少的与非-与非表达式。
Y AB AC AB AC AB AC
②用摩根定律去掉下面 的非号
①在最简与或表达式的基础上两次取反
3、最简或与表达式
括号最少、并且每个括号内相加的变量也最少的或与表达式。
Y AB AC (A B)(A C ) (A B)(A C ) A B A C
逻辑代数的公式和定理是推演、变 换及化简逻辑函数的依据。
11
2.3.4 逻辑函数简化的意义和最简的概 念
逻辑函数化简的意义:逻辑表达式越简单, 实现它的电路越简单,电路工作越稳定可靠。
例:化简Y=ABC+ABC+AB
解: Y=ABC+ABC+AB
3个与门和1个或门
公式A+A=1
=AB+AB =A
输入A = 输出Y, 不需要门
若两个逻辑函数相等,则它们的真值表一定相同;反之,若两个函数的真值表 完全相同,则这两个函数一定相等。因此,要证明两个逻辑函数是否相等,只要分 别列出它们的真值表,看看它们的真值表是否相同即可。
1
例2.3.1 用真值表证明摩根定律A•B=A+B,A+B=A •B
证明:列出真值表
A
B AB A•B A B
9
逻辑代数的运算顺序和书写方式有如下规定:
1、运算顺序和普通代数一样,应先算括号里内容,然后算乘法,最后算加法。 2、“•”一般 可省略,逻辑式求反时可以不再加括号。
如:(A•B+C)+(D•E)•F ==> AB+C+DEF
3、先或后与的运算式,或运算要加括号。
如: (A+B) •(C+D)不能写成A+B •C+D。
