实验8欧拉法_改进欧拉法_线性多步法
常微分方程数值解法-欧拉法、改进欧拉法与四阶龙格库塔法常微分方程数值解法

y( xn1)
y( xn
Байду номын сангаас
h)
y(xn )
hy'( xn )
h2 2!
y''( )
进一步: 令
h2 y( xn ) hy'( xn ) 2! y''( xn )
常微分方 yn1 y( xn1 ) , yn y( xn )
程数值解
法-欧拉法 yn1 yn hf ( xn , yn ) h2
、改进欧 y( xn1 ) yn1
2
max y''( x)
a xb
拉法和四
三、Euler方法
已 知 初 值 问 题 的 一 般 形式 为:
dy
dx
f (x, y)
a xb
(1)
y( x0 ) y0
常微分方 用差商近似导数 程数值解 问题转化为
yn1 yn dy
h
dx
法-欧拉法 yn1 yn hf ( xn , yn )
法-欧 y(拉0) 法1
、改进欧
拉法和四
四、几何意义
由 x0 , y0 出发取解曲线 y yx 的切线(存在!),则斜率
dy
f x0, y0
dx x y
,
0
0
常微分方 由于 f x0, y0 及 x0, y0 已知,必有切线方程。
由点斜式写出切程线方数程:值解
法、-改欧进拉欧法 ddxy y y0 x x0
常微分方 程数值解 能用解析方法求出精确解的微分方程为数不多,
而且有的方程即使有解析解,也可能由于解的表达
法-欧拉法 式非常复杂而不易计算,因此有必要研究微分方程
分别利用欧拉法和改进欧拉法求解微分方程组的数值解

分别利用欧拉法和改进欧拉法求解微分方程组的数值解欧拉法(Euler’s Method)和改进欧拉法(Improved Euler’s Method),是求解常微分方程数值解的两种常用方法。
它们都属于一阶精度的显式迭代算法。
首先,我们来介绍一下欧拉法。
欧拉法是一种简单的数值求解算法,它基于微分方程的定义,将微分方程转化为差分方程。
考虑一个一阶常微分方程 dy/dx = f(x, y),并给定初始条件 y(x0)= y0,我们希望求解在给定区间 [x0, xn] 上方程的数值解。
首先,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的欧拉迭代公式计算数值解:y[i+1] = y[i] + h * f(x[i], y[i])其中,x[i] = x0 + i * h,y[i] 是在点 x[i] 处的数值解。
通过不断迭代上述公式,我们可以获得[x0, xn] 上微分方程的数值解。
欧拉法的优点在于简单易懂,计算速度较快。
然而,欧拉法的缺点是精度较低,误差随着步长h 的增大而增大。
为了提高精度,我们可以使用改进欧拉法。
改进欧拉法,也称为龙格–库塔算法(Runge-Kutta Method)或四阶龙格–库塔方法,是一种基于欧拉法的改进算法。
改进欧拉法使用了更多的近似取值,以减小误差。
与欧拉法类似,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的公式计算数值解:k1 = h * f(x[i], y[i])k2 = h * f(x[i] + h/2, y[i] + k1/2)y[i+1] = y[i] + k2其中,k1 和 k2 是计算过程中的辅助变量。
通过不断迭代上述公式,我们可以获得 [x0, xn] 上微分方程的数值解。
改进欧拉法相对于欧拉法而言,计算精度更高。
第8章 常微分方程数值解法 本章主要内容: 1.欧拉法、改进欧拉法 2

第8章 常微分方程数值解法本章主要内容:1.欧拉法、改进欧拉法. 2.龙格-库塔法。
3.单步法的收敛性与稳定性。
重点、难点一、微分方程的数值解法在工程技术或自然科学中,我们会遇到的许多微分方程的问题,而我们只能对其中具有较简单形式的微分方程才能够求出它们的精确解。
对于大量的微分方程问题我们需要考虑求它们的满足一定精度要求的近似解的方法,称为微分方程的数值解法。
本章我们主要讨论常微分方程初值问题⎪⎩⎪⎨⎧==00)(),(yx y y x f dx dy的数值解法。
数值解法的基本思想是:在常微分方程初值问题解的存在区间[a,b]内,取n+1个节点a=x 0<x 1<…<x N =b (其中差h n = x n –x n-1称为步长,一般取h 为常数,即等步长),在这些节点上把常微分方程的初值问题离散化为差分方程的相应问题,再求出这些点的上的差分方程值作为相应的微分方程的近似值(满足精度要求)。
二、欧拉法与改进欧拉法欧拉法与改进欧拉法是用数值积分方法对微分方程进行离散化的一种方法。
将常微分方程),(y x f y ='变为()*+=⎰++11))(,()()(n xn x n n dtt y t f x y x y1.欧拉法(欧拉折线法)欧拉法是求解常微分方程初值问题的一种最简单的数值解法。
欧拉法的基本思想:用左矩阵公式计算(*)式右端积分,则得欧拉法的计算公式为:Nab h N n y x hf y y n n n n -=-=+=+)1,...,1,0(),(1 欧拉法局部截断误差11121)(2++++≤≤''=n n n n n x x y h R ξξ或简记为O (h 2)。
我们在计算时应注意欧拉法是一阶方法,计算误差较大。
欧拉法的几何意义:过点A 0(x 0,y 0),A 1(x 1,y 1),…,A n (x n ,y n ),斜率分别为f (x 0,y 0),f (x 1,y 1),…,f (x n ,y n )所连接的一条折线,所以欧拉法亦称为欧拉折线法。
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
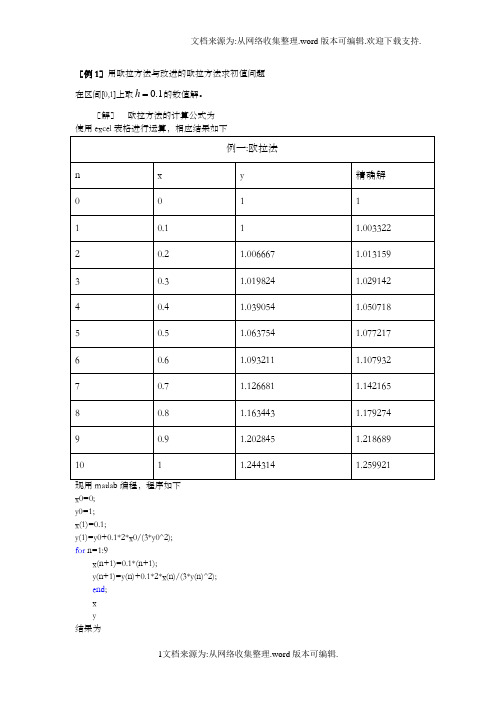
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
欧拉公式的改进

精度低 精度低, 计算量大 计算量大 多一个初值, 可能影响精度
Can’t you givethink me a formula Do OK, you Well, callyet mewithout greedy… let’s with all the advantages any it possible? make it of the disadvantages? possible.
最常用为四级4阶经典龙格-库塔法 /* Classical Runge-Kutta Method */ :
y i +1 K1 K2 K3 K4 = = = = = yi + h ( K1 + 2K 2 + 2K 3 + K 4 ) 6 f ( xi , yi ) h f ( xi + h , y + K1 ) i 2 2 f ( xi + h , yi + h K2 ) 2 2 f ( x i + h, yi + hK 3 )
Step 2: 将 K2 代入第1式,得到
yi +1 = yi + h 1 y( xi ) + 2[ y( xi ) + phy( xi ) + O( h2 )] = yi + (1 + 2 )h y( xi ) + 2 ph2 y( xi ) + O( h3 )
§2 Runge-Kutta Method
Step 3: 将 yi+1 与 y( xi+1 ) 在 xi 点的泰勒展开作比较
yi +1 = yi + (1 + 2 )h y( xi ) + 2 ph2 y( xi ) + O(h3 )
数值计算中的常微分方程数值模拟

数值计算中的常微分方程数值模拟在数值计算中,常微分方程(Ordinary Differential Equations,简称ODE)是一个重要的研究对象。
常微分方程的数值模拟是通过数值方法对其进行近似求解的过程,该过程对于模拟物理系统、生物学过程以及工程问题等具有重要意义。
本文将介绍常微分方程数值模拟的几种常用方法,并分析其特点与应用。
一、欧拉法(Euler's Method)欧拉法是最简单的常微分方程数值模拟方法之一,其基本思想是将连续的微分方程进行离散化,使用一阶差分近似代替微分。
具体步骤如下:1. 建立微分方程:设待求解的微分方程为dy/dx = f(x, y),其中f(x, y)为已知函数。
2. 初始化:选择初始条件y0 = y(x0),以及离散步长h。
3. 迭代求解:根据欧拉法的迭代公式yn+1 = yn + h * f(xn, yn)进行近似求解。
欧拉法的优点是简单易实现,但在处理复杂问题和大步长时存在精度较低的问题。
二、改进的欧拉法(Improved Euler's Method)为了提高欧拉法的精度,改进的欧拉法在迭代过程中使用两个不同的斜率近似值,从而对解进行更准确的预测并修正。
具体步骤如下:1. 建立微分方程:同欧拉法。
2. 初始化:同欧拉法。
3. 迭代求解:根据改进的欧拉法的迭代公式yn+1 = yn + h * (k1 +k2)/2进行近似求解,其中k1 = f(xn, yn),k2 = f(xn + h, yn + h * k1)。
改进的欧拉法在精度上优于欧拉法,但仍然不适用于高精度要求的问题。
三、龙格-库塔法(Runge-Kutta Methods)龙格-库塔法是一类常微分方程数值模拟方法,通过计算多个不同次数的斜率来逼近解。
其中,四阶龙格-库塔方法是最常用的一种方法。
具体步骤如下:1. 建立微分方程:同欧拉法。
2. 初始化:同欧拉法。
3. 迭代求解:根据四阶龙格-库塔方法的迭代公式yn+1 = yn + h * (k1 + 2k2 + 2k3 + k4)/6进行近似求解,其中k1 = f(xn, yn),k2 = f(xn + h/2, yn + h/2 * k1),k3 = f(xn + h/2, yn + h/2 * k2),k4 = f(xn + h, yn + h * k3)。
欧拉方法及其改进的欧拉方法的Matlab实现

11( n n y x y ++−。为了估计它,由Taylor展开得到的精确值1( n y x +是
2'
''
31( ( ( ( ( 2
n n n n h y x y x hy x y x O h +=+++ (5
2.欧拉方法、改进的欧拉方法及Matlab实现
下面主要讨论一阶常微分方程的初值问题,其一般形式为:
' 00
(,
( y f x y y x y ⎧=⎨
=⎩ (1我们知道,只要函数(, f x y适当光滑——譬如关于y满足利普希茨(Lipschitz条件
(, (, f x y f x y L y y −≤−
改进的欧拉方法是先用欧拉公式求1( n y x +的一个近似值1n y +,称为预测值,然后用梯形公式进行矫正并求得近似值1n y +。即
1111(, [(, (, ]
2n n n n n n n n n n y y f x y h h
y y f x y f x y ++++⎧=+⎪
⎨=++⎪⎩
(8 2.2.2改进的欧拉方法的误差估计
方法是一阶方法,因此它的精度不高。
2.2改进的欧拉方法
2.2.1改进的欧拉方法
用数值积分方法离散化问题(1,两端积分可得
1
1( ( (, ( (0,1, 2, n n
x n n x y x y x f x y x dx n ++−==∫
_改进欧拉方法

《微分方程数值解法》课程实验报告一. 改进欧拉方法背影材料欧拉公式是指以欧拉命名的诸多公式。
其中最著名的有,复变函数中的欧拉幅角公式--将复数、指数函数与三角函数联系起来; 拓扑学中的欧拉多面体公式;初等数论中的欧拉函数公式。
此外还包括其他一些欧拉公式,比如分式公式等等1.1建立模型⎪⎩⎪⎨⎧=++=0)0(y 1x142xy y , 设:1.022=-=a b h 05.0212=-=a b h 1.2利用C++编程实现:源程序:#include"stdio.h"#include"iostream"using namespace std;double x,x1,y,y1;int main(){double h;int n;cout<<endl<<"input x0=";cin>>x0;cout<<endl<<"input y0=";cin>>y0;cout<<endl<<"intput h=";cin>>h;cout<<endl<<"intput n=";cin>>n;mend_euler euler(h,n);getch();return 1;}class mend_euler{public:mend_euler(double h,int n);double f(double x,double y);private:double h;int n;};mend_euler::mend_euler(double a,int b){int i=1;h=a;n=b;while(i<=n){x1=x0+h;y1=y0+h/2*(f(x0,y0)+f(x1,y0+h*f(x0,y0))); cout<<endl;cout<<"x1="<<x1<<" y1="<<y1<<" y="<<x0/(1+x0*x0)<<" e="<<y1-x0/(1+x0*x0)<<endl;i++;x0=x1;y0=y1;}}double mend_euler::f(double x,double y){return 4*x*y/(1+x*x)+1;}1.3程序实现1.4总结:从本次实验结果我们可以看出在曲不同的步长H时欧拉公式的y 值由不同的精确值,从而在实际的应用中我们要根据实际情况取得相应的步长,从而达到精度和效率的最优化。
Euler方法与改进的Euler方法的应用

CENTRAL SOUTH UNIVERSITY 数值分析实验报告Euler 方法与改进的Euler 方法的应用一、问题背景在工程和科学技术的实际问题中,常需求解微分方程,但常微分方程中往往只有少数较简单和典型的常微分方程(例如线性常系数常微分方程等)可求出其解析解,对于变系数常微分方程的解析求解就比较困难,而一般的非线性常微分方程的求解困难就更不用说了。
大多数情况下,常微分方程只能用近似方法求解。
这种近似解法可分为两大类:一类是近似解析法,如级数解法、逐次逼近法等;另一类是数值解法,它给出方程在一些离散点上的近似值。
二、数学模型在具体求解微分方程时,需具备某种定解条件,微分方程和定解条件合在一起组成定解问题。
定解条件有两种:一种是给出积分曲线在初始点的状态,称为初始条件,相应的定解问题称为初值问题。
另一类是给出积分曲线首尾两端的状态,称为边界条件,相应的定解问题称为边值问题。
在本文中主要讨论的是给定初值条件的简单Euler 方法和改进的Euler 方法来求解常微分方程。
三、算法及流程Euler 方法是最简单的一种显式单步法。
对于方程()y x f dxdy ,= 考虑用差商代替导数进行计算,取离散化点列nh x x n +=0,L n ,2,1,0=则得到方程的近似式()()()()n n n n x y x f hx y x y ,1≈-+ 即()n n n n y x hf y y ,1+=+ 得到简单Euler 方法。
具体计算时由0x 出发,根据初值,逐步递推二得到系列离散数值。
简单Euler 方法计算量小,然而精度却不高,因而我们可以构造梯形公式()()[]η=++=+++0111,,2y y t f y t f h y y n n n n n n 其中()N a b h -=。
这是一个二阶方法,比Euler 方法精度高。
但是上述公式右边有1+n y ,因而是隐式差分方程,可以用迭代方法计算1+n y 。
欧拉法、改进的欧拉法、龙格-库塔法求解初值问题

欧拉法、改进的欧拉法、龙格-库塔法求解初值问题欧拉法、改进的欧拉法、龙格-库塔法求解初值问题简介通过求解简单的初值问题:dudx =f (x ,u )(1)u (x 0)=u 0(2)引⼊欧拉法、改进的欧拉法、龙格-库塔法等。
前期准备数值解法的基本思想就是先对x 和u(x)在区间[x0,∞)上进⾏离散化,然后构造递推公式,再进⼀步得到u(x)u(x) u(x)u(x)u(x)u(x)在这些位置的近似取值。
取定步长h ,令x n =x 0+nh (n =±1,±2,⋯)得到离散的位置:x 1,x 2,⋯,x n ,u(x)在这些点精确取值为:u (x 1),u (x 2),⋯,u (x n )利⽤数值解法得到的这些点的近似取值,u 1,u 2,⋯,u n欧拉法欧拉法的核⼼就是将导数近似为差商。
将导数近似为向前差商,则有:du dxx =x n≈u x n +1−u x nh代⼊(1)式,有:u x n +1=y x n +hf x n ‖u x n⽤u n +1和 u n 代替u (x n +1)和u (x n ),得:u n +1=u n +hf x n ,u n因此,若知道u 0我们就可以递归出u 1,u 2,⋯如果将导数近似为向后差商:du dxx =x n≈u x n −u x n −1h类似的,就可以得到:u n −1=u n −hf x n ,u n这样,若知道u 0我们就可以递归出u −1,u −2⋯改进的欧拉法对(1)式在[x n ,x n +1]上积分,可得:u x n +1=u x n +∫xn +1x nf (x ,u )dx其中,n =0,1,⋯⽤不同⽅式来近似上式的积分运算,就会得到不同的递推公式。
若使⽤左端点计算矩形⾯积并取近似:∫x n +1x nf (x ,u )dx ≈hf x n +1,u x n +1代⼊上式得:{|()()()()(())()|()()()()()(())u n +1=u n +hf (x n ,u n )若使⽤梯形的⾯积做近似:∫x n +1x nf (x ,y )dx ≈h2f x n ,u x n+f x n +1,ux n +1得到:u n +1=u n +h2f x n ,u n +f x n +1,u n +1欧拉法虽然精度偏低,但它是显式的,可直接得到结果。
最新Euler法与改进Euler法精品课件

作等价变换:
yn1
K1
f
h yn 2 ( xn , yn
(K1 )
K2)
K
2
f ( xn h, yn hK1 )
y( x0 ) y0
第二十一页,共40页。
二、改进(gǎijìn)的Euler法
梯形方法虽然提高(tí gāo)了精度,但算法复杂, 计算量大。如果实际计算时精度要求不太高,用梯形公 式求解时,每步可以迭代一次,由此导出一种新的方法 ——改进Euler法。这种方法实际上就是将Euler公式与 梯形公式结合使用:先用Euler公式求
由点斜式写出切线方程:
y y0 x x0 dy
y0 ( x x0 ) f ( x0 , y0 )
dx x y , 0 0
第十二页,共40页。
几何(jǐ hé)意义
等步长为h,则 x1 x0 h,可由切线算出y1 : y1 y0 hf(x0 , y0)
逐步计算出y y( x) 在 xn1点的值 : yn1 yn hf(xn , yn) n 0,1,2,
常微分方程数值(shùzí)解法
常微分方程(wēi fēn fānɡ chénɡ) 数值解法
-欧拉法、改进欧拉法和四阶龙格 库塔法
第一页,共40页。
常微分方程(wēi fēn fānɡ chénɡ)数值解法
常微分方程主要有: (1)变量可分离(fēnlí)的方程 (2)一阶线性微分方程(贝努利方程) (3)可降阶的一类高阶方程 (4)二阶常系数齐次微分方程 (5)二阶常系数非齐次微分方程 (6)全微分方程
能用解析方法求出精确解的微分方程为数不多,而且有的方 程即使( jíshǐ)有解析解,也可能由于解的表达式非常复杂而不易 计算,因此有必要研究微分方程的数值解法
计算方法 第七章 常微分方程数值解法

7.1.1 欧拉法及其截断误差
4、欧拉公式的截断误差是O(h2),公式是1 阶的。
因为
yi+ 1 ? yi
1
h f ( x i , y i ) = y ( x i ) + h y ¢( x i )
1 2
1
2n ) ( n y ( x ) y (( x)i 1 ) ( y i()x i ) y y ( ) ( x h i ) ( )yh ( ( x x i ) xi y x ) ( xi ) x y y 2 n! 2
y0 y( x0 )
i1 i i i
(欧拉公式)
9
7.1.1 欧拉法及其截断误差
例 取步长 h=0.1,用欧拉法求解初值问题
ì y ¢= x + y ï ï í ï y (0) = 1 ï î
y i 1 y i h f ( x i , y i ) , i 0 ,1 , 2 , y0 y( x0 )
y f ( x , y ), y( x0 ) y0
x [a , b ]
23
7.1 欧拉法和改进的欧拉法
欧拉公式
y i 1 y i h f ( x i , y i ) , i 0 ,1 , 2 , y0 y( x0 )
h y i 1 y i [ f ( x i , y i ) f ( x i 1 , y i 1 )] , i 0 ,1 , 2 , 2 y y( x ) 0 0
( p)
1.2 ? 1.24
1.528
y 2 = y 1 + 0 .1[( x1 + y 1 ) + ( x 2 + y 2 )] = 1 .2 4 + 0 .1(0 .2 + 1 .2 4 + 0 .4 + 1 .5 2 8) = 1 .5 7 6 8
实验8欧拉法_改进欧拉法_线性多步法

西华数学与计算机学院上机实践报告课程名称:计算方法C年级:2011级 上机实践成绩: 指导教师:严常龙姓名: 上机实践名称:解常微分方程初值问题学号: 上机实践日期:2012.12.22 上机实践编号:8上机实践时间: 一、目的1.通过本实验加深对欧拉法、改进欧拉法、线性多步法的构造过程的理解;2.能对上述四种方法提出正确的算法描述编程实现,观察计算结果的改善情况。
二、内容与设计思想自选常微分方程的初值问题,分别用欧拉法、改进欧拉法求解。
分别用以上两种方法求解常微分方程初值问题:2'()1,([0.0,1.4],0.1)(0)0.0y x y h y ⎧=+=⎨=⎩求解区间取步长三、使用环境操作系统:Windows7软件平台:VC++ 6.0四、核心代码及调试过程#include<math.h>#include<iostream.h>#define f(y) (y*y+1)#define m 0.0//初值为0#define h 0.1//步长为0.1#define n 14//迭代次数为14#define a 0.0//定义区间长度#define d 1.4void IEuro();//改进欧拉法void Euro();//欧拉法void main(){Euro();IEuro();}void Euro(){int i;float y[n+1];y[0]=m;//赋初值cout<<"-------------------欧拉法------------------------\n"; for(i=0;i<n;i++){if(i==0){y[i+1]=y[0]+h*f(y[0]);}else{y[i+1]=y[i-1]+2*h*f(y[i]);}//cout<<y[i]<<" ";}cout<<"欧拉法结果为:";cout<<y[i]<<" ";cout<<endl;}void IEuro(){int i;float y[n+1];y[0]=m;//赋初值cout<<"-----------------改进欧拉法----------------------\n"; for(i=0;i<n;i++){if(i==0)//预估{y[i+1]=y[0]+h*f(y[0]);}else{y[i+1]=y[i-1]+2*h*f(y[i]);}y[i+1]=y[i]+0.5*h*(f(y[i])+f(y[i+1]));//校估//cout<<y[i]<<" ";}cout<<"改进欧拉法结果为:";cout<<y[i]<<" ";cout<<endl;}五、总结通过本实验,我基本掌握用欧拉法、改进欧拉法求解常微分方程的初值问题。
欧拉法,改进欧拉法,斐波那契法原理及流程图

1欧拉法求微分方程方法说明欧拉(EUler)法是解常微分方程初值问题ydx= (4.1)最简单的数值方法,其具体做法是,将区间[a, b ]进行N 等分:式Iy (X + 方)=I y(X) + )dt[Λ(^O ) = 7O(4.2) 再对式(4 J)右端积分用矩形公式计算.则有t y(x+册=I yO)+ ⅛∕(x Jo))+«(/),(4. 3)在式(4. 3)右端取X =心,舍去余项。
则得Λ = Λ÷⅛r(⅞>Λ) 作为Wl)的近似值。
步长 N .并将式(4.1)写成等价的积分形在式(4. 3)右端取X=XI-y∞ = ∙vι,舍去余项,则得yι = 7ι + V 71)作为yE)的近似值.一般地,在式(4. 3)右端取舍去余项,则得‰ι = Λ +⅛r(兀,儿),“ IU…,“一1 (4. 4)作为班和】)的近似值.式(4. 4)为欧拉法计算公式.过点的积分曲线就是初值问题式(4. 1)的解.欧拉法的儿何意义是,过点4(心几)引斜率为5沟)的积分曲线的切线,此切线与直线XFl的交点为J⅞C⅛M),再过点引以J f OWL)为斜率的切线与直线2乃的交点为▲(乃宀),依此类推,从A-I(Vl>Λ-1)出发,作以Jr(VlJλ-I)为斜率的切线,此切线与直线X=兀交点为4(耳,儿).于是便得到过点A O A L- A ftI A fc的一条折线,见图4.1.过(心儿)的积分曲线则用此折线来代替.因此,这种方法亦称折线法.图4.1例:用欧拉法求微分方程y, = y,y(0) =1,h = 0.1,区间为_ y _欧拉法流程图如下:欧拉法程序如下:clear;clc;xl=0;x2=l;h=0.1;x0=0;yθ=i;N=(X2・xl)/h;%要计算的次数X(I)=X0;y(i)=yθ;for n=l:Nx(n+l)=x(n)+h;y (n+l)=y (n )+h * (y (n )-2 *x (n )∕y (n )); endX=XY=y2改进欧拉法求微分方程方法说明由于欧拉法采用矩形公式计算积分产生较大截断误差.改进欧拉法(乂称改进折线法)是采取梯形公式來计算式(4. 3)右端积分,则有Xτ+Λ) = Xx)+⅛/(XXX)÷∕(z+⅛y(^+⅛))]+^(∕)2 (5. 1)在式(5.1)右端取X = Xθ,舍去余项,则得^ι = Λ+∣[∕⅛>Λ)÷∕(^ι,Λ)]将乃作为巩小的近似值.在式(5.1)右端再取兀=丙丿(引=必,舍去余项,则得乃F+紳(W)+畑”)]将乃作为班乃)的近似值.一般地,在式(5.1)右端取X=Zy(XJ=儿,舍去余项.则得儿+】=儿 + 芬了E必)+∙∕(S必J],gQi,…,”一1(5 2)将7s+1作为∙y氐J的近似值.式(5. 2)为改进欧拉法计算公式.流程图如下:例:用改进欧拉法求微分方程y∙ = y-^,y(O) =1,11 =0.1,区间为E,1J y改进欧拉法程序如下:clear;clc;xl=0;x2=l;h=0.1;x0=0;yo=i;P(I)=o;N=(x2-xl)∕h;X(I)=X0;y(i)=yθ;for n=l:Nx(n+l)=x(n)+h;y(n+l)=y(n)+h*(y(n)-2*x(n)∕y(n));p(n+l)=y(n)+h*(y(n+l)-2*x(n)∕y(n+l));y(n+l)=(y(n+l)+p(n+l))∕2;endX=XY=y3斐波那契法求极值方法说明斐波那契法原理类似于黄金分割法,只是搜索区间的缩短率不再采用黄金分割数0.618o如图7.1所示,只要在[a, b]内取两点xl, x2,并计算岀f(xl),f(x2),通过比较,可将区间[a, b]缩短为[a, x2]或[xl,b]。
欧拉公式的改进

改进欧拉法 /* modified Euler’s method */
§1 Euler’s Method
Step 1: 先用显式欧拉公式作预测,算出 yi+1 = yi + h f ( xi , yi )
Step 2: 再将 yi+1 代入隐式梯形公式的右边作校正,得到
yi +1
=
yi
+
h 2
Step 3: 将 yi+1 与 y( xi+1 ) 在 xi 点的泰勒展开作比较
yi+1 = yi + (1+ 2 )h y( xi ) + 2 ph2 y( xi ) + O(h3 )
y( xi+1 ) =
y( xi ) + hy( xi ) +
h2 2
y( xi ) + O(h3 )
Hey! Isn’t the leading term of the local
由于未知数tryui+n1c同atSio时enem出ersr现tohra在otfwE等eucl式earn’的smma两ekte边haod,goho不22dy能(x直i )?接得到,故 称为隐式 /* implicit */ 欧拉us公e o式f it,…而前者称为显式 /* explicit */ 欧拉公式。 一般先用显式计算一个初值,再迭代求解。
迭代法m,et其ho迭d *代/,收而敛前性面与的欧三拉种公算式法相都似是。单步法 /* single-step method */。
中点欧拉公式 /* midpoint formula */
中心差商近似导数
y( x2 ) y( x0 ) +
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
main()
{
ol();
printf("\n");
gjol();
}
void gjol()
{
int i;
float y[n+1];
y[0]=m;//赋初值
printf("改进欧拉法\n");
for(i=0;i<n;i++)
{
if(i==0)//预估
{
y[i+1]=y[0]+h*f(y[0]);
}
printf("欧拉法结果为:\n");
printf("y[%d]=%f\n",i,y[i]);
}
显示结果:
五、总结
通过编程,我对运用欧拉公式求解常微分方程有了更深的理解,
六、附录
《数值计算方法与算法(第二版)》,张韵华主编,2012.1
}
else
{
y[i+1]=y[i-1]+2*h*f(y[i]);
}
y[i+1]=y[i]+0.5*h*(f(y[i])+f(y[i+1]));//校估
printf("y[%d]=%f\n",i,y[i]);
}
printf("改进欧拉法结果为:\n");
printf("y[%d]=%f\n",i,y[i]);
西华数学与计算机学院上机实践报告
课程名称:计算方法A
年级:2010级
上机实践成绩:
指导教师:严常龙
姓名:李国强
上机实践名称:解常微分方程初值问题
学号:362011080401114
上机实践日期:2013.12.25
上机实践编号:
上机实践时间:14:00
一、目的
1.通过本实验加深对欧拉法、改进欧拉法、线性多步法的构造过程的理解;
}
void ol()
{
int i;
float y[n+1];
y[0]=m;//赋初值
printf("欧拉法\n");
for(i=0;i<n;i++)
{
if(i==0)
{
y[i+1]=y[0]+h*f(y[0]);
}
else
{
y[i+1]=y[i-1]+2*h*f(y[i]);
}
printf("y[%d]=%f\n",i,y[i]);
2.能对上述四种方法提出正确的算法描述编程实现,观察计算结果的改善情况。
二、内容与设计思想
自选常微分方程的初值问题,分别用欧拉法、改进欧拉法求解。
分别用以上两种方法求解常微分方程初值问题:
三、使用环境
操作系统:Win 8
软件平台:Visual C++ 6.0
四、核心代码及调试过程
#include<stdio.h>
#include<math.h>
#define f(y) (y*y+1)
#define m 0.0//初值为0
#define h 0.1//步长为0.1
#define n 14//迭代次数为14
#define a 0.0//定义区间长度
#define d 1.4
void gjol();//改进欧拉法
