人教版七年级数学下册期末总复习学案+练习
2019-2020学年七年级数学下册 期末复习学案4 新人教版.doc

2019-2020学年七年级数学下册 期末复习学案4 新人教版【复习内容】二元一次方程组【知识梳理】二元一次方程(组)1.二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.2.二元一次方程组:含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.3.二元一次方程组的解:二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解. 4.二元一次方程组的解法. (1)代人消元法:解方程组的基本思路是“消元”一把“二元”变为“一元”,主要步骤是,将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代人另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代人消元法,简称代人法.(2)加减消元法:通过方程两边分别相加(减)消去其中一个未知数,这种解二元一次方程组的方法叫做加减消元法,简称加减法.【考点例题】1.写出其中一个解是⎩⎨⎧==35y x 的一个二元一次方程是 . 2.已知43x y =⎧⎨=⎩是方程组512ax by bx ay +=⎧⎨+=-⎩的解,则a b += . 3.已知12x t t y =+⎧⎪⎨=⎪⎩,请用含x 的代数式表示y ,则=y 4.方程x+2y=5的正整数解有A .一组B .二组C .三组D .四组5.方程组525x y x y =+⎧⎨-=⎩的解满足方程x+y -a=0,那么a 的值是A .5B .-5C .3D .-36.足球比赛的计分规则为胜一场得3分,平一场得1人,负一场得0分,一个队打14场,负5场,共得19分,那么这个队胜了A .3场B .4场C .5场D .6场7.如果21250x y x y -++--=.则x+y 的值是___________.8.解方程组(1)20325x y x y -=⎧⎨-=⎩ (2)⎩⎨⎧=-=+)2(132)1(42y x y x (3)32123x y x y ++== (4)解方程组13821325x y x y +=⎧⎨+=⎩9. 己知y=x 2 +px+q ,当x=1时,y=3:当x=-3时,y=7.求当x=-5时y 的值.10. 某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种无盖 的长方体纸盒.(长方形的宽与正方形的边长相等)(1)现有正方形纸板50张,长方形纸板l 00张,若要做竖式纸盒x 个,横式纸盒y 个. ①根据题意,完成以下表格:②若纸板全部用完,求x 、y 的值;(2)若有正方形纸板80张,长方形纸板n 张,做成上述两种纸盒,纸板恰好全部用完.已知162<n<172,求n的值.。
2019-2020学年七年级数学下册 期末复习学案3 新人教版.doc

2019-2020学年七年级数学下册 期末复习学案3 新人教版【知识梳理】幂的运算性质:①同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即n m n m a a a +=⋅(m 、n 为正整数);②同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即n m n m aa a -=÷(a ≠0,m 、n 为正整数,m>n );③幂的乘方法则:幂的乘方,底数不变,指数相乘,即n n n b a ab =)((n 为正整数); ④积的乘方法则:积的乘方,把积中各个因式分别乘方,再把所得的幂相乘即:(ab )n =a n b n 底数不变,指数相乘⑤零指数:10=a (a ≠0);⑥负整数指数:n n a a 1=-(a ≠0,n 为正整数); 【考点例题】1.计算:()2432x x -÷=___________.2.22)3)(2(x x --=3.一张薄的金箔的厚度为0.000000091m ,用科学记数法可表示为______________m .4.若3,2==y x a a ,则y x a 23-= .5.下列计算中,不正确的是( ).A 、1243a a a =⋅B 、(-2x 2y)3=-6x 6y 3C 、3ab 2•(-2a)=-6a 2b 2D 、(-5xy)2÷5x 2y =5y6. 计算(1)201)1()1()20101(---+--π (2)102322334)()2()(2a a a a a +-⋅-+;(3)(π-3)0-(12)-1+ ()200820092 1.53⎛⎫⨯- ⎪⎝⎭7. 若x =2m +1,y =3+8m ,则用x 的代数式表示y 为 .8.已知a=355,b=444,c=533,则有 ( )A .a <b <cB .c <b <aC .c <a <bD .a <c <b。
最新七年级数学人教版下学期期末总复习学案

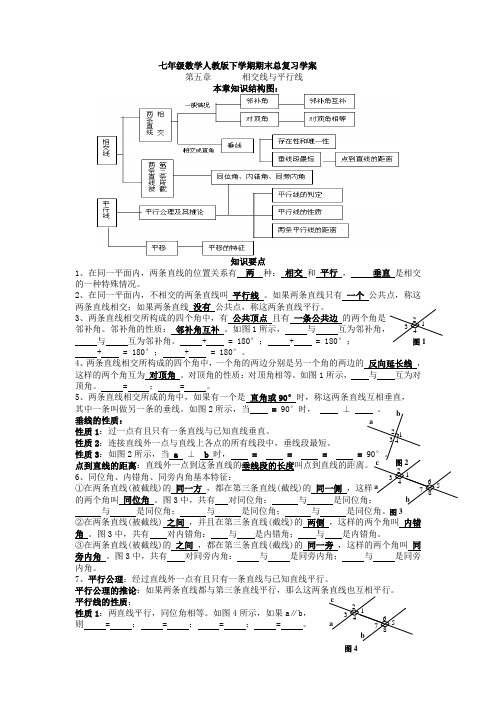
七年级数学人教版下学期期末总复习学案12第五章相交线与平行线3本章知识结构图:45知识要点61、在同一平面内,两条直线的位置关系有两种:相交和平行,垂直是相交的一种特殊情况。
782、在同一平面内,不相交的两条直线叫平行线。
如果两条直线只有一个9公共点,称这两条直线相交;如果两条直线没有公共点,称这两条直线平行。
3、两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两1011个角是邻补角。
邻补角的性质:邻补角互补。
如图1所示,与互为邻1213补角,14与互为邻补角。
+ =180°; + =180°;+ =180°; + =180°。
15164、两条直线相交所构成的四个角中,一个角的两边分别是另一个角的两边17的反向延长线,这样的两个角互为对顶角。
对顶角的性质:对顶角相等。
如18图1所示,与互为对顶角。
= ; = 。
195、两条直线相交所成的角中,如果有一个是直角或90°时,称这两条直20线互相垂直,其中一条叫做另一条的垂线。
如图2所示,当= 90°时,2122⊥。
23垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直。
2425性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
26性质3:如图2所示,当a⊥b时,= =2790°。
28点到直线的距离:直线外一点到这条直线的垂线段的长度叫点到直线的距29离。
306、同位角、内错角、同旁内角基本特征:31①在两条直线(被截线)的同一方,都在第三条直线(截线)的同一侧,32这样33的两个角叫同位角。
图3中,共有对同位角:与是同位34角;35与是同位角;与是同位角;与是同位36角。
37②在两条直线(被截线) 之间,并且在第三条直线(截线)的两侧,这样38的两个角叫内错角。
图3中,共有对内错角:与是内错角;与是内错角。
3940③在两条直线(被截线)的之间,都在第三条直线(截线)的同一旁,这样的两个角叫同旁内角。
七年级数学人教版下册期末总复习学案(谷风教育)

七年级数学人教版下学期期末总复习学案第五章相交线与平行线本章知识结构图:知识要点1、在同一平面内,两条直线的位置关系有两种:相交和平行,垂直是相交的一种特殊情况。
2、在同一平面内,不相交的两条直线叫平行线。
如果两条直线只有一个公共点,称这两条直线相交;如果两条直线没有公共点,称这两条直线平行。
3、两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
邻补角的性质:邻补角互补。
如图1所示,与互为邻补角,与互为邻补角。
+ =180°; + =180°;+ =180°; + =180°。
4、两条直线相交所构成的四个角中,一个角的两边分别是另一个角的两边的反向延长线,这样的两个角互为对顶角。
对顶角的性质:对顶角相等。
如图1所示,与互为对顶角。
= ; = 。
5、两条直线相交所成的角中,如果有一个是直角或90°时,称这两条直线互相垂直,其中一条叫做另一条的垂线。
如图2所示,当= 90°时,⊥。
垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直。
图113 4213 42ab性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
性质3:如图2所示,当 a ⊥ b 时, = = = = 90°。
点到直线的距离:直线外一点到这条直线的垂线段的长度叫点到直线的距离。
6、同位角、内错角、同旁内角基本特征:①在两条直线(被截线)的 同一方 ,都在第三条直线(截线)的 同一侧 ,这样 的两个角叫 同位角 。
图3中,共有 对同位角: 与 是同位角; 与 是同位角; 与 是同位角; 与 是同位角。
②在两条直线(被截线) 之间 ,并且在第三条直线(截线)的 两侧 ,这样的两个角叫 内错角 。
图3中,共有 对内错角: 与 是内错角; 与 是内错角。
③在两条直线(被截线)的 之间 ,都在第三条直线(截线)的 同一旁 ,这样的两个角叫 同旁内角 。
2013春七年级下册人教版数学期末总复习教案及练习试卷(修正版)

七年级数学人教版下学期期末总复习学案第五章 相交线与平行线(二)例题与习题:一、对顶角和邻补角:1.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个2.如图1-1,直线AB 、CD 、EF 都经过点O , 图中有几对对顶角。
( )3.如图1-2,若∠AOB 与∠BOC 是一对邻补角,OD OE 在∠BOC 内部,并且∠BOE =12∠COE ,∠DOE =72求∠COE 的度数。
( )二、垂线:已知:如图,在一条公路l 的两侧有A 、B 两个村庄.<1>现在乡政府为民服务,沿公路开通公交汽车,并在路边修建一个公共汽车站P ,同时修建车站P 到A 、B 两个村庄的道路,并要求修建的道路之和最短,请你设计出车站的位置,在图中画出点P 的位置,(保留作图的痕迹).并在后面的横线上用一句话说明道理. .<2>为方便机动车出行,A 村计划自己出资修建一条由本村直达公路l 的机动车专用道路,你能帮助A 村节省资金,设计出最短的道路吗?,请在图中画出你设计修建的最短道路,并在后面的横线上用一句话说明道理. .12121221(图1-2)三、同位角、内错角和同旁内角的判断1.如图3-1,按各角的位置,下列判断错误的是( )(A )∠1与∠2是同旁内角 (B )∠3与∠4是内错角 (C )∠5与∠6是同旁内角 (D )∠5与∠8是同位角2.如图3-2,与∠EFB 构成内错角的是_ ___,与∠FEB四、平行线的判定和性质:1.如图4-1, 若∠3=∠4,则 ∥ ; 若AB ∥CD,则∠ =∠ 。
2.已知两个角的两边分别平行,其中一个角为52°,则另一个角为_______.3.两条平行直线被第三条直线所截时,产生的八个角中, 角平分线互相平行的两个角是( ) A.同位角 B.同旁内角 C.内错角 D. 同位角或内错角4.如图4-2,要说明 AB ∥CD ,需要什么条件? 试把所有可能的情况写出来,并说明理由。
最新七年级下册数学期末复习导学案优秀名师资料

七年级下册数学期末复习导学案人教版七年级下册数学期末总复习学案平面直角坐标系考试相交线与平行线第六章第七章三角形第八章二元一次方程组第九章不等式与不等式组第十章数据的收集、整理与描述第十五章整式的乘除与因式分解第五章相交线与平行线(二)例题与习题:一、对顶角和邻补角:1.如图所示,?1和?2是对顶角的图形有( )1A.1个B.2个C.3个D.4个 2(如图1-1,直线AB、CD、EF都经过点O,图中有几对对顶角。
( )3(如图1-2,若?AOB与?BOC是一对邻补角,OD平分?OE在?BOC )12?COE,?DOE=72(图1-2)二、垂线:已知:如图,在一条公路l的两侧有A、B两个村庄.<1>现在乡政府为民服务,沿公路开通公交汽车,并在路边修建一个公共汽车站P,同时修建车站P到A、B两个村庄的道路,并要求修建的道路之和最短,请你设计出车站的位置,在图中画出点P的位置,(保留作图的痕迹)(并在后面的横线上用一句话说明道理( .<2>为方便机动车出行,A村计划自己出资修建一条由本村直达公路l的机动车专用道路,你能帮助A村节省资金,设计出最短的道路吗,,请在图中画出你设计修建的最短道路,并在后面的横线上用一句话说明道理( .三、同位角、 )(A)?1与?2是同旁___,与?FEB-1 四、平行线的判定和性质: 1.如图4-1,若?3=?4,则 1 283 45 6 图3 ? ;若AB?CD,则? =? 。
322.已知两个角的两边分别平行,其中一个角为52?,DC (1) 则另一个角为_______. 图4-13(两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是( )A.同位角B.同旁 D. 同位角或内错角4(如图4-2,要说明 AB?CD,需要什么条件,试把所有可能的情况写出来,并说明理由。
ADFEC(图4-2) B5(如图4-3,EF?GF,垂足为F,?AEF=150?, ?DGF=60?。
七年级数学人教版下学期期末总复习学案
七年级数学人教版下学期期末总复习学案第五章 相交线与平行线本章知识结构图:知识要点1、在同一平面内,两条直线的位置关系有 两 种: 相交 和 平行 , 垂直 是相交的一种特殊情况。
2、在同一平面内,不相交的两条直线叫 平行线 。
如果两条直线只有 一个 公共点,称这两条直线相交;如果两条直线 没有 公共点,称这两条直线平行。
3、两条直线相交所构成的四个角中,有 公共顶点 且有 一条公共边 的两个角是 邻补角。
邻补角的性质: 邻补角互补 。
如图1所示, 与 互为邻补角, 与 互为邻补角。
+ = 180°; + = 180°; + = 180°; + = 180°。
4、两条直线相交所构成的四个角中,一个角的两边分别是另一个角的两边的 反向延长线 ,这样的两个角互为 对顶角 。
对顶角的性质:对顶角相等。
如图1所示, 与 互为对顶角。
= ; = 。
5、两条直线相交所成的角中,如果有一个是 直角或90°时,称这两条直线互相垂直, 其中一条叫做另一条的垂线。
如图2所示,当 = 90°时, ⊥ 。
垂线的性质: 性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
性质3:如图2所示,当 a ⊥ b 时, = = = = 90°。
点到直线的距离:直线外一点到这条直线的垂线段的长度叫点到直线的距离。
6、同位角、内错角、同旁内角基本特征: ①在两条直线(被截线)的 同一方 ,都在第三条直线(截线)的 同一侧 ,这样 的两个角叫 同位角 。
图3中,共有 对同位角: 与 是同位角;与 是同位角; 与 是同位角; 与 是同位角。
②在两条直线(被截线) 之间 ,并且在第三条直线(截线)的 两侧 ,这样的两个角叫 内错角 。
图3中,共有 对内错角: 与 是内错角; 与 是内错角。
③在两条直线(被截线)的 之间 ,都在第三条直线(截线)的 同一旁 ,这样的两个角叫 同旁内角 。
七年级数学下册 期末复习学案3 新人教版

江苏省溧阳市汤桥初级中学2011-2012学年七年级数学下学期期末复习学案3 新人教版【知识梳理】幂的运算性质:①同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即n m n m a a a +=⋅(m 、n 为正整数);②同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即n m n m a a a -=÷(a ≠0,m 、n 为正整数,m>n ); ③幂的乘方法则:幂的乘方,底数不变,指数相乘,即n n n b a ab =)((n 为正整数); ④积的乘方法则:积的乘方,把积中各个因式分别乘方,再把所得的幂相乘 即:(ab )n =a n b n 底数不变,指数相乘⑤零指数:10=a (a ≠0); ⑥负整数指数:n n a a 1=-(a ≠0,n 为正整数); 【考点例题】1.计算:()2432x x -÷=___________.2.22)3)(2(x x --=3.一张薄的金箔的厚度为0.000000091m ,用科学记数法可表示为______________m .4.若3,2==y x a a ,则y x a 23-= .5.下列计算中,不正确的是( ).A 、1243a a a =⋅B 、(-2x 2y)3=-6x 6y 3C 、3ab 2•(-2a)=-6a 2b 2D 、(-5xy)2÷5x 2y =5y6. 计算(1)201)1()1()20101(---+--π (2)102322334)()2()(2a a a a a +-⋅-+;(3)(π-3)0-(12)-1+ ()200820092 1.53⎛⎫⨯- ⎪⎝⎭7. 若x =2m +1,y =3+8m ,则用x 的代数式表示y 为 .8.已知a=355,b=444,c=533,则有 ( )A.a<b<c B.c<b<a C.c<a<b D.a<c<b。
七年级下册人教版数学期末总复习教案)

七年级数学下学期期末总复习学案第五章 相交线与平行线(一)本章知识结构图:(二)例题与习题:一、对顶角和邻补角:1.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个 2.如图1-1,直线AB 、CD 、EF 都经过点O , 图中有几对对顶角。
( )3.如图1-2,若∠AOB 与∠BOC 是一对邻补角,OD 平分∠AOB ,OE 在∠BOC 内部,并且∠BOE =12∠COE ,∠DOE =72°。
求∠COE 的度数。
( )二、垂线:已知:如图,在一条公路l 的两侧有A 、B 两个村庄.<1>现在乡政府为民服务,沿公路开通公交汽车,并在路边修建一个公共汽车站P ,同时修建车站P 到A 、B 两个村庄的道路,并要求修建的道路之和最短,请你设计出车站的位置,在图中画出点P 的位置,(保留作图的痕迹).并在后面的横线上用一句话说明道理. .一般情况相交成直角相交线相交 两条直线 第三条所截两条直线被邻补角 垂线 邻补角互补 点到直线的距离同位角、内错角、同旁内角 平行线平行公理及其推论 平行线的性质 平行线的判定 平移 对顶角 对顶角相等 垂线段最短 存在性和唯一性两条平行线的距离 平移的特征 12121221D BE (图1-2) 图1-1<2>为方便机动车出行,A 村计划自己出资修建一条由本村直达公路l 的机动车专用道路,你能帮助A 村节省资金,设计出最短的道路吗?,请在图中画出你设计修建的最短道路,并在后面的横线上用一句话说明道理. .三、同位角、内错角和同旁内角的判断1.如图3-1,按各角的位置,下列判断错误的是( )(A )∠1与∠2是同旁内角 (B )∠3与∠4是内错角 (C )∠5与∠6是同旁内角 (D )∠5与∠8是同位角2.如图3-2,与∠EFB 构成内错角的是_ ___,与∠FEB 构成同旁内角的是_ ___.四、平行线的判定和性质: 1.如图4-1, 若∠3=∠4,则 ∥ ;若AB ∥CD,则∠ =∠ 。
2019-2020学年七年级数学下册 期末复习学案1 新人教版.doc

2019-2020学年七年级数学下册期末复习学案1 新人教版一、知识点:1、“三线八角”①如何由线找角:一看线,二看型。
同位角是“F”型;内错角是“Z”型;同旁内角是“U”型。
②如何由角找线:组成角的三条线中的公共直线就是截线。
③2、平行公理:如果两条直线都和第三条直线平行,那么这两条直线也平行。
简述:平行于同一条直线的两条直线平行。
补充定理:如果两条直线都和第三条直线垂直,那么这两条直线也平行。
简述:垂直于同一条直线的两条直线平行。
3、平行线的判定和性质:判定性质条件结论条件结论同位角相等两直线平行两直线平行同位角相等内错角相等两直线平行两直线平行内错角相等同旁内角互补两直线平行两直线平行同旁内角互补4、图形平移的性质:图形经过平移,连接各组对应点所得的线段互相平行(或在同一直线上)并且相等。
二、例题:例1:①如图,找出图中所有的同位角;找出图中所有的内错角;找出图中所有的同旁内角。
④BAC和∠是和被所截的内错角;∠BAC和∠是和被所截的内错角。
例2:如图,从下列三个条件中:(1)AD∥CB (2)AB∥CD (3)∠A=∠C,任选两个作为条件,另一个作为结论,编一道数学题,并说明理由。
已知:结论:理由:例3:如图,AD∥BC,∠A=∠C,BE、DF分别平分∠ABC和∠CDA,试说明BE∥DF的理由?例4:两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF 的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积。
三、作业:1、如图,AB∥CD,AD∥BC,∠A的2倍与∠C的3倍互补,求∠A和∠D的度数。
•2、如图,已知AB∥CD,直线EF分别交AB、CD于E、F,EG•平分∠BEF,若∠1=72°,求∠2的度数。
3、如图,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数.。
初一数学下册期末总复习学习教案合集(人教版)

初一数学下册期末总复习学习教案合集(人教版)七年级数学人教版下学期期末总复习学案考试内容第五章相交线与平行线第六章平面直角坐标系第七章三角形第八章二元一次方程组第九章不等式与不等式组第十章数据的收集、整理与描述第十五章整式的乘除与因式分解第五章相交线与平行线(一)本章知识结构图:(二)例题与习题:一、对顶角和邻补角:1.如图所示,1和2是对顶角的图形有毛A.1个B.2个C.3个D.4个2.如图1-1,直线AB、CD、EF都经过点O,图中有几对对顶角。
3.如图1-2,若AOB与BOC是一对邻补角,OD平分AOB,OE在BOC内部,并且BOE=COE,DOE=72。
求COE的度数。
二、垂线:已知:如图,在一条公路的两侧有A、B两个村庄.现在乡政府为民服务,沿公路开通公交汽车,并在路边修建一个公共汽车站P,同时修建车站P到A、B两个村庄的道路,并要求修建的道路之和最短,请你设计出车站的位置,在图中画出点P的位置,(保留作图的痕迹).并在后面的横线上用一句话说明道理. .为方便机动车出行,A村计划自己出资修建一条由本村直达公路的机动车专用道路,你能帮助A村节省资金,设计出最短的道路吗?,请在图中画出你设计修建的最短道路,并在后面的横线上用一句话说明道理. .三、同位角、内错角和同旁内角的判断1.如图3-1,按各角的位置,下列判断错误的是(A)1与2是同旁内角(B)3与4是内错角(C)5与6是同旁内角(D)5与8是同位角2.如图3-2,与EFB构成内错角的是_ ___,与FEB构成同旁内角的是_ ___.四、平行线的判定和性质:1.如图4-1,若4,则∥ ;若AB∥CD,则。
2.已知两个角的两边分别平行,其中一个角为52,则另一个角为_______.3.两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是A.同位角B.同旁内角C.内错角D. 同位角或内错角4.如图4-2,要说明AB∥CD,需要什么条件?试把所有可能的情况写出来,并说明理由。
最新人教版部编版七年级数学下册全册 期末知识点总结复习 专题训练

4.如图,∠1=∠2,∠3=40°,则∠4 等于( C ) A.120° B.130° C.140° D.40°
5.如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD =70°.
(1)求证:AB∥CD; (2)求∠C 的度数.
解:(1)证明:∵AE⊥BC,FG⊥BC, ∴AE∥GF. ∴∠2=∠A. ∵∠1=∠2, ∴∠1=∠A. ∴AB∥CD.
二、填空题(每小题 3 分,共 18 分) 9.将命题“两直线平行,同位角相等”写成“如果……那么……”的 形式是如果两直线平行,那么同位角相等.
10.将线段 AB 平移 1 cm,得到线段 A′B′,则点 A 到点 A′的距离
是 1cm
.
11.(1)如图 1,村庄 A 到公路 BC 最短的距离是 AD,根据
解:(1)BOC=180°. ∴∠BOC=135°. ∴∠AOC=45°. ∵OC 平分∠AOD, ∴∠COD=∠AOC=45°.
(2)OD⊥AB.理由如下: ∵∠COD=∠AOC=45°, ∴∠AOD=∠COD+∠AOC=90°. ∴OD⊥AB.
5.(2017·赤峰)直线 a∥b,直角三角形 ABC 的直角顶点 C 在直线 a 上.若∠1=35°,则∠2 等于( C )
A.65° B.50° C.55° D.60°
6.以下关于距离的几种说法中,正确的有( A ) ①连接两点间的线段长度叫做这两点的距离;
②连接直线外的点和直线上的点的线段叫做点到直线的距离;
解:(1)证明:∵BC∥OA, ∴∠B+∠AOB=180°. ∴∠AOB=180°-∠B=80°. 又∵∠A=100°, ∴∠A+∠AOB=180°.∴OB∥AC.
(3)不改变.理由如下: ∵BC∥OA, ∴∠OCB=∠AOC,∠OFB=∠AOF. ∵∠FOC=∠AOC, ∴∠AOF=2∠AOC. ∴∠OFB=2∠OCB,即∠OCB∶∠OFB 的值为 1∶2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学人教版下学期期末总复习学案考试内容第五章 相交线与平行线 第六章 平面直角坐标系第七章 三角形 第八章 二元一次方程组第九章 不等式与不等式组 第十章 数据的收集、整理与描述 第十五章 整式的乘除与因式分解第五章 相交线与平行线(一)本章知识结构图: (二)例题与习题:一、对顶角和邻补角:1.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个 2.如图1-1,直线AB 、CD 、EF 都经过点O ,图中有几对对顶角。
() 3.如图1-2,若∠AOB 与∠BOC 是一对邻补角,OD 平分∠AOB , OE 在∠BOC 内部,并且∠BOE =12∠COE ,∠DOE =72°。
求∠COE 的度数。
() 二、垂线: 已知:如图,在一条公路l 的两侧有A 、B 两个村庄.<1>现在乡政府为民服务,沿公路开通公交汽车,并在路边修建一个公共汽车站P ,同时修建车站P 到A 、B 两个村庄的道路,并要求修建的道路之和最短,请你设计出车站的位置,在图中画出点P 的位置,(保留作图的痕迹).并在后面的横线上用一句话说明道理..<2>为方便机动车出行,A 村计划自己出资修建一条由本村直达公路l 的机动车专用道路,你能帮助A 村节省资金,设计出最短的道路吗?,请在图中画出你设计修建的最短道路,并在后面的横线上用一句话说明道理..三、同位角、内错角和同旁内角的判断1.如图3-1,按各角的位置,下列判断错误的是( )(A )∠1与∠2是同旁内角 (B )∠3与∠4是内错角 (C )∠5与∠6是同旁内角 (D )∠5与∠8是同位角2.如图3-2,与∠EFB 构成内错角的是_ ___,与∠FEB _ ___.四、平行线的判定和性质: 1.如图4-1, 若∠3=∠4,则 ∥; 若AB ∥CD,则∠ =∠。
2.已知两个角的两边分别平行,其中一个角为52°,则另一个角为_______. 3.两条平行直线被第三条直线所截时,产生的八个角中, 角平分线互相平行的两个角是( ) A.同位角 B.同旁内角C.内错角D. 同位角或内错角4.如图4-2,要说明 AB ∥CD ,需要什么条件? 一般情况相交成直角相交线 相交两条直线第三条所截 两条直线被邻补角 垂线 邻补角互补点到直线的距离同位角、内错角、同旁内角 平行线平行公理及其推论 平行线的性质 平行线的判定平移 对顶角 对顶角相等 垂线段最短 存在性和唯一性 两条平行线的距离平移的特征12121221 D BE A C O(图1-2) 12345678图3-1 ⌒⌒⌒⌒A B C D 1432 (1) 图4-1 图1-1 F E DCBA(图4-2)FA CB ED (1)图3-2试把所有可能的情况写出来,并说明理由。
5.如图4-3,EF ⊥GF ,垂足为F ,∠AEF=150°, ∠DGF=60°。
试判断AB 和CD 的位置关系,并说明理由。
6.如图4-4,AB ∥DE ,∠ABC =70°,∠CDE =147°,求∠C 的度数.() 7.如图4-5,CD ∥BE ,则∠2+∠3−∠1的度数等于多少?() 8.如图4-6:AB ∥CD ,∠ABE =∠DCF ,求证:BE ∥CF .五、平行线的应用: 1.某人从A 点出发向北偏东60°方向走了10米,到达B 点,再从B 点方向向南偏西15°方向走了10米,到达C 点,则∠ABC 等于( )A.45°B.75°C.105°D.135°2.一位学员练习驾驶汽车,发现两次拐弯后,行驶方向与原来的方向相同,这两次的拐弯角度可能是( )A 第一次向右拐50°,第二次向左拐130°B 第一次向左拐50°,第二次向右拐50°C 第一次向左拐50°,第二次向左拐130°D 第一次向右拐50°,第二次向右拐50°3.如图5-2,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置, 若∠EFB =65°,则∠AED ′等于° 4.计算(图6-1)中的阴影部分面积。
(单位:厘米)5.如(图6-2)所示,已知大正方形的边长为10厘米,小正方形的边长为7厘米, 求阴影部分面积。
(结果保留π ) 6.求(图6-3)中阴影部分的面积(单位:厘米)7.下列命题中,真命题的个数为( )个 ① 一个角的补角可能是锐角;② ③ 平面内,过一点有且只有一条直线与已知直线垂直; ④ 平面内,过一点有且只有一条直线与已知直线平行;A.1B.2C.3D.48.已知:如图8-1,AD ⊥BC ,EF ⊥BC ,∠1=2。
求证:∠CDG=∠B. 9. 已知:如图8-2,A B ∥CD ,∠1=∠2,∠E=65°20′,求:∠F 的度数。
10.已知:如图8-3, AE ⊥BC , FG ⊥BC , ∠1=∠2, ∠D =∠3+60︒, ∠CBD =70︒ .(1)求证:AB ∥CD ; (2)求∠C 的度数。
()E21G F DC B A 3图8-1 1 3 2D BC AE F G 图8-3B 'DFCBAGCD E A BF图4-3 D B ECFA图4-6图6-1AB EFC D 12 图2图8-2图8-4图4-4321EA C BD图4-5 图5-2D图6-3 图6-211.如图8-4,在长方形ABCD 中,∠ADB =20°,现将这一长方形纸片沿AF 折叠,若使 AB ’∥BD ,则折痕AF 与AB 的夹角∠BAF 应为多少度?()12. 如图8-5, B 点在A 点的北偏西30︒方向, 距A 点100米, C 点在B 点的北偏东60︒, ∠ACB = 40︒ (1) 求A 点到直线BC 的距离;(100米) (2) 问:A 点在C 点的南偏西多少度 ? (写出计算和推理过程)()13.如图,在1010⨯的正方形网格中,每个小正方形的边长均为1个单位,将ABC △向下平移4个单位,得到A B C '''△,请你画出A B C '''△(不要求写画法).六、利用等积变换作图:1.如图△ ABC ,过A 点的中线能把三角形分成面积相同的两部分。
你能过AB 边上一点E作一条直线EF ,使它也将这个三角形分成两个面积相等的部分吗?2.有一块形状如图的耕地,兄弟二人要把它分成两等份,请你设计一种方案把它分成所需要的份数.如果只允许引一条直线,你能办到吗?3.如图,欲将一块四方形的耕地中间的一条折路MPN 改直,但不能改变折路两边的耕地面积的大小,应如何画线?4.已知:如图,五边形ABCDE ,用三角尺和直尺作一个三角形,使该三角形的面积与所给的五边形ABCDE 的面积相等。
第六章 平面直角坐标系(一)本章知识结构图:(二)例题与习题:一、填空: 1.已知点P(3a-8,a-1).(1) 点P在x 轴上,则P 点坐标为;(2) 点P 在第二象限,并且a 为整数,则P 点坐标为;(3) Q 点坐标为(3,-6),并且直线PQ ∥x 轴,则P 点坐标为.2.如图的棋盘中,若“帅” 位于点(1,-2)上,“相”位于点(3,-2)上, 则“炮”位于点___ 上.3.点)1,2(A 关于x 轴的对称点'A 的坐标是;点)3,2(B 关于y 轴的对称点'B 的坐标是;点)2,1(-C 关于坐标原点的对称点'C 的坐标是.BCE确定平面内点的位置 建立平面直角坐标系点 坐标(有序数对)P (x , y )A BCBM (北)AN (北)图8-5第4题 E ABDNB A CPM D 第3题4.已知点P 在第四象限,且到x 轴距离为52,到y 轴距离为2,则点P 的坐标为_____.5.已知点P 到x 轴距离为52,到y 轴距离为2,则点P 的坐标为.6. 已知),(111y x P ,),(122y x P ,21x x ≠,则⊥21P P 轴,21P P ∥轴;7.把点),(b a P 向右平移两个单位,得到点),2('b a P +,再把点'P 向上平移三个单位,得到点''P ,则''P 的坐标是; 8.在矩形ABCD 中,A (-4,1),B (0,1),C (0,3),则D 点的坐标为; 9.线段AB 的长度为3且平行与x 轴,已知点A 的坐标为(2,-5),则点B 的坐标为_____. 二、选择题:10.线段AB 的两个端点坐标为A (1D(3,0),则线段AB 与线段CD A.平行且相等 B.三、解答题: 1.已知:如图,)3,1(-A ,,2(-B 2.已知:)0,4(A ,),3(y B ,点C ⑴ 求点C 的坐标;⑵ 若10=∆ABC S ,求点B 3.已知:四边形ABCD (1)在平面直角坐标系中画出四边形(2)求四边形ABCD 的面积.(3)如果把原来的四边形ABCD 4. 已知:)1,0(A ,)0,2(B ,)3,4(C .⑴求△ABC 的面积;⑵ 设点P 在坐标轴上, 且△ABP 与△ABC 的面积相等, 求点P 的坐标.5.如图,是某野生动物园的平面示意图.6.如图,平移坐标系中的△ABC ,使AB 平移到A 置,再将111C B A ∆向右平移3个单位,得到2A ∆画出222C B A ∆,并求出△ABC 到222C B A ∆(一)本章知识结构图:1.A.第6题图C.钝角三角形D.锐角三角形或钝角三角形 2.如图是一副三角尺拼成图案,则∠AEB =_________°.3.在△ABC 中,若a=3,b=5,则c 边的取值范围________.4.如果三条线段的比是:(1)5:20:30 (2)5:10:15 (3)3:4:5 (4)3:3:5 (5)5:5:10 (6)7:7:2 那么其中可构成三角形的比有()种.A.2B.3C.4D.55.三角形的三边分别为3,8,1-2x ,则x 的取值范围是()A.0<x <2B.-5<x <-2C.-2<x <5D.x <-5或x >26.如果一个三角形两边上的高的交点在三角形的外部,那么这个三角形是___ ___三角形.7. 已知△ABC ,求作:(1)△ABC 的中线AD ;(2)△ABC 的角平分线AE ;8. 已知△ABC ,求作:△ABC 的高线AD 、CE 。
9.在△ABC 中,两条角平分线BD 、CE 相交于点O ,∠BOC=116°,那么∠A 的度数是______。
