编译原理-预测分析法(附源码)
编译原理笔记10 自上而下分析-预测分析程序与LL(1)文法
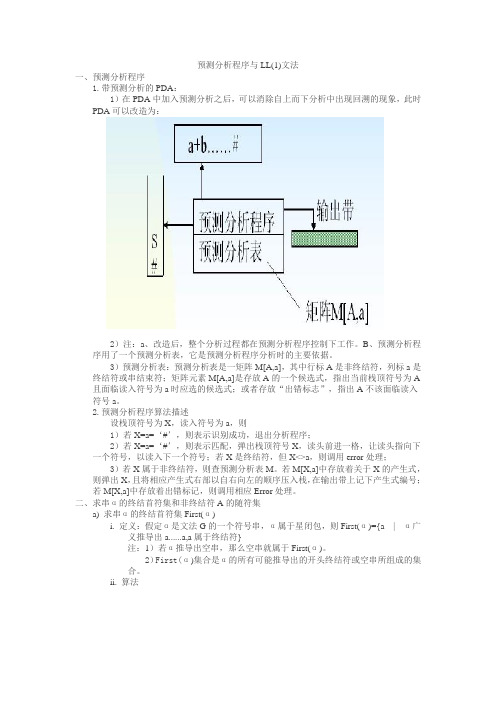
预测分析程序与LL(1)文法一、预测分析程序1.带预测分析的PDA:1)在PDA中加入预测分析之后,可以消除自上而下分析中出现回溯的现象,此时PDA可以改造为:2)注:a、改造后,整个分析过程都在预测分析程序控制下工作。
B、预测分析程序用了一个预测分析表,它是预测分析程序分析时的主要依据。
3)预测分析表:预测分析表是一矩阵M[A,a],其中行标A是非终结符,列标a是终结符或串结束符;矩阵元素M[A,a]是存放A的一个候选式,指出当前栈顶符号为A 且面临读入符号为a时应选的候选式;或者存放“出错标志”,指出A不该面临读入符号a。
2.预测分析程序算法描述设栈顶符号为X,读入符号为a,则1)若X=a=‘#’,则表示识别成功,退出分析程序;2)若X=a=‘#’,则表示匹配,弹出栈顶符号X,读头前进一格,让读头指向下一个符号,以读入下一个符号;若X是终结符,但X<>a,则调用error处理;3)若X属于非终结符,则查预测分析表M。
若M[X,a]中存放着关于X的产生式,则弹出X,且将相应产生式右部以自右向左的顺序压入栈,在输出带上记下产生式编号;若M[X,a]中存放着出错标记,则调用相应Error处理。
二、求串α的终结首符集和非终结符A的随符集a) 求串α的终结首符集First(α)i. 定义:假定α是文法G的一个符号串,α属于星闭包,则First(α)={a | α广义推导出a......a,a属于终结符}注:1)若α推导出空串,那么空串就属于First(α)。
2)First(α)集合是α的所有可能推导出的开头终结符或空串所组成的集合。
ii. 算法具体步骤:b) 求非终结符A的随符集Follow(A)i. 定义:假定S是文法G的开始符号,对于G的任何非终结符A,定义:ii. 算法1. 对文法开始符号S,将‘#’加入到Follow(S)中;2. 若B->αAβ是文法G的一个产生式,则将First(β)-空串加入到Folow(A)中;3. 若B->αA是文法G的一个产生式,或B->αAβ是文法G的一个产生式,且β推导出空串,则将Follow(B)加入到Follow(A)中;注:这里的文法必须消除左递归且提取了左因子后的文法。
预测分析程序代码

#include"stdio.h"#include"string.h" /**//*程序中用到strcpy()函数*//**//*全局变量定义*/char inputString[10]; /**//*用来存储用户输入的字符串,最长为20个字符*/char stack[10]; /**//*用来进行语法分析的栈结构*/int base=0; /**//*栈底指针*/int top=1; /**//*栈顶指针*/char VT[4]={'a','d','b','e'}; /**//*用来存放5个终结符*/char chanShengShi[10]; /**//*用来存放预测分析表M[A,a]中的一条产生式*/int firstCharIntex=0; /**//*如果a匹配产生式,则每次firstCharIntex 自增 1 *//**//*firstCharIntex用来存放用户输入串的第一个元素的下标*/ /**//*自定义函数声明*/char pop() ; /**//*弹出栈顶元素*/int push(char ch) ; /**//*向栈内添加一个元素,成功返回1,若栈已满则返回0*/int search(char temp) ; /**//*查找非终结符集合VT中是否存在变量temp,存在返回1,不存在返回0*/int M(char A, char a) ; /**//* 若预测分析表M[A,a]中存在产生式,则将该产生式赋给字符数组chanShengShi[10],并返回 1,若M[A,a]中无定义产生式则返回 0*/void init() ; /**//*初始化数组inputString[10] 、栈stack[10] 和chanShengShi[10]*/int yuCeFenXi() ; /**//* 进行输入串的预测分析的主功能函数,若输入串满足文法则返回 1,不满足则返回0*/void printStack(); /**//*打印栈内元素 */void printinputString(); /**//*打印用户输入串 *//**//*进入主函数*/void main(){//clrscr();yuCeFenXi(); /**//*调用语法预测分析函数*///getch();}/**//*函数的定义*/int yuCeFenXi(){char X; /**//*X变量存储每次弹出的栈顶元素*/char a; /**//*a变量存储用户输入串的第一个元素*/int i;int counter=1; /**//*该变量记录语法分析的步骤数*/init(); /**//*初始化数组*/printf("wen fa : "); /**//*输出文法做为提示*/printf("S -> aH ");printf("H -> aMd | d ");printf("M -> Ab | ");printf("A -> aM | e ");printf(" input string ,'#' is a end sign !!(aaabd#) "); /**//*提示用户输入将要测试的字符串*/scanf("%s",inputString);push('#');push('S');printf(" Counter-----Stack---------------Input string "); /**//*输出结果提示语句*/while(1) /**//*while循环为语法分析主功能语句块*/{ printf(" \n");printf(" %d",counter); /**//*输出分析步骤数*/printf(" "); /**//*输出格式控制语句*/printStack(); /**//*输出当前栈内所有元素*/X=pop(); /**//*弹出栈顶元素赋给变量X*/printinputString(); /**//*输出当前用户输入的字符串*/if( search(X)==0 ) /**//*在终结符集合VT中查找变量X的值,存在返回 1,否则返回 0*/{if(X == '#') /**//*栈已经弹空,语法分析结果正确,返回 1*/{printf("success ... "); /**//*语法分析结束,输入字符串符合文法定义*/return 1;}else{a = inputString[firstCharIntex];if( M(X,a)==1 ) /**//*查看预测分析表M[A,a]是否存在产生式,存在返回1,不存在返回0*/{for(i=0;i<10;i++) /**//* '$'为产生式的结束符,for循环找出该产生式的最后一个元素的下标*/{if( chanShengShi[i]=='$' ) break;}i-- ; /**//*因为 '$' 不是产生式,只是一个产生式的结束标志,所以i 自减1*/while(i>=0){push( chanShengShi[i] ); /**//*将当前产生式逆序压入栈内*/i-- ;}}else{printf(" error(1) !!"); /**//*若预测分析表M[A,a]不存在产生式,说明语法错误*/return 0;}}}else /**//*说明X为终结符*/{if( X==inputString[firstCharIntex] ) /**//*如果X等于a,说明a匹配*/{firstCharIntex++; /**//*输入串的第一个元素被约去,下一个元素成为新的头元素*/}else{printf(" error(2) !! ");return 0;}}counter++; }}void init(){int i;for(i=0;i<10;i++){inputString[i]=NULL; /**//*初始化数组inputString[10] */stack[i]=NULL; /**//*初始化栈stack[10] */chanShengShi[i]=NULL; /**//*初始化数组chanShengShi[10]*/}}int M(char A, char a) /**//*文法定义因实际情况而定,该文法为课本例题的文法*/{ /**//*该函数模拟预测分析表中的二维数组 */if( A=='S'&& a=='a' ) { strcpy(&chanShengShi[0],"aH$"); return 1; }if( A=='H'&& a=='a' ) { strcpy(&chanShengShi[0],"aMd$"); return 1; }if( A=='H'&& a=='d' ) { strcpy(&chanShengShi[0],"d$"); return 1; }if( A=='M'&& a=='a' ) { strcpy(&chanShengShi[0],"Ab$"); return 1; }if( A=='M'&& a=='d' ) { strcpy(&chanShengShi[0],"$"); return 1; }if( A=='M'&& a=='b' ) { strcpy(&chanShengShi[0],"$"); return 1; }if( A=='M'&& a=='e' ) { strcpy(&chanShengShi[0],"Ab$"); return 1; }if( A=='A'&& a=='a' ) { strcpy(&chanShengShi[0],"aM$"); return 1; }if( A=='A'&& a=='e' ) { strcpy(&chanShengShi[0],"e$"); return 1; }else return 0; /**//*没有定义产生式则返回0*/}char pop() /**//*弹出栈顶元素,用topChar返回*/{char topChar;topChar=stack[--top];return topChar;}int push(char ch){if( top>9 ){printf(" error : stack overflow "); /**//*栈空间溢出*/return 0;}else{stack[top]=ch; /**//*给栈顶空间赋值*/top++;return 1;} }int search(char temp){int i,flag=0; /**//*flag变量做为标志,若找到temp则赋1,否则赋0*/ for(i=0;i<4;i++){if( temp==VT[i] ) /**//*终结符集合中存在temp*/{flag=1;break;}}if(flag==1) return 1; /**//*flag==1说明已找到等于temp的元素*/else return 0;}void printStack() /**//*输出栈内内容*/{int temp;for(temp=1;temp<top;temp++){printf("%c",stack[temp]);}}void printinputString() /**//*输出用户输入的字符串*/{int temp=firstCharIntex ;printf(" "); /**//*该句控制输出格式*/do{printf("%c",inputString[temp]);temp++;}while(inputString[temp-1]!='#');printf(" ");}。
编译原理实验二 预测分析法

实验二预测分析法一、实验项目名称预测分析法二、实验目的根据某一LL(1)文法编制调试预测分析程序,以便对任意输入的符号串进行分析。
本次实验的目的主要是加深对预测分析法的理解。
三、实验环境Win8系统,VC++6.0软件,C语言开发工具四、实验内容本次实验的LL(1)文法为表达式文法:E→E+T | TT→T*F | FF→i | (E)编写识别表达式文法的合法句子的预测分析程序,对输入的任意符号串,给出分析过程及分析结果。
分析过程要求输出步骤、分析栈、剩余输入串和所用产生式。
如果该符号串不是表达式文法的合法句子,要给出尽量详细的错误提示。
五、实验步骤首先将终结符和非终结符以及预测分析表计算出来,并保存到数组中然后对输入的字符进行分析,将一个个终结符进行分配在分配的过程中输出每一步步骤对错误处,显示步骤数和错误字符六、源程序清单、测试数据、结果源程序:#include<iostream.h>#include<stdio.h>#include<string>using namespace std;char zhong[6]={'i','+','*','(',')','#'};char fzhong[5]={'E','R','T','Y','F'};char shu[20];1//R代表E' Y代表T'string biao[5][6]={{"TR","","","TR","",""},{"","+TR","","","@","@"}, //@代表空{"FY","","","FY","",""},{"","@","*FY","","@","@"},{"i","","","(E)","",""}};#define N 20;typedef char type;typedef struct{type *base;type *top;int stacksize;}sqstack;void initstack(sqstack &s){s.base=new type[2];if(!s.base)cout<<"错误";s.top=s.base;s.stacksize=N;}void push(sqstack &s,type e){if(s.top-s.base==s.stacksize)cout<<"栈满";*s.top++=e;}void pop(sqstack &s,type &e){if(s.top==s.base)cout<<"栈空";e=*--s.top;}type gettop(sqstack s){if(s.top==s.base)cout<<"栈空";return *(s.top-1);}int find1(char x){for(int i=0;i<5;i++){if(x==fzhong[i]){break;}}return i;}int find2(char x){for(int i=0;i<6;i++){if(x==zhong[i]){break;}}return i;}void showstack(sqstack fen){char a;sqstack x;initstack(x);while(fen.top!=fen.base){pop(fen,a);push(x,a);}3while(x.top!=x.base){pop(x,a);cout<<a;}}void fenxi(sqstack &fen){string str;int i=0,row=1,j;char ch1,ch2;// ch1=gettop(fen);while(1){if(gettop(fen)==shu[i]&&gettop(fen)!='#'){cout<<endl<<row++<<" ";showstack(fen);j=i;cout<<" ";while(shu[j]!='#'){cout<<shu[j];j++;}cout<<"# "<<shu[i]<<"被分配"<<endl;i++;pop(fen,ch2);}else if(gettop(fen)=='#'){cout<<row<<" # # 被接受";break;}else{str=biao[find1(gettop(fen))][find2(shu[i])];if(biao[find1(gettop(fen))][find2(shu[i])]==""){cout<<"第"<<row<<"行出现错误"<<gettop(fen)<<"与"<<shu[i]<<"无对应的关系"<<endl;break;}else if(biao[find1(gettop(fen))][find2(shu[i])]=="@"){cout<<row<<" ";showstack(fen);j=i;cout<<" ";while(shu[j]!='#'){cout<<shu[j];j++;}cout<<"# "<<gettop(fen)<<"->";for(j=0;j<str.length();j++){ cout<<str.at(j);}cout<<endl;row++;pop(fen,ch2);j=0;}else{cout<<row<<" ";showstack(fen);j=i;cout<<" ";while(shu[j]!='#'){cout<<shu[j];j++;}cout<<"# "<<gettop(fen)<<"->";5for(j=0;j<str.length();j++){ cout<<str.at(j);}row++;pop(fen,ch2);j=str.length()-1;while(j>=0){push(fen,str.at(j));j--;}cout<<endl;}}}}void main(){cout<<"这里是预测分析法程序测试!!!"<<endl;cout<<"请输入一串仅含i,+,*,(,)的字符串,并以#结束"<<endl;char a;sqstack fen;int i=0;while(a!='#'){cin>>a;shu[i]=a;i++;}cout<<"对输入串:"<<shu<<"的分析过程"<<endl;initstack(fen);push(fen,'#');push(fen,'E');fenxi(fen);}运行结果截图:测试一:测试二:7测试三:(错误测试)七、实验小结和思考预测分析法相对于RL法简单很多,而且预测分析表已经得到。
编译原理实验—预测分析器

strcat(VNT[t].VtoT,VNT[flag].VtoT);
}
for(j=0;j<s1;j++) //第三种情况的后半部分
for(k=0;k<length1;k++)
{
flag=0;
if(G[i].Right[j]==NT[k].Vnt&&Capital(G[i].Right[j+1]))
else return 0;
}
void FoldFirst(csc G[],db VNT[],int length)//将左部相同的产生式的非终结符合并起来 {
int i,j; for(i=0;i<length;i++)
for(j=i+1;j<length;j++) if(VNT[i].VN==VNT[j].VN&&VNT[i].VtoT[0]!=0&&VNT[j].VtoT[0]!=0) { strcat(VNT[i].VtoT,VNT[j].VtoT); VNT[j].VN='0'; }
if(flag==1) str[t++]=NT[i].Vt[j];
} for(j=0;j<strlen(VNT[i].VtoT);j++) //加入 Follow 中的非终结符 {
flag=1; for(k=0;k<t;k++)
} for(i=0;i<length;i++) {
s1=strlen(G[i].Right); for(k=0;k<length1;k++) //第三种情况的前半部分
预测分析法(编译原理)
实验二基于预测方法的语法分析程序的设计一、实验目的了解预测分析器的基本构成及用自顶向下的预测法对表达式进行语法分析的方法,掌握预测语法分析程序的手工构造方法。
二、实验内容1、了解编译程序的基于预测方法的语法分析过程。
2、根据预测分析原理设计一个基于预测方法的语法分析程序。
三、实验要求对给定文法G[S]:S->AT A->BU T->+AT|$ U->*BU|$ B->(S)|m其中,$表示空串。
1、判断上述文法G[S]是否LL(1)文法,若不是,将其转变为LL(1)文法;2、对转变后的LL(1)文法建立预测分析表;3、根据清华大学出版编译原理教材教材第五章P94的图5.11手工构造预测分析程序;4、用预测分析程序对任意给定的键盘输入串m+m*m#进行语法分析,并根据栈的变化状态输出给定串的具体分析过程。
四、运行结果从任意给定的键盘输入串:m+m*m#;输出:本实验重点有两个:一是如何用适当的数据结构实现预测分析表存储和使用;二是如何实现各规则右部串的逆序入栈处理。
建议:使用结构体数组。
六、分析与讨论1、若输入串不是指定文法的句子,会出现什么情况?2、总结预测语法分析程序的设计和实现的一般方法。
代码:#include<stdio.h>#include<stdlib.h>#include<string.h>#include<windows.h>struct stack1{char stack[10];}sta[][7]={"\0","+","*","(",")","m","#","S","\0","\0","AT","\0","AT","\0","A","\0","\0","BU","\0","BU","\0","T","+AT","\0","\0","$","\0","$","B","\0","\0","(S)","\0","m","\0","U","$","*BU","\0","$","\0","$"};//struct stack *head;char stack_1[10]={'\0'},stack_2[10]={'\0'},stack_3[10]={'\0'}; int i,j,k,len_1,len_2,len_3,mark=0;void main(){// void c_stack();void analyze_stack();void surplus_str();int rules();// printf("%s\t",sta[0][1].stack);// printf("\n");while(1){// system("cls");mark=0;printf("请输入串:\n");gets(stack_3);if(stack_3[0]=='0')break;stack_1[0]='S';len_3=strlen(stack_3);if(stack_3[len_3-1]!='#'){printf("字符串输入错误,字符串不以#号结束!\n");continue;}printf("分析栈\t\t剩余串\t\t\t\t\t\t规则\n");for(i=0;i<=100;i++){analyze_stack();surplus_str();rules();if(mark==1)break;if(stack_1[0]=='\0'&&stack_3[0]=='#'){printf("#\t\t#\t\t\t\t\t\t成功接受\n");break;}}}}void analyze_stack()//分析栈{printf("#%-15s",stack_1);len_1=strlen(stack_1);}void surplus_str()//剩余串//注意拼写的正确性,写成surlpus_str()报错,unresolved sxternal symbol_surplus_str;{printf("%-48s",stack_3);}int rules()//所用规则{int p,q,h;char temp;// printf("%d",len_1);if(stack_1[len_1-1]==stack_3[0]){printf("%c匹配\n",stack_3[0]);stack_1[len_1-1]='\0';for(h=1;h<=len_3-1;h++)stack_3[h-1]=stack_3[h];stack_3[len_3-1]='\0';}else if(stack_1[len_1-1]<'A'||stack_1[len_1-1]>'Z') {printf("报错\n");mark=1;return 0;}else if(stack_1[len_1-1]>='A'&&stack_1[len_1-1]<='Z') {for(j=1;j<=5;j++){if(stack_1[len_1-1]==sta[j][0].stack[0]){p=j;break;}}if(j>=6){printf("报错\n");mark=1;return 0;}for(k=1;k<=6;k++){if(stack_3[0]==sta[0][k].stack[0]){q=k;break;}}if(k>=7){printf("报错\n");mark=1;return 0;}if(sta[p][q].stack[0]=='\0'){printf("报错\n");mark=1;return 0;}strcpy(stack_2,sta[p][q].stack);len_2=strlen(stack_2);printf("%c->%s\n",stack_1[len_1-1],stack_2); stack_1[len_1-1]='\0';if(stack_2[0]=='$'){}else{for(h=0;h<len_2/2;h++){temp=stack_2[h];stack_2[h]=stack_2[len_2-1-h];stack_2[len_2-1-h]=temp;}strcat(stack_1,stack_2);}}return 0;}。
语法分析_预测分析法_实验报告

}
else if ( IsSymbolEnd(StackGet()) )
{
//栈顶为开始符
ProcessEnd();
}
else
{
//栈顶为非终结符
ProcessN();
}
}
void ProcessEnd()
{
if (StackGet() != ComingToken())
{
//非正常结尾
}
}
/*
*
*将产生式反向入栈
**/
void StackPushProfom(int buf[], int length)
{
int i;
_ASSERT(length > 0);
for (i = length - 1; i >= 0; i--)
{
StackPush(buf[i]);
}
}
/**
*由当前栈顶符及当前输入符取得产生式
}
}
void ProcessT()
{
if (StackGet() == ComingToken())
{
//match success, pop stack
StackPop();
//get next token
NextToken();
}
else
{
Leave(ANA_ERROR_UNEXPECTED_VALUE);
SELECT(F→( E )) SELECT(F→i)
= { ( } { i }
=
因而改写后的文法为LL(1)文法,可使用预测分析法自顶向下分析。
3)预测分析表
对每个表达式求其SELECT集。
编译原理预测分析法C语言的实验报告

题目:编写识别由下列文法所定义的表达式的预测分析程序。
E→E+T | E-T | TT→T*F | T/F |FF→(E) | i输入:每行含一个表达式的文本文件。
输出:分析成功或不成功信息。
(题目来源:编译原理实验(三)--预测(LL(1))分析法的实现)解答:(1)分析a) ∵E=>E+T=>E+T*F=>E+T*(E)即有E=>E+T*(E)存在左递归。
用直接改写法消除左递归,得到如下:E →TE’ E’ →+TE’ | −TE’|εT →FT’ T’ →*FT’ | /FT’|εF → (E) | i对于以上改进的方法。
可得:对于E’:FIRST( E’ )=FIRST(+TE’)∪FIRST(-TE’)∪{ε}={+,−,ε}对于T’:FIRST( T’ )=FIRST(*FT’)∪FIRST(/FT’)∪{ε}={*,∕,ε} 而且:FIRST( E ) = FIRST( T ) = FIRST( F )=FIRST((E))∪FIRST(i)={(,i }由此我们容易得出各非终结符的FOLLOW集合如下:FOLLOW( E )= { ),#}FOLLOW(E’)= FOLLOW(E)={ ),#}FOLLOW( T )= FIRST(E’)\ε∪FOLLOW(E’)={+,−,),#}FOLLOW( T’ ) = FOLLOW( T ) ={+,−,),#}FOLLOW( F )=FIRST(T’)\ε∪FOLLOW(T’)={*,∕,+,−,),#}由以上FOLLOW集可以我们可以得出SELECT集如下:对E SELECT(E→TE’)=FIRST(TE’)=FIRST(T)={ (,i }对E’ SELECT(E’ →+TE’)={ + }SELECT(E’ →−TE’)={ − }SELECT(E’ →ε)={ε,),#}对T SELECT(T→FT’)={(,i}对T’ SELECT(T’ →*FT’)={ * }SELECT(T’ →∕FT’)={ ∕ }SELECT(T’ →ε)={ε,+,−,),#}对F SELECT(F→(E) )={ ( }SELECT(F→i)={ i }∴SELECT(E’ →+TE’)∩SELECT(E’ →−TE’)∩SELECT(E’ →ε)=ΦSELECT(T’ →*FT’)∩SELECT(T’ →∕FT’)∩SELECT(T’ →ε)=ΦSELECT(F→(E) )∩SELECT(F→i)= Φ由上可知,有相同左部产生式的SELECT集合的交集为空,所以文法是LL(1)文法。
计算机编译原理---语法分析预测分析法

编译原理实验报告-语法分析2预测分析法目录1.摘要: (3)2、实验目的: (3)3、任务概述 (3)4、实验依据的原理 (3)5、程序设计思想 (5)6、实验结果分析 (9)7、总结 (18)8、程序代码 (18)1.摘要:用C/C++实现并运用预测分析法对Pascal的子集程序设计语言进行语法识别程序,并对语言进行判断,找出错误。
2、实验目的:通过预测分析法进行设计、编程、调试出一个语法分析程序,加深对预测分析法的语法分析原理的理解,掌握其设计方法。
3、任务概述1)将源程序转换成内码流,然后用预测分析法进行分析。
2)构造预测分析表,并利用分析表和一个栈来实现对Pascal的子集程序设计语言的分析程序。
4、实验依据的原理4.1Pascal的子集程序设计语言的文法Pascal的子集程序设计语言的文法如下:<程序>→<程序首部><分程序>。
<程序首部>→PROGRAM标识符;<分程序>→<常量说明部分><变量说明部分><过程说明部分> <复合语句> <常量说明部>→CONST<常量定义><常量定义后缀> |ε<常量定义>→标识符=无符号整数<常量定义后缀>→,<常量定义><常量定义后缀> |ε<变量说明部分>→VAR<变量定义><变量定义后缀> |ε<变量定义>→标识符<标识符后缀>:<类型>;<标识符后缀>→,标识符<标识符后缀> |ε<变量定义后缀>→<变量定义><变量定义后缀> |ε<类型>→INTEGER | LONG<过程说明部分>→<过程首部><分程序>;<过程说明部分后缀>|ε<过程首部>→PROCEDURE标识符<参数部分>;<参数部分>→(标识符: <类型>)|ε<过程说明部分后缀>→<过程首部><分程序>;<过程说明部分后缀>|ε<语句>→<赋值或调用语句>|<条件语句>|<当型循环语句>|<读语句>|<写语句>|<复合语句>|ε<赋值或调用语句>→标识符<后缀><后缀>→:=<表达式>|(<表达式>)|ε<条件语句>→IF<条件>THEN<语句><当型循环语句>→WHILE<条件>DO <语句><读语句>→READ(标识符<标识符后缀>)<写语句>→WRITE(<表达式><表达式后缀>)<表达式后缀>→,<表过式><表达式后缀>|ε<复合语句>→BEGIN<语句><语句后缀>END<语句后缀>→;<语句><语句后缀>|ε<条件>→<表达式><关系运算符><表达式>|ODD<表达式><表达式>→+<项><项后缀>|-<项><项后缀>|<项><项后缀> <项后缀>→<加型运算符><项><项后缀>|ε<项>→<因子><因子后缀><因子后缀>→<乘型运算符><因子><因子后缀>|e<因子>→标识符|无符号整数|(<表达式>)<加型运算符>→+|-<乘型运算型>→*|/<关系运算符>→ =|<>|<|<=|>|>=4.2内码对照5、程序设计思想5.1文法转化将上述文法转换成内码:128 →129 130 26 0 129→ 1 34 28 0 130→131 134 138 150 0131→ 2 132 133 28 0 131→0 132→34 20 33 0 133→27 132 133 0 133→0 134→3 135 136 0 134→0 135→34 147 29 137 28 0 136→135 136 0 136→0 137→4 0 137→5 0138→139 130 28 140 0 138→0 139→ 6 34 158 28 0140→139 130 28 140 0 140→0 141→142 0141→144 0 141→145 0 141→146 0141→148 0 141→150 0 141→0142→34 143 0 143→30 153 0 143→31 153 32 0 143→0 144→7 152 8 141 0 145→9 152 10 141 0146→11 31 34 147 32 0 147→27 34 147 0 147→0148→12 31 153 149 32 0 149→27 153 149 0 149→0150→13 141 151 14 0 151→28 141 151 0 151→0152→153 161 153 0 152→15 153 0 153→16 155 154 0 153→17 155 154 0 153→155 154 0 154→159 155 154 0 154→0 155→157 156 0 156→160 157 156 0 156→0 157→34 0 157→ 33 0157→31 153 32 0 158→31 34 29 137 32 0 158→0159→16 0 159→17 0 160→18 0160→19 0 161→20 0 161→21 0161→22 0 161→23 0 161→24 0161→25 05.2求非终结符的First集的方法:1.直接收取:若U->a…(其中a是终结符),把a收入到First(U)中;2.反复传送:若U->P…(其中P是非终结符),应把First(P)中的全部内容传送到First(U)中。
编译原理预测分析程序的实现

实验二预测分析表一、实验目的预测分析表的实现二、实验内容设有文法G:E→TE’E’→+TE’|εT→FT’T’→*FT’|εF→(E)|i;根据文法编写预测表分析总控程序,分析句子是否为该文法的句型。
当输入字符串:+i时,分析字符串是否为文法的句型三、实验步骤(详细的实验步骤)(1)文法E→TE’E’→+TE’|εT→FT’T’→*FT’|εF→(E)|i;(2)FIRST集FIRST(E)={(,i};FIRST(E’)={+, ε};FIRST(T)={(,i};FIRST(T’)={ *, ε};FIRST(F)={(,i};(3)FALLOW集FOLLOW(E)={),#};FOLLOW(E’)={),#};FOLLOW(T)={+,),#};FOLLOW(T’)={+,),#};FOLLOW(F)={*,+,),#};(4)预测分析表(5)分析过程步骤符号栈输入串应用句型0#E i1*i2+i3#1#E’T i1*i2+i3#E->TE’2#E’T’F i1*i2+i3#E->TE’3#E’T’i i1*i2+i3#F->i4# E’T’i1*i2+i3#5# E’T’F**i2+i3#T’->*FT’6# E’T’F*i2+i3#7# E’T’i i2+i3#F->i8# E’T’i2+i3#9#E’+i3#T’->ε10# E’T++i3#E’->+TE’11#E’T+i3#12# E’T’F i3#T->FT’13# E’T’i i3#F->i14# E’T’i3#15# E’#T’->ε16# #E’->ε(6)程序伪代码BEGIN首先把‘#’然后把文法开始符号推进STACK栈;把第一个输入符号读进a;FLAG:=TRUE;WHILE FLAG DOBEGIN把STACK栈顶符号托出去并放在X中;IF X属于VT THENIF X=a THEN 把下一输入符号读进a;ELSE ERROR;ELSE IF X=’#’ THENIF X=a THEN FLAG:=FALSE ELSE ERROR;ELSE IF M[A,a]={X->X1X2…Xk} THEN把Xk,X(k-1),…,X1一一推进栈ELSE ERROR;END OF WHILESTOPEND(7)运行结果截图注:为了将E和E’区分开,所以就有e来表示E’,因为在处理中E’会被当成两个字符来处理,所以就简化的表示了。
编译原理4.5.1-预测分析程序

对输入串 i+i*i# 进行分析 表达式文法的预测分析表 i + * ( ) # →ε →ε
E →TE' →TE' E' →+TE' →ε T →FT' →FT' T' →ε →*FT' →ε F →i →(E)
分析过程见黑板
输入串i+i*i# 输入串i+i*i#
G': E → TE' E'→ +TE'|ε T → FT' T'→ *FT'|ε F → (E) | i
把 ‘#’和S 推入 STACK 栈 和 p77 把ILE FIAG DO 把STACK栈顶符号上托出去, 并放入X 并放入X IF X∈VT THEN ∈ IF X=a THEN 把下一个输入符号读进 把下一个输入符号读进a ELSE ERROR ELSE IF X='#' THEN IF X=a THEN FLAG:=FALSE ELSE ERROR ELSE IF M[X, a]={ X→X1X2...XK } THEN 把XK,XK-1,…X1 一一推 进 STACK ELSE ERROR END OF WHILE;
2.预测分析程序的模型 2.预测分析程序的模型 输入串 …… a ……# # * . . . # 栈
总控程序 预测分析表
输出
2.预测分析程序的工作过程 预测分析程序的工作过程
"#" :句子括号 句子括号 "S" :文法的开始符号 文法的开始符号 "X" :存放当前栈顶符号的工作单元 存放当前栈顶符号的工作单元 "a" :存放当前输入符号 的工作单元 存放当前输入符号a的工作单元 存放当前输入符号
编译原理预测分析程序的实现

实验二预测分析表一、实验目的预测分析表的实现二、实验内容设有文法G:E→TE’E’→+TE’|εT→FT’T’→*FT’|εF→(E)|i;根据文法编写预测表分析总控程序,分析句子是否为该文法的句型。
当输入字符串: +i时,分析字符串是否为文法的句型三、实验步骤(详细的实验步骤)(1)文法E→TE’E’→+TE’|εT→FT’T’→*FT’|εF→(E)|i;(2)FIRST集FIRST(E)={(,i};FIRST(E’)={+, ε};FIRST(T)={(,i};FIRST(T’)={ *, ε};FIRST(F)={(,i};(3)FALLOW集FOLLOW(E)={),#};FOLLOW(E’)={),#};FOLLOW(T)={+,),#};FOLLOW(T’)={+,),#};FOLLOW(F)={*,+,),#};(4)预测分析表(5)分析过程步骤符号栈输入串应用句型0 #E i1*i2+i3#1 #E’T i1*i2+i3# E->TE’2 #E’T’F i1*i2+i3# E->TE’3 #E’T’i i1*i2+i3# F->i4 # E’T’i1*i2+i3#5 # E’T’F* *i2+i3# T’->*FT’6 # E’T’F *i2+i3#7 # E’T’i i2+i3# F->i8 # E’T’ i2+i3#9 #E’ +i3# T’->ε10 # E’T+ +i3# E’->+TE’11 #E’T +i3#12 # E’T’F i3# T->FT’13 # E’T’i i3# F->i14 # E’T’ i3#15 # E’ # T’->ε16 # # E’->ε(6)程序伪代码BEGIN首先把‘#’然后把文法开始符号推进STACK栈;把第一个输入符号读进a;FLAG:=TRUE;WHILE FLAG DOBEGIN把STACK栈顶符号托出去并放在X中;IF X属于VT THENIF X=a THEN 把下一输入符号读进a;ELSE ERROR;ELSE IF X=’#’ THENIF X=a THEN FLAG:=FALSE ELSE ERROR;ELSE IF M[A,a]={X->X1X2…Xk} THEN把Xk,X(k-1),…,X1一一推进栈ELSE ERROR;END OF WHILESTOPEND(7)运行结果截图注:为了将E和E’区分开,所以就有e来表示E’,因为在处理中E’会被当成两个字符来处理,所以就简化的表示了。
编译原理预测分析器C++源代码

预测分析器源代码:#include<iostream>#include<iomanip>#define MAX 100using namespace std;struct Stack{int data[MAX]; //栈中内容int top; //栈顶指针};int Yy_pushtab[13][4]={ //存放文法产生式右部符号的常数值{257,1,258,0},{256,0},{0},{260,259,0},{0},{260,259,2,0},{0},{262,261,0},{262,261,3,0},{0},{5,258,4,0},{6,0},{256,0}};int Yy_d[8][7]={ //LL(1)分析表{-1,0,-1,-1,0,-1,0},{2,1,-1,-1,1,-1,1},{-1,4,-1,-1,3,4,3},{-1,-1,-1,-1,7,-1,7},{-1,6,5,-1,-1,6,-1},{-1,-1,-1,-1,10,-1,11},{-1,9,9,8,-1,9,-1},{-1,12,-1,-1,12,-1,12}};//终结符集#(0)、;(1)、+(2)、*(3)、((4)、)(5)、num(6)int Terminal[7]={0,1,2,3,4,5,6};//非终结符集prgm(256)、prgm’(257)、expr(258)、term(259)、//expr’(260)、factor(261)、term’(262)、system_goal(263)int Nonterminal[8]={256,257,258,259,260,261,262,263};void InitStack(Stack &st) //初始化栈{st.top=-1;}void Push(Stack &st,int x) //压栈{if(st.top==MAX-1)cout<<" 栈已满,压栈失败!"<<endl;else{st.top++;st.data[st.top]=x;}}void Pop(Stack &st) //弹栈{if(st.top==-1)cout<<" 栈已空,弹栈失败!"<<endl;elsest.top--;}//判断是否为终结符,是返回1,否则返回0int Is_Vt(int a,int Terminal[7]){int i;for(i=0;i<7;i++){if(a==Terminal[i]) //a为输入符号常数return 1;}return 0;}//读入文法句子并将其转化为相应编码,返回输入串长度int Getchar(int length,char A[MAX],int B[MAX]){int i;cout<<" 输入字符串的长度length=";cin>>length;cout<<endl<<" 请输入该文法的句子:";for(i=0;i<length;i++){cin>>A[i]; //存放输入串switch(A[i]) //将输入串转为相应常数值存入数组B{case '#':B[i]=0;break;case ';':B[i]=1;break;case '+':B[i]=2;break;case '*':B[i]=3;break;case '(':B[i]=4;break;case ')':B[i]=5;break;default:B[i]=6;}}return length;}void PrintStack(Stack &st, int top) //输出栈中的内容{for (int i = 0; i <= top; i++){cout<<st.data[i] << " ";}cout << "\t\t\t";}int main(){Stack st;int what_to_do,ch,j,m;char A[MAX];int length=0,B[MAX];length=Getchar(length,A,B); //获得输入字符串InitStack(st); //初始化栈Push(st,263); //把开始符号的常数值压栈j=0;ch=B[j]; //指向第一个输入符号的编码cout<<endl<<" 分析栈(数值)"<<setw(15)<<"输入串"<<setw(20)<<"what_to_do"<<endl; //分析过程输出格式while(st.top!=-1) //分析栈非空{if(Is_Vt(st.data[st.top],Terminal)==1) //栈顶常数表示一个终结符{what_to_do=-1;if(st.data[st.top]!=ch) //栈顶常数与输入符号编码不同{cout<<" 输入串不是该文法的句子!"<<endl;return 0;}else{Pop(st); //栈顶出栈what_to_do=100; //表示输入符号与栈顶符号匹配PrintStack(st, st.top); //输出分析过程中栈中内容for(int p=j;p<length;p++) //输出分析过程中的输入串cout<<A[p];cout<<setw(12)<<what_to_do<<endl; //输入符与栈顶匹配j++;ch=B[j]; //读入下一个输入符号}}else //栈顶常数表示一个非终结符{m=st.data[st.top]-256; //获取数组Yy_d的第一个下标int t=0;for(int k=0;k<7;k++){if(ch==Terminal[k])t=k;}what_to_do=Yy_d[m][t];if(what_to_do==-1){cout<<" 语法错误!"<<endl;return 0;}else{PrintStack(st, st.top); //输出分析过程中栈中内容for(int p=j;p<length;p++) //输出分析过程中的输入串cout<<A[p];cout<<setw(12)<<what_to_do<<endl;Pop(st); //栈顶出栈int h=0;while(Yy_pushtab[what_to_do][h]!=0){Push(st,Yy_pushtab[what_to_do][h]);h++;}}}}cout<<" 分析成功:该输入串是文法的句子!"<<endl;return 0;}运行结果:。
预测分析表 编译原理

#include <stdio.h>#include <tchar.h>#include <string.h>int main(int argc, char* argv[]){char syn[15]; //语法栈int top; //栈顶指针char lookahead; //当前单词char exp[50]; //表达式区int m =0; //表达式指针char s[4][5]={"d","+","*","("}; //表中有空白的符号char string[3]={'E','T','F'}; //表中有同步记号的的非终结符int ll1[7][6]={{1,0,0,1,9,9}, //LL(1)分析表,9表示同步记号,第6行是#,第7行是){0,2,0,0,3,3},{4,9,0,4,9,9},{0,6,5,0,6,6},{8,9,9,7,9,9},{12,12,12,12,12,10},{13,13,13,13,11,13}};int i,j; //表行和列int code; //表项printf("************************语法分析器**********************\n");printf("请输入合法字符串:\n");scanf("%s",exp);top=1;lookahead=exp[m++];syn[0]='#';syn[1]='E';printf("***********************预测分析表*********************\n");printf("\ti\t *\t +\t (\t )\t #\n");printf(" E\tE->TE'\t\t\tE->TE'\n");printf(" E'\t\t\tE'->+TE'\t E'->ε\n");printf(" T\tT->FT'\t\t\tT->FT'\t\n");printf(" T'\t\tT'->*FT'\t\t T'->ε\t\n");printf(" F\tF->d\t\t\tF->(E)\n\n");printf("调用规则顺序:\n");while(1) { switch(syn[top]) //行{case 'E':i=0;break; case 'e':i=1;break;case 'T':i=2;break; case 't':i=3;break;case 'F':i=4;break; case '#':i=5;break;case ')':i=6;break;}switch(lookahead) //列{case 'd':j=0;break; case '+':j=1;break;case '*':j=2;break; case '(':j=3;break;case ')':j=4;break; case '#':j=5;break;}code=ll1[i][j];if(code==10){printf("语法分析结束\n"); //break;}else{switch(code){case 0:{//printf("出错,用户多输入了%s,跳过%s\n",s[j],s[j]);if(j==0){//lookahead=exp[m++];lookahead=exp[m++];}elselookahead=exp[m++];break;}case 1:{printf("E →TE′\n");syn[top]='e';syn[top+1]='T';top++;break;}case 2:printf("E′→+TE`\n");syn[top+1]='T';top++;lookahead=exp[m++];break;}case 3:{printf("E′→ε\n");syn[top]='\0';top--;break;}case 4:{printf("T →FT′\n");syn[top]='t';syn[top+1]='F';top++;break;}case 5:{printf("T′→* FT′\n");syn[top+1]='F';top++;lookahead=exp[m++];break;}case 6:{printf("T′→ε\n");syn[top]='\0';top--;break;}case 7:{printf("F →(E)\n");syn[top]=')';syn[top+1]='E';top++;lookahead=exp[m++];break;case 8:{printf("F →d\n");syn[top]='\0';top--;lookahead=exp[m++];lookahead=exp[m++];break;}case 9:{printf("弹栈,弹出非终结符%c,用户少输入了一个d\n",string[i/2]);syn[top]='\0';top--;break;}case 11:{syn[top]='\0';top--;lookahead=exp[m++];break;}case 13:{printf("弹栈,弹出终结符) ,用户少输入了一个右括号\n");syn[top]='\0';top--;break;}}}}return 0;}。
编译原理-语法分析程序设计(预测分析法)

1.实验目的构造文法的语法分析程序实验要求,2.实验要求采用预测分析法对输入的字符串进行语法分析。
3.实验环境V4.实验原理对文法G进行语法分析,文法G如下所示:*0. S→a */*1. S→^*2. S→(T)*3. T→SW **4. W→,SW*5. W→ε;5.软件设计与编程#include <stdio.h>#include <stdlib.h>#include <string.h>char str[100]; //存储待分析的句子const char T[ ] = "a^(),#"; //终结符,分析表的列符const char NT[ ] = "STW"; //非终结符,分析表的行符/*指向产生式右部符号串*/const char *p[] = {/*0. S→a */ "a",/*1. S→^ */ "^",/*2. S→(T) */ "(T)",/*3. T→SW */ "SW",/*4. W→,SW */ ",SW",/*5. W→ε; */ ""};//设M[i][j]=x,通过p[M[i][j]]=p[x]获取右部符号串。
const int M[][6] = {/* a ^ ( ) , # *//*S*/ { 0, 1, 2, -1, -1, -1 },/*T*/ { 3, 3, 3, -1, -1, -1 },/*W*/ { -1, -1,-1, 5, 4, -1 }};void init()//输入待分析的句子printf("请输入待分析的句子(以$结束):\n");scanf("%s",str);}int lin(char c);//非终结符转换为行号int col(char c);//终结转换为列号bool isNT(char c);//isNT判断是否是非终结符bool isT(char c);//isT判断是否是终结符。
编译原理:算术表达式预测分析程序设计

实验三:算术表达式预测分析程序设计LD1、实验目的:(1)掌握自上而下语法分析的要求与特点。
(2)掌握LL(1)语法分析的基本原理和基本方法。
(3)掌握相应数据结构的设计方法。
2、实验内容:编程实现给定算术表达式的预测分析器。
算术表达式文法如下:E→E+T | TT→T*F | FF→(E) | i3、设计说明:首先改写文法为LL(1)文法;构造LL(1)分析表,然后编写预测分析程序。
4、设计分析与步骤(1)将原算术表达式方法改写为LL(1)文法为:E-->TE'E'-->+TE'|εT-->FT'T'-->*FT'|εF-->(E)|i(2)计算文法中每一个非终结符的FIRST集和FOLLOW集FIRST FOLLOWE{ (,i }{ #,) }E’{ +,ε }{ ),# }T{ (,i }{ ),+,# }T’{ *,ε }{ ),+,# }F{ (,i }{ * }(3)构造预测分析表I()+*#E E-->TE’E-->TE’E’E’-->εE’-->+TE’E’-->εT T-->FT’T-->FT’T’T’-->εT’-->εT’-->*FT’T’-->εF F-->i F-->(E)(4)程序设计用vector<char>定义的A和B分别作为分析栈和输入栈,用string类型的INPUT获取用户输入的原始字符串。
用string类型的二维数组存储预测分析表。
1,#和E进分析栈A,#和倒序用户输入串压入用户栈B2,判断A和B栈顶不同时为#,如果是则下一步,如果不是则跳出判断3,根据A和B栈顶元素查分析表查找规则(1)如果查到一般规则,则进行相应的A的弹栈与压栈并比较两栈顶元素,如果相等则都弹栈(2)如果查到含空串的规则,则A弹栈并比较两栈顶元素,如果相等则都弹栈(3)如果查表越界则显示错误4,重复3直到两栈顶都是#元素显示分析成功5,提示用户输入0继续分析下一条,其它输入退出程序。
编译原理预测分析程序的实现

实验二预测分析表一、实验目的预测分析表的实现二、实验内容设有文法G:E→TE’E’→+TE’|εT→FT’T’→*FT’|εF→(E)|i;根据文法编写预测表分析总控程序,分析句子是否为该文法的句型。
当输入字符串: +i时,分析字符串是否为文法的句型三、实验步骤(详细的实验步骤)(1)文法E→TE’E’→+TE’|εT→FT’T’→*FT’|εF→(E)|i;(2)FIRST集FIRST(E)={(,i};FIRST(E’)={+, ε};FIRST(T)={(,i};FIRST(T’)={ *, ε};FIRST(F)={(,i};(3)FALLOW集FOLLOW(E)={),#};FOLLOW(E’)={),#};FOLLOW(T)={+,),#};FOLLOW(T’)={+,),#};FOLLOW(F)={*,+,),#};(4)预测分析表(5)分析过程步骤符号栈输入串应用句型0 #E i1*i2+i3#1 #E’T i1*i2+i3# E->TE’2 #E’T’F i1*i2+i3# E->TE’3 #E’T’i i1*i2+i3# F->i4 # E’T’i1*i2+i3#5 # E’T’F* *i2+i3# T’->*FT’6 # E’T’F *i2+i3#7 # E’T’i i2+i3# F->i8 # E’T’ i2+i3#9 #E’ +i3# T’->ε10 # E’T+ +i3# E’->+TE’11 #E’T +i3#12 # E’T’F i3# T->FT’13 # E’T’i i3# F->i14 # E’T’ i3#15 # E’ # T’->ε16 # # E’->ε(6)程序伪代码BEGIN首先把‘#’然后把文法开始符号推进STACK栈;把第一个输入符号读进a;FLAG:=TRUE;WHILE FLAG DOBEGIN把STACK栈顶符号托出去并放在X中;IF X属于VT THENIF X=a THEN 把下一输入符号读进a;ELSE ERROR;ELSE IF X=’#’ THENIF X=a THEN FLAG:=FALSE ELSE ERROR;ELSE IF M[A,a]={X->X1X2…Xk} THEN把Xk,X(k-1),…,X1一一推进栈ELSE ERROR;END OF WHILESTOPEND(7)运行结果截图注:为了将E和E’区分开,所以就有e来表示E’,因为在处理中E’会被当成两个字符来处理,所以就简化的表示了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
预测分析法实验报告一、实验项目名称预测分析法二、实验目的根据某一LL(1)文法编制调试预测分析程序,以便对任意输入的符号串进行分析。
本次实验的目的主要是加深对预测分析法的理解。
三、实验环境Windows 10Microsoft Visual Studio 2015四、实验内容本次实验的LL(1)文法为表达式文法:E→E+T | TT→T*F | FF→i | (E)编写识别表达式文法的合法句子的预测分析程序,对输入的任意符号串,给出分析过程及分析结果。
分析过程要求输出步骤、分析栈、剩余输入串和所用产生式。
如果该符号串不是表达式文法的合法句子,要给出尽量详细的错误提示五、源程序清单、测试数据、结果#include<iostream>#include<string>using namespace std;const int NUM = 20;//初始化的栈的大小//非终结符数组集char Var[5] = { 'E','R','T','M','F' };//终结符数组集char Ter[6] = { 'i','+','*','(',')','#' };string pred[5][6] ={ { "TR","","","TR","","" },{ "","+TR","","","@","@" },{ "FM","","","FM","","" },{ ""," @","*FM","","@","@" },{ "i","","","(E)","","" } };typedef struct {char *top;char *base;int stacksize;int num;}Stack;// 栈结构体void init(Stack *ss) {//初始化栈ss->base = (char *)malloc(NUM * sizeof(char));if (!ss->base)exit(1);ss->top = ss->base;ss->stacksize = NUM;ss->num = 0;}void push(Stack *ss, char c) {//入栈操作if (ss->top - ss->base >= ss->stacksize)exit(1);*(ss->top) = c;ss->top++;ss->num++;}void pop(Stack *ss) {//出栈操作if (ss->top == ss->base)exit(1);ss->top--;ss->num--;}char getTop(Stack *ss) {//取得栈顶元素if (ss->top == ss->base)exit(1);return *(ss->top - 1);}int isT(char c) {//判断是否为终结符int i = 0;int ret = 0;for (i = 0; i<6; i++) {if (Ter[i] == c){ret = 1; break;}}return ret;}string isInPred(char v, char t) {//查找预测分析表,并返回产生式右部int i, j;for (i = 0; i<5; i++){if (Var[i] == v)break;}for (j = 0; j<6; j++){if (Ter[j] == t)break;}if (pred[i][j] !=""){return pred[i][j];}elsereturn"";}void displayStack(Stack *stack) { //输出分析站的内容string str;int i = 0;Stack ss = *stack;while (ss.num != 0){str += getTop(&ss);pop(&ss);}for (i = str.length() - 1; i >= 0; i--){cout << str.at(i);}}void predict(Stack stack, string input)//预测分析总函数{int a = 1;char b;char ctop;//当前栈顶符号char cinput;//当前输入符号int i = 0, j = 0, count = 0;int error = 0;cout <<"步骤"<<'\t'<<"栈"<<'\t'<<"输入缓冲区"<<'\t'<<"所用的产生式"<<endl;cout << count++ <<'\t';displayStack(&stack);cout <<'\t'<<input<<'\t'<<""<< endl;while (getTop(&stack) != '#'){string produce = "";ctop = getTop(&stack);cinput = input.at(i);if (isT(ctop))//栈顶符号为终结符{if (ctop == cinput){pop(&stack);i++;}else{error = 1; break;}produce +="\"";produce += ctop;produce +="\"匹配";}else//栈顶符号位非终结符{string str = isInPred(ctop, cinput);if (str !=""){pop(&stack);if (str !="@"){for (j = str.length() - 1; j >= 0; j--)push(&stack, str.at(j));}produce += ctop;produce +="→";produce += str;}else{error = 1; break;}}//栈顶符号位非终结符cout << count++ <<'\t';displayStack(&stack);cout <<'\t'<<input.substr(i) <<"\t\t"<< produce << endl;}if (error)cout <<"不接受"<< endl;elsecout <<"接受"<< endl;}void main(){while (1) {int sel;//继续或者退出程序选择string input;//输入串int i = 0, j = 0;Stack stack;init(&stack);push(&stack, '#');push(&stack, 'E');cout <<"----------------文法如下--------------"<< endl;cout <<"E→E+T | T"<< endl;cout <<"T→T*F | F"<< endl;cout <<" F→i | (E)"<< endl;cout <<"----------------请输入表达式(以#结尾)--------------"<< endl;cin >> input;cout <<"“R表示“E'”,”M“表示“T'”,”@“表示“空”"<< endl;predict(stack, input);sel=0;if (sel == 0)exit(0);elsesystem("cls");}}六、实验小结和思考本次实验的文法是写在程序中的,不可以自行输入,难度不是很难,并没有太大问题,只是一些未初始化的小问题。
以后要积极做实验,做的程序要更加灵活。
