计算机控制系统总习题(及答案)
计算机控制系统部分习题参考答案1

第一章1.1 计算机控制系统是怎么样分类的?按功能和控制规律可各分几类?答:计算机控制系统可按功能分类,按控制规律分类和按控制方式分类。
按功能计算机控制系统的分类:(1)数据处理系统。
(2)直接数字控制(简记为DDC)。
(3)监督控制(简记为SCC)。
(4)分级控制。
(5)集散控制。
(6)计算机控制网络。
按照控制规律计算机控制系统的分类:(1)程序和顺序控制。
(2)比例积分微分控制(简称PID控制)。
(3)有限拍控制。
(4)复杂规律控制。
(5)智能控制。
1.2 计算机控制系统由哪些部分组成?并画出方框图。
答:计算机控制系统由控制对象、执行器、测量环节、数字调节器及输入输出通道等组成。
方框图:P115 图1.21 输出反馈计算机控制系统1.9 简述采样定理及其含义。
答:采样定理:如果采样角频率=2/T大于2,即≥2,则采样的离散信号(t)能够不失真地恢复原来的连续信号y(t)。
式中是连续信号y(t)的频谱特性中的最高角频率。
含义:要使采样信号(t)能够不失真地恢复原来的连续信号y(t),必须正确选择采样角频率,使≥1.10 多路巡回检测时,采样时间,采样周期T和通道数N之间的关系。
答:采样时间是足够短的时间,y(kT)y(kT+),0<<。
应满足 T≥N。
1.12 设有模拟信号(0~5)V和(2.5~5)V,分别用8位、10位和12位A/D转换器,试计算并列出各自的量化单位和量化误差。
答:量化单位q=,量化误差根据以上公式可求得(05)V:量化误差(2.5)V:量化误差1.14 试述数模转换器的作用?如何选择转换器的位数?答:数模转换器把数字量u(kT)转换成离散的模拟量(t)。
转换的精度取决模-数转换器的位数n,当位数足够多时,转换可以达到足够高的精度。
1.19 计算机控制系统有哪些主要的性能指标?如何衡量?答:计算机控制系统主要有动态指标,稳态指标和综合指标1.20 如何衡量系统的稳定性?答:用相角裕量和幅值裕量来衡量计算机控制系统的稳定程度。
计算机控制系统课后习题答案1

第一章课后参考答案1-1简述计算机控制系统的控制过程。
计算机控制系统的控制过程可以归纳为以下三个步骤:1)实时数据采集:对被控量进行采样测量,形成反馈信号;2)实时控制计算:根据反馈信号和给定信号,按一定的控制规律,计算出控制量;3)实时控制输出,向执行机构发出控制信号,实现控制作用。
1-2什么是实时性?有哪些因素影响系统的实时性?硬件:1)控制器计算速度2)传感器采集速度3)执行器反应时间4)A/D、D/A转换速度软件:1)操作系统调度2)中断响应处理方式(包括定时器)3)延时函数的设置实时性:即信号的输入、计算和输出都是在一定时间范围内即时完成的,超出这个时间就会失去控制时机,控制也就失去了意义。
1-3计算机控制系统的硬件由哪几部分组成?各部分作用是什么?计算机的硬件主要包括主机、输入输出通道和外部设备。
主机:主机是计算系统的核心,通过接口向系统的各个部分发出各种指令,对被控对象进行检测和控制。
输入输出通道:输入输出通道是计算机和生产对象之间进行信息交换的桥梁和纽带。
过程输入通道把生产对象的被控参数转换成计算机可以接收的数字信号,过程输出通道把计算机输出的控制命令和数据,转化成可以对生产对象进行控制的的信号。
过程输入输出通道包括模拟量输入输出通道和数字量输入输出通道。
外部设备:外部设备是实现计算机和外界进行信息交换的设备,简称外设,包括人机联系设备(操作台)、输入输出设备(磁盘驱动器、键盘、打印机、显示终端等)和外存贮器,其中操作台应具备显示功能,即根据操作人员的要求,能立即显示所要求的内容,还应有按键或开关,完成系统的启、停等功;操作台还要保证操作错误也不会造成恶劣后果,即应有保护功能。
1-4计算机控制系统的软件由哪几部分组成?各部分作用是什么?计算机控制系统软件分为系统软件、应用软件及数据库。
系统软件是有计算机生产厂家提供的专门用来使用和管理计算机的程序。
对用户来说,系统软件只是用来开发应用软件的工具,不需要自己设计。
计算机控制系统习题及答案

1.采样频率越高,采样数据描绘的曲线实际曲线。
为了提高控制精度,应尽可能。
2.在三相步进电机系统中,为了提高控制力矩,常常采用方法来实现。
3.在PID调节器中,比例系数KP的确定比微分和积分系数更重要,因为它关系到______。
4.采样/保持器有两种工作方式。
在采样方式中,采样-保持器的输出__________在保持状态时,采样-保持器的输出______。
5.在PID控制系统中,I的作用主要是______,它一般不单独使用的原因是__ _。
6.线性插值法最根本的问题是____________________。
7.CD4051是________路________向多路开关,当其INH端接_____伏时,芯片被选通。
8.在计算机控制系统中,采样周期T的确定很重要,因为它关系到_______,T太大_______。
9.步进电机的步距角指________,齿距角指______,拍是指________。
10.3相(A、B、C)步进电机有3种通电方式,是,和。
二、判断题(正确,在括号内划∨,错误,在括号内划╳,并改正(只对错误部分进行改正即可)(本题共5 小题,共10分)1. 在显示系统中,若为动态显示,需将待显示数变成显示码才能输出到显示器进行显示。
若在显示电路中增加一级锁存器,则可直接将待显示数输出到显示器进行显示。
()2. DAC0832是常用的8位D/A转换器,内部设有两级缓冲器,目的是使转换数椐得到充分缓冲,确保转换精度。
()3. 由于各种传感器提供的电压信号范围很宽,需要通过可编程增益放大器,对信号进行调整,使A/D转换器满量程信号达到均一化。
()4. 某系统采用程序判断滤波方式进行数据处理,发现总有一些杂波无法滤掉,原因是采样时间间隔太大()。
5. 在工业过程控制系统中,由于被控对象所处环境复杂,常使采样值偏离实际值。
所以一般要加入滤波环节,且常常将模拟滤波和数字滤波同时使用。
()三、简答题(本题共6 小题,共35 分)1.(本题6 分)简要说明多路开关的主要特点。
计算机控制试题及答案

计算机控制试题及答案一、单项选择题(每题1分,共10分)1. 计算机控制系统中,以下哪个不是典型的控制策略?A. 比例控制B. 积分控制C. 微分控制D. 模糊控制答案:D2. 在计算机控制系统中,系统响应时间指的是:A. 系统从接收到控制命令到开始执行的时间B. 系统从接收到控制命令到完成执行的时间C. 系统从接收到控制命令到输出结果的时间D. 系统从接收到控制命令到输出稳定结果的时间答案:D3. 以下哪个不是计算机控制系统的优点?A. 精度高B. 响应快C. 易于维护D. 能耗高答案:D4. 在计算机控制系统中,闭环控制系统与开环控制系统的主要区别在于:A. 是否有反馈B. 是否有传感器C. 是否有执行器D. 是否有控制器答案:A5. 计算机控制系统的稳定性分析通常采用哪种方法?A. 频率响应法B. 时域分析法C. 状态空间法D. 所有上述方法答案:D6. 在计算机控制系统中,以下哪个参数不是系统性能指标?A. 稳态误差B. 响应时间C. 系统复杂度D. 带宽答案:C7. 以下哪个不是计算机控制系统的组成部分?A. 传感器B. 执行器C. 显示器D. 电源答案:D8. 计算机控制系统中,以下哪个不是典型的干扰?A. 电源波动B. 温度变化C. 机械振动D. 人为操作答案:D9. 在计算机控制系统中,以下哪个不是控制器的设计方法?A. PID控制B. 模糊控制C. 神经网络控制D. 机械控制答案:D10. 计算机控制系统的实时性要求是指:A. 系统响应时间必须小于一个固定的阈值B. 系统响应时间必须大于一个固定的阈值C. 系统响应时间必须等于一个固定的阈值D. 系统响应时间可以是任意值答案:A二、多项选择题(每题2分,共10分)1. 计算机控制系统的输入设备包括:A. 传感器B. 键盘C. 鼠标D. 扫描仪答案:A2. 计算机控制系统的输出设备包括:A. 显示器B. 打印机C. 执行器D. 扬声器答案:C3. 计算机控制系统的设计目标通常包括:A. 稳定性B. 快速性C. 准确性D. 经济性答案:A, B, C, D4. 计算机控制系统的干扰可能来自:A. 电源B. 环境C. 人为操作D. 系统内部答案:A, B, C, D5. 计算机控制系统的稳定性分析方法包括:A. 根轨迹法B. 奈奎斯特准则C. 李雅普诺夫方法D. 频域分析答案:A, B, C, D三、简答题(每题5分,共20分)1. 简述计算机控制系统的工作原理。
计算机控制技术题库(附答案)

计算机控制技术题库(附答案)计算机控制技术练习题(附答案)⼀、填空题(每空2分,共20分)1.闭环负反馈控制的基本特征是。
2.闭环控制系统⾥,不同输出与输⼊之间的传递函数分母。
3.惯性环节的主要特点是,当其输⼊量发⽣突然变化时,其输出量不能突变,⽽是按变化。
4.静态误差系数是系统在典型外作⽤下精度的指标,静态误差系数越⼤,精度。
5.系统的相稳定裕度γM,定义为开环频率特性在截⽌频率ωc处。
6.离散系统稳定性与连续系统不同,它不仅与系统结构和参数有关,还与系统的有关。
7.零阶保持器是⼀个相位滞后环节,它的相频特性φ(ω)= 。
8.若已知闭环系统⾃然频率为ωn,经验上,采样频率ωs应取。
9.通常把叠加在被测信号上的⼲扰信号称为。
10.为使传感器特性与A/D变换器特性相匹配,通常应在传感器与A/D之间加⼊。
⼆、选择题(每题2分,共10分)1.在计算机控制系统⾥,通常当采样周期T减少时,由于字长有限所引起的量化误差将。
A 增⼤;B 减⼩;C 不变。
2.控制算法直接编排实现与串联编排实现相⽐,有限字长所引起的量化误差。
A 较⼤;B 较⼩;C 相当。
3.某系统的Z传递函数为G(z) = 0.5(z+0.5) / (z+1.2)(z-0.5) ,可知该系统是。
A稳定的;B不稳定的;C 临界稳定的。
4.若以电机轴的转⾓为输⼊量,电机轴的转速为输出量,则它的传递函数为环节。
A 积分;B 微分;C 惯性。
5.在确定A/D变换器精度时,通常要求它的精度应传感器的精度。
A ⼤于;B ⼩于;C 等于。
三、简答题(每⼩题5分,共20分)1.图1为⽔箱⽔位⾃动控制系统,试说明基本⼯作原理。
图12.已知单位负反馈闭环控制系统的单位阶跃响应的稳态误差为0.1,试问该系统为⼏型系统,系统的开环放⼤系数为多少?3.试简单说明系统稳定性与稳态误差相互⽭盾的关系。
4.试表述采样定理,并说明若⼀⾼频信号采样时不满⾜采样定理,采样后将会变成何种信号。
计算机控制系统:计算机控制系统概述习题与答案

1、智能仪表接入计算机有两种途径,一种是485串行方式,另一种是()。
A.FDDI网B.互联网InternetC.ATM网D.以太网Ethernet正确答案:D2、以太网络最典型的应用形式为顶层采用Ethernet,网络层和传输层一般采用国际标准()协议。
A. NetBEUIB.TCP/IPC.IPX/SPXD.RS-232-C正确答案:B3、D/A转换器误差的主要来源是()和保持器(采样点之间插值)的形式以及规定的时间间隔T来决定。
A.信号种类B.转换器种类C.信号大小D.转换器字长正确答案:D1、计算机控制系统的性能指标主要有()。
A.稳定性B.综合指标等C.稳态指标D.动态指标正确答案:A、B、C、D2、计算机控制系统的主要特点是()。
A.结构混合B.结构唯一C.信号混合D.信号唯一正确答案:A、C3、计算机控制系统的基本类型有()。
A.计算机监督控制系统B.总线控制系统C.集散控制系统D.集中式计算机控制系统正确答案:A、B、C、D三、判断题1、计算机控制系统主要从信号变换、对象建模与性能分析、控制算法设计、控制系统仿真、控制系统实现等5个方面系统讲述计算机控制系统分析和设计的基本理论和方法。
()正确答案:√2、计算机控制实验的基本要求是对课本中所涉及的计算机控制系统的相关理论进行仿真和控制实验研究,包括基础型实验,扩展型实验和研究型实验。
()正确答案:√3、分级控制系统由现场总线控制、计算机监督控制、直接数字控制三级组成。
()正确答案:×4、实验平台的“场所便利化”是指被控对象和控制系统小型化,安全性高、成本低,便于使用者携带和使用,在家中和宿舍等场所即可完成各种实验。
()正确答案:√5、实验平台的“场所便利化”是指被控对象和控制系统小型化,安全性高、成本低,便于使用者携带和使用,在家中和宿舍等场所即可完成各种实验。
()正确答案:√6、计算机控制系统就是由模拟器件参与并作为核心环节的自动控制系统,即应用模拟器件参与控制并借助一些辅助部件与被控对象相联系,以获得一定控制目的而构成的系统。
计算机控制系统题目(含答案)

n=v-j+q=2 对单位速度输入信号,选择
e (z)
1 (z)
v j
(1 ai z1 )(1
z 1 )q F1( z)
(1
z 1 )2 (1
f11z 1 )
i1
( z )
z
d
i1
(1 bi z 1 )F2 ( z)
(1
z 1 )( f21z 1
f 22 z 2 )
VOUT1 为单极性输出,若 D 为输入数字量,VREF 为基准参考电压,且为 n 位 D/A 转换器,则有
VOUT1
VREF
D 2n
VOUT2 为双极性输出,且可推导得到
VOUT2
(
R3 R1
VREF
R3 R2
VOUT1 )
VREF
(
D 2 n 1
1)
14、三相步进电机有哪几种工作方式?分别画出每种工作方式的各相通电顺序和电压波形图。(6 分)
步轨迹图,并标明进给方向和步数。[8 分]
(1) 插补计算过程如下表(4 分)
步数 偏差判别 坐标进给
偏差计算
坐标计算
终点判断
起点
F0=0
x0=0,y0=5
1
F0=0
-x
F1=F0-2x0+1=-9
x1=x0-1=4,y1=0
2
F1<0
+y
F2=F1+2y1+1=-8
x2=4,y2=y1+1=1
3
F2<0
对于三相步进电机则有单相三拍(简称单三拍)方式、双相三拍(简称双三拍)方式、三相六拍工作方式。 单三拍工作方式各相的通电顺序为:A→B→C→A→…,各相通电的电压波形:
(完整版)《计算机控制系统》课后题答案-刘建昌等科学出版社
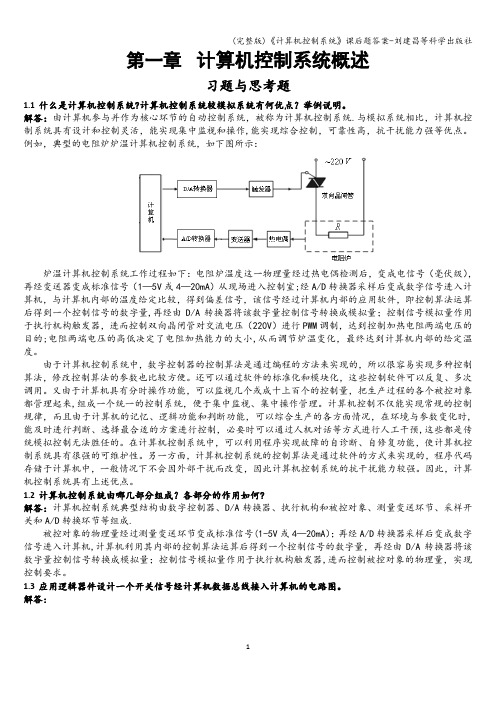
第一章计算机控制系统概述习题与思考题1.1什么是计算机控制系统?计算机控制系统较模拟系统有何优点?举例说明。
解答:由计算机参与并作为核心环节的自动控制系统,被称为计算机控制系统.与模拟系统相比,计算机控制系统具有设计和控制灵活,能实现集中监视和操作,能实现综合控制,可靠性高,抗干扰能力强等优点。
例如,典型的电阻炉炉温计算机控制系统,如下图所示:炉温计算机控制系统工作过程如下:电阻炉温度这一物理量经过热电偶检测后,变成电信号(毫伏级),再经变送器变成标准信号(1—5V或4—20mA)从现场进入控制室;经A/D转换器采样后变成数字信号进入计算机,与计算机内部的温度给定比较,得到偏差信号,该信号经过计算机内部的应用软件,即控制算法运算后得到一个控制信号的数字量,再经由D/A转换器将该数字量控制信号转换成模拟量;控制信号模拟量作用于执行机构触发器,进而控制双向晶闸管对交流电压(220V)进行PWM调制,达到控制加热电阻两端电压的目的;电阻两端电压的高低决定了电阻加热能力的大小,从而调节炉温变化,最终达到计算机内部的给定温度。
由于计算机控制系统中,数字控制器的控制算法是通过编程的方法来实现的,所以很容易实现多种控制算法,修改控制算法的参数也比较方便。
还可以通过软件的标准化和模块化,这些控制软件可以反复、多次调用。
又由于计算机具有分时操作功能,可以监视几个或成十上百个的控制量,把生产过程的各个被控对象都管理起来,组成一个统一的控制系统,便于集中监视、集中操作管理。
计算机控制不仅能实现常规的控制规律,而且由于计算机的记忆、逻辑功能和判断功能,可以综合生产的各方面情况,在环境与参数变化时,能及时进行判断、选择最合适的方案进行控制,必要时可以通过人机对话等方式进行人工干预,这些都是传统模拟控制无法胜任的。
在计算机控制系统中,可以利用程序实现故障的自诊断、自修复功能,使计算机控制系统具有很强的可维护性。
另一方面,计算机控制系统的控制算法是通过软件的方式来实现的,程序代码存储于计算机中,一般情况下不会因外部干扰而改变,因此计算机控制系统的抗干扰能力较强。
计算机控制系统复习题及答案

计算机控制系统复习题及答案《计算机控制系统》课程复习资料⼀、简答题:1.什么是计算机控制系统?它由哪⼏部分组成?各有什么作⽤。
2.计算机控制系统与连续控制系统主要区别是什么?计算机控制系统有哪些优点?3.计算机控制系统中的保持器有何作⽤,简述保持器的特点?4.简述PID调节器的作⽤,有哪⼏种改进型数字PID算法?5.计算机控制系统有哪四种形式的信号?各有什么特点?6.简要说明什么是计算机控制系统?模拟调节器与数字调节器有何区别?⼆、分析和计算题:1.已知⼀系统的闭环脉冲传递函数为-1-1-20.1z Y(z)Gc(z)==1-0.4z+0.8z R(z),其中输⼊为单位阶跃信号,求输出y(KT)。
2.已知⼀系统的闭环脉冲传递函数为-1-10.53+0.1zGc(z)=1-0.37z当输⼊为单位阶跃信号时,求输出y(KT)及y(∞)。
3.⽤长除法或Z反变换法或迭代法求闭环系统2z+0.5Gc(z)=8(z+0.1z-0.12)的单位阶跃响应。
4.已知低通数字滤波器0.5266zD(z)=z-0.4734,求D(z)的带宽ωm;并求当输⼊E(z)为阶跃信号时数字滤波器的控制算法。
取采样周期T=2ms。
5.设系统如图所⽰,试求:①系统的闭环脉冲传递函数。
②判定系统的稳定性。
③分别求系统对单位阶跃输⼊和单位斜坡输⼊时的稳态误差。
6.设函数的La⽒变换为25F(s)=s(s+4),试求它的Z变换F(z)。
7.数字控制系统如图所⽰,求当K=10,T=1s,a=1时,分别求当输⼊为单位阶跃、单位斜单位抛物线函数时的稳态误差。
8.已知单位负反馈系统的开环脉冲传递函数为 Gk(z)=K(0.1z+0.08)/[(z-1)(z-0.7)],问当K为何值时系统稳定。
9.已知系统单位负反馈的开环传递函数为:z +0.8Gk(z)=z(z -1)(z -0.7)问:K 为何值时系统稳定?10.已知单位反馈系统的⼴义对象的Z 传递函数为:-1-1-1-1-10.26z (1+2.78z )(1+0.2z )W1(z)=(1-z )(1-0.286z ),试按最少拍⽆波纹设计原则设计单位阶跃输⼊时,计算机的调节模型D(z),并求其控制算法。
计算机控制系统_课后答案全解

第1章习题B 习题B1-1 举例说明2-3个你熟悉的计算机控制系统,并说明与常规连续模拟控制系统相比的优点。
B1-2 利用计算机及接口技术的知识,提出一个用同一台计算机控制多个被控参量的分时巡回控制方案。
B1-3 题图B1-3是一典型模拟式火炮位置控制系统的原理结构图。
由雷达测出目标的高低角、方位角和斜距,信号经滤波后,由模拟式计算机计算出伺服系统高低角和方位角的控制指令,分别加到炮身的高低角和方位角伺服系统,使炮身跟踪指令信号。
为了改善系统的动态和稳态特性,高低角和方位角伺服系统各自采用了有源串联校正网络和测速反馈校正,同时利用逻辑电路实现系统工作状态的控制(如偏差过大时可断开主反馈,实现最大速度控制,当偏差小于一定值后实现精确位置控制)。
试将其改造为计算机控制系统,画出系统原理结构图。
题图B1-3典型模拟式火炮位置控制系统的原理结构图B1-4水位高度控制系统如题图B.1-4所示。
水箱水位高度指令由W1 电位计指令电压u r确定,水位实际高度h由浮子测量,并转换为电位计W2 的输出电压u h。
用水量Q1 为系统干扰。
当指令高度给定后,系统保持给定水位,如打开放水管路后,水位下降,系统将控制电机,打开进水阀门,向水箱供水,最终保持水箱水位为指令水位。
试把该系统改造为计算机控制系统。
画出原理示意图及系统结构图。
题图B1-4 水箱水位控制系统原理示意图B1-5 题图B1-5为一机械手控制系统示意图。
将其控制器改造为计算机实现,试画出系统示意图及控制系统结构图。
题图B1-5机械手控制系统示意图B1-6题图B1-6为仓库大门自动控制系统示意图。
试将其改造为计算机控制系统,画出系统示意图。
题图B1-6 仓库大门自动控制系统示意图B1-7车床进给伺服系统示意图如题图B1-7所示。
电动机通过齿轮减速机构带动丝杠转动,进而使工作台面实现直线运动。
该系统为了改善系统性能,利用测速电机实现测速反馈。
试将该系统改造为计算机控制系统,画出系统示意图。
计算机控制习题及答案

计算机控制习题及答案计算机控制习题及答案计算机控制是计算机科学中的一个重要领域,它涉及到计算机系统的硬件和软件之间的相互作用,以及人与计算机之间的交互。
对于学习计算机控制的学生来说,习题是非常重要的一部分,它可以帮助他们巩固所学的知识,提高解决问题的能力。
本文将介绍一些常见的计算机控制习题,并给出相应的答案。
1. 什么是计算机控制?计算机控制是指通过编程和软件设计,控制计算机系统的硬件和软件之间的相互作用。
它涉及到输入、处理和输出三个主要步骤,以及各种控制结构和算法的应用。
2. 什么是控制结构?控制结构是一种编程语言中用于控制程序执行流程的语句或指令。
常见的控制结构包括顺序结构、选择结构和循环结构。
顺序结构按照代码的顺序依次执行,选择结构根据条件判断选择不同的执行路径,循环结构根据条件重复执行一段代码。
3. 什么是条件语句?条件语句是一种选择结构,根据条件的真假来选择不同的执行路径。
在大多数编程语言中,条件语句通常使用if-else语句或switch语句来实现。
if-else语句根据条件的真假选择执行不同的代码块,switch语句根据条件的值选择执行不同的分支。
4. 什么是循环语句?循环语句是一种重复执行一段代码的结构。
在计算机控制中,循环语句通常使用for循环、while循环或do-while循环来实现。
for循环在执行前先判断条件,然后执行一段代码,再更新条件,直到条件不满足为止。
while循环和do-while 循环也是根据条件判断是否继续执行一段代码,但它们的判断条件在循环体内部。
5. 什么是函数?函数是一段封装了一系列操作的代码块,它可以接受参数并返回结果。
函数可以重复使用,提高代码的复用性和可维护性。
在计算机控制中,函数通常用于封装一些常用的操作,以便在程序中多次调用。
6. 什么是递归?递归是一种函数调用自身的技术。
在计算机控制中,递归通常用于解决可以分解为相同问题的子问题的问题。
递归函数必须有一个结束条件,否则会导致无限递归。
计算机控制系统总习题(及答案)
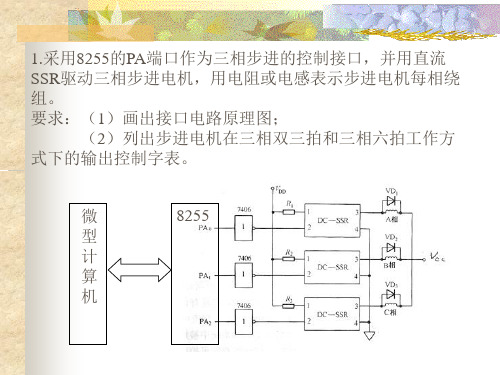
u(k )T 2T2 T 2T2 u(k 1)
e(k )(T 2T1 ) (T 2T1 )e(k 1)
T 2T2 T 2T1 T 2T1 u (k ) u(k 1) e(k ) e(k 1) T 2T2 T 2T2 T 2T2
2 1
2
1
1
z 3z Y ( z) 1 3z Y ( z) 2 2 z 2 3z z z 3z 2 Y ( z) A B z z 1 z 2 z z Y ( z ) 2 5 z 1 z2
2
z k 因为 Z [ ]a za
E( z) R( z)e ( z)
1 (1 z 1 ) 1 1 z 1
z 1 Y ( z ) R( z )( z ) 1 z 1
z 1 z 2 z 3 ...
9 z 1 (1 0.111z 1 ) G( z ) (1 z 1 )(1 0.0000454 1 ) z
( z ) z 1 1 ( z ) D( z ) G ( z ) 1 ( z )
(1 z 1 )(1 0.0000454 1 ) z z 1 . 1 1 9 z (1 0.111z ) (1 z 1 ) 0.1111 0.0000454 1 ) ( z (1 0.111z 1 )
v j i 1
1 ( z ) z d [ (1 bi z 1 )]F2 ( z ) f 21 z
u
i 1
根据上两式,有
e ( z) 1 ( z)
1 f 21 z 1 (1 z 1 )
根据多项式相等,其系数相等的的性质,有
计算机控制系统课后习题答案

1-1 什么是计算机控制系统?画出一个实际计算机控制系统原理结构图,并说明一个计算机控制系统由哪些部分组成及各部分的作用。
利用计算机参与控制的系统称为计算机控制系统。
1-2 简述计算机控制系统的控制过程。
实时数据采样实时计算控制量实时控制实时管理1-3 实时、在线方式和离线方式的含义是什么?(1)实时:所谓“实时”,是指信号的输入、计算和输出都是在一定时间围完成的,超出了这个时间就会失去控制时机,控制也就失去了意义。
(2)“在线”方式:生产过程和计算机系统直接连接,并接受计算机直接控制的方式称为在线或联机方式。
(3)“离线”方式:若生产过程设备不直接与计算机相连接,其工作不直接受计算机的控制的方式叫做“脱机”方式或“离线”方式。
1-4 计算机控制系统的硬件由哪几部分组成?各部分的作用是什么?主机:这是微型计算机控制系统的核心,通过接口它可以向系统的各个部分发出各种命令,同时对被控对象的被控参数进行实时检测及处理。
输入输出通道:这是微机和生产对象之间进行信息交换的桥梁和纽带。
(3)外部设备:这是实现微机和外界进行信息交换的设备,简称外设,包括人机联系设备(操作台)、输入输出设备(磁盘驱动器、键盘、打印机、显示终端等)和外存贮器(磁盘)。
(4)生产过程装置a.测量变送单元:为了测量各种参数而采用的相应检测元件及变送器。
b.执行机构:要控制生产过程,必须有执行机构。
1.5 计算机控制系统的软件由哪几部分组成?各部分的作用是什么?就功能来分,软件可分为系统软件、应用软件及数据库。
系统软件:它是由计算机设计者提供的专门用来使用和管理计算机的程序。
系统软件包括:a.操作系统:即为管理程序、磁盘操作系统程序、监控程序等;b.诊断系统:指的是调节程序及故障诊断程序;c.开发系统:包括各种程序设计语言、语言处理程序(编译程序)、服务程序(装配程序和编辑程序)、模拟主系统(系统模拟、仿真、移植软件)、数据管理系统等;d.信息处理:指文字翻译、企业管理等。
计算机控制系统复习题及答案

计算机控制系统复习题及答案《计算机控制系统》课程复习资料一、简答题:1.什么是计算机控制系统?它由哪几部分组成?各有什么作用。
2.计算机控制系统与连续控制系统主要区别是什么?计算机控制系统有哪些优点?3.计算机控制系统中的保持器有何作用,简述保持器的特点?4.简述PID 调节器的作用,有哪几种改进型数字PID 算法?5.计算机控制系统有哪四种形式的信号?各有什么特点?6.简要说明什么是计算机控制系统?模拟调节器与数字调节器有何区别?二、分析和计算题:1.已知一系统的闭环脉冲传递函数为-1-1-20.1zY(z)Gc(z)==1-0.4z+0.8zR(z),其中输入为单位阶跃信号,求输出y(KT)。
2.已知一系统的闭环脉冲传递函数为-1-10.53+0.1z Gc(z)=1-0.37z当输入为单位阶跃信号时,求输出y(KT)及y(∞)。
3.用长除法或Z 反变换法或迭代法求闭环系统2z +0.5Gc(z)=8(z +0.1z -0.12)的单位阶跃响应。
4.已知低通数字滤波器0.5266z D(z)=z -0.4734,求D (z )的带宽ωm;并求当输入E(z)为阶跃信号时数字滤波器的控制算法。
取采样周期T=2ms 。
5.设系统如图所示,试求:①系统的闭环脉冲传递函数。
②判定系统的稳定性。
③分别求系统对单位阶跃输入和单位斜坡输入时的稳态误差。
_6.设函数的La 氏变换为25F(s)=s (s +4),试求它的Z 变换F(z)。
7.数字控制系统如图所示,求当K=10,T=1s,a=1时,分别求当输入为单位阶跃、单位斜单位抛物线函数时的稳态误差。
8.已知单位负反馈系统的开环脉冲传递函数为 Gk(z)=K(0.1z+0.08)/[(z-1)(z-0.7)],问当K 为何值时系统稳定。
9.已知系统单位负反馈的开环传递函数为:z +0.8Gk(z)=z(z -1)(z -0.7)问:K 为何值时系统稳定?10.已知单位反馈系统的广义对象的Z 传递函数为:-1-1-1-1-10.26z (1+2.78z )(1+0.2z )W1(z)=(1-z )(1-0.286z ),试按最少拍无波纹设计原则设计单位阶跃输入时,计算机的调节模型D(z),并求其控制算法。
计算机控制系统复习题及答案

案4、采样定理的基本内容是什么?对频带受限的信号,当采样频率大于等于信号最高频率的两倍时,可以从采样值完全恢复原始的信号5、什么是数字滤波?常用的数字滤波有哪些方法?所谓数字滤波,就是在计算机中用某种计算方法对输入的信号进行数学处理,以便减少干扰在有用信号中的比重,提高信号的真实性。
程序判断法、中位值滤波法、算术平均滤波法、递推平均滤波法、加权递推平均滤波法、一阶惯性滤波法6、计算机控制系统中有哪几种地线?在计算机控制系统中,一般有以下几种地线:模拟地、数字地、安全地、系统地、交流地。
7、简述Smith预估控制的基本思想。
按照过程的动态特性建立一个模型加入到反馈控制系统中,使被延迟了τ时间的被控量超前反映到控制器,让控制器提前动作,从而可明显地减少超调量和加快控制过程。
8、工业控制计算机系统的干扰源有哪几类?各类干扰又有哪些具体形式?电源干扰(浪涌、尖峰、噪声、断电);空间干扰(静电和电场的干扰、磁场干扰、电磁辐射干扰);设备干扰9、RS-485串行总线采用什么传输方式?它与RS-422A串行通信总线的区别是什么?RS-485串行总线采用的是不平衡传输模式。
区别在于RS-485为半双工工作模式,而RS422A 为全双工工作方式,且RS-422A适用于两点之间进行高速,远距离通信,而RS-485适用于多点之间进行高速,远距离通信10、数字PID控制算法中,K P,T i,T D的物理调节作用分别是什么?Kp为比例增益,能减小误差,但不能消除稳态误差,但Kp加大会引起系统不稳定;Ti为积分时间常数,只要有足够的时间,积分控制将能完全消除误差,但积分作用太强会使系统超调加大,甚至使系统出现振荡;Td为微分时间常数,可以减小调整时间,从而改变系统的动态性能11、如何消除尖峰脉冲干扰?12、模拟量输入接口设计主要解决哪几个方面的问题?数据输出线的连接方式;选通信号、启动转换及读出控制信号的连接方法;电源和地线的处理;与计算机信息传递的方式。
计算机控制考试试题及答案

计算机控制考试试题及答案一、选择题1. 下列哪个不是计算机中常见的输入设备?A. 键盘B. 鼠标C. 打印机D. 扫描仪答案:C2. 以下关于计算机操作系统的描述中,正确的是?A. 操作系统是一种硬件设备B. 操作系统用于控制计算机的外设C. 操作系统是计算机软件的一部分D. 操作系统只能运行在个人电脑上答案:C3. 在Excel中,可以用来进行数据计算和分析的功能是?A. 排序B. 过滤D. 插入图表答案:C4. 下列哪个不是计算机网络的作用?A. 共享信息B. 远程控制C. 娱乐游戏D. 电子邮件答案:C5. 在计算机中,CPU是指什么?A. 中央处理器B. 中央存储器C. 控制处理单元D. 具有独立功能的电路板答案:A二、填空题1. 在计算机中,二进制系统使用的是 __________ 进制。
2. 在编写程序时,对程序的错误进行排查和修复的过程被称为__________。
答案:调试3. 在数据库管理系统中,用于检索和存储大量数据的语言是__________。
答案:SQL4. 在计算机网络中,IP地址是用来标识 __________ 的唯一地址。
答案:设备5. 在Word文档中,用于对文字进行加粗、斜体等格式设置的功能是 __________。
答案:字体三、简答题1. 请简要解释什么是操作系统,并举例说明操作系统的作用。
答案:操作系统是计算机软件的一部分,它负责管理和控制计算机硬件和应用程序的运行。
操作系统的作用包括:- 硬件管理:操作系统可管理计算机的硬件资源,如内存、CPU、硬盘等,合理分配资源以提高计算机的效率。
- 文件管理:操作系统可管理计算机中的文件和文件夹,包括创建、复制、移动、删除等操作,使用户能够方便地管理和访问文件。
- 进程管理:操作系统可管理计算机中的各个进程,包括进程的创建、调度、同步等操作,确保多个程序能够有效地共享计算机资源。
- 用户界面:操作系统提供了与计算机交互的接口,如图形界面(GUI)或命令行界面(CLI),使用户能够操作计算机并运行应用程序。
计算机控制系统习题参考答案

1
计算机控制系统习题参考答案
2) 直接数字控制系统:可完全取代模拟调节器,实现多回路的 PID 控制,而且只要改变 程序就可实现复杂的控制规律。
3) 监督控制系统:可考虑许多常规调节器不能考虑的因素,如环境温度和湿度对生产过 程的影响,可以进行在线过程操作的在线优化;可以实现先进复杂的控制规律,可靠性 好。
第二章 线性离散系统的数学描述和分析方法 P42
2-1 简述离散控制系统中信号变换的原理。 先经过采样过程,即采样开关按一定的周期进行闭合采样,使原来在时间上连续的 信号 f(t) 变成时间上离散、幅值上连续的离散模拟信号 f * (t) 。再经过量化过程,采用一组 数码来逼近离散模拟信号的幅值,将其转换成数字信号。 2-2 已知函数 f(t) ,求取 Z 变换 F(z) 。
10 ,采样周期 T=1s,采用零阶保持器,单位负反馈系 s(0.1s+1)
7
计算机控制系统习题参考答案
G(z)=Z[
1-e-Ts 10 10 9z -1 (1+0.11z -1 ) ]=(1-z −1 )Z[ 2 ]= ⋅ s s(0.1s+1) s (0.1s+1) (1-z -1 )(1-e-10 z -1 )
1)
f(t)=a mt
* -k mT -1 2mT -2 Z [ f(t) ] =Z f (t) = ∑ f(kT)z =1+a z +a z +... k=0 ∞
①ห้องสมุดไป่ตู้
①-① ⋅a mT ⋅ z -1 得:
Z[f(t)]=
1 1-a z
mT -1
2)
f(t)=1-e-at
1 1 (1-e-aT )z -1 F(z)=Z[1-e ]= -1 - -aT -1 = 1-z 1-e z (1-z -1 )(1-e-aT z -1 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
T z 1
D(z)U E((zz))D(s)sT2zz 1 1
1 T1s 1 T2 s
s 2 z 1 T z 1
D (z) U (z)(T 2 T 1 )z T 2 T 1
E (z) (T 2 T 2)z T 2 T 2
12
D (z)U (z)(T2 T 1)zT2 T 1 E (z) (T2 T 2)zT2 T 2
T 2 T 2
T 2 T 2 T 2 T 2
增量控制算法为:
u ( k ) u ( k ) u ( k 1 ) 2 T u ( k 1 ) T 2 T 1 e ( k ) T 2 T 1 e ( k 1 ) T 2 T 2 T 2 T 2 T 2 T 2
4 用Z变换求 y ( k 2 ) 1 .5 y ( k 1 的) 解0 .5 ,y ( k 已) 知0 初始条
件为
y( T)0.5 ,y( 2 T)0.75
解:对上述差分方程两边Z变换,利用延迟性质
n
Z[f(kn) ]zn[F(z) f(i)zi] i1 7
得 Z [y (k 2 ) 1 .5 y (k 1 ) 0 .5 y (k ) 0 ]
e ( k )T ( 2 T 1 ) ( T 2 T 1 ) e ( k 1 )
u (k ) T 2 T 2 u (k 1 ) T 2 T 1 e (k ) T 2 T 1 e (k 1 )
T 2 T 2
T 2 T 2 T 2 T 2
13
递推控制算法为:
u (k ) T 2 T 2u (k 1 ) T 2 T 1e (k ) T 2 T 1e (k 1 )
G (z)F(z)20 2 9 z z2 (z1)2 z1
F(z)z2z02(z2z1)2z9z1
查表 Z1[ z ]ak
za
Z1[ z ] 1 z 1
Z1[ z ]t kTk (z1)2 T T
6
F(z)z2z02(z2z1)2z9z1
所以 Z 1 [F (z) ]f(k ) 2 2 0 k 2 k 9
U E((z z))((T T 2 2 T T 2 1)) ((T T 2 2T T 1 2))zz 1 1
U ( z )T [ 2 ( T 2 ) ( T 2 T 2 ) z 1 ] [T ( 2 T 1 ) ( T 2 T 1 ) z 1 ] E ( z )
u ( k ) T 2 T 2 T 2 T 2 u ( k 1 )
因为 Z1[ z ]ak
za
所以 y (k ) 2 ( 1 )k 5 ( 2 )k,k 0 ,1 ,2 ,3
9
5 用Z变换求 c ( k 2 ) 1 .5 c ( k 1 ) 的 0 解.5 c ,( k 已) 知0 初始条件
为
c( 1 ) 0.5,c( 2)0.75
解:对上述差分方程两边Z变换,利用延迟性质
将初始条件代入得
z
zz
C (z)z23z2z1z2 10
因为 Z1[ z ]ak
za
C(z) z z z1 z2
所以
c(k) ( 1 )k( 2 )k,k0 ,1 ,2 ,3
11
作业: P139 4.2 4.4
1、某系统的连续控制器设计为 D(s)U(s)1T1s
E(s) 1T2s
试用双线性变换法、前向差分法、后向差分法分别求出数字 控制器D(z),并分别给出三种方法的递推控制算法。
带入初始值得
Y(z)z[21.5z10.5]z10.50.7 51.50.5 Y(z)z20 .51z.5 1z 11 .50.51 0.15.5 zz 1.05.z52z2
8
Y(z)2z3z3z2z2
Y(z) z
13z z2 3z2
Y(z) A B z z1 z2
Y(z)2 z 5 z z1 z2
z 2 [ Y ( z ) y ( T ) z y ( 2 T ) z 2 ] 1 . 5 z 1 [ Y ( z ) z ( T ) y 0 . 5 ] Y ( z ) 0 整理得
Y ( z ) z 2 [ 1 . 5 z 1 0 . 5 ] z 1 y ( T ) y ( 2 T ) 1 . 5 y ( T )
c2(s5)F(s)s5s52s51 5,
3
F(s)11 1 s2 5s 5(s5)
查表得
Z
1 s
z
z 1
Zs12
Tz (z 1)2
Zs1a
z zeaT
Tz 1z 1 z F(z)(z1)25z15ze5T
4
3 求 F(z)1(1zz32的1)(5zzZ2反1)62变z 换
f (k)
解:按要求整理得
1.采用8255的PA端口作为三相步进的控制接口,并用直流 SSR驱动三相步进电机,用电阻或电感表示步进电机每相绕 组。 要求:(1)画出接口电路原理图;
(2)列出步进电机在三相双三拍和三相六拍工作方 式下的输出控制字表。
微
8255
型
计
算
机
1
(2)双三拍工作方式下的控制字表
存贮地址编号
A口输出字
AD1
03H
AD2
06H
AD3
05H
三相六拍工作方式下的控制字表
存贮地址编号
A口输出字
AD1
01H
AD2
03H
AD3
02H
AD4
06H
AD5
04H
AD6
05H
2
2求
F(s)
的5Z变换
s2(s5)
F(z)
解:
F(s)cs121cs12sc25 c11s2F(s)s0s55s01
c12[s2F(s)]s0[s 55]s01 5,
F(z) 11z215z6 z (z2)(z1)2
G (z)F(zz)zc 12(zc 21)12zc 212
c1(z2)G (z)z21z1 (2z 11)z25 Nhomakorabea 20 z2
c21 (z1)2G (z)z11z1 2z 12z5 6 2 5 z1
c22 [(z1 )2G (z)]z 1[1z2 1 z 12z5 6] 9 z 1
n
Z[f(kn) ]zn[F(z) f(i)zi]
得
i1
Z [ c ( k 2 ) 1 .5 c ( k 1 ) 0 .5 c ( k ) 0 ]
z 2 [ C ( z ) c ( 1 ) z c ( 2 ) z 2 ] 1 . 5 z 1 [ C ( z ) z ( 1 ) c 0 . 5 ] C ( z ) 0
