新版混凝土结构设计规范二阶效应的设计规定简介
二阶效应在各个规范中的理解与区别

关于“二阶效应”的总结【《砼规》,《抗规》,《高规》】“二阶效应”分为“重力二阶效应P-Δ”和“挠曲二阶效应P-δ”重力二阶效应P-Δ:在地震等水平力作用下结构侧移时重力作用产生的附加内力挠曲二阶效应P-δ:偏心受压构件(主要是长细比大于17.5柱)由于自身挠曲产生的附加内力★《砼规》中的规定:《砼规》7.3.9条给出两种考虑“二阶效应”的方法:1)《砼规》7.3.10条的偏心距增大系数法存在问题:此法只针对于混凝土偏心受压构件(主要是柱),而且不论是否时地震工况,对于长细比大于17.5的偏心受压构件均应考虑。
虽然条文说明中认为此法可以同时考虑上述两种二阶效应,但从其增大系数的计算公式可知,此增大系数对挠曲二阶效应反映得较为充分,对重力二阶效应反映的则不够充分,或者不够准确,因为偏心距增大系数计算公式与结构的侧移量大小没有关系。
2)《砼规》7.3.12条的折减构件弹性抗弯刚度法(仿照美国规范)存在问题:《砼规》认为此法是“一种精度和效率较高得”考虑二阶效应的方法,是“一种理论上严密的”方法。
但是刚度得折减系数得取值很难精确,在不同荷载组合下,不同得构件得开裂程度都不一样。
取统一折减系数得方法,只能大概反映二阶效应的影响。
而且在程序实现时也会有新得问题,比如刚度减小,导致地震力减小,位移算是弹性还是塑性位移等等。
★《抗规》中的规定:《抗规》3.6.3条及条文说明规定,结构在地震作用下的重力附加弯矩大于初始弯矩的10%时,应考虑重力二阶效应的影响。
考虑方法是简化的内力增大系数1/(1-θ),θ是稳定系数,即附加弯矩占初始弯矩的倍数。
同时规定,对于混凝土柱,本条与《砼规》7.3.10不同时考虑。
★《高规》中的规定:《高规》5.4.1~5.4.3条规定,在水平力作用下,不满足5.4.1条刚重比的高层建筑,需要考虑水平力作用下重力二阶效应对结构内力和位移的影响。
其计算方法是5.4.3条的内力和位移增大系数。
二阶效应规范规定
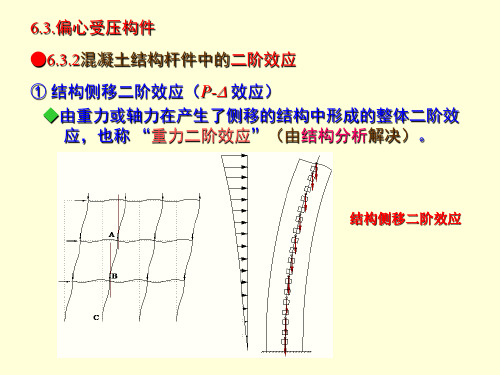
◆说明:轴向压力在挠曲杆件中产生的二阶效应(效应)
是偏压杆件中由轴向压力在产生了挠曲变形的杆件内引起 的曲率和弯矩增量。例如结构中常见的反弯点位于柱高中 部的偏压构件中,这种二阶效应虽能增大构件除两端区域 外各截面的曲率和弯矩,但增大后的弯矩通常不可能超过 柱两端控制截面的弯矩。因此,在这种情况下,效应不会 对杆件截面的偏心受压承载能力产生不利影响。但是,在 反弯点不在杆件高度范围内(即沿杆件长度均为同号弯矩) 的较细长且轴压比偏大的偏压构件中,经效应增大后的杆 件中部弯矩有可能超过柱端控制截面的弯矩。此时,就必 须在截面设计中考虑效应的附加影响。因后一种情况在工 程中较少出现,为了不对各个偏压构件逐一进行验算,本 条给出了可以不考虑效应的条件。
l c / i 34 - 12( M 1 / M 2 )
M1、M2—分别为偏心受压构件两端截面按结构分析确定的对
同一主轴的组合弯矩设计值,绝对值较大端为,绝对值 较小端为,当构件按单曲率弯曲时,取正值,否则取负 值 l c—构件的计算长度,可近似取偏心受压构件相应主轴 方向上下支撑点之间的距离; i—偏心方向的截面回转半径。
杆件挠曲二阶效应
● 6.2.3条: 弯矩作用平面内截面对称的偏心受压构件,当同一主轴 方向的杆端弯矩比M1/M2不大于0.9且设计轴压比不大于0.9时,若构 件的长细比满足下式要求时,可不考虑轴向压力在该方向挠曲杆件 中产生的附加弯矩影响;否则应按截面的两个主轴方向分别考虑轴 向压力在挠曲杆件中产生的附加弯矩影响。
Cm—构件端截面偏心距调节系数,当小于0.7时取0.7; hns—弯矩增大系数; N —与弯矩设计值M2相应的轴向压力设计值;
● 6.2.4条:考虑轴向压力在挠曲杆件中产生的二阶效应后控 制截面弯矩设计值应按下列公式计算:
混凝土二阶效应

6.3 偏心受压构件正截面承载力
2 大、小偏心受压破坏的设计判别(界限偏心距)
设计时可按下列条件进行判别: 当 ei 0.3h0 时,可能为大偏压,可能为小偏压,可按大偏压设计; 当 ei 0.3h0 时,按小偏压设计。
6.3.3 矩形截面非对称配筋偏心受压构件正截面受压承载力计算
④ 验算垂直于弯矩作用平面的受压承载力(按轴压构件),应满足
N Nu 0.9 ( fc A f yAs)
6.3.3矩形截面非对称配筋偏心受压构件正截面受压承载力计算
6.3 偏心受压构件正截面承载力
应用上式时注意以下几点:
1)公式中的 As 应取全部纵向钢筋的截面面积,包括受拉钢筋 As 和
e
h 2
as
ei
矩形截面非对称配筋小偏心受压构件截面应力计算图形
6.3.3 矩形截面非对称配筋偏心受压构件正截面受压承载力计算
6.3 偏心受压构件正截面承载力
2)基本公式
Ne
Nue
1 fcbx(h0
x) 2
fyAsh0
as
Ne
Nue
1
fcbx(
x 2
6.3 偏心受压构件正截面承载力
6.3.2 偏心受压构件的二阶效应
e 1.附加偏心距 ea、初始偏心距 i
可能产生附加偏心距 ea 的原因:
a.荷载作用位置的不定性;
b.混凝土质量的不均匀性;
c.施工的偏差等因素 。 《规范》6.2.5条规定:两类偏心受压构件的正截面承载力计算中, 均应计入轴向压力在偏心方向存在的附加偏心距。
5.4 偏心受压构件二阶效应

由受压构件自身挠曲产生的P-δ效应
《规范》规定,除排架结构柱外,其他偏心受压构件考
虑轴向压力在挠曲杆件中产生的二阶效应后,控制截面
的弯矩设计值应按下式进行计算。
M CmnsM 2
式中
Cm
0.7
0.3
M1 M2
偏心距调节系数(≥0.7)
ns
1
1
1300
M2 N
ea
/
h0
lc h
2
c
弯矩增 大系数
c
0.5 fc A N
截面曲率修正系数(≥1)
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)
由受压构件自身挠曲产生的P-Δ效应
P
P
FΔ
Δ
由侧移产生的二阶效应
由受压构件自身挠曲产生的P- Δ效应
(1)P-Δ效应产生的弯矩增大属于结构分析中考 虑几何非线性的内力计算问题; (2)在偏心受压构件截面计算时给出的内力设计 值已经包含了P-Δ效应,故不必再截面承载力计算 中再考虑。
P
M1
M1
M1
M2 P
M2
M2
杆端弯矩异号时的二阶效应
由受压构件自身挠曲产生的P-δ效应
考虑二阶效应的条件
杆端弯矩同号时,发生控制截面转移的情况是不普遍的, 为了减少计算工作量,《混凝土结构设计规范》规定, 当只要满足下述三个条件中的一个条件时, 就要考虑二阶效应:
① M1/M2>0.9 ② 轴压比N/fcA>0.9 ③ lci/i>34-12(M1/M2)
二阶效应: 轴向压力对偏心受压构件的侧移和挠曲产生附加弯矩 和附加曲率的荷载效应。 (1) P-δ效应
由挠曲产生的二阶效应。 (2) P-Δ效应
混凝土二阶效应

某高层建筑,在施工过程中出现混凝土结构开裂问题。通过 引入二阶效应分析,对施工方案进行调整,优化了混凝土配 合比和养护条件,成功避免了裂缝的产生,保证了工程质量 。
二阶效应在工程中的应用
结构优化设计
利用二阶效应理论,可以对混凝 土结构进行更为精确的力学分析 和优化设计,提高结构的承载能
力和稳定性。
试验方法
通过试验方法对混凝土试件进行压力 试验,可以获得其应力-应变曲线和相 关参数,进而评估二阶效应的影响。 这种方法较为直观,但需要考虑试件 与实际结构的差异。
03 混凝土二阶效应的实验研 究
实验设计
确定实验目的
验证混凝土二阶效应的存在, 研究其影响因素和作用机理。
选择实验材料
选择具有代表性的混凝土试样 ,确保试样质量和均匀性。
03
二阶效应还与结构的几何非线性和边界条件等因素有关,这些因素会导致结构 在受力过程中产生复杂的应力分布和变形形态。
二阶效应的影响因素
混凝土强度
混凝土强度是影响二阶效应的重要因素之一。高强度的混 凝土具有较大的非线性特征,因此在承受较大压力时更容 易产生二阶效应。
结构形式和尺寸
不同结构形式和尺寸的混凝土结构在承受压力时会产生不 同的二阶效应。例如,大跨度、高层和细长结构的二阶效 应更为显著。
导。
02 混凝土二阶效应基本理论
二阶效应的原理
01
混凝土二阶效应是指混凝土结构在承受压力时,不仅会产生弹性变形,还会产 生非弹性变形,即塑性变形。这种塑性变形会在结构内部产生二次应力,对结 构的承载能力和稳定性产生影响。
02
二阶效应的产生与混凝土材料的非线性特性有关,混凝土在受力过程中会发生 硬化和软化,导致其应力-应变关系呈现非线性特征。
混凝土结构重力二阶效应荷载分项系数

混凝土结构重力二阶效应荷载分项系数随着城市化进程的加快,高层建筑的需求越来越大,而混凝土结构作为一种常见的建筑结构形式,在高层建筑中得到了广泛应用。
然而,对于混凝土结构在设计和施工过程中所面临的问题,特别是重力二阶效应的荷载分项系数,一直是结构设计和工程实践中的热点和难点问题。
深入研究和分析混凝土结构重力二阶效应荷载分项系数的影响因素和计算方法,对于保证结构的安全性和可靠性具有重要意义。
1. 重力二阶效应概述重力二阶效应是指在垂直方向上,由于结构自重引起的非线性效应。
在混凝土结构中,由于结构的柔度和刚度存在一定的不一致性,使得结构在承载载荷时会产生较大的变形,在某些情况下会引起结构的不稳定和破坏。
重力二阶效应的考虑对于混凝土结构的设计和施工具有重要意义。
2. 影响因素重力二阶效应的大小受多种因素的影响,主要包括结构的几何形状、材料的性质、荷载的种类和分布等。
其中,结构的刚度和柔度是影响重力二阶效应的关键因素,而结构的几何形状和材料的性质则直接影响了结构的整体稳定性和承载能力。
荷载的种类和作用方式也会对重力二阶效应产生一定的影响。
3. 荷载分项系数为了准确地考虑重力二阶效应对结构的影响,相关标准和规范中引入了荷载分项系数的概念。
荷载分项系数是指在进行结构设计时,将荷载按照不同的分项作用计算,并将计算结果乘以相应的系数得到最终的设计荷载值。
在混凝土结构中,荷载分项系数的合理确定对于保证结构的安全和可靠性具有重要意义。
4. 系数计算方法确定荷载分项系数的方法通常包括经验法和理论分析法两种。
在实际工程中,可以根据结构的具体情况和设计要求选择合适的系数计算方法。
通常情况下,采用经验法进行系数的确定,结合理论分析进行修正和调整,可以得到较为合理和准确的系数值。
5. 相关规范和标准国内外关于混凝土结构重力二阶效应荷载分项系数的相关规范和标准是指导和保证工程实践的重要依据。
在进行混凝土结构设计和施工时,必须严格遵守相关规范和标准的规定,确保结构的安全性和可靠性。
混凝土结构的二阶效应

一、混凝土结构的二阶效应混凝土结构的二阶效应应由两部分组成:p-δ效应和P-Δ效应。
p-δ效应是指由于构件在轴向压力作用下,自身发生挠曲引起的附加效应,可称之为构件挠曲二阶效应,通常指轴向压力在产生了挠曲变形的构件中引起的附加弯矩,附加弯矩与构件的挠曲形态有关,一般中间大,两端部小。
P-Δ效应是指由于结构的水平变形而引起的重力附加效应,可称之为重力二阶效应,结构在水平力(风荷载或水平地震力)作用下发生水平变形后,重力荷载因该水平变形而引起附加效应,结构发生的水平侧移绝对值越大,P-Δ效应越显著,若结构的水平变形过大,可能因重力二阶效应而导致结构失稳。
1.重力二阶效应(P-Δ效应)计算计算P-Δ效应的近似方法有等效几何刚度的有限元法、等效水平力的有限元迭代法、折减弹性抗弯刚度的有限元、结构位移和构件内力增大系数法等。
1)等效几何刚度的有限元法在不考虑P-Δ效应影响时,是在结构的初始拓扑关系基础上建立结构的平衡方程。
一般可记为:[K]{u}=[F]考虑P-Δ效应影响时,对于结构的任一节点j,因P-Δ效应而引起的Mj=Gjuj,相应的等效附加水平力为Vj= 。
对于所有节点,则形成一个等效附加水平分力向量。
可以看出,考虑P-Δ效应相当于结构的初始刚度矩阵[K]修改为等效刚度矩阵[K-KG]。
新规范版的SATWE、TAT、PMSAP等软件都采用了等效几何刚度的有限元法,这种方法具有一般性,它既适用于采用刚性楼板假定的结构,也适用于存在独立弹性节点的结构。
与不考虑P-Δ效应的分析结果相比,结构的周期、位移和构件的内力都有所不同。
2)折减弹性抗弯刚度的有限元法折减弹性抗弯刚度的有限元法是今年来美国、加拿大等国设计规范推荐的一种考虑效益方法。
这种分析方法的基本思路是采用折减等效刚度,近似的考虑钢筋混凝土结构中各类构件在极限状态时因开裂而导致刚度减小现象,使分析结果与设计状态尽可能一致。
《混凝土结构设计规范》引进该方法,第7.3.12规定,当采用考虑二阶效应的弹性分析方法时,宜在结构分析中对钢筋混凝土构件的弹性抗弯刚度乘以一下折减系数:梁取0.4,柱取0.6,对未开裂的剪力墙和核心筒取0.7,对已开裂的剪力墙和核心筒壁取0.45。
二阶效应在各个规范中的理解与区别

关于“二阶效应”的总结【《砼规》,《抗规》,《高规》】“二阶效应”分为“重力二阶效应P-Δ”和“挠曲二阶效应P-δ”重力二阶效应P-Δ:在地震等水平力作用下结构侧移时重力作用产生的附加内力挠曲二阶效应P-δ:偏心受压构件(主要是长细比大于17.5柱)由于自身挠曲产生的附加内力★《砼规》中的规定:《砼规》7.3.9条给出两种考虑“二阶效应”的方法:1)《砼规》7.3.10条的偏心距增大系数法存在问题:此法只针对于混凝土偏心受压构件(主要是柱),而且不论是否时地震工况,对于长细比大于17.5的偏心受压构件均应考虑。
虽然条文说明中认为此法可以同时考虑上述两种二阶效应,但从其增大系数的计算公式可知,此增大系数对挠曲二阶效应反映得较为充分,对重力二阶效应反映的则不够充分,或者不够准确,因为偏心距增大系数计算公式与结构的侧移量大小没有关系。
2)《砼规》7.3.12条的折减构件弹性抗弯刚度法(仿照美国规范)存在问题:《砼规》认为此法是“一种精度和效率较高得”考虑二阶效应的方法,是“一种理论上严密的”方法。
但是刚度得折减系数得取值很难精确,在不同荷载组合下,不同得构件得开裂程度都不一样。
取统一折减系数得方法,只能大概反映二阶效应的影响。
而且在程序实现时也会有新得问题,比如刚度减小,导致地震力减小,位移算是弹性还是塑性位移等等。
★《抗规》中的规定:《抗规》3.6.3条及条文说明规定,结构在地震作用下的重力附加弯矩大于初始弯矩的10%时,应考虑重力二阶效应的影响。
考虑方法是简化的内力增大系数1/(1-θ),θ是稳定系数,即附加弯矩占初始弯矩的倍数。
同时规定,对于混凝土柱,本条与《砼规》7.3.10不同时考虑。
★《高规》中的规定:《高规》5.4.1~5.4.3条规定,在水平力作用下,不满足5.4.1条刚重比的高层建筑,需要考虑水平力作用下重力二阶效应对结构内力和位移的影响。
其计算方法是5.4.3条的内力和位移增大系数。
二阶效应规范规定
条: 弯矩作用平面内截面对称的偏心受压构件,当同一主轴方向的杆端弯矩比M1/M2不大于0.9且设计轴压比不大于0.9时,若构件的长细比满足下式要求时,可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响;否则应按截面的两个主轴方向分别考虑轴向压力在挠曲杆件中产生的附加弯矩影响。
M1、M2—分别为偏心受压构件两端截面按结构分析确定的对同一主轴的组合弯矩设计值,绝对值较大端为,绝对值较小端为,当构件按单曲率弯曲时,取正值,否则取负值 l c—构件的计算长度,可近似取偏心受压构件相应主轴方向上下支撑点之间的距离; i—偏心方向的截面回转半径。
Cm—构件端截面偏心距调节系数,当小于0.7时取0.7;
条:考虑轴向压力在挠曲杆件中产生的二阶效应后控制截面弯矩设计值应按下列公式计算:
N —与弯矩设计值M2相应的轴向压力设计值;
hns—弯矩增大系数;
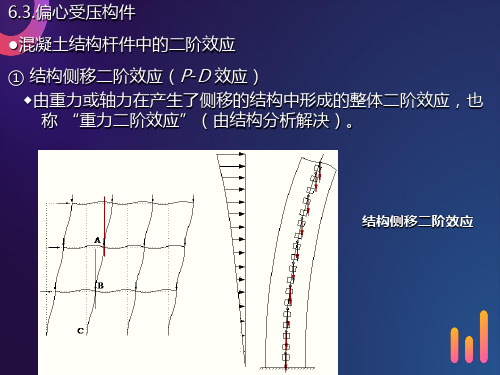
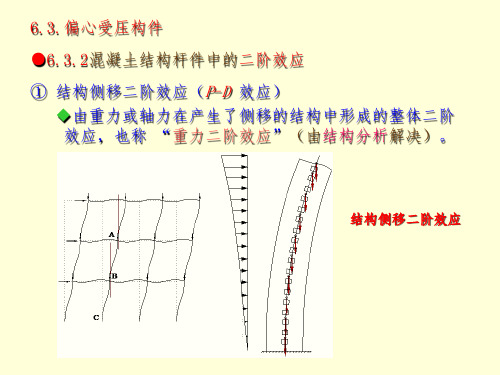
6.3.偏心受压构件 ●混凝土结构杆件中的二阶效应 ① 结构侧移二阶效应(P-D 效应) ◆由重力或轴力在产生了侧移的结构中形成的整体二阶效应,也称 “重力二阶效应”(由结构分析解决)。
结构侧移二阶效应
(P31) 当结构的二阶效应可能使作用效应显著增大时,在结构分析中应考虑二阶效应的不利影响。
01
混凝土结构的重力二阶效应可采用有限元分析方法计算,也可采用本规范附录B 的简化方法。当采用有限元分析方法时,宜考虑混凝土构件开裂对构件刚度的影响。
02
[考虑重力二阶效应的两种方法:有限元法;简化方法]
03ቤተ መጻሕፍቲ ባይዱ
杆件挠曲二阶效应(p-d 效应) 由轴压力在杆件自身挠曲后引起的局部二阶效应。通常起控制作用效应仅在少数偏压构件中形成,反弯点不在柱高范围内的较细长偏心压杆则有可能属于这类情况。 杆件挠曲二阶效应
凝土结构二阶效应条文解释

6
偏心受压构件旳二阶效应
▼问题:按P“ 层增大系数法”或“整体增大系数法”计算后, 是否需考虑 l0 效应?(某些软件两者均考虑) 现行措施: 法仅合用于有侧移框架构造,其他构造中旳柱
怎样考虑?
▼新修订规范处理措施:两种二阶效应分开考虑
计算弯矩增大系数时旳刚度折减系数可取为0.7。
12
偏心受压构件旳二阶效应-- P 效应
(1) 构件两端弯矩值相等
图示构件两端作用轴向压力N和相等 旳端弯矩M0 = N e0。在M0作用下,
构件将产生如图虚线所示旳弯曲变形 ,其中y0表达仅由弯曲引起旳侧移; 当N作用时,开始时各点力矩将增长 一种数值Ny0,并引起附加侧移而最 终至y。在M0和N同步作用下旳侧移 曲线如图a所示实线。
lc
——构件旳计算长度,近似取偏心受压构件相应主轴 方向两支撑点之间旳距离。
20
6.2.17 矩形截面偏心受压构件正截面受压承载力应符合下列规
定(图6.2.17) :
N 1 fcbx fyAs s As ( p0 fpy ) Ap p Ap
Ne
1
fcbx
h0
x 2
f yAs (h0
as) ( p0
fpy ) Ap (h0
ap )
e
ei
h 2
a
e
ei
h 2
a
ei e0 ea
21
6.2.17 此次对偏心受压构件二阶效应旳计算措施进行了修订, 即除排架构造柱以外,不再采用 l0 法。新修订旳措施主要希 望经过计算机进行构造分析时一并考虑由构造侧移引起旳二阶 效应。
新版混凝土结构设计规范二阶效应的设计规定简介_侯建国

第46卷增刊2013年10月武汉大学学报(工学版)Engineering Journal of Wuhan UniversityVol.46Sup.Oct.2013作者简介:侯建国(1955-),男,教授、博士生导师,主要从事结构可靠度基本理论与应用研究,E-mail:jghou@whu.edu.cn.文章编号:1671-8844(2013)S1-0056-13新版混凝土结构设计规范二阶效应的设计规定简介侯建国1,杨力1,叶亚鸿1,黄凯斌1,唐静1,李劲夫1,程献军2,王美华3(1.武汉大学土木建筑工程学院,湖北武汉 430072;2.黄冈市白莲河水库管理处,湖北黄冈 438218;3.山西中煤东坡煤业有限公司,山西朔州 037200)摘要:结构的二阶效应泛指作用在结构上的重力或构件中的轴向压力在产生了层间位移和挠曲变形后的结构或构件中引起的附加变形和相应的附加内力,包括结构整体的侧移二阶效应(P-Δ效应)和受压构件的挠曲效应(P-δ效应)两部分.简要介绍了我国新版GB 50010-2010《混凝土结构设计规范》关于二阶效应设计规定修订的主要内容和相关背景资料,可供相关工程技术人员借鉴和参考.与原规范GB 50010-2002《混凝土结构设计规范》相比,新规范关于二阶效应设计规定修订的要点为:1)结构的侧移二阶效应可采用有限元分析方法计算,也可采用规范附录B所给出的近似计算结构侧移二阶效应的增大系数法,不再采用原规范的η-l0法;2)对于构件自身挠曲引起的二阶效应(P-δ效应)的计算,则允许采用柱截面偏心距增大系数(或弯矩增大系数)的传统方法,但相应的计算公式作了重大修改.关键词:受压构件;二阶效应;增大系数中图分类号:TU 203 文献标志码:ABrief introduction to second-order effect design stipulationsin new edition of code for design of concrete structuresHOU Jianguo1,YANG Li 1,YE Yahong1,HUANG Kaibin1,TANG Jing1,LI Jinfu1,CHENG Xianjun2,WANG Meihua3(1.School of Civil and Architectural Engineering,Wuhan University,Wuhan 430072,China;2.Huanggang Bailianhe Reservoir Management Department,Huanggang 438218,China;3.Shanxi Zhongmei Dongpo Coal Co.,Ltd.,Shuozhou 037200,China)Abstract:Second-order effect is referred to the additional deformation and corresponding internal forcecaused by axial forces or gravity applied to the structural members and bars that have interbedded displace-ment and deflection.It may commonly consists of two parts:the lateral displacement second-order effect ofthe whole structure,commonly called P-Δeffect and deflection second-order effect of compression mem-bers,commonly called P-δeffect.Main revision contents and background materials of new edition of GB50010-2010 code for design of concrete structures is introduced,which can provide some references for theengineers and technicians concerned.In comparison with the concrete structures design code of GB 50010-2002,modifying second-order effect design stipulations of new code have following important points:1)Fi-nite element analysis can be used in calculation of analysis the lateral displacement second-order effect ofstructures.Magnifying coefficient method given in the appendix B of the code can also be used to calculateit approximately.Theη-l0method of former standard will fall out of use.2)The traditional method,ec-centricity magnification coefficient of columns cross-section method,can be used in deflection second-ordereffect of compression members calculation.But the corresponding calculation formula made significantchanges. 增刊侯建国,等:新版混凝土结构设计规范二阶效应的设计规定简介Key words:compression members;second-order effect;magnifying coefficient 我国新修订的国家标准GB 50010-2010《混凝土结构设计规范》[1]关于偏心受压构件的二阶效应的设计规定,较原规范GB 50010-2002《混凝土结构设计规范》[2]作了重大修改,本文就GB 50010-2010关于偏心受压构件二阶效应的设计规定修订的主要内容和相关背景资料情况作一简要介绍.1 二阶效应的有关概念结构的二阶效应泛指作用在结构上的重力或构件中的轴向压力在产生了层间位移和挠曲变形后的结构或构件中引起的附加变形和相应的附加内力,包括结构整体的侧移二阶效应(P-Δ效应)和受压构件的挠曲效应(P-δ效应)两部分(图1).以框架结构为例,在有侧移框架中,二阶效应主要是指竖向荷载在产生了侧移的框架中引起的附加变形和相应的附加内力,通常称为P-Δ效应,在这类框架的各个柱段中,P-Δ效应将增大柱端控制截面的弯矩;在有侧移框架或无侧移框架中,各柱的轴向压力还将由于各柱本身的挠曲变形引起附加变形和相应的附加弯矩,通常称为P-δ效应.P-δ效应通常会增大杆件中间区段截面的弯矩,特别是当杆件较细长、杆件两端弯矩同号且两端弯矩的比值接近于1.0时,就可能出现杆件中间区段截面考虑P-δ效应后的弯矩超过杆端弯矩的情况,从而使杆件中间区段的截面成为设计的控制截面.除底层柱底外,P-δ效应一般不增大柱端控制截面的弯矩.当受压构件的长细比较大时,结构整体的侧移二阶效应(即有侧移结构的P-Δ效应)和受压构件的挠曲效应(即有侧移结构或无侧移结构中受压构件的P-δ效应)不容忽视,结构设计中必须考虑二阶效应引起的附加弯矩对受压构件正截面受压承载力的不利影响,否则将会影响结构的安全.严格地讲,考虑P-Δ效应和P-δ效应进行结构分析,应考虑材料的非线性和裂缝、构件的曲率和层间侧移、荷载的持续作用、混凝土的收缩和徐变等因素.但要实现这样的分析,在目前条件下还有困难,工程分析中一般都采用简化的方法.结构的侧移二阶效应的计算属于结构整体层面的问题,一般在结构整体分析中考虑,GB 50010-2010给出了两种计算方法:有限元法和增大系数法;受压构件的挠曲效应计算属于构件层面的问题,一般在构件截面设计时考虑.对于图2所示的两端铰支且两端偏心距相等的“标准偏压柱”,在初始偏心距为e0的轴向压力N图1 有侧移框架的二阶效应(P-Δ效应和P-δ效应)的作用下产生挠曲变形,柱高度中点处的挠度为f2,Ne0称为柱的一阶弯矩,轴向压力N在产生了挠曲变形的各个柱截面中还将引起附加弯矩(即二阶弯矩),同时柱挠度也将相应增大,柱高中点截面的附加弯矩为Nf2,总弯矩为N(e0+f2),其中f2为考虑二阶效应后的柱高中点挠度(f2=f1+δ),δ则为二阶效应引起的附加挠度.我国规范GB50010-2010及其他国外规范(如ACI 318M-08[3]和BS 8110:1997[4]等)将“标准偏压柱”柱高中点截面考虑二阶效应后的总弯矩与未考虑二阶效应的弯矩(也称为“一阶弯矩”)之比称为“偏心距增大系数”(或“弯矩增大系数”)ηns,即ηns=N e0+f()2Ne0=1+f2e0(1)图2 标准偏压柱中的一阶弯矩与二阶弯矩以及一阶挠度与二阶挠度 又例如一个从规则框架中截出的楼层(图3),假定只受节点竖向荷载N1-N4和水平集中力(楼层剪力)Vi作用,且各柱反弯点均位于柱高中点.如果不考虑各柱轴向压力对在本层剪力作用下产生了侧移的该楼层的附加影响,则该楼层各柱在水平力作用下的侧移仅为Δl,对应的第j根柱的柱端弯矩为Mhj.但因N1-N4对已经产生了侧移的楼层的附加弯矩作用,将使这一有侧移楼层产生进一步的侧移,最后,楼层侧移将等于Δl+Δk,其中Δk为二阶效应引起的附加位移,而第j根柱柱端也将形成附加弯矩ΔMhj,从而使柱端弯矩变为Mhj+ΔMhj.如果考虑了这种二阶效应后该层框架的层间侧移为Δi,也75武汉大学学报(工学版)第46卷就是图3中的Δl+Δk,则这种二阶效应相当于施加给该楼层的一个附加“倾覆力矩”!NjΔi,其中!Nj为上部各柱传来的竖向荷载之和.该倾覆力矩也可以转化为一个“楼层附加剪力”ΔVi,该“楼层附加剪力”ΔVi与倾覆力矩!NjΔi的关系可以写成:ΔViHi=∑NjΔiΔVi=∑NjΔiHi(2)式中,Hi为该楼层层高.这一楼层这时所受的总楼层剪力即为Vi+ΔVi.人们通常把各柱轴向压力在有侧移框架中引起的水平荷载弯矩增量称为P-Δ弯矩,并把具有这种特征的二阶效应称为P-Δ效应.从图3还可以看出,当忽略各跨梁的轴向变形时,该楼层各柱的侧移总是相等的,于是各柱的(Δ1+Δk)/Δl也总是相等的.这就意味着,在弹性假定下,当假定各柱反弯点在考虑二阶效应前、后的位置保持不变时,虽然各柱柱端水平荷载弯矩并不一定相等,但各柱柱端水平荷载弯矩都将随层间位移的增大而按比例增大,因而各柱的比值(Mhj+ΔMhj)/Mhj都将是相等的.于是同层各柱在图3所示受力条件下的偏心距增大系数(或弯矩增大系数)ηs都可用下式表达:ηs=Mhj+ΔMhjMhj=Δl+ΔkΔl(3) 这是有侧移框架二阶效应规律中的一个很重要的结论,也可称为有侧移框架水平荷载弯矩二阶效应的“层效应”,这一规律首先是从结构分析理论方面得到确认的.1981年美国的J.S.Ford、D.C.Chang和J.E.Breen通过精确量测受竖向及水平荷载弯矩作用的钢筋混凝土多跨框架的试验进一步确认了这一事实[5],从而成为国际学术界公认的规律.图3 规则框架中的一个楼层在节点竖向力及水平层剪力作用下的一阶挠度Δl与二阶挠度Δk以及第j根柱的一阶弯矩Mhj与二阶弯矩ΔMhj 除此之外,同层各柱与无侧移框架柱类似,也将因柱本身的挠曲变形而由各自的轴向压力引起附加弯矩.与上面所述的P-Δ效应相对应,人们通常把由柱的挠曲变形引起的二阶效应称为P-δ效应.从图3还可以看出,当楼层侧移增大时,各跨梁的挠曲变形也将相应增大,使梁所承受的水平荷载弯矩和剪力也相应增大.由此可见,二阶效应不仅仅是增大框架柱各个截面的弯矩和相应剪力,也将增大框架梁的内力.美国规范ACI 318M-08就特别指出,在有侧移框架中,受弯构件应按节点处各受压构件总的增大后的端弯矩进行设计.在实际结构中,竖向荷载中的相当一部分不是节点荷载(例如竖向荷载作用在框架梁上或以偏心荷载的形式作用在框架节点处或排架柱顶),而且在某层楼盖标高处,上、下柱轴线也可能存在偏心,这些都将在结构构件中形成一阶竖向荷载弯矩.与此同时,结构还受水平荷载作用,并在结构构件中形成一阶水平荷载弯矩.例如,在某一多层多跨框架中,由竖向荷载引起的弯矩示意图如图4(a)所示,由水平荷载(假定自左向右作用)引起的弯矩示意图如图4(b)所示.当水平荷载由右向左作用时,图4(b)中的弯矩图将左右对调.应该说明的是,无论水平荷载作用方向如何,都将有一侧框架柱的柱端竖向荷载弯矩与水平荷载弯矩为同号叠加,另一侧框架柱的柱端竖向荷载弯矩与水平荷载弯矩则为异号叠加.在弯矩同号叠加的柱中,该柱段的柱端弯矩将由以下几部分组成(图5(a)):Mv为竖向荷载一阶弯矩,ΔMvδ为P-δ85 增刊侯建国,等:新版混凝土结构设计规范二阶效应的设计规定简介效应导致的竖向荷载一阶弯矩的降低值;Mh为由水平荷载引起的一阶弯矩,ΔMh为未考虑P-δ效应影响时由P-Δ效应引起的柱端弯矩增量,ΔM*h为考虑了P-δ效应对P-Δ效应的影响后的柱端弯矩增量.由于此时竖向荷载弯矩与水平荷载弯矩导致的柱段挠曲线有一定的相似性,且挠曲方向原则上相同,因此,在由Mv-ΔMvδ+Mh+ΔM*h所组成的线性分布弯矩图的基础上,应再叠加由柱段总的挠曲变形导致的P-δ效应沿柱高范围内各截面中引起的附加弯矩(图5(a)中的虚线). 而在竖向荷载弯矩与水平荷载弯矩反号叠加时,柱端弯矩将为-Mv+ΔMvδ+Mh+ΔM*h(图5(b)).在此基础上,再根据两部分弯矩反向叠加后所余弯矩引起的杆件挠曲状态,进一步叠加在这种挠曲状态下由P-δ效应沿柱高范围内各截面中引起的附加弯矩(图5(b)中的虚线).图4 规则框架中的竖向荷载弯矩与水平荷载弯矩图5 竖向荷载弯矩与水平荷载弯矩的不同叠加关系 在工程设计中,一般都是取图5(a)所示情况下由竖向荷载弯矩及水平荷载弯矩叠加后形成的较大柱端总弯矩M和相应轴向压力N作为截面设计的依据,其中较大柱端总弯矩从理论上应取为M=Mv-ΔMvδ+Mh+ΔM*h(4) 若将ΔMvδ这项有利影响忽略不计,并取:ηs=Mh+ΔM*hMh(5)则式(4)可以写成:M=Mv+ηsMh(6)式中:ηs称为水平荷载偏心距增大系数(或水平荷载弯矩增大系数),中国规范GB 50010-2010称为P-Δ效应增大系数.如前文所述,它可根据“层效应”确定,也就是对同层各柱的ηs,原则上应是相同的.具体确定方法将在后面说明.式(6)给出的一个重要结论是,实际工程常用的有侧移结构中,偏心距增大系数只应增大水平荷载弯矩,而不会增大竖向荷载弯矩.还应指出的是,式(4)中的ΔMvδ是由竖向荷载下的P-δ效应引起的,在ΔM*h中又包括了水平荷载作用下柱轴向压力的P-δ效应对P-Δ效应的影响,而图5(a)和5(b)中虚线所示的附加弯矩则是在Mv和Mh共同作用下,由轴向压力在杆件最后形成的挠曲状态下引起的.于是,这里自然涉及到不同受力状95武汉大学学报(工学版)第46卷态下的P-δ效应影响是否能够线性叠加的问题.从理论上来说,在考虑几何非线性的前提下,叠加原理是不适用的;也就是从数量计算上说,ΔMvδ和ΔM*h是不能简单地在一个式子中进行叠加的,因而式(4)只适用于解释各类一阶弯矩与二阶弯矩之间的关系,而不适用于具体的计算.具体进行计算时,则可利用已不涉及叠加原理的简化后的式(6).2 忽略二阶效应影响的准则对于有侧移或无侧移结构的偏心受压杆件,若杆件的长细比较大时,在轴向压力作用下,由于杆件自身挠曲变形的影响,通常会增大杆件中间区段截面的弯矩,即产生P-δ效应.只要杆件发生单曲率弯曲且两端的弯矩值比较接近时,就可能出现杆件中间区段截面考虑P-δ效应后的弯矩值超过杆端弯矩值的情况,从而使杆件中间区段的截面成为设计的控制截面;或者即使杆件发生双曲率弯曲,但如果杆件中的轴压比较大,也有可能发生考虑附加弯矩后的杆件中间区段截面的弯矩值超过杆端弯矩值的情况.轴向压力在挠曲杆件中产生的二阶效应(P-δ效应)是偏压构件中由轴向压力在产生了挠曲变形的构件内引起的曲率和弯矩增量.在结构中常见的反弯点位于柱高中部的偏压构件中,这种二阶效应虽能增大构件除两端区域外各截面的曲率和弯矩,但增大后的弯矩通常不可能超过柱两端控制截面的弯矩.因此,在这种情况下,P-δ效应不会对构件截面的偏心受压承载力产生不利影响.但是,当反弯点不在构件高度范围内(即沿构件长度均为同号弯矩)的较细长且轴压比偏大的偏压构件中,经P-δ效应增大后的构件中部弯矩有可能超过柱端控制截面的弯矩.此时,在截面设计中就必须考虑P-δ效应的附加影响.因后一种情况在实际工程中较少出现,为了不对各个偏压构件逐一进行验算,GB 50010-2010根据国外相关文献资料、规范以及近期国内对不同杆端弯矩比、不同轴压比和不同长细比的杆件进行计算验证的结果,给出了可以忽略杆件自身挠曲产生的P-δ效应影响的条件为:弯矩作用平面内截面对称的偏心受压构件,当同一主轴方向的柱端弯矩比M1/M2不大于0.9且轴压比不大于0.9时,若杆件的长细比满足下式的要求时,则可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响,否则应按截面的两个主轴方向分别考虑轴向压力在挠曲杆件中产生的附加弯矩影响:l0/i≤34-12(M1/M2)(7)式中:M1、M2分别为已考虑侧移影响的偏心受压构件两端截面按结构弹性分析确定的对同一主轴的组合弯矩设计值,绝对值较大端为M2,绝对值较小端为M1,当构件按单曲率弯曲时,M1/M2为正,否则为负;l0为构件的计算长度,可近似取偏心受压构件相应主轴方向上下支撑点之间的距离;i为偏心方向构件的截面回转半径,i=I/槡A,这里I为偏心方向构件的截面惯性矩,A为构件的截面面积.3 二阶效应的计算方法偏心受压长柱的二阶效应是一个与结构整体受力密切相关的问题,应从结构整体受力特征出发选择合适的计算方法,不宜简单地理解为只涉及单根构件截面设计中弯矩需要增大的问题.对于偏心受压长柱二阶效应附加弯矩的计算,目前已形成了实用简化方法和计算机辅助分析方法等多种方法并存的局面[6-7].现有的二阶效应计算方法大体上可以分为以下4类:考虑二阶效应的杆系结构非线性有限元法;考虑二阶效应的弹性有限元法(亦称为“采用折减刚度的弹性有限元法”);计算有侧移结构的二阶效应的各种弹性简化方法(包括迭代P-Δ法、层增大系数法、结构整体增大系数法、负刚度杆件法和负面积杆件法等)[8];以及柱截面偏心距增大系数(或弯矩增大系数)的传统方法等.美国规范ACI 318M-08同时给出了上述4种方法供工程设计人员根据实际情况和需要选用;欧洲规范EN 1992:2004给出了基于非线性二阶分析的一般方法和基于名义刚度的简化方法及基于名义曲率的简化方法[9];英国规范BS 8110:1997只选用了柱截面弯矩增大系数的传统方法;中国规范GB50010-2010规定,混凝土结构由侧移产生的重力二阶效应可采用有限元分析方法进行计算,也可采用近似计算偏压构件侧移二阶效应的增大系数法(包括层增大系数法和结构整体增大系数法),即对未考虑P-Δ效应的一阶弹性分析所得的构件端弯矩以及层间位移乘以增大系数进行计算;而对于构件自身挠曲引起的二阶效应(P-δ效应)的计算,则允许采用柱截面偏心距增大系数(或弯矩增大系数)的传统方法.3.1 考虑二阶效应的杆系结构非线性有限元法此法以有限元法为基础,需同时考虑钢筋混凝土结构的材料非线性和几何非线性(二阶效应),计算得到的结构内力已包括一阶内力和二阶效应引起的附加内力在内,构件设计时可直接采用有限元分析结果进行配筋计算.06 增刊侯建国,等:新版混凝土结构设计规范二阶效应的设计规定简介国外有些规范(如ACI 318M-08和EN 1992:2004等)已把这种方法作为基本方法列入了规范,如美国规范ACI 318M-08在10.10.1条中指出,除了10.10.2条允许的以传统的弯矩增大系数法为基础的各种近似计算方法之外,受压构件、约束梁及其他支承构件的设计均应采用由考虑材料非线性和开裂,以及构件曲率和侧移影响的二阶分析所得到的内力设计值进行设计.ACI 318M-08还给出了应用此法的两个限制条件:1)所分析结构构件的截面尺寸与实际采用的构件截面尺寸的差异应在10%以内;2)要论证采用此法所预测的极限荷载与试验报道的极限荷载的误差在15%以内.为了考虑分析中采用的构件特性与实际构件特性的差异,分析中构件的截面刚度应乘以一个小于1的刚度降低系数φk,ACI 318M-08建议φk可取为0.80.此法应认为是一个理论上比较合理、计算结果比较精确的方法.但应用此法必须具有考虑二阶效应的非线性有限元分析软件,计算工作量较大,实际应用不很方便.3.2 考虑二阶效应的弹性有限元法考虑二阶效应(几何非线性)的弹性有限元法是一种计算精度较高、计算效率较好的结构分析方法,它能够自动跟踪整体弹性结构和结构各构件在不同受力状态下的变形,从而能较准确地反映弹性结构中的P-Δ效应以及各构件中的P-δ效应给结构内力和变形带来的影响.国内外的相关规范大都推荐了这一方法,如美国规范ACI 318M-08推荐的有侧移框架二阶效应的几种近似计算方法中,将此法作为首选的方法.这种方法基于弹性假定,不受材料非弹性本构模型选择的影响,但考虑结构的几何非线性,也就是考虑二阶效应的影响.由于所计算的二阶效应是结构即将破坏时的情况,因而应采用构件即将破坏时的截面性质,而不是它的初始弹性性质.要准确计算构件即将破坏时的截面性质是十分困难的.目前各国规范都是采用把构件刚度适当折减的方法,使之接近于破坏时的刚度.故这种方法又称为“采用折减刚度的弹性有限元法”.刚度折减的原则是采用折减刚度后计算所得的内力和变形与考虑二阶效应及材料非线性的非线性有限元法的计算结果相符,并与试验的结果相近.由于这种方法对每一类构件取用一个统一的构件弹性刚度折减系数,其分析结果的精度自然要比非线性有限元法的分析结果略差.但与采用柱偏心距增大系数(或弯矩增大系数)的传统方法及采用刚度折减系数的层增大系数法相比,这种方法仍具有明显优势,其优点主要表现在:1)直接由结构分析求得已经包括二阶效应附加内力的结构内力,在各类构件(包括偏心受压柱)的截面设计中不再需要采取考虑二阶效应的专门措施.2)能更准确地反映不同类型结构的二阶效应规律,适用于范围更广的各类结构考虑二阶效应的结构分析,特别是适用于已不再适宜采用η-l0法(即偏心距增大系数法或弯矩增大系数法)或不再适宜采用层增大系数法的复杂结构或特殊结构.在国外各大型结构分析软件包中都已包含有该方法所用的考虑二阶效应的弹性有限元分析程序.这些软件包已陆续进入中国市场.因此,从国外软件包获取这种商业软件或自行编制相应商业软件均无理论上或技术上的困难.3.3 计算有侧移结构的二阶效应的弹性简化方法这种方法是从结构力学领域提出的计算有侧移结构各层柱的P-Δ效应附加弯矩的简化方法,包括迭代P-Δ法、层增大系数法、结构整体增大系数法、负刚度杆件法和负面积杆件法等[8],其中尤以层增大系数法的应用最为普遍.以层增大系数法为例,它所做的简化表现在,认为可以取某个楼层各柱的水平荷载一阶弯矩加P-Δ效应附加弯矩(即Mhj+ΔMhj)与水平荷载一阶弯矩Mhj之比,等于该楼层考虑P-Δ效应后的层间位移(即Δl+Δk)与未考虑P-Δ效应前的一阶层间位移Δl之比(参见式(3)).虽然这一假定可能会给二阶效应附加弯矩的计算结果带来某些误差,但对于竖向规则性较好(即没有刚度突变的)的多高层建筑结构,其计算结果仍具有足够的精度.因上述层间位移Δ1和附加层间位移Δk都是在弹性假定下求得的,因此,当用于非线性特征明显的钢筋混凝土结构时,与上述考虑二阶效应的弹性有限元法类似,也同样需要对构件的弹性刚度进行折减.各类构件的刚度折减系数的取值原则与考虑二阶效应的弹性有限元法相同.下面将层增大系数法的基本原理作一简要介绍.如图6所示,假定多层多跨框架在各层水平集中力Vi作用下产生的未考虑二阶效应的层间弹性位移为Δi.利用前述“楼层附加剪力”ΔVi与附加倾覆力矩!NijΔi之间的关系,某层各柱轴向压力Nij在产生了层间位移Δi的情况下所引起的附加倾覆力矩!NijΔi可用一个附加水平力ΔVi=(!NijΔi)/Hi来代替.于是,就可以再求出每层受Vi+ΔVi作用下的框架的各层层间位移,并重新计算出ΔVi,如此迭16武汉大学学报(工学版)第46卷代下去,直到计算出的前后两次层间位移之差小到一定精度为止.这时,各层层增大系数即为最后一次迭代求得的层间位移Δ*i与未考虑P-Δ效应的层间位移Δi之比,即:ηs=Δ*i/Δi(8)图6 P-Δ迭代法和层增大系数法的框架实例 上述方法即称为P-Δ迭代法.如果把通过迭代逐步增大的层间位移用一个无穷级数来表示,则在弹性假定下可以得到ηs的下列表达式:ηsi=11-γi∑NijΔiViHi(9)式中:Nij为所计算楼层各柱的轴向压力;Δi为该楼层不考虑二阶效应的弹性层间位移;Vi为该层层间剪力,即该层以上各层楼盖处作用的水平集中力之和;Hi为该层层高,"i则为考虑P-δ效应对P-Δ效应增大作用的系数,其取值通常应通过更精确的分析方法确定.当在钢筋混凝土结构中采用这一方法时,应设法考虑结构构件的非弹性受力特征,否则将得出明显偏于不安全的计算结果.常用的做法是在计算结构的一阶层间位移Δi时,在结构分析中对各构件的抗弯刚度乘以用在“考虑二阶效应的弹性有限元法”中的折减系数,从而可以通过一阶层间位移Δi近似反映结构构件的材料非线性对二阶效应的影响.美国规范ACI 318M-08和中国规范GB 50010-2010在考虑框架结构侧移影响的P-Δ效应分析中均推荐了考虑刚度折减系数的层增大系数法.3.4 柱截面偏心距增大系数(或弯矩增大系数)的传统方法 在上述3种方法尚未提出之前,从20世纪40~50年代起,世界各国的混凝土结构设计规范偏心受压构件截面设计中,都先后采用了通过柱截面偏心距增大系数(或弯矩增大系数)来考虑二阶效应的附加弯矩的传统简化方法.随着对二阶效应附加内力分布和变化规律的逐步深入了解,这一方法也在不同国家的规范中得到不同程度的改进.到目前为止,虽然各国规范大都采用了这一方法,但各国规范采用的具体做法在反映二阶效应规律的准确性方面仍有一定差异.这一方法的基本思路是先给出标准偏压柱偏心距增大系数(或弯矩增大系数)ηns的表达式,用来反映具有不同截面特征、受不同的M、N作用、且具有不同长细比的标准偏压柱柱高中点截面被二阶效应增大了的弯矩与未考虑二阶效应的弯矩的比值的变化规律.这种表达式一般应有足够的试验结果作为依据.有些表达式还经过了计算机非线性模拟分析的检验.当对结构中某根柱的控制截面进行设计时,则以与这一截面具有相同截面特征、受相同M、N作用的标准偏压柱作为其“等代柱”,然后通过为这根“等代柱”选择合适的柱长,也就是我国规范所规定的计算长度(国外规范称为等效长度)l0,使由该等代标准偏压柱的偏心距增大系数(或弯矩增大系数)ηns求得的该柱柱高中点截面的N(e0+δ)/Ne0值,能近似地反映所设计的柱截面在结构实际受力状态下的相应值.也就是说,在给出了偏心距增大系数(或弯矩增大系数)ηns的合理表达式之后,能否用它正确表达实际结构柱截面中的二阶效应的规律,关键在于所选择的计算长度(或等效长度)能不能正确反映结构中复杂的二阶效应规律.所以,“标准偏压柱”的计算长度(或等效长度)就成为这种方法中联系等代标准偏压柱与所设计的实际结构中的偏压柱的关键纽带.由此可见,要使采用柱截面偏心距增大系数(或弯矩增大系数)ηns的传统方法得到比较准确的二阶效应的计算结果,确定计算长度l0的合理取值是其关键所在.因此,国内外相关文献也把这种传统的计算二阶效应的简化方法简称为η-l0法.这个方法首先把一个结构中长度为l的受压构件折算为长度为l0的两端铰支的标准偏压柱,柱的计算长度可表示为l0=kl(10)式中:l为柱的实际长度;k为等效长度系数,即柱的计算长度与实际长度的比值.确定计算长度l0的原则就是使实际柱的挠度曲线与两端铰支的标准偏压柱的挠度曲线相当.如图7所示,两端固定无侧移柱的计算长度是实际长度的0.5倍,即k=0.5;两端铰支无侧移柱的计算长度是实际长度的1倍,即等于实际长度,此时k=1.其他情况下计算长度与实际长度的关系,即k值都可以按这个原则得到,目前大多基于弹性稳定理论来推算.26。
混凝土结构的二阶效应

一、混凝土结构的二阶效应混凝土结构的二阶效应应由两部分组成:p-δ效应和P-Δ效应。
p-δ效应是指由于构件在轴向压力作用下,自身发生挠曲引起的附加效应,可称之为构件挠曲二阶效应,通常指轴向压力在产生了挠曲变形的构件中引起的附加弯矩,附加弯矩与构件的挠曲形态有关,一般中间大,两端部小。
P-Δ效应是指由于结构的水平变形而引起的重力附加效应,可称之为重力二阶效应,结构在水平力(风荷载或水平地震力)作用下发生水平变形后,重力荷载因该水平变形而引起附加效应,结构发生的水平侧移绝对值越大,P-Δ效应越显著,若结构的水平变形过大,可能因重力二阶效应而导致结构失稳。
1.重力二阶效应(P-Δ效应)计算计算P-Δ效应的近似方法有等效几何刚度的有限元法、等效水平力的有限元迭代法、折减弹性抗弯刚度的有限元、结构位移和构件内力增大系数法等。
1)等效几何刚度的有限元法在不考虑P-Δ效应影响时,是在结构的初始拓扑关系基础上建立结构的平衡方程。
一般可记为:[K]{u}=[F]考虑P-Δ效应影响时,对于结构的任一节点j,因P-Δ效应而引起的Mj=Gjuj,相应的等效附加水平力为Vj= 。
对于所有节点,则形成一个等效附加水平分力向量。
可以看出,考虑P-Δ效应相当于结构的初始刚度矩阵[K]修改为等效刚度矩阵[K-KG]。
新规范版的SATWE、TAT、PMSAP等软件都采用了等效几何刚度的有限元法,这种方法具有一般性,它既适用于采用刚性楼板假定的结构,也适用于存在独立弹性节点的结构。
与不考虑P-Δ效应的分析结果相比,结构的周期、位移和构件的内力都有所不同。
2)折减弹性抗弯刚度的有限元法折减弹性抗弯刚度的有限元法是今年来美国、加拿大等国设计规范推荐的一种考虑效益方法。
这种分析方法的基本思路是采用折减等效刚度,近似的考虑钢筋混凝土结构中各类构件在极限状态时因开裂而导致刚度减小现象,使分析结果与设计状态尽可能一致。
《混凝土结构设计规范》引进该方法,第7.3.12规定,当采用考虑二阶效应的弹性分析方法时,宜在结构分析中对钢筋混凝土构件的弹性抗弯刚度乘以一下折减系数:梁取0.4,柱取0.6,对未开裂的剪力墙和核心筒取0.7,对已开裂的剪力墙和核心筒壁取0.45。
版图二阶效应

版图二阶效应二阶效应可以分为重力二阶效应(p−Δ)和构件挠曲二阶效应(p−δ),下面我们分别从这两者来探讨在混凝土结构设计中如何考虑二阶效应的影响:1.重力二阶效应当结构重力产生的附加弯矩大于初始弯矩的10%时需要考虑重力二阶效应,现行结构设计规范利用增大系数法(GB50010附录B、JGJ3-2010.5.4.3条和GB50010.3.6.3条文说明)考虑重力二阶效应的影响:M=Mns+ηsMs其中Ms为引起结构侧移的荷载所产生的一阶弹性分析构件端弯矩设计值(如水平地震作用);Mns为不引起结构侧移的一阶弹性分析构件端弯矩设计值(如对称结构在均布重力荷载作用下)。
上式使用了叠加原理的概念,即设计弯矩可以拆分为产生侧移荷载产生的弯矩和不产生侧移的荷载的弯矩之和,而重力二阶效应仅增加产生层间侧移的部分。
变形增量也同样使用增大系数法考虑:Δ=ηsΔ1上述的Δ为一阶弹性分析的层间位移,ηs为增大系数。
增大系数以框架结构举例:ηs=11−∑inGjDH0上式中D为侧移刚度;H0为计算楼层的层高;∑inGj为第i层以上全部重力荷载设计值之和。
对上式分母第二项略作化简可以得到:∑inGjΔuiViH0其中Δui层平均层间侧移;Vi为楼层剪力;可以发现,上式即为“重力附加弯矩与初始弯矩的比值”(具体定义参见何时需要考虑二阶效应?),由此可以发现,增大系数的表达式含义其实十分“朴素”,简单来说就是:考虑重力二阶效应弯矩值一阶弹性分析的弯矩值ηs=考虑重力二阶效应弯矩值一阶弹性分析的弯矩值关于增大系数的计算有下面两点值得注意:计算位移增大系数时,不对构件的刚度进行折减(JGJ3-2010.5.4.3条,GB50010.B.0.5)。
因为设计规范中给出的限值均为弹性位移限制,弹性位移限值需要和弹性位移计算结果所匹配。
计算内力增大系数时,对构件刚度进行折减,《高规》折减系数取0.5,《混规》则对不同构件选取不同的折减系数,见B.0.5条。
二阶效应规范规定
◆说明:轴向压力在挠曲杆件中产生的二阶效应(效应)
是偏压杆件中由轴向压力在产生了挠曲变形的杆件内引起 的曲率和弯矩增量。例如结构中常见的反弯点位于柱高中 部的偏压构件中,这种二阶效应虽能增大构件除两端区域 外各截面的曲率和弯矩,但增大后的弯矩通常不可能超过 柱两端控制截面的弯矩。因此,在这种情况下,效应不会 对杆件截面的偏心受压承载能力产生不利影响。但是,在 反弯点不在杆件高度范围内(即沿杆件长度均为同号弯矩) 的较细长且轴压比偏大的偏压构件中,经效应增大后的杆 件中部弯矩有可能超过柱端控制截面的弯矩。此时,就必 须在截面设计中考虑效应的附加影响。因后一种情况在工 程中较少出现,为了不对各个偏压构件逐一进行验算,本
lc / i 34 -12( M1 / M 2 )
M1、M2—分别为偏心受压构件两端截面按结构分析确定的对同 一主轴的组合弯矩设计值,绝对值较大端为,绝对值较 小端为,当构件按单曲率弯曲时,取正值,否则取负值
l c—构件的计算长度,可近似取偏心受压构件相应
主轴方向上下支撑点之间的距离;
i—偏心方向的截面回转半径。
条给出了可以不考虑效应的条件。
● 6.2.4条:考虑轴向压力在挠曲杆件中产生的二阶效应后 控制截面弯矩设计值应按下列公式计算:
M CmnsM 2
Cm
0.7
0.3
M1 M2
ns
1
1300(M 2
1 /N
ea
)
/
h0
lc h
2
c
c
0.5 fc A N
Cm—构件端截面偏心距调节系数,当小于0.7时取0.7; hns—弯矩增大系数; N —与弯矩设计值M2相应的轴向压力设计值;
混凝土结构的二阶效应

一、混凝土结构的二阶效应混凝土结构的二阶效应应由两部分组成:p-δ效应和P-Δ效应。
p-δ效应是指由于构件在轴向压力作用下,自身发生挠曲引起的附加效应,可称之为构件挠曲二阶效应,通常指轴向压力在产生了挠曲变形的构件中引起的附加弯矩,附加弯矩与构件的挠曲形态有关,一般中间大,两端部小。
P-Δ效应是指由于结构的水平变形而引起的重力附加效应,可称之为重力二阶效应,结构在水平力(风荷载或水平地震力)作用下发生水平变形后,重力荷载因该水平变形而引起附加效应,结构发生的水平侧移绝对值越大,P-Δ效应越显著,若结构的水平变形过大,可能因重力二阶效应而导致结构失稳。
1.重力二阶效应(P-Δ效应)计算计算P-Δ效应的近似方法有等效几何刚度的有限元法、等效水平力的有限元迭代法、折减弹性抗弯刚度的有限元、结构位移和构件内力增大系数法等。
1)等效几何刚度的有限元法在不考虑P-Δ效应影响时,是在结构的初始拓扑关系基础上建立结构的平衡方程。
一般可记为:[K]{u}=[F]考虑P-Δ效应影响时,对于结构的任一节点j,因P-Δ效应而引起的Mj=Gjuj,相应的等效附加水平力为Vj=。
对于所有节点,则形成一个等效附加水平分力向量。
可以看出,考虑P-Δ效应相当于结构的初始刚度矩阵[K]修改为等效刚度矩阵[K-KG]。
新规范版的SATWE、TAT、PMSAP等软件都采用了等效几何刚度的有限元法,这种方法具有一般性,它既适用于采用刚性楼板假定的结构,也适用于存在独立弹性节点的结构。
与不考虑P-Δ效应的分析结果相比,结构的周期、位移和构件的内力都有所不同。
2)折减弹性抗弯刚度的有限元法折减弹性抗弯刚度的有限元法是今年来美国、加拿大等国设计规范推荐的一种考虑效益方法。
这种分析方法的基本思路是采用折减等效刚度,近似的考虑钢筋混凝土结构中各类构件在极限状态时因开裂而导致刚度减小现象,使分析结果与设计状态尽可能一致。
《混凝土结构设计规范》引进该方法,第7.3.12规定,当采用考虑二阶效应的弹性分析方法时,宜在结构分析中对钢筋混凝土构件的弹性抗弯刚度乘以一下折减系数:梁取0.4,柱取0.6,对未开裂的剪力墙和核心筒取0.7,对已开裂的剪力墙和核心筒壁取0.45。
二阶效应在各个规范中的理解与区别

二阶效应在各个规范中的理解与区别第一篇:二阶效应在各个规范中的理解与区别关于“二阶效应”的总结【《砼规》,《抗规》,《高规》】“二阶效应”分为“重力二阶效应P-Δ”和“挠曲二阶效应P-δ”重力二阶效应P-Δ:在地震等水平力作用下结构侧移时重力作用产生的附加内力挠曲二阶效应P-δ:偏心受压构件(主要是长细比大于17.5柱)由于自身挠曲产生的附加内力★《砼规》中的规定:《砼规》7.3.9条给出两种考虑“二阶效应”的方法:1)《砼规》7.3.10条的偏心距增大系数法存在问题:此法只针对于混凝土偏心受压构件(主要是柱),而且不论是否时地震工况,对于长细比大于17.5的偏心受压构件均应考虑。
虽然条文说明中认为此法可以同时考虑上述两种二阶效应,但从其增大系数的计算公式可知,此增大系数对挠曲二阶效应反映得较为充分,对重力二阶效应反映的则不够充分,或者不够准确,因为偏心距增大系数计算公式与结构的侧移量大小没有关系。
2)《砼规》7.3.12条的折减构件弹性抗弯刚度法(仿照美国规范) 存在问题:《砼规》认为此法是“一种精度和效率较高得”考虑二阶效应的方法,是“一种理论上严密的”方法。
但是刚度得折减系数得取值很难精确,在不同荷载组合下,不同得构件得开裂程度都不一样。
取统一折减系数得方法,只能大概反映二阶效应的影响。
而且在程序实现时也会有新得问题,比如刚度减小,导致地震力减小,位移算是弹性还是塑性位移等等。
★《抗规》中的规定:《抗规》3.6.3条及条文说明规定,结构在地震作用下的重力附加弯矩大于初始弯矩的10%时,应考虑重力二阶效应的影响。
考虑方法是简化的内力增大系数1/(1-θ),θ是稳定系数,即附加弯矩占初始弯矩的倍数。
同时规定,对于混凝土柱,本条与《砼规》7.3.10不同时考虑。
★《高规》中的规定:《高规》5.4.1~5.4.3条规定,在水平力作用下,不满足5.4.1条刚重比的高层建筑,需要考虑水平力作用下重力二阶效应对结构内力和位移的影响。
高层设计中的二阶效应

P-δ与P-Δ效应及各国计算方法比较摘要:二阶效应是指轴向力作用在产生挠曲的构件上或竖向荷载作用在产生侧移的结构上引起的附加作用效应,属于结构分析设计中的几何非线性问题,在较精确的结构分析设计中必须加以考虑。
对这一问题国内外已进行了多年的系统研究,取得了重要进展。
本文就二阶效应的两种情况进行讨论分析并给出具体的例子。
关键词:混凝土,二阶效应,弯矩,结构1 混凝土结构的二阶效应概念结构物受力后将产生内力和变形,内力和变形是相互伴生和对应的两类物理量。
按现代控制论的观点,结构自身是一个非线性系统,结构所受荷载Fex是系统的激励,产生的内力Fin和变形D是结构在外部激励下的输出响应。
结构静力学中一般将内力作为状态变量,荷载作为输入变量,变形作为输出变量,而联系输入变量和状态变量的状态方程就是平衡方程,见式(1.1)(1.1)输出方程是联系内力和变形的物理方程,见式(1.2)(1.2)为了简化分析,结构静力学在建立平衡方程时往往忽略结构的微小变形,以结构变形前的状态作为平衡态,由此建立的平衡方程是一组线性方程,这种分析思路实际是将非线性系统简化为线性系统。
一般情况,结构的变形相对于结构自身的尺寸来说都很小,因此将结构简化为线性系统给结构分析带来的误差可以接受,这种结构分析处理方式称为结构的一阶分析,一阶分析得到的结构内力和变形分别称为结构的一阶内力和一阶变形。
系统状态变量的选取是相对的,若将结构的变形作为状态变量,也可以得到结构的状态方程,见式(1.3)(1.3)通过物理方程((1.2)可以得到两种状态方程的关系(1.4)状态方程(1.1)与(1.3)是对结构等效的描述,结构内力和变形是相互对等的变量。
状态方程(1.3)表明荷载与结构变形也是直接联系的,而结构一阶分析的简化处理忽略了这种直接联系,只是将结构变形作为结构内力的效应,这种简化处理存在概念性的误区,在某些情况下还会给结构分析带来较大的误差。
例如图1.1中柱顶铰接悬臂柱,柱端作用有轴向力和弯矩。
重力二阶效应201208

二阶效应
一、定义:
二阶效应由两部分组成:p-δ效应和P-Δ效应。
1.P-δ效应是指由于构件在轴向压力作用下,自身发生挠曲引起的附加效应,可称之为构件挠曲二阶效应,通常指轴向压力在产生了挠曲变形的构件中引起的附加弯矩,附加弯矩与构件的挠曲形态有关,一般中间大,两端部小。
2.P-Δ效应是指由于结构的水平变形而引起的重力附加效应,可称之为重力二阶效应,结构在水平力(风荷载或水平地震力)作用下发生水平变形后,重力荷载因该水平变形而引起附加效应,结构发生的水平侧移绝对值越大,P-Δ效应越显著,若结构的水平变形过大,可能因重力二阶效应而导致结构失稳。
控制P-Δ效应的方法:
(1)结构抗侧刚度不能太小:
a.弹性层间位移角限值;《抗规》5.5.1条及3.6.3条文说明
b.钢结构柱长细比的规定。
《抗规》8.3.1条
(2)刚重比上下限值;《高规》5.4.1条
三、规范对其实现方法
,2,
,n )
条(重力二阶效应下限值)
2
1
n
i i G =∑
,2,,n )
0M
,2,,n)(
,2,,n)(
剪力墙结构、框架-剪力墙结构、筒体结构:《高规》
5.4.3-3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下支撑点之间的距离;
i——偏心方向构件的截面回转半径。
3 二阶效应的计算方法
现有的二阶效应计算方法大体上可以分为以下四类: ➢考虑二阶效应的杆系结构非线性有限元法; ➢考虑二阶效应的弹性有限元法(亦称为“采用折减刚度的 弹性有限元法”); ➢计算有侧移结构的二阶效应的各种弹性简化方法(包括迭 代P-法、层增大系数法、结构整体增大系数法、负刚度杆 件法和负面积杆件法等); ➢柱截面偏心距增大系数(或弯矩增大系数)的传统方法等。
1 二阶效应的有关概念
在工程设计中,一般都是取图5a所示情况下由竖向荷载 弯矩及水平荷载弯矩叠加后形成的较大柱端总弯矩M和相应轴 向压力N作为截面设计的依据,其中较大柱端总弯矩从理论上 应取为:
M=Mv-Mv+Mh+ Mh*
(4)
若将Mv这项有利影响忽略不计,并取:
s
Mh
M
h
Mh
(5)
1 二阶效应的有关概念
1 二阶效应的有关概念
从理论上来说,在考虑几何非线性的前提下,叠加原理是 不适用的;也就是从数量计算上说,Mv和Mh*是不能简单 地在一个式子中进行叠加的,因而式(4)只适用于解释各类 一阶弯矩与二阶弯矩之间的关系,而不适用于具体的计算。具 体进行计算时,则可利用已不涉及叠加原理的简化后的式(6)。
则式(4)可以写成:
M = Mv+ s Mh
(6)
式中,s称为水平荷载偏心距增大系数(或水平荷载弯矩增
大系数),中国规范GB 50010-2010称为P-效应增大系数。
s可根据“层效应”确定,也就是对同层各柱的s,原
则上应是相同的。
实际工程常用的有侧移结构中,偏心距增大系数只应增大 水平荷载弯矩,而不会增大竖向荷载弯矩。
1 二阶效应的有关概念
结构的二阶效应泛指作用在结构上的重力或构件中的 轴向压力在产生了层间位移和挠曲变形后的结构或构件中 引起的附加变形和相应的附加内力,包括结构整体的侧移 二阶效应(P -△效应)和受压构件的挠曲效应(P -δ效应) 两部分。
1 二阶效应的有关概念
以框架结构为例,在有侧移框架中,二阶效应主要是 指竖向荷载在产生了侧移的框架中引起的附加变形和相应 的附加内力,通常称为P -△效应,在这类框架的各个柱段中, P -△效应将增大柱端控制截面的弯矩。
ns
N
e0
Ne0
f2
1
f2 e0
(1)
1 二阶效应的有关概念
有侧移框架水平荷载弯矩二阶效应的“层效应”的偏心距 增大系数(或弯矩增大系数)ηs都可用下式表达:
s
M hj M hj M hj
1 k 1
(3)
Hale Waihona Puke 这是有侧移框架二阶效应规律中的一个很重要的结论, 也可称为有侧移框架水平荷载弯矩二阶效应的“层效应” 。
图2 标准偏压柱中的一阶弯矩与二 阶弯矩以及一阶挠度与二阶挠度
1 二阶效应的有关概念
我国规范GB 50010-2010及其他国外规范(如ACI 318M-08 和BS 8110:1997等)将“标准偏压柱”柱高中点截面考虑二阶 效应后的总弯矩与未考虑二阶效应的弯矩(也称为“一阶弯
矩”)之比称为“偏心距增大系数”(或“弯矩增大系数”) ηns,即
讲授内容
1 二阶效应的有关概念 2 忽略二阶效应影响的准则 3 二阶效应的计算方法 4 GB 50010-2010二阶效应的设计规定 5 结语
前言
我国新修订的国家标准GB 50010-2010《混凝土结构设 计规范》关于偏心受压构件的二阶效应的设计规定,较原规 范GB 50010-2002《混凝土结构设计规范》作了重大修改, 本文就GB 50010-2010关于偏心受压构件二阶效应的设计规 定的修订情况作一简要介绍。
图1 有侧移框架的二阶效应
1 二阶效应的有关概念
在有侧移框架或无侧移框架中,各柱的轴向压力还将 由于各柱本身的挠曲变形引起附加变形和相应的附加弯矩,
通常称为P- 效应。
图1 有侧移框架的二阶效应
1 二阶效应的有关概念
P- 效应通常会增大杆件中间区段截面的弯矩,特别
是当杆件较细长、杆件两端弯矩同号且两端弯矩的比值接
受压构件的挠曲效应计算属于构件层面的问题,一般 在构件截面设计时考虑。
1 二阶效应的有关概念
一阶弯矩:Ne0 (e0为初始偏心距) 二阶弯矩 :轴向压力N在产生了挠曲
变形的各个柱截面中引起 的附加弯矩。
图2 标准偏压柱
1 二阶效应的有关概念
柱高中点截面的附加弯矩为N f2,总弯矩为N(e0+ f2), 其中f2为考虑二阶效应后的柱高中点挠度( f2 =f1 ),δ 则为二阶效应引起的附加挠度。
近于1.0时,就可能出现杆件中间区段截面考虑P- 效应后
的弯矩超过杆端弯矩的情况,从而使杆件中间区段的截面 成为设计的控制截面。
除底层柱底外,P- 效应一般不增大柱端控制截面的
弯矩。
1 二阶效应的有关概念
结构的侧移二阶效应的计算属于结构整体层面的问 题,一般在结构整体分析中考虑,GB 50010-2010给出了 两种计算方法:有限元法和增大系数法;
3 二阶效应的计算方法
美国规范ACI 318M-08同时给出了上述四种方法供工程 设计人员根据实际情况和需要选用;美国规范ACI 318M-08推 荐的有侧移框架二阶效应的几种近似计算方法中,将考虑二 阶效应的弹性有限元法作为首选的方法。
2 忽略二阶效应影响的准则
GB 50010-2010根据国外相关文献资料、规范以及近期国 内对不同杆端弯矩比、不同轴压比和不同长细比的杆件进行计 算验证的结果,给出了可以忽略杆件自身挠曲产生的P −δ 效应 影响的条件为:
2 忽略二阶效应影响的准则
弯矩作用平面内截面对称的偏心受压构件,当同一主轴方 向的柱端弯矩比M1/ M2不大于0.9且轴压比不大于0.9时,若杆 件的长细比满足式(7)的要求时,则可不考虑轴向压力在该 方向挠曲杆件中产生的附加弯矩影响,否则应按截面的两个主 轴方向分别考虑轴向压力在挠曲杆件中产生的附加弯矩影响:
l0 / i ≤ 34-12(M1/ M2)
(7)
2 忽略二阶效应影响的准则
l0 / i ≤ 34-12(M1/ M2)
(7)
式中:
M1、 M2——分别为已考虑侧移影响的偏心受压构件两端截面 按结构弹性分析确定的对同一主轴的组合弯矩设计 值,绝对值较大端为M2 ,绝对值较小端为M1 ,当 构件按单曲率弯曲时, M1/ M2为正,否则为负;
