函数与导数中任意性和存在性问题探究
利用导数研究存在性与任意性

利用导数研究存在性及任意性1.对,都有令,则; ,都有;,都有;.2.,使得,则;,使得;,都有;.3.,,使得;,,使得;,,使得且.21.(12分)已知函数2()(2),1x f x x e ax bx x =-++=是()f x 的一个极值点.(1)若1x =是()f x 的唯一极值点,求实数a 的取值范围;(2)讨论()f x 的单调性;(3)若存在正数0x ,使得0()f x a <,求实数a 的取值范围.21.(1)()(1)2x f x x e ax b '=-++,1x =是极值点()0f x '∴= ,故20a b +=, 2b a =- ()(1)(2)x f x x e a '=-+1x =是唯一的极值点20x e a ∴+≥恒成立或20x e a +≤恒成立由20x e a +≥恒成立得2x a e ≥-,又0x e > 0a ∴≥由20x e a +≤恒成立得2x a e ≤-,而x e -不存在最小值, 20x e a ∴+≤不可能恒成立.0a ∴≥ ………………4分(2)由(1)知,当0a ≥时,1x < , ()0f x '< ; 1x > , ()0f x '>.()f x ∴在(,1)-∞递减,在(1,)+∞上递增.当02ea -<<时,ln(2)1a -< ln(2)x a <-,()0f x '>; ln(2)1a x -<< , ()0f x '<; 1x >, ()0f x '>. ()f x ∴在(,ln(2))a -∞-、(1,)+∞上递增,在(ln(2),1)a -上递减。
当2ea <-时,()f x 在(,1)-∞、 (ln(2),)a -+∞上递增,在(ln(2),1)a -递减。
(完整版)函数导数任意存在”-型问题归纳总结,推荐文档

战略思想三: x R ,都有" f (x1) f (x) f (x2 )" f (x1), f (x2 ) 分别是 f (x) 的最小值和最大值, | x1 x2 | min 是同时出现最大值和最小值的最短区间.
y x1
x2 x
例 3.
已知函数
f
(x) 2sin( x 2
) ,若对 5
" f ( x1 x2 ) f (x1) f (x2 ) "恒成立的函数的个数是( )
2
2
A.0 B.1 C.2 D.3
解:本题实质就是考察函数的凸凹性,即满足条件" f ( x1 x2 ) f (x1) f (x2 ) "的函数,应是凸函
2
2
数的性质,画草图即知 y log2 2x 符合题意;
即 f (x) 在[1,1]上为增函数.
∵ f (1) 1,∴ x [1,1] ,恒有 f (x) 1; ∴要使 f (x) t2 2at 1 对所有 x [1,1] , a [1,1] 恒成立,
即要 t2 2at 1 1恒成立,故 t2 2at 0 恒成立,
令 g(a) 2at t2 ,只须 g(1) 0 且 g(1) 0 ,
x R ,都有"
f
(x1)
f (x)
f
(x2 )" 成立,则
| x1 x2 | 的最小值为____.
解 ∵对任意 x∈R,不等式 f (x1) f (x) f (x2 ) 恒成立,
∴ f (x1), f (x2 ) 分别是 f (x) 的最小值和最大值.
对于函数 y sin x ,取得最大值和最小值的两点之间最小距离是 π,即半个周期.
解得 t 2 或 t 0 或 t 2 .
函数与导数中任意性和存在性问题探究
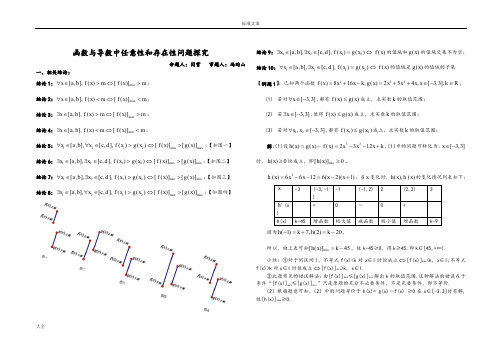
函数与导数中任意性和存在性问题探究命题人:闫霄 审题人:冯昀山一、相关结论:结论1:min [,],()[()]x a b f x m f x m ∀∈>⇔>; 结论2:max [,],()[()]x a b f x m f x m ∀∈<⇔<; 结论3:max [,],()[()]x a b f x m f x m ∃∈>⇔>; 结论4:min [,],()[()]x a b f x m f x m ∃∈<⇔<;结论5:1212min max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∀∈>⇔>;【如图一】 结论6:1212max min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∃∈>⇔>;【如图二】 结论7:1212min min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∃∈>⇔>;【如图三】 结论8:1212max max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∀∈>⇔>;【如图四】结论9:1212[,],[,],()()()x a b x c d f x g x f x ∃∈∃∈=⇔的值域和()g x 的值域交集不为空;结论10:1212[,],[,],()()()x a b x c d f x g x f x ∀∈∃∈=⇔的值域是()g x 的值域的子集【例题1】:已知两个函数232()816,()254,[3,3],f x x x k g x x x x x k R =+-=++∈-∈;(1) 若对[3,3]x ∀∈-,都有()()f x g x ≤成立,求实数k 的取值范围; (2) 若[3,3]x ∃∈-,使得()()f x g x ≤成立,求实数k 的取值范围; (3) 若对12,[3,3]x x ∀∈-,都有12()()f x g x ≤成立,求实数k 的取值范围;解:(1)设32()()()2312h x g x f x x x x k =-=--+,(1)中的问题可转化为:[3,3]x ∈-时,()0h x ≥恒成立,即min [()]0h x ≥。
函数导数任意存在”-型问题归纳总结

令 g(x)x 2 2x x ln xx [1,e] , 又 g (x)(x 1)(x 2 2ln x)(x ln x)2函数导数任意性和存在性问题探究导学语函数导数问题是高考试题中占比重最大的题型,前期所学利用导数解决函数图像切线、函数单调性、 函数极值最值等问题的方法, 仅可称之为解决这类问题的“战术” ,若要更有效地彻底解决此类问题还必须研究“战略,”因为此类问题是函数导数结合全称命题和特称命题形成的综合性题目 .常用战略思想如下:题型分类解析一.单一函数单一“任意”型f(x)上限战略思想一: “ x A , a ( )f ( x)恒成立”等价于“当x A 时, a ( ) f (x)max ;”f(x)下限“ x A , a ( ) f (x) 恒成立”等价于“当x A 时, a ( )f ( x) min ”.例 1 :已知二次函数 f (x) ax 2 x ,若 x [0,1] 时,恒有 | f (x)| 1,求实数 a 的取值范围 解: | f (x)| 1 ,∴ 1 ax 2 x 1;即 1 x ax 2 1 x ; 当 x 0 时,不等式显然成立,∴ a ∈R.21 1 1 1 当 0 x 1 时,由 1 x ax 21 x 得:2 a 2 , x x x x11 又∵(2 )max2 ,∴a 2, 2 a 0 ,xx综上得 a 的范围是 a [ 2,0] . .单一函数单一“存在”型x A ,使得 a ( ) f ( x)成立”等价于“当x A 时, a ( )f ( x) max取值范围解析:f (x) (a 2)x a(x ln x) x 2 2x . ∵x [1,e] ,∴ln x 1 x 且等号不能同时取,所以 ln x x ,即 x ln x 0 , x 2 2x因而 a x [1,e] ,x ln x ,而(x 12 1x )min 0,∴a 0.xx战略思想x A ,使得 a ( ) f (x) 成立”等价于“当x A 时,a ( ) f(x)min ”;f ( x)上限f ( x)下限例 2. 已知函数 f (x) aln x x 2(a R ),若存在 x [1,e] ,使得f (x) (a 2)x 成立,求实数 a 的当x [1, e]时,x 1 0,ln x 1,x 2 2ln x 0,从而g (x) 0 (仅当x=1 时取等号),所以g(x)在[1, e]上为增函数,故g(x) 的最小值为g(1) 1,所以 a 的取值范围是[ 1, ) .三.单一函数双“任意”型战略思想三:x R,都有" f(x1) f (x) f(x2)" f(x1), f (x2) 分别是f (x) 的最小值和最大值,|x1 x2 | min 是同时出现最大值和最小值的最短区间.例 3. 已知函数f (x) 2sin( x ) ,若对x R,都有" f (x1) f (x) f (x2)" 成立,则| x1 x2 |25的最小值为 __ .解∵对任意x∈R ,不等式f (x1) f (x) f (x2) 恒成立,∴f (x1), f (x2)分别是f (x) 的最小值和最大值对于函数y sin x ,取得最大值和最小值的两点之间最小距离是π,即半个周期x又函数f (x) 2sin( 2 5 )的周期为4,∴| x1 x2 |的最小值为 2.战略思想四:x1,x2 A, " f (x1 x2)f (x1) f (x2)"成立22f (x) 在 A 上是上凸函数 f ''(x) 02例 4. 在y 2x,y log2 2x,y x ,y cosx 这四个函数中,当0 x1 x2 1时,使" f (x1 x2)f(x1) f ( x2 )"恒成立的函数的个数是( )22A.0B.1C.2D.3解:本题实质就是考察函数的凸凹性,即满足条件" f(x1 x2)f (x1) f (x2)" 的函数,应是凸函22数的性质,画草图即知y log2 2x 符合题意;战略思想五:x1,x2 A,"f (x1) f (x2)0"成立f(x)在 A 上是增函数x1 x2例 5 已知函数f (x) 定义域为[ 1,1],f (1) 1,若m,n [ 1,1],m n 0时,都有f(m) f(n) 0" ,若f(x) t2 2at 1对所有x [ 1,1],a [ 1,1]恒成立,求实数t取值范围. mn解:任取1 x1 x2 1,则f (x1) f (x2) f (x1) f (x2) (x1 x2),x1 x2由已知 f (x1) f (x2) 0,又x1 x2 0,∴f (x1) f (x2) 0,x1 x2即f (x) 在[ 1,1]上为增函数.∵f (1) 1,∴x [ 1,1],恒有f (x) 1;2∴要使f (x) t2 2at 1对所有x [ 1,1],a [ 1,1]恒成立,即要t2 2at 1 1恒成立,故t2 2at 0 恒成立,2令g(a) 2at t2,只须g( 1) 0且g(1) 0,解得t 2或t 0或t 2.战略思想六:x1,x2 A,| f (x1) f (x2)| t ( t为常数)成立t= f (x)max f (x)min4 3 1例 6. 已知函数f (x) x4 2x3,则对任意t1,t2 [ ,2](t1 t2)都有| f(t1) f (t2)| 恒2成立,当且仅当t1 = __ ,t2 = ___ 时取等号.解:因为| f (x1) f (x2)| |[ f ( x)] max [ f ( x)] min |恒成立,4 3 1由f(x) x4 2x3,x [ ,2] ,23 27 1 5易求得[ f (x)]max f (3) 27,[ f (x)]min f ( 1) 5,2 16 2 16∴| f (x1) f (x2)| 2.战略思想七:x1,x2 A,| f (x1) f (x2)| t |x1 x2 ||f(x1) f(x2)| t | f '(x)| t(t 0)例7. 已知函数y f (x)满足:(1)定义域为[ 1,1] ;(2)方程f (x) 0 至少有两个实根1和1;(3)过f (x) 图像上任意两点的直线的斜率绝对值不大于 1.(1)证明:| f(0) | 1;(2)证明:对任意x1,x2 [ 1,1],都有| f (x1) f (x2)| 1.证明(1) 略;(2)由条件(2)知f( 1) f (1) 0,不妨设 1 x 1 x 2 1,由(3)知| f (x 1) f (x 2)| |x 1 x 2 | x 2 x 1, 又∵| f(x 1) f(x 2)| |f(x 1)| | f(x 2)| | f(x 1) f( 1)| |f(x 2) f(1)|x 1 1 1 x 2 2 (x 2 x 1) 2 | f(x 1) f(x 2)|;∴|f(x 1) f(x 2)| 133 例 8. 已知函数 f(x)x 3 ax b ,对于 x 1,x 2(0, )(x 1 x 2 )时总有 | f (x 1) f (x 2)| |x 1 x 2 |成3立,求实数 a 的范围 .3 ' 2解 由 f (x) x 3 ax b ,得 f '(x) 3x 2 a ,评注 由导数的几何意义知道,函数 y f (x)图像上任意两点 P(x 1,y 1),Q(x 2,y 2) 连线的斜率k y2 y1 (x 1 x 2 )的取值范围,就是曲线上任一点切线的斜率(如果有的话 )的范围,利用这个结论,可x 2 x1以解决形如 |f(x 1) f(x 2)| m|x 1 x 2||或| f(x 1) f(x 2)| m|x 1 x 2 | (m >0)型的不等式恒成立问题四.双函数“任意”+“存在”型: x 1A,x 2 B ,使得 f (x 1) g (x 2)成立 f (x)min g(x)min ;x 1 A, x 2B ,使得 f (x 1)g(x 2)成立f (x)maxg(x)max .总有 f (x 1) g( x 2 )成立,求实数 m 的取值范围 .解析:题意等价于 f(x)在(0,1)上的最大值大于或等于 g ( x)在[1,2] 上的最大值 2 2x 2 5x 2 1 f (x) 2 ,由 f '(x) 0得, x 或 x 2,x211 当 x (0, ) 时, f (x) 0,当 x ( ,1)时 f (x) 0 , 221 所以在( 0,1)上, f ( x)max f (1) 3 5ln2 .2当 x (0, 33)时,a f (x) 1 a ,∵| f(x 1) f(x 2)| |x 1 x 2 |,∴| f(x 1) f(x 2) | 1x 1 x 2a1 1a11a0战略思想八: 例 9 .已知函数2 f (x) 2xx 25ln x , g(x) xmx 4 ,若存在 x 1 (0,1) ,对任意 x 2 [1,2] ,又g(x)在[1,2]上的最大值为 max{g(1),g(2)} ,所以有所以实数 m 的取值范围是 m 8 5ln 2.战略思想九: “ x 1 A , x 2 B ,使得 f (x 1) g(x 2)成立”“f (x) 的值域包含于.g( x ) 的值域”.例 10.设函数 f (x)1x 3 1 x 2 5x 4.333(1)求 f (x) 的单调区间.32(2)设 a ≥1,函数 g(x) x 3 3a 2x 2a .若对于任意 x 1 [0,1] ,总存在 x 0 [0,1] ,使得 f (x 1) g( x 0 )成立,求 a 的取值范围.' 22 5 ' 2 2 5 5解析:( 1 ) f '(x) x 2x ,令 f '(x)≥0,即 x 2 x ≤ 0 ,解得: ≤ x ≤1,3 3 3 3 355f(x) 的单增区间为 [ ,1] ;单调减区间为 ( , ]和[1, ) .33(2)由(1)可知当 x [0,1]时, f ( x)单调递增, ∴当 x [0,1]时, f(x) [f (0), f (1)] , 即 f(x) [ 4, 3] ;又g '(x) 3x 2 3a 2,且 a ≥1,∴当x [0,1]时, g '( x) ≤ 0 , g( x)单调递减, ∴当 x [0,1] 时, g(x) [ g (1),g (0)] ,即 g(x) [ 3a 2 2a 1, 2a] , 又对于任意 x 1 [0,1] ,总存在 x 0 [0,1] ,使得 f (x 1) g(x 0)成立 [ 4, 3] [ 3a 2 2a 1, 2a] ,1a例 11 .已知函数 f(x) ln x ax 1(a R) ; x1(1) 当 a 时,讨论 f (x) 的单调性;222)设 g(x) x 2 2bx 4 ,1当 a 时,若对 x 1 (0, 2) , x 2 [1,2] ,使 f(x 1) g(x 2) ,求实数4f(21) g(1) f(21) g(2)3 5ln 2 5 m 3 5ln 2 8 2mm 8 5ln 21m (11 5ln 2)2m 8 5ln 2 ,f(x)上限f(x)下限即3a 2 2a 1 ≤ 3 ≤ 2a4,解得:≤a ≤3g(x)上限b 的取值范围;解:(1)(解答过程略去,只给出结论)当 a ≤0 时,函数 f(x)在( 0,1 )上单调递减,在( 1,+∞)上单调递增;1 当 a= 时,函数 f(x) 在( 0, +∞)上单调递减;2 11当 0<a< 时,函数 f (x) 在(0,1 )上单调递减,在 (1, 1)上单调递增,在 2'21, ) 上单调递减; a2 )函数的定义域为( 0 , +∞),f (x )=1-a+ a21xxax 2 x 1 aa= 1 时,由 f4x )=0 可得 x 1=1,x 2=3.因为a= 1∈(0, 1 ),x 2=3 (0,2),结合( 1)可知 42函数 f(x)在( 0,1 )上单调递减,在( 1,2 )上单调递增, 所以f(x) 在( 0,2 )上的最小值为 f(1)= - 12由于 对 x 1∈(0,2), x 2∈[1,2], 使 f(x 1) ≥g(x 2) ”等价于 “g(x)在[1,2]上的最小值不大于 f(x) 在( 0,2)上的最小值 f(1)= 1”2”※)又 g(x)=(x -b)2+4-b 2, x ∈[1,2], 所以当 b<1 时,因为 [g(x)] min =g(1)=5 - 2b>0, 此时与(※)矛盾; 当 b ∈[1,2]时, 因为 [g(x)] min =4 -b 2≥0,同样与(※)矛盾; 当 b ∈(2,+∞)时,因为 [g(x)] min =g(2)=8 -4b.1 17 解不等式 8- 4b ≤- ,可得b ≥ .2817 综上, b 的取值范围是[ ,+ ∞).8五.双函数“任意”+“任意”型战略思想十: x 1 A, x 2 B ,使得 f(x 1) g(x 2)成立 f (x)min g(x)max例 12. 已 知 函 数 f(x) 1x 3 x 2 3x 4,g(x)3 3 29x c,若对任x 1,x 2 [ 2,2] ,都有 f (x 1) g(x 2),求 c 的范围 .解:因为对任意的 x 1,x 2 [ 2,2] ,都有 f(x 1) g(x 2)成立,∴[ f ( x)] max [g(x)]min ,∵f '(x) x2 2x 3,令f '(x) 0得x 3,x 1x>3 或x<-1;f '(x) 0得1 x 3;∴f(x)在[ 2, 1]为增函数,在[ 1,2]为减函数.18 c∵f( 1) 3, f (2) 6,∴[ f (x)]max 3,.∴3 ,∴c 24.22 3 2例13.已知两个函数f(x) 8x2 16x k,g(x) 2x3 5x2 4x,x [ 3,3], k R;(1) 若对x [ 3,3] ,都有f (x) g(x)成立,求实数k 的取值范围;(2) 若x [ 3,3] ,使得f (x) g(x) 成立,求实数k的取值范围;(3) 若对x1,x2 [ 3,3] ,都有f (x1) g(x2)成立,求实数k的取值范围;解:(1)设h(x) g(x) f (x) 2x3 3x2 12x k ,(1)中的问题可转化为:x [ 3,3] 时,h(x) 0 恒成立,即[ h( x)] min 0.'2h'(x) 6x2 6x 12 6(x 2)(x 1);当x 变化时,h(x),h'(x) 的变化情况列表如下:因为h( 1) k 7, h(2) k 20 ,所以,由上表可知[ h( x)] min k 45,故k-45 ≥0,得k≥45,即k∈[45,+ ∞).小结:①对于闭区间I,不等式f(x)<k 对x∈I 时恒成立[f(x)] max <k, x ∈I;不等式f(x)>k 对x∈I 时恒成立[f(x)] min>k, x ∈I.②此题常见的错误解法:由[f(x)] max ≤[g(x)] min 解出k 的取值范围.这种解法的错误在于条件“ [f(x)] max ≤[g(x)] min”只是原题的充分不必要条件,不是充要条件,即不等价.( 2)根据题意可知, ( 2)中的问题等价于h(x)= g(x) -f(x) ≥0 在x ∈[-3,3]时有解,故[h(x)] max≥0.由( 1)可知[h(x)] max = k+7 ,因此k+7 ≥0,即k∈[7,+ ∞).(3)根据题意可知, (3)中的问题等价于 [f(x)] max ≤[g(x)] min ,x ∈[-3,3].由二次函数的图像和性质可得 , x ∈[-3,3]时, [f(x)] max =120 -k. 仿照( 1),利用导数的方法可求得 x ∈[-3,3]时, [g(x)] min =-21. 由 120 - k ≥-21 得 k ≥141,即 k ∈[141,+ ∞). 说明:这里的 x 1,x 2 是两个互不影响的独立变量从上面三个问题的解答过程可以看出 ,对于一个不等式一定要看清是对“ x ”恒成立,还是“ x ”使之成还是两个独立的变量 ,然后再根据不同的情况采取不同的等价条件 ,千万不要稀里糊涂的去猜六.双函数“存在”+“存在”型战略思想十一: x 1 A, x 2 B ,使得 f(x 1) g(x 2)成立f (x)min g(x)max ;x 1 A, x 2 B ,使得 f(x 1) g(x 2)成立f(x)max g(x)min .x 3 2例 14.已知函数 f (x) ln x 1, g(x) x 2 2bx 4.若存在 x 1 (0,2) , x 2 1,2 ,使4 4xf (x 1) g(x 2) ,求实数 b 取值范围1 f (x)在(0,1)上单调递增,在 (1,2)上单调递减,f(x)min f (1) .2依题意有 f ( x) min g(x)max ,所以 g(x)max12.又g(x) (x b)2 b 2 4,g(1) 1 从而g(2) 212,解得b 187.战略思想十二: “ x 1 A, x 2 B ,使得 f (x 1) g(x 2) 成立”等价于f (x) 的值域与 g(x) 的值域相交非空”3 219 1例 15 .已知函数 f(x) x 3 (1 a)x 2 a(a 2)x(a R) , g(x) x .是否存在实数 a ,存63在 x 11,1 , x 2 0,2 ,使得 f '(x 1) 2ax 1 g(x 2)成立?若存在,求出 a 的取值范围;若不存在,说明理由立,同时还要看清不等式两边是同一个变量, 解析: f (x) 1 1 32x 4 4x 2(x 1)(x 3)4x 219 1 1解析:在0,2 上g x x 是增函数,故对于x 0,2 ,g x ,66 3 32设h x f x 2ax 3x22x a a 2 ,当x 1,1 时,h(x) [-a2 2a 13,-a2 2a 5].3要存在x1 [ 1,1] ,x2 [0,2] 使得h x1 g x2 成立,只要[-a2 2a 13,-a2 2a 5] [ 13,6]33考虑反面,[-a2 2a 31,-a2 2a 5] [ 13,6]1 2 2 1 57 57则5 a 2a 或6< -a 2a 1,解得a 1 或a 1 ,3 3 3 357 57从而所求为1 a 1 .33。
函数任意性与存在性问题探析_翟丽

2015 年
函数任意性与存在性问题探析
翟 丽
( 江苏省扬州市新华中学, 225009 )
函数中的任意性与存在性问题, 也即函 数中的恒成立与能成立问题, 一直是高中数 也是高考的热点题型 . 学考试的重点和难点, 这一类问题主要涉及到函数的最值和值域, 常与导数工具相结合, 并且与数形结合 、 分类 讨论 、 转化与化归等数学思想紧密联系, 其基 本模式如下: ( 1 ) 对于任意的 x ∈ A, 不等式 m > f ( x) 成立 m > f ( x) 成立 m < f ( x) m > f( x) m < f( x)
f( x) = f 2 . 因 为 1 ∈ ( 0, e] ,所 以 m
min
( )
(i
f 2 ≤ f( 1 ) = 0 , 从而只要 f ( e) ≤ 0 , 解之得 m m≤ 2 2 2 , . 从而 ≤ m ≤ e -1 e e -1 m 的取值范围是 - ∞ , 2 . 综上, e -1 评注 上述题型包括两个函数, 并且含 有两个或者三个变量 . 这种双函数多变量中
设 a = 2, 若对任意给定的 x0 ∈
( 0, e] , e]上总存在 t1 , t2 ( t1 ≠ t2 ) , 在区间( 0 , 2 ) 成立, 使得 g ( x0 ) < f ( t i ) ( i = 1 , 求 m 的取 值范围 . 解 由 x0 的任意性, 知 g( x)
max
< f( t i ) ( i
(
]
g( x) =
ex , a 均为实数 . 其中 m, ex
( 1 ) ( 2 ) 略; ( 3 ) 设 a = 2 , 若对任意给定 e] , e]上总存在 t1 , t2 ( t1 的 x0 ∈ ( 0 , 在区间( 0 , ≠ t2 ) , 使得 f ( t1 ) = f ( t2 ) = g( x0 ) 成立, 求m 的取值范围 . 解 ( 3 ) g' ( x) = e( 1 - x) , 易得 g( x) 在 ex
浅议函数中任意性与存在性问题

浅议函数中任意性与存在性问题姻文/陈刚盐城市阜宁县陈集中学,江苏阜宁224400函数的任意性与存在性问题,是一种常见题型,也是高考的热点之一。
它们既有区别又有联系,意义和转化方法各不相同,容易混淆。
对于这类问题,利用函数与导数的相关知识,可以把相等关系转化为函数值域之间的关系,不等关系转化为函数最值大小的比较。
下面结合实例来看看函数中的任意性与存在性问题在解题中的区别。
1. 若函数()f x 的定义域为D ,对任意x D Î时有()0f x ³恒成立min ()0f x Û³;()0f x £恒成立max ()0f x Û£。
例1. 设函数32()29128f x x x x c =-++,若对任意[0,3]x Î,都有2()f x c <成立,则实数c 的取值范围是解析 因为32()29128f x x x x c =-++,由2()f x c < 所以32229128x x x c c -++<,所以32229128x x x c c -+<-令32()2912g x x x x =-+,欲使2()8g x c c <-对任意[0,3]x Î恒成立,则需使max ()g x <28c c -对任意[0,3]x Î成立即可。
所以 2()61812g x x x ¢=-+ 令()0g x ¢=,得121,2x x ==,当(0,1)x Î时,()0g x ¢>,所以函数()g x 在区间(0,1)上单调递增;当(1,2)x Î时,()0g x ¢<,所以函数()g x 在区间(1,2)上单调递减;当(2,3)x Î时,()0g x ¢>,所以函数()g x 在区间(2,3)上单调递增.又由(1)5,(3)9g g ==,故当[0,3]x Î时,max ()9g x =由题意得 298c c <-,得91c c ><-或。
函数中的任意性与存在性问题

龙源期刊网
函数中的任意性与存在性问题
作者:马军辉
来源:《新课程·教师》2013年第11期
任意与存在在逻辑上是互为否定的两个量词。
近几年全国各地的高考题以它们立意命题,已成为考查高中数学知识的热点。
尤其在函数与导数及不等式中频频出现,由于这类问题灵活多变,思辨性强,大多数学生望而生畏、束手无策。
本文通过对几道具有代表性、示范性的高考题进行改编并深入探究,通过一题多解、一题多变,总结出解决这类问题的思路与方法。
需要说明的是,通过分离参数最终转化为不含参数的新函数的最值问题,是我们解决这类问题的主要方法。
总之,处理函数中的任意性与存在性问题的主线是运用函数的最值,本文以一题多解、一题多变来培养学生思维的灵活性,加深对任意性与存在性问题的认识。
当然,在分析问题时还是要对问题进行适当的转化,找到最有效的解决途径,提炼出解题的思维与方法,提高思维能力与数学素养。
编辑薄跃华。
_任意性_存在性_问题剖析

类型五: “ 任意”、 “ 存在” ( 或“ 存在”、 “ 任意” )型
例5 ( 2 0 1 0年山东高考理 2 2 )已知函数 f ( x ) =l n x- 1-a a x+ -1 ( a ) . ∈R x ( 1 )当 a 1 时, 讨论 f ( x )的单调性; 2 1 时, 若对任意 x 1 4
4 0 x , 存在 x , x - 3 , 3 ] , 都有 f ( x ) <g ( x ) , 求实数 c 的 1 2∈ [ 1 2 取值范围. 分析: 存在 x , x -3 , 3 ] , 都有 f ( x ) <g ( x ) , 等价 1 2∈ [ 1 2
2 2 ( x ) ( x ) , 由f ( x ) =7 x - 2 8 x -c=7 ( x - 2 ) - 于f m i n <g m a x
2 2 1 1 a +b 2+ 2 为定值 2 2 ; O A O B ab 2 2 4 a b 2 2 2 A B| a +b. 2 2 | a +b
∴
2 2 4 a b 2 2 2 A B| a +b. 2 2 | a +b
这样结合平面几何知识由此题可知, 高考题第( Ⅱ)存 在半径 R 为
x +x 2 x +x +1 h ( x )= 2 , 则h ′ ( x )= , 故函数 h ( x ) 2 2 >0 2 x +1 ( 2 x +1 ) 2 在[ 1 , 2 ] 上是增函数, h ( x ) ( 1 )= , 所以实数 a 的取 m i n =h 3 值范围是 0 <a< 2 . 3
槡
2 2 a b 2 = a +b 2
= 的圆满足题意, 从而 8+4 3 槡
8×4 2 6 槡
证明: 设点 A ( | O A| c o s , | O A| s i n ) , 则点 B ( | O B| θ θ π π c o s ( , | O B| s i n ( ) , θ+ ) θ+ ) 2 2
专题08 巧辨“任意性问题”与“存在性问题(解析版)

2020高考数学压轴题命题区间探究与突破专题第一篇 函数与导数专题08 巧辨“任意性问题”与“存在性问题”一.方法综述含有参数的方程(或不等式)中的“任意性”与“存在性”问题,历来是高考考查的一个热点,也是高考复习中的一个难点.破解的关键在于将它们等价转化为熟悉的基本初等函数的最值或值域问题,而正确区分“任意性”与“存在性”问题也是解题的关键.本专题举例说明辨别“任意性问题”与“存在性问题”的方法、技巧.二.解题策略类型一 “∀x ,使得f(x)>g(x)”与“∃x ,使得f(x)>g(x)”的辨析(1)∀x ,使得f (x )>g (x ),只需h (x )min =[f (x )-g (x )]min >0.如图①.(2)∃x ,使得f (x )>g (x ),只需h (x )max =[f (x )-g (x )]max >0.如图②. 【例1】【2020·河南濮阳一中期末】已知函数1()ln (0),()a f x a x a g x x x x=-≠=--. (Ⅰ)求()f x 的单调区间;(Ⅱ)当0a >时,若存在0[1,]x e ∈,使得()()00f x g x <成立,求实数a 的取值范围.【解析】(I )()f x 的定义域为'221(0,),().a a x f x a x x x ++∞=--=- 所以,当0a >时,()'0f x <,()f x 在(0,)+∞上递减;当0a <时,()'0fx >,所以,()f x 在(0,)+∞上递增.(II )在[]1e ,上存在一点0x 使00()()f xg x <成立, 即函数1()ln a h x a x x x x=-++在[]1,e 上的最小值小于0, ()'222(1)1+1()1x x a a a h x x x x x+-⎡⎤⎣⎦=--+-=.①当1+a e ≥,即1a e ≥-时,()h x 在[]1,e 上单调递减, 所以()h x 在[]1,e 上的最小值为()h e ,由()10ah e e a e+=+-<, 得222111,1,111e e e a e a e e e +++>>-∴>---Q ; ②当11a +≤,即0a ≤时,0a >Q ,不合乎题意;③当11a e <+<,即01a e <<-时,()h x 的最小值为()1h a +,0ln(1)1,0ln(1),a a a a <+<∴<+<Q 故(1)2ln(1)2h a a a a +=+-+>. 此时(1)0h a +<不成立.综上所述,a 的取值范围是211e a >e +-. 【指点迷津】(1)这是较为常见的一类恒成立问题,运用数形结合的思想可知,当x 0≥0时,总有f (x 0)≥g (x 0),即f (x 0)-g (x 0)≥0(注意不是f (x )min ≥g (x )max ),可以转化为当x ≥0时,h (x )=f (x )-g (x )≥0恒成立问题.(2)存在x ≥0,使得f (x )≥g (x ),即至少有一个x 0≥0,满足f (x 0)-g (x 0)不是负数,可以转化为当x ≥0时,h (x )=f (x )-g (x )的函数值至少有一个是非负数. 【举一反三】【2020·江西瑞金一中期中】已知函数()()ln f x x x a b =++,曲线()y f x =在点()()1,1f 处的切线为210x y --=.(1)求a ,b 的值;(2)若对任意的()1,x ∈+∞,()()1f x m x ≥-恒成立,求正整数m 的最大值. 【解析】(1)由()()ln f x x x a b =++得:()ln 1f x x a '=++ 由切线方程可知:()1211f =-=()112f a '∴=+=,()11f a b =+=,解得:1a =,0b =(2)由(1)知()()ln 1f x x x =+则()1,x ∈+∞时,()()1f x m x ≥-恒成立等价于()1,x ∈+∞时,()ln 11x x m x +≤-恒成立令()()ln 11x x g x x +=-,1x >,则()()2ln 21x x g x x --'=-. 令()ln 2h x x x =--,则()111x h x x x-'=-=∴当()1,x ∈+∞时,()0h x '>,则()h x 单调递增()31ln30h =-<Q ,()422ln 20h =-> ()03,4x ∴∃∈,使得()00h x =当()01,x x ∈时,()0g x '<;()0,x x ∈+∞时,()0g x '>()()()000min0ln 11x x g x g x x +∴==-()000ln 20h x x x =--=Q 00ln 2x x ∴=- ()()()()0000min 0213,41x x g x g x x x -+∴===∈-()03,4m x ∴≤∈,即正整数m 的最大值为3类型二 “若1122x D x D ∃∈∃∈,,,使得()()12f x g x =”与“1122x D x D ∀∈∃∈,,使得()()12f x g x =”的辨析(1) 1122x D x D ∃∈∃∈,,使得()()12f x g x =等价于函数f (x )在D 1上的值域A 与g (x )在D 2上的值域B 的交集不是空集,即A ∩B ≠∅,如图③.其等价转化的目标是两个函数有相等的函数值.(2) 1122x D x D ∀∈∃∈,,使得()()12f x g x =等价于函数f (x )在D 1上的值域A 是g (x )在D 2上的值域B 的子集,即A ⊆B ,如图④.其等价转化的目标是函数y =f (x )的值域都在函数y =g (x )的值域之中. 说明:图③,图④中的条形图表示函数在相应定义域上的值域在y 轴上的投影. 【例2】【2020河北衡水中月考】已知函数()()()11ln 1f x a x x =---+,()1xg x xe -=.(1)求()g x 在区间(]0,e 上的值域;(2)是否存在实数a ,对任意给定的(]00,x e ∈,在[]1,e 存在两个不同的()1,2i x i =使得()()0i f x g x =,若存在,求出a 的范围,若不存在,说出理由. 【解析】(1)()()1'1xg x x e-=-,()0,1x ∈时,()'0g x >,()g x 单调递增,(]1,x e ∈时,()'0g x <,()g x 单调递减,()00g =,()11g =,()10e g e e e -=⨯>,∴()g x 在(]0,e 上值域为(]0,1. (2)由已知得1()1f x a x='--,且[]1,x e ∈, 当0a ≤时,()'0f x ≥,()f x 在[]1,e 上单调递增,不合题意. 当11a e≥-时,()'0f x ≤,()f x 在[]1,e 上单调递减,不合题意. 当101a e <<-时,()0f x '=得011x a=-.当1(1,)1x a∈-时()'0f x <,()f x 单调递减, 当1()1x e a ,∈-时,()'0f x >,()f x 单调递增,∴()min 11f x f a ⎛⎫= ⎪-⎝⎭.由(1)知()g x 在(]0,e 上值域为(]0,1,而()11f =,所以对任意(]00,x e ∈,在区间[]1,e 上总有两个不同的()1,2i x i =,使得()()0i f x g x =.当且仅当()1101fe f a ⎧≥⎪⎨⎛⎫≤ ⎪⎪-⎝⎭⎩,即()()()()()1111ln 1102a e a a ⎧--≥⎪⎨+-+≤⎪⎩, 由(1)得111a e ≤--. 设()()ln 11h a a a =+-+,10,1a e ⎛⎫∈- ⎪⎝⎭,()1'111a h a a a =-=--, 当10,1a e ⎛⎫∈- ⎪⎝⎭,()'0h a <,()h a 单调递减,∴()11110h a h e e⎛⎫>-=-> ⎪⎝⎭. ∴()0h a ≤无解.综上,满足条件的a 不存在. 【指点迷津】本例第(2)问等价转化的基本思想是:函数g (x )的任意一个函数值都与函数f (x )的某两个函数值相等,即f (x )的值域都在g (x )的值域中. 【举一反三】【2020·河南南阳一中期中】已知函数1()ln 1f x x x=+-, 32()324g x x a x a =--+, []0,1x ∈,其中0a ≥.(1)求函数()f x 的单调区间;(2)若对任意[]11,x e ∈,总存在[]20,1x ∈,使得()()12f x g x =成立,求a 的取值范围. 【解析】(1)函数()f x 的定义域为(0,)+∞,22111()x f x x x x-'=-+=, 令()0f x '>,解得1x >,令()0f x '<,解得01x <<,∴函数()f x 的减区间为(0,1),增区间为(1,)+∞;(2)依题意,函数()f x 在[]1,e 上的值域包含于函数g x ()在[]0,1上的值域,由(1)可知,函数()f x 在[]1,e 上单调递增,故值域为10,e ⎡⎤⎢⎥⎣⎦,由32()324g x x a x a =--+得22()333()()g x x a x a x a '=-=+-, ①当0a =时,()0g x '≥恒成立,故函数g()x 在[]0,1上单调递增,此时值域为[]224,3254,5a a a ⎡⎤-+--+=⎣⎦,故0a =不符合题意;②Q 当0a >时,()0g x '>的解集为(,)a +∞,()0g x '<的解集为(0,)a ,∴ 故函数()g x 在(0,)a 上单调递减,在(,)a +∞上单调递增,且2(0)42,(1)325g a g a a =-=--+,()i 当01a <<时,函数g()x 在(0,)a 上单调递减,在(,1)a 上单调递增,此时值域为{}32224,42,325a a max a a a ⎡⎤--+---+⎣⎦,则此时需要32240a a --+≤,即320a a +-≥,当01a <<时,320a a +-≥不可能成立,故01a <<不符合题意; ()ii 当1a ≥时,()0g x '≤在[]0,1上恒成立,则函数g()x 在[]0,1上单调递减,此时值域为2325,42a a a ⎡⎤--+-⎣⎦,则23250142a a a e ⎧--+≤⎪⎨-≥⎪⎩,解得1122a e ≤≤-; 综上所述,实数a 的取值范围为11,22e ⎡⎤-⎢⎥⎣⎦. 类型三 f (x ),g (x )是闭区间D 上的连续函数,“∀x 1,x 2∈D ,使得f (x 1)>g (x 2)”与“∃x 1,x 2∈D ,使得f (x 1)>g (x 2)”的辨析(1)f (x ),g (x )是在闭区间D 上的连续函数且∀x 1,x 2∈D ,使得f (x 1)>g (x 2),等价于f (x )min >g (x )max .其等价转化的目标是函数y =f (x )的任意一个函数值均大于函数y =g (x )的任意一个函数值.如图⑤.(2)存在x 1,x 2∈D ,使得f (x 1)>g (x 2),等价于f (x )max >g (x )min .其等价转化的目标是函数y =f (x )的某一个函数值大于函数y =g (x )的某些函数值.如图⑥.【例3】【2020·甘肃天水一中月考】已知函数(1)(1ln )()3x x f x m x++=-,()ln g x mx x =-+(R)m ∈.(1)求函数()g x 的单调区间与极值.(2)当0m >时,是否存在[]12,1,2x x ∈,使得12()()f x g x >成立?若存在,求实数m 的取值范围,若不存在,请说明理由.【解析】(1)1()(0)g x m x x =-+>', 当0m ≤时,1()0g x m x=-+>'恒成立,即函数()g x 的单调增区间为∞(0,+),无单调减区间,所以不存在极值.当0m >时,令1()0g x m x =-+=',得1x m =,当10x m <<时,()0g x '>,当1x m>时,()0g x '<,故函数()g x 的单调增区间为10m (,),单调减区间为1m+∞(,),此时函数()g x 在1x m =处取得极大值,极大值为111()ln 1ln g m m m m m=-⨯+=--,无极小值.综上,当0m ≤时,函数()g x 的单调增区间为()0+∞,,无单调减区间,不存在极值.当0m >时,函数()g x 的单调增区间为10m ⎛⎫ ⎪⎝⎭,,单调减区间为1m ⎛⎫+∞⎪⎝⎭,,极大值为1ln m --,无极小值 (2)当0m >时,假设存在[]12,1,2x x ∈,使得12()()f x g x >成立,则对[]1,2x ∈,满足max min ()()f x g x > 由(1)(1ln )()3x x f x m x++=-[]1,2x ∈()可得,221(1ln 1)(1)(1ln )ln ()x x x x x x x f x x x +++-++-=='. 令[]()ln 1,2h x x x x =-∈(),则1()10h x x'=-≥,所以()h x 在[]1,2上单调递增,所以()(1)1h x h ≥=,所以()0f x '>,所以()f x 在[]1,2上单调递增,所以max (21)(1ln 2)3(1ln 2)()(2)3322f x f m m +++==-=-由(1)可知,①当101m<≤时,即m 1≥时,函数()g x 在[]1,2上单调递减,所以()g x 的最小值是(2)2ln 2g m =-+.②当12m ≥,即102m <≤时,函数()g x 在[]1,2上单调递增, 所以()g x 的最小值是(1)g m =-.③当112m <<时,即112m <<时,函数()g x 在11,m ⎡⎤⎢⎥⎣⎦上单调递增,在1,2m ⎡⎤⎢⎥⎣⎦上单调递减.又(2)(1)ln 22ln 2g g m m m -=-+=-,所以当1ln 22m <<时,()g x 在[]1,2上的最小值是(1)g m =-.当ln 21m ≤<时,()g x 在[]1,2上的最小值是(2)ln 22g m =-所以当0ln 2m <<时,()g x 在[]1,2上的最小值是(1)g m =-,故3(1ln 2)32m m +->-, 解得3(1ln 2)4m +>,所以ln 20m >>. 当ln 2m ≤时,函数()g x 在[]1,2上的最小值是(2)ln 22g m =-,故3(1ln 2)3ln 222m m +->-, 解得3ln 22m +>,所以3ln 2ln 22m +≤<.故实数m 的取值范围是3ln 20,2+⎛⎫⎪⎝⎭【指点迷津】1.本例第(2)问从形的角度看,问题的本质就是函数f (x )图象的最低点低于g (x )图象的最高点.2.题设中,使得成立可转化为,进而求出参数.【举一反三】【2020·四川石室中学月考】已知函数()22ln f x x x =-+.(1)求函数()f x 的最大值; (2)若函数()f x 与()ag x x x=+有相同极值点. ①求实数a 的值;②若对于121,,3x x e ⎡⎤∀∈⎢⎥⎣⎦(e 为自然对数的底数),不等式()()1211f xg x k -≤-恒成立,求实数k 的取值范围.【解析】(1)22(1)(1)()2(0)x x f x x x x x+-'=-+=->, 由()0{0f x x >>'得01x <<,由()0{0f x x <>'得1x >,∴()f x 在(0,1)上为增函数,在(1,)+∞上为减函数, ∴函数()f x 的最大值为(1)1f =-; (2)∵()a g x x x=+,∴2()1a g x x =-',(Ⅰ)由(1)知,1x =是函数()f x 的极值点,又∵函数()f x 与()ag x x x=+有相同极值点, ∴1x =是函数()g x 的极值点,∴(1)10g a =-=',解得1a =, 经检验,当1a =时,函数()g x 取到极小值,符合题意;(ⅱ)∵211()2f ee =--,(1)1f =-,(3)92ln 3f =-+, ∵2192ln 321e -+<--<-, 即1(3)()(1)f f f e <<,∴1[,3]x e∀∈,min max ()(3)92ln 3,()(1)1f x f f x f ==-+==-,由(ⅰ)知1()g x x x =+,∴21()1g x x =-',当1[,1)x e∈时,()0g x '<,当(1,3]x ∈时,()0g x '>,故()g x 在1[,1)e 为减函数,在(1,3]上为增函数,∵11110(),(1)2,(3)333g e g g e e =+==+=,而11023e e <+<,∴1(1)()(3)g g g e <<,∴1[,3]x e ∀∈,min max 10()(1)2,()(3)3g x g g x g ====,①当10k ->,即1k >时,对于121,[,3]x x e ∀∈,不等式12()()11f xg x k -≤-恒成立 12max 1[()()]k f x g x ⇔-≥-12max [()()]1k f x g x ⇔≥-+,∵12()()(1)(1)123f x g x f g -≤-=--=-,∴312k ≥-+=-,又∵1k >,∴1k >, ②当10k -<,即1k <时,对于121,[,]x x e e ∀∈,不等式12()()11f xg x k -≤-,12min 1[()()]k f x g x ⇔-≤-12min [()()]1k f x g x ⇔≤-+,∵121037()()(3)(3)92ln 32ln 333f x g x f g -≥-=-+-=-+,∴342ln 33k ≤-+,又∵1k <, ∴342ln 33k ≤-+.综上,所求的实数k 的取值范围为34(,2ln 3](1,)3-∞-+⋃+∞. 类型四 “∀x 1∈D 1,∃x 2∈D 2,使f (x 1)>g (x 2)”与“∀x 1∈D 1,∃x 2∈D 2,使f (x 1)<g (x 2)”的辨析(1)∀x 1∈D 1,∃x 2∈D 2,使f (x 1)>g (x 2),等价于函数f (x )在D 1上的最小值大于g (x )在D 2上的最小值,即f (x )min >g (x )min (这里假设f (x )min ,g (x )min 存在).其等价转化的目标是函数y =f (x )的任意一个函数值大于函数y =g (x )的某一个函数值.如图⑦.(2)∀x 1∈D 1,∃x 2∈D 2,使f (x 1)<g (x 2),等价于函数f (x )在D 1上的最大值小于g (x )在D 2上的最大值,即f (x )max <g (x )max .其等价转化的目标是函数y =f (x )的任意一个函数值小于函数y =g (x )的某一个函数值.如图⑧. 【例4】【2020·江西抚州二中期末】已知函数()42ln af x a x x x-=-++. (1)当4a ≥时,求函数()f x 的单调区间;(2)设()26xg x e mx =+-,当22a e =+时,对任意[)12,x ∈+∞,存在[)21x ∈+∞,,使得()()2122f x e g x +≥,求实数m 的取值范围.【解析】(1)函数()f x 的定义域为(0,)+∞,224()1a a f x x x -'=-++2(2)[(2)]x x a x---=, 由()0f x '=,得2x =或2=-x a .当4a >即22a ->时,由()0f x '<得22x a <<-, 由()0f x '>得02x <<或2x a >-;当4a =即22a -=时,当0x >时都有()0f x '≥;∴当4a >时,单调减区间是(2,2)a -,单调增区间是(0,2),(2,)a -+∞;当4a =时,单调增区间是()0,∞+,没有单调减区间.(2)当22a e =+时,由(1)知()f x 在()22,e 上单调递减,在()2,e +∞上单调递增,从而()f x 在[)2,+∞上的最小值为22()6f e e =--.对任意[)12,x ∈+∞,存在[)21x ∈+∞,,使得()()2212g x f x e ≤+,即存在[)21x ∈+∞,,使()g x 的值不超过()22e f x +在区间[)2,+∞上的最小值26e -.由2266xe e mx ≥+--,22e e xm x-∴≤. 令22()xe e h x x-=,则当[)1,x ∈+∞时,max ()m h x ≤. ()()22222()x x e x e xh x e x ---'=Q ()232x x e xe e x+-=-,当[1,2]x ∈时()0h x '<;当[2,)x ∈+∞时,()22xxe xe e +-20xx xee >-≥,()0h x '<.故()h x 在[1,)+∞上单调递减,从而2max ()(1)h x h e e ==-,从而2m e e ≤-. 【指点迷津】“对任意x 1∈(0,2),总存在x 2∈[1,2],使f (x 1)≥g (x 2)”等价于“f (x )在(0,2)上的最小值大于或等于g (x )在[1,2]上的最小值”. 【举一反三】【2020重庆西南大学附中月考】已知函数()()()11ln x x f x x++=,()()ln g x x mx m R =-∈ .(1)求函数()g x 的单调区间;(2)当0m >时,对任意的[]11,2x ∈,存在[]21,2x ∈,使得()()123f x m g x ->成立,试确定实数m 的取值范围.【解析】(1)由()()ln 0g x x mx x =->,得()'1g x m x=-.当0m ≤时,()'0g x >,所以()g x 的单调递增区间是()0,∞+,没有减区间.当0m >时,由()'0g x >,解得10x m <<;由()'0g x <,解得1x m>,所以()g x 的单调递增区间是10,m ⎛⎫ ⎪⎝⎭,递减区间是1,m ⎛⎫+∞ ⎪⎝⎭.综上所述,当0m ≤时,()g x 的单调递增区间是()0,∞+,无递减区间;当0m >时,()g x 的单调递增区间是10,m ⎛⎫ ⎪⎝⎭,递减区间是1,m ⎛⎫+∞ ⎪⎝⎭. (2)当0m >时,对任意[]11,2x ∈,存在[]21,2x ∈,使得()()123f x m g x ->成立,只需()()min min 3f x m g x ->成立.由()()()11ln ln 1ln 1x x x f x x xxx++==+++,得()'2221ln 11ln x x xf x x xx x--=+-=.令()()ln 0h x x x x =->,则()'1x h x x-=.所以当()0,1x ∈时,()'0h x <,当()1,x ∈+∞时,()'0h x >.所以()h x 在()0,1上递减,在()1,+∞上递增,且()11h =,所以()()()min 110h x h x h ≥==>.所以()'0f x >,即()f x 在()0,∞+上递增,所以()f x 在[]1,2上递增,所以()()min 12f x f ==.由(1)知,当0m >时,()g x 在10,m ⎛⎫ ⎪⎝⎭上递增,在1,m ⎛⎫+∞ ⎪⎝⎭上递减,①当101m<≤即m 1≥时,()g x 在[]1,2上递减,()()min 2ln22g x g m ==-; ②当112m <<即112m <<时,()g x 在11,m ⎡⎫⎪⎢⎣⎭上递增,在1,2m ⎛⎤⎥⎝⎦上递减,()()(){}min min 1,2g x g g =,由()()()21ln22ln2g g m m m -=---=-, 当1ln22m <≤时,()()21g g ≥,此时()()min 1g x g m ==-, 当ln21m <<时,()()21g g <,此时()()min 2ln22g x g m ==-, ③当12m ≥即102m <≤时,()g x 在[]1,2上递增,()()min 1g x g m ==-, 所以当0ln2m <≤时,()()min 1g x g m ==-, 由0ln223m m m<≤⎧⎨->-⎩,得0ln2.m <≤当ln2m >时,()()min 2ln22g x g m ==-,由ln223ln22m m m>⎧⎨->-⎩,得 ln22ln2m <<-.∴ 02ln2m <<-.综上,所求实数m 的取值范围是()0,2ln2-.三.强化训练1.【2020·江西萍乡一中期中】已知函数ln ()xx af x e+=. (1)当1a =时,求()f x 的极值; (2)设()xg x xe a -=-,对任意12,(0,)x x ∈+∞都有()()11112xx e f x ax g x ->成立,求实数a 的取值范围.【解析】(1)当1a =时,ln 1()xx f x e+=,所以函数()f x 的定义域为(0,)+∞, 所以1ln ()xx x xf x xe--'=,且0x xe >, 令()1ln h x x x x =--,所以当01x <<时,10,ln 0x x x -><, 所以()1ln 0h x x x x =-->. 又()2ln h x x '=--,所以当1x >时,()2ln 0h x x '=--<,所以()h x 在(1,)+∞上单调递减,故()(1)0h x h <=. 同理当01x <<时,()0f x '>; 当1x >时,()0f x '<,所以()f x 在(0,1)是单调递增,在(1,)+∞单调递减, 所以当1x =时,()f x 的极大值为1(1)f e=,无极小值. (2)令()()xm x xe f x ax =-,因为对任意12,(0,)x x ∈+∞都有()()11112xx e f x ax g x ->成立,所以()()12min max m x g x >.因为()()ln xm x xe f x ax x x =-=, 所以()1ln m x x '=+.令()0m x '>,即1ln 0x +>,解得1x e>; 令()0m x '<,即1ln 0x +<,解得10x e<<.所以()m x 在10,e ⎛⎫ ⎪⎝⎭上单调递减,在1,e ⎛⎫+∞ ⎪⎝⎭上单调递增, 所以min 11()m x m e e⎛⎫==- ⎪⎝⎭. 因为()xg x xea -=-,所以()(1)xg x x e -'=-,当0x >时0x e ->,令()0g x '>,即10x ->,解得01x <<;令()0g x '<,即10x -<,解得1x >. 所以()g x 在(0,1)上单调递增,在(1,)+∞上单调递减, 所以max 1()(1)g x g a e==-, 所以11a e e->-, 所以2a e >,即实数a 的取值范围为2,e ⎛⎫+∞ ⎪⎝⎭. 2.【2020·河北邯郸期末】已知函数()f x 满足:①定义为R ;②2()2()9xxf x f x e e +-=+-. (1)求()f x 的解析式;(2)若12,[1,1]x x ∀∈-;均有()()21122(2)61x a x x f x -+-+-…成立,求a 的取值范围;(3)设2(),(0)()21,(0)f x xg x x x x >⎧=⎨--+≤⎩,试求方程[()]10g g x -=的解. 【解析】(1)2()2()9xx f x f x e e+-=+-Q ,…① 所以2()2()9xx f x f x ee ---+=+-即1()2()29xx f x f x e e-+=+-…② 由①②联立解得:()3xf x e =-.(2)设2()(2)6x x a x ϕ=-+-+,()()()1333x x x F x x e e xe x =--=+--,依题意知:当11x -≤≤时,min max ()()x F x ϕ≥()()33x x x x F x e e xe xe '+=-+=-+Q又()(1)0xF x x e ''=-+<Q 在(1,1)-上恒成立, 所以()F x '在[1,1]-上单调递减()(1)30min F x F e ∴'='=-> ()F x ∴在[1,1]-上单调递增,max ()(1)0F x F ∴==(1)70(1)30a a ϕϕ-=-≥⎧∴⎨=+≥⎩,解得:37a -≤≤实数a 的取值范围为[3,7]-. (3)()g x 的图象如图所示:令()T g x =,则()1g T =1232,0,ln 4T T T ∴=-==当()2g x =-时有1个解3-,当()0g x =时有2个解:(12)-、ln3,当()ln 4g x =时有3个解:ln(3ln 4)+、12(1ln 2)--. 故方程[()]10g g x -=的解分别为:3-,(12)-、ln3,ln(3ln 4)+、12(1ln 2)--3.【2020·天津滨海新区期末】已知函数()2ln h x ax x =-+.(1)当1a =时,求()h x 在()()2,2h 处的切线方程; (2)令()()22a f x x h x =+,已知函数()f x 有两个极值点12,x x ,且1212x x >,求实数a 的取值范围;(3)在(2)的条件下,若存在0122x ⎡⎤∈+⎢⎥⎣⎦,使不等式()()()()20ln 1112ln 2f x a m a a ++>--++对任意a (取值范围内的值)恒成立,求实数m 的取值范围. 【解析】()1当1a =时,()()12ln ,'2h x x x h x x=-+=-+2x =时,()()3'2,24ln 22h h =-=-+()h x ∴在()()2,2h 处的切线方程为()34ln 222y x +-=-- 化简得:322ln 220x y +-+=()2对函数求导可得,()()221'0ax ax f x x x-+=>令()'0f x =,可得2210ax ax -+=20440112a a a a ⎧⎪≠⎪∴->⎨⎪⎪>⎩,解得a 的取值范围为()1,2 ()3由2210ax ax -+=,解得121,1x x a a=-=+而()f x 在()10,x 上递增,在()12,x x 上递减,在()2,x +∞上递增12a <<Q2112x a ∴=+<+()f x ∴在122⎡⎤+⎢⎥⎣⎦单调递增 ∴在12⎡⎤⎢⎥⎣⎦上,()()max 22ln 2f x f a ==-+012x ⎡⎤∴∃∈+⎢⎥⎣⎦,使不等式()()()()20ln 1112ln 2f x a m a a ++>--++对a M ∀∈恒成立等价于不等式2(2ln 2ln 1112))()n (l 2a a m a a -+++>--++恒成立 即不等式2()ln 1ln 210a ma a m +--+-+>对任意的()12a a <<恒成立令()()2ln 1ln 21g a a ma a m =+--+-+,则()()121210,'1ma a m g g a a ⎛⎫-++ ⎪⎝⎭==+ ①当0m ≥时,()()'0,g a g a <在()1,2上递减()()10g a g <=不合题意②当0m <时,()1212'1ma a m g a a ⎛⎫-++ ⎪⎝⎭=+ 12a <<Q若1112m ⎛⎫-+> ⎪⎝⎭,即104m -<<时,则()g a 在()1,2上先递减 ()10g =Q12a ∴<<时,()0g a >不能恒成立若111,2m ⎛⎫-+≤ ⎪⎝⎭即14m ≤-,则()g a 在()1,2上单调递增 ()()10g a g ∴>=恒成立m ∴的取值范围为1,4⎛⎤-∞- ⎥⎝⎦4.【2020·全国高三专题练习】已知函数()321(1)32a x x ax f x +=-+.(Ⅰ)当1a =时,求曲线()y f x =在点(0,(0))f 处的切线方程; (Ⅱ)讨论函数()f x 的单调性;(Ⅲ)对于任意1x ,2[02]x ∈,,都有122()()3f x f x -≤,求实数a 的取值范围.【解析】(Ⅰ)当1a =时,因为()3213x x x f x =-+所以()221x x f x =-+',(0)1f '=.又因为(0)0f =,所以曲线()y f x =在点()0,(0)f 处的切线方程为y x =. (Ⅱ)因为()321(1)32a x x ax f x +=-+,所以2()(1)0f x x a x a '=-++=. 令()0f x '=,解得x a =或1x =. 若1a >,当()0f x '>即1x <或x a >时, 故函数()f x 的单调递增区间为()(),1,,a -∞+∞;当()0f x '<即1x a <<时,故函数()f x 的单调递减区间为()1,a . 若1a =,则22()21(1)0f x x x x '=-+=-≥,当且仅当1x =时取等号,故函数()f x 在(),-∞+∞上是增函数. 若1a <,当()0f x '>即x a <或1x >时, 故函数()f x 的单调递增区间为()(),,1,a -∞+∞;当()0f x '<即1<<a x 时,故函数()f x 的单调递减区间为(),1a .综上,1a >时,函数()f x 单调递增区间为(1)()a -∞∞,,,+,单调递减区间为(1,)a ; 1a =时,函数()f x 单调递增区间为(,)-∞+∞;1a <时,函数()f x 单调递增区间为()(1)a -∞∞,,,+,单调递减区间为(,1)a .(Ⅲ) 由题设,只要()()max min 23f x f x -≤即可. 令2()(1)0f x x a x a '=-++=,解得x a =或1x =.当0a ≤时,随x 变化,(),()f x f x ' 变化情况如下表:由表可知(0)0(1)f f =>,此时2(2)(1)3f f ->,不符合题意.当01a <<时,随x 变化,()()'f x f x , 变化情况如下表:由表可得3211112(0)0()(1)(2)62263f f a a a f a f ==-+=-=,,,,且(0)()f f a <,(1)(2)f f <,因()()2203f f -=,所以只需()(2)(1)(0)f a f f f ≤⎧⎨≥⎩,即3211262311026a a a ⎧-+≤⎪⎪⎨⎪-≥⎪⎩ ,解得113a ≤<. 当1a =时,由(Ⅱ)知()f x 在[]0,2为增函数, 此时()()()()max min 2203f x f x f f -=-=,符合题意. 当12a <<时,同理只需(1)(2)()(0)f f f a f ≤⎧⎨≥⎩,即3211226311062a a a ⎧-≤⎪⎪⎨⎪-+≥⎪⎩ ,解得513a <≤. 当2a ≥时,2()(1)32f f >=,()2()0(311)f f f =->,不符合题意. 综上,实数a 的取值范围是15,33⎡⎤⎢⎥⎣⎦.5.【2020·河南安阳期末】已知函数()ln f x x x x =+,()x xg x e=. (1)若不等式()()2f xg x ax ≤对[)1,x ∈+∞恒成立,求a 的最小值; (2)证明:()()1f x x g x +->.(3)设方程()()f x g x x -=的实根为0x .令()()()00,1,,,f x x x x F x g x x x ⎧-<≤⎪=⎨>⎪⎩若存在1x ,()21,x ∈+∞,12x x <,使得()()12F x F x =,证明:()()2012F x F x x <-.【解析】(1)()()2f xg x ax ≥,即()2ln x x x x x ax e +⋅≥,化简可得ln 1x x a e+≤. 令()ln 1xx k x e +=,()()1ln 1xx x k x e -+'=,因为1x ≥,所以11x ≤,ln 11x +≥. 所以()0k x '≤,()k x 在[)1,+∞上单调递减,()()11k x k e≤=.所以a 的最小值为1e.(2)要证()()1f x x g x +->,即()ln 10x xx x x e+>>.两边同除以x 可得11ln x x x e+>.设()1ln t x x x =+,则()22111x t x x x x-'=-=.在()0,1上,()0t x '<,所以()t x 在()0,1上单调递减.在()1,+∞上,()0t x '>,所以()t x 在()1,+∞上单调递增,所以()()11t x t ≥=. 设()1x h x e=,因为()h x 在()0,∞+上是减函数,所以()()01h x h <=. 所以()()t x h x >,即()()1f x x g x +->.(3)证明:方程()()f x g x x -=在区间()1,+∞上的实根为0x ,即001ln x x e=,要证()()2012F x F x x <-,由()()12F x F x =可知,即要证()()1012F x F x x <-.当01x x <<时,()ln F x x x =,()1ln 0F x x '=+>,因而()F x 在()01,x 上单调递增. 当0x x >时,()x x F x e =,()10xxF x e -'=<,因而()F x 在()0,x +∞上单调递减. 因为()101,x x ∈,所以0102x x x ->,要证()()1012F x F x x <-.即要证01011122ln x x x x x x e--<. 记()0022ln x xx xm x x x e--=-,01x x <<. 因为001ln x x e =,所以0000ln x x x x e =,则()00000ln 0x xm x x x e =-=.()0000022212121ln 1ln x x x x x xx x x xm x x x e e e---+--'=++=++-. 设()t t n t e =,()1t tn t e-'=,当()0,1t ∈时,()0n t '>.()1,t ∈+∞时,()0n t '<,故()max 1n t e=.且()0n t >,故()10n t e <<,因为021x x ->,所以002120x x x xe e ---<<.因此()0m x '>,即()m x 在()01,x 上单调递增.所以()()00m x m x <=,即01011122ln x x x x x x e --<.故()()2012F x F x x <-得证.6.【2020·山东邹平一中期末】已知函数()()sin ,ln f x x a x g x x m x =-=+. (1)求证:当1a ≤时,对任意()()0,,0x f x ∈+∞>恒成立; (2)求函数()g x 的极值; (3)当12a =时,若存在()12,0,x x ∈+∞且12x x ≠,满足()()()()1122f x g x f x g x +=+,求证:12249x x m <. 【解析】(1)()()sin 1cos f x x a x f x a x '=-∴=-,1cos 1x -≤≤Q ,()11cos 0a f x a x '∴≤=-≥,, ()sin f x x a x =-在()0+∞,上为增函数,所以当()0,x ∈+∞时,恒有()()00f x f >=成立; (2)由()()()ln ,10m x mg x x m x g x x x x+'=+∴=+=> 当()00m g x '≥>,()g x 在()0+∞,上为增函数,无极值 当()()0,00;0m x m g x x m g x ''<<<-<>->,,()g x 在()0m -,上为减函数,在(),m -+∞上为增函数,()x m x ∴=-,g 有极小值()ln m m m -+-,无极大值,综上知:当()0m g x ≥,无极值,当()0m g x <,有极小值()ln m m m -+-,无极大值. (3)当()11sin 22a f x x x ==-,在()0+∞,上为增函数, 由(2)知,当0m ≥,()g x 在()0+∞,上为增函数, 这时,()()f x g x +在()0+∞,上为增函数, 所以不可能存在()12,0,x x ∈+∞,满足()()()()1122f x g x f x g x +=+且12x x ≠ 所以有0m <现不防设()()()()1211220x x f x g x f x g x <<+=+,得:111222112sin ln 2sin ln 22x x m x x x m x -+=-+()()()2121211ln ln 2sin sin 2m x x x x x x --=---①1122sin sin x x x x -<-()()212111sin sin 22x x x x -->--② 由①②式可得:()()()2121211ln ln 22m x x x x x x -->--- 即()()21213ln ln 02m x x x x -->-> 又1221ln ln ,ln ln 0x x x x <->2121302ln ln x x m x x -∴->⨯>-③ 又要证12249x x m <,即证21294m x x > 120,0m x x <<<Q即证m ->④所以由③式知,只需证明:2121ln ln x x x x ->-2121ln 1x x x x -> 设211x t x =>,只需证1ln t t->即证()ln 01t t >> 令()()ln 1h t t t =-> 由()()()2101h t t h t '=>>,在()1+∞,上为增函数, ()()10h t h∴>=2121ln ln x x x x -∴>-,所以由③知,0m ->>成立, 所以12249x x m <成立. 7.【2020·陕西西安中学高三期末】已知函数21()ln 1()2f x x a x a R =-+∈. (1)讨论函数()f x 的单调性;(2)若20a -≤<,对任意[]12,1,2x x ∈,不等式121211()()f x f x m x x -≤-恒成立,求实数m 的取值范围.【解析】(1)∵依题意可知:函数()f x 的定义域为()0,∞+,∴2()a x af x x x x-'=-=,当0a ≤时,()0f x '>在()0,∞+恒成立,所以()f x 在()0,∞+上单调递增. 当0a >时,由()0f x'>得x ()0fx '<得0x <<综上可得当0a ≤时,()f x 在()0,∞+上单调递增; 当0a >时,()f x 在(上单调递减;在)+∞上单调递增.(2)因为20a -≤<,由(1)知,函数()f x 在[]1,2上单调递增,不妨设1212x x ≤≤≤,则121211()()f x f x mx x -≤-, 可化为2121()()m m f x f x x x +≤+, 设21()()ln 12m mh x f x x a x x x=+=-++,则12()()h x h x ≥, 所以()h x 为[]1,2上的减函数, 即2()0a mh x x x x=--≤'在[]1,2上恒成立,等价于3m x ax ≥-在[]1,2上恒成立, 设3()g x x ax =-,所以max ()m g x ≥,因20a -≤<,所以2()30>'=-g x x a ,所以函数()g x 在[]1,2上是增函数,所以max ()(2)8212g x g a ==-≤(当且仅当2a =-时等号成立) 所以12m ≥.8.【2020·浙江温州期末】已知函数()()2log ln a f x x x x =+-,1a >. (1)求证:()f x 在()1,+∞上单调递增;(2)若关于x 的方程()1f x t -=在区间()0,∞+上有三个零点,求实数t 的值;(3)若对任意的112,,x x a a -⎡⎤∈⎣⎦,()()121f x f x e -≤-恒成立(e 为自然对数的底数),求实数a 的取值范围.【解析】(1)()()2ln 1'21ln x f x xx a =⋅+-,∵1x >,∴()'0f x >,故()f x 在()1,+∞上单调递增.(2)()()()()2222ln ln ln 'ln x x a a f x x a +-=,令()()()222ln ln ln g x x x a a =+-,()()22'ln 0g x a x=+>,()10g =, 故当()0,1x ∈,()'0g x <,()1,x ∈+∞,()'0g x >,即()f x 在()0,1x ∈上单调递减;在()1,x ∈+∞上单调递增.()11f =, 若()()11f x t f x t -=⇔=±在区间()0,∞+上有三个零点,则11t -=,2t =.(3)()f x 在1,1x a -⎡⎤∈⎣⎦上单调递减;在(]1,x a ∈上单调递增.故()()min 11f x f ==,()()max 1max ,f x f f a a ⎧⎫⎛⎫=⎨⎬⎪⎝⎭⎩⎭, 令()()112ln h a f f a a a a a ⎛⎫=-=+-⎪⎝⎭,∴()0h a <, 故()max 1ln f x a a =+-,∴ln 1ln 1a a e a a e -≤-⇒-≤-, 因为1a >,设()ln a a a ϕ=-则1'()10a aϕ=->,故()ln a a a ϕ=-为增函数, 又()ln 1e e e e ϕ=-=-. ∴(]1,a e ∈.9.【2020·浙江台州期末】已知函数()ln f x a x x b =-+,其中,a b ∈R . (1)求函数()f x 的单调区间;(2)使不等式()ln f x kx x x a ≥--对任意[]1,2a ∈,[]1,x e ∈恒成立时最大的k 记为c ,求当[]1,2b ∈时,b c +的取值范围.【解析】(1)因()f x 的定义域为()0,∞+,()()'10af x x x=->, 当0a ≤时,()'0f x <,∴()f x 在()0,∞+上单调递减; 当0a >时,()'f x 在()0,∞+上单调递减,()'0f a =, ∴()f x 在()0,a 上单调递增,在(),a +∞单调递减; (2)()()l ln n f x kx x x f x x x a k x a ++⇒≤≥--()1ln ln a x x x x bx+-++=. ∵[]1,2a ∈,[]1,x e ∈,∴()1ln ln 1ln ln a x x x x b x x x x bx x+-+++-++≥, 令()()21ln ln ln 'x x x x b x x b g g x x x x+-++-+-=⇒=, 由(1)()ln p x x x b ⇒=-+-在()1,+∞上递增;(1)当()10p ≥,即1b =时[]1,x e ∈,()()0'0p x g x ≥⇒≥,∴()g x 在[]1,e 上递增;∴()()min 122c g x g b b c b ===⇒+==.(2)当()0p e ≤,即[]1,2b e ∈-时[]1,x e ∈,()()0'0p x g x ≤⇒≤,∴()g x 在[]1,e 上递减; ∴()()min 22b b c g x g e b c b e e ++===⇒+=+14,2e ee ⎡⎤∈++⎢⎥⎣⎦.(3)当()()10p p e <时,()ln p x x x b =-+-在上递增; 存在唯一实数()01,x e ∈,使得()00p x =,则当()01,x x ∈时()()0'0p x g x ⇒<⇒<.当()0,x x e ∈时()()0'0p x g x ⇒>⇒>. ∴()()00000mi 000n 1ln ln 1ln x x x x b x x x c g x g x +-++=+===.∴00000011ln ln b c x x x x x x +=++-=+.此时00ln b x x =-. 令()()()11ln '10x h x x x h x h x x x-=-⇒=-=>⇒在[]1,e 上递增, ()()01,11,b e x e ∈-⇒∈,∴12,b c e e ⎛⎫+∈+ ⎪⎝⎭.综上所述,42,2b c e ⎡⎤+∈+⎢⎥⎣⎦. 10.【2020·蒙阴实验中学期末】设函数()212ln 222af x ax x x -=+++,a R ∈. (1)当2a =时,求函数()f x 在点()()1,1f 处的切线方程; (2)2x =是函数()f x 的极值点,求函数()f x 的单调区间; (3)在(2)的条件下,()217ln 422g x x x x ⎛⎫=-++-⎪⎝⎭,若[)11,x ∀∈+∞,()20,x ∃∈+∞,使不等式()()1122mf xg x x x -≥+恒成立,求m 的取值范围. 【解析】(1)()f x 的定义域为()0,∞+,2a =时,()2ln 2f x x x =++,()12f x x x'=+, ()13f '=,()13f =,所以切线方程为()331y x -=-,即30x y -=.(2)()()22221222ax a x a f x ax x x+-+-'=++=, 2x =是函数的极值点,()8422204a a f +-+'==,可得1a =-,所以()2232(0)2x x f x x x-++'=>,令()0f x '>,即22320x x --<,解得1,22x ⎛⎫∈-⎪⎝⎭,结合定义域可知()f x 在()0,2上单调递增,在()2,+∞上单调递减. (3)令()()()2ln ln 26h x f x g x x x x x =-=+++,[)11,x ∀∈+∞,[)20,x ∃∈+∞, 使得()()1122m f x g x x x -≥+恒成立,等价于()()2min 21mh x x x x ≥+≥⎡⎤⎣⎦, ()12ln 2h x x x x x'=++-,因为1x ≥,所以2ln 0x x ≥,12x x+≥,即()'0h x ≥, 所以()h x 在[)1,+∞上单调递增,()()14h x h ≥=, 即()20,x ∃∈+∞使得函数4mx x+≤,即转化为240x x m -+≤在()0,∞+有解, ()22424x x m x m -+=--+,所以40m -+≤,4m ≤.。
导数题中“任意、存在”型的归纳辨析

导数题中“任意、存在”型的归纳辨析导数题是高考题中的常客,而且大都以压轴题的面目出现,所以拿下导数题是迈入高分段的标志。
导数题虽年年有,但却悄然之中发生着些改变。
这其中,尤以关于“任意”、“存在”的内容最为明显。
“任意”、“存在”可以说是导数题最为明显的特色,从早期单一型,发展到现今的混合型。
下面对此作一归纳。
一.单一函数单一“任意”型例1.已知函数()ln()f x x x a =-+的最小值为0,其中0a >。
(1)求a 的值;(2)若对任意的[0,)x ∈+∞,有2()f x kx ≤成立,求实数k 的最小值。
解析:(1)1()x a f x x a+-'=+,()f x ∴在(,1)a a --单调递减,在(1,)a -+∞单调递增,所min ()f x (1)01f a a =-=⇒=。
(2)设2()ln()g x kx x x a =-++,则问题等价于()0g x ≥对[0,)x ∈+∞恒成立,即min ()0g x ≥。
因为当0k ≤时,x →+∞时,()f x →-∞,所以0k >。
由22(21)()1kx k x g x x +-'=+,若2104k k-->,则当21(0,)4k x k -∈-时,()0g x '<,()g x 单调递减,()(0)0g x g <=,矛盾。
从而2104k k--≤,解得12k ≥。
即实数k 的最小值是12。
点评:“任意”的意思是不管x 取给定集合中的哪一个值,得到的函数值都要满足给定的不等式,它有两种形式:“对任意的x A ∈,()()a f x >≥恒成立”等价于“当x A ∈时,max ()()a f x >≥”;“对任意的x A ∈,()()a f x <≤恒成立”等价于“当x A ∈时,min ()()a f x <≤”。
二.单一函数单一“存在”型例 2. 已知函数2()ln f x a x x =+(a R ∈),若存在[1,]x e ∈,使得()(2)f x a x ≤+成立,求实数a 的取值范围。
(2021年整理)利用导数研究存在性与任意性专题

利用导数研究存在性与任意性专题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(利用导数研究存在性与任意性专题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为利用导数研究存在性与任意性专题的全部内容。
利用导数研究恒成立、存在性与任意性问题一、利用导数研究不等式恒成立问题[典例]设f(x)=e x-a(x+1).(1)若∀x∈R,f(x)≥0恒成立,求正实数a的取值范围;(2)设g(x)=f(x)+错误!,且A(x1,y1),B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围.[解](1)因为f(x)=e x-a(x+1),所以f′(x)=e x-a.由题意,知a>0,故由f′(x)=e x-a=0,解得x=ln a.故当x∈(-∞,ln a)时,f′(x)<0,函数f(x)单调递减;当x∈(ln a,+∞)时,f′(x)>0,函数f(x)单调递增.所以函数f(x)的最小值为f(ln a)=e ln a-a(ln a+1)=-a ln a.由题意,若∀x∈R,f(x)≥0恒成立,即f(x)=e x-a(x+1)≥0恒成立,故有-a ln a≥0,又a>0,所以ln a≤0,解得0<a≤1.所以正实数a的取值范围为(0,1].(2)设x1,x2是任意的两个实数,且x1<x2.则直线AB的斜率为k=错误!,由已知k>m,即错误!>m.因为x2-x1>0,所以g(x2)-g(x1)>m(x2-x1),即g(x2)-mx2>g(x1)-mx1.因为x1<x2,所以函数h(x)=g(x)-mx在R上为增函数,故有h′(x)=g′(x)-m≥0恒成立,所以m≤g′(x).而g′(x)=e x-a-错误!,又a≤-1<0,故g′(x)=e x+错误!-a≥2错误!-a=2错误!-a.而2错误!-a=2错误!+(错误!)2=(错误!+1)2-1≥3,所以m的取值范围为(-∞,3].[方法点拨]解决该类问题的关键是根据已知不等式的结构特征灵活选用相应的方法,由不等式恒成立求解参数的取值范围问题一般采用分离参数的方法.而第(2)问则巧妙地把直线的斜率与导数问题结合在一起,命题思路比较新颖,解决此类问题需将已知不等式变形为两个函数值的大小问题,进而构造相应的函数,通过导函数研究其单调性解决.[对点演练]已知f(x)=x ln x,g(x)=-x2+ax-3.(1)若对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.(2)证明:对一切x∈(0,+∞),ln x>错误!-错误!恒成立.解:(1)由题意知2x ln x≥-x2+ax-3对一切x∈(0,+∞)恒成立,则a≤2ln x+x+错误!,设h(x)=2ln x+x+错误!(x>0),则h′(x)=错误!.①当x∈(0,1)时,h′(x)<0,h(x)单调递减;②当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.所以h(x)min=h(1)=4,对一切x∈(0,+∞),2f(x)≥g(x)恒成立,所以a≤h(x)min=4,即实数a的取值范围是(-∞,4].(2)问题等价于证明x ln x>错误!-错误!(x>0).又f(x)=x ln x(x>0),f′(x)=ln x+1,当x∈错误!时,f′(x)<0,f(x)单调递减;当x∈错误!时,f′(x)>0,f(x)单调递增,所以f(x)min=f错误!=-错误!.设m(x)=错误!-错误!(x>0),则m′(x)=错误!,当x∈(0,1)时,m′(x)>0,m(x)单调递增,当x∈(1,+∞)时,m′(x)<0,m(x)单调递减,所以m(x)max=m(1)=-错误!,从而对一切x∈(0,+∞), f(x)>m(x)恒成立,即x ln x>xe x-错误!恒成立.即对一切x∈(0,+∞),ln x>错误!-错误!恒成立.二、利用导数研究存在性与任意性问题[典例] 设f(x)=错误!+x ln x,g(x)=x3-x2-3.(1)如果存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,求满足上述条件的最大整数M;(2)如果对于任意的s,t∈错误!,都有f(s)≥g(t)成立,求实数a的取值范围.[解] (1)存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,等价于[g(x1)-g(x2)]max≥M.由g(x)=x3-x2-3,得g′(x)=3x2-2x=3x错误!.由g′(x)<0,解得0<x<错误!;由g′(x)>0,解得x<0或x>错误!.又x∈[0,2],所以g(x)在区间错误!上单调递减,在区间错误!上单调递增,又g(0)=-3,g(2)=1,故g(x)max=g(2)=1,g(x)min=g错误!=-错误!.所以[g(x1)-g(x2)]max=g(x)max-g(x)min=1+错误!=错误!≥M,则满足条件的最大整数M=4.(2)对于任意的s,t∈错误!,都有f(s)≥g(t)成立,等价于在区间错误!上,函数f(x)min≥g(x)max.由(1)可知在区间错误!上,g(x)的最大值为g(2)=1.在区间错误!上,f(x)=错误!+x ln x≥1恒成立等价于a≥x-x2ln x恒成立.设h(x)=x-x2ln x,x∈错误!,则h′(x)=1-2x ln x-x,易知h′(x)在区间错误!上是减函数,又h′(1)=0,所以当1<x<2时,h′(x)<0;当错误!<x<1时,h′(x)>0.所以函数h(x)=x-x2ln x在区间错误!上单调递增,在区间[1,2]上单调递减,所以h(x)max=h(1)=1,所以实数a的取值范围是[1,+∞).[方法点拨]等价转化法求解双参数不等式双参数不等式问题的求解方法一般采用等价转化法.本例第(1)问是“存在性"问题,转化方法是:如果存在x 1,x 2∈[0,2]使得g (x 1)-g (x 2)≥M 成立,则可转化为M ≤[g (x 1)-g (x 2)]max ,即求解使不等式M ≤g (x )max -g (x )min 成立时的M 的最大取值;第(2)问是“恒成立”问题,转化方法是:如果对于任意的x 1,x 2∈错误!,都有f (x 1)≥g (x 2)成立,则可转化为在区间错误!上,f (x )min ≥g (x )max ,求解得到实数a 的取值范围.[对点演练]已知函数f (x )=ln x -ax +错误!-1(a ∈R ). (1)当0<a <错误!时,讨论f (x )的单调性;(2)设g (x )=x 2-2bx +4.当a =错误!时,若对任意x 1∈(0,2),存在x 2∈[1,2],使f (x 1)≥g (x 2),求实数b 的取值范围.解:(1)因为f (x )=ln x -ax +错误!-1,所以f ′(x )=错误!-a +错误!=-错误!,x ∈(0,+∞), 令f ′(x )=0,可得两根分别为1,错误!-1, 因为0<a <错误!,所以错误!-1>1>0,当x ∈(0,1)时,f ′(x )<0,函数f (x )单调递减;当x ∈⎝⎛⎭⎪⎫1,1a -1时,f ′(x )>0,函数f (x )单调递增;当x ∈错误!时,f ′(x )<0,函数f (x )单调递减. (2)a =错误!∈错误!,错误!-1=3∉(0,2),由(1)知,当x ∈(0,1)时,f ′(x )<0,函数f (x )单调递减;当x ∈(1,2)时,f ′(x )>0,函数f (x )单调递增,所以f (x )在(0,2)上的最小值为f (1)=-错误!.对任意x 1∈(0,2),存在x 2∈[1,2],使f (x 1)≥g (x 2)等价于g (x )在[1,2]上的最小值不大于f (x )在(0,2)上的最小值-错误!,(*)又g (x )=(x -b )2+4-b 2,x ∈[1,2],所以,①当b <1时,g (x )min =g (1)=5-2b >0,此时与(*)矛盾; ②当1≤b ≤2时,g (x )min =4-b 2≥0,同样与(*)矛盾; ③当b >2时,g (x )min =g (2)=8-4b , 且当b >2时,8-4b <0,解不等式8-4b ≤-12,可得b ≥错误!,所以实数b 的取值范围为错误!.。
任意性和存在性问题的教学思考

任意性和存在性问题的教学思考作者:李乐来源:《中学教学参考·理科版》2013年第03期任意性、存在性问题,是高考常考题型之一,我们教师在高考复习时多以“题海”战术来突破,不仅效率低,同时也加重了学生的负担,使相当一部分学生“丧失”了学习的兴趣.如何有效地指导学生突破是摆在每一位高三数学教师面前的任务.精选好题目,再适当地将原来的题目变形,这样既可以提高学生学习的兴趣,又能激发学生解答问题时思维的积极性、主动性,培养学生深入探究的思维品质,帮助学生更好地掌握所学的知识,达到举一反三的目的.下面就由一道例题展开,阐述自己的教学看法.【例题】已知函数f(x)=mxx2+n(m,n∈R)在x=1处取得极值2.(1)求f(x)的解析式;(2)设函数g(x)=x2-2ax+a,若对于任意x1∈R,总存在x2∈[-1,1],使得g(x2)解析:(1)f(x)=mxx2+n(m,n∈R),f′(x)=m(x2+n)-mx·2x(x2+n)2=mn-mx2(x2+n)2.因为f(x)=mxx2+n(m,n∈R)在x=1处取得极值2,所以f′(1)=0,f(1)=2.解得m=4,n=1,或m=0,n=-1,经检验m=0,n=-1不合题意,舍去;m=4,n=1符合题意,所以f(x)=4xx2+1.(2)f′(x)=4-4x2(x2+1)2=-4(x+1)(x-1)(x2+1)2,令f′(x)=0得x=-1或x=1.当x0,函数f(x)在(-1,1)单调递增;当x>1时,f′(x)0时,f(x)>0,所以当x=-1时,f(x)取得最小值-2,当x=1时,f(x)取得最大值为2.因为对于任意x1∈R,总存在x2∈[-1,1],使得g(x2)因为g(x)=x2-2ax+a=(x-a)2+a-a2,当a≤-1时,g(x)的最小值为g(-1)=1+3a,由1+3a当a≥1时,g(x)的最小值为g(1)=1-a,由1-a3;当-1综上,a∈(-∞,-1)∪(3,+∞).利用函数与导数的相关知识,把任意性、存在性问题转化为函数值域之间的关系问题.例题的第(2)问,是对于任意x1∈R,总存在x2∈[-1,1],使得g(x2)思考:把第(2)问条件改为“对于任意x2∈[-1,1],总存在x1∈R”,又该如何解决?变式1:已知函数f(x)=mxx2+n(m,n∈R)在x=1处取得极值2.(1)求f(x)的解析式;(2)设函数g(x)=x2-2ax+a,若对于任意x2∈[-1,1],总存在x1∈R,使得g(x2)解析:对于任意x1∈R,总存在x2∈[-1,1],使得g(x2)因为g(x)=x2-2ax+a=(x-a)2+a-a2,当a≤0时,g(x)的最大值为g(1)=1-a,由1-a当a>0时,g(x)的最大值为g(-1)=1+3a,由1+3a综上,a∈(-1,13).思考:把第(2)问条件再改为“对于任意x1∈R,任意x2∈[-1,1]”,又如何解决?变式2:已知函数f(x)=mxx2+n(m,n∈R)在x=1处取得极值2.(1)求f(x)的解析式;(2)设函数g(x)=x2-2ax+a,是否存在实数a,对于任意x1∈R,x2∈[-1,1],g(x2)解析:对于任意x1∈R,x2∈[-1,1],都有g(x2)当a≤0时,g(x)的最大值为g(1)=1-a,1-a当a>0时,g(x)的最大值为g(-1)=1+3a,1+3a综上,不存在实数满足条件.思考:把第(2)问条件改为“存在x1∈R,x2∈[-1,1]”,又如何解决?变式3:已知函数f(x)=mxx2+n(m,n∈R)在x=1处取得极值2.(1)求f(x)的解析式;(2)设函数g(x)=x2-2ax+a,若存在x1∈R,x2∈[-1,1],使得g(x2)评析:若存在x1∈R,x2∈[-1,1],使得g(x)当a≤-1时,g(x)的最小值为g(-1)=1+3a,由1+3a当a≥1时,g(x)的最小值为g(1)=1-a,由1-a当-1综上,a∈(-∞,-1]∪[1,+∞).本题通过互换任意性及存在性、全部变换为任意性、全部变换为存在性等变形,循序渐进,环环相扣,使学生处于一种愉悦的探索历程中,培养了学生思维的灵活性、变通性.通过这样的复习,还能使学生对如何解决任意性、存在性问题有了更深刻的理解.一道题在手,若能打开思维的窗扉,不仅可以培养学生的发散性思维能力及知识迁移能力,还可以开阔学生思路,培养学生的逻辑推理能力和想象力,提高学生的数学学习兴趣,提高数学课堂的有效性.精选、会用、善变,通过对一道数学题目的“变化”,让学生体会出“数学美”.教师借助一题多变进行教学,是提高教学质量、发展学生思维能力和增强学生解题能力的重要途径.(责任编辑金铃)。
函数中的任意和存在性问题

函数中的任意和存在性问题
当数学中的函数$f(x)$在某个定义域内“存在”,常常指的是函数在该定义域内存在定义,即对于该定义域内的每一个$x$,函数$f(x)$都有一个确定的输出值。
这意味着函数在该定义域内无未定义的点或不存在的点。
而“任意”则表示在某个条件下可以取任何值,通常出现在数学的定义或定理中。
例如,对于一个实数$x$,我们说“任意大的正实数”,表示该数可以取到比任何一个正实数都要大的值。
在数学中,存在和任意是两个基本的概念。
当我们讨论某个对象“存在”时,常常需要指明其定义域或范围,以确定其是否无未定义的点或是否符合条件。
而当我们使用“任意”时,通常需要指明在什么条件下可以取任意值,以确定其意义和约束条件。
需要注意的是,存在和任意这两个概念在不同的数学领域、分支或场景中可能有不同的定义和使用方式。
因此,在理解数学语言和符号时,需要仔细阅读定义和前提条件,并理解概念的含义和语境。
函数任意性与存在性问题探析

函数任意性与存在性问题探析函数的任意性与存在性问题是数学分析中的一个重要问题,涉及到了函数的构造和性质的研究。
在这个问题中,我们关注的是是否存在这样的函数,它具有我们期望的性质。
这篇文章将关注函数的任意性和存在性问题,从数学的角度对其进行探析。
函数的任意性问题指的是在一定的条件下,是否存在满足条件的函数。
在数学中,我们常常会提出一些条件,然后寻找满足这些条件的函数。
例如,我们可以要求函数在一些区间上连续、可微分、可积等等。
对于这些条件,我们需要判断是否存在满足条件的函数。
数学中,存在性问题往往是基于已有的数学定理和方法来研究的。
通过运用已有的数学工具和理论,我们可以判断是否存在满足条件的函数。
例如,当我们需要构造一个连续函数时,可以利用魏尔斯特拉斯逼近定理来进行构造;当我们需要构造一个可微分函数时,可以运用泰勒展开的方法;当我们需要构造一个可积函数时,可以利用黎曼和勒贝格定理等。
然而,存在性问题并不总是那么容易回答的。
有时,我们可能需要寻找一个不同寻常的函数来满足我们的条件。
对于这种情况,我们可能需要运用一些创造性的方法来构造函数。
例如,为了构造一个连续但无处可微的函数,我们可以考虑典型的例子,魏尔斯特拉斯函数。
这个函数在整个实数轴上连续,但在任何一点都不可微。
在一些情况下,我们可能会面临不存在满足条件函数的问题。
例如,对于方程f(x)=0,我们可能会想要找到一个函数f(x)来满足这个方程。
然而,根据零点存在性定理,除非满足一些条件,否则可能不存在这样的函数。
这就意味着,即使我们想要找到一个函数来满足一些方程,也不一定能找到。
因此,函数的任意性与存在性问题是一对相互关联的问题,互相影响。
在解决这些问题的过程中,我们需要充分考虑多种因素,如数学定理、方法、工具等。
对于存在性问题,我们可以根据已有的数学理论和定理来进行判断;对于任意性问题,我们需要构造一些特殊的函数,来满足我们给定的条件。
总之,函数的任意性与存在性问题是数学分析中的重要问题,在数学研究和应用中都具有重要意义。
高中数学函数中任意性与存在性的综合问题探讨

高中数学函数中任意性与存在性的综合问题探讨本课题经由高中一届学生的函数知识学习实际情况结合本人教学经验,结合新课程标准,综合分析相关原由,给出部分建设性教学建议,以便和广大教育工作者进行交流和参考。
标签:高中数学;新课程标准;任意性;存在性;教学一、选题理由学生对形如这类成立,求某个参数的取值范围。
学生基本上知道这是最值的比较,但是到底哪个是取最大值,哪个是取最小值来作比较,并不是特别清楚,可以说是模糊的,所以将这个课题选出来和大家一起探讨。
二、具体举例典例、已知函数,,如果对任意的,均存在,使得成立,求的取值范围.分析:这类问题是高中数学中《函数与导数》这一章节中的一类常见的问题,其考察的基本内容为用导数知识来求函数的最值问题,进而得到相应的参数的范围,而学生对于如下的两个被分解题目都能够进行求解分解一:已知函数,如果对任意的,恒成立,求的取值范围.分解二:已知函数,均存在,使得成立,求的取值范围.分解一为一个恒成立问题,分解二为一个存在性问题,所以单独求解这两个问题是比较简单的,而本例是一个将这两种情形糅合在一起的函数综合题,但是按照相应的思路拆分来看,问题就会迎刃而解了。
解析:先令,则原命题等价于已知函数如果对任意的,恒成立,这样就明显的转化为成立,其中.接下来就来处理,这样原命题就进一步可以理解为,已知函数,如果存在,使得成立.所以整个命题就为,其中,由二次函数在区间上的最值的相关知识易知因为,所以化简为当时,,所以在上,,在上,当时,在上,,在上,,在上,当时,在上,当时,在上,在上,在上,所以,综上所述,就有当时,函数在区间上为单调递增函数,故,解得此时的范围为当时,函数在上位单调递增函数,在上位单调递减函数,故,由于,所以所以,则在时恒成立此时的范围为综上所述,本题所求的的取值范围为点评:函数与导数这部分知识中间的恒成立问题和存在性问题是一类常见问题,对两者的综合考察也是一个常规考点,在此例子中将这样一个综合性问题进行分开分析,这样就变成了连个独立恒成立問题和存在性问题,进而就可以用熟悉的知识来进行求解了。
高中数学任意性与存在性问题探究

高中数学任意性与存在性问题探究函数中任意性和存在性问题探究近年的高考中,全称命题和存在性命题与导数的结合成为了一大亮点。
本文将结合高考试题对此类问题进行归纳探究。
一、相关结论:结论1:对于任意的x1∈[a,b]和x2∈[c,d],若f(x1)>g(x2),则有[f(x)]min>[g(x)]max;【如图一】结论2:存在x1∈[a,b]和x2∈[c,d],使得f(x1)>g(x2),则有[f(x)]max>[g(x)]XXX;【如图二】结论3:对于任意的x1∈[a,b]和存在x2∈[c,d],使得f(x1)>g(x2),则有[f(x)]min>[g(x)]XXX;【如图三】结论4:存在x1∈[a,b]和任意的x2∈[c,d],使得f(x1)>g(x2),则有[f(x)]max>[g(x)]max;【如图四】结论5:存在x1∈[a,b]和x2∈[c,d],使得f(x1)=g(x2),则f(x)的值域和g(x)的值域交集不为空;【如图五】例题1】:已知两个函数f(x)=8x+16x-k,g(x)=2x+5x+4x,x∈[-3,3],k∈R;1) 若对于任意的x∈[-3,3],都有f(x)≤g(x),求实数k的取值范围;2) 若存在x∈[-3,3],使得f(x)≤g(x),求实数k的取值范围;3) 若对于任意的x1,x2∈[-3,3],都有f(x1)≤g(x2),求实数k的取值范围;解:1)设h(x)=g(x)-f(x)=2x-3x-12x+k,问题可转化为:对于x∈[-3,3],h(x)≥常数成立,即[h(x)]XXX≥常数。
由结论1可知,当f(x1)>g(x2)时,[f(x)]min>[g(x)]max,即h(x)的最小值出现在f(x)和g(x)的交点处。
因此,我们可以求出h(x)的导数h'(x)并列出变化情况表格,得到[h(x)]min=k-45.因此,k≥45,即k∈[45,+∞)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数与导数中任意性和存在性问题探究命题人:闫霄 审题人:冯昀山 一、相关结论:结论1:min [,],()[()]x a b f x m f x m ∀∈>⇔>; 结论2:max [,],()[()]x a b f x m f x m ∀∈<⇔<; 结论3:max [,],()[()]x a b f x m f x m ∃∈>⇔>; 结论4:min [,],()[()]x a b f x m f x m ∃∈<⇔<;结论5:1212min max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∀∈>⇔>;【如图一】 结论6:1212max min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∃∈>⇔>;【如图二】 结论7:1212min min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∃∈>⇔>;【如图三】 结论8:1212max max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∀∈>⇔>;【如图四】 结论9:1212[,],[,],()()()x a b x c d f x g x f x ∃∈∃∈=⇔的值域和()g x 的值域交集不为空; 结论10:1212[,],[,],()()()x a b x c d f x g x f x ∀∈∃∈=⇔的值域是()g x 的值域的子集 【例题1】:已知两个函数232()816,()254,[3,3],f x x x k g x x x x x k R =+-=++∈-∈;(1) 若对[3,3]x ∀∈-,都有()()f x g x ≤成立,求实数k 的取值范围; (2) 若[3,3]x ∃∈-,使得()()f x g x ≤成立,求实数k 的取值范围; (3) 若对12,[3,3]x x ∀∈-,都有12()()f x g x ≤成立,求实数k 的取值范围;解:(1)设32()()()2312h x g x f x x x x k =-=--+,(1)中的问题可转化为:[3,3]x ∈-时,()0h x ≥恒成立,即min [()]0h x ≥。
'2()66126(2)(1)h x x x x x =--=-+;当x 变化时,'(),()h x h x 的变化情况列表如下:-3(-3,-1) -1 (-1,2) 2 (2,3) 3 h '(x)+-+h(x)k-45 增函数 极大值 减函数 极小值 增函数k-9因为(1)7,(2)20h k h k -=+=-,所以,由上表可知min [()]45h x k =-,故k-45≥0,得k ≥45,即k ∈[45,+∞). 小结:①对于闭区间I ,不等式f(x)<k 对x ∈I 时恒成立⇔[f(x)]max <k, x ∈I;不等式f(x)>k 对x ∈I 时恒成立⇔[f(x)]min >k, x ∈I.②此题常见的错误解法:由[f(x)]max ≤[g(x)]min 解出k 的取值范围.这种解法的错误在于条件“[f(x)]max ≤[g(x)]min ”只是原题的充分不必要条件,不是充要条件,即不等价. (2)根据题意可知,(2)中的问题等价于h(x)= g(x)-f(x) ≥0在x ∈[-3,3]时有解,故[h(x)]max ≥0.由(1)可知[h(x)]max = k+7,因此k+7≥0,即k ∈[-7,+∞). (3)根据题意可知,(3)中的问题等价于[f(x)]max ≤[g(x)]min ,x ∈[-3,3]. 由二次函数的图像和性质可得, x ∈[-3,3]时, [f(x)]max =120-k. 仿照(1),利用导数的方法可求得x ∈[-3,3]时, [g(x)]min =-21. 由120-k ≥-21得k ≥141,即k ∈[141,+∞). 说明:这里的x 1,x 2是两个互不影响的独立变量.从上面三个问题的解答过程可以看出,对于一个不等式一定要看清是对“∀x ”恒成立,还是“∃x ”使之成立,同时还要看清不等式两边是同一个变量,还是两个独立的变量,然后再根据不同的情况采取不同的等价条件,千万不要稀里糊涂的去猜..【例题2】:(2010年山东理科22) 已知函数1()ln 1()af x x ax a R x-=-+-∈; (1)当12a ≤时,讨论()f x 的单调性; (2)设2()24g x x bx =-+,当14a =时,若对1(0,2)x ∀∈,2[1,2]x ∃∈,使12()()f x g x ≥,求实数b 的取值范围;解:(1)(解答过程略去,只给出结论)当a ≤0时,函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;当a=21时,函数f(x)在(0,+∞)上单调递减; 当0<a<21时,函数()f x 递增区间为1(1,1)a -,递减区间为(0,1),1(1,)a-+∞;(2)函数的定义域为(0,+∞),f '(x )=x 1-a+21xa -=-221x a x ax -+-,a=41时,由f '(x )=0可得x 1=1,x 2=3. 因为a=41∈(0,21),x 2=3∉(0,2),结合(1)可知函数f(x)在(0,1)上单调递减,在(1,2)上单调递增,所以f(x) 在(0,2)上的最小值为f(1)= -21.由于“对∀x 1∈(0,2),∃x 2∈[1,2],使f(x 1) ≥g(x 2)”等价于“g(x)在[1,2]上的最小值不大于f(x) 在(0,2)上的最小值f(1)= -21”. (※)又g(x)=(x -b)2+4-b 2, x ∈[1,2],所以① 当b<1时,因为[g(x)]min =g(1)=5-2b>0,此时与(※)矛盾;② 当b ∈[1,2]时, 因为[g(x)]min =4-b 2≥0,同样与(※)矛盾; ③ 当b ∈(2,+∞)时,因为[g(x)]min =g(2)=8-4b.解不等式8-4b ≤-21,可得b ≥817. 综上,b 的取值范围是[817,+∞).二、相关类型题:类型一:直接求最值(往往需带参讨论) 例3: 类题: 例4: 类题:类型二:分离常数法求最值 例5:类题:例6: 类题:类型三:先进行变形简化,再求最值 例7: 类题:类型四:分离常数法+罗比达法则 洛必达法则简介:法则1 若函数f(x) 和g(x)满足下列条件:(1) ()lim 0x af x →= 及()lim 0x ag x →=;(2)在点a 的去心邻域内,f(x) 与g(x) 可导且g '(x)≠0;(3)()()limx a f x l g x →'=', 那么 ()()lim x a f x g x →=()()limx a f x l g x →'='。
法则2 若函数f(x) 和g(x)满足下列条件:(1)()lim 0x f x →∞= 及()lim 0x g x →∞=;(2)0A ∃>,f(x) 和g(x)在(),A -∞与(),A +∞上可导,且g '(x)≠0;(3)()()limx f x l g x →∞'=', 那么 ()()lim x f x g x →∞=()()limx f x l g x →∞'='。
法则3 若函数f(x) 和g(x)满足下列条件:(1) ()lim x af x →=∞及()lim x ag x →=∞;(2)在点a 的去心邻域内,f(x) 与g(x) 可导且g '(x)≠0;(3)()()limx a f x l g x →'=',那么 ()()lim x a f x g x →=()()limx a f x l g x →'='。
利用洛必达法则求未定式的极限是微分学中的重点之一,在解题中应注意: ○1将上面公式中的x→a,x→∞换成x→+∞,x→-∞,x a+→,x a-→洛必达法则也成立。
○2洛必达法则可处理00,∞∞,0⋅∞,1∞,0∞,00,∞-∞型。
○3在着手求极限以前,首先要检查是否满足00,∞∞,0⋅∞,1∞,0∞,00,∞-∞型定式,否则滥用洛必达法则会出错。
当不满足三个前提条件时,就不能用洛必达法则,这时称洛必达法则不适用,应从另外途径求极限。
○4若条件符合,洛必达法则可连续多次使用,直到求出极限为止。
例8:(2010年全国新课标理)设函数2()1xf x e x ax =---。
(1) 若0a =,求()f x 的单调区间; (2) 若当0x ≥时()0f x ≥,求a 的取值范围 原解:(1)0a =时,()1xf x e x =--,'()1xf x e =-.当(,0)x ∈-∞时,'()0f x <;当(0,)x ∈+∞时,'()0f x >.故()f x 在(,0)-∞单调减少,在(0,)+∞单调增加(II )'()12xf x e ax =--由(I )知1xe x ≥+,当且仅当0x =时等号成立.故'()2(12)f x x ax a x ≥-=-,从而当120a -≥,即12a ≤时,'()0 (0)f x x ≥≥,而(0)0f =, 于是当0x ≥时,()0f x ≥. 由1(0)xe x x >+≠可得1(0)xe x x ->-≠.从而当12a >时,'()12(1)(1)(2)x x x x x f x e a e e e e a --<-+-=--,故当(0,ln 2)x a ∈时,'()0f x <,而(0)0f =,于是当(0,ln 2)x a ∈时,()0f x <.综合得a 的取值范围为1,2⎛⎫-∞ ⎪⎝⎭原解在处理第(II )时较难想到,现利用洛必达法则处理如下: 另解:(II )当0x =时,()0f x =,对任意实数a,均在()0f x ≥;当0x >时,()0f x ≥等价于21x e x a x--≤ 令()21x e x g x x --=(x>0),则322()x x xe e x g x x -++'=,令()()220xxh x xe e x x =-++>,则()1xxh x xe e '=-+,()0x h x xe ''=>,知()h x '在()0,+∞上为增函数,()()00h x h ''>=;知()h x 在()0,+∞上为增函数,()()00h x h >=;()0g x '∴>,g(x)在()0,+∞上为增函数。
