IGBT驱动电阻计算详解
IGBT驱动电路的选择及驱动电阻的选择

IGBT驱动电路的选择及驱动电阻的选择IGBT驱动电路的选择绝缘栅双极型晶体管(IGBT)在今天的电力电子领域中已经得到广泛的应用,在实际使用中除IGBT自身外,IGBT 驱动器的作用对整个换流系统来说同样至关重要。
驱动器的选择及输出功率的计算决定了换流系统的可靠性。
驱动器功率不足或选择错误可能会直接导致IGBT 和驱动器损坏。
以下总结了一些关于IGBT驱动器输出性能的计算方法以供选型时参考。
IGBT 的开关特性主要取决于IGBT的门极电荷及内部和外部的电阻。
图1是IGBT 门极电容分布示意图,其中CGE 是栅极-发射极电容、CCE 是集电极-发射极电容、CGC 是栅极-集电极电容或称米勒电容(Miller Capacitor)。
门极输入电容Cies 由CGE 和CGC 来表示,它是计算IGBT 驱动器电路所需输出功率的关键参数。
该电容几乎不受温度影响,但与IGBT 集电极-发射极电压VCE 的电压有密切联系。
在IGBT数据手册中给出的电容Cies 的值,在实际电路应用中不是一个特别有用的参数,因为它是通过电桥测得的,在测量电路中,加在集电极上C 的电压一般只有25V(有些厂家为10V),在这种测量条件下,所测得的结电容要比VCE=600V 时要大一些(如图2)。
由于门极的测量电压太低(VGE=0V )而不是门极的门槛电压,在实际开关中存在的米勒效应(Miller 效应)在测量中也没有被包括在内,在实际使用中的门极电容Cin 值要比IGBT 数据手册中给出的电容Cies 值大很多。
因此,在IGBT数据手册中给出的电容Cies值在实际应用中仅仅只能作为一个参考值使用。
确定IGBT 的门极电荷对于设计一个驱动器来说,最重要的参数是门极电荷QG(门极电压差时的IGBT 门极总电荷),如果在IGBT 数据手册中能够找到这个参数,那么我们就可以运用公式计算出:图一门极驱动能量E = QG ? UGE = QG ? [ VG(on) - VG(off) ] 门极驱动功率PG = E ? fSW = QG ? [ VG(on) - VG(off) ] ? fSW 驱动器总功率P = PG + PS(驱动器的功耗)平均输出电流IoutAV = PG / ΔUGE = QG ? fSW 最高开关频率fSW max. = IoutAV(mA) / QG(μC) 峰值电流IG MAX =ΔUGE / RG min = [ VG(on) - VG(off) ] / RG min 其中的RG min = RG extern + RG intern fsw max. : 最高开关频率IoutAV : 单路的平均电流QG : 门极电压差时的IGBT门极总电荷RG extern : IGBT 外部的门极电阻RG intern : IGBT 芯片内部的门极电阻但是实际上在很多情况下,数据手册中这个门极电荷参数没有给出,门极电压在上升过程中的充电过程也没有描述。
IGBT驱动电流及驱动功率的计算

IGBT驱动电流及驱动功率的计算IGBT驱动电路的设计包括上下桥绝缘水平的选择、驱动电压水平的确定、驱动芯片驱动功率的确定、短路保护电路等等。
今天我们重点讨论一下驱动电流以及功率的确定,也就是说如何确定一个驱动芯片电流能力是不是可以驱动一个特定型号的IGBT,如果不能驱动该如何增强驱动输出能力。
01、驱动芯片峰值电流的计算在选择IGBT驱动芯片时,很重要的一步就是计算IGBT所需要的最大驱动电流,在不考虑门极增加Cge电容的条件下,可以把IGBT驱动环节简化为一个RLC电路,如下图阴影部分所示。
求解这个电路可以得到峰值电路的关系式如下:I peak:驱动环节可以输出的最大电流ΔU ge:门极电源最大值减去最小值R G,ext:外部门极电阻值,R G,int为器件内部的电阻值从上面公式可以看出最大驱动电流取决于门极电压水平,以及门极电阻值,一旦这两个参数确定后,所需要的最大驱动电流基本确定。
当然,在一些设计中会选用不同的开通关断电阻,那么就需要分别计算开通关断需要的电流。
依据上述计算的开通关断电流值可以初步选择芯片的驱动电流,芯片数据手册给出的峰值不能小于计算得到的电流值,并且适当考虑工程余量。
02、推挽电路放大电路增加驱动电流如果驱动芯片的输出电流不能驱动特定IGBT的话,比较简单的方法是采用推挽电路进一步增强驱动芯片的峰值电流输出能力。
采用三极管放大是一种常用的方式,其计算步骤如下:(1)根据选择的驱动电压水平以及门极电阻计算得到需求的最大峰值电流I peak (2)选择合适耐压的PNP/NPN三极管组成推挽电路(3)查所选择的三极管数据手册中的电流传输系数h FE,计算得到三极管的基极电流(4)计算驱动芯片输出极的输出电阻上述步骤给出了BJT作为推挽放大电路时一般的步骤,需要着重考虑的是BJT的耐压以及基级电阻的匹配。
由于使用BJT做推挽放大设计设计比较简单,因此在设计中得到广泛的应用。
在大功率应用场合比较常用的BJT三极管型号有MJD44/45H11(80V)等。
IGBT驱动电阻计算详解

IGBT驱动电路参数计算详解电阻大功率IGBT 模块在使用中驱动器至关重要,本文介绍在特定应用条件下IGBT门极驱动性能参数的计算方法,经验公式及有关CONCEPT 驱动板的选型标准,得出的一些参数值可以作为选择一款合适IGBT驱动器的基本依据。
1 门极驱动的概念IGBT存在门极-发射极电容Cge,门极-集电极电容Cgc,我们将IGBT的门极等效电容定义为Cg,门极驱动回路的等效电路如下图所示:其本质是:一个脉冲电压源向RC电路进行充放电,对于这个电压源,有2个物理量我们需要关心,1.它的功率;2.它的峰值电流。
2 驱动功率的计算驱动器是用来控制功率器件的导通和关断。
为了实现此功能,驱动器对功率器件的门极进行充电以达到门极开通电压VGE_on,或者是对门极进行放电至门极关断电压VGE_off。
门极电压的两种电平间的转换过程中,在驱动器门极驱动电阻及功率器件组成的回路中产生一定的损耗。
这个参数我们称为驱动功率PDRV。
驱动器必须根据其所驱动的功率器件所需的驱动功率来选择。
驱动功率可以从门极电荷量QGate,开关频率fIN,以及驱动器实际输出电压摆幅ΔVGate 计算得出:P DRV = Q Gate * f IN * ΔV Gate (Eq. 1)备注:P DRV: 驱动器每通道输出功率;f IN: IGBT开关频率;Q Gate :IGBT门极电荷,可从规格书第一页查出,不同IGBT该数值不同;ΔV Gate:门极驱动电压摆幅,等于驱动正压+U 和负压–U 之间差值。
如果门极回路放置了一个电容CGE (辅助门极电容),那么驱动器也需要对该电容进行充放电,如图1 所示:图1.带外接阻容的门级驱动只要CGE 在一个周期内被完全的充放电,那么RGE 值并不影响所需驱动功率。
驱动功率可以从以下公式得出:P DRV = Q GATE * f IN *ΔV GATE + C GE * f IN*ΔV GATE2(Eq. 2)这个功率是每个IGBT 驱动时必须的,但门极的充放电是没有能量损失的,这个功率实际上损失在驱动电阻及外部电路中。
IGBT基本参数详解讲解

第一部分IGBT模块静态参数1,:集射极阻断电压在可使用的结温范围内,栅极和发射极短路状况下,集射极最高电压.手册里一般为25℃下的数据,随着结温的降低,会逐渐降低。
由于模块内外部的杂散电感,IGBT在关断时最容易超过限值。
2,:最大允许功耗在25℃时,IGBT开关的最大允许功率损耗,即通过结到壳的热阻所允许的最大耗散功率。
其中,为结温,为环境温度。
二极管的最大功耗可以用同样的公式获得.在这里,顺便解释下这几个热阻,结到壳的热阻抗,乘以发热量获得结与壳的温差;芯片热源到周围空气的总热阻抗,乘以发热量获得器件温升;芯片结与PCB间的热阻抗,乘以单板散热量获得与单板的温差。
3,集电极直流电流在可以使用的结温范围流集射极的最大直流电流.根据最大耗散功率的定义,可以由最大耗散功率算出该值。
所以给出一个额定电流,必须给出对应的结和外壳的温度。
)4,可重复的集电极峰值电流规定的脉冲条件下,可重复的集电极峰值电流。
5,RBSOA,反偏安全工作区IGBT关断时的安全工作条件。
如果工作期间的最大结温不被超过,IGBT在规定的阻断电压下可以驱使两倍的额定电流。
6,短路电流短路时间不超过10us。
请注意,在双脉冲测试中,上管GE之间如果没有短路或负偏压,就很容易引起下管开通时,上管误导通,从而导致短路。
7,集射极导通饱和电压在额定电流条件下给出,Infineon的IGBT都具有正温度效应,适宜于并联。
随集电极电流增加而增加,随着增加而减小。
可用于计算导通损耗.根据IGBT的传输特性,计算时,切线的点尽量靠近工作点。
对于SPWM方式,导通损耗由下式获得,M为调制因数;为输出峰值电流;为功率因数.第二部分IGBT模块动态参数1,模块内部栅极电阻为了实现模块内部芯片的均流,模块内部集成了栅极电阻,该电阻值常被当成总的驱动电阻的一部分计算IGBT驱动器的峰值电流能力。
2,外部栅极电阻数据手册中往往给出的是最小推荐值,可以通过以下电路实现不同的和。
如何计算IGBT的驱动功率?

如何计算IGBT的驱动功率?展开全文确定门极电荷Qg和门极电容对于设计一个驱动器来说,最重要的参数莫过于门极电荷Qg的大小,同时确定实际的门极输入电容Cies的大小,因为Datasheet中给到的输入电容大小一般是个参考值,确定实际门极输入电容是一重要意义的。
我们可以通过测量门极的充电过程来确定实际输入结电容Cin的大小。
首先,在负载端没有输出电压的情况下,我们可以进行下面这样的计算:门极电荷Qg=∫idt=C*ΔV确定了门极电荷Qg之后,我们可以通过门极充电过程中的门极电压上升过程,示波器可以测量出ΔV,那么利用公式可以计算出实际的门极输入电容Cin=Qg/ΔV这里的测得的实际输入结电容Cin在我们的设计中是具有很大意义的。
1.关于Ciss在IGBT的Datasheet中,我们经常会看到一个参数Ciss,在实际电路应用中,这个参数其实并不算一个很有用的参数,是因为它是通过电桥测得的,由于测量电压太小而不能达到门极的门槛电压,实际开关过程中的miller效应并没有能包涵在内。
在测量电路中,一个25V的电压加在集电极上,在这种测量方法下测得的结电容要比Vce=0的时候要小一些,因此,规格书中的Ciss这个参数一般用于IGBT相互做对比时使用。
一般我们使用下面的经验公式根据规格书的Ciss来计算输入电容Cin的大小Cin=5Ciss2.驱动功率的计算接下来让我们看看应该如何来计算驱动功率。
在输入结电容中存储的能量可以通过如下公式计算:W=1/2*Cin*ΔU?其中,ΔU是门极上上升的整个电压,比如在±15V的驱动电压下,ΔU就是30V。
在每个周期,门极被充电两次,一个IGBT所需的驱动功率我们可以按下式计算:P=f*Cin*ΔU?如果门极电荷先前通过测量得到了,那么P=f*Qg*ΔU这个功率是每个IGBT驱动时所必须的,但门极的充放电时基本没有能量损失的,这个功率实际上损失在驱动电阻和外部电路中。
IGBT 的驱动特性及功率计算
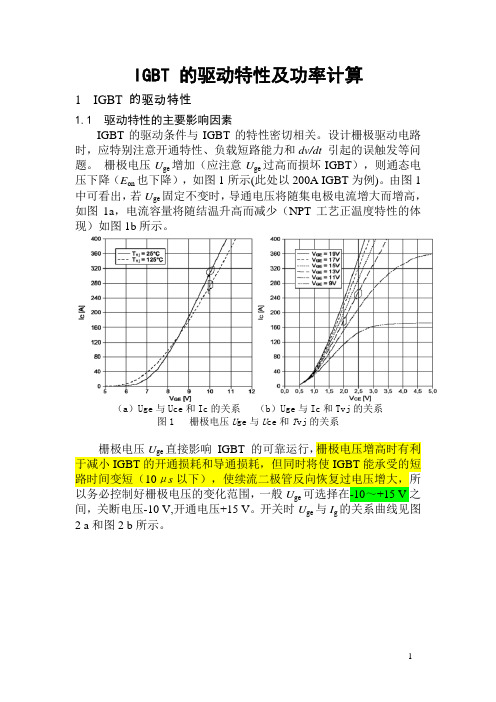
IGBT 的驱动特性及功率计算1 IGBT 的驱动特性1.1 驱动特性的主要影响因素IGBT的驱动条件与IGBT的特性密切相关。
设计栅极驱动电路时,应特别注意开通特性、负载短路能力和dv/dt 引起的误触发等问题。
栅极电压U ge增加(应注意U ge过高而损坏IGBT),则通态电压下降(E on也下降),如图1所示(此处以200A IGBT为例)。
由图1中可看出,若U ge固定不变时,导通电压将随集电极电流增大而增高,如图1a,电流容量将随结温升高而减少(NPT工艺正温度特性的体现)如图1b所示。
(a)Uge与Uce和Ic的关系(b)Uge与Ic和Tvj的关系图1 栅极电压U ge与U ce和T vj的关系栅极电压U ge直接影响IGBT 的可靠运行,栅极电压增高时有利于减小IGBT的开通损耗和导通损耗,但同时将使IGBT能承受的短路时间变短(10μs以下),使续流二极管反向恢复过电压增大,所以务必控制好栅极电压的变化范围,一般U ge可选择在-10~+15 V之间,关断电压-10 V,开通电压+15 V。
开关时U ge与I g的关系曲线见图2 a和图2 b所示。
(a)开通时 (b)关断时图2 开关时U ge与I c的关系曲线栅极电阻R g增加,将使IGBT的开通与关断时间增加,使开通与关断能耗均增加,但同时,可以使续流二极管的反恢复过电压减小,同时减少EMI的影响。
而门极电阻减少,则又使di/dt增大,可能引发IGBT误导通,但是,当R g减少时,可以使得IGBT关断时由du/dt 所带来误触发的可能性减小,同时也可以提高IGBT承受短路能量的能力,所以R g大小各有好坏,客户可根据自己设计特点选择。
图3为R g大小对开关特性的影响,损耗关系请参照图4所示。
图3 R g大小对开关特性的影响(di/dt 大小不同)图4 门极电阻R g与E on/E off由上述可得:IGBT 的特性随门极驱动条件的变化而变化,就象双极型晶体管的开关特性和安全工作区随基极驱动而变化一样。
IGBT的驱动特性及功率损耗计算

IGBT的驱动特性及功率损耗计算IGBT(Insulated Gate Bipolar Transistor)是一种常用的功率开关器件,广泛应用于电力电子领域。
IGBT的驱动特性和功率损耗计算是研究和设计IGBT电路时重要的考虑因素。
以下是对IGBT驱动特性和功率损耗计算的详细介绍。
一、IGBT的驱动特性1.输入阻抗:IGBT的输入阻抗较高,通常在几百欧姆到几兆欧姆之间,可以接受微弱的输入信号。
2.输入电容:IGBT的输入电容通常较大,约为几十皮法(pF),需要充放电过程来实现开关控制。
3.驱动电压:IGBT的驱动电压通常在12V至15V左右,在工作过程中,需要适当控制驱动电压的大小和时间,以保证其正常工作。
4.驱动电流:IGBT的驱动电流是驱动IGBT的关键参数,通常需要较大的驱动电流来保证IGBT的稳定工作。
5.驱动方式:常见的IGBT驱动方式有电流驱动和电压驱动两种。
电流驱动方式可以提供更好的保护性能和更高的驱动能力。
6.驱动信号:IGBT的驱动信号通常为脉宽调制(PWM)信号,通过控制脉宽来调节流过IGBT的电流,从而实现对电路的开关控制。
7.驱动时间:IGBT的驱动时间是指IGBT从关断到导通或从导通到关断的时间,通常需要较短的驱动时间来保证IGBT的快速开关。
IGBT在工作过程中会产生一定的功率损耗,包括导通损耗、关断损耗和开关损耗。
功率损耗的计算对于设计IGBT电路和散热系统非常重要。
1.导通损耗:IGBT在导通状态下会有一定的导通电压降和导通电流,导致功率损耗。
导通损耗可以通过以下公式计算:Pcon = Vce × Ic其中,Pcon为导通损耗,Vce为导通电压降,Ic为导通电流。
2.关断损耗:IGBT在关断过程中会有一定的关断电流和关断电压降,导致功率损耗。
关断损耗可以通过以下公式计算:Pdis = Vce × Ic × td其中,Pdis为关断损耗,Vce为关断电压降,Ic为关断电流,td为关断时间。
IGBT驱动电路的选择及驱动电阻的选择

IGBT驱动电路的选择及驱动电阻的选择IGBT驱动电路的选择绝缘栅双极型晶体管(IGBT)在今天的电力电子领域中已经得到广泛的应用,在实际使用中除IGBT自身外,IGBT 驱动器的作用对整个换流系统来说同样至关重要。
驱动器的选择及输出功率的计算决定了换流系统的可靠性。
驱动器功率不足或选择错误可能会直接导致IGBT 和驱动器损坏。
以下总结了一些关于IGBT驱动器输出性能的计算方法以供选型时参考。
IGBT 的开关特性主要取决于IGBT的门极电荷及内部和外部的电阻。
图1是IGBT 门极电容分布示意图,其中CGE 是栅极-发射极电容、CCE 是集电极-发射极电容、CGC 是栅极-集电极电容或称米勒电容(Miller Capacitor)。
门极输入电容Cies 由CGE 和CGC 来表示,它是计算IGBT 驱动器电路所需输出功率的关键参数。
该电容几乎不受温度影响,但与IGBT 集电极-发射极电压VCE 的电压有密切联系。
在IGBT数据手册中给出的电容Cies 的值,在实际电路应用中不是一个特别有用的参数,因为它是通过电桥测得的,在测量电路中,加在集电极上C 的电压一般只有25V(有些厂家为10V),在这种测量条件下,所测得的结电容要比VCE=600V 时要大一些(如图2)。
由于门极的测量电压太低(VGE=0V )而不是门极的门槛电压,在实际开关中存在的米勒效应(Miller 效应)在测量中也没有被包括在内,在实际使用中的门极电容Cin 值要比IGBT 数据手册中给出的电容Cies 值大很多。
因此,在IGBT数据手册中给出的电容Cies值在实际应用中仅仅只能作为一个参考值使用。
确定IGBT 的门极电荷对于设计一个驱动器来说,最重要的参数是门极电荷QG(门极电压差时的IGBT 门极总电荷),如果在IGBT 数据手册中能够找到这个参数,那么我们就可以运用公式计算出:图一门极驱动能量E = QG ? UGE = QG ? [ VG(on) - VG(off) ] 门极驱动功率PG = E ? fSW = QG ? [ VG(on) - VG(off) ] ? fSW 驱动器总功率P = PG + PS(驱动器的功耗)平均输出电流IoutAV = PG / ΔUGE = QG ? fSW 最高开关频率fSW max. = IoutAV(mA) / QG(μC) 峰值电流IG MAX =ΔUGE / RG min = [ VG(on) - VG(off) ] / RG min 其中的RG min = RG extern + RG intern fsw max. : 最高开关频率IoutAV : 单路的平均电流QG : 门极电压差时的IGBT门极总电荷RG extern : IGBT 外部的门极电阻RG intern : IGBT 芯片内部的门极电阻但是实际上在很多情况下,数据手册中这个门极电荷参数没有给出,门极电压在上升过程中的充电过程也没有描述。
IGBT门极驱动的计算

2008-11-19
IGBT门极驱动的计算
! 计算IGBT的门极电流
! 计算驱动电流
"
Iout≥3A,即电源的至 少要能提供3A的峰值电 流给IGBT的门极(此时 还没有考虑到Rg的误差)
驱动器输出电流不小于门极电流: IOUT
∆U I ≥ = G max R G min
Copyright © Infineon Technologies 2008. All rights reserved.
Page 2
IGBT门极驱动的计算
! 确定IGBT的门极电荷和门极电容
! 确定IGBT的门极电荷和门极电容
"
Q = ∫ idt = C • ∆U
" CIN =
Q ∆U
等效输入电容
PD=0.48W, 假设开 关频率是20kHz
假设驱动器本身消耗 0.5W的功率 P=0.98W, 即电源消耗 的最小平均功率,实际 计算的时候考虑一到两 倍的余量,因此功率约 为2W
Page 4
! 注释
"
每一个时钟周期内门极电荷各一次充放电
For internal use only Copyright © Infineon Technologies 2008. All rights reserved.
IGBT门极驱动的计算
! 计算驱动功率
! 计算驱动功率
"
输入电容中储存的能量: W = • CIN • ∆U 2
1 2
∆U=30V, 即门极电 压从-15V变化到+15V
" " " "
IGBT 在开关频率为f的条件下的驱动功率为:P = f • CIN • ∆U 2 或者,在门极电荷给定的条件下表述为:PD = f • Q • ∆U 除此之外还要考虑到驱动器本身的静态损耗:Pstatic 因此IGBT的驱动功率为: P = PD + Pstatic
IGBT驱动器输出计算

IGBT驱动器输出计算
IGBT驱动器输出计算
中心议题:
•栅极电荷体现IGBT 的特性
•如何测量和确定栅极电荷
•驱动器输出功率和栅极电流
•IGBT驱动器的选择
解决方案:
•输入电容CGC 和CGE 是计算IGBT 关键参数
•栅极导通电压VG(on)和关断电压VG(off)之差计算删极-发射极电压
•驱动器的最大平均输出电流必须大于计算值
绝缘栅双极型晶体管(IGBT)在电力电子领域已经普及,并被用于许多应用中,如变频器、电源和电子驱动器。
IGBT 具有较高的反向电压(高达
6.5kV),开关电流最大可达3kA。
除功率模块自身外,电力电子系统中的一个关键组件是IGBT 驱动器,它是功率晶体管和控制器之间重要的接口。
驱动器的选择及其准确输出功率的计算决定了转换器解决方案的可靠性。
驱动器功率不足或选择错误可能会导致模块和驱动器故障。
以下总结了一些计算用于开关IGBT 的驱动器输出性能的方法。
栅极电荷体现IGBT 的特性
IGBT 模块的开关特性主要取决于半导体电容(电荷)及内部和外部的电阻。
图1 是IGBT 电容的示意图,其中CGE 是栅极-发射极电容、CCE 是集电极-发射极电容、CGC 是栅极-集电极电容(或称为米勒电容)。
IGBT驱动电阻选取
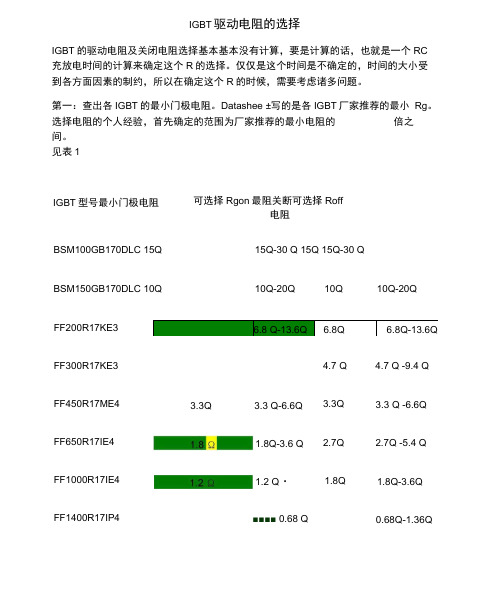
IGBT驱动电阻的选择IGBT的驱动电阻及关闭电阻选择基本基本没有计算,要是计算的话,也就是一个RC 充放电时间的计算来确定这个R的选择。
仅仅是这个时间是不确定的,时间的大小受到各方面因素的制约,所以在确定这个R的时候,需要考虑诸多问题。
第一:查出各IGBT的最小门极电阻。
Datashee ±写的是各IGBT厂家推荐的最小Rg。
选择电阻的个人经验,首先确定的范围为厂家推荐的最小电阻的倍之间。
见表1IGBT型号最小门极电阻可选择Rgon最阻关断可选择Roff电阻BSM100GB170DLC 15Q 15Q-30 Q 15Q 15Q-30 QBSM150GB170DLC 10Q 10Q-20Q 10Q 10Q-20QFF200R17KE3 6.8 Q-13.6Q 6.8Q 6.8Q-13.6Q FF300R17KE3FF450R17ME4 FF650R17IE4 FF1000R17IE4 FF1400R17IP4 3.3Q 3.3 Q-6.6Q4.7 Q3.3Q4.7 Q -9.4 Q3.3 Q -6.6Q2.7Q1.8Q■■■■ 0.68 Q2.7Q -5.4 Q1.8Q-3.6Q0.68Q-1.36Q1.8Q-3.6 Q1.2 Q・表1目前公司所用的IGBT驱动电阻可选择范围门极电阻的选择范围就如表1,具体的要进行双脉冲试验,才能最终确定最优化Rgon 和Rgoffo第二:确定Ron的功率。
计算公式:P = fs X QG XA U备注:P:每通道Rgon功率;fs: IGBT开关频率;QG: IGBT门极电荷,可从datashee中查出gate charge不同IGBT该数值不同;AU门极驱动电压摆幅,等于驱动正压+U和负压・U之间差值。
这里我们公司选择的是2SD315和SKYPER32o其?U=30V。
IGBT型号QG(datasheet Fs取值?U P(W可选择Rgon备注电阻功率备注BSM100GB170DLC 1.2uC 1.2K30V0.0432三0.125W BSM150GB170DLC 1.8uC 1.2K30V0.0648三0.125W FF200R17KE3 2.3uC 1.2K30V0.0828三0.125W FF300R17KE3 3.5uC 1.2K30V0.126三0.25W FF450R17ME4 4.6uC 1.2K30V0.1656三0.5W FF650R17IE47uC 1.2K30V0.252三0.5W FF1000R17IE410uC 1.2K30V0.36三1WFF1400R17IP413.5uC 1.2K30V0.486三1W第三:根据以上两个表格,来选择Ron和Roff的型号。
IGBT驱动参数计算详解

IGBT驱动参数计算详解大功率IGBT 模块在使用中驱动器至关重要,本文介绍在特定应用条件下IGBT门极驱动性能参数的计算方法,经验公式及有关CONCEPT 驱动板的选型标准,得出的一些参数值可以作为选择一款合适IGBT驱动器的基本依据。
1 门极驱动的概念IGBT存在门极-发射极电容Cge,门极-集电极电容Cgc,我们将IGBT的门极等效电容定义为Cg,门极驱动回路的等效电路如下图所示:其本质是:一个脉冲电压源向RC电路进行充放电,对于这个电压源,有2个物理量我们需要关心,1.它的功率;2.它的峰值电流。
2 驱动功率的计算驱动器是用来控制功率器件的导通和关断。
为了实现此功能,驱动器对功率器件的门极进行充电以达到门极开通电压VGE_on,或者是对门极进行放电至门极关断电压VGE_off。
门极电压的两种电平间的转换过程中,在驱动器门极驱动电阻及功率器件组成的回路中产生一定的损耗。
这个参数我们称为驱动功率PDRV。
驱动器必须根据其所驱动的功率器件所需的驱动功率来选择。
转载请注明出处驱动功率可以从门极电荷量QGate,开关频率fIN,以及驱动器实际输出电压摆幅ΔVGate 计算得出:P DRV = Q Gate * f IN * ΔV Gate (Eq. 1)备注:P DRV: 驱动器每通道输出功率;f IN: IGBT开关频率;Q Gate :IGBT门极电荷,可从规格书第一页查出,不同IGBT该数值不同;ΔV Gate:门极驱动电压摆幅,等于驱动正压+U 和负压–U 之间差值。
如果门极回路放置了一个电容CGE (辅助门极电容),那么驱动器也需要对该电容进行充放电,如图1 所示:图1.带外接阻容的门级驱动只要CGE 在一个周期内被完全的充放电,那么RGE 值并不影响所需驱动功率。
驱动功率可以从以下公式得出:P DRV = Q GATE * f IN *ΔV GATE + C GE * f IN*ΔV GATE2(Eq. 2)这个功率是每个IGBT 驱动时必须的,但门极的充放电是没有能量损失的,这个功率实际上损失在驱动电阻及外部电路中。
IGBT驱动器输出性能的计算

IGBT驱动器输出性能的计算IGBT驱动器输出性能的计算1、引言今天,绝缘栅双极型晶体管(IGBT)在电力电子领域已经普及,并被用于许多应用中,如变频器、电源和电子驱动器。
IGBT具有较高的反向电压(高达6.5kV),开关电流最大可达3kA。
除功率模块自身外,电力电子系统中的一个关键组件是IGBT驱动器,它是功率晶体管和控制器之间重要的接口。
驱动器的选择及其准确输出功率的计算决定了转换器解决方案的可靠性。
驱动器功率不足或选择错误可能会导致模块和驱动器故障。
以下总结了一些计算用于开关IGBT的驱动器输出性能的方法。
2、栅极电荷体现IGBT的特性IGBT模块的开关特性主要取决于半导体电容(电荷)及内部和外部的电阻。
图1是IGBT电容的示意图,其中CGE是栅极-发射极电容、CCE是集电极-发射极电容、CGC是栅极-集电极电容(或称为米勒电容)。
栅极电荷的特性由输入电容CGC和CGE来表示,它是计算IGBT驱动器电路所需输出功率的关键参数。
该电容几乎不受温度影响,但与电压关系密切,是IGBT集电极-发射极电压VCE的函数。
当在集电极-发射极电压非常低时这种依赖性大幅提高,电压高时依赖性下降。
当IGBT导通时,IGBT的特性由栅极电荷来体现。
图2显示了栅极-发射极电压VGE、栅极电流IG和相应的集电极电流IC作为时间的函数,从IGBT导通到饱和这段时间的简化波形。
正如IG=f(t)图所示,导通过程可以分为三个阶段。
分别是栅极-发射极电容的充电,栅极-集电极电容的充电和栅极-发射极电容的充电直至IGBT全饱和。
栅极电流IG对输入电容进行充电,IGBT的导通和关断特性由与充电过程有关的电压VGE和VCE来体现。
在关断期间,所描述的过程运行在相反的方向,电荷必须从栅极上移除。
由于输入电容的非线性,为了计算驱动器输出功率,输入电容可能只被应用到某种范围。
一种更为实际的确定驱动器输出功率的方法是利用栅极电荷特性。
图 1 IGBT 的电容图 2 简化的栅极充电波形3、如何测量和确定栅极电荷栅极电荷可以通过一个简化的测试电路进行测量。
IGBT栅极驱动电阻的选择和计算

的动态参数影响很大:驱动电阻越小,结电容充放电
速度越快,使得开关时间越短,进而降低了开关通态 损耗 [3]。但是,在开关管断开或者反并联二极管续流
结束后,结电容的存在会使得 IGBT 栅极电阻两端感
应出一个电平,严重时会使开关管误开通,或者在栅
极产生振铃,严重影响开关管的特性和系统安全。而
1 由栅极电阻引起的误动作
1.1 与 IGBT 结电容相关联的误开通
IGBT 的集电极 - 栅极和发射极 - 栅极之间存在着
结电容,分别是 CCG 和 CCE,是由器件的固有工艺结构 引起的。当 IGBT 关断时,由于线路中的感性,使得电
流并不会立即消失,而是寻找合适的通路。同时,突
变的电压会引起这一电流通路,结电容的存在使得关
Keywords:gate resistance;IGBT;dynamic characteristics
0 引 言
IGBT 是常用的电力电子开关元件,其驱动输入端 呈现容性。当使用 PWM 信号对 IGBT 进行控制驱动时, 信号会通过栅极驱动电阻对器件的输入端进行充放电。 因此,栅极电阻对 IGBT 的开关时间、损耗等开关参 数有重要影响,也决定了开关过程的 EMI 干扰和电压、 电流的上升下降速率。所以,栅极驱动电阻的大小对 IGBT 驱动电路的设计重要性不言而喻。现有的各种数 据手册中一般仅仅给出驱动电阻的测试典型值,并未 对其大小进行选择计算。因此,本文着眼于这一问题, 给出了驱动电阻的选择和计算方法。
HAN Peng-le (Henan Center for Patent Examination and Cooperation of the Patent Office of the State Intellectual Property Office,Zhengzhou
IGBT驱动全参数计算详解

IGBT驱动参数计算详解大功率IGBT 模块在使用中驱动器至关重要,本文介绍在特定应用条件下IGBT门极驱动性能参数的计算方法,经验公式及有关CONCEPT 驱动板的选型标准,得出的一些参数值可以作为选择一款合适IGBT驱动器的基本依据。
1 门极驱动的概念IGBT存在门极-发射极电容Cge,门极-集电极电容Cgc,我们将IGBT的门极等效电容定义为Cg,门极驱动回路的等效电路如下图所示:其本质是:一个脉冲电压源向RC电路进行充放电,对于这个电压源,有2个物理量我们需要关心,1.它的功率;2.它的峰值电流。
2 驱动功率的计算驱动器是用来控制功率器件的导通和关断。
为了实现此功能,驱动器对功率器件的门极进行充电以达到门极开通电压VGE_on,或者是对门极进行放电至门极关断电压VGE_off。
门极电压的两种电平间的转换过程中,在驱动器门极驱动电阻及功率器件组成的回路中产生一定的损耗。
这个参数我们称为驱动功率PDRV。
驱动器必须根据其所驱动的功率器件所需的驱动功率来选择。
请注明出处.igbt8.驱动功率可以从门极电荷量QGate,开关频率fIN,以及驱动器实际输出电压摆幅ΔVGate 计算得出:P DRV = Q Gate * f IN * ΔV Gate (Eq. 1)备注:P DRV: 驱动器每通道输出功率;f IN: IGBT开关频率;Q Gate :IGBT门极电荷,可从规格书第一页查出,不同IGBT该数值不同;ΔV Gate:门极驱动电压摆幅,等于驱动正压+U 和负压–U 之间差值。
如果门极回路放置了一个电容CGE (辅助门极电容),那么驱动器也需要对该电容进行充放电,如图1 所示:图1.带外接阻容的门级驱动只要CGE 在一个周期被完全的充放电,那么RGE 值并不影响所需驱动功率。
驱动功率可以从以下公式得出:P DRV = Q GATE * f IN *ΔV GATE + C GE * f IN*ΔV GATE2(Eq. 2)这个功率是每个IGBT 驱动时必须的,但门极的充放电是没有能量损失的,这个功率实际上损失在驱动电阻及外部电路中。
IGBT驱动参数的计算方法
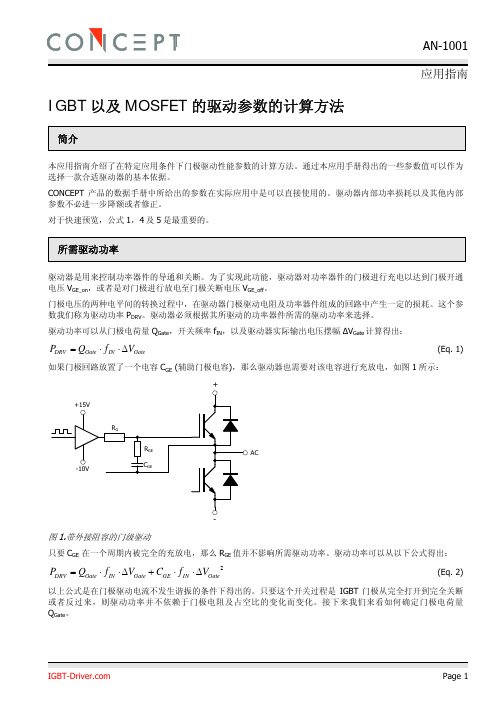
IGBT 以及MOSFET 的驱动参数的计算方法简介本应用指南介绍了在特定应用条件下门极驱动性能参数的计算方法。
通过本应用手册得出的一些参数值可以作为选择一款合适驱动器的基本依据。
CONCEPT 产品的数据手册中所给出的参数在实际应用中是可以直接使用的。
驱动器内部功率损耗以及其他内部参数不必进一步降额或者修正。
对于快速预览,公式1,4及5是最重要的。
所需驱动功率驱动器是用来控制功率器件的导通和关断。
为了实现此功能,驱动器对功率器件的门极进行充电以达到门极开通电压V GE_on ,或者是对门极进行放电至门极关断电压V GE_off 。
门极电压的两种电平间的转换过程中,在驱动器门极驱动电阻及功率器件组成的回路中产生一定的损耗。
这个参数我们称为驱动功率P DRV 。
驱动器必须根据其所驱动的功率器件所需的驱动功率来选择。
驱动功率可以从门极电荷量Q Gate ,开关频率f IN ,以及驱动器实际输出电压摆幅∆V Gate 计算得出:Gate IN Gate DRV V f Q P ∆⋅⋅= (Eq. 1)如果门极回路放置了一个电容C GE (辅助门极电容),那么驱动器也需要对该电容进行充放电,如图1所示:图1.带外接阻容的门级驱动只要C GE 在一个周期内被完全的充放电,那么R GE 值并不影响所需驱动功率。
驱动功率可以从以下公式得出:2Gate IN GE Gate IN Gate DRV V f C V f Q P ∆⋅⋅+∆⋅⋅= (Eq. 2)以上公式是在门极驱动电流不发生谐振的条件下得出的。
只要这个开关过程是IGBT 门极从完全打开到完全关断或者反过来,则驱动功率并不依赖于门极电阻及占空比的变化而变化。
接下来我们来看如何确定门极电荷量Q Gate 。
ACIN GH (output high)I OUT GL (output low)integration timegate charge: 11.4uC 门极电荷量Q Gate 绝不能从IGBT 或MOSFET 的输入电容C ies 计算得出。
IGBT 驱动器驱动能力的计算

际最大值仍有可能超过 DC/DC 变换器的额定功率, 为了作这种校核, 我们可以在驱动板的输 入电源与输入电容之间加分流器或探针,用示波器进行观察测试。 注意:由于内部有 DC/DC 变换器,驱动板的输入电流纹波,可以通过在副边加低电 感电容和选择低 ESR 方式就近驱动 IGBT 以减少引线长度来降低。
6
计算实例
对于一个 200A 的 IGBT 模块, 选择 EUPEC 公司的 BSM200GB120DN2, 工作频率在 8KHZ. 第一个参数门极电荷测量波形如图一所示: Q 及ΔU 值通过示波器可测得: Q=2150nAs ΔU=30V 门极电容 CIN=
Q 2150 As = =71.6nF U 30V
IGBT Drivers
Wang Yingbo
Correctly
Li Haijin
Calculated
Chen Shijun
(Wuhan Newrock Electric Technology co.,ltd, Wuhan,Hubei 430072,China) Abstract:The drivers of high power rate IGBT is important in power electronics. This paper introduces what you must know when dimensioning an IGBT driver, and choices about concept driver. Keywords: IGBT; driver; the gate charge
3
驱动功率的计算
在输入结电容中存贮的能量可通过如下计算: W= 1 2 CINΔU
2
这里,ΔU 是门极上上升的整个电压。比如,在±15V 驱动电压下,ΔU 是 30V。 在每个工作周期,门极被充电二次。一个 IGBT 所需的驱动功率计算如下: P=f ·CIN·ΔU
IGBT驱动器中栅极电阻Rg的作用及选取方法

IGBT驱动器中栅极电阻Rg的作用及选取方法一、栅极电阻Rg的作用1、消除栅极振荡绝缘栅器件(IGBT、MOSFET)的栅射(或栅源)极之间是容性结构,栅极回路的寄生电感又是不可避免的,如果没有栅极电阻,那栅极回路在驱动器驱动脉冲的激励下要产生很强的振荡,因此必须串联一个电阻加以迅速衰减。
2、转移驱动器的功率损耗电容电感都是无功元件,如果没有栅极电阻,驱动功率就将绝大部分消耗在驱动器内部的输出管上,使其温度上升很多。
3、调节功率开关器件的通断速度栅极电阻小,开关器件通断快,开关损耗小;反之则慢,同时开关损耗大。
但驱动速度过快将使开关器件的电压和电流变化率大大提高,从而产生较大的干扰,严重的将使整个装置无法工作,因此必须统筹兼顾。
二、栅极电阻的选取1、栅极电阻阻值的确定各种不同的考虑下,栅极电阻的选取会有很大的差异。
初试可如下选取:不同品牌的IGBT模块可能有各自的特定要求,可在其参数手册的推荐值附近调试。
2、栅极电阻功率的确定栅极电阻的功率由IGBT栅极驱动的功率决定,一般来说栅极电阻的总功率应至少是栅极驱动功率的2倍。
IGBT栅极驱动功率 P=FUQ,其中:F 为工作频率;U 为驱动输出电压的峰峰值;Q 为栅极电荷,可参考IGBT模块参数手册。
例如,常见IGBT驱动器(如TX-KA101)输出正电压15V,负电压-9V,则U=24V,假设 F=10KHz,Q=2.8uC可计算出 P=0.67w ,栅极电阻应选取2W电阻,或2个1W电阻并联。
三、设置栅极电阻的其他注意事项1、尽量减小栅极回路的电感阻抗,具体的措施有:a) 驱动器靠近IGBT减小引线长度;b) 驱动的栅射极引线绞合,并且不要用过粗的线;c) 线路板上的 2 根驱动线的距离尽量靠近;d) 栅极电阻使用无感电阻;e) 如果是有感电阻,可以用几个并联以减小电感。
2、IGBT 开通和关断选取不同的栅极电阻通常为达到更好的驱动效果,IGBT开通和关断可以采取不同的驱动速度,分别选取 Rgon和Rgoff(也称 Rg+ 和 Rg- )往往是很必要的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
IGBT驱动电路参数计算详解电阻大功率IGBT 模块在使用中驱动器至关重要,本文介绍在特定应用条件下IGBT门极驱动性能参数的计算方法,经验公式及有关CONCEPT 驱动板的选型标准,得出的一些参数值可以作为选择一款合适IGBT驱动器的基本依据。
1 门极驱动的概念IGBT存在门极-发射极电容Cge,门极-集电极电容Cgc,我们将IGBT的门极等效电容定义为Cg,门极驱动回路的等效电路如下图所示:其本质是:一个脉冲电压源向RC电路进行充放电,对于这个电压源,有2个物理量我们需要关心,1.它的功率;2.它的峰值电流。
2 驱动功率的计算驱动器是用来控制功率器件的导通和关断。
为了实现此功能,驱动器对功率器件的门极进行充电以达到门极开通电压VGE_on,或者是对门极进行放电至门极关断电压VGE_off。
门极电压的两种电平间的转换过程中,在驱动器门极驱动电阻及功率器件组成的回路中产生一定的损耗。
这个参数我们称为驱动功率PDRV。
驱动器必须根据其所驱动的功率器件所需的驱动功率来选择。
驱动功率可以从门极电荷量QGate,开关频率fIN,以及驱动器实际输出电压摆幅ΔVGate 计算得出:P DRV = Q Gate * f IN * ΔV Gate (Eq. 1)备注:P DRV: 驱动器每通道输出功率;f IN: IGBT开关频率;Q Gate :IGBT门极电荷,可从规格书第一页查出,不同IGBT该数值不同;ΔV Gate:门极驱动电压摆幅,等于驱动正压+U 和负压–U 之间差值。
如果门极回路放置了一个电容CGE (辅助门极电容),那么驱动器也需要对该电容进行充放电,如图1 所示:图1.带外接阻容的门级驱动只要CGE 在一个周期内被完全的充放电,那么RGE 值并不影响所需驱动功率。
驱动功率可以从以下公式得出:P DRV = Q GATE * f IN *ΔV GATE + C GE * f IN*ΔV GATE2(Eq. 2)这个功率是每个IGBT 驱动时必须的,但门极的充放电是没有能量损失的,这个功率实际上损失在驱动电阻及外部电路中。
注意:这个功率是表示在电路中实际需要的,而在驱动电路中的其它损耗(包括供电电源损耗)不包含在内。
驱动器中DC/DC 变换器的总输出功率在concept 公司智能驱动板说明书中被标明了,对于半桥电路驱动器,由于总变换器功率被标明了,因此总输出功率的一半即是每个通道的功率。
另外,还有一部分功率损失在驱动电路元件中。
总功率损耗通常是由一个静态的、固定的损耗加上最终驱动损耗组成。
Concept 驱动板静态损耗描述如下:IHD215/280/680 每个通道0.4WIHD580FX 每个通道0.8WIGD608/615AX 整个板0.5WIGD508/515EX(无光藕元件) 0.5W在IGD508/515 中,光藕的发送及接收所损失的功率应被计算在内。
光藕接收器所用的5V 电源是由外部16V 供电电源线性变换得来,这部分的损耗应该用+16V 乘以电流计算,而不是用+5V 计算。
每个通道的静态损耗也可通过测量得到,具体如下:断开输入侧的电压供应(DC/DC 变换器的逆流),16V 的电压直接加在Cs , COM 脚两端(等效副边电容)。
驱动板在静态时的消耗电流(没有输入脉冲时)同有脉冲工作时一样,能够直接从电路中的电流表读出。
以上公式是在门极驱动电流不发生谐振的条件下得出的。
只要这个开关过程是IGBT门极从完全打开到完全关断或者反过来,则驱动功率并不依赖于门极电阻及占空比的变化而变化。
接下来我们来看如何确定门极电荷量QGate。
3 门极电荷量QGate 绝不能从IGBT 或MOSFET 的输入电容Cies 计算得出。
Cies 仅仅是门极电荷量曲线在原点(VGE=0V)时的一阶近似值。
在IGBT 手册中的电容值Ciss,在实际电路应用中不是一个特别有用的参数,因为它是通过电桥测得的,由于测量电压太小而不能到达门极门槛电压,在实际开关中增加的内部回馈效应(Miller 效应)在测量中未被包括在内。
在测量电路中,一个25V 的电压加在集电极“C”上,在这种测量构架下,所测结电容要比Vce=0V 时要小一些。
因此,Ciss 仅仅只能在IGBT 互相作比较时使用。
我们在选择和设计IGBT 驱动器时经常会碰到一些问题和不确定因素。
部分原因是厂家对IGBT 描述的不够充分;另一方面是由于IGBT 手册中所给的输入结电容Ciss 值与在应用中的实际的输入结电容值相差甚远。
依据手册中的Ciss 值作设计,令许多开发人员走入歧途。
对于设计一个驱动器来讲,最重要的参数是门极电荷,在很多情况下,IGBT 数据手册中这个参数没有给出,另外,门极电压在上升过程中的充电过程也未被描述。
功率半导体的门极电荷量曲线是极其非线性的。
这就是为什么QGate 必须通过对门极电荷量曲线在VGE_off 到VGE_on 的区域内积分获得。
无论如何,门极的充电过程相对而言能够简单地通过测量得到。
因而要驱动一个IGBT,我们最好使用一个专用的驱动器。
除此之外,在设计中至少我们知道在应用中所需的门极电压(例如±15V)。
首先,在负载端没有输出电压的情况下,我们可以作如下计算。
门极电荷可以利用公式计算:Q=∫idt=CΔU确定了Q, 我们可以用示波器观测门极电压,同时电压的上升ΔU 在测量中也能在示波器上清楚的观测到。
(见下图2)利用公式CIN=Q/ΔU。
实际的输入电容能够通过计算得到。
尤其要注意的是,在应用中,实际的输入结电容CIN 在设计中是具有很大意义的。
Ciss 在折算中的经验公式对于SIEMENS 和EUPEC 的IGBT 而言,下面的经验公式经过验证是较为准确可信的。
CIN=5Ciss (Ciss 可从IGBT 手册中得到)如果QGate 在数据手册中已给出,在实际应用中一定要注意该参数给定的电压摆幅条件。
不同的电压摆幅条件下门极电荷量是不同的。
举个例子:如果VGE 从 0V 到 +15V 条件下的门极电荷量是QGate,那么没有办法很准确的得到VGE 从-10V 到+15V 条件下的门极电荷量。
在这样的情况下,如果没有电荷量图表(QGate vs. VGE),则实测电荷量QGate 是唯一的方法。
图2 显示的是一张典型的驱动器开通过程的波形图。
驱动器输出电流IOUT 正在对功率器件的门极进行充电。
因此,如图2 所示,输出电流曲线与时间轴围成的区域就是总的充电电荷量(见图4 所示的原理图)。
积分时间应宽到足以涵盖整个电压摆幅(参照输出:GH, GL) 。
积分时间包括驱动器输出电压至最终电压,或者是从驱动器开始输出电流至输出电流为零这段时间。
图2.用积分的方法来测量门极电荷量必须注意输出电流是否出现振荡。
在实际应用中,电荷量的测量值通常受电流振荡影响而变得不准确,其原因是过长的积分时间以及少量大数叠加而非大量小数叠加产生的不准确性。
因此,强烈建议使用驱动电流无振荡的设置来对门极电荷量进行测量。
驱动器输出电流振荡或可导致驱动器单元产生额外的功率损耗,这些损耗是由于钳位效应及输出级和控制回路的非线性产生的。
因此,驱动器最大可用功率通常是在输出电流不发生振荡的情况下得出的。
谐振门极驱动可以利用高频开关下的振荡现象来获得某种好处。
但这种驱动方法不在本应用指南讨论范围内。
4 峰值驱动电流公式驱动信号的上升沿及下降沿时刻,驱动器需要向门极电容充电及放电,需要送出峰值电流。
如下图,为IGBT导通过程中门极电流波形图。
门极驱动电路另一个重要的参数就是最大门极驱动电流IOUT,max。
门极电流由门极驱动电压和门极电阻决定,门极电阻由IGBT芯片或等于IGBT模块内置电阻,加上外置门极驱动电阻。
门极驱动电流IOUT,max 必须足够大以便在最大电压摆幅及最小门极电阻条件下提供足够的驱动电流。
其一阶最大值可以简写成:ÎOUT(1. Order)=△V/(Rinternal+Rexternal)ΔV为驱动电压摆幅,Rexternal为客户所选用的门极电阻,包括发射极回路中的电阻Rinternal为IGBT门极内阻,可从规格书查出,不同IGBT该数值不同。
若门极电流存在振荡现象,则建议在选择驱动器时,其峰值电流应满足IOUT,max>ÎOUT(1. Order)。
如果门极电流的振荡表现出低阻尼特性的话就必须引起注意。
此时,峰值电流电流会很大,且通常只能通过测量得到。
实践经验表明,在门极电流无振荡,且驱动电阻较小的情况下,电路中实际观察到的电流峰值低于ÎOUT(1. Order)的70%。
门极电流的减小是由于门极回路中的寄生电感导致的。
这个寄生电感在门极充电开始时限制电流的斜率。
因此,在门极回路电流无振荡出现的情况下,对于驱动小阻值门极电阻,我们只需根据如下要求选择驱动器,驱动器的门极电流至少需提供0.7 倍的衰减因子:在使用公式5 时,驱动器输出端的实际峰值电流需要进行实测以作确认。
举例:驱动器电压摆幅为25V(+15 / -10V),门极电阻为0.5Ω,IGBT 模块门极内阻为0.2Ω,则驱动器提供的最大峰值电流至少应为25A。
实际应用中的0.7 倍衰减因子的一个理论依据可以参照章节“最大驱动电流”。
5 输出电压摆幅的变化门极驱动器的输出电压摆幅在输出功率范围内会有轻微的变化。
这是因为驱动器高压隔离DC/DC 电源的外特性有些软所致。
最边界的计算值是通过最大电压摆幅得出的。
请在预期使用的功率范围内依据驱动器的数据手册得出电压摆幅,或者是在电路中进行实测。
严格来说,门极电荷量需在特定的门极电压摆幅下进行测量。
如果门极电荷量是在较大门极电压摆幅(在低频下)条件下得出,那么计算得出的驱动功率会比实际驱动功率大(在目标频率下)。
如果目标精度低于5%,实际上没有必要去考虑这个因素的影响。
6 最大运行温度除非另有说明,CONCEPT 驱动器在–40°C 到 85°C 的温度范围内能输出全功率。
如果没有关于降额说明,那么可以认为在全温度范围内都能输出全功率和额定电流。
温度等级是参考无强迫风冷,自然对流的环境温度而言。
即使是中级的强迫风冷(通过风扇形成环流)能够强烈地改善驱动器的热传导—提高驱动器的可靠性。
7 最大开关频率某些参数会影响最大可使用开关频率。
首先,前面章节所讨论得出的输出功率。
第二是门极电阻上的功耗变化。
门极电阻越大,在给定频率下驱动器推动级的功耗就越小。
第三是由于高开关频率而影响驱动器的温升。
图3 所示的是不同门极驱动电阻条件下,最大允许输出功率与开关频率的关系的曲线图。
该图只适用某个具体的驱动器,并不是通用的。
8 最大驱动电流实际应用中,驱动峰值电流的计算理论来源于以下问题:在没有振荡的情况下,门极回路中的实际峰值电流能达到多少?以下分析仅专注于门极电阻的变化而其他参数不变。
