大学复变函数考试卷试题及答案

大学复变函数期末考试试卷及答案(理工科所有专业)

2．设22-+=ni nin α),3,2,1( =n ,则=∞→n n αlim （）A. 0；B. 1；C. -1+i ；D. 1+i 。

3．满足不等式3211≤-+≤i z 的所有点z 构成的集合是（）。

A ．有界单连通区域； B. 无界单连通区域；C ．有界复连通闭域； D.无界复连通闭域。

4．下列函数中，不在复平面内解析的函数是( )A.1)(+=z ez f ； B ．-=z z f )( ；C ．nz z f =)( ； D ．)sin (cos )(y i y e z f x+=。

5A. ∑∞=+08)56(n nni ；C. ∑∞=02n n i ；三．计算题（每小题71．设z 1+=2．判定函数)2()()(222y xy i x y x z f -+--=在何处可导，在何处解析。

3．计算积分⎰-Cdz z z 4)2(sin π4.计算积分4=。

5.设,)1(2y x u -=试求解析函数iv u z f +=)(，使得i f -=)2(。

6.将函数)2)(1(1)(--=z z z f ，在圆环域21<<z 内展成洛朗级数。

四.证明函数yi(+=在复平面内不可导。

（7分）)zxf2参考答案一、填空题（本大题共8小题，每小题3 1．109 ， 2. 4 ，3. 0 ，4. 1，5. -3或二、单项选择题(本大题共7小题，每小题31. B ，2. B ，3.C,4. B,5. B .三、计算题（本大题共7小题，15-19 1.解：由i z 31+=得：)sin (cos2ππi z +=, （1分）624(cos 23166ππk i z k +=+=所以)18sin 18(cos 260ππi z +=，)1813sin 1813(cos 262ππi z += ,)25sin 1825(cos 264ππi z +=,5z 7分）2.解)2()2y xy i x -+,则(),(22y x y x u -=y u x x u ,12=∂∂-=∂∂ 只在21=y ,x v ∂∂-（6分）故只在21=y 处可导，处处不解析。

复变函数考试试题及参考答案

复变函数考试试题及参考答案下面是十道复变函数考试试题(一)的参考试题及答案：1.计算下列复数的幂函数：$z=1+i$,$n=3$。

答案：$(1+i)^3=-2+2i$。

2.计算下列复数的幂函数：$z=-2+i$,$n=4$。

答案：$(-2+i)^4=7-24i$。

3.求解方程：$z^2+4z+5=0$。

答案：可以使用求根公式求解，$(z+2)^2+1=0$，得到两个解：$z_1=-2+i$和$z_2=-2-i$。

4. 计算下列复数的极坐标形式：$z = 3e^{i \pi/6}$。

答案：$z = 3\cos(\pi/6) + 3i\sin(\pi/6) = \frac{3}{2} + \frac{3\sqrt{3}}{2}i$。

5.计算下列复数的共轭复数：$z=2-i$。

答案：$z^*=2+i$。

6. 将下列复数表示为共轭形式：$z = 4e^{i \pi/3}$。

答案：$z = 4\cos(\pi/3) + 4i\sin(\pi/3) = 4(\frac{1}{2} + \frac{\sqrt{3}}{2}i) = 2 + 2\sqrt{3}i$。

7.计算下列复数的实部和虚部：$z=3+2i$。

答案：实部为3，虚部为28.计算下列复数的模长：$z=-4+3i$。

答案：$，z， = \sqrt{(-4)^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5$。

9.求复数的幂函数：$z=-1-i$,$n=2$。

答案：$(-1-i)^2=1-2i-1=-2i$。

10. 求复数的幂函数：$z = \sqrt{3} + i$, $n = 3$。

答案：$(\sqrt{3} + i)^3 = -2\sqrt{3} + 2i$。

复变函数考试题及答案自考

复变函数考试题及答案自考一、选择题（每题2分，共20分）1. 下列哪个选项是复数z = 3 + 4i的共轭复数？A. 3 - 4iB. -3 + 4iC. -3 - 4iD. 3 + 4i答案：A2. 如果复变函数f(z)在点z₀处解析，那么它的导数f'(z₀)等于：A. 极限lim(Δz→0) [f(z₀ + Δz) - f(z₀)] / ΔzB. f(z₀)的实部C. f(z₀)的虚部D. f(z₀)的模答案：A3. Cauchy积分定理适用于：A. 仅在实数域B. 仅在复平面上的简单闭合曲线C. 仅在复平面上的开区域D. 所有以上情况答案：C4. 如果一个复变函数在某区域内除了一个孤立奇点外处处解析，那么这个函数在该区域内：A. 一定有原函数B. 一定没有原函数C. 可能是周期函数D. 以上都不对答案：A5. 复变函数f(z) = u(x, y) + iv(x, y)中，u和v分别表示：A. 实部和虚部B. 模和辐角C. 辐角和模D. 都不对答案：A6. 以下哪个是复变函数的柯西-黎曼方程？A. ∂u/∂x = ∂v/∂yB. ∂u/∂y = -∂v/∂xC. ∂u/∂x = ∂v/∂yD. ∂u/∂y = ∂v/∂x答案：B7. 复变函数的级数展开式中的系数是：A. 常数B. 复数C. 实数D. 以上都不对答案：B8. 如果一个复变函数在某个区域内处处连续，那么它的模：A. 也必定处处连续B. 可能不连续C. 必定不连续D. 以上都不对答案：A9. 复变函数的Taylor级数展开是关于：A. 模的展开B. 辐角的展开C. z的展开D. 共轭复数的展开答案：C10. 下列哪个是复变函数的Laurent级数展开的一个特性？A. 它只能展开在解析函数上B. 它包含负幂项C. 它只能展开在奇点附近D. 以上都是答案：B二、填空题（每题3分，共30分）11. 复数z = 2 - 3i的模是________。

《复变函数》考试试题与答案各种总结.docx

---《复变函数》考试试题（一）一、判断题（ 20 分）：1. 若 f(z) 在 z 0 的某个邻域内可导，则函数f(z) 在 z 0 解析 .2. 有界整函数必在整个复平面为常数.3. 若{ z n }收敛，则{Re z n } 与{Im z n }都收敛 .4. 若 f(z) 在区域 D 内解析，且f '( z)，则f ( z) C（常数） 5. 若函数 f(z) 在 z 0 处解析，则它在该点的某个邻域内可以展开为幂级数6. 若 z 0 是 f ( z)的 m 阶零点，则 z 0 是 1/f (z)的 m 阶极点 .lim f ( z)7. 若 zz 0存在且有限，则 z 0 是函数 f(z) 的可去奇点 .( ) ( ) ( ). ( ).( )()()8. 若函数 f(z) 在是区域 D 内的单叶函数，则f ' (z) 0( zD ).()9. 若 f(z)在区域 D 内解析 , 则对 D 内任一简单闭曲线Cf z dz.( )C( )10. 若函数 f(z) 在区域 D 内的某个圆内恒等于常数，则 f(z)在区域 D 内恒等于常数 . （）二. 填空题（ 20 分）1、|z z 0 |dz__________. （ n 为自然数）1 ( z z )n2.sin 2zcos 2z_________.3. 函数sin z的周期为 ___________.f (z)z 2 11，则f ( z)的孤立奇点有 __________.4.设5. 幂级数nz n 的收敛半径为 __________.n 06. 若函数 f(z) 在整个平面上处处解析，则称它是__________.lim z nlimz 1z 2 ...z n7. 若 n，则 nn______________.Res(e z8.n,0)________，其中 n 为自然数 .z---9.sin z的孤立奇点为 ________ .z若z 0 是 f (z)lim f (z)___10. 的极点，则z z.三. 计算题（ 40 分）：f (z)11. 设(z 1)( z 2) ，求 f ( z) 在 D { z : 0 | z | 1} 内的罗朗展式 .1dz.|z| 1cos z2.3. 设f ( z)3 271d{ z :| z | 3} ，试求 f ' (1 i ).Cz，其中 Cz 1w1 的实部与虚部 .4.求复数z四 . 证明题 .(20 分 )1. 函数f (z)在区域 D 内解析 . 证明：如果 | f ( z) |在 D 内为常数，那么它在D 内为常数 .2. 试证 : f ( z) z(1 z) 在割去线段 0Re z 1 的 z 平面内能分出两个单值解析分支,并求出支割线0 Re z 1上岸取正值的那支在 z 1的值 .《复变函数》考试试题（一）参考答案一．判断题1．× 2．√ ３．√ ４．√５．√6．√ ７．×８．×９．× 10．×二．填空题2 in1 2.1 ；3. 2k ， ( k z) ；4.z i ； 5.11.n；16. 整函数；7. ； 1 ； 9. 0； 10..8.(n 1)!三．计算题 .1. 解因为 0 z 1, 所以 0 z 1f ( z)1 1 1 z zn1 ( z )n.( z 1)(z 2) 1 z 2(1 )n 02 n 0 22---2.解因为z21Re s f (z)lim lim,cosz sin z1 z z z222Re s f (z)lim z2lim1 1 . cosz sin zz z z2 22所以1dz2i(Re s f (z)Re s f (z)0. z2 cosz z2z23.解令 ()3271,则它在 z 平面解析,由柯西公式有在z 3内,f (z)c ()dz2i(z) . z所以 f (1i )2i( z) z 1 i2i (136i )2(613i ) .4.解令 z a bi ,则w z 11212( a1bi )12( a1)2b2. z 1z 1222b22b( a 1) b( a 1)(a 1)z12(a1)z12bb2 .故 Re( z1)1( a1)2b2,Im(z1)(a1)2四. 证明题 .1.证明设在 D 内 f (z) C .令 f ( z) u iv ,2u2v2c2.则 f ( z)两边分别对 x, y 求偏导数,得uu x vv x0(1) uu y vv y0(2)因为函数在 D 内解析,所以 u x v y ,u y v x.代入 (2)则上述方程组变为uu x vv x0 .消去 u x得,(u2v2 )v x0 .vu x uv x01)若 u2v20 ,则 f (z)0 为常数.2)若 v x0,由方程(1) (2) 及C.R.方程有u x0,u y0 , v y0 .所以 u c1, v c2. ( c1 ,c2为常数).---所以 f ( z) c 1 ic 2 为常数 .2. 证明 f ( z)z(1 z) 的支点为 z 0,1 . 于是割去线段 0 Re z 1 的 z 平面内变点就不可能单绕 0 或 1 转一周 , 故能分出两个单值解析分支 .由于当 z 从支割线上岸一点出发 ,连续变动到 z0,1 时 , 只有 z 的幅角增加. 所以f ( z)z(1 z) 的幅角共增加. 由已知所取分支在支割线上岸取正值 , 于是可认为该分2z1的幅角为, 故 f ( 1)i2i .支在上岸之幅角为 0,因而此分支在2e22《复变函数》考试试题（二）一. 判断题 . （20 分）1. 若函数 f ( z)u( x, y) iv ( x, y) 在 D 内连续，则 u(x,y)与 v(x,y)都在 D 内连续 .( ) 2. cos z 与 sin z 在复平面内有界 .()3.若函数 f(z)在 z 解析，则 f(z)在 z 连续 .()0 04. 有界整函数必为常数 .一定不存在 .()5. 如 0是函数f(z)的本性奇点，则 lim f ( z) ()zz z 06. 若函数 f(z)在 z 0 可导，则 f(z)在 z 0 解析 .()7.若 f(z)在区域 D 内解析 , 则对 D 内任一简单闭曲线 Cf (z)dz0 .C( ) 8. 若数列 { z n } 收敛，则 {Re z n } 与 {Im z n } 都收敛 .() 9. 若 f(z)在区域 D 内解析，则 |f(z)|也在 D 内解析 .()10. 存在一个在零点解析的函数1 ) 0 1 1 1,2,... .f(z) 使 f (且 f ( ) ,nn 1 2n 2n( )二 . 填空题 . (20 分)1. 设 zi ，则 | z | __,arg z__, z __2.设 f (z) ( x 22xy) i(1 sin( x 2y 2 ), z x iy C ，则 limf ( z) ________.z 1i3.|z z 0| 1(zdz_________.z )n（ n 为自然数）---4.幂级数 nz n的收敛半径为__________ .n05.若 z0是 f(z)的 m 阶零点且 m>0，则 z0是f '( z)的 _____零点 .6.函数 e z的周期为 __________.7.方程 2z5z33z 8 0 在单位圆内的零点个数为________.8.设 f ( z)1，则 f (z) 的孤立奇点有_________.21z9.函数 f ( z) | z | 的不解析点之集为________.10. Res(z41,1) ____ . z三. 计算题 . (40 分)1.求函数sin( 2z3)的幂级数展开式 .2.在复平面上取上半虚轴作割线 . 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支，并求它在上半虚轴左沿的点及右沿的点 z i 处的值.i3.计算积分： I| z | dz，积分路径为（1）单位圆（ | z | 1）i的右半圆 .sin z dzz 2(z) 24.求2.四. 证明题 . (20 分)1. 设函数 f(z)在区域 D 内解析，试证： f(z)在 D 内为常数的充要条件是 f (z) 在D内解析 .2.试用儒歇定理证明代数基本定理 .《复变函数》考试试题（二）参考答案一.判断题 .1．√２．×３．√４．√ ５．× 6．×７．×８．√９．× 10．× .二.填空题---1.1 ，， i ；2. 3(1sin 2)i ；3.2 i n14. 1；5. m 1 . 0n；216.2k i ，( k z) .7. 0；8. i；9.R ；10. 0.三.计算题1.解 sin(2 z3 )( 1)n (2 z3 )2 n 1(1)n 22n 1 z6n3.n 0(2 n1)!n 0(2n1)!2.解令 z re i.2 ki则 f ( z)z re2,(k0,1).又因为在正实轴去正实值，所以k0 .所以 f (i)ie 4.3.单位圆的右半圆周为z e i,ide i e i 所以 zdz22i22 4.解.2 2 2i .即 u, v 满足 C.R.,且u x , v y , u y ,v x连续 , 故f ( z)在D内解析 .( 充分性 ) 令f ( z)u iv, 则 f ( z)u iv ,因为 f ( z) 与 f ( z) 在D内解析,所以u x v y , u y v x,且 u x ( v) y v y , u y( v x )v x.比较等式两边得u x v y u y v x0 .从而在 D 内 u, v 均为常数,故f ( z)在 D 内为常数.2. 即要证“任一n次方程a0 z n a1z n1a n 1z a n0(a00) 有且只有n 个根”.证明令 f (z)a0 z n a1z n 1a n1za n0 ,取 R max a1a n,1 ,当 za0在 C : z R 上时,有(z)a1 R n 1an 1R a n( a1a n )R n 1a0R n.f ( z) .由儒歇定理知在圆z R 内,方程 a0 z n a1z n 1a n 1z a n0与 a0 z n0有相---同个数的根 . 而 a 0 z n 0 在 z R 内有一个 n 重根 z 0 . 因此 n 次方程在 z R 内有 n 个根 .《复变函数》考试试题（三）一 . 判断题 . (20 分).1. cos z 与 sin z 的周期均为 2k .( )2. 若 f ( z) 在 z 0 处满足柯西 - 黎曼条件 , 则 f ( z) 在 z 0 解析 . ( )3. 若函数 f ( z) 在 z 0 处解析，则 f ( z) 在 z 0 连续 . ( )4. 若数列 { z n } 收敛，则 {Re z n } 与 {Im z n } 都收敛 .( )5.若函数 f ( z) 是区域 D 内解析且在 D 内的某个圆内恒为常数，则数 f ( z) 在区域 D 内为常数 . ( )6. 若函数 f ( z) 在 z 0 解析，则 f ( z) 在 z 0 的某个邻域内可导 . ()7.如果函数 f ( z) 在 D{ z :| z | 1} 上解析 , 且 | f (z) | 1(| z | 1) , 则| f ( z) | 1(| z | 1) .（）8.若函数 f ( z) 在 z 0处解析，则它在该点的某个邻域内可以展开为幂级数.( ) 9. 若 z 0 是 f ( z) 的 m 阶零点 , 则 z 0 是 1/ f ( z) 的 m 阶极点 . ( )10.若z 0 是 f (z)的可去奇点，则 Res( f ( z), z 0 ) 0. ( )二 . 填空题 . (20 分)1. 设 f ( z)1 ，则 f ( z) 的定义域为 ___________.2 z 12. 函数 e z 的周期为 _________.3. 若 z nn 2 i (1 1) n ，则 lim z n__________.1 nnn4. sin 2 z cos 2 z___________.dz5.|z z 0 | 1(z z )n（ n 为自然数）_________.6. 幂级数nx n 的收敛半径为 __________.n设 f (z) 1f z 的孤立奇点有z 2 1，则7.( ) __________.ez---9.若 z 是 f (z)的极点，则 lim f (z) ___ .z z 0z10.Res(en ,0) ____ .z三 . 计算题 . (40 分)11. 将函数 f ( z) z 2e z 在圆环域 0 z内展为 Laurent 级数 .2. 试求幂级数n!z n的收敛半径 .n nn3. 算下列积分：e zdz，其中 C是| z |1.Cz 2 (z29)4. 求 z92z6z 28z 2 0 在| z|<1内根的个数 .四 . 证明题 . (20 分)1.函数 f (z) 在区域 D 内解析 . 证明：如果 | f ( z) |在 D 内为常数，那么它在D 内为常数 .2.设 f (z) 是一整函数，并且假定存在着一个正整数 n ，以及两个正数 R 及 M ，使得当 | z|R 时| f ( z) |M | z |n，证明 f (z) 是一个至多 n 次的多项式或一常数。

复变函数期末试题及答案

复变函数期末试题及答案一、选择题（每题5分，共20分）1. 若复数 $ z = a + bi $（其中 $ a, b $ 为实数），则$ \bar{z} $ 表示（）A. $ a - bi $B. $ -a + bi $C. $ -a - bi $D. $ a + bi $答案：A2. 对于复变函数 $ f(z) = u(x, y) + iv(x, y) $，以下说法正确的是（）A. $ u $ 和 $ v $ 都是调和函数B. $ u $ 和 $ v $ 都是解析函数C. $ u $ 和 $ v $ 都是连续函数D. $ u $ 和 $ v $ 都是可微函数答案：A3. 若 $ f(z) $ 在 $ z_0 $ 处可导，则下列说法中正确的是（）A. $ f(z) $ 在 $ z_0 $ 处解析B. $ f(z) $ 在 $ z_0 $ 处连续C. $ f(z) $ 在 $ z_0 $ 处可微D. $ f(z) $ 在 $ z_0 $ 处的导数为0答案：C4. 已知 $ f(z) $ 是解析函数，且 $ f(z) $ 在 $ z_0 $ 处有孤立奇点，则 $ f(z) $ 在 $ z_0 $ 处的留数是（）A. 0B. $ \infty $C. 1D. $ -1 $答案：A二、填空题（每题5分，共20分）1. 若 $ z = x + yi $，且 $ |z| = 2 $，则 $ x^2 + y^2 = \_\_\_\_\_ $。

答案：42. 设 $ f(z) = z^2 $，则 $ f(2 + 3i) = \_\_\_\_\_ $。

答案：-5 + 12i3. 若 $ f(z) $ 在 $ z_0 $ 处解析，则 $ f(z) $ 在 $ z_0 $ 处的导数 $ f'(z_0) $ 等于 \_\_\_\_\_。

复变期末考试题及答案

复变期末考试题及答案复变函数期末考试题一、选择题（每题2分，共20分）1. 若复数 $ z = x + yi $，则 $ \overline{z} $ 是：A. $ x - yi $B. $ -x - yi $C. $ -x + yi $D. $ x + yi $2. 复平面上，单位圆上的点 $ z = e^{i\theta} $ 对应的实部是：A. $ \cos\theta $B. $ \sin\theta $C. $ \tan\theta $D. $ \sec\theta $3. 以下哪个是解析函数：A. $ f(z) = \frac{1}{z} $B. $ f(z) = z^2 $C. $ f(z) = \log z $D. $ f(z) = \sin z $4. Cauchy-Riemann方程是：A. $ \frac{\partial u}{\partial x} = \frac{\partialv}{\partial y} $B. $ \frac{\partial u}{\partial y} = -\frac{\partialv}{\partial x} $C. $ \frac{\partial u}{\partial x} = -\frac{\partialv}{\partial y} $D. 所有选项5. 若 $ f(z) $ 在 $ z_0 $ 处可导，则下列哪个说法是正确的：A. $ f(z) $ 在 $ z_0 $ 处连续B. $ f(z) $ 在 $ z_0 $ 处可微C. $ f(z) $ 在 $ z_0 $ 处解析D. 以上都是...二、填空题（每空3分，共30分）1. 复数 $ z = 3 + 4i $ 的模是 _________。

2. 如果 $ f(z) = z^3 + 2z^2 + z $，则 $ f'(z) = _________ $。

《复变函数》考试试题与各种总结

《复变函数》考试一试题（一）一、判断题（ 20 分）：1. 若 f(z) 在 z 0 的某个邻域内可导，则函数 f(z) 在 z 0 分析 .( )2. 有界整函数必在整个复平面为常数.()3. 若{ z n }收敛，则{Re z n } 与{Imz n }都收敛 .( )4. 若 f(z)在地区 D 内分析，且 f '( z)，则 f ( z)C（常数） . ( )5. 若函数 f(z) 在 z 0 处分析，则它在该点的某个邻域内能够睁开为幂级数 .( )6. 若 z 0 是f ( z)的 m 阶零点，则 z 0 是 1/f (z)的 m 阶极点 .()lim f ( z)7. 若 zz 0存在且有限，则 z 0 是函数 f(z) 的可去奇点 . ()8. 若函数 f(z) 在是地区 D 内的单叶函数，则f ' (z) 0(z D ) .( )9. 若 f ( z ) 在地区 D 内分析 , 则对 D 内任一简单闭曲线Cf (z)dz 0 .C( )10. 若函数 f(z) 在地区 D 内的某个圆内恒等于常数，则f(z) 在地区 D 内恒等于常数 . （）二. 填空题（ 20 分）1、dz__________. （ n 为自然数） |z z 0 |1 ( z z )n2.sin 2 z cos 2z _________.3. 函数sin z的周期为 ___________.f (z)z 214. 设 1，则f ( z)的孤立奇点有 __________.5. 幂级数nz n 的收敛半径为 __________.n 06. 若函数 f(z) 在整个平面上到处分析，则称它是__________.lim z nlimz 1z 2 ... z n7. 若 n，则 nn______________.Re s(e zn ,0)z，此中 n 为自然数 .9.sin z的孤立奇点为 ________ .z10. 若z0 是f (z)lim f (z) ___的极点，则z z.三. 计算题（ 40 分）：f (z)1(z1)( z 2) ，求 f ( z) 在 D { z : 0| z | 1}内的罗朗展式 .1. 设1dz.2.|z| 1cos zf ( z)3 2 71dC { z :| z | 3} ，试求 f ' (1 i ).3. 设Cz，此中z 1w1的实部与虚部 .4. 求复数z 四 . 证明题 .(20 分 )1. 函数 f (z)在地区D 内分析 . 证明：假如 | f ( z) |D 内在 D 内为常数，那么它在为常数 .2. 试证 : f (z) z(1z) 在割去线段 0 Re z 1 的 z 平面内能分出两个单值分析分支 ,并求出支割线 0 Re z 1登岸取正当的那支在z1的值 .《复变函数》考试一试题（一）参照答案一．判断题1．× 2．√ ３．√４．√ ５．√6．√７．×８．×９．× 10．×二．填空题2 i n 1 ； 3.2k ， ( kz) ； 4.z i ； 5. 11.n； 2.1 0 16. 整函数；7. ；8. 1 ；9. 0；10. .(n 1)!三．计算题 .1. 解因为0 z 1, 所以 0 z 1f ( z) 12) 1 1 z n 1 (z)n.( z 1)(z 1 z z ) n 0 2 n 0 22(122. 解因为z1Re s f (z) lim 2 lim 1z cosz sin z ,z z2 2 2Re s f (z) lim z 2 11. cosz limz z z sin z2 2 2所以 1 dz 2 i(Re s f (z) Re s f (z) 0 .z 2 cos zz 2 z 23. 解令 ( ) 3 2 7 1, 则它在 z 平面分析, 由柯西公式有在 z 3内,f (z)c ( )dz 2 i (z) . z所以f (1 i ) 2 i (z) z1 i2 i (13 6i ) 2 ( 6 13i ) .4. 解令 z a bi , 则w z 1 1 2 1 2( a 1 bi ) 1 2(a 1) 2b .z 1 z 1 ( a 1)2 b2 ( a 1)2 b2 (a 1)2 b2故z 112(a 1),z 1 2b. Re( )( a 1)2 b2Im( )(a 1)2 b2z 1 z 1四.证明题.1.证明设在D内 f ( z) C .令 f ( z) u iv ,则 f ( z)2u2v2c2.两边分别对 x, y 求偏导数 , 得uu xvv x 0 (1)uu y vv y 0(2)因为函数在 D 内分析 , 所以 u x v y , u y v x . 代入 (2) 则上述方程组变成uu xvv x 0 . 消去 u x 得, (u 2 v 2 ) v x 0 .vu xuv x 01)若 u 2 v 20 , 则 f ( z)0 为常数 .2) 若 v x0, 由方程 (1) (2)及 C.R. 方程有 u x 0, u y 0 ,v y 0 .所以 u c 1, v c 2 . ( c 1, c 2 为常数 ).所以f ( z)c 1 ic 2 为常数 .2. 证明 f ( z) z(1 z) 的支点为 z 0,1 . 于是割去线段 0 Re z1的 z 平面内变点就不行能单绕 0 或 1转一周 , 故能分出两个单值分析分支 .因为当 z 从支割线登岸一点出发, 连续改动到 z0,1 时 , 只有 z 的幅角增添. 所以f ( z)z(1 z) 的幅角共增添. 由已知所取分支在支割线登岸取正当 , 于是可以为该2分支在登岸之幅角为 0, 因此此分支在z1 的幅角为 , 故 f ( 1)2e2i2i .2《复变函数》考试一试题（二）一 . 判断题 . （20 分）1.若函数 f (z)u(x, y) iv ( x, y) 在 D 内连续，则 ux,y) 与 v x,y ) 都在 D 内连续.( (( )2. cosz与sinz 在复平面内有界 .( )3. 若函数 f ( z)在 z 0分析，则f ( z) 在z 0 连续 .()4. 有界整函数必为常数 .( )5.如 z 0 是函数 f ( z) 的天性奇点，则 lim ( ) 必定不存在 .()z z 0f z6. 若函数 f ( z) 在 z 0 可导，则f ( z) 在 z 0解析 .( )7. 若 f ( z) 在地区 D 内分析 , 则对 D 内任一简单闭曲线 Cf ( z)dz 0 .C( )8. 若数列 { z n } 收敛，则 {Re z n } 与 {Im z n } 都收敛 .( )9. 若 f ( z) 在区域D 内解析，则 | f ( z)| 也在D内分析.( )10. 存在一个在零点分析的函数f ( z) 使 f (1 ) 0 且 f ( 1) 1 , n 1,2,... . n12n2n( )二 . 填空题 . (20 分)1. 设 zi ，则 | z | __,arg z __, z __2. 设 f ( z) ( x 2 2 xy) i (1 sin( x 2 y 2 ), z x iy C ，则 lim f (z) ________.z 1 i3.dz_________.（ n 为自然数）|z z 0 | 1( z z )n4.幂级数nz n 的收敛半径为 __________ .n 05. 若 z 0 是 f ( z) 的 m 阶零点且 m>0，则 z 0 是 f '( z) 的_____零点 .6.函数 e z 的周期为 __________.7. 方程 2z 5 z 3 3z 8 0 在单位圆内的零点个数为 ________. 8. 设 f ( z)1 ，则 f ( z) 的孤立奇点有 _________. z 219. 函数 f (z) | z |的不分析点之集为 ________.10. Res(z 1,1) ____ .z4三 . 计算题 . (40分 )1.求函数sin(2z3)的幂级数睁开式 .2.在复平面上取上半虚轴作割线 . 试在所得的地区内取定函数z在正实轴取正实值的一个分析分支，并求它在上半虚轴左沿的点及右沿的点 z i 处的值.i3.计算积分： I| z | dz，积分路径为（1）单位圆（ | z| 1）i的右半圆 .sin z dzz 2( z) 24.求2.四. 证明题 . (20 分)1. 设函数 f ( z) 在地区 D内分析，试证：f ( z) 在 D 内为常数的充要条件是 f (z) 在D内分析 .2.试用儒歇定理证明朝数基本定理 .《复变函数》考试一试题（二）参照答案一. 判断题 .1．√２．×３．√４．√５．× 6．×７．×８．√９．× 10．× .二.填空题， i ； 2. 3 (1 sin 2)i ； 3. 2 i n 1； 5. m 1.，0 n ； 4.12 16. 2k i ，( k z) .7. 0；8. i ；9. R ；10. 0.三. 计算题1. 解 sin(2 z3 ) ( 1)n (2 z3 )2n 1 ( 1)n 22n 1 z6 n 3 .n 0 (2 n 1)! n 0 (2 n 1)!2. 解令 z re i .i 2 k则 f ( z)z re2,(k 0,1).又因为在正实轴去正实值，所以k 0 .i所以 f (i)e 4 .3. 单位圆的右半圆周为 ze i ,2.2izdz2deiei22i.所以i224. 解zsin z dz 2 i (sin z)2 i cos z2)2( zz2z 2=0.2四. 证明题 .1. 证明(必需性 ) 令 f ( z)c 1 ic 2 , 则 f ( z) c 1 ic 2 . ( c 1 ,c 2 为实常数 ).令 u( x, y) c 1, v( x, y) c 2 . 则 u x v yu yv x 0 .即 u, v 知足 C.R., 且 u x , v y ,u y , v x 连续 , 故 f (z) 在 D 内分析 .(充分性 ) 令 f ( z)u iv , 则 f (z) uiv ,因为 f ( z) 与 f ( z) 在 D 内分析 , 所以u x v y , u yv x , 且 u x ( v)y v y , u y ( v x ) v x .比较等式两边得 u x v yu y v x 0 . 进而在 D 内 u, v 均为常数 , 故 f (z) 在 D 内为常数.2. 即要证“任一n 次方程a 0 zna 1zn 1a n 1z an0 ( a 0 0) 有且只有 n个根” .证明令 f (z)a 0 z na 1z n 1a n 1z a n0 , 取 Rmax a 1a n,1 , 当a 0z在C : z R上时,有( z) a 1 R n 1a n 1 R a n ( a 1a n )R n 1 a 0 R n .f ( z) .由儒歇定理知在圆z R 内 , 方程 a 0 z n a 1z n 1 a n 1 z a n 0 与 a 0 z n 0 有相同个数的根 . 而 a0 z n 0 在z R 内有一个n 重根z 0 .所以n次方程在 z R 内有 n 个根.《复变函数》考试一试题（三）一. 判断题 . (20 分).1. cos z 与 sin z 的周期均为2k . ( )2. 若 f ( z) 在 z0处知足柯西 - 黎曼条件 , 则 f ( z) 在 z0分析 . ( )3. 若函数 f ( z) 在 z0处分析，则 f ( z) 在 z0连续 . ( )4. 若数列 { z n } 收敛，则 {Re z n } 与 {Im z n} 都收敛. ( )5.若函数 f ( z) 是地区 D 内分析且在 D 内的某个圆内恒为常数，则数 f ( z) 在区域 D内为常数 . ( )6. 若函数 f ( z) 在 z0分析，则 f ( z) 在 z0的某个邻域内可导 . ( )7. 假如函数 f ( z) 在D { z :| z | 1} 上分析,且 | f (z) | 1(| z | 1) , 则| f ( z) | 1(| z | 1) . （）8. 若函数 f ( z) 在 z0 处分析，则它在该点的某个邻域内能够睁开为幂级数.( ) 9. 若 z0是f ( z)的 m阶零点 , 则 z0是 1/ f ( z)的 m阶极点 . ( )10. 若z0是 f (z)的可去奇点，则 Res( f ( z), z0 ) 0. ( )二. 填空题 . (20 分)1. 设 f ( z) 1 ，则 f ( z) 的定义域为 ___________.z2 12. 函数 e z的周期为 _________.3. 若 z n n 2 i (1 1) n，则lim z n__________.1 n n n4. sin 2 z cos2 z ___________.dz5.|z z0 | 1(z z ) n_________. （n为自然数）6. 幂级数nx n的收敛半径为__________.n 07. 设 f (z) 11 ，则 f ( z) 的孤立奇点有 __________.z28. 设 e z1，则 z ___ .9.若z 0 是 f (z)的极点，则 lim f (z) ___.z z 0z10.Res(en ,0)____ .z三 . 计算题 . (40 分)11.将函数f ( z)z 2e z 在圆环域 0z内展为 Laurent级数 .2.试求幂级数n! z n 的收敛半径nn n.3. 算以下积分：e zdz，此中 C 是 | z | 1.Cz 2(z29)4. 求 z92z 6 z 2 8z2 0 在| z|<1 内根的个数 .四 . 证明题 . (20 分)1.函数 f (z) 在地区 D 内分析 . 证明：假如 | f ( z) |在 D 内为常数，那么它在D 内为常数 .2.设 f (z) 是一整函数，而且假设存在着一个正整数 n ，以及两个正数 R 及 M ，使适当 | z|R 时| f ( z) |M | z |n ，证明 f (z) 是一个至多 n 次的多项式或一常数。

完整版)复变函数测试题及答案

完整版)复变函数测试题及答案复变函数测验题第一章复数与复变函数一、选择题1.当 $z=\frac{1+i}{1-i}$ 时，$z+z+z$ 的值等于（）A) $i$ (B) $-i$ (C) $1$ (D) $-1$2.设复数 $z$ 满足 $\operatorname{arc}(z+2)=\frac{\pi}{3}$，$\operatorname{arc}(z-2)=\frac{5\pi}{6}$，那么 $z$ 等于（）A) $-1+3i$ (B) $-3+i$ (C) $-\frac{2}{3}+\frac{2\sqrt{3}}{3}i$ (D) $\frac{1}{3}+2\sqrt{3}i$3.复数 $z=\tan\theta-i\left(\frac{1}{2}\right)$，$0<\theta<\pi$，则 $[0<\theta<\frac{\pi}{2}$ 时，$z$ 的三角表示式是（）A) $\sec\theta[\cos(\pi+\theta)+i\sin(\pi+\theta)]$ (B)$\sec\theta[\cos\theta+i\sin\theta]$ (C) $-\sec\theta[\cos(\pi+\theta)+i\sin(\pi+\theta)]$ (D) $-\sec\theta[\cos\theta+i\sin\theta]$4.若 $z$ 为非零复数，则 $z^2-\bar{z}^2$ 与$2\operatorname{Re}(z)$ 的关系是（）A) $z^2-\bar{z}^2\geq 2\operatorname{Re}(z)$ (B) $z^2-\bar{z}^2=2\operatorname{Re}(z)$ (C) $z^2-\bar{z}^2\leq2\operatorname{Re}(z)$ (D) 不能比较大小5.设 $x,y$ 为实数，$z_1=x+1+\mathrm{i}y,z_2=x-1+\mathrm{i}y$ 且有 $z_1+z_2=12$，则动点 $(x,y)$ 的轨迹是（）A) 圆 (B) 椭圆 (C) 双曲线 (D) 抛物线6.一个向量顺时针旋转 $\frac{\pi}{3}$，向右平移 $3$ 个单位，再向下平移 $1$ 个单位后对应的复数为 $1-3\mathrm{i}$，则原向量对应的复数是（）A) $2$ (B) $1+3\mathrm{i}$ (C) $3-\mathrm{i}$ (D)$3+\mathrm{i}$7.使得 $z=\bar{z}$ 成立的复数 $z$ 是（）A) 不存在的 (B) 唯一的 (C) 纯虚数 (D) 实数8.设 $z$ 为复数，则方程 $z+\bar{z}=2+\mathrm{i}$ 的解是（）A) $-\frac{3}{3}+\mathrm{i}$ (B) $-\mathrm{i}$ (C)$\mathrm{i}$ (D) $-\mathrm{i}+4$9.满足不等式$|z+i|\leq 2$ 的所有点$z$ 构成的集合是（）A) 有界区域 (B) 无界区域 (C) 有界闭区域 (D) 无界闭区域10.方程 $z+2-3\mathrm{i}=2$ 所代表的曲线是（）A) 中心为 $2-3\mathrm{i}$，半径为 $2$ 的圆周 (B) 中心为 $-2+3\mathrm{i}$，半径为 $2$ 的圆周 (C) 中心为 $-2+3\mathrm{i}$，半径为 $2$ 的圆周 (D) 中心为 $2-3\mathrm{i}$，半径为 $2$ 的圆周11.下列方程所表示的曲线中，不是圆周的为（）A) $\frac{z-1}{z+2}=2$ (B) $z+3-\bar{z}-3=4$ (C) $|z-a|=1$ ($a0$)12.设 $f(z)=1-z$，$z_1=2+3\mathrm{i}$，$z_2=5-\mathrm{i}$，则 $f(z_1-z_2)$ 等于（）A) $-2-2\mathrm{i}$ (B) $-2+2\mathrm{i}$ (C)$2+2\mathrm{i}$ (D) $2-2\mathrm{i}$1.设 $f(z)=1$，$f'(z)=1+i$，则 $\lim_{z\to 0}\frac{f(z)-1}{z}=$ $f(z)$ 在区域 $D$ 内解析，且 $u+v$ 是实常数，则$f(z)$ 在 $D$ 内是常数。

(完整版)复变函数试题及答案

-5四123456五1一二三四2、、、、、、、、5、、、填（1611-计求将计计求设证使单判计B计证空e算函函算算将函明符选断算i1算明题n）9积数数积实单数：合题题题2题题（解，2分分积位在D条（（（，（（每不析fff2分圆件每每每z7每每小存zzz函CC3e小小小小小在题在zL数CIxz0=2题题题2题题区解的z221zzd1k402y321域2析z零226，共(Di分1k6a7，点分分分=1iD形0，x分z分80z且是zd，，，2，5内,c映,视））1满doC孤本共共共A±1解射iL答zs:足立质，2在…1析成题2134在的6的，x006C），z单情：2C所分分分(证，位a况f9有1i）））i y明圆的可23孤2711n：去)酌01C1立+w函52心情，1z奇iy数的邻给8点41D直域21的（2i，1线内n1f，分包9u，段分展zA式括，1，成也f0线15共洛在2性01n9朗）A变D21z0级处换内分数2的解1n）w留（析,数并nL指z1出,2 收敛）的域函数____________________________________________________________________________________________________________ f z
1 解： C 的参数方程为： z=i+t, 0 t 1 dz=dt
x
y
ix 2
dz ＝
1
t
1
it 2 dt =
1
i
C
0
23
2 解: z 1为 f z 一阶极点
z 1 为 f z 二阶极点
2
2k
1, 2 ) ， 4 ei ln 2 e 4
(k=0, 1, 2 )
5
i , 6 0, 7

大学《复变函数》试卷及答案

∴方程的解为
---------------------------- 6分
2．函数在复平面内何处可导，何处解析，并求
解：设，则
．四个偏导数在复平面上都连续，
由C—R方程得：．
故仅在直线上可导，在复平面上处处不解析．
--------------------------- 4分
且因为点在曲线上，所以．
大学《复变函数》试卷及答案
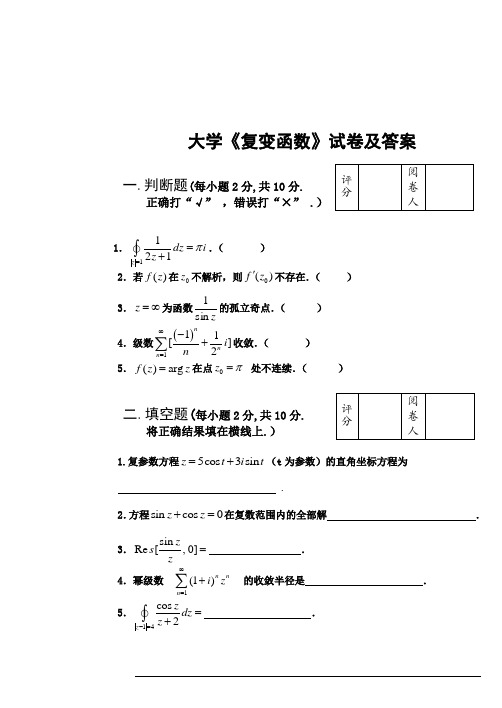
一.判断题(每小题2分,共10分.
正确打“√”，错误打“×”.）
评
分
阅
卷
人
1．．（）
2．若在不解析，则不存在．（）
3．为函数的孤立奇点．（）
4．级数收敛．（）
5．在点处不连续．（）
二.填空题(每小题2分,共10分.
将正确结果填在横线上.）
评
分
阅
卷
人
1.复参数方程（t为参数）的直角坐标方程为
3.下列结论错误的是（）
（A）是函数的二阶极点．（B）是函数的可去奇点．
（C）．(D) 是函数的本性奇点．
4.下列结论错误的是（）
（A）C为不通过原点的简则也为解析函数．
(C)在点解析的函数一定可以在点的邻域内展开成泰勒级数．
(D)对于任意的复数．
解：由于在平面上处处解析，所以积分
与路径无关，又的一个原函数为，
---------------------------- 5分
故
＝．
------------------------ 7分
2．．
解：在内有两个不解析点，分别为简单极
点、二级极点
，
------------------------ 5分

复变函数考试卷试题及答案

应用数理统计应用数理统计试题试题第 1 页共 4 页复变函数考试卷一、单项选择题（15分，每小题3分）分）1．设()2,00,0z z f z zz ì¹ï=íï=î，则()f z 的连续点集合为（的连续点集合为（）。

（A ）单连通区域）单连通区域（B ）多连通区域）多连通区域（C ）开集非区域）开集非区域（D ）闭集非闭区域）闭集非闭区域 2．设()(,)(,)f z u x y iv x y =+，那么(,)u x y 与(,)v x y 在点()00,x y 可微是()f z 在点000z x i y =+可微的（可微的（）。

()()()()A B C D 充分但非必要条件必要但非充分条件充分必要条件既非充分也非必要条件3．下列命题中，不正确的是（下列命题中，不正确的是（）。

()()()()()()()()()0R e s ,0I m 1.zz A f z f z B f z D z f z D C e i Dz e iwp w ¥¥=-=<<<+如果无穷远点是的可去奇点,那么若在区域内任一点的邻域内展开成泰勒级数,则在内解析.幂级数的和函数在收敛圆内是解析函数.函数将带形域0()映射为单位圆4．设c 是()1z i t =+，t 从1到2的线段，则arg d cz z ò（）。

()()()()()11444AB iC iD i ppp ++5．设()f z 在01z <<内解析且()0lim 1z zf z ®=，那么()()Res ,0f z =（）。

()()()()2211A iB iCD p p --二、填空题（15分，每空3分）分） 1．()Ln 1i -的主值为的主值为。

2．函数()()Re Im f z z z z ()=+仅在点z = 处可导。

(完整版)复变函数试题及答案

C是复数其实部等于1D是复数其模等于1
2、下列命题正确的是（）
A B零的辐角是零
C仅存在一个数z,使得 D
3、下列命题正确的是（）
A函数在平面上处处连续
B 如果存在,那么在解析
C每一个幂级数在它的收敛圆周上处处收敛
D如果v是u的共轭调和函数,则u也是v的共轭调和函数
4、根式的值之一是（）
1、的指数形式是
2、 =
3、若0<r<1，则积分
4、若是的共轭调和函数，那么的共轭调和函数是
5、设为函数 = 的m阶零点，则m =
6、设为函数的n阶极点，那么 =
7、幂级数的收敛半径R=
8、是函数的奇点
9、方程的根全在圆环内
10、将点 ,i,0分别变成0,i, 的分式线性变换
二、单选题（每小题2分）
1 2 3 4 5
四计算题（每小题6分，共36分）
1解： , 分
…5分
解得: 分
2解：被积函数在圆周的内部只有一阶极点z=0
及二阶极点z=1 分
= 2i(-2+2)=0 分
3解：
= …4分
（ <2）…6分
4解: 被积函数为偶函数在上半z平面有两个
一阶极点i,2i…1分
I= …2分
= …3分
= …5分
A可去奇点B一阶极点C一阶零点D本质奇点
6、函数，在以为中心的圆环内的洛朗展式
有m个，则m=( )
A 1 B2C3 D 4
7、下列函数是解析函数的为（）
A B
C D
8、在下列函数中，的是（）
A B
C D
9、设a ，C： =1，则（）

《复变函数》考试试题与答案各种总结

《复变函数》考试试题(一)一、判断题(20分):1、若f(z)在z 0的某个邻域内可导,则函数f(z)在z 0解析、 ( )2、有界整函数必在整个复平面为常数、 ( )3、若}{n z 收敛,则} {Re n z 与}{Im n z 都收敛、 ( )4、若f(z)在区域D 内解析,且0)('≡z f ,则C z f ≡)((常数)、 ( )5、若函数f(z)在z 0处解析,则它在该点的某个邻域内可以展开为幂级数、 ( )6、若z 0就是)(z f 的m 阶零点,则z 0就是1/)(z f 的m 阶极点、 ( )7、若)(lim 0z f z z →存在且有限,则z 0就是函数f(z)的可去奇点、 ( )8、若函数f(z)在就是区域D 内的单叶函数,则)(0)('D z z f ∈∀≠、 ( ) 9、若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C0)(=⎰Cdz z f 、( )10、若函数f(z)在区域D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数、( ) 二、填空题(20分)1、 =-⎰=-1||00)(z z nz z dz__________、(n 为自然数)2、=+z z 22cos sin _________、 3、函数z sin 的周期为___________、4、设11)(2+=z z f ,则)(z f 的孤立奇点有__________、5、幂级数nn nz∞=∑的收敛半径为__________、6、若函数f(z)在整个平面上处处解析,则称它就是__________、7、若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________、8、=)0,(Re n zz e s ________,其中n 为自然数、9、 zz sin 的孤立奇点为________ 、10、若0z 就是)(z f 的极点,则___)(lim 0=→z f z z 、三、计算题(40分):1、设)2)(1(1)(--=z z z f ,求)(z f 在}1||0:{<<=z z D 内的罗朗展式、2、 .cos 11||⎰=z dz z3、设⎰-++=C d z z f λλλλ173)(2,其中}3|:|{==z z C ,试求).1('i f +4、求复数11+-=z z w 的实部与虚部、四、证明题、(20分) 1、函数)(z f 在区域D 内解析、证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数、 2、试证: ()f z =0Re 1z ≤≤的z 平面内能分出两个单值解析分支,并求出支割线0Re 1z ≤≤上岸取正值的那支在1z =-的值、《复变函数》考试试题(一)参考答案一．判断题1.×2.√ ３.√ ４.√ ５.√ 6.√ ７.×８.×９.×10.× 二.填空题 1、 2101i n n π=⎧⎨≠⎩ ; 2、 1; 3、 2k π,()k z ∈; 4、 z i =±; 5、 16、整函数;7、 ξ;8、 1(1)!n -; 9、 0; 10、 ∞、三.计算题、1、解因为01,z << 所以01z <<111()(1)(2)12(1)2f z z z z z ==-----001()22nn n n z z ∞∞===-∑∑、 2、解因为22212Re ()limlim 1cos sin z z z z s f z z z ππππ→→=+===--, 22212Re ()limlim 1cos sin z z z z s f z z zππππ→-→-=--===-、所以22212(Re ()Re ()0cos z z z dz i s f z s f z z πππ==-==+=⎰、 3、解令2()371ϕλλλ=++, 则它在z 平面解析, 由柯西公式有在3z <内, ()()2()c f z dz i z z ϕλπϕλ==-⎰、所以1(1)2()2(136)2(613)z i f i i z i i i πϕππ=+''+==+=-+、 4、解令z a bi =+, 则 222222122(1)2(1)211111(1)(1)(1)z a bi a bw z z a b a b a b -+-+==-=-=-+++++++++、故 2212(1)Re()11(1)z a z a b -+=-+++, 2212Im()1(1)z bz a b-=+++、四、证明题、1、证明设在D 内()f z C =、令2222(),()f z u iv f z u v c =+=+=则、两边分别对,x y 求偏导数, 得 0(1)0(2)x x yy uu vv uu vv +=⎧⎨+=⎩因为函数在D 内解析, 所以,x y y x u v u v ==-、代入 (2) 则上述方程组变为00x x x x uu vv vu uv +=⎧⎨-=⎩、消去x u 得, 22()0x u v v +=、 1) 若220u v +=, 则 ()0f z = 为常数、2) 若0x v =, 由方程 (1) (2) 及 ..C R -方程有0,x u = 0y u =, 0y v =、所以12,u c v c ==、 (12,c c 为常数)、所以12()f z c ic =+为常数、2、证明()f z =0,1z =、于就是割去线段0Re 1z ≤≤的z 平面内变点就不可能单绕0或1转一周, 故能分出两个单值解析分支、由于当z 从支割线上岸一点出发,连续变动到0,1z = 时, 只有z 的幅角增加π、所以()f z =2π、由已知所取分支在支割线上岸取正值, 于就是可认为该分支在上岸之幅角为0, 因而此分支在1z =-的幅角为2π,故2(1)i f e π-==、《复变函数》考试试题(二)一. 判断题、(20分)1、若函数),(),()(y x iv y x u z f +=在D 内连续,则u (x,y )与v (x,y )都在D 内连续、 ( )2、 cos z 与sin z 在复平面内有界、 ( )3、若函数f (z )在z 0解析,则f (z )在z 0连续、 ( )4、有界整函数必为常数、 ( )5、如z 0就是函数f (z )的本性奇点,则)(lim 0z f z z →一定不存在、 ( )6、若函数f (z )在z 0可导,则f (z )在z 0解析、 ( )7、若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=⎰Cdz z f 、( )8、若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛、 ( ) 9、若f (z )在区域D 内解析,则|f (z )|也在D 内解析、 ( )10、存在一个在零点解析的函数f (z )使0)11(=+n f 且,...2,1,21)21(==n nn f 、( )二、填空题、 (20分)1、设i z -=,则____,arg __,||===z z z2、设C iy x z y x i xy x z f ∈+=∀+-++=),sin(1()2()(222,则=+→)(lim 1z f iz ________、3、=-⎰=-1||00)(z z n z z dz_________、(n 为自然数)4、幂级数0n n nz ∞=∑的收敛半径为__________ 、5、若z 0就是f (z )的m 阶零点且m >0,则z 0就是)('z f 的_____零点、6、函数e z 的周期为__________、7、方程083235=++-z z z 在单位圆内的零点个数为________、 8、设211)(zz f +=,则)(z f 的孤立奇点有_________、 9、函数||)(z z f =的不解析点之集为________、10、 ____)1,1(Res 4=-zz 、三、计算题、 (40分)1、求函数)2sin(3z 的幂级数展开式、2、在复平面上取上半虚轴作割线、试在所得的区域内取定函数z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点i z=处的值、3、计算积分:⎰-=iiz z Id ||,积分路径为(1)单位圆(1||=z )的右半圆、4、求dzz zz ⎰=-22)2(sin π、四、证明题、 (20分)1、设函数f (z )在区域D 内解析,试证:f (z )在D 内为常数的充要条件就是)(z f 在D 内解析、2、试用儒歇定理证明代数基本定理、《复变函数》考试试题(二)参考答案一. 判断题、1.√ ２.×３.√ ４.√ ５.×6.×７.×８.√ ９.×10.×、二、填空题1、1,2π-, i ; 2、 3(1sin 2)i +-; 3、2101i n n π=⎧⎨≠⎩; 4、 1; 5、 1m -、 6、 2k i π,()k z ∈、 7、 0; 8、 i ±; 9、 R ; 10、 0、三、计算题1、解 3212163300(1)(2)(1)2sin(2)(21)!(21)!n n n n n n n z z z n n +++∞∞==--==++∑∑、2、解令i z re θ=、则22(),(0,1)k if z k θπ+===、又因为在正实轴去正实值,所以0k =、所以4()if i eπ=、3、单位圆的右半圆周为i z e θ=, 22ππθ-≤≤、所以22222ii i iz dz de ei ππθθππ---===⎰⎰、4、解dz z zz ⎰=-22)2(sin π2)(sin 2ππ='=z z i 2cos 2ππ==z zi =0、四、证明题、1、证明 (必要性) 令12()f z c ic =+,则12()f z c ic =-、 (12,c c 为实常数)、令12(,),(,)u x y c v x y c ==-、则0x y y x u v u v ====、即,u v 满足..C R -, 且,,,x y y x u v u v 连续, 故()f z 在D 内解析、 (充分性) 令()f z u iv =+, 则 ()f z u iv =-, 因为()f z 与()f z 在D 内解析, 所以,x y y x u v u v ==-, 且(),()x y y y x x u v v u v v =-=-=--=-、比较等式两边得 0x y y x u v u v ====、从而在D 内,u v 均为常数,故()f z 在D 内为常数、2、即要证“任一 n 次方程 101100(0)n n n n a z a z a z a a --++⋅⋅⋅++=≠ 有且只有 n 个根”、证明令1011()0nn n n f z a z a z a z a --=++⋅⋅⋅++=, 取10max ,1n a a R a ⎧⎫+⋅⋅⋅+⎪⎪>⎨⎬⎪⎪⎩⎭, 当z 在:C z R =上时, 有 111110()()n n nn n n z a R a R a a a R a R ϕ---≤+⋅⋅⋅++<+⋅⋅⋅+<、()f z =、由儒歇定理知在圆 z R < 内, 方程10110n n n n a z a z a z a --++⋅⋅⋅++= 与 00na z = 有相同个数的根、而 00na z = 在 z R < 内有一个 n 重根 0z =、因此n 次方程在z R <内有n 个根、《复变函数》考试试题(三)一、判断题、 (20分)、1、 cos z 与sin z 的周期均为πk2、 ( ) 2、若f (z )在z 0处满足柯西-黎曼条件, 则f (z )在z 0解析、 ( )3、若函数f (z )在z 0处解析,则f (z )在z 0连续、 ( )4、若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛、 ( )5、若函数f (z )就是区域D 内解析且在D 内的某个圆内恒为常数,则数f (z )在区域D 内为常数、 ( )6、若函数f (z )在z 0解析,则f (z )在z 0的某个邻域内可导、 ( )7、如果函数f (z )在}1|:|{≤=z z D 上解析,且)1|(|1|)(|=≤z z f ,则)1|(|1|)(|≤≤z z f 、 ( )8、若函数f (z )在z 0处解析,则它在该点的某个邻域内可以展开为幂级数、( )9、若z 0就是)(z f 的m 阶零点, 则z 0就是1/)(z f 的m 阶极点、 ( ) 10、若z 就是)(z f 的可去奇点,则)),((Res 0=z z f 、( )二、填空题、 (20分)1、设11)(2+=z z f ,则f (z )的定义域为___________、2、函数e z的周期为_________、3、若n n n i n n z )11(12++-+=,则=∞→n z n lim __________、4、 =+z z 22cos sin ___________、5、 =-⎰=-1||00)(z z n z z dz_________、(n 为自然数) 6、幂级数∑∞=0n n nx 的收敛半径为__________、7、设11)(2+=z z f ,则f (z )的孤立奇点有__________、8、设1-=ze ,则___=z 、9、若0z 就是)(z f 的极点,则___)(lim 0=→z f z z 、10、 ____)0,(Res =n zze 、三、计算题、 (40分)1、将函数12()zf z z e =在圆环域0z <<∞内展为Laurent 级数、2、试求幂级数nn n z nn ∑+∞=!的收敛半径、3、算下列积分:⎰-C z z z ze )9(d 22,其中C 就是1||=z 、4、求0282269=--+-z z z z在|z |<1内根的个数、四、证明题、 (20分) 1、函数)(z f 在区域D 内解析、证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数、 2、设)(z f 就是一整函数,并且假定存在着一个正整数n ,以及两个正数R 及M ,使得当R z ≥||时n z M z f |||)(|≤,证明)(z f 就是一个至多n 次的多项式或一常数。

复变函数试题库(含答案)

复变函数一、选择题1. 设函数()(,)(,)f z u x y iv x y =+且),(y x u 是区域D 内的调和函数,则当),(y x v 在D 内是（ C ）时, )(z f 在D 内解析. A. 可导函数B.调和函数C.共轭调和函数2、复积分()nCdzz a -⎰的值为（ B ） (A) 0 (B) 0;2(C)(D)2i i ππ不存在 3、0z =是sin ()zf z z=的奇点类型是（ D ） (A) (B) (C)(D) 一阶极点本性奇点不是奇点可去奇点 4、计算12()i eπ-的结果是（ B ）(A) (B) (C)(D)i i i ±-05、下列函数在z S 处处解析的是（ C ）(A) (B) (C)(D)z z e z z z e z zRe z f()=f()=f()=f()= 6．当x 〈0, y 0≥时,argz=( C ).A. π-x y arctan; B. x yarctan ; C π+x y arctan ; D. π2arctan +xy.7．argz 1z 2=( A )..A ．argz 1+argz 2; B. argz 1+argz 2+2k π(k 是整数); C.argz 1+argz 2+2k 1π（k 1是某个整数）; D.argz 1+argz 2+π. 8.下列集合是有界闭区域的是（ C ） A 0<R z ≤;B Rez<2; C.1≤z 且Imz 0≥; D.1≥z 且 Rez>0 .9.方程z=t+)(R t ti∈在平面上表示的是（ B ）.A ．直线y=x; B. 双曲线 y=x1;C 椭圆周；D 圆周 10.函数)(z f =z 在0z =处（ A ）. A. 连续B. 可导C. 解析11.ii-+23=( A ). A ．i +1 i B +2. i C 32.+ i D -1.12.函数w=f(z)仅在点z 0可微，则w=f(z)在点z 0（ D ） A 解析； B 某邻域内处处解析； C.不解析。

复变函数考试题和答案

复变函数考试题和答案****一、选择题（每题5分，共30分）1. 复数 $ z = a + bi $ 的共轭复数为（）。

A. $ a - bi $B. $ a + bi $C. $ -a + bi $D. $ -a - bi $**答案：A**2. 复数 $ z = a + bi $ 的模长为（）。

A. $ \sqrt{a^2 + b^2} $B. $ \sqrt{a^2 - b^2} $C. $ \sqrt{a^2 + b} $D. $ \sqrt{a + b^2} $**答案：A**3. 函数 $ f(z) = \frac{1}{z} $ 在 $ z = 0 $ 处的性质是（）。

A. 可导B. 连续C. 可微D. 奇点**答案：D**4. 函数 $ f(z) = z^2 $ 在复平面上是（）。

A. 单叶函数B. 多叶函数C. 常数函数D. 线性函数**答案：A**5. 函数 $ f(z) = \sin(z) $ 是（）。

A. 整函数B. 亚纯函数C. 非解析函数D. 多项式函数**答案：A**6. 函数 $ f(z) = e^z $ 在复平面上是（）。

A. 整函数B. 亚纯函数C. 非解析函数D. 多项式函数**答案：A**二、填空题（每题5分，共20分）1. 复数 $ z = 3 + 4i $ 的共轭复数是 $ \_\_\_\_\_\_\_ $。

**答案：3 - 4i**2. 复数 $ z = 1 + i $ 的模长是 $ \_\_\_\_\_\_\_ $。

**答案：$ \sqrt{2} $**3. 函数 $ f(z) = z^3 $ 在 $ z = 1 $ 处的导数是 $ \_\_\_\_\_\_\_ $。

**答案：3**4. 函数 $ f(z) = \frac{1}{z-1} $ 的奇点是 $ \_\_\_\_\_\_\_ $。

复变函数考试题及答案

复变函数考试题及答案一、选择题（每题4分，共20分）1. 若函数f(z)=u(x,y)+iv(x,y)是解析函数，则以下关系式中正确的是（）。

A. u_x = v_yB. u_y = -v_xC. u_x = -v_yD. u_y = v_x答案：B2. 复变函数中，柯西-黎曼方程成立的条件是（）。

A. u和v都是调和函数B. u和v都是解析函数C. u和v都是连续函数D. u和v都是可微函数答案：D3. 以下哪个函数是解析函数？（）A. f(z) = |z|B. f(z) = z^2C. f(z) = z^3D. f(z) = z^4答案：B4. 函数f(z)=e^z的实部和虚部分别是（）。

A. u(x,y)=e^x*cos(y), v(x,y)=e^x*sin(y)B. u(x,y)=e^x*sin(y), v(x,y)=e^x*cos(y)C. u(x,y)=e^x*cos(y), v(x,y)=e^x*sin(y)D. u(x,y)=e^x*sin(y), v(x,y)=e^x*cos(y)答案：C5. 以下哪个函数是多值函数？（）A. f(z) = log(z)B. f(z) = sin(z)C. f(z) = cos(z)D. f(z) = z^2答案：A二、填空题（每题3分，共15分）1. 若f(z)=z^2，则f'(z)=________。

答案：2z2. 函数f(z)=z+1/z的极点是________。

答案：z=03. 函数f(z)=1/z的留数在z=0处为________。

答案：14. 函数f(z)=z^3的导数是________。

答案：3z^25. 函数f(z)=e^z的导数是________。

答案：e^z三、解答题（每题10分，共30分）1. 证明函数f(z)=z^2是解析函数，并求其导数。

答案：函数f(z)=z^2是解析函数，因为其满足柯西-黎曼方程。

设z=x+iy，则f(z)=(x+iy)^2=x^2-y^2+2ixy。

浙江大学大二数学专业《复变函数》考试A卷及答案

第 1 页共2页第 1 页共2页(A) 答案120分钟总分100分闭卷 2分，计10分）。

4π C. 3π- D.3π( B )。

z e C.f(z)=Lnz D.f(z)=Rez ( A )。

C.本性奇点 D.二阶极点 ( C )。

C.2 D.∞ B ）。

C.21D.020分)则z 的辐角主值为 π32 2cosz 圆 5、函数w=cosz 的解析范围为全平面 6、设z=3-4i ，则z ＝ 3+4i 7、积分⎰==+2102)1((z z dz z e z 08、函数z=)2)(1(--z z z的奇点为 1 和29、设f(z)=2)1(28--z z z ,则f(z)在z=0的留数Res[f(z),0]= -2 10、解析函数w=3z 在z=1处的伸缩率为 3 。

三、求下列积分(20分) 每题5分 1、dz i z zz ⎰=-22、dz i z zz ⎰=-23)(cos 1、原式＝2πii=-2π 2、原式＝2πi )(cos ''z iz ==-2πicosi 3、⎰=--32)1(25z dz z z z 4、⎰=--22))(9(z i z z z3、原式＝2πi{Res[f(z),0]+Res[f(z),1]} =2πi{-2+2}＝04、原式＝2πi i z z z =-29=-5π四、计算题(每题5分,计15分) 1、求i +1的值第 2 页共2页第 2 页共2页原式＝]224sin [cos2224ππππk i k +++ （k=0,1）k=0 原式=]8sin8[cos2ππi +k=1 原式=]89sin 89[cos 2ππi +2、求Ln(1-i)的值原式=ln2+i(-ππk 24+) k=1,2,…3、求10)1(i +的值原式=i i i 32)2(])1[(552==+ 五、(12分)将函数f(z)=)1)(2(1--z z (1)在0<|z-1|<1内展开为洛朗级数;(2) 在0<|z-2|<1内展开为洛朗级数.(1) f(z)=∑∞=----=--+--=-+--0)1(11111112111n n z z z z z z …6分(2) f(z)=∑∞=--+-=+---0)2()1(2112121n n n z z z z …6分六、(8分) 求f(z)=z321- 在z=0处的泰勒级数,并指出收敛范围。

复变函数试题及答案

复变函数试题及答案一、选择题（每题4分，共40分）1. 下列哪个函数在全平面上是解析的？A. f(z) = |z|^2B. f(z) = e^zC. f(z) = ln(z)D. f(z) = 1/z答案：B2. 设f(z) = u(x, y) + iv(x, y)是解析函数，其中u(x, y)和v(x, y)是实函数。

下列哪个条件是解析函数的充分必要条件？A. u满足柯西-黎曼方程B. v满足柯西-黎曼方程C. u和v满足柯西-黎曼方程D. u和v的一阶偏导数满足柯西-黎曼方程答案：C3. 设f(z) = u(r, θ)是解析函数，其中r和θ是极坐标系下的变量。

下列哪个条件是解析函数的充分必要条件？A. u满足极坐标下的柯西-黎曼方程B. f(z)在全平面上是解析的C. f(z)在圆心附近是解析的D. f(z)在正实轴上是解析的答案：A4. 设f(z) = u(x, y) + iv(x, y)是解析函数，其中u(x, y)和v(x, y)是实函数。

若u和v满足柯西-黎曼方程，则A. f(z)在全平面上是解析的B. f(z)在实轴上是解析的C. f(z)在虚轴上是解析的D. f(z)在解析的那部分上满足柯西-黎曼方程答案：A5. 设f(z) = u(x, y) + iv(x, y)是解析函数，其中u(x, y)和v(x, y)是实函数。

若f(z)在实轴上是解析的，则A. u(x, y)在全平面上是解析的B. v(x, y)在全平面上是解析的C. u(x, y)和v(x, y)满足柯西-黎曼方程D. u(x, y)和v(x, y)处处可微分答案：C二、填空题（每空5分，共30分）1. 若f(z) = x^2 - y^2 + 2xyi是解析函数，则它的共轭函数为________。

答案：f*(z) = x^2 - y^2 - 2xyi2. 设f(z) = u(x, y)是解析函数，且满足柯西-黎曼方程的实部形式，则函数f(z)可表示为f(z) = ________。