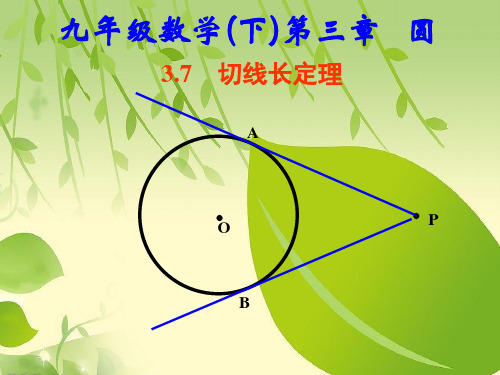
201X春九年级数学下册 第三章《圆》7 切线长定理习题课件(新版)北师大版
合集下载
九年级数学北师大版下册3.7切线长定理 课件

CB×AC=
1 2
r×AB+ 1 2
r×BC+ 1 2
r×AC
BA
D
CB
∴CB×AC= r×AB+ r×BC+ r×AC
10×24=r×10+r×24+r×26 ∴ r=4,
例1 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm, 求AF、BD、CE的长.
在弧AB上任取一点C,过点C作☉O的切线,分别交PA、
PB于点D、E.已知PA=7,∠P=40°.则
⑴ △PDE的周长是
;
⑵ ∠DOE= ____ . 解析:∵DC、DA是☉O的两条切线, P
点C、A是切点,∴DC=DA.
同理可得CE=EB.∵PA、PB是☉O的两
条切线,点A、B是切点,∴PA=PB=7.
2r=26.
例 如图3-33,Rt△ABC的两条直角边AC=10,BC=24,⊙O是 △ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
解法二:连接OD,OE,OF,设 O在DR=tr△. ABC中, AC=10, BCAB=24,AC 2 BC 2 102 242 26.
AC
E F
1 2
同理可得∠COE= 1 ∠COB.
2
∠DOE=∠DOC+∠COE=
12(∠AOC+
∠COB)=70°.
DA
C
O
E B
本课小结
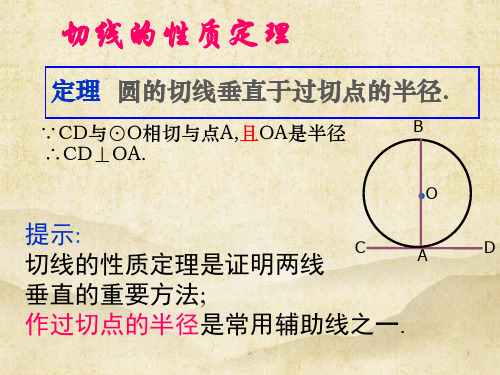
切线的6个性质: (1)切线和圆只有一个公共点. (2)切线和圆心的距离等于圆的半径. (3)切线垂直于过切点的半径. (4)经过圆心垂直于切线的直线必过切点. (5)经过切点垂直于切线的直线必过圆心. (6)切线长定理.
北师大版数学九年级下册3.7切线长定理 课件

②当PA=12,PD=8,求r,PO,CO,AB, ①∵PA,PB为切线
∴PA=PB
∵OA=OB
∴PO为AB的中垂线
解得r=5
∴PO⊥AB,且AD=BD ∴PO=5+8=13
②∵PA为切线
由得PO⊥AB且OA⊥PA
∴OA⊥PA
∴AO²=CO·PO(韦达定理)
∴在RT△APO中
∴CO=25/13
PA²+OA²=PO²
O
P
B
图2
3.切线长:从圆外一点可以引圆的两条切线, 这一点和切点之间_线_段_的_长_度_叫做圆的切线长 4.切线长定理:过圆外一点所作的圆的两条切 线长_相_等__。
教师点拨:(3分钟) 一:切线长:从圆外一点可以引圆的两条切线, 这一点和切点之间_线_段_的_长_度_叫做圆的切线长
注意:切线——是一条直线 切线长——线段的长度
∴x²+4²=(2+x )² 解得x=3 ∴PO=x+2=5 OA=x=3
教师点拨:(5分钟)
2、已知:如图,⊙O是△ABC的内切圆,切点分别
为D、E、F,(1)图中共有___3__对相等线段 (2)若AF=4,BD=6,CE=8,则△ABC的周长是 36
(3)若AB=9,BC=15,AC=12,则
二:切线长定理:过圆外一点所作的圆的两条 切线长 相等
几何语言:
A
∵PA,PB为⊙O的切线,切点为
A、B ∴PA=PB
O
P
B
图2
自学检测一:(5分钟)
1、如图,PA、PB分别与⊙O相切于点A、B
若PA=4,PD=2,则PO= 5 ;OA= 3 ;
2、已知:如图,⊙O是△ABC的内切圆,切点分别
九年级数学下册 第三章 圆 3.7 切线长定理教学课件 (

﹡7 切线长定理
【基础梳理】 1.切线长定义 过圆外一点作圆的切线,这点和切点之间的_线__段__长__叫做 这点到圆的切线长.
2.切线长定理
切线长定理 文字叙述 过圆外一点画圆的两条切线,它们的切线长_相__等__.
如图,∵AB,AC都是圆O的切线,切点 符号语言 分别是点B、点C.
∴AB=_A_C_
∴由勾股定理得,2OA2=OP2, 即OA2=8,∴OA=2 2 .即半径长为2 2 .
【微点拨】 切线长定理中的一二三 如图,PA,PB与☉O相切,切点分别是A,B,则此 图中包含信息有: 1.一条角平分线:即PO平分∠APB且平分∠AOB. 2.两个等腰三角形:△PAB,△AOB是等腰三角形. 3.三个垂直:即OA⊥PA,OB⊥PB,PO⊥AB.
知识点二 切线长定理的应用 【示范题2】如图,边长为1的正方形ABCD的边AB是☉O 的直径,CF是☉O的切线,E为切点,F点在AD上,BE是☉O 的弦,求△CDF的面积.
【备选例题】如图,PA,PB是☉O的切线,A, B为切点,AC是☉O的直径,∠P=60°. (1)求∠BAC的度数. (2)当OA=2时,求AB的长.
知识点一 切线长定理 【示范题1】如图,PA切☉O于A,PB切☉O于B,∠APB= 90°,OP=4,求☉O的半径.
【思路点拨】先判断四边形OAPB为正方形,再由勾股定 理求得圆的半径. 【自主解答】∵PA切☉O于B=90°,OA=OB,∴四边形OAPB为正方形, ∴AO=AP,∵OP=4,
【解析】(1)∵PA,PB是☉O的切线, ∴AP=BP. ∵∠P=60°, ∴∠PAB=60°, ∵AC是☉O的直径, ∴∠PAC=90°, ∴∠BAC=90°-60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°, ∴OP=4. 由勾股定理得:AP=2 3 . ∵AP=BP,∠APB=60°, ∴△APB是等边三角形, ∴AB=AP=2 3 .
【基础梳理】 1.切线长定义 过圆外一点作圆的切线,这点和切点之间的_线__段__长__叫做 这点到圆的切线长.
2.切线长定理
切线长定理 文字叙述 过圆外一点画圆的两条切线,它们的切线长_相__等__.
如图,∵AB,AC都是圆O的切线,切点 符号语言 分别是点B、点C.
∴AB=_A_C_
∴由勾股定理得,2OA2=OP2, 即OA2=8,∴OA=2 2 .即半径长为2 2 .
【微点拨】 切线长定理中的一二三 如图,PA,PB与☉O相切,切点分别是A,B,则此 图中包含信息有: 1.一条角平分线:即PO平分∠APB且平分∠AOB. 2.两个等腰三角形:△PAB,△AOB是等腰三角形. 3.三个垂直:即OA⊥PA,OB⊥PB,PO⊥AB.
知识点二 切线长定理的应用 【示范题2】如图,边长为1的正方形ABCD的边AB是☉O 的直径,CF是☉O的切线,E为切点,F点在AD上,BE是☉O 的弦,求△CDF的面积.
【备选例题】如图,PA,PB是☉O的切线,A, B为切点,AC是☉O的直径,∠P=60°. (1)求∠BAC的度数. (2)当OA=2时,求AB的长.
知识点一 切线长定理 【示范题1】如图,PA切☉O于A,PB切☉O于B,∠APB= 90°,OP=4,求☉O的半径.
【思路点拨】先判断四边形OAPB为正方形,再由勾股定 理求得圆的半径. 【自主解答】∵PA切☉O于B=90°,OA=OB,∴四边形OAPB为正方形, ∴AO=AP,∵OP=4,
【解析】(1)∵PA,PB是☉O的切线, ∴AP=BP. ∵∠P=60°, ∴∠PAB=60°, ∵AC是☉O的直径, ∴∠PAC=90°, ∴∠BAC=90°-60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°, ∴OP=4. 由勾股定理得:AP=2 3 . ∵AP=BP,∠APB=60°, ∴△APB是等边三角形, ∴AB=AP=2 3 .
3.7 切线长定理 北师大版数学九年级下册导学课件

第三章 圆
*7 切线长定理
学习目标
1 本节要点 切线长定理
2 学习流程
逐点 学练
本节 小结
作业 提升
பைடு நூலகம்
感悟新知
知识点 1 切线长定理
1. 切线长定义 过圆外一点画圆的切线,这点和切点之间 的线段长叫做这点到圆的切线长.
切线是直线,不可度量;切线 长是切线上切点与切点外一点 之间线段的长,可以度量.
∵ PA,PB,DE 是⊙ O 的切线,
∴ OA ⊥ PA,OB ⊥ PB,OC ⊥ DE.
∴∠ DAO= ∠ EBO=90°.∴∠ P+ ∠ AOB=180°.
∴∠ AOB=180°-50°=130°.
易知∠ AOD= ∠ DOC,∠ COE= ∠ BOE,
1
1
∴∠ DOE= 2 ∠ AOB= 2 ×130°=65°.
感悟新知
(1)若PA=10,求△ PDE 的周长; 解:∵ PA,PB,DE 分别切⊙ O 于点A,B,C, ∴ PA=PB,DA=DC,EC=EB. ∴ PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20. ∴△ PDE 的周长为20.
感悟新知
(2)若∠ P=50°,求∠ DOE 的度数. 解:如图3-7-2,连接OA,OC,OB.
2
∴ PO ⊥ AB. ∴∠ ABP+ ∠ BPO=90°. ∵ PB 是⊙ O 的切线,∴ OB ⊥ PB. ∴∠ ABP+ ∠ ABC=90°. ∴∠ ABC= ∠ BPO= 1 ∠ APB,即∠ APB=2 ∠ ABC.
2
感悟新知
(2)AC ∥ OP. 解:∵ BC 是⊙ O 的直径, ∴∠ BAC=90°,即AC ⊥ AB. 由(1)知OP ⊥ AB,∴ AC ∥ OP.
*7 切线长定理
学习目标
1 本节要点 切线长定理
2 学习流程
逐点 学练
本节 小结
作业 提升
பைடு நூலகம்
感悟新知
知识点 1 切线长定理
1. 切线长定义 过圆外一点画圆的切线,这点和切点之间 的线段长叫做这点到圆的切线长.
切线是直线,不可度量;切线 长是切线上切点与切点外一点 之间线段的长,可以度量.
∵ PA,PB,DE 是⊙ O 的切线,
∴ OA ⊥ PA,OB ⊥ PB,OC ⊥ DE.
∴∠ DAO= ∠ EBO=90°.∴∠ P+ ∠ AOB=180°.
∴∠ AOB=180°-50°=130°.
易知∠ AOD= ∠ DOC,∠ COE= ∠ BOE,
1
1
∴∠ DOE= 2 ∠ AOB= 2 ×130°=65°.
感悟新知
(1)若PA=10,求△ PDE 的周长; 解:∵ PA,PB,DE 分别切⊙ O 于点A,B,C, ∴ PA=PB,DA=DC,EC=EB. ∴ PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20. ∴△ PDE 的周长为20.
感悟新知
(2)若∠ P=50°,求∠ DOE 的度数. 解:如图3-7-2,连接OA,OC,OB.
2
∴ PO ⊥ AB. ∴∠ ABP+ ∠ BPO=90°. ∵ PB 是⊙ O 的切线,∴ OB ⊥ PB. ∴∠ ABP+ ∠ ABC=90°. ∴∠ ABC= ∠ BPO= 1 ∠ APB,即∠ APB=2 ∠ ABC.
2
感悟新知
(2)AC ∥ OP. 解:∵ BC 是⊙ O 的直径, ∴∠ BAC=90°,即AC ⊥ AB. 由(1)知OP ⊥ AB,∴ AC ∥ OP.
九年级数学下册 第三章 圆 3.7 切线长定理课件 北师大下册数学课件

第二十一页,共四十二页。
【学霸提醒(tíxǐng)】 切线长定理五类应用 1.求角度.
2.求线段的长度. 3.证线段相等.
4.证线段对应成比例.
5.证线段平行.
第二十二页,共四十二页。
【题组训练】
1.(2019·常州金坛区期中(qī zhōnɡ))如图,AB,AC,BD是☉O的
切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长
第二十七页,共四十二页。
解:(1)连接(liánjiē)CD,由AC是直径知CD⊥AB.
第二十八页,共四十二页。
∵DE,CE都是切线(qiēxiàn), ∴DE=CE,
∠EDC=∠ECD.
又∠B+∠ECD=90°, ∠BDE+∠EDC=90°; ∴∠B=∠BDE,∴BE=DE,从而BE=CE.
第二十九页,共四十二页。
PC,PD分别切☉O于点C,D.
第八页,共四十二页。
(1)请写出两个不同类型(lèixíng)的正确结论. (2)若CD=12,tan∠CPO= ,求1 PO的长.
2
第九页,共四十二页。
【规范解答】(1)不同类型(lèixíng)的正确结论有: ①PC=PD,②∠CPO=∠DPA,③CD⊥BA,④∠CEP=90°(答案
*7 切线长定理。如图,∵AB,AC都是。是点B、点C.。∴∠OCP=90°,在Rt△OPC中,。
No 1.(2019·深圳模拟)如图,AB是☉O的直径(zhíjìng),点C为。1.(2019·常州金坛区期中)如图,AB,AC,BD
是☉O的。★3.如图,☉O是四边形ABCD的内切圆,下列结论一定。解:(1)连接CD,由AC是直径 (zhíjìng)知CD⊥AB.。∴BE=r,即△ABC是一个等腰直角三角形,。正解:另一种情况,若点C在劣弧AB 上,如图C2
【学霸提醒(tíxǐng)】 切线长定理五类应用 1.求角度.
2.求线段的长度. 3.证线段相等.
4.证线段对应成比例.
5.证线段平行.
第二十二页,共四十二页。
【题组训练】
1.(2019·常州金坛区期中(qī zhōnɡ))如图,AB,AC,BD是☉O的
切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长
第二十七页,共四十二页。
解:(1)连接(liánjiē)CD,由AC是直径知CD⊥AB.
第二十八页,共四十二页。
∵DE,CE都是切线(qiēxiàn), ∴DE=CE,
∠EDC=∠ECD.
又∠B+∠ECD=90°, ∠BDE+∠EDC=90°; ∴∠B=∠BDE,∴BE=DE,从而BE=CE.
第二十九页,共四十二页。
PC,PD分别切☉O于点C,D.
第八页,共四十二页。
(1)请写出两个不同类型(lèixíng)的正确结论. (2)若CD=12,tan∠CPO= ,求1 PO的长.
2
第九页,共四十二页。
【规范解答】(1)不同类型(lèixíng)的正确结论有: ①PC=PD,②∠CPO=∠DPA,③CD⊥BA,④∠CEP=90°(答案
*7 切线长定理。如图,∵AB,AC都是。是点B、点C.。∴∠OCP=90°,在Rt△OPC中,。
No 1.(2019·深圳模拟)如图,AB是☉O的直径(zhíjìng),点C为。1.(2019·常州金坛区期中)如图,AB,AC,BD
是☉O的。★3.如图,☉O是四边形ABCD的内切圆,下列结论一定。解:(1)连接CD,由AC是直径 (zhíjìng)知CD⊥AB.。∴BE=r,即△ABC是一个等腰直角三角形,。正解:另一种情况,若点C在劣弧AB 上,如图C2
3.7北师大版九年级数学下册课件第三章圆第七节切线长定理.ppt
A
D
∴12
×10×24
=
1 2
×26r
+
1 2
×24r
+
1 2
×10r
∴r=4 即⊙O半径为4OF NhomakorabeaB
例题1图
E
C
例1:已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求⊙O 的半径。
解法2:连接OD,OE,OF,设OD=r 在Rt△ABC中,AC=10,BC=24
∴AB= AB2 BC2 102 242 26 ∵⊙O分别与AB,BC,CA相切于D,E,F ∴OD⊥AB,OE⊥BC,OF⊥AC,
BE=BD, AF=AD,CE=CF 又∵∠C=90°∴四边形OECF为正方形 ∴EC=FC=r∴BE=24-r,AF=10-r ∴AB=BD+AD=BE+AF=34-2r=26 ∴r=4 即⊙O半径为4
A D
O
F
B
例题1图
E
C
• 变式1:如图,△ABC的内切圆⊙O与BC,CA,AB分 别相切于点 D,E,F,且AB=9cm,BC=14cm,
CA=13cm,求AF,BD,CE的长。(知识技能2)
A
F
E
O
B
D
C
第2题
变式2:如图,P是⊙O外一点,PA与PB分别⊙O切于A、 B两点,DE也是⊙O的切线,切点为C,PA=PB=5cm, 求△PDE的周长。(知识技能1)
∵PA、PB分别是⊙O的切线,点A、B分别为切点,
(PA、PB分别与⊙O相切于点A、B)
∴PA=PB,∠APO=∠BPO.
A
O
春学期九年级数学下册第三章圆3.7切线长定理教学课件(北师大版)

① 分别连接圆心和切点; ② 连接两切点; ③ 连接圆心和圆外一点.
三角形 内切圆
应用
运用切线长定理,将相 等线段转化集中到某条 边上,从而建立方程.
重要结论
r abc 2
只适合于直角三角形
注意 切线长定理为证明线段相等、角相等提供了新
的方法.
练一练
1. PA、PB是⊙O的两条切线,A,B是切点,OA=3. (1)若AP=4,则OP= 5 ;
(2)若∠BPA=60 °,则OP= 6 .
A
O
P
B
2. PA、PB是☉O的两条切线,A、
B为切点,直线OP交☉O于点D、
A
E,交AB于C.
(1)写出图中所有的垂直关系; E O C D
P
OA⊥PA,OB ⊥PB,AB
B
⊥OP.
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC.
(3)写出图中所有的全等三角形;
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.
(4)写出图中所有的等腰三角形.
△ABP △AOB
A
E OCD
P
B
典例精析
例1 如图,PA、PB是☉O的两条切线,点A、B是切点,
相切,求☉O的半径r的取值范围.
A
F D O·
CE
B
解:设BC=3cm,由题意可知与BC、AC相切的最大
圆与BC、AC的切点分别为B、D,连接OB、OD,则四
边形BODC为正方形.
∴OB=BC=3cm,
A
∴半径r的取值范围为0<r≤3cm.
D
·O
C
B
课堂小结
切线长
三角形 内切圆
应用
运用切线长定理,将相 等线段转化集中到某条 边上,从而建立方程.
重要结论
r abc 2
只适合于直角三角形
注意 切线长定理为证明线段相等、角相等提供了新
的方法.
练一练
1. PA、PB是⊙O的两条切线,A,B是切点,OA=3. (1)若AP=4,则OP= 5 ;
(2)若∠BPA=60 °,则OP= 6 .
A
O
P
B
2. PA、PB是☉O的两条切线,A、
B为切点,直线OP交☉O于点D、
A
E,交AB于C.
(1)写出图中所有的垂直关系; E O C D
P
OA⊥PA,OB ⊥PB,AB
B
⊥OP.
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC.
(3)写出图中所有的全等三角形;
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.
(4)写出图中所有的等腰三角形.
△ABP △AOB
A
E OCD
P
B
典例精析
例1 如图,PA、PB是☉O的两条切线,点A、B是切点,
相切,求☉O的半径r的取值范围.
A
F D O·
CE
B
解:设BC=3cm,由题意可知与BC、AC相切的最大
圆与BC、AC的切点分别为B、D,连接OB、OD,则四
边形BODC为正方形.
∴OB=BC=3cm,
A
∴半径r的取值范围为0<r≤3cm.
D
·O
C
B
课堂小结
切线长
北师大版九年级数学下册第三章3.7切线长定理(共16张PPT)

(1)要把该四边形裁剪成一个面积最大的圆形纸片,你能否用 折叠的方法找出圆心,若能,请你度量出圆的半径。
(2)计算出最大的圆形纸片的半径。
B
E
A
O
C
D
课堂小结 A
1.切线长定义:在经过圆外一
点的切线上,这一点和切点之
间的线段的长叫做这点到圆的
切线长.
O
P
2.切线长定理:从圆外一点引
圆的两条切线,它们的切线长
B
相等,圆心和这一点的连线平
分两条切线的夹角.
3.切线是到圆心距离等于圆的 半径的直线
4. 圆的外切四边形的两组对边 的和相等.
三、应用新知,体验成功
1、填空:如图10,PA、PB分别与⊙O相切于点A、B,
(1)若PB=12,PO=13,则AO=
;
(2)若PO=10,AO=6,则PB= 5 ;
(3)若PA=4,AO=3,则PO= 8;PD= ;
CA=13cm,求AF,BD,CE的长。(知识技能2)
知识技能3
3.如图,过⊙O外一点P作⊙O的两条切线PA和PB,点A、点B为 切点,∠P=40°,点D在AB上,点E和点F分别在PB和PA上, 且AD=BE,BD=AF,求∠EDF。
1 5
3
4
2
数学理解4
4.如图,有一张四边形ABCD纸片,AB=AD=6cm,CB=CD=8cm, 且∠B=90°
•
14、谁要是自己还没有4日星期六下午10时22分30秒22:22:3021.9.4
•
15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月下午10时22分21.9.422:22September 4, 2021
(2)计算出最大的圆形纸片的半径。
B
E
A
O
C
D
课堂小结 A
1.切线长定义:在经过圆外一
点的切线上,这一点和切点之
间的线段的长叫做这点到圆的
切线长.
O
P
2.切线长定理:从圆外一点引
圆的两条切线,它们的切线长
B
相等,圆心和这一点的连线平
分两条切线的夹角.
3.切线是到圆心距离等于圆的 半径的直线
4. 圆的外切四边形的两组对边 的和相等.
三、应用新知,体验成功
1、填空:如图10,PA、PB分别与⊙O相切于点A、B,
(1)若PB=12,PO=13,则AO=
;
(2)若PO=10,AO=6,则PB= 5 ;
(3)若PA=4,AO=3,则PO= 8;PD= ;
CA=13cm,求AF,BD,CE的长。(知识技能2)
知识技能3
3.如图,过⊙O外一点P作⊙O的两条切线PA和PB,点A、点B为 切点,∠P=40°,点D在AB上,点E和点F分别在PB和PA上, 且AD=BE,BD=AF,求∠EDF。
1 5
3
4
2
数学理解4
4.如图,有一张四边形ABCD纸片,AB=AD=6cm,CB=CD=8cm, 且∠B=90°
•
14、谁要是自己还没有4日星期六下午10时22分30秒22:22:3021.9.4
•
15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月下午10时22分21.9.422:22September 4, 2021
北师大版九年级数学下册3.7切线长定理课件
自主学习课本94页的 PA=PB, DC=DA, EC=EB.
(1)找出图中所有相等的线段 运用切线长定理,将相等线段转化到某条边上,从而建立方程,求线段的长. (1)请同学们任意做一个⊙O ,并过圆外一点P做圆的两条切线,切点分别是A、B,测量切线长 PA、PB的长度,同时观察∠1,∠2 的关系。 如图,⊙O是四边形ABCD的内切圆,AB=16,CD=10,求四边形ABCD的周长. 例1 如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.
,
BF= BD =
.
方法小结:关键是熟练
运用切线长定理,将相等
线段转化集中到某条边上,
从而建立方程.
21
A
x
x
F
E O
13-x
9-x
C 9-x D
B
13-x
15
想一想 探索圆外切四边形边的关系
已DA知和:圆四结两O边分论组形别:对A相B圆 边切CD于的 和的L边外 相,MA切 等B,,四 。NB,边CP,。形CD的,
A
O
21
3
北师大版九年级数学下册
第三章 圆
3.7 切线长定理
21
4
新课导入
问题1 上节课我们学习了过圆上一点作已知圆
的切线,如果点P是圆外一点,又怎么作该圆
的切线呢?
问题2 过圆外一点作圆的切线,可以作几条?
A
A
P
O
O.
P
B
B
21
5
问题1:
思考:切线和切线长的区别和联系? 如图:PA,PB切圆于A,B两点,
直角三角形的两直角边分别是3cm,4cm,它的内切圆半径是 cm;外接圆半径是 cm.
(1)找出图中所有相等的线段 运用切线长定理,将相等线段转化到某条边上,从而建立方程,求线段的长. (1)请同学们任意做一个⊙O ,并过圆外一点P做圆的两条切线,切点分别是A、B,测量切线长 PA、PB的长度,同时观察∠1,∠2 的关系。 如图,⊙O是四边形ABCD的内切圆,AB=16,CD=10,求四边形ABCD的周长. 例1 如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.
,
BF= BD =
.
方法小结:关键是熟练
运用切线长定理,将相等
线段转化集中到某条边上,
从而建立方程.
21
A
x
x
F
E O
13-x
9-x
C 9-x D
B
13-x
15
想一想 探索圆外切四边形边的关系
已DA知和:圆四结两O边分论组形别:对A相B圆 边切CD于的 和的L边外 相,MA切 等B,,四 。NB,边CP,。形CD的,
A
O
21
3
北师大版九年级数学下册
第三章 圆
3.7 切线长定理
21
4
新课导入
问题1 上节课我们学习了过圆上一点作已知圆
的切线,如果点P是圆外一点,又怎么作该圆
的切线呢?
问题2 过圆外一点作圆的切线,可以作几条?
A
A
P
O
O.
P
B
B
21
5
问题1:
思考:切线和切线长的区别和联系? 如图:PA,PB切圆于A,B两点,
直角三角形的两直角边分别是3cm,4cm,它的内切圆半径是 cm;外接圆半径是 cm.
北师大版九年级数学下册第三章《 3-7 切线长定理》优课件(共20张PPT)

如图:用两根带有刻度的木条做一个夹角为60°的 工具尺,你能用它量出一个圆的半径吗?
若量出角的顶点到切点的距离为10cm,试求这个圆 半径的近似值。
三角形的外接圆: 三角形的内切圆:
学科网
A
A
O
B
C
B
I C
D
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月4日星期一2022/4/42022/4/42022/4/4 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/42022/4/42022/4/44/4/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/42022/4/4April 4, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
谢谢观赏
You made my day!
我们,还在路上……
学科网
A
O
·
P
B
① PA=PB
连结OA、OB、
② PO平分∠APB ∵PA、PB与⊙O相切,点
A、B是切点
∴OA⊥AP,OB⊥BP
A O
·
∴∠OAP=∠OBP=90°
∵OA=OB,OP=OP
1 ∴Rt△AOP≌Rt△BOP 2 P ∴PA=PB
∠1 =∠2
B
切线长定理
从圆外一点可以引圆的两条切 线,
B
┐ E
C
【例题】
【例1】△ABC的内切圆⊙O与BC,CA,AB分别相切于
点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)ห้องสมุดไป่ตู้
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)ห้องสมุดไป่ตู้
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
)
◆知识导航 ◆典例导学 ◆反馈演练 ( ◎第一阶 ◎第二阶 ◎第三阶
