曲线拟合
曲线拟合 归一化

曲线拟合归一化
目录
1.曲线拟合的定义和作用
2.归一化的定义和作用
3.曲线拟合和归一化在数据处理中的应用
4.曲线拟合和归一化的优缺点
5.结论
正文
曲线拟合是一种数学方法,用于在给定数据集上找到最佳匹配的曲线。
它可以帮助我们在数据中发现模式和趋势,从而更好地理解数据。
拟合的曲线可以是线性的,也可以是非线性的,具体取决于数据的特性。
曲线拟合在许多领域都有应用,包括经济学、物理学、生物学等。
归一化是一种数据处理的技术,它的主要目的是将数据转换到一个标准范围内,使得不同的特征之间的值可以进行直接的比较。
归一化的方法包括最大值和最小值归一化,以及标准差归一化等。
归一化可以提高模型的性能,特别是在数据量纲不同的情况下。
曲线拟合和归一化在数据处理中都有重要的应用。
曲线拟合可以用于拟合出数据集的函数关系,而归一化则可以将数据转换到同一量纲,方便后续的处理。
例如,在机器学习中,我们常常需要对输入数据进行归一化,以保证模型的稳定性和准确性。
曲线拟合和归一化都有其优缺点。
曲线拟合的优点是可以找出数据中的模式和趋势,但在数据量较少或者噪声较大的情况下,拟合的曲线可能会不准确。
归一化的优点是可以将数据转换到同一量纲,方便后续处理,但也可能会损失数据的原始信息。
总的来说,曲线拟合和归一化都是数据处理中常用的方法,它们可以帮助我们更好地理解和处理数据。
计算机 曲线 拟合公式

计算机曲线拟合公式
拟合曲线是指在已知一组数据的前提下,通过一定的数学方法,找出一个代表这组数据的曲线方程。
这个曲线方程可以用于对数据进行预测、分析和优化等操作。
常见的曲线拟合公式包括线性拟合、多项式拟合、指数拟合等。
1. 线性拟合
线性拟合是指拟合一个一次函数y=kx+b,其中k和b分别为
拟合曲线的斜率和截距。
通常使用最小二乘法来求解k和b。
最小二乘法是指通过最小化误差平方值的方法来确定k和b的值,误差平方值=∑(yi-(kxi+b))^2,其中yi为实际的数据值,
xi为自变量的取值。
通过求解误差平方值的导数,可以得到k
和b的值。
2. 多项式拟合
多项式拟合是指将一个多项式函数拟合到一组数据上。
多项式函数的一般形式为y=a0+a1*x+a2*x^2+…+an*x^n。
多项式拟
合的主要目的是通过多项式来描述数据中的非线性趋势。
常见的拟合方法包括最小二乘法、牛顿法、拉格朗日法等。
3. 指数拟合
指数拟合是指将一个指数函数y=a*exp(b*x)拟合到数据上。
这
种拟合常用于数据呈现出指数增长或衰减趋势的情况。
指数拟合的关键是通过对数变换将指数函数转化为线性函数,然后再进行线性拟合。
具体方法是对数据进行对数变换,然后用线性拟合的方法求解出a和b的值,再通过指数函数进行反推,得
到拟合曲线的方程。
以上是常见的曲线拟合公式及方法,拟合的具体选择要根据不同的数据趋势和实际需求进行决定。
曲线拟合方法

曲线拟合方法曲线拟合方法是在数据分析中应用广泛的一种数学模型,它能够有效地拟合一组数据,从而推断出它背后的现象,同时推断出现象的规律。
曲线拟合方法是最常用的无比可以满足实际应用要求的符号方法之一,在实际应用中可以清楚地看到它的优越性。
一、曲线拟合方法的定义曲线拟合方法是一种用来拟合数据的数学方法,即将一组数据拟合到一条曲线上,从而求解出拟合曲线的方程。
一般来说,曲线拟合方法是根据给定的数据集,通过最小二乘法来拟合出曲线的方程,以表述和描述该数据的特征。
曲线拟合方法给我们提供了一种比较直观和有效的数据分析工具,可以有效地发现数据中不同特征之间的关系,从而推断出它们背后的现象及其规律。
二、曲线拟合方法的基本思想曲线拟合方法的基本思想是将一组数据以曲线的形式,以拟合精度最高的方式拟合出曲线的方程。
有多种拟合方法,比如线性拟合、参数拟合、二次拟合、多项式拟合等,可以根据实际的数据特点,选择合适的拟合方法。
拟合方法的最终目的是使拟合曲线越接近原始数据,越接近实际情况,以此来求解出拟合曲线的方程,并且能够有效地反映出数据的规律特征。
三、曲线拟合方法的应用曲线拟合方法在实际工程中被广泛应用,它的应用非常广泛,可以用于各种数据的拟合,其中包括统计学中的数据拟合、物理学中拟合各种非线性函数曲线,以及优化、控制理论中根据给定数据拟合控制参数等。
曲线拟合方法可以有效地发现数据中不同特征之间的关系,从而推断出它们背后的现象,以及它们背后的规律,因此,曲线拟合方法在预测及数据分析中具有重要的作用。
四、曲线拟合方法的优缺点曲线拟合方法的优点在于它的拟合效果好,能够有效地发现数据中不同特征之间的关系,从而推断出它们背后的现象,以及它们背后的规律,因此它可以提供丰富、有价值的数据分析以及预测服务。
但是,曲线拟合方法也有一些缺点,比如它拟合的曲线不一定能够代表实际情况,有可能导致拟合出错误的结果,因此在使用时要注意控制拟合精度。
ai曲线拟合

ai曲线拟合
AI曲线拟合是指利用人工智能算法对给定的数据进行拟合,找到一个最佳的函数或曲线来描述数据的趋势和规律。
这个过程可以用于预测未来的数据点、揭示数据之间的关系、寻找最优解等。
在进行AI曲线拟合时,通常会使用一些常见的机器学习算法,如线性回归、多项式回归、支持向量回归、神经网络等。
具体的选择取决于数据的特点和需求。
在进行曲线拟合之前,需要先对原始数据进行预处理,包括数据清洗、归一化、特征选择等。
然后将数据分为训练集和测试集,用训练集来训练模型,再用测试集来评估模型的拟合效果。
在训练模型时,算法会尝试不同的拟合函数或曲线,通过调整函数的参数来使得模型与实际数据的差距最小化。
这个过程称为参数优化或模型训练。
最后,通过评估指标(如均方根误差、决定系数等)来判断模型的拟合效果,并根据需要对模型进行调整和改进。
需要注意的是,AI曲线拟合并不是万能的,它只能根据已有的数据找到一个最佳的拟合函数或曲线。
在使用时需要合理选择算法和模型,并结合领域知识和实际情况进行判断和解释。
第5章-1 曲线拟合(线性最小二乘法)讲解
求所需系数,得到方程: 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得:
a=0.912605
b=0.174034
所以线性拟合曲线函数为: y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数: y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
曲线拟合的最小二乘法
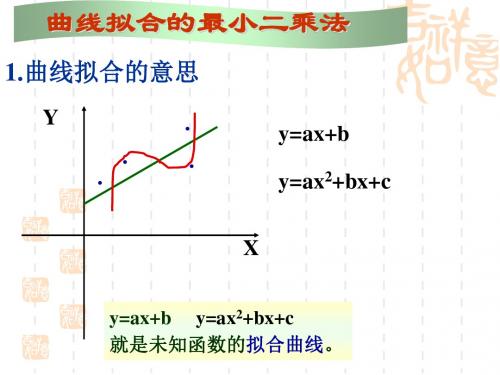
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为: y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
curvefitting拟合三元函数

curvefitting拟合三元函数曲线拟合是一种数学处理方法,旨在通过选择最佳拟合曲线来描述数据集的趋势和关系。
对于三元函数的曲线拟合,我们需要考虑三个变量之间的关系,并找到最适合数据的曲线模型。
一般而言,三元函数可以表示为f(x,y)=z,其中x、y和z分别是自变量和因变量。
我们的目标是找到合适的函数形式来描述x、y和z之间的关系。
根据数据集的分布情况,我们可以选择适当的函数模型进行拟合。
以下是一些常见的三元函数模型:1. 线性函数:f(x, y) = ax + by + c,其中a、b和c是拟合曲线的系数。
这个模型适合于变量之间的简单线性关系。
2. 多项式函数:f(x, y) = ax² + bxy + cy² + dx + ey + f。
这个模型适合于拟合包含二次或更高次项的数据。
3. 指数函数:f(x, y) = ab^(cx) + dy。
这个模型适用于自变量和因变量之间存在指数增长或衰减的情况。
4. 对数函数:f(x, y) = a + bln(x) + cln(y)。
这个模型适用于数据集呈现出对数增长或衰减的情况。
5.样条函数:样条函数是一种灵活的曲线拟合方法,适用于数据集呈现出复杂的曲线形状。
它通过在数据集中插入节点来逼近拟合曲线。
选择合适的函数模型后,我们需要使用数值优化方法来估计模型的参数。
最常用的方法之一是最小二乘法,它通过最小化观测值和拟合值之间的差异来确定最佳拟合曲线。
一旦拟合曲线的参数确定,我们可以使用这个曲线模型来预测和分析其他数据。
最后,我们需要评估拟合结果的质量。
可以使用统计指标如均方根误差(RMSE)或确定系数(R²)来衡量拟合曲线对原始数据的拟合程度。
总结起来,曲线拟合是一种重要的数学处理方法,用于找到最佳拟合曲线来描述三元函数数据集的关系。
它可以帮助我们理解和预测变量之间的关联性,并为进一步的分析和预测提供基础。
选择合适的函数模型、使用数值优化方法进行参数估计以及评估拟合结果的质量是进行曲线拟合的关键步骤。
曲线拟合
数模俱乐部
曲线拟合
现在我们使用上面求得的系数产生 y: y = (0.1032)x - 28.4909 图像为如图:
如何改善这种状况呢?我 们可以尝试拟合更高阶的多项式。让我们使用一个二次多项式看看。
数模俱乐部
曲线拟合
使用下面的步骤来做: >> p = polyfit(sqft,price,2); 这次有三个系数产生。次数设为 2的 polyfit 函数使用下面的形式给我们返 回系数: y = p1x + p2x + p3 我们把它们提取出来放进变量中并绘图: >> a = p(1); >> b = p(2); >> c = p(3); >> x = [1200:10:4000]; >> y = a*x^2+ b*x + c; >> plot(x,y,sqft,price,'o'), xlabel('房子平方英尺数'),ylabel('平均售价'), ... title('欢乐谷的房子平均售价与平方英尺数的关系'), axis([1200 4000 135 450])
数模俱乐部
曲线拟合
图象如图 所示。 虽然 4000 平方英尺的 房子的价格看起来有点 偏离正常,其它的数据 还是基本上一个直线的 周围的,让我们找出这 条最拟合这些数据的直线。 在我们尝试求出 y = mx + b 的过程中, 房子的 SQFT(平方英尺数)充当 x的角色而平均售价充当 y 的角色。使用 polyfit 找出我们需要的系数,我们只需把数据传递给它并告知它我们在求一 次的多项式。
曲线拟合
曲线拟合法

曲线拟合法
曲线拟合法是一种用于根据离散数据拟合出函数模型的方法,可以用来估计未知数据.是统计分析中经常使用的一种数学方法,它可以用来实现从数据中获取信息的目的。
曲线拟合的最常用的方法是最小二乘法,它的主要思想是将最小的均方误差捆绑到拟合的曲线上,使得它可以更好地描述数据曲线。
曲线拟合是一个复杂的过程。
它的目的是将一系列离散点拟合成一个曲线,该曲线可以刻画数据点之间的关系。
它可以帮助研究者更好地理解数据,并对数据进行进一步研究。
首先,研究者需要确定拟合曲线的函数形式,例如多项式,指数或对数函数,接着将参数估计出来,这一步通常使用标准的最小二乘估计方法。
有时候,参数的估计可能会受到多种因素的影响,但对于拟合曲线的准确性来说,参数的估计是非常重要的。
此外,在最小二乘估计方法中,也需要考虑多元变量之间的关系,这要求研究者针对每一种可能的关系预估参数。
另外,有许多类型的拟合方法,不同的拟合方法适用于不同的数据集,比如,动态拟合法、矩阵法和多元拟合法,这些方法可以帮助研究者在拟合表达式中找到更准确的参数值。
总的来说,曲线拟合法是一种有效的数据模型,它可以根据离散数据拟合出函数模型,这有助于研究者更全面地理解数据,并能够预测出未知点的值,有效地估计出参数。
它在统计学中有着广泛的应用,这种方法对于提高数据分析的精度,预测未知变量,并更加准确地描
述数据曲线都有着重要意义。
常用的曲线拟合方法

常用的曲线拟合方法常用的曲线拟合方法1. 多项式拟合•多项式拟合是最常见的曲线拟合方法之一,通过使用多项式函数来逼近实际数据的曲线。
•多项式拟合可以使用最小二乘法来确定最佳的拟合曲线。
•多项式拟合的优点是计算简单,易于理解和实现。
•多项式拟合的缺点是容易产生过拟合的问题,特别是在高次多项式的情况下。
2. 线性回归•线性回归是一种拟合直线的方法,适用于线性关系较强的数据。
•线性回归的目标是找到一条直线,使得所有数据点到该直线的距离之和最小。
•线性回归可以使用最小二乘法或者梯度下降法来求解最佳拟合直线。
•线性回归的优点是计算简单,易于解释。
•线性回归的缺点是对非线性关系的数据拟合效果不佳。
3. 指数拟合•指数拟合适用于呈指数增长或者指数衰减的数据。
•指数拟合的目标是找到一个指数函数,使得拟合曲线与实际数据的差异最小。
•指数拟合可以通过最小二乘法来求解最佳拟合曲线。
•指数拟合的优点是适用范围广,可以处理很多不同类型的数据。
•指数拟合的缺点是对于非指数型的数据拟合效果不佳。
4. 对数拟合•对数拟合适用于呈对数增长或者对数衰减的数据。
•对数拟合的目标是找到一个对数函数,使得拟合曲线与实际数据的差异最小。
•对数拟合可以通过最小二乘法来求解最佳拟合曲线。
•对数拟合的优点是适用范围广,可以处理很多不同类型的数据。
•对数拟合的缺点是对于非对数型的数据拟合效果不佳。
5. 非线性拟合•非线性拟合是一种通过使用非线性函数来逼近实际数据的曲线的方法。
•非线性拟合可以使用最小二乘法或者其他优化算法来求解最佳拟合曲线。
•非线性拟合的优点是可以适用于各种形状的数据曲线。
•非线性拟合的缺点是计算复杂度较高,收敛困难。
以上是常用的曲线拟合方法的简要介绍,不同的方法适用于不同类型的数据。
在实际应用中,需要根据数据的特点选取合适的拟合方法来进行数据处理和分析。
6. 平滑拟合•平滑拟合是一种通过平滑算法来逼近实际数据的曲线的方法。
•平滑拟合的目标是去除数据中的噪声和异常值,使得拟合曲线更加平滑。
拟合曲线的方法(一)

拟合曲线的方法(一)拟合曲线拟合曲线是一种数据分析方法,用于找到最符合给定数据的函数曲线。
在实际应用中,拟合曲线广泛应用于计算机图形学、统计学和机器学习等领域。
不同的方法可以应用于不同类型的数据和问题,下面将介绍几种常见的拟合曲线方法。
线性拟合线性拟合是最简单也是最常见的拟合曲线方法之一。
其基本思想是通过一条直线来拟合数据点。
线性拟合常用于描述两个变量之间的线性关系。
线性拟合的数学模型可以表示为:y=a+bx,其中y是因变量,x是自变量,a是截距,b是斜率。
线性拟合的目标是通过最小化实际数据点和拟合直线之间的误差来确定最佳的a和b。
多项式拟合多项式拟合是一种通过多项式函数来拟合数据点的方法。
多项式函数是由多个幂函数组成的函数,可以适应各种形状的数据。
多项式拟合的数学模型可以表示为:y=a0+a1x+a2x2+⋯+a n x n,其中y是因变量,x是自变量,a0,a1,…,a n是拟合函数的系数。
多项式拟合的目标是通过最小化实际数据点和拟合曲线之间的误差来确定最佳的系数。
曲线拟合曲线拟合是一种通过曲线函数来拟合数据点的方法。
曲线函数可以是任意形状的函数,可以适应各种复杂的数据。
常见的曲线拟合方法包括:贝塞尔曲线拟合贝塞尔曲线拟合是一种用于拟合平滑曲线的方法。
贝塞尔曲线由控制点和节点构成,通过调整控制点的位置来改变曲线的形状。
贝塞尔曲线拟合的目标是通过最小化实际数据点和贝塞尔曲线之间的误差来确定最佳的控制点和节点。
样条曲线拟合样条曲线拟合是一种用于拟合光滑曲线的方法。
样条曲线由多个局部曲线段组成,每个曲线段由一组控制点和节点定义。
样条曲线拟合的目标是通过最小化实际数据点和样条曲线之间的误差来确定最佳的控制点和节点。
非线性拟合非线性拟合是一种用于拟合非线性关系的方法。
非线性关系在现实世界中很常见,例如指数函数、对数函数等。
非线性拟合的数学模型可以表示为:y=f(x,θ),其中y是因变量,x是自变量,θ是模型的参数。
曲线拟合的实用方法与原理

曲线拟合的实用方法与原理曲线拟合是一种常用的数据分析方法,它可以通过寻找最佳拟合曲线来描述一组数据的趋势和关系。
在科学研究、工程技术、金融分析等领域中,曲线拟合被广泛应用于数据模型的建立、预测和优化等方面。
本文将介绍曲线拟合的实用方法和原理,帮助读者更好地理解和运用这一分析工具。
一、曲线拟合的基本概念曲线拟合是指通过一组已知数据点,寻找一条函数曲线来逼近这些数据点的过程。
拟合曲线的选择通常基于拟合误差最小化的原则,即找到一条曲线,使得它与实际数据点之间的误差最小。
二、常见的曲线拟合方法1. 最小二乘法最小二乘法是一种常见的曲线拟合方法,它通过最小化拟合曲线与实际数据点之间的残差平方和来确定最佳拟合曲线。
最小二乘法在实际应用中较为简单和灵活,能够拟合各种类型的曲线,如线性曲线、多项式曲线、指数曲线等。
2. 多项式拟合多项式拟合是一种通过多项式函数来拟合数据点的方法。
它可以通过最小二乘法来确定多项式的系数,从而得到最佳拟合曲线。
多项式拟合可以适用于不同阶数的多项式,阶数越高,拟合曲线越复杂,能够更好地逼近实际数据。
3. 曲线拟合工具除了最小二乘法和多项式拟合外,还有一些专门的曲线拟合工具可供使用。
例如,MATLAB和Python中的Scipy库提供了丰富的曲线拟合函数,可以根据实际需求选择合适的拟合方法和工具。
三、曲线拟合的实际应用曲线拟合在各个领域都有广泛的应用。
以下是几个典型的实际应用案例:1. 经济数据分析曲线拟合可以用于分析经济数据的趋势和关系。
例如,通过对历史GDP数据进行曲线拟合,可以预测未来的经济增长趋势,为政策制定和投资决策提供参考。
2. 工程建模在工程领域,曲线拟合可以用于建立物理模型和优化设计。
例如,通过对实验数据进行曲线拟合,可以得到物质的力学性质曲线,从而优化材料的设计和使用。
3. 股票价格预测曲线拟合可以用于股票价格的预测和交易策略的制定。
通过对历史股票价格数据进行曲线拟合,可以找到潜在的趋势和周期性,从而为投资者提供决策依据。
名词解释 曲线的拟合

名词解释曲线的拟合曲线的拟合是指通过一组已知的离散数据点,找到与这些数据点最匹配的数学函数曲线的过程。
它在许多领域有着广泛的应用,包括数学建模、统计学、机器学习和工程等。
曲线的拟合可以帮助我们理解数据之间的关系、预测未知数据点的值,以及寻找隐含在数据背后的规律和趋势。
在进行曲线的拟合之前,我们首先需要明确所使用的数据点以及期望的拟合函数类型。
常见的拟合函数包括线性函数、多项式函数、指数函数、对数函数等。
其中最简单的情况就是拟合一条直线,被称为线性回归。
而如果拟合的函数是一个高次的多项式,就被称为多项式拟合。
在实际应用中,我们根据数据的特点和需求选择合适的拟合函数类型。
曲线的拟合的关键在于确定拟合参数的取值,使得拟合函数与实际数据点尽可能地吻合。
我们使用拟合误差来衡量拟合的好坏。
拟合误差通常使用最小二乘法来计算,即将实际数据点到拟合函数曲线的距离平方求和最小化。
最小二乘法的优势在于能够将拟合误差平方化,避免正负误差相互抵消的情况产生。
在进行曲线的拟合过程中,我们可以使用一些常见的数学工具和算法。
例如,最小二乘法可以通过解线性方程组或最优化算法来求解最优拟合参数。
而在多项式拟合中,常常使用最小二乘多项式拟合,将实际数据点与多项式函数进行匹配。
此外,还有一些高级的拟合技术,如样条插值、非线性回归和神经网络等,可以在特定情况下提供更加精确和灵活的拟合结果。
曲线的拟合不仅仅是数学方法的应用,更是一门艺术。
在实际拟合过程中,我们需要不断地调整参数和拟合函数的选择,以寻找到最佳的拟合解。
拟合结果的质量取决于多个因素,包括数据的质量、调整参数的准确性,以及拟合函数的合理性等。
因此,拟合过程往往是一个经验丰富和反复试验的过程。
曲线的拟合还涉及到一些限制和问题。
例如,过度拟合是指拟合函数与实际数据点过于吻合,导致对未知数据的预测效果不佳。
解决过度拟合的方法之一是正则化,通过在拟合过程中引入惩罚项来控制模型参数的大小。
Ⅰ.时间序列数据11种曲线的拟合与外延预测法

Ⅰ.时间序列数据11 种曲线的拟合与外延预测法1. 11 种常用曲线方程时间序列数据常常要研究某变量随时间变化的趋势。
曲线拟合就是根据实际数据所呈现的趋势,拟合出误差最小的曲线方程。
SPSS的Trends 过程,其中的CURVEFIT 命令可一次性拟合出11 种常用的曲线方程。
本节介绍其拟合方法。
这11 种常用的曲线方程是:下述方程以“*”表示“乘”,“**”表示“乘方”。
(1) 直线回归方程(LINEAR,LIN):Y=b0+(b1*t)。
式中b0 为截距,b1 为直线的斜率,t 为自变量,Y 为因变量的估计值。
(2) 对数曲线方程(LOGARITHMIC,LOG):Y=b0+(b1*ln(t))。
令ln(t)=t',可得直线方程形式:Y=b0+(b1*t')。
(3) 反函数曲线方程(INVERSE,INV):Y=b0+(b1/t)。
令1/t=t',可得直线方程形式:Y=b0+(b1*t')。
(4) 二次曲线(抛物线)方程(QUADRA TIC,QUA):Y=b0+(b1*t)+(b2*t**2)。
(5) 三次曲线(三次抛物线)方程(CUBIC,CUB):Y=b0+(b1*t)+(b2*t**2)+(b3*t**3)。
(6) 复合曲线方程(COMPOUND,COM):Y=b0*(b1**t)或ln(Y)=ln(b0)+(ln(b1)*t)。
令ln(Y)=Y',ln(b0)=b0',ln(b1)=b1',可得直线方程形式:Y'=b0'+(b1*t)。
(7) 幂函数曲线方程(POWER,POW):Y=b0*(t**b1)或ln(Y)=ln(b0)+(b1*ln(t))。
令ln(Y)=Y',ln(b0)=b0',ln(t)=t',可得直线方程形式:Y'=b0'+(b1*t')。
(8) S 形曲线方程(S):Y=e**(b0+(b1/t))或ln(Y)=b0+(b1/t)。
第五章 曲线拟合

泰勒展开
arctgx x x3 x5 .....取. arctgx x 35
R(x) | arctg11| 0.2146
以x=0,x=1 作线性插值
arctgx x 1 arctg0 x 0 arctg1 0.7854x
0 1
1 0
R(x) (1 2 ) x(x 1) 0.0711
n
ck j Pk (x j ) y j j 1
m
cik ai ck (k 0,1...m)
i0
写成方程组形式
c00a0 c01a1 c0mam c0 c10a0 c11a1 c1mam c1
cm0a0 cm1a1 cmmam cm
二、正交多项式的曲线拟合
1.) 概念:
)2
j 1
j 1 i0
对ak求偏导数(k=0,1…m)
ak
nm
2
(
ai
x
i j
j1 i0
y
j
)
x
k j
0
m
m
n
化简得
ai
xik j
y
j
x
k j
i0 j 1
j 1
n
n
记
x
k j
Sk
y
j
x
k j
Tk
j 1
j 1 m
aiSki Tk (k 0,1m)
i0
写成矩阵形式
S0 S1 S2 Sm S1 S2 S3 Sm1 S2 S3 S4 Sm2 Sm Sm1 Sm2 S mm
0 (k 0,1,m)
ak
n
m
j[ ai Pi (x j ) y j ]Pk (x j ) 0
拟合曲线算法

拟合曲线算法
拟合曲线算法是一种在平面上用连续曲线近似描述离散数据点之间函数关系的方法。
它可以用于分析和预测数据,从而在科学、工程和数学等领域解决一系列问题。
拟合曲线算法主要包括以下几种:
1.线性拟合:通过最小化误差平方和,找到一条直线或多项式,使得这条直线或多项式与数据点之间的误差最小。
线性拟合常用的工具有最小二乘法、多项式拟合等。
2.非线性拟合:对于非线性数据关系,可以采用非线性函数拟合方法。
常见的非线性拟合算法有:多项式拟合、指数拟合、对数拟合、贝塞尔基函数拟合等。
3.曲线拟合:通过寻找一个连续的函数来近似描述数据点之间的关系。
曲线拟合可以分为一线性曲线拟合和非线性曲线拟合。
线性曲线拟合通常采用最小二乘法,非线性曲线拟合可以采用de Boor算法、Navier-Stokes算法等。
4.插值拟合:插值拟合是通过在数据点之间插入新的点,然后用一个连续的函数来描述这些点之间的关系。
常见的插值方法有拉格朗日插值、牛顿插值、三次样条插值等。
5.优化算法:在拟合曲线过程中,可以使用优化算法来寻找最优的拟合参数。
常见的优化算法有梯度下降、牛顿法、拟牛顿法、信赖域反射算法等。
总的来说,拟合曲线算法是一种通过寻找一个数学函数来描述数据点之间关系的方法,可以根据实际问题和数据特点选择合适的拟合算法。
在实际应用中,曲线拟合算法可以帮助我们更好地理解数据,预测趋势,并为决策提供依据。
曲线拟合方法浅析

曲线拟合方法概述工业设计 张静 1014201056引言:在现代图形造型技术中,曲线拟合是一个重要的部分,是曲面拟合的基础。
现着重对最小二乘法、移动最小二乘法、NURBS 三次曲线拟合法和基于RBF 曲线拟合法进行比较,论述这几种方法的原理及其算法,基于实例分析了上述几种拟合方法的特性,以分析拟合方法的适用场合,从而为图形造型中曲线拟合的方法选用作出更好的选择。
1 曲线拟合的概念在许多对实验数据处理的问题中,经常需要寻找自变量和对应因变量之间的函数关系,有的变量关系可以根据问题的物理背景,通过理论推导的方法加以求解,得到相应关系式。
但绝大多数的函数关系却很复杂,不容易通过理论推导得到相关的表达式,在这种情况下,就需要采用曲线拟合的方法来求解变量之间的函数关系式。
曲线拟合(Curve Fitting),是用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之问的函数关系的一种数据处理方法。
在科学实验或社会活动中,通过实验或观测得到量x 与y 的一组数据对(x i ,y i ),i =1,2,3…,m ,其中各x i 是彼此不同的。
人们希望用一类与数据的规律相吻合的解析表达式y =f(x)来反映量x 与y 之间的依赖关系。
即在一定意义下“最佳”地逼近或拟合已知数据。
f(x)称作拟合函数,似的图像称作拟合曲线。
2 曲线拟合的方法2.1最小二乘法最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配,是进行曲线拟合的一种早期使用的方法 一般最小二乘法的拟合函数是一元二次,可一元多次,也可多元多次。
该方法是通过求出数据点到拟合函数的距离和最小的拟合函数进行拟合的方法令f(x)=ax 2+bx+c ,计算数据点到该函数所表示的曲线的距离和最小 即:δ=∑-=n i y x f i i 02))((对上式求导,使其等于0,则可以求出f(x)的系数a,b,c ,从而求解出拟合函数。
2.2 移动最小二乘法移动最小二乘法在最小二乘法的基础上进行了较大的改进,通过引入紧支概念(即影响区域,数据点一定范围内的节点对该点的拟合函数值有影响),选取适合的权函数,算出拟合函数来替代最小二乘法中的拟合函数 从而有更高的拟合精度及更好的拟合光滑度。
verilog 曲线拟合

verilog 曲线拟合
Verilog是一种硬件描述语言,用于描述数字电路系统的结构和行为。
它主要用于电子系统的设计和验证,特别是在数字集成电路和FPGA(现场可编程门阵列)设计等领域。
在Verilog中,曲线拟合是一种用于确定最佳拟合曲线
的算法或技术。
这通常涉及使用数学模型来描述一组数据点,并找到最佳拟合这些点的曲线。
曲线拟合在Verilog中可能
用于各种目的,例如模拟电路行为、优化设计参数或进行信号处理等。
在Verilog中进行曲线拟合通常涉及以下步骤:
1.数据采集:首先,需要获取一组数据点作为输入,这些数据点可以是实际测量值、模拟结果或其他相关数据。
2.选择模型:选择适合于数据点的数学模型,例如多项式、指数、对数或其他函数形式。
选择合适的模型对于获
得准确的拟合结果至关重要。
3.拟合算法:使用适当的拟合算法来找到最佳拟合曲线的参数。
这可能涉及最小二乘法、非线性最小二乘法或其
他优化技术。
4.实现和验证:在Verilog中实现拟合算法,并对结果进行验证。
这包括比较实际数据和拟合曲线,以确保它们
之间的误差在可接受的范围内。
需要注意的是,Verilog本身不直接支持曲线拟合功能。
因此,通常需要借助其他工具或软件库来实现曲线拟合功能,例如使用MATLAB、Python或其他编程语言的曲线拟合库。
总之,Verilog是一种用于描述数字电路系统的硬件描述语言,而曲线拟合是一种数学技术,用于找到最佳拟合一组数据点的曲线。
在Verilog中实现曲线拟合通常需要借助其
他工具或软件库来实现。
曲线拟合的一般步骤

曲线拟合的一般步骤曲线拟合是数学中的一个重要概念,可以用于回归分析、模拟计算、数据预测等领域。
本文将简单介绍曲线拟合的一般步骤,帮助读者了解如何应用曲线拟合进行数据分析。
一、确定曲线类型在进行曲线拟合之前,首先需要确定所拟合的曲线类型。
曲线类型的选择取决于数据的特性和预测的目标。
例如,如果数据呈现出周期性变化的趋势,可以选择对数周期函数或三角函数进行拟合;如果数据呈现出指数增长的趋势,可以选择指数函数进行拟合。
选择合适的曲线类型有助于提高拟合的准确度和预测的精度。
二、收集数据收集数据是进行曲线拟合的前提。
数据的收集需要考虑采样的频率、样本量的大小等因素。
通常情况下,数据的样本量越大、采样的频率越高,得到的拟合曲线越精确。
在进行数据收集时,还需要考虑数据的可信度和数据的质量。
三、对数据进行处理在收集完数据之后,需要对数据进行处理。
数据处理的主要目的是为了减少数据存在的噪声,并消除异常数据对拟合的影响。
数据处理方法可以采用平滑处理、滤波处理、插值法等方法。
同时,还需要进行数据标准化,将不同尺度的数据进行标准化处理,以便进行合理的拟合。
四、选择拟合算法选择合适的拟合算法对于拟合的准确度和模型的复杂度有重要影响。
拟合算法通常分为参数拟合和非参数拟合两种。
其中,参数拟合根据已有数据,估计模型中的参数,并针对参数进行优化;非参数拟合则不需要对模型参数进行预先确定。
常用的参数拟合算法包括最小二乘法、梯度下降法、牛顿迭代法等;非参数拟合算法包括局部加权线性回归、核函数回归等。
五、拟合模型评估进行拟合之后,需要对拟合模型进行评估。
评估的目的是为了验证拟合模型的有效性、准确性和稳定性。
评估方法可以采用拟合优度、均方误差、残差分布等指标。
根据评估结果,进行参数调整和算法选择,逐步提高拟合的精度和模型的可行性。
总结曲线拟合是一项基础而重要的数据处理技术。
选择合适的曲线类型、收集准确的数据、对数据进行处理、选择合适的拟合算法、评估拟合模型,这是曲线拟合的一般步骤。
曲线拟合的最小二乘法原理及实现

曲线拟合的最小二乘法原理及实现任务名称简介在数据处理和统计分析中,曲线拟合是一种常见的技术,旨在通过数学函数找到最佳拟合曲线,以尽可能准确地描述给定数据集的变化趋势。
在曲线拟合的过程中,最小二乘法是一种常用的数学方法,用于选择最佳拟合曲线。
本文将详细介绍最小二乘法的原理和实现方法。
最小二乘法原理最小二乘法是一种通过最小化误差平方和来拟合数据的方法。
其基本原理是将数据集中的每个数据点与拟合曲线上对应点的差值进行平方,然后将所有差值的平方相加,得到误差平方和。
最小二乘法的目标是通过调整拟合曲线的参数,使得误差平方和达到最小值。
假设我们有一个包含n个数据点的数据集,每个数据点的横坐标为x,纵坐标为y。
我们希望找到一个拟合曲线,可以通过曲线上的点与数据点的差值来评估拟合效果。
拟合曲线的一般形式可以表示为:y = f(x, β)其中,β为拟合曲线的参数,f为拟合曲线的函数。
最小二乘法的基本思想是选择适当的参数β,使得误差平方和最小化。
误差平方和可以表示为:S(β) = Σ(y - f(x, β))^2其中,Σ表示求和操作,拟合曲线上的点的横坐标为x,纵坐标为f(x, β)。
为了找到误差平方和的最小值,我们需要对参数β进行求解。
最常用的方法是对参数β求导数,令导数为0,从而得到参数的估计值。
求解得到的参数估计值就是使得误差平方和最小化的参数。
最小二乘法实现步骤最小二乘法的实现可以分为以下几个步骤:1.确定拟合曲线的函数形式。
根据数据的特点和拟合的需求,选择合适的拟合曲线函数,例如线性函数、多项式函数等。
2.建立误差函数。
根据选择的拟合曲线函数,建立误差函数,即每个数据点与拟合曲线上对应点的差值的平方。
3.求解参数估计值。
对误差函数求导数,并令导数为0,求解得到参数的估计值。
4.进行拟合曲线的评估。
通过计算误差平方和等指标来评估拟合曲线的质量,可以使用残差平方和、R方值等指标。
5.优化拟合结果(可选)。
根据评估的结果,如有必要可以调整拟合曲线的参数或选择其他拟合曲线函数,以得到更好的拟合效果。
曲线拟合 拟合优度

曲线拟合拟合优度
曲线拟合是通过一个数学函数来近似描述一组离散数据点的过程。
拟合优度(Goodness of Fit)是用来评估拟合函数与实际数据的适应程度的指标。
一般来说,拟合优度越高,拟合函数与实际数据的吻合度越好。
常用的拟合优度指标包括:
1. 相关系数(Coefficient of Determination):常用符号为 R²,表示拟合函数的变异程度与实际数据的变异程度之比。
取值范围为 0 到 1,值越接近 1 表示拟合优度越高。
2. 均方误差(Mean Square Error):用于衡量拟合函数预测值与实际值之间的差距。
均方误差越小,拟合优度越高。
3. 标准残差(Standardized Residuals):计算每个数据点的残差(预测值与实际值之差)与拟合函数的标准差之比。
标准残差越接近 0,拟合优度越高。
需要注意的是,拟合优度不是唯一的评估指标,不同的拟合方法和数据集可能会选择不同的指标。
因此,在比较不同拟合模型或方法的优劣时,应综合考虑多个指标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
32
30
28
26
24
22
20
18 16
18
20
22
24
26
28
30
数据拟合函数表
cfit
fit
产生拟合的目标
用库模型、自定义模型、平滑样条或 内插方法来拟合数据 产生或修改拟合选项 产生目标的拟合形式 显示一些信息,包括库模型、三次样 条和内插方法等。 显示曲线拟合工具的信息 返回拟合曲线的属性 对于拟合曲线显示属性值
•输出结果为: •p = • Columns 1 through 5 • 0.0193 -0.0110 -0.0430 0.0073 0.2449 • Column 6 • 0.2961 •说明拟合的多项式为:
0.0193x 5 0.0110x 4 0.043x 3 0.0073x 2 0.2449x 0.2961
• 算例: >> years=1950:10:1990; >> service=10:10:30; >> wage = [150.697 199.592 187.625 179.323 195.072 250.287 203.212 179.092 322.767 226.505 153.706 426.730 249.633 120.281 598.243]; >> w = interp2(service,years,wage,15,1975) w= 190.6288
Method:用于指定插值的方法,linear:线性插值(默认方 法)。Cubic三次多项插值。Spline:三次样条插值。Nearst: 最近邻插值。
• 例
>> year=1900:10:2010; >> product=[75.995,91.972,105.711,123.203,131.669,... 150.697,179.323,203.212,226.505,249.633,256.344,267.893]; >> p1995 = interp1(year,product,1995) p1995 = 252.9885 >> x = 1900:10:2010; >> y = interp1(year,product,x,'cubic'); >> plot(year,product,'o',x,y)
• 最简单的插值方法是先根据基准数据,调用 MATLAB的绘图命令获得数据的图形表现,然 后估计所需点处的值。
6.8.1分段插值
• 算法分析:所谓分段插值就是通过插值点用折 线或低次曲线连接起来逼近原曲线。 • MATLAB实现 可调用内部函数。
– 命令1 interp1 格式1 yi = interp1(x,y,xi,’method’) 功能 :输入参数为原始数据点(x,y),xi为指定插 值点的横坐标,yi是在xi指定位置计算出的插值结果。
对于拟合结果求积分
对于新的观察量计算预测区间的边界
返回数据的描述统计量
估计一个拟合结果结果或拟合类型
画出数据点、拟合线、预测区间、异 常值点和残差
6.8 插值和样条(非参数拟合)
有时我们对拟合参数的提取或解释不感兴趣,只想得到一个平滑的 通过各数据点的曲线,这种拟合曲线的形式称之为非参数拟合。 • 非参数拟合的方法包括 • (1)插值法Interpolants • (2)平滑样条内插法Smoothing spline • 在多项式曲线拟合并不要求拟合曲线通过这些测量数据点。 而插值是在原始数据点之间按照一定的关系插入新的数据点,以 便更准确的分析数据的变化规律。他是在假定所给的基准数据完 全正确的情况下,研究如何“平滑”的估算出“基准数据”之间 其它函数值。
– 命令2 interp2
• 功能 二维数据内插值(表格查找) :是对两个变量的函数 z=f(x,y)进行插值。 • 格式 ZI = interp2(x,y,z,xi,yi,’method’) • 功能:输入参数为原始数据点(x,y,z);x,y为两个独 立向量,z为矩阵,是由x,y确定的点上的值。 • Z(i,:)=f(x,y(i))和Z(:,i)=f(x(i),y) • method计算二维插值: ’linear’:双线性插值算法(缺省算法); ’nearest’:最临近插值; ’spline’:三次样条插值; ’cubic’:双三次插值。
• • • • • • • • • •
>> y=polyval(a,T) %计算多项式在某一点处的值 y= 1.0e+003 * 0.7718 0.8132 0.8754 0.9502 1.0274 >> plot(T,R,'k+',T,y,'r*') >> hold on >> plot(T,y,'b') >> polyval(a,60) ans = 906.0212
x=[1 3 4 5 6 7 8 9 10]; y=[10 5 4 2 1 1 2 3 4]; [p,s]=polyfit(x,y,4); y1=polyval(p,x); plot(x,y,'go',x,y1,'b--')
10 9 8 7 6 5 4 3 2 1
1
2
3
4
5
6
7
8
9
10
>> poly2str(p,'t') ans = -0.0049945 t^4 + 0.11461 t^3 0.61143 t^2 - 1.1005 t + 11.5499
s=
R: [6x6 double] df: 0 normr: 2.3684e-016 mu = 0.1669 0.1499
自由度为 0 标准偏差为 2.3684e-016
例:根据表中数据进行4阶多项式拟合
X 1 3 4 4 5 2 6 1 7 1 8 2 9 3 10 4 F(x) 10 5
>> >> >> >> >>
1050
1000
950
900
850
800
750 20
30
40
50
60
70
80
90
100
• 例:已知年龄和运动能力的一组数据,试确定 二者的关系(根据图形指定次数)
• 年龄 17 19 21 23 25 27 29 • 第一人20.48 25.13 26.15 30.0 26.1 20.3 19.35 • 第二人24.35 28.11 26.3 31.4 26.92 25.7 21.3
fitoptions fittype cflibhelp
disp
get set
数据拟合函数表
excludedata
smooth confint differentiate
指定不参与拟合的数据
平滑响应数据
计算拟合系数估计值的置信区间边界
对于拟合结果求微分
integrate
predint datastates feval plot
•[p,s,mu]=polyfit(x,y,n) •返回多项式的系数,mu是一个二维向量 [u1,u2],u1=mean(x),u2=std(x),对数据进行预处理 x=(x-u1)/u2 例: x=1:20; y=sqrt(x)+sin(x); p=polyfit(x,y,5) [p,S]=polyfit(x,y,5) Plot(x,y,’o’,x,polyval(p,x),’-’)
• 例:已知的数据点来自函数
根据生成的数据进行插值处理,得出较平滑的曲线 直接生成数据。 >> x=0:.12:1; >> y=(x.^2-3*x+5).*exp(-5*x).*sin(x); >> plot(x,y,x,y,'o')
>> temp=[300,400,500,600]'; >> beta=1000*[3.33,2.50,2.00,1.67]'; >> alpha=10000*[0.2128,0.3605,0.5324,0.7190]'; >> ti=[321,400,571]'; >> propty=interp1(temp,[beta,alpha],ti); %propty=interp1(temp,*beta,alpha+,ti ,’linear’); >> [ti,propty] 例 对于temp,beta 、 ans = alpha分别有两组数据与 1.0e+003 * 之对应,用分段线性插值 0.3210 3.1557 2.4382 法计算当t=321, 440, 571 0.4000 2.5000 3.6050 时beta 、alpha的值。 0.5710 1.7657 6.6489
• • • •
[y,delta]=polyval(p,x,s) 产生置信区间y±delta。如果误差结果服从 标准正态分布,则实测数据落在y±delta区 间内的概率至少为50%。
• • • •
例 >> x=[0 0.0385 0.0963 0.1925 0.2888 0.385]; >> y=[0.042 0.104 0.186 0.338 0.479 0.612]; >> [p,s,mu]=polyfit(x,y,5)
y 0.2015x3 1.4385x2 2.7477x 5.4370
(2)Polyval函数
• • • • • 利用该函数进行多项式曲线拟合评价 y=polyval(p,x) 返回n阶多项式在x处的值,x可以是一个矩 阵或者是一个向量,向量p是n+1个以降序 排列的多项式的系数。
