解二元一次方程组练习题(经典)
二元一次方程组练习题多篇

二元一次方程组练习题多篇二元一次方程组练习题11)66x+17y=396725x+y=1200答案:x=48y=47(2)18x+23y=230374x-y=1998答案:x=27y=79(3)44x+90y=779644x+y=3476答案:x=79y=48(4)76x-66y=408230x-y=2940答案:x=98y=51(5)67x+54y=854671x-y=5680答案:x=80y=59(6)42x-95y=-141021x-y=1575答案:x=75y=48(7)47x-40y=85334x-y=2006答案:x=59y=48 (8)19x-32y=-1786 75x+y=4950答案:x=66y=95 (9)97x+24y=7202 58x-y=2900答案:x=50y=98 (10)42x+85y=6362 63x-y=1638答案:x=26y=62 (11)85x-92y=-2518 27x-y=486答案:x=18y=44 (12)79x+40y=2419 56x-y=1176答案:x=21y=19 (13)80x-87y=2156 22x-y=880答案:x=40y=12 (14)32x+62y=513457x+y=2850答案:x=50y=57(15)83x-49y=8259x+y=2183答案:x=37y=61(16)91x+70y=584595x-y=4275答案:x=45y=25(17)29x+44y=528188x-y=3608答案:x=41y=93(18)25x-95y=-435540x-y=2000答案:x=50y=59(19)54x+68y=328478x+y=1404答案:x=18y=34(20)70x+13y=352052x+y=2132答案:x=41y=50二元一次方程组练习题2实际问题与二元一次方程组题型归纳知识点一:列方程组解应用题的基本思想找出题目中的等式关系。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案)【1】一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).16.解下列方程组:(1)(2)17.方程组的解是否满足2x-y=8?满足2x-y=8的一对x,y的值是否是方程组的解?二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y 的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=,∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.2022年3月23日;第11页共10页。
二元一次方程组计算题20道带答案

二元一次方程组计算题20道带答案1.求解下列二元一次方程组:–3x - 2y = 7–2x + 4y = 10答案: x = 3, y = -12.解方程组:–2x + 5y = 11–3x - 7y = 8答案: x = 3, y = 13.求解二元方程组:–x + 2y = 9–3x - y = 3答案: x = 3, y = 34.解下列方程组:–4x + 2y = 10–2x - y = 9答案: x = 2, y = -55.解方程组:–5x - 3y = 4–x + 4y = 7答案: x = 2, y = 16.求解以下方程组:–8x + 3y = 21–2x - 5y = 7答案: x = 3, y = -37.解二元一次方程组:–3x + 2y = 13–4x - y = 6答案: x = 2, y = 58.解下列方程组:–7x + 3y = 17–5x - 2y = 11答案: x = 2, y = 39.求解二元方程组:–2x + 3y = 10–3x - y = 1答案: x = 2, y = 210.解方程组:–6x - 4y = 8–3x + 7y = 10答案: x = 2, y = 111.求解下列二元一次方程组:–5x + 2y = 11–x - 3y = 4答案: x = 2, y = 112.解方程组:–4x - 2y = 8–2x + 5y = 9答案: x = 2, y = 113.求解二元方程组:–x + 4y = 7–3x - y = 4答案: x = 2, y = 114.解下列方程组:–2x + 3y = 13–4x - y = 3答案: x = 2, y = 315.解方程组:–5x + 2y = 14–2x - 3y = 4答案: x = 2, y = 316.求解以下方程组:–3x - y = 4–5x + 2y = 11答案: x = 1, y = 117.解二元一次方程组:–4x + y = 9–x - 5y = -5答案: x = 2, y = 118.解下列方程组:–3x + 5y = 19–7x - 2y = 11答案: x = 2, y = 319.求解二元方程组:–2x - y = 1–3x + 4y = 11答案: x = 2, y = 320.解方程组:–4x - 3y = 5–x + 6y = 10答案: x = 2, y = 2以上为二元一次方程组计算题,每道题都已附有详细答案。
初中数学二元一次方程组经典练习题(含答案)

初中数学二元一次方程组经典练习题(含答案)解下列二元一次方程组:1. {x +y = 2 3x +7y =10;2.{x +3y = 810x −y =18;3.{3x +2y =1364x −3y =1;4.{ x+52+y−43=2x+20.3−y+70.4= −10 ;5.{ 4x −3y =−1 x 5=y 7 ;6. {3(x +2)=2(y +3)4(x −2)=3(y −3);7.{ x 5+y 7=10 x 3−y 4=3;8.{x 2+y 3=42x +7y =50 ;9.{12(x +3)+13(y −4)=52(x −3)+5(y +4)=70 ;10.{0.2x +0.5y =9x+22+y+105=15 ;11.{4(x −1) +3(y +1) =320%(x +1)+80%(y −1)=−3;12.{x+2y 2 +x−2y 3 = 113(x +2y )−4(x −2y )=30 ;参考答案1. {x +y = 23x +7y =10 ;解: {x +y = 2−−−−−−①3x +7y =10−−−−②①×3,得3x+3y=6-------③②-③,得4y=4,即y=1将y=1代入①,解得x=1故原方程组的解是: {x =1y =12.{x +3y = 810x −y =18; 解:{x +3y = 8−−−−−−−①10x −y =18−−−−−−②②×3,得 30x-3y=54----③①+③,得31x=62,即x=2将x=2代入①,得2+3y=8,y=2故原方程组的解是: {x =2y =23.{3x +2y =1364x −3y =1; 解:{3x +2y =136−−−−−−①4x −3y =1−−−−−−② ①×3,得9x+6y= 132------③ ②×2,得8x-6y=2-----④③+④,得17x= 172 ,x= 12 将x= 12代入②,2-3y=1,y= 13 故原方程组的解是: {x = 12y = 134.{ x+52+y−43=2 x+20.3−y+70.4= −10; 解:{ x+52+y−43=2 −−−−−−−① x+20.3−y+70.4= −10−−−−−−②①等号两边同时乘以6,得3(x+5)+2(y-4)=123x+15+2y-8=12整理,得3x+2y=5----------③②等号两边同时乘以0.3×0.4,得0.4(x+2)-0.3(y+7)=-1.2两边同时乘以10,得4(x+2)-3(y+7)=-124x+8-3y-21=-12整理,得4x-3y=1--------④③×3,得9x+6y=15------⑤④×2,得8x-6y=2-------⑥⑤+⑥,得17x=17,即x=1将x=1代入③,得3+2y=5,y=1故原方程组的解是: {x =1y =15.{ 4x −3y =−1 x 5=y 7 ; 解:{ 4x −3y =−1 −−−−−−−−−−−① x 5=y 7−−−−−−−−−−−−−−−② ②变化为x= 57 y--------------③ 将③代入①,得4×57y -3y=-1 20−217 y =-1,整理得y=7将y=7代入③,得x= 57 ×7,x=5 故原方程组的解是: {x =5y =76. {3(x +2)=2(y +3)4(x −2)=3(y −3); 解:{3(x +2)=2(y +3)4(x −2)=3(y −3)方程组去括号,得{3x +6=2y +64x −8=3y −9整理得{3x −2y =0−−−−①4x −3y +1=0−−②①×3,得9x-6y=0--------③②×2, 得8x-6y+2=0------④③-④,得x-2=0,即x=2将x=2代入①,得6-2y=0,y=3故原方程组的解是: {x =2y =37.{ x 5+y 7=10 x 3−y 4=3; 解:{ x 5+y 7=10 x 3−y 4=3 方程组去分母,得{ 7x +5y =350−−−−−−①4x −3y =36−−−−−−−②①×3,得21x+15y=1050---③②×5,得20x-15y=180----④③+④,得41x=1230,即x=30将x=30代入①,得210+5y=350,y=28故原方程组的解是: {x =30y =288.{x 2+y 3=4 2x +7y =50; 解:{x 2+y 3=4 2x +7y =50方程组去分母,得{3x +2y =24−−−−−−−① 2x +7y =50−−−−−−−②①×2,得6x+4y=48-----③②×3,得6x+21y=150---④④-③,得17y=102,即y=6将y=6代入① ,得3x+12=24,x=4故原方程组的解是: {x =4y =69.{12(x +3)+13(y −4)=52(x −3)+5(y +4)=70 ; 解:{12(x +3)+13(y −4)=5−−−−① 2(x −3)+5(y +4)=70−−−②①去分母,得3(x+3)+2(y-4)=30去括号,得3x+9+2y-8=30整理,得3x+2y-29=0-----------③②去括号,得2x-6+5y+20=70整理,得2x+5y-56=0-----------④③×2,得6x+4y-58=0------------⑤④×3,得6x+15y-168=0----------⑥⑥-⑤,得11y-110=0,即y=10将y=10代入③,得3x+20-29=0,x=3故原方程组的解是:{x=3 y=1010.{0.2x+0.5y=9x+2 2+y+105=15 ;解:{0.2x+0.5y=9−−−−−①x+22+y+105=15−−−−−−②①等号两边同时乘以10,得2x+5y=90------------------③②去分母,得5(x+2)+2(y+10)=150去括号,整理得5x+2y=120---④③×5,得10x+25y=450------⑤④×2,得10x+4y=240-------⑥⑤-⑥,得21y=210,即y=10将y=10代入③,得2x+50=90,x=20故原方程组的解是:{x=20 y=1011.{4(x −1) +3(y +1) =320%(x +1)+80%(y −1)=−3; 解:{4(x −1) +3(y +1) =3−−−−−−−−−①20%(x +1)+80%(y −1)=−3−−−−−−② ①去括号,得4x-4+3y+3=3,整理得4x+3y=4-----③ ②去百分号,得0.2(x+1)+0.8(y-1)=-3等号两边同时乘以10,得2(x+1)+8(y-1)=-30 去括号,得2x+2+8y-8=-30,整理得x+4y=-12----④ ④×4,得4x+16y=-48------------------------⑤ ⑤-③,得13y=-52,即y=-4将y=-4代入④,得x-16=-12,x=4故原方程组的解是: {x =4y =−412.{x+2y 2 +x−2y 3 = 11 3(x +2y )−4(x −2y )=30; 解:{x+2y 2 +x−2y 3 = 11 −−−−−−−−−−−−−−① 3(x +2y )−4(x −2y )=30−−−−−−② ①×6,得3(x+2y )+2(x-2y )=66----------------③③-②,得6(x-2y )=36,即x-2y= 6 -------④①×12,得6(x+2y )+4(x-2y )=132---------------⑤⑤+②,得9(x+2y)=162,即x+2y=18---⑥④+⑥,得2x=24,即x=12④-⑥,得-4y=-12,即y=3故原方程组的解是:{x=12 y=3。
二元一次方程组经典例题

二元一次方程组经典例题一、例题例1:解方程组2x + y = 5 x - y = 1解析:1. 观察方程组的特点- 这个方程组中y的系数分别为1和-1,可以采用加减消元法。
2. 消元求解- 将方程2x + y = 5与方程x - y = 1相加,得到(2x + y)+(x - y)=5 + 1。
- 化简得2x+y+x - y=6,即3x=6,解得x = 2。
3. 回代求y- 把x = 2代入x - y = 1中,得到2 - y = 1,解得y=1。
所以方程组的解为x = 2 y = 1例2:解方程组3x+2y = 8 2x - 3y=-5解析:1. 选择消元方法- 为了消去其中一个未知数,我们可以给第一个方程乘以3,第二个方程乘以2,然后再相加来消去y。
2. 消元计算- 方程3x + 2y = 8两边乘以3得9x+6y = 24。
- 方程2x - 3y=-5两边乘以2得4x-6y=-10。
- 将这两个新方程相加:(9x + 6y)+(4x-6y)=24+( - 10)。
- 化简得9x+6y + 4x-6y = 14,即13x=14,解得x=(14)/(13)。
3. 回代求y- 把x=(14)/(13)代入3x + 2y = 8中,得到3×(14)/(13)+2y = 8。
- 即(42)/(13)+2y = 8,移项得2y = 8-(42)/(13)。
- 2y=(104 - 42)/(13)=(62)/(13),解得y=(31)/(13)。
所以方程组的解为x=(14)/(13) y=(31)/(13)例3:某班有40名同学去看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元,问购买甲、乙两种票各多少张?设购买甲种票x张,购买乙种票y张。
根据题意可列方程组x + y = 40 10x+8y = 370解析:1. 消元方法选择- 由第一个方程x + y = 40可得y = 40 - x,我们可以采用代入消元法。
二元一次方程组经典练习题+答案解析100道

二元一次方程组练习题100道(卷一)(围:代数: 二元一次方程组)一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………( ) 2、方程组⎩⎨⎧=+-=5231y x xy 的解是方程3x -2y =13的一个解( )3、由两个二元一次方程组成方程组一定是二元一次方程组( )4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ,可以转化为⎩⎨⎧-=--=+27651223y x y x ( )5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程,则a 的值为±1( )6、若x +y =0,且|x |=2,则y 的值为2 …………( )7、方程组⎩⎨⎧=+-=+81043y x xm my mx 有唯一的解,那么m 的值为m ≠-5 …………( )8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有无数多个解 …………( ) 9、x +y =5且x ,y 的绝对值都小于5的整数解共有5组 …………( ) 10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解,反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………( )11、若|a +5|=5,a +b =1则32-的值为b a ………()12、在方程4x -3y =7里,如果用x 的代数式表示y ,则437yx +=( ) 二、选择:13、任何一个二元一次方程都有( ) (A )一个解; (B )两个解; (C )三个解; (D )无数多个解;14、一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( ) (A )5个 (B )6个 (C )7个 (D )8个 15、如果⎩⎨⎧=+=-423y x ay x 的解都是正数,那么a 的取值围是( )(A )a <2; (B )34->a ; (C )342<<-a ; (D )34-<a ; 16、关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解,那么m 的值是( )(A )2; (B )-1; (C )1;(D )-2;17、在下列方程中,只有一个解的是( ) (A )⎩⎨⎧=+=+0331y x y x(B )⎩⎨⎧-=+=+2330y x y x(C )⎩⎨⎧=-=+4331y x y x(D )⎩⎨⎧=+=+3331y x y x18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( )(A )15x -3y =6 (B )4x -y =7 (C )10x +2y =4 (D )20x -4y =3 19、下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114y x y x (B )⎩⎨⎧=+=+75z y y x(C )⎩⎨⎧=-=6231y x x(D )⎩⎨⎧=-=-1y x xyy x20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解,则a 、b 的值等于( )(A )a =-3,b =-14(B )a =3,b =-7 (C )a =-1,b =9(D )a =-3,b =14 21、若5x -6y =0,且xy ≠0,则yx yx 3545--的值等于( )(A )32 (B )23 (C )1 (D )-122、若x 、y 均为非负数,则方程6x =-7y 的解的情况是( ) (A )无解 (B )有唯一一个解 (C )有无数多个解 (D )不能确定 23、(A )14 (B )-4 (C )-12 (D )12 24、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为( ) (A )21=k ,b =-4 (B )21-=k ,b =4 (C )21=k ,b =4(D )21-=k ,b =-4 三、填空:25、在方程3x +4y =16中,当x =3时,y =________,当y =-2时,x =_______ 若x 、y 都是正整数,那么这个方程的解为___________;26、27、如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________; 28、29、方程|a |+|b |=2的自然数解是_____________; 30、如果x =1,y =2满足方程141=+y ax ,那么a =____________; 31、已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解,则a =______,m =______;32、若方程x -2y +3z =0,且当x =1时,y =2,则z =______;33、34、若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________; 35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________;36、四、解方程组五、解答题:47、甲、乙两人在解方程组 时,甲看错了①式中的x 的系数,解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ;乙看错了方程②中的y 的系数,解得⎪⎪⎩⎪⎪⎨⎧==19177681y x ,若两人的计算都准确无误,请写出这个方程组,并求出此方程组的解;48、使x +4y =|a |成立的x 、y 的值,满足(2x +y -1)2+|3y -x |=0,又|a |+a =0,求a 的值;49、代数式ax 2+bx +c 中,当x =1时的值是0,在x =2时的值是3,在x =3时的值是28,试求出这个代数式;50、要使下列三个方程组成的方程组有解,求常数a 的值。
专题 解二元一次方程组(计算题50题)(原卷版)
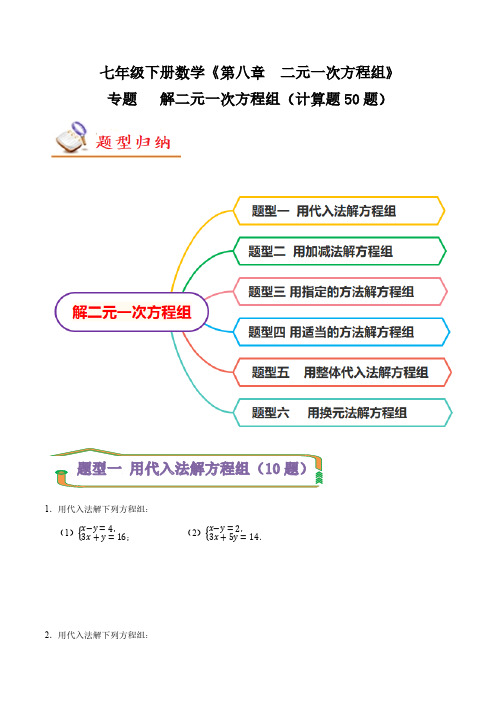
七年级下册数学《第八章二元一次方程组》专题解二元一次方程组(计算题50题)1.用代入法解下列方程组:(1)x−y=4,3x+y=16;(2)x−y=2,3x+5y=14.2.用代入法解下列方程组:(1)2x−y=33x+2y=8;(2)u+v=103u−2v=5.3.用代入法解下列方程组:(1)3x−y=2,9x+8y=17;(2)3x−4y=10x+3y=12.4.用代入法解下列方程组.(1)x+2y=4y=2x−3;(2)x−y=44x+2y=−2.5.用代入法解下列方程组:(1)5x+4y=−1.52x−3y=4(2)4x−3y−10=03x−2y=06.用代入法解下列方程组:(1)x−y=42x+y=5;(2)3x−y=29x+8y=17;(3)3x+2y=−8 6x−3y=−9.7.用代入法解下列方程组:(1)3x+2y=11,①x=y+3,②(2)4x−3y=36,①y+5x=7,②(3)2x−3y=1,①3x+2y=8,②8.用代入法解下列方程组:(1)5x+2y=15①8x+3y=−1②;(2)3(y−2)=x−172(x−1)=5y−8.9.用代入法解下列方程组:(1)x=6−5y3x−6y=4(2)5x+2y=15x+y=6(3)3x+4y=22x−y=5(4)2x+3y=73x−5y=110.用代入法解下列方程组:(1)2x+y=3x+2y=−6;(2)x+5y=43x−6y=5;(3)2x−y=63x+2y=2;(4)5x+2y=113y−x=−9;1.用加减法解下列方程组:(1)4x−y =143x +y =7 (2x−2y =7x−3y =−82.用加减法解下列方程组:(1)2m +7n =53m +n =−2(2)2u−5v =124u +3v =−2(3y 7=12+y 7=133.用加减法解下列方程组:(1)x−y =52x +y =4;(2)x−2y =33x +4y =−1.4.用加减法解下列方程组:(1)4x−3y =11,2x +y =13;(2)x−y =3,2y +3(x−y)=115.用加减法解下列方程组:(1)3μ+2t =76μ−2t =11 (2)2a +b =33a +b =4.6.(2023•市北区校级开学)用加减法解下列方程组:(1)3y−4x =04x +y =8; (2+y =3x−32y =−1.7.(2022秋•陕西期末)用加减法解下列方程组:(1)x−y =33x−8y =14; (2+2y =10=1+y 13.8.用加减法解下列方程组:(1)x +3=y ,2(x +1)−y =6; (2)x +y =2800,96%x +64%y =2800×92%.9.用加减法解下列方程组:(1)x−y =5,①2x +y =4;②(2)x−2y =1,①x +3y =6;②(3)2x−y =5,①x−1=12(2y−1).②10.用加减法解下列方程组:(1)x +3y =62x−3y =3 (2)7x +8y =−57x−y =4(3)y−1=3(x−2)y+4=2(x+1)(4+y4=1−y3=−1.1.(2022春•新田县期中)用指定的方法解下列方程组:(1)2x−5y=14①y=−x②(代入法);(2)2x+3y=9①3x+5y=16②(加减法).2.(2022春•安岳县校级月考)解下列方程组:(1)3x−y=75x+2y=8(用代入法);(2+n3=10−n4=5(用加减法).3.(2022春•大连期中)用指定的方法解下列方程组:(1)x−3y=42x+y=13(代入法);(2)5x+2y=4x+4y=−6(加减法).4.(2022春•宁远县月考)请用指定的方法解下列方程组(1)5a−b=113a+b=7(代入消元法);(2)2x−5y=245x+2y=31(加减消元法).5.(2021秋•蒲城县期末)请用指定的方法解下列方程组:(1)2x+3y=11①x=y+3②(代入消元法);(2)3x−2y=2①4x+y=10②(加减消元法).6.(2022秋•历下区期中)请用指定的方法解下列方程组:(1)m−n2=22m+3n=12(代入法);(2)6s−5t=36s+t=−15(加减法).7.(2022春•泰安期中)用指定的方法解下列方程组(1)3x+4y=19x−y=4(代入消元法);(2)2x+3y=−53x−2y=12(加减消元法);(35(x−9)=6(y−2)−y13=2.8.(2021秋•历下区期中)请用指定的方法解下列方程组:(1)3x+2y=14x=y+3;(代入法)(2)2x+3y=123x+4y=17.(加减法)9.(2021春•沙河口区期末)用指定的方法解下列方程组:(1)y=2x−33x+2y=8(代入法);(2)3x+4y=165x−6y=33(加减法).10.用指定的方法解下列方程组:(1)3x+4y=19x−y=4(代入法);(2)2x+3y=−53x−2y=12(加减法).1.(2022•苏州模拟)用适当的方法解下列方程组.(1)x+2y=9y−3x=1;(2x−34y=1=4.2.(2022秋•锦江区校级期末)用适当的方法解下列方程组.(1)x=2y−14x+3y=7;(2)3x+2y=22x+3y=28,.3.用适当的方法解下列方程组:(1)x+2y=0,3x+4y=6;(2=2y1)−y=11(3)x+0.4y=40,0.5x+0.7y=35;(4+n−m4=−14,5(n1)12=2.4.(2022•天津模拟)用适当的方法解下列方程组:(1)x +y =52x−y =4; (2=y 24−y−33=112.5.(2021•越城区校级开学)用适当的方法解下列方程组:(1)2x−3y =7x−3y =7. (2)0.3p +0.4q =40.2p +2=0.9q .6.(2022春•东城区校级月考)用适当的方法解下列方程组(1)x +y =52x +y =8; (2)2x +3y =73x−2y =4.7.(2021春•哈尔滨期末)用适当的方法解下列方程组(1)x +2y =93x−2y =−1 (2)2x−y =53x +4y =28.(2022春•椒江区校级期中)用适当的方法解下列方程组:(1)2x +3y =16①x +4y =13②; (2)2s t 3=3s−2t 8=3.9.(2022春•诸暨市期中)用适当的方法解下列方程组:(1)y=2x−1x+2y=−7(2+y3=7+y2=810.(2021春•南湖区校级期中)用适当的方法解下列方程组:(1)3x+2y=9x−y=8;(2=x y2=7.1.先阅读材料,然后解方程组:材料:解方程组x+y=4①3(x+y)+y=14②在本题中,先将x+y看作一个整体,将①整体代入②,得3×4+y=14,解得y=2.把y=2代入①得x=2,所以x=2 y=2这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组x−y−1=0①4(x−y)−y=5②.2.(2021秋•乐平市期末)解方程组3x−2y=8⋯⋯⋯①3(3x−2y)+4y=20⋯.②时,可把①代入②得:3×8+4y=20,求得y=﹣1,从而进一步求得x=2y=−1这种解法为“整体代入法“,请用这样的方法解下列方程组2x−3y=123(2x−3y)+5y=26.3.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1.③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0y=−1这种方法被称为“整体代入法”,请用这样的方法解下列方程组:=0=2y+1.4.(2022春•太和县期末)先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1,③然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0①y=−1②这种方法被称为“整体代入法”,+2y=9.5.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x这种方法被称为“整体代入法”,请用这样的方法解下列方程组:2x−3y−2=03(2x−3y)+y=7.1.用换元法解下列方程组+2y=12−1y=342.用换元法解下列方程组:(1)3(x+y)+2(x−y)=36(x+y)−4(x−y)=−16(2+x5y3=2−(x+5y)=5.3.(2022春•云阳县期中)阅读探索:解方程组(a−1)+2(b+2)=62(a−1)+(b+2)=6解:设a﹣1=x,b+2=y原方程组可以化为x+2y=62x+y=6,解得x=2y=2,即:a−1=2b+2=2∴a=3b=0,此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组(a4−1)+2(b5+2)=102(a4−1)+(b5+2)=11;(2)能力运用已知关于x,y的方程组a1x+b1y=c1a2x+b2y=c2的解为x=6y=7,求关于m、n的方程组a1(m−2)+b1(n+3)=c1a2(m−2)+b2(n+3)=c2的解.4+x−y10=3①−x−y10=−1②,你会解这个方程组吗?小明、小刚、小芳争论了一会儿,他们分别写出了一种方法:小明:把原方程组整理得8x+2y=90③2x+8y=−30④④×4﹣③得30y=﹣210,所以y=﹣7把y=﹣7代入③得8x=104,所以x=13,即x=13y=−7小刚:设x y6=m,x−y10=n,则m+n=3③m−n=−1④③+④得m=1,③﹣④得m=2,=1=2,所以x+y=6x−y=20,所以x=13y=−7.小芳:①+②得2(x y)6=2,即x+y=6.③①﹣②得2(x−y)10=4,即x﹣y=20.④③④组成方程组得x=13③﹣④得y =﹣7,即x =13y =−7.老师看过后,非常高兴,特别是小刚的方法独特,像小刚的这种方法叫做换元法,你能用换元法解下列方程组吗?+2x 3y 7=1−2x 3y 7=5.5.(2022春•卧龙区校级月考)阅读探索(1)知识积累解方程组(a−1)+2(b +2)=62(a−1)+(b +2)=6.解:设a ﹣1=x ,b +2=y .原方程组可变为x +2y =62x +y =6,解这个方程组得x =2y =2,即a−1=2b +2=2,所以a =3b =0,这种解方程组的方法叫换元法.(2)拓展提高运用上述方法解下列方程组:(m 3−1)+2(n 5+2)=43(m 3−1)−(n 5+2)=5.(3)能力运用已知关于x ,y 的方程组a 1x +b 1y =c 1a 2x +b 2y =c 2的解为x =3y =4,请直接写出关于m 、n 的方程组a 1(m +2)−b 1n =c 1a 2(m +2)−b 2n =c 2的解是 .。
二元一次方程组练习题(含答案)

二元一次方程组练习题(含答案) 二元一次方程组练题一.解答题(共16小题)1.解下列方程组:1)x+2y-1=23x-2y=52)1-yx+2/3=1/22y+3=3x3)5x+2y=11a4x-4y=6a4)2x+3y=73x-2y=15)2x-3y=75x+4y=176)2x+3y=13x-2y=57)3x-4y=-12x+5y=138)x(y+1)+y(1-x)=2x(x+1)-y-x^2=09)3x+y=72x-3y=-810)x^2+xy=2y-x+2=02.求适合的x,y的值。
已知关于x,y的二元一次方程y=kx+b的解有和。
1)求k,b的值。
2)当x=2时,y的值。
3)当y=3时,x的值为多少?解答:1.1)将第二个方程变形得到y=(3x-5)/2,代入第一个方程中,得到x=3,y=-2.2)将第一个方程变形得到y=(1/2-1+xy)/x,代入第二个方程中,得到x=3,y=-1.3)将第二个方程变形得到y=x-3/2,代入第一个方程中,得到x=2,y=1.4)将第二个方程变形得到y=(3x-1)/2,代入第一个方程中,得到x=2,y=1.5)将第一个方程变形得到y=(2x-7)/3,代入第二个方程中,得到x=1,y=-1.6)将第二个方程变形得到y=(3x-5)/2,代入第一个方程中,得到x=1,y=-1.7)将第二个方程变形得到y=(3x+1)/4,代入第一个方程中,得到x=5,y=2.8)将第一个方程变形得到y=(2-x^2)/(1-x),代入第二个方程中,得到x=1,y=1.9)将第二个方程变形得到y=(2x+8)/3,代入第一个方程中,得到x=1,y=1.10)将第一个方程变形得到y=2/x-x,代入第二个方程中,得到x=1,y=0.2.1)由于y=kx+b,所以当x=1时,y=k+b;当x=2时,y=2k+b。
又因为已知y=3时,x的值为多少,所以将y=kx+b代入得到kx+b=3,解得x=(3-b)/k。
二元一次方程组(例题、解方程组、练习及答案)
的x. y 的值.s+y=l 2x+y=3⑵2K -3y=-52y —12弩=4Cx-1)-2(2y+l)=43.解方程组:举-4y=24.解方程组: x+1.y~1 ~2'玄-11-L 2-2(x+2y)=3⑵L L1K +4(x+2y)=45解二元一次方程组练习及答案专题一:二元一次方程组解法精练一.解答题(共16小题)2.解下列方程组(s _t)-2(s+t)=10 5.解方程组上(日一t)+2Cs+t)=266.已知关于x,y 的二元一次方程y 二kx+b 的解有 (1)求k,b 的值. ⑵当x=2时,y 的值. ⑶当x 为何值时,y=3?7.解方程组:2y=3“至_y_7⑴[电文-10;=13_X "12,乙看错了方程组中的b.蓋二- £时,由于粗心,甲看错了方程组中的a,而得解为 (沪5而得解为尸°.(1)甲把a 看成了什么,乙把b 看成了什么? (2)求出原方程组的正确解.亠一空二5 14.I X0.315.解下列方程组:8.解方程组:卩(旳)(K -3y)=159.解方程组:10.解下列方程组: fs-y=4 ⑴4贵 11.解方程组: "T⑵[4(葢十7)-5(K-y)=212.解二元一次方程组: f 9s+2y=20(1).办十4尸10;乜(K -1)-4(y-4)=0⑵占〔厂"二3匕+5)鮎曲+5尸1013.在解方程组(1) 匹站3y=15 “x+1_y+4 ⑵f2x+y=4 16.解下列方程组:(1)时戈产5 p+y=l(2)■20^1+30^25^X2专题二:方程组解法强化训练 ■>二1+尸j3^-2/=6 2(右十为*175x+y+z=145 15 3.x+y —2z-5 仝%+4®二1124.5. 17 r0.25x+3ty+3)=156.匚(工十1)—1.5(^十刀二35 r 3(x-y 十E 二0'mJ4耳+2了+£=3i4 l 税25t+5v+z=6O 盲8.9.—2 4 J2 3 XH -/=60 J y +z =40 x+i=50 10. H 十JJ-H-Z=11<3A +J 二25z=4^11.L》+z -了工二号 5-3^+4-7y=1121」心+5我彳z +z-3j=5 13.乐十》)-4&p )二4土+二=118.21. fi-2j=7y x+1—二36y-1=3fx+|)16.y—1x二y-I2_y+2.2x=+13T" 33(x-0=4(卩一4)17.+500,[60%^+80%-7=500x72%.19.宝”一1)=3(兀+5)20.卜223A-3J-9=^±13r2(z+^+3(x-y)=1322.j-2z+3y=1123.尸(*)亠4决2刃=8724. 25. 弘+»=198jc-3y=6727. =-1=4IZ尹-1=128.30. SI兰工_气2十3-5巧P=〔23-_答案专题一1.x=6"X=1 「K=3、「K=3「⑵•卄8•解万程组:9•解方程组:1歼-1(y=0\y=0工二3114V——3⑷•y=-3•解方程组fl4•解方程组:鳥I尸4,尸亍6••(1)求k,b的值.k二言,b二号•7⑵当x=2时,y的值•把x=2代入,得y=p•(3)当x为何值时,y=3?把y=3代入,得x=1 7•解方程组:10•解下列方程组:17 \=60:'尸-2411•解方程组:⑴12⑵¥二广1712•解二元一次方程组:13.(1)甲把a看成了什么,乙把b看成了什么?fa=-2 [b=6(2)求出原方程组的正确解.P=152•解下列方程组专题二:=50rz=4rz=5K=5[75rz=-70rA=61.2.3.4.5.6.g1715•解下列方程组:⑴16•解下列方程组:⑴rx=-2cm =49.严=35L=2510.厂=30 12.J=_10 严=-17/4K=_19/413r=_5厂=17/15 厂1=714."11⑴15.J=-316.=1厂=20017.J=300 18. J -A =-1/4丫尹=3/819.29/6 -7/422. 23.CI ;rz =2324.f A =-11/2 25.f A =826.5=-127.rz=428.J -A =4.5 29.rz=6.530.。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).16.解下列方程组:(1)(2)第二十六章《二次函数》检测试题1,(2008年芜湖市)函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 ( )2,在一定条件下,若物体运动的路程s (米)与时间t (秒)的关系式为s =5t 2+2t ,则当t =4时,该物体所经过的路程为( )3,已知二次函数y =ax 2+bx +c (a ≠0)的图象如图2所示,给出以下结论:① a +b +c <0;② a -b +c <0;③ b +2a <0;④ abc >0 .其中所有正确结论的序号是( )A. ③④B. ②③C. ①④D. ①②③4,二次函数y =ax 2+bx +c 的图象如图3所示,若M =4a +2b +c ,N =a -b +c ,P =4a +2b ,则( )A.M >0,N >0,P >0B. M >0,N <0,P >0C. M <0,N >0,P >0D. M <0,N >0,P <05,如果反比例函数y =k x的图象如图4所示,那么二次函数y =kx 2-k 2x -1的图象大致为( )6y 所对应的函数值依次为:20,56,110,182,274,380,506,650.其中有一个值不正确,这个不正确的值是()A. 506B.380C.274D.18图3图4 A . B . 图5 图1A. y =x 2-2B. y =(x -2)2C. y =x 2+2D. y =(x +2)28如图6,小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h =3.5t -4.9t 2(t 的单位:s ,h 的单位:m )可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )A.0.71sB.0.70sC.0.63sD.0.36s9,如果将二次函数y =2x 2的图象沿y 轴向上平移1个单位,那么所得图象的函数解析式是 .10,平移抛物线y =x 2+2x -8,使它经过原点,写出平移后抛物线的一个解析式______ .11,若二次函数y =x 2-4x +c 的图象与x 轴没有交点,其中c 为整数,则c =12,二次函数y =ax 2+bx +c 的图像如图7所示,则点A (a ,b )在第___象限.13,已知抛物线y =x 2-6x +5的部分图象如图8,则抛物线的对称轴为直线x = ,满足y <0的x 的取值范围是 .14,已知一抛物线与x 轴的交点是)0,2( A 、B (1,0),且经过点C (2,8)。
二元一次方程组经典练习题+答案解析100道

二元一次方程组练习题100道(卷一)(范围:代数: 二元一次方程组)一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………( ) 2、方程组⎩⎨⎧=+-=5231y x xy 的解是方程3x -2y =13的一个解( )3、由两个二元一次方程组成方程组一定是二元一次方程组( )4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ,可以转化为⎩⎨⎧-=--=+27651223y x y x ( )5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程,则a 的值为±1( )6、若x +y =0,且|x |=2,则y 的值为2 …………( )7、方程组⎩⎨⎧=+-=+81043y x xm my mx 有唯一的解,那么m 的值为m ≠-5 …………( )8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有无数多个解 …………( ) 9、x +y =5且x ,y 的绝对值都小于5的整数解共有5组 …………( ) 10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解,反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………( )11、若|a +5|=5,a +b =1则32-的值为b a ………()12、在方程4x -3y =7里,如果用x 的代数式表示y ,则437yx +=( ) 二、选择:13、任何一个二元一次方程都有( ) (A )一个解; (B )两个解;(C )三个解; (D )无数多个解;14、一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( ) (A )5个 (B )6个 (C )7个 (D )8个 15、如果⎩⎨⎧=+=-423y x ay x 的解都是正数,那么a 的取值范围是( )(A )a <2; (B )34->a ; (C )342<<-a ; (D )34-<a ; 16、关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解,那么m 的值是( )(A )2; (B )-1; (C )1; (D )-2;17、在下列方程中,只有一个解的是( ) (A )⎩⎨⎧=+=+0331y x y x(B )⎩⎨⎧-=+=+2330y x y x(C )⎩⎨⎧=-=+4331y x y x(D )⎩⎨⎧=+=+3331y x y x18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( )(A )15x -3y =6 (B )4x -y =7 (C )10x +2y =4 (D )20x -4y =3 19、下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114yx y x (B )⎩⎨⎧=+=+75z y y x(C )⎩⎨⎧=-=6231y x x(D )⎩⎨⎧=-=-1y x xyy x20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解,则a 、b 的值等于( )(A )a =-3,b =-14(B )a =3,b =-7 (C )a =-1,b =9(D )a =-3,b =14 21、若5x -6y =0,且xy ≠0,则y x yx 3545--的值等于( )(A )32 (B )23 (C )1 (D )-122、若x 、y 均为非负数,则方程6x =-7y 的解的情况是( ) (A )无解 (B )有唯一一个解 (C )有无数多个解 (D )不能确定 23、(A )14 (B )-4 (C )-12 (D )12 24、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为( ) (A )21=k ,b =-4 (B )21-=k ,b =4 (C )21=k ,b =4(D )21-=k ,b =-4 三、填空:25、在方程3x +4y =16中,当x =3时,y =________,当y =-2时,x =_______ 若x 、y 都是正整数,那么这个方程的解为___________;26、27、如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________; 28、29、方程|a |+|b |=2的自然数解是_____________; 30、如果x =1,y =2满足方程141=+y ax ,那么a =____________; 31、已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解,则a =______,m =______;32、若方程x -2y +3z =0,且当x =1时,y =2,则z =______; 33、34、若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________; 35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________;36、四、解方程组 五、解答题:47、甲、乙两人在解方程组 时,甲看错了①式中的x 的系数,解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ;乙看错了方程②中的y 的系数,解得⎪⎪⎩⎪⎪⎨⎧==19177681y x ,若两人的计算都准确无误,请写出这个方程组,并求出此方程组的解;48、使x +4y =|a |成立的x 、y 的值,满足(2x +y -1)2+|3y -x |=0,又|a |+a =0,求a 的值;49、代数式ax 2+bx +c 中,当x =1时的值是0,在x =2时的值是3,在x =3时的值是28,试求出这个代数式;50、要使下列三个方程组成的方程组有解,求常数a 的值。
二元一次方程组经典练习题+答案解析100道(可编辑修改word版)

)
4
二、选择:
1、任何一个二元一次方程都有( )
(A)一个解;
(B)两个解;
(C)三个解;
(D)无数多个解;
2、如果
x y 3x 2 y
a
4
的解都是正数,那么
a
的取值范围是(
)
(A)a<2;
(B) a 4 ; (C) 2 a 4 ; (D) a 4 ;
3
3
3
3、关于
x、y
的方程组
x
y
பைடு நூலகம்
81 76 17 19
,若两人的计算都准确无误,请写出这个方程组,并求
出此方程组的解;
2、使 x+4y=|a|成立的 x、y 的值,满足(2x+y-1)2+|3y-x|=0,又|a|+a=0,求 a 的值;
3、要使下列三个方程组成的方程组有解,求常数 a 的值。 2x+3y=6-6a,3x+7y=6-15a,4x+4y=9a+9
2、某班学生到农村劳动,一名男生因病不能参加,另有三名男生体质较弱,教师安排他们与女生 一起抬土,两人抬一筐土,其余男生全部挑土(一根扁担,两只筐),这样安排劳动时恰需筐 68 个, 扁担 40 根,问这个班的男女生各有多少人?
3、甲、乙两人练习赛跑,如果甲让乙先跑 10 米,那么甲跑 5 秒钟就可以追上乙;如果甲让乙先跑 2 秒钟,那么甲跑 4 秒钟就能追上乙,求两人每秒钟各跑多少米?
x x
2 y
y 3m 9m
的解是方程
3x+2y=34
的一组解,那么
m
的值是(
)
(A)2;
(B)-1;
二元一次方程组练习题(含答案)

二元一次方程组练习题(含答案)1.解下列方程组:1) 5x + 2y = 11a,-4y = 6a;2) 4x + 3y - 1 = 0,2x + y - 2 = 0;3) x + 2y/3 - 1/3 = 2,x/3 + 1 - y/2 = 1/2;4) x - y/2 = 1,x + y/2 = 3.2.求解以下方程组:1) 2x + 3y = 7,x - y = 1;2) x + 2y = 5,2x + y = 7;3) 3x + 2y = 8,4x - 3y = -11.3.已知二元一次方程y = kx + b的解有(2,5)和(-1,0)。
1) 求k,b的值;2) 当x = 2时,y的值;3) 当y = 3/5时,x的值。
4.在解方程组2x + y = 5,x - y = 1时,甲看错了方程组中的a,而得到解x = 2,y = 1.乙看错了方程组中的b,而得到解x = 3,y = -1.1) 甲把a看成了什么,乙把b看成了什么?2) 求出原方程组的正确解。
参考答案与解析:1.解下列方程组:1) 5x + 2y = 11a,-4y = 6a。
将第二个方程式化简为y = -3/2a,代入第一个方程式中得到5x + 2(-3/2a) = 11a,化简得到x = (23/10)a,y = (-9/5)a。
2) 4x + 3y - 1 = 0,2x + y - 2 = 0.将第二个方程式中的y用第一个方程式中的x表示,得到y = 2 - 2x,代入第一个方程式中得到4x + 3(2 - 2x) - 1 = 0,化简得到x = 1/2,y = 1.3) x + 2y/3 - 1/3 = 2,x/3 + 1 - y/2 = 1/2.将第二个方程式中的x用第一个方程式中的y表示,得到x = 6 - 2y,代入第一个方程式中得到6 - 4y/3 = 2,化简得到y = 3/2,x = 0.4) x - y/2 = 1,x + y/2 = 3.将两个方程式相加得到2x = 4,化简得到x = 2,代入第一个方程式中得到y = 2.2.求解以下方程组:1) 2x + 3y = 7,x - y = 1.将第二个方程式中的x用第一个方程式中的y表示,得到x = y + 1,代入第一个方程式中得到2(y + 1) + 3y = 7,化简得到y = 1,x = 2.2) x + 2y = 5,2x + y = 7.将第一个方程式中的x用第二个方程式中的y表示,得到x = (7 - y)/2,代入第一个方程式中得到(7 - y)/2 + 2y = 5,化简得到y = 1,x = 2.3) 3x + 2y = 8,4x - 3y = -11.将第一个方程式中的x用第二个方程式中的y表示,得到x = (3y - 11)/4,代入第一个方程式中得到3(3y - 11)/4 + 2y = 8,化简得到y = 1,x = 1.3.已知二元一次方程y = kx + b的解有(2,5)和(-1,0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
|解二元一次方程组练习题1.(2013•梅州)解方程组.2.(2013•淄博)解方程组.【3.(2013•邵阳)解方程组:.4.(2013•遵义)解方程组.:5.(2013•湘西州)解方程组:.6.(2013•荆州)用代入消元法解方程组.】7.(2013•汕头)解方程组.8.(2012•湖州)解方程组.!9.(2012•广州)解方程组.10.(2012•常德)解方程组:—11.(2012•南京)解方程组.12.(2012•厦门)解方程组:.、13.(2011•永州)解方程组:.14.(2011•怀化)解方程组:.—16.(2010•南京)解方程组:.·17.(2010•丽水)解方程组:18.(2010•广州)解方程组:.…19.(2009•巴中)解方程组:.20.(2008•天津)解方程组:!21.(2008•宿迁)解方程组:.22.(2011•桂林)解二元一次方程组:.<23.(2007•郴州)解方程组:24.(2007•常德)解方程组:.~25.(2005•宁德)解方程组:`26.(2011•岳阳)解方程组:.27.(2005•苏州)解方程组:.28.(2005•江西)解方程组:,29.(2013•自贡模拟)解二元一次方程组:.—30.(2013•黄冈)解方程组:.解二元一次方程组练习题参考答案与试题解析一.解答题(共30小题)1.(2013•梅州)解方程组.-考点:解二元一次方程组;解一元一次方程.专题:计算题;压轴题.分析:①+②得到方程3x=6,求出x的值,把x的值代入②得出一个关于y的方程,求出方程的解即可.解答:>解:,①+②得:3x=6,解得x=2,将x=2代入②得:2﹣y=1,解得:y=1.∴原方程组的解为.点评:本题考查了解一元一次方程和解二元一次方程组的应用,关键是把二元一次方程组转化成一元一次方程,题目比较好,难度适中.2.(2013•淄博)解方程组.考点:解二元一次方程组.专题:计算题.分析:^先用加减消元法求出y的值,再用代入消元法求出x的值即可.解答:解:,①﹣2×②得,﹣7y=7,解得y=﹣1;把y=﹣1代入②得,x+2×(﹣1)=﹣2,解得x=0,故此方程组的解为:.点评:本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.3.(2013•邵阳)解方程组:.考点:解二元一次方程组.专题:计算题;压轴题.分析:#根据y的系数互为相反数,利用加减消元法其解即可.解答:解:,①+②得,3x=18,解得x=6,把x=6代入①得,6+3y=12,解得y=2,所以,方程组的解是.】点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.4.(2013•遵义)解方程组.考点:解二元一次方程组.专题:;计算题.分析:由第一个方程得到x=2y+4,然后利用代入消元法其解即可.解答:解:,由①得,x=2y+4③,③代入②得2(2y+4)+y﹣3=0,解得y=﹣1,"把y=﹣1代入③得,x=2×(﹣1)+4=2,所以,方程组的解是.点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.5.(2013•湘西州)解方程组:.考点:方程组的解.解答:解:,由①得:x=1﹣2y ③,把③代入②得:y=﹣1,把y=﹣1代入③得:x=3,]则原方程组的解为:.点评:此题考查了解二元一次方程组,解二元一次方程组常用的方法是加减法和代入法两种,般选用加减法解二元一次方程组较简单.6.(2013•荆州)用代入消元法解方程组.考点:-解二元一次方程组.专题:计算题.分析:把第一个方程整理为y=x﹣2,然后利用代入消元法求解即可.解答:解:,由①得,y=x﹣2③,-③代入②得,3x+5(x﹣2)=14,解得x=3,把x=3代入③得,y=3﹣2=1,所以,方程组的解是.点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.7.(2013•汕头)解方程组.;考点:解二元一次方程组.专题:计算题.分析:将方程组中的第一个方程代入第二个方程消去x求出y的值,进而求出x的值,即可得到方程组的解.解答:。
解:,将①代入②得:2(y+1)+y=8,将y=2代入①得:x=2+1=3,则方程组的解为.点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法."8.(2012•湖州)解方程组.考点:解二元一次方程组.分析:①+②消去未知数y求x的值,再把x=3代入②,求未知数y的值.解答:"解:①+②得3x=9,解得x=3,把x=3代入②,得3﹣y=1,解得y=2,∴原方程组的解是.点评:本题考查了解二元一次方程组.熟练掌握加减消元法的解题步骤是关键.9.(2012•广州)解方程组.&考点:解二元一次方程组.专题:计算题.分析:根据y的系数互为相反数,利用加减消元法求解即可.解答:#解:,①+②得,4x=20,解得x=5,把x=5代入①得,5﹣y=8,解得y=﹣3,所以方程组的解是.点评:本题考查了解二元一次方程组,有加减法和代入法两种,根据y的系数互为相反数确定选用加减法解二元一次方程组是解题的关键./10.(2012•常德)解方程组:考点:解二元一次方程组.专题:压轴题.分析:¥本题用加减消元法或代入消元法均可.解答:解:①+②得:3x=6,(3分)x=2,(4分)把x=2代入①得:y=3.(7分)∴.(8分)点评:)这类题目的解题关键是掌握方程组解法中的加减消元法和代入消元法.11.(2012•南京)解方程组.考点:解二元一次方程组.专题:计算题.先由①表示出x,然后将x的值代入②,可得出y的值,再代入①可得出x的值,继而得出了方程组的解.}分析:解答:解:由①得x=﹣3y﹣1③,将③代入②,得3(﹣3y﹣1)﹣2y=8,解得:y=﹣1.将y=﹣1代入③,得x=2.(故原方程组的解是.点评:此题考查了解二元一次方程的知识,属于基础题,注意掌握换元法解二元一次方程.12.(2012•厦门)解方程组:.考点:解二元一次方程组.探究型.)专题:分析:先用加减消元法求出x的值,再用代入消元法求出y的值即可.解答:解:,、故此方程组的解为:.点评:本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.13.(2011•永州)解方程组:.考点:解二元一次方程组.方程思想.,专题:分析:两个方程中,x或y的系数既不相等也不互为相反数,需要先求出x或y的系数的最小公倍数,即将方程中某个未知数的系数变成其最小公倍数之后,再进行加减.解答:解:,②×2﹣①得:5y=15,!y=3,把y=3代入②得:x=5,∴方程组的解为.点评:此题考查的知识点是解二元一次方程组,关键是用加减加减消元法解方程组时,将方程中某个未知数的系数变成其最小公倍数之后,再进行相加减.本题也可以用代入法求解.14.(2011•怀化)解方程组:.(考点:解二元一次方程组.分析:两方程相加即可求得x的值,然后代入第一个方程即可求得y的值.解答:解:,①+②得:6x=12,】∴x=2,把x=2①得:2+3y=8,解得:y=2,∴方程组的解集是:.点评:本题主要考查了二元一次方程组的解法,解方程组时一定要理解基本思想是消元.15.(2013•桂林)解二元一次方程组:.,考点:解二元一次方程组.分析:先把②变形为y=2x﹣1代入①求出x的值,再把x的值代入③即可求出y的值.解答:解:,由②得:y=2x﹣1③。
把③代入①得:3x+4x﹣2=19,解得:x=3,把x=3代入③得:y=2×3﹣1,即y=5故此方程组的解为.点评:本题考查的是解二元一次方程组,熟知解二元一次方程组的代入消元法是解答此题的关键.16.(2010•南京)解方程组:.)考点:解二元一次方程组.分析:此题x、y的系数较小,故可用加减消元法或代入消元法求解.解答:解:方法一:②×2,得2x+4y=10,③③﹣①,得3y=6,《解这个方程,得y=2,(3分)将y=2代入①,得x=1,(15分)所以原方程组的解是:.(6分)方法二:由①,得y=4﹣2x,③将③代入②,得x+2(4﹣2x)=5,解这个方程,得x=1,(13分)将x=1代入③,得y=2,(5分)所以原方程组的解是.(6分)#点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.17.(2010•丽水)解方程组:考点:解二元一次方程组.分析:;利用代入法或加减消元法均可解答.解答:解:解法1:(1)+(2),得5x=10,∴x=2,(3分)把x=2代入(1),得4﹣y=3,∴y=1,(2分)∴方程组的解是.(1分)解法2:由(1),得y=2x﹣3,③(1分)!把③代入(2),得3x+2x﹣3=7,∴x=2,(2分)把x=2代入③,得y=1,(2分)∴方程组的解是.(1分)点评:本题考查的是二元一次方程的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.18.(2010•广州)解方程组:.<考点:解二元一次方程组.分析:观察原方程组,两个方程的y系数互为相反数,可用加减消元法求解.解答:解:,①+②,得4x=12,$解得:x=3.将x=3代入①,得9﹣2y=11,解得y=﹣1.所以方程组的解是.点评:对二元一次方程组的考查主要突出基础性,题目一般不难,系数比较简单,主要考查方法的掌握.19.(2009•巴中)解方程组:.(考点:解二元一次方程组.专题:计算题.分析:可用加减消元法求解,①×2+②消去x求出y,再代入①求出x.解答:解:,①×2+②得:8y=40,y=5,把y=5代入①得:15﹣2x=17,得:x=﹣1,∴.此题考查的知识点是解二元一次方程组,这类题目的解题关键是掌握方程组解法中的加减消元法和代入法.。
点评:20.(2008•天津)解方程组:考点:解二元一次方程组.专题:@计算题.分析:通过观察本题用代入法较简单,把②变成y=的形式,直接代入①,进行解答即可.解答:解:由②得y=2x﹣1③,将③代入①得:3x+5(2x﹣1)=8,解得x=1,代入③得:y=1.(∴原方程组的解为.点评:这类题目的解题关键是掌握方程组解法中的代入消元法.21.(2008•宿迁)解方程组:.考点:解二元一次方程组.计算题.&专题:分析:本题两个未知数的系数的最小公倍数都是6,但y的系数的符号相反,为了少出差错可考虑用加减消元法先消去y,然后求解.解答:解:,(1)×2+(2)×3得:13x=26,:x=2并代入(2)得:y=3.∴原方程组的解是.点评:当所给方程组的两个未知数的系数的最小公倍数大小差不多时,应考虑先消去符号相反的未知数.22.(2011•桂林)解二元一次方程组:.考点:《解二元一次方程组.专题:计算题.分析:先把①代入②求出y的值,再把y的值代入①即可求出x的值,进而得出方程组的解.解答:解:把①代入②得:3y=8﹣2(3y﹣5),解得y=2(3分)~把y=2代入①可得:x=3×2﹣5(4分),解得x=1(15分)所以此二元一次方程组的解为.(6分)故答案为:.点评:本题考查的是解二元一次方程组的代入法,比较简单.23.(2007•郴州)解方程组:解二元一次方程组.(考点:分析:先把原方程组化简,再用代入消元法或加减消元法即可求解.解答:解:原方程组化为:,③﹣①得:2x=8,x=4.把x=4代入①得:4﹣y=3,y=1.;故原方程组的解为.点评:此题提高了学生的计算能力,解题时要注意观察方程组中各方程的特点,选择适当的解题方法会达到事半功倍的效果.24.(2007•常德)解方程组:.考点:解二元一次方程组.计算题.<专题:分析:解此题采用代入消元法最简单,解题时注意要细心.解答:解:由(1)得:x+3=3y,即x=3y﹣3.(3)由(2)得:2x﹣y=4,(4)>把(3)代入(4)得:y=2,把y=2代入(3)得:x=3.因此原方程组的解为.点评:此题考查了学生的计算能力,解题时要仔细审题,选择适宜的解题方法会达到事半功倍的效果.25.(2005•宁德)解方程组:—考点:解二元一次方程组.分析:用加减法,先把y的系数转化成相同的数,然后两式相加减消元,从而求另一未知数的值,然后把求得的值代入一方程求另一未知数.解答:解:解法一:把(x+y)=9代入②,得3×9+2x=33,∴x=3.(4分)把x=3代入①,得y=6.(7分)∴原方程组的解是.(8分)解法二:由①,得y=9﹣x③,(1分)把③代入②,得3(x+9﹣x)+2x=33,∴x=3.(4分)把x=3代入③,得y=6.(7分)∴原方程组的解是.(8分)点评:解二元一次方程组的基本思想是消元.消元的方法有代入法和加减法.26.(2011•岳阳)解方程组:.考点:解二元一次方程组.分析:把①代入②即可求得y,解得x的值,然后把x的值代入①即可求得y的值.;解答:解:把①代入②得:5x﹣3×3=1解得:x=2把x=2代入①得:y=1方程组的解集是:.点评:本题主要考查了二元一次方程组的解法,解方程组时一定要理解基本思想是消元.27.(2005•苏州)解方程组:.考点:解二元一次方程组.分析:先把方程组中的①化简,利用加减消元法或者代入消元法求解即可.解答:解:原方程组可化为,即,①+②得,6x=18,x=3.①﹣②得,﹣4y=﹣2,y=.故原方程组的解为.点评:解答此题的关键是掌握解二元一次方程组的加减消元法和代入消元法.28.(2005•江西)解方程组:考点:解二元一次方程组.分析:先把方程组化简再求解.解答:解:解法(1):由原方程组得把①代入②得2(6y﹣1)﹣y=9,即y=1;代入①得:x=5;∴原方程组的解为.解法(2):由得:x+1=6y,把①代入2(x+1)﹣y=11得:12y﹣y=11,即y=1;把y=1代入①得:x=5;∴原方程组的解为.点评:此题较简单,只要掌握了二元一次方程的代入法和加减消元法即可轻松解答.不论是哪种方法,解方程组的基本思想是消元.29.(2013•自贡模拟)解二元一次方程组:.考点:解二元一次方程组.专题:计算题.分析:把第一个方程整理得到2x+y=6y,再把(2x+y)看作一个整体代入第二个方程求解即可.解答:解:,由①得,2x+y=6y③,③代入②得,2×6y﹣5=7y,解得y=1,把y=1代入③得,2x+1=6,解得x=,所以,方程组的解是.点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单,本题利用整体代入求解更加简便.30.(2013•黄冈)解方程组:.考点:解二元一次方程组.专题:计算题.分析:把方程组整理成一般形式,然后利用代入消元法其求即可.解答:解:方程组可化为,由②得,x=5y﹣3③,③代入①得,5(5y﹣3)﹣11y=﹣1,解得y=1,把y=1代入③得,x=5﹣3=2,所以,原方程组的解是.点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.只要下功夫,一定有收获!。
