普通物理学第二版第三章课后习题答案
大学物理第二版 许瑞珍 贾谊明 编著 课后答案 1-3章
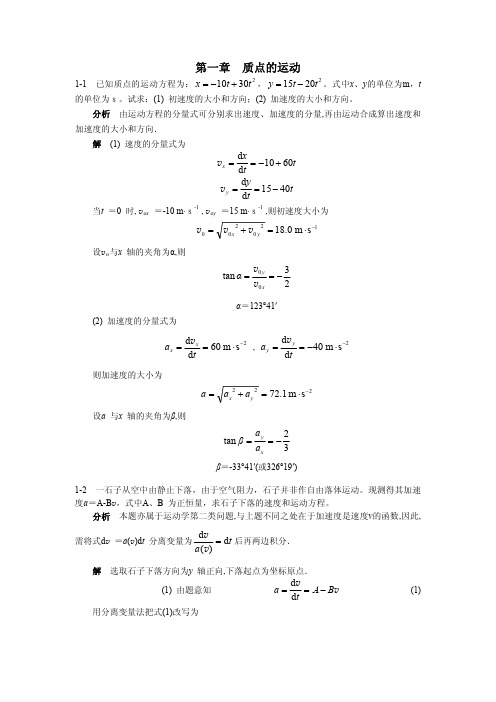
第一章 质点的运动1-1 已知质点的运动方程为:,。
式中x 、y 的单位为m ,t 的单位为s。
试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向。
23010t t x +-=22015t t y -=分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向.解 (1) 速度的分量式为t t xx 6010d d +-==v t ty y 4015d d -==v当t =0 时, v o x =-10 m·s-1 , v o y =15 m·s-1 ,则初速度大小为120200s m 0.18-⋅=+=y x v v v设v o 与x 轴的夹角为α,则23tan 00-==xy αv vα=123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta xx v , 2s m 40d d -⋅-==t a y y v则加速度的大小为222s m 1.72-⋅=+=y x a a a设a 与x 轴的夹角为β,则32tan -==x ya a β β=-33°41′(或326°19′)1-2 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动。
现测得其加速度a =A-B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程。
分析 本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v =a (v )d t 分离变量为t a d )(d =v v后再两边积分. 解 选取石子下落方向为y 轴正向,下落起点为坐标原点.(1) 由题意知 v vB A ta -==d d (1) 用分离变量法把式(1)改写为t B A d d =-vv(2)将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v vvvv得石子速度 )1(Bt e BA--=v 由此可知当,t →∞时,BA→v 为一常量,通常称为极限速度或收尾速度. (2) 再由)1(d d Bt e BAt y --==v 并考虑初始条件有 t e BA y t Bt y d )1(d 00⎰⎰--= 得石子运动方程)1(2-+=-Bt e BAt B A y1-3 一个正在沿直线行驶的汽船,关闭发动机后,由于阻力得到一个与速度反向、大小与船速平方成正比例的加速度,即a = - k v 2,k 为常数。
大学物理第三章-部分课后习题答案

大学物理第三章 课后习题答案3-1 半径为R 、质量为M 的均匀薄圆盘上,挖去一个直径为R 的圆孔,孔的中心在12R 处,求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。
分析:用补偿法〔负质量法〕求解,由平行轴定理求其挖去部分的转动惯量,用原圆盘转动惯量减去挖去部分的转动惯量即得。
注意对同一轴而言。
解:没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为:2112J MR =① 由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:2222213()()2424232c M R M R J J md MR =+=⨯⨯+⨯= ②由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:2121332J J J MR =-=3-2 如题图3-2所示,一根均匀细铁丝,质量为M ,长度为L ,在其中点O 处弯成120θ=︒角,放在xOy 平面内,求铁丝对Ox 轴、Oy 轴、Oz 轴的转动惯量。
分析:取微元,由转动惯量的定义求积分可得 解:〔1〕对x 轴的转动惯量为:2022201(sin 60)32Lx M J r dm l dl ML L ===⎰⎰ 〔2〕对y 轴的转动惯量为:20222015()(sin 30)32296Ly M L M J l dl ML L =⨯⨯+=⎰〔3〕对Z 轴的转动惯量为:22112()32212z M L J ML =⨯⨯⨯=3-3 电风扇开启电源后经过5s 到达额定转速,此时角速度为每秒5转,关闭电源后经过16s 风扇停止转动,已知风扇转动惯量为20.5kg m ⋅,且摩擦力矩f M 和电磁力矩M 均为常量,求电机的电磁力矩M 。
分析:f M ,M 为常量,开启电源5s 内是匀加速转动,关闭电源16s 内是匀减速转动,可得相应加速度,由转动定律求得电磁力矩M 。
解:由定轴转动定律得:1f M M J β-=,即11252520.50.5 4.12516f M J M J J N m ππβββ⨯⨯=+=+=⨯+⨯=⋅ 3-4 飞轮的质量为60kg ,直径为0.5m ,转速为1000/min r ,现要求在5s 内使其制动,求制动力F ,假定闸瓦与飞轮之间的摩擦系数0.4μ=,飞轮的质量全部分布在轮的外周上,尺寸如题图3-4所示。
大学物理第三章课后习题答案

r3
, k 为常量。试求两粒子相距为 r 时的势能,设力为零的
r = a cos ωt i + b sin ωt j , r 式中 a , b , ω 是正值常数,且 a ≻ b 。
(1)说明这质点沿一椭圆运动,方程为
�
x2 y 2 + = 1; a2 b2
(2)求质点在 A 点 (a ,0) 时和 B 点 (0, b ) 时的动能; (3)当质点从 A 点到 B 点,求力 F 所做的功,并求 F 的分力 Fx i 和 Fy j 所做的 功; (4) F 力是不是保守力? 12 . 如果物体从髙为 h 处静止下落,试求(1)时间为自变量; 12. (2)高度为自变量, 画出它的动能和势能图线,并证明两曲线中动能和势能之和相等。 . 一质量为 m 的地球卫星,沿半径为 3R e 的轨道运动, R e 为地球的半径,已知 13 13. 地球的质量为 M e ,求(1)卫星的动能; (2)卫星的引力势能; (3)卫星的机械 能。 . 如图所示, 14 14. 小球在外力作用下, 由静止开始从 A 点出发做匀加速运动,到达 B 点时撤消外力,小球 无摩擦的冲上竖直的半径为 R 的半圆环, 到达最高 点 C 时,恰能维持在圆环上做圆周运动,并以此速 度抛出而刚好落回到原来的出发点 A 处, 如图试求 小球在 AB 段运动的加速度为多大? . 如图所示,有一自动卸货矿车,满载时的质量 15 15. 为 M ,从与水平倾角 α = 30° 斜面上的点 A 由静 止下滑。设斜面对车的阻力为车重的 0.25 倍, 矿 车下滑距离 l 时,矿车与缓冲弹簧一道沿斜面运 动。当矿车使弹簧产生最大压缩形变时,矿车自 动卸货, 然后矿车借助弹簧的弹性力作用, 使之返回原位置 A 在装货。试问要完成这 一过程,空载时车的质量与满载时车的质 量之比应为多大? . 半径为 R 的光滑半球状圆塔的顶点 A 16 16. 上,有一木块 m ,今使木块获得水平速度
大学物理第三章部分课后习题答案

大学物理第三章部分课后习题答案3-1半径为R、质量为M的均匀薄圆盘上,挖去一个直径为R的圆孔,孔的中心在求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。
分析:用补偿法(负质量法)求解,由平行轴定理求其挖去部分的转动惯量,用原圆盘转动惯量减去挖去部分的转动惯量即得。
注意对同一轴而言。
解:没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为:1R处,2J11MR2①2由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:1MRMR3J2Jcmd2()2()2MR2②2424232由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:JJ1J213MR2323-2如题图3-2所示,一根均匀细铁丝,质量为M,长度为L,在其中点O处弯成120角,放在某Oy平面内,求铁丝对O某轴、Oy轴、Oz轴的转动惯量。
分析:取微元,由转动惯量的定义求积分可得解:(1)对某轴的转动惯量为:L20J某rdm(lin600)22M1dlML2L32(2)对y轴的转动惯量为:L1ML2M5Jy()2(lin300)2dlML20322L96(3)对Z轴的转动惯量为:1ML1Jz2()2ML2322122题图3-23-3电风扇开启电源后经过5达到额定转速,此时角速度为每秒5转,关闭电源后经过16风扇停止转动,已知风扇转动惯量为0.5kgm,且摩擦力矩Mf和电磁力矩M均为常量,求电机的电磁力矩M。
分析:Mf,M为常量,开启电源5内是匀加速转动,关闭电源16内是匀减速转动,可得相应加速度,由转动定律求得电磁力矩M。
解:由定轴转动定律得:MMfJ1,即52520.54.12Nm5163-4飞轮的质量为60kg,直径为0.5m,转速为1000r/min,现要求在5内使其制动,求制动力F,假定闸瓦与飞轮之间的摩擦系数0.4,飞轮的质量全部分布在轮的外周上,MJ1MfJ1J20.5尺寸如题图3-4所示。
分析:分别考虑两个研究对象:闸瓦和杆。
普通物理简明教程-胡盘新(第二版)大学物理习题-课后答案

ax =
a=
2
dυ x = −12t dt
2 1 2 2
补充作业1-01-方程求va
a是时间t的一次函数,既是 成正比关系变化,所以能用。
2 1
v − v ( 4 − 6t ) − ( 4 − 6t ) = = −6( t + t ) Δt t −t
2 1
a12 =
a1 + a2 = −6(t2 + t1 ) 2
Chenwq 1
1-2作业-方程求va
1-2. 一质点沿x轴运动,坐标与时间的变化关系为 x=4t-2t 3(SI制),试计算 (1)在最初2s内的平均速度,2s末的瞬时速度; (2)1s末到3s末的位移和平均速度; (3)1s末到3s末的平均加速度。此平均加速度是否可以 用a=(a1+a2)/2计算; (4)3s末的瞬时加速度。 解:(1)最初2s内的平均速度
2 2
2
船的加速度大小
1-10一辆铁路平板车装有货物,在货物与车底板之间的静 摩擦系数为0.25,如果火车以30km/s速度行驶,要使货物 不发生滑动,火车从刹车到完全静止所经过的最短路程是 多少? 解:
2
ax =
当x=s时
dυ x =− dt
h
2 3 2 2
(υ 0 ) = −
2
(l 2 − h )
前
前船接收抛物体前后
得v 前
前增大 中不变 后变小
(M + m)v 前=Mv + m(v + u)
Mv + mu m(u − v ) = =v+ >v M +m ( M + m)
得v 前 = v +
普通物理学第二版第三章课后习题答案

第三章 动量定理及动量守恒定律(习题)3.5.1质量为2kg 的质点的运动学方程为 j ˆ)1t 3t 3(i ˆ)1t 6(r 22+++-=(t 为时间,单位为s ;长度单位为m).求证质点受恒力而运动,并求力的方向大小。
解,j ˆ)3t 6(i ˆt 12v ++= j ˆ6i ˆ12a +=jˆ12i ˆ24a m F +==(恒量)012257.262412tg )N (83.261224F ==θ=+=-3.5.2质量为m 的质点在oxy 平面内运动,质点的运动学方程为ωω+ω=b,a, ,j ˆt sin b i ˆt cos a r为正常数,证明作用于质点的合力总指向原点。
解, ,j ˆt cos b i ˆt sin a v ωω+ωω-= r,j ˆt sin b i ˆt cos a a 22 ω-=ωω-ωω-= r m a m F ω-==3.5.3在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷粒,一方面逐出秸杆,筛面微微倾斜,是为了从较底的一边将秸杆逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才可能将谷粒筛出,若谷粒与筛面静摩擦系数为0.4,问筛沿水平方向的加速度至少多大才能使谷物和筛面发生相对运动。
解答,以谷筛为参照系,发生相对运动的条件是,g a ,mg f a m 000μ≥'μ=≥'a ' 最小值为)s /m (92.38.94.0g a 20=⨯=μ='以地面为参照系:解答,静摩擦力使谷粒产生最大加速度为,mg ma 0max μ= ,g a 0max μ=发生相对运动的条件是筛的加速度g a a0max μ=≥',a '最小值为)s /m (92.38.94.0g a20=⨯=μ='3.5.4桌面上叠放着两块木板,质量各为,m ,m 21如图所示。
2m 和桌面间的摩擦系数为2μ,1m 和2m 间的静摩擦系数为1μ。
大学物理第三章 部分课后习题答案

大学物理第三章 课后习题答案3-1 半径为R 、质量为M 的均匀薄圆盘上,挖去一个直径为R 的圆孔,孔的中心在12R 处,求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。
分析:用补偿法(负质量法)求解,由平行轴定理求其挖去部分的转动惯量,用原圆盘转动惯量减去挖去部分的转动惯量即得。
注意对同一轴而言。
解:没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为:2112J MR =① 由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:2222213()()2424232c M R M R J J md MR =+=⨯⨯+⨯= ②由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:2121332J J J MR =-=3-2 如题图3-2所示,一根均匀细铁丝,质量为M ,长度为L ,在其中点O 处弯成120θ=︒角,放在xOy 平面内,求铁丝对Ox 轴、Oy 轴、Oz 轴的转动惯量。
分析:取微元,由转动惯量的定义求积分可得 解:(1)对x 轴的转动惯量为:2022201(sin 60)32Lx M J r dm l dl ML L ===⎰⎰ (2)对y 轴的转动惯量为:20222015()(sin 30)32296Ly M L M J l dl ML L =⨯⨯+=⎰(3)对Z 轴的转动惯量为:22112()32212z M L J ML =⨯⨯⨯=3-3 电风扇开启电源后经过5s 达到额定转速,此时角速度为每秒5转,关闭电源后经过16s 风扇停止转动,已知风扇转动惯量为20.5kg m ⋅,且摩擦力矩f M 和电磁力矩M 均为常量,求电机的电磁力矩M 。
分析:f M ,M 为常量,开启电源5s 内是匀加速转动,关闭电源16s 内是匀减速转动,可得相应加速度,由转动定律求得电磁力矩M 。
解:由定轴转动定律得:1f M M J β-=,即11252520.50.5 4.12516f M J M J J N m ππβββ⨯⨯=+=+=⨯+⨯=⋅ 3-4 飞轮的质量为60kg ,直径为0.5m ,转速为1000/min r ,现要求在5s 内使其制动,求制动力F ,假定闸瓦与飞轮之间的摩擦系数0.4μ=,飞轮的质量全部分布在轮的外周上,尺寸如题图3-4所示。
大学物理学_第二版_第1-3章习题解答3

大学物理学习题答案习题一答案 习题一1.1 简要回答下列问题:(1) 位移和路程有何区别?在什么情况下二者的量值相等?在什么情况下二者的量值不相等?(2) 平均速度和平均速率有何区别?在什么情况下二者的量值相等?(3) 瞬时速度和平均速度的关系和区别是什么?瞬时速率和平均速率的关系和区别又是什么?(4) 质点的位矢方向不变,它是否一定做直线运动?质点做直线运动,其位矢的方向是否一定保持不变?(5) r ∆ 和r ∆ 有区别吗?v ∆ 和v ∆有区别吗?0dv dt= 和0d v dt = 各代表什么运动? (6) 设质点的运动方程为:()x x t =,()y y t =,在计算质点的速度和加速度时,有人先求出r =dr v dt = 及 22d ra dt=而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v = 及 a =你认为两种方法哪一种正确?两者区别何在?(7) 如果一质点的加速度与时间的关系是线性的,那么,该质点的速度和位矢与时间的关系是否也是线性的?(8) “物体做曲线运动时,速度方向一定在运动轨道的切线方向,法向分速度恒为零,因此其法向加速度也一定为零.”这种说法正确吗?(9) 任意平面曲线运动的加速度的方向总指向曲线凹进那一侧,为什么?(10) 质点沿圆周运动,且速率随时间均匀增大,n a 、t a 、a 三者的大小是否随时间改变? (11) 一个人在以恒定速度运动的火车上竖直向上抛出一石子,此石子能否落回他的手中?如果石子抛出后,火车以恒定加速度前进,结果又如何?1.2 一质点沿x 轴运动,坐标与时间的变化关系为224t t x -=,式中t x ,分别以m 、s 为单位,试计算:(1)在最初s 2内的位移、平均速度和s 2末的瞬时速度;(2)s 1末到s 3末的平均加速度;(3)s 3末的瞬时加速度。
解:(1) 最初s 2内的位移为为: (2)(0)000(/)x x x m s ∆=-=-= 最初s 2内的平均速度为: 00(/)2ave x v m s t ∆===∆ t 时刻的瞬时速度为:()44dxv t t dt==- s 2末的瞬时速度为:(2)4424/v m s =-⨯=-(2) s 1末到s 3末的平均加速度为:2(3)(1)804/22ave v v v a m s t ∆---====-∆ (3) s 3末的瞬时加速度为:2(44)4(/)dv d t a m s dt dt-===-。
大学物理第二版 许瑞珍 贾谊明 编著 课后答案 1-3章汇编

1-7 一人扔石头的最大出手速率为 v=25m/s,他能击中一个与他的手水平距离 L=50m,
高 h=13m 的目标吗?在此距离上他能击中的最大高度是多少?
解:由运动方程
x
vt
cos
,
y
vt
sin
1 2
gt 2
,消去
t
得轨迹方程
y
xtg
g 2v2
(tg 2
1) x 2
以x=05.0m ,v=25ms-1代入后得
l 2 v02t2 (H h)2
dl dt
v02t v02t 2 (H h)2
d 2l dt 2
(H h)2 v02 (H h)2 v02t 2 3/ 2
H v0
h
所以小车移动的速度 v
v02t
(H h)2 v02t 2
图 1-18 习题 1-4 图
小车移动的加速度 a
(H h)2 v02 (H h) 2 v02t 2 3/ 2
z
h 2
t
这是一条空间螺旋线。
在 O xy 平面上的投影为圆心在原点,半径为 R 的圆,螺距为 h
(2) vx
dx dt
R sin t
v
v
2 x
v
2 y
v
2 z
R2
h2 4 2
(3) ax R 2 cost a y R 2 sin t az 0
a
a
2 x
a
2 y
R 2
1-10 飞机以 100m·s-1的速度沿水平直线飞行,在离地面高为 100m时,驾驶员要把物品 投到前方某一地面目标处。问:(1)此时目标在飞机下方前多远?(2)投放物品时,驾驶 员看目标的视线和水平线成何角度?(3)物品投出 2s后,它的法向加速度和切向加速度各 为多少?
普通物理学第二版答案

普通物理学第二版答案【篇一:普通物理学第二版第七章课后习题答案】.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解答]?自?2?24?3600?7.27?10(rad/s)-7-5?公?2?365?24?3600?2.04?10(rad/s)??r?自an???r2?27.1.2 汽车发动机的转速在12s内由1200rev/min增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转?[解答]r(1)?????t?2??(3000?1200)?1/60122?1.57(rad/s)2(2)?2??02?(??)(3000?1200)2?15.7?420(转)222?2639(rad)26392?所以转数=7.1.3 某发动机飞轮在时间间隔t内的角位移为??at?bt?ct34球t时刻的角速度和角加速度.[解答]??at?bt?ct34(?:rad,t:s).23????d?dtd?dt?a?3bt?4ct?6bt?12ct27.1.4 半径为0.1m的圆盘在铅直平面内转动,在圆盘平面内建立o-xy坐标系,原点在轴上.x和y轴沿水平和铅直向上的方向.边缘上一点a当t=0时恰好在x轴上,该点的角坐标满足求(1)t=0时,(2)自t=0开始转45时,(3)转过90时,a点的速度和加速度在x和y轴上的投影.[解答]????1.2t?t(?:rad,t:s).2???1.2t?t??1.2?2t??2?t?0,??1.2,?a?r??j?0.12?j(m/s).(1) ??x?0,?y?0.12(m/s)2ax?an???2yr??0.144(m/s)2ay?r??0.2(m/s)(2)??45?时,?4,得t?0.47(s)??1.2t?t?2由???2.14(rad/s)???va???r?0.15?j?0.15?i??? ij k? 0 0?rcos? rsin?0???aa?dtdtxddtr(??sin??i??cos??j)22?1cos???sin?)?i?(??sin???cos?)?j?r[(??2??0.183?j?0.465?i(m/s)?ax??0.465(m/s),ay??0.183(m/s)22(3)当?2?90?时,由??1.2t?t???va??x?2???r???i??0.278?i(m/s)y2,得t?0.7895(s),??2.78(rad/s)??0.278(m/s),??0(m/s)ax??r???0.2(m/s)7.1.5 钢制炉门由两个各长1.5m的平行臂ab和cd支承,以角速度??10rad/s逆时针转动,求臂与铅直45时门中心g的速度和加速度.[解答]因炉门在铅直面内作平动,门中心g的速度、加速度与b或d点相同。
普通物理学第二版习题答案

普通物理学第二版习题答案普通物理学第二版习题答案普通物理学是一门研究物质运动规律的学科,它不仅是理工科学生的必修课,也是培养学生科学思维和解决问题能力的重要课程之一。
在学习普通物理学的过程中,习题是非常重要的一环,通过解习题可以帮助学生巩固知识、加深理解,并培养学生的分析和解决问题的能力。
本文将为大家提供《普通物理学第二版》习题的答案,帮助读者更好地掌握物理学知识。
第一章:运动的描述1. 一辆汽车以10 m/s的速度匀速行驶,经过5秒后,汽车的位移是多少?答案:位移等于速度乘以时间,即位移=速度×时间=10 m/s × 5 s = 50 m。
2. 一个物体以4 m/s的速度向东运动,经过2秒后,它的速度变为8 m/s,方向保持不变。
求物体的加速度。
答案:加速度等于速度的变化量除以时间,即加速度=(8 m/s - 4 m/s)/ 2 s = 2 m/s²。
第二章:牛顿定律和运动学1. 一个质量为2 kg的物体受到一个5 N的力,求物体的加速度。
答案:根据牛顿第二定律,加速度等于力除以质量,即加速度=5 N / 2 kg = 2.5 m/s²。
2. 一个质量为0.5 kg的物体受到一个10 N的力,求物体的加速度。
答案:加速度等于力除以质量,即加速度=10 N / 0.5 kg = 20 m/s²。
第三章:力和运动1. 一个物体受到一个10 N的向上的力和一个5 N的向下的力,求物体的净力和加速度。
答案:净力等于所有力的矢量和,即净力=10 N - 5 N = 5 N。
加速度等于净力除以质量,即加速度=5 N / 质量。
2. 一个物体受到一个20 N的向右的力和一个10 N的向左的力,求物体的净力和加速度。
答案:净力等于所有力的矢量和,即净力=20 N - 10 N = 10 N。
加速度等于净力除以质量,即加速度=10 N / 质量。
第四章:工作和能量1. 一个物体的质量为2 kg,高度为10 m,求物体的重力势能。
普通物理学第二版课后习题答案(全)

第一章 物理学和力学1.1国际单位制中的基本单位是那些?解答,基本量:长度、质量、时间、电流、温度、物质的量、光强度。
基本单位:米(m )、千克(kg )、时间(s )、安培(A )、温度(k )、摩尔(mol )、坎德拉(cd )。
力学中的基本量:长度、质量、时间。
力学中的基本单位:米(m )、千克(kg )、时间(s )。
1.2中学所学习的匀变速直线运动公式为,at 21t v s 20+= 各量单位为时间:s (秒),长度:m (米),若改为以h (小时)和km (公里)作为时间和长度的单位,上述公式如何?若仅时间单位改为h ,如何?若仅0v 单位改为km/h ,又如何?解答,(1)由量纲1LT v dim -=,2LT a dim -=,h/km 6.3h/km 360010h 36001/km 10s /m 33=⨯==--2223232h /km 36006.3h /km 360010)h 36001/(km 10s /m ⨯=⨯==--改为以h (小时)和km (公里)作为时间和长度的单位时,,at 36006.321t v 6.3s 20⨯⨯+=(速度、加速度仍为SI单位下的量值)验证一下:1.0h 3600s t ,4.0m/s a ,s /m 0.2v 20====利用,at 21t v s 20+=计算得:)m (2592720025920000720036004236002s 2=+=⨯⨯+⨯=利用,at 36006.321t v 6.3s 20⨯⨯+=计算得 )km (2.25927259202.71436006.321126.3s 2=+=⨯⨯⨯⨯+⨯⨯=(2). 仅时间单位改为h由量纲1LTv dim -=,2LTadim -=得h /m 3600h/m 3600h 36001/m s /m ===222222h /m 3600h /m 3600)h 36001/(m s /m ===若仅时间单位改为h ,得:,at 360021t v 3600s 220⨯+=验证一下:1.0h 3600s t ,4.0m/s a ,s /m 0.2v 20==== 利用,at 21t v s 20+=计算得:)m (2592720025920000720036004236002s 2=+=⨯⨯+⨯=利用,at 360021t v 3600s 220⨯+=计算得: )m (2592720025920000720014360021123600s 22=+=⨯⨯⨯+⨯⨯= (3). 若仅0v 单位改为km/h由量纲1LTv dim -=,得s/m 6.31h /km ,h /km 6.3)h 36001/(km 10s /m 3===-仅0v 单位改为km/h ,因长度和时间的单位不变,将km/h 换成m/s得,at 21t v 6.31s 20+=验证一下:1.0h 3600s t ,4.0m/s a ,s /m 0.2v 20====利用,at 21t v s 20+=计算得:)m (2592720025920000720036004236002s 2=+=⨯⨯+⨯=利用,at 21t v 6.31s 20+=计算得: )m (25927200259200007200360042136003600/11026.31s 23=+=⨯⨯+⨯⨯⨯=-1.3设汽车行驶时所受阻力f 与汽车的横截面积S 成正比,且与速率v 之平方成正比。
漆安慎《普通物理学教程:力学》第二版各单元课后习题思维方法分析

漆安慎《普通物理学教程:力学》第二版各单元课后习题思维方法分析《质点运动学》单元中的习题分析序号题型思维方法题目数对应习题题号1 已知运动学方程,求轨迹方程或位移比较法、等效法3 [2.1.1][2.1.2] [2.1.3] 2 已知初末位置和时间,求瞬时速度或瞬时速率的近似值比较法2 [2.2.1][2.2.2] 3 已知初末速度和时间,求平均加速度比较法1 [2.2.5] 4 已知质点直线运动的位移时间图像t x -图,求质点的速度图像法1 [2.3.1] 5 已知运动学方程,求速度和加速度比较法、微元法、极限法2 [2.2.6][2.3.2] 6 已知速度)(t v 或)(x v ,求加速度比较法、微元法、极限法2 [2.3.3][2.3.4] 7 已知两质点的位置关系,求两质点的加速度关系比较法、微元法、极限法1 [2.3.5] 8 坐标原点或计时起点的改变对运动学方程的影响比较法、等效法1 [2.3.6] 9 已知速度,求运动学方程或位移叠加法2 [2.4.2][2.5.3] 10 由加速度,求速度、运动学方程、位移叠加法、比较法4 [2.4.1][2.4.3][2.4.4] [2.5.1] 11 分运动与合运动问题:已知某一分运动,求另一分运动或合运动分析法、叠加法、演绎法2 [2.5.4][2.5.5] 12 相遇问题:已知两质点的加速度、初速度及开始时刻的位置关系,求何时或何地相遇叠加法、比较法3 [2.4.5][2.4.7] [2.5.2] 13 已知自然坐标系下的运动学方程(或切向速度),求切向速度(或切向加速度或合加速度)类比法、微元法、极限法、3 [2.6.1][2.6.2] [2.6.3] 叠加法14 相对运动问题等效法、叠加法6 [2.4.8][2.8.1][2.8.2] [2.8.3] [2.8.4][2.8.5] 《动量×牛顿运动定律×动量守恒定律》单元中的习题分析序号 题型思维方法 题目数 对应习题题号 1 已知运动学方程,求质点的受力情况(大小和方向)微元法、比较法、极限法 2 [3.4.1][3.4.2] 2 惯性系中牛顿运动定律的运用:已知运动情况(位置、速度或加速度间的关系),求力(或加速度)或相关物理量建模法、隔离法、演绎法、微元法、极限法、图示法 13 [3.4.3][3.4.4][3.4.5] [3.4.6] [3.4.7][3.4.8] [3.4.11][3.4.14] [3.4.15][3.4.16] [3.4.20][3.4.21] [3.4.22] 3 惯性系中牛顿运动定律的运用:已知受力情况(包括连续的变力)及初始条件(初速度或初位置(可根据坐标系的选择而定)),求运动情况(位置、位移、速度或角速度等)建模法、隔离法、微元法、演绎法、叠加法、极限法、图示法 5 [3.4.9][3.4.10] [3.4.12][3.4.13] [3.4.18] 4 非惯性系(直线加速系)中牛顿运动定律的运用:已知运动情况,求力或加速度建模法、隔离法、演绎法、等效法、叠加法、图示法 3 [3.4.5][3.5.1] [3.5.2] 5 非惯性系(直线加速系)中牛顿运动定律的运用:已知受力情况(包括惯性力)及初始条件,求运动情况(相对于非惯性系)建模法、隔离法、演绎法、等效法、叠加法、图示法 1 [3.5.3] 6 非惯性系(转动参考系)中牛顿运动定律的运用:已知受力情况(包括离心惯性力或科里奥利力)及初始条件,求运动情况建模法、隔离法、演绎法、等效法、叠加法、图示法 3 [3.5.4][3.5.5] [3.5.6] 7 已知受力情况(包括变力)(t F)及时间,求冲微元法、极限1 [3.6.1] 量 法、建模法、演绎法、叠加法8 已知质点的运动学方程)(t r r=,求质点动量 微元法、比较法、极限法、演绎法1 [3.6.2] 9 质点动量定理的应用等效法、演绎法3 [3.6.3][3.6.4] [3.6.5] 10 质点系动量定理的应用:已知各质点动量(或速度)变化及时间,求质点系所受合外力 建模法、演绎法、叠加法、等效法 2 [3.7.1][3.7.4] 11 质点系动量定理的应用:已知合外力(合加速度)及某些质点的速度(或加速度、位移)情况,求另外质点的速度(或加速度、位移)情况 建模法、演绎法、叠加法、等效法 4 [3.7.2][3.7.3][3.7.5] [3.7.6] 12 质心运动定理的应用:已知各质点动量(或速度)变化及时间,求质点系所受合外力 建模法、演绎法1 [3.7.1] 13 质心运动定理的应用:已知合外力(合加速度)及某些质点的速度(或加速度、位移)情况,求另外质点的速度(或加速度、位移)情况建模法、演绎法3 [3.7.2][3.7.3] [3.7.6] 14 在质心参考系中,求质点系质心的动量建模法、演绎法1 [3.7.7] 15 质点系动量守恒定律的应用建模法、演绎法、图示法3 [3.8.1][3.8.2] [3.8.3] 《动能和势能》单元中的习题分析序号 题型思维方法 习题数对应习题题号1 功的定义的应用:已知力或力的变化规律,求力(变力)的功微元法、极限法、建模法、演绎法、叠加3 [4.2.2][4.2.3] [4.2.4] 法2 质点动能定理与功的定义的应用:已知过程初末位置及过程中各个(变)力的(变化)情况及初速度(或末速度),求质点的末速度(或初速度)微元法、极限法、建模法、叠加法、演绎法3 [4.3.1][4.3.2] [4.3.4] 3 质点动能定理与功的定义的应用:已知过程的初末速度及过程中各个(变)力的(变化)情况及初位置,求质点的末位置微元法、极限法、建模法、叠加法、演绎法1 [4.3.3] 4 质点系动能定理的应用建模法、隔离法、演绎法、叠加法1 [4.3.7] 5 已知保守力做功,求对应势能的变化微元法、极限法、建模法、演绎法1 [4.4.1] 6 质点系机械能守恒定律的应用:由质点系机械能守恒,已知势能变化,求动能变化(或动能) 建模法、隔离法、演绎法3 [4.5.1][4.5.2] [4.5.3] 7 动量守恒定律、机械能守恒定律(或动能定理)与恢复系数在对心碰撞问题中的应用建模法、隔离法、分析法、演绎法、综合法9 [4.6.2][4.6.3][4.6.4] [4.6.5] [4.6.6][4.6.7] [4.6.8][4.6.9] [4.6.10] 8 动量守恒定律、机械能守恒定律(或动能定理)与恢复系数在非对心碰撞问题中的应用建模法、隔离法、分析法、演绎法、综合法2 [4.7.1][4.7.2] 《角动量×关于对称性》单元中的习题分析序号题型思维方法习题数对应习题题号1 质点对参考点的角动量守恒定律的应用:已知受力情况(主要是质点合力方向通过参考点)及建模法、演绎4 [5.1.1][5.1.7][5.1.9] 质点分别经过两点时相对于质点的位置矢量的大小及与速度的夹角,由质点经过其中一点的速度(速率)求经过另一点时的速度(速率)法、图示法[5.2.3] 2 已知质点的运动学方程,求质点所受的对某点(如原点)的力矩微元法、极限法、演绎法1 [5.1.2] 3 已知质点的受力情况(或给出)(tF)及初始条件(初位置、初速度),求某时刻质点所受的对某点(如原点)的力矩建模法、微元法、极限法、叠加法、演绎法2 [5.1.3][5.2.1] 4 已知质点对某点的运动情况(或给运动学方程),求质点对某点的角动量(或证明角动量守恒) 微元法、极限法、演绎法4 [5.1.4][5.1.5][5.1.8] [5.2.1] 5 已知质点的受力情况)(t F 及初始条件,求某时刻质点对某点的角动量微元法、极限法、叠加法、演绎法1 [5.1.6] 6 质点对轴的角动量守恒定律的应用建模法、演绎法、图示法1 [5.1.10] 7 质点系对参考点的角动量守恒定律的应用建模法、演绎法、分析法、综合法1 [5.2.2] 《万有引力定律》单元中的习题分析序号题型思维方法习题数对应习题题号1 万有引力定律和牛顿第二定律的应用建模法、演绎法4 [6.2.1][6.2.2][6.2.4] [6.2.5] 2 万有引力定律在连续物体内部的应用假设法、建模法、微元法、演绎法1 [6.2.3] 3 万有引力定律在两物体(或之一)不能看成质点微元法、极限法、演绎法、2 [6.2.6][6.2.7] 情况下的应用叠加法4 万有引力定律、牛顿第二定律与机械能守恒定律的应用建模法、演绎法、综合法2 [6.3.1][6.3.2] 《刚体力学》单元中的习题分析序号题型思维方法习题数对应习题题号1 已知刚体转动的运动学方程(角位移、角坐标))(tq,求角速度(或线速度)或角加速度(或线加速度)微元法、比较法、极限法2 [7.1.3][7.1.4] 2 已知刚体的定轴转动情况(转速或角速度)及整体平动情况,求刚体上某点相对于基本参考系(如地面)的线速度比较法、叠加法2 [7.1.6][7.1.7] 3 已知刚体的质量分布(密度分布),求刚体的质心位置微元法、极限法、建模法、演绎法、叠加法、对称法2 [7.2.1][7.2.2] 4 质心运动定理在刚体运动中的应用演绎法、图示法1 [7.2.3] 5 利用转动惯量定义或平行轴定理求刚体对轴的转动惯量微元法、极限法、演绎法、叠加法、对称法4 [7.3.1][7.3.2][7.3.3] [7.3.4] 6 刚体定轴转动定理与牛顿第二定律(或质心运动定理)在刚体运动中的应用建模法、隔离法、综合法、图示法5 [7.3.5][7.3.6][7.3.7] [7.3.8] [7.3.9] 7 质点系角动量守恒定律与机械能守恒定律在刚体运动中的应用建模法、演绎法、综合法4 [7.4.1][7.4.2][7.4.3] [7.5.1] 8 质心运动定理、转动定理、机械能守恒定律在建模法、隔离法、假设法、6 [7.5.2][7.5.3][7.5.4] 刚体平面运动中的应用演绎法、综合法[7.5.5] [7.5.6][7.5.7] 9 力的平衡方程、力矩平衡方程在刚体平衡问题中的应用建模法、演绎法、综合法3 [7.6.1][7.6.2] [7.6.3] 《弹性体的应力和应变》单元中的习题分析序号题型思维方法习题数对应习题题号1 已知弹性体轴向所受外力及横截面积,求弹性体两截面间的应力隔离法、整体法、演绎法、假设法1 [8.1.1] 2 已知弹性体内的应力最大值,求弹性体所能承受的最大外力建模法、隔离法、演绎法2 [8.1.2][8.1.3] 3 线应变的胡克定律及牛顿运动定律的应用建模法、隔离法、假设法、演绎法、综合法3 [8.1.4][8.1.5] [8.1.6] 4 剪切形变的胡克定律的应用演绎法2 [8.2.1][8.3.1] 5 由压缩拉伸弹性势能密度公式求弯曲形变势能微元法、极限法、建模法、演绎法、叠加法1 [8.3.3] 《振动》单元中的习题分析序号题型思维方法习题数对应习题题号1 通过建立系统动力学方程,由动力学特征判断假设法、演绎1 [9.2.1] 系统是否做简谐运动法2 通过建立简谐运动的动力学方程求系统(如弹簧振子)的固有频率(周期)建模法、隔离法、演绎法5 [9.2.1][9.2.2][9.2.3] [9.2.5] [9.3.1] 3 非惯性系中,通过建立简谐运动的动力学方程求系统(如单摆)的固有周期(频率)建模法、隔离法、等效法、演绎法、极限法1 [9.2.4] 4 已知系统做简谐运动及其初始条件,求运动学方程或相关物理量演绎法、微元法、比较法、极限法、综合法2 [9.2.6][9.2.7] 5 计时起点改变对简谐振动运动学方程的影响比较法、等效法1 [9.2.8] 6 求对称物体绕某点做微小摆动的周期建模法、演绎法、对称法2 [9.2.10][9.2.11] 7 已知物体与振动系统(如单摆或弹簧振子)发生碰撞,求碰撞后振动系统的运动学方程建模法、隔离法、分析法、演绎法、极限法、综合法4 [9.2.12][9.2.13] [9.2.14][9.2.15] 8 已知振动系统的参数(或运动学方程),求系统的总能量(或动能)建模法、演绎法2 [9.3.1][9.3.2] 《波动和声》单元中的习题分析序号题型思维方法习题数对应习题题号1 由已知条件,求波方程比较法、演绎法4 [10.2.2][10.2.3] [10.2.4][10.2.10] 2 已知波方程,求波的频率、振幅、速度、波长比较法、演绎法1 [10.2.5] 3 计时起点改变对波方程形式的影响比较法、等效法1 [10.2.6] 4 由已知条件求固体中传播横波和纵波的波速建模法、演绎法1 [10.3.1] 5 已知纵波在流体中的波速,求流体的体积模量演绎法、比较法1 [10.3.2] 6 已知两列波,求波叠加最强(或弱)的位置或叠加后的波行为演绎法、比较法、叠加法2 [10.5.2][10.5.3] 7 已知入射波方程,求反射波方程比较法、演绎法3 [10.5.4][10.5.5] [10.5.6] 8 波的干涉的应用演绎法、比较法1 [10.5.9] 9 驻波在弦振动中的应用演绎法、比较法2 [10.5.10][10.5.11] 10 开普勒效应的应用比较法、演绎法4 [10.6.1][10.6.2] [10.6.3][10.6.4] 《流体力学》单元中的习题分析序号题型思维方法习题数对应习题题号1 求静止流体内某点(处)的压强演绎法、叠加法4 [11.2.1][11.2.2] [11.2.4][11.2.5] 2 求静止流体内压强(或压力)分布微元法、极限法、建模法、演绎法、叠加法4 [11.2.3][11.2.7] [11.2.8][11.2.10] 3 求相对于非惯性系静止的流体的压强分布微元法、极限法、建模法、等效法、演绎1 [11.2.6] 法、叠加法4 伯努利方程与连续性原理的应用建模法、演绎法、综合法3 [11.4.3][11.4.4] [11.4.5] 5 动量定理在运动流体对挡壁的压力求解中的应用微元法、演绎法1 [11.5.1] 。
普通物理学第二版课后习题答案(全)

�得算计 用利 2 , 2 ta � t 0 v � s 1 h0.1 � s0063 � t , 2s/m0.4 � a ,s / m0.2 � 0 v
2 6.3 , 2 ta � t 0 v �s 1 1
:下一证验
s/m 成换 h/mk 将�变不位单的间时和度长因�h/mk 为改位单 0 v 仅 6.3 s/m � h / mk 1 0063 (/ m k 3 � 0 1 � s / m ,h / mk6.3 � ) h 1 得 得,
2
。误无果成此断判纲量据根。1 为纲量的边两子式出看以可�答解 �否误有果成此断 判纲量据根步初否能你 �1 纲量即数纯为 1 和 、�、 0、 1 01 � 量 质 的 体
9 2� 3�
物 些 某 示 表 p m和2 m、1m、M 中 其 1 1 m 2m m ] ) ( 01 � 1[ 2 ) ( 92 �01 � � M m 3 1m 3 �
1�
TL � v mid
纲量由
h/mk 为改位单 0 v 仅若 .�3� ) m(00272952 � 00002952 � 0027 � 2 1 � 4 � 20063 � � 1 � 2 � 0063 � s 2 1 �得算计 用利 2 , ta 0063 � � t 0 v0063 � s 2 2 1 ) m(00272952 � 00002952 � 0027 � 2 0063 � 4 � � 0063 � 2 � s 1
t2 �
程方迹轨得 t 去消 , 3 � t 2 � y , t 4 � x .① � 解 2
。移位的点质 1=t 至 1-=t 自求.�2� �迹轨的
点质求
.�1� � k 2 � j i e � r 为程方学动运点质 2.1.2 ˆ ˆ t2 e � ˆ t2 � �
