八枚硬币的判定树
减治法

子问题 的规模是n/2 子问题的解
原问题的解
图5.1 减治法的典型情况(减半技术)
对于给定的整数a和非负整数n,计算an的值。
利用减治法,如果n=1,可以简单地返回a的值,如果n是偶数并且n>1,可 以把该问题的规模减半,即计算an/2的值,而且规模为n的解an和规模减半 的解an/2之间具有明显的对应关系:an=(an/2)2,如果n是奇数并且n>1,可 以先用偶指数的规则计算a(n-1),再把结果乘以a。所以,应用减治技术得到 如下计算方法:
排序问题中的减治法
堆排序
选择问题
堆排序
例
28 25 36 18 32 28 36 25 18 16 32 25 16 36 25 18 16 36 28 32
28
18 16
32
堆排序是利用堆(假设利用大根堆)的特性进 行排序的方法,其基本思想是:首先将待排序 的记录序列构造成一个堆,此时,选出了堆中 所有记录的最大者即堆顶记录,然后将它从堆 中移走(通常将堆顶记录和堆中最后一个记录 交换),并将剩余的记录再调整成堆,这样又 找出了次大的记录,以此类推,直到堆中只有 一个记录为止。
n 1 n 1
查找问题中的减治法
折半查找
二叉查找树
折半查找
在有序表{ 7, 14, 18, 21, 23, 29, 31, 35, 38, 42, 46, 49, 52 }中查找值为14的 记录的过程如图所示。
0 1
7
2
14
3
18
4
21
5
23
6
29
7
31
8
35
9
38
10
42
离散数学Data_G_11-2

《离散数学》
page: 29
11.5 树 11.5.4 哈夫曼编码与哈夫曼树 最优二叉树(哈夫曼树)的构造方法(N-S图):
各个结点独立成树(森林) 当森林中树的数目大于1 找两棵权值最小的树 合并这两棵权值最小的树(权为二者之和)
2013年11月16日星期六
《离散数学》
2013年11月16日星期六
《离散数学》
page: 25
11.5 树 11.5.4 哈夫曼编码与哈夫曼树 前缀—字符串中前边的一部分。 如,字符串s1s2s3…sn是长度为n的字符串,则其长度 为1,2,3..n-1的前缀分别是:? s1 s 1s 2 s 1s 2s 3 s1s2s3…sn-1
前缀码—彼此不互为前缀的一组编码。 如:{0,10,110,1111},{1,01,001,000} 和 {1,,11,101,001,0011},{xi,xia,xiang} 前缀码 非前缀码
证明模式: 1)⇒ 2)⇒ 3)⇒ 4) ⇒ 5)⇒ 6)⇒ 1)
2013年11月16日星期六
《离散数学》
page: 1
11.5 树 11.5.1 无向树 叶结点(叶子)--无向树中度为1的结点(顶点)。 (n,m)树—具有个n结点,m条边的树。 结论1:非平凡无向树中至少有两个叶结点。 证明:设非平凡无向树为(n,m)树,其中m=n-1
《离散数学》
page: 10
11.5 树 11.5.3 二叉树 二叉树的主要性质: 性质1:二叉树的第i层上最多可有2i-1个结点。
层:层结点数 1: 21-1=1 2: 22-1=2 B C D F A E H
3: 23-1=4
4: 24-1=8 …… i: 2i-1
数据结构第七章 树和森林

7.5 树的应用
➢判定树
在实际应用中,树可用于判定问题的描述和解决。
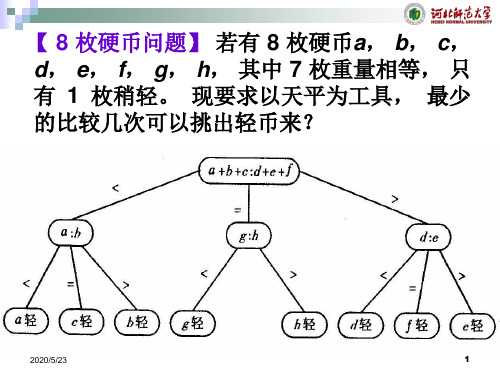
•设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,其中有一枚且 仅有一枚硬币是伪造的,假硬币的重量与真硬币的重量不同,可能轻, 也可能重。现要求以天平为工具,用最少的比较次数挑选出假硬币, 并同时确定这枚硬币的重量比其它真硬币是轻还是重。
的第i棵子树。 ⑺Delete(t,x,i)在树t中删除结点x的第i棵子树。 ⑻Tranverse(t)是树的遍历操作,即按某种方式访问树t中的每个
结点,且使每个结点只被访问一次。
7.2.2 树的存储结构
顺序存储结构 链式存储结构 不管哪一种存储方式,都要求不但能存储结点本身的数据 信息,还要能够唯一的反映树中各结点之间的逻辑关系。 1.双亲表示法 2.孩子表示法 3.双亲孩子表示法 4.孩子兄弟表示法
21
将二叉树还原为树示意图
A BCD
EF
A
B
C
E
D
F
A
B
C
E
D
F
22
练习:将下图所示二叉树转化为树
1 2
4
5
3
6
2 4
1 53
6
23
7.3.2 森林转换为二叉树
由森林的概念可知,森林是若干棵树的集合,只要将森林中各棵树 的根视为兄弟,森林同样可以用二叉树表示。 森林转换为二叉树的方法如下:
⑴将森林中的每棵树转换成相应的二叉树。 ⑵第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树 的根结点作为前一棵二叉树根结点的右孩子,当所有二叉树连起来 后,此时所得到的二叉树就是由森林转换得到的二叉树。
相交的集合T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是 一棵树。树T1,T2,…,Tm称为这个根结点的子树。 • 可以看出,在树的定义中用了递归概念,即用树来定义树。因此, 树结构的算法类同于二叉树结构的算法,也可以使用递归方法。
第二章 生成树

第二章树教学安排的说明章节题目:§2.1树的特性;§2.2割边与割点,§2.3生成树学时分配:共2课时本章教学目的与要求:会正确表述关于树的一些基本概念(如树、生成树、割边与割点),会用避圈法和破圈法找生成树,会用树的方法描述一些简单的实际问题.课 堂 教 学 方 案课程名称:§2.1树的特性;§2.2割边与割点;§2.3 生成树授课时数:2学时授课类型:理论课教学方法与手段:讲授法教学目的与要求:会正确表述关于树的一些基本概念(如树、生成树、割边与割点),会用避圈法和破圈法找生成树,会用树的方法描述一些简单的实际问题. 教学重点、难点:(1) 理解树的概念以及树的等价命题;(2) 掌握割边与割点的概念;(3) 理解生成树的定义;(4) 掌握找生成树的两种方法——避圈法和破圈法。
教学内容:树是图论中的一个重要概念。
树是一种极为简单而又非常重要的特殊图,它在计算机科学以及其它许多领域都有广泛的应用。
在1847年克希霍夫就用树的理论来研究电网络,1857年凯莱在计算有机化学中222n C H 的同分异构物数目时也用到了树的理论。
各类网络的主干网通常都是树的结构。
本节介绍树的基本知识,其中谈到的图都假定是简单图。
2.1 树的特性定义2.1.1 连通无圈的无向图称为无向树,简称为树(Undirected tree )。
记作T ,树中的悬挂点(或称T 中度数为1的顶点)又称为树叶(leave )(或叶顶点),其它顶点称为树枝(Branch Point 或内点(Inner Point))。
诸连通分支均为树的图称为森林(forest ),树是森林。
例1 图1中(a ),(b )为树,(c )为森林。
图1由于树无环也无重边(否则它有圈),因此树必定是简单图。
树还有等价命题:设T 是一个无向(,)n m 图,则以下关于T 的命题是等价的。
(1) T 是树;(2)T 无圈且1m n =-;(3) T 连通且1m n =-;(4)T 无圈,但增加任一新边,得到且仅得到一个圈。
算法实验报告(8枚硬币)

实验名称减治法在组合问题中的应用——8枚硬币问题实验室实验目的或要求1. 实验题目在8枚外观相同的硬币中,有一枚是假币,并且已知假币与真币的重量不同,但不知道假币与真币相比较轻还是较重。
可以通过一架天平来任意比较两组硬币,设计一个高效的算法来检测这枚假币。
2.实验目的1)深刻理解并掌握减治法的设计思想并理解它与分治法的区别;2)提高应用减治法设计算法的技能。
3)理解这样一个观点:建立正角的模型对于问题的求解是非常重要的。
3. 实验要求1)设计减治算法实现8枚硬币问题;2)设计实验程序,考察用减治技术设计的算法是否高效;3)扩展算法,使之能处理n枚硬币中有一枚假币的问题。
4. 实现提示假设用一个数组B[n]表示硬币,元素B[i]中存放第i枚硬币的重量,其中n-1个元素的值都是相同的,只有一个元素与其他元素值不同,则当n=8时即代表8枚硬币问题。
由于8枚硬币问题限制只允许使用天平比较轻重,所以,算法中只能出现元素相加和比较的语句实验原理(算法基本思想)利用三分法if (p == q){}else if (q - p == 1){if (p > 0){if (arr[p] == arr[0])coin(arr, n, p + 1, q);elsecoin(arr, n, p, q - 1);}else if (q < n - 1){if (arr[p] == arr[n - 1])coin(arr, n, p + 1, q);elsecoin(arr, n, p, q - 1);}}else if (p < q){int temp = (q - p + 1) / 3;int sum1 = 0, sum2 = 0;for(int i = 0; i < temp; i++){sum1 += arr[p + i];sum2 += arr[q - i];}if (sum1 == sum2)//在中间{coin(arr, n, p + temp, q - temp);}else//在两边,不在中间{if (sum1 == arr[p + temp] * temp)//左边的和中间的相等,在右边{coin(arr, n, q - temp + 1, q);}else{coin(arr, n, p, p + temp - 1);}程序代码//******************************************************//* *n枚硬币问题* *//* *通用减治算法* * //* *算法分析与设计* *//******************************************************#include <stdio.h>#include <iostream>#include <stdlib.h>using namespace std;void coin(int arr[], int n, int p, int q){if (n == 2){cout<<"无法判断\n";return;}if (p == q){cout<<"假币的序号为:"<<p+1<<endl;cout<<"假币的重量为:"<<arr[p]<<endl;}else if (q - p == 1){if (p > 0){if (arr[p] == arr[0])coin(arr, n, p + 1, q);elsecoin(arr, n, p, q - 1);}else if (q < n - 1){if (arr[p] == arr[n - 1])coin(arr, n, p + 1, q);elsecoin(arr, n, p, q - 1);}}else if (p < q){int temp = (q - p + 1) / 3;int sum1 = 0, sum2 = 0;for(int i = 0; i < temp; i++){sum1 += arr[p + i];sum2 += arr[q - i];}if (sum1 == sum2)//在中间{coin(arr, n, p + temp, q - temp);}else//在两边,不在中间{if (sum1 == arr[p + temp] * temp)//左边的和中间的相等,在右边{coin(arr, n, q - temp + 1, q);}else{coin(arr, n, p, p + temp - 1);}}}}void ShowCoin(){while(1){int i,n;cout<<"请输入几枚硬币:"<<endl;cin>>n;if(n==0) break;int *arr=new int[n];cout<<"请输入各硬币的重量:"<<endl;for(i=0;i<n;i++)cin>>arr[i];coin(arr, n, 0, n - 1);}}(写不完时,可另加附页。
32.二叉树与最优二叉树

0 1 2 3 4 5 30% 20% 15% 10% 10% 5% 6 5% 7 5%
求传输它们的最佳前缀 码。
参考答案: 0 01 1 11 2 3 4 5 6 7 1001
001 101 0000 0001 1000
教师:田检
30
教师:田检
60 20 10 15 10 15 0 01 10 5 0 00 1 5 0 00 00 5 0 00 01 0 10 10 0 11 0 10 0 11 1 20 10
40 20
25
35
10 1 11
1 10
图 9.2.11
w0=20; w1=15;w2=10;w3=10; w4=10; w5=5; w6=10; w7=5; w8=10;w9=5。
教师:田检
26
解 (1)令i对应树叶权为wi,wi=100i,则 w0=20;w1=15;
w2=10;w3=10; w4=10;w5=5; w6=10;w7=5; w8=10;w9=5。 构造一棵带权5,5,5,10,10,10,10,10,15, 20的最优二叉树。
教师:田检
27
1 00 0 —10 1 —01 0 2 —11 1 3 —11 0 4 —01 11 5 —00 01 6 —01 10 7 —00 00 1 8 —00 1 9 —00 00 0
31
16 16
10 10
最优二叉树不唯一!
6
6
4
6 3
1
3
2
4
6
3
1 2
3
教师:田检
18
练习 1:求带权为 2,4,7,8,10,12的最优二叉树 43
ACM超级经典算法大集合

超级经典算法大集合:老掉牙河内塔费式数列巴斯卡三角形三色棋老鼠走迷官(一)老鼠走迷官(二)骑士走棋盘八个皇后八枚银币生命游戏字串核对双色、三色河内塔背包问题(KnapsackProblem)数、运算蒙地卡罗法求PI Eratosthenes筛选求质数超长整数运算(大数运算)长PI最大公因数、最小公倍数、因式分解完美数阿姆斯壮数最大访客数中序式转后序式(前序式)后序式的运算关于赌博洗扑克牌(乱数排列)Craps赌博游戏约瑟夫问题(JosephusProblem)集合问题排列组合格雷码(GrayCode)产生可能的集合m元素集合的n个元素子集数字拆解排序得分排行选择、插入、气泡排序Shell 排序法- 改良的插入排序Shaker 排序法-改良的气泡排序Heap 排序法- 改良的选择排序快速排序法(一)快速排序法(二)快速排序法(三)合并排序法基数排序法搜寻循序搜寻法(使用卫兵)二分搜寻法(搜寻原则的代表)插补搜寻法费氏搜寻法矩阵稀疏矩阵多维矩阵转一维矩阵上三角、下三角、对称矩阵奇数魔方阵4N 魔方阵2(2N+1) 魔方阵1.河内之塔说明河内之塔(Towers of Hanoi)是法国人M.Claus(Lucas)于1883年从泰国带至法国的,河内为越战时北越的首都,即现在的胡志明市;1883年法国数学家Edouard Lucas曾提及这个故事,据说创世纪时Benares有一座波罗教塔,是由三支钻石棒(Pag)所支撑,开始时神在第一根棒上放置64个由上至下依由小至大排列的金盘(Disc),并命令僧侣将所有的金盘从第一根石棒移至第三根石棒,且搬运过程中遵守大盘子在小盘子之下的原则,若每日仅搬一个盘子,则当盘子全数搬运完毕之时,此塔将毁损,而也就是世界末日来临之时。
解法如果柱子标为ABC,要由A搬至C,在只有一个盘子时,就将它直接搬至C,当有两个盘子,就将B当作辅助柱。
如果盘数超过2个,将第三个以下的盘子遮起来,就很简单了,每次处理两个盘子,也就是:A->B、A ->C、B->C这三个步骤,而被遮住的部份,其实就是进入程式的递回处理。
假币问题与三神问题的决策树

假币问题与三神问题的决策树1. 引言假币问题和三神问题是经典的决策问题,涉及到如何在一系列选择中作出最佳决策。
在本文中,我们将探讨这两个问题,并通过决策树的方式解决它们。
2. 假币问题假币问题是一个关于如何找出一枚假币的问题。
假设有一堆硬币,其中有一枚是假币,假币的重量要么轻一些,要么重一些。
通过称重,我们需要确定哪一枚硬币是假币,以及它是轻还是重。
2.1 问题分析假币问题可以通过构建一个决策树来解决。
首先,我们可以将硬币分成几个相等的组,然后用天平来比较它们的重量。
2.2 决策树设计根据硬币的数量,我们可以设计如下的决策树:1.将硬币平均分成三组。
–如果天平是平衡的,那么假币一定在剩下的一组中。
•将这组硬币平均分成两组,重复步骤1。
–如果天平不平衡,那么假币一定在较轻或较重的那一组中。
•将这一组硬币平均分成两组,重复步骤1。
通过不断地递归,我们最终可以找到假币以及它是轻还是重。
3. 三神问题三神问题是一个关于如何识别出撒谎的神的问题。
假设有三个神,其中一个总是说真话,另一个总是说假话,第三个则随机说真话或假话。
你可以提问一个问题,然后根据神的回答来判断哪一个是撒谎的神。
3.1 问题分析三神问题可以通过构建一个决策树来解决。
我们可以设计一系列的问题,通过分析神的回答来确定哪一个是撒谎的神。
3.2 决策树设计根据问题的设计和神的回答,我们可以设计如下的决策树:1.提问一个问题,例如:“天气是晴天吗?”–如果三个神的回答都一样,那么他们中的两个是撒谎的神。
–如果两个神的回答一样,而第三个神的回答不同,那么说不同话的神是撒谎的神。
–如果三个神的回答都不一样,那么说真话的神是撒谎的神。
通过逐步提问,我们可以确定哪一个是撒谎的神。
4. 总结假币问题和三神问题是具有挑战性的决策问题。
通过构建决策树,我们可以逐步缩小选择范围,最终找到最佳的解决方案。
通过本文的讨论,希望读者对决策树这种解决问题的工具有更深入的了解,并能将其应用于实际生活中的决策问题中。
第九章 树
例题 判断下列哪些图是树?
v1 v2 v3 v2 v1 v3 v1 v2 v4 v3
v4
v5
v4
v5
v5
(a)
(b)
(c)
解: 图(a)是树, 因为它连通又不包含回路。图(b), (c)不 是树, 因为图(b)虽连通但有回路, 图(c)虽无回路但不连 通。 在图(a)中, v1、 v4、 v5为均为叶, v2、 v3均为分 支节点。
(1)
(2)
(3)
余树可能不连通,也可能含回路。
2018/2/4
11
定理9.3 任何连通图G至少存在一棵生成树. 推论1 设n阶无向连通图G有m条边,则 m≥n-1. 推论2 设n阶无向连通图G有m条边,T是G的生 成树,T'是T的余树,则T'中有m-n+1条边.
(1)
(2)
(3)
m=8,n=5
2018/2/4 12
T有5个树枝a, b, c, d, e, 因而有5个 基本割集:Sa={a,g,f } ; Sb={b,g,h } ; Sc={c,f,h } ; Sd={d,i,h } ; Se={e,f,i}.
基本割集系统为{Sa,Sb,Sc, Sd,Se}.
2018/2/4
a b
c d
e
g
h
i
16
定义9.5 设无向连通带权图G=<V,E,W>,T是 G的一棵生成树.T各边带权之和称为T的权,记 作W(T).G的所有生成树中带权最小的生成树 称为最小生成树. 问题的提出: 要在 n 个城市间建立通信联络 网。顶点:表示城市,权:城市间通信线路的 花费代价。希望此通信网花费代价最小。
d
20
b
减治法

第5章减治法(Decrease and Conquer)减治法的基本思想规模为n的原问题的解与较小规模(通常是n/2)的子问题的解之间具有关系:(1)原问题的解只存在于其中一个较小规模的子问题中;(2)原问题的解与其中一个较小规模的解之间存在某种对应关系。
由于原问题的解与较小规模的子问题的解之间存在这种关系,所以,只需求解其中一个较小规模的子问题就可以得到原问题的解。
2减治法的基本思想一旦建立了这种关系,就可以从顶至下(递归),也可以从底至上(非递归)的来运用Example, n!A top down (recursive) solutionA bottom up (iterative) solution3减治法的类型减治法有三种变种:1)减去一个常量2)减去一个常数因子3)减去的规模是可变的gcd(m, n)4减(一)治技术a problem of size nsubproblemof size n-1a solution to thesubprobleme.g., n!a solution tothe original problem5减(半) 治技术a problem of size nsubproblemof size n/2a solution to thesubprobleme.g., Binary searcha solution tothe original problem67典型的分治法subproblem 2 of size n /2subproblem 1 of size n /2a solution to subproblem 1 a solution to the original problema solution to subproblem 2a problem of size ne.g., mergesort减治与分治的区别考虑以下指数问题: 计算a n减一法Bottom-up: iterative (brute Force) Top-down:recursive分治法:减常因子法:a n= a*a*a*a*...*aa n= a n-1* a if n > 1= a if n = 1a n= a ⎣n/2 ⎦* a ⎡n/2⎤if n > 1= a if n = 1a n = (a n/2 ) 2if n is even and positive= (a(n-1)/2 ) 2 * a if n is odd and > 1 = a if n = 1O (log2n) O (n log2n)89111)2/(0)(>=⎩⎨⎧+=n n n T n T 所以,通常来说,应用减治法处理问题的效率是很高的,一般是O (log 2n)数量级。
分治算法——精选推荐

分治过程
比较过程
分析
从图例可以看出,当有8个金块的时候,方法1需 要比较15~16次,方法2只需要比较10次,那么形成 比较次数差异的根本原因在哪里? 其原因在于方法2对金块实行了分组比较。 对于N枚金块,我们可以推出比较次数的公式: 假设n是2的次幂,c(n)为所需要的比较次数。 方法1: c(n)=2n-1 方法2:c(n) = 2c(n/2 ) + 2。 由c(2)=1, 使用迭代方法可知c(n) = 3n/2 - 2。在本 例中,使用方法2比方法1少用了2 5%的比较次
2. 左邻括号的运算符为“/”,则括号必须保留,即 … /(s1 op s2)… 形式。
3. 左邻括号的预算符为“*”或“-”。而op为“+”或“-”,则保留括 号,即…*(s1+s2)… 或 … -(s1+s2)… 或 … *(s1s2)… 或 … -(s1-s2)…
4. 右邻括号的运算符为“*”或“/”,而op为“+”或“-”,原式中的 op运算必须优先进行,因此括号不去除,即(s1+s2)* …
方法1
假设袋中有n 个金块。可以用函数M a x通过n-1次
比较找到最重的金块。找到最重的金块后,可以从 余下的n-1个金块中用类似的方法通过n-2次比较找 出最轻的金块。这样,比较的总次数为2n-3。
算法如下:
max:=a[1];min:=a[1]; for i:=2 to n do {2n-2次比较} begin
样例 输入:1 -5 -4 20 输出:-2.00 2.00 5.00
分析
如果精确到小数点后两位,可用简单的枚举法:将x从100.00 到100.00(步长0.01) 逐一枚举,得到20000 个 f(x),取其值与0最接近的三个f(x),对应的x即为答 案。而题目已改成精度为小数点后4位,枚举算法时间 复杂度将达不到要求。
八枚硬币问题

题目:八枚硬币问题姓名:龚晓峰学号:3110100687课程名称:应用运筹学年级与专业:2011级理科试验班类所在学院:求是学院丹青学园八枚硬币问题一.原题设有八枚硬币,其中有一枚硬币是假币,且知道假币比真币轻。
那么通过一个天平找出假币所需的最少次数是多少?答案是两次而不是三次。
下面分析:解法一:设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,先选取两组各三枚硬币,分别为a,b,c和f,g,h。
如果a+b+c=f+g+h,那么d和e中较轻的那枚时假币。
如果a+b+c>f+g+h,那么假币必在f,g,h中,比较f和g,如果f=g,那么h是假币;如果f>g,那么g是假币;如果f<g,那么f是假币。
如果a+b+c<f+g+h,则同上可得出相应结果。
a+b+c?f+g+ha+b+c>f+g+ha+b+c=f+g+ha+b+c<f+g+hf<gf=gf=gd>ed<ea>ba=ba<bg是假币h是假币f是假币e是假币d是假币b是假币c是假币a是假币f>gf<g解法二:设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,先选取两组各三枚硬币,分别为a,b,c和f,g,h。
如果a+b+c=f+g+h,那么d和e中较轻的那枚时假币。
如果a+b+c<f+g+h,那么假币必在a,b,c中,再比较a+d+f和c+e+g,如果a+d+f=c+e+g,那么b是假币;如果a+d+f>c+e+g,那么c是假币;如果a+d+f<c+e+g,那么a是假币。
如果a+b+c>f+g+h,则同上可得出相应结果。
a+b+c<f+g+ha+b+c=f+g+h a+b+c>f+g+h a+d+f<c+e+g a是假币a+d+f=c+e+g b 是假币c是假币a+d+f>c+e+gd>ed<e d是假币e 是假币a+d+f<c+e+ha+d+f=c+e+ha+d+f>c+e+hf 是假币g是假币h是假币a+b+c?f+g+h解法一和解法二的区别在于解法二的第二次比较并没有用到第一次比较的结果。
树形图法求概率

由树形图可以看出,共有8种 等可能的结果,能确定哪两人 先玩的有6种 6 3 所以P(两只手同向)=
8
4
谁赢了?
有两个可以自由转动的均匀转盘A、B,分别 被分成4等份、3等份,并在每份内均标 有数字,如图所示,丁洋和王倩同学用这 两个转盘游戏,游戏规则如下:①分别转 动转盘A和转盘B;②两个转盘停止后, 将两个指针所指份内的数字相加(若指针 恰好停在等分线上,那么重转一次,直到 指针指向某一份为止);③如果和为0, 丁洋获胜,否则王倩获胜 1.用树形图求丁洋获胜的概率 2. 你认为这个游戏公平吗?请说明理由。
3 1 由图可知:P(丁洋获胜)= 12 4
王倩获胜的概率为P= 3 4
1 3 4 4
所以游戏不公平。
游戏规则可修改为:和为正数丁洋胜,否则王倩胜
摸球实验
袋中有1只红球,2只白球, 它们除了颜色外无任何 区别,任意摸出一个球, 记下球的颜色,放回袋 中,搅匀后再任意摸出 一个球,记下球的颜色。 为了研究两次摸球出现 情况的概率,画出如下 树形图: P(两次都摸到白球)= 1.请你把树形图补充完整 2.根据树形图求两次都摸到 白球的概率是多少?
1 3
所以我选择去昌明 超市购物
反思小结
1.明确完成一次试验需要几个步骤;根据一次实 验中几个步骤的顺序直接画出树形图。 2.注意:画树形图要注意同一级的树枝必须 是等可能的;最后一级的“树枝”条数是试 验中所有等可能的结果个数 3..列表法和树形图法都是列举法,列表 法应用于实验中涉及两个元素或两个步 骤,而树形图法既可以是两个元素也可 以是多个元素或多个步骤,而且中 学
掷一枚硬币,求正面向上的概率 掷两枚硬币,求正面全部向上的概率 掷三枚硬币,求正面全部向上的概率
图论之二部图图形解析

*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图,本节先介绍二部图的基本概念和主要结论,然后介绍它的一个重要应用—匹配。
定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ,满足(1)12V V V = ,12V V φ= ;(2)(,)e u v E ∀=∈,均有1u V ∈,2v V ∈。
则称G 为二部图或偶图(Bipartite Graph 或Bigraph),1V 和2V 称为互补顶点子集,常记为12,,G V V E =。
如果1V 中每个顶点都与2V 中所有顶点邻接,则称G 为完全二部图或完全偶图(Complete Bipartite Graph),并记为,r s K ,其中12,r V s V ==。
由定义可知,二部图是无自回路的图。
图7-55中,(),(),(),(),(a b c d e 都是二部图,其中(),(),(),(b c d e 是完全二部图1,32,32,43,3,,,K K K K 。
图7-55二部图示例显然,在完全二部图中,r s K 中,顶点数n r s =+,边数m rs =。
一个无向图如果能画成上面的样式,很容易判定它是二部图。
有些图虽然表面上不是上面的样式,但经过改画就能成为上面的样式,仍可判定它是一个二部图,如图7-56中()a 可改画成图()b ,图()c 可改画成图()d 。
可以看出,它们仍是二部图。
图7-56二部图示例定理7.5.1 无向图,G V E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。
证明 先证必要性。
设G 是具有互补节点子集1V 和2V 的二部图。
121(,,,,)k v v v v 是G 中任一长度为k 的回路,不妨设11v V ∈,则211m v V +∈,22m v V ∈,所以k 必为偶数,不然,不存在边1(,)k v v 。
再证充分性。
设G 是连通图,否则对G 的每个连通分支进行证明。
八硬币集中四坏硬币的最优测试方法

2 引 理
引理 1 n 枚硬币中含有 m 枚等质量偏重的问题硬币, 则理论上用一台不带砝码的天
平, 检测 m 枚坏硬币的最优过程存在, 测试次数为 log3 m [2].
22 <
33 =
27.
211202103
所以此方法可以入选.
类似的, 可以判断 (3, 3, 2) 可以入选而 (1, 1, 6) 与 (4, 4, 0) 则不行.
此处, 我们选择 (2, 2, 4) 的情况进行证明.
设硬币组合为 C = {a, b, c, d , e, f , g , h }. 取 X = {a, b}, Y = {c, d }, Z = {e, f , g , h }. 第
Abstract: W e give a so lu tion to the p rob lem of testing 4 defectives from 8 item s. T he m ethod u sed in th is p ap er is sha rp , since in telling ou t the defectives from the good ones, the num ber of the testing tim es is m in im a l. Keywords: group testing; com b ina to ria l op tim iza tion; defective elem en t p rob lem
图4 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
树的应用举例——八枚硬币问题
设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,其中有且仅有一枚硬币是假币,并且假币的重量与真币的重量不同,可能轻,也可能重。
现要求以天平为工具,用最少的比较次数挑选出假币,并同时确定这枚假币的重量比其它真币是轻还是重。
问题的解决是经过一系列的判断,这些判断构成了树结构,可以用判定树来描述这个判定过程。
解决这个问题的最自然的想法就是把硬币分成两组,也就是一分为二。
但是,如果一分为三的话,会获得更少的比较次数。
从八枚硬币中任取六枚a,b,c,d,e,f,在天平两端各放三枚进行比较。
假设a,b,c三枚放在天平的一端,d,e,f三枚放在天平的另一端,可能出现三种比较结果:
⑴a+b+c > d+e+f
⑵a+b+c=d+e+f
⑶a+b+c < d+e+f
若a+b+c >d+e+f,可以肯定这六枚硬币中必有一枚为假币,同时也说明,为真币。
这时可将天平两端各去掉一枚硬币,假设去掉和,同时将天平两端的硬币各换一枚,假设硬币,作了互换,然后进行第二次比较,比较的结果同样可能有三种:
①a+e>d+b:这种情况表明天平两端去掉硬币c,f且硬币b,e互换后,天平两端的轻重关系保持不变,从而说明了假币必然是a,d中的一个,这时我们只要用一枚真币(例如h)和a进行比较,就能找出假币。
若a>h,则a是较重的假币;若a=h,则d为较轻的假币;不可能出现a
②a+e=d+b:此时天平两端由不平衡变为平衡,表明假币一定在去掉的两枚硬币c,f中,同样用一枚真币(例如h)和c进行比较,若c>h,则c是较重的假币;若c=h,则f为较轻的假币;不可能出现c
③a+e:此时表明由于两枚硬币b,e的对换,引起了两端轻重关系的改变,那么可以肯定b或e中有一枚是假币,同样用一枚真币(例如h)和b进行比较,若b>h,则b是较重的假币;若b=h,则e为较轻的假币;不可能出现b 对于结果⑵和⑶的情况,可按照上述方法作类似的分析。
图5-42给出了判定过程,图中大写字母H和L分别表示假币较其它真币重或轻,边线旁边给出的是天平的状态。
八枚硬币中,每一枚硬币都可能是或轻或重的假币,因此共有16种结果,反映在树中,则有16个叶子结点,从图中可看出,每种结果都需要经过三次比较才能得到。
