遗传算法求解函数极值
遗传算法求函数最大值实验报告

遗传算法求函数最大值实验报告遗传算法是一种模拟自然界进化过程的优化算法,它通过模拟生物进化过程中的遗传、交叉和变异等机制,逐步优化解空间中的个体,以找到问题的最优解。
在本次实验中,我们利用遗传算法来求解一个函数的最大值。
下面我们将详细介绍实验的过程和结果。
首先,我们选择了一个简单的函数作为实验对象,即f(x) = x^2,在x的范围为[-10, 10]。
我们的目标是找到使函数值最大的x。
首先,我们需要定义遗传算法中的基本元素,包括编码方式、适应度函数、选择策略、交叉和变异操作等。
在本实验中,我们选择二进制编码方式,将x的范围[-10, 10]离散化为10位的二进制编码。
适应度函数即为f(x) = x^2,它表示个体的适应度。
选择策略采用轮盘赌选择算法,交叉操作采用单点交叉,变异操作采用随机位变异。
接下来,我们需要初始化种群,并迭代进行交叉和变异操作,直到满足终止条件。
在每一代中,我们根据适应度函数对种群中的个体进行评估,并根据选择策略选择父代个体进行交叉和变异操作。
通过交叉和变异操作,产生新的子代个体,并替代原有种群中的个体。
在本次实验中,我们设置了100个个体的种群,并进行了100代的迭代。
实验结果显示,经过多次迭代,算法逐渐优化到了最优解。
最终找到了使函数值最大的x,即x=10,对应的函数值为100。
总结起来,本次实验利用遗传算法求解函数的最大值,展示了遗传算法在优化问题中的应用。
通过适当选择编码方式、适应度函数和操作策略,我们可以有效地找到问题的最优解。
在后续的研究中,我们可以进一步探索遗传算法在更复杂问题上的应用,并通过改进算法的参数和操作策略来提高算法的性能。
matlab遗传算法计算函数区间最大值和最小值

matlab遗传算法计算函数区间最大值和最小值下面是用matlab实现遗传算法计算函数区间最大值和最小值的示例代码:首先定义函数(此处以f(x)=x*sin(10*pi*x)+1为例):matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;end然后设置遗传算法参数:matlaboptions = gaoptimset('Generations', 1000, 'PopulationSize', 50,'StallGenLimit', 200, 'TolCon', 1e-10);其中,Generations表示遗传算法的迭代次数,PopulationSize表示种群大小,StallGenLimit表示在连续多少代没有改变时停止迭代,TolCon表示收敛精度。
接着,编写遗传算法主函数:matlab[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);其中,第一个参数为要优化的函数,第二个参数为变量维度,后面的参数为变量的取值范围。
最后,输出结果:matlabfprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);其中,-fval表示函数最大值,fval表示函数最小值。
完整代码如下:matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;endoptions = gaoptimset('Generations', 1000, 'PopulationSize', 50, 'StallGenLimit', 200, 'TolCon', 1e-10);[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);fprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);参考资料:[1][2]。
简述极值原理的应用方法

简述极值原理的应用方法1. 概述极值原理(Extreme Value Principle)是应用于数学分析、最优化和物理学中的一项基本原理。
其基本思想是在一个有限集合中存在最大值和最小值。
在实际应用中,极值原理常常用于求解最优化问题和优化算法。
2. 应用方法2.1. 寻找极值点的方法寻找函数的极值点是极值原理的一种常见应用方法。
以下是几种常用的方法:•导数法:对于连续可导的函数,通过求解导数为零的方程来找到函数的极值点。
其中,导数为零的点可能是极大值点、极小值点或驻点。
•二分法:对于有界函数,可以通过二分法来逼近极值点。
该方法需要先确定一个区间,在该区间内通过逐步缩小区间范围的方式来找到极值点的近似值。
•牛顿法:牛顿法是通过函数的一阶和二阶导数来逼近极值点。
该方法通过迭代计算,不断逼近极值点。
2.2. 极值在实际问题中的应用极值原理不仅在数学分析中有应用,还在实际问题中有广泛的应用。
以下是一些实际问题中极值原理的应用方法:•最优化问题:极值原理在最优化问题中有重要应用。
例如,在生产过程中,为了提高效益、降低成本,需要确定某个变量的最优值,这可以通过极值原理来解决。
最优化问题的求解可以利用上述提到的找极值点的方法。
•经济决策:在经济决策中,极值原理可以用于确定最优的投资策略、定价策略和市场策略,从而使企业获得最大利润。
例如,在确定产品的最优价格时,可以利用极值原理来确定最大利润对应的价格。
•机器学习:在机器学习中,极值原理可以用于求解最优化问题,例如线性回归和逻辑回归。
这些问题可以通过优化算法来求解,而这些优化算法的基础就是极值原理。
2.3. 优化算法的应用优化算法是一类通过迭代方法逼近极值点的算法。
以下是几种常见的优化算法:•梯度下降法:梯度下降法是一种通过迭代调整参数值的方法来求解最优化问题。
该方法通过计算函数的梯度(导数)方向,从而找到可使目标函数值下降的参数值。
•遗传算法:遗传算法是一种基于进化原理的优化算法。
实验五:遗传算法求解函数最值问题实验

EJdoublefitness(constCh^crrcscrcRc)
{
doublek,y;
decode(cx# y);
retiurnf(x, y)+5;
2•交叉操作
首先是根据交叉概率probCross选择要交叉的个体进行交叉
//根据交叉槪率进行交叉
for(inti=pre = -1;i<N; i++)
//根据变异概率迸行变异
for (inti=0;i<N; i++)
if(randQm61() < probMutation)
mutate(group[i]);
变异时先随机生成变异的位置,然后把改位的01值翻转。
//变异操作
Hvoidmutate(ChrcfnosomeS c)
{
//随机选行翻转
inti-rand()%len; c-g[i] =
//骑越
boolflag-令;
for(inti = j=0; i<1.亡n;i++)
swap(d.g[l]Jc2.g[i]);
if(i== crosspcint[j])
//妇杲若干个交叉点重合”则效果叠加 "偃数个交叉点效果瑁当于没有交叉点while(j<
flag = [flag;
3.变异操作
首先是根据变异概率probMutation选择要变异的个体
经过一定的进化之后得到最终种群,从中选择最优的个体即可得
到最终的结果。
//获取种群最优你
-intgetOptimal(Ch^crescr:-oup[mxn]doubled—double&』doubled\)
遗传算法求函数极大值(matlab实现)

遗传算法求函数最大值(matlab实现)一、题目:寻找f(x)=x2,,当x在0~31区间的最大值。
二、源程序:%遗传算法求解函数最大值%本程序用到了英国谢菲尔德大学(Sheffield)开发的工具箱GATBX,该工具箱比matlab自带的GATOOL使用更加灵活,但在编写程序方面稍微复杂一些Close all;Clear all;figure(1);fplot('variable*variable',[0,31]); %画出函数曲线%以下定义遗传算法参数GTSM=40; %定义个体数目ZDYCDS=20; %定义最大遗传代数EJZWS=5; %定义变量的二进制位数DG=0.9; %定义代沟trace=zeros(2, ZDYCDS); %最优结果的初始值FieldD=[5;-1;2;1;0;1;1]; %定义区域描述器的各个参数%以下为遗传算法基本操作部分,包括创建初始种群、复制、交叉和变异Chrom=crtbp(GTSM, EJZWS); %创建初始种群,即生成给定规模的二进制种群和结构gen=0; %定义代数计数器初始值variable=bs2rv(Chrom, FieldD); %对生成的初始种群进行十进制转换ObjV=variable*variable; %计算目标函数值f(x)=x2 while gen<ZDYCDS %进行循环控制,当当前代数小于定义的最大遗传代数时,继续循环,直至代数等于最大遗传代数FitnV=ranking(-ObjV); %分配适应度值SelCh=select('sus', Chrom, FitnV, DG); %选择,即对个体按照他们的适配值进行复制SelCh=recombin('xovsp', SelCh, 0.7); %交叉,即首先将复制产生的匹配池中的成员随机两两匹配,再进行交叉繁殖SelCh=mut(SelCh); %变异,以一个很小的概率随机地改变一个个体串位的值variable=bs2rv(SelCh, FieldD); %子代个体的十进制转换ObjVSel=variable*variable; %计算子代的目标函数值[Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel);%再插入子代的新种群,其中Chrom为包含当前种群个体的矩阵,SelCh为包好当前种群后代的矩阵variable=bs2rv(Chrom, FieldD); %十进制转换gen=gen+1; %代数计数器增加%输出最优解及其序号,并在目标函数图像中标出,Y为最优解,I 为种群的%序号[Y, I]=max(ObjV);hold on; %求出其最大目标函数值plot(variable(I), Y, 'bo');trace(1, gen)=max(ObjV); %遗传算法性能跟踪trace(2, gen)=sum(ObjV)/length(ObjV);end%以下为结果显示部分,通过上面计算出的数值进行绘图variable=bs2rv(Chrom, FieldD); %最优个体进行十进制转换hold on, grid;plot(variable,ObjV,'b*'); %将结果画出三、运行结果:由图可见该函数为单调递增函数,即当X=31时,该取得最大值f(x)max=961。
神经网络遗传算法函数极值寻优-非线性函数极值

%% 清空环境变量clccleartic%% 训练数据预测数据提取及归一化%下载输入输出数据load data input output%从1到2000间随机排序k=rand(1,4000);[m,n]=sort(k);%找出训练数据和预测数据input_train=input(n(1:3900),:)';output_train=output(n(1:3900),:)';input_test=input(n(3901:4000),:)';output_test=output(n(3901:4000),:)';%选连样本输入输出数据归一化[inputn,inputps]=mapminmax(input_train); [outputn,outputps]=mapminmax(output_train);%% BP网络训练% %初始化网络结构net=newff(inputn,outputn,5);net.trainParam.epochs=100;net.trainParam.lr=0.1;net.trainParam.goal=0.0000004;%网络训练net=train(net,inputn,outputn);%% BP网络预测%预测数据归一化inputn_test=mapminmax('apply',input_test,inputps);%网络预测输出an=sim(net,inputn_test);%网络输出反归一化BPoutput=mapminmax('reverse',an,outputps);%% 结果分析figure(1)plot(BPoutput,':og')hold onplot(output_test,'-*');legend('预测输出','期望输出','fontsize',12)title('BP网络预测输出','fontsize',12)xlabel('样本','fontsize',12)ylabel('输出','fontsize',12)print -dtiff -r600 4-3%预测误差error=BPoutput-output_test;figure(2)plot(error,'-*')title('神经网络预测误差')figure(3)plot((output_test-BPoutput)./BPoutput,'-*');title('神经网络预测误差百分比')errorsum=sum(abs(error))tocsave data net inputps outputps%%Codefunction ret=Code(lenchrom,bound)%本函数将变量编码成染色体,用于随机初始化一个种群% lenchrom input : 染色体长度% bound input : 变量的取值范围% ret output: 染色体的编码值flag=0;while flag==0pick=rand(1,length(lenchrom));ret=bound(:,1)'+(bound(:,2)-bound(:,1))'.*pick; %线性插值,编码结果以实数向量存入ret 中flag=test(lenchrom,bound,ret); %检验染色体的可行性end%%Crossfunction ret=Cross(pcross,lenchrom,chrom,sizepop,bound)%本函数完成交叉操作% pcorss input : 交叉概率% lenchrom input : 染色体的长度% chrom input : 染色体群% sizepop input : 种群规模% ret output : 交叉后的染色体for i=1:sizepop %每一轮for循环中,可能会进行一次交叉操作,染色体是随机选择的,交叉位置也是随机选择的,%但该轮for循环中是否进行交叉操作则由交叉概率决定(continue控制)% 随机选择两个染色体进行交叉pick=rand(1,2);while prod(pick)==0pick=rand(1,2);endindex=ceil(pick.*sizepop);% 交叉概率决定是否进行交叉pick=rand;while pick==0pick=rand;endif pick>pcrosscontinue;endflag=0;while flag==0% 随机选择交叉位pick=rand;while pick==0pick=rand;endpos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置,即选择第几个变量进行交叉,注意:两个染色体交叉的位置相同pick=rand; %交叉开始v1=chrom(index(1),pos);v2=chrom(index(2),pos);chrom(index(1),pos)=pick*v2+(1-pick)*v1;chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束flag1=test(lenchrom,bound,chrom(index(1),:)); %检验染色体1的可行性flag2=test(lenchrom,bound,chrom(index(2),:)); %检验染色体2的可行性if flag1*flag2==0flag=0;else flag=1;end %如果两个染色体不是都可行,则重新交叉endendret=chrom;。
遗传算法求多元函数的极值

遗传算法求多元函数的极值
遗传算法是一种基于生物进化理论的优化算法,可以用来求解多元函数的极值。
下面介绍遗传算法求解多元函数极值的基本流程:
确定目标函数:首先需要确定待优化的目标函数,将其转化为一个优化问题。
确定变量范围和初始种群:对于每个变量,需要确定其可行域范围,并生成一个随机的初始种群。
适应度函数的定义:根据目标函数确定适应度函数,并将其作为评估个体优劣的标准。
选择操作:选择操作是遗传算法的核心,通过适应度函数选择个体,以保留优良个体。
遗传操作:包括交叉和变异两种操作。
交叉操作是指将两个个体的染色体部分进行交换,从而产生新个体;变异操作是指对某个个体的染色体部分进行随机变换,从而产生新个体。
繁殖新种群:通过选择和遗传操作,生成新的种群,并根据适应度函数进行排序。
判断停止条件:根据实际情况设定停止条件,如达到最大迭代次数、收敛到一定程度等。
输出结果:在满足停止条件后,输出当前最优解和最优适应度值。
需要注意的是,遗传算法求解多元函数极值需要根据实际情况调整参数和优化算法流程,以达到最优结果。
遗传算法求函数极值

遗传算法求函数极值遗传算法是一种基于模拟生物进化过程的优化算法,它通过模拟生物的进化过程中的遗传、交叉和变异等操作,对问题的解空间进行,并到满足最优条件的解。
它被广泛应用于求解各种复杂问题,包括函数极值问题。
在使用遗传算法求函数极值的过程中,首先需要明确问题的目标函数。
目标函数是一个将自变量映射到一个实数值的函数,它描述了问题的优化目标。
例如,我们可以考虑一个简单的目标函数f(x),其中x表示自变量,f(x)表示因变量。
遗传算法的基本流程如下:1.初始化种群:随机生成一组初始解,也就是种群。
种群中的每个个体都是一个可能的问题解,而个体中的染色体则表示了问题解的具体数值。
2.适应度评估:对于种群中的每个个体,通过计算目标函数的值,评估每个个体的适应度。
适应度越高的个体,越有可能成为下一代个体的基因。
3.选择操作:根据个体的适应度,选择一些个体作为下一代遗传操作的基因。
4.交叉操作:从选择出的个体中随机选择一对个体,进行交叉操作。
交叉操作通过交换两个个体的染色体信息,产生新的个体。
5.变异操作:对交叉操作生成的新个体进行变异操作。
变异操作通过改变个体染色体中的部分基因,引入新的解,以增加问题解的多样性。
6.新种群产生:基于交叉和变异操作,生成新的种群。
7.终止条件判断:如果满足终止条件(例如达到最大迭代次数、找到了满足要求的解等),则停止算法;否则,返回第2步。
通过以上步骤的循环迭代,遗传算法可以到问题的最优解,即函数的极值。
由于遗传算法充分利用了进化算法的生物特点,具有全局能力和自适应优化能力,因此在函数极值求解中得到了广泛的应用。
遗传算法的关键在于如何进行适应度评估、选择操作、交叉操作和变异操作。
适应度评估是指根据目标函数计算个体的适应度值,一般情况下适应度越高的个体越有可能成为下一代的基因。
选择操作可以采用轮盘赌选择、最优选择等方式,根据个体的适应度选择一定数量的个体进行交叉和变异。
交叉操作通过交换染色体信息,产生新的个体;变异操作通过改变个体染色体中的部分基因,引入新的解。
求极值的方法

求极值的方法在数学中,求极值是一个非常重要的问题,它涉及到函数的最大值和最小值,对于优化问题和实际应用都具有重要意义。
本文将介绍一些常见的求极值的方法,帮助读者更好地理解和掌握这一数学概念。
一、导数法。
求极值的常见方法之一是利用导数。
对于给定的函数,我们可以通过求导数来找到函数的极值点。
具体来说,我们首先求出函数的导数,然后令导数等于零,解出方程得到极值点的横坐标,再代入原函数求得纵坐标,就可以得到函数的极值点。
二、二阶导数法。
除了利用一阶导数来求极值外,我们还可以利用二阶导数。
对于函数的极值点,其一阶导数为零,而且二阶导数的符号可以告诉我们这个极值点是极大值还是极小值。
当二阶导数大于零时,函数在该点取得极小值;当二阶导数小于零时,函数在该点取得极大值。
三、拉格朗日乘数法。
对于带有约束条件的极值问题,我们可以使用拉格朗日乘数法。
这种方法适用于多元函数的极值求解,通过引入拉格朗日乘数,将带有约束条件的极值问题转化为无约束条件的极值问题,然后利用导数或者其他方法求解。
四、牛顿法。
牛顿法是一种迭代求解的方法,可以用来求函数的零点,同时也可以用来求函数的极值点。
通过不断迭代,我们可以逼近函数的极值点,从而得到极值的近似解。
五、凸优化方法。
对于凸函数的极值问题,我们可以使用凸优化方法来求解。
凸优化是一类特殊的优化问题,其解具有良好的性质和稳定性,因此在实际问题中有着广泛的应用。
六、遗传算法。
除了传统的数学方法外,我们还可以利用遗传算法来求解极值问题。
遗传算法是一种模拟生物进化过程的优化方法,通过不断迭代和选择,可以得到函数的极值点。
综上所述,求极值的方法有很多种,不同的方法适用于不同的问题,我们可以根据具体情况选择合适的方法来求解。
希望本文对读者有所帮助,能够更好地理解和掌握求极值的方法。
遗传算法求函数极值

智能优化算法第一次作业--------------遗传算法洪文杰S151000853 问题:用遗传算法求解f(x)=xsin(10π*x)+的最大值,x取[-1,2].一、分析:遗传算法基本思路二、实例简介1. 产生初始种群s1= 13 (01101)s2= 24 (11000)s3= 8 (01000)s4= 19 (10011)2. 计算适应度假定适应度为f(s)=s^2 ,则f (s1) = f(13) = 13^2 = 169 f (s2) = f(24) = 24^2 = 576 f (s3) = f(8) = 8^2 = 64f (s4) = f(19) = 19^2 = 3613. 选择染色体的选择概率为:染色体的累计概率为:根据上面的式子,可得到:例如设从区间[0, 1]中产生4个随机数:r1 = , r2 =r3 = , r4 =4. 交叉基本遗传算法(SGA)中交叉算子采用单点交叉算子。
单点交叉运算5. 变异6. 至下一代,适应度计算→选择→交叉→变异,直至满足终止条件三、解决问题四、实验结果源代码:/*问题:用遗传算法求解f(x)=xsin(10π*x)+的最大值,x取[-1,2].*/ /*洪文杰2016-3-9. 智能优化算法第一次作业*/#include<iostream>//#includ<>#include<>#include<>#include<>#include<>using namespace std;#define NUMBER 50//种群规模#define GENE_NUMBER 10000//迭代次数int Unit[NUMBER][30];//初始种群int Unit_choose[NUMBER][30];//选择、交叉、变异后的种群int Number[NUMBER];//被选择的个体编号float Fitness[NUMBER];//适应度float select_probability[NUMBER];//选择概率float accumula_probability[NUMBER] ;//积累概率float f_max=;//最大值float f_x=;//最大值对应的自变量int hwj_coding(int start,int end);//编码void hwj_initial_population(int num);//产生初始种群void hwj_fitness(int num);//适应度计算void hwj_choose();//选择个体int hwj_binary_search(int l, int r,float temp);//查找选择//void hwj_N_M(int a[],int b[],int N, int M);//从M个数中选N个不一样的数void hwj_cross(int num,float cross);//交叉后的得到种群void hwj_aberrance(int num,float aberrance);//变异后的得到的种群void hwj_max(int num);//找到最适应的个体int main(){int strat,end;//区间int Num;//编码大小float cross=;//交叉概率float aberrance = ;//变异概率int key=1;cout<<"请输入求解区间:"<<endl;cin>>strat>>end;Num=hwj_coding(strat,end);cout<<"Num:"<<Num<<endl;// cout<<"--------------------------1-----------------"<<endl;hwj_initial_population(Num);// cout<<"--------------------------2初始种群-----------------"<<endl;/* for(int i=0;i<NUMBER;i++){for(int j=0;j<Num;j++){cout<<Unit[i][j]<<' ';}cout<<endl;}*/while(key!=GENE_NUMBER){hwj_fitness(Num);// cout<<"--------------------------3适应度-----------------"<<endl;// for(int i=0;i<NUMBER;i++){// cout<<Fitness[i]<<endl;// }hwj_choose();// cout<<"--------------------------4被选择的个体-----------------"<<endl; /* for(int i=0;i<NUMBER;i++){for(int j=0;j<Num;j++){cout<<Unit_choose[i][j]<<' ';}cout<<endl;}*/hwj_cross(Num,cross);/* cout<<"--------------------------5交叉后的种群-----------------"<<endl;for(int i=0;i<NUMBER;i++){for(int j=0;j<Num;j++){cout<<Unit[i][j]<<' ';}cout<<endl;}*/hwj_aberrance(Num,aberrance);/* cout<<"--------------------------6变异后的种群-----------------"<<endl;for(int i=0;i<NUMBER;i++){for(int j=0;j<Num;j++){cout<<Unit[i][j]<<' ';}cout<<endl;}*/key++;hwj_max(Num);}cout<<"最大值是对应的x值是:"<<endl;cout<<f_x<<endl;cout<<"最大值为:"<<f_max<<endl;return 0;}int hwj_coding(int start,int end){//种群编码float precision;int temp=2;int sum;int N=1;cout<<"请输入精度范围:"<<endl;cin>>precision;if(precision==0){cout<<"对不起精度不能为零:"<<endl;return 0;}else{sum=(end-start)/precision;cout<<"sum:"<<sum<<endl;while(temp<sum){temp*=2;N++;}return N;}}void hwj_initial_population(int num){//生成初始种群srand(time(NULL));for(int i=0;i<NUMBER;i++){for(int j=0;j<num;j++){Unit[i][j]=rand()%2;}}}void hwj_fitness(int num){//计算适应度float sum;int temp;temp=1;sum=;for(int j=num-1;j>=0;j--){sum+=Unit[i][j]*temp;temp*=;}Fitness[i]=sum*3/;// cout<<Fitness[i];// cout<<"--------------+++++";Fitness[i]=Fitness[i]*sin(10**Fitness[i])+;// cout<<Fitness[i]<<endl;}}int hwj_binary_search(int l,int r,float temp){for(int i=0;i<NUMBER;i++){if(temp<=accumula_probability[i]&&temp>accumula_probability[i-1]){ return i;}}return -1;}void hwj_choose(){//选择个体float sum=;float temp;int i;sum+=Fitness[i];}select_probability[0]=Fitness[0]/sum;temp=accumula_probability[0]=select_probability[0];for(i=1;i<NUMBER;i++){select_probability[i]=Fitness[i]/sum;temp+=select_probability[i];accumula_probability[i]=temp;// cout<<accumula_probability[i]<<endl;}for(i=0;i<NUMBER;i++){// srand(time(NULL));temp=(rand()%1000000)/;// cout<<temp;Number[i]=hwj_binary_search(0,NUMBER,temp);// cout<<Number[i]<<endl;for(int j=0;j<NUMBER;j++){Unit_choose[i][j]=Unit[Number[i]][j];}}}/*void hwj_N_M(int a[],int b[],int N,int M){//从M个数中选N个不一样的数int i=1;srand(time(NULL));a[0]=rand()%M;b[a[0]]=1;while(i!=N){a[i]=rand()%M;if(b[a[i]]==0){i++;b[a[i]]=1;cout<<a[i]<<endl;}}// cout<<a[i]<<' '<<b[a[i]]<<endl;}*/void hwj_cross(int num,float cross){//交叉后的得到种群int num_cross=NUMBER*cross;int k;//交叉点int i , j;if(num_cross%2!=0){num_cross=num_cross+1;}//需要交叉的个体数int cro[NUMBER];//被交叉的个体编号int temp[NUMBER];//是否交叉数组一览for(i=0;i<NUMBER;i++){cro[i]=-1;temp[i]=0;}// hwj_N_M(cro,temp,num_cross,NUMBER);srand(time(NULL));cro[0]=rand()%NUMBER;temp[cro[0]]=1;i=1;while(i!=num_cross){cro[i]=rand()%NUMBER;if(temp[cro[i]]==0){temp[cro[i]]=1;i++;}}// for(int i=0;i<NUMBER;i++){// cout<<temp[i]<<" "<<cro[i]<<endl;// }// cout<<num_cross<<endl;for(i=0;i<num_cross/2;i++){srand(time(NULL));k=rand()%num;for(j=0;j<num;j++){if(j<=k){Unit[i][j]=Unit_choose[cro[num_cross-i]][j];Unit[i+num_cross/2][j]=Unit_choose[cro[i]][j];}else{Unit[i][j]=Unit_choose[cro[i]][j];Unit[i+num_cross/2][j]=Unit_choose[cro[i]][j];}}}for(i=0;i<NUMBER;i++){// cout<<temp[i]<<endl;if(temp[i]==0){for(j=0;j<num;j++){Unit[num_cross][j]=Unit_choose[i][j];}num_cross++;}}}void hwj_aberrance(int num,float aberrance){//变异后的得到的种群int num_aberrance=NUMBER*aberrance;//变异的个体数int k;//变异点int abe[NUMBER];//变异的个体编号int temp[NUMBER];//是否变异数组一览int i,j,p;for(i=0;i<NUMBER;i++){abe[i]=-1;temp[i]=0;}// hwj_N_M(cro,temp,num_cross,NUMBER);srand(time(NULL));abe[0]=rand()%NUMBER;temp[abe[0]]=1;i=1;while(i!=num_aberrance){abe[i]=rand()%NUMBER;if(temp[abe[i]]==0){temp[abe[i]]=1;i++;}}for( i=0;i<NUMBER;i++){for( j=0;j<num_aberrance;j++){if(i==abe[j]){k=rand()%num;for( p=0;p<num;p++){if(p==k){if(Unit[i][p]==1){Unit[i][p]==0;}else{Unit[i][p]==1;}}}}}}}void hwj_max(int num){hwj_fitness(num);// float max=;int i;int temp=1;float sum=;int k;for(i=0;i<NUMBER;i++){// cout<<Fitness[i]<<endl;if(Fitness[i]>f_max){f_max=Fitness[i];k=i;}}for(int j=num-1;j>=0;j--){sum+=Unit[k][j]*temp;temp*=;}f_x=sum*3/;}。
遗传算法求解函数极值的应用

现 在 我们 用 遗 传 算 法 来 解 答 :
1遗传 编 码
由 于 X 的 定 义 域 是f 1 1 整 数 ,5 24, 以可 以用 0。5 的 1< ^ 所 四 位 的二 进 制 来 表 示 此 问 题 如:0 0表 示 X= 1 1 00 0. 1 1表示,
k ey wor s Ge ei g rt msCo i gCh ieHy rd; rain d : n tcAlo i h ; d n ; oc ; b i Va ic o
遗 传 算 法 (e e ca oi ms 简 称 G 是 根 据 自然 gnt l rh , i g t A) 界 的 “ 竞 天 择 . 者 生 存 ” 象 而 提 出来 的 一 种 随 机 搜 物 适 现 索 算 法 , 是 霍 兰 德 ( ol d 于 17 H ln ) a 9 5年 在 他 的 著 作 《 d p o nN tr n rfi yt s 中 首 次 提 出 来 A a t ni a a ad a ic lSs m } i ul t a i e } 的 此 算 法 将 优 化 问 题 看 作 是 自 然 界 中 生 物 的 进 化 过 程 .通 过 模 拟 大 自然 中 生 物 进 化 过 程 中 的 遗 传 规 律 , 来
关 键词 : 遗传 算 法 ; 码 ; 编 选择 ; 交 ; 杂 变异
中图分 类号 : P 8 T 1
文献标识码 : A
文章编号 :0 9 3 4 (0 72 — 0 0 — 2 1 0 — 0 42 0 )1 4 8 2 0
ZH O U ZH AN G i h n Li Zh —s u
遗传算法求四元函数极值

遗传算法求四元函数极值遗传算法是一种启发式搜索算法,可以用来求解函数的极值问题。
对于四元函数,我们可以采用以下步骤来求解其极值:1.确定变量范围:对于四元函数,我们需要确定每个变量的取值范围。
2.初始化种群:以随机方式生成一组初始解作为种群的第一代。
3.评价适应度:根据目标函数的值,评价每个个体的适应度。
4.选择交叉操作:从种群中选择适应度较高的个体,并对它们进行交叉操作,生成新的个体。
5.变异操作:对于一部分个体,进行变异操作,以增加种群的多样性。
6.更新种群:将新生成的个体加入到种群中,并淘汰适应度较低的个体。
7.检查终止条件:如果达到了预设的终止条件,算法停止;否则,继续进行第3步。
可以通过多次迭代,不断优化种群中的个体,直到得到满意的极值或达到最大迭代次数为止。
对于四元函数极值问题,考虑以下四元函数:f(x1,x2,x3,x4)=x1^2+x2^2+x3^2+x4^2。
假设变量范围均在[-5,5]之间,则可以采用以下Python代码来实现遗传算法求解极值:``` python。
import numpy as np。
def fitness(x):。
return sum(x**2)。
def selection(population, fitness):。
idx = np.random.choice(len(population), size=len(population), replace=True, p=fitness/fitness.sum())。
return population[idx]。
def crossover(parents, p_crossover=0.9):。
offspring = np.empty_like(parents)。
for i in range(len(parents)//2):。
p1, p2 = parents[2*i], parents[2*i+1]。
if np.random.rand() < p_crossover:。
实验五:遗传算法求解函数最值问题实验

实验五:遗传算法求解函数最值问题实验一、实验目的使用遗传算法求解函数在及y的最大值。
二、实验内容使用遗传算法进行求解,篇末所附源代码中带有算法的详细注释。
算法中涉及不同的参数,参数的取值需要根据实际情况进行设定,下面运行时将给出不同参数的结果对比。
定义整体算法的结束条件为,当种群进化次数达到maxGeneration时停止,此时种群中的最优解即作为算法的最终输出。
设种群规模为N,首先是随机产生N个个体,实验中定义了类型Chromosome表示一个个体,并且在默认构造函数中即进行了随机的操作。
然后程序进行若干次的迭代,在每次迭代过程中,进行选择、交叉及变异三个操作。
1.选择操作首先计算当前每个个体的适应度函数值,这里的适应度函数即为所要求的优化函数,然后归一化求得每个个体选中的概率,然后用轮盘赌的方法以允许重复的方式选择选择N个个体,即为选择之后的群体。
但实验时发现结果不好,经过仔细研究之后发现,这里在x、y 取某些值的时候,目标函数计算出来的适应值可能会出现负值,这时如果按照把每个个体的适应值除以适应值的总和的进行归一化的话会出现问题,因为个体可能出现负值,总和也可能出现负值,如果归一化的时候除以了一个负值,选择时就会选择一些不良的个体,对实验结果造成影响。
对于这个问题,我把适应度函数定为目标函数的函数值加一个正数,保证得到的适应值为正数,然后再进行一般的归一化和选择的操作。
实验结果表明,之前的实验结果很不稳定,修正后的结果比较稳定,趋于最大值。
2.交叉操作首先是根据交叉概率probCross选择要交叉的个体进行交叉。
这里根据交叉参数crossnum进行多点交叉,首先随机生成交叉点位置,允许交叉点重合,两个重合的交叉点效果互相抵消,相当于没有交叉点,然后根据交叉点进行交叉操作,得到新的个体。
3.变异操作首先是根据变异概率probMutation选择要变异的个体。
变异时先随机生成变异的位置,然后把改位的01值翻转。
极大值的计算方法

极大值的计算方法在数学中,极大值是一个与函数相关的概念,它指的是函数取得最大值的点。
求函数的极大值是数学中常见的问题之一,在不同的领域,极大值计算方法也不尽相同。
本文将介绍几种常见的极大值计算方法。
一、导数法在一元函数中,求解极值可以利用导数的概念。
如果函数在某个点处导数为零,那么这个点可能是极值点。
具体来说,如果函数在某点处导数为零,而在该点的左侧导数为正,右侧导数为负,那么这个点就是函数的局部最大值。
反之,如果函数在某点处导数为零,而在该点的左侧导数为负,右侧导数为正,那么这个点就是函数的局部最小值。
但是,需要注意的是,导数为零并不总是意味着极值存在。
事实上,一些特殊的函数在某些情况下也会出现导数为零而不是极值的问题。
因此,我们需要结合具体情况进行分析。
二、二分查找法在一些具有单峰函数性质的问题中,可以使用二分查找法求解极值。
单峰函数是指函数有一个唯一的极大值或极小值,且以此为分割点两侧函数值呈单调性变化。
对于这种函数,我们可以采用二分查找法来逼近极值。
具体做法是:先随机选择一个起点,然后计算其一侧的函数值。
如果这一侧的函数值递减,那么极值可能存在于这一侧。
此时,再从这一侧中间随机选取一个点,重复进行计算比较,直到一个足够小的精度范围内得到极值点。
三、梯度下降法梯度下降法是一种常用的优化算法,也可以用来寻找函数的极值点。
其基本思路是通过不断迭代,在每次迭代的过程中向函数值降低的方向移动,直到收敛到极值点。
具体实现时,需要先选定一个起始点,然后计算该点处函数的梯度(即函数对各个自变量的偏导数向量)。
按照负梯度的方向更新自变量,得到相邻的一个点。
不断重复这个过程,直到收敛到某个点或达到最大迭代次数。
四、蒙特卡洛法蒙特卡洛法是一种随机化的算法,可以应用于一些难以直接求解的问题中。
在极值计算中,我们可以使用蒙特卡洛法模拟函数值的随机取样,通过统计这些样本中的最大值来估计极值点。
具体做法是:根据一定的概率分布生成随机点,然后计算这些点的函数值。
五种典型启发式算法对比总结
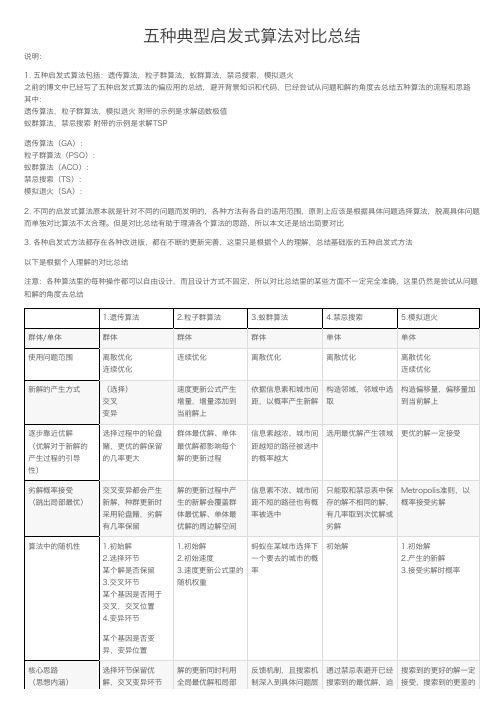
五种典型启发式算法对⽐总结说明:1. 五种启发式算法包括:遗传算法,粒⼦群算法,蚁群算法,禁忌搜索,模拟退⽕之前的博⽂中已经写了五种启发式算法的偏应⽤的总结,避开背景知识和代码,已经尝试从问题和解的⾓度去总结五种算法的流程和思路其中:遗传算法,粒⼦群算法,模拟退⽕ 附带的⽰例是求解函数极值蚁群算法,禁忌搜索 附带的⽰例是求解TSP遗传算法(GA):粒⼦群算法(PSO):蚁群算法(ACO):禁忌搜索(TS):模拟退⽕(SA):2. 不同的启发式算法原本就是针对不同的问题⽽发明的,各种⽅法有各⾃的适⽤范围,原则上应该是根据具体问题选择算法,脱离具体问题⽽单独对⽐算法不太合理。
但是对⽐总结有助于理清各个算法的思路,所以本⽂还是给出简要对⽐3. 各种启发式⽅法都存在各种改进版,都在不断的更新完善,这⾥只是根据个⼈的理解,总结基础版的五种启发式⽅法以下是根据个⼈理解的对⽐总结注意:各种算法⾥的每种操作都可以⾃由设计,⽽且设计⽅式不固定,所以对⽐总结⾥的某些⽅⾯不⼀定完全准确,这⾥仍然是尝试从问题和解的⾓度去总结1.遗传算法2.粒⼦群算法3.蚁群算法4.禁忌搜索5.模拟退⽕群体/单体群体群体群体单体单体使⽤问题范围离散优化连续优化连续优化离散优化离散优化离散优化连续优化新解的产⽣⽅式(选择)交叉变异速度更新公式产⽣增量,增量添加到当前解上依据信息素和城市间距,以概率产⽣新解构造邻域,邻域中选取构造偏移量,偏移量加到当前解上逐步靠近优解(优解对于新解的产⽣过程的引导性)选择过程中的轮盘赌,更优的解保留的⼏率更⼤群体最优解、单体最优解都影响每个解的更新过程信息素越浓、城市间距越短的路径被选中的概率越⼤选⽤最优解产⽣领域更优的解⼀定接受劣解概率接受(跳出局部最优)交叉变异都会产⽣新解,种群更新时采⽤轮盘赌,劣解有⼏率保留解的更新过程中产⽣的新解会覆盖群体最优解、单体最优解的周边解空间信息素不浓、城市间距不短的路径也有概率被选中只能取和禁忌表中保存的解不相同的解,有⼏率取到次优解或劣解Metropolis准则,以概率接受劣解算法中的随机性 1.初始解2.选择环节某个解是否保留3.交叉环节某个基因是否⽤于交叉,交叉位置4.变异环节某个基因是否变异,变异位置1.初始解2.初始速度3.速度更新公式⾥的随机权重蚂蚁在某城市选择下⼀个要去的城市的概率初始解 1.初始解2.产⽣的新解3.接受劣解时概率核⼼思路(思想内涵)选择环节保留优解,交叉变异环节解的更新同时利⽤全局最优解和局部反馈机制,且搜索机制深⼊到具体问题层通过禁忌表避开已经搜索到的最优解,迫搜索到的更好的解⼀定接受,搜索到的更差的(算法特⾊)产⽣新解最优解信息⾯使算法搜索新的最优解以概率接受解。
二进制编码遗传算法求函数极大值

二进制编码遗传算法求函数极大值二进制编码遗传算法是一种用于求解函数极大值的优化方法。
通过将函数的自变量编码为二进制字符串,然后利用遗传算法进行搜索,以找到函数的极大值。
下面是详细步骤:1. 确定问题:首先,明确需要求解的函数以及自变量的取值范围。
例如,假设我们要寻找函数f(x) = x^2 + 3x - 2在[0, 10]范围内的最大值。
2. 二进制编码:将自变量x的取值范围划分为若干个区间,然后用二进制字符串表示每个区间。
例如,如果将区间[0, 10]划分为5个区间,那么二进制编码的长度为log2(5) = 3。
3. 构建初始种群:根据二进制编码规则,生成一定数量的初始个体。
每个个体表示一个可能的解。
例如,生成10个个体。
4. 评估适应度:将每个个体解码为自变量x,计算对应的函数值f(x)。
然后,根据函数值计算每个个体的适应度。
适应度越高,表示个体对应的解越有可能为极大值。
5. 选择操作:采用轮盘赌选择法等策略,从当前种群中选择一部分优秀个体作为父代,用于产生下一代。
6. 交叉操作:对选定的父代个体进行交叉,生成一定数量的子代。
交叉操作可以采用单点交叉、多点交叉等方法。
7. 变异操作:对子代个体进行变异,即随机改变某些位上的二进制值。
变异操作有助于保持种群的多样性。
8. 更新种群:根据新的个体适应度重新构建种群。
9. 终止条件:当满足终止条件(如达到最大遗传代数、找到满足精度要求的极大值等)时,算法结束。
10. 结果输出:输出找到的极大值以及对应的自变量值。
通过以上步骤,二进制编码遗传算法可以用于求解函数的极大值。
需要注意的是,二进制编码遗传算法的性能受到种群数量、编码长度、交叉率、变异率等因素的影响,需要根据实际情况调整参数。
利用遗传算法求函数的极小值

1、利用遗传算法求出下面函数的极小值:z=2-exp[-(x2+y2)], x,y∈[-5,+5]对于此函数,求某一极值、或说最值时,由于x、y定义域与系数相同,x与y相对于z 来说是地位等同的,因此可以转换成求该函数极值:;继而转换成了一种单变量函数。
函数的实现:(1)ga_main脚本文件% GA main program% Edited by Bian Xuezi% n ---- 种群规模% ger ---- 迭代次数% pc ---- 交叉概率% pm ---- 变异概率% v ---- 初始种群(规模为n)% f ---- 目标函数值% fit ---- 适应度向量% vx ---- 最优适应度值向量% vmfit ---- 平均适应度值向量clear all;close all;clc;tic;n=20;ger=100;pc=0.70;pm=0.009;% 生成初始种群v=init_population(n,20);[N,L]=size(v);disp(sprintf('Number of generations:%d',ger)); disp(sprintf('Population size:%d',N));disp(sprintf('Crossover probability:%.3f',pc)); disp(sprintf('Mutation probability:%.3f',pm)); % 待优化问题xmin=-5;ymin=-5;xmax=5;ymax=5;f='-2+exp(-x.^2-y.^2)';%初始化sol=0.1;vmfit=[];it=1;vx=[];%C=[];% 计算适应度,并画出图形x=decode(v(:,1:10),xmin,xmax);y=decode(v(:,11:20),ymin,ymax);fit=eval(f);figure(1);[X,Y]=meshgrid(-5:0.1:5,-5:0.1:5);Z=-2+exp(-X.^2-Y.^2);mesh(X,Y,Z);grid on;hold on;plot3(x,y,fit,'k*');title('染色体的初始位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 开始进化while it<=ger%Reproduction(Bi-classist Selection) vtemp=roulette(v,fit);%Crossoverv=crossover(vtemp,pc);%MutationM=rand(N,L)<=pm;%M(1,:)=zeros(1,L);v=v-2.*(v.*M)+M;%Resultsx=decode(v(:,1:10),xmin,xmax);y=decode(v(:,11:20),ymin,ymax);fit=eval(f);[sol,indb]=max(fit);v(1,:)=v(indb,:);media=mean(fit);vx=[vx sol];vmfit=[vmfit media];it=it+1;end%%%% 最后的结果disp(sprintf('\n')); %空一行% 显示最优解及最优值disp(sprintf('Maximum found[x,f(x)]:[%.4f,%.4f,%.4f]',x(indb),y(indb),sol)); % 图形显示最优结果figure(2);[X,Y]=meshgrid(-5:0.1:5,-5:0.1:5);Z=-2+exp(-X.^2-Y.^2);mesh(X,Y,Z);grid on;hold on;plot3(x,y,fit,'k*');title('染色体的最终位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 图形显示最优及平均函数值变化趋势figure(3);plot(vx);%title('最优,平均函数值变化趋势'); xlabel('Generations');ylabel('f(x,y)');hold on;plot(vmfit,'r');hold off;runtime=toc(2)Crossover函数%Crossoverfunction v=crossover(vtemp,pc) [N,L]=size(vtemp);C(:,1)=rand(N,1)<=pc;I=find(C(:,1)==1);I';j=1;for i=1:2:size(I)if i>=size(I)break;endsite=fix(1+L*rand(1));temp=vtemp(I(i,1),:);vtemp(I(i,1),site:end)=vtemp(I(i+1,1),site:end); vtemp(I(i+1,1),site:end)=temp(:,site:end);%j=j+2;endv=vtemp;(3)decode函数%Decodify bitstringsfunction x=decode(v,min,max)% x ----真实值% v ----待解码的已编码的0-1串v=fliplr(v);[s,c]=size(v);aux=0:1:c-1 ;%21;aux=ones(s(1),1)*aux;x1=sum((v.*2.^aux)');x=min+(max-min)*x1./(2^c-1); % ; (4)init_population函数function v=init_population(n1,s1)v=round(rand(n1,s1));(5)roulette函数function vtemp=roulette(v,fit)N=size(v);fitmin=abs(min(fit));fit=fitmin+fit;%fitS=sum(fit);for i=1:NSI=S*rand(1);for j=1:Nif SI<=sum(fit(1:j))vtemp(i,:)=v(j,:);breakendendend。
MATLAB神经网络(4)神经网络遗传算法函数极值寻优——非线性函数极值寻优

MATLAB神经⽹络(4)神经⽹络遗传算法函数极值寻优——⾮线性函数极值寻优4.1 案例背景y = {x_1}^2 + {x_2}^24.2 模型建⽴神经⽹络训练拟合根据寻优函数的特点构建合适的BP神经⽹络,⽤⾮线性函数的输⼊输出数据训练BP神经⽹络,训练后的BP神经⽹络就可以预测函数输出。
遗传算法极值寻优把训练后的 BP 神经⽹络预测结果作为个体适应度值,通过选择、交叉和变异操作寻找函数的全局最优值及对应输⼊值。
⽹络结构:2-5-1训练数据:3900,测试数据:1004.3 编程实现%% 基于神经⽹络遗传算法的系统极值寻优%% 清空环境变量clcclearinput=2*randn(2,2000);output=sum(input.*input);[inputn,inputps]=mapminmax(input);[outputn,outputps]=mapminmax(output);%% BP⽹络训练% %初始化⽹络结构net=newff(inputn,outputn,[10,5]);% 配置⽹络参数(迭代次数,学习率,⽬标)net.trainParam.epochs=500;net.trainParam.lr=0.1;net.trainParam.goal=0.000004;%⽹络训练net=train(net,inputn,outputn);%% 初始化遗传算法参数%初始化参数maxgen=200; %进化代数,即迭代次数sizepop=20; %种群规模pcross=[0.4]; %交叉概率选择,0和1之间pmutation=[0.2]; %变异概率选择,0和1之间lenchrom=[1 1]; %每个变量的字串长度,如果是浮点变量,则长度都为1bound=[-5 5;-5 5]; %数据范围individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %将种群信息定义为⼀个结构体avgfitness=[]; %每⼀代种群的平均适应度bestfitness=[]; %每⼀代种群的最佳适应度bestchrom=[]; %适应度最好的染⾊体%% 初始化种群计算适应度值% 初始化种群for i=1:sizepop%随机产⽣⼀个种群individuals.chrom(i,:)=Code(lenchrom,bound);x=individuals.chrom(i,:);%计算适应度individuals.fitness(i)=fun(x,inputps,outputps,net); %染⾊体的适应度end%找最好的染⾊体[bestfitness bestindex]=min(individuals.fitness);bestchrom=individuals.chrom(bestindex,:); %最好的染⾊体avgfitness=sum(individuals.fitness)/sizepop; %染⾊体的平均适应度% 记录每⼀代进化中最好的适应度和平均适应度trace=[avgfitness bestfitness];%% 迭代寻优% 进化开始for i=1:maxgenif(mod(i,10)==0)iend% 选择individuals=Select(individuals,sizepop);avgfitness=sum(individuals.fitness)/sizepop;%交叉individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);% 变异individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound); % 计算适应度for j=1:sizepopx=individuals.chrom(j,:); %解码individuals.fitness(j)=fun(x,inputps,outputps,net);end%找到最⼩和最⼤适应度的染⾊体及它们在种群中的位置[newbestfitness,newbestindex]=min(individuals.fitness);[worestfitness,worestindex]=max(individuals.fitness);% 代替上⼀次进化中最好的染⾊体if bestfitness>newbestfitnessbestfitness=newbestfitness;bestchrom=individuals.chrom(newbestindex,:);endindividuals.chrom(worestindex,:)=bestchrom;individuals.fitness(worestindex)=bestfitness;avgfitness=sum(individuals.fitness)/sizepop;trace=[trace;avgfitness bestfitness]; %记录每⼀代进化中最好的适应度和平均适应度endfunction fitness = fun(x,inputps,outputps,net)% 函数功能:计算该个体对应适应度值% x input 个体% fitness output 个体适应度值%数据归⼀化x=x';inputn_test=mapminmax('apply',x,inputps);%⽹络预测输出an=sim(net,inputn_test);%⽹络输出反归⼀化fitness=mapminmax('reverse',an,outputps);%% 结果分析[r,c]=size(trace);plot(trace(:,2),'r-');title('适应度曲线','fontsize',12);xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);axis([0,200,0,1])x=bestchrom;disp([bestfitness x]);fun([0,0],inputps,outputps,net)ans =0.0507在遗传算法中没有y = {x_1}^2 + {x_2}^2函数的原型,由于神经⽹络的误差,最后的计算值离真实值有⼀定偏差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{
for(i=1;i<=N-1;i++)
{
p1=&group[i-1];
p2=&group[i];
if(p1->cost>p2->cost) //值大的往后排
{
Copy_unit(p1,&temp);
Copy_unit(p2,p1);
{
p->path[j]=RandomInteger(0,9); //end
}
Calculate_cost(p); //计算该种群的函数值
}//end初始化种群
}
/*种群进化,进化代数由genmax决定*/
void Evolution(struct unit group[N])
{
int i,j;
int temp1,temp2,temp3,temp4,temp5;
return(p->cost);
}
/*复制种群中的p1到p2中*/
void Copy_unit(struct unit *p1,struct unit *p2)
{
int i;
for(i=0;i<=num_C-1;i++)
p2->path[i]=p1->path[i];
p2->cost=p1->cost;
temp1=N*pc/2;
temp2=N*(1-pc);
temp3=N*(1-pc/2);
temp4=N*(1-ps);
temp5=N*ps;
for(i=1;i<=genmax;i++)
{
//选择
for(j=0;j<=temp4-1;j++)
{ Copy_unit(&group[j],&group[j+temp5]); }
int RandomInteger(int low,int high);
void Initial_gen(struct unit group[N]);
void Sort(struct unit group[N]);
void Copy_unit(struct unit *p1,struct unit *p2);
#define num_C 12 //个体的个数,前6位表示x1,后6位表示x2
#define N 100 //群体规模为100
பைடு நூலகம்#define pc 0.9 //交叉概率为0.9
#define pm 0.1 //变异概率为10%
#define ps 0.6 //进行选择时保留的比例
#define genmax 2000 //最大代数200
}
cross_point=RandomInteger(1,num_C-1); //交叉位随机生成
//交叉,生成子代
//子代1
//子代1前半部分直接从父代复制
for(i=0;i<=cross_point-1;i++) son1[i]=p3->path[i];
for(i=cross_point;i<=num_C-1;i++)
if((!flag>(flag_v>100))?(5*100*pm):(100*pm))
{
i=RandomInteger(0,N-1); //确定发生变异的个体
j=RandomInteger(0,num_C-1); //确定发生变异的位
k=RandomInteger(0,num_C-1);
p=&group[i]; //变异
void Print_optimum(struct unit group[N],int k);
/*定义个体信息*/
typedef struct unit
{
int path[num_C]; //每个个体的信息
double cost; //个体代价值
};
struct unit group[N]; //种群变量group
void Cross(struct unit *p3,struct unit *p4)
{
int i,j,cross_point;
int son1[num_C],son2[num_C];
for(i=0;i<=num_C-1;i++) //初始化son1、son2
{
son1[i]=-1;
son2[i]=-1;
}
/*生成一个介于两整型数之间的随机整数*/
int RandomInteger(int low,int high)
{
int k;
double d;
k=rand();
k=(k!=RAND_MAX)?k:(k-1); //RAND_MAX是VC中可表示的最大整型数
d=(double)k/((double)(RAND_MAX));
Calculate_cost(p4); //计算子代p2的函数值
}
/*变异*/
void Varation(struct unit group[N],int flag_v)
{
int flag,i,j,k,temp;
struct unit *p;
flag=RandomInteger(1,100);
//在进化后期,增大变异概率
void Cross(struct unit *p3,struct unit *p4);
void Varation(struct unit group[N],int i);
void Evolution(struct unit group[N]);
float Calculate_cost(struct unit *p);
题目:生成两个整型,求在这两个整形之间cost=x1+x2-10*(cos(2*3.14*x1)+cos(2*3.14*x2))函数的最小值
源程序:
#include "stdio.h"
#include "stdlib.h"
#include "conio.h"
#include "math.h"
#include "time.h"
}
else if(p->path[6]<6)
{
x2=0-(p->path[7]+p->path[8]*0.1+p->path[9]*0.01+p->path[10]*0.001+p->path[11]*0.0001);
}
p->cost=x1+x2-10*(cos(2*3.14*x1)+cos(2*3.14*x2));
temp=p->path[j];
p->path[j]=p->path[k];
p->path[k]=temp;
Calculate_cost(p); //重新计算变异后的函数值
}
}
/*将种群中个体按函数值从小到大排序*/
void Sort(struct unit group[N])
{
int i,j;
struct unit temp,*p1,*p2;
//交叉
for(j=0;j<=temp1-1;)
{
Cross(&group[temp2+j],&group[temp3+j]);
j+=2;
}
//变异
Varation(group,i);
}
Sort(group);
Print_optimum(group,i-1); //输出当代(第i-1代)种群
}
/*交叉*/
}
printf("当x1=%f x2=%f\n",x1,x2);
printf("函数最小值为:%f \n",p->cost);
}
运行结果:
1
2
3
4
int num_gen=0; //记录当前达到第几代
int main()
{
int i,j;
srand((int)time(NULL)); //初始化随机数发生器
Initial_gen(group); //初始化种群
Evolution(group); //进化:选择、交叉、变异
getch();
return 0;
for(j=0;j<=num_C-1;j++) //补全p1
{
son1[i]=p4->path[j];
}//end子代1
//子代2
//子代1后半部分直接从父代复制
for(i=cross_point;i<=num_C-1;i++) son2[i]=p4->path[i];
for(i=0;i<=cross_point-1;i++)
Copy_unit(&temp,p2);
}
}//end一轮排序
}//end排序
}
/*计算某个个体的函数值*/
float Calculate_cost(struct unit *p)
{
double x1,x2;
x1=0;
if(p->path[0]>5)
{
x1=p->path[1]+p->path[2]*0.1+p->path[3]*0.01+p->path[4]*0.001+p->path[5]*0.0001;
