计数第06讲_标数法(学生版)A4

合集下载

【精选】奥数：计数之对应法.学生版

前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法，比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等，这里再集中学习一下计数中其他常见的方法，主要有归纳法、整体法、对应法、递推法．对这些计数方法与技巧要做到灵活运用．将难以计数的数量与某种可计量的事物联系起来，只要能建立一一对应的关系，那么这两种事物在数量上是相同的．事实上插入法和插板法都是对应法的一种表现形式．模块一、图形中的对应关系【例 1】在8×8的方格棋盘中，取出一个由三个小方格组成的“L ”形（如图），一共有多少种不同的方法？【考点】计数之图形中的对应关系【难度】3星【题型】解答【解析】注意：数“不规则几何图形”的个数时，常用对应法．第1步：找对应图形每一种取法，有一个点与之对应，这就是图中的A 点，它是棋盘上横线与竖线的交点，且不在棋盘边上．第2步：明确对应关系从下图可以看出，棋盘内的每一个点对应着4个不同的取法（“L ”形的“角”在2×2正方形的不同“角”上）．第3步：计算对应图形个数由于在 8×8的棋盘上，内部有7×7=49（个）交叉点，第4步：按照对应关系，给出答案故不同的取法共有49×4=196（种）．评注:通过上面两个范例我们知道,当直接去求一个集合元素的个数较为困难的时候,可考虑采用相等的原则,把问题转化成求另一个集合的元素个数．【答案】196【例 2】在8×8的黑白相间染色的国际象棋棋盘中，以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个？【考点】计数之图形中的对应关系【难度】3星【题型】解答例题精讲教学目标7-6-3计数之对应法【解析】首先可以知道题中所讲的13⨯长方形中间的那个小主格为黑色，这是因为两个白格不相邻，所以不能在中间．显然，位于棋盘角上的黑色方格不可能被包含在这样的长方形中．下面分两种情况来分析：第一种情况，一个位于棋盘内部的黑色方格对应着两个这样的13⨯长方形(一横一竖)；第二种情况，位于边上的黑色方格只能对应一个13⨯长方形．由于在棋盘上的32个黑色方格中，位于棋盘内部的18个，位于边上的有12个，位于角上的有2个，所以共有1821248⨯+=个这样的长方形．本题也可以这样来考虑：事实上，每一行都有6个13⨯⨯=个．由于棋盘上⨯长方形，所以棋盘上横、竖共有13⨯长方形68296的染色具有对称性，因此包含两个白色小方格与一个黑色小方格的长方形正好与包含两个黑色小方格与一个白色小方格的长方形具有一一对应关系，这说明它们各占一半，因此所求的长方形个数为96248÷=个．【答案】48【巩固】用一张如图所示的纸片盖住66⨯方格表中的四个小方格，共有多少种不同的放置方法？【考点】计数之图形中的对应关系【难度】3星【题型】解答【解析】如图，将纸片中的一个特殊方格染为黑色，下面考虑此格在66⨯方格表中的位置．易见它不能位于四个角上；若黑格位于方格表中间如图浅色阴影所示的44⨯正方形内的某格时，纸片有4种不同的放法，共计44464⨯⨯=种；若黑格位于方格表边上如图深色阴影所示的方格中时，纸片的位置随之确定，即只有1种放法，此类放法有4416⨯=种．所以，纸片共有641680+=种不同的放置方法．【答案】80种【例3】图中可数出的三角形的个数为．【考点】计数之图形中的对应关系【难度】4星【题型】填空【解析】这个图不像我们以前数三角形那样规则，粗看似乎看不出其中的规律，不妨我们取出其中的一个三角形，发现它的三条边必然落在这个图形中的三条大线段上，而每三条大线段也正好能构成一个三角形，因此三角形的个数和三条大线段的取法是一一对应的关系，图中一共有8条大线段，因此有3856C =个三角形．【答案】56个三角形【例 4】如图所示，在直线AB 上有7个点，直线CD 上有9个点．以AB 上的点为一个端点、CD上的点为另一个端点的所有线段中，任意3条线段都不相交于同一个点，求所有这些线段在AB 与CD 之间的交点数．【考点】计数之图形中的对应关系【难度】4星【题型】解答C D BA【解析】常规的思路是这样的：直线AB 上的7个点，每个点可以与直线CD 上的9个点连9根线段，然后再分析这些线段相交的情况．如右图所示，如果注意到下面这个事实：对于直线AB 上的任意两点M 、N 与直线CD 上的任意两点P 、Q 都可以构成一个四边形MNQP ，而这个四边形的两条对角线MQ 、NP 的交点恰好是我们要计数的点，同时，对于任意四点(AB 与CD 上任意两点)都可以产生一个这样的交点，所以图中两条线段的交点与四边形有一一对应的关系．这说明，为了计数出有多少个交点，我们只需要求出在直线AB 与CD 中有多少个满足条件的四边形MNQP 就可以了！从而把问题转化为：在直线AB 上有7个点，直线CD 上有9个点．四边形MNQP 有多少个？其中点M 、N 位于直线AB 上，点P 、Q 位于直线CD 上．这是一个常规的组合计数问题，可以用乘法原理进行计算：由于线段MN 有2721C =种选择方式，线段PQ 有2936C =种选择方式，根据乘法原理，共可产生2136756⨯=个四边形．因此在直线AB 与CD 之间共有756个交点．【答案】756个交点模块二、数字问题中的对应关系【例 5】有多少个四位数，满足个位上的数字比千位数字大，千位数字比百位大，百位数字比十位数字大？【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【解析】由于四位数的四个数位上的数的大小关系已经非常明确，而对于从0～9中任意选取的4个数字，它们的大小关系也是明确的，那么由这4个数字只能组成1个符合条件的四位数(题目中要求千位比百位大，所以千位不能为0，本身已符合四位数的首位不能为0的要求，所以进行选择时可以把0包含在内)，也就是说满足条件的四位数的个数与从0～9中选取4个数字的选法是一一对应的关系，那么满足条件的四位数有410109872104321C ⨯⨯⨯==⨯⨯⨯个．【答案】210个【巩固】三位数中，百位数比十位数大，十位数比个位数大的数有多少个？【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【解析】相当于在10个数字中选出3个数字，然后按从大到小排列.共有10×9×8÷（3×2×1）=120种．实际上，前铺中每一种划法都对应着一个数．【答案】120种【例 6】数3可以用4种方法表示为一个或几个正整数的和，如3，12+，21+，111++．问：1999表示为一个或几个正整数的和的方法有多少种？【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【解析】我们将1999个1写成一行，它们之间留有1998个空隙，在这些空隙处，或者什么都不填，或者填上“＋”号．例如对于数3，上述4种和的表达方法对应：1 1 1，1+1 1，1 1+1，1+1+1．可见，将1999表示成和的形式与填写1998个空隙处的方式之间是一一对应的关系，而每一个空隙处都有填“＋”号和不填“＋”号2种可能，因此1999可以表示为正整数之和的不同方法有1998199822222⨯⨯⨯=个相乘种．【答案】19982种【例 7】请问至少出现一个数码3，并且是3的倍数的五位数共有多少个？【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【关键词】小学数学竞赛【解析】五位数共有90000个，其中3的倍数有30000个．可以采用排除法，首先考虑有多少个五位数是3的倍数但不含有数码3.首位数码有8种选择，第二、三、四位数码都有9种选择．当前四位的数码确定后，如果它们的和除以余数为0，则第五位数码可以为0、6、9；如果余数为1，则第五位数码可以为2、5、8；如果余数为2，则第五位数码可以为1、4、7.可见只要前四位数码确定了，第五位数码都有3种选择，所以五位数中是3的倍数但不含有数码3的数共有8999317496⨯⨯⨯⨯=个．所以满足条件的五位数共有300001749612504-=个．【答案】12504个模块三、对应与阶梯型标数法【例 8】游乐园的门票1元1张，每人限购1张．现在有10个小朋友排队购票，其中5个小朋友只有1元的钞票，另外5个小朋友只有2元的钞票，售票员没有准备零钱．问有多少种排队方法，使售票员总能找得开零钱？【考点】计数之对应与阶梯型标数法【难度】5星【题型】解答【解析】与类似题目找对应关系．要保证售票员总能找得开零钱，必须保证每一位拿2元钱的小朋友前面的若干小朋友中，拿1元的要比拿2元的人数多，先将拿1元钱的小朋友看成是相同的，将拿2元钱的小朋友看成是相同的，可以利用斜直角三角模型．在下图中，每条小横线段代表1元钱的小朋友，每条小竖线段代表2元钱的小朋友，因为从A 点沿格线走到B 点，每次只能向右或向上走，无论到途中哪一点，只要不超过斜线，那么经过的小横线段都不少于小竖线段，所以本题相当于求下图中从A 到B 有多少种不同走法．使用标数法，可求出从A 到B 有42种走法．A B 424228145141494553221111111但是由于10个小朋友互不相同，必须将他们排队，可以分成两步，第一步排拿2元的小朋友，5个人共有5120=！种排法；第二步排拿到1元的小朋友，也有120种排法，所以共有5514400⨯=！！种排队方法．这样，使售票员能找得开零钱的排队方法共有421440060480⨯=(种)．【答案】604800种【例 9】学学和思思一起洗5个互不相同的碗（顺序固定），思思洗好的碗一个一个往上摞，学学再从最上面一个一个地拿走放入碗柜摞成一摞，思思一边洗，学学一边拿，那么学学摞好的碗一共有种不同的摞法．【考点】计数之对应与阶梯型标数法【难度】5星【题型】解答【关键词】学而思杯，5年级，第7题【解析】方法一：如下所示，共有42种不同的摞法：54321----，45321----，35421----，53421----，34521----，54231----，45231----，25431----，52431----，24531----，52341----，25341----，23541----，23451----，54312----，45312----，53412----，35412----，34512----，54132----，45132----，15432----，51432----，14532----，51342----，15342----，13542----，13452----，54123----，45123----，15423----，51423----，14523----，12543----，51243----，15243----，12453----，12354----，12534----，15234----，51234----， 12345----。

标数法——学生版

A
B
5. 如图所示，有一个棋子要从左下角走到右上角，每步只能向右、向上或者向右上移动一格，一共有多少种不同的走法？
6. 用 10 个形如“
”的棋子覆盖 2 10 的棋盘（“
”）；有多少种不同的摆法？
7. 一场足球比赛的结束后，甲乙两队的进球数为 3 : 4，且整场比赛中甲队的进球数量从未领先乙队，请问，两队在比赛中的进球顺序有多少种情况？
11
标数法 +
基本图形中的标数法
如图，每次只能向右或向上走 1 步（1）从 A 走到 C 的最短路线有多少条？（2）从 A 走到 D 的最短路线有多少条？（3）从 A 走到 B 的最短路线有多少条？
B
CD
A
如图，每次只能向右或向上走 1 步，从 A 点走到 B
养老院
学校
市中心
学校
市中心
2
如图为一幅街道图，从 A 出发经过十字路口 B，但不经过 C 走到 D 的不同的最短路线有
条.
D
BC A
特殊图形中的标数法
一只蜜蜂从 A 处出发，回到家里 B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？
A
B
3
一只蜜蜂从 A 处出发，回到家里 B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？
A
标数法的综合应用
（1）一段楼梯有 10 级台阶，盛盛每一步只能上一级或两级台阶，要登上第 10 级台阶，共有几种不同的走法？
（2）若盛盛每一步能上一级或两级或三级台阶，要登上第 10 级台阶，共有几种不同的走法？（3）若盛盛每一步只能上一级或三级台阶，要登上 10 级台阶，共有几种不同的走法？

标数法

一、加法原理概念引入生活中常有这样的情况，就是在做一件事时，有几类不同的方法，而每一类方法中，又有几种可能的做法．那么，考虑完成这件事所有可能的做法，就要用加法原理来解决．例如:王老师从北京到天津，他可以乘火车也可以乘长途汽车，现在知道每天有五次火车从北京到天津，有4趟长途汽车从北京到天津．那么他在一天中去天津能有多少种不同的走法？分析这个问题发现，王老师去天津要么乘火车，要么乘长途汽车，有这两大类走法，如果乘火车，有5种走法，如果乘长途汽车，有4种走法．上面的每一种走法都可以从北京到天津，故共有5+4=9种不同的走法．在上面的问题中，完成一件事有两大类不同的方法．在具体做的时候，只要采用一类中的一种方法就可以完成．并且两大类方法是互无影响的，那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数．二、加法原理的定义一般地，如果完成一件事有k 类方法，第一类方法中有1m 种不同做法，第二类方法中有2m 种不同做法，…，第k 类方法中有k m 种不同做法，则完成这件事共有12 k N m m m =+++……种不同方法，这就是加法原理．加法原理运用的范围：完成一件事的方法分成几类，每一类中的任何一种方法都能完成任务，这样的问题可以使用加法原理解决．我们可以简记为：“加法分类，类类独立”．分类时，首先要根据问题的特点确定一个适合于它的分类标准，然后在这个标准下进行分类；其次，分类时要注意满足两条基本原则：① 完成这件事的任何一种方法必须属于某一类； ② 分别属于不同两类的两种方法是不同的方法．知识要点第8讲标数法只有满足这两条基本原则，才可以保证分类计数原理计算正确．运用加法原理解题时，关键是确定分类的标准，然后再针对各类逐一计数．通俗地说，就是“整体等于局部之和”．三、加法原理解题三部曲1、完成一件事分N 类；2、每类找种数（每类的一种情况必须是能完成该件事）；3、类类相加树形图法、标数法及简单的递推一、树形图法“树形图法”实际上是枚举的一种，但是它借助于图形，可以使枚举过程不仅形象直观，而且有条理又不重复遗漏，使人一目了然．【例 1】（难度等级 ※※※）A 、B 、C 三个小朋友互相传球，先从A 开始发球(作为第一次传球)，这样经过了5次传球后，球恰巧又回到A 手中，那么不同的传球方式共多少种？(2005年《小数报》数学邀请赛)【解析】如图，A 第一次传给B ，到第五次传回A 有5种不同方式．同理，A 第一次传给C ，也有5种不同方式．所以，根据加法原理，不同的传球方式共有5510+=种．C B CC B AAB A B CCBA【巩固】（难度等级 ※※※）一只青蛙在A ，B ，C 三点之间跳动，若青蛙从A 点跳起，跳4次仍回到A 点，则这只青蛙一共有多少种不同的跳法？【解析】 6种，如图，第1步跳到B ，4步回到A 有3种方法；同样第1步到C 的也有3种方法．根据加法原理，共有336+=种方法．AA A BCAB C BA【例 2】（难度等级 ※※※）甲、乙二人打乒乓球，谁先连胜两局谁赢，若没有人连胜头两局，则谁先胜三局谁赢，打到决出输赢为止．问：一共有多少种可能的情况？【解析】如下图，我们先考虑甲胜第一局的情况：图中打√的为胜者，一共有7种可能的情况．同理，乙胜第一局也有 7种可能的情况．一共有 7＋7=14（种）可能的情况．二、标数法适用于最短路线问题，需要一步一步标出所有相关点的线路数量，最终得到到达终点的方法总数．标数法是加法原理与递推思想的结合．【例 3】（难度等级 ※※）如图所示，沿线段从A 到B 有多少条最短路线？GFE D C BA111064332111AB【解析】图中B 在A 的右上方，因此从A 出发，只能向上或者向右才能使路线最短，那么反过来想，如果到达了某一个点，也只有两种可能：要么是从这个点左边的点来的，要么是从这个点下边的点来的．那么，如果最后到达了B ，只有两种可能：或者经过C 来到B 点，或者经D 来到B 点，因此，到达B 的走法数目就应该是到达C 点的走法数和到达D 点的走法数之和，而对于到达C 的走法，又等于到达E 和到达F 的走法之和，到达D 的走法也等于到达F和到达G的走法之和，这样我们就归纳出：到达任何一点的走法都等于到它左侧点走法数与到它下侧点走法数之和，根据加法原理，我们可以从A点开始，向右向上逐步求出到达各点的走法数．如图所示，使用标号方法得到从A到B共有10种不同的走法．【巩固】（难度等级※※）如图，从A点到B点的最近路线有多少条？BA10204111111B6243310A【解析】使用标号法得出到B点的最近路线有20条．【例 4】（难度等级※※）如图，某城市的街道由5条东西向马路和7条南北向马路组成，现在要从西南角的A处沿最短的路线走到东北角B出，由于修路，十字路口C不能通过，那么共有＿＿＿＿种不同走法．AA【解析】本题是最短路线问题．要找出共有多少种不同走法，关键是保证不重也不漏，一般采用标数法．如上图所示，共有120种．另解：本题也可采用排除法．由于不能经过C，可以先计算出从A到B的最短路线有多少条，再去掉其中那些经过C的路线数，即得到所求的结果．对于从A到B的每一条最短路线，需要向右6次，向上4次，共有10次向右或向上；而对于每一条最短路线，如果确定了其中的某6次是向右的，那么剩下的4次只能是向上的，从而该路线也就确定了．这就说明从A到B的最短路线的条数等于从10次向右或向上里面选择6次向右的种数，为610C．一般地，对于m n⨯的方格网，相对的两个顶点之间的最短路线有mm nC+种．本题中，从A到B的最短路线共有610C种；从A到C的最短路线共有26C种，从C到B的最短路线共有24C种，根据乘法原理，从A到B且必须经过C的最短路线有2264C C⨯种，所以，从A到B且不经过C的最短路线有622106421090120C C C-⨯=-=种．【例 5】（难度等级※※※）如图所示，从A点到B点，如果要求经过C点或D点的最近路线有多少条？【解析】1、方格图里两点的最短路径，从位置低的点向位置高的点出发的话，每到一点（如C、D点）只能向前或者向上．2、题问的是经过C点，或者D点；那么A到B点就可以分成两条路径了A--C---B；A---D---B，那么也就可以分成两类．但是需要考虑一个问题——A到B点的最短路径会同时经过C和D点吗？最短路径只能往上往前，经过观察发现C、D不会同时出现在最短路径上了．3、A---C---B，那么C就是必经之点了，就需要用到乘法原理了．A---C，最短路径用标数法标出，同样C---B点用标数法标注，然后相乘A---D---B，同样道理．最后结果是735+420=1155条．【例 6】如图1为一幅街道图，从A出发经过十字路口B，但不经过C走到D的不同的最短路线有条.【解析】到各点的走法数如图2所示.ACBD1118126666633211DB CA图1图2所以最短路径有18条.【例 7】小王在一年中去少年宫学习56次，如图所示，小王家在P点，他去少年宫都是走最近的路，且每次去时所走的路线正好互不相同，那么少年宫在________点处．EC【解析】本题属最短路线问题．运用标数法分别计算出从小王家P点到A、B、C、D、E点的不同路线有多少条，其中，路线条数与小王学习次数56相等的点即为少年宫．因为，从小王家P点到A点共有不同线路84条；到B点共有不同线路56条；到C点共有不同线路71条；到D点共有不同线路15条；到E点共有不同线路36条．所以，少年宫在B点处．【例 8】（难度等级※※※）在下图的街道示意图中，有几处街区有积水不能通行，那么从A 到B的最短路线有多少种？AB1111111111455511136162151422 1111 1311B A【解析】因为B在A的右下方，由标号法可知，从A到B的最短路径上，到达任何一点的走法数都等于到它左侧点的走法数与到它上侧点的走法数之和．有积水的街道不可能有路线经过，可以认为积水点的走法数是0．接下来，可以从左上角开始，按照加法原理，依次向下向右填上到各点的走法数．如右上图，从A到B的最短路线有22条．【例 9】（难度等级※※※）在下图的街道示意图中，C处因施工不能通行，从A到B的最短路线有多少条？CBA6033311122221111CBA【解析】因为B 在A 的右上方，由标号法可知，从A 到B 的最短路径上，到达任何一点的走法数都等于到它左侧点的走法数与到它下侧点的走法数之和．而C 是一个特殊的点，因为不能通行，所以不可能有路线经过C ，可以认为到达C 点的走法数是0．接下来，可以从左下角开始，按照加法原理，依次向上向右填上到各点的走法数．如图，从A 到B 的最短路线有6条．【巩固】（难度等级 ※※※）在下图的街道示意图中，C 处因施工不能通行，从A 到B 的最短路线有多少种？CB A【解析】因为B 在A 在右下方，由标号法可知，从A 到B 的最短路径上，到达任何一点的走法数都等于到它左侧点的走法数与到它上侧点的走法数之和.而C 是一个特殊的点，因为不能通行，所以不可能有路线经过C ，可以认为到达C 点的走法数是0.接下来，可以从左上角开始，按照加法原理，依次向下向右填上到各点的走法数.如图，从A 到B 的最短路线有6条．【例 10】（难度等级 ※※※）如下表，请读出“我们学习好玩的数学”这9个字，要求你选择的9个字里能连续(即相邻的字在表中也是左右相邻或上下相邻)，这里共有多少种完15111310146151132【解析】方法一：标数法．第一个字只能选位于左上角的“我”，以后每一个字都只能选择前面那个字的下方或右方的字，所以本题也可以使用标号法来解：(如右上图，在格子里标数)共70种不同的读法．方法二：组合法．仔细观察我们可以发现，按“我们学习好玩的数学”走的路线就是向右走四步，向下走四步的路线，而向下和向右一个排列顺序则代表了一种路线．所以总共有4870C 种不同的读法．【例 11】（难度等级 ※※※）如图，沿着“北京欢迎你”的顺序走（要求只能沿着水平或竖直方向走），一共有多少种不同的走法？北北京北北京欢京北欢迎欢你113112*********【解析】沿着“北京欢迎你”的顺序沿水平或竖直方向走，北以后的每一个字都只能选择上面的或左右两边的字，按加法原理，用标号法可得右上图．所以一共有11种走法．【巩固】（难度等级 ※※※）如下表，请读出“我们学习好玩的数学”这9个字，要求你选择的9个字里能连续(即相邻的字在表中也是左右相邻或上下相邻)，这里共有多少351511113451014610151512013570321【解析】第一个字只能选位于左上角的“我”，以后每一个字都只能选择前面那个字的下方或右方的字，所以本题也可以使用标号法来解：(在格子里标数)共70种不同的读法．【例 12】（难度等级※※※）在下图中，用水平或者垂直的线段连接相邻的字母，当沿着这些线段行走是，正好拼出“APPLE”的路线共有多少条？A|A—P—A| | |A—P—P—P—A| | | | |A—P—P—L—P—P—A| | | | | | |A—P—P—L—E—L—P—P—A1|1—3 —1| | |1—2—7 —2—1| | | | |1—2—4—15—4—2—1| | | | | | | 1—2—4—8—31—8—4—2—1【解析】要想拼出英语“APPLE”的单词，必须按照“A→P→P→L→E”的次序拼写．在图中的每一种拼写方式都对应着一条最短路径．如下图所示，运用标号法原理标号得出共有31种不同的路径．【巩固】如图1，用水平线或竖直线连结相邻汉字，沿着这些线读下去，正好可以读成“祖国明天更美好”，那么可读成“祖国明天更美好”的路线有条.【解析】如图2所示，利用加法原理，将读到各个字的路线数写在每个字下方，共有不同的路线721127-=(条).祖祖国祖祖国明国祖祖国明天明国祖祖国明天更天明国祖祖国明天更美更天明国祖祖国明天更美好美更天明国祖图1祖1祖1国3祖1祖1国2明7国2祖1祖1国2明4天15明4国2祖1祖1国2明4天8更31天8明4国2祖1祖1国2明4天8更16美63更16天8明4国2祖1祖1国2明4天8更16美32好127美32更16天8明4国2祖1图2【巩固】(第三届“希望杯”2试试题)右图中的“我爱希望杯”有______种不同的读法.杯杯杯杯杯望望望望希希希爱爱我161511353211111111杯杯杯杯杯望望望望希希希爱爱我【解析】“我爱希望杯”的读法也就是从“我”走到“杯”的方法.如上右图所示，共16种方法.【例 13】如图1所示，科学家“爱因斯坦”的英文名拼写为“Einstein”，按图中箭头所示方向有种不同的方法拼出英文单词“Einstein”.i111111i图1图2【解析】由E n s t e i n→i→→→→→→的拼法如图2所示.根据加法原理可得共有303060+=(种)不同拼法.【例 14】（难度等级※※※）图中有10个编好号码的房间，你可以从小号码房间走到相邻的大号码房间，但不能从大号码走到小号码，从1号房间走到10号房间共有多少种不同的走法？【解析】我们可以把这个图展开，用箭头标出来就更直观了，然后采用我们学的标数法．【例 15】（难度等级 ※※※）国际象棋中“马”的走法如图1所示，位于○位置的“马”只能走到标有×的方格中，类似于中国象棋中的“马走日”．如果“马”在88⨯的国际象棋棋盘中位于第一行第二列（图2中标有△的位置），要走到第八行第五列（图2中标有＠的位置），最短路线有________条．【2008年北京“数学解题能力展示”读者评选活动】第@图图1题@图2【解析】最后一步的可能如图1，倒数第二步的可能如图2，倒数第三步的可能如图3．最后36312++=（种）．图3图2@11112122图1@111122163321111@【例 16】（难度等级 ※※※）从北京出发有到达东京、莫斯科、巴黎和悉尼的航线，其他城市间的航线如图所示(虚线表示在地球背面的航线)，则从北京出发沿航线到达其他所有城市各一次的所有不同路线有多少？【解析】第一站到东京的路线有10条：⎧⎪⎪⎪⎧→→⎪→⎨⎪→→⎩⎪⎪⎧⎧→→⎪⎪⎨→⎪⎪⎩→→→⎨⎨→⎧⎪⎪→⎨⎪⎪→⎩⎩⎪⎪⎧⎧→⎪→⎪⎨⎪→⎪⎩→⎪⎨→⎧⎪⎪→⎨⎪⎪→⎩⎩⎩莫斯科巴黎悉尼纽约悉尼巴黎莫斯科巴黎悉尼纽约悉尼巴黎北京东京莫斯科纽约悉尼巴黎悉尼纽约巴黎莫斯科纽约莫斯科巴黎悉尼纽约莫斯科巴黎莫斯科纽约同理，第一站到悉尼、巴黎、莫斯科的路线各有10条，不同的路线共有10440⨯=条．【例 17】一个实心立方体的每个面分成了四部分．如图所示，从顶点P 出发，可找出沿图中相连的线段一步步到达顶点Q 的各种路径．若要求每步沿路径的运动都更加靠近Q ，则从P 到Q 的各种路径的数目为几？QP1818666333322111111QP【解析】因为正方体每个面的对面也有同样的路径，最靠近Q 的有三个点，从P 点到这三个点都是18种路径．故有18354⨯=三、简单递推：斐波那契数列的应用对于某些难以发现其一般情形的计数问题，可以找出其相邻数之间的递归关系，有了这一递归关系就可以利用前面的数求出后面的数，这种方法称为递推法．【例 18】（难度等级※※※）一楼梯共10级，规定每步只能跨上一级或两级，要登上第10级，共有多少种不同走法？【解析】登1级2级3级4级 ......10级1种方法2种3种5种 ......？我们观察每级的种数，发现这么一个规律：从第三个数开始，每个数是前面两个数的和；依此规律我们就可以知道了第10级的种数是89.其实这也是加法的运用：假如我们把这个人开始登楼梯的位置看做A0，那么登了1级的位置是在A1，2级在A2... A10级就在A10．到A3的前一步有两个位置；分别是A2和A1．在这里要强调一点，那么A2到A3既然是一步到了，那么A2、A3之间就是一种选择了；同理A1到A3也是一种选择了．同时我们假设到n级的选择数就是An ．那么从A0到A3就可以分成两类了：第一类：A0 ---- A1 ------ A3，那么就可以分成两步．有A1×1种，也就是A1种；(A1 ------ A3是一种选择)第二类：A0 ---- A2 ------ A3，同样道理有A2．类类相加原理：A3 = A1＋A2，依次类推An = An-1 + An-2．【例 19】（难度等级※※※）1×2的小长方形(横的竖的都行)覆盖2×10的方格网，共有多少种不同的盖法．【解析】如果用12⨯的长方形盖2n ⨯的长方形，设种数为n a ,则11a =，22a =,对于3n ≥，左边可能竖放1个12⨯的，也可能横放2个12⨯的，前者有-1n a 种，后者有-2n a 种，所以-1-2n n n a a a =+,所以根据递推，覆盖210⨯的长方形一共有89种．【例 20】（难度等级 ※※※）如下图，一只蜜蜂从A 处出发，回到家里B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？BAAB 1357946821235813213455891【解析】蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬近相邻大号码的蜂房．明确了行走路径的方向，就可以运用标数法进行计算．如右图所示，小蜜蜂从A 出发到B 处共有89种不同的回家方法．【巩固】小蜜蜂通过蜂巢房间，规定只能由小号房间进入大号房间问小蜜蜂由A 房间到达B 房间有多少种方法？【解析】斐波那契数列第八项．21种．【例 21】每对小兔子在出生后一个月就长成大兔子，而每对大兔子每个月能生出一对小兔子来．如果一个人在一月份买了一对小兔子，那么十二月份的时候他共有多少对兔子？【解析】第一个月，有1对小兔子；第二个月，长成大兔子，所以还是1对；第三个月，大兔子生下一对小兔子，所以共有2对；第四个月，刚生下的小兔子长成大兔子，而原来的大兔子又生下一对小兔子，共有3对；第五个月，两对大兔子生下2对小兔子，共有5对； ……这个特点的说明每月的大兔子数为上月的兔子数，每月的小兔子数为上月的大兔子数，即上上月的兔子数，所以每月的兔子数为上月的兔子数与上上月的兔子数相加．依次类推可以列出下表：经过月数：---1---2---3---4---5---6---7---8---9---10---11---12 兔子对数：---1---1---2---3---5---8--13--21--34--55--89--144 所以十二月份的时候总共有144对兔子．【例 22】树木生长的过程中，新生的枝条往往需要一段“休息”时间供自身生长，而后才能萌发新枝．一棵树苗在一年后长出一条新枝，第二年新枝“休息”，老枝依旧萌发新枝；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则依次“休息”．这在生物学上称为“鲁德维格定律”．那么十年后这棵树上有多少条树枝？【解析】一株树木各个年份的枝桠数，构成斐波那契数列：1，2，3，5，8，13，21，34，55，89，……所以十年后树上有89条树枝．【例 23】对一个自然数作如下操作：如果是偶数则除以2，如果是奇数则加1，如此进行直到得数为1操作停止．问经过9次操作变为1的数有多少个？【解析】可以先尝试一下，倒推得出下面的图：2410131112514302831643215167683421其中经1次操作变为1的1个，即2，经2次操作变为1的1个，即4，经3次操作变为1的2个，是一奇一偶，以后发现，每个偶数可以变成两个数，分别是一奇一偶，每个奇数变为一个偶数，于是，经1、2、…次操作变为1的数的个数依次为：1，1，2，3，5，8，…这一串数中有个特点：自第三个开始，每一个等于前两个的和，即即经过9次操作变为1的数有34个.为什么上面的规律是正确的呢？道理也很简单. 设经过n 次操作变为1的数的个数为n a ,则1a =1，2a =1，3a =2，… 从上面的图看出，1n a +比n a 大.一方面，每个经过n 次操作变为1的数，乘以2，就得出一个偶数，经过1n +次操作变为1；反过来，每个经过1n +次操作变为1的偶数，除以2，就得出一个经过n 次操作变为1的数. 所以经过n 次操作变为1的数与经过1n +次操作变为1的偶数恰好一样多.前者的个数是n a ,因此后者也是n a 个.另一方面，每个经过n 次操作变为1的偶数，减去1，就得出一个奇数，它经过1n +次操作变为1，反过来.每个经过1n +次操作变为1的奇数，加上1，就得出一个偶数，它经过n 次操作变为1. 所以经过n 次操作变为1的偶数经过1n +次操作变为1的奇数恰好一样多.而由上面所说，前者的个数就是1n a -,因此后者也是1n a -.经过n +1次操作变为1的数，分为偶数、奇数两类，所以11n n n a a a +-=+，即上面所说的规律的确成立.。

小学数学竞赛计数之归纳法.教师版与学生版

前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法，比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等，这里再集中学习一下计数中其他常见的方法，主要有归纳法、整体法、对应法、递推法．对这些计数方法与技巧要做到灵活运用．从条件值较小的数开始，找出其中规律，或找出其中的递推数量关系，归纳出一般情况下的数量关系．【例 1】如图所示，在2×2方格中，画一条直线最多穿过3个方格；在3×3方格中，画一条直线最多穿过5个方可知；那么在5×5方格中，画一条直线，最多穿过个方格。

【考点】计数之归纳法【难度】2星【题型】填空【关键词】希望杯，四年级，复赛，第14题，6分【解析】边长每多1，穿过的方格多2，那么5×5的最多穿过3+2+2+2=9个方格【答案】9【例 2】一条直线分一个平面为两部分．两条直线最多分这个平面为四部分．问5条直线最多分这个平面为多少部分?【考点】计数之归纳法【难度】3星【题型】解答【解析】方法一：我们可以在纸上试着画出1条直线，2条直线，3条直线，……时的情形，于是得到下表：由上表已知5条直线最多可将这个平面分成16个部分，并且不难知晓，当有n条直线时，最多可将平面分成2+2+3+4+…+n=()12n n++1个部分．方法二：如果已有k条直线，再增加一条直线，这条直线与前k条直线的交点至多k个，因而至多被分成k+1段，每一段将原有的部分分成两个部分，所以至多增加k+1个部分．于是3条直线至多将平面分为4+3=7个部分，4条直线至多将平面分为7+4=11个部分，5条直线至多将平面分为11+5=16个部分．一般的有k条直线最多将平面分成：1+1+2+…+k=()12k k++1个部分，所以五条直线可以分平面为16个部分．例题精讲教学目标7-6-1.计数之归纳法【答案】16【巩固】平面上5条直线最多能把圆的内部分成几部分？平面上100条直线最多能把圆的内部分成几部分？【考点】计数之归纳法【难度】4星【题型】解答【解析】假设用a k 表示k 条直线最多能把圆的内部分成的部分数，这里k ＝0，1，2，……a 0＝1a 1=a 0+1＝2 a 2=a 1＋2=4 a 3=a 2＋3=7 a 4=a 3+4＝11 ……故5条直线可以把圆分成16部分，100条直线可以把圆分成5051部分【答案】5051部分【例 3】平面上10个两两相交的圆最多能将平面分割成多少个区域？【考点】计数之归纳法【难度】4星【题型】解答【解析】先考虑最简单的情形．为了叙述方便，设平面上k 个圆最多能将平面分割成k a 个部分．141312111098765432187652134431221从图中可以看出，12a =，24221a ==+⨯，38422a ==+⨯，414823a ==+⨯，…… 可以发现k a 满足下列关系式：()121k k a a k -=+-．实际上，当平面上的(1k -)个圆把平面分成1k a -个区域时，如果再在平面上出现第k 个圆，为了保证划分平面的区域尽可能多，新添的第k 个圆不能通过平面上前()1k -个圆之间的交点．这样，第k 个圆与前面()1k -个圆共产生2(1)k ⨯-个交点，如下图：这2(1)k ⨯-个交点把第k 个圆分成了2(1)k ⨯-段圆弧，而这2(1)k ⨯-段圆弧中的每一段都将所在的区域一分为二，所以也就是整个平面的区域数增加了2(1)k ⨯-个部分．所以，()121k k a a k -=+-．那么，10987292829272829a a a a =+⨯=+⨯+⨯=+⨯+⨯+⨯=12122...272829a =+⨯+⨯++⨯+⨯+⨯ ()2212...78992=+⨯+++++=．故10个圆最多能将平面分成92部分．【答案】92【例 4】 10个三角形最多将平面分成几个部分？【考点】计数之归纳法【难度】4星【题型】解答【解析】设n 个三角形最多将平面分成n a 个部分．1n =时，12a =；2n =时，第二个三角形的每一条边与第一个三角形最多有2个交点，三条边与第一个三角形最多有236⨯=（个）交点．这6个交点将第二个三角形的周边分成了6段，这6段中的每一段都将原来的每一个部分分成2个部分，从而平面也增加了6个部分，即2223a =+⨯．3n =时，第三个三角形与前面两个三角形最多有4312⨯=（个）交点，从而平面也增加了12个部分，即：322343a =+⨯+⨯． …… 一般地，第n 个三角形与前面()1n -个三角形最多有()213n -⨯个交点，从而平面也增加()213n -⨯个部分，故()()222343213224213332n a n n n n ⎡⎤=+⨯+⨯++-⨯=++++-⨯=-+⎣⎦；特别地，当10n =时，2103103102272a =⨯+⨯+=，即10个三角形最多把平面分成272个部分．【答案】272【例 5】一个长方形把平面分成两部分，那么3个长方形最多把平面分成多少部分？【考点】计数之归纳法【难度】4星【题型】解答【解析】一个长方形把平面分成两部分．第二个长方形的每一条边至多把第一个长方形的内部分成2部分，这样第一个长方形的内部至多被第二个长方形分成五部分．同理，第二个长方形的内部至少被第一个长方形分成五部分．这两个长方形有公共部分(如下图，标有数字9的部分)．还有一个区域位于两个长方形外面，所以两个长方形至多把平面分成10部分．第三个长方形的每一条边至多与前两个长方形中的每一个的两条边相交，故第一条边被隔成五条小线段，其中间的三条小线段中的每一条线段都把前两个长方形内部的某一部分一分为二，所以至多增加3×4=12个部分．而第三个长方形的4个顶点都在前两个长方形的外面，至多能增加4个部分．所以三个长方形最多能将平面分成10+12+4=26．【小结】n 个图形最多可把平面分成部分数：直线：()112n n ⨯++；圆：()21n n +⨯-；三角形：()231n n +⨯⨯- ；长方形：()241n n +⨯⨯-．【答案】26【例 6】在平面上画5个圆和1条直线，最多可把平面分成多少部分? 【考点】计数之归纳法【难度】5星【题型】解答【解析】先考虑圆．1个圆将平面分成2个部分．这时增加1个圆，这个圆与原有的1个圆最多有两个交点，成为2条弧，每条弧将平面的一部分一分为二，增加了2个部分，所以2个圆最多将平面分成4个部分．当有3个圆时，第3个圆与原有的2个产生4个交点而增加4个部分，所以3个圆最多将平面分成8个部分．同样的道理，5个圆最多将平面分成22个部分．再考虑直线．直线与每个圆最多有2个交点，这样与5个圆最多有10个交点．它们将直线分成11条线段或射线，而每条线段又将平面的一部分一分为二，2条射线增加了一部分，因此5个圆和1条直线最多可将平面分成32个部分．【答案】32【例 7】在一个西瓜上切6刀，最多能将瓜皮切成多少片？【考点】计数之归纳法【难度】4星【题型】解答【解析】将西瓜看做一个球体，球体上任意一个切割面都是圆形，所以球面上的切割线是封闭的圆周，考虑每一次切割能增加多少瓜皮片．当切1刀时，瓜皮被切成两份，当切第2刀时，由于切割线相交，所以瓜皮被切成4分，……，切第n次时，新增加的切割线与原来的切割线最多有()n-个交点．这21些交点将第n条切割线分成()21n-，所以21n-段，也就是说新增加的切割线使瓜皮数量增加了()在西瓜上切6刀，最多能将瓜皮切成11212223242532++⨯+⨯+⨯+⨯+⨯=片．【答案】32【例 8】在一大块面包上切6刀最多能将面包切成多少块．（注：面包是一个立体几何图形，切面可以是任何方向）【考点】计数之归纳法【难度】5星【题型】解答【解析】题目相当于6个平面能将空间划分为多少个部分．通过找规律来寻找递推关系，显然的1个平面能将空间划分成2块，2个平面能将空间划分成4块，3个平面能将空间划分成8个平面，当增加到第四个平面时，第四个平面这能将原来空间中的8个部分中的其中几个划分．如图：注意到第四个平面与其他三个平面相交形成3条直线，这三条直线将第四个平面分割成7个部分，而每一部分将原来三个平面划分的8个空间中的7个划分成两份，所以4个平面能将空间划分成+=个部分．8715同样的第五个平面与前四个平面分别相交成4条直线，这四条直线能将第5个平面分割成++++=个部分，每一部分都划分原空间中的某一区域，所以第五个平面能使空间中的区1123411域增加到151126+==个部分．当增加到6个平面时，第六个平面共被划分成11234516+++++=个部分，所以第6个平面能将空间中的区块数增加到261642+=个部分．所以6刀能将面包切成42块．【答案】427-6-1.计数之归纳法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法，比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等，这里再集中学习一下计数中其他常见的方法，主要有归纳法、整体法、对应法、递推法．对这些计数方法与技巧要做到灵活运用．从条件值较小的数开始，找出其中规律，或找出其中的递推数量关系，归纳出一般情况下的数量关系．【例 9】如图所示，在2×2方格中，画一条直线最多穿过3个方格；在3×3方格中，画一条直线最多穿过5个方可知；那么在5×5方格中，画一条直线，最多穿过个方格。

小学奥数加法原理之树形图及标数法.学生版

1.使学生掌握加法原理的基本内容；2.掌握加法原理的运用以及与乘法原理的区别；3.培养学生分类讨论问题的能力，了解分类的主要方法和遵循的主要原则．加法原理的数学思想主旨在于分类讨论问题，教授本讲的目的也是为了培养学生分类讨论问题的习惯，锻炼思维的周全细致．一、加法原理概念引入生活中常有这样的情况，就是在做一件事时，有几类不同的方法，而每一类方法中，又有几种可能的做法．那么，考虑完成这件事所有可能的做法，就要用加法原理来解决．例如:王老师从北京到天津，他可以乘火车也可以乘长途汽车，现在知道每天有五次火车从北京到天津，有4趟长途汽车从北京到天津．那么他在一天中去天津能有多少种不同的走法？分析这个问题发现，王老师去天津要么乘火车，要么乘长途汽车，有这两大类走法，如果乘火车，有5种走法，如果乘长途汽车，有4种走法．上面的每一种走法都可以从北京到天津，故共有5+4=9种不同的走法．在上面的问题中，完成一件事有两大类不同的方法．在具体做的时候，只要采用一类中的一种方法就可以完成．并且两大类方法是互无影响的，那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数．二、加法原理的定义一般地，如果完成一件事有k 类方法，第一类方法中有1m 种不同做法，第二类方法中有2m 种不同做法，…，第k 类方法中有k m 种不同做法，则完成这件事共有12 k N m m m =+++……种不同方法，这就是加法原理．加法原理运用的范围：完成一件事的方法分成几类，每一类中的任何一种方法都能完成任务，这样的问题可以使用加法原理解决．我们可以简记为：“加法分类，类类独立”．分类时，首先要根据问题的特点确定一个适合于它的分类标准，然后在这知识要点教学目标7-1-3.加法原理之树形图及标数法个标准下进行分类；其次，分类时要注意满足两条基本原则： ① 完成这件事的任何一种方法必须属于某一类； ② 分别属于不同两类的两种方法是不同的方法．只有满足这两条基本原则，才可以保证分类计数原理计算正确．运用加法原理解题时，关键是确定分类的标准，然后再针对各类逐一计数．通俗地说，就是“整体等于局部之和”．三、加法原理解题三部曲 1、完成一件事分N 类；2、每类找种数（每类的一种情况必须是能完成该件事）；3、类类相加枚举法：枚举法又叫穷举法，就是把所有符合条件的对象一一列举出来进行计数．分类讨论的时候经常会需要把每一类的情况全部列举出来，这时的方法就是枚举法．枚举的时候要注意顺序，这样才能做到不重不漏．模块一、树形图法“树形图法”实际上是枚举的一种，但是它借助于图形，可以使枚举过程不仅形象直观，而且有条理又不重复遗漏，使人一目了然．【例 1】 A 、B 、C 三个小朋友互相传球，先从A 开始发球(作为第一次传球)，这样经过了5次传球后，球恰巧又回到A 手中，那么不同的传球方式共多少种？【考点】加法原理之树形图法【难度】3星【题型】解答【关键词】2005年，小数报【解析】如图，A 第一次传给B ，到第五次传回A 有5种不同方式．同理，A 第一次传给C ，也有5种不同方式．所以，根据加法原理，不同的传球方式共有5510+=种．C B CC B AAB A B CCBA【答案】10例题精讲【巩固】一只青蛙在A ，B ，C 三点之间跳动，若青蛙从A 点跳起，跳4次仍回到A 点，则这只青蛙一共有多少种不同的跳法？【考点】加法原理之树形图法【难度】3星【题型】解答【解析】 6种，如图，第1步跳到B ，4步回到A 有3种方法；同样第1步到C 的也有3种方法．根据加法原理，共有336+=种方法．AA A BCAB C BA【答案】6【例 2】甲、乙二人打乒乓球，谁先连胜两局谁赢，若没有人连胜头两局，则谁先胜三局谁赢，打到决出输赢为止．问：一共有多少种可能的情况？【考点】加法原理之树形图法【难度】3星【题型】解答【解析】如下图，我们先考虑甲胜第一局的情况：图中打√的为胜者，一共有7种可能的情况．同理，乙胜第一局也有 7种可能的情况．一共有 7＋7=14（种）可能的情况．【答案】14【例 3】如图，从起点走到终点，要求取出每个站点上的旗子，并且每个站点只允许通过一次，有种不同的走法。

奥数标数法练习计数之标数法经典例题讲解

奥数标数法练习计数之标数法经典例题讲解解答：第1步：在起点A处标1。

再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点C处标1＋1＝2。

同理重复点F，点D，点E，点G，点H，点I【第三篇】分析:既然要走最短路线,自然是不能回头走,所以从A地到B地的过程中只能向右或向下走.我们首先来确认一件事,如下图从A地到P点有m种走法,到Q点有n种走法,那么从A地到B 地有多少种走法呢?就是用加法原理,一共有m+n种走法.这个问题明白了之后,我们就可以来解决这道例题了:首先由于只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不可以走回头路).我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.【第四篇】有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字可以重复) 这是一道数论的题目,但是我们也可以使用标数法来解答,并且非常直观.到第一站可以有5种选择,每种选择有一种走法,那么下一站,走1号门就只有一种走法(就是第一站走的2号门),走2号门就有2种走法(第一站走1号或3号门)走3号门也是2种走法(第一站走2号门或4号门)走4号门2种走法(第一站走3号门或者5号门)走5号门只有一种走法(第一站走的是4号门)我们发现在这一站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们可以将数字标全.这道题的答案就是42种,虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.可以用到标数法的问题有很多，大家掌握这种方法之后可以解决很多平时看起来很麻烦的题目。

苏教版数学四年级下册计数的基本方法—标数法(试题)

苏教版数学四年级下册计数的基本方法—标数法（试题）例1.苏珊从A步行到Z,行走方向都是向东或向南,路线如图所示。

那么苏珊从A到Z有多少条不同的行走路线?例2.按图中箭头所指的方向行走,从A到I共有多少条不同的路线?例3.按图中箭头方向所指行走,从A到G有多少种不同的路线?例4.一只蜜蜂从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?例5.如图所示,科学家“爱因斯坦”的英文名拼写为“Einstein”,按图中箭头所示方向有多少种不同的方法拼出英文单词“Einstein”?例6.在右图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出“APPLE”的路线共有多少条？例7.图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间,从1号房间走到10号房间共有多少种不同走法?例8.图中是A、B、C的公路网,汽车从A出发经过B到C可以选择不绕远路的不同路线共有多少种?例9.在右边的街道示意图中,C处因施工不能通行,从A到B的最短路线有多少条?例10.如图,从A到B沿网格线不经过线段CD和EF的最短路径的条数是多少条?例11.如图所示,从A点沿线段走最短路径到B点,每次走一步或两步,共有多少种不同走法?(注:路线相同步骤不同,认为是不同走法)例12.甲队和乙队进行的一场足球赛的最终比分是4:2,已知甲队先进一球,而乙队在比赛过程中始终没有领先过,那么两队的入球次序共有多少种不同的可能？综合练习1.(1)某镇街道分布如图,一个居民要从A处前往B处,如果规定只能走从左到右或从上到下的方向,那么该居民共有可选择的不同路线的条数是多少?(2)如图,从A到B,只许向下或向右走,一共有多少种不同的路线?2.(1)如图,如果只允许向下移动,从A到B共有多少种不同的路线?(2)如图,要从A点到B点,要求每一步都是向右,向上或者斜上方,问共有多少种不同的走法?3.(1)在图中,从甲地到乙地最近的道路共有多少条?(2)如图,由A地到B地,若规定只能往右或往下走,共有多少种不同的路线?4.如图,按照箭头方向组成“明心奥数”四个字的不同路线,一共有多少条？5.(1)如图,一个正方形大厅,分隔成25个小间,每相邻两间之间都可相通,位于它的对角线位置上的四间作为休息室,其余布置成展览室从A处出发,使走过的房间数最少而到达休息室的不同走法共有多少种?(2)在右上图中,可以有多少种不同的方法来连成“迎接澳门回归”这句话?6.图中是一个道路图,圆圈处有128个孩子,这群孩子从圆圈处开始,经过每个路口时都有一半人向上走,另一半人向右走那么A、B、C、D四个路口,按照经过路口的人数从多到少排列依次是多少?7.图中是某城市道路交通图。

小学奥数计数之标数法经典例题讲解【三篇】

小学奥数计数之标数法经典例题讲解【三篇】
解答：蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”
这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。

明确了行
走路径的方向，就可使用标数法实行计算。

如图所示，小蜜蜂从A出发到B处共有89种不同的回家方法。

【第二篇】
例1．按图中箭头所指的方向行走，从A到I共有多少条不同的路线？
解答：
第1步：在起点A处标1。

再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点
C处标1＋1＝2。

奥数标数法练习计数之标数法经典例题讲解

奥数标数法练习计数之标数法经典例题讲解【第一篇】一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？如图所示，小蜜蜂从A出发到B处共有89种不同的回家方法。

【第二篇】例1．按图中箭头所指的方向行走，从A到I共有多少条不同的路线？解答：第1步：在起点A处标1。

再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点C处标1＋1＝2。

同理重复点F，点D，点E，点G，点H，点I【第三篇】分析：既然要走最短路线,自然是不能回头走,所以从A地到B地的过程中只能向右或向下走.我们首先来确认一件事,如下图从A地到P点有m种走法,到Q点有n种走法,那么从A地到B地有多少种走法呢?就是用加法原理,一共有m+n种走法.这个问题明白了之后,我们就能够来解决这道例题了：首先因为只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不能够走回头路).我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.【第四篇】有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字能够重复)这是一道数论的题目,但是我们也能够使用标数法来解答,并且非常直观.到第一站能够有5种选择,每种选择有一种走法,那么下一站,走1号门就只有一种走法(就是第一站走的2号门),走2号门就有2种走法(第一站走1号或3号门)走3号门也是2种走法(第一站走2号门或4号门)走4号门2种走法(第一站走3号门或者5号门)走5号门只有一种走法(第一站走的是4号门)我们发现在这个站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们能够将数字标全.这道题的答案就是42种,虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.能够用到标数法的问题有很多，大家掌握这种方法之后能够解决很多平时看起来很麻烦的题目。

标数法

训练题
(7)
》的选择题
3
的条件应为“
……使
AE EB
=
FC DF
=
2
007.
……”,填空题 1 的解答“ ……p
=
2 xy x+ y
=
40 2
011470 .
……”应为“ ……p =
2 xy x+ y
=
50 2
140 017
.
……”;《数学奥林匹克高中训练题
(10) 》的选择题 6 的解答在分类 (1) 中遗漏了一
f (1 , n) = 4 ×1 + 3 (2 n - 2)
= 4 + 6 n - 6 = 6 n - 2.
中等数学
算公式.
首先 ,显然有
f (3 ,1) = f (1 ,3) = 16 ,
f (3 ,2) = f (2 ,3) = 50.
其次 ,当 n = 3 时 ,
A 、C 两类格点各有 4
次 ,故合乎条件的正方形的个数为1244 = 31.
参考文献 : [1 ] 董迎新. 中考加分题对教学的启示 [J ] . 中小学数学
(教师版) ,2004 (122) . [2 ] 周士藩. 对一道中考加分题的思考 [J ] . 中小学数学
(教师版) ,2004 (3) . [3 ] 季小冬. 对一道中考加分题的再思考[J ] . 中小学数学
补充为 30 ,而文 [ 3 ] 补充得出的正确答案为
32. 由此可见 ,这一问题看似简单 ,但稍不留
神 ,就会导致解题失误.
本文介绍解决这类计数问题的一种行之
有效的方法 ———标数法 ,它能很好地避免上

【推荐】小学奥数训练专题加法原理之树形图及标数法.学生版.doc

1.使学生掌握加法原理的基本内容；2.掌握加法原理的运用以及与乘法原理的区别；3.培养学生分类讨论问题的能力，了解分类的主要方法和遵循的主要原则．加法原理的数学思想主旨在于分类讨论问题，教授本讲的目的也是为了培养学生分类讨论问题的习惯，锻炼思维的周全细致．一、加法原理概念引入生活中常有这样的情况，就是在做一件事时，有几类不同的方法，而每一类方法中，又有几种可能的做法．那么，考虑完成这件事所有可能的做法，就要用加法原理来解决．例如:王老师从北京到天津，他可以乘火车也可以乘长途汽车，现在知道每天有五次火车从北京到天津，有4趟长途汽车从北京到天津．那么他在一天中去天津能有多少种不同的走法？分析这个问题发现，王老师去天津要么乘火车，要么乘长途汽车，有这两大类走法，如果乘火车，有5种走法，如果乘长途汽车，有4种走法．上面的每一种走法都可以从北京到天津，故共有5+4=9种不同的走法．在上面的问题中，完成一件事有两大类不同的方法．在具体做的时候，只要采用一类中的一种方法就可以完成．并且两大类方法是互无影响的，那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数．二、加法原理的定义一般地，如果完成一件事有k 类方法，第一类方法中有1m 种不同做法，第二类方法中有2m 种不同做法，…，第k 类方法中有k m 种不同做法，则完成这件事共有12 k N m m m =+++……种不同方法，这就是加法原理．加法原理运用的范围：完成一件事的方法分成几类，每一类中的任何一种方法都能完成任务，这样的问题可以使用加法原理解决．我们可以简记为：“加法分类，类类独立”．分类时，首先要根据问题的特点确定一个适合于它的分类标准，然后在这个标准下进行分类；其次，分类时要注意满足两条基本原则： ① 完成这件事的任何一种方法必须属于某一类； ② 分别属于不同两类的两种方法是不同的方法．只有满足这两条基本原则，才可以保证分类计数原理计算正确．运用加法原理解题时，关键是确定分类的标准，然后再针对各类逐一计数．通俗地说，就是“整体等于局部之和”．三、加法原理解题三部曲1、完成一件事分N 类；2、每类找种数（每类的一种情况必须是能完成该件事）；3、类类相加枚举法：枚举法又叫穷举法，就是把所有符合条件的对象一一列举出来进行计数．分类讨论的时候经常会需要把每一类的情况全部列举出来，这时的方法就是枚举法．枚举的时候要注意顺序，这样才能做到不重不漏．知识要点教学目标7-1-3.加法原理之树形图及标数法模块一、树形图法“树形图法”实际上是枚举的一种，但是它借助于图形，可以使枚举过程不仅形象直观，而且有条理又不重复遗漏，使人一目了然．【例 1】 A 、B 、C 三个小朋友互相传球，先从A 开始发球(作为第一次传球)，这样经过了5次传球后，球恰巧又回到A 手中，那么不同的传球方式共多少种？【考点】加法原理之树形图法【难度】3星【题型】解答【关键词】2005年，小数报【解析】如图，A 第一次传给B ，到第五次传回A 有5种不同方式．同理，A 第一次传给C ，也有5种不同方式．所以，根据加法原理，不同的传球方式共有5510+=种．C B CC B AB A B CCBA【答案】10【巩固】一只青蛙在A ，B ，C 三点之间跳动，若青蛙从A 点跳起，跳4次仍回到A 点，则这只青蛙一共有多少种不同的跳法？【考点】加法原理之树形图法【难度】3星【题型】解答【解析】 6种，如图，第1步跳到B ，4步回到A 有3种方法；同样第1步到C 的也有3种方法．根据加法原理，共有336+=种方法．AA A BCAB C BA【答案】6【例 2】甲、乙二人打乒乓球，谁先连胜两局谁赢，若没有人连胜头两局，则谁先胜三局谁赢，打到决出输赢为止．问：一共有多少种可能的情况？【考点】加法原理之树形图法【难度】3星【题型】解答【解析】如下图，我们先考虑甲胜第一局的情况：图中打√的为胜者，一共有7种可能的情况．同理，乙胜第一局也有 7种可能的情况．一共有 7＋7=14（种）可能的情况．例题精讲【答案】14【例 3】如图，从起点走到终点，要求取出每个站点上的旗子，并且每个站点只允许通过一次，有种不同的走法。

四年级数学：标数法

四年级数学：标数法标数法：是一种技巧性很强的方法，掌握好了方法，可以快速解决相关题型。

标数法的技巧：1、把起点标为1；2、之后每个点上的数=所有来这个点的“正确”方向上各自最近点上数之和。

如果只有一个正确方向过来这个点，那么就把唯一的一个方向上最近的点上数挪过来。

3、如果目标在起点的右上方，那么必须往右，往上或者往右上方向走。

如右图：（1）某个点，从左边来，从下边来，所有数为A+B，（2）某个点，只能从左边来，把A数挪过来。

（3）某个点，只能往上走，把B数挪过来。

一、基础例题1、如图小明要从家去学校，图中的线段是街道。

小明只能沿着街道从家去学校，那么请问小明最短最合理的路线有多少种？2、从学校到图书馆，所走路线最短最合理的走法一共有多少种？3、图中的线路表示的是小刚从家到学校所能经过的所有街道，问小刚上学一共有多少条不同的最短路线？4、如图，要从点A到点B去，问最短的线路有多少种？5、现在要从点A到点B去，但是C点正在施工，不能经过。

问最短的路线有多少种？6、小明要从学校去少年宫，但是不能经过A点，问最短路线有多少种？7、如图是一街道的平面图，从A点到B点有多少种最近的走法？8、小明从A点步行到Z点,只能往右或者往下走，路线如图所示，那么小明从A 点到Z点的最短路线有多少条？二、拓展例题1、按照图中箭头所指的方向行走，那么从A点到I点一共有多少条不同的路线？2、按照图中箭头所指的方向行走，那么从A点到G点一共有多少条不同的路线？3、一只小蜜蜂呀，从点A出发，A回到家B，每次只能从一个蜂房爬向右侧相邻的蜂房而不准逆行，一共有多少种回家的方法？（右侧：正右，右上，右下三种都算右侧方向。

）4、如图所示，科学家爱因斯坦的英文名拼写为“Einstein”按照图中箭头所指方向有多少种不同的方法拼出英文单词“Einstein”？5、图中有10方格编好号码的方向，你可以从小号码房间走到相邻的大号码房间，但是不能从大号码房间走到小号码房间，从1号房间走到10号房间共有多少种不同的走法？6、图中是关于A、B、C的公路网，汽车从A点到B点再到C点可以选择不绕远路的不同路线各有几种？7、在右边的街道示意图中，C处因为施工不可以通过，问从A点到B点的最短路线有多少条？8、如图所示从A点到B点沿着网格线不经过线段CD和EF的最短路线的条数有多少条？作业：1、从点A到点B的最短路线有几条？只可以向右或者向下走。

小学计数知识学习习题：标数法(含答案)

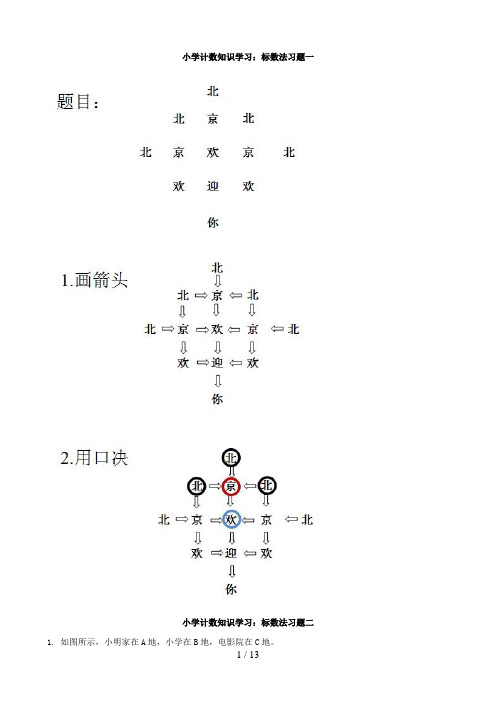
小学计数知识学习：标数法习题一小学计数知识学习：标数法习题二1. 如图所示，小明家在A地，小学在B地，电影院在C地。

1.小明从家里去学校，走最短的线路，有多少种走法?2.小明从家里去电影院，走最短线路，有多少种走法?小学计数知识学习：标数法习题三如图，从一楼到二楼有12梯，小明一步只能上1梯或2梯，问小明从1楼上到2楼有多少种走法？小学计数知识学习：标数法习题四一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？解答：蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。

明确了行走路径的方向，就可运用标数法进行计算。

如图所示，小蜜蜂从A出发到B处共有89种不同的回家方法。

小学计数知识学习：标数法习题五例1．按图中箭头所指的方向行走，从A到I共有多少条不同的路线？解答：第1步：在起点A处标1。

再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点C处标1＋1＝2。

同理重复点F，点D，点E，点G，点H，点I小学计数知识学习：标数法习题六分析:既然要走最短路线,自然是不能回头走,所以从A地到B地的过程中只能向右或向下走. 我们首先来确认一件事,如下图从A地到P点有m种走法,到Q点有n种走法,那么从A地到B地有多少种走法呢?就是用加法原理,一共有m+n种走法.这个问题明白了之后,我们就可以来解决这道例题了:首先由于只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不可以走回头路).我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.小学计数知识学习：标数法习题七有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字可以重复)这是一道数论的题目,但是我们也可以使用标数法来解答,并且非常直观.到第一站可以有5种选择,每种选择有一种走法, 那么下一站,走1号门就只有一种走法(就是第一站走的2号门),走2号门就有2种走法(第一站走1号或3号门)走3号门也是2种走法(第一站走2号门或4号门)走4号门2种走法(第一站走3号门或者5号门)走5号门只有一种走法(第一站走的是4号门)我们发现在这一站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们可以将数字标全.这道题的答案就是42种,虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.可以用到标数法的问题有很多，大家掌握这种方法之后可以解决很多平时看起来很麻烦的题目。

小学五六年级奥数学竞赛第6讲计数方法之标数法、递推法

【例3】(★★★★) 在下图中，左下角有1枚棋子，每次可以向上，向右，或沿对角线的方向向右上走任意多步，但不能不走。那么走到右上角一共有多少种方法？
【例4】(★★★★★) 中10片莲叶如右图排列．青蛙在莲叶间跳跃，每次只能从一，池塘中片莲叶跳到相邻的另一片莲叶．一只青蛙盘算着从其中一片莲叶上起跳，连跳4步，那么它有种不同的跳法．
【例6】(★★★) 如下图，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？
A
B
【例7】(★★★) 一个楼梯共有12级台阶，规定每步可以迈1级台阶或2级台阶，最多可以迈3级台阶，从地面到最阶一共可以有多少种不同的走法？
重点例题：例3、例4、例5、例7、例8
2
【例8】(★★★) 在平面上画8个圆，最多可以把平面分成_______部分。
本讲总结 ①标数法与递推法都是加法原理 ②按最后一步进行分类，做加法 ③标数时要注意限制条件 ④ 平 ④分平面问题要确定交点个数要确点个
【例9】(★★★★) 一个长方形把平面分成两部分，那么个长方形把平面分成两部分那么10个长方形最多把平面分成 _______部分.
计数方法之标数法、递推法
【例1】(★★) 如图所示科学家“爱因斯坦”的英文名拼写为“ 如图所示，科学家爱因斯坦的英文名拼写为 Einstein Einstein”，按按图中箭头所示方向有______种不同的方法拼出英文单词 “Einstein”。
【例2】(★★) 如图，为一幅街道图，从A出发经过十字路口B，但不经过C走到D的不同的最短路线有多少条？
○
1
【例5】(★★★★★) 游乐园门票1元1张，每人限购1张.现有10个小朋友排队购买，其中5个小朋友只有1元的钞票，另外5个小朋友只有2元的钞票，售票员没有零钱。10个小朋友排队，不同的排队方法总共有10！＝3628800种，问其中有种问其中有______种排队方法，售票员总能找的开种排队方法售票员总能找的开零钱。

小奥四年级标数法教学内容

小奥四年级标数法四年级计数问题：标数法难度：高难度如图，某城市的街道由5条东西向马路和7条南北向马路组成，现在要从西南角的处沿最短的路线走到东北角出，由于修路，十字路口不能通过，那么共有＿＿＿＿种不同走法．解答：四年级计数问题：标数法难度：中难度如图为一幅街道图，从A出发经过十字路口B，但不经过C走到D的不同的最短路线有条.解答：计数习题标数法和加法原理的综合应用（★★★★）有20个相同的棋子，一个人分若干次取，每次可取1个，2个，3个或4个，但要求每次取之后留下的棋子数不是3或4的倍数，有（）种不同的方法取完这堆棋子.【分析】把20、0和20以内不是3或4的倍数的数写成一串，用标号法把所有的方法数写出来：考点说明：本题主要考察学生对于归纳递推思想的理解，具体来说就是列表标数法的使用，难度一般，只要发现了题目中的限制条件，写出符合条件的剩余棋子数，然后进行递推就可以了。

<评价> ：计数问题在各大考试中所占的分量越来越重，计数的知识也学习的比较早，标号法是加乘原理中加法原理的内容，在四年级以前已经学习过，但是灵活应用学习过的知识才是学习最重要的意义，六年级上（第十一级）第10讲会将计数问题与应用题或者最值问题进行综合学习，学习后能力会有进一步的提高。

计数方法与技巧（标数法例题1）计数方法与技巧（标数法例题2）计数方法与技巧（标数法例题3）1. 如图所示，小明家在A地，小学在B地，电影院在C地。

1.小明从家里去学校，走最短的线路，有多少种走法?2.小明从家里去电影院，走最短线路，有多少种走法?如图，从一楼到二楼有12梯，小明一步只能上1梯或2梯，问小明从1楼上到2楼有多少种走法？一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？解答：蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。

小奥四年级标数法

：计数问题在各大考试中所占的分量越来越重，计数的知识也学习的比较早，标号法是加乘原理中加法原理的内容，在四年级以前已经学习过，但是灵活应用学习过的知识才是学习最重要的意义，六年级上（第十一级）第10讲会将计数问题与应用题或者最值问题进行综合学习，学习后能力会有进一步的提高。

明确了行走路径的方向，就可运用标数法进行计算。

计数第06讲_标数法(学生版)A4

【精选】奥数：计数之对应法.学生版

标数法——学生版

标数法

小学数学竞赛 计数之归纳法.教师版与学生版

小学奥数 加法原理之树形图及标数法.学生版

奥数标数法练习 计数之标数法经典例题讲解

苏教版数学四年级下册 计数的基本方法—标数法(试题)

小学奥数计数之标数法经典例题讲解【三篇】

奥数标数法练习 计数之标数法经典例题讲解

标数法

【推荐】小学奥数训练专题 加法原理之树形图及标数法.学生版.doc

四年级数学：标数法

小学计数知识学习习题：标数法(含答案)

小学五六年级奥数学竞赛第6讲计数方法之标数法、递推法

小奥四年级标数法教学内容

小奥四年级标数法

小学数学竞赛计数之归纳法.教师版与学生版

小学奥数加法原理之树形图及标数法.学生版

奥数标数法练习计数之标数法经典例题讲解

苏教版数学四年级下册计数的基本方法—标数法(试题)

奥数标数法练习计数之标数法经典例题讲解

【推荐】小学奥数训练专题加法原理之树形图及标数法.学生版.doc