高级数理逻辑第3讲全解
高级数理逻辑

设R为A上的一个等价关系,则 A/R={[a]R|a∈A}称为A关于R的商集。 等价类的性质
∪[a]R=A [a]R=[b]R iff aRb [a]R≠Ф
A/R是A的一个划分。
映射
复合关系
设R是由A到B的一个二元关系,S是由B到C的一个二元关 系,则
R◦S={<x,z>|存在y ∈B,使得<x,y>∈R且<y,z>∈S}称为R 与S的复合关系
逆关系
设R是由A到B的一个二元关系,则 R-1= {<y,x>|<x,y>∈R} 称为R的逆关系。
关系的性质
设R是A上的一个二元关系 自反
✓ 所有中学生打网球。 ✓ 王君不打网球。 ➢ 王君不是中学生。
可推导性关系的内因
表象:前提、结论的真值
语义范畴
内因:前提、结论的逻辑形式
语法范畴
两个例子的逻辑形式相同
✓ S中的所有元有R性质。 ✓ a没有R性质。 ➢ a不是S中的元。
数理逻辑的研究内容
形式语言
无二义性、精确的、普遍适用的符号语言 自然语言存在二义性、不精确 语义:涉及符号、表达式的具体涵义 语法:仅涉及表达式的形式结构
ZF公理体系
外延公理
S=T iff (x)(x S x T)为真
子集公理
S T iff (x)(x S x T)为真
空集存在公理幂集P(A) = {a | a为A的子集}
集合的运算
对于集S,T 并
SUT {x | x S x T}
交
SI T {x | x S x T}
数理逻辑讲义

数理逻辑的一般介绍我们在中学时代就能进行一些证明了, 但并非所有的人都能回答到底什么是证明. 大概来说, 所谓的证明就是把认为某一断言是正确的理由明确地表述出来. 在这一过程中, 我们通常都需要把一些人们已接受的命题作为讨论的基础. 在此基础上, 如果我们能够把该断言推导出来, 该断言就是被认为是被证明了, 因而也就会被人们接受. 于是, 一个很自然的问题就是: 推导究竟为何物? 这个问题就属于逻辑的范畴.逻辑研究推理, 而数理逻辑则研究数学中所用的推理. 由于这种推理在计算机科学中有许多有广泛的应用, 数理逻辑也就成为计算机科学的重要基础之一.很明显, 我们不能够证明一切命题. 如上所述, 当我们证明某一断言(结论) 的时候需要一些其它的命题(前提)作为推理的基础. 我们还可以要求对这些前提进行证明. 如果一直这样要求下去, 或迟或早, 我们会遇这样的情况: 我们进行了“循环” 证明, 即把要证明的命题作为前提来使用, 或者我们无法再作任何证明, 因为没有更为明显的命题可以用来作为前提了.这样,我们就必须不用证明而接受某些命题,我们把这类命题称为“公理”; 其它由这些公理而证明的命题则被称为“定理”.所谓的命题, 直观上是关于某些概念之间的关系. 因而, 我们要求公理是那些根据概念可以明显地接受的命题. 由概念,公理和定理所组成的全体就是公理系统.以上对公理系统的描述要求我们知道公理系统的确切含义. 然而, 从推理的角度来说, 我们并不需要如此. 让我们来看下面的例子:(1).每个学生都是人,(2).王平是学生, (3).王平是人.我们可以由(1) 和(2)推导出(3), 也就是说,如果(1) 和(2)是正确的, 我们就可以断定(3)是正确的. 在这个推理过程中我们并不需要知道“王平”, “学生”, “人” 的含义如何, 把它们换成任何其它的名词, 这一推理都成立. 使(3) 成为(1) 和(2) 的逻辑推论是依据这样的事实: 如果(1)和(2)为真, 则(3)为真. 换句话说, 我们从命题的形式上就可以判断某一推理是否在逻辑上成立, 而无需考虑它的实际含义. 所以我们在研究逻辑的时候往往只需要进行形式的考察就行了, 不必考虑其含义.当我们对某一类研究对象指定了一个公理系统时, 这个公理系统所表示的含义就确定了. 但是在很多情况下, 我们会发现这个公理系统也适合于其它的一些对象. 于是当代数学建立了许多公理系统框架(如各种代数结构). 在这种公理系统框架中, 真正重要的并不是各种公理系统所表达的特定含义的不同, 而是它们的系统构造方面的区别. 这就告诉我们, 在对公理系统进行研究时, 仅对公理系统的形式进行考察是有实际意义的, 在某些情况下这种形式上的考察可以使我们的研究更具有一般性.基于如上认识以及其它的一些考虑(如从计算机科学的角度进行研究等), 我们将对公理系统的语法部分和语义部分进行分别研究. 公理系统的语义部分研究公理系统的含义, 它属于"模型论" 的研究范围, 我们将在今后作一些初步的介绍. 现在,我们对公理系统的语法部分进行粗略的描述.公理系统的语法部分称为形式系统. 它由语言, 公理和推理规则这样三个部分组成.任何推理必须在一定的语言环境中进行, 所以形式系统首先需要有它的语言. 自然语言(如英语, 中文等)具有很丰富的表达能力, 但通常会产生二义性. 例如"是" 在自然语言中可以表示“恒等” (如: 我们的英语老师是张卫国.), “属于” (如: 王小平是学生.), “包含” (如: 学生是人.) 等不同的含义. 同时, 我们还希望公理系统的语言结构能尽可能地反映它的语义并能有效地进行推理. 因而, 我们通常在形式系统中使用人工设计的形式语言.1设A 是一个任给的集合. 我们把A 称为字母表, 把A 中的元素称为符号. 我们把有穷的符号序列称为A的表达式. 一个以A 为其字母表的语言是A 的表达式集合的一个子集, 我们把这个子集中的元素称为公式. 因为我们希望这个语言能够表达我们所研究的对象, 我们要求公式能反映某些事实. 虽然理论上以A 为其字母表的语言可以是A 的表达式集合的任何子集, 我们将只讨论那些能将公式和其它表达式有效地区分开的语言. 我们将用L(F)表示公理系统F 的语言.形式系统的第二个部分是它的公理. 我们对公理的唯一要求是它们必须是该公理系统语言中的公式.最后, 为了进行推理我们需要推理规则. 每个推理规则确保某个公式(结论) 可由其它一些公式(前提) 推导出来.给定公理系统F, 我们可以把F 中的定理定义如下:1). F 的公理是F 的定理;2). 如果F 的某一推理规则的前提都是定理, 则该推理规则的结论也是定理;3). 只有1)和2)所述的是定理.这种定义方式和自然数的定义方式相类似, 称为广义递归定义. 它和通常的定义方式在形式上有所区别. 为了说明它的合理性, 我们对F的定理进行进一步的描述. 设S0 是F 的公理集. 根据1), S0 中的元素是定理. 设S1 是公式集, 它的元素都是F 的某一推理规则的结论, 而该推理规则的前提都是S0 中的元素. 根据2), S1 中元素是定理. 设S2 是公式集,它的元素都是F 的某一推理规则的结论, 而该推理规则的前提都是S0 或S1 中的元素. 根据2), S2 中元素是定理. 如此下去, 我们得到S2 ,S3 ,.... 最后, 设S N 是公式集, 它的元素都是F 的某一推理规则的结论, 而该推理规则的前提都是S0 或S1 ,...S N中的元素. 根据2), S N 中元素是定理并且我们得到了F中的所有定理. 我们将经常使用这种定义方式. 为了书写方便, 在今后的广义递归定义中我们将不再把类似3)的条款列出.如此定义的F 中定理为我们提供了一种证明方法. 当要证明F 中的定理都具有某一性质P 时, 我们可以采用下述步骤:1). 证明F 的公理都具有性质P;2). 证明如果F 的每个推理规则的所有前提具有性质P, 则它的结论具有性质P.这种证明方法称为施归纳于F的定理. 一般说来, 如果集合C 是由广义递归定义的, 我们可用类似的方法证明C中的元素都具有性质P. 这种证明方法称为施归纳于C中的元素. 2)中的前提称为归纳假设.现在我们就可以定义什么是证明了. 所谓F 中的一个证明是一个有穷的F 的公式序列, 该序列中的每一个公式要么是公理, 要么F 的某个推理规则以该序列中前面的公式所为前提而推导出的结论. 如果A 是证明P 的最后的公式, 则称P 是A 的证明.定理公式A 是F 的定理当且仅当A 在F 中有证明.证明首先根据定理的定义可以看出任何证明中的任何公式都是定理, 所以如果A 有证明, 则A 是定理. 我们施归纳于F 的定理来证明其逆亦真. 如果A 是公理, 则A 本身就是A 的证明. 如果A 是由F 的某一推理规则以B1 ,...,B n 为前提推导而得的结论, 由归纳假设, B1 ,...,B n 都有证明. 我们把这些证明按顺序列出来即可得到A 的一个证明. 证完今后, 我们将用 F .... 表示"....是F 的定理".一阶理论2今后, 我们将主要讨论一类特殊的公理系统. 这类公理系统称为一阶理论. 一阶理论是一种逻辑推理系统, 它具有很强的表达能力和推理能力, 并且在数学, 计算机科学及许多其它的科学领域中有广泛的应用. 事实上, 目前使用的大多数计算机语言和数学理论都是一阶理论.如前所述, 一阶理论的第一个部分是它的语言. 我们把一阶理论的语言称为一阶语言. 如同其它的形式语言一样, 一阶语言应包括一个符号表和一些能使我们把公式和其它表达式区分开的语法规则.首先, 我们定义一阶语言的符号表, 它由三类功能不同的符号组成. 它们是:a) 变元x,y,z,...;b) n元函数符号f,g,..., 及n元谓词符号p,q,...;c) 联结词符号和量词符号⌝,∨和∃.为了今后的方便, 我们假定一阶语言的变元是按一定顺序排列的, 并且我们把这种排列顺序称为字母顺序. 我们称0 元函数符号是常元符号. 注意: 一个任给的一阶理论并没有要求必须有函数符号: 一个一阶理论可能没有函数符号, 可能有有穷多个函数符号, 也可能有无穷多的函数符号. 我们要求任何一阶理论必须包括一个二元谓词符号, 并用"=" 来表示它. 和函数符号一样, 一个给定的一阶语言可能有有穷或无穷多个(甚至没有) 其它的谓词符号. 函数符号和除=外的谓词符号称为非逻辑符号, 而其它的符号称为逻辑符号.在定义公式之前, 我们必须先定义"项":(1.1) 定义在一阶语言中, 项是由下述广义递归方式定义的:a) 变元是项;b) 如果u1 ,...,u n 是项, f是n元函数符号, 则fu1 ...u n 是项.然后, 我们定义公式如下:(1.2) 定义在一阶语言中, 公式是由下述广义递归方式定义的:a) 如果u1 ,...,u n 是项, p是n元谓词符号, 则pu1 ...u n 是(原子) 公式,b) 如果u,v 是公式, x 是变元, 则⌝u, ∨uv 和∃xu是公式.如前所述, 相应于公式的定义, 我们有一种广义归纳的证明方法. 我们将把这种证明方法称为施归纳于长度. 有时我们还用施归纳于高度的证明方法, 而所谓的高度是公式中含有⌝,∨,和∃的数量.如果一个表达式b包括另一个表达式a, 则称第二个表达式a在第一个表达式b中出现, 即如果u,v,w 是表达式, 则v在uvw 中出现. 这里, 我们不仅要求a的符号都包括在b中, 而且要求这些符号的排列顺序和a一样并且中间不插有任何其它的符号. 我们把b包括a的次数称为a在b中出现的次数.接下来, 我们要讨论关于一阶语言的一些性质. 这种讨论不仅可以使我们加深对一阶语言的认识, 同时还能帮助我们理解其它的形式系统. 首先要考虑的是唯一可读性问题, 也就是说, 我们将要证明一阶语言中的任何公式不可能有不同的形式. 这一性质说明一阶语言在结构上是不会产生二义性的. 为了简化书写, 我们把公式和项统称为合式表达式. 于是, 根据定义可以知道所有的合式表达式都具有uv1 ...v n 的形式, 其中u 是n 元(函数或谓词) 符号, v1 ,...,v n 是合式表达式.我们说两个表达式u和v是可比较的, 如果存在一个表达式w (w 可以是空表达式) 使u=vw. 显然, 如果uv和u'v'是可比较的, 则u 和u'是可比较的; 如果uv和uv' 是可比较的, 则v 和v'是可比较的.3(1.3) 引理如果u1 ,...,u n ,u'1 ,...,u'n 是合式表达式(u1 和u'1 都不是空表达式), 而且u1 ...u n 和u'1 ...u'n 是可比较的,则对于一切i=1,...,n, u i =u'i .证明施归纳于u1 ...u n 的长度k.如果k=1, 则u1 ...u n 只有一个符号. 所以, n=1. 于是u1 ...u n =u1 且u'1 ...u'n =u'1 . 由于u1 和u'1 都是合式表达式, 它们只可能是变元或常元符号. 由于它们是可比较的, 所以u1 =u'1 .假定当k〈m时引理成立, 并设k=m.由于u1 是合式表达式, 我们可以把它写成vv1 ...v s , 其中v 是s 元符号, v1 ,...,v s 是合式表达式. 由上, u'1 和u1 是可比较的, v 也是u'1 的第一个符号. 于是, 由于u'1 是合式表达式, 它具有vv'1 ...v's 的形式. 由上所述的性质, v1 ...v s 和v'1 ...v's 是可比较的. 由于|v1 ...v s |<|u1 |≤|u1 ...u n |, 根据归纳假设, 对于一切j=1,...,s, v j =v'j , 所以, u1 =u'1 . 由此而得, u2 ...u n 和u'2 ...u'n 是可比较的, 且|u2 ...u n |<|u1 ...u n |, 所以, 由归纳假设, 对于一切i=2,...,n, u i =u'i .于是, 引理得证#(1.4) 唯一可读性定理每一个合式表达只能以唯一的方式写成uv1 ...v n 的形式, 其中, u 是n 元符号, v1 ,...,v n 是合式表达式.证明设w,w'是同一个合式表达式书写形式, 我们必须证明它们的结构是相同的. 首先, 它们必须都有相同的第一个符号,这样, u和n就唯一确定了, 从而, w=uv1...v n 且w'=uv'1...v'n, 其中v i ,v'j 是合式表达式(i,j=1,...,n). 我们还需证明对一切i=1,...,n, v i=v'i. 因为w 和w'是同一个表达式, 因而是可比较的. 于是, 根据引理(1.3), 对于一切i=1,...,n, v i=v'i #下面的定理说明如果一个合式表达式不可能由两个(或更多) 合式表达式的某些部分组成.(1.5) 引理合式表达式u中的任何符号w都是u中某一合式表达式的第一个符号.证明施归纳于u的长度k. 如果k=1, 则u是变元或常元符号. 于是任何在u中出现的符号就是u本身, 从而引理成立.假定当k<m时引理成立, 并设k=m.设u 是vv1 ...v n , 其中v是n元符号, v1 ,...,v n 是合式表达式. 如果w是v, 则它是u的第一个符号. 否则, 存在i=1,...,n, 使w 在v i 中出现. 由于|v i |<|u|, 根据归纳假设, w 是v i 中的某一合式表达式的第一个符号, 当然也是u中的某一合式表达式的第一个符号. 证完. #(1.6) 出现定理设u是n元符号, v1 ,...,v n 是合式表达式. 如果一个合式表达式v在uv1 ...v n 出现, 而且v不是整个uv1 ...v n , 则v在某一v i 出现.证明如果v的第一个符号就是定理中的u, 则v=uv'1 ...v'n , 其中v'1 ,...,v'n 是合式表达式, 且由定理条件, u和v是可比较的. 于是根据引理(1.3), 对于一切i=1,...,n, v i =v'i , 即v=uv1 ...v n . 矛盾.现假定v的第一个符号在某一v i 中出现. 根据引理(1.5), 该符号是某一合式表达式v'的第一个符号. 显然, v和v'是可比较的, 因而由引理(1.3), v=v', 即v在v i 中出现.4#为了方便起见, 我们今后将用大写字母A,B,...表示公式, 用f,g,...表示函数符号, 用p,q,...表示谓词符号, 用x,y,...表示变元, 用a,b,...表示常元符号.现在我们定义两类性质不同的变元, 即自由变元和约束变元.(1.7) 定义a) 如果x 在原子公式中出现, 则x是自由变元;b) 如果x是A 和B 中的自由变元, 且y 不是x, 则x 是⌝A, ∨AB和∃yA中的自由变元.a') x 是∃xA中的约束变元;b') 如果x是A 或B 中的约束变元, 则x 是⌝A, ∨AB和∃yA中的约束变元.注意: x可以在A 中既是自由变元又是约束变元.我们将用u[x/a]表示在表达式u 中将所有的自由变元x换成项a而得的表达式. 设A 是公式, 在很多情况下, A[x/a]关于a 所表示的含义与A 关于x所表示的含义是一样的, 但并非总是如此. 例如, 若A 是∃y=x2y, 而a 是y+1, 则A 是说x 是偶数, 但A[x/a]却不是说y+1是偶数. 这表明并非所有的代入都会保持原有的含义. 于是我们有下述定义:(1.8) 定义 a 被称为是在A 中可代入x的, 如果i) 如果A是原子公式,则a 是在A中可代入x 的;ii) 如果a 在B中可代入x 且对于a 中的任何变元y, ∃yB不含有自由变元x,则a 是在∃yB中可代入x 的;iii) 如果a 在A, B中可代入x, 则a 在⌝A和A∨B中是可代入x 的.今后, 当使用A[x/a] 时, 我们总是假定a是在A 中可代入x的. 类似地, 我们将用u[x1/ a1 ,...,x n/ a n ]表示在表达式u 中将所有的自由变元x1 ,...,x n 分别换成项a1 ,...,a n 而得的表达式, 同时还假定它们都是可代入的.在我们的一阶语言定义中项和公式的写法对于证明和理论分析比较方便, 但和通常的阅读方式不一致. 为了克服这一弱点, 我们引进一些定义符号:(A∨B) 定义为∨AB; (A→B) 定义为(⌝A∨B); (A&B) 定义为⌝(A→⌝B);(A↔B) 定义为((A→B)&(B→A)); ∀xA 定义为⌝∃x⌝A.注意: 定义符号只是为了方便而引进的记号, 它们不是语言中的符号. 当我们计算公式的长度时, 必须把它们换成原来的符号. 同样, 当用施归纳于长度或高度进行证明时也不能把它们作为符号来处理. 今后, 我们将在展示公式时用定义符号, 而在证明时用定义(1.1) 和(1.2).我们称:⌝A 为 A 的否定; A∨B 为 A 和B 的析取(A 或者B); A&B 为 A 和B 的合取(A并且B);A→B 为 A 蕴含B; A↔B 为A等价于B; ∃xA 为关于x的存在量词(存在x 使得A);∀xA 为关于x的全称量词(对一切x 使得A).作业:1) 施归纳于长度证明如果u是公式(项), x 是变元, a是项, 则u[x/a]是公式(项).2) 证明如果uv和vv'是合式表达式, 则v和v'中必有一个是空表达式.一阶理论的逻辑公理和规则形式系统的公理和规则可以分为两类: 逻辑公理和逻辑规则, 非逻辑公理和非逻辑规则. 逻辑公理和逻辑规则指的是那些所有形式系统都有的公理, 而非逻辑公理和非逻辑规则仅在5某些特定的形式系统中才有. 但是, 当形式系统足够丰富时,我们并不需要非逻辑规则. 假定在一个形式系统F 中有一条非逻辑规则使我们可以由B1 ,...,B n 推导出A, 只要F 有足够多的逻辑规则, 我们只需要在F 中加进一条公理B1 →...→B n →A (这里, B1 →...→B n →A表示B1 →(...→(B n →A)...).)就不再需要那条非逻辑规则了. 因此, 我们今后假定我们的形式系统中没有非逻辑规则. 今后我们将把逻辑规则简称为规则. 由于我们仅对形式系统进行一般讨论, 我们的兴趣主要是那些逻辑公理和规则.下面是逻辑公理:1) 命题公理: ⌝A∨A;2) 代入公理: A[x/a]→∃xA;3) 恒等公理: x=x;4) 等式公理: x1 =y1 →...→x n =y n →fx1 ...x n =fy1 ...y n ;或x1 =y1 →...→x n =y n →px1 ...x n →py1 ...y n .注意: 以上并不是仅有四条公理, 而是四类公理. 如命题公理并非一条公理, 而是对于任何公式A 我们有一条命题公理. 所以, 以上的公理实际上是公理模式.以下是规则:1) 扩展规则: 如果A, 则B∨A;2) 收缩规则: 如果A∨A, 则A;3) 结合规则: 如果A∨(B∨C), 则(A∨B)∨C;4) 切割规则: 如果A∨B且⌝A∨C, 则B∨C;5) ∃-引入规则: 如果A→B且x 不是B 中的自由变元, 则∃xA→B.如同上面的公理, 这些规则也不是五条规则, 而是五个规则模式.现在, 我们定义一阶理论如下:(1.9) 定义一个一阶理论T (简称理论T)是具有如下特征的形式系统:1) T 的语言L(T)是一阶语言;2) T 的公理是以上列出的四组公理和一些其它的非逻辑公理;3) T 的规则是以上列出的五组规则.由于一阶理论的逻辑符号, 逻辑公理和规则已经确定, 一阶理论之间的区别在于它们的非逻辑符号和非逻辑公理. 因此, 当我们希望讨论某一具体的一阶理论时只需要把它的非逻辑符号和非逻辑公理指明就行了.例.1) 数论NN 的非逻辑符号为: 常元0, 一元函数符号S, 二元函数符号+和*, 和二元谓词符号<. N 的非逻辑公理为:N1 Sx≠0; N2 Sx=Sy→x=y; N3 x+0=x; N4 x+Sy=S(x+y); N5 x*0=0;N6 x*Sy=(x*y)+x; N7 ⌝(x<0); N8 x<Sy↔x<y∨x=y; N9 x<y∨x=y∨y<x.2) 群GG 只有一个非逻辑符号, 即二元函数符号*. G 的非逻辑公理为:G1 (x*y)*z=x*(y*z); G2 ∃x(∀y(x*y=y)&∀y∃z(z*y=x)).根据我们在第一节所述, 一阶理论T 的定理可以定义为:1) 每一条命题公理, 代入公理, 恒等公理, 等式公理和非逻辑公理是定理;2) 如果A 是定理, 则A∨B是定理;3) 如果A∨A是定理, 则A 是定理;64) 如果A∨(B∨C) 是定理, 则(A∨B)∨C 是定理;5) 如果A∨B和⌝A∨C是定理, 则B∨C是定理;6) 如果A→B是定理且x 不是B 中的自由变元, 则∃xA→B是定理.与此对应, 我们可以用如下广义归纳法证明一阶理论T 中的定理都具有某一性质P:1) 每一条命题公理, 代入公理, 恒等公理, 等式公理和非逻辑公理具有性质P;2) 如果A 具有性质P, 则A∨B具有性质P;3) 如果A∨A具有性质P, 则A 具有性质P;4) 如果A∨(B∨C) 具有性质P, 则(A∨B)∨C 具有性质P;5) 如果A∨B和⌝A∨C具有性质P, 则B∨C具有性质P;6) 如果A→B具有性质P且x 不是B 中的自由变元, 则∃xA→B具有性质P.下面我们证明一阶理论的逻辑公理是相互独立的.(1.10) 定理一阶理论的逻辑公理和规则是互相独立的.证明当我们希望证明某一命题A 是独立于某个命题集Γ和规则集Δ时, 我们需要找到一个性质P 使A 不具有性质P, 而Γ中的每一命题具有性质P 且Δ中的每一规则保持性质P (即如果该规则的前提具有性质P, 则其结论具有性质P); 当我们希望证明某一规则R 是独立于Γ和Δ时, 我们需要找到一个性质P 使R 不保持性质P, 而Γ中的每一命题具有性质P 且Δ中的每一规则保持性质P. 这样就可以断言: 在由Γ为其公理集, Δ为其规则集的形式系统中, 每一定理都具有性质P. 由于A不具有性质P (或R 不保持性质P), 所以, A (或R)是不可能由Γ和Δ来证明的. 这样, A(或R)就独立于Γ和Δ了. 我们将根据这个思想来证明本定理.1) 对于命题公理. 定义f 如下:f(A)=T 若 A 是原子公式; f(⌝A)=F; f(A∨B)=f(B); f(∃xA)=T.可以证明: f(⌝⌝(x=x)∨⌝(x=x))=F, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=T.2) 对于代入公理. 定义f 如下:f(A)=1 若A 是原子公式; f(⌝A)=1 如果f(A)=0, f(⌝A)=0 若f(A)=1;f(A∨B)=max{f(A),f(B)}; f(∃xA)=0.可以证明: f((x=x)→∃x(x=x))=0, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=1.3) 对于恒等公理. 定义f 如下:f(A)=0 若A是原子公式; f(⌝A)=1 如果f(A)=0, f(⌝A)=0 若f(A)=1; f(A∨B)=max{f(A)},f(B); f(∃xA)=f(A).可以证明: f((x=x))=0, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=1.4) 对于等式公理. 首先在L(T)中加进常元e1 ,e2 和e3 而得L'. 然后定义f 如下:f(e i =e j )=1 iff i≤j; f(⌝A)=1 如果f(A)=0, f(⌝A)=0 若f(A)=1; f(A∨B)=max{f(A),f(B)}; f(∃xA)=T iff 存在i 使f(A[x/e i ])=T .可以证明: f((x=y→x=z→x=x→y=z))=0, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A[x/e i ])=1, 其中, x是A 中的自由变元.5) 对于扩展规则. 定义f 如下:f(A)=1 若 A 是原子公式; f(⌝A)=1 如果f(A)=0, 否则, f(A)=0; f(A∨B)=1 如果f(A)=f(⌝B), 否则f(A∨B)=0; f(∃xA)=f(A).可以证明: f((x=x∨(⌝(x=x)∨x=x)))=0, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=1.6) 对于收缩规则. 定义f 如下:7f(A)=T 若 A 是原子公式; f(⌝A)=f(∃xA)=F; f(A∨B)=T.可以证明: f(⌝⌝(x=x))=F, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=T.7) 对于结合规则. 定义f 如下:f(A)=0 若 A 是原子公式; f(⌝A)=1-f(A); f(A∨B)=f(A)*f(B)*(1-f(A)-f(B)); f(∃xA)=f(A).可以证明: f(⌝(⌝(x=x)∨⌝(x=x)))>0, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=0.8) 对于切割规则. 定义f 如下:f(A)=1 若 A 是原子公式; f(⌝A)=1 如果f(A)=0或A是原子公式, 否则f(⌝A)=0; f(A∨B)=max{f(A),f(B)}; f(∃xA)=f(A).可以证明: f(⌝⌝(x=x)))=0, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=1.9) 对于E-引入规则. 定义f 如下:f(A)=1 若A是原子公式; f(⌝A)=1 如果f(A)=0, f(⌝A)=0 若f(A)=1; f(A∨B)=max{f(A),f(B)}; f(∃xA)=T.可以证明: f(∃y⌝(x=x)→⌝(x=x))=0, 而且对于任何可由其它的逻辑公理和规则证明的命题A, f(A)=1.结构和模型现在我们讨论一阶理论的语义部分. 为此我们先引进一些集论的记号: 集合或类是把一些我们想要研究的对象汇集在一起, 从而我们可以把它看作是一个整体. 如果A 和B 是集合, 一个由A 到B 的映射 F (记作F: A→B)是一个A 和B 之间的对应, 在这个对应中A 中的每一个元素a 都对应着一个唯一的B中元素 b (称为F在a 上的值, 记作F(b) ). 我们把n个A 中元素按一定顺序排列而得的序列称为A 的一个n 元组, 并用(a1,...,a n )表示由A 中元素a1,...,a n 按此顺序排列的n 元组. 把由A 的所有n 元组成的集合记为A n, 然后把由A n 到B的映射称为由A 到B 的n元函数. 我们把A n 的子集称为A 上的n 元谓词. 如果P是A 上的n 元谓词, 则P(a1 ,...,a n )表示(a1 ,...,a n )∈P.真值函数根据我们对公式和项的定义, 我们可以先用函数符号和谓词符号以及变元构造一些简单的公式, 然后用联结词得到比较复杂的公式, 如"A 并且B" 等等. 我们用符号"&" 表示"并且", 即若A 和B 是公式, "A&B" 表示"A 和B同时成立".于是一个很自然的问题是怎样知道A&B 的真假? 这里, A&B 的一个很重要的特征是: 只需要知道A 和B 的真假就能确定A&B 的真假, 而不必知道A 和B 的具体含义. 为了表示这一特征, 我们引进真值. 真值是两个不同的字母T 和F, 而且当公式A 为真时, 我们用T 表示其真值; 当公式A 为假时, 我们用F 表示其真值. 于是, A&B 的真值就由A 和B 的真值确定了.有了真值的概念, 我们就可以定义真值函数了. 所谓的真值函数是由真值集T,F 到真值集T,F 的函数. 由此, 我们可以把以上的讨论叙述为: 存在二元真值函数H& 使得: 若a 和b 分别是A 和B 的真值, 则H& (a,b) 是A&B 的真值. 我们定义H& 为:H& (T,T)=T, H& (T,F)=H& (F,T)=H& (F,F)=F.我们用"∨" 表示"或者", 并定义H∨如下:8H∨(F,F)=F, H∨(T,F)=H∨(F,T)=H∨(T,T)=T.于是当a 和b 分别是A 和B 的真值时, H∨(a,b)就是A∨B的真值.我们用"→" 表示"如果...则...", 并定义H→如下:H→(T,F)=F, H→(F,F)=H→(F,T)=H→(T,T)=T.于是当a 和b 分别是A 和B 的真值时, H→(a,b)就是A→B的真值.我们用"↔" 表示"当且仅当", 并定义H↔如下:H↔(F,T)=H↔(T,F)=F, H↔(F,F)=H↔(T,T)=T.于是当a 和b 分别是A 和B 的真值时, H↔(a,b)就是A↔B的真值.我们用"⌝" 表示"非", 并定义H⌝如下:H⌝(F)=T, H⌝(T)=F.于是当a 是A 的真值时, H⌝(a)就是⌝A的真值.容易证明, &,→, 和↔可由⌝和∨定义. 事实上所有的真值函数都可以由⌝和∨定义.作业1. 证明: 任何真值函数f(a1 ,...,a n )都可以由H⌝和H∨定义.2. 设H d , H s 是真值函数, 其定义为:H d (a,b)=T 当且仅当a=b=F; H s (a,b)=F 当且仅当a=b=T.证明: 任何真值函数f(a1 ,...,a n )都可以由H d (或H s )定义.结构现在我们讨论一阶语言的语义部分(称为它的结构). 所谓一个语言的语义, 当然是表示该语言中所指称的对象范围和每一个词和句子所表达的含义. 一阶语言的语义也是如此. 如前定义, 一阶语言中的符号有函数符号和谓词符号, 这些都应在它的语义中有具体的含义. 把这些组合起来, 我们就可以得到如下定义:(1.11) 定义称三元组M=〈|M|,F,P〉是一个结构,如果:1) |M|是一个非空集合,它称为是L 的论域, |M| 中的元素称为是M 的个体;2) F是|M|上的函数集合;3) P是|M|上的谓词集合.定义设L是一阶语言,M是一个结构。
数理逻辑(Mathematical Logic)

数理逻辑(MathematicalLogic)数理逻辑(Mathematical logic)是用数学方法研究诸如推理的有效性、证明的真实性、数学的真理性和计算的可行性等这类现象中的逻辑问题的一门学问。
其研究对象是对证明和计算这两个直观概念进行符号化以后的形式系统。
数理逻辑是数学基础的一个不可缺少的组成部分。
数理逻辑的研究范围是逻辑中可被数学模式化的部分。
以前称为符号逻辑(相对于哲学逻辑),又称元数学,后者的使用现已局限于证明论的某些方面。
历史背景“数理逻辑”的名称由皮亚诺首先给出,又称为符号逻辑。
数理逻辑在本质上依然是亚里士多德的逻辑学,但从记号学的观点来讲,它是用抽象代数来记述的。
某些哲学倾向浓厚的数学家对用符号或代数方法来处理形式逻辑作过一些尝试,比如说莱布尼兹和朗伯(Johann Heinrich Lambert);但他们的工作鲜为人知,后继无人。
直到19世纪中叶,乔治·布尔和其后的奥古斯都·德·摩根才提出了一种处理逻辑问题的系统性的数学方法(当然不是定量性的)。
亚里士多德以来的传统逻辑得到改革和完成,由此也得到了研究数学基本概念的合适工具。
虽然这并不意味着1900年至1925年间的有关数学基础的争论已有了定论,但这“新”逻辑在很大程度上澄清了有关数学的哲学问题。
在整个20世纪里,逻辑中的大量工作已经集中于逻辑系统的形式化以及在研究逻辑系统的完全性和协调性的问题上。
本身这种逻辑系统的形式化的研究就是采用数学逻辑的方法.传统的逻辑研究(参见逻辑论题列表)较偏重于“论证的形式”,而当代数理逻辑的态度也许可以被总结为对于内容的组合研究。
它同时包括“语法”(例如,从一形式语言把一个文字串传送给一编译器程序,从而转写为机器指令)和“语义”(在模型论中构造特定模型或全部模型的集合)。
数理逻辑的重要著作有戈特洛布·弗雷格(Gottlob Frege)的《概念文字》(Begriffsschrift)、伯特兰·罗素的《数学原理》(Principia Mathematica)等。
数理逻辑-大纲
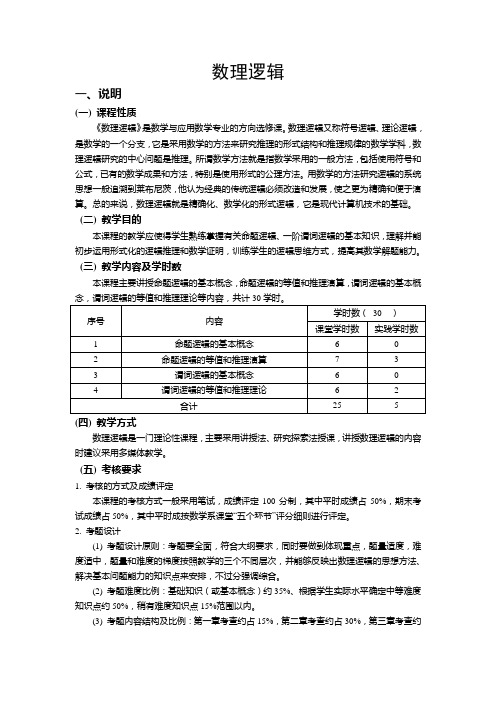
数理逻辑一、说明(一) 课程性质《数理逻辑》是数学与应用数学专业的方向选修课。
数理逻辑又称符号逻辑、理论逻辑,是数学的一个分支,它是采用数学的方法来研究推理的形式结构和推理规律的数学学科,数理逻辑研究的中心问题是推理。
所谓数学方法就是指数学采用的一般方法,包括使用符号和公式,已有的数学成果和方法,特别是使用形式的公理方法。
用数学的方法研究逻辑的系统思想一般追溯到莱布尼茨,他认为经典的传统逻辑必须改造和发展,使之更为精确和便于演算。
总的来说,数理逻辑就是精确化、数学化的形式逻辑,它是现代计算机技术的基础。
(二) 教学目的本课程的教学应使得学生熟练掌握有关命题逻辑、一阶谓词逻辑的基本知识,理解并能初步运用形式化的逻辑推理和数学证明,训练学生的逻辑思维方式,提高其数学解题能力。
(三) 教学内容及学时数本课程主要讲授命题逻辑的基本概念,命题逻辑的等值和推理演算,谓词逻辑的基本概念,谓词逻辑的等值和推理理论等内容,共计30学时。
序号内容学时数(30 )课堂学时数实践学时数1 命题逻辑的基本概念 6 02 命题逻辑的等值和推理演算7 33 谓词逻辑的基本概念 6 04 谓词逻辑的等值和推理理论 6 2合计25 5 (四) 教学方式数理逻辑是一门理论性课程,主要采用讲授法、研究探索法授课,讲授数理逻辑的内容时建议采用多媒体教学。
(五) 考核要求1. 考核的方式及成绩评定本课程的考核方式一般采用笔试,成绩评定100分制,其中平时成绩占50%,期末考试成绩占50%,其中平时成按数学系课堂“五个环节”评分细则进行评定。
2. 考题设计(1) 考题设计原则:考题要全面,符合大纲要求,同时要做到体现重点,题量适度,难度适中,题量和难度的梯度按照教学的三个不同层次,并能够反映出数理逻辑的思想方法、解决基本问题能力的知识点来安排,不过分强调综合。
(2) 考题难度比例:基础知识(或基本概念)约35%、根据学生实际水平确定中等难度知识点约50%,稍有难度知识点15%范围以内。
01-高等数理逻辑课程介绍_

{
{
{
□
z
描述问题的逻辑工具 常用的逻辑: 命题逻辑 谓词逻辑 多值逻辑 直觉主义逻辑 模态逻辑 时态逻辑 描述逻辑 二阶逻辑
{ { { { { { { {
l 逻辑方法是求解问题的一种独特方法.
{
□
z
抽象问题类的性质研究 使用不同的逻辑体系描述具体问题, 针对问题的求解, 需要关注以下 性质:
{ {
□
z
数学分析中的 % - $ 语言语句. / $ 时, 对任意的 % > 0 , 存在 $ > 0 , 当 0=|x-a|< |f(x)-b|< % . □ 数学语句的符号化. “函数 f 在点 a 的极限是 b ”常被写为: ] % > 0 ^ $ > 0 ] x(0=|x-a|< / $ >|f(x)-b|< % ) . □
z z
z
无限集合初步 公理集合论初步 自然数的逻辑理论
z
z
z
z
z
z
z
z
z
z
z
z
z
命题逻辑完备性定理及紧致性 命题逻辑公理的独立性 可满足问题及相关判定算法 谓词逻辑的模型及无限模型 一目谓词逻辑的可判定性 非欧几何简介 实闭域的可判定性 谓词逻辑的完备性 谓词逻辑公理的独立性 可计算性及半可判定性 不完备性定理与非标准模型 直觉主义逻辑 模态逻辑 □
解答: 设定以下的命题变元:
根据对三个情形的约定可得语句 9 1 : (p1 ) r 3 ) [ (q 1 ) p3 ) [ (r 1 ) p 2 ). 根据无并列第一及第三可得语句 9 2 \ (p 1 [q 1 ) [\ (p 1 [ r 1 ) [\ (q1 [ r 1 ) [\ (p 3 [r 3 ). 根据对名次唯一性约定可得语句 9 3 \ (p 1 [p 2 ) [\ (p 1 [ p 3 ) [\ (p 2 [ p3 ) [\ (r 1 [ r 3 ). 所以问题可以被描述为: 91 [ 92[ 93 . 用真值表方法可以求得唯一赋值 v: v(q 1 )=v(p 2 )=v(r 3 )=1,v(p 1 )=v(p 3 )=v(r 1 )=0. 使得 v( 9 1 [ 9 2 [ 9 3 )=1 这表明从一到三的排名是:B,A,C. □ 命题逻辑计算复杂性分析
数理逻辑PPT课件

.
4
数理逻辑
正如著名的计算机软件大师 戴克斯特拉 (E.W.Dijkstra)曾经说过:我 现在年纪大了,搞了这么多年软件,错误 不知犯了多少,现在觉悟了。我想,假如 我早在数理逻辑上好好下点功夫的话,我 就不会犯这么多错误。不少东西逻辑学家 早就说过了,可是我不知道。要是我能年 轻20岁的话,我就会回去学逻辑。
P∧Q的真值为真,当且 T T T
仅当P和Q的真值均为真。
.
11
命题逻辑
• 或者“∨”(析取)
表示“或者”,“或者”有二义性,看下面 两个例子:
例1. 灯泡或者线路有故障。 例2. 第一节课上数学或者上英语。
例1中的或者是可兼取的或。即或者“∨”
例2中的或者是不可兼取的或,也称之为异或、 排斥或。即“ ”.
.
12
命题逻辑
P:灯泡有故障。 Q:线路有故障。 例1中的复合命题可 表示为:P∨Q,读 成P或者Q,P∨Q的 真值为F,当且仅当 P与Q均为F。
P Q P∨Q FF F FT T TF T
TT T
.
13
命题逻辑
P:第一节上数学。
Q:第一节上英语。
P Q P Q
例2中的复合命题
可写成P Q,读 成P异或Q。
P Q的真值为F,
FF F FT T TF T
TT F
当且仅当P与Q的真值相同。
.
14
命题逻辑
• 蕴含(条件)“”
表示“如果… 则 …”,“当...则...”,“若... 那么...”,“假如...那么...”
例如: P表示:缺少水分。
Q表示:植物会死亡。
PQ:如果缺少水分,植物就会死亡。
PQ:也称之为蕴含式,读成“如果P则
北师大版选修高中数学 第三章 推理与证明 分析法名师点拨

2.综合法和分析法各有优缺点.从寻求解题思路 来看,综合法由因导果,往往枝节横生,不容易奏效; 分析法执果索因,常常根底渐远,有希望成功.就表 达证明过程而论,综合法形式简洁,条理清晰;分析 法叙述繁琐,文辞冗长.也就是说分析法利于思考, 综合法宜于表述.因此,在实际解题时,常常把分析 法和综合法结合起来运用,先以分析法为主寻求解题 思路,再用综合法有条理地表述解答或证明过程.有 时要把分析法和综合法结合起来交替使用,才能成 功.
∵a+2 b≤ ab,b+2 c≤ bc,a+2 c≤ ac ∵a,b,c 是不全相等的正数 ∴a+2 b·b+2 c·a+2 c< ab bc ac=abc 即a+2 b·b+2 c·c+2 a<abc ∴logxa+2 b+logxb+2 c+logxc+2 a<logxa+logxb+logxc
用分析法证明命题“若P,则Q”时的模式如下: 为了证明命题Q为真,只需证明命题P1为真,从而 有… 只需证明命题P2为真,从而有… 只需证明命题P为真,而已知P为真,故Q必真.
[特别提醒] 当所证结论与所给条件之间的关系 不明确时,常采用分析法证明,但更多的时候是综合 法与分析法结合使用,先看条件能够提供什么,再看 结论成立需要什么,从两头向中间靠拢,逐步接通逻 辑思路.
应用综合法和分析法证明问题时的注意点 1.运用综合法解题时,要保证前提条件正确, 推理要合乎逻辑规律,只有这样才能保证结论的正 确性. 2.利用分析法证明问题时一定注意语言要清楚、 明白.
1.在解决问题时,我们经常把综合到中间结论Q;根据结论的结构特点去转化条件,得 到中间结论P.若由P可以推出Q成立,就可以证明结 论成立.
∵a,b,c 不全相等,∴a+2 b·b+2 c·a+2 c> ab· bc· ac= abc.
数理逻辑课件 数理逻辑ch3

p
q
i( 3 i 9)满足p U q
3.2.2 LTL的语义—路径的概念
12)π╞ ФWψ当且仅当存在某个i≥ 1,使得 πi╞ψ且对所有j=1,2,…i-1,有πj╞Ф或对所有 的k≥1,有πk ╞ Ф (W弱直到)
13)π╞ ФRψ当且仅当或者存在某个i≥1,使得 πi╞Ф,且对所有j=1,2,…i,有πj╞ψ或对所有 的k≥1,有πk ╞ψ
理方法。该方法用于有限状态的并发的、反应式系 统,利用穷举搜索的方法来判定系统是否满足给定 的一个或一组规范。
7
3.1.2 模型检测的验证方法
模型检测过程的大体步骤 – 由用户描述的一个模型开始 – 判断用户所断言的假设在模型中是否有效 – 若无效,则产生由执行轨迹构成的反例
8
3.1.2 模型检测的验证方法
3.2.1 LTL的语法(线性时态逻辑)
定义:线性时态逻辑(LTL)有下列用Backus Naur(巴科斯范式)给出的语法 Ф::= ┬∣┴∣p∣(┐Ф)∣(Ф∧Ф)∣(Ф∨Ф)∣( Ф→Ф)∣(×Ф)∣(FФ)∣(GФ)∣(ФUФ)∣( ФWФ)∣(ФRФ) 其中:┬:表示永真(重言式) (不加约束) ┴:表示永假(矛盾式) (所有约束) X:表示下一个状态 (next) F:表示某未来状态 (Future) G:表示所有未来状态 (Globally)
– 模型检测:有限状态并发系统的自动化验证技术
1
第3章 通过模型检测进行验证
[关键词]
验证的动机 线性时态逻辑 模型检测:系统、工具和性质 分支时间逻辑 CTL*与LTL和CTL的表达能力 模型检测算法
2
3.1 验证的动机(目的)
1)能够验证计算机系统的正确性
例:一个系统生产出来,必须有验证过程才能应用. 如 window95、97、2000、xp,office97等
第三四讲——产生式及一阶谓词

专家系统的开发过程
专家系统是一个复杂的智能软件,与一般软件 类似,但又有不同的特点。
一般软件处理的对象是数值、文字、图形等信 息,且有固定的算法序列,而专家系统软件处理的 对象是以符号表示的知识,在运行过程中常有回溯 发生,因此专家系统的开发过程与一般软件的开发 有所不同。
专家系统的创始人费根鲍姆教授把开发专家系 统的技术称之为知识工程,即以知识获取、知识表 示、知识运用(推理)为中心。根据这个思想,可把 专家系统的开发过程分为以下几个阶段。
14
2019/12/15
例:初始状态 Start 目标状态 Goal
R冲1:突if 原P 则a:nd Q then Goal
R2:if选R取最an久d 以S 前t被he触n 发P 的或根本没有被触发的规则
R3:if如W果出an现d R“平t局he”n Q,选取R其4:中if的T第a一nd个U规则then Q
接口,完成信息适的用性和有效性密切相关的。
内部形式和人可接
间假设和中间结 果
收的形式之间进行
转换。
用
推
理
动态库
用
户
执
知识
户
界
行
获取
机
面
构
知识库
推理机根据动态库的当 前状态,利用知识库中 的知识进行推理。
包括:1与当前问题有关的数据信
解 释 息;2 一般知识和领域知识。规
机构
则、网络和过程等形式表示。
以人类专家知识为基础的专家系统的问题求解,从本质
上都可以看作是从初始状态到目标状态的推导变换过程,
因而都可用产生式系统来求解。
2019/12/15
21
2019/12/15
高级数理逻辑

1.2 数理逻辑的发展过程
第五阶段:公理集合论促进了数理逻辑形式 系统的产生 英国唯心主义哲学家、逻辑学家、数 学家罗素在集合论的研究过程中,于1903 年提出了著名的罗素悖论(数学史上的第 三次危机)。罗素悖论动摇了集合论的基 础,促使人们去研究数学中的矛盾性。从 而提出了公理集合论。公理集合论的产生 和发展,促进了形式系统的产生。
10
1.1 基本概念
语义 涉及符号和符号表达式的涵义。 语法 涉及符号表达式的形式结构,不考虑 任何对语言的解释。
两者既有区别又有联系。
---------------------------------------------------------11
1.2 数理逻辑的发展过程
逻辑学→数理逻辑→形式逻辑→计算逻辑 第一阶段:逻辑学思想的提出 亚里士多德提出建立探索人类推理、 思维原则的学科,从而有了逻辑的概念。
14
1.2 数理逻辑的发展过程
第四阶段:发展为独立的学科 十九世纪末二十世纪初,数理逻辑有 了比较大的发展,1884年,德国数学家弗 雷格出版了《数论的基础》和《符号论》, 在书中引入量词的符号,使得数理逻辑的 符号系统更加完备。对建立这门学科做出 贡献的,还有美国人皮尔斯,他也在著作 中引入了逻辑符号。从而使现代数理逻辑 最基本的理论基础逐步形成,成为一门独 立的学科。
---------------------------------------------------------16
1.2 数理逻辑的发展过程
第六阶段:形式推理自动化的产生 1965年Robinson提出了归结原理 (Principle of Resolution),归结原理提 出了基于形式描述的,利用计算机的推理 方法。从而使机器定理证明和计算机辅助 软件工程得到长足的发展。
北邮高级数理逻辑课件

形式系统由{∑, TERM, FORMULA, AXIOM, RULE}等5个部分构成,其中 称为符号表,TERM 为项集;FORUMULA 为公式集;AIXIOM 为公理集;RULE 为推理规则集。
:1、 符号表∑为非空集合,其元素称为符号。
2、 设∑*为∑上全体字的组合构成的集合。
项集TERM 为∑*的子集,其元素称为项;项集TERM 有子集V ARIABLE 称为变量集合,其元素称为变量。
F(X) a, X,3、 设∑*为∑上全体字的组合构成的集合。
公式结FORMULA 为∑*的子集,其元素称为公式;公式集有子集ATOM ,其元素称为原子公式。
A(f(a,x1,y)), A →B4、 公理集AXIOM 是公式集FROMULA 的子集,其元素称为公理。
5、 推理规则集RULE 是公式集FORMULA 上的n 元关系集合,即RULE=)}2(|{n FORMULA r n n n r ⊆∧≥∧∃是正整数,其元素称为形式系统的推理规则。
其中公式集和项集之间没有交叉,即TERM ∩FORMULA =φ,公式和项统称为表达式。
由定义可知,符号表∑、项集TERM 、公式集FORMULA 是形式系统的语言部分。
而公理集AXIOM 、推理规则集RULE 为推理部分形式系统特性1、 符号表∑为非空、可数集合(有穷、无穷都可以)。
2、 项集TERM 、公式集FORMULA 、公理集AXIOM 和推理规则集RULE 是递归集合,即必须存在一个算法能够判定给定符号串是否属于集合(可判定的)。
3、 形式系统中的项是用来描述研究的对象,或者称为客观世界的。
而公式是用来描述这些研究对象的性质的。
这个语言被称为对象语言。
定义公式和项产生方法的规则称为词法。
公理:I))((A B A →→ II))()(())(((C A B A C B A →→→→→→ III ))())()(((A B B A →→⌝→⌝证明:A →A(1)A →(A →A)((A →(B →C))→((A →B)→(A →C))((A →(B →A))→((A →B)→(A →A))((A →((A →A)→A))→((A →(A →A))→(A →A))A →((A →A)→A))(A →(A →A))→(A →A)(A →(A →A))A →ABB A A →, 已知:R 是一个有关公式的性质证明:R 对于所有公式有效I. 对于)(FSPC Atom p ∈,则)(P RII. 假设公式A 和B 都具有RIII. )(FSPC Atom A ∈∀,且)(A R ,则)(A R ⌝IV. B A ,∀是公式,如果)(A R 且)(B R ,则)(B A R →根据:形式系统的联结词只有两个→⌝,,因为在命题逻辑的语义上,其他联结词可以有这两个联结词表示。
高等数理逻辑 课程介绍

z
z
f 是1 元函数符号. A: ] xy(f(x)=f(y) >x=y). B : ^ y] x( \ f(x)=y). □
谓词逻辑用于解决实际问题 初等几何是可判定的 初等几何的逻辑研究
z z
z
z
选定一阶语言 将平面几何命题表示为一阶语言算术语句 在实数范围内成立的算术语句 在实数范围内成立的算术语句的集合是可判定的
0重 1重 2重 3重
{
{
{
□
z
描述问题的逻辑工具 常用的逻辑: 命题逻辑 谓词逻辑 多值逻辑 直觉主义逻辑 模态逻辑 时态逻辑 描述逻辑 二阶逻辑
{ { { { { { { {
l 逻辑方法是求解问题的一种独特方法.
{
□
z
抽象问题类的性质研究 使用不同的逻辑体系描述具体问题, 针对问题的求解, 需要关注以下 性质:
{
{
{
{ z
{
{
{
{ z
{
{
{
{
{ z
{
{
{
{
高等数理逻辑
课程基本内容:
z
常用的描述语言——朴素集合论
{ {
{
{
{
{
{
集合 映射 等势 无限 可数 无限集合的应用 集合论假设
全部
□
z
严格的描述语言——公理集合论
{
{
{
{
集合论模型 公理的相容性及独立性 全集 正规公理 自然数集合与自然数 归纳法与递归定义 集合 { ochcp 0 ,{0} occcchccccp,{{0}} occcccccchccccccccp,{{{0}}} occcccccccccchccccccccccccp, l }.
《数理逻辑》第三章

马琦 2010.9.11 maqi08@所有人是要死的。
所有人是要死的。
苏格拉底是人。
苏格拉底是人。
苏格拉底是要死的。
∴ 苏格拉底是要死的。
显然这是一个有效论证的例子。
但是如果我们试图要用第一章的方法 来处理,把这一论证符号化,我们得 到的是 p,q, ∴ r。
按第一章的理论, 这不是有效的论证形式。
在这种情形下,有效性并不 依赖于作为简单语句的前提和结 论间的关系,而是依赖于语句内 部所含成分之间的关系以及语句 本身的形式。
如果我们希望寻找 对应的“论证形式”,把它变得 更清楚些,那么论证形式应写作所有的 A 是 B, , C 是一个 A, , ∴ C 是 B。
。
主语:语句所判断的对象。
谓语:对象所具有的“性质”。
苏格拉底是人。
苏格拉底是人。
我写书。
我写书。
平方是-1的数不是实数。
平方是 的数不是实数。
的数不是实数 A(s) B(i) R(j) 或 ~R(j)用大写字母A,B,C,…表示谓语,用小写字母表示主语。
复合语句也可以用这样的方法译成符号。
每一个整数都有质因数。
“每一个整数都有质因数。
” 是一整数, 有质因数。
对所有的 x, 若 x 是一整数,则 x 有质因数。
, 对所有的 x,(I(x)→P(x)). , →全称量词“所有的人是要死的。
” 所有的人是要死的。
对所有的 x,(A(x)→M(x)). , →存在量词“有些猪有翅膀。
” 有些猪有翅膀。
至少存在一个对象 x,使 x 是猪 , 并且 x 有翅膀。
有翅膀。
短语“对所有的 x”称为全称量词 全称量词, 全称量词 用符号 (∀x)表示。
∀ (∀x) (A(x)→M(x)) ∀ →短语“至少存在一个对象 x 使得” 存在量词,用符号(∃x)表示。
称为存在量词 存在量词 ∃ (∃x) (P(x)∧W(x)) ∃ ∧更一般的, 代表谓词符号, 更一般的,如果 A 代表谓词符号,那么我们可以有意义的写成 (∀x) A(x) 每一个对象有 所确定的性质 ∀ 每一个对象有A所确定的性质 (∃x) A(x) 某个对象有 所确定的性质 ∃ 某个对象有A所确定的性质例3.2并非所有的鸟会飞。
第五章 高级数理逻辑

26
当涉及归纳定义的集S上的函数f的递归定 义和递归定义原理时,应当要求S中的元有 唯一的生成过程 例 M={0,1},g1是一元函数,且有g1(0)=1, g1(1)=0,故S={0,1}中的0和1可以由M生成, 也可以由g1生成,即生成过程不唯一.
27
例 令h(0)=h1(0)=0和h(1)=h1(1)=1,则按照 递归定义S上的函数f如下:
19
归纳证明
使用如上定理作出的证明,称为归纳证明, 即用归纳法作出的证明。 命题“对于任何n∈N,R(n)”是归纳命题, 其中n是归纳变元,这是说,当证明归纳命 题时,要对n做归纳。
第一步,称为(归纳的)基始,是证明定理中
的(i),即0有性质R。 第二步,称为归纳步骤,是证明其中的(ii),即 后继运算保存R性质。归纳步骤中的假设R(n) 称为归纳假设。
28
f(x)=h(x) 对于任何x∈M f(g1(x))=h1(f(x)) 对于任何x∈S 当0,1 ∈M时,有 f(0)=h(0)=0和f(1)=h(1)=1 但是此外,也有 f(0)= f(g1(1))=h1(f(1)) =h(1)=1 f(1)= f(g1(0))=h1(f(0)) =h(0)=0
22
递归定义原理
在归纳定义的集上定义函数,可以采用递 归定义的方法。 定理2 设g和h是N上的已知函数,则存在唯 一的N上的函数f,使得
f(0)=g(0),
f(n’)=h(f(n))
或 f(n’)=h(n, f(n)) .
对于任何n∈N,f(n)的值能够由上述定义f 的方程通过f(0),f(1),…,f(n-1)计算出来。称 这种定义为递归定义。
高级数理逻辑第3讲

3命题逻辑形式系统(FSPC)-续3.4 命题逻辑语义P(X)→Q(F(X-a)) A(X)-->A(X)X是复数,则(x-a)平方大于等于0;X=RPx是复数Q(x)代表的是大于等于0F代表的是平方X复数T(P(X))=0.5P(X)→(Q(X)→P(X))A→B3.4.1基本概念1、什么是形式系统的语义(1)形式系统与具体的系统无关(2)能够用形式系统来描述现实系统(3)把从形式系统解释成“→”现实系统的过程成为语义语义有多种类型:指称语义,克里普克语义,操作语义,公理语义等2.语义构成(指称语义)语义主要有两部分:(1)结构:(有两个主要部分构成)*确定研究对象集合,论域或个体域*把形式系统中的变量到论域中的一组规则映射规则(2)域值:指一组给公式赋值的规则根据这项规则将-Atomic→Value中3.4.2 命题逻辑语义1、语义结构由于没有变量,所以只有第二部分赋值,值域为{0,1}赋值规则: I.{}1,0∈V PII. ⎪⎩⎪⎨⎧===⌝0,11,0)(V VVA A AT(~A)= 当T (A )=0时,T(~A)=1。
当T (A )=1时,T(~A)=0。
III. ⎪⎩⎪⎨⎧=====∧00,01,1)(VV VV VB A B A B A 或 当T(A)=T(B)=1时,T(B A ∧)=1,其他情况T(B A ∧)=0。
IV. ⎪⎩⎪⎨⎧=====∨00111)(VV V V VB A B A B A ,或, 当T(A)=1或者T (B )=1情况下,T (B A ∨)=1,其他情况T (B A ∨)=0。
V. ⎩⎨⎧===→,否则或,0101)(V V B A B A当T(A)=0时候,T (B A →)=1,当T(B)=1时候,T (B A →)=1。
其他情况下T (B A →)=0。
A BVI. ⎪⎩⎪⎨⎧≠==↔VV VV VBA BA B A ,,01)( 2、 语义的特殊公式1) 公式A 为永真式,重言式tautologies ,如果对一切赋值v ,1=VA .A →A=~AvA(A →A)=1, A →(B →A)=12) 公式A 为永假式,矛盾式contradictions,如果对一切赋值v ,0=VA~A^A=03) A ,B 为逻辑等价的,如果对于一切赋值v ,VVB A =,记做A ╞B(A |=|B )T(A)=T(B),对于任意T A-->A A-->(B-->A)4) 可满足的,公式A 为可满足的,如果至少存在一个赋值v ,1=VA3、 真值计算有了赋值映射,我们可以计算任意公式的真值。
第三章 关系运算2(实例讲解)

PNAME 螺丝 门扣 门锁 开关 水龙头
COLOR 银色 红色 红色 白色 蓝色
WEIGHT 0.5 5 20 2 50
JNO JNAME JCITY BALANCE
J1 办公室 青岛 50000 工程
J2 居家装 山东 50000 修
SNO S1 S1 S3
PNO P3 P5 P4
JNO J1 J2 J1
SNO S1 S3 S1
SNA ME 喜多
天奴
喜多
SAD DR
上海 浦东
广州 汕头
上海 浦东
PNO P3 P4 P5
JNO J1 J1 J2
PRIC QTY PNA
E
ME
5
5
门锁
15 1
开关
10 2
水龙 头
COL WEI OR GHT 红色 20
白色 2
蓝色 50
JNO JNAME JCITY BALANCE
11. 检索使用了全部零件的工程名称JNAME。
π JNAME(J⋈(π JNO,PNO(SPJ)÷π PNO(P))
12.检索使用零件包含编号为S1的供应商所供应的全部零件的工程 编号JNO。
π JNO,PNO(σ SNO=‘S1’(SPJ))÷π PNO(σ SNO=‘S1’(SPJ))
课后3.12
2.检索使用了编号为P3零件的工程编号和名称。 {t|(u)(v)(J(u)∧SPJ(v)∧v[2]=‘P3’∧u[l]=v[3]∧t[l]=u[1]
∧t[2]=u[2])} 3.检索至少使用了编号为P3和P5零件的工程编号JNO。 {t|(u)(v)(SPJ(u)∧SPJ(v)∧u[3]=v[3]∧u[2]=‘P3’
高级数理逻辑

集合归纳定义的一般情况
设M为集合,gi为ni元函数,i=1,2,…,k。 两种等价的定义:
(1)M⊆S (2)对于任何x1,x2,…,xni,若x1,x2,…,xni ∈S,则 gi (x1,x2,…,xni ) ∈S (3)只有由(有限次使用)(1)和(2)生成的元素才是S 中元素
集合S是满足以下(1)和(2)的T中的最小集: (1)M⊆T (2)对于任何x1,x2,…,xni,若x1,x2,…,xni ∈T,则 gi (x1,x2,…,xni ) ∈T
课程的主要内容?经典逻辑?命题逻辑?谓词一阶逻辑?非经典逻辑?构造型逻辑?模态逻辑集合论?19世纪下半叶cantor提出朴素集合论?1903年russel提出集合论悖论产生数学的第三次危机?1908年zermelo提出公理化集合论zf体系集合论?集合论是数学的基石?基本概念?集合元素?序偶笛卡尔积?关系?映射?等价关系?相容关系?序关系集合元素?若干事物组成的整体被称为集合集合中的每个事物被称为元素
自然数集的归纳定义
后继 两种等价定义
(1)0∈N (2)对于任何n,若n∈N,则n’ ∈N(n’为n的后继) (3)只有由(有限次使用)(1)和(2)生成的n ∈N
N是满足以下(1)和(2)的S中的最小集: (1)0∈S (2)对于任何n,若n∈S,则n’ ∈S(n’为n的后继)
基于自然数集的归纳证明原理
笛卡尔积
ST { x, y | x S y T}
扩展(n>2)
有序n元组
<a1, a2, …, an>=<< a1, a2, …, an-1 >, an >
n阶笛卡尔积
S1 S2 ...Sn { x1, x2,..., xn | x1 S1 x2 S2 ... xn Sn}
数理逻辑讲稿

数理逻辑讲稿数理逻辑又称符号逻辑、理论逻辑。
它是数学的一个分支,是用数学方法研究逻辑或形式逻辑的学科。
其主要特征之一是“形式化”,就是将数理逻辑的研究对象“数学推理形式化,推理都有前提、结论和推理规则,这些前提和结论都是命题。
一个推理系统包含命题、公理和推理规则,“形式化”即为将这样的推理系统符号化而形成一个形式系统。
用数学的方法研究逻辑的系统思想一般追溯到十七世纪莱布尼茨,他设想过能不能创造一种“通用的科学语言”,可以把推理过程象数学一样利用公式来进行计算,从而得出正确的结论。
由于当时的社会条件,他的想法并没有实现。
但是它的思想却是现代数理逻辑部分内容的萌芽,从这个意义上讲,莱布尼茨可以说是数理逻辑的先驱。
后人基本是沿着莱布尼茨的思想进行工作的。
1847年,英国数学家布尔发表了《逻辑的数学分析》,建立了“布尔代数”,并创造一套符号系统,利用符号来表示逻辑中的各种概念。
布尔建立了一系列的运算法则,利用代数的方法研究逻辑问题,初步奠定了数理逻辑的基础。
十九世纪末二十世纪初,数理逻辑有了比较大的发展,1884年,德国数学家弗雷格出版了《数论的基础》一书,在书中引入量词的符号,使得数理逻辑的符号系统更加完备。
对建立这门学科做出贡献的,还有美国人皮尔斯,他也在著作中引入了逻辑符号。
从而使现代数理逻辑最基本的理论基础逐步形成,成为一门独立的学科。
数理逻辑就是精确化、数学化的形式逻辑。
它是现代计算机技术的基础。
数理逻辑的内容两个最基本的也是最重要的组成部分,就是“命题演算”和“谓词演算”。
命题演算是研究关于命题如何通过一些逻辑连接词构成更复杂的命题以及逻辑推理的方法。
命题是指具有具体意义的又能判断它是真还是假的句子。
在谓词演算里,把命题的内部结构分析成具有主词和谓词的逻辑形式,然后研究这样的命题之间的逻辑推理关系。
数理逻辑的发展数理逻辑这门学科建立以后,发展比较迅速,促进它发展的因素也是多方面的。
比如,非欧几何的建立,促使人们去研究非欧几何和欧氏几何的无矛盾性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3命题逻辑形式系统(FSPC)-续3.4 命题逻辑语义P(X)→Q(F(X-a)) A(X)-->A(X)X是复数,则(x-a)平方大于等于0;X=RPx是复数Q(x)代表的是大于等于0F代表的是平方X复数T(P(X))=0.5P(X)→(Q(X)→P(X))A→B3.4.1基本概念1、什么是形式系统的语义(1)形式系统与具体的系统无关(2)能够用形式系统来描述现实系统(3)把从形式系统解释成“→”现实系统的过程成为语义语义有多种类型:指称语义,克里普克语义,操作语义,公理语义等2.语义构成(指称语义)语义主要有两部分:(1)结构:(有两个主要部分构成)*确定研究对象集合,论域或个体域*把形式系统中的变量到论域中的一组规则映射规则(2)域值:指一组给公式赋值的规则根据这项规则将-Atomic→Value中3.4.2 命题逻辑语义1、语义结构由于没有变量,所以只有第二部分赋值,值域为{0,1}赋值规则: I.{}1,0∈VPII.⎪⎩⎪⎨⎧===⌝0,11,0)(VVVA A A T(~A)= 当T (A )=0时,T(~A)=1。
当T (A )=1时,T(~A)=0。
III. ⎪⎩⎪⎨⎧=====∧00,01,1)(VV VVVB A B A B A 或当T(A)=T(B)=1时,T(B A ∧)=1,其他情况T(B A ∧)=0。
IV. ⎪⎩⎪⎨⎧=====∨00111)(VV VVVB A B A B A ,或,当T(A)=1或者T (B )=1情况下,T (B A ∨)=1,其他情况T (B A ∨)=0。
V.⎩⎨⎧===→,否则或,0101)(VVB A B A当T(A)=0时候,T (B A →)=1,当T(B)=1时候,T (B A →)=1。
其他情况下T (B A →)=0。
A BVI. ⎪⎩⎪⎨⎧≠==↔VV VVVBA BA B A ,,01)( 2、 语义的特殊公式1) 公式A 为永真式,重言式tautologies ,如果对一切赋值v ,1=VA .A →A=~AvA(A →A)=1, A →(B →A)=12) 公式A 为永假式,矛盾式contradictions,如果对一切赋值v ,0=VA~A^A=03) A ,B 为逻辑等价的,如果对于一切赋值v ,V V B A =,记做A ╞B(A |=|B )T(A)=T(B),对于任意T A-->A A-->(B-->A)4) 可满足的,公式A 为可满足的,如果至少存在一个赋值v ,1=VA3、 真值计算有了赋值映射,我们可以计算任意公式的真值。
通常真值计算的方法有:真值表计算方法和二叉树计算方法等。
1) 真值表真值表是计算真值的简单工具。
利用这个工具可以计算任意公式的真值。
例如:公式)(r q p ⌝∨→的真值表如下:p qr)(r q p ⌝∨→0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 0 1111 1 1 12) 二叉树利用二叉树,可视化地计算公式的真值。
例如:计算下面公式的真值,并给出他是否是重言式。
))(()(r q q p A ∧⌝→∨=A 1=p 0=pr q ∧⌝)( ))((r q q ∧⌝→1=q 0=q 1=q 0=q0 r 0 11=r 0=r1故A 不为重言式,是可满足的 3) 习题求以下公式的真值表:(1))()(q p q p ∨⌝∧⌝∧(2))()(p q q p →↔→(3))())()((r q p r q r p →∨↔→∧→pqr))(())()((r q p r q r p →∨↔→∧→0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1113.5 逻辑推论(逻辑演算)有了公式的真值以后,对于一些公式我们可以比较公式的真值得大小。
从而可以讨论公式真值之间的关系。
讨论公式之间真值关系的就是我们在语义上进行演算的主要内容。
3.5.1 基本概念(1)逻辑推论:设∑是一个FSPC 上的公式集合,A 是FSPC 上的任一公式。
A 为∑的逻辑结果,记做∑|=A ,当且仅当对任何赋值映射v ,如果v∑=1时,则1=vA 。
|=读作逻辑蕴涵。
(2)逻辑等价:设公式A 和公式B 分别为FSPC 上的两个公式。
A 和B 为逻辑等价的,记做A|=|B 当且仅当A|=B 和B|=A 同时成立。
(3)永真式:如果A 为永真式,则公式集合∑为空集,即|=A 。
3.5.2逻辑推论的主要方法(1)永真式代入原理(principle of substitution)设A(P)为一含有命题变元P的永真式,那么将A中P的每一次出现代换为公式B,所得公式A(B)仍为永真式。
C-->(B-->C) == C-->(X-->C)(2)替换原理(principle of replacement)设命题公式A含有子公式C(C为命题公式),如果C|=|D,那么将A中子公式C提换为命题公式D,所得公式B满足A|=│B。
(3)逻辑等价性:逻辑等价且有自反性、对称性和传递性。
(4)对偶原理:设A是原子公式和联结符号∨∨,以原子公,组成的公式,并且在A中交换∧∧⌝,式与其否定互换得到的公式A′,称A′为A的对偶;A|=│⌝A′A∨B=~(~A ∧~B)(5)演绎定理:设∑为FSPC的公式集合,A和B分别为FSPC上的公式。
∑|=BA→成立的充分必要条件是:A∑|=B。
,已知:存在一个证明序列A1,A2,……An=A→B,An+1=A,An+2=B求证:存在另一个证明序列:从A∑出发能够得到B。
,已知:对于任意一个赋值映射f,如果f(∑)=1,则f(A→B)=1;求证:对于任意的赋值映射f,如果f(∑,A)=1,则f(B)=1证明:已知:对于任意的赋值映射f,如果f满足f(∑)=1,则f(A→B)=1.求证:对于任意的赋值映射f1,f1满足f1(∑)=1,且f1(A)=1;则f1(B)=1.证明:任意的赋值映射f,f满足f1(∑)=1,且f(A)=1.由于f1(∑)=1,则f1(A→B)=1;由于f1(A→B)=1,并且f1(A)=1;条件:f(∑)=1,且f(A)=1, f(A→B)=1,证明:f(B)=1由已知:f(A→B)=1.因此,f(B)=1.因此,对于任意的赋值映射f,f满足f(∑)=1,且f(A)=1;则f(B)=1.必要性:已知:对于任意的赋值映射f,f满足f(∑)=1,且f(A)=1;则f(B)=1.求证:对于任意的赋值映射f1,如果f1满足f1(∑)=1,则f1(A→B)=1.对于任意的赋值映射f,使得f(∑)=1.F1(∑)=1,f1(A)=0 f1(A→B)=1F1(∑)=1,f1(A)=1 ,f1(B)=1, f1(A→B)=1假设f1(A)=0;f1(A→B)=1.假设f1(A)=1, 由于已知条件可以知道f(B)=1.因此,f(A→B)=1.证明:a)首先证明充分性:已知∑╞BA→,证明A,∑╞B成立。
对于任意赋值映射v,如果v∑=1成立,则1)A成立。
B→v(=对于1→vA成立有两种情况,为了证明A,∑╞B成立,只需考虑,使v A=1 B(=)的情况。
如果赋值映射v,满足v∑=1,v A=1且1A,则有v B=1。
因此,A,∑╞B→v(=)B 成立。
b)证明必要性:已知 A ,∑╞B ,证明∑╞B A →成立。
已知:如果对于任意的赋值映射1=∑v且1=v A 则1=v B ;要证明∑╞B A →:即证明对于任意赋值映射v ,满足1=∑v,则有1)(=→vB A 成立。
任取赋值映射v ,满足1=∑v,则有:当vA =0时,,1)(=→vB A 有∑╞B A →当v A =1时,由已知vB =1, 因此∑╞B A →3.5.3 逻辑推论性质1、公理为重言式A1 ╞v )(A B A →→A2 ╞v ))()(())((C A B A C B A →→→→→→A3 ╞v )()(A B B A →→⌝→⌝2、推理规则保真性设A 和B 为FSPC 上的公式;如果|=A 且|=B A →成立,则|=B 成立。
3、重要永真式T 1 P P P P →⌝∨, T(P)<=T(P)T 2 )(),(Q P Q Q P P ∨→∨→ P<=Max(P,Q)T 3 Q Q P P Q P →∧→∧, Min(P,Q)<=PT 4 )())()((R P R Q Q P →→→∧→ P<=Q, Q<=R, P<=RT 5 )()()(R P R Q Q P ↔→↔∧↔ P=Q,Q=R, P=R4、重要等价式E 1 )(P ⌝⌝╞│P ~~P=1-(1-P)=PE 2 P P ∨╞│P P P ∧,╞│P (等幂律)E 3Q P ∨╞│Q P P Q ∧∨,╞│P Q ∧ (交换律)E 4 )(R Q P ∧∨╞│)()(R P Q P ∨∧∨E 5 )(R Q P ∨∧╞│)()(R P Q P ∧∨∧ (分配律)E 6 )(Q P ∨⌝╞│)()(Q P ⌝∧⌝ (德摩根定律))(Q P ∧⌝╞│)()(Q P ⌝∨⌝E 7 Q P ∨⌝)(╞│QP →E 8 Q P →╞│)()(P Q ⌝→⌝E 9)(R Q P →→╞│R Q P →∧)(~Pv(Q →R) ==~Pv(~QvR)=(~Pv~Q)vR=~(Q ∧P)vR=(P ∧Q)→R如果P=1,则Q R=1;如果min(Q,P)=1,则R=1.E 10 Q P ↔╞│)()(P Q Q P →∧→(~PvQ) ∧(~QvP)=((~PvQ)∧~Q)v((~PvQ) ∧P)=(~Q ∧~P)v(P ∧Q) E 11 Q P ↔╞│))()(()(Q P Q P ⌝∧⌝∨∧E 12 )(Q P P ∧∨╞│P Max(P, Min(P,Q))=P MIN(P,Q)<P)(Q P P ∨∧╞│P MIN(P,MAX(P,Q))=PMAX(P,Q)>=P. (吸收律)3.6 公式化简 3.6.1 基本概念有了赋值规则和上述的等价公式后,我们就可以将公式进行等价形式的转化。
转换的目标是获得一个标准的公式形式,从而使公式计算更简单,同时使计算机能够进行基于符号的演算和推理过程。
范式是常用的公式的标准形式。
1、范式:设A 和B 为FSPC 上的两个公式,称公式B 为公式A 的析取(合取)范式,如果B |=│A ,并且B 型如:)(321321m m C C C C C C C C ∧∧∧∧∨∨∨∨{C1, C2, C3, …,Cm} {L1Vl2, L2v~L1} {L2} P(x), ~P(5+y)= x=5+y, P(5+y) ~P(5+y) 其中,),,3,2,1(m i C i =称为B 的子句(Clause ),子句型如: Ci=)(321321n n L L L L L L L L ∨∨∨∨∧∧∧∧其中),,3,2,1(n j L j =为原子公式或其否定式,被称为文字。
