用枚举法设计算法
谈谈用枚举算法解决问题的编程思路与步骤方法

谈谈用枚举算法解决问题的编程思路与步骤方法一.问题上海市普通高中在信息科技学科中开展《算法与程序设计》教学,教材中有一章名为“算法实例”的内容,其中有一节介绍“枚举算法”。
教材中关于枚举算法的描述:有一类问题可以采用一种盲目的搜索方法,在搜索结果的过程中,把各种可能的情况都考虑到,并对所得的结果逐一进行判断,过滤掉那些不合要求的,保留那些符合要求的。
这种方法叫做枚举算法(enumerative algorithm)。
枚举法就是按问题本身的性质,一一列举出该问题所有可能的解,并在逐一列举的过程中,检验每个可能解是否是问题的真正解,若是,我们采纳这个解,否则抛弃它。
在列举的过程中,既不能遗漏也不应重复。
生活和工作中,人们经常会不经意间运用“枚举算法”的基本原理,进行问题的解决。
比如,让你用一串钥匙,去开一把锁,但是不知道具体是用哪一把钥匙,你就会一把一把地挨个地逐个尝试,最终打开锁为止。
又如,要对1000个零件,进行合格检验,等等。
二.用枚举算法的思想编写程序的思路与步骤枚举算法,归纳为八个字:一一列举,逐个检验。
在实际使用中,一一列举;采用循环来实现,逐个检验:采用选择来实现。
下面,通过一个问题的解决来说明这一类问题的解决过程的方法与步骤;例1:在1—2013这些自然数中,找出所有是37倍数的自然数。
这个问题就可以采用枚举算法来解决:1).一一列举;采用循环来实现;循环需要确定范围:本循环控制变量假设用i,起始值是1,终止值是2013。
2).逐个检验:采用选择来实现;选择需要列出判断的关系表达式:i Mod 37 = 0这样,就可以写出整个求解的VB代码:Dim i As IntegerFor i = 1 To 2013If i Mod 37 = 0 ThenPrint iEnd IfNext i说白了,用枚举算法解决问题,其实是利用计算机的高速度这一个优势,就好比上题完全可以使用一张纸和一支笔,采用人工的方法完成问题的解,从1开始,一一试除以37,这样计算2013次,也可以找到问题的答案。
【算法】枚举法
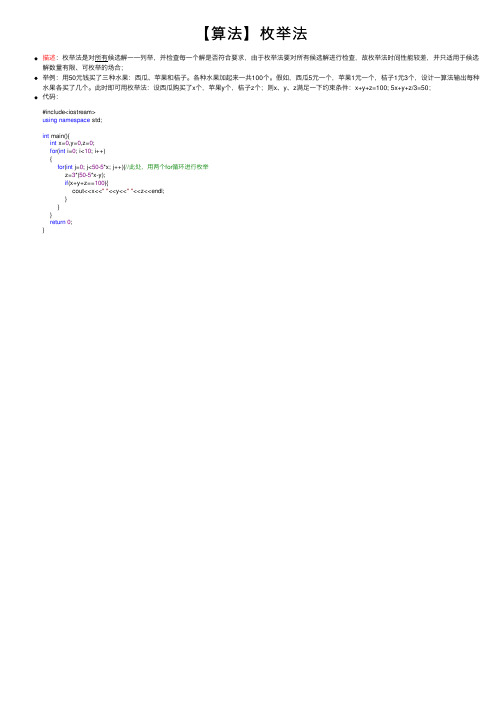
【算法】枚举法
描述:枚举法是对所有候选解⼀⼀列举,并检查每⼀个解是否符合要求,由于枚举法要对所有候选解进⾏检查,故枚举法时间性能较差,并只适⽤于候选解数量有限、可枚举的场合;
举例:⽤50元钱买了三种⽔果:西⽠、苹果和桔⼦。
各种⽔果加起来⼀共100个。
假如,西⽠5元⼀个,苹果1元⼀个,桔⼦1元3个,设计⼀算法输出每种⽔果各买了⼏个。
此时即可⽤枚举法:设西⽠购买了x个,苹果y个,桔⼦z个;则x、y、z满⾜⼀下约束条件:x+y+z=100; 5x+y+z/3=50;
代码:
#include<iostream>
using namespace std;
int main(){
int x=0,y=0,z=0;
for(int i=0; i<10; i++)
{
for(int j=0; j<50-5*x; j++){//此处,⽤两个for循环进⾏枚举
z=3*(50-5*x-y);
if(x+y+z==100){
cout<<x<<""<<y<<""<<z<<endl;
}
}
}
return0;
}。
枚举算法的步骤

枚举算法的步骤介绍枚举算法是一种简单却有效的解决问题的方法。
它通过穷举所有可能的解决方案来找到问题的解。
本文将详细介绍枚举算法的步骤,包括问题描述、解设计、穷举和解决方案验证。
通过深入了解枚举算法的步骤,读者可以更好地理解和应用这一算法。
问题描述首先,我们需要明确问题的描述。
问题描述应该清晰而具体,直观地表达问题的要求和限制。
在枚举算法中,问题描述是我们开始设计解决方案的基础。
解设计解设计是指为了解决问题而设计的解决方案的结构和思路。
在枚举算法中,解设计是整个算法的核心。
下面是解设计的一些重要步骤:确定问题解空间问题解空间是指问题的所有可能的解决方案构成的空间。
在枚举算法中,我们需要明确问题解空间的结构和范围,以便穷举所有可能的解。
制定解决方案的表示解决方案的表示是指如何表示问题的解。
这个表示应该能够表示问题的所有可能解,并能够在算法中被穷举和验证。
设计解穷举的算法解穷举是指枚举算法中穷举解空间的过程。
设计解穷举的算法需要考虑解的范围和解的顺序,以便能够穷举所有可能的解,并将其作为解决方案的候选。
解决方案的验证解决方案的验证是指对穷举出来的解进行筛选和验证,以确认其是否满足问题的要求和限制。
解决方案的验证是保证最终解是正确的关键。
穷举穷举是指枚举算法中对解空间进行遍历的过程。
在穷举过程中,我们逐个尝试解空间中的解,并对其进行验证。
为了实现穷举,我们需要使用循环和条件判断等控制结构。
一般来说,我们会使用嵌套循环来穷举所有可能的组合。
解决方案验证解决方案验证是指对穷举出来的解进行筛选和验证的过程。
通过解决方案验证,我们可以确定哪些解是满足问题要求和限制的。
解决方案验证可以包括以下步骤:检查解的有效性首先,我们需要检查解是否满足问题的约束条件。
这些约束条件可以是数学方程、逻辑条件等。
如果解不满足约束条件,那么该解是无效的,我们应该继续穷举其他解。
检查解的优劣除了满足约束条件外,我们还需要评估解的优劣。
谈谈用枚举算法解决问题的编程思路与步骤方法

谈谈用枚举算法解决问题的编程思路与步骤方法一.问题上海市普通高中在信息科技学科中开展《算法与程序设计》教学,教材中有一章名为“算法实例”的内容,其中有一节介绍“枚举算法”。
教材中关于枚举算法的描述:有一类问题可以采用一种盲目的搜索方法,在搜索结果的过程中,把各种可能的情况都考虑到,并对所得的结果逐一进行判断,过滤掉那些不合要求的,保留那些符合要求的。
这种方法叫做枚举算法(enumerative algorithm)。
枚举法就是按问题本身的性质,一一列举出该问题所有可能的解,并在逐一列举的过程中,检验每个可能解是否是问题的真正解,若是,我们采纳这个解,否则抛弃它。
在列举的过程中,既不能遗漏也不应重复。
生活和工作中,人们经常会不经意间运用“枚举算法”的基本原理,进行问题的解决。
比如,让你用一串钥匙,去开一把锁,但是不知道具体是用哪一把钥匙,你就会一把一把地挨个地逐个尝试,最终打开锁为止。
又如,要对1000个零件,进行合格检验,等等。
二.用枚举算法的思想编写程序的思路与步骤枚举算法,归纳为八个字:一一列举,逐个检验。
在实际使用中,一一列举;采用循环来实现,逐个检验:采用选择来实现。
下面,通过一个问题的解决来说明这一类问题的解决过程的方法与步骤;例1:在1—2013这些自然数中,找出所有是37倍数的自然数。
这个问题就可以采用枚举算法来解决:1).一一列举;采用循环来实现;循环需要确定范围:本循环控制变量假设用i,起始值是1,终止值是2013。
2).逐个检验:采用选择来实现;选择需要列出判断的关系表达式:i Mod 37 = 0这样,就可以写出整个求解的VB代码:Dim i As IntegerFor i = 1 To 2013If i Mod 37 = 0 ThenPrint iEnd IfNext i说白了,用枚举算法解决问题,其实是利用计算机的高速度这一个优势,就好比上题完全可以使用一张纸和一支笔,采用人工的方法完成问题的解,从1开始,一一试除以37,这样计算2013次,也可以找到问题的答案。
枚举算法(修改)

控件属性值的设置如下表 对象名 Form1 List1 Command1 属性名 Caption list Caption 属性值 涂抹数字推算 空白 计算
高中信息技术必修2:算法与程序设计
②分析算法流程,编写代码; Private Sub Command1_Click() Dim j As Integer, n As Integer, c As Integer c=0 List1.Clear For j = 0 To 99 n = 25006 + j * 10 ’生成每一种可能解 If n Mod 37 = 0 Or n Mod 67 = 0 Then ‘判断是否满足条件 List1.AddItem Str(n) c=c+1 End If Next j List1.AddItem "总计有" + Str(c) + "个五位数" End Sub ③运行调试程序;(点击打开)
课堂练习
高中信息技术必修2:算法与程序设计
单据中被涂抹数字的推算问题,请将划线处填写完整: Private Sub Command1_Click() Dim j As Integer, n As Integer, c As Integer c=0 List1.Clear n=25006 ________________’(1) Do while n<=25996 If n Mod 37 = 0 Or n Mod 67 = 0 Then List1.AddItem Str(n) c=c+1 End If n=n+10 ________________’(2) Loop List1.AddItem "总计有" + Str(c) + "个五位数" End Sub
python枚举法1~100算法

枚举法是一种通过列举所有可能情况来解决问题的方法。
对于1到100的数字,我们可以使用Python的for循环来枚举所有的数字。
以下是一个简单的Python程序,使用枚举法找出1到100之间的所有奇数:python复制代码for i in range(1, 101):if i % 2 != 0:print(i)这个程序会打印出1到100之间的所有奇数。
range(1, 101)函数生成一个从1到100的数字序列,然后for 循环遍历这个序列。
在循环中,我们使用if语句检查当前的数字是否是奇数(即除以2的余数不等于0),如果是,就打印出来。
如果你想找出1到100之间的所有素数,你可以使用一个稍微复杂的算法,比如埃拉托斯特尼筛法(Sieve of Eratosthenes)。
这个算法的基本思想是,从2开始,把所有的偶数都标记为合数,然后找出所有的未被标记的数字,这些数字就是素数。
以下是一个使用Python实现的埃拉托斯特尼筛法的例子:python复制代码def sieve_of_eratosthenes(n):primes = [True] * (n+1)primes[0] = primes[1] = Falsefor i in range(2, int(n**0.5)+1):if primes[i]:for j in range(i**2, n+1, i):primes[j] = Falsereturn [p for p in range(2, n+1) if primes[p]]print(sieve_of_eratosthenes(100))这个程序会打印出1到100之间的所有素数。
8算法策略之枚举法

8算法策略之枚举法蛮⼒法蛮⼒法是基于计算机运算速度快这⼀特性,在解决问题时采取的⼀种“懒惰”的策略。
这种策略不经过(或者说是经过很少的)思考,把问题的所有情况或所有过程交给计算机去⼀⼀尝试,从中找出问题的解。
蛮⼒策略的应⽤很⼴,具体表现形式各异,数据结构课程中学习的:选择排序、冒泡排序、插⼊排序、顺序查找、朴素的字符串匹配等,都是蛮⼒策略具体应⽤。
⽐较常⽤还有枚举法、盲⽬搜索算法等。
枚举法枚举( enumerate)法(穷举法)是蛮⼒策略的⼀种表现形式,也是⼀种使⽤⾮常普遍的思维⽅法。
它是根据问题中的条件将可能的情况⼀⼀列举出来,逐⼀尝试从中找出满⾜问题条件的解。
但有时⼀⼀列举出的情况数⽬很⼤,如果超过了我们所能忍受的范围,则需要进⼀步考虑,排除⼀些明显不合理的情况,尽可能减少问题可能解的列举数⽬。
⽤枚举法解决问题,通常可以从两个⽅⾯进⾏算法设计:1)找出枚举范围:分析问题所涉及的各种情况。
2)找出约束条件:分析问题的解需要满⾜的条件,并⽤逻辑表达式表⽰。
【例1】百钱百鸡问题。
中国古代数学家张丘建在他的《算经》中提出了著名的“百钱百鸡问题”:鸡翁⼀,值钱五;鸡母⼀,值钱三;鸡雏三,值钱⼀;百钱买百鸡,翁、母、雏各⼏何?算法设计1:通过对问题的理解,读者可能会想到列出两个三元⼀次⽅程,去解这个不定解⽅程,就能找出问题的解。
这确实是⼀种办法,但这⾥我们要⽤“懒惰”的枚举策略进⾏算法设计:设x,y,z分别为公鸡、母鸡、⼩鸡的数量。
尝试范围:由题意给定共100钱要买百鸡,若全买公鸡最多买100/5=20只,显然x的取值范围1~20之间;同理,y的取值范围在1~33之间,z的取值范围在1~100之间。
约束条件: x+y+z=100 且 5*x+3*y+z/3=100算法1如下:main( ){ int x,y,z;for(x=1;x<=20;x=x+1)for(y=1;y<=34;y=y+1)for(z=1;z<=100;z=z+1)if(100=x+y+z and 100=5*x+3*y+z/3){print("the cock number is",x);print("the hen number is", y);print("the chick number is“,z);}}算法分析:以上算法需要枚举尝试20*34*100=68000次。
python枚举算法例子简单

python枚举算法例子简单枚举算法是一种常用的算法思想,它通过列举所有可能的情况来解决问题。
枚举算法在解决一些简单问题时非常有效,但对于复杂的问题可能会导致计算量过大,因此需要谨慎使用。
以下是一些常见的使用枚举算法解决问题的例子:1.查找数组中的最大值和最小值:给定一个整数数组,我们可以使用枚举算法来查找其中的最大值和最小值。
我们可以使用两个变量分别记录当前找到的最大值和最小值,然后遍历数组,依次比较每个元素与当前最大值和最小值的大小关系,更新最大值和最小值。
2.找到数组中的两个元素使其和为给定值:给定一个整数数组和一个目标值,我们可以使用枚举算法来找到数组中的两个元素,使其和等于目标值。
我们可以使用两层循环遍历数组中的所有元素,对于每对元素,判断它们的和是否等于目标值。
如果找到了满足条件的元素,就输出它们的索引或值。
3.找到数组中的三个元素使其和为给定值:类似地,我们也可以使用枚举算法来找到数组中的三个元素,使其和等于给定值。
这可以通过使用三层循环遍历数组中的所有元素来实现。
对于每三个元素的组合,判断它们的和是否等于目标值。
如果找到了满足条件的三个元素,就输出它们的索引或值。
4.穷举法解决密码破解问题:某种密码由4个数字组成,每个数字的范围是0-9之间的一个整数。
穷举法可以用来解决这类密码破解问题。
我们可以使用四层循环来穷举所有可能的密码组合,并与已知密码进行比对,直到找到正确的密码。
这种方法在密码位数较少、可能取值较少的情况下比较实用。
5.枚举所有子串:给定一个字符串,枚举所有可能的子串是一个常见的问题。
我们可以使用两层循环来遍历字符串的所有可能的起始和结束索引,并输出对应的子串。
这种方法可以帮助我们快速检查字符串中是否包含指定的子串。
以上例子只是枚举算法的一些基本应用,实际上枚举算法可以应用在很多不同的问题中。
但需要注意的是,由于枚举算法需要遍历所有可能的情况,所以在解决复杂问题时会导致计算量过大,效率较低。
第十课 枚举算法(ppt)

二、用VB程序实现:如果一个三维数等于 它的每个数字立方的和,则此数称为“水仙 花数”,如153=1^3+5^3+3^3,故153 是水仙花数。求100—999之间的全部水仙 花数。
板书设计
一、认识枚举算法
现实生活中有一类问题可以采用搜索的方法解决,如密码破解、寻找素数等,在搜索的过程中,列举所有 可能的结果,并逐一判断,排除其中不符合要求的结果,这种方法称为枚举算法,也称为“穷举法”。 方法:
二、多重循环
在一个循环体内又包含了循环结构,称为多重循环或循环嵌套,如二重循环的结构为: For i=初值 To 终值
For j=初值 To 终值 循环体
Next j Next i
三、枚举算法的程序实例:百钱买百鸡
作业布置
程序实现: 一张单据上有一个5位数的编码,其千位数和百位数 已经变得模糊不清,但是直到这个5位数是57或67的倍数,现在要设 计一个算法,输出所有满足这些条件的5位数,并统计这样的数的个 数。
5*i+3*j+k/3=100 百钱的计算
i+j+k=100 百鸡的计算(鸡的数量)
该问题可转化为对i,j,k各种不同的组合进行搜索, 从而找到鸡和钱的总数均为100的组合。在计算机程序 中,可认利用二重循环枚举解决这类问题。
知识链接
多重循环:在一个循环体内又
例:
包含了循环结构,称为多重循
For i=1 To 4
对象名
Form1 Command1
Label1
属性名
Caption Caption Caption
属性值
百钱买百鸡问题
求解
一百个铜钱买了一百 只鸡,其中公鸡一只 5钱,母鸡一只3钱, 小鸡一钱3只,问一 百只鸡中公鸡、母鸡、
枚举算法举例

用变量i表示十位上的数;变量n表示这个5位数。
列举范围:0——9
检验条件:n能被5或者11整除。
即:(n mod 7=0) or (n mod 11=0)
开始
i=0
i<10
N
Y
n=14708+i*10
N
(n mod 7=0) or (n mod 11=0)
Y 输出n
i=i+1
if i mod 7=0 then print i
end if i=i+1 loop
枚举算法的设计步骤
• 确定列举范围 • 明确检验条件 • 确定循环控制方式和列举方式
枚举算法只适用于可能解的个数不太多的情况。
一张单据上有一个5位数的编号,万位数是1,千位 数是4,百位数是7,个位数是8,十位数已经模糊不清 ,只知道该5位数是7或11的倍数,找出所有满足这些条 件的5位数并输出。
i=1
i<=1000
F
T
i mod 3=0
F
T 输出 i
i mod 7=0 and i mod 11=0
i mod 77=0
i=i+1
结束
鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱 一,百钱买百鸡,问翁、母、雏பைடு நூலகம்几何?
鸡翁 鸡母 鸡雏
一一列举: a 初值: 0 终值: 20
递增值: 1
b
c
0
0
33
F
T
i mod 3=0
F
T 检验 输出 i
检验:
i mod 3=0
F
T
输出 i
i=i+1
结束
算法设计与分析:枚举三步

• 共枚举63次
模拟面试-2
问题描述:给定长度为n的单调不下降数列0 , ⋯ , −1 和一个数,求满足
条件 ≥ 的最小值。不存在的情况下输出n。
输入样例:
n=5
a = {2, 3, 3, 5, 6}
k =4
输出样例:
3
模拟面试-3
问题描述:有N条绳子,它们的长度分别为 。如果从它们中切割出K条长
度相同的绳子的话,这K条绳子每条最长能有多长?答案保留到小数点后2
位。
输入样例:
N=4
K = 11
L = {8.02, 7.43, 4.57, 5.39}
输出样例:
2.00 (每条绳子分别可以得到4条、3条、2条、2条,共计11条。)
模拟面试-4
给一个很长的数字串S:123456891011121314…,它是由所有的自
枚举三步
1. 确定枚举对象 枚举对象也可以理解为是问题解的表达形式,一般需
要用若干参数来描述
参数之间需要相互独立,而且,参数数目越少,问题解的搜索空间的维度也
相应地小;
每个参数的取值范围越小,问题解的搜索空间也越小。
2. 逐一列举可能解 根据枚举对象的参数构造循环,一一列举其表达式
的每一种取值情况。
3. 逐一验证可能解 根据问题解的要求,一一验证枚举否则,抛弃之。
模拟面试-1
问题描述:编写算法解如下数字迷:ABCAB * A = DDDDDD
方案1:
• 枚举范围:A:3-9 B:0-9 C:0-9
• 工枚举700次
方案2:
• 将算式变形为除法:DDDDDD / A = ABCAB
枚举算法之算法实现

之程序实现
什么是枚举算法
“鸡、兔同笼问题” 鸡、兔共79只,200只脚在笼里走,试问多有少只
鸡?多少只兔? 枚举法就是按问题本身的性质,一一列举出该问
题所有可能的解,并在逐一列举的过程中,检验 每个可能解是否是问题的真正解,若是,我们采 纳这个解,否则抛弃它。
解题过程
解题过程分两步: 逐一列举可能的解的范围。这个过程用循环结构
90890123 00 01 02 03 …… 98 99
J
让变量J依次取0到99这100个不同的值,同时对于J的每个 确定的值乘以10加上25006这样就能形成一个可能解.
J
乘以10
0
00
1
10
2
20
……
98
980
99
990
加上25006 25006 25016 25026
25986
25996
验证条件: N MOD 37=0 OR N MOD 67=0
SUCCESS
THANK YOU
2019/10/28
for循环
Private Sub Command1_Click() Dim j As Integer '定义一个中间被涂抹的两位数变量 Dim n As Integer '定义被求的结果5位数变量 Dim c As Integer '定义被求的符合要求的五位数个数变量 c=0 List1.Clear For j = 0 To 99 n = 25006 + j * 10 If n Mod 37 = 0 Or n Mod 67 = 0 Then List1.AddItem Str(n) c=c+1 End If Next j List1.AddItem "总计有" + Str(c) + "个五位数"
枚举算法之算法实现

枚举算法之算法实现枚举算法是一种常用的算法设计思想,其核心思想是通过遍历所有可能的解空间,逐一枚举所有可能的解,并通过比较得到最优解。
枚举算法的实现一般包括以下几个步骤:1.确定问题的解空间:首先需要明确问题的解空间是什么,即问题的可能解有哪些。
对于一些简单的问题,解空间可能是固定的范围,如整数的解空间是[0,n];对于一些复杂的问题,解空间可能需要通过一些规律和约束来确定。
2.枚举所有可能的解:确定了解空间后,就可以通过循环或递归来枚举解空间中的所有可能解。
如果解空间是一个固定的范围,可以使用循环来遍历解空间中的每一个值;如果解空间是不定的,可以使用递归来遍历解空间中的每一个可能。
3.判断解的有效性:对于问题的解,可能不是所有的解都是有效的解,需要通过一些条件来判断解的有效性。
如果解无效,可以直接跳过或排除该解,减少后续的计算量。
4.比较得到最优解:在枚举的过程中,需要将当前枚举得到的解与当前最优解进行比较,并根据问题的要求更新最优解。
最优解可以是最大值、最小值、最优组合等,根据具体问题而定。
枚举算法的实现需要一定的时间复杂度,因为需要遍历解空间中的所有解。
对于解空间较大的问题,枚举算法的时间复杂度可能会非常高,甚至是指数级的。
在实际应用中,需要根据具体问题的规模和要求来选择是否使用枚举算法。
下面以两个例子来说明枚举算法的实现。
1. 求解在一个整数数组中找到两个数之和等于给定值的问题。
假设给定一个整数数组arr和目标值target,需要找到两个数a和b,使得a + b = target。
可以使用枚举算法来遍历数组中的每一个数,并用目标值减去当前数字,看是否存在解。
具体实现如下:```pythondef findTwoSum(arr, target):for i in range(len(arr)):for j in range(i + 1, len(arr)):if arr[i] + arr[j] == target:return [i, j]return []arr = [2, 7, 11, 15]target = 9print(findTwoSum(arr, target)) # 输出[0, 1]```2.求解在一个字符串中找到最长的回文子串的问题。
研究生课程算法设计与分析之枚举算法

输出:每组测试样例的结果输出占一行,第一个数字表示满 足条件的编码个数,后面按升序输出所有满足条件的编码, 数字与数字之间用空格隔开。
?? 0 9 5
m钱n鸡
任务描述:我国古代数学家张丘建在《算经》中出了一 道题“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值 钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?”, 现在假定各鸡种的价格不变,拥有的钱数为m,需要购 买的鸡数为n,试求出所有可能的购买方案总数。
✓ 解的高准确性和全面性 ✓ 实现简单,枚举算法通过循环来逐一列举和验证可能解 ✓ 效率提升空间比较大
枚举三步
1. 确定枚举对象 枚举对象也可以理解为是问题解的 表达形式,一般需要用若干参数来描述
参数之间需要相互独立,而且,参数数目越少,问题解 的搜索空间的维度也相应地小;
每个参数的取值范围越小,问题解的搜索空间也越小。
逐一列举 逐一验证
✓✓ ““EEvveenn””状状态态,,天天平平任任意意一一端端出出现现ss,,则则ss不不可可 能能为为重轻的的假假币币;;
✓✓ ““UUpp””状状态态,,天天平平左右端端没没有有出出现现ss,,则则ss不不可可能能 为为重轻的的假假币币;;
✓✓ ““DDoowwnn””状状态态,,天天平平右左端端没没有有出出现现ss,,则则ss不不可可 能能为为重轻的的假假币币;;
输入:第一行包含一个正整数,表示测试数据的组数。每组测试 数据有三行,每行表示一次称重的结果。张三和助手事先把银币 标号为A~L。每次称重的结果用3个以空格隔开的字符串表示:天 平左边放置的银币标号,天平右边放置的银币标号,以及平衡状 态。其中平衡状态用“up”、“down”和“even”表示,分别表示 右端高、右端低和平衡。另外,每次称重天平左右的银币数总是 相等的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h
8
当且仅当问题可能的解不太多时,才能用穷举法
h
2•
1.问题 一张标签上有一个5位数的编号,其千位数和百位数处
已经变得模糊不清,如右图。但知道这个5位数是57或67 的倍数。现在要设计一个算法,输出所有满足这些条件 的5位数,并统计这样的数的个数。
h3ຫໍສະໝຸດ 枚举法一个实例 复原一份数字被涂抹的单据的算法
其真正解n:能被57或67整除,若n是真正解,则输出n, 并在计数器c中计数。
真
计数器C计数; 输出真正解;
h
假
输出计数器C的值 结束
7
程序:
main() { int n,c,j; c=0; for (j=0;j<100;j=j+1) { n=10047+j*100;
If(n%57==0||n%67==0) {c=c+1; printf(“%d\n”,n);} }
Printf(“Count=%d\n”,c)
NO: 1??47
能填入的数: 00,01,02,…98,99
产能生的可解:10047,10147 …… 19947 (100个)
h
4•
用穷举法解决问题:
在算法中使用的变量:
c: 计数器,用于记录算法执行过程中已经找到的真正解的个数。
j: 本变量的作用如下: 依次产生应填在千位和百位上的数值(0到99)。
第三章 用枚举法设计算法
一、学习目的: 1、通过一个具体实例,理解什么是穷举法 2、如何利用穷举法解决问题 3、了解计数器的用法
h
1•
枚举法(也叫穷举算法):
就是按照问题的本身的性质,通过多重循环,一 一列出问题所有可能的解,然后检验每个可能的解是 否是问题的真正解,若是,采纳(输出)这个解,否 则放弃它。这种解决问题的算法
在重复处理过程中记录已经进行的重复的次数, 并用它来控制重复的次数;
n: 存储一个可能解。
表达式:n%57==o或n%67==0确定真正解
h
5
h
6
根据空举法用for()语句来实现找真解n及真解的个数c: 开始
计数器置C=0;
返回
J=0;
真 J<100?
n←10047+j*100; n正解吗?
假
J←j+1
