第4讲 MATLAB矩阵分析及绘图
MATLAB矩阵操作教程

MATLAB矩阵操作教程第一章:MATLAB中的矩阵介绍1.1 什么是矩阵矩阵是由数个行和列组成的矩形数组,可以用于表示数据和进行数值计算。
1.2 创建矩阵在MATLAB中,可以使用矩阵生成算符进行矩阵的创建,如使用方括号,分号和逗号分隔元素。
1.3 矩阵索引MATLAB中的矩阵索引从1开始,可以使用括号和索引访问矩阵中的元素。
1.4 矩阵运算MATLAB提供了丰富的矩阵运算函数,如加法、减法、乘法、除法等,可用于执行矩阵操作。
第二章:MATLAB矩阵的基本操作2.1 矩阵转置可以使用单引号将矩阵转置,即将矩阵的行变为列,列变为行。
使用方括号和逗号将矩阵进行水平或垂直合并。
2.3 矩阵切片可以使用冒号运算符和索引,对矩阵进行切片操作,提取出所需的子矩阵。
2.4 矩阵重塑使用reshape函数可以改变矩阵的形状,重新组织矩阵元素的排列顺序。
2.5 矩阵求逆使用inv函数求矩阵的逆矩阵,如果矩阵不可逆,则会报错。
第三章:MATLAB矩阵的高级操作3.1 特征值与特征向量使用eig函数可以计算矩阵的特征值和特征向量,以进行其他相关计算。
3.2 矩阵分解MATLAB中提供了多种矩阵分解函数,如LU分解、QR 分解、奇异值分解等,可用于求解线性方程组、矩阵逆等问题。
使用左除运算符(\)和右除运算符(/)可以求解形如AX=B的线性方程组。
3.4 矩阵迭代可以使用循环结构和条件判断,在MATLAB中实现矩阵的迭代计算。
第四章:MATLAB中的矩阵应用4.1 数据处理与分析使用MATLAB可以进行各种数据处理和分析,如平均值计算、数据拟合、统计分析等。
4.2 信号处理利用MATLAB中的矩阵操作函数,可以进行信号滤波、频谱分析、波形生成等信号处理操作。
4.3 图像处理MATLAB中的矩阵操作函数可用于图像的载入、处理、显示和保存,如图像滤波、边缘检测、图像分割等。
4.4 机器学习利用MATLAB中的矩阵操作与机器学习算法相结合,可以进行分类、回归、聚类等机器学习任务。
1第四讲MATLAB矩阵课件PPT

学习内容
一.变量和数据操作 二.数组和矩阵的创建 三.数组和矩阵的寻访和操作 四.数组和矩阵运算
22
MATLAB矩阵简介
从结构上讲,矩阵(数组)是MATLAB数 据存储的基本单元。
从运算角度讲,矩阵形式的数据有多种 运算形式,例如向量运算,矩阵运算, 数组运算等。
19
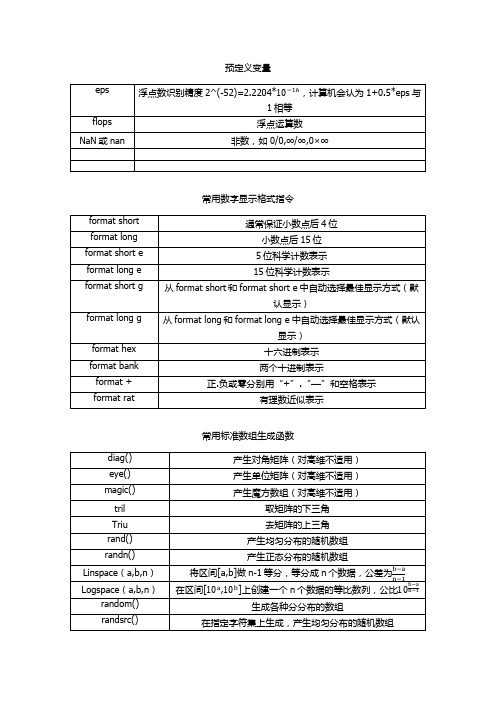
5.数据的输出格式
MATLAB用十进制数表示一个常数,具体 可采用日常记数法和科学记数法(如 3.5e5)两种表示方法。
在一般情况下,MATLAB内部每一个数据 元素都是用双精度数来表示和存储的。
20
5.数据的输出格式
数据输出时用户可以用format命令设置或 改变数据输出格式,
format命令的格式为:format+格式符 注:格式符决定数据的输出格式,格式符的 形式可以为 compact; losse;bank; short;long;short e;long e等。
8
一、变量和数据操作
1. 变量命名 在MATLAB 中,变量名是以字母开头,后接
字母、数字或下划线的字符序列,但不得 使用空格和标点符号,最多63个字符。如 my_var_201是合法的变量而my,var201就 不是变量名
9
变量命名命名规则(续)
在MATLAB中,变量名区分字母的大小 写,如变量myvar和MyVar表示两个不同 的变量,sin是MATLAB定义的正弦函数 名,但SIN,Sin等都不是。
1 0 % x1 2 5 % x2 2 0 % x3 5 % x4 1 2 %
x1 x2 x3 x4 1
2
0
x1
16 x2
10 x3
15x4
第四讲 MATLAB绘图

希腊字母、上标、下标、数学符号、字型:
\ alpha \ beta \ gamma \ pi \ tall
\ Delta
\ delta
\ Omega
a2 a^{2} a2 a _{2} \ inf ty \ times \ oplus \ otimes
t = -pi:pi/100:pi; y = sin(t); plot(t,y) axis([-pi pi -1 1]) xlabel('-\pi \leq {\itt} \leq \pi’, 'FontSize',16) ylabel('sin(t) ', 'FontSize',16) title('Graph of the sine function') text(1,-1/3,'{\itNote the odd symmetry.}')
plot(x1, y1, 选项1, x2, y2, 选项2, …, xn, yn, 选项n) plot (x, y, ‘color_linestyle_marker’) 例 : plot (x, y, ‘y:square’)
color_linestyle_marker
Color strings are 'c', 'm', 'y', 'r', 'g', 'b', 'w', and 'k'. These correspond to cyan, magen, white, and black.
%加图形标题
xlabel('independent variable X');
《MATLAB矩阵分析》幻灯片

020
120
006
136
>> diag(ans) ans =
?
例: 矩阵生成函数例如
>>A=pascal(3)
>>diag(A)
ans = 111
123
ans = 1 2 6
136
>> diag(ans)
>>tril(A)
ans =
ans =
100
100
020
120
006
136
>> diag(ans) ans =
(5) 伴随矩阵 MATLAB生成伴随矩阵的函数是 compan(p),其中p是一个多项式的系数 向量,高次幂系数排在前,低次幂排在后。 例如,为了求多项式的x3-7x+6的伴随矩 阵,可使用命令: p=[1,0,-7,6]; compan(p)
(6) 帕斯卡矩阵 我们知道,二次项(x+y)n展开后的系数随 n的增大组成一个三角形表,称为杨辉三角 形。由杨辉三角形表组成的矩阵称为帕斯 卡(Pascal)矩阵。函数pascal(n)生成一个 n阶帕斯卡矩阵。
• 杨辉三角是一个由数字排列成的三角形数表,一般形式如下: 1 11 121 1331 14641 1 5 10 10 5 1 1 6 15 20 15 6 1 ...................................................... 杨辉三角最本质的特征是,它的两条斜边都是由数字1组成的,而其 余的数那么是等于它肩上的两个数之和。
《MATLAB矩阵分析》幻 灯片
本课件PPT仅供大家学习使用 学习完请自行删除,谢谢! 本课件PPT仅供大家学习使用 学习完请自行删除,谢谢!
Matlab中的矩阵操作详解

Matlab中的矩阵操作详解引言:Matlab是一种强大的数值计算工具,广泛应用于各个领域,尤其在科学研究和工程设计中。
矩阵操作是Matlab的重要特性之一,它使得我们可以方便地处理和分析大量的数据。
本文将详细介绍Matlab中的矩阵操作,包括矩阵的定义、创建、操作和应用,旨在帮助读者更好地掌握这一方面的知识。
一、矩阵的定义和创建在Matlab中,矩阵是由行和列组成的矩形数据结构。
我们可以用一对方括号“[]”来表示一个矩阵,行与行之间用分号“;”隔开。
例如,下面是一个3行4列的矩阵的定义:A = [1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12];除了直接定义矩阵,Matlab还提供了一些特殊的函数来创建矩阵。
例如,我们可以使用zeros函数创建一个所有元素都为零的矩阵:B = zeros(2, 3);这样就创建了一个2行3列的零矩阵。
同样地,我们还可以使用ones函数创建所有元素都为1的矩阵,eye函数创建单位矩阵,rand函数创建随机矩阵等等。
二、矩阵的基本操作在Matlab中,我们可以对矩阵进行各种操作,包括矩阵的加减乘除运算,矩阵的转置和逆等。
以下是一些常见的矩阵操作示例:1. 矩阵加法和减法:可以直接使用"+"和"-"运算符进行矩阵的加法和减法。
例如,假设有两个矩阵A和B,它们的维度相同,可以通过以下代码实现矩阵的加法和减法:C = A + B; % 矩阵相加D = A - B; % 矩阵相减2. 矩阵乘法:在Matlab中,我们可以使用"*"运算符来实现矩阵的乘法。
但需要注意的是,矩阵乘法的维度满足一定的条件。
例如,如果矩阵A的维度是m×n,矩阵B的维度是n×p,那么矩阵A乘以矩阵B的结果矩阵C的维度就是m×p。
以下是一些矩阵乘法的示例:C = A * B; % 矩阵相乘3. 矩阵转置和逆:在Matlab中,我们可以使用"'"运算符来实现矩阵的转置。
MATLAB画图矩阵处理

Matlab图像读入: X=Imread(‘zab1.jpg’); 图像输出: Imshow(X); 注意:图像要在工作目录下 图像处理:
融合(矩阵加法), 边界提取等(edge)
二、矩阵 1. 矩阵的生成 >>a=[1 2 3 -4; 5 6 7 8; -1 3 -5 7] %生成矩阵 >>b=[a; 2 4 6 8] % 添加一行 >>c=[b,b(4,:)’] % 将b的第四行转置为一列添在后面 >>d=ones(2) %2×2的全 1 矩阵 >>f=ones(3,1) %全1向量 >>I=eye(3) %3×3的单位矩阵 >> v=repmat(0,[3,5,7]) %三维矩阵 >>C=cat(3,zeros(3,5),ones(3,5),randn(3,5),rand(3,5))
3 矩阵函数
>>sin(a)+2.*a >>b.^2 >>b^2 >>det(b) %行列式的值 >> rank(b) %矩阵的秩 >>a1=sum(a) %矩阵 a 各列元素的和 >>sum(a1) %向量 a1 各分量的和 >>a1=max(a) %矩阵 a 各列元素的最大元 >>max(a1) %向量 a1 各分量的的最大元
2. 矩阵的运算 >>h=A’ %矩阵转置 >>A±B %矩阵(与数)加减 >>A.*B , A./B %矩阵对应元素相乘,除 >>X=A*B %矩阵相乘 >>X=A.^2 %矩阵各元素乘方 >>X=inv(A) %方阵A求逆 >>X=A\B %左除,A*X=B, X=inv(A)*B, 解方程 >>X=A/B %右除,X*B=A, X=A*inv(B) >>size(A) %矩阵A的维数 >>length(a) %向量 a 元素的个数
matlab第4讲

2013-7-9
Matlab Language
14
6、算术运算 (续)
2013-7-9
Matlab Language
15
6、算术运算 (续)
【例5-2】点幂“.^”举 例 >>a=1:6
a= 1 2 3 4 5 6
>>a=a.^2
a= 1 4 9 16 25 36
>>b=b.^2
b= 1 4
>>b=reshape(a,2,3)
2013-7-9
Matlab Language
22
【例7-1】求向量的最大值 >>x=[-43,72,9,16,23,47]; >>y=max(x) %求向量x中的最大值 y= 72 >>[y,l]=max(x) %求向量x中的最大值及其该元素的位置 y= 72 l= 2
2013-7-9
Matlab Language
7
5、多维数组 (续)
三维数组元素的寻址:可以(行、列、页)来确定。 以维数为 3×4×2 的三维数组为例,其寻址方式如 下图所示:
数组 A 是三维数组,其中 A(:,:,1)代表第一页的二 维数组,A(:,:,2)代表第二页的二维数组。
Matlab Language
8
2013-7-9
5、多维数组 (续)
标量关系进行比较,并给出结果,形成一个维数与原来相同
的0、1矩阵。 3、当一个标量与一个矩阵比较时,该标量与矩阵的各元素进行
比较,结果形成一个与矩阵维数相等的0、1矩阵。
2013-7-9
Matlab Language
17
7、关系运算 (续) 【例】建立5阶方阵A,判断其元素能否被3整除。
matlab数组,矩阵,绘图
由各元胞创建
由各元胞内容 创建
取多个元胞元素内容 [X4,X5,X6]=deal(A{[1,2,4]})
结构数组
创建结构数组
直接使用赋 值指令创建 结构数组 利用 struct 函数创建
PS(1).name='张三' PS(1).billing=150 PS(1).test=[9,75,60;188,44,100] PS(2).name='欧阳';PS(2).billing=203; PS(2).test=[11,65,82;155,74,93] PS(1)=struct('name','张三','billing',150,'test',[9,75,60;188,44,100]); PS(2)=struct('name','欧阳','billing',203,'test',[11,65,82;155,74,93])
字符串转换函数 Abs double Setstr Fprintf Sscanf Sprintf Int2str Str2num Num2str Str2mat Lower Upper 字符串到 ASCII 码的转换 ASCII 码转换成字符串 按照给定的格式把文本写到文件中或显示屏上 按照给定的格式将字符串转换成数字 按照给定的格式将数字转换成字符串 整数转换成字符串 字符串转换成数字 数字转换成字符串 字符串转换成一个文本矩阵 字符串变为小写 字符串转换成大写
ij
flipud(A) fliplr(A) rot90(A) [x,D]=Eig(A) reshape
将 A 阵上下翻转 将 A 阵左右翻转 将 A 阵逆时针旋转 90 度 A 为 n 阶方阵,A*x=x*D,D 的对角元素的特征值,x 的列是特征 向量 保持数组总元素个数不变的情况下,改变行数和列数
Matlab基础知识(详细分析:矩阵)共10张PPT

矩阵包括数值矩阵、符号矩阵、特殊矩阵等三种基本样式。
第一章
工作台窗口和数组编辑器(Workspace Browser and Array Editor)
4 MATLAB自带图形集
矩阵包括数值矩阵、符号矩阵、特殊矩阵等三种基本样式。
>> Null = [ ]
%生成一个空矩阵
%% 改变图像的映**色
Imageext
MATLAB优化算法案例分析与应用
%% MATtLrAaBv的eLl ogo
%% L-形薄膜的12Байду номын сангаас模态
MATLAB优化算法案例分析与应用
图1-16 四个首尾相接的圆环
Column 12
MATLAB优化算法案例分析与应用
1 MATLAB简介
第一章
当前路径窗口(Current Directory Browser)
c) 启动平台(Launch Pad)
d) 编辑调试窗口(The Edit/Debug Window)
e) 工作台窗口和数组编辑器(Workspace Browser and Array Editor) f) 帮助空间窗口(Help Browser) g) 当前路径窗口(Current Directory Browser)
第一章
MATLAB优化算法案例分析与应用
第1章 Matlab基础知识
第一章
MATLAB优化算法案例分析与应用
•1.1 MATLAB简介
MATLAB桌面上可以得到和访问的窗口
a) 命令窗口(The Command Window)
b) 命令历史窗口(The Command History Window)
帮4 助MA空【T间L例A窗B】口自(带实H图数e形lp值集Br矩ow阵ser输)入实例
第4讲 MATLAB矩阵分析及绘图

2 矩阵的转置与旋转
(1)矩阵的转置 转置运算符是单撇号(‘)。 (2)矩阵的旋转 利用函数rot90(A,k)将矩阵A旋转90º 的k倍,当k为1时可省略。
(3)矩阵的左右翻转
对矩阵实施左右翻转是将原矩阵的第一列和最后一列 调换,第二列和倒数第二列调换,…,依次类推。 MATLAB对矩阵A实施左右翻转的函数是fliplr(A)。 (4)矩阵的上下翻转
当选项省略时,MATLAB规定,线型一律用实线,颜色将
根据曲线的先后顺序依次。
要设置曲线样式可以在plot函数中加绘图选项,其调用格 式为: plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)
>> x=0:pi/15:2*pi;
>> y1=sin(x); y2=cos(x); >> plot(x,y1,'b:+',x,y2,'g-.*')
>> y=[1 2 3;4 5 6;7 8 9];
>> plot(x,y);
(2) 当x,y是同维矩阵时,则以x,y对应列元素为横、纵
坐标分别绘制曲线,曲线条数等于矩阵的列数。 >> x=[1 2 3;4 5 6;7 8 9]; >> y=[7 8 9;1 2 3;4 5 6]; >> plot(x,y); (3) 对只包含一个输入参数的plot函数,当输入参数是实矩阵 时,则按列绘制每列元素值相对其下标的曲线,曲线条数等 于输入参数矩阵的列数。 >> x=[1 2 3;4 5 6;7 8 9]; >> plot(x,y);
MATLAB矩阵运算与绘图实践

MATLAB矩阵运算与绘图实践一、MATLAB矩阵运算的基本概念与操作MATLAB是一种强大的数学软件工具,可以用于矩阵运算和绘图实践。
在MATLAB中,矩阵是一种基本的数据类型,具有简洁而强大的数据处理功能。
1.1 矩阵的定义和表示矩阵是一个二维的数组,由行和列组成。
在MATLAB中,可以使用方括号进行矩阵的定义和表示。
例如,A = [1 2 3; 4 5 6]定义了一个2行3列的矩阵A。
1.2 矩阵的运算MATLAB提供了一系列的矩阵运算函数,包括加法、减法、乘法、转置等。
例如,可以使用A+B进行矩阵的加法运算,A-B 进行矩阵的减法运算,A*B进行矩阵的乘法运算。
1.3 矩阵的索引与切片在MATLAB中,可以使用索引和切片操作来访问矩阵的特定元素或子矩阵。
例如,可以使用A(1,2)来访问矩阵A的第1行第2列的元素,使用A(1,:)来访问矩阵A的第1行的所有元素。
1.4 矩阵的运算速度优化MATLAB中的矩阵运算通常使用向量化操作,可以显著提高运算速度。
向量化操作是指将循环结构转换为矩阵运算表达式的操作。
例如,可以使用A.*B进行矩阵的逐元素相乘运算,而不是使用循环结构逐个相乘。
二、MATLAB矩阵运算的高级应用2.1 矩阵的特征值和特征向量在MATLAB中,可以使用eig函数计算矩阵的特征值和特征向量。
特征值和特征向量是矩阵的重要属性,可以用于矩阵的分类和分析。
2.2 矩阵的奇异值分解奇异值分解(SVD)是一种常用的矩阵分解方法,在MATLAB中可以使用svd函数进行奇异值分解。
SVD可以将一个矩阵分解为三个矩阵的乘积,可以用于矩阵的降维和数据压缩。
2.3 矩阵的LU分解LU分解是一种常用的矩阵分解方法,可以将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积,在MATLAB中可以使用lu函数进行LU分解。
LU分解可以用于矩阵的求解和矩阵方程的求解。
三、MATLAB绘图实践的基本技巧与命令3.1 绘图函数的选择在MATLAB中,有多种绘图函数可以用于实现不同类型的图形。
matlab矩阵操作基础ppt课件

精品ppt
1
MATLAB作为线性系统的一种分析和仿真 工具,是理工科大学生应该掌握的技术工具,它 作为一种编程语言和可视化工具,可解决工程、 科学计算和数学学科中许多问题。 MATLAB建立在向量、数组和矩阵的基 础上,使用方便,人机界面直观,输出结果可 视化。
矩阵是MATLAB的核心
(1)MATLAB的每条命令后,若为逗号或无标点符号,
则显示命令的结果;若命令后为分号,则禁止显示结果.
(2)“%” 后面所有文字为注释.
(3) “...”表示续行.
精品ppt
6
3、数学函数
函数 sin(x) cos(x) tan(x) abs(x) min(x) sqrt(x) log(x) sign(x)
例 m=[1 2 3 4 ;5 6 7 8;9 10 11 12] p=[1 1 1 1 2222 3 3 3 3]
精品ppt
13
特殊矩阵的建立:.
a=[ ]
产生一个空矩阵,当对一项操作无结 果时,返回空矩阵,空矩阵的大小为零.
b=zeros(m,n) 产生一个m行、n列的零矩阵
c=ones(m,n) 产生一个m行、n列的元素 全为1的矩阵
精品ppt
9
3、数组的方向
前面例子中的数组都是一行数列,是行方向分布的. 称之为行向量. 数组也可以是列向量,它的数组操作和运 算与行向量是一样的,唯一的区别是结果以列形式显示.
产生列向量有两种方法: 直接产生 例 c=[1;2;3;4] 转置产生 例 b=[1 2 3 4]; c=b’
说明:以空格或逗号分隔的元素指定的是不同列的 元素,而以分号分隔的元素指定了不同行的元素.
a./b= [a1/b1,a2/b2,…,an/bn]
MATLAB矩阵分析与处理

THANKS
线性判别分析(LDA)
寻找最佳投影方向,使得同类数据投 影后尽可能接近,不同类数据投影后 尽可能远离。
数据可视化
散点图
展示两个变量之间的关系。
柱状图
展示一个或多个分类变量的频 数分布。
热力图
展示矩阵或数据集中的数值大 小,通过颜色的深浅表示数值 的大小。
可视化树
展示层次结构数据的图形表示 ,如决策树、组织结构图等。
矩阵的属性
维度
描述矩阵的行数和列数。
大小
描述矩阵中元素的数量。
类型
描述矩阵中元素的数据类型。
矩阵的基本操作
01
加法
对应元素相加。
02
减法
对应元素相减。
03
数乘
所有元素乘以一个数。
04
转置
将矩阵的行和列互换。
02 矩阵运算
矩阵加法与减法
矩阵加法
对应元素相加,结果矩阵与原矩阵具 有相同的维度。
矩阵减法
处理效果。
机器学习中的矩阵运算
数据矩阵的建立
在机器学习中,数据通常以矩阵形式表示,每一行表示一个样本,每一列表示一个特征。
矩阵运算在机器学习中的应用
通过矩阵运算,如线性代数运算、矩阵分解、特征值分解等,可以用于构建机器学习模型 ,如线性回归、逻辑回归、决策树等。
模型评估与优化
使用Matlab中的机器学习工具箱,可以对机器学习模型进行评估和优化,如交叉验证、 网格搜索等。
数值分析中的矩阵运算
数值分析中的矩阵运算
数值分析中涉及大量的矩阵运算,如矩阵乘法、矩阵除法、矩阵求 逆等。
矩阵运算在数值分析中的应用
通过这些矩阵运算,可以求解线性方程组、求解特征值问题、进行 矩阵分解等。
MATLAB简介,矩阵及其运算,绘图与数据可视化实验报告总结

MATLAB简介,矩阵及其运算,绘图与数据可视化实验
报告总结
一.实验目的
1.了解MATLAB的基本使用方法。
2.掌握MATLAB数据对象的特点和运算规则。
3.掌握MATLAB中建立矩阵的方法和矩阵的处理方法。
二.实验内容
浏览MATLAB的start菜单,了解所安装的模块和功能。
建立自己的工作目录,使用MATLAB将其设置为当前工作目录。
使用path命令和工作区浏览两种方法。
使用Help帮助功能,查询inv、plot、max、round等函数的用法和功能。
使用help命令和help菜单。
建立一组变量,如x=0:pi/10:2*pi,y=sin(x),在命令窗口显示这些变量;在变量窗口打开这些变量,观察其值并使用绘图菜单绘制y。
分多行输入一个MATLAB命令。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x1=x(k);
%取y1与y2相等点的x坐标
y3=0.2*exp(-0.5*x1).*cos(4*pi*x1); %求y1与y2值相等点的y坐标 plot(x,y1,x,y2,'k:',x1,y3,'bp');
5.3 图形标注与坐标控制
1.图形标注
有关图形标注函数的调用格式为:
title(图形名称) xlabel(x轴说明) ylabel(y轴说明) text(x,y,图形说明)
例:用求逆矩阵的方法解线性方程组
x 2 y 3z 5 x 4 y 9 z 2 x 8 y 27 z 6
4.4 矩阵求值
1.方阵的行列式值 把一个方阵看作一个行列式,并对其按行列式的规则求值, 这个值就称为矩阵所对应的行列式的值。 在MATLAB中,求方阵A所对应的行列式的值的函数是 det(A)。
5.2 设置曲线样式
MATLAB提供了一些绘图选项,用于确定所绘曲线
的线型、颜色和数据点标记符号,它们可以组合使用。
线型 线方式: - 实线 :点线 -. 虚点线 - - 波折线。
线型 点方式: . 圆点 +加号 * 星号 x x形 o 小圆 颜色:b蓝 ;g绿;r红; c青; m紫; y黄; k黑; w白;
>> y=[1 2 3;4 5 6;7 8 9];
>> plot(x,y);
(2) 当x,y是同维矩阵时,则以x,y对应列元素为横、纵
坐标分别绘制曲线,曲线条数等于矩阵的列数。 >> x=[1 2 3;4 5 6;7 8 9]; >> y=[7 8 9;1 2 3;4 5 6]; >> plot(x,y); (3) 对只包含一个输入参数的plot函数,当输入参数是实矩阵 时,则按列绘制每列元素值相对其下标的曲线,曲线条数等 于输入参数矩阵的列数。 >> x=[1 2 3;4 5 6;7 8 9]; >> plot(x,y);
yi a bxi
此外,常用的函数还有reshape(A,m,n),它在矩阵总元 素保持不变的前提下,将矩阵A重新排成m×n的二维矩阵。
2、用于专门学科的特殊矩阵
魔方矩阵
魔方矩阵有一个有趣的性质,其每行、每列及两条 对角线上的元素和都相等。对于n阶魔方阵,其元素由
1,2,3,…,n2共n2个整数组成。MATLAB提供了求魔方矩阵
第5章 MATLAB绘图
5.1 二维数据曲线图
5.1.1 绘制单根二维曲线 plot函数的基本调用格式为: plot(x,y)
其中x和y为长度相同的向量,分别用于存储x坐标和y坐标数据。
例5-1 在0≤x≤2区间内,绘制曲线 y=2e-0.5xcos(4πx) 程序如下: x=0:pi/100:2*pi; y=2*exp(-0.5*x).*cos(4*pi*x);
>> A=[1 2 3;4 5 6;7 8 9];
>> triu(A) ans = 1 2 0 5 0 0 >> tril(A,-1) ans = 0 0 0 4 0 0 7 8 0 >> tril(A,1) ans = 1 2 0 4 5 6 7 8 9
3 6 9
>> triu(A,1) ans = 0 2 3 0 0 6 0 0 0
2 1.5
1
0.5
0
-0.5
-1
plot(x,y)
-1.5
-2
0
1
2
3
4
5
6
7
例5-2 绘制曲线。 程序如下: t=0:0.1:2*pi; x=t.*sin(3*t); y=t.*sin(t).*sin(t); plot(x,y);
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0 -6
-4
-2
0
2
4
6
plot函数最简单的调用格式是只包含一个输入参数:
纵坐标范围默认在最大最 小值之间。
4.图形保持
hold on/off命令控制是保持原有图形还是刷新原有图
形,不带参数的hold命令在两种状态之间进行切换。
例4-5 采用图形保持,在同一坐标内绘制曲线 y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)。 程序如下: x=0:pi/100:2*pi; y1=0.2*exp(-0.5*x).*cos(4*pi*x); plot(x,y1) hold on y2=2*exp(-0.5*x).*cos(pi*x); plot(x,y2); hold off
plot(x)
在这种情况下,当x是实向量时,以该向量元素的下标为 横坐标,元素值为纵坐标画出一条连续曲线,这实际上是绘 制折线图。
5.1.2 绘制多根二维曲线
1.plot函数的输入参数是矩阵形式
(1) 当x是向量,y是有一维与x同维的矩阵时,则绘制出多根不 同颜色的曲线。曲线条数等于y矩阵的另一维数,x被作为这 些曲线共同的横坐标。 >> x=[1 2 3];
例:建立3*3,3*2的和矩阵A同样大小的零矩阵 Zero(3,3) Zero(3,2) Zero(size(A))
例(1)在区间[20,50]内均匀分布的5阶随机矩阵
(2)均值为0.6,方差为0.1的5阶正态分布随机矩阵
任意[a,b]区间上均匀分布的随机数: yi a (b a) xi 均值为a,方差为b^2的随机数:
MATLAB对矩阵A实施上下翻转的函数是flipud(A)。
4.3 矩阵的逆
1.矩阵的逆 对于一个方阵A,如果存在一个与其同阶的方阵B,使得: A· B=B· (I为单位矩阵)则称B为A的逆矩阵,当然,A也是B的 A=I 逆矩阵。 求一个矩阵的逆是一件非常烦琐的工作,容易出错,但在 MATLAB中,求一个矩阵的逆非常容易。求方阵A的逆矩阵可调 用函数inv(A)。 例 求方阵A的逆矩阵,并验证其互逆。
2.矩阵的秩和迹
(1)矩阵的秩 矩阵线性无关的行数与列数称为矩阵的秩。在MATLAB中, 求矩阵秩的函数是rank(A)。 (2)矩阵的迹 矩阵的迹等于矩阵的对角线元素之和,也等于矩阵的特征 值之和。在MATLAB中,求矩阵的迹的函数是trace(A)。
3.矩阵的特征值与特征向量
在MATLAB中,计算矩阵A的特征值和特征向量的函数 是eig(A),常用的调用格式有3种:
>> plot(x1,y1,x2,y2,x3,y3)
3.具有两个纵坐标标度的图形
在MATLAB中,如果需要绘制出具有不同纵坐标标 度的两个图形,可以使用plotyy绘图函数。调用格式为: plotyy(x1,y1,x2,y2)
其中x1,y1对应一条曲线,x2,y2对应另一条曲线。横坐标的标 度相同,纵坐标有两个,左纵坐标用于x1,y1数据对,右纵坐
(1) E=eig(A):求矩阵A的全部特征值,构成向量E。
(2) [V,D]=eig(A):求矩阵A的全部特征值,构成对角阵D, 并求A的特征向量构成V的列向量。
例 用求特征值的方法解方程。3x5-7x4+5x2+2x-18=0 p=[3,-7,0,5,2,-18]; A=compan(p); %求伴随矩阵A x1=eig(A) %求A的特征值 x2=roots(p) %直接求多项式p的零点
例5-6 在同一坐标内,分别用不同线型和颜色绘制曲线 y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx),标记两曲线交叉点。 程序如下:
x=linspace(0,2*pi,1000); y1=0.2*exp(-0.5*x).*cos(4*pi*x); y2=2*exp(-0.5*x).*cos(pi*x); k=find(abs(y1-y2)<1e-2); %查找y1与y2相等点(近似相等)的下标
标用于x2,y2数据对。
例5-4 用不同标度在同一坐标内绘制曲线 y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)。
程序如下:
x=0:pi/100:2*pi;
y1=0.2*exp(-0.5*x).*cos(4*pi*x); y2=2*exp(-0.5*x).*cos(pi*x); plotyy(x,y1,x,y2);
的函数magic(n),其功能是生成一个n阶魔方阵。 观察magic(5),其元
素为1~25,每行每列
及对角线的和均为65 例: 将101~125等25个数填 入一个5行5列的表格中,使 其每行每列及对角线的和均 为565。
4.2 矩阵的结构变换
1、对角阵与三角阵
(1)对角阵 只有对角线上有非0元素的矩阵称为对角矩阵,对角线上的元素相等的 对角矩阵称为数量矩阵,对角线上的元素都为1的对角矩阵称为单位矩阵。 提取矩阵的对角线元素
2.含多个输入参数的plot函数 调用格式为: plot(x1,y1,x2,y2,…,xn,yn)
(1)
当输入参数都为向量时,x1和y1,x2和y2,…,xn和yn 分别组成一组向量对,每一组向量对的长度可以不同。 每一向量对可以绘制出一条曲线,这样可以在同一坐标
内绘制出多条曲线。
>> x1=linspace(0,2*pi,100); >> y1=sin(x1); >> x2=linspace(0,3*pi,70); >> y2=1+sin(x2); >> plot(x1,y1,x2,y2)
(2) 当输入参数有矩阵形式时,配对的x,y按对应列元
素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的 列数。
>> x1=linspace(0,2*pi,100); >> y1=sin(x1); >> x2=linspace(0,3*pi,100); >> y2=1+sin(x2); >> x3=[x1;x2]'; >> y3=[y1+2;y2+2]';
