(C语言)10进制转换2,8,16进制
(C语言)10进制转换2,8,16进制

(C语言)10进制转换2,8,16进制作者:vinseven#include"stdio.h"#include"conio.h"#include"malloc.h"#include"windows.h"#define ElemType intvoid menu();void TenToTwo();void TenToEight();void TenToSixteen();void InitStack(struct sNode **HS);void Push(struct sNode **HS,ElemType x);ElemType Pop(struct sNode **HS);ElemType Peek(struct sNode **HS);int EmptyStack(struct sNode **HS);void ClearStack(struct sNode **HS);int ten;/*要输入的10进制数*/int x;/*把将要插入到栈中的元素暂时存进 x 中*/struct sNode hs;struct sNode{ElemType data;struct sNode *next;};void main(){menu();getch();}void menu(){char choice;int flag=1;while(1){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 1,10进制转换2进制\n\n\n");printf("\t\t\t 2,10进制转换8进制\n\n\n");printf("\t\t\t 3,10进制转换16进制\n\n\n");printf("\t\t\t 0,退出\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入编号:");while(flag){fflush(stdin);choice=getch();switch(choice){case '1':{system("cls");TenToTwo();flag=0;break;}case '2':{system("cls");TenToEight();flag=0;break;}case '3':{system("cls");TenToSixteen();flag=0;break;}case '0':{printf("\n\t\t\t按任意键退出");getch();exit(0);}default:{printf("\n\t\t\t无此选项可选!请重新输入!\n");flag=1;break;}}}system("cls");flag=1;}}/*10进制转换2进制界面*/void TenToTwo(){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换2进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数:");scanf("%d",&ten);while(ten!=0){x=ten%2;Push(&hs,x);ten=ten/2;}printf("\t\t\t二进制数为:");while(!EmptyStack(&hs))printf("%d",Pop(&hs));getch();}/*10进制转换8进制界面*/void TenToEight(){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换8进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数:");scanf("%d",&ten);while(ten!=0){x=ten%8;Push(&hs,x);ten=ten/8;}printf("\t\t\t八进制数为:");while(!EmptyStack(&hs))printf("%d",Pop(&hs));getch();}/*10进制转换16进制界面*/void TenToSixteen(){int temp;printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换16进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数:");scanf("%d",&ten);while(ten!=0){x=ten%16;Push(&hs,x);ten=ten/16;}printf("\t\t\t十六进制数为:");while(!EmptyStack(&hs)){temp=Pop(&hs);switch(temp){case 1:case 2:case 3:case 4:case 5:case 6:case 7:case 8:case 9:printf("%d",temp);break;case 10:printf("A");break;case 11:printf("B");break;case 12:printf("C");break;case 13:printf("D");break;case 14:printf("E");break;case 15:printf("F");break;}}getch();}/*关于栈的函数*//*1,初始化链栈为空*/void InitStack(struct sNode **HS) {*HS=NULL;}/*2,向栈中插入一个元素*/void Push(struct sNode **HS,ElemType x){struct sNode *newp;newp=malloc(sizeof(struct sNode));if(newp==NULL){printf("内存动态空间用完,退出运行!");system("pause");exit(0);}newp->data=x;newp->next=*HS;*HS=newp;}/*3,从栈中删除一个函元素并返回它*/ ElemType Pop(struct sNode **HS){struct sNode *p;ElemType temp;if(*HS==NULL){printf("栈空!无法删除!");system("pause");exit(0);}p=*HS;*HS=p->next;temp=p->data;free(p);return temp;}/*4,读取栈顶元素*/ElemType Peek(struct sNode **HS){if(*HS==NULL){printf("栈空!无法读取栈顶结点!");system("pause");exit(1);}return (*HS)->data;}/*5,检查链栈是否为空,空返回1,否则返回0*/ int EmptyStack(struct sNode **HS){if(*HS==NULL)return 1;elsereturn 0;}/*6,清除链栈为空*/void ClearStack(struct sNode **HS){struct sNode *cp,*np;cp=*HS;while(cp!=NULL){np=cp->next;free(cp);cp=np;}*HS=NULL; }。
二进制八进制十进制十六进制之间的转换方法

二进制八进制十进制十六进制之间的转换方法....一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分① 整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(__-__)2 分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即__-__(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25; 第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5; 第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0; 第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
进制转换规则

进制转换规则一、求余法。
适用范围:十进制转换为→二进制、八进制、十六进制。
要将十进制转换为多少进制,那么就对几求余。
例如:①、23转换为二进制,就是不停的对2求余数(第一次用本数对2求余,从第二次开始都用上一次的商除以2,直到商的值为0为止)。
23除以2的商为11 余数为111除以2的商为5 余数为15除以2的商为2 余数为12除以2的商为1 余数为01除以2的商为0 余数为1将余数从下到上写就可以得到23的二进制为10111;②、23转换为八进制,就是不停的对8求余(第一次用本数对8求余,从第二次开始都用上一次的商除以8,直到商的值为0为止。
)23除以8的商为2 余数为72除以8的商为0 余数为2同理将余数从下到上写可以得到23的八进制数位27③、27转换为十六进制,就是不停的对16求余(第一次用本数对16求余,从第二次开始都用上一次的商除以16,直到商的值为0为止。
)27除以16的商为1 余数为111除以16的商为0 余数为1同理将余数从下到上写可以得到27的十六进制数位1B(11在十六进制数中用字母B表示)。
二、乘方。
N制数的右边第一位为N的0次方,前一位为N的1次方,依次类推。
例如:2进制的右边第一位就为2的0次方,前一位2的1次方,依次类推。
适用范围:将二进制、八进制、十六进制转换为十进制。
例如:①、将27O转换为十进制。
右边第一位表示8的0次方,该位上的数位7,就表示有7个8的0次方。
右边第二位表示8的1次方,该位上的数位2,就表示有2个8的1次方。
所以这个八进制数就等于7个8的0次方与2个8的1次方之和即为:7×81082⨯+=7+16=23,所以八进制的23O转换为十进制就为23。
(数字后有字母O表示八进制。
)②、将1BH转换为十进制。
右边第一位表示16的0次方,该位上的数位B,就表示有B,十六进制B表示11即是说有11个8的0次方。
右边第二位表示16的1次方,该位上的数位1,就表示有1个16的1次方。
一篇教程教你学会Python进制转换(十进制转二进制、八进制、十六进制)

⼀篇教程教你学会Python进制转换(⼗进制转⼆进制、⼋进制、⼗六进制)⼀、导⾔导语:在计算机进⾏数据交换时,常常会有⼀个进制转换的过程,我们知道计算机只认0 和 1.在内存系统中,基本基于⼆进制进⾏运算的,但是有时候数据过于庞⼤,为了⽅便存储管理,计算机会使⽤⼗六进制存储数据,但是怎么实现数据转换呢?我们⼈类由⼗根⼿指头,所以⾃然就使⽤⼗进制啦,每当我们数数字到10之后,于是就重0 开始继续数,所以逢⼗进⼀就这么来了。
对于其它进制呢,也是同样的,⽐如最常见的⼆进制,也就是逢⼆进⼀,慢慢来,依次类推,所以数学的世界是多么的奇妙呀!今天给⼤家带来的是使⽤ Python 实现进制转换,内容包括如下:dec(⼗进制)—> bin(⼆进制)dec(⼗进制)—> oct(⼋进制)dec(⼗进制)—> hex(⼗六进制)⼆、各种进制介绍在转换之前,我们先了解以下各种进制⼗进制(Decimal)我们所熟知的⼗进制,其实是从 0 开始,数到 9 之后,就跳到 10,这样就变成了 10,数数⼤家总会把⼆进制(Binary)⼆进制同理,从 0 开始也就是 00(前⾯的⼀个0可以省去,但是为了更好的描述,所以保留),到 01,也变成了 10【对应⼗进制中的 3】,然后是 11【对应⼗进制中的 4】,100【⼗进制中的5】。
以此类推因为⼆进制的英⽂单词是 binary,所以在计算机运算的过程中,使⽤⼆进制会⽤如下⽅法,0b11(4),0b1101(13)等等⼋进制(Octal)理解了⼆进制,在理解⼋进制就很容易了,⼋进制是逢⼋进⼀,范围是 0~7,对⽐⼀下⼆进制,就很好理解啦!!⼗六进制(Hexadecimal)⼗六进制就可能会相对复杂⼀点点,⼗六进制是⽤数字 0~9 和英⽂字母 A - F(⼤⼩写随意) 表⽰,因此 A代表 10, F代表15。
为什么在计算机领域中,⼗六进制⽤途会如此⼴泛呢?给⼤家看⼀个对⽐:当数据⽐较⼤的时候,⼆进制显然不再那么使⽤,再看使⽤⼗六进制,就简短很多。
十进制数转换成二进制,八进制,十六进制(c语言)

}
int InitStack(SqStack &S)
{
S.base=(int *)malloc(STACK_INIT_SIZE*sizeof(int));
if(!S.base) exit(OVERFLOW);
S.top=S.base;
S.stacksize=STACK_INIT_SIZE;
return OK;
}
int GetTop(SqStack S,int &e)
{
if(S.top==S.base) return ERROR;
e=*(S.top-1);
return OK;
}
int Push(SqStack &S,int e)
{
if((S.top-S.base)>=S.stacksize)
SqStack S;
InitStack(S);
printf("请选择转换类型:1:十进制->二进制 2:十进制->八进制 3:十进制->十六进制 \n");
printf("请输入你的选择:");
scanf("%d",&Cho);
switch(Cho)
{
case 1:cj=2;printf("你选择的是十进制转换成二进制\n\n");printf("请输入要转换的十进制数:");scanf("%d",&N);break;
if(S.top!=S.base) return 0;
}
default:printf("请从1-3中选择!");
二进制 八进制 十进制 十六进制之间的转换方法

一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
十六进制八进制二进制之间的彼此专换方式

十六进制、八进制、二进制之间的彼此专换方式一、十六进制举例说明10进制的32表示成绩是:2016进制的32表示成10进制就是:3×16^1+2×16^0=50编程中,咱们常常利用的仍是10进制.毕竟C/C++是高级语言。
比如:int a = 100,b = 99;不过,由于数据在计算机中的表示,最终以二进制的形式存在,所以有时候利用二进制,可以更直观地解决问题。
但太长了。
比如int 类型占用4个字节,32位。
比如100,用int类型的二进制数表达将是:0000 0000 0000 0000 0110 0100面对这么长的数进行思考或操作,没有人会喜欢。
因此,C,C++ 没有提供在代码直接写二进制数的方式。
用16进制或8进制可以解决这个问题。
因为,进制越大,数的表达长度也就越短。
不过,为何恰恰是16或8进制,而不其它的,诸如9或20进制呢?二、八、16,别离是2的1次方,3次方,4次方。
这一点使得三种进制之间可以超级直接地彼此转换。
8进制或16进制缩短了二进制数,但维持了二进制数的表达特点。
在下面的关于进制转换的课程中,你可以发现这一点。
二、转换二进制转换十进制二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:101100100,转换为10进制为:356用横式计算0 X2^0 + 0X 2^1 + 1X 2^2 + 0X2^3 + 0X2^4 + 1 X2^5 + 1 X2^6 + 0 X 2^7 + 1X 2^8 = 3560乘以多少都是0,所以咱们也可以直接跳过值为0的位:1X 2^2 + 1 X2^5 + 1X 2^6 + 1X 2^8 = 3564 + 32 + 64 + 256 =356八进制转换十进制八进制就是逢8进1。
八进制数采用0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方……所以,设有一个八进制数:1507,转换为十进制为:839,具体方式如下:可以用横式直接计算:7 * 8^0 + 0 * 8^1 + 5 * 8^2 + 1 * 8^3 = 839也可以用竖式表示第0位7 * 8^0 = 7第1位0 * 8^1 = 0第2位 5 * 8^2 = 320第3位 1 * 8^3 = 512十六进制转换十进制16进制就是逢16进1,但咱们只有0~9这十个数字,所以咱们用A,B,C,D,E,F这六个字母来别离表示10,11,12,13,14,15。
输入数,使十进制转换成二进制、八进制、十六进制

源程序public static void main(String args[]){System.out.println("请输入要转换的进制(2,8,16),其他数字表示退出");Scanner reader=new Scanner(System.in);int a=reader.nextInt();System.out.println("请输入要转换的10进制数:");int b=reader.nextInt();int d=b;Stack <Integer> s=new Stack<Integer>();Stack <String> c=new Stack<String>();if(a!=2&&a!=8&&a!=16){System.out.println("退出");}else{if(a==2||a==8){while(b!=0){s.push(b%a);b=b/a;}}while(b!=0){if(b%a>9){if(b%a-9==1)c.push("a");if(b%a-9==2)c.push("b");if(b%a-9==3)c.push("c");if(b%a-9==4)c.push("d");if(b%a-9==5)c.push("e");if(b%a-9==6)c.push("f");}else{c.push(b%a+"");}b=b/a;}}}System.out.println(d+"的"+a+"进制为:");while(!s.isEmpty()){System.out.print(s.pop());}while(!c.isEmpty()){System.out.print(c.pop());}}测试数据: 2 1024结果:请输入要转换的进制(2,8,16),其他数字表示退出2请输入要转换的10进制数:10241024的2进制为:10000000000测试数据:8 255结果:请输入要转换的进制(2,8,16),其他数字表示退出8请输入要转换的10进制数:255255的8进制为:377测试数据:16 1023结果:请输入要转换的进制(2,8,16),其他数字表示退出16请输入要转换的10进制数:10231023的16进制为:3ff调试过程:因为十六进制需要a,b,c,d,e,f等字母入栈,所以先考虑二进制和八进制,声明一个integer类型的栈,将余数入栈。
10进制浮点数转化为16进制c语言

10进制浮点数转化为16进制c语言以10进制浮点数转化为16进制C语言在计算机中,浮点数是一种用来表示带有小数部分的数值类型。
而在C语言中,我们经常需要将浮点数转化为16进制的形式进行处理。
本文将介绍如何将10进制浮点数转化为16进制,并给出相应的C语言代码示例。
要将10进制浮点数转化为16进制,首先需要了解浮点数的存储方式。
在计算机中,浮点数一般采用IEEE 754标准进行存储。
IEEE 754标准规定了浮点数的位数分配,其中包括符号位、指数位和尾数位。
对于32位单精度浮点数,符号位占1位,指数位占8位,尾数位占23位。
对于64位双精度浮点数,符号位占1位,指数位占11位,尾数位占52位。
在C语言中,可以使用union联合体来实现浮点数和整数之间的转换。
具体的代码如下所示:```c#include <stdio.h>typedef union {float f;unsigned int i;} FloatInt;void printHex(float f) {FloatInt fi;fi.f = f;printf("%f in hex: 0x%x\n", f, fi.i);}int main() {float f = 3.14;printHex(f);return 0;}```在上述代码中,我们定义了一个FloatInt联合体,其中包含了一个float类型的成员变量f和一个unsigned int类型的成员变量i。
通过将浮点数赋值给f,我们可以通过访问i来获取浮点数的16进制表示。
在main函数中,我们定义了一个浮点数f并赋值为3.14,然后调用printHex函数将其转化为16进制并输出。
运行上述代码,输出结果如下:3.140000 in hex: 0x4048f5c3```可以看到,浮点数3.14在16进制中的表示为0x4048f5c3。
需要注意的是,上述代码中使用的是单精度浮点数类型float。
c语言_各种进制转换

c语言各种进制转换计算机中常用的数的进制主要有:二进制、八进制、十六进制。
2进制,用两个阿拉伯数字:0、1;8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;10进制,用十个阿拉伯数字:0到9;16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这五个字母来分别表示10,11,12,13,14,15。
字母不区分大小写。
以下简介各种进制之间的转换方法:一、二进制转换十进制例:二进制“1101100”1101100 ←二进制数6543210 ←排位方法例如二进制换算十进制的算法:1*26 + 1*25 + 0*24 + 1*23 + 1* 22 + 0*21 + 0*20↑ ↑说明:2代表进制,后面的数是次方(从右往左数,以0开始)=64+32+0+8+4+0+0=108二、二进制换算八进制例:二进制的“10110111011”换八进制时,从右到左,三位一组,不够补0,即成了:010 110 111 011然后每组中的3个数分别对应4、2、1的状态,然后将为状态为1的相加,如:010 = 2110 = 4+2 = 6111 = 4+2+1 = 7011 = 2+1 = 3结果为:2673三、二进制转换十六进制十六进制换二进制的方法也类似,只要每组4位,分别对应8、4、2、1就行了,如分解为:0101 1011 1011运算为:0101 = 4+1 = 51011 = 8+2+1 = 11(由于10为A,所以11即B)1011 = 8+2+1 = 11(由于10为A,所以11即B)结果为:5BB四、二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:计算:0 * 20 + 0 * 21 + 1 * 22 + 0 * 23 + 0 * 24 + 1 * 25 + 1 * 26 + 0 * 27 = 100五、八进制数转换为十进制数八进制就是逢8进1。
2进制 , 8进制 , 10进制 , 16进制

2进制, 8进制, 10进制, 16进制,介绍及相互转换及快速转换的方法为什么要使用进制数数据在计算机中的表示,最终以二进制的形式存在,就是各种<黑客帝国>电影中那些0101010…的数字;我们操作计算机,实际就是使用程序和软件在计算机上各种读写数据,如果我们直接操作二进制的话,面对这么长的数进行思考或操作,没有人会喜欢。
C,C++语言没有提供在代码直接写二进制数的方法。
用16进制或8进制可以解决这个问题。
因为,进制越大,数的表达xx也就越短。
之所以使用16或8进制,而不其它的,诸如9或20进制.是因为2、8、16,分别是2的1次方、3次方、4次方。
这一点使得三种进制之间可以非常直接地互相转换;8进制或16进制既缩短了二进制数,还能保持了二进制数的表达特点。
转换还方便.进制的介绍进制:是计算机中数据的一种表示方法。
N进制的数可以用0~(N-1)的数表示,超过9的用字母A-F表示.10进制先说我们最熟悉的10进制,就是用0~9的数表示,逢10进1 .16进制如果是16进制,它就是由0-9,A-F组成,与10进制的对应关系是:0-9对应0-9;A-F对应10-15;字母不区分大小写。
2进制和8进制2进制由0-1组成8进制由0-7组成进制的转换公式二进制转换十进制八进制转换十进制十六进制转换十进制如何快速的进行2进制,10进制,16进制的相互转换先记住二进制的8421首先我们来看一个二进制数:1111,它是多少呢?你可能还要这样计算:1×2º+1×2¹+1×2²+1×2³=1×1+1×2+1×4+1×8=15。
我们必须直接记住1111每一位的权值,并且是从高位往低位记,:8、4、2、1。
即,最高位的权值为2³=8,然后依次是2²=4,2¹=2,2º=1。
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
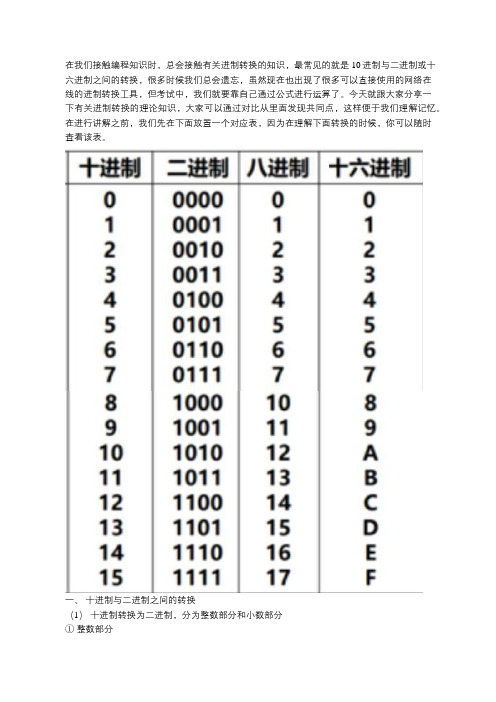
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
十进制与十六进制转换方法

十进制与十六进制转换方法
十进制(Decimal)和十六进制(Hexadecimal)之间的转换是计算机科学中常见的操作。
下面是两者之间的转换方法:
1. 从十进制转换到十六进制:
首先,确定十进制数的范围。
确保这个数是一个整数,如果不是,你需要将它转换为整数(例如,通过除以10的适当次幂)。
使用除法来找到最大的十六进制位数。
例如,如果你正在转换一个十进制数,你可以用它除以16,并记录余数和商。
余数将是最低位的十六进制数字,而商可以再次除以16。
重复这个过程,每次都取余数和商,直到商为0。
所有这些余数连接在一起形成转换后的十六进制数。
2. 从十六进制转换到十进制:
读取十六进制数的每一位。
使用乘法来转换每一位。
例如,十六进制中的“A”或“10”代表10进制的10,而“B”或“11”代表10进制的11。
将每一位的十进制值乘以相应的基数(对于十六进制,基数是16)并加在一起。
此外,也有在线工具和应用程序可以帮助进行这两种转换,如果觉得手动转换比较困难的话。
十六进制、八进制、二进制之间的相互专换方法

十六进制、八进制、二进制之间的相互专换方法一、十六进制举例说明10进制的32表示成16进制就是:2016进制的32表示成10进制就是:3×16^1+2×16^0=50编程中,我们常用的还是10进制.毕竟C/C++是高级语言。
比如:int a = 100,b = 99;不过,由于数据在计算机中的表示,最终以二进制的形式存在,所以有时候使用二进制,可以更直观地解决问题。
但二进制数太长了。
比如int 类型占用4个字节,32位。
比如100,用int类型的二进制数表达将是:0000 0000 0000 0000 0110 0100面对这么长的数进行思考或操作,没有人会喜欢。
因此,C,C++ 没有提供在代码直接写二进制数的方法。
用16进制或8进制可以解决这个问题。
因为,进制越大,数的表达长度也就越短。
不过,为什么偏偏是16或8进制,而不其它的,诸如9或20进制呢?2、8、16,分别是2的1次方,3次方,4次方。
这一点使得三种进制之间可以非常直接地互相转换。
8进制或16进制缩短了二进制数,但保持了二进制数的表达特点。
在下面的关于进制转换的课程中,你可以发现这一点。
二、转换二进制转换十进制二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:101100100,转换为10进制为:356用横式计算0 X2^0 + 0X 2^1 + 1X 2^2 + 0X2^3 + 0X2^4 + 1 X2^5 + 1 X2^6 + 0 X 2^7 + 1X 2^8 = 3560乘以多少都是0,所以我们也可以直接跳过值为0的位:1X 2^2 + 1 X2^5 + 1X 2^6 + 1X 2^8 = 3564 + 32 + 64 + 256 =356八进制转换十进制八进制就是逢8进1。
八进制数采用0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方……所以,设有一个八进制数:1507,转换为十进制为:839,具体方法如下:可以用横式直接计算:7 * 8^0 + 0 * 8^1 + 5 * 8^2 + 1 * 8^3 = 839也可以用竖式表示第0位7 * 8^0 = 7第1位0 * 8^1 = 0第2位 5 * 8^2 = 320第3位 1 * 8^3 = 512十六进制转换十进制16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。
很完整的2、8、10、16进制转换方法

很完整的2、8、10、16进制转换方法最近在研究C语言,因为要用到各进制间转换,所以收集了一些资料…这是一节“前不着村后不着店”的课。
不同进制之间的转换纯粹是数学上的计算。
不过,你不必担心会有么复杂,无非是乘或除的计算。
生活中其实很多地方的计数方法都多少有点不同进制的影子。
比如我们最常用的10进制,其实起源于人有10个指头。
如果我们的祖先始终没有摆脱手脚不分的境况,我想我们现在一定是在使用20进制。
至于二进制……没有袜子称为0只袜子,有一只袜子称为1只袜子,但若有两袜子,则我们常说的是:1双袜子。
生活中还有:七进制,比如星期。
十六进制,比如小时或“一打”,六十进制,比如分钟或角度……我们找到问号字符(?)的ASCII值是63,那么我们可以把它转换为八进值:77,然后用‘\77′来表示’?'。
由于是八进制,所以本应写成‘\077′,但因为C,C++规定不允许使用斜杠加10进制数来表示字符,所以这里的0可以不写。
事实上我们很少在实际编程中非要用转义符加八进制数来表示一个字符,所以,6.2.4小节的内容,大家仅仅了解就行。
6.2.5 十六进制数转换成十进制数2进制,用两个阿拉伯数字:0、1;8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;10进制,用十个阿拉伯数字:0到9;16进制,用十六个阿拉伯数字……等等,阿拉伯人或说是印度人,只发明了10个数字啊?16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这五个字母来分别表示10,11,12,13,14,15。
字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X * 16的N次方。
假设有一个十六进数 2AF5, 那么如何换算成10进制呢?用竖式计算:2AF5换算成10进制:第0位: 5 * 16^0 = 5第1位: F * 16^1 = 240第2位: A * 16^2 = 2560第3位: 2 * 16^3 = 8192 +————————————-10997直接计算就是:5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 = 10997(别忘了,在上面的计算中,A表示10,而F表示15)现在可以看出,所有进制换算成10进制,关键在于各自的权值不同。
2、8、10、16进制转换

直接计算就是:
5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 = 10997
(别忘了,在上面的计算中,A表示10,而F表示15)
现在可以看出,所有进制换算成10进制,关键在于各自的权值不同。
假设有人问你,十进数 1234 为什么是 一千二百三十四?你尽可以给他这么一个算式:
现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1
“将商继续除以2,直到商为0……最后将所有余数倒序排列”
好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!
6转换成二进制,结果是110。
比如,十进制数 1234转换成二制数,如果要一直除以2,直接得到2进制数,需要计算较多次数。所以我们可以先除以16,得到16进制数:
被除数 计算过程 商 余数
1234 1234/16 77 2
77 77/16 4 13 (D)
4 4/16 0 4
结果16进制为: 0x4D2
同样是120,转换成16进制则为:
被除数 计算过程 商 余数
120 120/16 7 8
7 7/16 0 7
120转换为16进制,结果为:78。
6. 十六----> 十
16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。字母不区分大小写。
1. 十 -----> 二
给你一个十进制,比如:6,如果将它转换成二进制数呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(C语言)10进制转换2,8,16进制作者:vinseven#include"stdio.h"#include"conio.h"#include"malloc.h"#include"windows.h"#define ElemType intvoid menu();void TenToTwo();void TenToEight();void TenToSixteen();void InitStack(struct sNode **HS);void Push(struct sNode **HS,ElemType x);ElemType Pop(struct sNode **HS);ElemType Peek(struct sNode **HS);int EmptyStack(struct sNode **HS);void ClearStack(struct sNode **HS);int ten;/*要输入的10进制数*/int x;/*把将要插入到栈中的元素暂时存进 x 中*/struct sNode hs;struct sNode{ElemType data;struct sNode *next;};void main(){menu();getch();}void menu(){char choice;int flag=1;while(1){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 1,10进制转换2进制\n\n\n");printf("\t\t\t 2,10进制转换8进制\n\n\n");printf("\t\t\t 3,10进制转换16进制\n\n\n");printf("\t\t\t 0,退出\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入编号:");while(flag){fflush(stdin);choice=getch();switch(choice){case '1':{system("cls");TenToTwo();flag=0;break;}case '2':{system("cls");TenToEight();flag=0;break;}case '3':{system("cls");TenToSixteen();flag=0;break;}case '0':{printf("\n\t\t\t按任意键退出");getch();exit(0);}default:{printf("\n\t\t\t无此选项可选!请重新输入!\n");flag=1;break;}}}system("cls");flag=1;}}/*10进制转换2进制界面*/void TenToTwo(){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换2进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数:");scanf("%d",&ten);while(ten!=0){x=ten%2;Push(&hs,x);ten=ten/2;}printf("\t\t\t二进制数为:");while(!EmptyStack(&hs))printf("%d",Pop(&hs));getch();}/*10进制转换8进制界面*/void TenToEight(){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换8进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数:");scanf("%d",&ten);while(ten!=0){x=ten%8;Push(&hs,x);ten=ten/8;}printf("\t\t\t八进制数为:");while(!EmptyStack(&hs))printf("%d",Pop(&hs));getch();}/*10进制转换16进制界面*/void TenToSixteen(){int temp;printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换16进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数:");scanf("%d",&ten);while(ten!=0){x=ten%16;Push(&hs,x);ten=ten/16;}printf("\t\t\t十六进制数为:");while(!EmptyStack(&hs)){temp=Pop(&hs);switch(temp){case 1:case 2:case 3:case 4:case 5:case 6:case 7:case 8:case 9:printf("%d",temp);break;case 10:printf("A");break;case 11:printf("B");break;case 12:printf("C");break;case 13:printf("D");break;case 14:printf("E");break;case 15:printf("F");break;}}getch();}/*关于栈的函数*//*1,初始化链栈为空*/void InitStack(struct sNode **HS) {*HS=NULL;}/*2,向栈中插入一个元素*/void Push(struct sNode **HS,ElemType x){struct sNode *newp;newp=malloc(sizeof(struct sNode));if(newp==NULL){printf("内存动态空间用完,退出运行!");system("pause");exit(0);}newp->data=x;newp->next=*HS;*HS=newp;}/*3,从栈中删除一个函元素并返回它*/ ElemType Pop(struct sNode **HS){struct sNode *p;ElemType temp;if(*HS==NULL){printf("栈空!无法删除!");system("pause");exit(0);}p=*HS;*HS=p->next;temp=p->data;free(p);return temp;}/*4,读取栈顶元素*/ElemType Peek(struct sNode **HS){if(*HS==NULL){printf("栈空!无法读取栈顶结点!");system("pause");exit(1);}return (*HS)->data;}/*5,检查链栈是否为空,空返回1,否则返回0*/ int EmptyStack(struct sNode **HS){if(*HS==NULL)return 1;elsereturn 0;}/*6,清除链栈为空*/void ClearStack(struct sNode **HS){struct sNode *cp,*np;cp=*HS;while(cp!=NULL){np=cp->next;free(cp);cp=np;}*HS=NULL; }。
