第3章 相对位置(建筑)
7年级上册 第03章 人类的家园——地球(单元综合测试)(教师版含解析)

浙教版七年级上科学同步学习精讲精练第3章人类的家园——地球单元综合测试(测试时间:100分钟,总分100分)一、选择题(每题2分,共40分)1.我国主要位于()A.太平洋板块B.亚欧板块C.印度洋板块D.大西洋板块【答案】B【解析】地质学家经过长期研究,提出了板块构造学说.板块构造学说认为,地球岩石圈是由板块拼合而成的.全球主要有六大板块,其中太平洋板块几乎全部是海洋,其余板块既包括大陆,又包括海洋.海洋与陆地的相对位置是不断变化的.我国位于亚洲东部,太平洋西岸,在板块上属于亚欧板块。
2.下列地貌形态的形成,主要是由风力侵蚀作用引起的是()【答案】D【解析】地表形态是内力作用和外力作用共同作用的结果。
内力作用主要包括:地壳运动、火山和地震活动;外力作用主要包括:风力、流水、冰川、波浪、生物等。
火山湖是由火山喷发后火山口水聚集形成的,不是风力侵蚀形成的,A错误;海岸边的怪石是在海水的侵蚀下形成的,B错误;喜马拉雅山的角峰冰斗谷是在冰川作用下形成的,C错误;沙漠中的石蘑菇是风力侵蚀作用的结果,D正确。
3.我国首都北京(116°E、40°N)位于()A.东半球、北半球、低纬度B.西半球、北半球、中纬度C.东半球、北半球、中纬度D.西半球、南半球、低纬度【答案】C【解析】南北半球与南北纬度的分界线是赤道,以北为北半球(北纬),以南为南半球(南纬);东西半球分界线是20°W和160°E组成的经线圈,20°W以东、160°E以西为东半球,20°W以西、160°E以东为西半球;纬度划分,0°~30°为低纬度地区,30°~60°为中纬度地区,60°~90°为高纬度地区,据此可判断,我国首都北京(40°N、116°E)位于东半球、北半球、中纬度。
4.地球是我们共同的家园。
运营管理-第三章 运营系统的选址和合理布置

得分(0~100)
地点1 (3)
地点2 (4)
地点3 (5)
100
70
80
80
80
100
50
90
70
40
80
60
90
60
80
80
90
60
50
80
100
加权得分
地点1 (2) (3)
地点2 (2) (4)
0.15100=15 0.0580=4 0.3050=15 0.0540=2 0.2090=18 0.1580=12 0.1050=5 71
2 ) 、 根 据 生 产 系 统 功 能 布 置 ( Production System Layout by Function)
a、仓储布置(Storage Layout) • 在仓库中安排物资的存放 • 原则:最大限度地利用仓储空间,以最低
成本保管、处理物资 • 要考虑的因素:订货次数、物品间的相关
• 目标:使分配到各个工作地的作业所需要的时间大致相 等,从而使生产线上各活动同步进行,实现工人和设备 的最大利用
• 可能遇到的困难 • 设备问题 • 基本作业的时间差异不能通过分配作业组而解决 • 生产或装配所要求的技术顺序 对理想的分配有约束力
生产线的平衡-工作地数量的确定
• 工作地数量的确定
运营系统的选址和合理布置
企业选址(Location)
• 选址规划:确定工厂或服务设施的位置。 涉及两个层面:第一个层面是选位,即选 择一定的区域,如国家、地区、省市等; 第二个层面是定址,即选择工厂或服务设 施的具体地址。
• 战略性决策
企业选址考虑的因素
建筑制图与识图-第三章

三、平面立体表面上点和线的投影
(一)利用“从属性法”和“积聚性法”作图
从属性法 当点位于立体表面的某条棱边上时,该点的投影必定在棱线的
投影上。此时,可利用线上点的“从属性”求出该点的投影。
积聚性法
(梯梯为台)。由于正面投影中的m′n′可见,因此 可判定该直线位于四棱台的前棱面上。由于M点在 棱边上,故可利用“从属性法”求出其他两面投影 ;N点所在的表面为侧垂面,其侧面投影具有积聚 性,因此可先利用表面的积聚性求出n''点,然后再 利用n''点和n′点求出n点。
图3-7 利用“从属性法”和 “积聚性法”求立体表面上点
(c)
图3-11 圆柱投影图的作图步骤
二、圆锥
圆锥是由圆锥面和圆底面所围成的回转体。其中,圆锥面是由母线绕与其相交并且 成一定角度的轴线回转而成的。母线与轴线的交点称为锥顶。圆锥面的所有素线都交于 锥顶,并且对底面的倾角相等。母线上任意一点的运动轨迹形成的圆称为纬圆。
(一)投影分析 将圆锥的轴线垂直于H面放置在三投
影面体系中,如图3-12所示,其三面投影 特性如下。
图3-12 圆锥的三面投影
二、圆锥
H面投影 为一水平圆,反映圆锥底面的实形,同时也是圆锥面的投影。
V面和W 面投影
均为等腰三角形,且三角形的底边为圆锥底面的积聚投影。V面投影中, 三角形的左、右两边分别是圆锥面最左、最右素线(素线也是转向轮廓线 )的投影;W面投影中,三角形的左、右两边分别是圆锥面最前、最后素 线的投影。
一、棱柱
(四)正六棱柱的作图步骤
(1)画出正六棱柱的对称中心线、底面基线及45°辅助线,以确定各投影图的位置, 如图3-3(a)所示。 (2)先画出反映主要形状特征的投影图,即画H面投影图中的正六边形,然后按照 “长对正”的投影规律及正六棱柱的高度画出V面投影。正六边形可采用等分圆周的方 法绘制,结果如图3-3(b)所示。 (3)根据“高平齐、宽相等”的投影规律画出W面投影,最后擦去多余的图线并加深, 结果如图3-3(c)所示。
房屋建筑学---第三章建筑剖面

绝大多数建筑属于一般功能要求的,可采用矩形,如住宅、学 校、办公楼、旅馆、商店等。
某些有特殊功能要求的房间,须选择合适的剖面。 1.视线要求(影剧院观众厅、体育馆比赛大厅、阶梯教室等 )
* 地面的升起坡度---设计视点选择、 座位排列方式、排距、 视线升高值C
3
h
第三章 建筑剖面设计
8
第三章 建筑剖面设计
3.1.3 采光、通风的要求
为满足通风要求, 对公共厨房等在操作过程中散 发大量蒸汽和油烟的房间,可在顶部设排气窗,形成 各异的剖面形状。
9
h
第三章 建筑剖面设计
第一节 完
休息一会儿吧!
10
h
第三章 建筑剖面设计
3.2 房屋各部分高度的确定
11
h
第三章 建筑剖面设计
地面坡度大于1:6时,应做成台阶
中学演示教室的地面升起
上:对位排列,逐排升高
下:错位排列,隔排升高
5
重庆大学建筑城规学院
建筑技术研究所绘制
h
第三章 建筑剖面设计
3.1.1 使用要求对剖面的影响
2.音质要求—顶棚形式的确定 (如剧院、电影院、会堂)
观众厅声学特点: * 声能分布均匀 * 防止回声 * 避免声聚焦
房屋建筑学
第三章 建筑剖面设计
3.1 房间的剖面形状 3.2 房屋各部分高度的确定 3.3 房屋的层数 3.4 建筑空间的组合与利用
1
h
第三章 建筑剖面设计
3.1 房间的剖面形状
房间的剖面形状分为矩形、非矩形两类。
使用要求 结构、材料和施工的影响 采光、通风、艺术构思等要求
2
h
第三章 建筑剖面设计
房屋建筑混凝土结构设计第3章课后自测答案

第3章多层建筑框架结构3.1 框架结构设计的基本要求题目1()是为了避免厂房因基础不均匀沉降而引起的开裂和损坏而设置的。
选择一项:A. 隔离带B. 伸缩缝C. 防震缝D. 沉降缝正确答案是:沉降缝题目2伸缩缝从()开始,将两个温度区段的上部结构完全分开,留出一定宽度的缝隙,当温度变化时,结构可自由地变形,防止房屋开裂。
选择一项:A. 地基底面B. 基础底面C. 基础顶面D. 地基顶面正确答案是:基础顶面3.2 框架结构布置及柱梁截面尺寸题目1采用(),有利于提高框架结构建筑的横向侧移刚度,并且由于横向跨度小于纵向跨度,故而楼板的跨度较为经济合理。
选择一项:A. 纵向框架承重体系B. 斜向框架承重体系C. 混合承重体系D. 横向框架承重体系正确答案是:横向框架承重体系题目2采用(),其优点在于开间布置比较灵活,但房屋的横向刚度较差,楼板的跨度也较大,因此在实际工程中采用较少。
选择一项:A. 混合承重体系B. 斜向框架承重体系C. 横向框架承重体系D. 纵向框架承重体系正确答案是:纵向框架承重体系题目3采用(),其优点是有利于抵抗来自纵横两个方向的风荷载和地震作用,框架结构具有较好的整体工作性能。
选择一项:A. 混合承重体系B. 横向框架承重体系C. 纵向框架承重体系D. 斜向框架承重体系正确答案是:混合承重体系3.3 框架结构计算简图题目1在框架结构内力和位移计算中,考虑到(),计算框架梁截面惯性矩I时应考虑其影响。
选择一项:A. 框架柱的稳定性影响B. 框架节点的塑性铰影响C. 现浇楼板可以作为框架梁的有效翼缘的作用D. 框架梁的抗扭刚度影响正确答案是:现浇楼板可以作为框架梁的有效翼缘的作用题目2计算框架梁截面惯性矩I时应考虑现浇楼板对它的影响,为方便设计,对现浇楼盖,中框架梁的截面惯性矩取为()。
(I0为矩形截面梁的截面惯性矩)选择一项:A. 1.2 I0B. 1.5I0C. 2 I0D. I0正确答案是:2 I03.4 框架结构的内力计算之分层法题目1采用分层法进行框架结构竖向荷载作用下的内力计算时,可近似地按无侧移框架进行分析。
第3章建筑剖面设计剖析

第3章 建筑剖面设计
5.室内空间比例 室内的空间比例对人的心理行为影响很大。高而 窄的空间易使人产生兴奋、激昂、向上的情绪,具有严肃感,但过高就 会觉得不亲切;宽而矮的空间易使人感到宁静、开阔、亲切,但过低又 会使人感觉压抑、沉闷。设计净高时,应巧妙运用空间比例的变化,使 物质功能与精神感受密切结合,从而获得理想的艺术效果。
图3-8 房间的最小净高
第3章 建筑剖面设计
2. 房间的采光和通风 房间的采光和通风不仅会影响房间的剖面形状, 而且还会影响房间的高度。当窗户面积不变时,侧窗上沿的高度愈高,对室 使用规范说明 内远窗点的照度愈有利。如图3-10所示为单侧采光时室内照度的变化示意图 ,可以看出,沿进深方向室内照度衰减很大。因此,进深大的房间,为满足 房间的采光要求,常需提高窗上沿的高度,此时房间的净高也需相应增高。
图3-8 房间的最小净高
图3-10 室内照度变化示意图
第3章 建筑剖面设计
在房间的剖面设计中,要保证良好的通风,需注意室内进出风口在剖面 上的高低位置。在炎热地区,通过设置高低窗,利用空气的气压差,可形成 室内穿堂风(参见图3-11),此时要注意房间的净高要求。
(a)教室
图3-11 房间剖面中进出风口的位置和通风线路示意图
第3章 建筑剖面设计
使用规范说明
(a)画廊
(b)阶梯教室
图3-5 天窗的剖面形状对室内照明分布的影响
第3章 建筑剖面设计
为满足通风的要求,一般在墙的两侧或一侧设窗,进行空气对流。对
于有特殊要求的房间或湿度较大、温度较高的房间(如厨房),除了在墙 使用规范说明
面两侧开窗以外,还需在屋顶开设排气窗,如图3-6所示。
(b) H1—净高;H2—层高
红色警戒教程攻略(精品)

第1章红色警戒2中的常用快捷键第2章红色警戒2 (RED ALERT 2)经济篇第3章红色警戒2 (RED ALERT 2)防御篇第4章红色警戒2(RED ALERT 2)中的常规兵种第5章红色警戒2(RED ALERT 2)步兵篇第6章红色警戒2(RED ALERT 2)空军篇第7章红色警戒2(RED ALERT 2)抢占建筑第8章红色警戒2(RED ALERT 2)海军陆战队第9章红色警戒2(RED ALERT 2)速推篇第10章红色警戒2(RED ALERT 2)战术意识的培养第11章红色警戒2(RED ALERT 2)的禁忌打法篇第1章红色警戒2中的常用快捷键关于红色警戒2的快捷键,红警家园有不少此类文章,但我们还是把它集中在本文,方便各位红警玩家阅读。
首先让我们了解一下红警里的常用快捷键,他将使你更加熟练的操作红警、提高建造和发展速度。
A:点取玩家,结盟。
(建议不要等看到盟友后再结盟,因为结盟以后盟友之间所探索的地图可以共享,如果直到看到盟友后才结盟,不仅容易误伤!还浪费了许多时间去探索地图。
强烈建议一开局不久时,利用等待建造完毕时,立即结盟):警示信标,提示盟友。
可以配合交谈键。
选取,按dl键,取消。
(有的版本没有这项功能。
特别是在多人联线时,比较有用。
比如己已经没有任何战斗力,或者已经完全被击败,全图已开,而盟友没有全图时你可以帮助盟友指示箱子的位置,以及基地的位置。
点击信标后,回车,可以敲入一些提示性的语言,比如:红色老家!)C:欢呼,气势。
D:能使美国大兵、辐射工兵等蹲下或站起;坦克变形等;尤里里的苏军米格直升机D,可以架小型巨炮。
可是很多兵种只有在以后版本才有D的功能。
大家可以多试试。
:兵营栏。
F:聚焦跟踪。
(这个功能尤其要掌握。
很多刚开始玩红警的朋友,忘了把己的部队派到那里了,这个时候F功能就可以起很大的作用了。
比如你想知道1编队在那里,你可以按1,然后按F,马上就可以切换到1编队的位置)G:警戒。
画法几何与土木建筑制图 第3章 点、直线的投影及两直线的相对位置

V
a'
X
ax
Z
az
A
a''
O
a
ay
Y
(a)立体图
a' X aX
a
Z
aZ
a''
YW O aYW aYH YH
V
a'
b' W
a'
b' Z
a''(b''
X
A
O B)
X
a b
Y
立体图
a
投影特性: a''b'' 积聚为一点
ab ∥a'b'∥OX
ab= a'b'=AB
O
b
YH 投影图
a''(b'')
YW
2. 投影面平行线投影特性
V
a'
X
Z
b' W
B
αγ
A
a b
正平线
a' α
b''
X
a''
b' Z γ
O
Y
立体图
a
正平线投影特性:
b'
X
Z
a'
a''
工程制图第3章答案

3.两直线交叉
交叉两直线各组同面投影不会都平行,特殊情况下可能有一两组 平行;其各组同面投影交点的连线与相应的投影轴不垂直,即不符合 点的投影规律。
重影点 反之,如果两直线的投影既不符合平行两直线的投影特性,也不 符合相交两直线的投影特性,则该两直线空间为交叉两直线。
4.两直线垂直
一般情况下,在投影图中不能确定空间两直线是否垂直, 但当直线处于特殊位置时可以直接从投影图中判断:
三、正投影的基本性质
1. 实形性
2.积聚性
∟
三、正投影的基本性质
3.类似性
4.平行性
三、正投影的基本性质
5.定比性
6.从属性
3-2 三视图的形成及其投影关系
一、 三视图的形成
1. 三投影面体系的建立
物体的一个投影不能确定空间物体的形状。
怎吗办?
建立三面投影体系
2.三视图的形成
主视图
左 视图
[例3-4] 已知点A(15,10,12),求作点A的三面投影图。
作图步骤如下:
1.自原点O沿OX轴向左量取x=15,得点 ax 2.过ax作OX轴的垂线,在垂线上自ax向下量取y=10,得点A的水平投影a 向上量取z=12,得点A的正面投影a
3.根据点的投影规律,可由点的两个投影作出第三投影 a 。
★ 我们只讨论直线与平面中至少有一个处于特殊位置的情况。
[例3-11] 求一般位置直线MN与铅垂面ABC的交点 分析: 作图:
判可见性:
[例3-12] 求铅垂线MN与一般位置平面△ABC的交点 分析: 作图:
判可见性:
⒉ 两平面相交
两平面相交其交线为直线,交线是两平面的共 有线,同时交线上的点都是两平面的共有点。
工程图学 第3章 直线

2
a X 4 c a 1(2)
d
O b d
3
4. 垂直两直线的投影
两直线夹角,其投影有下列三种情况: ①相互垂直两直线都平行某一投影面,在所平行的投 影面上的投影反映直角。 ②相互垂直的两直线,其中一条直线平行某一投影 面,在所平行的投影面上的投影反映直角。 ——称为直角投影定理(蒙日直角定理)
利用这一特性,在不作侧面投影的情况下,可以在两面投影上找点或 判断已知点是否在直线上。
例1 已知线段AB的投影图,试将AB分成1:2两段,求分点C 的投影。 b c a X b
O
c
a 1
2
3
例2
已知点C在线段AB上,求点C的正面投影。
V
b
c
b B A a c c b C O X c
a(b)
X
O
YW
a
b
Y
投影特性: 1、ab 积聚 成一点 2 、 ab OX ; ab OX 3 、 ab = ab =AB
投影面垂直线的投影特性: 1、在垂直的投影面上的投影积聚为一点; 2、在另外两个投影面上的投影反映其实长,且平行于 相应的投影轴。 读图原则: 一直线只要有一个投影积聚为一点,这条直线必定是 投影面的垂直线,垂直于该积聚投影所在的投影面。
2.相交两直线 d k a X c K D O b b B a k
d b
X
c
c b k
O
C Ac a
k
d
a
d 两相交直线在同一投影面上的投影仍相交,且交点属于 两直线。 反之,若两直线在同一投影面上的投影相交,且 交点属于两直线,则该两直线相交。
例6:过C点作水平线CD与AB相交。
国开电大建筑制图基础第3章自测参考答案

题目1.1.构成形体最基本的几何元素是()。
a. 平面b. 曲线c. 直线d. 点【答案】:点题目2.2.在投影理论中,对于物体只研究其形状、大小、位置,而它的物理性质、化学性质都不涉及到,这种物体称为()。
a. 球体b. 形体c. 旋转体d. 刚体【答案】:形体题目3.3.点的正面投影和侧面投影的连线垂直于()。
a. 不能确定b. OX轴c. OZ轴d. OY轴【答案】:OZ轴题目4.4.点在某一投影面上的投影是()。
a. 曲线b. 点c. 平面d. 直线【答案】:点题目5.5.投影法中规定空间点选用字母是应()。
a. 右上角加一撇的小写字母b. 右上角加两撇的小写字母c. 大写字母d. 小写字母【答案】:大写字母题目6.6.投影法中规定,空间点在H面的投影选用字母是应()。
a. 小写字母b. 右上角加一撇的小写字母c. 右上角加两撇的小写字母d. 大写字母【答案】:小写字母题目7.7.投影法中规定,空间点在V面的投影选用字母是应()。
a. 大写字母b. 右上角加一撇的小写字母c. 小写字母d. 右上角加两撇的小写字母【答案】:右上角加一撇的小写字母题目8.8.投影法中规定,空间点在W面的投影选用字母是应()。
a. 右上角加一撇的小写字母b. 小写字母c. 大写字母d. 右上角加两撇的小写字母【答案】:右上角加两撇的小写字母题目9.9.如果空间点的位置用A(x,y,z)形式表示,那么它的H面投影的坐标应为()。
a. a (0,y,0)b. a(x,0,z)c. a(x,y,0)d. a(0,y,z)【答案】:a(x,y,0)题目10.10.如果空间点的位置用A(x,y,z)形势表示,那么它的V面投影的坐标应为()。
a. a’(0,y,0)b. a’(x,0,z)c. a’(0,y,z)d. a’(x,y,0)【答案】:a’(x,0,z)题目11.11.如果空间点的位置用A(x,y,z)形势表示,那么它的W面投影的坐标应为()。
第3章 点、线、面答案

2.在△ABC内作距V面为15mm的正平线。
2.过点C作直线CD与直线AB相交,交点距V面15mm。
3.作直线MN平行AB,且与CD、EF相交。
4.判断两直线的相对位置。
5.用字母标出交叉两直线重影点的投影。
3-7平面的投影(找出平面Ⅰ的另两视图,判断空间位置)
1.
2.
3.
4.
3-8平面的投影
1.已知点K属于△ABC平面,完成△ABC的正面投影。
第3章点、直线、平面的投影
3-1点的投影
1.完成点A的轴测图和点A的三面投影图。
2.标出正四棱锥顶点Ⅰ、Ⅱ的其他两面投影,并判断Ⅰ、Ⅱ两点的相对位置。点Ⅰ在点Ⅱ的左、前、下方。
3.已知点B距H面20mm、距V面15mm、距W面30mm,试作出点B的三面投影。
4.已知点的两面投影,求第三面投影。点E在W面上,点F在H面。
3-3直线的投影
1.已知点A在点B的左方15mm、下方10mm、前方10mm,求A、B两点的三面投影。
2.在正五棱台的主视图、左视图上标出A、B两点的投影,并比较两点的相对位置。点B在点A的右、前、上方。
3.已知A、B两点在W面的投影重影,完成A、B两点的三面投影。
4.已知正三棱锥的俯视图,其锥顶S距H面25mm,又知锥底位于H面上,试补画主、左视图。
3-4直线的投影
1.作直线AB的H面投影,并标出它与V、W面的倾角β和γ。
2.求作正平线CD的三面投影,已知CD长25mm,与H面倾角为30°。
3.求侧垂线EF的三面投影,已知EF长30mm,距V面15mm,距H面20mm,端点E距W面40mm。
4.已知点M在直线CD上,并与H、V面的距离相等,完成点M的投影。
中国建筑史第3章第五讲(民居)

少见 罕见
的纯客家
圆
闽西永定、龙岩、上杭、粤东嘉应梅县、 南部 漳平;闽西南平和、诏 大埔、平远、 散见 五华、潮州 安、南靖、云霄等 闽西所有县;闽北各县、粤东嘉应、 闽南诏安、平和、南靖、潮州、南雄 云霄、同安及闽东闽清 及深圳、香 港
(一)木构抬梁、穿斗与混合式: 主要分布地区:北京、江浙、皖南、 江西、湖南、湖北、云、贵、川等。 抬梁和穿斗两种技术在汉代便已成 熟。此后在住宅中普遍应用,范围甚广。 北方多抬梁式,以北京四合院为代表;南 方多穿斗式,如云南白族住宅的主体部分。 皖南、江浙、江西一带住宅中,山墙边贴 用穿斗式,以较密集的柱梁横向穿插结合, 辅以墙体,增强抗风性能;明间为使空间 开敞、庄重,虽然柱梁交接还是横向榫卯 关系,具穿斗特征,但已改及大梁上再抬 上部梁架,为抬梁、穿斗混合式。
在此时期,人类才首次获得充足、稳定的 食物。也才建立了相对稳定的居民点。这就是 最初的聚落。到新石器时代,中国大部分地区 已从事农耕。其中距今约6000—9000年前的湖 南澧(li)县彭头山遗址、河南郑州裴李岗遗址、 河北武安磁山遗址、浙江余姚河姆渡遗址等, 是我国所知的最早和最具典型性的农耕遗址。 人类第一次劳动大分工,即农业的出现而 形成固定的居民点----聚落;人类第二次劳动 大分工,即商业从农业中分离出来,聚落分化 成以农业为主的乡村和以非农业为主而以商业 手工业为主的城市。这是从原始社会向奴隶社 会过渡时期产生的。随之,由于生活方式和生 活环境的不同,以城市达官贵人的住宅和乡村 中乡绅庶民的住宅为代表,在漫长的历史发展 中也自成轨迹。
(八)阿以旺: 主要分布地区:新疆南部。 “阿以旺”是新疆维吾尔族住宅常见的一种, 有三四百年的历史。土木结构,平屋顶,带外廊。 所谓“阿以旺”,即是一种带有天窗的夏室(大 厅),中留井孔采光,天窗高出屋面约40-80cm, 供起居、会客之用,后部做卧室,亦称冬室,各 室也用井孔采光。“阿以旺”顶部以木梁排木檩, 厅内周边设土台,高40-50cm,用于日常起居。室 内壁龛甚多,用石膏花纹作装饰,龛内可放被褥 或杂物。墙面喜用织物装饰,并以此质地和大小、 多少来标识主人身份与财富。屋侧有庭院,夏日 葡萄架下,可作息生活。
机械制图与CAD(含习题集)( (3)

助线的方法,作出交点K的水平投影k。由于正垂线EF在正面积 聚,可不必判断可见性。在水平投影上,直线EF有一部分被平
面ACD遮挡,交点K是直线可见部分和不可见部分的分界点。从 正面投影知,直线段FK在平面ACD的下方(也可用重影点法比 较交叉直线段FK与CD的上下位置来间接判断),因此直线段FK
水平线DⅢ平行,平面ABC上的正平线BⅠ和平面DEF上的正平线 DE平行,并且水平线和正平线相交,因此可判断平面ABC与平 面DEF平行。
第3章 几何元素间的相对位置 图3-6 两平面平行
第3章 几何元素间的相对位置
【例3-4】 如图3-7所示,已知平面ABCD和平面外一点 E的两面投影,试过点E作平面平行于平面ABCD。 分析 要保证所作平面平行于平面ABCD,必须作出一对相交直 线与已知平面ABCD平行。如图3-7(b)所示,为作图方便, 可过点E作相交直线分别与平面ABCD上的CD和AD平行。
第3章 几何元素间的相对位置 图3-1 直线平行于平面
第3章 几何元素间的相对位置 图3-2 直线平行于特殊平面
第3章 几何元素间的相对位置
【例3-1】 如图3-3(a)所示,试判断直线DE是否 平行于平面ABC。
解 欲判别直线与平面是否平行,就应判断是否在平面上 可否作一条与该直线平行的直线。如图3-3(b)所示,作图 步骤如下:
的水平投影不可见部分应用虚线画出。直线段KE的水平投影可 见,应用粗实线画出。
第3章 几何元素间的相对位置
解 如图3-9(b)所示,其作图步骤如下: (1)根据交点K的共有性,在直线的积聚性投影上直接找 到交点的正面投影k′;
工程制图第3章答案

投 射 方 向
90°
2. 特性
中心投影法
物体位置改 变,投影大 小也改变。
投 影 特 性
●
投射中心、物体、投影面三者之间的相 对距离对投影的大小有影响。 用于建筑图样中的透视图绘制。
● 度量性较差。 ●
平行投影法
物体位置改 变,投影大 小不改变。
投 影 特 性
● ● ●
投影大小与物体和投影面之间的距离无关。 度量性较好。 工程图样多数采用正投影法绘制。
a a ⊥OX;
⊥OZ;
水平投影到X轴的距离等于侧面投影到Z轴的距离,即
a ax = aaz
[例3-3] 根据点A和B的两个投影求第三个投影。 (二求三)
求法:
a:
长对正 宽相等
:
高平齐 宽相等
二、点的投影与空间直角坐标的关系
空间点A到W面的距离,等于点A的x坐标;即: 空间点A到V面的距离,等于点A的y坐标;即: 空间点A到H面的距离,等于点A的z坐标;即:
[例3-12] 求铅垂线MN与一般位置平面△ABC的交点
分析: 作图:
判可见性:
⒉ 两平面相交
两平面相交其交线为直线,交线是两平面的共 有线,同时交线上的点都是两平面的共有点。
要讨论的问题:
● 求两平面的交线。 ● 判别两平面之间的相互遮挡关系,即:判别可见性。
解决问题的方法:
若相交两平面之一为投影面垂直面或投影面平行 面时,则可利用该平面有积聚性的投影,在有积聚性 的投影图上直接求得交线,再根据交线是两平面的共 有线,求出另外的投影。
平 面 投 影 图
应 用 举 例
2. 投影面平行面
正平面
轴 测 投 影 图 平 面 投 影 图
第三章 建筑间距
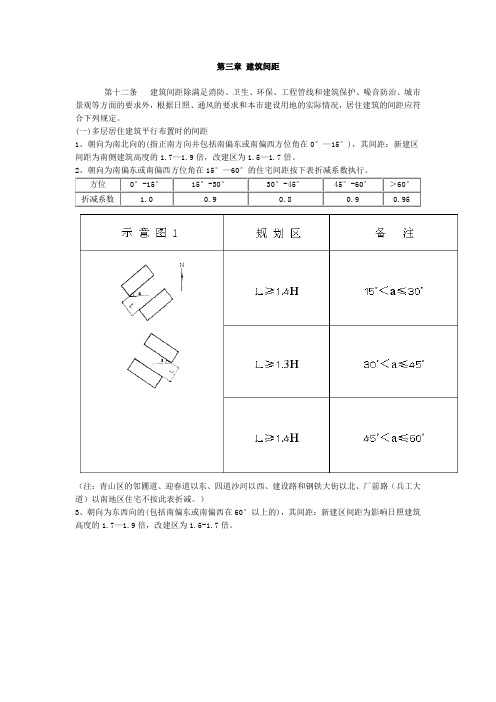
第三章建筑间距第十二条建筑间距除满足消防、卫生、环保、工程管线和建筑保护、噪音防治、城市景观等方面的要求外,根据日照、通风的要求和本市建设用地的实际情况,居住建筑的间距应符合下列规定。
(一)多层居住建筑平行布置时的间距1、朝向为南北向的(指正南方向并包括南偏东或南偏西方位角在0°—15°),其间距:新建区间距为南侧建筑高度的1.7—1.9倍,改建区为1.5—1.7倍。
2、朝向为南偏东或南偏西方位角在15°—60°的住宅间距按下表折减系数执行。
(注:青山区的邻圃道、迎春道以东、四道沙河以西、建设路和钢铁大街以北、厂前路(兵工大道)以南地区住宅不按此表折减。
)3、朝向为东西向的(包括南偏东或南偏西在60°以上的),其间距:新建区间距为影响日照建筑高度的1.7—1.9倍,改建区为1.5-1.7倍。
4、低层住宅和多层住宅间距按本项1—3项执行。
5、在核算多层、低层条式住宅建筑间距时,当阴台或阳台累计长度大于(等于)居住建筑长度的1/2时,按本项1—4项执行,应自遮挡建筑物的主体算至被遮挡建筑物的阳台;当阴台或阳台累计长度小于居住建筑长度的1/2时,按本款1—4执行,应自遮挡建筑物的主体算至被遮挡建筑物的主体。
6、在核算建筑间距时,建筑高度按以下规定计算(1)平屋面至女儿墙顶,无女儿墙算至檐口。
(2)坡屋面北坡屋顶坡度小于35°,高度计算至檐口;大于35°时,屋脊线平行于相关建筑的算至屋脊线,垂直于相关建筑的算至山墙斜坡高度的中点。
㈡低层、多层居住建筑垂直布置且居住建筑的短边与另一建筑长边重合大于(等于)短边的1/2时,应符合下列规定,小于1/2的不计遮挡因素。
1、低层、多层居住建筑南北向垂直布置时,其间距不得小于遮挡建筑高度的1.0倍。
2、低层、多层居住建筑东西向垂直布置时,其间距不得小于东侧建筑的0.8倍。
3、低层、多层居住建筑当其山墙宽度大小14米时,则按平行布置间距规定控制。
建筑装饰设计 第3章 建筑装饰设计与相关学科

建筑装饰设计
(五)厨房家具
在进行厨 房设计时,首 先应考虑合理 的作业流程。
图计。厨柜一般分为低柜和吊 柜两种形式,设计可参考柜子的设计,
图3-15 厨柜厚度的设计
建筑装饰设计
第二节 建筑装饰设计与环境心理学
一、符合行为模式和心理特征的设计
90° 98° 104° 105° 95° 98° 105° 110° 104° 94°
下部 支撑点的高度
— — — — 190 mm 250 mm 190 mm 250 mm 190 mm 250 mm
支撑面的角度
— — — — 100° 94° 94° 104° 105° 129°
建筑装饰设计
动范围、人的活动方向等内容构成,是影响室内空间造型、 几何尺寸的重要因素。 1.静点位置
通过分析静点位置,可以使功能分区更合理,而且还可 以结合人的活动尺度对静电位置的周围空间进行布置。
2.人体三维活动范围 人体三维活动范围是指人的上下、左右、前后正常活动
范围和极限。通过人体三维活动范围的研究,可以在满足人 们正常活动的情况下尽量的节约空间
(一)人与环境因素 设计要以人为本,设计者就要对所设计的室内空间的
各种有损健康的因素加以限制。这种危害可能来自噪声污 染、光污染、辐射污染、视觉污染、温差影响等,设计者 可以通过人体工程学的研究为室内装饰设计提供科学的依 据。
建筑装饰设计
(二)人与空间因素 人体空间一般是由人在室内的静点位置、人体三维活
(三)智能玻璃幕墙技术
智能玻璃幕墙属于智能建筑的一部分,它从广义上包 括玻璃幕墙、通风系统、空调系统、环境监测系统、楼宇 自动控制系统。其技术核心是一种有别于传统幕墙的热通 道幕墙。它主要由一个单层玻璃幕墙和一个双层玻璃幕墙 组成。
第三章 几何元素间的相对位置

第3章 几何元素间的相 对位置
主讲:黎启柏 2009.8
3.1 平行问题
3.1.1直线与直线平行 1)对一般直线,只要两直线的同名投影平行 就能确定空间中两条直线平行 2)对投影面的平行线,这样的条件不够
对投影面的平行线
与投影面平行的直线
只有两直线的同名投影 平行不能确定空间中两 条直线平行 如何确定某一直线为特 殊直线?
此定理可推广到 正平面和侧平面
此定理可推广到正平面和侧平面
推论:若一直线垂直于平面,则此直线的各 若一直线垂直于平面,
的投影一定垂直于该平面的同名迹线
例3-8:过点M作直线垂直于平面ABC
解:作正平线AE和水平线CF, 则所求直线MN⊥AE和CF, 于是过m作mn⊥cf,m’n’⊥a’e’为所求
例3-13 过直线MN作一平面,垂直 于△ABC确定的平面
想法:在直线上找一 点做平面ABC的垂线, 即此垂线和MN确定 的平面为所求解: 1)在△ABC上容易作 水平线AD和正平线A E 2)作 mk⊥ad,m’k’⊥a’e’ 3)MN和MK确定的平△ABC确定的平面
1)直线与直线相交如果2直线相交,则各个投影面上的同名投影也相 交,且这些交点符合空间点的投影规律
2)两直线交叉-既不平行也不相交
如果2直线交叉,则投影面上的同名投影也可能相交, 但这些交点不符合空间点的投影规律 应用重影点可以方便地判断两直线的空间位置
3.2.2 直线与平面相交
直线若与平面不平行就必然 相交,交点称穿点 1)平面为特殊位置平面 若平面为特殊位置平面,可 利用投影的积聚性,简便地 求出穿点 例:ABC为水平面,MN为直 线,求穿点? 被平面遮挡部分为不可见线 段,用虚线表示,以提高投 影图的表现力 可见性判断方法:从正面投 影向下看
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(三)垂直问题
掌握线面垂直、面面垂直的投影特性及作图方法。
(四)点、线、面综合题
1.熟练掌握点、线、面的基本作图方法; 2.能对一般画法几何综合题进行空间分析,了解综合题的一般解题 步骤和方法。
3. 1 平行问题
• 直线与平面平行
• 两平面平行
3.1.1 直线与平面平行
A B
C
若:AB∥CD 则:AB∥P
a
n● d(e) m
●
2 ● h(f)
●
作图 ① 求交线 ② 判别可见性
c
b
1
点Ⅰ在MC上,点Ⅱ在 FH上,点Ⅰ在前,点Ⅱ在 后,故mc 可见。
⑶
f a f m● a d m d ●
b k● n'
●
投影分析
ΔDEF的正面投影积聚
e
作图
① 求交线
c b
●
k
●
n
c
N点的水平投影n位于 Δdef 的外面,说明点N位 于ΔDEF所确定的平面内 e ,但不位于ΔDEF这个图 形内。 所以ΔABC和ΔDEF的 交线应为MK。 ② 判别可见性
例4 求两平面的交线
PV n
2
1
m m
k
l
QV
两一般位置平 面相交,求交 线步骤: 1.用求直线 与平面交点的 方法,作出两 平面的两个共 有点K、E。 2.连接两个 共有点,画出 交线KE。
eห้องสมุดไป่ตู้
2
e k l
1
示意图
n
两一般位置平面相交求交线的方法 示意图
B M 利用求一般位置 线面交点的方法找出 交线上的两个点,将 其连线即为两平面的 交线。
2
k
示意图
1
以正垂面为辅助平面求线面交点
示意图
A
Ⅱ
F
C
Ⅰ
B
E
过EF作正垂面Q
以铅垂面为辅助平面求直线EF与ΔABC平面的交点
步骤: 2’ k 1’ PH 1 k 2 1.过EF作铅 垂平面P。 2.求P平面与 ΔABC的交线 ⅠⅡ。 3.求交线 ⅠⅡ与EF的交 点K。
示意图
以铅垂面为辅助平面求线面交点
A E
示意图
K E Ⅰ
Ⅱ F
C
B
F
过EF作铅垂面P
直线EF与平面 ABC相交,判别可见性。
f
( 2 )
1 k 3 4 利 用 重 影 点 判 别 可 见 性
e
2
k 1
4 (3 )
示意图 e
直线EF与平面 ABC相交,判别可见性。
利 用 重 影 点 判 别 可 见 性
1 (2)
[例5]试过K点作一直线平行于已知平面ΔABC,并与直线EF 相交 。
综合性问题解法
分析
过已知点K作平面P平行于 ABC;直线EF与平面P交于H; 连接KH,KH即为所求。 K F H E
作图
PV m 1 2 n
1.过点K作平面 KMN// ABC平面。
2.求直线EF与平面 KMN的交点H 。
e n c f
d
●
① 求交线 ② 判别可见性
从正面投影上可看出,在交 线左侧,平面ABC在上,其水 平投影可见。
m
b
还可通过重影点 判别可见性
⑵
空间及投影分析:
d′
a′
●
h′
m′
●
b′ e′
X
n′
●
1'(2')
f′
c′
平面DEFH是一铅垂面, 它的水平投影有积聚性,其 与ac、bc的交点m 、n 即为 两个共有点的水平投影,故 mn即为交线MN的水平投影。
C A B a(b) c d D F e(f) h(g) G a(b) E H a' d' b' X c e(f) d h(g) f' g' O c' e' h'
当平面为投影面的垂直面时,只要平面有积聚性的投影和直 线的同面投影平行,或直线也为该投影面的垂线,则直线与平面 必定平行。
3.1.2 两平面平行
② 判别两平面之间的相互遮挡关系,即: 判别可见性。
特殊位置线面相交
直线与特殊位置平面相交 判断直线的可见性 特殊位置直线与一般位置平面相交
3.2.1直线与特殊位置平面相交
交点的一个投影是平面积聚性投影与直线的同面投影的 交点,另一个投影可在直线的另一个投影上找到。
V
P B
b'
F a' k'
f'
A
E a e
k C
b k c
e'
a f PH H e
c'
f
b
k c
— 判断直线的可见性
利用积聚性直接 判断出可见性
V
b' k'
f'
P B
F a'
A
E a e
k C
b k c
e'
a f PH H e
c'
f
b
k c
例1 求直线MN与平面ABC的交点K并判别可见性。
⑴ 平面为特殊位置
b
1(2)
●
k' 1' (2' )
2
k1
3.2.2 一般位置平面与特殊位置平面相交
求两平面交线的问题可以看作是求两个 共有点的问题,由于特殊位置平面的某个投 影有积聚性,交线可直接求出。
1.求交线 2.判断平面的可见性
—— 求交线
m
M B K F m C c PH P
b
f n k l
c
a k b
b c d
X
e
f a
X
b c d
f
d
e g
a c a b d e f
a
c
b
f e
g
两一般位置平面平行
两特殊位置平面平行
[例1] 判断平面ABDC与平面EFHM是否平行,已知 AB∥CD∥EF∥MH
a c m e k f
h
O
X
b b
d
d
f k m
由于ek 不平行 于ac,故 两平面 不平行
空间及投影分析:
n
a
X
k ●
m
m a
2 ●
●
c
c n
平面ABC是一铅垂面, 其水平投影积聚成一条直 线,该直线与mn的交点即 为K点的水平投影。
① 求交点 ② 判别可见性 由水平投影可知,KN 段在平面前,故正面投影 上kn为可见。
●
k 1 b
还可通过重影点 判别可见性。
—直线为特殊位置 b k a
c
b n
例7
试过定点K作特殊位置平面的法线。
h
PV k
SV k h
h
k
k
k h QH h k
h
例8 平面由两平行线AB、CD给定,试判断直线MN 是否垂直于定平面。
a
e b X d f
c
m
n O m
b
e d
a
c f
n
3.3.2 两平面垂直
A
P
B
几何条件:若一直线垂直于一定平面,则包含这条直线的所 有平面都垂直于该平面。
Ⅱ Ⅰ Ⅲ
Ⅳ 3
示意图
(4)
3.2.4 两一般位置平面相交
求两平面交线的问题可以看作是求两个 共有点的问题, 其作图方法可以有:
1.利用求一般位置线面交点的方法找出交线上 的两个点,将其连线即为两平面的交线。 2.用三面共点的方法找出交线上的两个点,将 其连线即为两平面的交线。
•两一般位置平面相交求交线 •判别可见性
A A
Ⅰ Ⅱ
B
Ⅰ
B
Ⅱ
两平面垂直 两平面不垂直
反之,两平面相互垂直,则由属于第一个平面的任意一 点向第二个平面作的垂线必属于第一个平面。
例10 平面由 BDF给定,试过定点K作已知平面的垂面
h
f c g k b O g b h
h
3.连接KH,KH即 为所求。
h
n
2
m 1
3.3 垂直问题
直线与平面垂直
两平面互相垂直
3.3.1 直线与平面垂直
V
A
C E B D
几何条件:若一直线垂直于一平面,则必垂直于属于该平面 的一切直线。
n
V
A C E a
k d
e
c
b
X
B
a k n d e
O
D
c
b
定理1:若一直线垂直于一平面、则直线的水平投影必垂直于属 于该平面的水平线的水平投影;直线的正面投影必垂直 于属于该平面的正平线的正面投影。
几何条件: 若一个平面内的相交两直线与另一个 平面内的相交两直线对应平行,则此两平 面平行。这是两平面平行的作图依据。 两平面平行的作图问题有: 判别两已知平面是否相互平行; 过一点作一平面与已知平面平行; 已知两平面平行,完成其中一平面的 所缺投影。
两平面平行
Ⅰ
Ⅱ
Ⅲ
AB∥ⅠⅡ;AC∥ⅠⅢ; 则:P∥Q
a l
A L
N b n k a l
m
f c
n
f
— 判断平面的可见性
例3 求两平面的交线, MN并判别可见性。 ⑴ a
d a
●
b m(n) e ●
f c
空间及投影分析:
平面ABC与DEF都为 正 垂面,它们的交线为一条正垂 线,两平面正面投影的交点即 为交线的正面投影,交线的水 平投影垂直于OX轴。
