第一章习题解答
第一章 习题答案

第一章 习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a ,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1-1 所示。
1-2 题1-2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电解 c u 增高,偏差电压 r 。
此时,-=r e u u 使c u 过程:系统中,加热炉是被控对象,炉温是被控量,给定量是由给定电位器设定的电压r u (表征炉温的希望值)。
系统方框图见图解1-3。
1-4 题1-4图是控制导弹发射架方位的电位器式随动系统原理图。
图中电位器1P 、2P 并联后跨接到同一电源0E 的两端,其滑臂分别与输入轴和输出轴相联结,组成方位角的给定元件和测量反馈元件。
输入轴由手轮操纵;输出轴则由直流电动机经减速后带动,电动机采用电枢控制的方式工作。
试分析系统的工作原理,指出系统的被控对象、被控量和给定量,画出系统的方框图。
题1-4图 导弹发射架方位角控制系统原理图解 当导弹发射架的方位角与输入轴方位角一致时,系统处于相对静止状态。
当摇动手轮使电位器1P 的滑臂转过一个输入角i θ的瞬间,由于输出轴的转角i o θθ≠,于是出现一个误差角o i e θθθ-=,该误差角通过电位器1P 、2P 转换成偏差电压o i e u u u -=,e u 经放大后驱动电动机转动,在驱动导弹发射架转动的同时,通过输出轴带动电位器2P 的滑臂转过一定的角度o θ,直至i o θθ=时,o i u u =,偏差电压0=e u ,电动机停止转动。
这时,导弹发射架停留在相应的方位角上。
只要o i θθ≠,偏差就会产生调节作用,控制的结果是消除偏差e θ,使输出量o θ严格地跟随输入量i θ的变化而变化。
电路理论习题解答 第一章

1.5
u /V
内阻不为零
+ us
R0
I
+
u
RL
−
伏安关系曲线
−
I/A 0.15
0
1.5
u /V
注:这里的伏安关系曲线只能在第一象限,原因也是,一旦出了第一象限, u 和 I 的比值就 变为负的了,反推出的 RL 就变为负值了,与题意不符。
V
V
1.5V
1.5V
R 内阻为零时 内阻不为零时
R
1-9 附图是两种受控源和电阻 RL 组成的电路。现以 RL 上电压作为输出信号,1)求两电路的电 压增益(A,gmRL);2)试以受控源的性质,扼要地说明计算得到的结果。
1) 如果不用并联分压(在中学就掌握的东西),当然也可以用两个回路的 KVL 方程和顶部 节点的 KCL 方程,得出上面的 H(jω)的表达式,但是显然这样做是低效的。 2) 事实上,本课程的目的是希望学习者能够根据不同的题目,尽可能采用多种方法中的一 种最简单的方法去解决问题。因此, a) 只要没有要求,任意的逻辑完整的解题思路都是可取的; b) 学习者可以视自己的练习目的选择一种简单熟悉的方法、或者一种较为系统的方法、 或者多种方法来完成习题。
第一章习题答案 1-1 已知电路中某节点如图,I1=-1A,I2=4A,I4=-5A,I5=6A,用 KCL 定律建立方程并求解 I3 ( 4A )
图 1-1 解:由 KCL 定律:任一集中参数电路中的任一节点,在任一时刻,流入该节点的电流之和与 流出该节点的电流之和相同。 即: I1+I3+I4+I5=I2 =〉-1+(-5)+6+I3=4 =〉I3=4(A)
1 2
第一章部分习题解答

第一章部分习题解答1.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z ,知321z z z Δ的三个顶点均在单位圆上。
因为 33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+−+−=21212z z z z ++=所以, 12121−=+z z z z ,又 )())((122122112121221z z z z z z z z z z z z z z +−+=−−=−()322121=+−=z z z z故 321=−z z ,同理33231=−=−z z z z ,知321z z z Δ是内接于单位圆1=z 的一个正三角形。
2.证明:z 平面上的直线方程可以写成C z a z a =+(a 是非零复常数,C 是实常数) 证 设直角坐标系的平面方程为C By Ax =+将)(i 21Im ),(21Re z z z y z z z x −==+==代入,得C z B A z B A =−+−)i (21)i (21令)i (21B A a +=,则)i (21B A a −=,上式即为C z a z a =+。
3.求下列方程(t 是实参数)给出的曲线。
(1)t z i)1(+=; (2)t b t a z sin i cos +=;(3)t t z i+=; (4)22it t z +=,解(1)⎩⎨⎧∞<<−∞==⇔+=+=t t y tx t y x z ,)i 1(i 。
即直线x y =。
(2)π20,sin cos sin i cos i ≤<⎩⎨⎧==⇔+=+=t t b y ta x tb t a y x z ,即为椭圆12222=+b y a x ;(3)⎪⎩⎪⎨⎧==⇔+=+=t y t x t t y x z 1ii ,即为双曲线1=xy ; (4)⎪⎩⎪⎨⎧==⇔+=+=22221ii t y t x t t y x z ,即为双曲线1=xy 中位于第一象限中的一支。
物理化学 答案 第一章_习题解答

-
知此气体的 Cp,m=29.10 J·K 1,求过程的ΔU、ΔH、Q 和 W 。 解: (1)等容
ΔU = n ⋅ Cv ,m (T2 − T1 ) = 1 × (29.1 − 8.314) × 75 = 1559 J ΔH = n ⋅ C p ,m (T2 − T1 ) = 1 × 29.1 × 75 = 2183 J
η = −Wr / Q1 = (T1 − T2 ) / T1 = (500 − 300) / 600 = 40%
第二个卡诺热机效率
η ′ = −Wr / Q1′ = (T1 − T2′) / T1 = (500 − 250) / 600 = 50%
∵
η =η′
∴两个热机的效率不相同
(2)第一个热机吸收的热量: Q1 =
γ =1.4,试求 Cv,m。若该气体的摩尔热容近似为常数,试求在等容条件下加热该气体至 t2=
80℃所需的热。 解:∵ γ =
C p,m Cv , m
=
Cv , m + R Cv , m
= 1.4
∴ Cv, m =
R
γ
=
8.314 = 20.79 J ⋅ K -1 ⋅ mol-1 0.4
Qv = n ⋅ Cv ,m ⋅ ΔT = =
4
3 3 ⎧ ⎧ ⎪V1 = 5dm ⎪V2 = 6dm Q (可 ) = 0 ⎯⎯⎯⎯ → ⎨ ⎨ ⎪T1 = 298.15 K ⎪T2 = 278.15 K ⎩ ⎩
由理想气体绝热可逆过程方程式可知
T2 / T1 = (V1 / V2 ) Cv ,m =
R / Cv , m
运筹学教程(第三版)习题答案(第一章)

b 3/2 1
c x1 0 1 0
d x2 1 0 0
0 x3 5/14
0 x4 -3/4
-2/14 10/35 -5/14d+2/14c 3/14d-10/14c
School of Management
运筹学教程
第一章习题解答
之间时最优解为图中的A点 当c/d在3/10到5/2之间时最优解为图中的 点 ; 当 在 到 之间时最优解为图中的 c/d大于 且c大于等于 时最优解为图中的 点;当c/d 大于5/2且 大于等于 时最优解为图中的B点 大于等于0时最优解为图中的 大于 小于3/10且 d大于 时最优解为图中的 点 ; 当 c/d大于 大于0时最优解为图中的 小于 且 大于 时最优解为图中的C点 大于 5/2且c小于等于 时或当 小于 小于等于0时或当 小于3/10且d小于 时最优解 小于0时最优解 且 小于等于 时或当c/d小于 且 小于 为图中的原点。 为图中的原点。
page 7 14 March 2012
School of Management
运筹学教程
第一章习题解答
对下述线性规划问题找出所有基解, 1.3 对下述线性规划问题找出所有基解,指出哪 些是基可行解,并确定最优解。 些是基可行解,并确定最优解。
max Z = 3 x1 + x 2 + 2 x 3 12 x1 + 3 x 2 + 6 x 3 + 3 x 4 = 9 8 x + x − 4 x + 2 x = 10 1 2 3 5 st 3 x1 − x 6 = 0 x j ≥ 0( j = 1, L , 6) ,
School of Management
《电磁场与电磁波》课后习题解答第一章

n(x2
y2
z2)
(x2 y2 z2)2 (x2 y2 z2)
(n 3)rn
【习题 1.20 解】
1
已知 r (x2 y2 z2 )2
r xex yey zez
所以
(1)
r
(ex
x
ey
y
ez
z
)
(
xex
yey
zez )
ex ey ez
xyz
Bx ex By ey Bz ez
取一线元: dl exdx eydy ezdz
则有
B dl
ex ey ez Bx By Bz 0 dx dy dz
则矢量线所满足的微分方程为
dx dy dz Bx By Bz
或写成
dx dy dz =k(常数) a2 z a3 y a3x a1z a1 y a2x
对(3)(4)分别求和
(4)
d (a1x) d (a2 y) d (a3 z) 0 xdx ydy zdz 0
d (a1x a2 y a3 z) 0 d(x2 y2 z2) 0
所以矢量线方程为
a1x a2 y a3 z k1
x2 y2 z2 k2
【习题 1.6 解】
ex ey ez A B (ex 9ey ez ) (2ex 4ey 3ez ) 1 9 1
2 4 3
31ex 5ey 14ez
【习题 1.3 解】
已知 A ex bey cez , B ex 3ey 8ez ,
(1)要使 A B ,则须散度 A B 0
所以从 A B 1 3b 8c 0 可得: 3b 8c 1
即 12ex 9ey ez • aex bey 12a 9b 0 ⑴
物理初二第一章练习题答案

物理初二第一章练习题答案1. 速度和加速度的关系根据物理学的基本概念,速度是物体运动的一个重要参量,而加速度则表示物体速度变化的快慢。
在初二的物理学习中,我们常常需要研究速度和加速度之间的关系。
以下是第一章练习题的答案:题目1:一个从静止开始的物体以恒定的加速度3 m/s²沿着一条直线运动,求它在5秒后的速度是多少?答案:根据物理学中的加速度公式v = u + at,其中v是末速度,u是初速度,a是加速度,t是时间。
给定初速度u=0,加速度a=3 m/s²,时间t=5秒。
代入公式计算可得v = 0 + 3 × 5 = 15 m/s。
题目2:一辆汽车在道路上以25 m/s的速度匀速行驶,经过10秒后它的位置是多少?答案:根据物理学中的位移公式s = ut,其中s是位移,u是速度,t 是时间。
给定速度u=25 m/s,时间t=10秒。
代入公式计算可得s = 25 ×10 = 250 m。
题目3:一个物体的速度从10 m/s增加到20 m/s,经过2秒的时间,求它的加速度是多少?答案:根据物理学中的加速度公式a = (v - u) / t,其中a是加速度,v是末速度,u是初速度,t是时间。
给定初速度u=10 m/s,末速度v=20 m/s,时间t=2秒。
代入公式计算可得a = (20 - 10) / 2 = 5 m/s²。
2. 动量守恒定律在物理学中,动量守恒定律是一个重要的原理,它指出在一个系统内,所有物体的总动量在没有外力作用的情况下保持不变。
以下是第一章练习题中涉及到动量守恒定律的答案:题目1:一辆质量为1000 kg的小轿车以20 m/s的速度向东行驶,和一辆质量为1500 kg的卡车以15 m/s的速度向东行驶发生碰撞,碰撞后两车结合在一起,求结合后的速度是多少?答案:根据动量守恒定律,碰撞前的总动量等于碰撞后的总动量。
小轿车的动量为mv1,卡车的动量为mv2,碰撞后的总动量为(m1 +m2)v。
《初等数论》各章习题参考解答

《初等数论》各章习题参考解答第一章习题参考解答1.解:因为25的最小倍数是100,9的最小倍数是,所以满足条件的最小正整数11111111100a =。
2.解:3在100!的分解式中的指数()1001001001003100!33113148392781⎡⎤⎡⎤⎡⎤⎡⎤=+++=+++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦, 在100!的分解式中的指数()1001001001001002100!50251261942481664⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++=++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,∴ ()9448474847100!2343123,,61k k k k =⋅⋅=⋅⋅=⋅=。
故 max 47n =,min 3M k =,(),61k =。
故 当M 最小值是3的倍数,但不是2的倍数。
3.解:112121n n n n x x ++++++等价于()()21221n n n x x x ++-+-,从而3x ³(n 就不会太大,存在反向关系)。
由()()22121n nn x x x -+-?+,得()()2212n n n x x -+?,即()()()121122nn x x -+?。
若2n ³,则()()()()251221114242nn x xx x-?+??,导致25140x x -+?,无解。
所以,只有1n =,335314x x x +-?,只能是37,14x +=,从而4,11x =。
综上所述,所求正整数对()()(),4,111,1x n =、。
4.解:按题意,2m n >>,记*,m n k k N =+?;则()222211111n n k nk n k k a a a a a a a a a a a a +++-+-?-+--++-22211111n k k n k k a a a a a a a a a ++?---+?-+-,故 存在无穷多个正整数a 满足2111n k k a a a a ++-+-。
(完整版)自动控制原理_第一章课后习题解答

第一章1.1 图1.18是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变,试说明系统工作原理并画出系统方块图。
c+-SM___ 1Q浮浮浮浮浮浮2Q浮浮浮浮浮浮浮浮浮浮浮浮fi-+解:系统的控制任务是保持液面高度不变。
水箱是被控对象,水箱液位是被控变量。
电位器用来设置期望液位高度*c(通常点位器的上下位移来实现) 。
当电位器电刷位于中点位置时,电动机不动,控制阀门有一定的开度,使水箱的流入水量与流出水量相等,从而使液面保持在希望高度*c上。
一旦流出水量发生变化(相当于扰动),例如当流出水量减小时,液面升高,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一定的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液体流量减少。
这时,水箱液位下降.浮子位置相应下降,直到电位器电刷回到中点位置为止,系统重新处于平衡状态,液位恢复给定高度。
反之,当流出水量在平衡状态基础上增大时,水箱液位下降,系统会自动增大阀门开度,加大流入水量,使液位升到给定高度*c。
系统方框图如图解1. 4.1所示。
1.2恒温箱的温度自动控制系统如图1.19所示。
(1) 画出系统的方框图;(2) 简述保持恒温箱温度恒定的工作原理;(3) 指出该控制系统的被控对象和被控变量分别是什么。
M放大器电机减速器调压器 220~热电偶电阻丝- +- +图1.19 恒温箱的温度自动控制系统解:恒温箱采用电加热的方式运行,电阻丝产生的热量与调压器电压平方成正比,电压增高,炉温就上升。
调压器电压由其滑动触点位置所控制,滑臂则由伺服电动机驱动.炉子的实际温度用热电偶测量,输出电压作为反馈电压与给定电压进行比较,得出的偏差电压经放大器放大后,驱动电动机经减速器调节调压器的电压。
在正常情况下,炉温等于期望温度T ,热电偶的输出电压等于给定电压。
此时偏差为零,电动机不动,调压器的滑动触点停留在某个合适的位置上。
运筹学教程(第三版)习题答案(第一章)

x1 0 0 0 0.75
maxZ 3x1 x2 2x3
12x1 3x2 6x3 3x4 9
(1)
st
8x1 3x1
x2 x6
4x3 0
2x5
10
xj 0( , j 1, ,6)
基可行解
x2
x3
x4
x5
x6
3 0 0 3.5 0
0 1.5 0 8 0
00350
0 0 0 2 2.25
运筹学教程
第一章习题解答
讨论cl.,5d的上值题如(1何)中变,化若,目使标该函问数题变可为行m域ax的Z每=个cx顶1 +点d依x2, 次使目标函数达到最优。
解:得到最终单纯形表如下:
Cj→
c
CB 基 b x1
d x2 3/2 0
c x1 1 1
j
0
d
0
0
x2
x3
x4
1
5/14
-3/4
0
-2/14
X 0是 max Z CX 的最优解,故
CX 0 CX * 0;
X *是 max Z C * X 的最优解,故
C * X * C * X 0 0;
(C * C )( X * X 0 )
C(X 0 X *) C*(X * X 0) 0
page 24 5/25/2020
School of Management
C T X ( 2 ) , 所以 X 也是最优解。
page 23 5/25/2020
School of Management
运筹学教程
第一章习题解答
1.10 线性规划问题max Z=CX,AX=b,X≥0,设 X0为问题的最优解。若目标函数中用C*代替C后,问题 的最优解变为X*,求证
基础化学习题解答(第一章)

习题解答(第一章物质结构基础)思考与习题1.填空题(1)原子核外电子运动具有波粒二象性、能量变化不连续的特征,其运动规律可用量子力学来描述。
(2)当主量子数为3时,包含有3s、3p、3d三个亚层,各亚层为分别包含1、3、5个轨道,分别能容纳2、6、10个电子。
(3)同时用n、l、m和m s四个量子数可表示原子核外某电子的运动状态;用n、l、m 三个量子数表示核外电子运动的一个轨道;而n、l两个量子数确定原子轨道的能级。
(4)改错的现象称为能级交错。
3d4S(6)原子序数为35的元素,其基态原子的核外电子分布式为1s22s22p63s23p63d104s24p5,用原子实表示为[Ar]3d104s24p5,其价电子构型为4s24p5,价电子构型的轨道表示式为;该元素位于元素周期表的第ⅦA 族,第四周期,元素符号是Br 。
(7)等价轨道处于全充满(p6、d10、f14)、半充满(p3、d5、f7)和全空(p0、d0、f0)状态时,具有较低的能量,比较稳定。
这一规律通常又称为洪德规则的特例。
(8)原子间通过共用电子对而形成的化学键,叫做共价键。
共价键的本质是原子轨道的重叠,其形成条件是两个具有自旋相反单电子的原子轨道,尽可能达到最大重叠。
(9)表征化学键性质的物理量,统称为键参数,常用的有键能、键长、键角。
(10)H2S分子的构型为V形,中心原子S采取sp3不等性杂化,键角∠HSH<109°28′(提示:填写>,=或<)。
(11)完成下表2.选择题(1)下列原子轨道中,属于等价轨道的一组是( C )。
A .2s ,3sB .2p x ,3p xC .2p x ,2p yD .3d xy ,4d xy(2)下列用一套量子数表示的电子运动状态中,能量最高的是( B )。
A .4,1,-1,-12B .4,2,0,-12C .4,0,0,+12D .3,1,1,+12(3)下列不存在的能级是( C )。
第一章习题解答及参考答案

∫
−∞
sin (ωx ) d x =1 πx x
又有
ω x ω sin π ( ω π x ) = ω sin c ω sin = π (ω π x ) π πx π π sin (ωx ) ∞ = ω →∞ πx 0 lim x=0 x≠0
∞
∞ ∞ x comb eiπx = ∑ δ ( x − m )eimπ = ∑ δ ( x − m )cos mπ 2 m = −∞ m = −∞
当 m = 奇数时, comb( x ) + comb( x )e
iπx
=0;
∞
当 m = 偶数时,令 m = 2n ,则 cos 2πx = 1 ,并且有:
1 2 1 − 2
dξ = 1 5 −x 2
3 5 ≤ x ≤ 时(见图(c)), 2 2
∫1Biblioteka 2 x−2dξ =④ 当x>
5 1 和 x < − 时,重叠面积等于零。 2 2
卷积后所得图形如附图 1-3 所示。
附图 1-3 习题[1-5](2)卷积结果的函数图形
[1-6]试用卷积定理计算下列各式。 (1) sinc ( x ) ∗ sinc ( x ) (2) F sinc ( x ) sinc ( 2 x )
∞ 1/ 2 x − ξ −1 x − ξ −1 x −1 dξ = ∫− ∞ rect(ξ ) rect dξ = ∫−1 / 2 rect 2 2 2
其中
x − ξ − 1 1 x − 2 ≤ ξ ≤ x rect = 2 其他 0 1 1 1 1 3 1 ≤ ξ ≤ ;当 ξ = − 时有 − ≤ x ≤ ,而当 ξ = 时有 2 2 2 2 2 2
《一元函数微积分》习题解答第一章

《一元函数微积分》 习题1—11.确定下列函数的定义域: (1)912-=x y ;解:要使函数有意义,则:092>-x 即 3>x 或3-<x .所以函数定义域:),3()3,(+∞⋃--∞.(2)x y a arcsin log =;解:要使函数有意义,则0arcsin >x ,即10≤<x .所以函数定义域:(0,1]. (3)2111x x y --+=; 解:01012≠+≥-x x 且,即111-≠≤≤-x x 且.所以函数定义域:(-1,1].(4))32(log 213-+-=x x y a ; 解:03202>-≠-x x 且,即232>≠x x 且.所以函数定义域:),2()2,23(+∞⋃. (5))4(log 21arccos 2x x y a -+-=; 解:0412112>-≤-≤-x x 且,则2231<<-≤≤-x x 且。
所以函数定义域:)2,1[- (6)xy πsin 1=.解:0sin ≠x π,则Z k k x ∈≠,.(其中是Z 整数集),函数定义域:_Z 或}{Z k k x x ∈≠,.2.求函数⎪⎩⎪⎨⎧=≠=000,1sin x x xy 的定义域和值域,并求⎪⎭⎫⎝⎛π2f 和)0(f . 解:定义域:),(+∞-∞. 当0≠x 时,01≠x ,故11sin 1≤≤-x. 所以值域:[-1,1]. 12sin )2(==ππf ,0)0(=f .3.下列各题中,函数)(x f 和)(x g 是否相同,为什么? (1) 2)(,)(x x g x x f ==;解: 不同 因为||)(2x x x g ==,即)(x g 的值域是全体非负实数,而)(x f 的值域是全体实数.(2) 2sin 21)(,cos )(2x x g x x f -==; 解: 相同因为)(x f 和)(x g 的定义域均为实数R ,值域为[-1,1],且)(cos 2sin21)(2x f x xx g ==-= (3)1)(,11)(2-=+-=x x g x x x f ; 解: 不同因为)1(111)(2≠-=+-=x x x x x f .两函数的定义域不同. (4)0)(,)(x x g xxx f ==. 解: 相同因为)0(1)(),0(1)(0≠==≠==x x x g x xxx f 定义域均为非零实数,在定义域内函数值恒等于1.4.设x x f sin )(=, 证明:)2cos(2sin2)()(x x x x f x x f ∆+∆=-∆+. 证明: 由三角函数知:)2cos(2sin 2sin )sin()()(xx x x x x x f x x f ∆+∆=-∆+=-∆+.5.设5)(2++=bx ax x f 且38)()1(+=-+x x f x f ,试确定a , b 的值.解: 因为 5)(2++=bx ax x f故)5()2(5)1()1()1(22+++++=++++=+b a x b a ax x b x a x f 由题设3852)()1(+=++=-+x a ax x f x f 所以有:82=a 且3=+b a 得:1,4-==b a .6.下列函数哪些是偶函数? 哪些是奇函数?哪些既非奇函数又非偶函数? (1) )1(22x x y -=; 解: 定义域:),(+∞-∞)()1(])(1[)()(2222x f x x x x x f =-=---=-所以函数是偶函数. (2)323x x y -=; 解: 定义域:),(+∞-∞32323)()(3)(x x x x x f +=---=-,)()(x f x f ≠-且)()(x f x f -≠-.所以函数既非奇函数又非偶函数.(3)2211x x y +-=;解: 定义域:),(+∞-∞)(11)(1)(1)(2222x f xx x x x f =+-=-+--=- 所以函数是偶函数. (4))1)(1(+-=x x x y 解: 定义域:),(+∞-∞x x x x x x f -=+-=3)1)(1()(,)()()()(33x f x x x x x f -=+-=---=-.所以函数是奇函数. (5)1cos sin +-=x x y ; 解: 定义域:),(+∞-∞1cos sin 1)cos()sin()(+--=+---=-x x x x x f ,则)()(x f x f ≠-且)()(x f x f -≠-所以函数既非奇函数又非偶函数.(6)2xx a a y -+=.解: 定义域:),(+∞-∞)(2)(x f a a x f xx =+=--所以函数是偶函数.7.设)(x f 为定义在),(+∞-∞上的任意函数,证明:(1))()()(1x f x f x F -+=为偶函数; (2) )()()(2x f x f x F --=为奇函数.证明: 由题设)(x f 为定义在),(+∞-∞的函数, 则)(),(21x F x F 的定义域也为),(+∞-∞ (1) )()()()()()()(111x F x f x f x F x f x f x F =+-=-⇒-+= ,. 故)(1x F 是偶函数. (2) )()()()()()()(222x F x f x f x F x f x f x F -=--=-⇒--= ,.故)(2x F 为奇函数.8. 证明: 定义在),(+∞-∞上的任意函数可以表示为一个奇函数与一个偶函数和. 证明: 设)(x f 是定义在),(+∞-∞上的任意函数.由7题知 )()()(1x f x f x F -+=为偶函数,)()()(2x f x f x F --=为奇函数. 且 )(21)(21)(21x F x F x f +=. 故命题成立.9. 设)(x f 为定义在),(L L -上的奇函数,若)(x f 在),0(L 上单增, 证明: )(x f 在)0,(L -上也单增.证明: 由题设知对于任意),(L L x -∈有:)()(x f x f -=-不妨设任意的1x ,2x 满足021<<<-x x L , 则012>-<->x x L .)(x f 在),0(L 上单增, 则)()(21x f x f ->- ,)(x f 奇函数)()(),()(2211x f x f x f x f -=--=-∴即 )()(21x f x f ->- )()(21x f x f < 所以)(x f 在)0,(L -上也单增.10. 下列各函数中哪些是周期函数? 对于周期函数,指出其周期: (1) )2cos(-=x y ;解:)2cos()22cos(-=+-x x π, 函数是周期函数且周期π2=T . (2) x y 4cos =; 解: x x x 4cos )24cos()2(4cos =+=+ππ, 函数是周期函数且周期2π=T .(3) x y πsin 1+=;解: )2(sin 1)2sin(1sin 1++=++=+x x x ππππ,函数是周期函数且周期2=T . (4) x x y cos =; 解: 非周期函数 (5) x y 2sin =; 解: )](2cos 1[21)]22cos(1[21)2cos 1(21sin 2ππ+-=+-=-=x x x x , 函数是周期函数且周期π=T . (6) x x y tan 3sin +=解: )32(3sin )23sin(3sin ππ+=+=x x x , )tan(tan π+=x x ,故原函数的周期为两函数x x tan ,3sin 的周期π32和π最小公倍数. 所以周期为π2=T .11. 下列各组函数中哪些不构成复合函数? 把能构成复合函数的写,成复合函数,并指出定义域. (1) 3x y =,t x sin =;解: 构成复合函数t y 3sin =, 定义域: ),(+∞-∞. (2) ua y =,2x u =;解: 构成复合函数2x a y =, 定义域: ),(+∞-∞. (3) u y a log =,232+=x u ;解: 构成复合函数)22(log 2+=x y a , 定义域: ),(+∞-∞. (4) u y =,2sin -=x u ;解: 不构成复合函数u y =要求0≥u , 但是2sin -=x u 的值域:]1,3[--. (5) u y =,3x u =; 解: 构成复合函数3x y =, 定义域: ),0[+∞.(6) u y a log =, 22-=x u .解: 构成复合函数)2(log 2-=x y a , 定义域: ),2()2,(+∞⋃--∞.12. 下列函数是由哪些简单函数复合而成的?(1) 321)1(++=x y ;解: 3u y =,1)1(2++=x u . (2) 2)1(ln 3+=x y ;解: u y 3=, 2v u =, 1ln +=x v .(3) )13(sin 3+=x y ;解: 3u y =, v u sin =, 13+=x v . (4) 32cos log x y a =.解: 3u y =, v u a log =, 2w v =, x w cos =.13. 求下列函数的反函数: (1) x y sin 2=;]2,2[ππ-∈x 解: 原函数的定义域:]2,2[ππ-∈x , 值域:]2,2[-. 反解: 2arcsin yx =. 得反函数: 2arcsinx y =. (2) )2(log 1++=x y a ;解: 原函数的定义域: ),2(+∞-, 值域:),(+∞-∞. 反解: 21-=-y a x .得反函数: 21-=-x ay反函数的定义域),(+∞-∞:, 值域: ),2(+∞-.(3) 122+=x xy .解: 121112112122+-=+-+=+=xx x x x y 由于112>+x, 则11210<+<x . 原函数的定义域: ),(+∞-∞, 值域:.)1,0( 反解: yy x-=12, y y x -=1log 2.得反函数: xx y -=1log 2反函数的定义域: )1,0(, 值域: ),(+∞-∞.14. 某批发商店按照下列价格表整盒在批发销售某种盒装饮料:当购货量小于或等于20盒时,每盒2.50元;当购货量小于或等于50盒时,其超过20盒的饮料每盒2.30元; 当购货量小于或等于100盒时,其超过50盒的饮料每盒2.00元; 当购货量大于100时,其超过100盒的饮料每盒1.80元;设x 是销售量, y 是总价, 试建立总价y 和销售量x 之间的函数关系式,并作出它的图形. 解: 由题知: 当200≤≤x 时, x y 5.2=;当5020≤<x 时, 43.2)20(3.2205.2+=-+⨯=x x y ;当10050≤<x 时, 192)50(2)2050(3.2205.2+=-+-⨯+⨯=x x y ; 当100>x 时, 398.1)100(8.1219+=-+=x x y⎪⎪⎩⎪⎪⎨⎧>+≤<+≤<+≤≤=100398.110050192502043.22005.2x x x x x x x xy 图形(略)15. 设某商品的市场供应函数p p S Q 480)(+-==, 其中Q 为供应量, p 为市场价格. 商品的单位生产成本是1.5元, 试建立总利润L 与市场价格p 的函数关系式. 解: 供应函数p p S Q 480)(+-==则总利润120864)480)(5.1()5.1(2+-=+--=-=p p p p Q p L .16. 用p 代表单价, 某商品的需求函数为p p D Q 500007)(-==, 当Q 超过1 000时成本函数为Q C 2500020+=, 试确定能达到损益平衡的价格 (提示: 当总收入=总成本时,便达到损益平衡).解: 当1000>Q 时 1000500007)(>-==p p D Q 则价格120<p . 达到损益平衡, 则 C pQ =即: )500007(25000202500020)500007(p Q p p -+=+=-039001652=+-p p得282.107165±=p又因为价格120<p , 故59.28=p答: 当需求量超过1000时,达到损益平衡的价格是28.59.17. 在半径为r 的球内嵌入一个内接圆柱, 试将圆柱的体积V 表示为圆柱的高h 的函数, 并求此函数的定义域.解: 设圆柱的半径为R, 则满足4)2(22222h r h r R -=-=圆柱的体积: 3222241)4(h h r h h r h R V ππππ-=-==. 定义域: )2,0(r18. 已知华氏温度F 与摄氏温度℃的线性关系, 在101325帕(一个标准大气压)下, 水的冰点温度不32F 或0℃, 水的沸点温度为212F 或100℃.(1) 写出华氏温度F 与摄氏温度℃的函数关系; (2) 画出该函数的图形;(3) 摄氏20℃相当于华氏几度?解: (1)由华氏温度F 与摄氏温度℃的线性关系, 设当摄氏温度为x ℃时, 华氏温度为y F , 则有关系式 b ax y += 其中a , b 为常数. 由题知:⎩⎨⎧==⇒⎩⎨⎧+=+⋅=328.1100212032b a b a b a 函数关系: 328.1+=x y (其中x 的度量单位是℃, y 的度量单位是F) (2) 函数图形(略)(3) 摄氏20℃时, y =1.8⨯20℃+32=68(F) 习题1-2 1.(1)0;(2)1;(3)-1;(4)发散 2.(1)证明:0>∀ε,要使ε<=-+nn 1111,即ε1>n 。
完整版高等代数习题解答(第一章)

完整版高等代数习题解答(第一章)高等代数题解答第一章多项式补充题1.当a,b,c取何值时,多项式f(x)=x-5与g(x)=a(x-2)^2+b(x+1)+c(x^2-x+2)相等?提示:比较系数得a=-1,b=-1,c=6.补充题2.设f(x),g(x),h(x)∈[x],f^2(x)=xg^2(x)+x^3h^2(x),证明:假设f(x)=g(x)=h(x)不成立。
若f(x)≠0,则∂(f^2(x))为偶数,又g^2(x),h^2(x)等于或次数为偶数,由于g^2(x),h^2(x)∈[x],首项系数(如果有的话)为正数,从而xg^2(x)+x^3h^2(x)等于或次数为奇数,矛盾。
若g(x)≠0或h(x)≠0,则∂(xg^2(x)+x^3h^2(x))为奇数,而f^2(x)为偶数,矛盾。
综上所证,f(x)≠g(x)或f(x)≠h(x)。
1.用g(x)除f(x),求商q(x)与余式r(x):1)f(x) =x^3-3x^2-x-1,g(x) =3x^2-2x+1;2)f(x) =x^4-2x+5,g(x) =x^2-x+2.1)解法一:待定系数法。
由于f(x)是首项系数为1的3次多项式,而g(x)是首项系数为3的2次多项式,所以商q(x)必是首项系数为1的1次多项式,而余式的次数小于2.于是可设q(x)=x+a,r(x)=bx+c。
根据f(x)=q(x)g(x)+r(x),即x^3-3x^2-x-1=(x+a)(3x^2-2x+1)+bx+c,右边展开,合并同类项,再比较两边同次幂的系数,得a=-1/3,b=-2/3,c=-1,故得q(x)=x-1/3,r(x)=-x-1/3.2)解法二:带余除法。
用长除法得商q(x)=x^2+x-1,余式r(x)=-5x+7.2.m,p,q适合什么条件时,有1)x^2+mx-1/x^3+px+q;2)x^2+mx+1/x^4+px^2+q.解:1)将x^3+px+q除以x^2+mx-1得商为x+m+1/(x+m-1),所以当m≠1时有解。
第一章 习题解答 物理化学

第一章习题解答1.1 物质的体膨胀系数αV与等温压缩率κT的定义如下:试导出理想气体的、与压力、温度的关系解:对于理想气体:PV=nRT , V= nRT/P求偏导:1.2 气柜储存有121.6kPa,27℃的氯乙烯(C2H3Cl)气体300m3,若以每小时90kg的流量输往使用车间,试问储存的气体能用多少小时?解:将氯乙烯(M w=62.5g/mol)看成理想气体:PV=nRT , n= PV/RT n=121600⨯300/8.314⨯300.13 (mol)=14618.6molm=14618.6⨯62.5/1000(kg)=913.66 kgt=972.138/90(hr)=10.15hr1.3 0℃,101.325kPa的条件常称为气体的标准状况,试求甲烷在标准状况下的密度?解:将甲烷(M w=16g/mol)看成理想气体:PV=nRT , PV =mRT/ M w甲烷在标准状况下的密度为=m/V= PM w/RT=101.325⨯16/8.314⨯273.15(kg/m3)=0.714 kg/m31.4 一抽成真空的球形容器,质量为25.0000g。
充以4℃水之后,总质量为125.0000g。
若改充以25℃,13.33kPa的某碳氢化合物气体,则总质量为25.0163g。
试估算该气体的摩尔质量。
水的密度按1 g.cm-3计算。
(答案来源:)解:球形容器的体积为V=(125-25)g/1 g.cm-3=100 cm3将某碳氢化合物看成理想气体:PV=nRT , PV =mRT/ M wM w= mRT/ PV=(25.0163-25.0000)⨯8.314⨯300.15/(13330⨯100⨯10-6) M w =30.51(g/mol)1.5 两个容器均为V的玻璃球之间用细管连接,泡内密封着标准状况下的空气。
若将其中一个球加热到100℃,另一个球则维持0℃,忽略连接细管中的气体体积,试求该容器内空气的压力。
理论力学作业解答
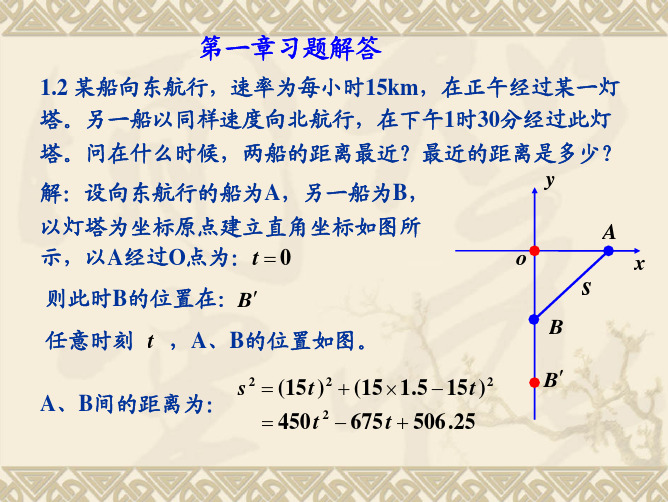
1.2 某船向东航行,速率为每小时15km,在正午经过某一灯 塔。另一船以同样速度向北航行,在下午1时30分经过此灯 塔。问在什么时候,两船的距离最近?最近的距离是多少? y 解:设向东航行的船为A,另一船为B, 以灯塔为坐标原点建立直角坐标如图所 示,以A经过O点为:t = 0 则此时B的位置在:B′ 任意时刻 t ,A、B的位置如图。 A、B间的距离为:
d ( − kv 0 cos α tg θ ) 1 dt = k ( g + kv 0 cos α tg α ) − kv 0 cos α tg θ
对上式积分可得:
1 ∫0 dt = k
t
∫α
−α
d ( − kv 0 cos α tg θ ) ( g + kv 0 cos α tg α ) − kv 0 cos α tg θ
v v0
α
v mg
θ
x
α v v
dv m = − mkv − mg sin θ (1) dt v2 m = mg cos θ ( 2)
随着质点运动,切线方 向与 x 轴夹角减少,故有:
ρ
ds ρ =− dθ
(3)
dv m = − mkv − mg sin θ (1) dt v2 m = mg cos θ ( 2)
s 2 = (15 t ) 2 + (15 × 1 .5 − 15 t ) 2 = 450 t 2 − 675 t + 506 .25
A
o
s
B B′
x
s = 450 t − 675 t + 506 .25
2 2
y
A
当 A、B相距最近时有: d (s2 ) = 900 t − 675 = 0 dt 可得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 流体力学一.填空题1. 某设备的真空表读数为500mmHg ,设备外环境大气压强为640mmHg ,则它的绝对压强为_________Pa 。
该设备的绝对压强=640-500=140mmHg =140×133.32=1.866×104Pa 。
2. 流体在圆形直管内作滞流(层流)流动时,其速度分布呈_________形曲线,中心最大速度为平均速度的____________倍。
此时摩擦系数λ与__________无关,只随__________加大而_______________。
抛物线,2,ε/d ,Re ,减小。
3.牛顿粘性定律表达式为_____τ=μy ∆∆μ_______,它只适用于___牛顿____型流体。
4.内摩擦力是流体________________的表现,所以又称为___________力或者__________________力。
粘性, 粘滞,粘性摩擦5.流体在圆形直管内流动时,在湍流区则摩擦系数λ与________及________有关。
在完全湍流区则λ与雷诺系数的关系线趋近于___________线。
Re ,ε/d ,水平6.粘度的物理意义是___促使流体流动产生单位速度梯度的剪应力。
___。
7.在定态流动系统中,水连续地从粗圆管流入细圆管,粗管内径为细管的2倍。
则细管内水的流速为粗管内流速的________倍。
据=21u u (12d d )2=(112d d )2=(2)2=4 8. 流体在圆管内流动时的摩擦阻力可分为__________________和_____________两种。
局部阻力的计算方法有___________法和_________法。
直管阻力,局部阻力,阻力系数,当量长度。
9.在静止的同一种连续流体的内部,各截面上__位___能与___静压___能之和为常数。
10. 法定单位制中,粘度的单位为_________________,在cgs 制中粘度的单位为_______________________,他们之间的关系是________________。
Pa·S ;p 或cp ; 1cp =1×10-2 p =1×10-3Pa·S (11. 流体在管内作湍流流动时,在管壁处速度为_____零_____,邻近管壁处存在_____滞流(或层流)内____层,且Re 值越大,则该层厚度越_____薄(或小)_______。
12.实际流体在直管内流过时,各截面上的总机械能_____不______守恒。
因实际流体流动时有________摩擦阻力__________。
13. 流体在一段装有若干个管件的直管l 中流过的总能量损失的通式为__________,它的单位为_________________。
∑f h =d l l e ∑+λ.22u (2分) J/Kg (1分)二.选择题1. 流体在圆形直管内作定态流动,雷诺准数Re =1500,则其摩擦系数应为( )(A ) 0.032 (B )0.0427 (C )0.0267 (D )无法确定0427.0150064Re 64===λ 应选(B )2. 在静止流体内部各点的静压强相等的必要条件是( D )(A ) 同一种流体内部 (B ) 连通着的两种流体(C ) 同一种连续流体 (D ) 同一水平面上,同一种连续的流体3. 在一水平变径管道上,细管截面A 及粗管截面B 与U 管压差计相连,当流体流过时,U 管压差计测量的是(C )(A )A 、B 两截面间的总能量损失 (B )A 、B 两截面间的动能差(C )A 、B 两截面间的压强差 (D )A 、B 两截面间的局部阻力4. 在阻力平方区内,摩擦系数λ( c )(A ) 为常数,与Re ,ε/d 均无关(B ) 随Re 值加大而减小(C ) 与Re 值无关,是ε/d 的函数(D ) 是Re 值与ε/d 的函数5. 流体在圆形直管中作滞流流动时,其直管阻力损失与流速u 的关系为( )(A ) 与u 2成正比(B ) 与u 成正比(C ) 与u 1.75成正比(D ) 与u 0.55成正比2.2u d l h f λ=, 当流体作滞流时,:64Re 64代入可得μρλdu == ρμρμρμ222322642..64d l u d l u u d l du h f === 应选(B )三.解答题1.什么是理想流体?引入理想流体的概念有什么意义?(1) 流动时没有阻力的流体,即总能量损失为零,称这种流体为理想气体。
(2) 自然界中不存在理想流体,但引入这个概念可使复杂的流体流动问题得以简化。
2. 何谓有效功(净功)?有效功率?轴功率?(1) 在流动过程中,输送机械对1Kg 流体所做的功称为有效功(净功)。
以We 表示,单位为J/Kg 。
(2分)(2) 单位时间内输送机械对流体所做的有效功称为有效功率。
以Ne 表示,单位为W 。
而s e e w W N .=(2分)(3) 有效功率Ne 与输送机械的效率η的比值称为轴功率。
以N 表示,单位为W 。
即ηNeN =(2分)3.化工厂哪些计算要应用流体静力学基本方程式?主要应用与以下三个方面:(1) 压强差与压强的测量。
(2) 测量容器内的液面位置(3)计算液封高度。
(4.扼要说明柏努利方程式和流体静力学基本方程式的关系。
静止流体∑====-0,0,02121f h W e u u 。
此时柏努利方程式即可化简为静力学基本方程式。
所以,静力学基本方程式是柏努利方程式的一个特例。
5.液体及气体的粘度随温度、压强的变化情况如何?1、 液体粘度随温度升高而减小,气体则相反。
(2分)2、 液体粘度基本上不随压强而变,除了极高及极低的压强外,气体粘度几乎不随压强而变。
3、6. 何谓滞流内层?由于在管壁附近流体速度很小,且湍流时管壁处速度也为零,故离管壁很近的一薄层流体运动必然是滞流,这层流体称为滞流内层。
四.计算题1.空气中各组分的摩尔分数为:0.21O 2、0.78N 2、0.01Ar 。
(1)求标准状况下空气的平均密度ρ0;(2)求绝对压强为3.8×104Pa 、温度为20℃时空气的平均密度ρ;比较两者的结果。
(1)求空气的ρ0:已知M O2=32,M N2=28,M Ar =40。
单位均为kg/kmol 。
①先求出标准状况下空气的平均密度Mm :Mm= M O2•χO2+ M N2•χN2+ M Ar •χAr =32×0.21+28×0.78+40×0.01=28.96kg/kmol (2分) ②293.1273315.896.2833.101000=⨯⨯==RT M P m ρkg/m 3(2分) (2)求3.8×104Pa 、20℃时空气的平均密度ρ:452.0)20273(1033.101273108.3293.134000=+⨯⨯⨯⨯⨯==T P PT ρρkg/m 3(2分) 由计算结果可看出:空气在标准状况下的密度与其在3.8×104Pa 、20℃状态下的密度相差很多,故气体的密度一定要标明状态。
(1分) (共7分)2.水在附图所示的水平管内流动,在管壁A 处连接一U 形管压差计,指示液为汞,密度为13600kg/m 3,U形管开口右支管的汞面上注入一小段水(此小段水的压强可忽略不计),当地大气压Pa 为101.33Pa ,水的密度取1000kg/m 3,其它数据见附图,求A 处的绝对压强为多少Pa ?(1)取U 形管中处于同一水平面上的B 、C 、D 三点,根据等压点的判定条件可得到P B =P C ,P C =P D ,于是可得P B =P C =P D (2分)(2)根据静力学基本方程式可得:P D =Pa+R ρHg g =Pa+0.25ρHg g =P B (2分)P A =P B +h ρH2O g =P D + h ρH2O g = Pa+0.25ρHg g +0.20ρH2O g (2分)于是A 处的绝对压强:P A =101330+0.25×13600×9.81+0.20×1000×9.81=136646Pa=136.646kPa (2分) (共8分)3. 某车间输水管路为φ60×3.5mm 的钢管,流速为4m/s ,因生产情况有变动,预使流速减至2.5m/s 左右,而用水量不变。
拟采用两个改进方案:(1)换一根粗管;(2)增加一根管子。
求两种方案各应选用管子的型号。
(1)换一根粗管。
体积流量Vs 不变, ===2211A u A u v s (1分) 体积流量为:5.244)053.0(422⨯=⨯=粗d v s ππ(1分) 所换一根粗管的直径067.05.2)053.0(42=⨯=粗d m 。
可选用附录23中(一)无缝热轧钢管,规格为φ76×3.5mm (2分)(2)增加一根管子。
Vs 不变,总体积流量为两根管子内体积流量之和,用d 增表示所增加管子的内径。
(1分)5.245.2)053.0(44)053.0(4222⨯+⨯⨯=⨯⨯=增d v s πππ(2分) 可解出 041.05.2)053.0(5.2)053.0(422=⨯-⨯=增d m 。
可选用附录23中(一)无缝热轧钢管,规格为φ50×3.5mm 。
(2分) (共9分)4. 实验室为了控制流动为定态流动,采用带溢流装置的高位槽。
(如本题附图)槽内水经φ89×3.5mm 的管子送至密闭设备内。
在水平管路上装有压强表,读数为6×104Pa 。
已知由高位槽至压强表安装的截面间总能量损失105/kg 。
每小时需要水2.85×104kg 。
求高位槽液面至压强表安装处的垂直距离h 。
解:(1)取高位槽水液面为1-1’截面,压强表安装位置为2-2’截面,以水平管的中心线为基准水平面,如图中所示。
(3分)(2)可列出柏努利方程:212222121122-∑+++=+++f e h P u g z w P u g z ρρ (2分)各量确定如下:z 1=h (待求值),z 2=0,P 1=0(表压),P 2=6×104Pa (表压),u 1≈0,u 2可求出,w e =0 (2分)(3)求2u :取3/1000m kg =水ρ,而m mm d 082.0825.32892=⨯-==5.1)082.0(4100036001085.2)(4/242222=⨯⨯===ππρωρωd A u s s m/s (2分) (4)将以上各值代入柏式,可求出z 1:1010001062)5.1(000081.9421+⨯++=+++z 。
