大学物理实验报告 英文版
大学物理实验报告英文版--声速测量

Physical Lab Report : Measurement of speed of soundWriter: No.Experiment date: 31.10.2012&7.11.2012Report date:10.11.2012In this class,we start to do an experiment b y only one person,which is named“measurement of speed of sound”.In fact,we are required to measure the wavelength and the frequency at the same same according to the formula“λf v =” .We can measure the frequency using the oscilloscope.And there are several about 15 minutes,I become familiar with them and begin operating my experiment.Experiment ing the resonance methodIn order to make the error smaller,I first move S2 to the position about mm x 100= ,then ,I move the S2 until first received amplitude reaches maximum.At the same time,I set the digital indicator to “mm 0”and record it,which makes following records easier.When f =38.629Hz,the records are as followed:There are two methods available to get an average distance from which we calculate the wavelength.The average,49.42mm =so mm 98.9=λ.then,m/s mm f v 346.898.98Hz 629.38=⨯==λ.The averagemm 48.42=.so ./12.34696.8Hz 629.38,96.8s m mm f v mm =⨯===λλCombining the method A and B,the average speed of sound is m/s 346.51v 1=.Experiment ing phase comparison methodIn this experiment,I was excited to see the so-called Lissajous curves.But I met a problem when I try to read the position of S 2 when the curv es collapses into straight line to “ ”,while it is OK to read when it shows“ ”.Thus,I found a solution to deal with this problem-----I only recorded the position of S 2 when the Lissajous curve showed “ ”.Then I must be careful that the phase between two record is 2π when doing data analysis later.Also,there are two methods to get the wavelength:A.Successive subtraction method:x 9-x 1 x 10-x 2 x 11-x 3 x 12-x 4x 13-x 5x 14-x 6x 15-x 7x 16-x 8Unit(mm ) 79.26 80.64 80.73 80.85 80.47 82.55 82.64 83.05 )(8mm x∆=λ 9.9010.0810.0910.1010.0510.3210.3310.38The average mm 15.10=λ.then,m/s mm f v 350.8115.01Hz 563.34=⨯==λ.e a linear fit x i -x 1=(i -1)λ/2i2 3 4 5 6 7 8 9 10 11 12 13141516)(11mm i x x i --=λ8.9 9.90 9.83 9.99 9.77 9.84 9.86 9.90 9.96 10.05 10.0310.0310.1110.1210.14The average ./17.34290.9Hz 563.34,90.9s m mm f v mm =⨯===λλCombining the method A and B,the average speed of sound is m/s 346.49v 2=Experiment ing timing methodIn fact,timing method is the first method I thought of when I want to measure the speed of sound.Because the basic formula “tLv ∆∆=”is almost the first physical formula we have learned. Now comes the problem that how to calculate the v since we have the formula as a principle.Then I recalled the first experiment we did to measure the spring constant.We made a linear fit of ∆x vs m ,the slope of which is just the k.Similarly,I collect all the data and then make a linear fit of L ∆ vs ∆t,the slope of which is just the speed of sound.The data recorded is as followed: t/μs 404 433 460 490 519 546 575 605 634 L/mm100110120130140150160170180After putting all the data to SI unit ,the form is: t/s 0.000404 0.000433 0.00046 0.00049 0.000519 0.000546 0.000575 0.000605 0.000634 L/m0.10.110.120.130.140.150.160.170.18Then I use a mathematic tool to make a linear fit of L vs t ,the graph is :According to the graph,we see R 2=0.9999,indicating that L and t are quite linearly correlative.Besides,we know the slope is the speed of sound,i.e,we conclude that m/s 348.40v 3=.Experiment ing timing method to measure the speed of sound in waterAfter finishing the first three experiments measuring the speed of sound in air,I filled the apparatus with water,and did the experiment similar to the experiment 3 to measure the sound speed in water. The data recorded is as followed: t/μs 94 100 107 114 121 127 134 141 148 L/mm100110120130140150160170180After putting all the data to SI unit ,the form is: t/s 0.00094 0.000100 0.000107 0.000114 0.000121 0.000127 0.000134 0.000141 0.000148 L/m0.10.110.120.130.140.150.160.170.18Then I use the mathematic tool to make a linear fit of L vs t ,the graph is :Also,from the graph,I see R 2=0.9997,indicating that L and t in water are also well linearly correlative.Similarly,weconclude that the speed of sound in water m/s 1477.4v water =.Discussion and conclusionThere are several factors contributing to the errors:①The distance between S1 and S2 is not always appropriate.For example,maybe I set the initial distance to be 100mm,but as I move S2 slowly away from S1,the distance become larger,which may make the transmission less sensitive,causing errors in the time.②In the experiment using resonance method,we need to judge that the oscillation amplitude in the detected signal reaches the maximum.Thus comes the problem how to judge.It ’s all up to ourselves!And this is also where errors come.③During a method,I had to keep the frequency unchanging,however,though I had try my best to keep it constant,it still changed,which can ’t be avoided by person.④As a matter of fact,when the sound transmit for a short distance,it may not strictly obey a simple harmonic wave,but we simplify the complexity when doing data analysis.Conclusion for the experimentwe use three methods to measure the sound of speed in air,the results are: m/s 346.51v 1= , m/s 346.49v 2= , m/s 348.40v 3= Besides the speed of sound in water is m/s 1477.4v water =.That is to say,the speed in water is approximately 4.3 times of that in air.In fact,this is very important in life.For example ,sonar is an application.It can measure the distance as well as explore things in water.This confirms that physics is always around our life and very useful .。
最新物理实验报告(英文)

最新物理实验报告(英文)Abstract:This report presents the findings of a recent physics experiment conducted to investigate the effects of quantum entanglement on particle behavior at the subatomic level. Utilizing a sophisticated setup involving photon detectors and a vacuum chamber, the experiment aimed to quantify the degree of correlation between entangled particles and to test the limits of nonlocal communication.Introduction:Quantum entanglement is a phenomenon that lies at the heart of quantum physics, where the quantum states of two or more particles become interlinked such that the state of one particle instantaneously influences the state of the other, regardless of the distance separating them. This experiment was designed to further our understanding of this phenomenon and its implications for the fundamental principles of physics.Methods:The experiment was carried out in a controlled environment to minimize external interference. A pair of photons was generated and entangled using a nonlinear crystal. The photons were then separated and sent to two distinct detection stations. The detection process was synchronized, and the data collected included the time, position, and polarization state of each photon.Results:The results indicated a high degree of correlation between the entangled photons. Despite being separated by a significant distance, the photons exhibited a consistent pattern in their polarization states, suggesting a strong entanglement effect. The data also showed that the collapse of the quantum state upon measurement occurred simultaneously for both particles, supporting the theory of nonlocality.Discussion:The findings of this experiment contribute to the ongoing debate about the nature of quantum entanglement and its potential applications. The consistent correlations observed between the entangled particles provide strong evidence for the nonlocal properties of quantum mechanics. This has implications for the development of quantum computing and secure communication technologies.Conclusion:The experiment has successfully demonstrated the robustness of quantum entanglement and its potential for practical applications. Further research is needed to explore the broader implications of these findings and to refine the experimental techniques for probing the quantum realm.References:[1] Einstein, A., Podolsky, B., & Rosen, N. (1935). Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47(8), 777-780.[2] Bell, J. S. (1964). On the Einstein Podolsky RosenParadox. Physics, 1(3), 195-200.[3] Aspect, A., Grangier, P., & Roger, G. (1982). Experimental Tests of Realistic Local Theories via Bell's Theorem. Physical Review Letters, 49(2), 91-94.。
大学物理实验报告英文版--温度传感器

Physical Lab Report :Temperature SensorsWriter: No:This time in the lab, I come to do something about temperature sensors.Before the experiment, I know that temperature sensors are very widely used lab equipment.From the guide, I can find their outputs changes as a function of temperature.The most commonly used ones in the lab are Platinum resistors and semiconductor thermocouples.In this experiment, I will describe the working principle of Platinum thermo-resistors, Semi-conductor thermo-resistor, and PN diode temperature sensor, and make measurements with them in the lab.At the beginning, I use the ice water to get the reference point to zero degree is 2 degree.So, when I deal with the data, I have changed the temperature into correct ones already.1.Semi-conductor thermo-resistorWithin range, the resistanc-temperature relation is ⎪⎭⎫⎝⎛=T B A R T expIf we calibrate the resistance at a temperature T 0 to be R 0, we can rewrite this relation into⎪⎪⎭⎫⎝⎛-+=0011ln ln T T B R R TAfter I change the unit of temperature into K, I use computer to make a linear fit and get a graph as follows:The slope of the line is equal to 1555.6, it means B=1555.6 K.which is a little bit smaller than the reference.2.Platinum thermo-resistorsA platinum resistor has a temperature-resistance relation of ()201TB AT R R T ++=R/Ω 4000 37023473 3106 2868 2544 2303 2101 1744 1569 1343 1282 1212 1146 1089 118967 896 838 773 724 668 624 586 561 538 505T/C27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 72 75 78 83 88 93 98U/ V 0.1150.11830.12120.12350.1260.12830.13030.13210.13410.13620.1380.13970.14130.1430.14460.14650.14790.14940.15160.15410.15620.1583T/C 14 11 8 5 2 0 -2 -4 -6 -7 -8U/V 0.1064 0.10570.10490.10440.10360.1030.10240.10180.10120.10080.1003From the graph ,I get the coefficient of x2 is B=2.8*10-7 o C-2,the coefficient of x is A=6*10-4 C-13.PN diode temperature sensorT/C 35 38 42 45 47 51 53 55 57 59 61 64 66 98 99 101 103U/V 0.470.4620.450.44140.43660.42460.42010.41380.40750.40170.39580.38840.38350.29610.29290.28840.283T/C 69 72 74 76 78 80 83 85 87 88 90 92 94 96 105 106 110Semiconductor diodes begin conducting electricity only if a certain threshold voltage or cut-in voltage is present in the forward direction.The voltage drop across a forward-biased diode varies only a little with the current, and is a function of temperature; this effect can be used as a temperature sensor.Within a given range of temperature, the resistance varies linearly with temperature.U=-0.0025T+0.5425, as the I=100μA,so,R=-25T+5424,the temperature is 25Error analysis:1.The temperature is tested indirectly, so the measured temperature is a little slower or higher than the correct one,If not precise, then our result of the coefficient is not that correct.2.The ice-water is made by human, even its temperature is near 0, however, there still exists some worry weather it is 0 degree.。
英语作文物理电学实验报告

英语作文物理电学实验报告Physics Experiment Report on Electric Circuits。
Introduction。
Electric circuits are important in our daily lives as they form the basis of all electrical devices. In this experiment, we investigated the behavior of electric circuits, including Ohm's law, Kirchhoff's laws, and the behavior of resistors in series and parallel.Materials。
Power supply。
Ammeter。
Voltmeter。
Resistors (varying values)。
Wires。
Breadboard。
Procedure。
1. Set up the circuit as shown in the diagram below, using a breadboard to connect the components.2. Measure the voltage across the resistor using the voltmeter and record the value.3. Measure the current flowing through the resistor using the ammeter and record the value.4. Repeat steps 2-3 for different values of resistors.5. Connect resistors in series and parallel and measure the voltage and current across each resistor.Results。
物理实验报告 英文

物理实验报告英文Title: Investigating the Behavior of Light: A Physics Experiment Report Introduction:In this report, we will discuss the experimental setup, procedure, and results of a physics experiment aimed at investigating the behavior of light. Light, as a fundamental entity, exhibits various phenomena that are crucial for understanding the nature of our universe. By conducting this experiment, we aimed to deepen our knowledge of light's properties and its interaction with different materials.Experimental Setup:The experiment was conducted in a controlled laboratory environment with the following equipment:1. Light Source: A laser beam was used as the primary light source. Its monochromatic nature ensured a consistent wavelength throughout the experiment.2. Optical Bench: An optical bench with adjustable components, such as lenses, mirrors, and prisms, was used to manipulate and direct the laser beam.3. Photodetector: A photodetector was employed to measure the intensity of the laser beam after passing through various materials or undergoing different optical processes.Procedure:1. Refraction: The first part of the experiment focused on investigating thephenomenon of refraction. A glass prism was placed on the optical bench, and the laser beam was directed towards it. By varying the angle of incidence, we observed the corresponding change in the angle of refraction. The intensity of the laser beam was measured using the photodetector at different angles.2. Diffraction: In the second part, we explored the phenomenon of diffraction. A diffraction grating was placed in the path of the laser beam. By rotating the grating, we observed the diffraction pattern formed on a screen placed at a specific distance from the grating. The intensity of the diffracted light was measured using the photodetector.3. Interference: The final part of the experiment focused on the interference of light waves. Two narrow slits were placed in the path of the laser beam, creating two coherent sources of light. A screen was placed at a specific distance from the slits, and the interference pattern was observed. The intensity of the interference pattern was measured using the photodetector.Results and Discussion:1. Refraction: As the angle of incidence increased, the angle of refraction also increased. This confirmed the relationship between the two angles predicted by Snell's law. The intensity of the laser beam decreased as the angle of refraction increased, indicating the loss of energy during the refraction process.2. Diffraction: By rotating the diffraction grating, we observed a series of bright and dark fringes on the screen. The distance between the fringes decreased as the grating rotation angle increased, indicating a smaller wavelength ofdiffracted light. The intensity of the laser beam varied at different angles, demonstrating the constructive and destructive interference of light waves.3. Interference: The interference pattern displayed alternating bright and dark fringes. The intensity of the bright fringes was higher, indicating constructive interference, while the dark fringes represented destructive interference. The distance between the fringes increased as the distance from the slits to the screen increased, confirming the relationship between fringe separation and wavelength.Conclusion:Through this experiment, we gained valuable insights into the behavior of light. We observed and analyzed the phenomena of refraction, diffraction, and interference, which are fundamental to the understanding of optics. The results obtained aligned with the theoretical predictions, reinforcing our understanding of light's properties and its interaction with various materials. Conducting experiments such as these allows us to bridge the gap between theoretical knowledge and practical applications, ultimately leading to advancements in the field of physics.。
大学物理实验报告 英文版

大学物理实验报告Ferroelectric Control of Spin PolarizationABSTRACTA current drawback of spintronics is the large power that is usually required for magnetic writing, in contrast with nanoelectronics, which relies on “zero-current,” gate-controlled operations. Efforts have been made to control the spin-relaxation rate, the Curie temperature, or the magnetic anisotropy with a gate voltage, but these effects are usually small and volatile. We used ferroelectric tunnel junctions with ferromagnetic electrodes to demonstrate local, large, and nonvolatile control of carrier spin polarization by electrically switching ferroelectric polarization. Our results represent a giant type of interfacial magnetoelectric coupling and suggest a low-power approach for spin-based information control.Controlling the spin degree of freedom by purely electrical means is currently an important challenge in spintronics (1, 2). Approaches based on spin-transfer torque (3) have proven very successful in controlling the direction of magnetization in a ferromagnetic layer, but they require the injection of high current densities. An ideal solution would rely on the application of an electric field across an insulator, as in existing nanoelectronics. Early experiments have demonstrated the volatile modulation of spin-based properties with a gate voltage applied through a dielectric. Notable examples include the gate control of the spin-orbit interaction in III-V quantum wells (4), the Curie temperature T C (5), or the magnetic anisotropy (6) in magnetic semiconductors with carrier-mediated exchange interactions; for example, (Ga,Mn)As or (In,Mn)As. Electric field–induced modifications of magnetic anisotropy at room temperature have also been reported recently in ultrathin Fe-based layers (7, 8).A nonvolatile extension of this approach involves replacing the gate dielectric by a ferroelectric and taking advantage of the hysteretic response of its order parameter (polarization) with an electric field. When combined with (Ga,Mn)As channels, forinstance, a remanent control of T C over a few kelvin was achieved through polarization-driven charge depletion/accumulation (9, 10), and the magnetic anisotropy was modified by the coupling of piezoelectricity and magnetostriction (11, 12). Indications of an electrical control of magnetization have also been provided in magnetoelectric heterostructures at room temperature (13–17).Recently, several theoretical studies have predicted that large variations of magnetic properties may occur at interfaces between ferroelectrics and high-T C ferromagnets such as Fe (18–20), Co2MnSi (21), or Fe3O4 (22). Changing the direction of the ferroelectric polarization has been predicted to influence not only the interfacial anisotropy and magnetization, but also the spin polarization. Spin polarization [i.e., the normalized difference in the density of states (DOS) of majority and minority spin carriers at the Fermi level (E F)] is typically the key parameter controlling the response of spintronics systems, epitomized by magnetic tunnel junctions in which the tunnel magnetoresistance (TMR) is related to the electrode spin polarization by the Jullière formula (23). These predictions suggest that the nonvolatile character of ferroelectrics at the heart of ferroelectric random access memory technology (24) may be exploited in spintronics devices such as magnetic random access memories or spin field-effect transistors (2). However, the nonvolatile electrical control of spin polarization has not yet been demonstrated.We address this issue experimentally by probing the spin polarization of electrons tunneling from an Fe electrode through ultrathin ferroelectric BaTiO3 (BTO) tunnel barriers (Fig. 1A). The BTO polarization can be electrically switched to point toward oraway from the Fe electrode. We used a half-metallic La0.67Sr0.33MnO3(LSMO) (25) bottom electrode as a spin detector in these artificial multiferroic tunnel junctions (26, 27). Magnetotransport experiments provide evidence for a large and reversible dependence of the TMR on ferroelectric polarization direction.Fig. 1(A) Sketch of the nanojunction defined by electrically controlled nanoindentation. A thin resist is spin-coated on the BTO(1 nm)/LSMO(30 nm) bilayer. The nanoindentation is performed with a conductive-tip atomic force microscope, and the resultingnano-hole is filled by sputter-depositing Au/CoO/Co/Fe. (B) (Top) PFM phase image of a BTO(1 nm)/LSMO(30 nm) bilayer after poling the BTO along 1-by-4–μm stripes with either a negative or positive (tip-LSMO) voltage. (Bottom) CTAFM image of an unpoled area of a BTO(1 nm)/LSMO(30 nm) bilayer. Ω, ohms. (C) X-ray absorption spectra collected at room temperature close to the Fe L3,2 (top), Ba M5,4 (middle), and TiL3,2 (bottom) edges on an AlO x(1.5 nm)/Al(1.5 nm)/Fe(2 nm)/BTO(1 nm)/LSMO(30 nm)//NGO(001) heterostructure. (D) HRTEM and (E) HAADF images of the Fe/BTO interface in a Ta(5 nm)/Fe(18 nm)/BTO(50 nm)/LSMO(30 nm)//NGO(001) heterostructure. The white arrowheads in (D) indicate the lattice fringes of {011} planes in the iron layer. [110] and [001] indicate pseudotetragonal crystallographic axes of the BTO perovskite.The tunnel junctions that we used in this study are based on BTO(1 nm)/LSMO(30 nm) bilayers grown epitaxially onto (001)-oriented NdGaO3 (NGO) single-crystal substrates (28). The large (~180°) and stable piezoresponse force microscopy (PFM) phase contrast (28) between negatively and positively poled areas (Fig. 1B, top) indicates that the ultrathin BTO films are ferroelectric at room temperature (29). The persistence of ferroelectricity for such ultrathin films of BTO arises from the large lattice mismatch with the NGO substrate (–3.2%), which is expected to dramatically enhance ferroelectric properties in this highly strained BTO (30). The local topographical and transport properties of the BTO(1 nm)/LSMO(30 nm) bilayers were characterized by conductive-tip atomic force microscopy (CTAFM) (28). The surface is very smooth with terraces separated by one-unit-cell–high steps, visible in both the topography (29) and resistance mappings (Fig. 1B, bottom). No anomalies in the CTAFM data were observed over lateral distances on the micrometer scale.We defined tunnel junctions from these bilayers by a lithographic technique based on CTAFM (28, 31). Top electrical contacts of diameter ~10 to 30 nm can be patterned by this nanofabrication process. The subsequent sputter deposition of a 5-nm-thick Fe layer, capped by a Au(100 nm)/CoO(3.5 nm)/Co(11.5 nm) stack to increase coercivity, defined a set of nanojunctions (Fig. 1A). The same Au/CoO/Co/Fe stack was deposited on another BTO(1 nm)/LSMO(30 nm) sample for magnetic measurements. Additionally, a Ta(5 nm)/Fe(18 nm)/BTO(50 nm)/LSMO(30 nm) sample and a AlO x(1.5 nm)/Al(1.5nm)/Fe(2 nm)/BTO(1 nm)/LSMO(30 nm) sample were realized for structural and spectroscopic characterizations.We used both a conventional high-resolution transmission electron microscope (HRTEM) and the NION UltraSTEM 100 scanning transmission electron microscope (STEM) to investigate the Fe/BTO interface properties of the Ta/Fe/BTO/LSMO sample. The epitaxial growth of the BTO/LSMO bilayer on the NGO substrate was confirmed by HRTEM and high-resolution STEM images. The low-resolution, high-angle annular dark field (HAADF) image of the entire heterostructure shows the sharpness of theLSMO/BTO interface over the studied area (Fig. 1E, top). Figure 1D reveals a smooth interface between the BTO and the Fe layers. Whereas the BTO film is epitaxially grown on top of LSMO, the Fe layer consists of textured nanocrystallites. From the in-plane (a) and out-of-plane (c) lattice parameters in the tetragonal BTO layer, we infer that c/a = 1.016 ± 0.008, in good agreement with the value of 1.013 found with the use of x-ray diffraction (29). The interplanar distances for selected crystallites in the Fe layer [i.e.,~2.03 Å (Fig. 1D, white arrowheads)] are consistent with the {011} planes ofbody-centered cubic (bcc) Fe.We investigated the BTO/Fe interface region more closely in the HAADF mode of the STEM (Fig. 1E, bottom). On the BTO side, the atomically resolved HAADF image allows the distinction of atomic columns where the perovskite A-site atoms (Ba) appear as brighter spots. Lattice fringes with the characteristic {100} interplanar distances of bcc Fe (~2.86 Å) can be distinguished on the opposite side. Subtle structural, chemical, and/or electronic modifications may be expected to occur at the interfacial boundarybetween the BTO perovskite-type structure and the Fe layer. These effects may lead to interdiffusion of Fe, Ba, and O atoms over less than 1 nm, or the local modification of the Fe DOS close to E F, consistent with ab initio calculations of the BTO/Fe interface (18–20).To characterize the oxidation state of Fe, we performed x-ray absorption spectroscopy (XAS) measurements on a AlO x(1.5 nm)/Al(1.5 nm)/Fe(2 nm)/BTO(1 nm)/LSMO(30 nm) sample (28). The probe depth was at least 7 nm, as indicated by the finite XAS intensity at the La M4,5 edge (28), so that the entire Fe thickness contributed substantially to the signal. As shown in Fig. 1C (top), the spectrum at the Fe L2,3 edge corresponds to that of metallic Fe (32). The XAS spectrum obtained at the Ba M4,5 edge (Fig. 1C, middle) is similar to that reported for Ba2+ in (33). Despite the poor signal-to-noise ratio, the Ti L2,3 edge spectrum (Fig. C, bottom) shows the typical signature expected for a valence close to 4+ (34). From the XAS, HRTEM, and STEM analyses, we conclude that theFe/BTO interface is smooth with no detectable oxidation of the Fe layer within a limit of less than 1 nm.After cooling in a magnetic field of 5 kOe aligned along the [110] easy axis of pseudocubic LSMO (which is parallel to the orthorhombic [100] axis of NGO), we characterized the transport properties of the junctions at low temperature (4.2K). Figure 2A (middle) shows a typical resistance–versus–magnetic field R(H) cycle recorded at a bias voltage of –2 mV (positive bias corresponds to electrons tunneling from Fe to LSMO). The bottom panel of Fig. 2A shows the magnetic hysteresisloop m(H) of a similar unpatterned sample measured with superconducting quantuminterference device (SQUID) magnetometry. When we decreased the magnetic field from a large positive value, the resistance dropped in the –50 to –250 Oe range and then followed a plateau down to –800 Oe, after which it sharply returned to thehigh-resistance state. We observed a similar response when cycling the field back to large positive values. A comparison with the m(H) loop indicates that the switching fields in R(H) correspond to changes in the relative magnetic configuration of the LSMO and Fe electrodes from parallel (at high field) to antiparallel (at low field). The magnetically softer LSMO layer switched at lower fields (50 to 250 Oe) compared with the Fe layer, for which coupling to the exchange-biased Co/CoO induces larger and asymmetric coercive fields (–800 Oe, 300 Oe). The observed R(H) corresponds to a negative TMR = (R ap–R p)/R ap of –17% [R p and R ap are the resistance in the parallel (p) and antiparallel (ap) magnetic configurations, respectively; see the sketches in Fig. 2A]. Within the simple Jullière model of TMR (23) and considering the large positive spin polarization of half-metallic LSMO (25), this negative TMR corresponds to a negative spin polarization for bcc Fe at the interface with BTO, in agreement with ab initio calculations (18–20).Fig. 2(A) (Top) Device schematic with black arrows to indicate magnetizations. p, parallel; ap, antiparallel. (Middle) R(H) recorded at –2 mV and 4.2 K showing negative TMR. (Bottom) m(H) recorded at 30 K with a SQUID magnetometer. emu, electromagnetic units. (B) (Top) Device schematic with arrows to indicate ferroelectric polarization. (Bottom) I(V DC) curves recorded at 4.2 K after poling the ferroelectric down (orange curve) or up (brown curve). The bias dependence of the TER is shown in the inset.As predicted (35–38) and demonstrated (29) previously, the tunnel current across a ferroelectric barrier depends on the direction of the ferroelectric polarization. We also observed this effect in our Fe/BTO/LSMO junctions. As can be seen in Fig. 2B, after poling the BTO at 4.2 K to orient its polarization toward LSMO or Fe (with a poling voltage of VP–≈ –1 V or VP+≈ 1 V, respectively; see Fig. 2B sketches),current-versus-voltage I(V DC) curves collected at low bias voltages showed a finite difference corresponding to a tunnel electroresistance as large as TER = (I VP+–I VP–)/I VP–≈ 37% (Fig. 2B, inset). This TER can be interpreted within an electrostatic model (36–39), taking into account the asymmetric deformation of the barrier potential profile that is created by the incomplete screening of polarization charges by different Thomas-Fermi screening lengths at Fe/BTO and LSMO/BTO interfaces.Piezoelectric-related TER effects (35, 38) can be neglected as the piezoelectric coefficient estimated from PFM experiments is too small in our clamped films (29). TER measurements performed on a BTO(1 nm)/LSMO(30 nm) bilayer with the use of a CTAFM boron-doped diamond tip as the top electrode showed values of ~200%(29). Given the strong sensitivity of the TER on barrier parameters and barrier-electrode interfaces, these two values are not expected to match precisely. We anticipate that the TER variation between Fe/BTO/LSMO junctions and CTAFM-based measurements is primarily the result of different electrostatic boundary conditions.Switching the ferroelectric polarization of a tunnel barrier with voltage pulses is also expected to affect the spin-dependent DOS of electrodes at a ferromagnet/ferroelectric interface. Interfacial modifications of the spin-dependent DOS of the half-metallic LSMO by the ferroelectric BTO are not likely, as no states are present for the minority spins up to ~350 meV above E F (40, 41). For 3d ferromagnets such as Fe, large modifications of the spin-dependent DOS are expected, as charge transfer between spin-polarized empty and filled states is possible. For the Fe/BTO interface, large changes have been predicted through ab initio calculations of 3d electronic states of bcc Fe at the interface with BTO by several groups (18–20).To experimentally probe possible changes in the spin polarization of the Fe/BTO interface, we measured R(H) at a fixed bias voltage of –50 mV after aligning the ferroelectric polarization of BTO toward Fe or LSMO. R(H) cycles were collected for each direction of the ferroelectric polarization for two typical tunnel junctions of the same sample (Fig. 3, B and C, for junction #1; Fig. 3, D and E, for junction #2). In both junctions at the saturating magnetic field, high- and low-resistance states are observed when the ferroelectric polarization points toward LSMO or Fe, respectively, with a variation of ~ 25%. This result confirms the TER observations in Fig. 2B.Fig. 3(A) Sketch of the electrical control of spin polarization at the Fe/BTO interface.(B and C) R(H) curves for junction #1 (V DC = –50 mV, T = 4.2 K) after poling the ferroelectric barrier down or up, respectively. (D and E) R(H) curves for junction #2 (V DC = –50 mV, T= 4.2 K) after poling the ferroelectric barrier down or up, respectively.More interestingly, here, the TMR is dramatically modified by the reversal of BTO polarization. For junction #1, the TMR amplitude changes from –17 to –3% when the ferroelectric polarization is aligned toward Fe or LSMO, respectively (Fig. 3, B and C). Similarly for junction #2, the TMR changes from –45 to –19%. Similar results were obtained on Fe/BTO (1.2 nm)/LSMO junctions (28). Within the Jullière model (23), these changes in TMR correspond to a large (or small) spin polarization at the Fe/BTO interface when the ferroelectric polarization of BTO points toward (or away from) the Fe electrode. These experimental data support our interpretation regarding the electrical manipulation of the spin polarization of the Fe/BTO interface by switching the ferroelectric polarization of the tunnel barrier.To quantify the sensitivity of the TMR with the ferroelectric polarization, we define a term, the tunnel electromagnetoresistance, as TEMR = (TMR VP+–TMR VP–)/TMR VP–. Largevalues for the TEMR are found for junctions #1 (450%) and #2 (140%), respectively. This electrical control of the TMR with the ferroelectric polarization is repeatable, as shown in Fig. 4 for junction #1 where TMR curves are recorded after poling the ferroelectric up, down, up, and down, sequentially (28).Fig. 4TMR(H) curves recorded for junction #1 (V DC = –50 mV, T = 4.2 K) after poling the ferroelectric up (VP+), down (VP–), up (VP+), and down (VP–).For tunnel junctions with a ferroelectric barrier and dissimilar ferromagnetic electrodes, we have reported the influence of the electrically controlled ferroelectric barrier polarization on the tunnel-current spin polarization. This electrical influence over magnetic degrees of freedom represents a new and interfacial magnetoelectric effect that is large because spin-dependent tunneling is very sensitive to interfacial details. Ferroelectrics can provide a local, reversible, nonvolatile, and potentially low-power means of electrically addressing spintronics devices.Supporting Online Material/cgi/content/full/science.1184028/DC1Materials and MethodsFigs. S1 to S5References∙Received for publication 30 October 2009.∙Accepted for publication 4 January 2010.References and Notes1. C. Chappert, A. Fert, F. N. Van Dau, The emergence of spin electronics indata storage. Nat. Mater. 6,813 (2007).2.I. Žutić, J. Fabian, S. Das Sarma, Spintronics: Fundamentals andapplications. Rev. Mod. Phys. 76,323 (2004).3.J. C. Slonczewski, Current-driven excitation of magnetic multilayers. J.Magn. Magn. Mater. 159, L1(1996).4.J. Nitta, T. Akazaki, H. Takayanagi, T. Enoki, Gate control of spin-orbit interaction in an inverted In0.53Ga0.47As/In0.52Al0.48Asheterostructure. Phys. Rev. Lett. 78, 1335 (1997).5.H. Ohno et al., Electric-field control offerromagnetism. Nature 408, 944 (2000).6. D. Chiba et al., Magnetization vector manipulation by electricfields. Nature 455, 515 (2008).7.M. Weisheit et al., Electric field–induced modification of magnetism inthin-film ferromagnets. Science315, 349 (2007).8.T. Maruyama et al., Large voltage-induced magnetic anisotropy changein a few atomic layers of iron.Nat. Nanotechnol. 4, 158 2009).9.S. W. E. Riester et al., Toward a low-voltage multiferroic transistor:Magnetic (Ga,Mn)As under ferroelectric control. Appl. Phys.Lett. 94, 063504 (2009).10.I. Stolichnov et al., Non-volatile ferroelectric control of ferromagnetismin (Ga,Mn)As. Nat. Mater. 7, 464(2008).11. C. Bihler et al., Ga1−x Mn x As/piezoelectric actuator hybrids: A modelsystem for magnetoelastic magnetization manipulation. Phys. Rev.B 78, 045203 (2008).12.M. Overby, A. Chernyshov, L. P. Rokhinson, X. Liu, J. K. Furdyna, GaMnAs-based hybrid multiferroic memory device. Appl. Phys.Lett. 92, 192501 (2008).13. C. Thiele, K. Dörr, O. Bilani, J. Rödel, L. Schultz, Influence of strain on themagnetization and magnetoelectric effect inLa0.7A0.3MnO3∕PMN-PT(001)(A=Sr,Ca). Phys.Rev.B 75, 054408 (2007).14.W. Eerenstein, M. Wiora, J. L. Prieto, J. F. Scott, N. D. Mathur, Giantsharp and persistent converse magnetoelectric effects in multiferroic epitaxial heterostructures. Nat. Mater. 6, 348 (2007).15.T. Kanki, H. Tanaka, T. Kawai, Electric control of room temperatureferromagnetism in a Pb(Zr0.2Ti0.8)O3/La0.85Ba0.15MnO3 field-effect transistor. Appl.Phys. Lett. 89, 242506 (2006).16.Y.-H. Chu et al., Electric-field control of local ferromagnetism using amagnetoelectric multiferroic. Nat. Mater. 7, 478 2008).17.S. Sahoo et al., Ferroelectric control of magnetism in BaTiO3∕Feheterostructures via interface strain coupling. Phys. Rev. B 76, 092108 (2007). 18. C.-G. Duan, S. S. Jaswal, E. Y. Tsymbal, Predicted magnetoelectric effectin Fe/BaTiO3 multilayers: Ferroelectric control of magnetism. Phys. Rev.Lett. 97, 047201 (2006).19.M. Fechner et al., Magnetic phase transition in two-phase multiferroicspredicted from first principles.Phys. Rev. B 78, 212406 (2008).20.J. Lee, N. Sai, T. Cai, Q. Niu, A. A. Demkov, preprint availableat /abs/0912.3492v1.21.K. Yamauchi, B. Sanyal, S. Picozzi, Interface effects at ahalf-metal/ferroelectric junction. Appl. Phys. Lett. 91, 062506 (2007).22.M. K. Niranjan, J. P. Velev, C.-G. Duan, S. S. Jaswal, E. Y. Tsymbal, Magnetoelectric effect at the Fe3O4/BaTiO3 (001) interface: A first-principles study. Phys. Rev. B 78, 104405 (2008).23.M. Jullière, Tunneling between ferromagnetic films. Phys. Lett.A 54, 225 (1975).24.J. F. Scott, Applications of modern ferroelectrics. Science 315, 954 (2007).25.M. Bowen et al., Nearly total spin polarization in La2/3Sr1/3MnO3 fromtunneling experiments. Appl. Phys. Lett. 82, 233 (2003).26.J. P. Velev et al., Magnetic tunnel junctions with ferroelectric barriers:Prediction of four resistance states from first principles. Nano Lett. 9, 427 (2009).27. F. Yang et al., Eight logic states of tunneling magnetoelectroresistancein multiferroic tunnel junctions.J. Appl. Phys. 102, 044504 (2007).28.Materials and methods are available as supporting materialon Science Online.29.V. Garcia et al., Giant tunnel electroresistance for non-destructivereadout of ferroelectric states. Nature460, 81 (2009).30.K. J. Choi et al., Enhancement of ferroelectricity in strained BaTiO3 thinfilms. Science 306, 1005(2004).31.K. Bouzehouane et al., Nanolithography based on real-time electricallycontrolled indentation with an atomic force microscope for nanocontactelaboration. Nano Lett. 3, 1599 (2003).32.T. J. Regan et al., Chemical effects at metal/oxide interfaces studied byx-ray-absorption spectroscopy.Phys. Rev. B 64, 214422 (2001).33.N. Hollmann et al., Electronic and magnetic properties of the kagomesystems YBaCo4O7 and YBaCo3M O7 (M=Al, Fe). Phys. Rev. B 80, 085111 (2009).34.M. Abbate et al., Soft-x-ray-absorption studies of the location of extracharges induced by substitution in controlled-valence materials. Phys. Rev.B 44, 5419 (1991).35. E. Y. Tsymbal, H. Kohlstedt, Tunneling across aferroelectric. Science 313, 181 (2006).36.M. Ye. Zhuravlev, R. F. Sabirianov, S. S. Jaswal, E. Y. Tsymbal, Giantelectroresistance in ferroelectric tunnel junctions. Phys. Rev.Lett. 94, 246802 (2005).37.M. Ye. Zhuravlev, R. F. Sabirianov, S. S. Jaswal, E. Y. Tsymbal, Erratum:Giant electroresistance in ferroelectric tunnel junctions. Phys. Rev.Lett. 102, 169901 2009).38.H. Kohlstedt, N. A. Pertsev, J. Rodriguez Contreras, R. Waser, Theoreticalcurrent-voltage characteristics of ferroelectric tunnel junctions. Phys. Rev.B 72, 125341 (2005).39.M. Gajek et al., Tunnel junctions with multiferroic barriers. Nat.Mater. 6, 296 (2007).40.M. Bowen et al., Spin-polarized tunneling spectroscopy in tunneljunctions with half-metallic electrodes.Phys. Rev. Lett. 95, 137203 (2005).41.J. D. Burton, E. Y. Tsymbal, Prediction of electrically induced magneticreconstruction at the manganite/ferroelectric interface. Phys. Rev.B 80, 174406 (2009).42.We thank R. Guillemet, C. Israel, M. E. Vickers, R. Mattana, J.-M. George,and P. Seneor for technical assistance, and C. Colliex for fruitful discussions on the microscopy measurements. This study was partially supported by theFrance-U.K. Partenariat Hubert Curien Alliance program, the French RéseauThématique de Recherche Avancée Triangle de la Physique, the European Union (EU) Specific Targeted Research Project (STRep) Manipulating the Coupling inMultiferroic Films, EU STReP Controlling Mesoscopic Phase Separation, U.K. Engineering and Physical Sciences Research Council grant EP/E026206/I, French C-Nano Île de France, French Agence Nationale de la Recherche (ANR) Oxitronics, French ANR Alicante, the European Enabling Science and Technology through European Elelctron Microscopy program, and the French Microscopie Electronique et Sonde Atomique network. X.M.acknowledges support from Comissionat per a Universitats i Recerca (Generalitat de Catalunya).。
关于物理实验的英语作文

关于物理实验的英语作文英文回答:The Scientific Method and Experiment Design.The scientific method is a systematic approach totesting hypotheses and theories. It involves making observations, developing hypotheses, conducting experiments, and drawing conclusions based on the results. Experiment design is an important part of the scientific method because it ensures that the experiment is conducted in away that will yield meaningful results.There are five basic steps in the scientific method:1. Make observations: The first step in the scientific method is to make observations about the world around you. These observations can be about anything, but they shouldbe specific and detailed.2. Develop a hypothesis: A hypothesis is a tentative explanation for the observations you have made. It is important to develop a hypothesis that is testable, meaning that it can be tested through an experiment.3. Conduct an experiment: An experiment is a controlled test of a hypothesis. It involves manipulating one variable (the independent variable) while holding all other variables constant (the controlled variables). The results of the experiment can be used to support or refute the hypothesis.4. Draw conclusions: After conducting an experiment, you need to draw conclusions about your results. These conclusions should be based on the data you collected and should be consistent with your hypothesis.5. Communicate your results: The final step in the scientific method is to communicate your results to others. This can be done through writing a scientific paper, giving a presentation, or creating a poster.Experiment design is an important part of thescientific method because it ensures that the experiment is conducted in a way that will yield meaningful results. There are many factors to consider when designing an experiment, including:The type of experiment: There are many different types of experiments, including controlled experiments, observational studies, and case studies. The type of experiment you choose will depend on the question you are trying to answer.The sample size: The sample size is the number of participants in your experiment. The sample size should be large enough to ensure that the results are statistically significant.The independent variable: The independent variable is the variable that you are manipulating in your experiment. The independent variable should be the only variable that you change in your experiment.The controlled variables: The controlled variables are all of the variables that you are holding constant in your experiment. The controlled variables should be kept constant so that they do not affect the results of your experiment.The data collection method: The data collection method is the way that you collect data in your experiment. The data collection method should be reliable and valid.By following the steps of the scientific method and using careful experiment design, you can ensure that your experiment will yield meaningful results.中文回答:科学方法和实验设计。
英文版物理实验

physics lab reportDetermination of the Gravitation Constant gby Means of a Simple PendulumAimThis experiment was performed to determine the gravitational acceleration of objects close to the surface of the earth, by observing the motion of a simple pendulum.IntroductionA simple pendulum, figure 1, displaced through a small angle θ, will oscillate back and forth about its equilibrium position with period T . T is the time the pendulum takes to make one complete back-and-forth motion. The bob is hung from a rigid support on a string of length L .Figure 1: The simple pendulum.For oscillations where the angle θ is small, the period T is related to the length L of the string and the gravitation constant g byT L g=2πSquaring both sides of this equation yieldsTL g224=πIf one measures the period of a pendulum as a function of the length of the string, then a plot of T 2 as a function of L will yield a straight line with a gradient G ; andg G=42πExperimental MethodA simple pendulum was produced from a length of string and a fishing sinker. The sinker was displaced through an angle less than 10 degrees and released. For five different lengths of string between 23 and 100 cm, the period of oscillation wasmeasured. In each measurement, the pendulum was allowed to oscillate 50 times. The total time for 50 oscillations was measured with a stopwatch, and the period was calculated by dividing the total time for 50 oscillations by 50. The stopwatchmeasures time to 0.01 seconds. However, it is estimated that the total reaction time of the experimenter was 0.2 seconds. Thus the uncertainty of any original measurement of time was taken to be 0.2 seconds. With a metre rule, the length of the string was measured to the nearest millimetre. The length of the string was measured from the support to the centre of the bob.Results and CalculationsTable 1 shows the results of the experiment, and the plot of T 2 versus L is given in figure 2.Table 1: Pendulum data.The uncertainty in each measurement of length is 0.001 m. The uncertainty in each measurement of time for 50 oscillations, δT 1 is 0.2 s. Thus the uncertainty in any measurement of the period isδδT T ===15002500004..s sThe period is squared prior to plotting. The relative uncertainty in the period squared is twice the relative uncertainty in the period:δδ().T TT TT2220008==sString Length (m) Time for 50 oscillations (s)Time T for one oscillation (s) Period squared (s 2)0.975 97.3 1.95 3.80 0.812 88.7 1.77 3.13 0.597 75.6 1.51 2.28 0.411 61.9 1.24 1.54 0.235 45.9 0.918 0.843Solving for δT ,δδδ()()(.T TTTT T T22220008===s)Thus the uncertainty in T 2 is proportional to T . The largest data point is forT 2 = 3.80 s 2. The uncertainty in this datum is δ()(.(.).T 22000819500156==s)s s . The maximum uncertainty in T 2 is thus 0.4 %. The error bars associated with T 2 are too small to plot on a graph. Similarly, the error bars associated with L are also too small to plot on the graph.00.511.522.533.540.2350.4110.5970.8120.975length (m)T 2Figure 2: Plot of T 2as a function of L .A straight line fits the data well. The gradient of the line of best fit can be calculated fromG ==--==rise runsmsms m(..)(..).../3505009001430076395222andg G===44s mm /s22ππ39599922./.To work out the uncertainty in the gradient, an alternative line of best fit was selected, and its gradient is given byG alt smsms m=--==(..)(..).../375250095064125031403222The uncertainty in G is the difference of these 2 gradients:δG G G =±-=±-±()(..)//alt s m =0.08s m 40339522The percent uncertainty in G , and thus in g isδδG Gg g===0083952..%Thus the experimentally determined value of the gravitation constant is g = 9.99 m/s 2 ± 2 %.DiscussionThe accepted value 1 of g is 9.81 m/s 2. The accuracy of the results isaccuracy m sm sobserved expectedexpected=-=-=+g g g (..)/./%999981981222The experimentally determined value of g agrees with the accepted value to within the experimental uncertainty. Thus this experiment was a successful and accurate determination of g , even with the simple apparatus.The bob used in this experiment is in the shape of a triangular wedge. The centre of mass was estimated (guessed) for the bob, and the length of the string wasconsistently measured to that point. The accuracy of the length of the string did not matter in this experiment so long as the length was always measured in the same way. The gravitation constant was determined from the change in T 2 as L changed. This change is static, regardless of where the end of the string was taken to be. Any errors in estimating where the string ended will merely shift the plot up or down. It will not affect the gradient. An interesting further experiment would be to collect more data points for small L , and see if the plotted data pass through the origin.Another interesting investigation would be to perform the experiment for large angles of displacement θ. The theory assumes that this angle is small. Further experiments could investigate how the determination of g in this technique is affected by an increasing angle of displacement.ConclusionBy means of a simple pendulum, the value of the gravitation constant was determined to be g = 9.99 m/s 2 ± 2 %. This agreed with the accepted value, 9.81 m/s 2, to within the experimental uncertainty.References1. Deakin University (1997), SEP101 Unit Guide .2. Halliday, D., Resnick, R., and Walker, J. (1993), Fundamentals of Physics , 4th edn(extended), John Wiley & Sons, New York. 3. Ohanian, H.C. (1994), Principles of Physics , Norton, New York.1Halliday, Resnick and Walker give g to one decimal place: g = 9.8 m/s 2. However, Ohanian gives it to two decimal places: g = 9.81 m/s 2.。
大学物理实验报告英文版--X光

Experiment report of X-rayPrinciple:When we speak of attenuation of x-rays, we mean the decrease in intensity that occurs when the radiation passes through matter. This attenuation is caused mainly by the two effects: scattering and absorption.Although absorption and attenuation are different physical phenomena, the transilluminated object is often referred to -inaccurately- as an absorber; this should more properly be termed an attenuator. However, this description will follow the traditional usage in some places and refer to absorbers instead of attenuators.The scattering of x-ray quanta at the atoms of the attenuator material causes a part of the radiation to change direction. This reduces the intensity in original direction. This scattering can be either elastic or entail an energy loss or shift in wavelength, i.e. Inelastic scattering.When x-ray hits a fluorescence material, it excites the material, making fluorescence lights. This is the principle of a fluorescence screen. When x-ray is used in imaging, the transmitted light will carry interior information of the object.A more sophisticated x-ray detector is the so-called Geiger-Muller counter, an instrument for detecting the presence of and measuring ionizing radiation such as the x-rays. It converts the intensity of the x-ray into counting rates. We will use such a device in our lab.Attenuation of x-rays:When passing through a material, x-ray can be attenuated by E&M interactions. For a slab of thickness x, the transmission (defined as the ratio of the transmittedradiation to the incoming), x=. µ is the attenuation coefficient, with a dimensionT eμ-of 1/distance. µis a character of the material, and it varies, for example, as a function of atomic number. We will study this dependence in this lab. Bragg Diffraction da 0Like normal lights, when x-ray transmit through material with regular optical pattern (e.g. lattice), diffraction will happen if the wavelength of the x-ray is close to the lattice space. Such diffraction on the crystal is the so-called Bragg Diffraction. If the lattice spacing is d, and the x-ray and the crystal surface forms an angle θ, the angle where maximum diffraction happens will satisfy2sin ,1,2,d n n θλ==where n is an integer and λ is the wavelength.Lab equipment:The equipment is an x-ray lab system made by Leybold Inc. A schematic is shown below.The x-ray is generated by an electron beam with controllable energy (via the potential) and current. The x-ray is going into the detection chamber to the right. There is a removableaperture which focuses the x-ray, a rotatable sample holder, and a rotatable G-M counter. At the right end of the wall, there is a fluorescence screen for imagine.Operation details of the device will be given by the manual. Basically, you need to set the high voltage (U) which determine the energy of the x-ray, the current (I), and the angle of the sample holder (target) or the detector. A knob can be used to make the adjustment on selected parameters. “Coupled” movement means one moves the target and the detector together, the former by an angle α, and the latter by an angle 2α. Make sure the lead glass window is closed before you turn on the high voltage.Attenuator (target)Left: aluminum attenuator mounted on a curved plate with thickness of 0,0.5,1.0,1.5,2.0,2.5, and 3mm. One can select different thickness by selecting angle.Right: attenuation of different materials, all with a thickness of 0.5 mm, including Polystyrene (average Z=6), Aluminum (13), Iron (26), Copper (29), Zirconium(40) andSilver(47).2.Install the aperture. Install the Zr foil onto the aperture. This is to filter out the Kαline. Squeeze the NaCl crystal onto the sample holder.In this part of the procedure we need to make sure that the X ray beam, the crystal surface and the detector is aligned. Use the following alignment procedure by the Bragg Diffraction, the process is omitted.data:The first peak appears when it ’s 7.5 degree.1. analysis:2sin ,1,2,d n n θλ== Then, 9102sin 20.5640210sin 7.5 1.4724101d n θλ--⨯⨯⨯︒===⨯ m. That is, the wavelength of X ray is 101.472410-⨯ m.2.Measure the X ray attenuation to different thickness:Install the Zr foil onto the aperture. Set HV=21 kV, I=0.05 mA, ∆β=0, ∆t=100 s.Hit target key. Change the angle sequentially to 0, 10, 20, 30, 40, 50, 60 degree (the thickness of the attenuation increase by 0.5mm each step).For each of this setting, hit “scan ” to take the data, and hit “replay ” to get the average rate.attenuation of different thicknessthickness(mm) 0.5 1 1.5 2 2.5 3 Data(1/s) 21.4 9.6 4.4 2.8 1.7 1Fit the rate as a function of thickness (with background subtraction) to get the attenuation coefficient.Fit the data in origin with exponential fit (mode = expdec1),through equation x=. We form the graph of 1/T and x.So, we get thatT eμ-Hence,So, the attenuation coefficient is110.263783.79097tμ===.Measure the X ray attenuation to materials with different atomic mass:a)Remove the Zr filter. Insert the curved attenuator holder B (different target) intothe annulus slot on the plastic mount. Set HV = 30 kV, I=1 mA, ∆β=0, ∆t=100 s. Hittarget key. Change the angle sequentially to 0, 10, 20, 30, 40, 50, 60 degree,each corresponding to a given material.b)For each of this setting, hit “scan” to take the data, and hit “replay” to getthe average rate.c)For the scan with Zr filter.attenuation of different Z, with ZrZ 6 13 26 29 40 47 Data(1/s) 9117.9 7627.4 72.9 7.7 108.9 14.4No exact rule can be found.Install the Zr filter. Repeat of Z number.The graph turns out:attenuation of different Z, without ZrZ 6 13 26 29 40 47Data(1/s) 9025.4 9027.8 8308.4 75.2 5.2 74.8Plot the rate as a function of Znumber.Also,no exact rule can be found.Conclusion:1.the wavelength of X ray is 10⨯m.1.472410-2.The rate has no exact relationship with Z.Error:Whether I check the background or not will have a influence on the wavelength. The light in the room will maybe influence the data I got. When I did the experiment with the light on, thus the light will be stronger.。
(完整word版)英文实验报告模板

Determination of heavy metals in soil by atomic absorption spectrometry(AAS)Name: XuFei Group: The 3rd groupDate: Sep。
20th 2012Part 1 The introduction1。
1The purposes(1)Learn how to operate the atomic absorption spectrometry;(2)Learn how to do the pretreatment of soil samples;(3)Get familiar with the application of atomic absorption spectrometry。
1.2The principlesAtomic Absorption Spectrometry (AAS) is a technique for measuring quantities of chemical elements present in environmental samples by measuring the absorbed radiation by the chemical element of interest。
This is done by reading the spectra produced when the sample is excited by radiation. The atoms absorb ultraviolet or visible light and make transitions to higher energy levels 。
Atomic absorption methods measure the amount of energy in the form of photons of light that are absorbed by the sample。
物理实验报告英文

物理实验报告英文Title: Investigating the Effects of Temperature on the Viscosity of Liquids Introduction:In this experiment, we aim to explore the relationship between temperature and the viscosity of liquids. Viscosity refers to a fluid's resistance to flow, and it plays a crucial role in various fields, including chemical engineering, medicine, and geology. Understanding how temperature affects viscosity can provide valuable insights into the behavior of different liquids and their applications in various industries.Experimental Setup:To conduct this experiment, we used a viscometer, a device specifically designed to measure the viscosity of liquids. The viscometer consists of a cylindrical container with a small opening at the bottom and a stopwatch to measure the time it takes for a certain volume of liquid to flow through the opening. We selected three different liquids for our experiment: water, vegetable oil, and glycerin.Procedure:1. We started by setting up the viscometer and ensuring it was clean and free from any residue.2. We filled the viscometer with water and allowed it to reach room temperature.3. Using the stopwatch, we measured the time it took for a fixed volume of water to flow through the opening.4. We repeated the process three times and calculated the average time.5. Next, we heated the water to a specific temperature using a water bath.6. Again, we measured the time it took for the water to flow through the viscometer at the elevated temperature.7. We repeated steps 5 and 6 for different temperatures, ranging from room temperature to 80°C.8. Finally, we repeated the entire process using vegetable oil and glycerin, following the same temperature range.Results and Analysis:Upon analyzing the data obtained from the experiment, we observed a clear trend between temperature and viscosity for all three liquids. As the temperature increased, the viscosity of the liquids decreased. This phenomenon can be explained by the kinetic theory of matter, which states that as temperature increases, the kinetic energy of the molecules also increases. Consequently, the intermolecular forces holding the liquid together weaken, allowing the molecules to move more freely, resulting in reduced viscosity.Additionally, we found that the rate of viscosity decrease varied among the liquids. Water exhibited the most significant change in viscosity with temperature, followed by vegetable oil and glycerin. This difference can be attributed to the molecular structure and composition of each liquid. Water, being a polar molecule, experiences stronger intermolecular forces, leading to a more significant decrease in viscosity with increasing temperature.Conclusion:In conclusion, our experiment successfully demonstrated the relationship between temperature and the viscosity of liquids. The results indicate that as temperature increases, the viscosity of liquids decreases due to the weakening of intermolecular forces. This knowledge has practical applications in various industries, such as the design of lubricants, the optimization of chemical reactions, and the understanding of fluid dynamics. Further studies can explore the effects of pressure, concentration, and other factors on viscosity to deepen our understanding of fluid behavior.。
英文的物理实验报告

英文的物理实验报告英文的物理实验报告IntroductionIn the field of science, conducting experiments and documenting the results is an essential part of the research process. This holds true for physics as well, where experimental reports play a crucial role in presenting and analyzing the findings. In this article, we will explore the structure and content of an English physics experiment report, highlighting its importance and providing tips for effective writing.Experimental SetupThe first section of a physics experiment report typically outlines the experimental setup. Here, the writer describes the apparatus used, including any instruments, equipment, and materials. It is essential to provide sufficient details so that readers can understand and replicate the experiment if needed. Clear and concise language should be used to ensure accuracy and avoid any ambiguity.MethodologyThe methodology section explains the step-by-step procedure followed during the experiment. It should be written in a logical and sequential manner, allowing readers to understand the experimental process easily. It is advisable to use active voice and past tense when describing the actions performed during the experiment. Additionally, any calculations or formulas used should be clearlystated, ensuring transparency and reproducibility.Data Collection and AnalysisAfter conducting the experiment, the next step is to collect and analyze the data obtained. In this section, the writer presents the raw data gathered during the experiment. This can be done using tables, graphs, or charts, depending on the nature of the data. It is important to label and title all figures appropriately, providing units of measurement and clear legends.Once the data is presented, the analysis begins. The writer interprets the data, looking for patterns, trends, and relationships. Statistical methods, such as calculating averages or standard deviations, may be employed to support the analysis. It is crucial to provide a clear and logical explanation of the findings, relating them back to the objectives of the experiment.DiscussionThe discussion section is where the writer provides a deeper analysis of the results obtained. This is an opportunity to compare the findings with existing theories or prior research. Any discrepancies or unexpected outcomes should be addressed and explained. The writer may also suggest possible sources of error or limitations of the experiment, demonstrating a critical understanding of the experimental process.ConclusionThe conclusion summarizes the key findings of the experiment and their implications. It should be concise and to the point, highlighting the significanceof the results. The writer may also mention any recommendations for further research or improvements to the experimental setup. It is important to avoid introducing any new information in the conclusion, as it should serve as a summary of the report.ReferencesIn scientific writing, it is crucial to acknowledge the sources of information used. The references section provides a list of all the references cited in the report. The writer should follow a specific citation style, such as APA or MLA, and provide complete and accurate information for each reference. This ensures credibility and allows readers to explore the sources further if desired.ConclusionWriting an English physics experiment report requires careful attention to detail and a clear understanding of the scientific method. By following the structure outlined above and focusing on clarity and accuracy, researchers can effectively communicate their experimental findings. Experiment reports serve as a valuable tool for the scientific community, facilitating knowledge sharing and promoting further research and discovery.。
关于物理实验的英语作文

关于物理实验的英语作文英文回答:An experiment is a scientific procedure that involves testing a hypothesis through controlled observation and data collection. It is a systematic way of investigating a phenomenon by isolating variables and manipulating them to determine their effects. Experiments can be used to test theories, validate hypotheses, and develop new knowledge in various fields of science, including physics.In physics, experiments play a crucial role in understanding the fundamental laws of nature. They allow scientists to test the validity of their theories, such as Newton's laws of motion or the laws of thermodynamics, by observing the behavior of physical systems under controlled conditions. Experiments also help in testing new theories or modifying existing ones based on the observed results.The design of a physics experiment involves identifyingthe variables to be tested, controlling for other variables that could influence the results, and determining appropriate measurement techniques. Experiments are often conducted in laboratories or controlled environments to minimize external influences and ensure accurate data collection.Data analysis is an essential aspect of any experiment. The collected data is analyzed using statistical techniques or mathematical models to identify patterns and relationships. The results are then interpreted and compared with the original hypothesis to draw conclusions about the phenomenon being investigated.Experiments in physics have contributed significantly to our understanding of the universe, from the laws that govern the motion of celestial bodies to the behavior of elementary particles. They have led to major discoveries, such as the laws of conservation of energy and momentum, the theory of relativity, and the development of quantum mechanics.中文回答:实验的定义。
大学物理波动光学英文实验报告

Diffraction grating modeling by RCWA and CM methods: diffraction efficiency synchronism studiesIvan Richter,Petr Honsa,and Pavel FialaCzech Technical University in Prague,Faculty of Nuclear Sciences and Physical EngineeringDepartment of Physical Electronics,Břehová7,11519Prague l,CZECH REPUBLICPhone:+420221912285,Fax:+42026884818,Email:richter@troja.fjfi.cvut.czAbstract:This contribution concentrates on modeling of diffraction processes in opticaldiffraction gratings(ODG).First,the approach to characterization of mechanisms and diffractionprocesses is briefly presented,together with the regions with typical diffraction regimes.Differenttypes of diffraction efficiency volume phase synchronism are then described.Different situationsare analyzed and compared concerning ODG of different types,different refractive index/reliefmodulation profiles,various modulation strengths,and incident wave polarization influence.Asexamples,the cases of conical and Littrow mounts are discussed in detail.As rigorous modelingtools,both rigorous coupled wave analysis,and coordinate transformation methods are used,implemented,and modified.2002Optical Society of AmericaOCIS codes:050.1950Diffraction gratings,050.1970Diffractive optics1.Introduction and modeling toolsIn the last years,diffractive optics modeling,i.e.both analysis(direct problem)and synthesis(inverse problem)in diffractive optics has obtained an immense attention and interest,especially due to an increasing amount of practical applications of optical diffraction gratings(ODG)and diffractive optical elements and systems.Technological possibilities of grating fabrication methods to produce e.g.high-aspect ratio diffractive structures with periods(or minimum feature sizes)comparable and smaller than the wavelength of light have also enlarged rapidly.Hence, originally-used scalar theoretical methods(analytical methods of transmittance,two wave Kogelnik's methods,thin film decomposition,etc.)became inapplicable soon,and the rigorous methods had to start their developments and beings.Apart from design,fabrication and application driven rigorous modeling,diffraction processes characterization in ODG is also important itself since it can provide a deep insight into the physical mechanisms,can separate and identify their influences,and allows to find some regions(of important parameters)with typical diffraction regimes.In this sense,it is very useful and needful for all other types of modeling.Therefore,based on our previous studies[1-8],the purpose of this contribution is mainly to present,discuss and interpret on various examples new and physically interesting results concerning the behavior of the diffraction efficiency synchronism for selected grating and experimental parameters of diffraction gratings.As rigorous modeling tools,both rigorous coupled wave analysis(RCWA)and coordinate transformation methods(CM)have been implemented and applied within this contribution.RCWA,as a standard technique for the analysis of diffraction grating properties,nowadays represents an efficient and stable modelling tool[9].Our RCWA model has implemented several modifications and improvements,and was successfully applied in our previous studies[10].The coordinate transformation method has also shown a great potential in rigorous diffraction modelling,and become a strong counterpart of RCWA methods,efficiently applicable especially to specific types of surface-relief gratings[11].This method is based on the introduction of a new coordinate system transforming a generally complicated grating surface corrugation into a simple plane surface,hence simplifying the boundary-matching problem by a great extent.Our CM model,based mainly on the Li's valuable reformulation[12]and modifications of the classical algorithm,has also been recently successfully implemented and tested.We have confirmed that while CM has appeared fast and efficient for smooth profiles,and for both input polarizations,it has showed considerably slower convergence for profiles with discontinuities.On the other hand,RCWA is practically ideal for gratings with multilevel profiles.Both methods have been found complementary,with different areas of applicability,and thus both methods are used within this contribution.2.Diffraction efficiency synchronismAs has been shown in[1-3,7],by using the proper way of interpretation,i.e.by studying the diffraction efficiency of a given diffraction order in the representation defined by the relevant independent variables(as e.g.the period to wavelength ratio(Λ/λ) and the grating depth to wavelength ratio(d/λ) − for a fixed angle of incidence),it is possible to efficiently describe and explain the complex behavior of grating diffraction efficiencies.The main advantage of such a description is that the whole class of gratings can be described altogether,and character of the diffraction efficiency synchronization(i.e.volume phase synchronism[1,2])can thus be effectively studied.This also allows one to determine the regions with typical diffraction regimes in the(Λ/λ, d/λ)representation,as has been studied previously[1,2],the synchronism periodicity and structuring[7],as well as to study the behavior within resonant regions of diffraction(threshold and guiding effects[3,8]).From a practical point of view,however,the effects of varying some important grating and diffraction setup parameters,using mainly the(Λ/λ, d/λ)synchronism,are of great importance.Hence,in this contribution,these influences have been studied and will be presented(the effects of the angle of incidence,of grating relief profiles,of input polarization,and of the value of refractive index).3.The case of conical diffractionAs an example,Fig.1shows a comparison of volume phase synchronisms for the case of conical mount(90deg.) and classical mount(0deg.),for both TE and TM polarizations,for the case of binary gratings,with the incidence angle of30deg.As can be seen,whereas the classical mount provides the Bragg synchronization,in the case of conical mount,there is no such effect.4.Different types of synchronisms,the case of Littrow mountThe diffraction efficiency dependence characterization is clearly a complicated multi-parameter problem,complexly describable using some type of proper characterization.In this sense,although the selected(Λ/λ, d/λ)synchronism appears as one of the most beneficial,other types can be also very useful(angular synchronism,combinedsynchronisms).As the second example,Fig.2shows a comparison of such combined synchronisms,again for the case of binary gratings,comparing both TE and TM polarizations.Here,at each periodΛ/λ,the incident angle is appropriately changed in order to ensure the proper Littrow mount.In the contribution,the interpretation of such behavior will be given,and usefulness of the approach will be shown.5.ConclusionsTo summarize the contribution,we have contributed to a better understanding of diffraction processes in optical diffraction gratings,by presenting and interpreting various simulation results based on rigorous diffraction modeling of RCWA and CM.The influence of important parameters on the synchronism has been evaluated,and different situations have been analyzed and discussed.6.AcknowledgmentsThis work has been partially supported by the Grant Agency of Czech Republic with contract No.202/01/D004and by the Ministry of Education of the Czech Republic Research plan CEZ:J04/98:210000022.7.References[1]I.Richter,Z.Ryzí,and P.Fiala,"Analysis of binary diffraction gratings:comparison of different approaches,"J.Modern Optics45,1335(1998).[2]P.Fiala,I.Richter,and Z.Ryzí,"Analysis of diffraction processes in gratings,"Proceedings of SPIE3820,131(1999).[3]I.Richter and P.Fiala,"Threshold and resonance effects in diffraction gratings,"Proceedings of SPIE4095,58(2000).[4]I.Richter,P.Fiala,"Volume phase synchronism in diffraction gratings:various studies,"EOS Topical Meeting Digest Series30,32(2001)(EOS Topical Meeting on Diffractive Optics,Budapest,Hungary).[5]P.Honsa,I.Richter,and P.Fiala,"Rigorous analysis of surface-relief diffraction gratings:a comparison of CM and RCWA methods,"EOSTopical Meeting Digest Series30,74(2001)(EOS Topical Meeting on Diffractive Optics,Budapest,Hungary).[6]P.Fiala,M.Matějka,I.Richter,and M.Škereň,"Diffractive optics:analysis,design,and fabrication of diffractive optical elements,"Proceedings of the New Trends in Physics Conference345,(2001)(Technical University in Brno Press,Brno,Czech Republic,2001).[7]I.Richter,P.Fiala,and P.Honsa,"Volume phase synchronism in diffraction gratings:a comparison for different situations,"Proceedings ofSPIE4438,in print(2001).[8]I.Richter and P.Fiala,"Mechanisms connected with a new diffraction order formation in surface-relief gratings,"Optik111,237(2000).[9]M.G.Moharam and T.K.Gaylord,"Diffraction analysis of dielectric surface-relief gratings,"J.Opt.Soc.Am.72,1385(1982).[10]I.Richter,P.-C.Sun,F.Xu,and Y.Fainman,"Design Considerations of Form Birefringent Microstructures,"Applied Optics34,2421(1995).[11]J.Chandezon,M.T.Dupuis,G.Cornet,and D.Maystre,"Multicoated gratings:a differential formalism applicable in the entire opticalregion,"J.Opt.Soc.Am.72,839(1982).[12]L.Li,J.Chandezon,G.Granet,and J.-P.Plumey,"Rigorous and efficient grating-analysis method made easy for optical engineers,"AppliedOptics38,304(1999).。
大学物理实验 4-2实验报告(英文版)

1 0.0512 0.0511
2 0.0511 0.0510
3 0.0513 0.0512
4 0.0512 0.0511
5 0.0515 0.0514
6 0.0513 0.0512
������0 = 0.0001������������ ������������������ =0.0512cm Data analysis: 1.������������ = ������ 2 + ∆2 ������������ = 0.004������������ 2.������������ = 1������������������������ = 5������������������������ = 0.02������������ ������������������ ± ������������ =0.512±0.004mm L± ������������ =83.25±0.5cm D± ������������ = 298.72 ± 1cm l± ������������ = 7.55 ± 0.02cm 3.
������ ������ ������ ∆������
can be known by counting the number of the weights. L can be measuredby the tape; A can be counted by using the microcalliper.∆L is too small to measure directly, we must use the Elastic modulus instrument. Light lever principle is used to measurethe small change amplification. By using reflector we can make the small length change big, in the end, we get E=8DLmg/π������ 2 l(X-������0 ). D is the distance between the reflector and the ruler, l is the length of light leverage. L is the primitive length of the steel, d is the radius of it. Procedure: 1. Adjusting instrument device Adjusting the reflector and then we can see the ruler through the telescope. Adjusting the telescope so that we can see the scale on the ruler clearly. 2. Put eight weights on the hook; write down the X on the ruler
关于物理实验的英语作文

Physics Experiments: Exploring the Laws ofNaturePhysics, the science that delves into the fundamental principles governing the universe, often finds itself at the forefront of scientific exploration. At the heart of physics lies the conduct of experiments, which are not just means to test hypotheses but also gateways to deeper understanding and potential breakthroughs.The process of conducting a physics experiment begins with the formulation of a hypothesis, a tentative explanation for a phenomenon that is yet to be proven or disproven. This hypothesis is then translated into a testable prediction, often expressed as a mathematical relationship or equation. The next step is to design the experiment, choosing appropriate equipment, setting up the necessary conditions, and ensuring the safety of the procedure.During the experimental phase, meticulous attention to detail is crucial. Measurements must be precise, and any deviations from the expected results must be carefully noted. Data collection is often a laborious task, involvingthe use of specialized instruments and techniques. However, the effort is worth it, as the data obtained can provide valuable insights into the nature of physical phenomena.Once the data has been collected, the analysis phase begins. This involves the use of statistical methods and mathematical models to interpret the data and test the hypothesis. The results of the analysis can either confirmor refute the original hypothesis, leading to a deeper understanding of the underlying physical principles.The importance of physics experiments cannot be overstated. They not only validate our understanding of the physical world but also serve as the foundation for technological advancements. The development of new materials, the optimization of energy systems, and the exploration of space are all reliant on the insights gained from physics experiments.Moreover, the skills developed through conducting physics experiments are invaluable. They foster ascientific mindset, teaching us to be objective, analytical, and critical thinkers. These skills are transferable tovarious fields, enhancing our ability to solve complex problems and make informed decisions.In conclusion, physics experiments are essential to our understanding of the universe and the advancement ofscience and technology. They require careful planning, precision, and meticulous analysis, but the rewards are immense. As we continue to delve deeper into the mysteriesof the physical world, physics experiments will remain at the forefront of our efforts to unlock its secrets.**物理实验:探索自然法则**物理学,这门探索宇宙基本法则的科学,经常站在科学探索的前沿。
大学物理实验报告英文版--全息照相

physical lab report:HolographyWriter:[Backgrounds]Lights are electromagnetic waves.A monochromatic optical wave can be mathematically expressed as a waveequation:2cos()r x A tπωφλ=+-where A is the amplitude and)2(λπϕωrt-+carries phase information. The way we viewany given object is to observe the brightness (amplitude), color (wavelength), and shape/distance (phase).A conventional photograph records the focused image of an object on a photographic film or plate. A hologram is a photographic recording of an optical interference pattern. The amplitude and phase of light coming from the object are stored in the hologram. The phase information enables us to reconstruct the original wavefront and hence obtain a three-dimensional image in space.The holography you experience in this lab will consist of two steps, a) recording: the amplitude and phase information of an object is recorded on a film, b) viewing: illuminating the film to reconstruct the object that was being filmed.This experiment uses a 658nm diode laser as a source of coherent light which irradiates the objects, and also provides a reference beam of uniform amplitude and phase. [Process]1.RecordingAt the very beginning,we prepare light path according to Fig. First,we have a dark environment .Then we adjust the path length of the reference and object beam, so that the path difference is small. Then,we adjust the devices so that both the object and reference beams are irradiating the film area uniformly.Teacher told us that the ratio between the object and reference beams should better be between 1:1 to 1:10. Then my partner keep adjusting the optics till these conditions are met. Successfully we get an optical film (wrapped in black paper) and mount it onto the holder. Then ,we expose the film to light for about 0.5 second, then dismount the film.Figure 1: recording of a hologram2.Film developmentAfter getting a film,we take it to the dark room to develop. There are three bath basins: developer, stop bath (water), and fixer. According to the instructor, we immerse the film into development liquid. My partner flip the film up and down with the tweezers and we wait till the gray-scale is similar to the color on the bottom of the basin. This usually takes 2 minutes and 25 seconds.Later,we rinse the film in the water basin for 25 seconds, and we take it to the fixer. I immerse it in the fixer for 3 minutes. We take the film to the viewing room and dry the film.3.ViewingThe principle to reconstruct image from a hologram is via light diffraction. If a laser beam irradiates onto the film exactly like the object beam, diffraction will happen on the pattern recorded on the hologram. See figure below.Figure 2: illustration of image reconstruction in hologram..We are all excited to get ready to view the film. Before viewing, we have a high expectation about it.We Use a viewing beam to irradiate the film. After having made sure the emulsion side is facing the beam, we adjust our viewing angle on the other side of the film to observe an expected 3-D image of the object.HOWEVER unfortunately,we are unlucky to find the image.No matter what angle we try,we can’t find it.We suppose it is because the angle is too large to find.So we try once again,LUCKLY,we finally find the 3-D image! -------A lovely white horse!![Feeling]In this experiment,we have a deep impression of the 3-D image. I think this experience is very unforgettable.In deed,this is where physics is attractive to us.。
大学物理实验报告英文版--测薄透镜焦距
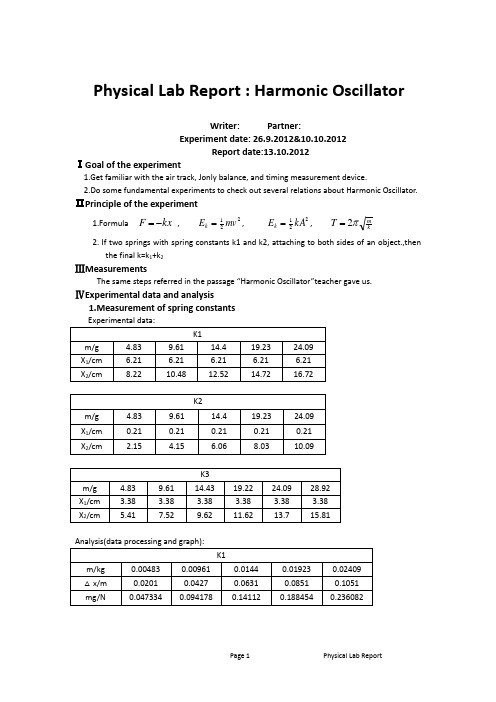
Physical Lab Report : Harmonic OscillatorWriter: Partner:Experiment date: 26.9.2012&10.10.2012Report date:13.10.2012ⅠGoal of the experiment1.Get familiar with the air track, Jonly balance, and timing measurement device.2.Do some fundamental experiments to check out several relations about Harmonic Oscillator.ⅡPrinciple of the experiment1.Formula kx F -= , 221mv E k =, 221kA E k =, kmT π2=2. If two springs with spring constants k1 and k2, attaching to both sides of an object.,then the final k=k 1+k 2ⅢMeasurementsThe same steps referred in the passage “Harmonic Oscillator ”teacher gave us.ⅣExperimental data and analysis1.Measurement of spring constantsFrom the graph,we know that k1=2.2202N/m,and R2=0.9995 shows that mg and △x are very linearly relative.k2m/kg 0.00483 0.00961 0.0144 0.01923 0.02409△x/m 0.0194 0.0394 0.0585 0.0782 0.0988mg/N 0.047334 0.094178 0.14112 0.188454 0.236082From the graph,we know that k2=2.3872N/m,and R2=0.9999 shows that mg and △x are quite linearly relative.K3m/kg 0.00483 0.00961 0.01443 0.01922 0.02409 0.02892△x/m 0.0203 0.0414 0.0624 0.0825 0.1033 0.1244mg/N 0.047334 0.094178 0.141414 0.188356 0.236082 0.283416From the graph,we know that k 3=2.2759N/m,and R 2=0.9999 shows that mg and △x are quite linearly relative.2.Study the relationship between oscillation period and the mass of the oscillator Experimental data m/g 181.1 185.89 190.68 195.51 200.29 10T/ms 12634.112784.412940.5 13098.513251.2m s /g22.07Analysis(data processing and graph)M=m+m s /3M/kg0.188456667 0.193246667 0.198036667 0.202866667 0.207646667 22A T -1.596204828 1.634408834 1.674565403 1.715707023 1.755943014 T/s 1.263411.278441.294051.309851.32512From the graph,we know that T 2 and M are quite linearly relative.And kM T π2=,sokM T 224π==8.3496N/m,we can figure out k=4.7282N/m. And k 1+k 2=2.2202+2.3872=4.6074N/m,the error rate is 2.62%,which is acceptable .3.Study the relationship between oscillation amplitude and period.Experimental data: m=192.41g ms=22.07gA/cm 10 20 30 35 40 50 10T/ms12618.612617.312620.712622.112619.612615.1Analysis(data processing and graph) A/m 0.10.20.30.350.40.5T/s 1.26186 1.26173 1.26207 1.26221 1.26196 1.26151From the graph,R 2=0.0303 says that A and T have little relation.4.Study the relation between v max 2 and A 2m=192.41g m s =22.07g M=m+m s /3=199.77g v max /cm/s 48.8 96.52 143.27 166.94 190.84 239.23 A/cm10203035405022/m A0.01 0.04 0.09 0.1225 0.16 0.2522max )//(s m v0.238144 0.93161104 2.05262929 2.78689636 3.64199056 5.72309929From the graph ,we can know v max2 and A2 are strictly linearly relative.ⅤDiscussion and conclusionIn this experiment,I have become familiar with some experimental device and have had some results about Harmonic Oscillator:1.The spring constants are k1=2.2202N/m,k2=2.3872N/m,k3=2.2759N/m.2. In the range of permitted errors,T2 and M are linearly relative.3.In the range of permitted errors,A and T have no relation.4.In the range of permitted errors,v max2 and A2 are linearly relative.Errors analysis:1.Ignorance the affection of air friction.2.Errors when doing data processing.3.Errors of the measurement devices.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理实验报告Ferroelectric Control of Spin PolarizationABSTRACTA current drawback of spintronics is the large power that is usually required for magnetic writing, in contrast with nanoelectronics, which relies on “zero-current,” gate-controlled operations. Efforts have been made to control the spin-relaxation rate, the Curie temperature, or the magnetic anisotropy with a gate voltage, but these effects are usually small and volatile. We used ferroelectric tunnel junctions with ferromagnetic electrodes to demonstrate local, large, and nonvolatile control of carrier spin polarization by electrically switching ferroelectric polarization. Our results represent a giant type of interfacial magnetoelectric coupling and suggest a low-power approach for spin-based information control.Controlling the spin degree of freedom by purely electrical means is currently an important challenge in spintronics (1, 2). Approaches based on spin-transfer torque (3) have proven very successful in controlling the direction of magnetization in a ferromagnetic layer, but they require the injection of high current densities. An ideal solution would rely on the application of an electric field across an insulator, as in existing nanoelectronics. Early experiments have demonstrated the volatile modulation of spin-based properties with a gate voltage applied through a dielectric. Notable examples include the gate control of the spin-orbit interaction in III-V quantum wells (4), the Curie temperature T C (5), or the magnetic anisotropy (6) in magnetic semiconductors with carrier-mediated exchange interactions; for example, (Ga,Mn)As or (In,Mn)As. Electric field–induced modifications of magnetic anisotropy at room temperature have also been reported recently in ultrathin Fe-based layers (7, 8).A nonvolatile extension of this approach involves replacing the gate dielectric by a ferroelectric and taking advantage of the hysteretic response of its order parameter (polarization) with an electric field. When combined with (Ga,Mn)As channels, forinstance, a remanent control of T C over a few kelvin was achieved through polarization-driven charge depletion/accumulation (9, 10), and the magnetic anisotropy was modified by the coupling of piezoelectricity and magnetostriction (11, 12). Indications of an electrical control of magnetization have also been provided in magnetoelectric heterostructures at room temperature (13–17).Recently, several theoretical studies have predicted that large variations of magnetic properties may occur at interfaces between ferroelectrics and high-T C ferromagnets such as Fe (18–20), Co2MnSi (21), or Fe3O4 (22). Changing the direction of the ferroelectric polarization has been predicted to influence not only the interfacial anisotropy and magnetization, but also the spin polarization. Spin polarization [i.e., the normalized difference in the density of states (DOS) of majority and minority spin carriers at the Fermi level (E F)] is typically the key parameter controlling the response of spintronics systems, epitomized by magnetic tunnel junctions in which the tunnel magnetoresistance (TMR) is related to the electrode spin polarization by the Jullière formula (23). These predictions suggest that the nonvolatile character of ferroelectrics at the heart of ferroelectric random access memory technology (24) may be exploited in spintronics devices such as magnetic random access memories or spin field-effect transistors (2). However, the nonvolatile electrical control of spin polarization has not yet been demonstrated.We address this issue experimentally by probing the spin polarization of electrons tunneling from an Fe electrode through ultrathin ferroelectric BaTiO3 (BTO) tunnel barriers (Fig. 1A). The BTO polarization can be electrically switched to point toward oraway from the Fe electrode. We used a half-metallic La0.67Sr0.33MnO3(LSMO) (25) bottom electrode as a spin detector in these artificial multiferroic tunnel junctions (26, 27). Magnetotransport experiments provide evidence for a large and reversible dependence of the TMR on ferroelectric polarization direction.Fig. 1(A) Sketch of the nanojunction defined by electrically controlled nanoindentation. A thin resist is spin-coated on the BTO(1 nm)/LSMO(30 nm) bilayer. The nanoindentation is performed with a conductive-tip atomic force microscope, and the resultingnano-hole is filled by sputter-depositing Au/CoO/Co/Fe. (B) (Top) PFM phase image of a BTO(1 nm)/LSMO(30 nm) bilayer after poling the BTO along 1-by-4–μm stripes with either a negative or positive (tip-LSMO) voltage. (Bottom) CTAFM image of an unpoled area of a BTO(1 nm)/LSMO(30 nm) bilayer. Ω, ohms. (C) X-ray absorption spectra collected at room temperature close to the Fe L3,2 (top), Ba M5,4 (middle), and TiL3,2 (bottom) edges on an AlO x(1.5 nm)/Al(1.5 nm)/Fe(2 nm)/BTO(1 nm)/LSMO(30 nm)//NGO(001) heterostructure. (D) HRTEM and (E) HAADF images of the Fe/BTO interface in a Ta(5 nm)/Fe(18 nm)/BTO(50 nm)/LSMO(30 nm)//NGO(001) heterostructure. The white arrowheads in (D) indicate the lattice fringes of {011} planes in the iron layer. [110] and [001] indicate pseudotetragonal crystallographic axes of the BTO perovskite.The tunnel junctions that we used in this study are based on BTO(1 nm)/LSMO(30 nm) bilayers grown epitaxially onto (001)-oriented NdGaO3 (NGO) single-crystal substrates (28). The large (~180°) and stable piezoresponse force microscopy (PFM) phase contrast (28) between negatively and positively poled areas (Fig. 1B, top) indicates that the ultrathin BTO films are ferroelectric at room temperature (29). The persistence of ferroelectricity for such ultrathin films of BTO arises from the large lattice mismatch with the NGO substrate (–3.2%), which is expected to dramatically enhance ferroelectric properties in this highly strained BTO (30). The local topographical and transport properties of the BTO(1 nm)/LSMO(30 nm) bilayers were characterized by conductive-tip atomic force microscopy (CTAFM) (28). The surface is very smooth with terraces separated by one-unit-cell–high steps, visible in both the topography (29) and resistance mappings (Fig. 1B, bottom). No anomalies in the CTAFM data were observed over lateral distances on the micrometer scale.We defined tunnel junctions from these bilayers by a lithographic technique based on CTAFM (28, 31). Top electrical contacts of diameter ~10 to 30 nm can be patterned by this nanofabrication process. The subsequent sputter deposition of a 5-nm-thick Fe layer, capped by a Au(100 nm)/CoO(3.5 nm)/Co(11.5 nm) stack to increase coercivity, defined a set of nanojunctions (Fig. 1A). The same Au/CoO/Co/Fe stack was deposited on another BTO(1 nm)/LSMO(30 nm) sample for magnetic measurements. Additionally, a Ta(5 nm)/Fe(18 nm)/BTO(50 nm)/LSMO(30 nm) sample and a AlO x(1.5 nm)/Al(1.5nm)/Fe(2 nm)/BTO(1 nm)/LSMO(30 nm) sample were realized for structural and spectroscopic characterizations.We used both a conventional high-resolution transmission electron microscope (HRTEM) and the NION UltraSTEM 100 scanning transmission electron microscope (STEM) to investigate the Fe/BTO interface properties of the Ta/Fe/BTO/LSMO sample. The epitaxial growth of the BTO/LSMO bilayer on the NGO substrate was confirmed by HRTEM and high-resolution STEM images. The low-resolution, high-angle annular dark field (HAADF) image of the entire heterostructure shows the sharpness of theLSMO/BTO interface over the studied area (Fig. 1E, top). Figure 1D reveals a smooth interface between the BTO and the Fe layers. Whereas the BTO film is epitaxially grown on top of LSMO, the Fe layer consists of textured nanocrystallites. From the in-plane (a) and out-of-plane (c) lattice parameters in the tetragonal BTO layer, we infer that c/a = 1.016 ± 0.008, in good agreement with the value of 1.013 found with the use of x-ray diffraction (29). The interplanar distances for selected crystallites in the Fe layer [i.e.,~2.03 Å (Fig. 1D, white arrowheads)] are consistent with the {011} planes ofbody-centered cubic (bcc) Fe.We investigated the BTO/Fe interface region more closely in the HAADF mode of the STEM (Fig. 1E, bottom). On the BTO side, the atomically resolved HAADF image allows the distinction of atomic columns where the perovskite A-site atoms (Ba) appear as brighter spots. Lattice fringes with the characteristic {100} interplanar distances of bcc Fe (~2.86 Å) can be distinguished on the opposite side. Subtle structural, chemical, and/or electronic modifications may be expected to occur at the interfacial boundarybetween the BTO perovskite-type structure and the Fe layer. These effects may lead to interdiffusion of Fe, Ba, and O atoms over less than 1 nm, or the local modification of the Fe DOS close to E F, consistent with ab initio calculations of the BTO/Fe interface (18–20).To characterize the oxidation state of Fe, we performed x-ray absorption spectroscopy (XAS) measurements on a AlO x(1.5 nm)/Al(1.5 nm)/Fe(2 nm)/BTO(1 nm)/LSMO(30 nm) sample (28). The probe depth was at least 7 nm, as indicated by the finite XAS intensity at the La M4,5 edge (28), so that the entire Fe thickness contributed substantially to the signal. As shown in Fig. 1C (top), the spectrum at the Fe L2,3 edge corresponds to that of metallic Fe (32). The XAS spectrum obtained at the Ba M4,5 edge (Fig. 1C, middle) is similar to that reported for Ba2+ in (33). Despite the poor signal-to-noise ratio, the Ti L2,3 edge spectrum (Fig. C, bottom) shows the typical signature expected for a valence close to 4+ (34). From the XAS, HRTEM, and STEM analyses, we conclude that theFe/BTO interface is smooth with no detectable oxidation of the Fe layer within a limit of less than 1 nm.After cooling in a magnetic field of 5 kOe aligned along the [110] easy axis of pseudocubic LSMO (which is parallel to the orthorhombic [100] axis of NGO), we characterized the transport properties of the junctions at low temperature (4.2K). Figure 2A (middle) shows a typical resistance–versus–magnetic field R(H) cycle recorded at a bias voltage of –2 mV (positive bias corresponds to electrons tunneling from Fe to LSMO). The bottom panel of Fig. 2A shows the magnetic hysteresisloop m(H) of a similar unpatterned sample measured with superconducting quantuminterference device (SQUID) magnetometry. When we decreased the magnetic field from a large positive value, the resistance dropped in the –50 to –250 Oe range and then followed a plateau down to –800 Oe, after which it sharply returned to thehigh-resistance state. We observed a similar response when cycling the field back to large positive values. A comparison with the m(H) loop indicates that the switching fields in R(H) correspond to changes in the relative magnetic configuration of the LSMO and Fe electrodes from parallel (at high field) to antiparallel (at low field). The magnetically softer LSMO layer switched at lower fields (50 to 250 Oe) compared with the Fe layer, for which coupling to the exchange-biased Co/CoO induces larger and asymmetric coercive fields (–800 Oe, 300 Oe). The observed R(H) corresponds to a negative TMR = (R ap–R p)/R ap of –17% [R p and R ap are the resistance in the parallel (p) and antiparallel (ap) magnetic configurations, respectively; see the sketches in Fig. 2A]. Within the simple Jullière model of TMR (23) and considering the large positive spin polarization of half-metallic LSMO (25), this negative TMR corresponds to a negative spin polarization for bcc Fe at the interface with BTO, in agreement with ab initio calculations (18–20).Fig. 2(A) (Top) Device schematic with black arrows to indicate magnetizations. p, parallel; ap, antiparallel. (Middle) R(H) recorded at –2 mV and 4.2 K showing negative TMR. (Bottom) m(H) recorded at 30 K with a SQUID magnetometer. emu, electromagnetic units. (B) (Top) Device schematic with arrows to indicate ferroelectric polarization. (Bottom) I(V DC) curves recorded at 4.2 K after poling the ferroelectric down (orange curve) or up (brown curve). The bias dependence of the TER is shown in the inset.As predicted (35–38) and demonstrated (29) previously, the tunnel current across a ferroelectric barrier depends on the direction of the ferroelectric polarization. We also observed this effect in our Fe/BTO/LSMO junctions. As can be seen in Fig. 2B, after poling the BTO at 4.2 K to orient its polarization toward LSMO or Fe (with a poling voltage of VP–≈ –1 V or VP+≈ 1 V, respectively; see Fig. 2B sketches),current-versus-voltage I(V DC) curves collected at low bias voltages showed a finite difference corresponding to a tunnel electroresistance as large as TER = (I VP+–I VP–)/I VP–≈ 37% (Fig. 2B, inset). This TER can be interpreted within an electrostatic model (36–39), taking into account the asymmetric deformation of the barrier potential profile that is created by the incomplete screening of polarization charges by different Thomas-Fermi screening lengths at Fe/BTO and LSMO/BTO interfaces.Piezoelectric-related TER effects (35, 38) can be neglected as the piezoelectric coefficient estimated from PFM experiments is too small in our clamped films (29). TER measurements performed on a BTO(1 nm)/LSMO(30 nm) bilayer with the use of a CTAFM boron-doped diamond tip as the top electrode showed values of ~200%(29). Given the strong sensitivity of the TER on barrier parameters and barrier-electrode interfaces, these two values are not expected to match precisely. We anticipate that the TER variation between Fe/BTO/LSMO junctions and CTAFM-based measurements is primarily the result of different electrostatic boundary conditions.Switching the ferroelectric polarization of a tunnel barrier with voltage pulses is also expected to affect the spin-dependent DOS of electrodes at a ferromagnet/ferroelectric interface. Interfacial modifications of the spin-dependent DOS of the half-metallic LSMO by the ferroelectric BTO are not likely, as no states are present for the minority spins up to ~350 meV above E F (40, 41). For 3d ferromagnets such as Fe, large modifications of the spin-dependent DOS are expected, as charge transfer between spin-polarized empty and filled states is possible. For the Fe/BTO interface, large changes have been predicted through ab initio calculations of 3d electronic states of bcc Fe at the interface with BTO by several groups (18–20).To experimentally probe possible changes in the spin polarization of the Fe/BTO interface, we measured R(H) at a fixed bias voltage of –50 mV after aligning the ferroelectric polarization of BTO toward Fe or LSMO. R(H) cycles were collected for each direction of the ferroelectric polarization for two typical tunnel junctions of the same sample (Fig. 3, B and C, for junction #1; Fig. 3, D and E, for junction #2). In both junctions at the saturating magnetic field, high- and low-resistance states are observed when the ferroelectric polarization points toward LSMO or Fe, respectively, with a variation of ~ 25%. This result confirms the TER observations in Fig. 2B.Fig. 3(A) Sketch of the electrical control of spin polarization at the Fe/BTO interface.(B and C) R(H) curves for junction #1 (V DC = –50 mV, T = 4.2 K) after poling the ferroelectric barrier down or up, respectively. (D and E) R(H) curves for junction #2 (V DC = –50 mV, T= 4.2 K) after poling the ferroelectric barrier down or up, respectively.More interestingly, here, the TMR is dramatically modified by the reversal of BTO polarization. For junction #1, the TMR amplitude changes from –17 to –3% when the ferroelectric polarization is aligned toward Fe or LSMO, respectively (Fig. 3, B and C). Similarly for junction #2, the TMR changes from –45 to –19%. Similar results were obtained on Fe/BTO (1.2 nm)/LSMO junctions (28). Within the Jullière model (23), these changes in TMR correspond to a large (or small) spin polarization at the Fe/BTO interface when the ferroelectric polarization of BTO points toward (or away from) the Fe electrode. These experimental data support our interpretation regarding the electrical manipulation of the spin polarization of the Fe/BTO interface by switching the ferroelectric polarization of the tunnel barrier.To quantify the sensitivity of the TMR with the ferroelectric polarization, we define a term, the tunnel electromagnetoresistance, as TEMR = (TMR VP+–TMR VP–)/TMR VP–. Largevalues for the TEMR are found for junctions #1 (450%) and #2 (140%), respectively. This electrical control of the TMR with the ferroelectric polarization is repeatable, as shown in Fig. 4 for junction #1 where TMR curves are recorded after poling the ferroelectric up, down, up, and down, sequentially (28).Fig. 4TMR(H) curves recorded for junction #1 (V DC = –50 mV, T = 4.2 K) after poling the ferroelectric up (VP+), down (VP–), up (VP+), and down (VP–).For tunnel junctions with a ferroelectric barrier and dissimilar ferromagnetic electrodes, we have reported the influence of the electrically controlled ferroelectric barrier polarization on the tunnel-current spin polarization. This electrical influence over magnetic degrees of freedom represents a new and interfacial magnetoelectric effect that is large because spin-dependent tunneling is very sensitive to interfacial details. Ferroelectrics can provide a local, reversible, nonvolatile, and potentially low-power means of electrically addressing spintronics devices.Supporting Online Material/cgi/content/full/science.1184028/DC1Materials and MethodsFigs. S1 to S5References∙Received for publication 30 October 2009.∙Accepted for publication 4 January 2010.References and Notes1. C. Chappert, A. Fert, F. N. Van Dau, The emergence of spin electronics indata storage. Nat. Mater. 6,813 (2007).2.I. Žutić, J. Fabian, S. Das Sarma, Spintronics: Fundamentals andapplications. Rev. Mod. Phys. 76,323 (2004).3.J. C. Slonczewski, Current-driven excitation of magnetic multilayers. J.Magn. Magn. Mater. 159, L1(1996).4.J. Nitta, T. Akazaki, H. Takayanagi, T. Enoki, Gate control of spin-orbit interaction in an inverted In0.53Ga0.47As/In0.52Al0.48Asheterostructure. Phys. Rev. Lett. 78, 1335 (1997).5.H. Ohno et al., Electric-field control offerromagnetism. Nature 408, 944 (2000).6. D. Chiba et al., Magnetization vector manipulation by electricfields. Nature 455, 515 (2008).7.M. Weisheit et al., Electric field–induced modification of magnetism inthin-film ferromagnets. Science315, 349 (2007).8.T. Maruyama et al., Large voltage-induced magnetic anisotropy changein a few atomic layers of iron.Nat. Nanotechnol. 4, 158 2009).9.S. W. E. Riester et al., Toward a low-voltage multiferroic transistor:Magnetic (Ga,Mn)As under ferroelectric control. Appl. Phys.Lett. 94, 063504 (2009).10.I. Stolichnov et al., Non-volatile ferroelectric control of ferromagnetismin (Ga,Mn)As. Nat. Mater. 7, 464(2008).11. C. Bihler et al., Ga1−x Mn x As/piezoelectric actuator hybrids: A modelsystem for magnetoelastic magnetization manipulation. Phys. Rev.B 78, 045203 (2008).12.M. Overby, A. Chernyshov, L. P. Rokhinson, X. Liu, J. K. Furdyna, GaMnAs-based hybrid multiferroic memory device. Appl. Phys.Lett. 92, 192501 (2008).13. C. Thiele, K. Dörr, O. Bilani, J. Rödel, L. Schultz, Influence of strain on themagnetization and magnetoelectric effect inLa0.7A0.3MnO3∕PMN-PT(001)(A=Sr,Ca). Phys.Rev.B 75, 054408 (2007).14.W. Eerenstein, M. Wiora, J. L. Prieto, J. F. Scott, N. D. Mathur, Giantsharp and persistent converse magnetoelectric effects in multiferroic epitaxial heterostructures. Nat. Mater. 6, 348 (2007).15.T. Kanki, H. Tanaka, T. Kawai, Electric control of room temperatureferromagnetism in a Pb(Zr0.2Ti0.8)O3/La0.85Ba0.15MnO3 field-effect transistor. Appl.Phys. Lett. 89, 242506 (2006).16.Y.-H. Chu et al., Electric-field control of local ferromagnetism using amagnetoelectric multiferroic. Nat. Mater. 7, 478 2008).17.S. Sahoo et al., Ferroelectric control of magnetism in BaTiO3∕Feheterostructures via interface strain coupling. Phys. Rev. B 76, 092108 (2007). 18. C.-G. Duan, S. S. Jaswal, E. Y. Tsymbal, Predicted magnetoelectric effectin Fe/BaTiO3 multilayers: Ferroelectric control of magnetism. Phys. Rev.Lett. 97, 047201 (2006).19.M. Fechner et al., Magnetic phase transition in two-phase multiferroicspredicted from first principles.Phys. Rev. B 78, 212406 (2008).20.J. Lee, N. Sai, T. Cai, Q. Niu, A. A. Demkov, preprint availableat /abs/0912.3492v1.21.K. Yamauchi, B. Sanyal, S. Picozzi, Interface effects at ahalf-metal/ferroelectric junction. Appl. Phys. Lett. 91, 062506 (2007).22.M. K. Niranjan, J. P. Velev, C.-G. Duan, S. S. Jaswal, E. Y. Tsymbal, Magnetoelectric effect at the Fe3O4/BaTiO3 (001) interface: A first-principles study. Phys. Rev. B 78, 104405 (2008).23.M. Jullière, Tunneling between ferromagnetic films. Phys. Lett.A 54, 225 (1975).24.J. F. Scott, Applications of modern ferroelectrics. Science 315, 954 (2007).25.M. Bowen et al., Nearly total spin polarization in La2/3Sr1/3MnO3 fromtunneling experiments. Appl. Phys. Lett. 82, 233 (2003).26.J. P. Velev et al., Magnetic tunnel junctions with ferroelectric barriers:Prediction of four resistance states from first principles. Nano Lett. 9, 427 (2009).27. F. Yang et al., Eight logic states of tunneling magnetoelectroresistancein multiferroic tunnel junctions.J. Appl. Phys. 102, 044504 (2007).28.Materials and methods are available as supporting materialon Science Online.29.V. Garcia et al., Giant tunnel electroresistance for non-destructivereadout of ferroelectric states. Nature460, 81 (2009).30.K. J. Choi et al., Enhancement of ferroelectricity in strained BaTiO3 thinfilms. Science 306, 1005(2004).31.K. Bouzehouane et al., Nanolithography based on real-time electricallycontrolled indentation with an atomic force microscope for nanocontactelaboration. Nano Lett. 3, 1599 (2003).32.T. J. Regan et al., Chemical effects at metal/oxide interfaces studied byx-ray-absorption spectroscopy.Phys. Rev. B 64, 214422 (2001).33.N. Hollmann et al., Electronic and magnetic properties of the kagomesystems YBaCo4O7 and YBaCo3M O7 (M=Al, Fe). Phys. Rev. B 80, 085111 (2009).34.M. Abbate et al., Soft-x-ray-absorption studies of the location of extracharges induced by substitution in controlled-valence materials. Phys. Rev.B 44, 5419 (1991).35. E. Y. Tsymbal, H. Kohlstedt, Tunneling across aferroelectric. Science 313, 181 (2006).36.M. Ye. Zhuravlev, R. F. Sabirianov, S. S. Jaswal, E. Y. Tsymbal, Giantelectroresistance in ferroelectric tunnel junctions. Phys. Rev.Lett. 94, 246802 (2005).37.M. Ye. Zhuravlev, R. F. Sabirianov, S. S. Jaswal, E. Y. Tsymbal, Erratum:Giant electroresistance in ferroelectric tunnel junctions. Phys. Rev.Lett. 102, 169901 2009).38.H. Kohlstedt, N. A. Pertsev, J. Rodriguez Contreras, R. Waser, Theoreticalcurrent-voltage characteristics of ferroelectric tunnel junctions. Phys. Rev.B 72, 125341 (2005).39.M. Gajek et al., Tunnel junctions with multiferroic barriers. Nat.Mater. 6, 296 (2007).40.M. Bowen et al., Spin-polarized tunneling spectroscopy in tunneljunctions with half-metallic electrodes.Phys. Rev. Lett. 95, 137203 (2005).41.J. D. Burton, E. Y. Tsymbal, Prediction of electrically induced magneticreconstruction at the manganite/ferroelectric interface. Phys. Rev.B 80, 174406 (2009).42.We thank R. Guillemet, C. Israel, M. E. Vickers, R. Mattana, J.-M. George,and P. Seneor for technical assistance, and C. Colliex for fruitful discussions on the microscopy measurements. This study was partially supported by theFrance-U.K. Partenariat Hubert Curien Alliance program, the French RéseauThématique de Recherche Avancée Triangle de la Physique, the European Union (EU) Specific Targeted Research Project (STRep) Manipulating the Coupling inMultiferroic Films, EU STReP Controlling Mesoscopic Phase Separation, U.K. Engineering and Physical Sciences Research Council grant EP/E026206/I, French C-Nano Île de France, French Agence Nationale de la Recherche (ANR) Oxitronics, French ANR Alicante, the European Enabling Science and Technology through European Elelctron Microscopy program, and the French Microscopie Electronique et Sonde Atomique network. X.M.acknowledges support from Comissionat per a Universitats i Recerca (Generalitat de Catalunya).。
