模式识别作业三
模式识别作业题(2)

答:不是最小的。首先要明确当我们谈到最小最大损失判决规则时,先验概率是未知的, 而先验概率的变化会导致错分概率变化, 故错分概率也是一个变量。 使用最小最大损 失判决规则的目的就是保证在先验概率任意变化导致错分概率变化时, 错分概率的最 坏(即最大)情况在所有判决规则中是最好的(即最小)。 4、 若 λ11 = λ22 =0, λ12 = λ21 ,证明此时最小最大决策面是来自两类的错误率相等。 证明:最小最大决策面满足 ( λ11 - λ22 )+( λ21 - λ11 ) 容易得到
λ11 P(ω1 | x) + λ12 P(ω2 | x) < λ21 P(ω1 | x) + λ22 P(ω2 | x) ( λ21 - λ11 ) P (ω1 | x) >( λ12 - λ22 ) P (ω2 | x) ( λ21 - λ11 ) P (ω1 ) P ( x | ω1 ) >( λ12 - λ22 ) P (ω2 ) P ( x | ω2 ) p( x | ω1 ) (λ 12 − λ 22) P(ω2 ) > 即 p( x | ω2 ) ( λ 21 − λ 11) P (ω1 )
6、设总体分布密度为 N( μ ,1),-∞< μ <+∞,并设 X={ x1 , x2 ,… xN },分别用最大似然 估计和贝叶斯估计计算 μ 。已知 μ 的先验分布 p( μ )~N(0,1)。 解:似然函数为:
∧Байду номын сангаас
L( μ )=lnp(X|u)=
∑ ln p( xi | u) = −
i =1
N
模式识别第三章作业及其解答
模式识别大作业

一、问题描述现有sonar 和wdbc 这两个样本数据集,取一半数据作为训练样本集,其余数据作为测试样本集,通过编程实现分别用C 均值算法对测试样本集中的数据进行分类,进行10次分类求正确率的平均值。
二、算法描述1.初始化:选择c 个代表点,...,,321c p p p p2.建立c 个空间聚类表:C K K K ...,213.按照最小距离法则逐个对样本X 进行分类:),(),,(min arg J i iK x add p x j ∂=4.计算J 及用各聚类列表计算聚类均值,并用来作为各聚类新的代表点(更新代表点)5.若J 不变或代表点未发生变化,则停止。
否则转2.),(1∑∑=∈=ci K x i i p x J δ6.计算正确率:将dtat(i,1)与trueflag(i,1)(i=1~n )进行比较,统计正确分类的样本数,并计算正确率将上述过程循环10次,得到10次的正确率,并计算平均正确率ave算法流程图三、实验数据表1 实验数据四、实验结果表2 实验结果准确率(%)注:表中准确率是十次实验结果的平均值五、程序源码用C均值算法对sonar分类(对wdbc分类的代码与之类似)clc;clear;accuracy = 0;for i = 1:10data = xlsread('sonar.xls');data = data';%初始划分2个聚类rand(:,1:size(data,2)) = data(:,randperm(size(data,2))'); %使矩阵元素按列重排A(:,1) = rand(:,1);B(:,1) = rand(:,2); %选取代表点m = 1;n = 1;for i = 3:size(rand,2)temp1 = rand(:,i) - A(:,1);temp2 = rand(:,i) - B(:,1);temp1(61,:) = [];temp2(61,:) = []; %去掉标号后再计算距离if norm(temp1) < norm(temp2)m = m + 1; %A类中样本个数A(:,m) = rand(:,i);elsen = n + 1; %B类中样本个数B(:,n) = rand(:,i);endend%划分完成m1 = mean(A,2);m2 = mean(B,2);%计算JeJ = 0;for i = 1:mtemp = A(:,i) - m1;temp(61,:) = []; %去掉标号的均值J = J + norm(temp)^2;endfor i = 1:ntemp = B(:,i) - m2;temp(61,:) = [];J = J + norm(temp)^2;endtest = [A,B];N = 0; %Je不变的次数while N < m + nrarr = randperm(m + n); %产生1-208即所有样本序号的随机不重复序列向量y = test(:,rarr(1,1));if rarr(1,1) <= m %y属于A类时if m == 1continueelsetemp1 = y - m1;temp1(61,:) = [];temp2 = y - m2;temp2(61,:) = [];p1 = m / (m - 1) * norm(temp1);p2 = n / (n + 1) * norm(temp2);if p2 < p1test = [test,y];test(:,rarr(1,1)) = [];m = m - 1;n = n + 1;endendelse %y属于B类时if n == 1continueelsetemp1 = y - m1;temp1(61,:) = [];temp2 = y - m2;temp2(61,:) = [];p1 = m / (m + 1) * norm(temp1);p2 = n / (n - 1) * norm(temp2);if p1 < p2test = [y,test];test(:,rarr(1,1)) = [];m = m + 1;n = n - 1;endendendA(:,1:m) = test(:,1:m);B(:,1:n) = test(:,m + 1:m + n);m1 = mean(A,2);m2 = mean(B,2);%计算JetempJ = 0;for i = 1:mtemp = A(:,i) - m1;temp(61,:) = []; %去掉标号的均值tempJ = tempJ + norm(temp)^2;endfor i = 1:ntemp = B(:,i) - m2;temp(61,:) = [];tempJ = tempJ + norm(temp)^2;endif tempJ == JN = N + 1;elseJ = tempJ;endend %while循环结束%判断正确率correct = 0;false = 0;A(:,1:m) = test(:,1:m);B(:,1:n) = test(:,m + 1:m + n);c = mean(A,2);if abs(c(61,1) - 1) < abs(c(61,1) - 2) %聚类A中大多为1类元素for i = 1:mif A(61,i) == 1correct = correct + 1;elsefalse = false + 1;endendfor i = 1:nif B(61,i) == 2correct = correct + 1;elsefalse = false + 1;endendelse %聚类A中大多为2类元素for i = 1:mif A(61,i) == 2correct = correct + 1;elsefalse = false + 1;endendfor i = 1:nif B(61,i) == 1correct = correct + 1;elsefalse = false + 1;endendendaccuracy = accuracy + correct / (correct + false);endaver_accuracy = accuracy / 10fprintf('用C均值算法对sonar进行十次分类的结果的平均正确率为%.2d %%.\n',aver_accuracy*100)六.实验心得本算法确定的K 个划分到达平方误差最小。
模式识别作业三道习题

K7 ( X ) K6 ( X ) 1 第八步:取 X 4 w2 , K 7 ( X 4 ) 32 0 ,故 0 K8 ( X ) K 7 ( X ) 0 第九步:取 X 1 w1 , K8 ( X 1 ) 32 0 ,故 1 K 9 ( X ) K8 ( X ) 0 第十步:取 X 2 w1 , K9 ( X 2 ) 32 0 ,故 1 K10 ( X ) K9 ( X )
2
K ( X , X k ) exp{ || X X k || 2} exp{[( x 1 xk 1) 2 ( x 2 xk 2 ) 2]} x1 X = x2 ,训练样本为 X k 。 其中
模式识别大作业

模式识别专业:电子信息工程班级:电信****班学号:********** 姓名:艾依河里的鱼一、贝叶斯决策(一)贝叶斯决策理论 1.最小错误率贝叶斯决策器在模式识别领域,贝叶斯决策通常利用一些决策规则来判定样本的类别。
最常见的决策规则有最大后验概率决策和最小风险决策等。
设共有K 个类别,各类别用符号k c ()K k ,,2,1 =代表。
假设k c 类出现的先验概率()k P c以及类条件概率密度()|k P c x 是已知的,那么应该把x 划分到哪一类才合适呢?若采用最大后验概率决策规则,首先计算x 属于k c 类的后验概率()()()()()()()()1||||k k k k k Kk k k P c P c P c P c P c P P c P c ===∑x x x x x然后将x 判决为属于kc ~类,其中()1arg max |kk Kk P c ≤≤=x若采用最小风险决策,则首先计算将x 判决为k c 类所带来的风险(),k R c x ,再将x 判决为属于kc ~类,其中()min ,kkk R c =x可以证明在采用0-1损失函数的前提下,两种决策规则是等价的。
贝叶斯决策器在先验概率()k P c 以及类条件概率密度()|k P c x 已知的前提下,利用上述贝叶斯决策规则确定分类面。
贝叶斯决策器得到的分类面是最优的,它是最优分类器。
但贝叶斯决策器在确定分类面前需要预知()k P c 与()|k P c x ,这在实际运用中往往不可能,因为()|k P c x 一般是未知的。
因此贝叶斯决策器只是一个理论上的分类器,常用作衡量其它分类器性能的标尺。
最小风险贝叶斯决策可按下列步骤进行: (1)在已知)(i P ω,)(i X P ω,i=1,…,c 及给出待识别的X 的情况下,根据贝叶斯公式计算出后验概率:∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…,x(2)利用计算出的后验概率及决策表,按下面的公式计算出采取i a ,i=1,…,a 的条件风险∑==cj j j i i X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…,a 进行比较,找出使其条件风险最小的决策k a ,即()()1,min k i i aR a x R a x ==则k a 就是最小风险贝叶斯决策。
模式识别(三)课后上机作业参考解答

“模式识别(三).PDF”课件课后上机选做作业参考解答(武大计算机学院袁志勇, Email: yuanzywhu@) 上机题目:两类问题,已知四个训练样本ω1={(0,0)T,(0,1)T};ω2={(1,0)T,(1,1)T}使用感知器固定增量法求判别函数。
设w1=(1,1,1)Tρk=1试编写程序上机运行(使用MATLAB、 C/C++、C#、JA V A、DELPHI等语言中任意一种编写均可),写出判别函数,并给出程序运行的相关运行图表。
这里采用MATLAB编写感知器固定增量算法程序。
一、感知器固定增量法的MATLAB函数编写感知器固定增量法的具体内容请参考“模式识别(三).PDF”课件中的算法描述,可将该算法编写一个可以调用的自定义MATLAB函数:% perceptronclassify.m%% Caculate the optimal W by Perceptron%% W1-3x1 vector, initial weight vector% Pk-scalar, learning rate% W -3x1 vector, optimal weight vector% iters - scalar, the number of iterations%% Created: May 17, 2010function [W iters] = perceptronclassify(W1,Pk)x1 = [0 0 1]';x2 = [0 1 1]';x3 = [1 0 1]';x4 = [1 1 1]';% the training sampleWk = W1;FLAG = 0;% iteration flagesiters = 0;if Wk'*x1 <= 0Wk =Wk + x1;FLAG = 1;endif Wk'*x2 <= 0Wk =Wk + x2;FLAG = 1;endif Wk'*x3 >= 0Wk=Wk-x3;FLAG = 1; endif Wk'*x4 >= 0Wk =Wk -x4; FLAG = 1; enditers = iters + 1; while (FLAG) FLAG = 0; if Wk'*x1 <= 0Wk = Wk + x1; FLAG = 1; endif Wk'*x2 <= 0Wk = Wk + x2; FLAG = 1; endif Wk'*x3 >= 0 Wk = Wk - x3; FLAG = 1; endif Wk'*x4 >= 0 Wk = Wk - x4; FLAG = 1; enditers = iters + 1; endW = Wk;二、程序运行程序输入:初始权向量1W , 固定增量大小k ρ 程序输出:权向量最优解W , 程序迭代次数iters 在MATLAB 7.X 命令行窗口中的运行情况: 1、初始化1[111]T W = 初始化W 1窗口界面截图如下:2、初始化1kρ=初始化Pk 窗口界面截图如下:3、在MATLAB 窗口中调用自定义的perceptronclassify 函数由于perceptronclassify.m 下自定义的函数文件,在调用该函数前需要事先[Set path…]设置该函数文件所在的路径,然后才能在命令行窗口中调用。
江南大学模式识别课后答案

课程作业十二 一、Agent 体系中的 Agent 联盟的工作方式? 二、机器人规划的基本任务是什么?
3.树根的代价即为解树的代价,计算时是从树叶开始自下而上逐层 计算而求得的,根是指初始节点 S0。 X 是与节点的两种计算公式为: 《1》g(x)=∑{c(x,yi)+g(yi)} 1≤i≤n 称为和代价法。
《2》g(x)=max{c(x,yi)+g(yi)} 1≤i≤n 称为最大代价法。
课程作业五 一、写出下面命题的产生式规则: 1.如果学生的学习刻苦了,那成绩一定会上升。 2.如果速度慢了,则时间一定会长。
¬f(B)∨¬f(D)
--(5)
则:(1)、(4)èf(B) ∨¬f(C) --(6)
(2)、(6) èf(B)
--(7)
(5)、(7) è¬f(D)
--(8)
(8)、(3) èf(C) 所以,最后得出 C 是罪犯。
课程作业四 简答题: 1、什么是启发式搜索,什么是启发式信息。启发式搜索具体有哪些 搜索。 2、状态图表示中的三元组分别是什么? 3、解树的代价是指什么?写出 X 是与节点的两种计算公式。
参考答案: 1、SSP 即业务交换点,实际就是交换机,只用来完成基本呼叫处理。 SSP 即业务控制点,位于 SSP 之上,用来存放智能服务程序和数据。 SCP、SSP 的实时连接通过公共信道信令网实现。SSP 将业务请求提交 给 SCP,SCP 通过查询智能业务数据库,将业务请求解释为 SSP 所能够 进行的处理,这些处理再由 SCP 下达给 SSP。
模式识别第三次作业

模式识别作业三运行环境:Anaconda-sypder2019.11.71.2.1.写出实现batch perception算法的程序。
(a) a = 0开始,将程序应用在第一类和第二类训练数据上;(b)程序应用在第三类和第四类训练数据上。
(记录收敛步数)选择感知器准则函数:J p(a)=∑(−a t y)y∈Yy是被错分的样本,则a t y ≤0,则J p(a)≥0。
对向量J p(a)求a梯度:∇J p(a)=∑(−y)y∈Y得到梯度下降的迭代公式:a(k+1)=a(k)+eta(k)∑yy∈Y由此写出代码(见PCF.py)输出图像:得到收敛步数:即:(a)收敛步数为23步:;(b)收敛步数为16步。
2.编写Ho-Kashyap算法,分别应用在第一类和第三类,以及第二类和第四类数据上。
已知准则函数:J s(a,b)=||Ya −b||2则J s(a,b)关于a的梯度是:∇a J s=Y t(Ya−b)则J s(a,b)关于b的梯度是:∇b J s=−2(Ya−b)对于任意的b,令:a=Y+bb(k +1)=b(k)−η12[∇b J s −|∇b J s|]整理得到:b(1)>0b(k +1)=b(k)−2η(k)e+(k)其中e+(k)是误差向量的正数部分。
[e(k)+|e(k)|]e+(k)= 12a(k)=Y+b(k)由此,写出Ho-Kashyap算法(见HK.py)输出图像:由于第一类和第三类不完全可分,所以无法用一条直线将其分开。
向量a和迭代步数:计算第一类和第三类时,由于不完全可分,则迭代会无止境的进行,这是需要设置最大迭代步数,这里设置为50次。
3.请写一个程序,实现MSE 多类扩展方法。
每一类用前8 个样本来构造分类器,用后两个样本作测试。
请给出你的正确率。
MSE多类扩展–可以直接采用c 个两类分类器的组合,且这种组合具有与两类分类问题类似的代数描述形式由此写出算法(见MSE.py)用测试样本测试,输入分别为第一类两个、第二类两个、三类两个、第四类两个,输出判别结果:从测试结果来看,全部判别正确,正确率为100%。
模式识别习题及答案

模式识别习题及答案模式识别习题及答案模式识别是人类智能的重要组成部分,也是机器学习和人工智能领域的核心内容。
通过模式识别,我们可以从大量的数据中发现规律和趋势,进而做出预测和判断。
本文将介绍一些模式识别的习题,并给出相应的答案,帮助读者更好地理解和应用模式识别。
习题一:给定一组数字序列,如何判断其中的模式?答案:判断数字序列中的模式可以通过观察数字之间的关系和规律来实现。
首先,我们可以计算相邻数字之间的差值或比值,看是否存在一定的规律。
其次,我们可以将数字序列进行分组,观察每组数字之间的关系,看是否存在某种模式。
最后,我们还可以利用统计学方法,如频率分析、自相关分析等,来发现数字序列中的模式。
习题二:如何利用模式识别进行图像分类?答案:图像分类是模式识别的一个重要应用领域。
在图像分类中,我们需要将输入的图像分为不同的类别。
为了实现图像分类,我们可以采用以下步骤:首先,将图像转换为数字表示,如灰度图像或彩色图像的像素矩阵。
然后,利用特征提取算法,提取图像中的关键特征。
接下来,选择合适的分类算法,如支持向量机、神经网络等,训练模型并进行分类。
最后,评估分类结果的准确性和性能。
习题三:如何利用模式识别进行语音识别?答案:语音识别是模式识别在语音信号处理中的应用。
为了实现语音识别,我们可以采用以下步骤:首先,将语音信号进行预处理,包括去除噪声、降低维度等。
然后,利用特征提取算法,提取语音信号中的关键特征,如梅尔频率倒谱系数(MFCC)。
接下来,选择合适的分类算法,如隐马尔可夫模型(HMM)、深度神经网络(DNN)等,训练模型并进行语音识别。
最后,评估识别结果的准确性和性能。
习题四:如何利用模式识别进行时间序列预测?答案:时间序列预测是模式识别在时间序列分析中的应用。
为了实现时间序列预测,我们可以采用以下步骤:首先,对时间序列进行平稳性检验,确保序列的均值和方差不随时间变化。
然后,利用滑动窗口或滚动平均等方法,将时间序列划分为训练集和测试集。
模式识别大作业

模式识别大作业(总21页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如 vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率 vs. 图2先验概率 vs.图3先验概率 vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2); error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
模式识别大作业-许萌-1306020
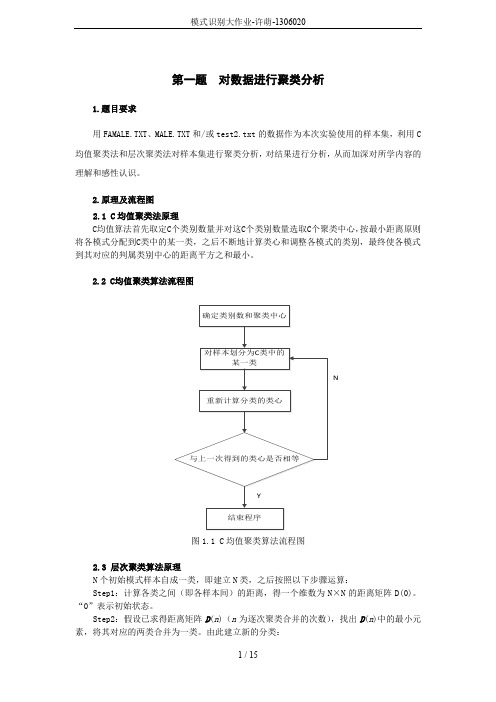
第一题对数据进行聚类分析1.题目要求用FAMALE.TXT、MALE.TXT和/或test2.txt的数据作为本次实验使用的样本集,利用C 均值聚类法和层次聚类法对样本集进行聚类分析,对结果进行分析,从而加深对所学内容的理解和感性认识。
2.原理及流程图2.1 C均值聚类法原理C均值算法首先取定C个类别数量并对这C个类别数量选取C个聚类中心,按最小距离原则将各模式分配到C类中的某一类,之后不断地计算类心和调整各模式的类别,最终使各模式到其对应的判属类别中心的距离平方之和最小。
2.2 C均值聚类算法流程图N图1.1 C均值聚类算法流程图2.3 层次聚类算法原理N个初始模式样本自成一类,即建立N类,之后按照以下步骤运算:Step1:计算各类之间(即各样本间)的距离,得一个维数为N×N的距离矩阵D(0)。
“0”表示初始状态。
Step2:假设已求得距离矩阵D(n)(n为逐次聚类合并的次数),找出D(n)中的最小元素,将其对应的两类合并为一类。
由此建立新的分类:Step3:计算合并后所得到的新类别之间的距离,得D (n +1)。
Step4:跳至第2步,重复计算及合并。
直到满足下列条件时即可停止计算:①取距离阈值T ,当D (n )的最小分量超过给定值 T 时,算法停止。
所得即为聚类结果。
②或不设阈值T ,一直到将全部样本聚成一类为止,输出聚类的分级树。
2.4层次聚类算法流程图N图1.2层次聚类算法流程图3 验结果分析对数据文件FAMALE.TXT 、MALE.TXT 进行C 均值聚类的聚类结果如下图所示:图1.3 C 均值聚类结果的二维平面显示将两种样本即进行聚类后的样本中心进行比较,如下表:从下表可以纵向比较可以看出,C 越大,即聚类数目越多,聚类之间差别越小,他们的聚类中心也越接近。
横向比较用FEMALE,MALE 中数据作为样本和用FEMALE,MALE ,test2中),1(),1(21++n G n G数据作为样本时,由于引入了新的样本,可以发现后者的聚类中心比前者都稍大。
模式识别大作业
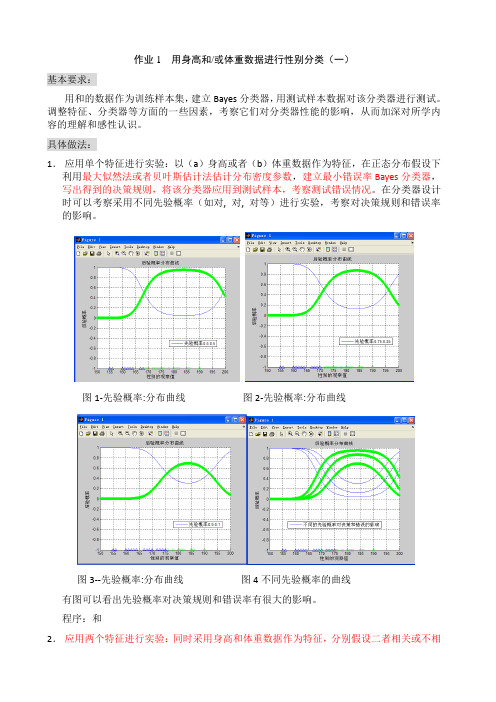
作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes 分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率vs. 图2先验概率vs.图3先验概率vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
模式识别第3章部分习题解答

Problem 1
• a When θ = 1 p(x|θ) = Plot as follows:
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 2 4 6 8 10 exp(-x)
e−x , x ≥ 0 0 others
When x = 2 we get: p(x|θ) = Plot as follows:
0.2 0.18 0.16 0.14 0.12 0.1 0.08 0.06 0.04 0.02 0 0 0.5 1 1.5 2
θe−2θ , x ≥ 0 0 others
x*exp(-2*x)
2.5
3
3.5
4
4.5
5
• b
x1 , · · · , xn p(x|θ), and xi are independently. Then we define the log-likelihood as follows:
Which is Eqs.46.
P (X |θ) =
i=1
xi θi (1 − θi )( 1 − xi )
hence,
n d
P (X 1 , ..., X n |θ) =
k=1 i=1
θi i (1 − θi )(1 − xk i)
xk
And the likelihood function:
n d k xk i ln θi + (1 − xi ) ln(1 − xi ) k=1 i=1
n
n
xi = 0
i=1
1 n
n i=1
xi
n→∞
xi −(x + 1)e−x |∞ 0 = 1
Problem 2
模式识别_作业3

作业一:设以下模式类别具有正态概率密度函数: ω1:{(0 0)T , (2 0)T , (2 2)T , (0 2)T }ω2:{(4 4)T , (6 4)T , (6 6)T , (4 6)T }(1)设P(ω1)= P(ω2)=1/2,求这两类模式之间的贝叶斯判别界面的方程式。
(2)绘出判别界面。
答案:(1)模式的均值向量m i 和协方差矩阵C i 可用下式估计:2,111==∑=i x N m i N j ij i i2,1))((11=--=∑=i m x m x N C i N j Ti ij i ij i i 其中N i 为类别ωi 中模式的数目,x ij 代表在第i 个类别中的第j 个模式。
由上式可求出:T m )11(1= T m )55(2= ⎪⎪⎭⎫ ⎝⎛===1 00 121C C C ,⎪⎪⎭⎫⎝⎛=-1 00 11C 设P(ω1)=P(ω2)=1/2,因C 1=C 2,则判别界面为:24442121)()()(2121211112121=+--=+--=----x x m C m m C m x C m m x d x d T T T(2)作业二:编写两类正态分布模式的贝叶斯分类程序。
程序代码:#include<iostream>usingnamespace std;void inverse_matrix(int T,double b[5][5]){double a[5][5];for(int i=0;i<T;i++)for(int j=0;j<(2*T);j++){ if (j<T)a[i][j]=b[i][j];elseif (j==T+i)a[i][j]=1.0;elsea[i][j]=0.0;}for(int i=0;i<T;i++){for(int k=0;k<T;k++){if(k!=i){double t=a[k][i]/a[i][i];for(int j=0;j<(2*T);j++){double x=a[i][j]*t;a[k][j]=a[k][j]-x;}}}}for(int i=0;i<T;i++){double t=a[i][i];for(int j=0;j<(2*T);j++)a[i][j]=a[i][j]/t;}for(int i=0;i<T;i++)for(int j=0;j<T;j++)b[i][j]=a[i][j+T];}void get_matrix(int T,double result[5][5],double a[5]) {for(int i=0;i<T;i++){for(int j=0;j<T;j++){result[i][j]=a[i]*a[j];}}}void matrix_min(int T,double a[5][5],int bb){for(int i=0;i<T;i++){for(int j=0;j<T;j++)a[i][j]=a[i][j]/bb;}}void getX(int T,double res[5],double a[5],double C[5][5]) {for(int i=0;i<T;i++)double sum=0.0;for(int j=0;j<T;j++)sum+=a[j]*C[j][i];res[i]=sum;}}int main(){int T;int w1_num,w2_num;double w1[10][5],w2[10][5],m1[5]={0},m2[5]={0},C1[5][5]={0},C2[5][5]={0};cin>>T>>w1_num>>w2_num;for(int i=0;i<w1_num;i++){for(int j=0;j<T;j++){cin>>w1[i][j];m1[j]+=w1[i][j];}}for(int i=0;i<w2_num;i++){for(int j=0;j<T;j++){cin>>w2[i][j];m2[j]+=w2[i][j];}}for(int i=0;i<w1_num;i++)m1[i]=m1[i]/w1_num;for(int i=0;i<w2_num;i++)m2[i]=m2[i]/w2_num;for(int i=0;i<w1_num;i++){double res[5][5],a[5];for(int j=0;j<T;j++)a[j]=w1[i][j]-m1[j];get_matrix(T,res,a);for(int j=0;j<T;j++){for(int k=0;k<T;k++)C1[j][k]+=res[j][k];}matrix_min(T,C1,w1_num);for(int i=0;i<w2_num;i++){double res[5][5],a[5];for(int j=0;j<T;j++)a[j]=w2[i][j]-m2[j];get_matrix(T,res,a);for(int j=0;j<T;j++){for(int k=0;k<T;k++)C2[j][k]+=res[j][k];}}matrix_min(T,C2,w2_num);inverse_matrix(T,C1);inverse_matrix(T,C2);double XX[5]={0},C_C1[5]={0},C_C2[5]={0};double m1_m2[5];for(int i=0;i<T;i++){m1_m2[i]=m1[i]-m2[i];}getX(T,XX,m1_m2,C1);getX(T,C_C1,m1,C1);getX(T,C_C2,m2,C1);double resultC=0.0;for(int i=0;i<T;i++)resultC-=C_C1[i]*C_C1[i];for(int i=0;i<T;i++)resultC+=C_C2[i]*C_C2[i];resultC=resultC/2;cout<<"判别函数为:"<<endl;cout<<"d1(x)-d2(x)=";for(int i=0;i<T;i++)cout<<XX[i]<<"x"<<i+1;if(resultC>0)cout<<"+"<<resultC<<endl;elseif(resultC<0)cout<<resultC<<endl;return 0;}运行截图:。
中科院模式识别第三次(第五节)-作业-答案-更多

第5章:线性判别函数第一部分:计算与证明1. 有四个来自于两个类别的二维空间中的样本,其中第一类的两个样本为(1,4)T 和(2,3)T ,第二类的两个样本为(4,1)T 和(3,2)T 。
这里,上标T 表示向量转置。
假设初始的权向量a=(0,1)T ,且梯度更新步长ηk 固定为1。
试利用批处理感知器算法求解线性判别函数g(y)=a T y 的权向量。
解:首先对样本进行规范化处理。
将第二类样本更改为(4,1)T 和(3,2)T . 然后计算错分样本集:g(y 1) = (0,1)(1,4)T = 4 > 0 (正确) g(y 2) = (0,1)(2,3)T = 3 > 0 (正确) g(y 3) = (0,1)(-4,-1)T = -1 < 0 (错分) g(y 4) = (0,1)(-3,-2)T = -2 < 0 (错分) 所以错分样本集为Y={(-4,-1)T , (-3,-2)T }.接着,对错分样本集求和:(-4,-1)T +(-3,-2)T = (-7,-3)T第一次修正权向量a ,以完成一次梯度下降更新:a=(0,1)T + (-7,-3)T =(-7,-2)T 再次计算错分样本集:g(y 1) = (-7,-2)(1,4)T = -15 < 0 (错分) g(y 2) = (-7,-2)(2,3)T = -20 < 0 (错分) g(y 3) = (-7,-2)(-4,-1)T = 30 > 0 (正确) g(y 4) = (-7,-2)(-3,-2)T = 25 > 0 (正确) 所以错分样本集为Y={(1,4)T , (2,3)T }.接着,对错分样本集求和:(1,4)T +(2,3)T = (3,7)T第二次修正权向量a ,以完成二次梯度下降更新:a=(-7,-2)T + (3,7)T =(-4,5)T 再次计算错分样本集:g(y 1) = (-4,5)(1,4)T = 16 > 0 (正确) g(y 2) = (-4,5)(2,3)T = 7 > 0 (正确) g(y 3) = (-4,5)(-4,-1)T = 11 > 0 (正确) g(y 4) = (-4,5)(-3,-2)T = 2 > 0 (正确)此时,全部样本均被正确分类,算法结束,所得权向量a=(-4,5)T 。
模式识别第三章作业

1. 在一个10类的模式识别问题中,有3类单独满足多类情况1,其余的类别满足多类情况2。
问该模式识别问题所需判别函数的最少数目是多少?答:25个判别函数。
将10类问题看作4类满足多类情况1的问题,先将3类单独满足多类情况1的类找出来,再将剩下的7类全部划到第4类中。
再对第四类运用多类情况2的判别法则进行分类,此时需要7*(7-1)/2=21个判别函数。
所有一共需要4+21=25个判别函数;2. 一个三类问题,其判别函数如下:d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-1(1) 设这些函数是在多类情况1条件下确定的,绘出其判别界面和每一个模式类别的区域(2)设为多类情况2,并使:d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。
绘出其判别界面和多类情况2的区域。
(3)设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的,绘出其判别界面和每类的区域3.两类模式,每类包括5个3维不同的模式,且良好分布。
如果它们是线性可分的,问权向量至少需要几个系数分量?假如要建立二次的多项式判别函数,又至少需要几个系数分量?(设模式的良好分布不因模式变化而改变。
)解:由总项数公式()!!!rw n rn rN Cr n++==,得1 44N C==;23210N C+==所以如果它们是线性可分的,则权向量至少需要4个系数分量;如要建立二次的多项式判别函数,则至少需要10个系数分量4.用感知器算法求下列模式分类的解向量w:ω1: {(0 0 0)T, (1 0 0)T, (1 0 1)T, (1 1 0)T}ω2: {(0 0 1)T, (0 1 1)T, (0 1 0)T, (1 1 1)T}解:将属于2ω的模式样本乘以(-1)进行第一轮迭代:取C=1,令w(1)= (0 0 0 0)Tw T(1)x①=(0 0 0 0)(0 0 0 1)T=0;故w(2)=w(1)+x①=(0 0 0 1)Tw T(2)x②=(0 0 0 1)(1 0 0 1)T=1>0,故w(3)=w(2)=(0 0 0 1)Tw T(3)x③=(0 0 0 1)(1 0 1 1)T=1>0,故w(4)=w(3)=(0 0 0 1)Tw T(4)x④=(0 0 0 1)(1 1 0 1)T=1>0,故w(5)=w(4)=(0 0 0 1)Tw T(5)x⑤=(0 0 0 1)(0 0 -1 -1)T=-1<0,故w(6)=w(5)+x⑤=(0 0 -1 0)Tw T(6)x⑥=(0 0 -1 0)(0 -1 -1 -1)T=1>0,故w(7)=w(6)=(0 0 -1 0)Tw T(7)x⑦=(0 0 -1 0)(0 -1 0 -1)T=0,故w(8)=w(7)+x⑦=(0 -1 -1 -1)Tw T(8)x⑧=(0 -1 -1 -1)(-1 -1 -1 -1)T=3>0,故w(9)=w(8)=(0 -1 -1 -1)T第二轮迭代:w T(9)x①=(0 -1 -1 -1)(0 0 0 1)T=-1<0;故w(10)=w(9)+x①=(0 -1 -1 0)Tw T(10)x②=(0 -1 -1 0)(1 0 0 1)T=0,故w(11)=w(10)+x②=(1 -1 -1 1)Tw T(11)x③=(1 -1 -1 1)(1 0 1 1)T=1>0,故w(12)=w(11)=(1 -1 -1 1)Tw T(12)x④=(1 -1 -1 1)(1 1 0 1)T=1>0,故w(13)=w(12)=(1 -1 -1 1)Tw T(13)x⑤=(1 -1 -1 1)(0 0 -1 -1)T=0,故w(14)=w(13)+x⑤=(1 -1 -2 0)T w T(14)x⑥=(1 -1 -2 0)(0 -1 -1 -1)T=3>0,故w(15)=w(14)=(1 -1 -2 0)T w T(15)x⑦=(1 -1 -2 0)(0 -1 0 -1)T=1>0,故w(16)=w(15)=(1 -1 -2 0)T w T(16)x⑧=(1 -1 -2 0)(-1 -1 -1 -1)T=2>0,故w(17)=w(16)=(1 -1 -2 0)T 第三轮迭代:…w T(24)x⑧=(2 -2 -2 0)(-1 -1 -1 -1)T=2>0,故w(25)=w(24)=(2 -2 -2 0)T 第四轮迭代:w T(25)x①=(2 -2 -2 0)(0 0 0 1)T=0;故w(26)=w(25)+x①=(2 -2 -2 1)T…w T(32)x⑧=(2 -2 -2 1)(-1 -1 -1 -1)T=1>0,故w(33)=w(32)=(2 -2 -2 1)T 第五轮迭代:….该轮迭代全部大于0所以w=(2 -2 -2 1)TMatlab 运行结果5.用多类感知器算法求下列模式的判别函数:ω1: (-1 -1)Tω2: (0 0)Tω3: (1 1)T解:将模式样本写成增广形式:x①=(-1 -1 1)T, x②=(0 0 1)T, x③=(1 1 1)T取初始值w1(1)=w2(1)=w3(1)=(0 0 0)T,C=1。
模式识别作业(全)

模式识别大作业一.K均值聚类(必做,40分)1.K均值聚类的基本思想以及K均值聚类过程的流程图;2.利用K均值聚类对Iris数据进行分类,已知类别总数为3。
给出具体的C语言代码,并加注释。
例如,对于每一个子函数,标注其主要作用,及其所用参数的意义,对程序中定义的一些主要变量,标注其意义;3.给出函数调用关系图,并分析算法的时间复杂度;4.给出程序运行结果,包括分类结果(只要给出相对应的数据的编号即可)以及循环迭代的次数;5.分析K均值聚类的优缺点。
二.贝叶斯分类(必做,40分)1.什么是贝叶斯分类器,其分类的基本思想是什么;2.两类情况下,贝叶斯分类器的判别函数是什么,如何计算得到其判别函数;3.在Matlab下,利用mvnrnd()函数随机生成60个二维样本,分别属于两个类别(一类30个样本点),将这些样本描绘在二维坐标系下,注意特征值取值控制在(-5,5)范围以内;4.用样本的第一个特征作为分类依据将这60个样本进行分类,统计正确分类的百分比,并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志(正确分类的样本点用“O”,错误分类的样本点用“X”)画出来;5.用样本的第二个特征作为分类依据将这60个样本再进行分类,统计正确分类的百分比,并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来;6.用样本的两个特征作为分类依据将这60个样本进行分类,统计正确分类的百分比,并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来;7.分析上述实验的结果。
8.60个随即样本是如何产生的的;给出上述三种情况下的两类均值、方差、协方差矩阵以及判别函数;三.特征选择(选作,15分)1.经过K均值聚类后,Iris数据被分作3类。
从这三类中各选择10个样本点;2.通过特征选择将选出的30个样本点从4维降低为3维,并将它们在三维的坐标系中画出(用Excell);3.在三维的特征空间下,利用这30个样本点设计贝叶斯分类器,然后对这30个样本点利用贝叶斯分类器进行判别分类,给出分类的正确率,分析实验结果,并说明特征选择的依据;。
模式识别与机器学习_作业_中科院_国科大_来源网络 (6)

Lecture5 答案作业一:写出上下文无关文法,其终止符集V T={a,b}能生成语言L(G)={ab,ba,aba,bab,abab,baba,…}答案:上下文无关文法:G=(V,T,S,P),V={S,A,B},T={a,b},P如下:S->aAb|aAba|bBa|bBabA->baA|∈B->abB|∈作业二:求一有限态自动机,它只能接受由“偶数个a”与/或“偶数个b”组成的任意字符串,例如:aa, bb, abab, abba, baba等。
答案:其中文法为:G=(V,T,S,P),V={S,A,B,C},T={a,b},P如下:S->aA|bBA->aS|bC|aB->aC|bS|bC->aB|bA其有限态自动机为:作业三:自己定义基元,用PDL文法生成0到5的字符,字符笔划用七划样式。
答案:文法G = (V N, V T, P, S),其中V N={S,S0,S1,S2,S3,S4,S5,A,B,C,D},V T={ a↓, b→, (, ),+,*,~,-},P:S->S0|S1|S2|S3|S4|S5,A->((~a+b)+a),B->((a+b)+~a),C->(b+a),D->((~b+a)+b) S0->A*B,S1->(a+a),S2->C+D,S3->((C-b)+a)-b,S4->((a+b)-a)+a,S5->D+a+(~b)作业四:试用树文法生成单位边长的立方体,定义三个基元为立方体的三种方向的边。
答案:对于该树状结构。
可以对应有一个上下文无关文法G=({S, A}, {$, a, b, c}, P, S)P: S->$AAA,A->aAA,A->bA,A->c,A->cAA,A->aA,A->b,A->bAA,A->cA,A->a则G T’=({S, A}, {$, a, b, c, (, )}, P’, S)P’: S->($AAA),A->(aAA),A->(bA),A->(c),A->(cAA),A->(aA),A->(b),A->(bAA), A->(cA),A->(a)由G生成:S=>$AAA=>$aAAAA=>$abAAAA=>$abcAAA=>$abccAA=>$abcccAAA=>$abcccaAAA =>$abcccabAA=>$abcccabbA=>$abcccabbbAA=>$abcccabbbcAA=>$abcccabbbcaA=>$abcc cabbbcaa由G T’生成:S=>($AAA)=>($(aAA)AA)=>($(a(bA)A)AA)=>($(a(b(c))A)AA)=>($(a(b(c))(c))AA)=>( $(a(b(c))(c))(cAA)A)=>($(a(b(c))(c))(c(aA)A)A)=>($(a(b(c))(c))(c(a(b))A)A)=>($( a(b(c))(c))(c(a(b))(b))A)=>($(a(b(c))(c))(c(a(b))(b))(bAA))=>($(a(b(c))(c))(c(a (b))(b))(b(cA)A))=>($(a(b(c))(c))(c(a(b))(b))(b(c(a))A))=>($(a(b(c))(c))(c(a(b) )(b))(b(c(a))(a)))作业五:给出字符串样本集为{aaacc, aaacb, aacc, bacb, aaa, abc, bb, cc}推断一个有限态文法。
模式识别小作业

(1)神经网络模式识别识别加入20%噪声的A-Z 26个字母。
程序代码clear;close all;clc;[alphabet,targets]=prprob;[R,Q]=size(alphabet);[S2,Q]=size(targets);S1=10;P=alphabet;net=newff(minmax(P),[S1,S2],{'logsig' 'logsig'},'traingdx'); net.LW{2,1}=net.LW{2,1}*0.01;net.b{2}=net.b{2}*0.01;T=targets;net.performFcn='sse';net.trainParam.goal=0.1;net.trainParam.show=20;net.trainParam.epochs=5000;net.trainParam.mc=0.95;[net,tr]=train(net,P,T);netn=net;netn.trainParam.goal=0.6;netn.trainParam.epochs=300;T=[targets targets targets targets];for pass=1:10;P=[alphabet,alphabet,...(alphabet+randn(R,Q)*0.1),...(alphabet+randn(R,Q)*0.2)];[netn,tr]=train(netn,P,T);endnetn.trainParam.goal=0.1;netn.trainParam.epochs=500;netn.trainParam.show=5;P=alphabet;T=targets;[netn,tr]=train(netn,P,T);noise_percent=0.2;for k=1:26noisyChar=alphabet(:,k)+randn(35,1)*noise_percent;subplot(6,9,k+floor(k/9.5)*9);plotchar(noisyChar);de_noisyChar=sim(net,noisyChar);de_noisyChar=compet(de_noisyChar);answer=find(de_noisyChar==1);subplot(6,9,k+floor(k/9.5)*9+9);plotchar(alphabet(:,answer));endset(gcf,'Position',[10,60,900,700], 'color','w')运行结果(2)实现最小错误率和最小风险bayes决策w1=input('input the priorp of a1\n');w2=input('input the priorp of a2\n');p1=input('input the similarp of w1\n');p2=input('input the similarp of w2\n');s=input('input the table\n');posteriorp1=w1*p1; %约去总体概率密度的w1的后验概率posteriorp2=w2*p2; %。
模式识别作业三

改为
y1=1/(2*pi)*exp(-((x-xx(i))/h).^2/2);%正态窗窗口函数
y=y+y1;%累加
即可。
由上图可见,在h=2和4左右时,图像效果较好,而且符合h越大,图像越平坦的结论,平坦度要看y轴的坐标值的变化率,下面有两个h更大的图,可以看出y轴的坐标值的变化率很小,很平坦
这下,我们得到了意料之中的图像,在h=6左右时,效果较好。
然而,在这里,我们可以发现用方窗得到理想曲线的方法,那就是我之前的错误——方窗叠加(每次y不清零),但是要注意这时体积也会变,v=n(n+1)/2(一维)。
(2)正态窗
代码几乎不变,只要将上面的
s=find(abs(x-xx(i))<=0.5*h);%找到在此方窗窗口内的点
解:(1)方窗
%%方窗
xx=[5.2 5.6 5 8 2.5];%样本点
x=-5:0.01:15;%画图点
y=zeros(size(x));%纵坐标值
f=4;%f^2为窗口数
forh=1:f^2%窗口宽度,逐渐递增
fori=1:5%逐一累加窗口函数
s=find(abs(x-xx(i))<=0.5*h);%找到在此方窗窗口内的点
(3)指数窗
同样,代码只用改为
y1=exp(-abs((x-xx(i))/h));%指数窗窗口函数
y=y+y1;%累加
即可。得到
由上图可见,在h=4左右时,图像效果较好。
总结:由3个窗口图像我们知道这批数据大概是按正态分布的,所以用正态窗的效果较好。
第5章
1.设有如下三类模式样本集ω1,ω2和ω3,其先验概率相等,求Sw和Sb
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用K-L变换,分别把特征空间维数降到二维和一维,并画出样本在该空间中的位置。
解:应用类间散布矩阵。均值为
,
由公式
得
特征值为 ,对应的特征向量为
原图中点的位置:
新坐标公式
1、化到一维,
(1)用 来, 得
图为,可见效果很不理想,很多重合
然后我将h的循环关闭,直接令h=20,如果是h越大越好的话,那么图像应该更好,但是图像是:
看来图像并不好看,很平坦,符合h越大,图像越平坦的结论,那么,原来的图那里错了呢?
原来
y=zeros(size(x));%纵坐标值
f=4;%f^2为窗口数
forh=1:f^2%窗口宽度,逐渐递增
这里y在h循环时,y并没有清零,导致图像累加了,然后我修改程序,得到:
(3)指数窗
同样,代码只用改为
y1=exp(-abs((x-xx(i))/h));%指数窗窗口函数
y=y+y1;%累加
即可。得到
由上图可见,在h=4左右时,图像效果较好。
总结:由3个窗口图像我们知道这批数据大概是按正态分布的,所以用正态窗的效果较好。
第5章
1.设有如下三类模式样本集ω1,ω2和ω3,其先验概率相等,求Sw和Sb
由于 与 无关,所以令其为a,所以
而后验概率可以直接写成正态形式:
利用对应系数相等得:
由上式解得:
2.设对于一个二类(ω1,ω2)识别问题,随机抽取ω1类的5个样本X=(x1,x2,…. x5),即ω1=(x1,x2,…. x5)
{x1=5.2,x2=5.6,x3=5,x4=8,x5=2.5}
试用方窗函数、正态窗函数和指数窗函数,估计P(x|ω1),并讨论其性能。
这下,我们得到了意料之中的图像,在h=6左右时,效果较好。
然而,在这里,我们可以发现用方窗得到理想曲线的方法,那就是我之前的错误——方窗叠加(每次y不清零),但是要注意这时体积也会变,v=n(n+1)/2(一维)。
(2)正态窗
代码几乎不变,只要将上面的
s=find(abs(x-xx(i))<=0.5*h);%找到在此方窗窗口内的点
(2)用 来化, ,得
图为,可见,可分性很好
2、划到2维
(1)用 来,得到
图为,效果不好,重叠
(2)用 来,得
图为,可见,可分性很好
所以
2.两类的一维模式,每一类都是正态分布,其中
。设这里用0-1代价函数,且 。试绘出其密度函数,画判别边界并标示其位置。
解:由题
两类问题的0-1代价问题即最小错误率Bayes决策,且
所以决策边界为g(x)=p(x|w1)- p(x|w2)=0即:x=1
密度函数图像即判别边界图为:
3.设以下模式类别具有正态概率密度函数:
ω1:{(1 0)t, (2 0)t, (1 1)t}
ω2:{(-1 0)t, (0 1)t, (-1 1)t}
ω3:{(-1 -1)t, (0 -1)t, (0 -2)t}
解:3类的均值向量为
所以
(Ci为第i类协方差矩阵)
得 , ,
类间: ,由
所以,
2.设有如下两类样本集,其出现的概率相等:
ω1:{(0 0 0)T, (1 0 0)T, (1 0 -1)T, (1 1 0)T}
(a)设 ,求该两类模式之间的贝叶斯判别边界的方程式。
(b)绘出其判别界面。
解:(1)由题
x11=1/4*(0+2+2+0)=1; x12=1/4*(0+0+2+2)=1
x21=1/4*(4+6+6+4)=5; x22=1/4*(4+4+6+6)=5
所以u1=(1,1), u2=(5,5),算得协方差矩阵为:
第三次模式识别作业
(3、4、5章)
第3章
1.分别写出在以下两种情况(1)(2)
下的最小错误率(基本的)贝叶斯决策规则。
答:判别函数为:g(x)=p(w1)·p(x|w1)- p(w2)·p(x|w2)
(1)当时,g(x)= p(w1)- p(w1)- p(x|w2)
E1=E2=I=
所以
判别面方程:g1(x)=g2(x)即
x1+x2-6=0
(2)判别界面图为
第4章
1.设总体概率分布密度为 , ,并设,分别用最大似然估计和贝叶斯估计计算 。已知 的先验分布为
解:(1)极大似然法
先对 取对数,
然后对 求导,并令其等于0,得
即
(2)贝叶斯估计法
,
所以由贝叶斯公式,则可得后验概率:
y(s)=y(s)+1;%把它们对应的纵坐标值加1
改为
y1=1/(2*pi)*exp(-((x-xx(i))/h).^2/2);%正态窗窗口函数
y=y+y1;%累加
即可。
由上图可见,在h=2和4左右时,图像效果较好,而且符合h越大,图像越平坦的结论,平坦度要看y轴的坐标值的变化率,下面有两个h更大的图,可以看出y轴的坐标值的变化率很小,很平坦
y(s)=y(s)+1;%把它们对应的纵坐标值加1
end
subplot(f,f,h);%开窗口
plot(x,y/h);%画图,y/h是除以体积
d=num2str(h);%为标题准备
title(['窗口宽度h=',d]);%标题
gridon
end
由上图可以看出h越大,图像越好看,这与h越大,图像越平坦的结论不符,为什么呢??
解:(1)方窗
%%方窗
xx=[5.2 5.6 5 8 2.5];%样本点
x=-5:0.01:15;%画图点
y=zeros(size(x));%纵坐标值
f=4;%f^2为窗口数
forh=1:f^2%窗口宽度,逐渐递增
fori=1:5%逐一累加窗口函数
s=find(abs(x-xx(i))<=0.5*h);%找到在此方窗窗口内的点
