最新全国高中数学联赛预赛试题及答案汇总
2024年全国高中数学联赛北京赛区预赛一试试题(解析版)

2024年全国高中数学联赛北京赛区预赛一试试题考试时间:8:00-9:20填空题(1-8题每题8分,第9题16分,第10,11题每题20分,共120分)1.设整数集合{}12345A a a a a a =,,,,,若A 中所有三元子集的三个元素之积组成的集合为{}30,15,10,6,5,3,26,10,15B =------,,则集合A =.2.已知函数()201ln 102x x f x x x +<⎧⎪=⎨⎛⎫+≥ ⎪⎪⎝⎭⎩,,若关于x 的方程()()f f x m =恰有三个不相等的实数根123,,x x x 且满足123x x x <<,则()1229ln 4x x ++的取值范围是.3.从1,2,,2024 中任取两个数()a b a b ≤,,则37a b +的值中,个位数字为8的数有个.4.设复数z 满足32i 6z -=,令21107457iz z z z -+=-+,则1z 的最大值是.5.已知函数()*,1,,,N ,,,x x f x q q x p q p q p q p p ⎧⎪=+⎨=∈>⎪⎩若为无理数若其中且互质,则函数()f x 在区间89,910⎛⎫ ⎪⎝⎭上的最大值为.6.对于0c >,若非零实数a b ,满足224240a ab b c -+-=,且使2a b +最大,则342a b c -+的最小值为.7.已知函数()44cos sin sin4f x x x a x b =++-,且π6f x ⎛⎫+ ⎪⎝⎭为奇函数.若方程+=0在[]0,π上有四个不同的实数解1234,,,x x x x ,则12344x x x x f +++⎛⎫ ⎪⎝⎭的平方值为.8.已知{}1,2,,2625A ⊆ ,且A 中任意两个数的差的绝对值不等于4,也不等于9,则A 的最大值为.9.设多项式202320240()i i f x x cx ==+∑,其中{}1,0,1i c ∈-.记N 为()f x 的正整数根的个数(含重根).若()f x 无负整数根,N 的最大值是.10.在棱长为4的正方体1111ABCD A B C D -中,E 为棱1AA 上的一点,且11,A EF =为截面1A BD 上的动点,则AF FE +的最小值等于.11.数列{}n a 定义如下:设()()2!!2024!n n n +写成既约分数后的分母为(),n A n a 等于()2A n 的最大质因数,则n a 的最大值等于.2024年全国高中数学联赛北京赛区预赛二试试题考试时间:9:40-12:3012.设,,a b c 是三个正数,求证:++13.如图所示,锐角ABC V 的三条高线AD ,BE ,CF 交于点H ,过点F 作//FG AC 交直线BC 于点G ,设 CFG 的外接圆为O O ,与直线AC 的另一个交点为P ,过P 作//PQ DE 交直线AD 于点Q ,连接OD ,OQ .求证:OD OQ =.14.有n 个球队参加比赛,球队之间的比赛计划已经安排好了.但是每场比赛的主场客场还没有分配好.这时每个球队都上报了自己能够接受的客场比赛的最大次数.最终组委会发现这些次数加在一起恰好是比赛的总场次,并且组委会还发现任意挑出若干支球队,他们能够接受的客场次数之和都要大于等于他们之间的比赛总场次.请问组委会能否安排好主客场使得每支球队都满意,请证明你的结论.15.设12n a a a ,,,为n 个两两不同的正整数且12n a a a 恰有4048个质因数.如果12n a a a ,,,中任意多个数相乘均不是一个整数的4049次方,求n 的最大值.1.{}2,1,1,3,5--【分析】依据总的乘积,绝对值最大的乘积,绝对值最小的乘积去分析集合A 中的各元素即可.【详解】A 中所有三元子集共有35C 10=个,A 中的每个元素在这些三元子集中均出现了10365⨯=次,故()()()()()()()612345301510653261015a a a a a =-⨯-⨯-⨯-⨯-⨯-⨯⨯⨯⨯,1234530a a a a a =,因为集合B 中的元素有6个负数4个正数,故集合A 中的元素有2个负数3个正数,所以1234530a a a a a =,不妨设12345a a a a a ≤≤≤≤,三个元素之积绝对值最大时,34530a a a =-,121a a =-,又A 为整数集合,所以11a =,21a =-或者11a =-,21a =;三个元素之积绝对值最小时,1232a a a =,又121a a =-,所以32a =-,4515a a =,因为集合A 中的元素有2个负数3个正数,故4a 、5a 均为正整数,所以43a =,55a =,故{}2,1,1,3,5A =--.故答案为:{}2,1,1,3,5--.【点睛】关键点点睛:本题考查集合的子集,关键是理解题目的意思,并从“总的乘积,绝对值最大的乘积,绝对值最小的乘积”这些不同的角度去分析集合A 中的各元素.2.11,1ln 22ln 2⎡⎫+⎪⎢⎣⎭【分析】求出嵌套函数解析式4,2,1(())ln 2,20,211ln ln 11,022x x f f x x x x x ⎧⎪+<-⎪⎪⎪⎛⎫=+-≤<⎨ ⎪⎝⎭⎪⎪⎡⎤⎛⎫++≥⎪ ⎪⎢⎥⎝⎭⎪⎣⎦⎩,作出其图象,得到0ln 2m ≤<,化简得()121ln 229221ln 4ln 2x x m ⎛⎫- ⎪+=- ⎪++ ⎪⎝⎭,设右边为新函数,根据其单调性得到范围.【详解】当2x <-时,则20x +<,则()()224f f x x x =++=+,当20x -≤<时,022x £+<,则()()()11ln 21ln 222f f x x x ⎡⎤⎛⎫=++=+ ⎪⎢⎥⎣⎦⎝⎭,当0x ≥时,()()11ln ln 1122f f x x ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦,即4,2,1(())ln 2,20,211ln ln 11,022x x f f x x x x x ⎧⎪+<-⎪⎪⎪⎛⎫=+-≤<⎨ ⎪⎝⎭⎪⎪⎡⎤⎛⎫++≥⎪ ⎪⎢⎥⎝⎭⎪⎣⎦⎩方程(())f f x m =恰有三个不相等的实数根等价于直线y m =与函数(())y f f x =的图象有三个不同交点,因此0ln 2m ≤<.此时14x m +=且21ln 22x m ⎛⎫+= ⎪⎝⎭,则14x m =-,()2ln 4ln 2x m +=+,从而()121ln 22921221ln 4ln 2ln 2x m x m m ⎛⎫- ⎪++==- ⎪+++ ⎪⎝⎭,设()1ln 2221ln 2h m m ⎛⎫- ⎪=- ⎪+ ⎪⎝⎭,则其在[0,ln 2)上单调递增,因此()1229ln 4x x ++的取值范围是11,1ln 22ln 2⎡⎫+⎪⎢⎣⎭.故答案为:11,1ln 22ln 2⎡⎫+⎪⎢⎣⎭.【点睛】关键点点睛:本题的关键是利用分段函数的解析式求出()()y f f x =的表达式,然后利用转化法、数形结合思想进行求解.。
2024年全国高中数学联赛江西省预赛试题与答案

2024年全国高中数学联赛江西省预赛试题(考试时间:6月23日上午9:3012:00−−)一、填空题(每小题7分,共56分)1. .设集合{2,3,4,,4050}A =,集合{(,)|log 8log 6,,}a b B a b b a a A b A =+=∈∈,则集合B 的元素个数为 . 2 .设复数z 满足242||021z z z −+=−,则|1|z +的值为 .3.P 的正四面体ABCD 面BCD 的中心,,M N 分别是面,ABD ACD 上的动点, 则PM MN NP ++的最小值为 .4.222444cos 20cos 40cos 80sin 20sin 40sin 80++++的值为 . 5.设,b c 为实数,满足关于x 的方程2()()0f x bf x c ++=有6个互不相等的实数解,其中11()||||2f x x x x x=−−++,则(2025)(2024)f b f c ++的最小值为 . 6.正实数,,x y z 满足2222248x y x y z ++=,则428log log log x y z ++的最大值为 .7.平面上同时和三直线34,(5),043y x y x y ==−−=相切的所有圆的半径的乘积为 . 8. 已知正整数n 的所有正因数排列为: 1231,d d d =<<<则在1,2,3,,2024中使得1088d =的所有数之和为 .二、解答题(共64分) 9 (14分)双曲线2222:1x y a bΓ−=的左右顶点,A B 的距离为4,,M N 是Γ右支上不重合的两动点且满足20BN AM k k +=(,AM BN k k 是相应直线的斜率).求动直线MN 经过的定点的坐标.10.(15分)实数,,a b c 满足44ab bc ca ++=,求222(4)(4)(4)a b c +++的最小值.11.(15分)点H 为锐角ABC ∆的垂心,H 与边BC 切于点M 且与边,AB AC 无交点,,BD CE 分别与H 切于点,D E (均异于M ), ,CF BG 为ABC ∆的高.证明:,,,D E F G 四点共线. 12.(20分)是否存在实数λ和2024次的实系数多项式()P x 和()Q x 满足对任意实数x ,都有22(1)(2)P x x Q x x λ−+=++.请说明理由.2024年全国高中数学联赛江西省预赛参考答案(6月23日上午−−9:3012:00)一、填空题(每小题7分,共56分)1.设集合{2,3,4,,4050}=A ,集合=+=∈∈B a b b a a A b A a b {(,)|log 8log 6,,},则集合B 的元素个数为 .答案:68.解:由题=b a log 2或4,又=<<==63396940504096648224,所以集合B 的元素个数为−+−=(631)(71)68.2.设复数z 满足−+=−z z z 21||0422,则+z |1|的值为 . 答案:2.解:由题≠z 21, 所以 −+=−−z z z z |21|||0(42)(21)22.从而−=−−z z z 2(21)|21|||1222,得=z ||设−=z bi 21(其中∈b R ),再由==+z bi |2||1|得=b 72,所以+=+==z bi 2|1||3|21.3.P 是棱长为的正四面体ABCD 面BCD 的中心,M N ,分别是面ABD ACD ,上的动点,则++PM MN NP 的最小值为 .答案解:如图1,点S T ,分别是点P 关于面ABD ,面ACD 的对称点,线段PS ST ,分别和面ABD 交于点Q M ,0,线段PT ST ,分别和面ACD 交于点R N ,0,点E F ,分别是棱DB DC ,的中点.则线段ST 的长度与++PM MN NP 相等,且是所求的最小值.点P 和线PS 在面ACE ,点P 和线PT 在面ABF 上,从而QR 在面AEF 上,且QR EF ST ////,=ST QR 2.为便于计算边长比例和角度,我们先设正四面体的棱长为6,则==EA EC,=EP 从而⋅∠==⋅−PEQ 2273cos 227612,===EA EC EP EQ EQ EQ 391,所以8822,99ST QR EF BC ==⋅=故4.222444cos 20cos 40cos 80sin 20sin 40sin 80++++的值为 . 答案:43. 解:注意到,22222222222cos 20cos 40cos 80cos 20cos (6020)cos (6020)1313cos 20(cos 20sin 20)(cos 20sin 20)222233(cos 20sin 20);22++=+−++=+−++=+=444444444222sin 20sin 40sin 80sin 20sin (6020)sin (6020)3131sin 20(cos 20sin 20)(cos 20sin 20)222299(cos 20sin 20).88++=+−++=+−++=+=故所求值为43. 5.设,b c 为实数,满足关于x 的方程2()()0f x bf x c ++=有6个互不相等的实数解,其中11()||||2f x x x x x=−−++,则(2025)(2024)f b f c ++的最小值为 . B 图1答案:20231012. 解: ()f x 的定义域{|0}D x x =≠关于原点对称,且对任意x D ∈,()()f x f x −=,所以()f x 是偶函数,且22,01,()22, 1.x x f x x x −+<<⎧⎪=⎨−⎪⎩画出()f x 的图像,如图2.由图可得:原方程有6个互不相等的实数解当且仅当关于t 的一元二次方程20t bt c ++=的两个根12,t t 满足120,02t t =<<,此时20,(2,0)c b t ==−∈−.再结合函数图像得最小值为22023(1)(2024)022*******f f −+=+−=.6.正实数,,x y z 满足2222248x y x y z ++=,则428log log log x y z ++的最大值为 .答案:13. 解:由2222248244x y x y z x y =++⋅得3624x y z ,其中不等式在222242x y x y z ===,即12,4x y z ===时取到等号,所以 36242864641log log log log log 4.3x y z x y z ++== 故所求最大值为13. 7.平面上同时和三直线34,(5),043y x y x y ==−−=相切的所有圆的半径的乘积为 .答案:36.图2解:设满足条件圆的圆心坐标为(,)a b ,半径为R ,将直线方程化成标准方程再由点到直线的距离公式得|34||4320|||55a b a b R b −+−===,所以 222(3)(3)0,25(34)(4320)(25)(210)0.a b a b b a b a b a b a b −+=⎧=−=+−⇔⎨+−−−=⎩当3a b =时,得(55)(510)0b b −−=,解得121, 2.b b == 当13a b =−时,得55(5)(10)033b b −−−=,解得343, 6.b b ==− 故所有圆的半径的乘积为123636⨯⨯⨯=.8.已知正整数n 的所有正因数排列为: 1231,d d d =<<<则在1,2,3,,2024中使得1088d =的所有数之和为 .答案:2376.解: 注意到388211=⨯的全部(31)(11)8+⨯+=个正因数从小到大依次为: 1,2,4,8,11,22,44,88.要使1088d =当且仅当n 是88的倍数且另有2个小于88的正因数.当n 只有2和11两个素因子时,此时增加n 中11的幂次不影响其小于88的正因数个数,626488=,得5211(1)k n k =⨯,又2024n ,所以5211352n =⨯=.当n 有三个以上素因子时,若第3个素因子23p <,则,2,4p p p 是n 的小于88且不整除88的正因数,与1088d =矛盾,所以23p.再注意到3202421123=⨯⨯,所以,此种情形符合题意的只有2024n =.故所求和为35220242376+=.二、解答题(共64分)9.(14分) 双曲线2222:1x y a b Γ−=的左右顶点,A B 的距离为4.,M N 是Γ右支上不重合的两动点且满足20BN AM k k +=(,AM BN k k 是相应直线的斜率).求动直线MN 经过的定点的坐标.解:设直线0:MN x my x =+,1122(,),(,)M x y N x y .由题得24a =,02,x >120,y y <0102(2)(2)0,x y x y −⋅+>从而 0102(2)(2)0.x y x y −++≠联立2222044b x y b x my x ⎧−=⎨=+⎩,,得22222200(4)2(4)0b m y mb x y x b −++−=,则 22200121222222(4),,44mb x b x y y y y b m b m −−+==−− 从而222001212220(4)4().42mb x x my y y y b m x −−==+−又由20BN AM k k +=得 120221************2012022200102022200102012010(2)22222(2)4()(2)2(4)(2)24(2)(4)2()(2)2my y x y y x y x y x y y x y my y x y x y y x y x x y x y x x x y x y x y y x y x ++++−=⋅==−−+−−+++−+++===−−+−−++−, 即有00242,x x +=−+解得06x =,所以直线MN 过定点(6,0).10.(15分)实数,,a b c 满足44ab bc ca ++=,求222(4)(4)(4)a b c +++的最小值.解: (1)令222(4)(4)(4)D a b c =+++.我们先考虑,,a b c 均是正数情形,此时22222222(4)(4)164()(4)4(),a b a b a b ab a b ++=+++=−++所以2222222(4)(4)(4)((4)4())(4)(2(4)2())a b c ab a b c ab c a b +++=−+++−++ 22(2()8)806400,ab bc ca =++−==等号成立当且仅当42()2ab a b c−+=,即 4()abc a b c =++且44ab bc ca ++=.注意到(,,)(2,4,6)a b c =符合取等条件,故在,,a b c 均是正数情形,D 的最小值为6400.注意到题设条件的对称性,在,,a b c 均是负数情形,D 的最小值也为6400.(2)若0abc =,即,,a b c 中存在取值为0情形,由题不妨设0c =,此时44ab =. 2222(4)(4)(4)4446400.D a b c =+++>⋅>(3)最后考虑,,a b c 的取值为两负一正或一负两正情形,由对称性,不妨设0ab >,此时44()44ab a b c =−+>,也有24446400.D >⋅>综上,D 的最小值为6400,在(,,)(2,4,6)a b c =时取得该最小值.11.(15分)点H 为锐角ABC ∆的垂心,H 与边BC 切于点M 且与边,AB AC 无交点,,BD CE 分别与H 切于点,D E (均异于点M ), ,CF BG 为ABC ∆的高.证明:,,,D E F G 四点共线.证明:如图3,联结,,,,HD HE FD DE EG得,,,HF FB HD DB HG GC HE EC ⊥⊥⊥⊥,BH 平分DBC ∠,CH 平分EBC ∠,且有,,,;,,,H D F B H E G C 分别四点共圆.又360()DHE BHC DHB EHC ∠=−∠+∠+∠360(9090)BHC HBC HCB =−∠+−∠+−∠ 36022BHC A =−∠=∠,所以90180HDE A ABG HDF ∠=−∠=∠=−∠, 故180HDE HDF ∠+∠=,所以,点F 在直线DE 上.同理点G 在直线DE 上.所以,,,D E F G 四点共线.12.(20分)是否存在实数λ和2024次的实系数多项式()P x 和()Q x 满足对任意实数x ,都有22(1)(2)P x x Q x x λ−+=++.请说明理由.解: 不存在.对任意非零多项式()h x ,用deg(())h x 表示其次数.我们这里证明一般的结论:当()P x 不是常数多项式,即deg(())1P x 时,不存在实数λ和实系数多项式()P x 和()Q x 满足对任意实数x ,都有22(1)(2)P x x Q x x λ−+=++.(反证法) 假设存在满足条件的实数λ和多项式()P x 和()Q x .设deg(())P x m =,则1m ,2deg((1))2deg(())2P x x P x m −+==.由代数基本定理方程2(1)(1)P x x P −+=最多有2m 个互异实根.另一方面,由题得对任意实数x ,22(1)(2)P x x Q x x λ++=−+.所以图322222(1)(2)((2)2(2))((2)(2)1)(57).P x x Q x x Q x x P x x P x x λλ−+=++=+−++=++++=++ 令22()1,()57,f x x x g x x x =−+=++则(),()f x g x 均在[1,)+∞上严格单调递增,()()f x g x <,(1)1,(1)13f g ==,从而可按如下方式规范定义取值在[1,)+∞上的数列{}n a 和{}n b :111,1,()()n n n a n b g a f a +===.此时,对任意1n ,有111,1n n n n a a b b ++>>>,1(())(())()(())n n n n P f a P g a P b P f a +===.递推得21(1)(())(())(1),n n n P a a P f a P f a P −+===即严格单调递增的实数列{}n a 的每一项都是方程2(1)(1)P x x P −+=的实根,这与2(1)(1)P x x P −+=最多有2m 个互异实根矛盾,故假设不成立,结论得证.。
2024年全国高中数学联赛

2024年全国中学生数学奥林匹克竞赛(预赛)暨2024年全国高中数学联合竞赛一试试题(A )一、填空题:本大题共8小题,每小题8分,满分64分.1.若实数m >1满足98m log log =2024,则32m log log 的值为.2.设无穷等比数列{a n }的公比q 满足0<q <1.若{a n }的各项和等于{a n }各项的平方和,则a 2的取值范围是.3.设实数a ,b 满足:集合A ={x ∈R |x 2-10x +a ≤0}与B ={x ∈R |bx ≤b 3}的交集为4,9 ,则a +b 的值为.4.在三棱锥P -ABC 中,若PA ⏊底面ABC ,且棱AB ,BP ,BC ,CP 的长分别为1,2,3,4,则该三棱锥的体积为.5.一个不均匀的骰子,掷出1,2,3,4,5,6点的概率依次成等差数列.独立地先后掷该骰子两次,所得的点数分别记为a ,b .若事件a +b =7发生的概率为17,则事件“a =b ”发生的概率为.6.设f (x )是定义域为R 、最小正周期为5的函数.若函数g (x )=f (2x )在区间0,5 上的零点个数为25,则g (x )在区间[1,4)上的零点个数为.7.设F 1,F 2为椭圆Ω的焦点,在Ω上取一点P (异于长轴端点),记O 为△PF 1F 2的外心,若PO ∙F 1F 2 =2PF 1 ∙PF 2 ,则Ω的离心率的最小值为.8.若三个正整数a ,b ,c 的位数之和为8,且组成a ,b ,c 的8个数码能排列为2,0,2,4,0,9,0,8,则称(a ,b ,c )为“幸运数组”,例如(9,8,202400)是一个幸运数组.满足10<a <b <c 的幸运数组(a ,b ,c )的个数为.二、解答题:本大题共3小题,满分56分.解答应写出文字说明、证明过程或演算步骤.9.(本题满分16分)在ΔABC 中,已知cos C =sinA +cosA 2=B sin +cosB 2,求cos C 的值.10.(本题满分20分)在平面直角坐标系中,双曲线Γ:x 2-y 2=1的右顶点为A .将圆心在y 轴上,且与Γ的两支各恰有一个公共点的圆称为“好圆”.若两个好圆外切于点P ,圆心距为d ,求d PA的所有可能的值.11.(本题满分20分)设复数z ,w 满足z +w =2,求S =z 2-2w +w 2-2z 的最小可能值.2024年全国中学生数学奥林匹克竞赛(预赛)暨2024年全国高中数学联合竞赛加试试题(A卷)一.(本题满分40分)给定正整数r,求最大的实数C,使得存在一个公比为r的实数等比数列a nn≥1,满足a n≥C对所有正整数n成立.(x 表示实数x到与它最近整数的距离.)二.(本题满分40分)如图,在凸四边形ABCD中,AC平分∠BAD,点E,F分别在边BC,CD上,满足EF||BD,分别延长FA,EA至点P,Q,使得过点A,B,P的圆ω1及过点A,D,Q的圆w2均与直线AC相切.证明:B,P,Q,D四点共圆.(答题时储将图画在答卷纸上)三.(本题满分50分)给定正整数n.在一个3×n的方格表上,由一些方格构成的集合S称为“连通的”,如果对S 中任意两个不同的小方格A,B,存在整数l≥2及S中l个方格A=C1,C2,…,C l=B,满足C i与C i+1有公共边(i=1, 2,⋯,l-1).求具有下述性质的最大整数K:若将该方格表的每个小方格任意染为黑色或白色,总存在一个连通的集合S,使得S中的黑格个数与白格个数之差的绝对值不小于K.四.(本题满分50分)设A,B为正整数,S是一些正整数构成的一个集合,具有下述性质:(1)对任意非负整数k,有A K∈S;(2)若正整数n∈S,则n的每个正约数均属于S;(3)若m,n∈S,且m,n互素,则mn∈S;(4)若n∈S,则An+B∈S.证明:与B互素的所有正整数均属于S.。
解析版-2024年全国高中数学联赛福建赛区预赛试卷

2024 年全国高中数学联赛福建赛区预赛 暨 2024 年福建省高中数学竞赛试卷参考答案(考试时间: 2024 年 6 月 22 日上午 9:00-11:30, 满分 160 分)一、填空题 (共 10 小题, 每小题 6 分, 满分 60 分. 请直接将答案写在题中的横线上) 1. 在 △ABC 中,已知 AB =4,BC =2,AC =2√3 ,若动点 P 满足 |CP⃗⃗⃗⃗⃗ |=1 ,则 AP ⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ 的最大值为 . 【答案】 5【解答】取 AB 中点 O ,则AP ⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =14[(PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ )2−(PA ⃗⃗⃗⃗⃗ −PB ⃗⃗⃗⃗⃗ )2]=14[(2PO ⃗⃗⃗⃗⃗ )2−BA⃗⃗⃗⃗⃗ 2]=PO ⃗⃗⃗⃗⃗ 2−14×42=PO ⃗⃗⃗⃗⃗ 2−4由 AB =4,BC =2,AC =2√3 ,知 AB 2=CA 2+CB 2 ,于是 CA ⊥CB . 所以 CO =12AB =2 .又 |CP⃗⃗⃗⃗⃗ |=1 ,所以 |PO ⃗⃗⃗⃗⃗ | 的最大值为 CO +1=3 . 所以 AP⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ 的最大值为 32−4=5 . 2. 已知 z 1,z 2,z 3 为方程 z 3=−i 的三个不同的复数根,则 z 1z 2+z 2z 3+z 3z 1= . 【答案】 0【解答】设 z =x +yi (x,y ∈R ) 为方程 z 3=−i 的复数根, 则 z 3=(x +yi )3=x 3+3x 2(yi )+3x (yi )2+(yi )3=−i . 即 x 3+3x 2yi −3xy 2−y 3i =−i,x 3−3xy 2+(3x 2y −y 3)i =−i . 由 x,y ∈R ,得 {x 3−3xy 2=03x 2y −y 3=−1,解得 {x 1=0y 1=1 , {x 2=√32y 2=−12,{x 3=−√32y 3=−12.于是 z 1=i, z 2=√32−12i, z 3=−√32−12i . 所以 z 2+z 3=(√32−12i)+(−√32−12i)=−i ,z 2z 3=(√32−12i)(−√32−12i)=(−12i)2−(√32)2=−14−34=−1.因此 z 1z 2+z 2z 3+z 3z 1=z 1(z 2+z 3)+z 2z 3=i ×(−i )−1=0 .3. 设a=66⋯6⏟10个6,b=33⋯3⏟6个3,则a,b的最大公约数为 .【答案】 33【解答】用(x,y)表示正整数x,y的最大公约数.则(a,b)=(66⋯6⏟10个6,33⋯3⏟6个3)=(33⋯3⏟10个3,33⋯3⏟6个3)=3(11⋯1⏟10个1,11⋯1⏟6个1) .设m=11⋯1⏟10个1, n=11⋯1⏟6个1,则由m=11⋯1⏟10个1=104×11⋯1⏟6个1+1111 ,可知(m,n)=(1111,11⋯1⏟6个1) .同理可得, (m,n)=(1111,11⋯1⏟6↑1)=(11,1111)=(11,11)=11 .所以(a,b)=3(m,n)=33 .4. 某校三个年级举办乒乓球比赛, 每个年级选派 4 名选手参加比赛. 组委会随机将这 12 名选手分成 6 组, 每组 2 人, 则在上述分组方式中每组的 2 人均来自不同年级的概率为 .【答案】64385【解答】设三个年级为甲、乙、丙.12名选手随机分成6组,每组2人的分组方式有: C122C102C82C62C42C22A66=11×9×7×5×3×1种.下面考虑每组的2人均来自不同年级的分组情形.先考虑甲年级4名选手的配对方式: 由于每组2人均来自不同年级, 因此需从乙, 丙两个年级中每个年级各取 2 名选手与甲年级的 4 名选手配对. 故有C42×C42×A44=36×24种方式.再考虑余下 4 人的配对方式,此时乙、丙年级各有 2 人,其分组方式有2×1种.所以每组的 2 人均来自不同年级的分组方式有36×24×2种.所以每组的 2 人均来自不同年级的概率为36×24×211×9×7×5×3×1=64385.5. 如图,在棱长为 6 的正方体ABCD−A1B1C1D1中,点E,F分别为 AB,BC 的中点,点 G 在棱 CC 1 上. 若平面 EFG 与底面 ABCD 所成角的余弦值为 3√1717,则平面 EFG 截正方体 ABCD −A 1B 1C 1D 1 所得截面多边形的周长为 . 【答案】 6√13+3√2【解答】如图,以 D 为原点,射线 DA,DC,DD 1 分别为 x 轴, y 轴,(第 5 题图) z 轴非负半轴建立空间直角坐标系.(第 5 题答题图)则 E (6,3,0),F (3,6,0) . 设 G (0,6,t ) ,则 EF ⃗⃗⃗⃗⃗ =(−3,3,0) , EG ⃗⃗⃗⃗⃗ =(−6,3,t ) . 设 m ⃗⃗ =(x,y,z ) 为平面 EFG 的一个法向量,则{m ⃗⃗ ⋅EF⃗⃗⃗⃗⃗ =−3x +3y +0=0m ⃗⃗ ⋅EG⃗⃗⃗⃗⃗ =−6x +3y +tz =0 ,于是 m ⃗⃗ =(t,t,3) 为平面 EFG 的一个法向量.又 n ⃗ =(0,0,1) 为平面 ABCD 的一个法向量,且平面 EFG 与底面 ABCD 所成角的余弦值 为 3√1717, 所以 |cos⟨m ⃗⃗ ,n ⃗ ⟩|=|m⃗⃗⃗ ⋅n ⃗ |m ⃗⃗⃗ |⋅|n ⃗ ||=√2t 2+9⋅1=3√1717. 结合 t >0 ,解得 t =2 . 所以 G (0,6,2),CG =2 .延长 EF 交直线 DC 于点 M ,由 E,F 分别为 AB,BC 的中点,知点 M 在 DC 延长线上, 且 CM =3 . 由 CG DD 1=26=39=MCMD 知, M,G,D 1 三点共线.于是 GD 1 是截面多边形的一条边.延长 FE 交直线 DA 于点 N ,连接 D 1N 交 AA 1 于点 P ,则 D 1P 也是截面多边形的一条边. 另由AN =3=12A 1D 1 可知, AP =12A 1P ,所以 AP =2,A 1P =4 .连接 PE ,则五边形 EFGD 1P 为平面 EFG 截正方体 ABCD −A 1B 1C 1D 1 所得的截面多边形. 易知 EF =√32+32=3√2,FG =√32+22=√13,GD 1=√42+62=2√13 ,D 1P =√62+42=2√13, PE =√22+32=√13.所以截面五边形的周长为 6√13+3√2 .注: 作 CH ⊥EF 与 H ,则 GH ⊥EF,∠GHC 为二面角 G −EF −D 的平面角,于是 tan∠GHC =CGCH =3√22=2√23,因此 CG =2 。
2023年全国高中数学联赛江西省预赛数学试题及参考答案

.
解:由边长为1正六面体被一个平面所截的面积最大的平面是边长为
6⋅ ⋅
√
⋅
√
=
√
的正六边形,故最大面积为
.
6、若锐角, , 满足 + + = 2,则
是
√
.
1 / 5
+
+的最小值解:由111
+
+
填空题(每小题 7 分,共 56 分)
一、
1、用 12 种不同的动物图案制作成一些动物卡片,使得每张卡片上都有其中的 4 种不同的动物图案,
且制作过程中要求任取的两张卡片有且仅有一种动物是相同的,则最多能制作的卡片数量为
.
解:将 12 种不同的动物图案编号为 1,2,…,12,如果考虑相同的一种动物是 1 号,最多有 3 种,
2023 年全国高中数学联赛江西省预赛试题
一、
(考试时间:2023 年 5 月 21 日上午 9 : 30 12 : 00 )
填空题(每小题 7 分,共 56 分)
1 、用 12 种不同的动物图案制作成一些动物卡片,使得每张卡片上都有其中的 4 种不同的动物图案,
且制作过程中要求任取的两张卡片有且仅有一种动物是相同的,则最多能制作的卡片数量为
2
2
4
4
sin A cos B sin B cos C sin C cos 4 A
2
.
7 、设 A, B 为双曲线 W :
x2 y2
1 与实轴的交点, P (0,1) 为双曲线外一点, PA, PB 分别交双曲线于另
2024年全国中学生数学奥林匹克竞赛(预赛)暨2024年全国高中数学联赛一试(A卷)试题(含答案)

2024年全国中学生数学奥林匹克竞赛(预赛)暨2024年全国高中数学联合竞赛一试(A 卷)参考答案及评分标准说明:1. 评阅试卷时,请依据本评分标准. 填空题只设8分和0分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不得增加其他中间档次.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中第9小题4分为一个档次,第10、11小题5分为一个档次,不得增加其他中间档次.一、填空题:本大题共8小题,每小题8分,满分64分.1. 若实数1m 满足98log (log )2024m ,则32log (log )m 的值为 . 答案:4049.解:323898log (log )log (3log )12log (log )1220244049m m m .2. 设无穷等比数列{}n a 的公比q 满足01q .若{}n a 的各项和等于{}n a 各项的平方和,则2a 的取值范围是 .答案:1,0(0,2)4. 解:因为数列{}n a 的各项和为11a q,注意到{}n a 各项的平方依次构成首项为21a 、公比为2q 的等比数列,于是2{}n a 的各项和为2121a q. 由条件知211211a a q q,化简得11a q . 当(1,0)(0,1)q 时,22111(1),0(0,2)244a q q q . 3. 设实数,ab 满足:集合2{100}A x x x a R 与3{}B x bx b R 的交集为[4,9],则a b 的值为 .答案:7.解:由于2210(5)25x x a x a ,故A 是一个包含[4,9]且以5x 为中点的闭区间,而B 是至多有一个端点的区间,所以必有[1,9]A ,故9a .进一步可知B 只能为[4,) ,故0b 且34b b ,得2b .于是7a b .4. 在三棱锥P ABC 中,若PA 底面ABC ,且棱,,,AB BP BC CP 的长分别为1,2,3,4,则该三棱锥的体积为 .答案:34. 解:由条件知PA AB ,PA AC .因此PA AC .在ABC 中,22219131cos 22132AB BC AC B AB BC ,故sin B .所以1sin 2ABC S AB BC B 又该三棱锥的高为PA ,故其体积为1334ABC V S PA . 5. 一个不均匀的骰子,掷出1,2,3,4,5,6点的概率依次成等差数列.独立地先后掷该骰子两次,所得的点数分别记为,a b .若事件“7a b ”发生的概率为17,则事件“a b ”发生的概率为 . 答案:421. 解:设掷出1,2,,6 点的概率分别为126,,,p p p .由于126,,,p p p 成等差数列,且1261p p p ,故16253413p p p p p p . 事件“7a b ”发生的概率为1162561P p p p p p p . 事件“a b ”发生的概率为2222126P p p p . 于是22221216253411()()()333P P p p p p p p . 由于117P ,所以21143721P . 6. 设()f x 是定义域为R 、最小正周期为5的函数.若函数()(2)x g x f 在区间[0,5)上的零点个数为25,则()g x 在区间[1,4)上的零点个数为 .答案:11.解:记2x t ,则当[0,5)x 时,[1,32)t ,且t 随x 增大而严格增大.因此,()g x 在[0,5)上的零点个数等于()f t 在[1,32)上的零点个数.注意到()f t 有最小正周期5,设()f t 在一个最小正周期上有m 个零点,则()f t 在[2,32)上有6m 个零点,又设()f t 在[1,2)上有n 个零点,则625m n ,且0n m ,因此4,1m n .从而()g x 在[1,4)上的零点个数等于()f t 在[2,16)[1,16)\[1,2) 上的零点个数,即311m n .7. 设12,F F 为椭圆 的焦点,在 上取一点P (异于长轴端点),记O 为12PF F 的外心,若12122PO F F PF PF ,则 的离心率的最小值为 .答案 解:取12F F 的中点M ,有12MO F F ,故120MO F F . 记1212,,PF u PF v F F d ,则121212PO F F PM F F MO F F 12211()()2PF PF PF PF 222v u , 222121222cos PF PF uv F PF u v d ,故由条件知222222v u u v d ,即22232u v d . 由柯西不等式知222281(3)1()33d u v u v (当3v u 时等号成立).所以 的离心率d e u v .当::u v d 时, 的离心率e 取到最小值8. 若三个正整数,,a b c 的位数之和为8,且组成,,a b c 的8个数码能排列为2,0,2,4,0,9,0,8,则称(,,)a b c 为“幸运数组”,例如(9,8,202400)是一个幸运数组.满足10a b c 的幸运数组(,,)a b c 的个数为 .答案:591.解:对于幸运数组(,,)a b c ,当10a b c 时,分两类情形讨论. 情形1:a 是两位数,,b c 是三位数.暂不考虑,b c 的大小关系,先在,,a b c 的非最高位(五个位置)中选三个位置填0,剩下五个位置还未填,任选其中两个填2,最后三个位置填写4,8,9,这样的填法数为3255C C 3!600 .再考虑其中,b c 的大小关系,由于不可能有b c ,因此b c 与b c 的填法各占一半,故有300个满足要求的幸运数组.情形2:,a b 是两位数,c 是四位数.暂不考虑,a b 的大小关系,类似于情形1,先在,,a b c 的非最高位(五个位置)中选三个位置填0,剩下五个位置填2,2,4,8,9,这样的填法数为600.再考虑其中,a b 的大小关系.若a b ,则必有20a b ,c 的四个数字是0,4,8,9的排列,且0不在首位,有33!18 种填法,除这些填法外,a b 与a b 的填法各占一半,故有600182912个满足要求的幸运数组. 综上,所求幸运数组的个数为300291591 .二、解答题:本大题共3小题,满分56分.解答应写出文字说明、证明过程或演算步骤.9. (本题满分16分) 在ABC 中,已知sin cos sin cos cos 22A AB B C,求cos C 的值.解:由条件知cos 44C A B. …………4分 假如44A B,则2C ,cos 0C ,但sin 04A ,矛盾. 所以只可能44A B .此时0,2A B ,2C A . …………8分注意到cos 04C A ,故2C ,所以,42A B ,结合条件得cos cos 2sin 22sin cos 244C A A A A2C ,又cos 0C ,化简得28(12cos )1C ,解得cos C…………16分 10.(本题满分20分)在平面直角坐标系中,双曲线22:1x y 的右顶点为A .将圆心在y 轴上,且与 的两支各恰有一个公共点的圆称为“好圆”.若两个好圆外切于点P ,圆心距为d ,求d PA 的所有可能的值. 解:考虑以0(0,)y 为圆心的好圆2220000:()(0)x y y r r .由0 与 的方程消去x ,得关于y 的二次方程2220002210y y y y r .根据条件,该方程的判别式22200048(1)0y y r ,因此220022y r .…………5分对于外切于点P 的两个好圆12, ,显然P 在y 轴上.设(0,)P h ,12, 的半径分别为12,r r ,不妨设12, 的圆心分别为12(0,),(0,)h r h r ,则有2211()22h r r ,2222()22h r r .两式相减得2212122()h r r r r ,而120r r ,故化简得122r r h. …………10分 进而221211222r r r r ,整理得 221122680r r r r .① 由于12d r r ,(1,0)A ,22212()114r r PA h ,而①可等价地写为2212122()8()r r r r ,即228PA d ,所以d PA…………20分 11.(本题满分20分)设复数,z w 满足2z w ,求2222S z w w z 的最小可能值.解法1:设i (,)z a b a b R ,则2i w a b ,故2222242(1)i 642(3)i S a a b b a a a b b a ,22222464a a b a a b2222(1)5(3)5a b a b . ①…………5分记1t a .对固定的b ,记255B b ,求22()(4)f t t B t B 的最小值.由()(4)f t f t ,不妨设2t .我们证明0()()f t f t ,其中0t . 当0[2,]t t 时,04[2,4]t t ,22200()()()((4))((4))f t f t B t B t B t2222220000(4)((4))(28)(28)t t t t t t t t0 (用到02t t 及228y x x 在[2,) 上单调增). …………10分当0[,)t t 时,22200()()(4)(4)f t f t t B t B t B222200(4)(4)t t t t 000()8t t t t t t0 (用到04t t ). …………15分所以200()(4)1616S f t B t .当0b (①取到等号),011a t 时,S 取到最小值16.…………20分解法2:设1i,1i (,)R z x y w x y x y ,不妨设其中0x . 计算得2222(41)(24)i z w x x y x y ,2222(41)(24)i w z x x y x y .所以22Re(2)Re(2)S z w w z 22224141x x y x x y . …………5分利用a b a b ,可得8S x ,① 亦有22222212(1)2(1)S x y x y x . ②…………10分注意到方程282(1)x x 2.当2x 时,由①得816S x .当02x 时,由②得222(1)2(12))16S x .因此当2,0x y 时,S 取到最小值16. …………20分 解法3:因为2w z =−,所以我们有222(2)2411z z z z z22(2)26411z z z z z从而上两式最右边各项分别是z 到复平面中实轴上的点1−1−,33+的距离,所以把i z x y =+换成其实部x 时,都不会增大.因此只需 考虑函数22()2464f x x x x x +−+−+在R 上的最小值.…………10分因为1313−−<<−+<,因此我们有以下几种情况:1.若1x≤−,则2()24f x x x=−,在这一区间上的最小值为(116f−=+;2.若(13x∈−−,则()88f x x=−+,在这一区间上的最小值为(316f=−+…………15分3.若31x∈−,则2()24f x x x=−+,在这一区间上的最小值为((3116f f=−+=−+;4.若13x∈− ,则()88f x x=−,在这一区间上的最小值为(116f−+=−+;5.若3x≥+,则2()24f x x x=−,在这一区间上的最小值为(316f=+.综上所述,所求最小值为((3116f f=−+=−.…………20分。
2023年全国高中数学联合竞赛(A)卷参考答案及评分标准

2023年全国中学生数学奥林匹克竞赛(预赛)暨2023年全国高中数学联合竞赛加试(A 卷)参考答案及评分标准说明:1.评阅试卷时,请严格按照本评分标准的评分档次给分.2.如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,10分为一个档次,不得增加其他中间档次.一.(本题满分40分)如图, 是以AB 为直径的固定的半圆弧, 是经过点A 及 上另一个定点T 的定圆,且 的圆心位于ABT 内.设P 是 的弧 TB(不含端点)上的动点,,C D 是 上的两个动点,满足:C 在线段AP 上,,C D 位于直线AB 的异侧,且CD AB .记CDP 的外心为K .证明:(1) 点K 在TDP 的外接圆上;(2) K 为定点. ΩωPD ABT C证明:(1) 易知PCD 为钝角,由K 为CDP 的外心知2(180)2PKD PCD ACD .由于90APB ,CD AB ,故PBA ACD ATD .……………10分 所以2180PTD PKD PTA ATD ACD PTA PBA . 又,K T 位于PD 异侧,因此点K 在TDP 的外接圆上. ……………20分(2) 取 的圆心O ,过点O 作AB 的平行线l ,则l 为CD 的中垂线,点K 在直线l 上. ……………30分由,,,T D P K 共圆及KD KP ,可知K 在DTP 的平分线上,而9090DTB ATD PBA PAB PTB ,故TB 为DTP 的平分线.所以点K 在直线TB 上.显然l 与TB 相交,且l 与TB 均为定直线,故K 为定点. ……………40分 ωΩl D P OK B ATC二.(本题满分40分)正整数n 称为“好数”,如果对任意不同于n 的正整数m ,均有2222n m n m ⎧⎫⎧⎫⎪⎪⎪⎪≠⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭,这里,{}x 表示实数x 的小数部分. 证明:存在无穷多个两两互素的合数均为好数.证明:引理:设n 是正奇数,且2模n 的阶为偶数,则n 是好数.引理的证明:反证法.假设n 不是好数,则存在异于n 的正整数m ,使得2222n m n m .因此22n n 与22m m 写成既约分数后的分母相同.由n 为奇数知22n n 是既约分数,故2m 的最大奇因子为2n ,从而m 的最大奇因子为n .设2t m n ,其中t 为正整数(从而m 是偶数).于是22222m m t m n. 由22222m t n n n可得2222(mod )m t n n ,故 222(mod )m t n n . (*)设2模n 的阶为偶数d .由(*)及阶的基本性质得2(mod )m t n d ,故2m t n 是偶数.但2m t 是偶数,n 是奇数,矛盾.引理得证.……………20分回到原问题.设221(1,2,)k k F k .由于1221k k F ,而k F 221k,因此2模k F 的阶为12k ,是一个偶数.对正整数l ,由221(mod )l k F 可知21(mod )l k F ,故由阶的性质推出,2模2k F 的阶被2模k F 的阶整除,从而也是偶数.因2k F 是奇数,由引理知2k F 是好数.……………30分对任意正整数,()i j i j ,211(,)(,(21)2)(,2)1i i j i i i j i F F F F F F F ,故123,,,F F F 两两互素.所以222123,,,F F F 是两两互素的合数,且均为好数. ……………40分三.(本题满分50分) 求具有下述性质的最小正整数k :若将1,2,,k 中的每个数任意染为红色或者蓝色,则或者存在9个互不相同的红色的数129,,,x x x 满足1289x x x x +++< ,或者存在10个互不相同的蓝色的数1210,,,y y y 满足12910y y y y +++< .解:所求的最小正整数为408.一方面,若407k =时,将1,55,56,,407 染为红色,2,3,,54 染为蓝色,此时最小的8个红数之和为1555661407++++= ,最小的9个蓝数之和为231054+++= ,故不存在满足要求的9个红数或者10个蓝数.对407k <,可在上述例子中删去大于k 的数,则得到不符合要求的例子. 因此407k ≤不满足要求. ……………10分 另一方面,我们证明408k =具有题述性质.反证法.假设存在一种1,2,,408 的染色方法不满足要求,设R 是所有红数的集合,B 是所有蓝数的集合.将R 中的元素从小到大依次记为12,,,m r r r ,B 中的元素从小到大依次记为12,,,n b b b ,408m n +=.对于R ,或者8R ≤,或者128m r r r r +++≥ ;对于B ,或者9B ≤,或者129n b b b b +++≥ .在1,2,,16 中至少有9个蓝色的数或至少有8个红色的数.情形1:1,2,,16 中至少有9个蓝色的数.此时916b ≤.设区间9[1,]b 中共有t 个R 中的元素12,,,(08)t r r r t ≤< .记12t x r r r =+++ ,则112(1)2x t t t ≥+++=+ . 因为12912,,,,,,,t b b b r r r 是9[1,]b 中的所有正整数,故{}{}12912,,,,,,,1,2,,9t b b b r r r t =+ .于是 12912(9)n b b b b t x ≤+++=++++- 1(9)(10)2t t x =++-. (*) ……………20分 特别地,116171362n b ≤⨯⨯=.从而9R ≥. 对任意(1)i i m t ≤≤-,由(*)知1(9)(10)2t i n r b i t t x i +≤+≤++-+.从而 811811(9)(10)2t m t t i r r r r r x t t x i -+=⎛⎫ ⎪≤+++++≤+++-+ ⎪⎝⎭∑ 11(9)(10)(8)(8)(9)(7)22t t t t t t x =++-+---- 111(9)(10)(8)(8)(9)(7)(1)222t t t t t t t t ≤++-+----⋅+ 2819396407t t =-++≤(考虑二次函数对称轴,即知1t =时取得最大). 又136n b ≤,这与,n m b r 中有一个为408矛盾. ……………40分情形2:1,2,,16 中至少有8个红色的数.论证类似于情形1.此时816r ≤.设区间8[1,]r 中共有s 个B 中的元素12,,,(09)s b b b s ≤< .记1s y b b =++ ,则1(1)2y s s ≥+. 因为12128,,,,,,,s b b b r r r 是8[1,]r 中的所有正整数,故 {}{}12128,,,,,,,1,2,,8s b b b r r r s =+ . 于是1(8)(9)2m r s s y ≤++-. 特别地,116171362m r ≤⨯⨯=.从而10B ≥. 对任意(1)i i n s ≤≤-,有1(8)(9)2s i m b r i s s y i +≤+≤++-+.从而 911911(8)(9)2s n s s i b b b b b y s s y i -+=⎛⎫ ⎪≤+++++≤+++-+ ⎪⎝⎭∑ 11(9)(8)(9)(8)(9)(10)22s s s s y s s =-++--+--111(9)(8)(9)(8)(1)(9)(10)222s s s s s s s s ≤-++--⋅++-- 2727369395s s =-++≤(在2s =时取得最大), 又136m r ≤,这与,n m b r 中有一个为408矛盾.由情形1、2知408k =具有题述性质.综上,所求最小正整数k 为408. ……………50分四.(本题满分50分)设4110a -=+.在20232023⨯的方格表的每个小方格中填入区间[1,]a 中的一个实数.设第i 行的总和为i x ,第i 列的总和为i y ,12023i ≤≤.求122023122023y y y x x x 的最大值(答案用含a 的式子表示). 解:记2023n =,设方格表为(),1,ij a i j n ≤≤,122023122023y y y x x x λ= . 第一步:改变某个ij a 的值仅改变i x 和j y ,设第i 行中除ij a 外其余1n -个数的和为A ,第j 列中除ij a 外其余1n -个数的和为B ,则jij i ij y B a x A a +=+.当A B ≥时,关于ij a 递增,此时可将ij a 调整到,a λ值不减.当A B ≤时,关于ij a 递减,此时可将ij a 调整到1,λ值不减.因此,为求λ的最大值,只需考虑每个小方格中的数均为1或a 的情况. ……………10分第二步:设{}1,,1,ij a a i j n ∈≤≤,只有有限多种可能,我们选取一组ij a 使得λ达到最大值,并且11n nij i j a ==∑∑最小.此时我们有,,1,.i j ij i j a x y a x y ⎧>⎪=⎨≤⎪⎩(*) 事实上,若i j x y >,而1ij a =,则将ij a 改为a 后,行和及列和变为,i j x y '',则11j j j i i iy y a y x x a x '+-=>'+-, 与λ达到最大矛盾,故ij a a =.若i j x y ≤,而ij a a =,则将ij a 改为1后,λ不减,且11n nij i j a ==∑∑变小,与ij a 的选取矛盾.从而(*)成立.通过交换列,可不妨设12n y y y ≤≤≤ ,这样由(∗)可知每一行中a 排在1的左边,每一行中的数从左至右单调不增.由此可知12n y y y ≥≥≥ .因而只能12n y y y === ,故每一行中的数全都相等(全为1或全为a ).……………20分 第三步:由第二步可知求λ的最大值,可以假定每一行中的数全相等.设有k 行全为a ,有n k -行全为1,0k n ≤≤.此时()()()n nk k n k n k ka n k ka n k na nn a λ-+-+-==. 我们只需求01,,,n λλλ 中的最大值. ()11(1)1111()(1)nn n k k n k n kk a n k a n a ka n k a k a n n a λλ++++--⎛⎫- ⎪==+ ⎪+--+⎝⎭. 因此1111(1)n k k a a k a n λλ+⎛⎫- ⎪≥⇔+≥ ⎪-+⎝⎭ 11(1)n n x x k x n-⇔+≥-+(记n x a =) 2111(1)n n x x x k x n-++++⇔≥-+ 2111n n x x x n k x -++++-⇔≤- 211(1)(1)1n n x x x x x--+++++++=+++ . 记上式右边为y ,则211(2)1n n n n x x y x x ---+-++=+++ . 下面证明(1010,1011)y ∈. ……………30分 首先证明1011y <.1011y < 2021202220222021101110111011x x x x ⇔+++<+++1010101210132021202210111010210101011x x x x x x ⇔+++<++++ .由于220221x x x <<<< ,故101010101012011(1011)101110121011101222k k k x x x =-<⋅⋅<⋅⋅∑101110110k k kx +=<∑. ……………40分 再证明1010y >,等价于证明2021202200(2022)1010kk k k k x x ==->∑∑. 由于2021202100(2022)(2022)10112023k k k k x k ==->-=⨯∑∑, 20222022010101010202310102023k k x x a =<⨯<⨯∑,只需证明1011202310102023a ⨯>⨯,而410111101010a -=+<,故结论成立. 由上面的推导可知1k k λλ+≥当且仅当1010k ≤时成立,从而1011λ最大.故 2023max 101120231011(10111012)2023a aλλ+==. ……………50分。
2023全国高中数学联赛山东省预赛试题(答案)

2023全国数学联赛山东省预赛试题(答案)一、填空题(每小题8分,共80分)1、已知},33811|{1Z x x A x ,},032|{N x x x x B ,则集合},,|{B y A x xy m m C 的元素个数是答案:7解析:由已知得}2,1,0,1,2{ A ,}2,1,0{ B ,所以}4201124{,,,,, C 2、已知:3tan sin 41))2,0((,则 是答案:18解析:由已知得)6sin (22sin 2,所以易得183、已知关于x 的方程023 c b x a x x 的三个非零实数根成等比数列,则33b c a 的值是答案:0解析:设这三个根是2,,dq dq d ,则由韦达定理得c qd b q d q d q d adq dq d 33322222整理得c ab3)(,所以033 b c a 4、正方体1111D C B A ABCD 的底面1111D C B A 内有一个动点M ,且CAD BM 1//平面,则MD D 1tan 的最大值是答案:2解析:由已知点M 在线段11C A 上运动,所以2tan 111MD DD MD D ,且当点M 是11C A 中点时等号成立.5、数列}{n a 中,11 a ,),2,1(211na a nn ,那么n a 答案:),2,1(1)2(32na nn 解析:由递推关系得)1(211nnn a a a ,)2(121nnn a a a 所以2122111n n n n a a a a ,所以nn n n a a a a )2(21)2(21111 所以),2,1(1)2(32na nn6、已知0,, z y x ,则zy x x zz yy xf539164222222的最小值是答案:55解析:由柯西不等式得y x y x24122,z y z y441422,xz x z8411622所以zy x x zz yy xf539164222222555539842)(z y x xz z y y x 且当x z y 2 时取等号7、设ABC 的内心为I ,而且满足0652 IC IB IA ,则B cos 的值是答案:85解析:设ABC 的三边长为c b a ,,,由熟悉的结论:0 IC c IB b IA a 得6:5:2:: c b a ,所以85cosB 8、已知双曲线H :221x y 上第一象限内一点M ,过M 的作H 的切线l ,与双曲线H 切于M ,交H 的渐近线于P ,Q 两点(P 在第一象限),R 与Q 在同一渐近线上.则RP RQ的最小值为.答案:21解析:设点00(,)M xy ,11(,)P x y ,22(,)Q x y ,则00:10l x x y y .02121=x y y x x y 且2211222200x y x y ,12211221212x x y y y y x x,注意到02121=x y y x x y 1201222x x y y y x1201222x x y y y x即M 为PQ 的中点.222221111||||4444RP RQ RM P Q P OP QO Q.考虑到M 在第一象限,故22O Q21142RP RQ O Q9、小张参加一次十道选择题的测试,做对一道得一分,做错一道扣一分,不做得零分.他的目标是至少得7分,7分及格.小张现在确定他前六道题的答案是正确的,而剩下的每道题做对的概率为21,小张应该做______多少道题,及格的概率最大答案:7或9解析:做对6道题.再做一道题及格的概率为1P p ,再做两道题及格的概率为22P p ,再做三道题及格的概率为322233(1)(32)P p C p p p p ,再做四道题及格的概率为433344(1)(43)P p C p p p p .显然1234P P P P ,.因此,只需比较1P 与3P 的大小.当13P P ,即2(32)pp p时,解得112p .因此,当112p 时,13P P ,此时回答九道题及格的概率最大;当102p 时,13P P ,此时回答七道题及格的概率最大;当12p 时,13P P ,此时回答七道题或回答九道题及格的概率最大10、设实数y x ,使得y x ,22y x ,33y x 均为素数,则y x 的值是答案:3解析:设p y x ,q y x22,r y x 33,期中r q p ,,都是素数,pq yx y xy x22所以)(21p pq x,)(21p pq y代入r y x 33整理得)4(332p rp q故23|q p ,所以3 p 或q p ,经检验只能3 p 二、解答题(共70分)11、(本题15分)已知:O 是ABC 的外心,E D ,分别是边AB AC ,上的点.线段CE BD DE ,,的中点分别为R Q P ,,.DE OH垂足为H .求证:H R Q P ,,,四点共圆证明:设ADE 的三个内角分别为E D A ,,,ABC 的外接圆半径为R 由ACRP AB QP//,//知EQPH sinsin,A QPR sinsin ,DHPR sinsin又2,2CD PRBE PQ ,故HR Q P ,,,四点共圆 QPRPHQPH PR RPH PQ sinsin sinAPHECD DBE sin sin 2sin 2DEPH AD CD AE BE 2 )()()()(2222EHDH EH DH ODRDER2222EHDH OE ODDEOH得证12、(本题15分)在区间)2,2(32n n 中任取1212 n 个奇数.求证:在所取出的数中,必有两个数,其中一个数的平方不能被另一个数整除.13、(本题20分)已知:c b a ,,为正实数.证明:)(9)2)(2)(2(222ca bc ab c b a 证明:由抽屉原理,c b a ,,中必有两个数同时不大于1,或同时比小于1,设为b a ,则由0)1)(1(22 b a 得22221b a b a 所以)2)(422()2)(2)(2(22222222 c b a b a c b a )11)(1(3222c b a 2)(3c b a )(9ca bc ab 14、(本题20分)1010 的表格上填入1到100,第i 行第j 列填入j i )1(10.每次操作如下:取一个格子,或者将此格数字减少2,将两个相对的邻格同时加1;或者将此格数字增加2,将两个相对的邻格同时减1.证明:如果经过一些步骤后表格中又得到1到100的数字,则它们是按原来的顺序排列的.证明:设一开始填数字k 的格子为k a ,令 1001i iia A 则A 在操作中是不变量,始终为33835010012 i i 又因此数为表格中1到100所能得到的最大值,故等号成立,所以顺序不变.。
2023年全国高中数学联赛江西省预赛试题(附参考答案 )

.
− 1,所以函数() = ( + 1) ( + 1)的单调递增区间是
( − 1, +∞).
4、已知关于的方程|( − 1)( − 3)| = 有四个不同的实根,则的取值范围是
.
解:由 = 与 = −( − 1)( − 3)在区间(1,3)内相切,可得 = 4 ± 2√3,再由切点横坐标必
.
解: 内(包括边界)的点与内(包括边界)点的最短距离为到的中点(
的距离,故直线即为线段的中垂线,所以直线的方程为: −
= − ( −
, )
),
即 − 5 − 25 = 0,也即 = − 5.
3、函数() = ( + 1) ( + 1)的单调递增区间是
须在区间(1,3)内,所以 = 4 + 2√3不合条件,故的取值范围是0 < < 4 − 2√3
5、边长为1正六面体被一个平面所截的最大截面面积为
.
解:由边长为1正六面体被一个平面所截的面积最大的平面是边长为
6⋅ ⋅
√
⋅
√
=
√
的正六边形,故最大面积为
.
6、若锐角, , 满足 + + = 2,则
一点, ,过, 的切线相交于 ,若是一个正三角形,且面积为
是
,则双曲线 的方程
.
解:设(−, 0), (, 0), (− , ), ( , )
从而的直线方程为 = − + 1,于是有 = − + 1
2 / 5
中 (1,1,1), (2,1,1), (2,2,1), (1,2,1), (1,2,2), (1,1,2), (2,1,2), (2,2,2),
2023年全国高中数学联赛北京赛区预赛试题答案
2023 中国数学奥林匹克预赛北京赛区预赛一试试题参考解答
2023 年 5 月 21 日 8 : 00 − 9 : 20 前 8 题每题 8 分, 第 9 题 16 分, 第 10, 11 题每题 20 分
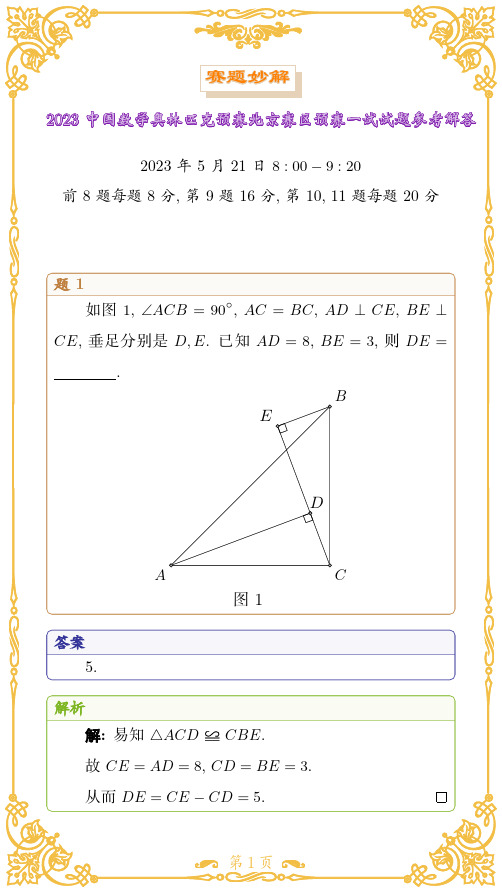
题1 如图 1, ∠ACB = 90◦, AC = BC, AD ⊥ CE, BE ⊥
2 3
=⇒ =⇒
f (3) = 1 或 3, f (3) = 2 或 3.
这样的 f 一共有 13 个.
第3页
题5
已知向量 |−→a | = 1,
−→ b
=
2,
且
−→a ,
−→ b
夹角为
120◦.
若 −→a + t−→b 与 t−→a + −→b 的夹角为锐角, 则 t 的取值范围是
.
答案
√
√
5 − 21 , 1 ∪ 1, 5 + 21 .
3 其它所有数均可选入.
故 |S|max = 2023 − 674 + 1 = 1350.
题3 已知函数 f (x) = sin ωx + sin 2x, 其中 ω ∈ N+, ω ⩽
2023. 若 f (x) < 2 恒成立, 则满足题设的常数 ω 的个数为 .
答案 1770.
解析
解: 只要考虑 sin 2x = 1 ⇐⇒ x =
√
3
=⇒ x2 = 3 − 2 2 (x > 0)
√6
√
=⇒ x =
2√− 1 , y =
2+1 √.
6
6
(n + m)2 = m2 + n2 + 2mn
= 1 + 4xy = 5 (n > 0, m > 0)
2024年全国高中数学联赛(浙江预赛)试题(含答案)

2024年全国中学生奥林匹克数学竞赛浙江赛区初赛试题本卷共15道题目,12道填空题,3道解答题,所有答案填写在答题纸上,满分150分一、填空题(每小题8分,共计96分)1.设集合10,21x A xx ⎧−⎫=≤⎨⎬−⎩⎭集合2{20}B x x x m =++≤。
若A B ⊆,则实数m 的取值范围为 。
2.设函数{}{}:1,2,32,3,4f → 满足 ()()1()ff x f x −=,则这样的函数有_______个。
3.函数22sin sin 1sin 1x x y x ++=+的最大值与最小值之积为 。
4.已知数列{}n x满足:11,12n x x x n +==≥,则通项n x =__________。
5 .已知四面体A BCD −的外接球半径为1,1,60BC BDC =∠=,则球心到平面BDC 的距离为______________。
6.已知复数z 满足24510(1)1zz =−=,则z =__________________。
7.已知平面上单位向量,a b 垂直,c 为任意单位向量,且存在(0,1)t ∈,使得向量(1)a t b +−与向量c a −垂直,则a b c +−的最小值为__________________________。
8. 若对所有大于2024的正整数n ,成立202420240, ii n i i na C a ==∈∑,则12024a a +=_________。
9.设实数,,(0,2]a b c ∈,且3b a ≥或43a b +≤,则max{,,42}b a c b c −−−的最小值为 ___ __ __。
10.在平面直角坐标系xOy 上,椭圆E 的方程为221124x y +=,1F 为E 的左焦点;圆C 的方程为222())x a y b r −+−=( ,A 为C 的圆心。
直线l 与椭圆E 和圆C 相切于同一点(3,1)P 。
则当1OAF ∠最大时,实数r =_____________________。
完整版-2023年数学联赛试题及答案(学科竞赛圈)

2023年全国中学生数学奥林匹克竞赛(预赛)暨2023年全国高中数学联合竞赛一试(A 卷)参考答案及评分标准说明:1. 评阅试卷时,请依据本评分标准. 填空题只设8分和0分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不得增加其他中间档次.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中第9小题4分为一个档次,第10、11小题5分为一个档次,不得增加其他中间档次.一、填空题:本大题共8小题,每小题8分,满分64分.1. 设复数910i z (i 为虚数单位),若正整数n 满足2023n z ,则n 的最大值为 .答案:2.解: 22910181n nn n z z .因21812023z ,而当3n 时, 181132023nn n z ,故n 的最大值为2. 2. 若正实数,a b 满足lg 2b a ,lg lg 5a b a b ,则lg ()ab ab 的值为 . 答案:20.解:因为lg lg lg lg 102a a b b b a ,所以lg lg lg lg lg lg lg ()()()52220ab a b a b b a ab ab a b a b .3. 将一枚均匀的骰子独立投掷三次,所得的点数依次记为,,x y z ,则事件“777C C C x y z ”发生的概率为 . 答案:127. 解:由于162534777777C C C C C C ,因此当,,{1,2,3,4,5,6}x y z 时,事件“777C C C x y z ”发生当且仅当“{1,6},{2,5},{3,4}x y z ”成立,相应的概率为321627 . 4. 若平面上非零向量,, 满足 ,2|| ,3|| ,则|| 的最小值为 .答案:23. 解:由 ,不妨设(,0),(0,)a b ,其中,0a b ,并设(,)x y ,则由2|| 得2by a ,由3|| 得3ax b . 所以2232||2223b a x y xy a b . 取3,2a b ,此时6x y ,|| 取到最小值23.5. 方程sin cos2x x 的最小的20个正实数解之和为 .答案:130 .解:将2cos212sin x x 代入方程,整理得(2sin 1)(sin 1)0x x ,解得532,2,2()662Z x k k k k . 上述解亦可写成2()36Z k x k ,其中0,1,,19k 对应最小的20个正实数解,它们的和为1902219202013036326k k . 6. 设,,a b c 为正数,a b .若,a b 为一元二次方程20ax bx c 的两个根,且,,a b c 是一个三角形的三边长,则a b c 的取值范围是 .答案:7,518. 解:由条件知2222()()()ax bx c a x a x b ax a ab x a b ,比较系数得22,b a ab c a b ,故24,11a a b c a a,从而 24231a a a b c a a a a a. 由于201a a b a,故112a .此时显然0b c .因此,,,a b c 是一个三角形的三边长当且仅当a c b ,即4211a a a a a,即2(1)0a a a ,结合112a ,解得15122a . 令23()f x x x x ,则()abc f a .显然当0x 时()f x 连续且严格递增,故a b c 的取值范围是151,22f f,即7,518 . 7. 平面直角坐标系xOy 中,已知圆 与x 轴、y 轴均相切,圆心在椭圆2222:1(0)x y a b a b内,且 与 有唯一的公共点(8,9).则 的焦距为 .答案:10.解:根据条件,可设圆心为(,)P r r ,则有222(8)(9)r r r ,解得5r 或29r .因为P 在 内,故5r . 椭圆 在点(8,9)A 处的切线为2289:1x y l a b ,其法向量可取为2289,n a b . 由条件,l 也是圆 的切线,故n 与PA 平行,而(3,4)PA ,所以223227a b. 又2264811a b,解得22160,135a b .从而 的焦距为22210a b .8. 八张标有,,,,,,,A B C D E F G H 的正方形卡片构成下图.现逐一取走这些卡片,要求每次取走一张卡片时,该卡片与剩下的卡片中至多一张有公共边(例如可按,,,,,,,D A B E C F G H 的次序取走卡片,但不可按,,,,,,,D B A E C F G H 的次序取走卡片),则取走这八张卡片的不同次序的数目为 .A BCD E F G H答案:392.解:如左下图重新标记原图中的八张卡片.现将每张卡片视为顶点,有公共边的两张卡片所对应的顶点之间连一条边,得到一个八阶图,该图可视为右下图中的2m n 阶图(,)G m n 在3,3m n 时的特殊情况.231-3-20P -1G (m , n )P n ...210-1-2-m ... 取卡片(顶点)的规则可解释为:(i) 若顶点P 已取走,则以下每步取当前标号最小或最大的顶点,直至取完; (ii) 若顶点P 未取走,则必为某个(,)(,0)G m n m n 的情形,此时若0m ,则将P 视为1 号顶点,归结为(i)的情形;若0,0m n ,则将P 视为1号顶点,归结为(i)的情形;若,1m n ,则当前可取P 或m 号顶点或n 号顶点,分别归结为(i)或(1,)G m n 或(,1)G m n 的情形.设(,)G m n 的符合要求的顶点选取次序数为(,)f m n ,本题所求即为(3,3)f . 由(i)、(ii)知1(,0)2(0)m f m m ,1(0,)2(0)n f n n ,且(,)2(1,)(,1)(,1)m n f m n f m n f m n m n .由此可依次计算得(1,1)12f ,(1,2)(2,1)28f f ,(1,3)(3,1)60f f ,(2,2)72f ,(2,3)(3,2)164f f ,(3,3)392f ,即所求数目为392.二、解答题:本大题共3小题,满分56分.解答应写出文字说明、证明过程或演算步骤.9. (本题满分16分)平面直角坐标系xOy 中,抛物线2:4y x ,F 为 的焦点,,A B 为 上的两个不重合的动点,使得线段AB 的一个三等分点P 位于线段OF 上(含端点),记Q 为线段AB 的另一个三等分点.求点Q 的轨迹方程.解:设1122(,),(,)A x y B x y .不妨设AP PQ QB ,则121222,33x x y y P. 易知(1,0)F .由于点P 位于线段OF 上,故122[0,1]3x x ,12203y y . ……………4分可设12,2y t y t ,则2212,4t x x t .此时有2122[0,1]32x x t ,且由,A B 不重合知0t ,所以2(0,2]t . ……………8分设(,)Q Q Q x y ,则21212232,343Q Q x x y y x t y t ,有243Q Q y x . 注意到2330,42Q x t ,故点Q 的轨迹方程为243(0)32y x x . ……………16分10.(本题满分20分)已知三棱柱111:ABC A B C 的9条棱长均相等.记底面ABC 所在平面为 .若 的另外四个面(即面111111111,,,A B C ABB A ACC A BCC B )在 上投影的面积从小到大重排后依次为23,33,43,53,求 的体积.解:设点111,,A B C 在平面 上的投影分别为,,D E F ,则面11111,,A B C ABB A 1111,ACC A BCC B 在 上的投影面积分别为,,,DEF ABED ACFD BCFE S S S S .由已知及三棱柱的性质,DEF 为正三角形,且,,ABED ACFD BCFE 均为平行四边形.由对称性,仅需考虑点D 位于BAC 内的情形(如图所示).显然此时有ABED ACFD BCFE S S S . ……………5分 XFE B D C A由于,,,23,33,43,53DEF ABED ACFD BCFE S S S S ,故,ABED ACFD S S 必为23,33的排列,53BCFE S ,进而43DEF S ,得DEF 的边长为4,即正三棱柱 的各棱长均为4. ……………10分 不妨设23,33ABED ACFD S S ,则333,2ABD ACD S S . 取射线AD 与线段BC 的交点X ,则23ABD ACD BX S CX S ,故85BX .因此 2242cos60195AX AB BX AB BX , 而58ABD ACD ABC AD S S AX S ,故192AD . ……………15分 于是 的高221352h AA AD . 又43ABCS ,故 的体积615ABC V S h . ……………20分11.(本题满分20分)求出所有满足下面要求的不小于1的实数t :对任意,[1,]a b t ,总存在,[1,]c d t ,使得()()1a c b d .解:记[1,]t I t ,()()S a c b d .假如2t ,则当a b t 时,对任意,t c d I ,均有2(1)1S t ,不满足要求. 假如312t ,则当1,2a b t 时,对任意,t c d I ,均有 21a c t ,12t b d .若,a c b d 同正或同负,则2(1)1S t ,其余情况下总有01S ,不满足要求. ……………5分 以下考虑322t 的情形.为便于讨论,先指出如下引理. 引理:若1,2u v ,且52u v ,则1uv . 事实上,当32u v 时,22225312244u v u v uv . 当32u v 时,1131222uv .引理得证. 下证对任意,t a b I ,可取11,t c d I ,使得111()()1S a c b d .① 若12a b ,则取111c d ,此时 1(1)(1)(1)(1)S a b a b , 其中31311,12222a b b a ,且5(1)(1)2()2a b a b ,故由引理知11S . 若12a b ,则取1132t c d I ,此时 13322S a b, 其中331,222a b ,且3353222a b a b ,故由引理知11S . ……………15分 注意到,当,t a b I 时,可取2t c I ,使得21a c (例如,当[1,1]a 时取20c ,当(1,]a t 时取21c ),同理,可取2t d I ,使得21b d .此时22222()()1S a c b d a c b d . ②根据①、②,存在一个介于12,c c 之间的实数c ,及一个介于12,d d 之间的实数d ,使得()()1a c b d ,满足要求.综上,实数t 满足要求当且仅当322t . ……………20分2023年全国中学生数学奥林匹克竞赛(预赛)暨2023年全国高中数学联合竞赛加试(A 卷)参考答案及评分标准说明:1.评阅试卷时,请严格按照本评分标准的评分档次给分.2.如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,10分为一个档次,不得增加其他中间档次.一.(本题满分40分)如图, 是以AB 为直径的固定的半圆弧, 是经过点A 及 上另一个定点T 的定圆,且 的圆心位于ABT 内.设P 是 的弧 TB(不含端点)上的动点,,C D 是 上的两个动点,满足:C 在线段AP 上,,C D 位于直线AB 的异侧,且CD AB .记CDP 的外心为K .证明:(1) 点K 在TDP 的外接圆上;(2) K 为定点. ΩωPD ABT C证明:(1) 易知PCD 为钝角,由K 为CDP 的外心知2(180)2PKD PCD ACD .由于90APB ,CD AB ,故PBA ACD ATD .……………10分 所以2180PTD PKD PTA ATD ACD PTA PBA . 又,K T 位于PD 异侧,因此点K 在TDP 的外接圆上. ……………20分(2) 取 的圆心O ,过点O 作AB 的平行线l ,则l 为CD 的中垂线,点K 在直线l 上. ……………30分由,,,T D P K 共圆及KD KP ,可知K 在DTP 的平分线上,而9090DTB ATD PBA PAB PTB ,故TB 为DTP 的平分线.所以点K 在直线TB 上.显然l 与TB 相交,且l 与TB 均为定直线,故K 为定点. ……………40分 ωΩl D P OK B ATC二.(本题满分40分)正整数n 称为“好数”,如果对任意不同于n 的正整数m ,均有2222n m n m ⎧⎫⎧⎫⎪⎪⎪⎪≠⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭,这里,{}x 表示实数x 的小数部分. 证明:存在无穷多个两两互素的合数均为好数.证明:引理:设n 是正奇数,且2模n 的阶为偶数,则n 是好数.引理的证明:反证法.假设n 不是好数,则存在异于n 的正整数m ,使得2222n m n m .因此22n n 与22m m 写成既约分数后的分母相同.由n 为奇数知22n n 是既约分数,故2m 的最大奇因子为2n ,从而m 的最大奇因子为n .设2t m n ,其中t 为正整数(从而m 是偶数).于是22222m m t m n. 由22222m t n n n可得2222(mod )m t n n ,故 222(mod )m t n n . (*)设2模n 的阶为偶数d .由(*)及阶的基本性质得2(mod )m t n d ,故2m t n 是偶数.但2m t 是偶数,n 是奇数,矛盾.引理得证.……………20分回到原问题.设221(1,2,)k k F k .由于1221k k F ,而k F 221k,因此2模k F 的阶为12k ,是一个偶数.对正整数l ,由221(mod )l k F 可知21(mod )l k F ,故由阶的性质推出,2模2k F 的阶被2模k F 的阶整除,从而也是偶数.因2k F 是奇数,由引理知2k F 是好数.……………30分对任意正整数,()i j i j ,211(,)(,(21)2)(,2)1i i j i i i j i F F F F F F F ,故123,,,F F F 两两互素.所以222123,,,F F F 是两两互素的合数,且均为好数. ……………40分三.(本题满分50分) 求具有下述性质的最小正整数k :若将1,2,,k 中的每个数任意染为红色或者蓝色,则或者存在9个互不相同的红色的数129,,,x x x 满足1289x x x x +++< ,或者存在10个互不相同的蓝色的数1210,,,y y y 满足12910y y y y +++< .解:所求的最小正整数为408.一方面,若407k =时,将1,55,56,,407 染为红色,2,3,,54 染为蓝色,此时最小的8个红数之和为1555661407++++= ,最小的9个蓝数之和为231054+++= ,故不存在满足要求的9个红数或者10个蓝数.对407k <,可在上述例子中删去大于k 的数,则得到不符合要求的例子. 因此407k ≤不满足要求. ……………10分 另一方面,我们证明408k =具有题述性质.反证法.假设存在一种1,2,,408 的染色方法不满足要求,设R 是所有红数的集合,B 是所有蓝数的集合.将R 中的元素从小到大依次记为12,,,m r r r ,B 中的元素从小到大依次记为12,,,n b b b ,408m n +=.对于R ,或者8R ≤,或者128m r r r r +++≥ ;对于B ,或者9B ≤,或者129n b b b b +++≥ .在1,2,,16 中至少有9个蓝色的数或至少有8个红色的数.情形1:1,2,,16 中至少有9个蓝色的数.此时916b ≤.设区间9[1,]b 中共有t 个R 中的元素12,,,(08)t r r r t ≤< .记12t x r r r =+++ ,则112(1)2x t t t ≥+++=+ . 因为12912,,,,,,,t b b b r r r 是9[1,]b 中的所有正整数,故{}{}12912,,,,,,,1,2,,9t b b b r r r t =+ .于是 12912(9)n b b b b t x ≤+++=++++- 1(9)(10)2t t x =++-. (*) ……………20分 特别地,116171362n b ≤⨯⨯=.从而9R ≥. 对任意(1)i i m t ≤≤-,由(*)知1(9)(10)2t i n r b i t t x i +≤+≤++-+.从而 811811(9)(10)2t m t t i r r r r r x t t x i -+=⎛⎫ ⎪≤+++++≤+++-+ ⎪⎝⎭∑ 11(9)(10)(8)(8)(9)(7)22t t t t t t x =++-+---- 111(9)(10)(8)(8)(9)(7)(1)222t t t t t t t t ≤++-+----⋅+ 2819396407t t =-++≤(考虑二次函数对称轴,即知1t =时取得最大). 又136n b ≤,这与,n m b r 中有一个为408矛盾. ……………40分情形2:1,2,,16 中至少有8个红色的数.论证类似于情形1.此时816r ≤.设区间8[1,]r 中共有s 个B 中的元素12,,,(09)s b b b s ≤< .记1s y b b =++ ,则1(1)2y s s ≥+. 因为12128,,,,,,,s b b b r r r 是8[1,]r 中的所有正整数,故 {}{}12128,,,,,,,1,2,,8s b b b r r r s =+ . 于是1(8)(9)2m r s s y ≤++-. 特别地,116171362m r ≤⨯⨯=.从而10B ≥. 对任意(1)i i n s ≤≤-,有1(8)(9)2s i m b r i s s y i +≤+≤++-+.从而 911911(8)(9)2s n s s i b b b b b y s s y i -+=⎛⎫ ⎪≤+++++≤+++-+ ⎪⎝⎭∑ 11(9)(8)(9)(8)(9)(10)22s s s s y s s =-++--+--111(9)(8)(9)(8)(1)(9)(10)222s s s s s s s s ≤-++--⋅++-- 2727369395s s =-++≤(在2s =时取得最大), 又136m r ≤,这与,n m b r 中有一个为408矛盾.由情形1、2知408k =具有题述性质.综上,所求最小正整数k 为408. ……………50分四.(本题满分50分)设4110a -=+.在20232023⨯的方格表的每个小方格中填入区间[1,]a 中的一个实数.设第i 行的总和为i x ,第i 列的总和为i y ,12023i ≤≤.求122023122023y y y x x x 的最大值(答案用含a 的式子表示). 解:记2023n =,设方格表为(),1,ij a i j n ≤≤,122023122023y y y x x x λ= . 第一步:改变某个ij a 的值仅改变i x 和j y ,设第i 行中除ij a 外其余1n -个数的和为A ,第j 列中除ij a 外其余1n -个数的和为B ,则jij i ij y B a x A a +=+.当A B ≥时,关于ij a 递增,此时可将ij a 调整到,a λ值不减.当A B ≤时,关于ij a 递减,此时可将ij a 调整到1,λ值不减.因此,为求λ的最大值,只需考虑每个小方格中的数均为1或a 的情况. ……………10分第二步:设{}1,,1,ij a a i j n ∈≤≤,只有有限多种可能,我们选取一组ij a 使得λ达到最大值,并且11n nij i j a ==∑∑最小.此时我们有,,1,.i j ij i j a x y a x y ⎧>⎪=⎨≤⎪⎩(*) 事实上,若i j x y >,而1ij a =,则将ij a 改为a 后,行和及列和变为,i j x y '',则11j j j i i iy y a y x x a x '+-=>'+-, 与λ达到最大矛盾,故ij a a =.若i j x y ≤,而ij a a =,则将ij a 改为1后,λ不减,且11n nij i j a ==∑∑变小,与ij a 的选取矛盾.从而(*)成立.通过交换列,可不妨设12n y y y ≤≤≤ ,这样由(∗)可知每一行中a 排在1的左边,每一行中的数从左至右单调不增.由此可知12n y y y ≥≥≥ .因而只能12n y y y === ,故每一行中的数全都相等(全为1或全为a ).……………20分 第三步:由第二步可知求λ的最大值,可以假定每一行中的数全相等.设有k 行全为a ,有n k -行全为1,0k n ≤≤.此时()()()n nk k n k n k ka n k ka n k na nn a λ-+-+-==. 我们只需求01,,,n λλλ 中的最大值. ()11(1)1111()(1)nn n k k n k n kk a n k a n a ka n k a k a n n a λλ++++--⎛⎫- ⎪==+ ⎪+--+⎝⎭. 因此1111(1)n k k a a k a n λλ+⎛⎫- ⎪≥⇔+≥ ⎪-+⎝⎭ 11(1)n n x x k x n-⇔+≥-+(记n x a =) 2111(1)n n x x x k x n-++++⇔≥-+ 2111n n x x x n k x -++++-⇔≤- 211(1)(1)1n n x x x x x--+++++++=+++ . 记上式右边为y ,则211(2)1n n n n x x y x x ---+-++=+++ . 下面证明(1010,1011)y ∈. ……………30分 首先证明1011y <.1011y < 2021202220222021101110111011x x x x ⇔+++<+++1010101210132021202210111010210101011x x x x x x ⇔+++<++++ .由于220221x x x <<<< ,故101010101012011(1011)101110121011101222k k k x x x =-<⋅⋅<⋅⋅∑101110110k k kx +=<∑. ……………40分 再证明1010y >,等价于证明2021202200(2022)1010kk k k k x x ==->∑∑. 由于2021202100(2022)(2022)10112023k k k k x k ==->-=⨯∑∑, 20222022010101010202310102023k k x x a =<⨯<⨯∑,只需证明1011202310102023a ⨯>⨯,而410111101010a -=+<,故结论成立. 由上面的推导可知1k k λλ+≥当且仅当1010k ≤时成立,从而1011λ最大.故 2023max 101120231011(10111012)2023a aλλ+==. ……………50分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年全国高中数学联赛预赛试题及答案«Skip Record If...»2012年全国高中数学联合竞赛(四川初赛)一、单项选择题(本大题共6个小题,每小题5分,共30分)1、设集合«Skip Record If...»,«Skip Record If...»,则«Skip Record If...»=()A、«Skip Record If...»B、«Skip Record If...»C、«Skip Record If...»D 、«Skip Record If...»2、正方体«Skip Record If...»中«Skip Record If...»与截面«Skip Record If...»所成的角是()A、«Skip Record If...»B、«Skip Record If...»C、«Skip Record If...»D、«Skip Record If...»3、已知«Skip Record If...»,«Skip Record If...»,则“«Skip Record If...»”是“«Skip Record If...»在«Skip Record If...»上恒成立”的()A、充分但不必要条件B、必要但不充分条件C、充要条件D、既不充分也不必要条件4、设正三角形«Skip Record If...»的面积为«Skip Record If...»,作«Skip Record If...»的内切圆,再作内切圆的内接正三角形,设为«Skip Record If...»,面积为«Skip Record If...»,如此下去作一系列的正三角形«Skip Record If...»,其面积相应为«Skip Record If...»,设«Skip Record If...»,«Skip Record If...»,则«Skip Record If...»=()A 、«Skip Record If...»B 、«Skip Record If...» C、«Skip Record If...» D 、25、设抛物线«Skip Record If...»的焦点为«Skip Record If...»,顶点为«Skip Record If...»,«Skip Record If...»是抛物线上的动点,则«Skip Record If...»的最大值为()A 、«Skip Record If...»B 、«Skip Record If...» C、«Skip Record If...»D 、«Skip Record If...»6、设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并放入半径为«Skip Record If...»的一个实心球,此时球与容器壁及水面恰好都相切,则取出球后水面高为()A、«Skip Record If...»B、«Skip Record If...»C、«Skip Record If...»D、«Skip Record If...»二、填空题(本大题共6个小题,每小题5分,共30分)7、如图,正方形«Skip Record If...»的边长为3,«SkipRecord If...»为«Skip Record If...»的中点,«Skip Record If...»与«Skip Record If...»相交于«Skip Record If...»,则«Skip Record If...»的值是.8、«Skip Record If...»的展开式中的常数项是.(用具体数字作答)9、设等比数列«Skip Record If...»的前«Skip Record If...»项和为«Skip Record If...»,满足«Skip Record If...»,则«Skip Record If...»的值为.10、不超过2012的只有三个正因数的正整数个数为.11、已知锐角«Skip Record If...»满足«Skip Record If...»,则«Skip Record If...»的最大值是.12、从1,2,3,4,5组成的数字不重复的五位数中,任取一个五位数«Skip Record If...»,满足条件“«Skip Record If...»”的概率是.三、解答题(本大题共4个小题,每小题20分,共80分)13、设函数«Skip Record If...»,(I)求函数«Skip Record If...»在«Skip Record If...»上的最大值与最小值;(II)若实数«Skip Record If...»使得«Skip Record If...»对任意«Skip Record If...»恒成立,求«Skip Record If...»的值.14、已知«Skip Record If...»,满足«Skip Record If...»,(I)求«Skip Record If...»的最小值;(II)当«Skip Record If...»取最小值时,求«Skip Record If...»的最大值.15、直线«Skip Record If...»与双曲线«Skip Record If...»的左支交于«Skip Record If...»、«Skip Record If...»两点,直线«Skip Record If...»经过点«Skip Record If...»和«Skip Record If...»的中点,求直线«Skip Record If...»在«Skip Record If...»轴的截距«Skip Record If...»的取值范围.16、设函数«Skip Record If...»在«Skip Record If...»上的最大值为«Skip Record If...»(«Skip Record If...»).(I)求数列«Skip Record If...»的通项公式;(II)求证:对任何正整数«Skip Record If...»,都有«Skip Record If...»成立;(III)设数列«Skip Record If...»的前«Skip Record If...»项和为«Skip Record If...»,求证:对任意正整数«Skip Record If...»,都有«Skip Record If...»成立.2012年全国高中数学联合竞赛(四川初赛)参考解答一、选择题(本大题共6个小题,每小题5分,共30分)1、C2、A3、A4、B5、B6、D二、填空题(本大题共6个小题,每小题5分,共30分)7、«Skip Record If...» 8、«Skip Record If...» 9、0 10、14 11、«Skip Record If...» 12、«Skip Record If...»三、解答题(本大题共4个小题,每小题20分,共80分)13、解:(I)由条件知«Skip Record If...»,(5分)由«Skip Record If...»知,«Skip Record If...»,于是«Skip Record If...»所以«Skip Record If...»时,«Skip Record If...»有最小值«Skip Record If...»;当«Skip Record If...»时,«Skip Record If...»有最大值«Skip Record If...».(10分)(II)由条件可知«Skip Record If...»对任意的«Skip Record If...»恒成立,∴«Skip Record If...»∴«Skip Record If...»∴«Skip Record If...», (15分)由«Skip Record If...»知«Skip Record If...»或«Skip Record If...»。
