(完整word版)高等代数多项式习题解答

合集下载

高等代数课后答案高等教育出版社

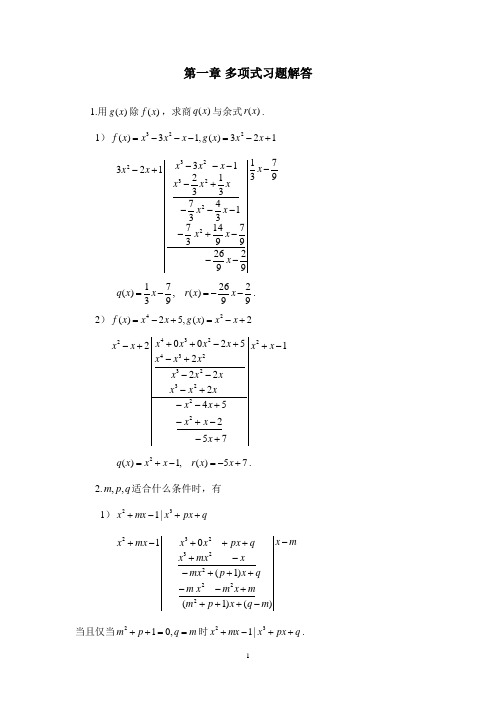
高等代数习题答案（一至四章）第一章多项式习题解答1、（1）由带余除法，得17(),39q x x =-262()99r x =--（2）2()1q x x x =+-，()57r x x =-+2、（1）2100p m q m ⎧++=⎨-=⎩ ，（2）由22(2)010m p m q p m ⎧--=⎪⎨+--=⎪⎩得01m p q =⎧⎨=+⎩或212q p m =⎧⎨+=⎩。

3、（1）432()261339109,q x x x x x =-+-+()327r x =- （2）q （x ）=22(52)x ix i --+，()98r x i =--4、（1）有综合除法：2345()15(1)10(1)10(1)5(1)(1)f x x x x x x =+-+-+-+-+- （2）234()1124(2)22(2)8(2)(2)f x x x x x =-+++-+++（3）234()24(75)5()(1)()2()()f x i x i i x i i x i x i =+-++--+-+++5、（1）x+1 （2）1 （3）21x -- 6、（1）u （x ）=-x-1 ，v （x ）=x+2 （2）11()33u x x =-+，222()133v x x x =-- （3）u （x ）=-x-1, 32()32v x x x x =+--7、02u t =⎧⎨=⎩或23u t =-⎧⎨=⎩8、思路：根具定义证明证：易见d （x ）是f （x ）与g （x ）的公因式。

另设()x ϕ是f （x ）与g （x ）的任意公因式，下证()()x d x ϕ。

由于d （x ）是f （x ）与g （x ）的一个组合，这就是说存在多项式s （x ）与t （x ），使 d （x ）=s （x ）f （x ）+t （x ）g （x ）。

从而()()x f x ϕ，()()x g x ϕ，可得()()x d x ϕ。

高等代数二练习题答案

高等代数二练习题答案一、多项式运算1. 给定多项式 $ p(x) = x^3 - 3x^2 + 2x - 1 $ 和 $ q(x) =x^2 + 1 $，求 $ p(x) $ 除以 $ q(x) $ 的商和余数。

2. 计算多项式 $ r(x) = 2x^3 - 5x^2 + 7x - 3 $ 和 $ s(x) =x - 2 $ 的乘积。

3. 证明多项式 $ t(x) = x^4 - 5x^3 + 6x^2 + 8x - 9 $ 可以分解为两个二次多项式的乘积。

二、矩阵运算1. 给定矩阵 $ A = \begin{bmatrix} 1 & 2 \\ 3 & 4\end{bmatrix} $ 和 $ B = \begin{bmatrix} 5 & 6 \\ 7 & 8\end{bmatrix} $，求矩阵 $ A $ 与 $ B $ 的乘积。

2. 若矩阵 $ C = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} $，求 $ C $ 的逆矩阵。

3. 判断矩阵 $ D = \begin{bmatrix} 2 & 1 \\ 1 & 2\end{bmatrix} $ 是否可对角化，并给出相应的对角矩阵。

三、线性方程组1. 解线性方程组：\[\begin{align*}x + 2y - z &= 1 \\3x - y + 2z &= 0 \\2x + y + z &= -1\end{align*}\]2. 判断下列线性方程组是否有唯一解：\[\begin{align*}x + y &= 3 \\2x + 2y &= 6\end{align*}\]3. 用克拉默法则解线性方程组：\[\begin{align*}x - y + z &= 2 \\2x + y - z &= 1 \\-x + 2y + z &= 3\end{align*}\]四、特征值与特征向量1. 求矩阵 $ E = \begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix} $ 的特征值和对应的特征向量。

高等代数习题答案

高等代数(北大版第三版)习题答案I I(总95页)-本页仅作为预览文档封面，使用时请删除本页-高等代数（北大第三版）答案目录第一章多项式第二章行列式第三章线性方程组第四章矩阵第五章二次型第六章线性空间第七章线性变换第八章 —矩阵第九章欧氏空间第十章双线性函数与辛空间注：答案分三部分，该为第二部分，其他请搜索，谢谢！12．设A 为一个n 级实对称矩阵，且0<A ，证明：必存在实n 维向量0≠X ，使0<'A X X 。

证因为0<A ，于是0≠A ，所以()n A rank =，且A 不是正定矩阵。

故必存在非退化线性替换Y C X 1-=使()BY Y ACY C Y AX X '=''='-12222122221n p p p y y y y y y ----+++=++ ，且在规范形中必含带负号的平方项。

于是只要在Y C Z 1-=中，令p y y y === 21,1,021=====++n p p y y y 则可得一线性方程组 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++=+++=+++=++++++1102211,122,111,122111212111n nn n n n n p p p n pn p p n n x c x c x c x c x c x c x c x c x c x c x c x c ，由于0≠C ，故可得唯一组非零解()ns s s s x x x X ,,,21 =使()0111000<--=----+++='p n AX X s s，即证存在0≠X ，使0<'A X X 。

13．如果B A ,都是n 阶正定矩阵，证明：B A +也是正定矩阵。

证因为B A ,为正定矩阵，所以BX X AX X '',为正定二次型，且 0>'A X X ， 0>'B X X ，因此()0>'+'=+'BX X AX X X B A X ，于是()X B A X +'必为正定二次型，从而B A +为正定矩阵。

高等代数-第4章习题及解答

第四章多项式4.1习题,()(),..(-)-(-)()()-(-)()--(-)(-)Z a c ad bc q Z s t ad bc q a c a c b d ab cd ad bc a c b d ab cd a c q a c b d q ab cd ∈-+∴∃∈+==++=++=+1. 设a,b,c,d 已知(a-c)(ad+bc),求证(a-c)(ab+cd)证明：又由（）得（）（）即 ,,-()()b d q Zb d q Z ac ab cd ∈∴+∈-+即有 121212,65(-3)13,65(-2)5,65-,65(-3)13(-2)571865-(6528)65(-65)-2828m m m m r c c m c m c c c m m r ⨯⨯∃⨯+⨯==-+∴=2. 一个整数被5除余3，被13除余2，求它被65除的余数解：设所求数为由题知即有令，，则有故有 1723582957,581-143,-143202,0231414a b a b a b a b b a b a b a ==-=-==-=-=-=-=+=⋅+=⋅+3. 对于下列的整数，分别求出以除所得的商和余数：（1）, （2）, （3）, （4）解：）由带余除法，可表示为故商为，余数为；）同理得故商为，余数为；）由知商为，余数为； 49595b a =+ ）由知商为，余数为。

.()001a b a b b aq q Z b q b a q q a b≠≤=∈≠∴≠∴=≥∴≤4. 证明：若a b,b 0,则证明：由可得又又1,) 1.b ∈=1 1 1115. 设a,b 是不全为零的整数，且a=da ,b=db ,d,a ,b Z.证明d 是a 与b 的一个最大公因数的充分必要条件是(a1111111111[] 4.1.3,,..01(,)1[](,)1''1''1,''u v Z s t ua vb d uda vdb d d ua vb a b a b u a v b a bu v u a v b d d d⇒∃∈+=+=≠∴+=∴=⇐=+=+=+=证明：根据定理得即又故有即则有综上所述，结论得证6.(,)1,(,) 1.,(1),,..()()(1),,1,1a b a b ab a b ab d d Z d u v Z s t u a b vab d ua u va b d u v a Z u va Za b =+=+=∈≠∴∃∈++=∴++=∈∴+∈= 证明：若则证明：反证假设（）且故（）与（）矛盾 ,17.1..,()(),,.a b ab a b p ab p a p b p p mn a b k k Z p abp b b k p a p b p k m b m k m k n b n k n k p ∴+===+∈∴+ （）设是一个大于的整数且具有以下性质：对于任意整数，，若，则或证明是一个素数证明：令又当不整除，有，不整除又有，不整除或；不整除或若为合数，那,m k n k p p k p b p 么由可知必为素数，否则同理可证当不整除时，也必为素数4.2习题224324321.,,(21)(1)251\2(2)(21)()12521-2,1,31k h m x hx x kx x x mx x x k h x hk x h k x h k hk m k h m h k +--+=++--=--+--++--=⎧⎪--====⎨⎪+=-⎩求使解：对于左边即有解之得432322.()242,()25 4.()(),()(),()().f x x x x xg x x x x f x g x f x g x f x g x =+---=--++- 设计算432443270765432()()4292()()6()0254()()()23913131868kki k i k i f x g x x x x x f x g x x x g x x x x x f x g x a b x x x x x x x x -==+=+--+-=+-=⋅+--+∴==+--++--∑∑解：由题得令323122223.()59-73,()(53),()().-15-50[()()]3691()()04.()0().()0()()()f x x x xg x x x f x g x f x g x x f x g x s f x f x f x f x f x f x ︒=-++=++⨯=±∂===≠≠=⋅∴ 设求乘积的次数及其系数和解：根据得令则有的系数和证明：当时，是偶次多项式证明：又有根据定理2 4.2.12()()()()(),()()2f x f x f x f x f x n n N f x n ︒︒︒︒︒∂⋅=∂+∂∂=∈∴∂=的（）知（）（）（）再令（）结论得证2225.(),(),()..()()(),()()()0.(),(),()1221222132212f x g x h x f x xg x xh x f x g x h x g x g f x f h x hg h f g g h f h g h f g f ︒︒︒︒︒︒=+===∂=∂=∂=>=+<=+==+= 设是实数域上的多项式证明如下若是则证明：令（）（）（）当时，有当时，有当时，有或 2222214()(),(),()(),(),()()()()06.(),(),()()0(),()1()0(),()h f x f x g x h x f x g x h x f x g x h x f x g x h x f x g x i h x f x xg x x xh x x +========-= 又由题可知是偶次多项式，又由于是实数域上的多项式故的次数不存在即求一组满足上题结论的不全为零的复系数多项式解：令，即， 222()()0()()0(),()1xg x xh x f x f x g x i h x ∴+===== 满足条件即，4.3 习题3221.()321,()321,()()()().f x x x xg x x x g x f x q x r x =-+-=-+设求用除所得的商式和余数232322217393213212133751337147399299172(),()3999()()()()x x x x x x x x x x x x x x x q x x r x f x g x q x r x --+-+--+-+--+--=-=-=+解：故即[]2432322412*********.,,(1)()?012,1(1)()3.()(()()),()(()()),:()(()()()()),(),()m p q x mx x px q p m m m r q m p m m q m x mx x px q g x f x f x g x f x f x g x u x f x u x f x u x u x F x ++++⎧+=-=⎨=-⎩=-=-+++++-+在适合什么条件时，解：由题知当余式时有即当时有设证明其中为中任意两个12121212121211()(()()),()(()())()(()()()())()(()()()())()(),()()3()()(i g x f x f x g x f x f x g x f x f x f x f x g x f x f x f x f x g x f x g x f x u x F x i +-∴++-+-+∃∀∈=多项式证明：即根据多项式整除性质）可知 1122112221,2)..()()(),()()()2()()(1,2)..()(()()()())4.(1)(),(1)(),(1)().11(1)(),(1)(i o s t g x u x f x g x u x f x u x F x i s t g x u x f x u x f x x f x x f x x f x x x f x x f ∃∀∈=+-+-≠±-+ 再根据性质）得若则证明：1212)(),()[]()()(1)(1)()()(1)(2)x u x u x F x f x u x x f x u x x ∴∃∈=+⎧⎨=-⎩221()()(1)(-1)-(2)(1)()(-1)()2u x u x x x f x x -⨯⨯+= 得212()()()[]2(-1)()21-1()0o u x u x u x F x x f x x x f x -∃=∈=== 故即或时，可得出同样结论成立1212121221212125.(1)()(()()),()()()()(2)()()(),()()()()1(),()1,()1()(()())()()()g x f x f x g x f x g x f x g x f x f x g x f x g x f x g x x f x x f x x g x f x f x g x f x f x +==+=-+ 若则且对吗？若则或对吗？解：（）不对如：令可见而不整除和（21212122()-1,()1,()1()()()()()()g x x f x x f x x g x f x f x g x f x f x ==+=-）不对如：令可见而不整除和(1)(2)6.(1)(1),.,1()1(1)(1),(1)(1).(1)(1)(0),1(1)1,(1)(1)(1)(d n n d q d q d q d d n d n n qd r d q r r d n d x x d n d n d n n qd x x x x x x x x x n qd r r d x x x x x x x x --+--⇐=-=-=-+++--⇒--=+≤<-==-+---- 证明：的充分必要条件是（这里是正整数）证明设，即则即设，令则且212121)(1)(1)0,0.7.()110220()32.(),()[]..(1)()10()(1)(2)()2d q d r x x x r d r d n f x x x f x x x u x u x F x s t x u x f x x u x -∴--≤<=++++∃∈++=++ ,又故，即设被除的余式为，被除的余式为，求被除的余式解：设， 23120()(2)()[]..()32(3)(1)(2)-(2)(1)()32--10(1)434-10(1)f x u x F x s t f x x x u r x x f x x x u u x r x =∃∈=+++⨯+⨯+=+++=+ 又，（）有（）（）（）由（），（）可得习题4.4432424322432312(1)43243221(-1)1.1)()242,()322;2)()441,() 1.()24221)()()2222f x x x x x g x x x x x f x x x x x g x x x f x x x x x x x A x g x x x x x x x x x +-+=+---=+---=--++=--⎛⎫⎛⎫+----⎛⎫==−−−→ ⎪ ⎪ ⎪+---+---⎝⎭⎝⎭⎝⎭−计算以下各式多项式的最大公因式：解：由 11333221()1()21()42222222200x x xx x x x x x x x x x -++-⎛⎫⎛⎫⎛⎫⎛⎫----−−→−−−→−−−→−−−→ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭224324312(4)222212(-)2(1)12()221(1)()2()44132)()()112333212x x d x x f x x x x x x x A x g x x x x x x x x x x x x +++-++∴=-⎛⎫⎛⎫--++--⎛⎫==−−−→ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫--⎛⎫−−−−→−−−→−−−→ ⎪ ⎪ ⎪-+---+⎝⎭⎝⎭⎝⎭−−−→ 由 2311110()1x x x d x -⎛⎫⎛⎫⎛⎫→→ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭∴=2.(),()(),,0,(()(),()())((),()).((),())()()(),()()()()()),()()())(),()(f x g x F x a b c d F ad bc af x bg x cf x dg x f x g x f x g x d x d x f x d x g x d x af x bg x d x cf x dg x h x h x af ∈∈-≠++==∴++∃∀另而，，，并且证明证明：令即有（（又设（)()),()()())-0()()())-()())---()()())()())--()(),()(),()x bg x h x cf x dg x ad bc d bf x af x bg x cf x dg x ad bc ad bc c ag x af x bg x cf x dg x ad bc ad bch x f x h x g x h x d ++≠∴=++=+++∴ （有（（（（从而有 ()()()()())()(()(),()())((),())x af x bg x cf x dg x d x af x bg x cf x dg x f x g x ++=++= 即（，即 :3.()0,()((),())(()()(),()).()0(),..()()()()()()-()()1((),())(()())((),())(()()(g x h x f x g x f x h x g x g x g x h x s t f x g x h x r x r x f x g x h x f x g x g x r x f x g x f x h x g x ≠=-≠∃=+===-设为任意多项式，证明：证明：故即由引理可知，即 ),())g x1122121212124.1)(,)2)(,)(,)(,,,),,,().1(,),,,,(,),[],..f g hf gh f g f g f f f g g f g g f g h F x f g d d f d g dh fh dh gh dh hf hg f g d u v F x s t uf vg d ===∃∈+=∴证明：是与的最大公因式；此处都是的多项式证明：）设即从而有即是与的公因式又由得 112211211212211211221214.4.42)(,),(,),(,[]),;,,,,(,),(,),,,ufh vgh dhdh fh gh f g m f g n m n F x m f m g m f m g mn f f mn f g mn f g mn g g f g m f g n k k l +===∈==∃ 由定理知是与的最大公因式设即从而有又由知 211112222121211221221121212122112112212122112[],..,(,,,)(,)(,)(,,,)l F x s t k f l g m k f l g nk k f f k f l g l k f g l l g g mn mn f f f g f g g g f g f g f f f g f g g g ∈+=+=+++=== 即有由此可知从而有4323243232324323235.(),()()()()()((),()):1)()343,()310232)()421659,()25453431033113333102301310u x v x u x f x v x g x f x g x f x x x x x g x x x x f x x x x x g x x x x x x x x x x x x x x x x +==+---=++-=--++=--+⎛⎫+--------→ ⎪++-⎝⎭+2求使解：）（A(x),I ）=222322222232230159935993913310230156553296331393555591393132563555555x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ⎛⎫⎪⎪ ⎪+-⎝⎭⎛⎫----⎛⎫---- ⎪→→ ⎪- ⎪++---- ⎪⎝⎭⎝⎭⎛-+⎛⎫-+------ ⎪ ⎪→→--+ ⎪------+- ⎪⎝⎭⎝33-x -x 22243232323231550**321,()55122342165910332540125401x x x x x x x v x x x x x x x x x x x x x x ⎫ ⎪ ⎪ ⎪ ⎪⎭⎛⎫-+- ⎪→ ⎪ ⎪⎝⎭-∴-=⎛⎫⎛⎫--+---++ ⎪→ ⎪ ⎪--+ ⎪⎝⎭--+⎝⎭2 u(x)= 2)（A(x),I ）=22222222121223231333332222412(2)1333312231330**1223(),()33x xx x x x x x x x xx x x x x x x x x x x u x v x ⎛⎫-++⎛⎫--+--- ⎪⎪ ⎪⎪→→ ⎪ ⎪--++--+-+- ⎪ ⎪⎝⎭⎝⎭⎛⎫--+- ⎪→ ⎪ ⎪⎝⎭--+∴==4322432436.()1,()(1),,,()().(),()2,()()()()(,,)()(2)(2)(2)1of x Ax Bxg x x A B f x g x f x g x g x f x g x ax bx c a b c F f x ax b a x c b a x b c x c Ax Bx a A =++=-∂==++∈∴=+-+-++-+=++=设试决定使与的最大公因式为二次多项式解：由于（）即为最大公因式故不妨设即有 -23,2,13,-4202013,-4b a B a bc A B c b a b c c A B ⎧⎪=⎪⎪=====-+=⎨⎪-=⎪=⎪⎩∴== 解得即7.(),()((),())()()()(),((),())1((),())()()()()*()()()()()()()()()()*(),()[].f x g x f x g x u x f x v x g x u x v x f x g x u x f x v x g x u x f x v x g x f x u x f x v x g x g x m x n x F x s =+==+++∃∈设不全为零，且证明：证明：（）有，再由（） .()()[()()()()]()()[()()()()]1-()()()()()()11-()())()()()()221()t f x m x u x f x v x g x g x n x u x f x v x g x m x u x f x m x v x g x n x v x g x n x u x f x f x =+=+== 即（）（）（（）将（）代入（），消去得1-()()1-()()()()()()()()(),(),()01-()()()()()()()()()()()()1()()()()4.4.5((),())1m x u x n x v x g x m x v x g x n x u x f x g x g x n x v x m x u x m x n x u x v x m x n x u x v x m x n x u x v x u x v x =≠∴-+=∴==（）（）不全为零即令由定理得8.((),()) 1.((),()) 1.,,((),()) 1.1()()()[]()()()()()()((),())1n m n o n n n f x g x n f x g x m n f x g x g x g x k x F x g x k x g x g x g x k x f x g x ===∃∈=∴==设令是任意正整数，证明：由此进一步证明：对于任意正整数都有证明：易见 , 即 s.t. (1)又 ()()1()()1()((),())1()(),()[]()()()()()()nn m m m f x g x f x g x k x f x g x x f x l x F x f x l x f x f x f x l x ∴∃∈+=+==∃∈=∴=o u(x),v(x)F[x] s.t. u(x)v(x) (2)v(x) 将（1）代入（2）得 u(x) 由定理4.4.5 知 2易见 f 即 s.t. ((),())1'''()()'()()11'()()'()()1()((),())1n n mn m n f x g x u x f x v x g x u x f x v x g x l x f x g x =∴∃∈+=+== (3)又u (x),v (x)F[x] s.t. (4) 将（3）代入（4）得由定理4.4.5知 [][]1111119.((),()) 1.((),()())((),()())(()(),()()) 1.((),()())()()(),()()()()[()()]()()()]f x g x f x f x g x g x f x g x f x g x f x g x f x f x g x d x d x F x u x v x F x u x f x v x f x g x d x u x v x =+=+=+=+=∈∴∃∈++=+设证明：证明：令 ()s.t. 即 [1()()()()((),())1()1((),()())1((),()())1(()(),()())1f x v xg x d x f x g x d x f x f x g x g x f x g x f x g x f x g x +===+=+=+=故即同理可证得再根据互素性质可知10.()0,()0,:1(),()()()()(),((),())12(),()(),()()()()(),((),())11((),())()1,()()f x g x h x f x g x h x f x h x f x g x h x f x h x g x h x f x g x h x f x g x f x g x d x f x d x m ≠≠===≠=设证明）若对于任意多项式由可得到则必有）若对于任意多项式由可得到则必有证明：）假设则有(),()()()()()()()()()()()()()()x g x d x n x m x f x f x g x h x h x f x g x m x f x m x ︒︒=∂<∂∴ 其中（）（）又（为任意多项式）即有()()((),())12((),())()1()()()()()()()()(),()()()()()()()1((f x m x f x g x f x g x d x f x d x m x h x m x g x f x g x m x g x g x m x f x g x g x m x f x ==≠==∴ 但不整除，从而矛盾，故）假设，且令即有（）又),())()()()()()()()1((),())1g x d x f x m x f x g x g x m x f x g x ︒︒︒︒=∴∂>∂∂>∂∴= （）（）故（）（）与（）矛盾1212111212112211.(),(),,()().1)((),(),,())(((),,()),((),,())),112(),(),,()(),(),,()()()()()()()n n k k n n n n f x f x f x F x f x f x f x f x f x f x f x k n f x f x f x u x u x u x F x u x f x u x f x u x +∈=≤≤-∈+++设证明：）互素的充分且必要条件是存在多项式，使得1211121()11((),(),,())(),((),,()(),((),,()()()(),1,2,,()(),1,2,,;()(),1,2,,()(),n n k k n i s t f x f x f x f x d x f x f x d x f x f x d x d x f x i nd x f x s k d x f x t k k nd x d x +=====∴==++∴证明：）设21212()()()(),1,2()(),1,2,,;()(),1,2,,()(),1,2,,()(),2((),(),,())1i s t i n d x d x c x d x i d x f x s k d x f x t k k nc x f x i nc xd x f x f x f x ===++∴=∴= 设结论得证。

高等代数多项式习题解答(供参考)

第一章多项式习题解答1.用)(x g 除)(x f ，求商)(x q 与余式)(x r .1）123)(,13)(223+-=---=x x x g x x x x f92926)(,9731)(--=-=x x r x x q . 2）2)(,52)(24+-=+-=x x x g x x x f75)(,1)(2+-=-+=x x r x x x q .2.q p m ,,适合什么条件时，有1）q px x mx x ++-+32|1当且仅当m q p m ==++,012时q px x mx x ++-+32|1.本题也可用待定系数法求解.当q px x mx x ++-+32|1时，用12-+mx x 去除q px x ++3，余式为零，比较首项系数及常数项可得其商为q x -.于是有q x mq x q m x mx x q x q px x ++--+=-+-=++)1()()1)((2323.因此有m q p m ==++,012.2）q px x mx x ++++242|1由带余除法可得当且仅当0)1()2()(22=--++--=m p q x m p m x r 时q px x mx x ++++242|1.即⎩⎨⎧=--+=--010)2(22m p q m p m ，即⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 本题也可用待定系数法求解.当q px x mx x ++++242|1时，用12++mx x 去除q px x ++24，余式为零，比较首项系数及常数项可得其商可设为q ax x ++2.于是有比较系数可得.0,1,0=+=++=+mq a p q ma a m 消去a 可得⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p3.求)(x g 除)(x f 的商)(x q 与余式)(x r .1）;3)(,852)(35+=--=x x g x x x x f解：运用综合除法可得商为109391362)(234+-+-=x x x x x q ，余式为.327)(-=x r2）i x x g x x x x f 21)(,)(23+-=--=.解:运用综合除法得:商为)25(22i ix x +--,余式为i 89+-.4.把)(x f 表成0x x -的方幂和，即表示成 +-+-+202010)()(x x c x x c c 的形式.1）1,)(05==x x x f ；2）;2,32)(024-=+-=x x x x f3）.1,73)1(2)(0234-=++-+-+=x i x x i ix x x f分析：假设)(x f 为n 次多项式，令0c 即为0x x -除)(x f 所得的余式，商为10021)()()(--++-+=n n x x c x x c c x q .类似可得1c 为0x x -除商)(x q 所得的余式，依次继续即可求得展开式的各项系数.解：1）解法一：应用综合除法得.5)(x x f =1)1(5)1(10)1(10)1(5)1(2345+-+-+-+-+-=x x x x x .解法二：把x 表示成1)1(+-x ，然后用二项式展开2）仿上可得432)2()2(8)2(22)2(2411)(+++-+++-=x x x x x f .3）因为5.求)(x f 与)(x g 的最大公因式1）1)(,143)(23234--+=---+=x x x x g x x x x x f解法一：利用因式分解因此最大公因式为1+x .解法二：运用辗转相除法得因此最大公因式为1+x .2）13)(,14)(2334+-=+-=x x x g x x x f .解：运用辗转相除法得（注意缺项系数补零）3）.124624)(,110)(23424+++-=+-=x x x x x g x x x f)()()22(24)()(123x r x f x x x x f x g +=---=，因此.122))(),((2--=x x x g x f6.求)(),(x v x u 使:))(),(()()()()(x g x f x g x v x f x u =+1）;22)(,242)(234234---+=---+=x x x x x g x x x x x f解：运用辗转相除法得：因此2)())(),((22-==x x r x g x f .且有)()()()(11x r x q x g x f +=，),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=.2）;452)(,951624)(23234+--=++--=x x x x g x x x x x f解：运用辗转相除法得：因此1)())(),((2-=-=x x r x g x f .且有)()()()(11x r x q x g x f +=，),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=.3）.1)(,144)(2234--=++--=x x x g x x x x x f解：运用辗转相除法得：因此.1)())(),((2==x r x g x f 且有)()()()(11x r x q x g x f +=，),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=.7.设u tx x x g u x x t x x f ++=++++=323)(,22)1()(的最大公因式是一个二次多项式，求u t ,的值.解：运用带余除法有由题意可得，)(1x r 即为)(),(x g x f 的最大公因式.因此有01≠+t .进一步])1(21[)1()2()1()1()(22222t t u x t t t u t t x r +--++-++-+=. 要使)(1x r 为)(),(x g x f 的最大公因式的充要条件是.0)(2=x r 即解得8.证明：如果),(|)(),(|)(x g x d x f x d 且)(x d 为)(x f 与)(x g 的一个组合，那么)(x d 是)(x f 与)(x g 的一个最大公因式.证明：由)(|)(),(|)(x g x d x f x d 可知)(x d 是)(x f 与)(x g 的一个公因式.下证)(x f 与)(x g 的任意一个公因式是)(x d 的因式.由)(x d 为)(x f 与)(x g 的一个组合可知，存在多项式)(),(x v x u ，使得)()()()()(x g x v x f x u x d +=.设)(x ϕ是)(x f 与)(x g 的任意一个公因式，则)(|)(),(|)(x g x x f x ϕϕ.故即).(|)(x d x ϕ因此)(x d 是)(x f 与)(x g 的一个最大公因式.9.证明：)()(())(),(())()(),()((x h x h x g x f x h x g x h x f =的首项系数为1）.证明：存在多项式)(),(x v x u ，使得)()()()())(),((x g x v x f x u x g x f +=.所以有)()()()()()()())(),((x h x g x v x h x f x u x h x g x f +=.即)())(),((x h x g x f 是)()(x h x f 与)()(x h x g 的一个组合.显然有)(|))(),((),(|))(),((x g x g x f x f x g x f .从而)()(|)())(),((),()(|)())(),((x h x g x h x g x f x h x f x h x g x f .由第8题结果)())(),((x h x g x f 是)()(x h x f 与)()(x h x g 的一个最大公因式.又)(x h 是首项系数为1的，因此).())(),(())()(),()((x h x g x f x h x g x h x f =10.如果)(x f ，)(x g 不全为零，证明1))(),(()(,)(),(()((=x g x f x g x g x f x f . 证明：由)(x f ,)(x g 不全为零可得其最大公因式不为零多项式，即.0))(),((≠x g x f 又存在多项式)(),(x v x u ，使得)()()()())(),((x g x v x f x u x g x f +=.于是))(),(()()())(),(()()(1x g x f x g x v x g x f x f x u +=. 因此1))(),(()(,)(),(()((=x g x f x g x g x f x f . 11.如果)(x f ，)(x g 不全为零，且))(),(()()()()(x g x f x g x v x f x u =+，那么1))(),((=x v x u .证明：由)(x f ,)(x g 不全为零可得.0))(),((≠x g x f 由有于是1))(),((=x v x u .12.证明：如果,1))(),((,1))(),((==x h x f x g x f 那么.1))()(),((=x h x g x f证法一、由条件1))(),((,1))(),((==x h x f x g x f 可得存在多项式)(),(11x v x u ； )(),(22x v x u 使得1)()()()(11=+x g x v x f x u ，1)()()()(22=+x h x v x f x u .两式相乘得1)()()()()()]()()()()()()()()([21211221=+++x h x g x v x v x f x h x v x u x g x v x u x f x u x u . 因此有.1))()(),((=x h x g x f证法二、反证法证明.显然.0))()(),((≠x h x g x f 若,1))()(),((≠x h x g x f 则存在不可约多项式)(x p ，使得)(x p 为)(x f 与)()(x h x g 的公因式.因此有)(|)(x f x p 且)()(|)(x h x g x p .由)(x p 的不可约性有)(|)(x g x p 或)(|)(x h x p .若)(|)(x g x p ，则)(x p 为)(x f 与)(x g 的一个公因式，与1))(),((=x g x f 相矛盾.若)(|)(x h x p ，则)(x p 为)(x f 与)(x h 的一个公因式，与1))(),((=x h x f 相矛盾.因此1))()(),((≠x h x g x f 不成立，即有.1))()(),((=x h x g x f13.设)(),(),(),(,),(),(2121x g x g x g x f x f x f n m 都是多项式，而且求证：1))()()(),()()((2121=x g x g x g x f x f x f n m .证明：由),,2,1(1))(),((1n j x g x f j ==，反复利用第12题结果可得1))()()(),((211=x g x g x g x f n .类似可得再反复利用12题结果可得1))()()(),()()((2121=x g x g x g x f x f x f n m .14.证明：如果,1))(),((=x g x f 那么.1))()(),()((=+x g x f x g x f证明：方法一.由,1))(),((=x g x f 存在多项式)(),(x v x u 使得1)()()()(=+x g x v x f x u .从而有,1)())()(())()()((,1))()()(()())()((111111=+-++=++-x g x v x u x g x f x u x g x f x v x f x v x u 因此有.1))()(),((,1))()(),((=+=+x g x f x g x g x f x f 由12题结果结论成立.方法二：用反证法.若.1))()(),()((≠+x g x f x g x f 则存在不可约多项式)(x p ，使得)(x p 为)()(x g x f 与)()(x g x f +的公因式.即)()(|)(x g x f x p 且)()(|)(x g x f x p +.由)(x p 的不可约性及)()(|)(x g x f x p ，有)(|)(x f x p 或)(|)(x g x p .若)(|)(x f x p ，又)()(|)(x g x f x p +，因此有)]())()([(|)(x f x g x f x p -+，即)(|)(x g x p ，也即)(x p为)(x f 与)(x g 的一个公因式，与1))(),((=x g x f 相矛盾.类似可得当)(|)(x g x p 时也与已知1))(),((=x g x f 矛盾.所以.1))()(),()((=+x g x f x g x f15.求下列多项式的公共根：解法一：利用因式分解可得因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 解法二：运用辗转相除法求出)(x f 与)(x g 的最大公因式，最大公因式的根即为所求的公共根.因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 16.判别下列多项式有无重因式：1）;84275)(2345-+-+-=x x x x x x f解：,4421205)('234+-+-=x x x x x f运用辗转相除法可得.)2(44))('),((22-=+-=x x x x f x f 因此2-x 为)(x f 的三重因式.解法二：试根可得2为)(x f 的根)1()2()2()2()43)(2()(23232234++-=----=++--=x x x x x x x x x x x x f .因此2-x 为)(x f 的三重因式.2).344)(24--+=x x x x f解：).12(4484)('33-+=-+=x x x x x f 1))('),((=x f x f .故)(x f 无重因式.17.求t 值使13)(23-+-=tx x x x f 有重根.解法一：要使)(x f 有重根，则1))('),((≠x f x f ..63)('2t x x x f +-= 当,033=-t 即3=t 时 ),(|)(',)1(3363)('22x f x f x x x x f -=+-=2)1())('),((-=x x f x f ，因此1为)(x f 的三重根.当0415=+t ，即415-=t 时，21))('),((+=x x f x f ，21-为)(x f 的二重根. 解法二：设b a x ab a x b a x b x a x x f 22232)2()2()()()(-+++-=--=.因此有由第一个方程有a b 26-=，代人第三个方程有,0132,1)23(232=+-=-a a a a 即 0)12()1(2=+-a a .因此有⎪⎩⎪⎨⎧===,3,1,1t b a 或⎪⎪⎩⎪⎪⎨⎧-==-=.415,4,21t b a即当3=t 时1为)(x f 的三重根；当415-=t 时，21-为)(x f 的二重根. 18.求多项式q px x ++3有重根的条件.解：令q px x x f ++=3)(.显然当0==q p 时，0为)(x f 的三重根.当0≠p 时， p x x f +=23)('，q x p x xf q px x x f ++=++=32)('31)(3， )427()42729)(32()('222p q p p q x p q x p x f ++-+=. 要使)(x f 有重根，则1))('),((≠x f x f .即,042722=+pq p 即.027423=+q p 显然 0==q p 也满足.027423=+q p 因此)(x f 有重根的条件是.027423=+q p19.如果,1|)1(242++-Bx Ax x 求.,B A解法一：利用整除判定方法，1|)1(242++-Bx Ax x 的充要条件是用2)1(-x 除124++Bx Ax ，余式为零.)31()42()32()1(12224B A x A B A B Ax Ax x Bx Ax --++++++-=++.因此有0)31()42(=--++B A x A B ，即解法二：要使1|)1(242++-Bx Ax x 成立，则1至少是124++Bx Ax 的二重根.因此1既是124++Bx Ax 的根，也是其导数的根.而Bx Ax Bx Ax 24)'1(324+=++.故有解法三：利用待定系数法.令D x D C x D C A x A C Ax D Cx Ax x Bx Ax +-++-+-+=++-=++)2()2()2()()1(12342224因此有⎪⎪⎩⎪⎪⎨⎧==-=+-=-.1,02,2,02D D C B D C A A C 解得⎪⎪⎩⎪⎪⎨⎧==-==.1,2,2,1D C B A 20.证明：!!212n x x x n++++ 不能有重根. 证明：令,!!21)(2n x x x x f n++++= 则因此有,!)(')(n x x f x f n +=从而有)!),('())('),((n x x f x f x f n =.!n x n因式只有)0(≠c c 及)1,0(n k c cx k ≤≤≠.而)1,0(n k c cx k ≤≤≠显然不是)('x f 的因式.因此有1)!),('())('),((==n x x f x f x f n. 所以)(x f 没有重根.21.如果a 是)('''x f 的一个k 重根，证明a 是的一个3+k 重根.证明：显然有0)(")(')(===a g a g a g .由a 是)('''x f 的一个k 重根可得a 是)(''x g 的一个1+k 重根，设a 是)(x g 的s 重根，则3,12+=+=-k s k s .本题常见错误证法.错误证法一：由a 是)('''x f 的一个k 重根就得出a 是)(''x f 的一个1+k 重根，a 是)('x f 的一个2+k 重根，a 是)(x f 的一个3+k 重根，于是从而a 是)(x g 的3+k 重根.事实上，由a 是)('''x f 的一个k 重根推不出a 是)(''x f 的一个1+k 重根，a 是)('x f 的一个2+k 重根，a 是)(x f 的一个3+k 重根.如3)()()()(23+-+-+-=+a x a x a x x f k ，则1)(2))(3()('2+-+-+=+a x a x k x f k ， 2))(2)(3()(''1+-++=+k a x k k x f .a 既不是)(x f 的根，也不是)('x f 与)(''x f 的根.错误证法二：由得出a 是)(''x g 的1+k 重根，直接得出a 是)(x g 的3+k 重根，缺了a 是)(x g 与)('x g 的根验证.22.证明：0x 是)(x f 的k 重根的充分必要条件是,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k证明：必要性.设0x 是)(x f 的k 重根，从而0x x -是)(x f 的k 重因式，从而是)('x f 的1-k 重因式，是)(''x f 的2-k 重因式，...，是)()1(x f k -的单因式，而不是)()(x f k 的因式.因此0x 是)(x f ，)('x f ，)(''x f ，...，)()1(x f k -的根，而不是)()(x f k 的根.故有,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k充分性.由,0)()(')(0)1(00====-x f x f x f k 而0)(0)(≠x f k 可知0x 是)(x f ，)('x f ，)(''x f ，...，)()1(x f k -的根，而不是)()(x f k 的根.因此0x 是)()1(x f k -的单根，是)()2(x f k -二重根，依此类推，是)(x f 的k 重根.23.举例说明断语“如果α是)('x f 的m 重根，那么α是)(x f 的1+m 重根”是不对的.解：例如2)()(1+-=+m x x f α，m x m x f ))(1()('α-+=.α是)('x f 的m 重根，但α不是)(x f 的根.24.证明：如果),(|)1(n x f x -那么)(|)1(n n x f x -.证明：由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 因此有 ),()1()(x h x x f -=从而有).()1()(n n n x h x x f -=即)(|)1(n n x f x -.证法二：要证)(|)1(n n x f x -，只要证1-n x 在复数域上的各个根都是)(n x f 的根.1-n x 的根为.1,,2,1,0,2sin 2cos -=+=n k nk i n k x k ππ由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 从而0)1()(==f x f n k .即,2sin 2cos nk i n k x k ππ+= 1,,2,1,0-=n k 都是)(n x f 的根.因此有)(|)1(n n x f x -.25.证明：如果)()(|)1(32312x xf x f x x +++，那么证明：要证)(|)1(),(|)1(21x f x x f x --成立，只要证1是)(1x f 和)(2x f 的根. 12++x x 的两个根为231,23121i i --=+-=εε.由)()(|)1(32312x xf x f x x +++可得)()1()()(23231x g x x x xf x f ++=+.于是即0)1(231)1(,0)1(231)1(2121=+-=--f i f f i f .故有.0)1()1(21==f f 所以 )(|)1(),(|)1(21x f x x f x --.26.求多项式1-n x 在复数范围内和在实数范围内的因式分解.解：1-n x 的根为.1,,2,1,0,2sin 2cos-=+=n k nk i n k k ππε故在复数范围内的分解式为)())()(1(112-----=-n n x x x x x εεε . 在实数范围内，因k n k -=εε，)0(n k <<.当n 为奇数时，1-n x 的根中一个为实根，其余为虚根，其分解式为 ]1)([]1)(][1)()[1(12121222212++-++-++--=-+---x x x x x x x x n n n n n εεεεεε .当n 为偶数时，1-n x 的根中二个为实根，即,1±其余为虚根，其分解式为27.求下列多项式的有理根.1);1415623-+-x x x解：多项式可能的有理根为.14,7,2,1±±±±由系数取值可知，x 取负数时，多项式的值均为负的，故该多项式没有负根.检验得2为其根，进一步运用综合除法可得即)74)(2(14156223+--=-+-x x x x x x ，显然742+-x x 没有有理根.因此1415623-+-x x x 仅有一个有理根2，且为单根.2);157424---x x x解：多项式可能的有理根为.41,21,1±±± 因此有)1()12()444()21(1574222224--+=--+=---x x x x x x x x x ，显然12--x x 没有有理根.因此21-为157424---x x x 的二重根. 3).3111462345----+x x x x x解：多项式可能的有理根为.3,1±±检验得1-为其根，进一步运用综合除法可得故)3()1()12)(3()1(3111464222345-+=++-+=----+x x x x x x x x x x x .即1-为其四重跟，3为单根.28.下列多项式在有理数域上是否可约？1);12+x解：显然12+x 无有理根，又为二次的，故在有理数域上不可约. 2);2128234++-x x x解：取素数2=p ，满足艾森斯坦判别法的条件，因此在有理数域上不可约.3）;136++x x解：令,1+=y x).(3918211561)1()1(1)(234563636y g y y y y y y y y x x x f =++++++=++++=++=取素数,3=p )(y g 满足艾森斯坦判别法条件，因此在有理数域上不可约，从而)(x f 在有理数域上不可约.4）p px x p ,1++为奇素数；解：令1-=y x ，由p 为奇数可得由组合数定义)11(-≤≤p k C k p 均为整数，且12)1()1()1(⋅-+--= k k k p p p C k p ，分子中有因子p ，分母个各数均小于p ，又p 为素数，因此约分时p 不会被约去，因此有k pC p |，取素数为p ，)(y g 满足艾森斯坦判别式条件，因此)(y g 在有理数域上不可约，从而)(x f 在有理数域上不可约.5）k kx x ,144++为整数.解：令,1+=y x 则有取素数,2=p )(y g 满足艾森斯坦判别法条件，因此在有理数域上不可约，从而)(x f 在有理数域上不可约.。

【最新试题库含答案】高等代数习题及答案(1)

高等代数习题及答案(1)篇一：高等代数习题解答(第一章)高等代数习题解答第一章多项式补充题1．当a,b,c取何值时，多项式f(x)?x?5与g(x)?a(x?2)2?b(x?1) ?c(x2?x?2)相等？6136提示：比较系数得a??,b??,c?. 555补充题2．设f(x),g(x),h(x)??[x]，f2(x)?xg2(x)?x3h2(x)，证明：f(x)?g(x)?h(x)?0．证明假设f(x)?g(x)?h(x)?0不成立．若f(x)?0，则?(f2(x))为偶数，又g2(x),h2(x)等于0或次数为偶数，由于g2(x),h2(x)??[x]，首项系数（如果有的话）为正数，从而xg2(x)?x3h2(x)等于0或次数为奇数，矛盾．若g(x)?0或h(x)?0则?(xg2(x)?x3h2(x))为奇数，而f2(x)?0或?(f2(x))为偶数，矛盾．综上所证，f(x)?g(x)?h(x)?0．1．用g (x) 除 f (x)，求商q (x)与余式r (x)：1）f (x) = x3- 3x2 -x-1，g (x) =3x2 -2x+1；2）f (x) = x4 -2x+5，g (x) = x2 -x+2．1）解法一待定系数法．由于f (x)是首项系数为1的3次多项式，而g (x)是首项系数为3的2次多项式，1所以商q(x)必是首项系数为的1次多项式，而余式的次数小于 2．于是可设 31 q(x) =x+a , r(x) =bx+c 3根据 f (x) = q(x) g(x) + r(x)，即1 x3-3x2 -x-1 = (x+a)( 3x2 -2x+1)+bx+c 3右边展开，合并同类项，再比较两边同次幂的系数，得21 ?3?3a?, ?1??2a??b, ?1?a?c 337262解得 a?? , b?? , c?? ，故得 99917262q(x)?x?, r(x)??x?.3999解法二带余除法．3-21 1 -3-1 -11 ???21 3374 ?-1 337147 ? 399262 ? 9917 ? 39?得17262q(x)?x?, r(x)??x?. 39992） q(x)?x2?x?1,r(x)??5x?7. r(x)??2．m,p,q适合什么条件时，有1）x2?mx?1x3?px?q;2）x2?mx?1x4?px2?q.?1除x3?px1）解 x2?mx得余式为： ?q262x?. 99 r(x)?(p?m2?1)x?(q?m)，?p?m2?1?0;令r(x)?0，即 ? ?q?m?0.故x2?mx?1x3?px?q的充要条件是?m?q; ? 2p?m?1?0.??1除x4?px2?q得余式为： 2）解 x2?mxr(x)??m(p?m2?2)x?(q?p?m2?1)，2???m(p?m?2)?0;令r(x)?0，即 ? 2??q?p?m?1?0. 解得x2?mx?1x4?px2?q的充要条件是?m?0; ? 或 p?q?1??q?1; ?2p?2?m.?3．求g(x)除f(x)的商q(x)与余式r(x)：。

高等代数习题北大第四版答案一到四章

上式说明 ( f ( x), g( x)) h( x) 是 f (x)h(x) 与 g( x)h( x) 的一个组合。
另一方面，由 ( f (x), g( x)) | f ( x) 知 ( f (x), g(x))h(x) | f ( x)h( x) ，
同理可得 ( f ( x), g( x)) h( x) | g( x) h( x) ，
于是 u(x) = −q2 (x) = −x −1
。
v(x) = 1+ q1 (x )q2 (x ) = 1+1i(x + 1) = x + 2
2）仿上面方法，可得 ( f (x), g( x)) = x−1，且 u(x) = − 1 x + 1 ,v(x) = 2 x 2 − 2 x −1。
33
33
１０．如果 f (x), g( x) 不全为零，证明：
⎛ ⎜ ⎝
(
f
f ( x) ( x), g( x))
, (
f(
g( x) x), g(
x))
⎞ ⎟ ⎠
=1。
证存在 u(x), v( x) 使 ( f ( x), g( x)) = u( x) f ( x) + v( x) g( x) ，
又因为 f (x), g(x) 不全为０，所以 ( f (x), g(x)) ≠ 0 ，
39
99
2）同理可得 q(x) = x 2 + x −1, r( x) = −5x + 7 。
2． m, p, q 适合什么条件时，有
1） x 2 + mx −1 | x3 + px + q ，
2） x 2 + mx + 1| x4 + px2 + q 。

(完整版)高等代数多项式习题解答

第一章多项式习题解答1.用)(x g 除)(x f ，求商)(x q 与余式)(x r .1）123)(,13)(223+-=---=x x x g x x x x f9731929269791437134373132131232223232----+----+----+-x x x x x x x x x x x x x x 92926)(,9731)(--=-=x x r x x q . 2）2)(,52)(24+-=+-=x x x g x x x f17525422225200222223232342342-++--+-+--+---+-+-+++-x x x x x x x xx x x x x x x x x x x x x x75)(,1)(2+-=-+=x x r x x x q .2.q p m ,,适合什么条件时，有1）q px x mx x ++-+32|1m x m q x p m mx m x m qx p mx x mx x q px x x mx x --++++--+++--++++-+)()1()1(01222223232 当且仅当m q p m ==++,012时q px x mx x ++-+32|1.本题也可用待定系数法求解.当q px x mx x ++-+32|1时，用12-+mx x 去除q px x ++3，余式为零，比较首项系数及常数项可得其商为q x -.于是有q x mq x q m x mx x q x q px x ++--+=-+-=++)1()()1)((2323.因此有m q p m ==++,012.2）q px x mx x ++++242|1由带余除法可得)1()2()1)(1(2222224m p q x m p m m p mx x mx x q px x --++--++-+-++=++ 当且仅当0)1()2()(22=--++--=m p q x m p m x r 时q px x mx x ++++242|1.即⎩⎨⎧=--+=--010)2(22m p q m p m ，即⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 本题也可用待定系数法求解.当q px x mx x ++++242|1时，用12++mx x 去除q px x ++24，余式为零，比较首项系数及常数项可得其商可设为q ax x ++2.于是有)1)((2224++++=++mx x q ax x q px x.)()1()(234q x mq a x q ma x a m x ++++++++=比较系数可得.0,1,0=+=++=+mq a p q ma a m 消去a 可得⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 3.求)(x g 除)(x f 的商)(x q 与余式)(x r .1）;3)(,852)(35+=--=x x g x x x x f解：运用综合除法可得327109391362327117083918605023---------商为109391362)(234+-+-=x x x x x q ，余式为.327)(-=x r2）i x x g x x x x f 21)(,)(23+-=--=.解:运用综合除法得:ii ii i i i 892521892421011121+----+-------商为)25(22i ix x +--,余式为i 89+-. 4.把)(x f 表成0x x -的方幂和，即表示成 +-+-+202010)()(x x c x x c c 的形式.1）1,)(05==x x x f ；2）;2,32)(024-=+-=x x x x f3）.1,73)1(2)(0234-=++-+-+=x i x x i ix x x f分析：假设)(x f 为n 次多项式，令])()()[()()()()(10021000202010--++-+-+=-++-+-+=n n nn x x c x x c c x x c x x c x x c x x c c x f0c 即为0x x -除)(x f 所得的余式，商为10021)()()(--++-+=n n x x c x x c c x q .类似可得1c 为0x x -除商)(x q 所得的余式，依次继续即可求得展开式的各项系数.解：1）解法一：应用综合除法得.5110141110416311563143211143211111111111100000115)(x x f =1)1(5)1(10)1(10)1(5)1(2345+-+-+-+-+-=x x x x x .解法二：把x 表示成1)1(+-x ，然后用二项式展开1)1(5)1(10)1(10)1(5)1(]1)1[(234555+-+-+-+-+-=+-=x x x x x x x2）仿上可得812226122412210412112082422128442302012-----------------432)2()2(8)2(22)2(2411)(+++-+++-=x x x x x f . 3）因为i iii i i i i i i i i i ii ii i i 2111510157104141173121-----------+-------+---- .)()(2))(1()(5)57(73)1(2)(432234i x i x i i x i i x i ix x i ix x x f +++-++-+-+=++-+-+=5.求)(x f 与)(x g 的最大公因式1）1)(,143)(23234--+=---+=x x x x g x x x x x f解法一：利用因式分解),13)(1(143)(3234--+=---+=x x x x x x x x f).1()1(1)(223-+=--+=x x x x x x g因此最大公因式为1+x .解法二：运用辗转相除法得)(3438)(01122132)(1434343)(41432112321212314121)(3122123423422223232x q x x q x x x x x x x x r x x x x x x x x x x r x x x x x x x x x x x x q =+=---------=--+---+--=------++--++-= 因此最大公因式为1+x .2）13)(,14)(2334+-=+-=x x x g x x x f .解：运用辗转相除法得（注意缺项系数补零）2564411627)(125627)(2565391649216491633323)(10310031004911916)(920910310132310323110391031)(13221232323423422223232--=--=+-+-+-+--=-++-+-+-++-+++--=+--++--+++-+-=x x q x x r x x x x x x x r x x x x x x x x x x x x x x x x r x x x x x x x x x x x x q .1))(),((=x g x f3）.124624)(,110)(23424+++-=+-=x x x x x g x x x f)()()22(24)()(123x r x f x x x x f x g +=---=，),()22)((241)122()22)(22()(21223x r x x r x x x x x x x f ++-=---+--= ,)()122(22)(24122231x x r x x x x x x x r -=--=--=- 因此.122))(),((2--=x x x g x f6.求)(),(x v x u 使:))(),(()()()()(x g x f x g x v x f x u =+1）;22)(,242)(234234---+=---+=x x x x x g x x x x x f解：运用辗转相除法得：)()(1022)(222422)(222221)(3133123423422323242342x q x x q x x xx x r x x x x x x x x x x r xx x x x x x x x x x x x q ==--=---+---+-=--+----++= 因此2)())(),((22-==x x r x g x f .且有 )()()()(11x r x q x g x f +=，),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..2)()(1)(,1)()(212+=+=--=-=x x q x q x v x x q x u2）;452)(,951624)(23234+--=++--=x x x x g x x x x x f解：运用辗转相除法得：)(96)(20999966936)(810249516241)(32422324523131)(3122123423422223232x q x x q x x x xx x x x r xx x x x x x x x x r x x x x x x x x x x x x q =+=+-+-+-+--=+--++--+-=+--+---++--+-= 因此1)())(),((2-=-=x x r x g x f .且有)()()()(11x r x q x g x f +=，),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..13232)3131(21)()(1)(,3131)()(2212--=+---=--=+-==x x x x x q x q x v x x q x u 3）.1)(,144)(2234--=++--=x x x g x x x x x f解：运用辗转相除法得：)(32)(3331431441)(21211)(121222342342222x q x x x r x x x x x x x x x x x x r x x xx x x x x q =--=++-++---++--=-----+= 因此.1)())(),((2==x r x g x f 且有)()()()(11x r x q x g x f +=，),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..23)1)(3(1)()(1)(,1)()(232212--+=+-+=+=--=-=x x x x x x q x q x v x x q x u7.设u tx x x g u x x t x x f ++=++++=323)(,22)1()(的最大公因式是一个二次多项式，求u t ,的值.解：运用带余除法有),()()2()1(1)(22)1()(12323x r x g u x t x t u tx x u x x t x x f +=+--++⋅++=++++= 由题意可得，)(1x r 即为)(),(x g x f 的最大公因式.因此有01≠+t .进一步),(])1(211)[()(221x r t t x t x r x g ++-++= ])1(21[)1()2()1()1()(22222t t u x t t t u t t x r +--++-++-+=. 要使)(1x r 为)(),(x g x f 的最大公因式的充要条件是.0)(2=x r 即⎩⎨⎧=--+=-++-+,0)]2()1[(,0)2()1()1(222t t u t t u t t 解得⎪⎩⎪⎨⎧--=+-=⎪⎩⎪⎨⎧+-=--=⎪⎩⎪⎨⎧±==⎩⎨⎧-==.2111,117;2111,117;231,0;4,0i t i u i t i u i t u t u 8.证明：如果),(|)(),(|)(x g x d x f x d 且)(x d 为)(x f 与)(x g 的一个组合，那么)(x d 是)(x f 与)(x g 的一个最大公因式.证明：由)(|)(),(|)(x g x d x f x d 可知)(x d 是)(x f 与)(x g 的一个公因式.下证)(x f 与)(x g 的任意一个公因式是)(x d 的因式.由)(x d 为)(x f 与)(x g 的一个组合可知，存在多项式)(),(x v x u ，使得)()()()()(x g x v x f x u x d +=.设)(x ϕ是)(x f 与)(x g 的任意一个公因式，则)(|)(),(|)(x g x x f x ϕϕ.故)()()()(|)(x g x v x f x u x +ϕ即).(|)(x d x ϕ因此)(x d 是)(x f 与)(x g 的一个最大公因式.9.证明：)()(())(),(())()(),()((x h x h x g x f x h x g x h x f =的首项系数为1）. 证明：存在多项式)(),(x v x u ，使得)()()()())(),((x g x v x f x u x g x f +=.所以有)()()()()()()())(),((x h x g x v x h x f x u x h x g x f +=.即)())(),((x h x g x f 是 )()(x h x f 与)()(x h x g 的一个组合.显然有)(|))(),((),(|))(),((x g x g x f x f x g x f .从而)()(|)())(),((),()(|)())(),((x h x g x h x g x f x h x f x h x g x f .由第8题结果)())(),((x h x g x f 是)()(x h x f 与)()(x h x g 的一个最大公因式.又)(x h 是首项系数为1的，因此).())(),(())()(),()((x h x g x f x h x g x h x f =10.如果)(x f ，)(x g 不全为零，证明1))(),(()(,)(),(()((=x g x f x g x g x f x f . 证明：由)(x f ,)(x g 不全为零可得其最大公因式不为零多项式，即.0))(),((≠x g x f 又存在多项式)(),(x v x u ，使得)()()()())(),((x g x v x f x u x g x f +=.于是))(),(()()())(),(()()(1x g x f x g x v x g x f x f x u +=. 因此1))(),(()(,)(),(()((=x g x f x g x g x f x f . 11.如果)(x f ，)(x g 不全为零，且))(),(()()()()(x g x f x g x v x f x u =+，那么1))(),((=x v x u .证明：由)(x f ,)(x g 不全为零可得.0))(),((≠x g x f 由))(),(()()()()(x g x f x g x v x f x u =+有.1))(),(()()())(),(()()(=+x g x f x g x v x g x f x f x u 于是1))(),((=x v x u .12.证明：如果,1))(),((,1))(),((==x h x f x g x f 那么.1))()(),((=x h x g x f 证法一、由条件1))(),((,1))(),((==x h x f x g x f 可得存在多项式)(),(11x v x u ； )(),(22x v x u 使得1)()()()(11=+x g x v x f x u ，1)()()()(22=+x h x v x f x u .两式相乘得1)()()()()()]()()()()()()()()([21211221=+++x h x g x v x v x f x h x v x u x g x v x u x f x u x u . 因此有.1))()(),((=x h x g x f证法二、反证法证明.显然.0))()(),((≠x h x g x f 若,1))()(),((≠x h x g x f 则存在不可约多项式)(x p ，使得)(x p 为)(x f 与)()(x h x g 的公因式.因此有)(|)(x f x p 且)()(|)(x h x g x p .由)(x p 的不可约性有)(|)(x g x p 或)(|)(x h x p .若)(|)(x g x p ，则)(x p 为)(x f 与)(x g 的一个公因式，与1))(),((=x g x f 相矛盾.若)(|)(x h x p ，则)(x p 为)(x f 与)(x h 的一个公因式，与1))(),((=x h x f 相矛盾.因此1))()(),((≠x h x g x f 不成立，即有.1))()(),((=x h x g x f13.设)(),(),(),(,),(),(2121x g x g x g x f x f x f n m 都是多项式，而且).,,2,1;,,2,1(,1))(),((n j m i x g x f j i ===求证：1))()()(),()()((2121=x g x g x g x f x f x f n m .证明：由),,2,1(1))(),((1n j x g x f j ==，反复利用第12题结果可得1))()()(),((211=x g x g x g x f n .类似可得.,,2,1))()()(),((21m i x g x g x g x f n i ==再反复利用12题结果可得1))()()(),()()((2121=x g x g x g x f x f x f n m .14.证明：如果,1))(),((=x g x f 那么.1))()(),()((=+x g x f x g x f 证明：方法一.由,1))(),((=x g x f 存在多项式)(),(x v x u 使得1)()()()(=+x g x v x f x u .从而有,1)())()(())()()((,1))()()(()())()((111111=+-++=++-x g x v x u x g x f x u x g x f x v x f x v x u 因此有.1))()(),((,1))()(),((=+=+x g x f x g x g x f x f 由12题结果结论成立.方法二：用反证法.若.1))()(),()((≠+x g x f x g x f 则存在不可约多项式)(x p ，使得)(x p 为)()(x g x f 与)()(x g x f +的公因式.即)()(|)(x g x f x p 且)()(|)(x g x f x p +.由)(x p 的不可约性及)()(|)(x g x f x p ，有)(|)(x f x p 或)(|)(x g x p .若)(|)(x f x p ，又)()(|)(x g x f x p +，因此有)]())()([(|)(x f x g x f x p -+，即)(|)(x g x p ，也即)(x p 为)(x f 与)(x g 的一个公因式，与1))(),((=x g x f 相矛盾.类似可得当)(|)(x g x p 时也与已知1))(),((=x g x f 矛盾.所以.1))()(),()((=+x g x f x g x f15.求下列多项式的公共根：.12)(;122)(23423++++=+++=x x x x x g x x x x f解法一：利用因式分解可得);1)(1(122)(223+++=+++=x x x x x x x f ).1)(1(12)(22234+++=++++=x x x x x x x x g因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 解法二：运用辗转相除法求出)(x f 与)(x g 的最大公因式，最大公因式的根即为所求的公共根.),1(2)1)(()(2++--=x x x x f x g ).1)(1()(2+++=x x x x f因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 16.判别下列多项式有无重因式： 1）;84275)(2345-+-+-=x x x x x x f 解：,4421205)('234+-+-=x x x x x f运用辗转相除法可得.)2(44))('),((22-=+-=x x x x f x f 因此2-x 为)(x f 的三重因式.解法二：试根可得2为)(x f 的根)1()2()2()2()43)(2()(23232234++-=----=++--=x x x x x x x x x x x x f .因此2-x 为)(x f 的三重因式. 2).344)(24--+=x x x x f解：).12(4484)('33-+=-+=x x x x x f 1))('),((=x f x f .故)(x f 无重因式. 17.求t 值使13)(23-+-=tx x x x f 有重根.解法一：要使)(x f 有重根，则1))('),((≠x f x f ..63)('2t x x x f +-=),12(33)(')3131(13)(23+-+-=-+-=x t x f x tx x x x f .415)41523)(12(63)('2++-+=+-=t x x t x x x f当,033=-t 即3=t 时),(|)(',)1(3363)('22x f x f x x x x f -=+-=2)1())('),((-=x x f x f ，因此1为)(x f 的三重根. 当0415=+t ，即415-=t 时，21))('),((+=x x f x f ，21-为)(x f 的二重根.解法二：设b a x ab a x b a x b x a x x f 22232)2()2()()()(-+++-=--=. 因此有⎪⎩⎪⎨⎧==+=+.1,2,3222b a t ab a b a 由第一个方程有a b 26-=，代人第三个方程有,0132,1)23(232=+-=-a a a a 即0)12()1(2=+-a a .因此有⎪⎩⎪⎨⎧===,3,1,1t b a 或⎪⎪⎩⎪⎪⎨⎧-==-=.415,4,21t b a即当3=t 时1为)(x f 的三重根；当415-=t 时，21-为)(x f 的二重根.18.求多项式q px x ++3有重根的条件.解：令q px x x f ++=3)(.显然当0==q p 时，0为)(x f 的三重根.当0≠p 时， p x x f +=23)('，q x px xf q px x x f ++=++=32)('31)(3，)427()42729)(32()('222p q p p q x p q x p x f ++-+=. 要使)(x f 有重根，则1))('),((≠x f x f .即,042722=+pq p 即.027423=+q p 显然 0==q p 也满足.027423=+q p 因此)(x f 有重根的条件是.027423=+q p19.如果,1|)1(242++-Bx Ax x 求.,B A解法一：利用整除判定方法，1|)1(242++-Bx Ax x 的充要条件是用2)1(-x 除124++Bx Ax ，余式为零.)31()42()32()1(12224B A x A B A B Ax Ax x Bx Ax --++++++-=++.因此有0)31()42(=--++B A x A B ，即⎩⎨⎧-==⎩⎨⎧=--=+.2,1.031,042B A B A A B 解法二：要使1|)1(242++-Bx Ax x 成立，则1至少是124++Bx Ax 的二重根.因此1既是124++Bx Ax 的根，也是其导数的根.而Bx Ax Bx Ax 24)'1(324+=++.故有⎩⎨⎧-==⎩⎨⎧=+=++.2,1.024,01B A B A B A 解法三：利用待定系数法.令Dx D C x D C A x A C Ax D Cx Ax x Bx Ax +-++-+-+=++-=++)2()2()2()()1(12342224因此有⎪⎪⎩⎪⎪⎨⎧==-=+-=-.1,02,2,02D D C B D C A A C 解得⎪⎪⎩⎪⎪⎨⎧==-==.1,2,2,1D C B A 20.证明：!!212n x x x n++++ 不能有重根.证明：令,!!21)(2n x x x x f n++++= 则,)!1(!21)('12-++++=-n x x x x f n因此有,!)(')(n x x f x f n +=从而有)!),('())('),((n x x f x f x f n =.!n x n因式只有)0(≠c c 及)1,0(n k c cx k ≤≤≠.而)1,0(n k c cx k ≤≤≠显然不是)('x f 的因式.因此有1)!),('())('),((==n x x f x f x f n.所以)(x f 没有重根.21.如果a 是)('''x f 的一个k 重根，证明a 是)()()](')('[2)(a f x f a f x f ax x g +-+-=的一个3+k 重根. 证明：)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=).('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=显然有0)(")(')(===a g a g a g .由a 是)('''x f 的一个k 重根可得a 是)(''x g 的一个1+k 重根，设a 是)(x g 的s 重根，则3,12+=+=-k s k s .本题常见错误证法.错误证法一：由a 是)('''x f 的一个k 重根就得出a 是)(''x f 的一个1+k 重根，a 是)('x f 的一个2+k 重根，a 是)(x f 的一个3+k 重根，于是)(2)()()()](')('[2)(3x h a x a f x f a f x f a x x g k +-=+-+-=从而a 是)(x g 的3+k 重根.事实上，由a 是)('''x f 的一个k 重根推不出a 是)(''x f 的一个1+k 重根，a 是)('x f 的一个2+k 重根，a 是)(x f 的一个3+k 重根. 如3)()()()(23+-+-+-=+a x a x a x x f k ，则1)(2))(3()('2+-+-+=+a x a x k x f k ，2))(2)(3()(''1+-++=+k a x k k x f .a 既不是)(x f 的根，也不是)('x f 与)(''x f 的根.错误证法二：由)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=)('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=得出a 是)(''x g 的1+k 重根，直接得出a 是)(x g 的3+k 重根，缺了a 是)(x g 与)('x g 的根验证.22.证明：0x 是)(x f 的k 重根的充分必要条件是,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k证明：必要性.设0x 是)(x f 的k 重根，从而0x x -是)(x f 的k 重因式，从而是)('x f 的1-k 重因式，是)(''x f 的2-k 重因式，...，是)()1(x f k -的单因式，而不是)()(x f k 的因式.因此0x 是)(x f ，)('x f ，)(''x f ，...，)()1(x f k -的根，而不是)()(x f k 的根.故有,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k充分性.由,0)()(')(0)1(00====-x f x f x f k 而0)(0)(≠x f k 可知0x 是)(x f ，)('x f ，)(''x f ，...，)()1(x f k -的根，而不是)()(x f k 的根.因此0x 是)()1(x f k -的单根，是)()2(x f k -二重根，依此类推，是)(x f 的k 重根.23.举例说明断语“如果α是)('x f 的m 重根，那么α是)(x f 的1+m 重根”是不对的.解：例如2)()(1+-=+m x x f α，m x m x f ))(1()('α-+=.α是)('x f 的m 重根，但α不是)(x f 的根.24.证明：如果),(|)1(n x f x -那么)(|)1(n n x f x -.证明：由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 因此有),()1()(x h x x f -=从而有).()1()(n n n x h x x f -=即)(|)1(n n x f x -.证法二：要证)(|)1(n n x f x -，只要证1-n x 在复数域上的各个根都是)(n x f 的根.1-n x 的根为.1,,2,1,0,2sin 2cos-=+=n k nk i n k x k ππ由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 从而0)1()(==f x f nk .即,2sin 2cos nk i n k x k ππ+=1,,2,1,0-=n k 都是)(n x f 的根.因此有)(|)1(n n x f x -.25.证明：如果)()(|)1(32312x xf x f x x +++，那么).(|)1(),(|)1(21x f x x f x --证明：要证)(|)1(),(|)1(21x f x x f x --成立，只要证1是)(1x f 和)(2x f 的根.12++x x 的两个根为231,23121ii --=+-=εε.由)()(|)1(32312x xf x f x x +++可得)()1()()(23231x g x x x xf x f ++=+.于是,0)()1()()(,0)()1()()(2223222321112312131121=++=+=++=+εεεεεεεεεεεεg f f g f f即0)1(231)1(,0)1(231)1(2121=+-=--f if f i f .故有.0)1()1(21==f f 所以 )(|)1(),(|)1(21x f x x f x --.26.求多项式1-n x 在复数范围内和在实数范围内的因式分解. 解：1-n x 的根为.1,,2,1,0,2sin 2cos -=+=n k nk i n k k ππε故在复数范围内的分解式为)())()(1(112-----=-n n x x x x x εεε .在实数范围内，因k n k -=εε，)0(n k <<.当n 为奇数时，1-n x 的根中一个为实根，其余为虚根，其分解式为]1)([]1)(][1)()[1(12121222212++-++-++--=-+---x x x x x x x x n n n n nεεεεεε .当n 为偶数时，1-n x 的根中二个为实根，即,1±其余为虚根，其分解式为].1)([]1)(][1)()[1)(1(11212222212++-++-++-+-=-+---x x x x x x x x x n n n n nεεεεεε27.求下列多项式的有理根. 1);1415623-+-x x x解：多项式可能的有理根为.14,7,2,1±±±±由系数取值可知，x 取负数时，多项式的值均为负的，故该多项式没有负根.检验得2为其根，进一步运用综合除法可得074114821415612-----即)74)(2(14156223+--=-+-x x x x x x ，显然742+-x x 没有有理根.因此1415623-+-x x x 仅有一个有理根2，且为单根.2);157424---x x x解：多项式可能的有理根为.41,21,1±±±444222026242113121570421------------因此有)1()12()444()21(1574222224--+=--+=---x x x x x x x x x ，显然12--x x 没有有理根.因此21-为157424---x x x 的二重根.3).3111462345----+x x x x x解：多项式可能的有理根为.3,1±±检验得1-为其根，进一步运用综合除法可得1213630351133511038601138601311146111--------------故)3()1()12)(3()1(3111464222345-+=++-+=----+x x x x x x x x x x x .即1-为其四重跟，3为单根.28.下列多项式在有理数域上是否可约？ 1);12+x解：显然12+x 无有理根，又为二次的，故在有理数域上不可约. 2);2128234++-x x x解：取素数2=p ，满足艾森斯坦判别法的条件，因此在有理数域上不可约. 3）;136++x x 解：令,1+=y x).(3918211561)1()1(1)(234563636y g y y y y y y y y x x x f =++++++=++++=++=取素数,3=p )(y g 满足艾森斯坦判别法条件，因此在有理数域上不可约，从而)(x f 在有理数域上不可约.4）p px x p ,1++为奇素数；解：令1-=y x ，由p 为奇数可得1)1()1(1)(+-+-=++=y p y px x x f p p).()(1222211y g p y p C y C y C yC y p p p p p p p p p =-++--+-=---- 由组合数定义)11(-≤≤p k C kp 均为整数，且12)1()1()1(⋅-+--= k k k p p p C k p，分子中有因子p ，分母个各数均小于p ，又p 为素数，因此约分时p 不会被约去，因此有kpC p |，取素数为p ，)(y g 满足艾森斯坦判别式条件，因此)(y g 在有理数域上不可约，从而)(x f 在有理数域上不可约. 5）k kx x ,144++为整数. 解：令,1+=y x 则有).(2)1(4641)1(4)1(1423444y g y k y y y y k y kx x =+++++=++++=++取素数,2=p )(y g 满足艾森斯坦判别法条件，因此在有理数域上不可约，从而)(x f 在有理数域上不可约.。

高等代数第一章答案(多项式)

若()()()x m x l x h +=，且()()x m x p |，()()x l x p |/，则()()x h x p |/。

证法1：由()()x m x p |/有 ()()()x p x m x m 1=。

由()()x l x p |/有()()()()()0,1≠+=x r x r x p x l x l 。

于是 ()()()()()()()()x r x p x l x m x m x l x h ++=+=11。

因()0≠x r ，故()()x h x p |/。

证明2：用反证法。

问：若()()()()x g x h x f x h |,|//，则()()()()x g x f x h +|成立吗？试举例说明。

答：不一定。

例如 ()()()1,1,+=-==x x g x x f x x h ，则()()()()x g x h x f x h |,|//，但()()()()x g x f x h +|。

例如 ()()()2,1,+=-==x x g x x f x x h ，则()()()()x g x h x f x h |,|//，且()()()()x g x f x h +/|。

例求m l ,，使()2523+++=x lx x x f 能被()12++=mx x x g 整除。

解法1：因()()3=∂x f ，()()2=∂x g ，故商()x q 满足()()1=∂x q ，且设()p x x q +=，则由 ()()()x g x q x f =，可得()()p x pm x p m x x lx x +++++=+++1252323，l m p pm p =+=+=,51,2，从而 4,2,2===l m p 。

高等代数作业第一章多项式答案

.高等代数第一次作业第一章多项式 §1—§ 3一、填空题1. 如果 f ( x)|g( x) , g( x) | h( x) ，则。

f ( x) | h( x)2. 若 f ( x) | g( x) h( x) , f ( x)|g (x) ，则。

f ( x) | h( x)3. 若 f ( x)|g(x) , / ，则。

高等代数习题及参考答案

17．求值，使有重根。
解易知有三重根时，。若令
，比较两端系数，得
由（1），（3）得，解得的三个根为，将的三个根分别代入（1），得。再将它们代入（2），得的三个根。
当时有3重根；当时，有2重根。
18．求多项式有重根的条件。
解令，则，显然当时，只有当才有三重根。
3）。
解利用剩余除法试根，可得
1）有一个有理根2。
2）有两个有理根（即有2重有理根）。
3）有五个有理根（即一个单有理根3和一个4重有理根）。
28．下列多项式在有理数域上是否可约？
1）；
2）；
3）；
4）为奇素数；
5）为整数。
解1）因为都不是它的根，所以在有理数域里不可约。
2）利用艾森斯坦判别法，取，则此多项式在有理数域上不可约。
指数组
对应的方幂乘积
4 2 0
4 1 1
3 3 0
3 2 1
2 2 2
原式= (1)
只要令 ,则原式左边。另一方面，有，
代入（1）式，得。再令，得。
令，得
（2）
令得
（3）
由（2），（3）解得。因此
原式。
4）原式=
指数组
对应的方幂乘积
2 2 0 0
2 1 1 0
1 1 1 1
设原式
高等代数
第一章多项式
1．用除，求商与余式：
1）；
2）。
解1）由带余除法，可得；
2）同理可得。
2．适合什么条件时，有
1），
2）。
解1）由假设，所得余式为0，即，

(完整版)高等代数多项式

第二章多项式1．设f (x )，g (x )和h (x )是实数域上的多项式．证明：若f (x )2 = x g (x )2+x h (x )2，那么 f (x ) = g (x ) = h (x ) = 0．1．求f (x )被g (x )除所得的商式和余式：(i) 14)(24--=x x x f ,13)(2--=x x x g(ii) 13)(235-+-=x x x x f ,23)(3+-=x x x g证明：kx f x )(|必要且只要)(|x f x2．令)(),(),(,)(2121x g x g x f x f 都是数域F 上的多项式，其中0)(1≠x f 且)()(21x g x g |)()(21x f x f ，)(1x f |)(1x g ．证明：)(2x g |)(2x f ．3．实数m, p , q 满足什么条件时多项式12++mx x 能够整除多项式q px x ++4？、4．设F 是一个数域，F a ∈．证明：a x -整除nn a x -．5．考虑有理数域上多项式 1)1)(2()1()(-+++++=n k n k x x x x fn k x x )1()2(++⋅⋅⋅+，这里n 和k 都是非负整数．证明：1+k x |1)1()()1(++++-n k x x f x ．6．证明：1-d x 整除1-nx 必要且只要d 整除n1．计算以下各组多项式的最大公因式：(i)32103)(,343)(23234-++=---+=x x x x g x x x x x f ；(ii) i x i x i x i x x f ----+-+-+=1)21()42()22()(234；i x i x x g -+-+=1)21()(2．2．设)()()(1x f x d x f =，)()()(1x g x d x g =．证明：若)())(),((x d x g x f =，且)(x f 和)(x g 不全为零，则1))(),((=x g x f ，反之，若1))(),((=x g x f ，则)(x d 是)(x f 与)(x g 的一个最大公因式．从而可知)(x ϕ|)(x f ，)(x ϕ|)(x g ．既)(x ϕ是)(x f 、)(x g 的一个公因式，所以)(x ϕ|)(x d ．由定义知))(),(()(11x g x f x d =．3．证明：(i) h g f ),(是fh 和gh 的最大公因式；4．、设432()242f x x x x x =+---，432()2f x x x x x =+--2-都是有理数Q 域上的多项式．求u (x ),][)(x Q x v ∈使得))(),(()()()()(x g xd f x v x g x u x f =+．5．设(f , g )=1．令n 是任意正整数，证明：( f , g n ) = 1．由此进一步证明，对于任意正整数m ，n ，都有( f m , g n ) = 1．、6．设( f , g ) = 1．证明：( f , f + g ) = ( f + g , g ) = 1．证明：因为( f , g ) = 1．所以有u ,v 使uf + vg = 1，进而有( u – v ) f + v ( g + f ) = 1, 所以( f , g + f ) = 1.同理( g + f , g ) = 1利用互素性质得( f g , f + g ) = 17．证明：对于任意正整数n 都有( f , g )n = ( f n , g n )．8．证明：若是f ( x )与g ( x )互素，并且的次数都大于0．那么定理2.3.3里的可以如此选取，u ( x )次数低于g ( x )的次数，v ( x )次数低于f ( x )的次数，并且这样的u ( x )与v ( x )是唯一的．9．决定k ，使2(6)42x k x k ++++与2(2)2x k x k +++的最大公因式是一次的．10．证明：如果 ( f ( x ) , g ( x ) ) =１，那么对于任意正整数m ，( f ( x m ) , g ( x m ) ) =１ 11．设f ( x ) , g ( x )是数域F 上的多项式．f ( x )与g ( x )的最小公陪式指的是F [x ]中满足以下条件的一个多项式m ( x )：(a) f (x ) | m (x ) 且 g (x ) | m (x )；(b) h (x )∈F [x ] 且 f (x ) | h (x )，g (x ) | h (x )，那么m (x ) | h (x )．(i) 证明： F [x ]中任意两个多项式都有最小公倍式，并且除了可能的零次因式差别外，是唯一的．(ii)设f (x )， g (x )都是最高次项系数是１的多项式．令[ f (x ), g (x )]表示 f (x )与g (x )的最高次项系数是１的那个最小公倍式．证明： f (x ) g (x )= (f (x ) , g (x )) [ f (x ), g (x )]．12．设g (x )|)()(1x f x f n ⋅⋅⋅，并且(f i (x ), g (x )) =1, i =1,1,,2-⋅⋅⋅n . 证明 g (x ) | f n (x )．13．设][)(,),(1x F x f x f n ∈⋅⋅⋅．证明：(i) ()(,),(1x f x f n ⋅⋅⋅)=(()(,),(1x f x f k ⋅⋅⋅), ()(,),(1x f x f n k ⋅⋅⋅+)), 1≤k ≤n -1.(ii))(,),(1x f x f n ⋅⋅⋅互素的充要条件是存在多项式][)(,),(1x F x u x u n ∈⋅⋅⋅使得1)()()()(11=+⋅⋅⋅+x u x f x u x f n n14．设][)(,),(1x F x f x f n ∈⋅⋅⋅．令I ={+⋅⋅⋅+)()(11x g x f f n (x ) g n (x )|][)(x F x g i ∈, 1≤i ≤n } ．比照定理１.４.２，证明：)(,),(1x f x f n ⋅⋅⋅有最大公因式．［提示：如果)(,),(1x f x f n ⋅⋅⋅不全为零，取d (x )是中次数最底的一个多项式，则d (x )就是)(,),(1x f x f n ⋅⋅⋅的一个最大公因式．］2.4 多项式的分解1．在有理数域上分解以下多项式为不可约因式的乘积：2．分别在复数域，实数域和有理数域上分解多项式x ４+1为不可约因式的乘积．3．证明：g (x )２|f (x )２，当且仅当g (x )|f (x )． 4．5． (i)求f (x )= x 5-x 4-2x 3+2x 2+x -1在Q (x )内的典型分解式； 6．(ii)求f (x )= 2x 5-10x ４+16x 3-16x 2+14x -6在R (x )内的典型分解式．7．证明：数域F 上一个次数大于零的多项式f (x )是F [x ]中某一不可约多项式的幂的充分必要条件是对于任意g (x )∈F [x ],或者(f (x ), g (x )) =1,或者存在一个正整数m 使得f (x )|g (x )m .8．设p (x )是F [x ]中一个次数大于零的多项式.如果对于任意f (x ), g (x )∈F [x ]，只要p (x )|f (x )g(x )就有p (x )| f (x )或p (x )| g(x ),那么p (x )不可约．2.5 重因式1. 证明下列关于多项式的导数的公式： a) )(')('))'()((x g x f x g x f +=+； b))(')()()('))'()((x g x f x g x f x g x f +=2. 设)(x p 是)(x f 的导数)('x f 的1-k 重因式．证明： a) )(x p 未必是)(x f 的k 重因式；b))(x p 是)(x f 的k 重因式的充分必要条件是)(|)(x f x p3. 证明有理系数多项式!!21)(2n x x x x f n++++= 没有重因式． 4. a,b 应该满足什么条件，下列的有理系数多项式才能有重因式？a) b ax x ++33 b) b ax x ++445. 证明：数域F 上的一个n 次多项式)(x f 能被它的导数整除的充分必要条件是：n b x a x f )()(-=，这里a,b 是F 中的数．2.6 多项式函数多项式的根1.设f (x )=2x 5-3x 4-5x 3+1.求f (3),f (-2).2.数环R 的一个数c 说是f (x )∈R(x )的一个k 重根，如果f (x )可以被(x -c )k 整除，但不能被(x -c )k +1整除．判断5是不是多项式f (x )=3x 5-224x 3+742x 2+5x +50的根.如果是的话,是几重根?3.设2x 3-x 2+3x -5=a (x -2)3+b (x -2)2+c (x -2)+d .求a,b,c,d .4.将下列多项式f (x )表成x-a 的多项式.a) f (x )= x 5 ,a =1; b) f (x )=x 4-2x 2+3,a =-2.5.求一次数小于4的多项式,使f (2)=3,f (3)=-1,f (4)=0,f (5)=2.6.求一个2次多项式,使它在x =0,,2ππ处于函数 sin x 有相同的值．结果：24()()f x x x ππ=--7.令f (x ) , g (x ),是两个多项式,并且f (x 3) +x g (x 3)可以被x 2+x +1.证明: f (1) = g (1) =0. 8.令c 是一个复数,且是Q [x ]中一个非零多项式的根.令J ={ f (x )∈Q [x ] | f (c ) = 0}．b) p (x )在Q [x ]中不可约.如果c =32+,求上述的p (x )．9.设C [x ]中多项式f (x )≠0且f (x )| f (x n ),n 是一个对于1的整数.证明: f (x )的根只能是零或单位根.2.7 复数和实数域上多项式1.设n 次多项式n n na x a x a x f +++=-10)( 的根是n αα,,1 .a) 求以n c c αα,,1 为根的多项式,这里c 是一个数;b) 以n a 1,,11α(假定0,,1≠n αα )为根的多项式.2.设f (x )是一个多项式,用)(x f 表示把f (x )的系数分别换成它们的共轭数后所得多项式.证明:a) 若是g (x )|f (x ),那么)(x g |)(x f ;b) 若是d (x )是f (x )和)(x f 的一个最大公因式,并且d (x )的最高次项系数是1,那么d (x )是一个实系数多项式.3.给出实系数四次多项式在实数域上所有不同类型的典型分解式.4.在复数和实数域上分解x n -2为不可约因式的乘积.5.证明:数域F 上任意一个不可约多项式在复数域内没有重根.2.8 有理数域上多项式1.证明以下多项式在有理域上不可约: a) x 4-2x 3+8x -10; b) 2x 5+18x 4+6x 2+6 c) x 4-2x 3+2x -3 d) x 6+x 3+12利用艾森斯坦判断法,证明:若是t p p p ,,,21 是t 个不相同的素数,而n 是一个大于1的整数,那么nt p p p 21是一个无理数.3.设f (x )是一个整数系数多项式,证明:若是f (0)和f (1)都是奇数,那么f (x )不能有整数根.4.求以下多项式的有理数根: a) x 3-6x 2+15x -14; b) 4x 4-7x 2-5x -1;c) x 5-x 4-25x 3+2x 2-21x -3.2.9 多元多项式1.写出一个数域F 上三元三次多项式的一般形式.2.设 f (n x x ,,1 )是一个r 次齐次多项式.t 是任意数.证明：f (n tx tx ,,1 )=t r f (n x x ,,1 ).3. 设f (n x x ,,1 )是数域F 上一个n 元齐次多项式,证明:如果f (n x x ,,1 )=g (n x x ,,1 )h (n x x ,,1 ),则g ,h 也是n 元齐次多项式.4.把多项式x 3+y 3+z 3+3xyz 写成两个多项式的乘积.5.设F 是数域. f ,g ∈F [n x x ,,1 ]是F 上n 元多项式. 如果存在h ∈F [n x x ,,1 ]使得f =gh ,那么就说g 是f 的一个因式.或者说g |f .a) 证明,每一f 都可以被零次多项式c 和cf 整除c ∈F , c ≠0.b) f ∈F [n x x ,,1 ]说是不可约的,如果除了a)中那种类型的因式外f 没有其它因式,证明在F [x ,y ]里多项式x ,y ,x +y ,x 2-y 都不可约.c) 举反例证明,当n ≥2时,类似于一元多项式的带余除法不成立.d) f ,g ∈F [n x x ,,1 ]说是互素的,如果除了零次多项式外,它们没有次数大于零的公因式.证明x ,y ∈F [x ,y ]是互素的多项式.能是否找到u (x ,y ), v (x ,y ) ∈F [x ,y ],使得x u (x ,y )+y v (x ,y )=1?2.10 对称多项式1. 写出某一数环R 上三元三次对称多项式的一般形式.2.令R [n x x ,,1 ]是数环R 上n 元多项式环, S 是由一切n 元对称多项式组成的R [n x x ,,1 ]的子集.证明存在R [n x x ,,1 ]到S 的一个双射.3.把下列多元多项式表成初等对称多项式的多项式: a) ∑231xx ; b) ∑41x; c) 32221x x x ∑;4.证明:如果一个三次多项式x 3+ax 2+bx +c 的一个根的平方等于其余两个根的平方和那么这个多项式的系数满足以下关系: 2324)22(2)2(c ab a b a a +-=-.5.设n αα,,1 是某一数域F 上多项式x n +a 1x n -1++ a n -1x +a n 在复数域内的全部根.证明:2,,n αα的每一个对称多项式都可以表成F 上关于1α的多项式.。

高等代数习题(北大第四版)答案一到四章.docx

高等代数答案第一章多项式1 •用 g{x)除 /(.r),求商 </(.r)与余式 r(.r):1) /*(.r) = .r 3 - 3.r 2 - x-1,= 3.r 2 - 2.r +1: 2) f(x} = x 4 — 2.r+ 5,烈A ) = H -才+ 2 •解1)由带余除法，可得彳(才)=丄x--,/(.r) = - —.r--； 3 9 99 2 )同理可得久工)=X 2 + X- 1,心=-5.V+ 1 .2. m 、p 、q 适介什么条件时，冇1) x 1 + w.r-11 .t 3 + px+ q 、2) .r 2 + 7//.V+ 11 x 4 + + q o解I)由假设，所得余式为0,即(P+1 +〃小才+(0-刃) = 0,所以当+ 1 + - ° 时有才2 + my-11 x 3 + px*q° q- m- 02)类似可得(劝(2 — Q -刃?=0, j ：是当加=o 时，代入(2)可得〃=夕+ 1：而当［乡+ 1-p- ftl・=02-p-nr =0 时，代入(2〉可得0 = 1。

了时,皆有 f + 〃/・丫+11 x 4 + pf + q o p + 〃厂=23. 求g(.x)除/(X )的商0⑴与余式：1) /*(.r) = Zr 5 - 5-r 3 - 8.i ,g(.r) = .r+ 3 ：2) f(x) = 一 , 一不 g(.v)=才一 l + 2/ o0(・丫) = 2r 4 - +13” 一 39才 +109解1)；心)=-327°).(.丫) = '-2灯-(5+2/)。

/// = 0综上所诉,当 □攵.；p=q+\ -心)=-9 + 8/4. 把/(才)表示成才一兀的方幕和，即表成C Q +q(・Y-旺)+Q(才一・®)2 + ... + C…(X -X Q y+ …的形式：1) /(才)"，兀 T；2) /*(.r) = .r4 - 2.x2 + 3,x0 = -2；3) /(r) = x + 2/x一(l + /).r2一3x+ 7 + /,兀=-/«解1)由综合除法,可得/(x) = 1+ 5(x-1) + 10(r -1)2 +10(x-l)3^5(x -l)4+(r-l)5；2) 由综合除法，可得x4 -21^ + 3 = 11 - 24(.r+ 2) + 22(.r+ 2)2 -8(.r+ 2)3 + (.r+ 2)4:3) 由综介除法，可得.r4 + 2/：? - (1 + /).? -3x + (7 + z)= (7+5/)-5(x+/)4- (- 1一/比+/予-2«+/)+ (r+ // o5. 求/(貯与肌工)的最大公因式：1) /(才)=.r4 + .r5 -3, - 4才- 1£(才)=,+ , -.丫-1 ；2) /(.r) = .r4 -4.? + l,^(.r) =.? -3,r +1 ：3) f .r) - .r4 - lO.r2 + l,g(") - .r4 -心力 + 6A2 + 4/2r+ 1。

线性代数(含全部课后题详细答案)1第一章一元多项式习题及解答.docx

A 组1.判别Q (厉)二｛0 +勿亦|0,处0｝是否为数域？解是.2.设/(x) = x3 4-x2 4-x+l, g(兀)=兀2+3兀+ 2,求 /(兀)+ g(x)，/(x)-g(x), f(x)g(x). 解/(x) + g (x) = x3 4- 2x2 + 4x + 3 ,/(兀)-g(x)"-2x-l,f(x)g(x) = x5 +4x4 +6兀'+6兀$ +5x + 2 .3.设/(%) = (5x-4),993(4x2 -2x-l),994 (8x3 -1 lx+2)'995,求 /(%)的展开式中各项系数的和.解由于/(兀)的各项系数的和等于/⑴，所以/(I) = (5-4严3(4-2- 1尸94(8-11 + 2)1995 =-1.4.求g(兀)除以/(兀)的商q(x)与余式心).(1)f (x) —— 3%2— x — 1, g(兀)=3F - 2兀+1 ；(2)/(x) = x4 -2x4-5, g(x) = x2 -x + 2 .解（1）用多项式除法得到x 73x~ — 2x +13_93X + 3—x —x-i3 37 ° 14 7-- 无_+ —x --3 9 926 2-- X ---9 9所以'恥）十岭心）W（2）用多项式除法得到x4— 2x + 5兀4 —”丫" + 2 兀2— 2x~ — 2 兀+5 jy?—兀~ + 2 兀-x2-4x4-5-兀? + X - 2—5x + 7所以，q(x) = x2 +x-l, r(x) = -5x + 7 .5.设是两个不相等的常数，证明多项式/(兀)除以(x-a)(x-b)所得余式为af(b)_bg)a-b a-h证明依题意可设/(x) = (x - a)(x - b)q(x) + cx+d,则”(a) = ca + d,[f(b) = cb + d.解得F=(/a) --,\d = (af(b)-bf(a))/(a-b).故所得余式为a-b a-b6.问m,p,q适合什么条件时，/(兀)能被g(x)整除？(1) /(x) = x3 + px + q , g(x) = x2 + nvc-1；(2) f(x) = x4 + px2 +q , g(兀)=x2 + mx+l.解(1)由整除的定义知，要求余式r(x) = 0 .所以先做多项式除法,3x2 + mx -1x-in“+ “X + q3 2x + mx^ - x-mx1 +(〃 + l)x + g2 2一 mx_ — m^x + m°(# +1 + 加〜)兀 + (g —m)要求厂(x) = (/? + l +加2)兀+ (§ —加)=0 ,所以(“ + 1 +加2) = 0, q-m = 0.即p = -l-m2, q - m时, 可以整除.（2）方法同上.先做多项式除法，所得余式为厂（兀）=加（2 — ”一nr ）兀+ （1 + @ —卩一加〜），所以 m （2-p-/772） = 0, 1 + ^ - p - m 2= 0 ,即 m = 0, p = q + \ 或“二 2— 加［q = l 时，可以整除.7. 求/（兀）与gCr ）的最大公因式:(1) f (x) — x 4 + — 3%2 — 4x — 1, g (x)=兀彳 + — x — 1 ； (2) f(x) = x 4— 4x 3+ 1, g(x) = x 3— 3x 2+1 ；(3) /(x) = x 4 -10x 2 +1, g(x) = x 4 -4A /2X 3 +6X 2 +4A /2X +1 .解（1）用辗转相除法得到用等式写出來，就是所以(/(x),g(x)) = x + l ・（2）同样地,<8 4 / 3 3= -X + — — -X-—(3 344-2x 2-3x-l1 1 --- X 4——2 -- 4 X 3+ X 2- X - 1 x 4 + x 3- 3x 2- 4x- 11 2 3 , -2x 2 — 3兀—12 21 2 3 1 -- X ----- X ---—2兀~ — 2兀2 4 433-- X ----X -144一丄 184—X H - 3 3 0心宀丄兀2 24 3 2牙+牙-X - Xf(x) = xg(x)^(-2x 2-3x-l),g(x) =所以(/⑴,g (兀)) = 1.⑶ 同样用辗转相除法，可得(/(x),g(x)) = F —2血兀一1.8.求 w(x),仄兀)使 w(x) f\x) + v(x)g(ji) = (/(x), g(%))：(1) f (x) = %4 4- 2x^ — %2 — 4x — 2, (x) = %4 + x — x~ — 2x — 2 : (2) /(x) = 4x 4-2x 3-16x 2+5x4-9, g(x) = 2兀3-x 2-5x+4:(3) /(x) = x A-x 3-4x 2 +4x + l, g (兀)=x 2 -x-l.解(1)利用辗转相除法，可以得到/(x) = g (A ：) + (x 3-2x)'g (兀)=(x+l)(x 3 - 2x) + (x 2 -2),x — 2兀=x(^x~ — 2).因而，(/(x),g(x)) = x 2-2,并且(/(兀),g (兀))=/ 一 2 = g (兀)_ (兀+1)(疋 _ 2兀) =g (兀)一(X +1) (f(x) -g (兀))=(一兀一 1)/(兀)+ (兀+2)g(x),所以 u(x) = -x-\, v(x) = x + 21 10 -- X H --- 3 9x 3 - 3x 2x-13 1 2 2X H —X X 3 3 10 2 2~~'- ---- X H 兀+ 13 -- 3 10 ° 10 20 X --- 兀 3 9 916~~1T —X ------ 9 927 441 --------- X ---------------16 256-3x 2+—x1649一一539 兀+ --- 27 256(2)利用辗转相除法，可以得到/(x) = 2xg(x)-(6x 2 +3兀-9),(\ 1Ag(x) = —(6x_ + 3兀一9) ——% + — — (% — 1), —(6x - + 3x — 9) = —(x —1)(6% + 9).因而，(/⑴,g(Q) = x-1，并且(1 1 …厶— —X + _ f (x) + _兀_—x~\ I 3 3丿 (3 3丿] 1 2 7 2fi/f 以 W (X )= X H —, V (X )= — --- X — \ •3 3 3 3(3) 利用辗转相除法，可以得到fM = X —3)g(x) + (x — 2),g(x) = (x+l)(x-2) + l ・因而( f(x), g(x)) = 1 ,并且(/(兀),g(x)) = 1 = g(x) - (x+1)(兀一 2)=g (兀)-(兀+1)(/(兀)-(x 2 一3)gCr))—(—兀―1) f (x) + (兀'+ 兀2 — 3兀—2)g(x),所以u (兀)= -x-l, v(x) = x 3 +x 2 -3x-2.9.设/(x) = %3+ (14-t)x 2+ 2x + 2w, g(x)二F+zx + u 的最大公因式是一个二次多项式，求/，凤的值.解利用辗转相除法，可以得到/(%) = g(x) + (l + /)兀2 +(2-/)兀 + « ,(/(x), g(x)) = x-l = -(6x 2+ 3x-9)+ | _g(x)I d J J(I ] \= (/(x)-2xg(x)) --x+- -g(x)\ 3丿 <2 o 2 d ,、 U 3 广—---- 兀+ (1 + r t-2(l +r)2(尸 + r—w)(i+r) + (t— 2)~u[(l + t)2 — (r —2)]由题意，/(x)与g(Q的最大公因式是一个二次多项式，所以(广 + / —w)(l + /) + (f— 2)~(T H?皿(l + r)2-(r-2)] A ；=0,(l + O2解得u = o^t = -4.10.设(x —I)[(A/+ B F+I),求A和B.由题意要求知解用(兀一1)2 去除f\x) = Ar4 + Bx2 +1 ,得余式”(x) = (4A + 2B)兀+1 -3人一B,斤（兀）=0,即4A + 2B = 0,1-3A-B = O,解得A = l,B = -2.11.证明:如果(/(x),g(x)) = l, (/(x),/z(x)) = l,那么(/(x), g(x)/z(x)) = l. 证明由条件可知,存在络(兀)和片⑴ 使得旳(兀)/(兀)+岭⑴g(x) = l,存在如(兀)和卩2(兀)使得u2(x)f(x) + v2(x)h(x) = 1.用/?(兀)乘以第一式得坷(x)f(x)h(x) + V, (x)g(x)h(x) = h(x),代入第二式得u2(x)f(x) + v2 (x) [u t (x)f(x)h(x) 4-Vj (x)g(x)/z(x)] = 1, 即[w2(兀)+ u\ (x)v2(x)h(x)]f(x) + [v, (x)v2(x)]g(x)h(x) = 1,所以(/(x),g(x)/z(x)) = l.12.证明：如果/(x)与g(x)不全为零，且/心)/(兀)+ 咻)g(兀)=(/(%), g(Q)，证明由于w(x)/(x) + v(x)g(x) = (/(x),g(x)), /(X )与 g(x)不全为零，所以(/(x)，g(x))HO.两边同时除以(/(Hg(Q)HO,有所以(弘(兀),咻)) = 1 .13.证明：如果〃(兀)|/(兀),〃(兀)|g(x),且〃(兀)为/(兀)与g(x)的一个组合，那么〃(兀)是/G)与 g(x)的一个最大公因式.证明由题意知d(x)是/(X )与g(x)的公因式.再由条件设d(x) = w(x)/(x) + v(x)^(x) •又设h(x) 为/(x)与g(x)的任一公因式，即/z(x)|/(x), h(x)\g(x),则由上式有h(x)\d(x).故而”(兀)是/(兀)与 g(x)的一个最大公因式.14.证明：(.fO)/2(X ), gO)/2(X )) = (.f(X ), g(x))〃(x),其中力(兀)的首项系数为 1.证明显然(/(x), g(x))/?(x)是f{x)h{x)与g(x)h(x)的一个公因式.下面來证明它是最大公因式. 设 /心),v(x)满足 w(x)/(x) + v(x)g(x) = (/(x), g(X>),贝iJu(x)f(x)h(x) + v(x)g(x)h(x) = (/(x),g(x))/z(x).由上题结果知，(/(兀),g(X ))/7(X )是/(X )/?(X )与g(JC”7(X )的一个最大公因式，又首项系数为1,所以(/(x)A(x), ^(%)/?(%)) = (/(x), ^(x))/i(x)・/⑴ g (兀)、(/(兀),g (兀))’(f(x),g(x))丿证明设〃(兀)=(/(兀),g(x)),则存在多项式M (x), v(x),使d(x) = u(x)f(x) + v(x)g(x)・因为/(X )与g (尢)不全为零，所以d(x)HO.上式两边同时除以〃(兀)，有故 /(兀) _____________ g (x)l (/(x),g(x))‘(/(x),g(x))‘u(x) /(X ) (/(%), g(x)) + v(x) g(x) (y (x ),^(x ))15.设多项式/(x)与gS)不全为零，证明1 = u(x)/(兀)(/(兀),g(x))+咻)g(x) (/(兀),g(x))=1成立.16. 分别在复数域、实数域和有理数域上分解兀4+ 1为不可约因式之积.在有理数域上兀°+1是不可约多项式.否则，若+ +1可约，有以下两种可能.(1) 兀4+1有一次因式，从而它有有理根，但/(±1)工0,所以卍+1无有理根.(2) x 4+ 1 无一次因式，设x 4+1 = (x 2+处 +方)(F +cx + d),其中 a,b y c,cl 为整数.于是a + c = O, b+ 〃 + ac = O, cut + be = 0 , bd = \,又分两种情况：① b = d = \,又 a = —c,从而由 b + 〃 + ac = O,得 a 2=2,矛盾； ② b = d = — \,则 a 2= —2 ,矛盾.综合以上情况，即证.17. 求下列多项式的有理根： (1) /(x) = x 3-6x 2+15兀一 14 ；(2) ^(X ) = 4X 4-7X 2-5X -1；(3) /z(x) = x 5+ %4— 6x^ — 14x~ — 1 lx — 3 ・解(1)由于/(x)是首项系数为1的整系数多项式，所以有理根必为整数根，且为-14的因数.-14的因数有：±1, ±2, ±7, ±14,计算得到:/(D = -4, /(-1) = -36, /(2) = 0, /(-2) = -72,/(7) = 140, /(-7) = -756, /(14) = 1764, /(一 14) = —4144,故x = 2是/(兀)的有理根.再由多项式除法可知，x = 2是于(兀)的单根.⑵ 类似(1)的讨论可知，g(x)的可能的有理根为:故x = --是巩兀)的有理根.再由多项式除法可知，兀二-丄是/(劝的2重根.2 2⑶ 类似地，加兀)的可能的有理根为：±1,±3,计算得到解在实数域上的分解式为X4+ 1 = (X 2 + 1)2-2X 2 =(X 2+V2X + 1)(X 2-V2X +1).在复数域上的分解式为x + ----------1 2 2%4+ 1 = f亠迈亠近、X ---------- 12 2/±1, ±1 ±?计算得到g(l) = -9,g(-1) = 1, g(］、r 、171=-5, g —=0, g — 一 —‘ g —〔2< 264 ,4丿11A(l) = -28, /?(-l) = 0,(3) = 0,加一3) = -96.故x = -l, x = 3是//(兀)的有理根.再由多项式除法可知，x = -\是/z(x)的4重根，兀=3是//(兀)的单根.18.若实系数方程x34- px + q = 0有一根a + bi (a,b为实数，/?工0),则方程x3 + px-q = 0有实根2—证明设原方程有三个根不失一般性，令=a + bi,从而有a2 =a-bi,由根与系数的关系可知0 = $ + 冬 + 他=(° + 勿)+ (a - bi) + ,所以冬二-2d，即(-2a)‘ + /?(-2a) + g = 0，故(2a)' + p(2a)-q = 0.这说明x3 + /zr-g = 0有实根2a .19.证明：如果(%-i)|/(r),那么证明因为u-i)|/(z),所以/(r)= /(i)= 0.因此，令y(x)=(x-i)g(x),则有E =(*-i)g(;),即(伙-1)|/(疋).20.下列多项式在有理数域上是否可约？(1)土 (%) = F+1；(2)/；(X)= X4-8?+12X2+2；(3)人(x) = x" +『+1 ；(4)厶(无)=* + "； + 1,门为奇素数；(5)厶(兀)=兀°+4尬+ 1, A为整数.解(1) ./；(兀)的可能的有理根为：±1,而/(±1) = 2,所以它在有理数域上不可约.(2)由Eisenstein判别法，取素数p = 2,则2不能整除1,而2|(-8), 2|12, 2|2,但是2?不能整除2,所以该多项式在有理数域上不可约.(3)令x=y + l,代入厶(x) = P+x'+l有^(y) = ^(y + l) = / + 6/+15/+21/+18y24-9y4-3.取素数0 = 3,由Eisenstein判别法知，g(y)在有理数域上不可约，所以/(兀)在有理数域上不可约.(4)令兀= y_l,代入f4(x) = x p 4-px + 1,得g(y)=厶(y j) = -+ cy~2——C；-2y2 + (Cf* + p)y-p，取素数p,由Eisenstein判别法知，g(y)在有理数域上不可约，所以£(兀)在有理数域上不可约.(5)令x=y + l,代入农(兀)=兀4+4Ax+l,得g(.y)=厶(y +1) = y" + 4y‘ + 6y2 + (4k + 4)y + 4R + 2 ,収素数p = 2,由Eisenstein判别法知，g(y)在有理数域上不可约，所以点(兀)在有理数域上不可约.1•设/(X)，g(X)，加兀)是实数域上的多项式，(1)若/2U) = xg2(x) + x/z2(x),则/(x) = g(x) = h{x) = 0 .(2)在复数域上，上述命题是否成立？证明(1)当g(兀)=/2(兀)=0时，有严⑴=0,所以/(%) = 0 ,命题成立.如果g(x), /z(x)不全为零，不妨设g(x)H0・当h(x) = 0时，a(xg2(x) + x/i2U)) = l + 2a^(x)为奇数；当加兀)工0时，因为g(x),瓜兀)都是实系数多项式，所以Xg2(x)与兀胪(兀)都是首项系数为正实数的奇次多项式，于是也有d(xg2(x) + x/『(x))为奇数.而这时均有/2(x)^0 ,且df\x) = 2df(x)为偶数,矛盾.因此有g(兀)=力(兀) = 0,从而有f(x) = 0 .(2)在复数域上，上述命题不成立.例如，设f(x) = 0 , g(x) = x\ h(x) = ix,1,其中斤为自然数, 有/2 (x) = xg2 (x)xh2 (x),但g(x) / 0 ,力(兀)工0.2.设/(x), g(x)9 h(x)e P[x],满足(x2 4-l)h(x)4-(x-l)/(x) + (x+2)g(x) = 0,(x2 + l)/?(x) + (x+ l)/(x) + (x - 2)^(%) = 0.证明(X2+1)|(/U), g(X))・证明两式相加得到2(x2 + l)h(x) + 2x(/(x) + g(兀))=0.由(x2+l,兀)=1可知(x2 + l)|(/(x) + g(x)).两式相减得到-2f(x) + 4g(x) = 0, f(x) = 2g(x).故(x2 + l)|/(x), (x2+l)|g(x), BP(X2+1)|(/(X),g(x)).3・设gi(x)g2(x)\f{(x)f2(x),证明(1)若/(x)|g](x)，/(X)H0,则g2(x)\f2(x)；(2)若g2(x)|/；(x)/；(x),是否有g2(x)\f2(x)?解(1)因为gi(兀)g2(兀)庞(兀)£(兀)，/O)|gi(X)，故存在多项式h(x), h}(x)使得fl(x)f 2(x) = g](x)g 2(x)h(x\ g](兀)=Z (x)h }(x).于是/；(兀)£(兀)=/(兀)人(兀)g2(x)力(兀)•由于土(兀)工0,故有 f 2(x) = h l (x)g 2(x)h(x),即g 2(x)\f 2(x).(2)否•例如取 g {(x) = x-2 , ^2(X ) = X 2-1 , (x) = (x-l)(x-2), (x) = (x + l)(x4-2).虽然 gSx)g 2(x)\f^x)f 2(x)且 g 2(x)\f {(x)f 2(x),但 g 2(x)不能整除 f 2(x).4.当R 为何值时，/(x) = X 2 +伙+ 6)x + 4k + 2和g(x) = F+(£ + 2)x + 2R 的最大公因式是一次的？并求出此吋的最大公因式.解显然 g(x) = (x + £)(x+2).当(/(x),g(Q) = x + 2时'/(一2) = 4 — 2伙+ 6) + 4£ + 2 = 0‘ 则k = 3.当(于(兀),g(Q )=兀 + £ 时’/(一灯=k 2 - k(k + 6) + 4Z: + 2 = 0 ‘ 则 k = l.这时(/(x), g(x))=兀+1. 5.证明：对于任意正整数斤，都有(/(x),g(Q)"=(/"(x),g"(x))・证明由题意可知/(%)与&(兀)不全为零.令(/(x), g(x)) = d(x),Z 、” g(x) 、d(x)丿/心)/"(兀)+ 咚)g"(兀)=d\x).又由 d(x)\f(x), d(x)|g(x),有 d n (x) f l \x), d"(x) g"(x),因此 d"(x)是厂(x)与 g"(x)的首项系数为1的最大公因式，从而有(广(x),g"(x))= 〃"(兀)=(/(x),g(x))" •6.设 / (x) = af(x) + bg(x), g[ (x) = c/(x) + dg(x),且 ad - be H 0 ,证明(/(x),g(x)) = (/](x), g](X ))・证明设(/(x), g(x)) = d(x),则 d(x)\f(x\d(x)\g(x).由于 “所以对任意正整如，有爲J 寫〕"卜于是有u{x) +咻) 则〃(兀)工0,从而fi (兀)=妙(x) + bg(x) , g] (x) = (x) + dg (x),故d (x)| (x), d (x)|g t (x).又设h(x)\ (x), /z(x)|(x),由上式及ad-bc^O ,可得从而/?(x)|/(x), h(x)\g(x),于是h(x)\d(x),即〃(兀)也是/；(兀)和g|(x)的最大公因式，即(/(x), g(x)) = (/；(x),&(兀))・7.设 /(x) = t/(x)/(x), g(Q 二 dCr)g](x),且/O)与 gd)不全为零，证明〃(兀)是/O)与 gCO的一个最大公因式的充分必要条件是(/(劝,g|(x)) = 1.证明必要性.若〃(x)是/(兀)与g (兀)的一个最大公因式，则存在多项式w(x),v(x)使W (x)/(x) +v(x)g(x) = d(x),于是u(x)d(x)f t (x) + v(x)d(x)g l (x) = d(x).由/(力与g (兀)不全为零知如工0,因此有u(x)f l (x) + v(x)g l (x) = l f 即(土(兀),g©))i •充分性.若(f l (x),g l (x)) = l ,则存在多项式u(x),v(x),使 u(x)f l (x)+ v(x)g l (x) = l. 两边同吋乘〃(兀)有u(x)f(x) + v(x)g(x) = d(x)・由d(x)是/(x)与g(x)的一个公因式知，d(x)是f(x)与g(x)的一个最大公因式.8.设于(兀)和g(x)是两个多项式，证明(f(x), g(x)) = l 当且仅当(f(x)-l-g(x), f(x)g(x)) = l. 证明必要性.设(f(x)9g(x)) = l,若f(x) + g(x)与/⑴g(x)不互素，则有不可约公因式p(x), 使p(x)lf(x)g(x)f所以 p(x)| /(X )或 0(x)|g(x).不妨设 p(x)\ /(x),由 P (x)|(/(x) + g (兀))可知 p(x)|g(x),因此 P (兀)是 /(兀)和g“)的公因式,与/(%), g (x)互素矛盾,故蚀+g (兀)与蚀g (兀)互素.充分性.设(/(兀)+ gO) J(x)g (兀)) = 1,则存在w(x), v(x)使(/(兀)+ g (兀))心)+ /(x)g(x)v(x) = 1 , f(x)u(x) + g (兀)(臥兀)+d ad-be zw- h ad 一gi (兀)， g(x) -c ad -be a ad -be g](x)，/(x)v(x)) = 1, 上式说明(/(兀),g(兀)) = 1.9.如果(x2 +x + l)|/j(x3) + x/^(x3),那么(x-l)|/；(x), 0 — 1)|/；(兀)・T；®所以，^3=£23 = 1.证明X2+X + l的两个根为£\= 士护和£2=因为U2+x+l)|(/；(^3) + x/；(^3)),所以(兀一£|)(x - £2)|/；(X')+/(F)，故有y 窗)+ £/(郃)=0,［爪哥)+ £2£(哥)=0,即解得/(l) = /；(l) = o,从而(兀—1)|久(兀)，(x-1)|/；(%).10.若f(x)\f(x H),则/(x)的根只能是零或单位根.证明因为f(x)\f(x n),故存在多项式g(x),使/(x n) = /(x)^(x).设。

高等代数北大编第1章习题参考答案

高等代数北大编第1章习题参考答案第一章多项式一、习题及参考解答1．用)(x g 除)(x f ，求商)(x q 与余式)(x r ： 1）123)(,13)(223+-=---=x x x g x x x x f ； 2）2)(,52)(24+-=+-=x x x g x x x f 。

解 1）由带余除法，可得92926)(,9731)(--=-=x x r x x q ； 2）同理可得75)(,1)(2+-=-+=x x r x x x q 。

2．q p m ,,适合什么条件时，有 1）q px x mx x ++-+32|1， 2）q px x mx x ++++242|1。

解 1）由假设，所得余式为0，即0)()1(2=-+++m q x m p ，所以当=-=++0012m q m p 时有q px x mx x ++-+32|1。

2）类似可得=--+=--010)2(22m p q m p m ，于是当0=m 时，代入（2）可得1+=q p ；而当022=--m p 时，代入（2）可得1=q 。

综上所诉，当??+==10q p m 或=+=212m p q 时，皆有q px x mx x ++++242|1。

3．求()g x 除()f x 的商()q x 与余式：1）53()258,()3f x x x x g x x =--=+； 2）32(),()12f x x x x g x x i =--=-+。

解 1）432()261339109()327q x x x x x r x =-+-+=-；2）2()2(52)()98q x x ix i r x i=--+=-+。

4．把()f x 表示成0x x -的方幂和，即表成2010200()()...()n n c c x x c x x c x x +-+-++-+L 的形式：1）50(),1f x x x ==；2）420()23,2f x x x x =-+=-；3）4320()2(1)37,f x x ix i x x i x i =+-+-++=-。

高等代数课后答案高等教育出版社

另设()x ϕ是f （x ）与g （x ）的任意公因式，下证()()x d x ϕ。

由于d （x ）是f （x ）与g （x ）的一个组合，这就是说存在多项式s （x ）与t （x ），使 d （x ）=s （x ）f （x ）+t （x ）g （x ）。

从而()()x f x ϕ，()()x g x ϕ，可得()()x d x ϕ。

完整版高等代数习题解答(第一章)

完整版高等代数习题解答(第一章)高等代数题解答第一章多项式补充题1.当a,b,c取何值时，多项式f(x)=x-5与g(x)=a(x-2)^2+b(x+1)+c(x^2-x+2)相等？提示：比较系数得a=-1,b=-1,c=6.补充题2.设f(x),g(x),h(x)∈[x]，f^2(x)=xg^2(x)+x^3h^2(x)，证明：假设f(x)=g(x)=h(x)不成立。

若f(x)≠0，则∂(f^2(x))为偶数，又g^2(x),h^2(x)等于或次数为偶数，由于g^2(x),h^2(x)∈[x]，首项系数（如果有的话）为正数，从而xg^2(x)+x^3h^2(x)等于或次数为奇数，矛盾。

若g(x)≠0或h(x)≠0，则∂(xg^2(x)+x^3h^2(x))为奇数，而f^2(x)为偶数，矛盾。

综上所证，f(x)≠g(x)或f(x)≠h(x)。

1.用g(x)除f(x)，求商q(x)与余式r(x)：1）f(x) =x^3-3x^2-x-1，g(x) =3x^2-2x+1；2）f(x) =x^4-2x+5，g(x) =x^2-x+2．1）解法一：待定系数法。

由于f(x)是首项系数为1的3次多项式，而g(x)是首项系数为3的2次多项式，所以商q(x)必是首项系数为1的1次多项式，而余式的次数小于2.于是可设q(x)=x+a,r(x)=bx+c。

根据f(x)=q(x)g(x)+r(x)，即x^3-3x^2-x-1=(x+a)(3x^2-2x+1)+bx+c，右边展开，合并同类项，再比较两边同次幂的系数，得a=-1/3,b=-2/3,c=-1，故得q(x)=x-1/3,r(x)=-x-1/3.2）解法二：带余除法。

用长除法得商q(x)=x^2+x-1，余式r(x)=-5x+7.2.m,p,q适合什么条件时，有1）x^2+mx-1/x^3+px+q;2）x^2+mx+1/x^4+px^2+q.解：1）将x^3+px+q除以x^2+mx-1得商为x+m+1/(x+m-1)，所以当m≠1时有解。

(完整word版)高等代数多项式习题解答

第一章多项式习题解答1. 用g(x)除f(x)，求商q(x)与余式r(x).5x2. m, p,q 适合什么条件时，有 1) x 2 mx 11 x 3 px qq(x)x 2 x 1, r(x)5x 7.x 3 0x 2 px q xp 10,q m 时 x 2 mx 11 x 3 px1) f(x)x 3 3x 2 2x3x 232x 3xx 1 3 2 2 1x —x -x3 3 7 24 1 x x 3 37 2 14 7 —x ■ x — 3 9 926 2 —x9 9q(x) £ r (x )26 x92) f(x)2x 5, g(x)4 x 4x0x 3 0x 2 x 3 2x 2 x 3 2x 22x 32x x 2xx2x2x 54x 5 x 2 mx 1当且仅当m 2 i,g(x)x 2x 1 1—x 3 3x 2本题也可用待定系数法求解 .当X 2 mx 1| x 3 px q 时，用x 2 mx 1去除x 3 px q ，余式为零，比较首项系数及常数项可得其商为 x q.于是有因此有m 2 p 1 0, q m .2) x 2 mx 11 x 4 2px q由带余除法可得42/ 2x px q (x mx1)( x2mx 2p 1 m ) m(2pm 2)x (q 1 pm 2) 当且仅当r(x) m(2 p 2m )x (q 1 p m 2) 0 时2x 42mx 11 x pxq .即m(2 p m 2) 2m，即 mQ 或 p 2小m 2,q 1p 0q 1 p,q 1.本题也可用待定系数法求解.当x 2 mx 1|x 4px 2 q 时，用x 2 mx 1去除x 4 px 2 q ，余式为零，比较首项系数及常数项可得其商可设为 x 2 ax q .于是有3. 求 g(x)除 f (x)的商 q(x)与余式 r(x). 531) f (x) 2x 5x 8x, g(x) x 3; 解：运用综合除法可得 32580 6 18 39 1173272 6 1339 109 327商为 q(x) 2x 4 6x 3 13x 2 39x 109，余式为 r(x) 327.4 2x pxq (x 2ax q)( 2x mx 1)(m a)x 3 (ma2q 1)x(a mq)x q.ma q 1 p,a mq 0.消去a 可得m 0,或2p m 2,q 1 p,q 1.x 4 比较系数可得m a 0,2px q (x q)(x mx 1)x 3 (m q)x 2(mq 1)x q .2) f(x) x 3 x 2x,g(x) x 1 2i .解:运用综合除法得：1 2i 11 1 0 1 2i4 2i 9 8i 1 2i5 2i9 8i商为x 2 2ix (5 2i),余式为9 8i .c 0即为x X o 除f (x)所得的余式，商为q(x) q 可得C 1为x x o 除商q(x)所得的余式，依次继续即可求得展开式的各项系数解：1)解法一：应用综合除法得•1 1 o o o o o11111 111111 112 3 4 1 1 2 3 4 51 3 6 1 1 3 6 1o1 4 1 1 4 1o 14.把 f(; x)表成x X °的方幂和，即表示成CoC 1(X X o ) C 2(X X o )2的形1) f(x) 5x12) f(x) 4x 2x 23, xo2;3) f(x) 4x2ix 3 (1 i)x 2 3x 7 i,x o1分析：假设 f(x) 为n 次多项式，令f(x)C o G (x X o ) C 2(X X o )2C n (x X o )n式.x o )n1]C o (x X o )[G C 2(x x o )C n (x C 2(x X 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

)C n (x x °)n1.类似f(x) x5 (x 1)55(x 1)4 10(x 1)310(x 1)2 5(x 1) 1 .1 5f(x) x 5 (x 1)5 5(x 1)4 10(x 1)3 10(x 1)25(x 1) 1 .21 6 22 21 83) 因为1 2i13 7i11 4i 1i i 4 7 5ii0 11 0ii 151 2if(x) x 4 2ix 3 (1 i)x 2 3x 7 i(7 5i) 5(x i) (1 i)(x i)25.求 f (x)与g (x)的最大公因式1) f(x)x 4 x 3 3x 2 4x 1,g(x) x 3 x 2 x 1解法一:利用因式分解f(x)43^2*x x 3x 4x31 (x 1)( x3x 1),55x [(x 1) 1]5432(x 1)5( x 1)10(x 1)10(x 1)5(x 1) 12 )仿上可得2 1 0 2 0 32 4 4 82 12 2 4 112 8202 14 10 242 12解法二：把x 表示成(x 1) 1，然后用二项式展开f(x) 11 24(x 2)2322(x 2)8( x 2)4(x 2).2i(x i)3 (x i)4.g(x) x3 x2 x 1 (x 1)2(x 1).因此最大公因式为x 1.解法二：运用辗转相除法得q2（x ）3 2x x x 13 3 2 1x x x2 21 2 3 1x x2 21 2 3 1x x —2 4 4”2（X）3 3x4 44 3x x 3x24x 14 3 2x x x x「1（2x23x 12x22xx 1x 18 -x3q(x)43 q3(x)因此最大公因式为x 1.4 3 3 22) f (x) x 4x 1,g(x) x 3x 1 .解：运用辗转相除法得（注意缺项系数补零）q2（x ）9 312 2x —x —x3 310 2 2一x —x 13 310 2 10 20—x 一x3 9 916 11r2(x) 一x —9 93 210 x 3x 0x 14 ,3^2x 4x 0x4 小3 2x 3x 0x0x 1x3 小 2x 0x x 13 x 3x20x 1n(x) 3x2x 2-2 333x -—x1649 x 21649 539—x16 256“(x)27256x 1 qdx)27 441—x --------16 256(f(x),g(x)) 1.3)f (x) x4 10x21,g(x) x44-2x3 6x24・2x 1.g(x) f (x) 4.2(x3 2.2x2 x) f (x) R(x)，f (x) (x3 2 .2x2 x)(x 2 2) 2(x 22x 1)14” 2rdx)(x 2-2) D(X),—r1(x) x32P2x24、2x x(x22・2x 1) D(x)x,因此(f (x), g(x)) x22 2x 1.6•求u(x),v(x)使 u(x)f(x) v(x)g(x) (f(x),g(x)): 1) f (x) x 4 2x 3 x 2 4x 2,g(x)解：运用辗转相除法得:因此(f(x), g(x)) r 2(x) x 2 2.且有q 2(x)f(x) [i q i (x)q 2(x)]g(x). u(x)q 2(x)x i, v(x) i q i (x)q 2(x) x 2.4322) f (x) 4x 2x i6x 5x 9, g (x) 解：运用辗转相除法得:43223) f (x) x x 4x 4x i, g(x) x x i.x 4 x 3 x 2 2x 2;q 2（x ）f(x) g(x)q i (x)r i (x) , g(x) r i (x)q 2(x)D(x), A(x)「2(x)q 3(x).于是「2(x) g (x ) r i (x)q 2(x)g (x ) [f(x) g(x)q i (x)]q 2(x)c 322x x 5x 4;i-x i 2x 3 x 2 5x 4 4x 4 2x 3i6x 2 5x 9 332x 3 x 23x4x 4 2x 3i0x 2 8x2x 2 2x 4 r i (x)6x 2 3x92x 2 x 3 6x 26xD(x)x i9x 99x 9q i (x) q 3(x因此（f （x ）, g （x ）） r 2（x ） x 〔.且有f(x) g(x)q i (x)r i (x) , g(x) r i (x)q 2(x) “(x), A (X ) b(x)q 3(x).于是「2（X ） g (x ) r i (x)q 2(x) g (x ) [f(x) g(x)q i (x)]q 2(x)q 2(x)f(x) [i q i (x)q 2(x)]g(x).u(x) q 2(x)v(x)i q i (x)q 2(x)i 2x( ^x -) -x 2 -x i.3 3 33x 1 x q i (x) q 3(x q 2（x2x6x 922 2解：运用辗转相除法得:■ 2q 2(x) x 1 x x 1 x 22x x 1x 2I D(x) 1因此(f(x),g(x)) D (X ) 1.且有q 2(x)f(x) [1 qdx)q 2(x)]g(x).u(x) q 2(x) x 1,v(x) 1 q-i (x)q 2(x)1 (x 23)(x 1) x 3 x 2 3x 2.7.设f (x) x 3 (1 t)x 2 2x 2u, g(x) x 3 tx u 的最大公因式是一个二次多项式，求t, u 的值.解：运用带余除法有f(x) x 3(1 t)x 2 2x 2u (x 3 tx u) 1 (1 t)x 2(2 t)x u g(x) r 1(x),Hx)即为f(x),g(x)的最大公因式.因此有1 t 0 .进g(x) n(x)[ x畀11 t (1 t)2解得如果 d(x) | f (x),d(x)| g(x),且 d(x)为 f (x)与 g(x)的一个组合，那么43,2x x 4x4 3 2x x x4x13x 2 4x 13x 2 3x 3 「1(X ) x 2q 1(x )f(x) g(x)q 1(x) r 1(x) , g(x) h(x)q 2(x)D(x), r'x) a(x)q 3(x).于是 a (x) g (x ) r 1(x)q 2(x) g (x ) [f(x) g(x)q 1(x)]q 2(x)由题意可得,D(x),r 2(x)2 2t(1 t) u(1 t) (2 t) x zv(1 t)2u[1 (1 t)2]. 要使r,x)为 f(x),g(x)的最大公因式的充要条件是「2(X )0.即 t(1 t)2 u(1 u[(1 t)2(t t) (2 t)2 2)] 0,0,u 0, u t 4; t0,1 3i 7歼i, 1 v'Tii8证明:2xd(x)是f(x)与g(x)的一个最大公因式证明：由d(x) | f (x),d(x) | g(x)可知d(x)是f (x)与g(x)的一个公因式.下证f(x)与g(x)的任意一个公因式是d(x)的因式•由d(x)为f (x)与g(x)的一个组合可知，存在多项式u(x),v(x)，使得d(x) u(x) f (x) v(x)g(x).设(x)是f (x)与g(x)的任意一个公因式，则(x) | f(x), (x)|g(x).故(x)|u(x)f(x) v(x)g(x)即(x)|d(x).因此d(x)是f (x)与g(x)的一个最大公因式.9.证明：(f (x)h(x), g(x)h(x)) (f (x), g(x))h(x)(h(x)的首项系数为1). 证明：存在多项式u(x),v(x)，使得(f (x),g(x)) u(x)f (x) v(x)g(x).所以有(f (x), g(x))h(x) u(x) f (x)h(x) v(x)g(x)h(x).即(f (x), g(x))h(x)是f(x)h(x)与g(x)h(x)的一个组合.显然有(f (x), g(x))| f(x), (f(x), g(x))|g(x).从而(f (x), g(x))h(x) | f (x)h(x),(f (x), g(x))h(x) | g(x)h(x).由第8 题结果(f (x), g(x))h(x)是f (x)h(x)与g(x)h(x)的一个最大公因式.又h(x)是首项系数为1 的，因此(f (x)h(x),g(x)h(x)) (f(x),g(x))h(x).f(x) g(x))10如果f (x)，g(x)不全为零，证明((f (x),g(x)' (f (x),g(x)证明：由f(x),g(x)不全为零可得其最大公因式不为零多项式，即(f (x), g(x)) 0.又存在多项式u(x), v(x)，使得(f (x),g(x)) u(x)f (x) v(x)g(x).于是1 u(x)空v(x)凹.(f (x), g(x)) (f (x),g(x))因此，型)1.(f (x),g(x) (f (x),g(x)11 如果f(x) , g(x)不全为零，且u(x) f(x) v(x)g(x) (f (x), g(x)),那么(u(x),v(x)) 1 .证明：由f (x), g(x)不全为零可得(f (x), g(x)) 0.由u(x)f(x) v(x)g(x) (f (x),g(x))有u(x) f(x) v(x) g(x) 1.(f(x), g(x)) (f(x),g(x))于是(u(x),v(x)) 1.12. 证明：如果(f (x), g(x)) 1,(f (x),h(x)) 1,那么(f(x), g(x)h(x)) 1.证法一、由条件(f(x),g(x)) 1, (f (x), h(x)) 1 可得存在多项式5(x),v1(x)；U2(x),v2(x)使得U1(x)f(x) v1(x)g(x) 1，U2(x)f(x) v2(x)h(x) 1 .两式相乘得[U1(x)U2(x) f (x) U2(x)w(x)g(x) 5(x)v2(x)h(x)] f (x) w(x)v2(x)g(x)h(x) 1. 因此有(f(x),g(x)h(x))1.证法二、反证法证明.显然(f (x), g(x)h(x)) 0.若(f (x), g(x)h(x)) 1,则存在不可约多项式p(x)，使得p(x)为f (x)与g(x)h(x)的公因式.因此有p(x) | f (x)且p(x) |g(x)h(x).由p(x)的不可约性有p(x) | g(x)或p(x) | h(x).若p(x) | g(x)，则p(x)为f (x)与g(x)的一个公因式，与(f(x), g(x)) 1相矛盾.若p(x) |h(x)，则p(x)为f (x)与h(x)的一个公因式，与(f(x), h(x)) 1相矛盾.因此( f (x),g(x)h(x)) 1不成立，即有( f(x),g(x)h(x)) 1.13. 设f1(x), f2(x), , f m(x),g1(x),g2(x), g n(x) 都是多项式，而且( f i(x),g j(x)) 1,(i 1,2, ,m; j 1,2, ,n).求证：( f1(x) f2(x) f m(x),g1(x)g2(x) g n(x)) 1.证明：由( f1(x),g j(x)) 1( j 1,2, , n) ，反复利用第12题结果可得( f1(x),g1(x)g2(x) g n(x)) 1.类似可得(f i (x), g1(x)g2(x) g n(x)) 1,i 2, ,m.再反复利用12 题结果可得(f1(x) f2(x) f m(x), g1(x)g2(x) g n(x)) 1.14. 证明：如果(f (x),g(x)) 1,那么(f (x)g(x), f(x) g(x)) 1.证明：方法一.由(f(x),g(x)) 1,存在多项式u(x), v(x)使得u(x)f(x) v( x)g(x) 1 .从而有(u1(x) v1(x)) f (x) v1(x)( f(x) g(x)) 1,u1(x)(f (x) g(x)) ( u1(x) v1(x))g(x) 1, 因此有( f (x), f (x) g(x)) 1,(g(x), f (x) g(x)) 1.由12题结果结论成立.方法二：用反证法.若(f (x)g(x), f (x) g(x)) 1.则存在不可约多项式p(x),使得p(x)为f (x)g(x)与f (x) g(x)的公因式.即p(x)| f (x)g(x) 且p(x)| f (x) g(x).由p(x)的不可约性及p(x) | f (x)g (x)，有p(x)| f (x)或p(x) |g(x).若p(x) | f(x)，又p(x)| f (x) g(x)，因此有p(x) |[( f(x) g(x)) f (x)]，即p(x) | g(x)，也即p(x) 为f (x)与g(x)的一个公因式，与(f(x), g(x)) 1相矛盾.类似可得当p(x)| g(x)时也与已知(f (x),g(x)) 1 矛盾.所以(f (x)g(x), f (x) g(x)) 1.15. 求下列多项式的公共根：3 24 3 2f(x) x 2x 2x 1;g(x) x x 2x x 1.解法一：利用因式分解可得3 2 2f(x) x 2x 2x 1 (x 1)( x x 1);4 3 2 2 2g(x) x x 2x x 1 (x 1)( x x 1).因此(f (x), g(x)) x2 x 1. f (x)与g(x)的公共根为1 fi.解法二：运用辗转相除法求出f(x)与g(x)的最大公因式，最大公因式的根即为所求的公共根.2 2g(x) f (x)(x 1) 2(x x 1), f (x) (x x 1)(x 1).因此(f(x),g(x)) X2 x 1.f(x)与g(x)的公共根为寸日16.判别下列多项式有无重因式:1) f (x) x5 5x4 7x3 2x24x 8；解：f'(x) 5x420x321x24x 4,运用辗转相除法可得(f (x), f'(x)) 2 x 4x 4 (x 2)2. 因此x 2为f (x)的三重因式.解法二：试根可得2为f (x) 的根4 3 2(x x x 2) 3(x 2) (x2 x 1).f(x) (x 2)(x 3x x 4) (x 2)2 3 2因此x 2为f (x)的三重因式.2) f (x) x4 4x2 4x 3.解：f' (x) 4x3 8x 4 4(x3 2x 1). (f (x), f '(x)) 1.故f (x)无重因式.17.求t 值使f (x) x3 3x2 tx 1 有重根.解法一：要使f(x)有重根，则(f(x),f'(x)) 1. f'(x) 3x2 6x t.3 2 1 1 ______ t 3_ 八f (x) x 3x tx 1 (— x )3 3f'(x) W(2x D,2f '(x) 3x 6x t (2x 1)(3x2 t匹4t 3t 3 0,即t 3时3f'(x) 3x 2 6x 3 3(x 1)2, f'(x)| f(x), (f (x), f'(x)) (x 1)2,因此1为f (x)的三重根.当t 解法1T 0，即 t15広时，(f(x),f '(x))1x2，b)x 2 (a1—为f (x)的二重根.22 22ab)x a b .二：设 f(x)(x a)2(x b)3x (2a因此有2a b 3,2a 2ab t,a 2b 1.由第一个方程有b 6 2a，代人第三个方程有a 2(3 2a) 1,2a 3 3a 2 10,即(a 1)2(2a 1)0.因此有1a 1,a-， b 1,或 b 4, t 3, t ㊇. 4151即当t 3时1为f (x)的三重根；当t 一时，—为f (x)的二重根.4 2(23p x q)(29_x 峯)(p 3 2p 4p要使f(x)有重根，则(f (x), f'(x)) 1.即p 竺 0,即4p 3 27q 20.显然4pp q 0也满足4p 3 27q 2 0.因此f (x)有重根的条件是4p 3 27q 2 0.19.如果(x 1)2| Ax 4 Bx 2 1,求 A,B.解法一：利用整除判定方法，(x 1)2|A X 4 Bx 2 1的充要条件是用(x 1)2除18.求多项式x 3 px q 有重根的条件解：令f(x) xpx q .显然当p q0时, 0为f (x)的三重根.当 p 0时,f'(x)3x 2f(x)x 3f'(x) 人2 '■4pAx 4 Bx 2 1，余式为零. Ax 4 Bx 2 1 (x 1)2(Ax 22 Ax B 3A)(2B 4A)x (1 3A B)因此有(2B4A)x(1 3AB) 0 ，即卩2B 4A 0,A 1,1 3A B 0. B 2.解法二：要使(x 1)2 |Ax 4 Bx 2 1成立，则 1至少是Ax 4 Bx 2 1 的二 •重根. 因此1既是Ax 4 Bx 2 1的根，也是其导数的根 .而(Ax 4 Bx 231)' 4 Ax2Bx .故有1 A B 0, A 1,4A 2B 0. B2.解法三：利用待定系数法•令42224Ax 4Bx 21 (x 1)2(Ax 2Cx D) Ax 4(C2A)x 3 (A 2C D)x 2 (C 2D)x D因此有n 1X(n 1)!'nn., xxX ・，一因此有 f(x) f'(x) ,从而有(f(x),f'(x)) (f'(x),). 因式只有 C (c 0)n!n! n!及cx k (c 0,1 kn) .而 cx k (c 0,1 k n)显然不是f'(x)的因式.因此有nx(f(x), f'(x)) (f'(x),—)1.n!所以f(x)没有重根.C 2A 0,A 1, A 2C D B, ” eB 2,解得C 2D 0, C 2, D 1.D 1.2 n20.证明：1 x — —不能有重根.证明：令 f(x)x2!+,则n!f'(x)2x2! 2!n!n21.如果a是f'''(x)的一个k重根，证明a是x a g(x) —[f'(x) f'(a)] f(x) f(a)的一个k 3重根.证明：1 x a x a 1g'(x) 2【f'(x) f'(a)] 〒f''(x) f'(x) 〒f''(x) 2【f'(x) f'(a)],1 x a i x ag''(x) -f''(x) 〒f“'(x) 2f''(x) 〒f'''(x).显然有g(a) g'(a) g"(a) 0.由a是f '''(x)的一个k重根可得a是g''(x)的一个k 1重根，设a是g(x)的s重根，贝U s 2 k 1,s k 3.本题常见错误证法.错误证法一：由a是f'''(x)的一个k重根就得出a是f''(x)的一个k 1重根，a是f'(x)的一个k 2重根，a是f (x)的一个k 3重根，于是x ag(x) [f'(x)2( )k 3 f'(a)] f(x) f(a) (X a) h(x)2从而a是g(x)的k 3重根.事实上，由a是f'''(x)的一个k重根推不出a是f''(x)的一个k 1重根，a是f'(x)的一个k 2重根，a是f (x)的一个k 3重根.如 f (x) (x a)k 3 (x a)2 (x a) 3，则f '(x) (k 3)(x a)k 2 2(x a) 1，f''(x) (k 3)(k 2)( x a)k 32.a 既不是f (x)的根，也不是f'(x)与f''(x)的根.错误证法二：由1 x a x a 1g'(x) 2【f'(x) f'(a)] f''(x) f'(x) f''(x) ?[f'(x) f'(a)],f'(x)的k 1重因式，是f''(x)的k 2重因式，…，是f(k1)(x)的单因式，而不是f(k)(x)的因式•因3 x a 1 x ag''(x) -f''(x) —f'''(x) ?f“(x) — f'''(x)得出a是g''(x)的k 1重根，直接得出a是g(x)的k 3重根，缺了a是g(x)与g'(x)的根验证.22证明：X。

(完整word版)高等代数多项式习题解答

高等代数__课后答案__高等教育出版社

高等代数二练习题答案

高等代数习题答案

高等代数-第4章习题及解答

高等代数多项式习题解答(供参考)

【最新试题库含答案】高等代数习题及答案(1)

高等代数习题 北大第四版 答案一到四章

(完整版)高等代数多项式习题解答

高等代数第一章答案(多项式)

高等代数作业第一章多项式答案

高等代数 习题及参考答案

(完整版)高等代数多项式

高等代数习题(北大第四版)答案一到四章.docx

线性代数(含全部课后题详细答案)1第一章一元多项式习题及解答.docx

高等代数北大编第1章习题参考答案

高等代数__课后答案__高等教育出版社

完整版高等代数习题解答(第一章)

(完整word版)高等代数多项式习题解答

高等代数课后答案高等教育出版社

高等代数习题北大第四版答案一到四章

高等代数习题及参考答案

高等代数课后答案高等教育出版社