电磁感应定律单杆模型共24页文档
高考物理复习 电磁感应杆模型

5.最大速度vm 电容器充电量: Q0 CE
放电结束时电量: Q CU CBlvm
电容器放电电量: Q Q0 Q CE CBlvm
对杆应用动量定理:mvm BIl t BlQ
vm
m
BlCE B2l2C
题型五 电容放电式:
6.达最大速度过程中 的两个关系
v1=0时:电流最大,
Im
Blv0 R1 R2
v2=v1时:电流 I=0
3.两棒的运动情况
安培力大小:
两棒的相对速度变小,感应电 流变小,安培力变小.棒1做加 速度变小的加速运动,棒2做
加速度变小的减速运动,最 终两棒具有共同速度。
随着棒2的减速、棒1的加速,两棒 的相对速度v2-v1变小,回路中电流 也变小。
4.变化
(1)两棒都受外力作用
(2)外力提供方式变化
题型五 电容放电式:
4.最终特征:匀速运 动,但此时电容器带 电量不为零
1.电路特点 电容器放电,相当于电源;导体棒受安 培力而运动。
2.电流的特点 电容器放电时,导体棒在安培力作用下
开始运动,同时产生阻碍放电的反电动
势,导致电流减小,直至电流为零,此 时UC=Blv 3.运动特点 a渐小的加速运动,最终做匀速运动。
1.电路特点:导体棒相当于电源。
6、三个规律
2.安培力的特点:安培力为阻力, 并随速度减小而减小。
(1)能量关系:
1 2
mv02
0
Q,
QR Qr
F BIL B2l2v Rr
(2)动量关系:BIl t 0 mv0 q n Bl s
R r
高考物理双基突破二专题电磁感应中的单杆模型精讲.doc

专题32 电磁感应中的“单杆”模型单杆模型是电磁感应中常见的物理模型,此类题目所给的物理情景一般是导体棒垂直切割磁感线,在安培力、重力、拉力作用下的变加速直线运动或匀速直线运动,所涉及的知识有牛顿运动定律、功能关系、能量守恒定律等。
1.此类题目的分析要抓住三点:(1)杆的稳定状态一般是匀速运动(达到最大速度或最小速度,此时合力为零)。
(2)整个电路产生的电能等于克服安培力所做的功。
(3)电磁感应现象遵从能量守恒定律。
如图甲,导体棒ab 从磁场上方h 处自由释放,当进入磁场后,其速度随时间的可能变化情况有三种,如图乙,全过程其能量转化情况是重力势能转化为动能和电能,电能再进一步转化为导体棒和电阻R 的内能。
2.单杆模型中常见的情况及处理方法: (1)单杆水平式开始时a =Fm ,杆ab 速度v ⇒感应电动势E =开始时a =Fm ,杆ab 速度v ⇒感应电动势E =BLv ,经过Δt 速度为v +Δv ,此时感应=Blv R,安培力F =BIL=B2L2v R ,做减速运动:v ⇒F ⇒a,当v =0时,F =0,a =0,杆保持静止此时a =BLEmr,杆ab 速度v ⇒感应电动势BLv ⇒I ⇒安培力F =BIL ⇒加速度a ,当E感=E 时,v 最大,且v m =E BLBLv ⇒I ⇒安培力F 安=BIL ,由F -F 安=ma 知a ,当a =0时,v 最大,v m =FRB2L2【题1】如图所示,间距为L ,电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R 的电阻连接,导轨上横跨一根质量为m ,电阻也为R 的金属棒,金属棒与导轨接触良好。
整个装置处于竖直向上、磁感应强度为B 的匀强磁场中.现使金属棒以初速度v 0沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q 。
下列说法正确的是A .金属棒在导轨上做匀减速运动B .整个过程中电阻R 上产生的焦耳热为mv202C .整个过程中金属棒在导轨上发生的位移为qRBLD .整个过程中金属棒克服安培力做功为mv202【答案】D【题2】如图所示,足够长的平行金属导轨内有垂直纸面向里的匀强磁场,金属杆ab 与导轨垂直且接触良好,导轨右端与电路连接.已知导轨相距为L ,磁场的磁感应强度为B ,R 1、R 2和ab 杆的电阻值均为r ,其余电阻不计,板间距为d 、板长为4d ,重力加速度为g ,不计空气阻力.如果ab 杆以某一速度向左匀速运动时,沿两板中心线水平射入质量为m 、带电荷量为+q 的微粒恰能沿两板中心线射出,如果ab 杆以同样大小的速度向右匀速运动时,该微粒将射到B 板距其左端为d 的C 处。
完整版电磁感应定律单杆导轨模型含思路分析

单杆+导轨”模型1.单杆水平式(导轨光滑)注:加速度a的推导,a=F合/m (牛顿第二定律),F合=F-F安,F安=BIL ,匸E/R 整合一下即可得到答案。
v变大之后,根据上面得到的a的表达式,就能推出a变小这里要注意,虽然加速度变小,但是只要和v同向,就是加速运动,是a减小的加速运动(也就是速度增加的越来越慢,比如1s末速度是1, 2s末是5, 3s末是6, 4s末是6.1,每秒钟速度的增加量都是在变小的)2.单杆倾斜式(导轨光滑)BLv T【典例1】如图所示,足够长的金属导轨固定在水平面上,金属导轨宽度L二1.0 m,导轨上放有垂直导轨的金属杆P,金属杆质量为m= 0.1 kg,空间存在磁感应强度B= 0.5 T、竖直向下的匀强磁场。
连接在导轨左端的电阻R= 3.0約金属杆的电阻r 二1.0約其余部分电阻不计。
某时刻给金属杆一个水平向右的恒力F, 金属杆P由静止开始运动,图乙是金属杆P运动过程的v—t图象,导轨与金属杆间的动摩擦因数尸0.5。
在金属杆P运动的过程中,第一个2 s内通过金属杆P的电荷量与第二个2 s内通过P的电荷量之比为3 : 5。
g取10 m/s2。
求:(1)水平恒力F的大小;⑵前4 s内电阻R上产生的热量。
【答案】(1)0.75 N (2)1.8 J【解析】(1)由图乙可知金属杆P先做加速度减小的加速运动,2 s后做匀速直线运动当t= 2 s时,v= 4 m/s,此时感应电动势E= BLv感应电流1=吕R+ rB2I2v安培力F = BIL =R+ r根据牛顿运动定律有F —F '―卩m= 0解得 F = 0.75 N o过金JI杆p的电荷量厂"二磊^甘十);△型BLx所以尸驚qa为尸的位移)设第一个2 s內金属杆P的位移为Xi ;第二个肚内P的位移为助则二号g,又由于如:血=3 : 5麻立解得«=8mj IL=<8m前4 s内由能量守恒定律得其中 Q r : Q R = r : R = 1 : 3解得 Q R = 1.8 J o注:第二问的思路分析,要求 R 上产生的热量,就是焦耳热,首先想到的是公式Q=l2Rt ,但是在这里,前2s 的运动过程中,I 是变化的,而且也没办法求出I 的有效值来(电荷量对应的是电流的平均值,求焦耳热要用有效值,两者不一样), 所以这个思路行不通。
电磁感应中的“杆+导轨”模型

电磁感应中的“杆+导轨”模型电磁感应中的“杆+导轨”模型一、单棒模型阻尼式:在单棒模型中,导体棒相当于电源,根据洛伦兹力的公式,可以得到安培力的特点为阻力,并随速度减小而减小,加速度随速度减小而减小,最终状态为静止。
根据能量关系、动量关系和瞬时加速度,可以得到公式B2l2v R rF和q mv/Bl,其中q表示流过导体棒的电荷量。
需要注意的是,当有摩擦或者磁场方向不沿竖直方向时,模型的变化会受到影响。
举例来说,如果在电阻不计的光滑平行金属导轨固定在水平面上,间距为L、导轨左端连接一阻值为R的电阻,整个导轨平面处于竖直向下的磁感应强度大小为B的匀强磁场中,一质量为m的导体棒垂直于导轨放置,a、b之间的导体棒阻值为2R,零时刻沿导轨方向给导体棒一个初速度v,一段时间后导体棒静止,则零时刻导体棒的加速度为0,零时刻导体棒ab两端的电压为BLv,全过程中流过电阻R的电荷量为mv/Bl,全过程中导体棒上产生的焦耳热为0.二、发电式在发电式中,导体棒同样相当于电源,当速度为v时,电动势E=Blv。
根据安培力的特点,可以得到公式22Blv/l=Blv/(R+r)。
加速度随速度增大而减小,最终特征为匀速运动。
在稳定后的能量转化规律中,F-BIl-μmg=m*a,根据公式可以得到a=-(F-μmg)/m、v=0时,有最大加速度,a=0时,有最大速度。
需要注意的是,当电路中产生的焦耳热为mgh时,电阻R中产生的焦耳热也为mgh。
1.如图所示,相距为L的两条足够长的光滑平行金属导轨MN、PQ与水平面的夹角为θ,N、Q两点间接有阻值为R的电阻。
整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下。
将质量为m、阻值也为R的金属杆cd垂直放在导轨上,杆cd由静止释放,下滑距离x时达到最大速度。
重力加速度为g,导轨电阻不计,杆与导轨接触良好。
求:1)杆cd下滑的最大加速度和最大速度;2)上述过程中,杆上产生的热量。
电磁感应的单棒模型

电磁感应的单棒模型例.如图:水平面上有两根相距为L=0.5m的足够长的平行光滑金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R=3.0Ω的定值电阻,导体棒ab的电阻为r=1.0Ω质量m=0.5kg,与导轨接触良好.整个装置处于方向竖直向下的匀强磁场中,磁感应器强度B=2T,问:(1)若导体棒在水平拉力作用下以8m/s的速度向右匀速直线运动,求该水平拉力多大?(2)第(1)题中若某时刻,该水平拉力突然变成3N,导体棒接下去将做什么运动?求出该导体棒的最终速度?当该导体棒速度达到最大速度10m/s时,求此时导体棒的加速度。
(3)写出导体棒最终速度v m与所加水平外力F的关系式,画出v m-F拉图像(4)若要该导体棒由静止开始做a=2m/s2的匀加速直线运动,写出所需水平拉力F拉与时间的关系式练习1:如图,两根相距L=0.4m、电阻不计的平行光滑金属导轨水平放置,一端与阻值R=0.15Ω的电阻相连。
导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T。
一根质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上,并与导轨垂直。
棒在外力作用下从x=0处以初速度v0=2m/s沿导轨向右运动,运动过程中电阻上消耗的功率不变。
求:(1)电路中的电流;(2)金属棒在x=2m处的速度;(3)金属棒从x=0运动到x=2m过程中安培力做功的大小;(4)金属棒从x=0运动到x=2m过程中外力的平均功率。
练习2:如图所示,光滑竖直导轨顶端连接着一个电阻R=4Ω,导体棒质量m=0.8kg,电阻r=1Ω,磁感应强度B=4T,磁场、导体棒与轨道平面两两垂直,现导体棒由静止开始竖直下落,下落过程与导轨保持良好接触,导轨足够长且导轨间距L=0.5m,重力加速度取g=10m/s2,问:(1)该导体棒最终速度v m(2)当v=5m/s的时候的加速度。
完整版电磁感应中的单双杆模型

电磁感应中的单双杆问题-、单杆问题(一) 与动力学相结合的问题1、水平放置的光滑金属轨道上静止一根质量为m的金属棒MN,电阻为R,左端连接-电动势为E,内阻为r的电源,其他部分及连接处电阻不计,试求:金属棒在轨道上的最大速度?2、水平放置的光滑金属轨道上静止一根质量为m的金属棒MN ,电阻为R,左端连接一电阻为R,MN在恒力F的作用下从静止开始运动,其他部分及连接处电阻不计,试求:金属棒在轨道上的最大速度?3、金属导轨左端接电容器,电容为 整个装置处于垂直纸面磁感应强度为 速度v ,试求金属棒的最大速度?C ,轨道上静止一长度为 L 的金属棒cd , B 的匀强磁场当中,现在给金属棒一初_P< X X ~p< X X1 (k 乂(二)与能量相结合的题型 1、倾斜轨道与水平面夹角为,整个装置处于与轨道相垂直的匀强磁场当中,导轨顶端连有一电阻R ,金属杆的电阻也为 R 其他电阻可忽略,让金属杆由静止释放,经过一段时 求: 间后达到最大速度V m ,且在此过程中电阻上生成的热量为 (1 )金属杆达到最大速度时安培力的大小(2)磁感应强度B 为多少(3 )求从静止开始到达到最大速度杆下落的高度2. ( 20 分)如图所示,竖直平面内有一半径为r 、内阻为R i 、粗细均匀的光滑半圆形金属环,在 M 、N 处与相距为2r 、电阻不计的平行光滑 金属轨道ME 、NF 相接,EF 之间接有电阻 R 2,已知R i = 12R , R 2MNATCDB[xR■ ■ ■ ■ *=4R 。
在MN 上方及CD 下方有水平方向的匀强磁场 I 和II ,磁感应强度大小均为 B 。
现有质量为m 、电阻不计的导体棒 ab ,从半圆环的最高点 A 处由静止下落,在下落过程中导体 棒始终保持水平,与半圆形金属环及轨道接触良好,两平行轨道中够长。
已知导体棒 ab 下落r/2时的速度大小为 W ,下落到MN 处的速度大小为 V 2。
(完整版)高分策略之电磁感应中的杆+导轨模型

电磁感应现象中的杆4导轨模型一、单棒问题、含容式单棒问题三、无外力双棒问题竇力愣况分析动力学观点 *动量现点 运动情况伽能冒观点 牛輛定律 平衡羞件动能定理〕 幡■守恒无外力等距式1¥杆1做a渐小的加速运动杆2做a渐小的减速运动V1=V2I = 0无外力不等距式» 1杆1做a渐小的减速运动杆2做a渐小的加速运动a= 0I = 0L1V1 = L2V2四、有外力双棒问题题型一阻尼式单棒模型如图。
1 •电路特点:导体棒相当于电源。
4.运动特点:速度如图所示。
a减小的减速运动基本模型运动特点有外力等距式i厂F12杆1做a渐大的加速运动杆2做a渐小的加速运动有外力不等距式杆1做a渐小的加速运动杆2做a渐大的加速运动最终特征a i=a2, A v 恒定I恒定a i M a2, a i、a2恒定I恒定2•安培力的特点:安培力为阻力,并随速度减小而减小。
F B=BII= B+r3.加速度特点:加速度随速度减小而减小,a==5 •最终状态:静止 6.三个规律(1)能量关系:「'• ■ , -0 = Q ,=【典例1】如图所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为 L 的区域内,那么(【答案】B由上述二式可得' ,- •,即B 选项正确。
【典例2】如图所示,AB 杆受一冲量作用后以初速度 V 0=4m/s 沿水平面内的固定轨道运动,经一段时间后而停止. AB 的质量为m=5g 导轨宽为L=0.4m ,电阻为R=2Q ,其余的电阻不计,磁 感强度B=0.5T ,棒和导轨间的动摩擦因数为卩=0.4 ,测得杆从运动到停止的过程中通过导线的(2)动量关系:BII t 0 mv 0(3)瞬时加速度: a ==-有一个边长为a ( a<L )的正方形闭合线圈以初速V 0垂直磁场边界滑过磁场后速度变为V ( V<V 0)A. 完全进入磁场中时线圈的速度大于( v o +v ) /2B. 安全进入磁场中时线圈的速度等于( V o +V ) /2C. 完全进入磁场中时线圈的速度小于(V o +V ) /2D. 以上情况A B 均有可能,而C 是不可能的【解析】设线圈完全进入磁场中时的速度为对于线圈进入磁场的过程,据动量定理可得:对于线圈穿出磁场的过程,据动量定理可得:V x 。
专题32+电磁感应中的“单杆”模型(精讲)-高考物理双基突破(二)+Word版含解析.doc

单杆模型是电磁感应中常见的物理模型,此类题目所给的物理情景一般是导体棒垂直切割磁感线,在安培力、重力、拉力作用下的变加速直线运动或匀速直线运动,所涉及的知识有牛顿运动定律、功能关系、能量守恒定律等。
1.此类题目的分析要抓住三点:(1)杆的稳定状态一般是匀速运动(达到最大速度或最小速度,此时合力为零)。
(2)整个电路产生的电能等于克服安培力所做的功。
(3)电磁感应现象遵从能量守恒定律。
如图甲,导体棒ab 从磁场上方h 处自由释放,当进入磁场后,其速度随时间的可能变化情况有三种,如图乙,全过程其能量转化情况是重力势能转化为动能和电能,电能再进一步转化为导体棒和电阻R 的内能。
2.单杆模型中常见的情况及处理方法: (1)单杆水平式开始时a =Fm ,杆ab 速度v ⇒感开始时a =Fm ,杆ab 速度v ⇒感应电动势E =BLv ,经过Δt势E =BLv ,电流I =ER =Blv R ,安培力F =BIL =B 2L 2vR,做减速运动:v ⇒F ⇒a ,当v =0时,F =0,a =0,杆保持静止此时a =BLEmr ,杆ab 速度v ⇒感应电动势BLv ⇒I ⇒安培力F =BIL ⇒加速度a ,当E感=E 时,v 最大,且v m =E BL应电动势E =BLv ⇒I ⇒安培力F 安=BIL ,由F -F安=ma 知a ,当a =0时,v 最大,v m =FRB 2L 2【题1】如图所示,间距为L ,电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R 的电阻连接,导轨上横跨一根质量为m ,电阻也为R 的金属棒,金属棒与导轨接触良好。
整个装置处于竖直向上、磁感应强度为B 的匀强磁场中.现使金属棒以初速度v 0沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q 。
下列说法正确的是A .金属棒在导轨上做匀减速运动B .整个过程中电阻R 上产生的焦耳热为mv 202C .整个过程中金属棒在导轨上发生的位移为qRBLD .整个过程中金属棒克服安培力做功为mv 202【答案】D【题2】如图所示,足够长的平行金属导轨内有垂直纸面向里的匀强磁场,金属杆ab 与导轨垂直且接触良好,导轨右端与电路连接.已知导轨相距为L ,磁场的磁感应强度为B ,R 1、R 2和ab 杆的电阻值均为r ,其余电阻不计,板间距为d 、板长为4d ,重力加速度为g ,不计空气阻力.如果ab 杆以某一速度向左匀速运动时,沿两板中心线水平射入质量为m 、带电荷量为+q 的微粒恰能沿两板中心线射出,如果ab 杆以同样大小的速度向右匀速运动时,该微粒将射到B 板距其左端为d 的C 处。
电磁场中的单杆模型

R
v0 B
d
O
x
解 : (1)金属杆在导轨上先是向右做加速度为a 的匀减速直 线运动,到导轨右方最远处速度为零,后又沿导轨向左做 加速度为a 的匀加速直线运动.当过了y 轴后,由于已离 开了磁场区,故回路不再有感应电流.
以t1表示金属杆做匀减速运动的时间,有 t1 = v0 / a .
从而,回路中感应电流持续的时间 T=2t1=2v0/ a .
➢ [06上海物理卷.12] 如图所示,平行金属导轨与水平
面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂 直穿过导轨平面.有一导
体棒ab,质量为m,导体
棒的电阻与固定电阻R1和 R2的阻值均相等,与导轨
B
a
R1
θ
之间的动摩擦因数为μ,
R2
导体棒ab沿导轨向上滑动,
b θ
当上滑的速度为v时,受到安培力的大小为F.此时
解后小结
➢→与“导体单棒”组成的闭合回路 中 的磁通量发生变化
➢→导体棒产生感应电动势 ➢→感应电流 ➢→导体棒受安培力 ➢→合外力 ➢→加速度
三、单杆在磁场中变速运动
倾 角 为 30° 的 斜 面 上 , 有 一 导 体 框 架 , 宽 为
1m,不计电阻,垂直斜面的匀强磁场磁感应
强 度 为 0.2T , 置 于 框 架 上 的 金 属 杆 ab , 质 量
向左运动时F-f=ma
F=ma+f=0.22(牛) 方向与x轴相反 ④
(3)开始时 v=v0, f=ImB l=B2l 2v0/R
F+f=ma, F=ma-f=ma-B2l 2v0/R
∴ 当v0<maR/B2l 2=10米/秒 时,
F>0 方向与x轴相反 ⑥
am
高考回归复习—电磁感应之含动量定理的单杆综合题模型(word 含答案)

高考回归复习—电磁感应之含动量定理的单杆综合题模型1.如图所示,两光滑平行金属导轨置于水平面内,两导轨间距为L,左端连有阻值为R的电阻,一金属杆置于导轨上,金属杆右侧存在一磁感应强度大小为B、方向竖直向下的有界匀强磁场区域。
已知金属杆质量为m,电阻也为R,以速度0v向右进入磁场区域,做减速运动,到达磁场区域右边界时速度恰好为零。
金属杆与导轨始终保持垂直且接触良好,导轨电阻忽略不计。
求:(1)金属杆运动全过程中,在电阻R上产生的热量RQ(2)金属杆运动全过程中,通过电阻R的电荷量q(3)磁场左右边界间的距离d2.如图所示,质量为m的跨接杆ab可以无摩擦地沿水平的导轨滑行,两轨间宽为L,导轨与电阻R连接,放在竖直向下的匀强磁场中,磁感强度为B。
杆从x轴原点O以大小为v0的水平初速度向右滑行,直到静止。
已知杆在整个运动过程中速度v和位移x的函数关系是:220xv v B LmR=-。
(杆及导轨的电阻均不计。
)(1)试求杆所受的安培力F随其位移x变化的函数式;(2)若杆在运动过程中水平方向只受安培力作用,请求出杆开始运动到停止运动过程中通过R的电量q;(3)若杆在运动过程中水平方向只受安培力作用,请求出杆开始运动到停止运动过程中R产生的热量Q。
3.如图所示,两光滑金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=0.1T、方向竖直向下的有界磁场中,电阻R=3Ω,桌面高H=0.8m,金属杆ab的质量m=0.2kg,电阻r=1Ω,在导轨上距桌面h=0.2m的高处由静止释放,落地点距桌面左边缘的水平距离s=0.4m,g=10m/s2. 求:(1)金属杆进入磁场时,R上的电流大小;(2)整个过程中R上产生的热量.(3)整个过程中通过R的电荷量.4.如图所示,光滑的金属导轨固定在绝缘水平面上,导轨足够长,电阻不计,两轨间距为L,其左端连接一阻值为R的电阻.导轨处在竖直向下的匀强磁场中,磁感应强度大小为B,一质量为m的金属棒,放置在导轨上,其电阻为r,某时刻一水平力F垂直作用在金属棒中点,金属棒从静止开始做匀加速直线运动,已知加速度大小为a,金属棒始终与导轨接触良好.(1)从力F作用开始计时,请推导F与时间t关系式;(2)F作用时间0t后撤去,求金属棒能继续滑行的距离S.5.如图所示,在方向竖直向上、磁感应强度大小为B的匀强磁场中,有两条相互平行且相距为d的光滑固定金属导轨P1P2P3和Q1Q2Q3,两导轨间用阻值为R的电阻连接,导轨P1P2、Q1Q2的倾角均为θ,导轨P2P3、Q2Q3在同一水平面上,P2Q2⊥P2 P3,倾斜导轨和水平导轨用相切的小段光滑圆弧连接.质量为m的金属杆CD从与P2Q2处时的速度恰好达到最大,然后沿水平导轨滑动一段距离后停下.杆CD始终垂直导轨并与导轨保持良好接触,空气阻力、导轨和杆CD的电阻均不计,重力加速度大小为g,求:(1)杆CD到达P2Q2处的速度大小v m;(2)杆CD沿倾斜导轨下滑的过程通过电阻R的电荷量q1以及全过程中电阻R上产生的焦耳热Q;(3)杆CD沿倾斜导轨下滑的时间Δt1及其停止处到P2Q2的距离s.6.水平桌面上固定着两相距为L的平行金属导轨,导轨右端接电阻R,在导间存在宽度均为d的有界匀强磁场区域I和Ⅱ,磁感应强度为B,方向竖直向下。
高中物理模型讲解:电磁场中的单杆模型

高中物理模型讲解:电磁场中的单杆模型在电磁场中,“导体棒”主要是以“棒生电”或“电动棒”的内容出现,从组合情况看有棒与电阻、棒与电容、棒与电感、棒与弹簧等;从导体棒所在的导轨有“平面导轨”、“斜面导轨”“竖直导轨”等。
一、单杆在磁场中匀速运动例1、如图1所示,,电压表与电流表的量程分别为0~10V和0~3A,电表均为理想电表。
导体棒ab与导轨电阻均不计,且导轨光滑,导轨平面水平,ab棒处于匀强磁场中。
图1(1)当变阻器R接入电路的阻值调到30,且用=40N的水平拉力向右拉ab棒并使之达到稳定速度时,两表中恰好有一表满偏,而另一表又能安全使用,则此时ab棒的速度是多少?(2)当变阻器R接入电路的阻值调到,且仍使ab棒的速度达到稳定时,两表中恰有一表满偏,而另一表能安全使用,则此时作用于ab棒的水平向右的拉力F2是多大?解析:(1)假设电流表指针满偏,即I=3A,那么此时电压表的示数为U==15V,电压表示数超过了量程,不能正常使用,不合题意。
因此,应该是电压表正好达到满偏。
当电压表满偏时,即U1=10V,此时电流表示数为设a、b棒稳定时的速度为,产生的感应电动势为E1,则E1=BLv1,且E1=I1(R1+R并)=20Va、b棒受到的安培力为F1=BIL=40N解得(2)利用假设法可以判断,此时电流表恰好满偏,即I2=3A,此时电压表的示数为=6V可以安全使用,符合题意。
由F=BIL可知,稳定时棒受到的拉力与棒中的电流成正比,所以。
二、单杠在磁场中匀变速运动例2、如图2甲所示,一个足够长的“U”形金属导轨NMPQ固定在水平面内,MN、PQ两导轨间的宽为L=0.50m。
一根质量为m =0.50kg的均匀金属导体棒ab静止在导轨上且接触良好,abMP恰好围成一个正方形。
该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中。
ab棒的电阻为R=0.10Ω,其他各部分电阻均不计。
开始时,磁感应强度。
图2(1)若保持磁感应强度的大小不变,从t=0时刻开始,给ab 棒施加一个水平向右的拉力,使它做匀加速直线运动。
高中物理┃模型讲解:电磁场中的单杆模型.doc

高中物理┃模型讲解:电磁场中的单杆模型在电磁场中,“导体棒”主要是以“棒生电”或“电动棒”的内容出现,从组合情况看有棒与电阻、棒与电容、棒与电感、棒与弹簧等;从导体棒所在的导轨有“平面导轨”、“斜面导轨”“竖直导轨”等。
一、单杆在磁场中匀速运动例1、如图1所示,,电压表与电流表的量程分别为0~10V和0~3A,电表均为理想电表。
导体棒ab与导轨电阻均不计,且导轨光滑,导轨平面水平,ab棒处于匀强磁场中。
图1(1)当变阻器R接入电路的阻值调到30,且用=40N的水平拉力向右拉ab棒并使之达到稳定速度时,两表中恰好有一表满偏,而另一表又能安全使用,则此时ab棒的速度是多少?(2)当变阻器R接入电路的阻值调到,且仍使ab棒的速度达到稳定时,两表中恰有一表满偏,而另一表能安全使用,则此时作用于ab棒的水平向右的拉力F2是多大?解析:(1)假设电流表指针满偏,即I=3A,那么此时电压表的示数为U==15V,电压表示数超过了量程,不能正常使用,不合题意。
因此,应该是电压表正好达到满偏。
当电压表满偏时,即U1=10V,此时电流表示数为设a、b棒稳定时的速度为,产生的感应电动势为E1,则E1=BLv1,且E1=I1(R1+R并)=20Va、b棒受到的安培力为F1=BIL=40N解得(2)利用假设法可以判断,此时电流表恰好满偏,即I2=3A,此时电压表的示数为=6V可以安全使用,符合题意。
由F=BIL可知,稳定时棒受到的拉力与棒中的电流成正比,所以。
二、单杠在磁场中匀变速运动例2、如图2甲所示,一个足够长的“U”形金属导轨NMPQ 固定在水平面内,MN、PQ两导轨间的宽为L=0.50m。
一根质量为m=0.50kg的均匀金属导体棒ab静止在导轨上且接触良好,abMP恰好围成一个正方形。
该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中。
ab棒的电阻为R=0.10Ω,其他各部分电阻均不计。
开始时,磁感应强度。
电磁感应专题-单杆模型
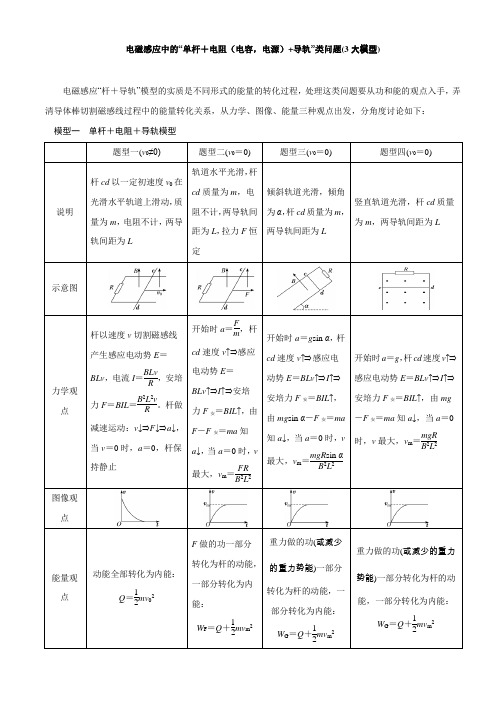
电磁感应中的“单杆+电阻(电容,电源)+导轨”类问题(3大模型)电磁感应“杆+导轨”模型的实质是不同形式的能量的转化过程,处理这类问题要从功和能的观点入手,弄清导体棒切割磁感线过程中的能量转化关系,从力学、图像、能量三种观点出发,分角度讨论如下:模型一单杆+电阻+导轨模型× × × × × × × × ×× × × ×× × × × ×× ×v θ cdabM Nl1、[母题] (2020·淮安模拟)如图所示,相距为L 的两条足够长的光滑平行金属导轨MN 、PQ 与水平面的夹角为θ,N 、Q 两点间接有阻值为R 的电阻。
整个装置处于磁感应强度为B 的匀强磁场中,磁场方向垂直导轨平面向下。
将质量为m 、阻值也为R 的金属杆cd 垂直放在导轨上,杆cd 由静止释放,下滑距离x 时达到最大速度。
重力加速度为g ,导轨电阻不计,杆与导轨接触良好。
求: (1) 杆cd 下滑的最大加速度和最大速度; (2)、速度为v (小于最大速度)时的加速度 (3)上述过程中,杆上产生的热量。
(4)[变式] 若已知金属杆与导轨之间的动摩擦因数为μ。
现用沿导轨平面向上的恒定外力F 作用在金属杆cd 上,使cd 由静止开始沿导轨向上运动,求cd 的最大加速度和最大速度。
2、如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l =0.5 m ,左端接有阻值R =0.3 Ω的电阻。
一质量m =0.1 kg 、电阻r =0.1 Ω的金属棒MN 放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B =0.4 T 。
棒在水平向右的外力作用下由静止开始以a =2 m/s 2的加速度做匀加速运动,当棒的位移x =9 m 时撤去外力,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q 1∶Q 2=2∶1。
