平抛运动斜面距离问题的解法赏析
与斜面有关的平抛运动例析

.
落 地 时 间
g
, 落 地 点 到 斜坡 顶 端 的 距 离
( 2 )因小球距离斜坡最远 ( B点 ) 速度方向角
t a n 8 : : 羔 生
告
V
破解关键:密切 关注两个过程 的连接 点,抓住平抛的突破 口一
一
・ .
.
小球达到距离斜坡最远所 需时间
霉
筹
V0
对 于第二问,需要弄清 楚什么时候小球离斜面最远 ?小眯的速
度方 向与斜面平行时,那当然 马上 分解速度 ,建立速度三角形利用
移三角形,另一种是分速度 ,建立速度三角 形,结合运动学公式求 解 。当然在 处理平抛运动时还必须利用分运动的独立性和等时性 。 而与斜面关联 的平抛运动又是高中物理常考的题型和重点的题型。
而
= 腼
2 7 5都市家教
r o t l
斜面顶端与平台的高度差 h = O . 8 m,重力加速度 g = l O e r / s 2,s i n 5 3 。
t = — — — — = — — — — — 一
・
.
2v .ta
:0 . 8 ,c o s 5 3 。 : 0 . 6 ,求①小球水平抛 出的 初速度 v O 是多少?② 斜面顶端与平 台边缘 的水平距离 S 是多少 ?⑨若斜面顶端高 H= 2 O . 8 m ,则小球离 开平台后经多长时间 t 到达斜面底端?
求:①小球需经过多长 时间落至 蝌 坡上?落地点到斜坡项端 的距离 是多大 ? ②小球被抛 出多久距离斜坡最远 ?
破解关键:这种题型,对于第一问,—定要抓住突破 口:小球
… s
= 厨
水平方向上的速度为 0 ,所 以小球在 B点的速度为:
数理结合,五种方法求解斜面上抛体最远距离

数理结合,五种方法求解斜面上抛体最远距离题:从倾角为θ的斜面上O 点,以初速度V 0 水平抛出一个小球,落至斜面B 点。
求:从抛出开始经多长时间小球离斜面的距离最大?最大距离是多大?解法一:设小球抛出t 秒后,当速度方向与斜面平行时,小球离斜面的距离达到最大,此时小球速度方向与初速度方向成θ角。
根据“平抛运动任意时刻末速度的反向延长线经过水平位移的中点”。
设图中M 点为末速度反向延长线与水平位移的交点,线段MN 的长即为所求的最远距离H 。
解:当末速度方向与斜面平行时,物体离斜面距离最大,tan y y v v gt v θ==可得:0tan v t g θ=因为平抛运动中任意时刻末速度的反向延长线经过水平位移的中点。
所以2x OM =由几何关系可知最远距离: 200sin tan sin =sin sin 222v t v xH MN OM gθθθθθ====解法二:利用斜抛思想求解,将物体初速度v 0、重力加速度g 都分解成沿着斜面和垂直斜面方向的两个分量。
在垂直斜面方向上,物体做的是以v 0y 为初速度、g y 为加速度的类竖直上抛运动。
物体上升到顶端的时间等于它从抛出至离斜面最远的运动时间。
可得:00sin tan t=cos oyy v v v g g gθθθ==物体在垂直于斜面方向“上升”的最大高度20000sin tan tan sin =222y v tv v v H g gθθθθ==解法三:以抛出点O 为坐标原点,建立图示水平竖直坐标系斜面直线方程为()tan h x x θ= 抛体轨迹方程为22220011()222x g h gt g x v v ===(下同) 抛物线上某点00(,)p x h 的导函数为该点处的切线斜率,当切线与斜面平行时,该点距斜面最远2'()22gh x x v =0020'()2tan 2gh x x v θ==200tan v x gθ=42220000220tan tan ()22v v g h h x v g gθθ===所以离斜面tan 0x h θ-=距离最远的点为22200tan tan (,)2v v p g gθθ利用点到直线距离公式可得:20tan sin 2v H gθθ==解法四:设抛物线上某点00(,)p x h 距斜面最远,其切线与斜面平行20'()22gh x x v = 002=h '()22gk x x v =切 200tan v x gθ=可得:000tan x v t v gθ==42220000220tan tan ()22v v g h h x v g gθθ===抛物线上点00(,)p x h 的切线方程为:00)h h k x x -=-切(22200tan tan tan ()2v v h x g gθθθ-=-xx222200tan tan tan 2v v h x g gθθθ-=-可得切线方程:220tan tan 02v x h gθθ--= 与斜面tan 0x hθ-=的距离为:20tan sin 2v H g θθ==解析五:抛物线上任意一点00(,)p x h 到直线tan 0x h θ-=的距离为:H ==H =0x =当点(p 020tan sin =2v H g θθ=以上解法,各有所长,解法一、二突出了物理过程的理解与应用,其余解法展示了学生扎实的数学基本功,体现了数学知识在物理学习上的应用,起到了相辅相成的作用。
平抛运动与斜面、曲面结合的问题

平抛运动与斜面、曲面结合的问题高考试题呈现方式及命题趋势纵观近几年的高考试题,平抛运动考点的题型大多数不是单纯考查平抛运动而是平抛运动与斜面、曲面结合的问题,这类问题题型灵活多变,综合性强,既可考查基础又可考查能力,因此收到命题专家的青睐,在历年高考试题中属于高频高点。
求解思路解答平抛试题,首先要掌握平抛运动的规律和特点,同时也要明确联系平抛的两个分运动数量关系的桥梁,除时间t 外,还有两个参量:速度偏角α,tan yx v v α=位移偏角θ,tan y xθ= 两者关系:tan 2tan αθ=。
平抛运动与斜面、曲面结合的问题,命题者用意用于考查学生能否寻找一定的几何图形中几何角的关系,考查学生运用数学知识解决物理问题的能力。
知识准备结论:做平抛运动的物体经时间t 后,其速度t v 与水平方向的夹角为α(速度偏角),位移s 与水平方向的夹角为θ(位移偏角),则有tan 2tan αθ=证明:速度偏角0tan yx v gt v v α== 位移偏角2001112tan tan 22gt y gt x v t v θα==== 即:tan 2tan αθ=说明:以上结论对于做平抛运动的物体在任意时刻此式都成立,与物体运动速度大小,运动时间等外界因素无关!试题分类归纳一、抛点和落点都在斜面上存在以下规律:(1)位移与水平方向的夹角就为斜面的倾角(2)物体的运动时间与初速度成正比;由20012tan gt y gt x v t v θ===,知02tan v t g θ=,0v 确定时t 就确定了。
(3)物体落在斜面上时的速度方向平行;(4)当物体的速度方向与斜面平行时,物体离斜面的距离最远。
1.如图所示,从倾角为θ的足够长的斜面顶端P 以速度v 0抛出一个小球,落在斜面上某处Q 点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变为2v 0,小球仍落在斜面上,则以下说法正确的是( )A .夹角α将变大B .夹角α与初速度大小无关C .小球在空中的运动时间不变D .PQ 间距是原来间距的3倍[答案] B2.如图所示,ab bc cdde ef ====,当小球以速度水平0v 抛出后落于b 点,当以02v 。
模型10 斜面上的平抛运动

模型10 斜面上的平抛运动平抛运动与斜面模型组合是一种常见的题型,也是高考考查的热点题型,具体有以下两种情况。
模型解题方法方法应用分解速度,构建速度矢量三角形水平方向:v x=v0竖直方向:v y=gt合速度:v=方向:tan θ=分解位移,构建位移矢量三角形水平方向:x=v0t竖直方向:y=gt2合位移:s=方向:tan θ=【典例1】如图所示,倾角为θ的斜面上有A、B、C三点,现从这三点分别以不同的初速度水平抛出一小球,三个小球均落在斜面上的D点,今测得AB∶BC∶CD=5∶3∶1,由此可判断()A.A、B、C处三个小球运动时间之比为1∶2∶3B.A、B、C处三个小球的运动轨迹可能在空中相交C.A、B、C处三个小球的初速度大小之比为1∶2∶3D.A、B、C处三个小球落在斜面上时速度与初速度间的夹角之比为1∶1∶1【答案】D【解析】选D。
A、B、C处三个小球下降的高度之比为9∶4∶1,根据平抛运动的时间t=知,A、B、C处三个小球运动时间之比为3∶2∶1,故A项错误;因最后三个小球落到同一点,抛出点不同,轨迹不同,故三个小球的运动不可能在空中相交,故B项错误;三个小球的水平位移之比为9∶4∶1,根据x=v0t知,初速度之比为3∶2∶1,故C项错误;对于任意一球,因为平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,三个小球落在斜面上,位移与水平方向夹角相等,即位移与水平方向夹角正切值相等,则三个小球在D点速度与水平方向上的夹角的正切值相等,也就是三个小球在D点的速度与水平方向的夹角相等,故D项正确。
【变式训练1】第十六届中国崇礼国际滑雪节在张家口市崇礼区的长城岭滑雪场隆重举行.如图1所示,跳台滑雪运动员经过一段加速滑行后从A点水平飞出,落到斜坡上的B点.A、B两点间的竖直高度h=45 m,斜坡与水平面的夹角α=37°,不计空气阻力(取sin37°=0.6,cos37°=0.8,g取10 m/s2).求:(1)运动员水平飞出时初速度v0的大小;(2)设运动员从A点以不同的水平速度v0飞出,落到斜坡上时速度大小为v,请通过计算确定v与v0的关系式,并在图2中画出v-v0的关系图象.【答案】(1)20 m/s (2)v =132 v 0 图见解析 【解析】(1)运动员离开A 点后做平抛运动,竖直方向上,h =12gt 2 根据几何关系可知,水平位移x =h tan α=60 m 水平方向上,v 0=x t=20 m/s. (2)竖直方向上的位移y =12gt 2 水平方向上位移x =v 0t根据平抛运动规律可知tan α=y x =gt 2v 0竖直分速度v y =gt根据平行四边形定则可知,合速度v =v 20+v 2y联立解得v =132v 0,作图如下.【典例2】如图所示,在斜面顶端a 处以速度v a 水平抛出一小球,经过时间t a 恰好落在斜面底端P 处;今在P 点正上方与a 等高的b 处以速度v b 水平抛出另一小球,经过时间t b 恰好落在斜面的中点处。
模型10 斜面上的平抛运动(解析版)

【变式训练 3】(多选)如图所示,一质点以速度 v0 从倾角为 θ 的斜面底端斜向上抛出,落到斜面上的 M 点且速 度水平向右。现将该质点以 2v0 的速度从斜面底端朝同样方向抛出,落在斜面上的 N 点。下列说法正确的是 ( )。
【解析】(1)设石块击中物块的过程中,石块运动的时间为 t 对物块,运动的位移 s=vt 对石块,竖பைடு நூலகம்方向有(l+s)sin37°= gt2 水平方向有(l+s)cos37°=v0t 解得 v0=20m/s。 (2)对物块有 x1=vt 对石块,竖直方向有 h= gt2
解得 t= =4s
水平方向有 +x1=v1t 联立可得 v1=41.7m/s。 【典例 3】(多选)如图所示,从倾角为 θ 的斜面上某点先后将同一小球以不同的初速度水平抛出,小球均落在斜 面上,当抛出的速度为 v1 时,小球到达斜面时速度方向与斜面的夹角为 α1;当抛出速度为 v2 时,小球到达斜面时 速度方向与斜面的夹角为 α2,则( )。
根据几何关系可知,水平位移 x=tahnα=60 m
水平方向上,v0=xt=20 m/s.
(2)竖直方向上的位移 y=12gt2
水平方向上位移 x=v0t 根据平抛运动规律可知 tanα=yx=2gvt0 竖直分速度 vy=gt
根据平行四边形定则可知,合速度 v= v20+v2y
联立解得 v=
13 2
【变式训练 2】如图所示,在倾角为 37°的固定斜坡上有一人,前方有一物块沿斜坡匀速下滑,且速度 v=15 m/s, 在二者相距 l=30 m 时,此人以速度 v0 水平抛出一石块打击物块,人和物块都可看成质点。(已知 sin 37°=0.6,g=10 m/s2)
(1)若物块在斜坡上被石块击中,求 v0 的大小。 (2)当物块在斜坡末端时,物块离人的高度 h=80 m,此刻此人以速度 v1 水平抛出一石块打击物块,同时物块开始 沿水平面运动,物块速度 v=15 m/s,若物块在水平面上能被石块击中,求速度 v1 的大小。 【答案】(1)20m/s (2)41.7m/s
平抛运动最远距离与斜面的关系

平抛运动最远距离与斜面的关系1.平抛运动最远距离与斜面的夹角有关。
The maximum distance of projectile motion is related to the angle of the incline.2.当斜面倾角为45度时,平抛运动的最远距离最大。
The maximum distance of projectile motion is the greatest when the incline is 45 degrees.3.斜面的摩擦力会影响平抛运动的最远距离。
The friction of the incline will affect the maximum distance of projectile motion.4.较小的斜面倾角会减小平抛运动的最远距离。
A smaller incline angle will decrease the maximum distance of projectile motion.5.较大的斜面倾角会增加平抛运动的最远距离。
A larger incline angle will increase the maximum distance of projectile motion.6.斜面的高度会影响平抛运动的最远距离。
The height of the incline will affect the maximum distance of projectile motion.7.斜面倾角越大,平抛运动的最远距离越小。
The larger the incline angle, the smaller the maximum distance of projectile motion.8.斜面倾角越小,平抛运动的最远距离越大。
The smaller the incline angle, the greater the maximum distance of projectile motion.9.斜面的光滑程度也会对平抛运动的最远距离产生影响。
斜面上的平抛运动模型及类平抛运动模型高三物理一轮复习专题

一.必备知识和方法斜面上的平抛运动问题是一种常见的题型,在解答这类问题时除要运用平抛运动的位移和速度规律,还要充分运用斜面倾角,找出斜面倾角同位移和速度与水平方向夹角的关系,从而使问题得到顺利解决。
1.从斜面上某点水平抛出,又落到斜面上的平抛运动的五个规律〔推论〕 (1)位移方向相同,竖直位移与水平位移之比等于斜面倾斜角的正切值。
(2)刚落到侧面时的末速度方向都平行,竖直分速度与水平分速度(初速度)之比等于斜面倾斜角正切值的2倍。
(3)运动的时间与初速度成正比⎝ ⎛⎭⎪⎫t =2v 0tan θg 。
(4)位移与初速度的二次方成正比⎝ ⎛⎭⎪⎫s =2v 20tan θg cos θ。
(5)当速度与斜面平行时,物体到斜面的距离最远,且从抛出到距斜面最远所用的时间为平抛运动时间的一半。
2.常见的模型模型方法分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系 分解速度,构建速度的矢量三角形 分解位移,构建位移三角形,隐含条件:斜面倾角θ等于位移与水平方向的夹角 根本 规律水平:v x =v 0竖直:v y =gt 合速度:v =v 2x +v 2y水平:v x =v 0 竖直:v y =gt 合速度:v =v 2x +v 2y水平:x =v 0t 竖直:y =12gt 2 合位移:方向:tan θ=v xv y 方向:tan θ=v yv xs =x 2+y 2 方向:tan θ=yx 运动 时间由tan θ=v 0v y =v 0gt 得t =v 0g tan θ由tan θ=v y v 0=gtv 0得t =v 0tan θg由tan θ=y x =gt2v 0得t=2v 0tan θg3.类平抛运动模型〔1〕模型特点:物体受到的合力恒定,初速度与恒力垂直,这样的运动叫类平抛运动。
如果物体只在重力场中做类平抛运动,那么叫重力场中的类平抛运动。
学好这类模型,可为电场中或复合场中的类平抛运动打根底。
与斜面有关的平抛运动

与斜面有关的平抛运动与斜面有关的平抛运动,包括两种情况:(1)物体从空中抛出落在斜面上;(2)物体从斜面上抛出落在斜面上.在解答该类问题时,除要运用平抛运动的位移和速度规律外,还要充分利用斜面倾角,找出斜面倾角同位移和速度的关系,从而使问题得到顺利解决.两种情况的特点及分析方法对比如下:方法内容斜面飞行时间总结分解速度水平方向:v x=v0竖直方向:v y=gt合速度:v=v x2+v y2特点:tan θ=v xv y=v0gtt=v0g tan θ分解速度,构建速度三角形分解位移水平方向:x=v0t竖直方向:y=12gt2合位移:s=x2+y2特点:tan θ=yx=gt2v0t=2v0tan θg分解位移,构建位移三角形【例1】如图所示,以9.8 m/s的水平初速度v 0抛出的物体,飞行一段时间后,垂直地撞在倾角为30°的固定斜面上,这段飞行所用的时间为(不计空气阻力,g取9.8 m/s2)()A.23s B.223s , C. 3 s D.2 s【例2】如图所示,AB为固定斜面倾角为30°,小球从A点以初速度v0水平抛出,恰好落到B点.求:(空气阻力不计,重力加速度为g)(1)A、B间的距离及小球在空中飞行的时间;(2)从抛出开始,经过多长时间小球与斜面间的距离最大?最大距离为多大?【例3】如图所示,B 为竖直圆轨道的左端点,它和圆心O 的连线与竖直方向的夹角为α.一小球在圆轨道左侧的A 点以速度v 0平抛,恰好沿B 点的切线方向进入圆轨道.已知重力加速度为g ,则A 、B 之间的水平距离为( )A.v 20tan αgB.2v 20tan αgC.v 20g tan αD.2v 20g tan α【例4】如图所示,在倾角为37°的斜面上从A 点以6 m/s 的初速度水平抛出一个小球,小球落在B 点,求:(g 取10 m/s 2,sin 37°=0.6,cos 37°=0.8,不计空气阻力)(1)A 、B 两点间的距离和小球在空中飞行的时间;(2)小球刚碰到斜面时的速度方向与水平方向夹角的正切值.【例5】如图所示,一个小球从高h =10 m 处以水平速度v 0=10 m/s 抛出,撞在倾角θ=45°的斜面上的P 点,已知AC =5 m .g =10 m/s 2,不计空气阻力,求:(1)P 、C 之间的距离;(2)小球撞击P 点时速度的大小和方向.课后作业1.如图所示,位于同一高度的小球A、B分别以v1和v2的速度水平抛出,都落到了倾角为30°的斜面上的C点,小球B恰好垂直打在斜面上,则v1、v2之比为()A.1∶2B.2∶1 C.3∶2 D.2∶32.如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10 m处的O 点,以5 m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,不计空气阻力,这段飞行所用的时间为(g取10 m/s2)()A.2 s B. 2 s C.1 s D.0.5 s3.如图所示,一个倾角为37°的斜面固定在水平面上,在斜面底端正上方的O点将一小球以速度v0=3 m/s水平抛出,经过一段时间后,小球垂直打在斜面P点处.(小球可视为质点,不计空气阻力,取重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8),则()A.小球击中斜面时的速度大小为5 m/sB.小球击中斜面时的速度大小为4 m/sC.小球做平抛运动的水平位移是1.6 mD.小球做平抛运动的竖直位移是1 m4.将一小球以水平速度v0=10 m/s从O点向右抛出,经 3 s小球恰好垂直落到斜面上的A点,不计空气阻力,g=10 m/s2,B点是小球做自由落体运动在斜面上的落点,如图所示,下列判断正确的是()A.斜面的倾角是60°B.小球的抛出点距斜面的竖直高度约是15 mC.若将小球以水平速度v0′=5 m/s向右抛出,它一定落在AB的中点P的上方D.若将小球以水平速度v0′=5 m/s向右抛出,它一定落在AB的中点P处5.如图所示,在斜面顶端先后水平抛出同一小球,第一次小球落到斜面中点,第二次小球落到斜面底端,从抛出到落至斜面上(忽略空气阻力)( )A.两次小球运动时间之比t 1∶t 2=1∶2B.两次小球运动时间之比t 1∶t 2=1∶2C.两次小球抛出时初速度之比v 01∶v 02=1∶2D.两次小球抛出时初速度之比v 01∶v 02=1∶46.如图所示,从斜面上的A 点以速度v 0水平抛出一个物体,飞行一段时间后,落到斜面上的B 点,已知AB =75 m ,α=37°,不计空气阻力,g =10 m/s 2,sin 37°=0.6,下列说法正确的是( )A.物体的位移大小为60 mB.物体飞行的时间为6 sC.物体的初速度v 0大小为20 m/sD.物体在B 点的速度大小为30 m/s7.如图所示,可视为质点的小球,位于半径为3m 半圆柱体左端点A 的正上方某处,以一定的初速度水平抛出小球,其运动轨迹恰好能与半圆柱体相切于B 点.过B 点的半圆柱体半径与水平方向的夹角为60°,则初速度为(不计空气阻力,重力加速度g 取10 m/s 2)( )A.553 m/sB.4 3 m/sC.3 5 m/sD.152m/s8.如图所示,一小球从平台上水平抛出,恰好落在平台前一倾角为α=53°的固定斜面顶端并刚好沿斜面下滑,已知平台到斜面顶端的高度为h =0.8 m ,不计空气阻力,g =10 m/s 2,sin 53°=0.8,cos 53°=0.6,求: (1)小球水平抛出的初速度大小v 0; (2)斜面顶端与平台边缘的水平距离x .与斜面有关的平抛运动参考答案【例1】【答案】 C【解析】 如图所示,把末速度分解成水平方向的分速度v 0和竖直方向的分速度v y ,则有:tan 30°=v 0v y ,v y =gt ,联立得:t=v 0g tan 30°=3v 0g= 3 s ,故C 正确. 【例2】【答案】 (1)4v 0 23g 23v 03g (2)3v 03g 3v 0 212g【解析】 (1)设飞行时间为t ,则有:水平方向位移l AB cos 30°=v 0t 竖直方向位移l AB sin 30°=12gt 2解得:t =2v 0g tan 30°=23v 03g ,l AB =4v 023g .(2)方法二(结合斜抛运动分解)如图所示,把初速度v 0、重力加速度g 都分解成沿斜面和垂直斜面的两个分量.在垂直斜面方向上,小球做的是以v 0y 为初速度、g y 为加速度的“竖直上抛”运动.小球到达离斜面最远处时,速度v y =0, 由v y =v 0y -g y t ′可得:t ′=v 0y g y =v 0sin 30°g cos 30°=v 0g tan 30°=3v 03g小球离斜面的最大距离y =v 0y22g y =v 0 2sin 2 30°2g cos 30°=3v 0 212g.【例3】【答案】 A【解析】 如图所示,对在B 点时的速度进行分解,小球运动的时间t =v y g =v 0tan αg,则A 、B 间的水平距离x =v 0t =v 20tan αg,故A 正确,B 、C 、D 错误.【例4】【答案】 (1)6.75 m 0.9 s (2)32【解析】 (1)如图所示,小球落到B 点时位移与初速度的夹角为37°,设运动时间为t . 则tan 37°=h x =12gt 2v 0t =56t又因为tan 37°=34,解得:t =0.9 s所以x =v 0t =5.4 m则A 、B 两点间的距离l =xcos 37°=6.75 m(2)设小球落到B 点时速度方向和水平方向的夹角为α,则tan α=v y v 0=gt v 0=32.【例5】【答案】 (1)5 2 m (2)10 2 m/s 方向垂直于斜面向下 【解析】 (1)设P 、C 之间的距离为L ,根据平抛运动规律有: AC +L cos θ=v 0t ,h -L sin θ=12gt 2联立解得:L =5 2 m ,t =1 s.(2)小球撞击P 点时的水平速度v 0=10 m/s 竖直速度v y =gt =10 m/s所以小球撞击P 点时速度的大小v =v 02+v y 2=10 2 m/s设小球撞击P 点时的速度方向与水平方向的夹角为α,则tan α=v yv 0=1 解得:α=45°故小球撞击P 点时速度方向垂直于斜面向下.课后作业1.【答案】C【解析】球A 做平抛运动,根据分位移公式,有x =v 1t ,y =12gt 2,又tan 30°=yx ,联立解得v 1=32gt ;小球B 恰好垂直打到斜面上,则有tan 30°=v 2v y =v 2gt ,则得v 2=33gt ,可得v 1∶v 2=3∶2,故C 正确,A 、B 、D 错误. 2.【答案】C【解析】设小球撞到斜面AB 中的一点D 上,则小球的水平运动的时间与竖直下落的时间相等,设飞行时间为t ,则根据几何关系可得v 0t =10 m -12gt 2,代入数据解得t =1 s ,故选项C正确. 3.【答案】 A【解析】 P 点小球的速度方向与斜面垂直,则有:tan 37°=v 0v y ,解得:v y =v 0tan 37°=334 m/s=4 m/s ,小球击中斜面时的速度大小为:v =v 20+v 2y =32+42 m/s =5 m/s ,A 正确,B 错误;小球运动的时间:t =v y g =410 s =0.4 s ,可知水平位移:x =v 0t =3×0.4 m =1.2 m ,竖直位移:y =12gt 2=12×10×0.42 m =0.8 m ,C 、D 错误.4.【答案】 C【解析】 设斜面倾角为θ,对小球在A 点的速度进行分解有tan θ=v 0gt,解得θ=30°,A 错误;小球距过A 点水平面的距离为h =12gt 2=15 m ,所以小球的抛出点距斜面的竖直高度一定大于15 m ,B 错误;若小球的初速度为v 0′=5 m/s ,过A 点做水平面,小球落到水平面的水平位移是小球以初速度v 0=10 m/s 抛出时的一半,延长小球运动的轨迹线,可知小球应该落在P 、A 之间,C 正确,D 错误。
专题02 平抛运动的描述——解析版

专题2 平抛运动的描述(教师版)一、目标要求二、知识点解析1.平抛运动的定义将物体以一定的速度抛出,如果物体只受重力的作用,这时的运动叫做抛体运动;做抛体运动的物体只受到重力作用,既加速度g不变,因此抛体运动一定是是匀变速运动.抛体运动开始时的速度叫做初速度.如果初速度是沿水平方向的,这个运动叫做平抛运动.平抛运动是匀变速曲线运动.平抛运动的特征:①具有水平方向的初速度②只受重力作用2.平抛运动的基本规律(1)水平方向:匀速直线运动.(2)竖直方向:自由落体运动,加速度为g.3.平抛运动的运动规律v的方向相同;竖直方向为y轴,正方向向下;物以抛出点为原点取水平方向为x轴,正方向与初速度(,),下面将就质点任意时刻的速度、位移进行讨论.体在任意时刻t位置坐标为P x yy(1)速度公式:水平方向和竖直方向速度:0x y v v v gt =⎧⎪⎨=⎪⎩因此物体的实际速度为:0y x v v gtv v tan α⎧===⎪⎪⎨⎪==⎪⎩(2)位移公式水平方向和竖直方向位移:0212x v t y gt =⎧⎪⎨=⎪⎩因此实际位移为:02S y gt x v tan θ⎧⎪==⎪⎨⎪==⎪⎩注意:显然,位移和速度的夹角关系为:12tan tan θα=,即v 的反向延长线交于OA 的中点O ’.这一结论在运算中经常用到.(3)轨迹公式 由0x v t =和212y gt =可得2202g y x v =,所以平抛运动的轨迹是一条抛物线. 4.平抛运动的几个重要结论(1)运动时间:t =(2)落地的水平位移:x x v t v ==,即水平方向的位移只与初速度0v 和下落高度h 有关.(3)落地时速度:v =0v 和下落高度h 有关平抛运动 (4)两个重要推论:表示速度矢量v 与水平方向的夹角,故 表示位移矢量与水平方向的夹角,故 ①平抛运动中,某一时刻速度与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍. ②根据示意图,我们可知,平抛运动中,某一时刻速度的反向延长线与x 轴的交点为水平位移的中点. 5.求解平抛运动飞行时间的四种方法(1)已知物体在空中运动的高度,根据212h gt =,得到t = (2)已知水平射程x 和初速度0v ,也可以求出物体在空中运动的时间0x t v =(3)已知物体在空中某时刻的速度方向与竖直方向的夹角θ与初速度0v 的大小,根据0v gttan θ=可以求得时间.(4)已知平抛运动的位移方向与初速度方向的夹角α及初速度0v 的大小,根据200122gtgt v t v tan α==可求出时间.6.类平抛运动有时物体的运动与平抛运动很相似,也是在某个方向物体做匀速直线运动,另一垂直方向做初速度为零的匀加速直线运动.对这种运动像平抛又不是平抛,通常称为平抛运动,处理方法与平抛运动一样,只是a 不同而已.如图所示倾角为θ.一物块沿上方顶点P 水平射入,而从右下方顶点Q 离开.xα0tan y xv gt v v α==θ21tan tan 222x x y gt gt x v t v θα====7.斜面上的平抛运动解决这类问题应该注意一下几点: (1)斜面的倾角θ是一个很重要的条件(2)当物体做平抛运动,落到斜面上时,若已知斜面倾角,则相当于间接告诉合速度或者合位移的方 向.这个类问题主要就是将平抛运动规律与几何知识综合起来.①当物体的起点和落点均在斜面上此类问题的特点是物体的位移与水平方向的夹角即为斜面的倾角.一般要从位移关系入手,根据位移中分运动和合运动的大小和方向(角度)关系进行求解.例如:两个相对的斜面,倾角分别为037和053,在顶点把两个小球以相同初速度分别向左、向右水平抛出,小球都落在斜面上,若不计空气阻力,是求解A 、B 两个小球落到斜面上的时间之比是多少.a :从位移关系入手,我们可以求出水平方向和竖直方向的位移大小:2012x v t y gt ,== b :由于物体的位移与水平方向的夹角即为斜面的倾角可知:tan y x θ=,()201tan 2gt v t θ=,0tan v t g θ2=,所以:tan 379tan 5316A B t t ︒==︒ ②当物体的起点在斜面外,落点在斜面上 解决这类问题应该注意一下几点: (1)斜面的倾角θ是一个很重要的条件(2)当物体做平抛运动,落到斜面上时,是垂直打到斜面上,所以水平方向的速度和竖直方向的速度有以下关系:0tan yv v θ=根据这个公式再加上水平方向和竖直方向的位移关系就可以方便的求解.例如:在倾角为37°的斜面底端的正上方H 处平抛一个小球,该小球垂直打在斜面上的一点,求小球抛出时的初速度.a :从位移关系入手,我们可以求出水平方向和竖直方向的位移大小:2012x v t y gt ,==,由图可知, 2012tan 37H gt v t-︒=. b :由速度关系得:0tan 37v gt ︒=,解之得:0v = 8.斜抛运动的基本概念(1)定义:斜向上或斜向下抛出的物体只在重力(不考虑空气阻力)作用下的运动叫做斜抛运动. (2)斜抛运动的特点:水平方向速度不变,竖直方向仅受重力,加速度为g .(3)斜抛运动的分解:斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下 抛运动的合运动. (4)斜抛运动的方程如图所示,斜上抛物体初速度为v ,与水平方向夹角为θ,则速度:x yv v v v gt cos sin θθ=⎧⎪⎨=-⎪⎩位移:212x v t y v t gt cos sin θθ=⎧⎪⎨=-⎪⎩轨迹方程:可得:xt v cos θ=,代入y 可得2222gx y x v tan cos θθ=-可以看出:y =0时 (1)x =0是抛出点位置.(2)22v x gsin θ=是水平方向的最大射程.(3)飞行时间:2v t gsin θ=三、考查方向题型1:平抛运动的基本规律典例一:(多选)关于平抛运动,下列说法中正确的是( ) A .落地时间仅由抛出点高度决定B .抛出点高度一定时,落地时间与初速度大小有关C .初速度一定的情况下,水平飞出的距离与抛出点高度无关D .抛出点高度一定时,水平飞出距离与初速度大小成正比 【答案】AD【解析】AB .平抛运动在竖直方向上做自由落体运动,由 h =212gt 得 t则知平抛运动的时间由抛出点高度决定,与初速度无关,故A 正确,B 错误;CD .平抛运动的水平距离 x =v 0t=v 抛出点高度一定时,水平飞出距离与初速度的大小成正比,故C 错误,D 正确.题型2:平抛运动的计算典例二:(2020江苏·多选)如图所示,小球A 、B 分别从2l 和l 的高度水平抛出后落地,上述过程中A 、B 的水平位移分别为l 和2l 。
抛体模型的运动学问题与功能动量(解析版)
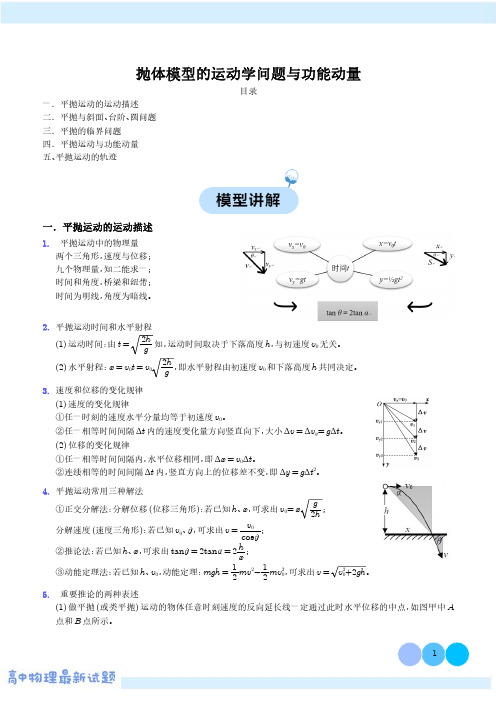
抛体模型的运动学问题与功能动量目录一.平抛运动的运动描述二.平抛与斜面、台阶、圆问题三.平抛的临界问题四.平抛运动与功能动量五、平抛运动的轨迹一.平抛运动的运动描述1.平抛运动中的物理量两个三角形,速度与位移;九个物理量,知二能求一;时间和角度,桥梁和纽带;时间为明线,角度为暗线。
2.平抛运动时间和水平射程(1)运动时间:由t =2h g 知,运动时间取决于下落高度h ,与初速度v 0无关。
(2)水平射程:x =v 0t =v 02h g,即水平射程由初速度v 0和下落高度h 共同决定。
3.速度和位移的变化规律(1)速度的变化规律①任一时刻的速度水平分量均等于初速度v 0。
②任一相等时间间隔Δt 内的速度变化量方向竖直向下,大小Δv =Δv y =g Δt 。
(2)位移的变化规律①任一相等时间间隔内,水平位移相同,即Δx =v 0Δt 。
②连续相等的时间间隔Δt 内,竖直方向上的位移差不变,即Δy =g Δt 2。
4.平抛运动常用三种解法①正交分解法:分解位移(位移三角形):若已知h 、x ,可求出v 0=x g2h;分解速度(速度三角形):若已知v 0、θ,可求出v =v 0cos θ;②推论法:若已知h 、x ,可求出tan θ=2tan α=2hx ;③动能定理法:若已知h 、v 0,动能定理:mgh =12mv 2-12mv 20,可求出v =v 20+2gh 。
5.重要推论的两种表述(1)做平抛(或类平抛)运动的物体任意时刻速度的反向延长线一定通过此时水平位移的中点,如图甲中A 点和B 点所示。
(2)做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其速度方向与水平方向的夹角为θ,位移与水平方向的夹角为α,则tan θ=2tan α,如图乙所示。
二.平抛与斜面、台阶、圆问题1.斜面上平抛运动的时间的计算斜面上的平抛(如图),分解位移(位移三角形)x =v 0t ,y =12gt 2,tan θ=y x ,可求得t =2v 0tan θg。
平抛运动斜面距离问题的解法赏析

平抛运动斜面距离问题的解法赏析无锡市堰桥中学 周维新平抛运动是生活中常见的运动,也是高中物理曲线运动中典型的运动形式。
因此平抛运动高考中的重点和热点。
学生在处理较为简单的问题时,进行分解合成处理还能完成,但是对于较为复杂的问题时就感觉到束手无策。
本文就平抛运动中较为复杂的斜面距离问题的解法作如下探讨。
例题:如图,AB 斜面倾角为37°,小球从A 点以初速度v 0=20m/s 水平抛出,恰好落到B 点,求: (1)物体在空中飞行的时间;AB间的距离;(2)小球在B点时速度的大小和方向; (3)从抛出开始经多少时间小球与斜面间的距离最大,最大距离是多少g=10m/s 2;1、分解法第(3)问的传统解法将平抛运动分解到斜面方向和垂直于斜面方向:沿斜面方向:V //=V 0cos37º=20×0.8=16m/s ,a //=gsin37º=10×0.6=6m/s 2匀加速直线运动。
垂直斜面方向:V ⊥= V 0sin37º=20×0.6=12m/s ,a ⊥=gcos37º=10×0.8=8m/s2匀减速直线运动。
当垂直斜面方向的速度减为零时,球离斜面距离最远。
t===1.5s ,最远距离S==。
此种解法沿用了离地最高必有在垂直地面方向的速度为零的结论。
球离斜面距离最大,则球在垂直斜面上的速度必为零。
因而本解法采用正交分解,可以巩固学生的运动合成与分解知识,同时拓展对平抛运动的处理方法。
平抛运动分解为两个方向的匀变速直线运动,学生较易理解但运算较繁。
2、追击解法设斜面上有一个点,该点沿斜面作匀速直线运动。
该点的水平分速度v 0=20m/s 与小球的平抛初速度相等,竖直方向的分速度v y = v 0tan37°=15m/s ,所以小球由A 点平抛运动到B 点时,该点也恰好从A 点匀速运动到B 点,在运动过程中该点始终在小球的正下方。
第16讲 斜面上的平抛运动模型及类平抛运动模型(解析版)

第16讲 斜面上的平抛运动模型及类平抛运动模型一.知识总结斜面上的平抛运动问题是一种常见的题型,在解答这类问题时除要运用平抛运动的位移和速度规律,还要充分运用斜面倾角,找出斜面倾角同位移和速度与水平方向夹角的关系,从而使问题得到顺利解决。
1.从斜面上某点水平抛出,又落到斜面上的平抛运动的五个规律(推论) (1)位移方向相同,竖直位移与水平位移之比等于斜面倾斜角的正切值。
(2)刚落到侧面时的末速度方向都平行,竖直分速度与水平分速度(初速度)之比等于斜面倾斜角正切值的2倍。
(3)运动的时间与初速度成正比⎝ ⎛⎭⎪⎫t =2v 0tan θg 。
(4)位移与初速度的二次方成正比⎝ ⎛⎭⎪⎫s =2v 20tan θg cos θ。
(5)当速度与斜面平行时,物体到斜面的距离最远,且从抛出到距斜面最远所用的时间为平抛运动时间的一半。
2.常见的模型模型方法分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系 分解速度,构建速度的矢量三角形分解位移,构建位移三角形,隐含条件:斜面倾角θ等于位移与水平方向的夹角基本 规律水平:v x =v 0竖直:v y =gt 合速度:v =v 2x +v 2y水平:v x =v 0 竖直:v y =gt 合速度:v =v 2x +v 2y水平:x =v 0t 竖直:y =12gt 2 合位移: s =x 2+y 2方向:tanθ=v xv y方向:tanθ=v yv x方向:tanθ=yx运动时间由tanθ=v0v y=v0gt得t=v0g tanθ由tanθ=v yv0=gtv0得t=v0tanθg由tanθ=yx=gt2v0得t=2v0tanθg3.类平抛运动模型(1)模型特点:物体受到的合力恒定,初速度与恒力垂直,这样的运动叫类平抛运动。
如果物体只在重力场中做类平抛运动,则叫重力场中的类平抛运动。
学好这类模型,可为电场中或复合场中的类平抛运动打基础。
(2).类平抛运动与平抛运动的区别做平抛运动的物体初速度水平,物体只受与初速度垂直的竖直向下的重力,a=g;做类平抛运动的物体初速度不一定水平,但物体所受合力与初速度的方向垂直且为恒力,a=F合m。
斜面上平抛运动问题

斜面上的平抛运动问题一、情景描述:如果物体是从斜面上平抛的,若以斜面为参考系,平抛运动有垂直(远离)斜面和平行斜面两个方向的运动效果,如果题目要求讨论相对斜面的运动情况,如求解离斜面的最远距离等,往往沿垂直斜面和平行斜面两个方向进行分解,这种分解方法初速度、加速度都需要分解,难度较大,但解题过程会直观简便。
平抛运动中的“两个重要结论”是解题的关键,一是速度偏向角α,二是位移偏向角β,画出平抛运动的示意图,抓住这两个角之间的联系,即tan α=2tan β,如果物体落到斜面上,则位移偏向角β和斜面倾角θ相等,此时由斜面的几何关系即可顺利解题。
推论Ⅰ:做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为φ,则tan θ=2tan φ。
证明:如右图所示,由平抛运动规律得tan θ=v y v x =gt v 0, tan φ=y 0x 0=12·gt 2v 0t =gt 2v 0, 所以tan θ=2tan φ。
推论Ⅱ:做平抛(或类平抛)运动的物体,任意时刻的瞬时速度方向的反向延长线一定通过此时水平位移的中点。
证明:如右图所示,tan φ=y 0x 0tan θ=2tan φ=y 0x 0/2即末状态速度方向的反向延长线与x 轴的交点B 必为此时水平位移的中点。
注意:(1)在平抛运动过程中,位移矢量与速度矢量永远不会共线。
(2)它们与水平方向的夹角关系为tan θ=2tan φ,但不能误认为θ=2φ。
【典例精析】:如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上, 物体与斜面接触时速度与水平方向的夹角φ满足( )A .tan φ=sin θB .tan φ=cos θC .tan φ=tan θD .tan φ=2tan θ[解析]竖直速度与水平速度之比为:tan φ=gt v 0,竖直位移与水平位移之比为:tan θ=gt 22v 0t,故tan φ=2tan θ, D 正确。
“平抛遇到斜面”类问题剖析

例 3 如 图 5 从 倾 角 为 的 ,
足 够 长 的 斜 面 上 的 A 点 , 后 将 先 同 一 小 球 以 不 同 的初 速 度 水 平 向
右 抛 出 . 一 次 初 速 度 为 , 落 第 球
到 斜 面 上 的 瞬 时 速 度 方 向 与 斜 面 图 5
~ 夹 角 为 a , 二 次 初 速 度 为 z, 第 球 的速度减为零时 , 球 距斜 面的距离 最大 , 过程 的时 间 t 小 此 一
、
图 4 示 , b 做水平线 A , 以 2 所 过 点 B 当
的 速 度 水 平 抛 出 时 , 下 落 到 水 平 线 若 AB上 , 其 运 动 时 间 与 以 口的 速 度 水 则 平 抛 出 时 的运 动 时 间 相 同 , 水 平 位 移 其
图 1
例 1 如 图 1所 示 , 面 倾 角 为 0 斜 ,
~
定 值 与 初 速 度 无 关 . 案 为 B 答 .
然后利用速度的合成得出此时小球的速度 一 。. _
点 评 : 法 运 算 量 较 大 , 很 容 易得 出一 个 “ 产 品 ” 一 此 但 副 一 最 大 距 离 H. 用上 述 两 法 求 最 大距 离 H , 常 烦 琐 . 若 非 二 、 造 水 平 面 巧 断 下 落 点 构 例 2 如 图 3 斜 面 上 有 n 6 c d四个 点 ,b c c , n , 、、、 a =b d 从 点 正 上 方 0 点 以速 度 水 平 抛 出 一 个 小 球 , 落 在 斜 面 上 b 它
, .
胪
. n
c + g 0
C a <a .。 z
点 评 : 题 也 可 以 沿 水 平 方 向 和 竖直 方 向 分 解 , 出 两 个 本 求
平抛运动与斜面、曲面结合的问题(解析版)--高考物理热点模型
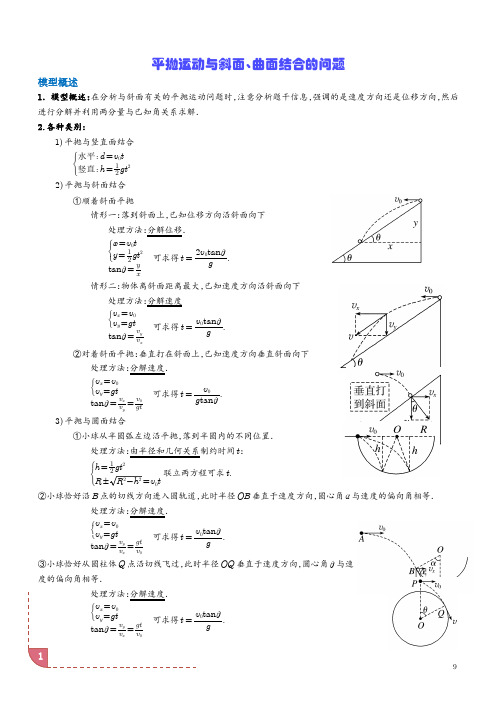
1平抛运动与斜面、曲面结合的问题模型概述1.模型概述:在分析与斜面有关的平抛运动问题时,注意分析题干信息,强调的是速度方向还是位移方向,然后进行分解并利用两分量与已知角关系求解.2.各种类别:1)平抛与竖直面结合水平:d =v 0t竖直:h =12gt 22)平抛与斜面结合①顺着斜面平抛情形一:落到斜面上,已知位移方向沿斜面向下处理方法:分解位移.x =v 0t y =12gt 2tan θ=yx可求得t =2v 0tan θg .情形二:物体离斜面距离最大,已知速度方向沿斜面向下处理方法:分解速度v x =v 0v y =gt tan θ=v y vx可求得t =v 0tan θg .②对着斜面平抛:垂直打在斜面上,已知速度方向垂直斜面向下处理方法:分解速度.v x =v 0v y =gt tan θ=v x v y=v 0gt可求得t =v 0g tan θ.3)平抛与圆面结合①小球从半圆弧左边沿平抛,落到半圆内的不同位置.处理方法:由半径和几何关系制约时间t :h =12gt2R ±R 2-h 2=v 0t联立两方程可求t .②小球恰好沿B 点的切线方向进入圆轨道,此时半径OB 垂直于速度方向,圆心角α与速度的偏向角相等.处理方法:分解速度.v x =v 0v y =gt tan θ=v y v x=gt v可求得t =v 0tan θg .③小球恰好从圆柱体Q 点沿切线飞过,此时半径OQ 垂直于速度方向,圆心角θ与速度的偏向角相等.处理方法:分解速度.v x =v 0v y =gt tan θ=v y v x=gt v可求得t =v 0tan θg .4)与圆弧面有关的平抛运动:题中常出现一个圆心角,通过这个圆心角,就可找出速度的方向及水平位移和竖直位移的大小,再用平抛运动的规律列方程求解.典题攻破1.平抛运动与斜面结合的问题1.(2024·辽宁·模拟预测)如图所示,斜面的倾角为θ,斜面的长度为L 。
【问题】斜面上平抛运动问题

【关键字】问题斜面上的平抛运动问题一、情景描述:如果物体是从斜面上平抛的,若以斜面为参考系,平抛运动有笔直(远离)斜面和平行斜面两个方向的运动效果,如果题目要求讨论相对斜面的运动情况,如求解离斜面的最远距离等,往往沿笔直斜面和平行斜面两个方向进行分解,这种分解方法初速度、加速度都需要分解,难度较大,但解题过程会直观简便。
平抛运动中的“两个重要结论”是解题的关键,一是速度偏向角α,二是位移偏向角β,画出平抛运动的示意图,抓住这两个角之间的联系,即tanα=2tanβ,如果物体落到斜面上,则位移偏向角β和斜面倾角θ相等,此时由斜面的几何关系即可顺利解题。
推论Ⅰ:做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为φ,则tanθ=2tanφ。
证明:如右图所示,由平抛运动规律得tanθ==,tanφ==·=,所以tanθ=2tanφ。
推论Ⅱ:做平抛(或类平抛)运动的物体,任意时刻的瞬时速度方向的反向延长线一定通过此时水平位移的中点。
证明:如右图所示,tanφ=tanθ=2tanφ=即末状态速度方向的反向延长线与x轴的交点B必为此时水平位移的中点。
注意:(1)在平抛运动过程中,位移矢量与速度矢量永远不会共线。
(2)它们与水平方向的夹角关系为tanθ=2tanφ,但不能误认为θ=2φ。
【典例精析】:如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足()A.tanφ=sinθ B.tanφ=cosθC.tanφ=tanθ D.tanφ=2tanθ[解析]竖直速度与水平速度之比为:tanφ=,竖直位移与水平位移之比为:tanθ=,故tanφ=2tanθ, D正确。
(注意:只要落点在斜面上,该结论与初速度大小无关)关于物体在斜面上运动,若选取鞋面为参照物时,我们可以更具所需将速度沿加速度方向和笔直于加速度方向分解、将加速度沿速度方向和笔直于速度方向分解或者两者同时进行分解从而进行有效阶梯【典例精析】:如右图所示,足够长斜面OA的倾角为θ,固定在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中经过多长时间离斜面最远?最远距离是多少?解法一:常规分解方法(不分解加速度)当小球的速度方向与斜面平行时,小球与斜面间的距离最大。
简谈解决斜面平抛运动的数学技巧

简谈解决斜面平抛运动的数学技巧高中物理是一门综合性比较高的学科,尤其是与数学学科的交叉应用比较多,大量应用到一些数学中的处理技巧与方法。
应用数学处理物理问题的能力是高考考纲所列的五种能力之一,学生利用数学知识研究物理问题也是高考考查的重点内容。
本文以斜面上的平抛运动为例,让学生体会数学在物理中的应用。
例:从倾角为θ的斜面上A点,以初速度V0沿水平方向抛出一个小球,落在斜面B上,求:从抛出到落到斜面上时,小球离斜面的最远距离。
【解法一】平抛运动的基本公式和推论从抛出点开始计时,经过时间t小球与斜面的距离最在;如图1所示,当小球的速度V与斜面平行时,小球离斜面距离达到最远,即此时速度与水平面的夹角为θ。
此时=tanθ=,则t=作速度的反向延长线,交初速度方向的延长线交于M点,根据平抛运动的结论:M点为水平位移的中点,所以,小球距离斜面的最大距离:MN=AMsinθ=sinθ=v0tsinθ=v0sinθ=【解法二】运动的分解如图2所示,将平抛运动的初速度v0和加速度g沿着斜面和垂直于斜面分解,在垂直于斜面方向vx=v0 sinθax=gcosθ小球做匀变速直线运动,平行于斜面方向vx=v0cosθ vy=v0sinθ小球做匀加速直线运动。
所以,当小球在垂直于斜面方向的速度减为0的时,小球距离斜面最远。
hmax==【解法三】解析几何法(1)切线方程法由于做平抛运动的小球的数学解析式为:x=vot y=gt则做平抛运动的小球的解析式为:y0=同理可设斜面0A的解析式为y1=xtanθ如图3,将直线OA沿y轴方向向上移动b个单位,得到一个新的解析式为:y2=xtanθ-b。
当y2与y0只有一个交点时,xtanθ-b=即-xtanθ+b=0由于方程只有一个解,所以△=(ta nθ)-4×=0则b=最大高度h=bcosθ==(2)点到直线距离法根据点到直线的距离公式:xtanθ-y=0,抛物线上的任意一点的坐标是(x0,)则点到直线的距离d==cosθx-将x0视为未知数,刚dmin=cosθ·==【解法四】平面几何法如图4所示,取平抛运动过程中一点A,过A点作水平线与斜面分别交于C、D两点。
平抛运动与斜面相结合问题的解题策略

平抛运动与斜面相结合问题的解题策略作者:刘玲来源:《中学物理·高中》2015年第02期我们先来看看2013年上海高考的第19题:轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h,山坡倾角为θ,由此可算出A.轰炸机的飞行高度B.轰炸机的飞行速度C.炸弹的飞行时间D.炸弹投出时的动能分析与解根据A点的高度可知A点到底端的水平位移,即炸弹的水平位移,由于炸弹垂直击中目标A,可知速度与水平方向的夹角为斜面的倾角,再抓住平抛运动速度与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,可得知平抛运动竖直位移.从而得出轰炸机的飞行高度.故A正确.求出平抛运动的竖直位移,根据y=12gt2得出炸弹平抛运动的时间,根据时间和水平位移求出轰炸机的初速度.故B、C正确.由于炸弹的质量未知,则无法求出炸弹投出时的动能.故D错误.所以本题的答案为A、B、C.分析与解当小球初速度变为v时,其落点位于c点,根据平抛运动的特点,初速度越大,则落点越远,显然v>v0,由于斜面上a、b、c三点等距,如图3所示,设想做一条过b点的水平线,当小球从a点抛出的初速度变成2v0时,小球恰好在c点正上方通过这条水平线上的点c1,然后落到斜面上c点下面的点d,因此可以判断v从对这两道高考题的分析可以看出,当平抛运动与斜面相结合时,解题的基本方法有如下几点:(1)熟练掌握平抛运动的规律;(2)斜面的倾角十分关键,是解决这类问题的突破口.它隐含的可能是速度的方向角(即速度与水平方向的夹角),则斜面的倾角的三角函数就联系了水平速度、竖直速度和实际速度;它也可能隐含的是位移的方向角(即位移和水平方向的夹角),则斜面的倾角的三角函数就联系了水平位移、竖直位移和实际位移.平抛运动速度与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,即vt的反向延长线与x轴的交点是水平位移的中点.下面根据这这个解题的基本方法我们来研究几道例题.例题1如图5,在倾角为θ的斜面上A点,以水平的初速度v0抛出一小球,小球落在斜面上的B点,不计空气阻力,从小球抛出开始计时,求:(1)小球经过多长时间落到B点?A、B两点间的距离L为多大?(2)小球经过多长时间距斜面最远?最远距离h为多少?(3)若以不同的初速度将小球水平抛出,试证明小球到达斜面速度方向与斜面的夹角α为一定值.分析与解(1)小球落到B点时,位移与水平方向的夹角与斜面倾角相等,即斜面的倾角为位移的方向角,其水平位移x与竖直位移y满足例题3如图9,从离地面的高度为h的固定点A,将甲球以速度v0抛出,抛射角为α,0。
平抛物体离斜面最远的计算

平抛物体离斜面最远的计算一、解题思路咱们来看看平抛物体离斜面最远的这个事儿哈。
你想啊,平抛运动它是水平方向上做匀速直线运动,竖直方向上做自由落体运动。
那对于离斜面最远这个情况呢,咱们得找到一个特殊的点。
这个点就是当物体的速度方向和斜面平行的时候,它离斜面最远啦。
为啥呢?你可以想象一下,要是速度方向还没平行,那它就还在靠近或者远离斜面的过程中,一旦平行了,就到了那个最远的状态了。
那咱们怎么去计算这个最远的距离呢?首先得设一些参数。
设斜面的倾角是θ,平抛的初速度是v₀,抛出点离斜面的高度是h。
然后呢,咱们根据平抛运动的规律来分析。
二、具体计算1. 速度关系水平方向速度vₓ = v₀,竖直方向速度vᵧ = gt。
当速度方向和斜面平行的时候,tanθ = vᵧ/vₓ = gt/v₀,这样就能算出时间t =v₀tanθ/g。
2. 位移关系水平位移x = v₀t = v₀²tanθ/g。
竖直位移y = 1/2gt² =v₀²tan²θ/2g。
那我们把物体的运动轨迹和斜面放在一个坐标系里看,设物体在斜面上投影点的坐标为(X,Y),根据几何关系,Y = x tanθ。
物体离斜面的距离d可以用一个向量的方法来算。
假设物体的位置坐标是(x,y),斜面方程是y = x tanθ,根据点到直线的距离公式d = y - x tanθ /√(1 + tan²θ)。
把x和y的值代入进去,d = 1/2gt² - v₀t tanθ /√(1 +tan²θ)。
再把t = v₀tanθ/g代入,就能算出d的具体表达式啦。
三、总结哈哈,这样咱们就把平抛物体离斜面最远的计算搞清楚啦。
其实啊,物理里面很多这种看似复杂的问题,只要咱们把基本的运动规律搞明白,设好参数,一步步分析,就能够解决的。
就像这个问题,从平抛运动的基本规律出发,到速度关系,再到位移关系,最后算出距离,每一步都很关键呢。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平抛运动斜面距离问题的解法赏析
无锡市堰桥中学 周维新
平抛运动是生活中常见的运动,也是高中物理曲线运动中典型的运动形式。
因此平抛运动高考中的重点和热点。
学生在处理较为简单的问题时,进行分解合成处理还能完成,但是对于较为复杂的问题时就感觉到束手无策。
本文就平抛运动中较为复杂的斜面距离问题的解法作如下探讨。
例题:如图,AB 斜面倾角为37°,小球从A 点以
初速度v 0=20m/s 水平抛出,恰好落到B 点,求:
(1)物体在空中飞行的时间;AB 间的距离;
(2)小球在B 点时速度的大小和方向; (3)从抛出开始经多少时间小球与斜面间的距离最大,最大距离是多少g=10m/s 2;
1、分解法
第(3)问的传统解法将平抛运动分解到斜面方向和垂直于斜面方向:沿斜面方向:V //=V 0cos37º=20×0.8=16m/s ,a //=gsin37º=10×0.6=6m/s 2匀加速直线运动。
垂直斜面方向:V ⊥= V 0sin37º=20×0.6=12m/s ,a ⊥=gcos37º=10×0.8=8m/s 2匀减速直线运动。
当垂直斜面方向的速度减为零时,球离斜面距离最远。
t===1.5s ,最远距离S==。
此种解法沿用了离地最高必有在垂直地面方向的速度为零的结论。
球离斜面距离最大,则球在垂直斜面上的速度必为零。
因而本解法采用正交分解,可以巩固学生的运动合成与分解知识,同时拓展对平抛运动的处理方法。
平抛运动分解为两个方向的匀变速直线运动,学生较易理解但运算较繁。
B A
2、追击解法
设斜面上有一个点,该点沿斜面作匀速直线运动。
该点的水平分速度
v
20m/s与小球的平抛初速度相等,竖直方向的分速度v y= v0tan37°=15m/s,所0=
以小球由A点平抛运动到B点时,该点也恰好从A点匀速运动到B点,在运动
过程中该点始终在小球的正下方。
在竖直方向,小球自由落体追击该点匀速直线
运动,当小球在竖直方向上的速度等于该点的竖直方向上的速度时,两点间有最
大距离,此时小球与斜面间的距离也最大。
解答如下:
研究对象:点V点x= 20m/s V点y= 15m/s
小球:V球x= 20m/s V球y=gt
当V球y= V点y时,点和球之间有最大距离y CD(如图)
t===1.5s y CD= y点-y球=V点y t-=15×1.5-5×
1.52=11.25m
则球与斜面间大最大距离S=y CD cos37º=9m
追击解法也采用运动的分解,但增加了研究对象,充分利用追击问题中的规
律:两物速度相同时距离有极值。
思维独特,想法新颖,运算较为简便,具有一
定创造性,有利与学生发散性思维的培养。
3、数学几何法
在数学中,直线和曲线间的距离最大时,必有曲线的切线与直线平行。
结合物理中的知识,平抛曲线的切线为速度的方向。
即小球
在与斜面距离最大的位置C点的速度V C与水平方向的夹
角为37º。
由此可以求得此时竖直方向的分速度V Cy=
v
tan37º=15 m/s,平抛运动竖直方向作自由落体运动,可求得时间t===1.5s,0
下落高度h==5×1.52=11.25m。
此时小球水平方向运动距离X=v0t=20×1.5=30m,又数学几何知识可知y CD=Xtan37º-h
则球与斜面间大最大距离S=y CD cos37º=(20×1.5×0.75-11.25)×0.8=9m 数学几何法同样运用运动分解,把物理和数学中几何知识相结合。
切入点非常清晰,但几何关系稍稍复杂。
该解法可以提高学生的数学应用能力及知识的综合应用能力。
总的来说这三种都抓住了“球与斜面距离最大”这一物理要求,分别得到相应的物理条件:分解法转化为垂直斜面方向的速度为零;追击法转化为两者速度相等;数学几何法转化为速度方向平行于斜面。
但总的来说都归到平抛运动处理的基本思想:化曲为直—分解。
通过对这些解法的讨论和分析,教师强化平抛运动的处理的基本方法是分解合成,同时训练学生的思维,提升学生对物理条件的分析建模能力,提高学生对知识的综合用能力。
如有侵权请联系告知删除,感谢你们的配合!。
