图像与追及问题
用图像法解追及问题

用图像法解追及问题(说明:六种情况下,两物同时、同地、同向出发)1、 t=t 0以前,后面的物体 与前面间的物体间的距 离增大。
2、 t=t 0时,两物体相距最远为x 0 x 。
3、 t=t 0以后,后面的物体 与前面物体韹距离减 小。
4、 能追及且只能相遇一 次。
5、 说明:X o 为在t o 时间内做匀速运动的物体通过 的距离。
(一) 匀 加 速 追 匀 速(三) 匀 加 速 追 匀 减 速t 0t时(二) 匀 速 追 匀 减例题:甲、乙两质点同时开始在彼此靠近的两水平轨道上同向运动,甲在前,乙在后,相距为x。
甲的初速度(四)匀减速追匀速(五)匀速追匀减速(六)匀减速追匀匀加速II 1 1L■011t 0t2t开始追及时,后面的物体与前面物体间的距离在减小,当两物体速度相等时,即t t o时刻:1、若X X0,则恰能追及,两物体只能相遇一次,这民是避免相撞的临界条件。
2、若X X o,则不能追及,此时两物体有最小距离为X)x。
3、若x x0,则相遇两次,设1时刻治x0,两物体第一次相遇,则t2时刻两物体第二次相遇。
为零,加速度为a,做匀加速直线运动。
关于两质点在相遇前的运动,某同学作如下分析:设两质点相遇前,它们韹距离为 x ,贝U x !at 22离x 有最小值,也就是两质点速度相等时,两质点间的距离最近。
你觉得他的分析是否正确?如果认为是正确的, 请求出它们间的最小距离;如果不正确, 请说明理由,并作出正确分析。
思维导图:M 在前此加速遇相遇前/两者之间的距离变能相遇是不确定的,这完全取决于两质点点的初始距离x 与v o 、a 之间的大小关系,所以该同学的分析不正确。
变大直到A 点,A 点后,v ?> v 乙,距离又变小直到二次相遇;(3)若x2相同速度,甲仍在前,乙在后,还没有相遇,距离还是 x 匹,以后呦>v 乙,就更不能相遇2a注意:弄清追及和被追物体因速度变化而引起两者间距离的变化过程,是解追及和相遇问题的关键,而两者速度相等是相距最远(或最近)此题也可用解析法:了。
高中物理 第二章 拓展课 运动图像与追及相遇问题教案

拓展课运动图像与追及相遇问题核心要点运动图像问题[要点归纳]1.x-t图像与v-t图像的比较比较内容x-t图像v-t图像图像物理意义反映的是位移随时间的变化规律反映的是速度随时间的变化规律①表示物体从位移为正处开始一直做反向匀速直线运动并过零位移处表示物体先做正向匀减速直线运动,再做负向匀加速直线运动②表示物体静止不动表示物体做正向匀速直线运动③表示物体从位移为零处开始做正向匀速运动表示物体从静止开始做正向匀加速直线运动④表示物体做加速直线运动表示物体做加速度逐渐增大的加速运动图像与坐标轴围成的“面积”的意义无实际意义表示相应时间内的位移(1)根据图像斜率可以求出物体的速度。
(2)由图像判断物体运动的方向。
(3)根据图像可以求出一段时间内的位移或发生一段位移所用的时间。
(4)在同一坐标系中若画出几个物体的位移图像,可比较它们运动的快慢,也可知道它们相遇(两图线的交点)的时刻。
3.v-t图像的应用(1)由图像判断物体运动的方向。
(2)根据图像的斜率可以求出物体的加速度。
(3)根据图像可以求出某一时刻的速度或某段时间内速度的变化量。
(4)根据图线与t 轴所围图形面积求物体的位移。
(5)根据图像可以判断物体的运动性质。
(6)在同一坐标系中,若画出几个物体的速度图像,可比较它们速度变化的快慢,也可知道它们速度相等(两图线的交点)的时刻。
[试题案例][例1] (多选)质点做直线运动的v -t 图像如图所示,规定向右为正方向,则该质点在前8 s 内的平均速度及质点运动的总路程为( ) A.总路程为2 mB.平均速度为0.25 m/s ,方向向左C.总路程为8 mD.平均速度为1 m/s ,方向向左解析 v -t 图像中,图线与时间轴围成的面积表示位移的大小,时间轴上方的面积表示的位移为正值,下方的面积表示的位移为负值,由图知,前8 s 内的总位移x =3×22 m -5×22m =-2 m ,平均速度v -=xt=-0.25 m/s ,负号表示方向向左,故选项B 正确,D 错误;总路程为s =3×22 m +5×22 m =8 m ,选项C 正确,A 错误。
高一物理必修1第二讲图像和追及相遇专题
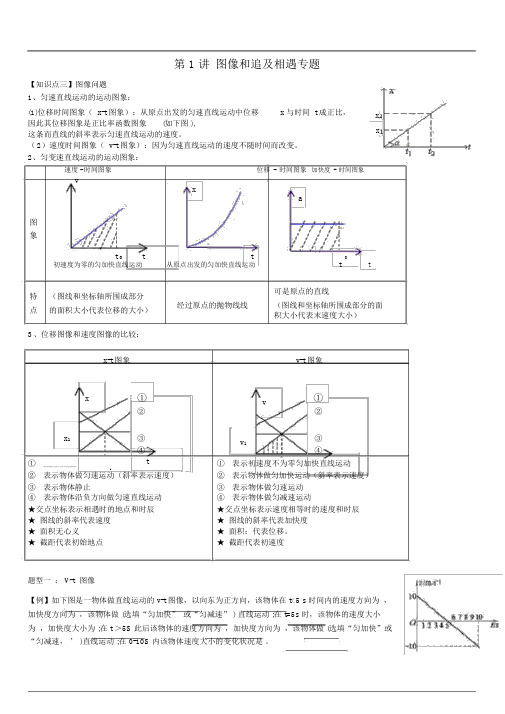
第 1 讲图像和追及相遇专题【知识点三】图像问题1、匀速直线运动的运动图象:(1)位移时间图象( x-t 图象):从原点出发的匀速直线运动中位移x 与时间 t 成正比,x 因此其位移图象是正比率函数图象(如下图 ),x 这条而直线的斜率表示匀速直线运动的速度。
(2)速度时间图象( v-t 图象):因为匀速直线运动的速度不随时间而改变。
2、匀变速直线运动的运动图象:速度 - 时间图象位移-时间图象加快度-时间图象vxa图象t 0 t tt 0t初速度为零的匀加快直线运动从原点出发的匀加快直线运动特(图线和坐标轴所围成部分可是原点的直线经过原点的抛物线线(图线和坐标轴所围成部分的面点的面积大小代表位移的大小)积大小代表末速度大小)3、位移图像和速度图像的比较:x-t 图象v-t 图象x ①v ①②②x1 ③v1③④④①t ①表示初速度不为零匀加快直线运动表示初始地点坐标不为零的匀速直线运动1②表示物体做匀速运动(斜率表示速度)②表示物体做匀加快运动(斜率表示速度)③表示物体静止③表示物体做匀速运动④表示物体沿负方向做匀速直线运动④表示物体做匀减速运动★交点坐标表示相遇时的地点和时辰★交点坐标表示速度相等时的速度和时辰★ 图线的斜率代表速度★ 图线的斜率代表加快度★ 面积无心义★ 面积:代表位移。
★ 截距代表初始地点★ 截距代表初速度题型一: V-t 图像【例】如下图是一物体做直线运动的 v-t 图像,以向东为正方向,该物体在 t<5 s 时间内的速度方向为,加快度方向为,该物体做 (选填“匀加快” 或“匀减速” ) 直线运动 ;在 t=5s 时,该物体的速度大小为,加快度大小为 ;在 t >5S 此后该物体的速度方向为,加快度方向为,该物体做 (选填“匀加快”或“匀减速,’ )直线运动 ;在 0-10S 内该物体速度大小的变化状况是。
【例】质点做直线运动的A 0.25m/s向右B 0.25m/s向左v-t 图像如下图,规定向右为正方向,则该质点在前8s 内均匀速度的大小和方向分别为( )C 1m/sD 1m/s 向右向左【例】某物体沿直线运动,其v-t 图象如下图,以下说法正确的选项是()A在 1s 内和第 6s 内的速度方向相反B在 1s 内和第 6s 内的加快度方向相反C第 2s 内的加快度为零D第 6s 末物体回到原出发点【例】如下图,一起学沿向来线行走,现用频闪照相记录了他行走中映该同学运动的速度-时间图像的是()9 个地点的图片,察看图片,能比较正确反【例】一枚火箭由地面竖直向上发射,其v-t 图象如下图,由图象可知()A 0 ~ t a段火箭的加快度小于t a-t b段火箭的加快度B 在 0-t b段火箭是上涨的,在t b-t c段火箭是着落的C t b时辰火箭离地面最远D t c时辰火箭回到地面【例】(2013 海南卷)一物体做直线运动,其加快度随时间变化的a-t 图象如下图。
专题2-6运动学图像和追及相遇问题【练】-2023-2024学年高一物理同步讲(004)
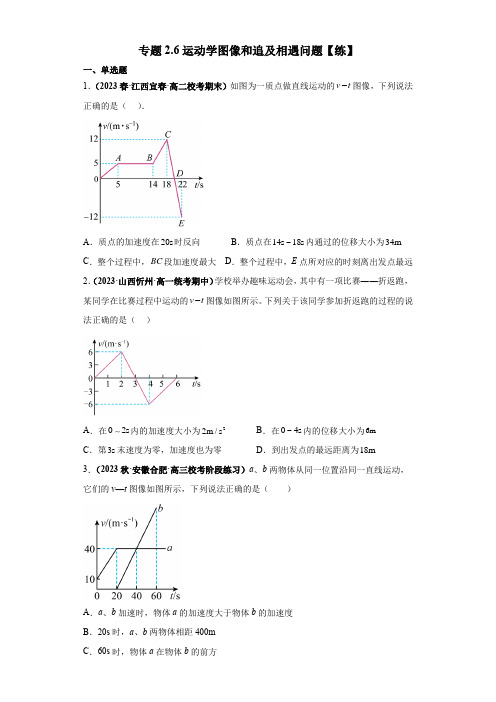
专题2.6运动学图像和追及相遇问题【练】一、单选题1.(2023春·江西宜春·高二校考期末)如图为一质点做直线运动的v t-图像,下列说法正确的是().~内通过的位移大小为34m A.质点的加速度在20s时反向B.质点在14s18sC.整个过程中,BC段加速度最大D.整个过程中,E点所对应的时刻离出发点最远2.(2023·山西忻州·高一统考期中)学校举办趣味运动会,其中有一项比赛――折返跑,-图像如图所示。
下列关于该同学参加折返跑的过程的说某同学在比赛过程中运动的v t法正确的是()A.在02s内的加速度大小为2~内的位移大小为6m2m/s B.在04sC.第3s末速度为零,加速度也为零D.到出发点的最远距离为18m 3.(2023秋·安徽合肥·高三校考阶段练习)a、b两物体从同一位置沿同一直线运动,它们的v—t图像如图所示,下列说法正确的是()A.a、b加速时,物体a的加速度大于物体b的加速度B.20s时,a、b两物体相距400mC.60s时,物体a在物体b的前方D .40s 时,a 、b 两物体速度相等,相距200m 4.(2023秋·广东河源·高三统考期末)正在行驶的某无人驾驶汽车发现正前方6m 处的斑马线上有行人,立即启动刹车程序。
已知汽车从发现行人到停下来的速度—时间()v t -图像如图所示,则可判定该汽车( )A .停在斑马线前0.5m 的地方B .停在斑马线前1.0m 的地方C .恰好在斑马线前停止D .已越过斑马线0.5m5.(2023秋·湖南永州·高三永州市第一中学校考阶段练习)高铁改变生活,地铁改变城市!地铁站距短需要频繁启停,为缩短区间的运行时间需要较大的启动加速度。
0=t 时刻,一列高铁和一列地铁沿各自所在的长直轨道由静止启动,0240s ~内的v t -图像如图所示。
下列说法正确的是( )A .甲是地铁的v t -图像,乙是高铁的v t -图像B .地铁和高铁加速过程的加速度大小之比为53:C .地铁和高铁加速过程的平均速度大小之比为31:D .0240s ~内,地铁和高铁的位移大小之比为58:6.(2023春·云南红河·高一开远市第一中学校校考期中)如图所示为A 、B 两物体在同一直线坐标系中运动的x t -图像,则下列关于物体运动的说法正确的是( )A .A 物体在7s 末速度方向改变B .两物体在第5s 末相遇C .A 物体在27s 时间内位移为4mD .05s 内两物体的平均速度不相同7.(2023秋·浙江嘉兴·高一统考期末)如图甲所示为甲物体做直线运动的x t -图像,如图乙所示为乙物体做直线运动的v t -图像。
用图像法解追及问题

用图像法解追及问题 LELE was finally revised on the morning of December 16, 2020用图像法解追及问题(说明:六种情况下,两物同时、同地、同向出发)题:甲、乙两质点同时开始在彼此靠近的两水平轨道上同向运动,甲在前,乙在后,相距为x。
甲的初速度为零,加速度为a,做匀加速直线运动。
关于两质点在相遇前的运动,某同学作如下分析:设两质点相遇前,它们韹距离为x ∆,则2012x at x v t ∆=+-,当0v t a=时,两质点的的距离x ∆有最小值,也就是两质点速度相等时,两质点间的距离最近。
你觉得他的分析是否正确?如果认为是正确的,请求出它们间的最小距离;如果不正确,请说明理由,并作出正确分析。
思维导图:)若此时202v a<时,前,距离变大直到A 点,A 点后,v 甲乙>v ,距离又变小直到二次相遇;(3)若202v x a >时,两者具有相同速度,甲仍在前,乙在后,还没有相遇,距离还是202v x a -,以后v 甲乙>v ,就更不能相遇了。
相同速度时有最小距离,即202v x a-。
注意:弄清追及和被追物体因速度变化而引起两者间距离的变化过程,是解追及和相遇问题的关键,而两者速度相等是相距最远(或最近)的临界条件。
此题也可用解析法:根据题意:甲、乙相遇的须满足:2012x at v t +=, 即20102at v t x -+=(1) 当2214402b ac v ax -=-⨯>,即满足202v x a <,方程有两解,即甲、乙相遇两次;(2) 当2214402b ac v ax -=-⨯=,即202v x a =时,甲、乙相遇一次;(3) 当2214402b ac v ax -=-⨯<,即202v x a >时,方程无解,甲、乙不能相遇。
1.3匀变速直线运动图像和追及相遇问题(解析版)

1.3匀变速直线运动图像和追及相遇问题一、v -t 图像1.图像的意义:v -t 图像反映了做直线运动的物体的速度随时间变化的规律,它只能描述物体做直线运动的情况.2.图像的斜率:v -t 图线(或切线)的斜率表示物体的加速度.斜率的绝对值表示加速度的大小,斜率为正表示加速度沿规定的正方向,但物体不一定做加速运动;斜率为负,则加速度沿负方向,物体不一定做减速运动. 3.v -t 图线与t 轴所围“面积”表示这段时间内物体的位移.t 轴上方的“面积”表示位移沿正方向,t 轴下方的“面积”表示位移沿负方向,如果上方与下方的“面积”大小相等,说明物体恰好回到出发点.用函数法解决非常规图像问题 二、三类图像 (1)a -t 图像由Δv =a Δt 可知图像中图线与横轴所围面积表示速度变化量,如图甲所示. (2)xt-t 图像 由x =v 0t +12at 2可得x t =v 0+12at ,截距b 为初速度v 0,图像的斜率k 为12a ,如图乙所示.(3)v 2-x 图像由v 2-v 02=2ax 可知v 2=v 02+2ax ,截距b 为v 02,图像斜率k 为2a ,如图丙所示.三、追及相遇问题1.追及相遇问题的实质就是分析两物体在相同时间内能否到达相同的空间位置. 2.追及相遇问题的基本物理模型:以甲车追乙车为例.(1)无论v 甲增大、减小或不变,只要v 甲<v 乙,甲、乙的距离不断增大.(2)若v甲=v乙,甲、乙的距离保持不变.(3)无论v甲增大、减小或不变,只要v甲>v乙,甲、乙的距离不断减小.3.分析思路可概括为“一个临界条件”“两个等量关系”.(1)一个临界条件:速度相等.它往往是物体间能否追上或两者距离最大、最小的临界条件,也是分析、判断问题的切入点;(2)两个等量关系:时间等量关系和位移等量关系.通过画草图找出两物体的位移关系是解题的突破口.4.常用分析方法(1)物理分析法:抓住“两物体能否同时到达空间某位置”这一关键,认真审题,挖掘题目中的隐含条件,建立物体运动关系的情境图.能否追上的判断方法(临界条件法)物体B追赶物体A:开始时,两个物体相距x0,当v B=v A时,若x B>x A+x0,则能追上;若x B=x A+x0,则恰好追上;若x B<x A+x0,则不能追上.(2)二次函数法:设运动时间为t,根据条件列方程,得到关于二者之间的距离Δx与时间t的二次函数关系,Δx=0时,表示两者相遇.①若Δ>0,即有两个解,说明可以相遇两次;②若Δ=0,一个解,说明刚好追上或相遇;③若Δ<0,无解,说明追不上或不能相遇.当t=-b2a时,函数有极值,代表两者距离的最大或最小值.(3)图像法:在同一坐标系中画出两物体的运动图像.位移-时间图像的交点表示相遇,分析速度-时间图像时,应抓住速度相等时的“面积”关系找位移关系.区分x-t图像和v-t图像1.无论x-t图像、v-t图像是直线还是曲线,所描述的运动都是直线运动,图像的形状反映了x与t、v与t的函数关系,而不是物体运动的轨迹.2.x-t图像中两图线的交点表示两物体相遇,v-t图像中两图线的交点表示该时刻两物体的速度相等,并非相遇.3.位置坐标x-y图像则能描述曲线运动,图线交点表示物体均经过该位置,但不一定相遇,因为不知道时间关系.例题1.如图为一质点做直线运动的v-t图像,下列说法正确的是()A .BC 段表示质点通过的位移大小为34 mB .在18~22 s 时间内,质点的位移为24 mC .整个过程中,BC 段的加速度最大D .整个过程中,E 点所对应的时刻离出发点最远 【答案】A 【解析】BC 段,质点的位移为x =5+122×4 m =34 m ,选项A 正确;在18~22 s 时间内,质点的位移为x =12×22 m +(-12×22) m =0 m ,选项B 错误;由题图看出,CE 段图线斜率的绝对值最大,则CE 段对应过程的加速度最大,选项C 错误;由题图看出,在0~20 s 时间内,速度均为正值,质点沿正方向运动,在20~22 s 时间内速度为负值,质点沿负方向运动,所以整个过程中,D 点对应时刻离出发点最远,选项D 错误.(多选)雨雪天气时路面湿滑,汽车在紧急刹车时的刹车距离会明显增加.如图所示为驾驶员驾驶同一辆汽车在两种路面紧急刹车时的v -t 图像,驾驶员的反应时间为1 s .下列说法正确的是( )A .从t =0到停下,汽车在湿滑路面的平均速度大于在干燥路面的平均速度B .从t =1 s 到停下,汽车在湿滑路面的平均速度大于在干燥路面的平均速度C .从t =0到停下,汽车在湿滑路面的行驶距离比在干燥路面的行驶距离多15 mD .从t =1 s 到停下,汽车在湿滑路面的加速度是在干燥路面的加速度的0.75倍 【答案】CD【解析】从t =0到停下,汽车在湿滑路面的位移为x 1=30×1 m +4×302m =90 m平均速度为v 1=905 m/s =18 m/s 汽车在干燥路面的位移为x 2=30×1 m +3×302 m =75 m平均速度为v 2=754m/s =18.75 m/s ,x 1-x 2=15 m ,故A 错误,C 正确;从t =1 s 到停下,汽车在湿滑路面的平均速度v 1′=302m/s =15 m/s ,汽车在干燥路面的平均速度 v 2′=302m/s =15 m/s ,故B 错误; 从t =1 s 到停下,汽车在湿滑路面的加速度大小a 1=304m/s 2=7.5 m/s 2,汽车在干燥路面的加速度大小a 2=303 m/s 2=10 m/s 2,则从t =1 s 到停下,汽车在湿滑路面的加速度是在干燥路面的加速度的0.75倍,故D 正确.在平直的公路上有甲、乙两辆汽车,它们运动的位置-时间图像如图所示。
高一运动图像与追及问题

图像与追击相遇1. 下图中表示三个物体运动位置和时间的函数关系图象,下列说法正确的是( )A. 运动速率相同,3B. 运动速率相同,3秒内经过路程相同,起点位置不同.C. 运动速率不同,3秒内经过路程不同,但起点位置相同.D. 均无共同点.2右图所示为A 和B 两质点的位移—时间图象,以下说法中正确的是( ) A. 当t=0时,A 、B 两质点的速度均不为零.B. 在运动过程中,A 质点运动得比B 快.C. 当t=t 1时,两质点的位移相等.D. 当t=t 1时,两质点的速度大小相等.3.某物体沿直线运动的v-t 图象如图所示,由图可以看出物体 ( )A . 沿直线向一个方向运动B . 沿直线做往复运动C . 加速度大小不变 D . 做匀速直线运动 4如图所示是甲、乙两物体的v 一t A .甲做匀加速运动,乙做匀减速运动 B .甲、乙两物体相向运动 C .乙比甲晚1s 出发 D .5s 末两物体相遇5慢车以10cm/s 2的加速度从车站启动开出,同时在距车站2km 处,与慢车平行的另一轨道上,有一以72km/h 的速度迎面开来的列车开始做匀减速运动,以便到站停下,问两车何时相遇.6两辆一样的汽车沿水平直线一前一后匀速行驶,速度均为v0。
若前车突然以恒定加速度刹车,在它刚停车后,后车以与前车相同的加速度开始刹车。
已知前车在刹车过程中所前进的距离为s。
若要保证两车在上述情况下不相撞,则两车在匀速行驶时应保持多大的距离?7.一辆巡逻车最快能在10 s内由静止加速到最大速度50 m/s,并能保持这个速度匀速行驶.在平直的高速公路上,该巡逻车由静止开始启动加速,追赶前方2 000 m处正以35 m/s 的速度匀速行驶的一辆违章卡车求:巡逻车至少需要多少时间才能追上卡车?图像与追击相遇答案1B 2AB 3BC 4C5 另车到站停下,末速度0的平方-初速度的平方=2as,算出加速度a1为0.1m/s2两车错车说明两车相遇,两车走的位移之和等于全程2000m分别求出两车的位移慢车走的位移s1=1/2at^2=0.05t^2另车走的位移s2=20t-1/2 a1 t^2=20t-0.05t^2然后s2+s2=2000=20t解得t=100s6 开始时,A、B两车的速度相同,两者之间距离保持恒定。
高中物理【运动学图像和追及相遇问题】
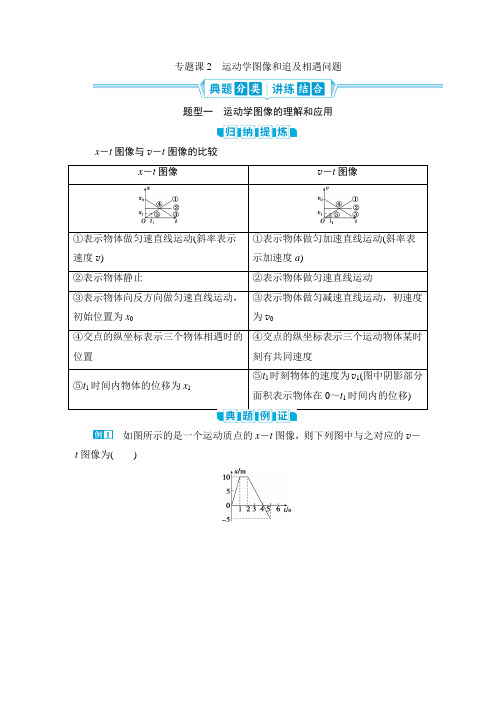
专题课2运动学图像和追及相遇问题题型一运动学图像的理解和应用x-t图像与v-t图像的比较x-t图像v-t图像①表示物体做匀速直线运动(斜率表示速度v)①表示物体做匀加速直线运动(斜率表示加速度a)②表示物体静止②表示物体做匀速直线运动③表示物体向反方向做匀速直线运动,初始位置为x0③表示物体做匀减速直线运动,初速度为v0④交点的纵坐标表示三个物体相遇时的位置④交点的纵坐标表示三个运动物体某时刻有共同速度⑤t1时间内物体的位移为x1⑤t1时刻物体的速度为v1(图中阴影部分面积表示物体在0~t1时间内的位移)如图所示的是一个运动质点的x-t图像,则下列图中与之对应的v-t图像为()[解析]根据位移—时间图像可知,第1 s内质点做匀速运动,第2 s内质点静止,后3 s反向匀速运动。
[答案] B如图所示,在位移—时间图像和速度—时间图像中,给出四条图线1、2、3、4代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是()A.图线1表示物体做曲线运动B.x-t图像中t1时刻v1>v2C.v-t图像中0至t3时间内3和4的平均速度大小相等D.两图像中,t2、t4时刻分别表示2、4开始反向运动[解析]图线1是位移—时间图像,表示物体做变速直线运动,A错误;x -t图线上某点斜率的绝对值的大小表示速度的大小,B正确;v-t图像中0至t3时间内3和4位移不同,所以平均速度大小不相等,C错误;t2时刻2开始反向运动,t4时刻4加速度方向变化但运动方向不变,D错误。
[答案] B题型二追及相遇问题1.解题关键(1)一个条件:速度相等。
这是两物体是否追上(或相撞)、距离最大、距离最小的临界点,是解题的切入点。
(2)两个关系:时间关系和位移关系。
通过画示意图找出两物体位移之间的数量关系,是解题的突破口。
2.常用方法(1)物理分析法抓住“两物体能否同时到达空间某位置”这一关键,认真审题,挖掘题中的隐含条件,建立物体运动关系的图景,并画出运动情况示意图,找出位移关系。
物理学霸笔记04运动图像及追及相遇问题

条 件 , 如 “ 刚 好 ”、 “ 恰 好 ”、 “ 最 多 ”、 “ 至 少 ” 等 , 它们往往对应一个临界状态,满足相应的临界条件。 特别提醒: ( 1 )在分析追及与相遇问题时,可用以下方法: ①临界条件法:当二者速度相等时,二者相距最远(最 近 )。 ②图象法:画出 x – t 图象或 v – t 图象,然后利用图象 进行分析求解。 ③数学判别式法:设相遇时间为 t ,根据条件列方程,得 到 关 于 t 的 一 元 二 次 方 程 , 用 判 别 式 进 行 讨 论 , 若 Δ >0 , 即 有 两 个 解 , 说 明 可 以 相 遇 两 次 ; 若 Δ =0 , 说 明 刚 好 追 上 或 相 遇 ; 若 Δ <0 , 说 明 追 不 上 或 不 能 相 遇 。 ( 2 )在追及问题中,若后者能追上前者,则追上时,两 者处于同一位置,后者的速度一定大于前者的速度;若后 者追不上前者,则当后者的速度与前者相等时,两者相距 最近。 ( 3 )在相遇问题中,同向运动的两物体追及即相遇;相 向运动的物体,当各自发生的位移大小之和等于开始时两 物体之间的距离时即相遇。 例:甲、乙两汽车同一条平直公路上同向运动,其速度— 时 间 图 象 分 别 如 图 中 甲 、 乙 两 条 曲 线 所 示 。 已 知 两 车 在 t2 时刻并排行驶,下列说法正确的是
考 点 04 运 动 图 像 及 追 及 相 遇 问 题 一、三种运动图像 1 .位移—时间( x – t )图像 ( 1 )位移—时间图像反映了做直线运动的物体的位移随 时间变化的规律,图像并非物体运动的轨迹。 ( 2 )位移—时间图像只能描述物体做直线运动的情况, 这是因为位移—时间图像只能表示物体运动的两个方向: t 轴上方代表正方向, t 轴下方代表负方向;如果物体做 曲线运动,则画不出位移—时间图像。 ( 3 )位移—时间图线上每一点的斜率表示物体在该时刻 的速度,斜率的大小表示速度的大小,斜率的正负表示速 度的方向。 2 .速度—时间( v – t )图像 ( 1 )速度—时间图像反映了做直线运动的物体的速度随 时间变化的规律,它也只能描述物体做直线运动的情况。 ( 2 )速度—时间图线上每一点的斜率表示物体该时刻的 加速度。斜率的大小表示加速度的大小,斜率为正表示加 速度沿规定的正方向,但物体不一定做加速运动,斜率为 负则加速度沿负方向,物体不一定做减速运动。 ( 3 )速度—时间图线与 t 轴所围面积表示这段时间内物 体的位移。 t 轴上方的面积表示位移沿正方向, t 轴下方 的面积表示位移沿负方向,如果上方与下方的面积大小相 等,说明物体恰好回到出发点。 3 .位置坐标( x – y )图像
第一章第三课时 图像法和追击问题
甲刹车经时间t(t>0.5 所示.
s),甲、乙两车的运动情景如图
1 2 32 甲车位移为x1=v0t-2a1t =16t-2t 甲车速度为v1=v0-a1t=16-3t 1 乙车位移为x2=v0×0.5+v0(t-0.5)-2a2(t-0.5)2 4 =16×0.5+16(t-0.5)-2(t-0.5)2 乙车速度为v2=v0-a2(t-0.5)=16-4(t-0.5) 二车免碰的临界条件是速度相等且位置相同,因此有v1 =v2,x1+x0=x2 其中,x0就是它们不相碰应该保持的最小距离. 解以上方程组可得x0=1.5 m.Βιβλιοθήκη 【答案】1.5 m
例1、(2008年四川高考理综卷23 )A、B两辆汽车 在笔直的公路上同向行驶。当 B车在A车前84 m处时, B车速度为4 m/s,且正以2 m/s2的加速度做匀加速运 动;经过一段时间后,B车加速度突然变为零。A车 一直以20 m/s的速度做匀速运动。经过12 s后两车相 遇。问B车加速行驶的时间是多少?
9、(07全国卷Ⅰ)甲、乙两运动员在训练交接棒的 过程中发现:甲经短距离加速后能保持9m/s的速度跑 完全程;乙从起跑后到接棒前的运动是匀加速的。为 了确定乙起跑的时机,需在接力区前适当的位置设置 标记。在某次练习中,甲在接力区前S0=13.5m处作了 标记,并以v=9m/s的速度跑到此标记时向乙发出起跑 口令。乙在接力区的前端听到口令时起跑,并恰好在 速度达到与甲相同时被甲追上,完成交接棒。已知接 力区的长度为L=20m。 求:(1)此次练习中乙在接棒前的加速度a (2)在完成交接棒时乙离接力区末端的距离。
由上述分析知当两车之间距离最大时: v 自=v 汽=at 汽车从启动到与自行车速度相等所经历的时间: v汽 v自 6m/s t= a = a =3m/s2=2s 所以:Δsmax=s 自-s 汽 1 2 =v 自 t-2at 1 =6×2-2×3×22m =6m
高考物理复习:运动图像 追及与相遇问题

不知道甲、乙初始位置关系,故无法判断两者间距离如何变化,选项B错误。
1 +2
乙在t1到t2时间内的位移小于做匀减速直线运动的位移,故平均速度v< 2 ,
选项C正确。
归纳总结(1)无论x-t图像、v-t图像是直线还是曲线,所描述的运动都是直线
运动,图像的形状反映的是x与t、v与t的函数关系,而不是物体运动的轨迹。
运动图像
追及与相遇问题
内
容
索
引
01
第一环节
必备知识落实
02
第二环节
关键能力形成
第一环节
必备知识落实
知识点一
运动图像
1.直线运动的x-t图像
(1)图像的物理意义。
反映了做直线运动的物体的位移随时间变化的规律。
(2)图线斜率的意义。
①图线上某点切线的斜率大小表示物体速度的大小。
②图线上某点切线的斜率正负表示物体速度的方向。
线的斜率表示速度,速度一直向同一方向运动,选项A错误。速度先增加后
16
减小,选项B错误 m/s=0.8 m/s,
选项C正确。速度从0增大到最大又减小为0,瞬时速度有两次为0.8 m/s,选
项D错误。
3.汽车正以10 m/s的速度在平直公路上前进,突然发现正前方距离s处有
一辆自行车以4 m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做
匀减速运动,加速度大小为6 m/s2,若汽车恰好不碰上自行车,则s大小为( A )
A.3 m
B.4 m
C.5 m
D.6 m
解析:设汽车关闭油门经过时间t与自行车速度相等,在该段时间内汽车和
1 +2
t
2
自行车位移分别为x1和x2,根据运动学公式有v2=v1-at, x1=
高中物理课件--运动图像-追及与相遇问题

1.分析追及问题的方法技巧可概括为“一个
栏 目
临界条件”、“两个等量关系”.
开 关
(1)一个临界条件——速度相等.它往往是物
体间能否追上或(两者)距离最大、最小的临
界条件,也是分析判断问题的切入点.
(2)两个等量关系:时间关系和位移关系,通
过画草图找出两物体的位移关系是解题的
突破口.
运动图像 追及与相遇问题
将 x≤x0 代入上式得 a≥(v12-x0v2)2
运动图像 追及与相遇问题
建模感悟
在一条直线上运动的两物体,后面物体的速度只要大于前面物体的
速度,两物体之间的距离将会越来越小,就有相撞的危险,若后面
本 刹车,做匀减速运动,而货车仍保持原速度前进.求客车的加速度符
课
栏 合什么条件,客车与货车才不会相撞?
目
开 关
解析 以货车为参照物,客车的初速度为 v0,则
v0=v1-v2
客车的末速度 vt=0(两车速度相等),客车相对货车的位移为 x≤x0,
由匀变速运动的公式有
围面积相等都说明两物体相遇.
(2)数学分析法:设在 t 时刻两物体能相遇,然后根据几何关系列
出关于 t 的方程 f(t)=0,若其方程无正实数解,则两物体不可能
相遇,如有正实数解,则两物体可能相遇.
(3)相对运动法:选择合适参考系,列出相应方程求解.
运动图像 追及与相遇问题
跟踪训练 3 如图 6 所示,直线
(2)若后者追不上前者,则当后者的速度与前者的速度相等
时,两者相距 最近 .
运动图像 追及与相遇问题
【深度思考】
追及问题中,“刚好能追上”、
本 课 栏
“刚好追不上”以及两物体间
高一物理图像、追及和相遇问题

13
2.甲、乙两物体相距x,它们同时同向运动,乙在前面做初速度 为零、加速度为a1的匀加速运动,甲在后面做初速度为v0,加 速度为a2的匀加速运动,则以下判断正确的是( A.若a1=a2,它们只能相遇一次 B.若a1>a2,它们可能相遇两次 C.若a1>a2,它们只能相遇两次 )
D.若a1<a2,它们不能相遇
的位置时,具有相同的速度.
12
1.甲、乙、丙三辆汽车以相同的速度同时经过某一个路标,以后 甲车一直做匀速直线运动,乙车先加速后减速,丙车先减速 后加速,它们经过下一路标时的速度又相同,则( A.甲车先通过下一个路标 B.乙车先通过下一个路标 C.丙车先通过下一个路标 )
D.三车同时到达下一个路标
答案:B
上或恰好追不上的临界条件是两物体速度相等,即v甲=v乙. 判断此种追赶情形能否追上的方法是:假定在追赶过程中两者在同
一位置,比较此时的速度大小,若v甲>v乙,则能追上;v甲<v乙,则追不
上,如果始终追不上,当两物体速度相等即v甲=v乙时,两物体的间 距最小.
9
(3)速度大者减速(如匀减速直线运动)追速度小者(如 匀速运动) ①两者速度相等,追者位移仍小于被追者位移,则永
车再次相遇,故D错.
答案:C
共 32 页 18
2.a、b两物体从同一位置沿同一直线运动,它们的速度图象如 图专2-3所示,下列说法正确的是( B.20 s时,a、b两物体相距最远 C.60 s时,物体a在物体b的前方 D.40 s时,a、b两物体速度相等,相距200 m ) A.a、b加速时,物体a的加速度大于物体b的加速度
共 32 页
24
解析:对设问(1) 解法1:汽车开动后速度由零逐渐增大,而自行车速度是定值, 当汽车的速度还小于自行车的速度时,两者距离越来越大, 当汽车的速度大于自行车的速度时,两者距离越来越小.所 以当两车的速度相等时,两车之间距离最大. 有v汽=at=v自,
第3讲 运动图像 追及相遇问题

()
(2)[v-t图像]如图所示是甲、乙两物体运动的速度—时间图像,下列说法正确
的是
()
A.0~5 s内,甲物体的加速度大小为0.75 m/s2
B.3 s时,乙物体的加速度大小为1 m/s2
C.0~5 s内,甲物体的位移大小为236 m
D.0~5 s内,乙物体的位移大于13.5 m
解析:(1) x-t 图像的斜率表示速度,可知 t=3 s 时,两车具有相同的速度, A 错误;a 车做匀速运动,而 b 车的速度一直减小,B 错误;在运动过程中的 任意时刻,b 车的位移坐标始终不大于 a 车的位移坐标,故 b 车始终没有超过 a 车,C 正确;因在 0~3 s 内,a 车的位移小于 b 车的位移,由 v =ΔΔxt 可知, a 车的平均速度小于 b 车的平均速度,D 错误。
(2) 根据 v-t 图像的斜率表示加速度,得 0~5 s 内甲物体的加速度大小为 a 甲=ΔΔvt =43 m/s2,选项 A 错误;乙物体的图像不是四分之一圆,所以点(3,3) 处切线的斜率不是 1,选项 B 错误;根据 v=-4 m/s+43t,得 t=5 s 时甲物体 的速度大小为83 m/s,则 0~5 s 内甲物体的位移大小为 x 甲=3×2 4 m-2×2 83 m =130 m,选项 C 错误;根据图像与坐标轴围成的面积表示位移,知 0~5 s 内 乙物体的位移大于1×2 3+3×3+3×2 2m=13.5 m,选项 D 正确。 答案:(1)C (2) D
对点清 1.x-t 图像的信息 (1)x-t 图像某点切线的斜率表示物体在该时刻的速度。 (2)纵坐标之差表示该段时间内的位移。 (3)两 x-t 图线的交点表示两物体在该位置、该时刻相遇。 2.v-t 图像的信息
2.[图像选择类问题]
运动学图像及追击相遇问题

2.3.典型运动的图象x -t 图v -t 图a -t 图匀速直线运动匀加速直线运动匀减速直线运动加速度均匀增大的加速运动加速度均匀减小的加速运动【注意】x -t 图、v -t 图、a -t 图描述的都是物体的直线运动,都不是物体运动的轨迹,图象的形状由x 与t 、v 与t 、a 与t 的函数关系决定。
追及相遇问题——一定能追上的情况如果乙做匀速运动或匀减速运动,甲在乙的身后做匀加速运动,只要时间足够长,甲的速度一定会大于乙的速度,最终一定能追上乙。
如果两者做的都是匀加速直线运动,只要甲的加速度大于乙,则最终也是一定能追上的。
【典例】甲乙两人同向运动,开始时乙以速度v 做匀速直线运动,甲在乙身后Δx 的位置,初速度为v ,开始做加速度为a 的匀加速直线运动。
(1)画出甲、乙两物体的v -t 图;(2)求甲追上乙的时间t ;(3)甲追上乙之前二者之间的最大距离x 。
【解析】(1)甲、乙两物体的v -t 图如图所示。
t 之前甲的速度比乙小,甲乙间 的距离不断增大,但此后甲的速度比乙大,不断拉近与乙的距离,2t 时刻甲终于21m 114. 5.又把二者之间的距离追至刚开始的Δx,此后甲继续追赶,直至时刻t 追上乙,接下来就会把乙甩在身后了。
(2)根据列出运动学方程,可得解得甲追上乙的时间为(3)图中阴影部分面积S 加上Δx 就是甲乙之间的最大距离,,,可得追及相遇问题——追上需要条件的情况物体甲想追上前面的物体乙,则甲的速度必须比乙的速度大。
如果乙做的是匀速运动或者匀加速运动,甲做的是匀减速运动或匀速运动,若刚开始甲的速度比乙小,则肯定追不上。
如果开始时甲的速度比乙大,则必须满足在甲、乙速度相等之前甲必须追上乙,如果此时还追不上乙,那么之后乙的速度反超甲,那就再也追不上了。
【典例】以匀减速直线运动追匀加速运动为例,甲、乙两物体同时同向运动,甲在乙的后面Δx处,物体甲做匀减速直线运动,初速度为v,减速度大小为a;物体乙做匀加速直线运动,初速度为v,加速度大小为a,则甲能追上乙得满足什么条件?【解析】甲必须在乙的速度超过自己之前追上乙,否则一旦乙的速度超过自己,那么将无法追上了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
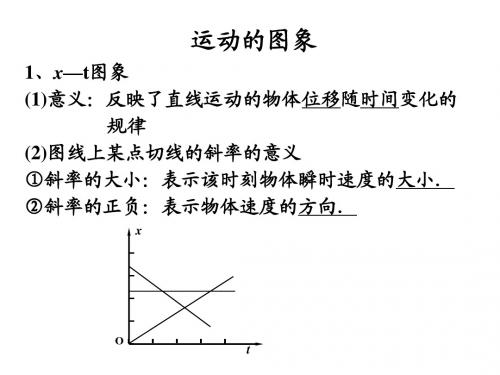
图像与追及问题x—t图与v—t图一、匀速直线运动图像1.位移-时间图像(1)物理意义:由x=vt可知,图像是通过原点的一条倾斜直线。
如图所示,它反映做匀速直线运动的物体位移随时间变化的规律。
(2)图线信息:①任一时刻对应的位移x;②图线上某点切线的斜率大小表示物体速度大小,斜率为正,表示速度方向为正,远离参考原点;斜率为负,表示速度方向为负,向参考原点运动.1.如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置—时间(xt)图线。
由图可知()A.在时刻t1,a车追上b车B.在时刻t2,a、b两车运动方向相反C.在t1到t2这段时间内,b车的速率先减少后增加D.在t1到t2这段时间内,b车的速率一直比a车的大2。
如图所示,某滑块初速度v0沿表面粗糙且足够长的固定斜面,从顶端下滑,直至速度为零.对于该运动过程若用h、s、v、a分别表示滑块的下降高度、位移、速度和加速度的大小,t表示时间,则下列图像最能正确描述这一运动规律的是( )2.速度—时间图像(1)平行于时间轴的直线如图.(2)“面积”对应“位移"大小.原因:x=vt二、匀变速直线运动图像1.速度—时间图像在vt图像中,匀变速直线运动为一条直线,直线的斜率为加速度,图1中的加速度为正,图2中的加速度为负.2。
位移的表达“面积”对应“位移”,S△OA2为正,说明位移方向与正方向相同,S△2B4为负,说明位移方向与正方向相反.1.一质点沿x轴做直线运动,其vt图像如图所示。
质点在t=0时位于x=5 m处,开始沿x轴正向运动。
当t=8 s时,质点在x轴上的位置为( )A.x=3 m B.x=8 mC.x=9 m ﻩﻩD.x=14 m2。
一质点在外力作用下做直线运动,其速度v随时间t变化的图像如图所示,在图中标出的时刻中,质点所受合外力的方向与速度方向相同的有()A.t1 ﻩB。
t2C.t3 D.t43。
甲、乙两物体在t=0时刻经过同一位置沿x轴运动,其v。
t图像如图所示,则( )A.甲、乙在t=0到t=1 s之间沿同一方向运动B。
乙在t=0到t=7 s之间的位移为零C.甲在t=0到t=4 s之间做往复运动D.甲、乙在t=6s时的加速度方向相同4.质点做直线运动的速度-时间图像如图所示,该质点()A.在第1秒末速度方向发生了改变B.在第2秒末加速度方向发生了改变C.在前2秒内发生的位移为零D.第3秒末和第5秒末的位置相同5.以不同初速度将两个物体同时竖直向上抛出并开始计时,一个物体所受空气阻力可忽略,另一物体所受空气阻力大小与物体速率成正比,下列用虚线和实线描述两物体运动的v。
t图像可能正确的是()6.如图所示,水平地面上有一静止平板车,车上放一物块,物块与平板车表面间的动摩擦因数为0。
2,t=0时,车受水平外力作用开始沿水平面做直线运动,其v。
t图像如图所示。
t=12 s后车静止不动.平板车足够长,物块不会从车上掉下,g取10 m/s2。
关于物块的运动,以下描述正确的是()A。
0-6 s加速,加速度大小为4 m/s2,6-12 s减速,加速度大小为4 m/s2B.0—6 s加速,加速度大小为2 m/s2,6-12 s减速,加速度大小为2 m/s2 C.0—6 s加速,加速度大小为2 m/s2,6-12 s先加速后减速,加速度大小为2 m/s2D.0-6 s加速,加速度大小为2 m/s2,6—12 s先加速后减速,加速度大小为4 m/s27.一列车沿直线轨道从静止出发由A地驶向B地,并停在B地,列车做加速运动时,其加速度最大值为a1;做减速运动时,其加速度的绝对值的最大值为a2。
要让列车由A地到B 地所用的时间最短,图中列车的vt图像应是(其中tanα=a1;tanβ=a2)()8.(2014·河北衡水)从同一地点同时开始沿同一方向做直线运动的两个物体A、B的速度图像如图实线所示.在0-t0时间内,下列说法中错误的是()A.A物体的加速度不断减小,速度不断增大B。
B物体的加速度不断减小,速度不断减小C。
A、B物体的位移都不断增大D.A、B两个物体的平均速度大小都大于错误!7。
一个物体做变加速直线运动,依次经过A、B、C三点,B为AC的中点.物体在AB 段的加速度恒为a1,在BC段的加速度恒为a2,已知物体经过A、B、C三点的速度为vA、vB、vC,有vA<vC,且vB=错误!,则加速度a1和a2的大小为()A.a1<a2 B.a1=a2C.a1>a2 ﻩD.条件不足无法确定10.(2015·菏泽模拟)下列图像能正确反映物体在直线上运动,经2 s又回到初始位置的是()高考调研规律(三)追及、相遇问题技巧归纳追及、相遇问题的实质,就是分析两物体在相同时间内能否到达相同的位置.当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距越来越大或越来越小,这时就会涉及追及、相遇和避免碰撞等问题.1.追及问题的方法技巧“一个临界条件”“两个等量关系"(1)一个临界条件:“速度相等”.“刚好能追上”“刚好追不上”以及两物体间有最大距离或最小距离的条件是速度相等,它往往是物体间能否追上或两者距离最大、最小的临界条件,也是分析判断问题的切入点.(2)两个等量关系:时间关系和位移关系,通过画草图找出两物体的位移关系是解题的突破口.(3)追及与时间过量:若被追赶的物体做匀减速直线运动,一定要注意判断追上前该物体是否已经停止运动.2。
能否追上的判断方法做匀速直线运动的物体B追赶从静止开始做匀加速直线运动的物体A:开始时,两个物体相距x0.若vA=vB时,xA+x0<xB,则能追上;若vA=vB时,xA+x0=xB,则恰好不相撞;若vA=vB时,xA+x0〉xB,则不能追上.1. A、B两辆汽车在笔直的公路上同向行驶,当B车在A车前84 m处时,B车速度为4m/s,且正以2 m/s2的加速度做匀加速运动;经过一段时间后,B车加速度突然变为零,A车一直以20 m/s的速度做匀速运动,经过12 s后两车相遇.求B车加速行驶的时间.2。
甲车以10 m/s的速度在平直的公路上匀速行驶,乙车以4m/s的速度与甲车平行同向做匀速直线运动,甲车经过乙车旁边开始以大小为0.5 m/s2的加速度刹车,从甲车刹车开始计时,求:(1)乙车在追上甲车前,两车相距的最大距离;(2)乙车追上甲车所用的时间。
3。
公路上行驶的两汽车之间应保持一定的安全距离,当前车突然停止时,后车司机可以采取刹车措施,使汽车在安全距离内停下而不会与前车相撞,通常情况下,人的反应时间和汽车系统的反应时间之和为1 s,当汽车在晴天干燥沥青路面上以108 km/h 的速度匀速行驶时,安全距离为120 m,设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5,若要求安全距离仍为120 m,求汽车在雨天安全行驶的最大速度.4。
某煤矿运输部有一新采购的水平浅色足够长传送带以 4.0 m/s的恒定速度运动,若使该传送带改做加速度大小为3。
0 m/s2的匀减速运动,并且在传送带开始做匀减速运动的同时,将一煤块(可视为质点)无初速度放在传送带上.已知煤块与传送带间的动摩擦因数为0.10,重力加速度取10 m/s2,求煤块在浅色传送带上能留下的痕迹长度和相对于传送带运动的位移大小. (计算结果保留两位有效数字)5.甲乙两车在公路上沿同一方向做直线运动,它们的v。
t图像如图所示.两图像在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合可能是()A.t′=t1,d=S B.t′=\f(1,2)t1,d=错误!SC。
t′=错误!t1,d=错误!SD.t′=错误!t1,d=错误!S6。
甲乙两车在一平直道路上同向运动,其vt图像如图所示,图中△OPQ和△OQT的面积分别为s1和s2(s1>s2).初始时,甲车在乙车前方s0处.( )A。
若s0=s1+ s2,两车不会相遇B.若s0<s1,两车相遇2次C.若s0= s1,两车相遇1次D.若s0= s2,两车相遇1次7.如图所示,甲、乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的。
为了确定乙起跑的时机,需在接力区前适当的位置设置标记.在某次练习中,甲在接力区前x0=13.5m处作了标记,并以v=9 m/s的速度跑到此标记时向乙发出起跑口令。
乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒。
已知接力区的长度L=20 m.求:(1)此次练习中乙在接棒前的加速度a;(2)在完成交接棒时乙离接力区末端的距离.8.一辆摩托车能达到的最大速度为30 m/s,要想在3 min内由静止起沿一条平直公路追上前面1 000m处正以20 m/s的速度匀速行驶的汽车,则摩托车必须以多大的加速度启动?(保留2位有效数字)利用速率-时间图像解路程问题1.如图所示,两光滑斜面的总长度相等,高度也相等,两球a、b由静止从顶端下滑,小球在转折处的速度大小不变,如果a球到达底端的时间为ta,b球到达底端的时间为tb,则两球到达底端的时间关系()A。
ta>tb ﻩB.ta<tbC.ta=tb ﻩﻩD。
无法判断2。
如图所示,游乐场中,从高处A到水面B处有两条长度相同的光滑轨道.甲、乙两小孩沿不同轨道同时从A处自由滑向B处,下列说法正确的有( )A.甲的切向加速度始终比乙的大B.甲、乙在同一高度的速度大小相等C.甲、乙在同一时刻总能到达同一高度D.甲比乙先到达B处3。
一个固定在水平面上的光滑物块,其左侧面是斜面AB,右侧面是曲面AC,如图所示。
已知AB和AC的长度相同.两个小球p、q同时从A点分别沿AB和AC由静止开始下滑,比较它们到达水平面所用的时间()A。
p小球先到B。
q小球先到C.两小球同时到D。
无法确定。
