《大学物理简明教程》课后习题答案(全)之欧阳光明创编
大学物理简明教程_课后答案_1章

问题1.1 关于行星运动的地心说和日心说的根本区别是什么?答:地心说和日心说的根本区别在于描述所观测运动时所选取的参考系不同。
1.2 牛顿是怎样统一了行星运动的引力和地面的重力?答:用手向空中抛出任一物体,按照惯性定律,物体应沿抛出方向走直线,但是它最终却还会落到地面上。
这说明地球对地面物体都有一种吸引力。
平抛物体的抛速越大,落地时就离起点越远,惯性和地球吸引力使它在空中划出一条曲线。
地球吸引力也应作用于月球,但月球的不落地,牛顿认为这不过是月球下落运动曲线的弯曲度正好与地球表面的弯曲程度相同。
这样牛顿就把地球对地面物体的吸引力和地球对月球的吸引力统一起来了。
牛顿认为这种引力也作用在太阳和行星、行星与行星之间,称为万有引力。
并认为物体所受的重力就等于地球引力场的引力。
这样牛顿就统一了行星运动的引力和地面的重力。
1.3 什么是惯性? 什么是惯性系?答:任何物体都有保持静止或匀速直线运动状态的特性,这种特性叫惯性。
我们把牛顿第一定律成立的参考系叫惯性系。
而相对于已知惯性系静止或做匀速直线运动的参考系也是惯性系。
1.4 人推动车的力和车推人的力是作用力与反作用力,为什么人可以推车前进呢?答:人推动车的力和车推人的力是作用力与反作用力,这是符合牛顿第三定律的。
但这两两个力是分别作用在两个物体上的。
对于车这个研究对象来说,它就只受到人推动车的力(在不考虑摩擦力的情况下),所以人可以推车前进。
1.5 摩擦力是否一定阻碍物体的运动?答:不一定。
例如汽车前进时,在车轮与路面之间实际上存在着两种摩擦力:静摩擦和滚动摩擦。
前者是驱使汽车前进的驱动力,后者是阻碍汽车前进的阻力。
再如,拖板上放上一物体,拉动拖板,物体可以和拖板一起运动,其原因就是拖板给予了物体向前的摩擦力。
1.6 用天平测出的物体的质量,是引力质量还是惯性质量?两汽车相撞时,其撞击力的产生是源于引力质量还是惯性质量?1答:用天平测出的物体的质量和引力有关,是地球对物体和砝码的引力对天平刀口支撑点力矩平衡测出的质量,所以是引力质量。
大学物理简明教程课后习题加答案43页

大学物理简明教程习题解答习题一1-1 |r ∆|与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆; (2)t d d r 是速度的模,即t d d r ==v tsd d . t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆtr t d d d d d d r rr += 式中t rd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢),所以式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=,故它们的模即为而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作其二,可能是将22d d d d t r tr 与误作速度与加速度的模。
在1-1题中已说明t r d d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r 也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-=222d d d d t r t r a θ径。
大学物理简明教程课后习题加答案

大学物理简明教程习题解答习题一1-1 |r ∆|与r ∆有无不同t d d r 和t d d r 有无不同 t d d v 和t d d v有无不同其不同在哪里试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即t d d r ==v t sd d .t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中t rd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,t v d d 是加速度a 在切向上的分量. ∵有ττ(v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττ+=式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确为什么两者差别何在解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=,jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a tr v ==其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
大学物理简明教程课后习题及答案(2020年7月整理).pdf

图 1-4
解: 设人到船之间绳的长度为 l ,此时绳与水面成 角,由图可知
将上式对时间 t 求导,得
l2 = h2 + s2
2l dl = 2s ds dt dt
题 1-4 图
根据速度的定义,并注意到 l , s 是随 t 减少的,
∴
v绳
=
−
dl dt
=
v0 , v船
=
−
ds dt
即
v船
=
− ds dt
dt v=
v表示(加表速轨度道的节模线,方即向单位矢ddt)v,,=所dd以tv 是 +加v速d度
a
在切向上的分量.
dt dt dt
dv
式中 dt 就是加速度的切向分量. drˆ 与 dˆ ( dt dt 的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为 x = x ( t ), y = y ( t ),在计算质点的速度和加速度时,有人先求
dr
d2r
出 r= x 2 + y 2 ,然后根据 v = dt ,及 a = dt 2 而求得结果;又有人先计算速度和加速度
的分量,再合成求得结果,即
v=
dx
2
+
dy
2
dt dt 及 a =
d2 dt
x
2
2
+
d2 dt
y
2
2
你认为两种方法哪一种正确?为什么?两者差别何在? 解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有
7
j
m
48
2-3 质点在流体中作直线运动,受与速度成正比的阻力 kv ( k 为常数)作用, t =0 时质点的
《大学物理简明教程》课后答案

《大学物理简明教程》课后答案习题11-1 |r ∆|与r ∆ 有无不同?t d d r 和t d d r 有无不同? t d d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即td d r==v t s d d . trd d 只是速度在径向上的分量. ∵有r r ˆr =(式中r ˆ叫做单位矢),则tˆr ˆt r t d d d d d d rrr += 式中trd d 就是速度径向上的分量, ∴trt d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即tva d d=,t v d d 是加速度a 在切向上的分量.∵有ττ(v =v 表轨道节线方向单位矢),所以tv t v t v d d d d d d ττ += 式中dt dv就是加速度的切向分量. (tt r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-5 质点沿x 轴运动,其加速度和位置的关系为 a =2+62x ,a 的单位为2s m -⋅,x 的单位为 m. 质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值. 解: ∵ xvv t x x v t v a d d d d d d d d ===分离变量: x x adx d )62(d 2+==υυ 两边积分得c x x v ++=322221 由题知,0=x 时,100=v ,∴50=c∴ 13s m 252-⋅++=x x v1-7 一质点沿半径为1 m 的圆周运动,运动方程为 θ=2+33t ,θ式中以弧度计,t 以秒计,求:(1) t =2 s 时,质点的切向和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少?解: t tt t 18d d ,9d d 2====ωβθω (1)s 2=t 时, 2s m 362181-⋅=⨯⨯==βτR a2222s m 1296)29(1-⋅=⨯⨯==ωR a n(2)当加速度方向与半径成ο45角时,有145tan ==︒na a τ即 βωR R =2 亦即 t t 18)9(22= 则解得 923=t 于是角位移为rad 67.29232323=⨯+=+=t θ习题22-3 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk ev )(0-;(2) 由0到t 的时间内经过的距离为x =(km v 0)[1-t m k e )(-];(3)停止运动前经过的距离为)(0k mv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量. 答: (1)∵ tvm kv a d d =-= 分离变量,得m tk v v d d -=即 ⎰⎰-=v v t mtk v v 00d d m kte v v -=ln ln 0∴ tm k e v v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d(3)质点停止运动时速度为零,即t →∞, 故有 ⎰∞-=='00d km v t ev x tm k (4)当t=km时,其速度为 ev e v ev v km m k 0100===-⋅- 即速度减至0v 的e1.2-6 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m ==2-7 设N 67j i F -=合.(1) 当一质点从原点运动到m 1643k j i r++-=时,求F 所作的功.(2)如果质点到r 处时需0.6s ,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化.解: (1)由题知,合F为恒力,∴ )1643()67(k j i j i r F A++-⋅-=⋅=合J 452421-=--= (2) w 756.045==∆=t A P (3)由动能定理,J 45-==∆A E k2-8 如题2-18图所示,一物体质量为2kg ,以初速度0v =3m ·s -1从斜面A 点处下滑,它与斜面的摩擦力为8N ,到达B 点后压缩弹簧20cm 后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度.解: 取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原 长处为弹性势能零点。
《大学物理简明教程》课后习题

《大学物理简明教程》习题解答习题一1-1 |r ∆|与r ∆有无不同?td d r 和td d r 有无不同? td d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r ϖϖ-=∆;(2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即t v a d d ϖϖ=,t v d d 是加速度a 在切向上的分量.∵有ττϖϖ(v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττϖϖϖ+=式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τϖϖΘ与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =trd d ,及a =22d d t r而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r ϖϖϖ+=,jt y i t x t r a jt y i t x t r v ϖϖϖϖϖϖϖϖ222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x yx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a tr v ==其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
大学物理(上)课后习题答案之欧阳生创编

第1章质点运动学P21时间:2021.02.08创作人:欧阳生1.8一质点在xOy 平面上运动,运动方程为:x =3t +5, y =21t 2+3t -4. 式中t 以 s 计,x ,y 以m 计。
⑴以时间t 为变量,写出质点位置矢量的表示式;⑵求出t =1 s 时刻和t =2s 时刻的位置矢量,计算这1秒内质点的位移;⑶计算t =0 s 时刻到t =4s 时刻内的平均速度;⑷求出质点速度矢量表示式,计算t =4 s 时质点的速度;(5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算t =4s 时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式)。
解:(1)jt t i t r)4321()53(2-+++=m⑵1=t s,2=t s时,j i r5.081-=m ;2114r i j =+m∴213 4.5r r r i j∆=-=+m⑶0t =s 时,054r i j =-;4t =s 时,41716r i j =+ ∴140122035m s 404r r ri ji j t --∆+====+⋅∆-v ⑷1d 3(3)m s d ri t j t-==++⋅v ,则:437i j =+v 1s m -⋅(5) 0t =s 时,033i j =+v ;4t =s 时,437i j =+v (6)2d 1 m s d a j t-==⋅v这说明该点只有y 方向的加速度,且为恒量。
1.9质点沿x 轴运动,其加速度和位置的关系为226a x =+,a 的单位为m/s2,x 的单位为m 。
质点在x=0处,速度为10m/s,试求质点在任何坐标处的速度值。
解:由d d d d d d d d x a tx tx===v v v v 得:2d d (26)d a x x x ==+v v两边积分2100d (26)d xx x =+⎰⎰vv v 得:232250x x =++v∴1m s -=⋅v1.11一质点沿半径为1 m 的圆周运动,运动方程为θ=2+33t ,式中θ以弧度计,t 以秒计,求:⑴t =2s 时,质点的切向和法向加速度;⑵当加速度的方向和半径成45°角时,其角位移是多少? 解:t t t t 18d d ,9d d 2====ωβθω⑴s 2=t 时,2s m 362181-⋅=⨯⨯==βτR a⑵当加速度方向与半径成ο45角时,有:tan 451n a a τ︒==即:βωR R =2,亦即t t 18)9(22=,解得:923=t 则角位移为:322323 2.67rad 9t θ=+=+⨯=1.13一质点在半径为0.4m 的圆形轨道上自静止开始作匀角加速度转动,其角加速度为α=0.2 rad/s2,求t =2s 时边缘上各点的速度、法向加速度、切向加速度和合加速度。
物理学简明教程1-9章课后习题答案

物理学简明教程1-9章课后习题答案(总115页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v . (1) 根据上述情况,则必有( )(A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r(C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s(D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s(2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v(C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts t ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故ts t d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x .下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r 表示速度矢量;在自然坐标系中速度大小可用公式ts d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D). 1 -3 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -4 质点的运动方程为23010t t x +-=22015t t y -=式中x ,y 的单位为m,t 的单位为s.试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向.分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向.解 (1) 速度的分量式为t tx x 6010d d +-==v t ty y 4015d d -==v 当t =0 时, v 0x =-10 m·s-1 , v 0y =15 m·s-1 ,则初速度大小为120200s m 0.18-⋅=+=y x v v v 设v 0与x 轴的夹角为α,则23tan 00-==x yαv v α=123°41′(2) 加速度的分量式为2s m 60d d -⋅==t a x x v , 2s m 40d d -⋅-==ta y y v 则加速度的大小为222s m 1.72-⋅=+=y x a a a 设a 与x 轴的夹角为β,则32tan -==x y a a β β=-33°41′(或326°19′)1 -5 质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m·s-1 ,求质点的运动方程.分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决.由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =.如a =a (t )或v =v (t ),则可两边直接积分.如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分.解 由分析知,应有⎰⎰=tt a 0d d 0v v v 得 03314v v +-=t t (1)由 ⎰⎰=tx x t x 0d d 0v 得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m·s-1代入(1)、(2)得v 0=-1 m·s-1, x 0= m于是可得质点运动方程为75.0121242+-=t t x1 -6 飞机以100 m·s-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问:(1) 此时目标在飞机正下方位置的前面多远 (2) 投放物品时,驾驶员看目标的视线和水平线成何角度(3) 物品投出s后,它的法向加速度和切向加速度各为多少?题 1-13 图分析 物品空投后作平抛运动.忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动.到达地面目标时,两方向上运动时间是相同的.因此,分别列出其运动方程,运用时间相等的条件,即可求解.此外,平抛物体在运动过程中只存在竖直向下的重力加速度.为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β.由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得.解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x =vt , y =1/2 gt 2飞机水平飞行速度v =100 m·s -1 ,飞机离地面的高度y =100 m,由上述两式可得目标在飞机正下方前的距离m 4522==gy x v(2) 视线和水平线的夹角为 o 5.12arctan==x y θ (3) 在任意时刻物品的速度与水平轴的夹角为vv v gt αx y arctan arctan == 取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为2s m 88.1arctan sin sin -⋅=⎪⎭⎫ ⎝⎛==v gt g αg a t 2s m 62.9arctan cos cos -⋅=⎪⎭⎫ ⎝⎛==v gt g g a n α1 -7 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t 时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b (3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v 其加速度的切向分量和法向分量分别为b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为R )(402222bt b a a a a t tn -+=+=v 其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n 20)(arctan arctan v (2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v = (3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为b s s s t 2200v =-= 因此质点运行的圈数为bRR s n π4π220v == 1 -8 一升降机以加速度 m·s-2上升,当上升速度为 m·s-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距 m .计算:(1)螺丝从天花板落到底面所需要的时间;(2)螺丝相对升降机外固定柱子的下降距离.分析 在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 =y 1(t )和y 2 =y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解;另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度.升降机厢的高度就是螺丝(或升降机)运动的路程.解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为20121at t y +=v 20221gt t h y -+=v 当螺丝落至底面时,有y 1 =y 2 ,即20202121gt t h at t -+=+v v s 705.02=+=ag h t (2) 螺丝相对升降机外固定柱子下降的距离为m 716.021202=+-=-=gt t y h d v 解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′=g +a ,螺丝落至底面时,有2)(210t a g h +-= s 705.02=+=ag h t (2) 由于升降机在t 时间内上升的高度为2021at t h +='v 则 m 716.0='-=h h d题 1-8 图1 -9 一无风的下雨天,一列火车以v 1= m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v2 .(设下降的雨滴作匀速运动)题 1-19 图分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得1o 12s m 36.575tan -⋅==v v 1 -10 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿?分析 这也是一个相对运动的问题.可视雨点为研究对象,地面为静参考系S,汽车为动参考系S′.如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足h l αarctan≥.再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1.题 1-20 图解 由122v v v -='[图(b)],有θθcos sin arctan221v v v -=α 而要使h l αarctan ≥,则 hl θθ≥-cos sin 221v v v ⎪⎭⎫ ⎝⎛+≥θh θl sin cos 21v v 1 -11 用水平力F N 把一个物体压着靠在粗糙的竖直墙面上保持静止.当F N 逐渐增大时,物体所受的静摩擦力F f 的大小( )(A) 不为零,但保持不变(B) 随F N 成正比地增大(C) 开始随F N 增大,达到某一最大值后,就保持不变(D) 无法确定分析与解 与滑动摩擦力不同的是,静摩擦力可在零与最大值μF N 范围内取值.当F N 增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态.由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A).1 -12 一段路面水平的公路,转弯处轨道半径为R ,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率( )(A) 不得小于gR μ (B) 必须等于gR μ(C) 不得大于gR μ (D) 还应由汽车的质量m 决定分析与解 由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μF N .由此可算得汽车转弯的最大速率应为v =μRg .因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑.应选(C).1-13 一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则( )(A) 它的加速度方向永远指向圆心,其速率保持不变(B) 它受到的轨道的作用力的大小不断增加(C) 它受到的合外力大小变化,方向永远指向圆心(D) 它受到的合外力大小不变,其速率不断增加分析与解 由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力F N 作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关.重力的切向分量(m g cos θ) 使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程Rm θmg F N 2sin v =-可判断,随θ 角的不断增大过程,轨道支持力F N 也将不断增大,由此可见应选(B).*1 -14 图(a)示系统置于以a =1/4 g 的加速度上升的升降机内,A 、B 两物体质量相同均为m ,A 所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为( )(A) 5/8 mg (B) 1/2 mg (C) mg (D) 2mg分析与解本题可考虑对A、B 两物体加上惯性力后,以电梯这个非惯性参考系进行求解.此时A、B 两物体受力情况如图(b)所示,图中a′为A、B 两物体相对电梯的加速度,m a为惯性力.对A、B 两物体应用牛顿第二定律,可解得FT=5/8 mg.故选(A).讨论对于习题2 -5 这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力.如以地面为惯性参考系求解,则两物体的加速度a A和a B均应对地而言,本题中a A和a B的大小与方向均不相同.其中a A应斜向上.对a A、a B、a和a′之间还要用到相对运动规律,求解过程较繁琐.有兴趣的读者不妨自己尝试一下.1 -15 在如图(a)所示的轻滑轮上跨有一轻绳,绳的两端连接着质量分别为1 kg和2 kg的物体A和B,现以50 N的恒力F向上提滑轮的轴,不计滑轮质量及滑轮与绳间摩擦,求A和B的加速度各为多少?题 1-15 图分析 在上提物体过程中,由于滑轮可以转动,所以A 、B 两物体对地加速度并不相同,故应将A 、B 和滑轮分别隔离后,运用牛顿定律求解,本题中因滑轮质量可以不计,故两边绳子张力相等,且有T 2F F =.解 隔离后,各物体受力如图(b )所示,有滑轮 02T =-F FA A A A T a m g m F =-B B B B T a m g m F =-联立三式,得 2.15A =a 7.2s m B 2=⋅-a ,2s m -⋅讨论 如由式a m m g m m F )()(B A B A +=+-求解,所得a 是A 、B 两物体构成的质点系的质心加速度,并不是A 、B 两物体的加速度.上式叫质心运动定理.1 -16 一质量为m 的小球最初位于如图(a)所示的A 点,然后沿半径为r 的光滑圆轨道ADCB 下滑.试求小球到达点C 时的角速度和对圆轨道的作用力.题 1-16 图分析 该题可由牛顿第二定律求解.在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度a t,与其相对应的外力F t是重力的切向分量mg sin α,而与法向加速度a n 相对应的外力是支持力F N 和重力的法向分量mg cos α.由此,可分别列出切向和法向的动力学方程F t=m d v/d t 和F n =ma n .由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量.该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便.但它不能直接给出小球与圆弧表面之间的作用力.解 小球在运动过程中受到重力P 和圆轨道对它的支持力F N .取图(b)所示的自然坐标系,由牛顿定律得t m αmg F t d d sin v =-= (1) Rm m αmg F F N n 2cos v =-= (2) 由tαr t s d d d d ==v ,得v αr t d d =,代入式(1),并根据小球从点A 运动到点C 的始末条件,进行积分,有()⎰⎰-=απαα2/sin 0d rg d vv v v得 αrg cos 2=v则小球在点C 的角速度为r αg rω/cos 2==v 由式(2)得 αmg αmg rm m F N cos 3cos 2=+=v 由此可得小球对圆轨道的作用力为αmg F F N Ncos 3-=-=' 负号表示F ′N 与e n 反向.1 -17 光滑的水平桌面上放置一半径为R 的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v 0 ,求:(1) t 时刻物体的速率;(2) 当物体速率从v 0减少2/0v 时,物体所经历的时间及经过的路程.题 1-17 图分析 运动学与动力学之间的联系是以加速度为桥梁的,因而,可先分析动力学问题.物体在作圆周运动的过程中,促使其运动状态发生变化的是圆环内侧对物体的支持力F N 和环与物体之间的摩擦力F f ,而摩擦力大小与正压力F N ′成正比,且F N 与F N ′又是作用力与反作用力,这样,就可通过它们把切向和法向两个加速度联系起来了,从而可用运动学的积分关系式求解速率和路程.解 (1) 设物体质量为m ,取图中所示的自然坐标,按牛顿定律,有Rm ma F n N 2v == tma F t d d f v -=-= 由分析中可知,摩擦力的大小F f=μF N ,由上述各式可得tR μd d 2v v -= 取初始条件t =0 时v =v 0 ,并对上式进行积分,有⎰⎰-=v v v v 020d d μR t t tμR R 00v v v += (2) 当物体的速率从v 0 减少到2/0v 时,由上式可得所需的时间为v μR t =' 物体在这段时间内所经过的路程⎰⎰''+==t t t tμR R t s 0000d d v v v 2ln μR s =第二章动量守恒定律和能量守恒定律2 -1对质点系有以下几种说法:(1) 质点组总动量的改变与内力无关;(2) 质点组总动能的改变与内力无关;(3) 质点组机械能的改变与保守内力无关.下列对上述说法判断正确的是( )(A) 只有(1)是正确的(B) (1)、(2)是正确的(C) (1)、(3)是正确的 (D) (2)、(3)是正确的分析与解在质点组中内力总是成对出现的,它们是作用力与反作用力.由于一对内力的冲量恒为零,故内力不会改变质点组的总动量.但由于相互有作用力的两个质点的位移大小以及位移与力的夹角一般不同,故一对内力所作功之和不一定为零,应作具体分析,如一对弹性内力的功的代数和一般为零,一对摩擦内力的功代数和一般不为零,对于保守内力来说,所作功能使质点组动能与势能相互转换,因此保守内力即使有可能改变质点组的动能,但也不可能改变质点组的机械能.综上所述(1)(3)说法是正确的.故选(C).2 -2有两个倾角不同、高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则( )(A) 物块到达斜面底端时的动量相等(B) 物块到达斜面底端时动能相等(C) 物块和斜面(以及地球)组成的系统,机械能不守恒(D) 物块和斜面组成的系统水平方向上动量守恒分析与解对题述系统来说,由题意知并无外力和非保守内力作功,故系统机械能守恒.物体在下滑过程中,一方面通过重力作功将势能转化为动能,另一方面通过物体与斜面之间的弹性内力作功将一部分能量转化为斜面的动能,其大小取决其中一个内力所作功.由于斜面倾角不同,故物体沿不同倾角斜面滑至底端时动能大小不等.动量自然也就不等(动量方向也不同).故(A)(B)(C)三种说法均不正确.至于说法(D)正确,是因为该系统动量虽不守恒(下滑前系统动量为零,下滑后物体与斜面动量的矢量和不可能为零.由此可知,此时向上的地面支持力并不等于物体与斜面向下的重力),但在水平方向上并无外力,故系统在水平方向上分动量守恒.2 -3如图所示,质量分别为m1和m2的物体A和B,置于光滑桌面上,A和B之间连有一轻弹簧.另有质量为m1和m2的物体C和D分别置于物体A与B 之上,且物体A和C、B和D之间的摩擦因数均不为零.首先用外力沿水平方向相向推压A和B,使弹簧被压缩,然后撤掉外力,则在A和B弹开的过程中,对A、B、C、D 以及弹簧组成的系统,有( )(A) 动量守恒,机械能守恒(B) 动量不守恒,机械能守恒(C) 动量不守恒,机械能不守恒 (D) 动量守恒,机械能不一定守恒分析与解由题意知,作用在题述系统上的合外力为零,故系统动量守恒,但机械能未必守恒,这取决于在A、B 弹开过程中C 与A 或D 与B 之间有无相对滑动,如有则必然会因摩擦内力作功,而使一部分机械能转化为热能,故选(D).2 -4 如图所示,子弹射入放在水平光滑地面上静止的木块后而穿出.以地面为参考系,下列说法中正确的说法是( )(A) 子弹减少的动能转变为木块的动能(B) 子弹-木块系统的机械能守恒(C) 子弹动能的减少等于子弹克服木块阻力所作的功(D) 子弹克服木块阻力所作的功等于这一过程中产生的热分析与解 子弹-木块系统在子弹射入过程中,作用于系统的合外力为零,故系统动量守恒,但机械能并不守恒.这是因为子弹与木块作用的一对内力所作功的代数和不为零(这是因为子弹对地位移大于木块对地位移所致),子弹动能的减少等于子弹克服阻力所作功,子弹减少的动能中,一部分通过其反作用力对木块作正功而转移为木块的动能,另一部分则转化为热能(大小就等于这一对内力所作功的代数和).综上所述,只有说法(C)的表述是完全正确的.2 -5 质量为m 的物体,由水平面上点O 以初速为v 0 抛出,v 0与水平面成仰角α.若不计空气阻力,求:(1) 物体从发射点O 到最高点的过程中,重力的冲量;(2) 物体从发射点到落回至同一水平面的过程中,重力的冲量.分析 重力是恒力,因此,求其在一段时间内的冲量时,只需求出时间间隔即可.由抛体运动规律可知,物体到达最高点的时间gαt sin Δ01v =,物体从出发到落回至同一水平面所需的时间是到达最高点时间的两倍.这样,按冲量的定义即可求得结果.另一种解的方法是根据过程的始、末动量,由动量定理求出.解1 物体从出发到达最高点所需的时间为gαt sin Δ01v = 则物体落回地面的时间为gt t αsin Δ2Δ0122v == 于是,在相应的过程中重力的冲量分别为 j j F I αsin Δd 011Δ1v m t mg t t -=-==⎰j j F I αsin 2Δd 022Δ2v m t mg t t -=-==⎰解2 根据动量定理,物体由发射点O 运动到点A 、B 的过程中,重力的冲量分别为j j j I αm y m mv Ay sin 001v v -=-=j j j I αm y m mv By sin 2002v v -=-=2 -6 高空作业时系安全带是非常必要的.假如一质量为 kg 的人,在操作时不慎从高空竖直跌落下来,由于安全带的保护,最终使他被悬挂起来.已知此时人离原处的距离为 m ,安全带弹性缓冲作用时间为 s .求安全带对人的平均冲力. 分析 从人受力的情况来看,可分两个阶段:在开始下落的过程中,只受重力作用,人体可看成是作自由落体运动;在安全带保护的缓冲过程中,则人体同时受重力和安全带冲力的作用,其合力是一变力,且作用时间很短.为求安全带的冲力,可以从缓冲时间内,人体运动状态(动量)的改变来分析,即运用动量定理来讨论.事实上,动量定理也可应用于整个过程.但是,这时必须分清重力和安全带冲力作用的时间是不同的;而在过程的初态和末态,人体的速度均为零.这样,运用动量定理仍可得到相同的结果.解1 以人为研究对象,按分析中的两个阶段进行讨论.在自由落体运动过程中,人跌落至2 m 处时的速度为 gh 21=v (1)在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有()12Δv v m m t -=+P F (2)由式(1)、(2)可得安全带对人的平均冲力大小为()N 1014.1Δ2ΔΔ3⨯=+=+=tgh mg t m Δmg F v 解2 从整个过程来讨论.根据动量定理有N 1014.1/2Δ3⨯=+=mg g h tmg F 2 -7 如图所示,在水平地面上,有一横截面S = m 2 的直角弯管,管中有流速为v = m·s-1 的水通过,求弯管所受力的大小和方向.题 3-12 图分析 对于弯曲部分AB 段内的水而言,由于流速一定,在时间Δt 内,从其一端流入的水量等于从另一端流出的水量.因此,对这部分水来说,在时间Δt 内动量的增量也就是流入与流出水的动量的增量Δp =Δm (v B -v A );此动量的变化是管壁在Δt 时间内对其作用冲量I 的结果.依据动量定理可求得该段水受到管壁的冲力F ;由牛顿第三定律,自然就得到水流对管壁的作用力F′=-F .解 在Δt 时间内,从管一端流入(或流出) 水的质量为Δm =ρυS Δt ,弯曲部分AB 的水的动量的增量则为Δp =Δm (v B -v A ) =ρυS Δt (v B -v A )依据动量定理I =Δp ,得到管壁对这部分水的平均冲力()A B t S ρt v v v -==ΔΔI F 从而可得水流对管壁作用力的大小为N 105.2232⨯-=-=-='v S ρF F作用力的方向则沿直角平分线指向弯管外侧.2 -8 质量为m′ 的人手里拿着一个质量为m 的物体,此人用与水平面成α角的速率v 0 向前跳去.当他达到最高点时,他将物体以相对于人为u 的水平速率向后抛出.问:由于人抛出物体,他跳跃的距离增加了多少(假设人可视为质点)分析 人跳跃距离的增加是由于他在最高点处向后抛出物体所致.在抛物的过程中,人与物之间相互作用力的冲量,使他们各自的动量发生了变化.如果把人与物视为一系统,因水平方向不受外力作用,故外力的冲量为零,系统在该方向上动量守恒.但在应用动量守恒定律时,必须注意系统是相对地面(惯性系)而言的,因此,在处理人与物的速度时,要根据相对运动的关系来确定.至于,人因跳跃而增加的距离,可根据人在水平方向速率的增量Δv 来计算.解 取如图所示坐标.把人与物视为一系统,当人跳跃到最高点处,在向左抛物的过程中,满足动量守恒,故有()()u m m αm m -+'='+v v v cos 0式中v 为人抛物后相对地面的水平速率, v -u 为抛出物对地面的水平速率.得u m m m α'++=cos 00v v 人的水平速率的增量为u m m m α'+=-=cos Δ0v v v 而人从最高点到地面的运动时间为gαt sin 0v = 所以,人跳跃后增加的距离()gm m αm t x '+==sin ΔΔ0v v 2 -9 一质量为 kg 的球,系在长为 m 的细绳上,细绳的另一端系在天花板上.把小球移至使细绳与竖直方向成30°角的位置,然后从静止放开.求:(1) 在绳索从30°角到0°角的过程中,重力和张力所作的功;(2) 物体在最低位置时的动能和速率;(3) 在最低位置时的张力.题 2-9 图分析 (1) 在计算功时,首先应明确是什么力作功.小球摆动过程中同时受到重力和张力作用.重力是保守力,根据小球下落的距离,它的功很易求得;至于张力虽是一变力,但是,它的方向始终与小球运动方向垂直,根据功的矢量式⎰⋅=s d F W ,即能得出结果来.(2) 在计算功的基础上,由动能定理直接能求出动能和速率.(3) 在求最低点的张力时,可根据小球作圆周运动时的向心加速度由重力和张力提供来确定.解 (1) 如图所示,重力对小球所作的功只与始末位置有关,即。
大学物理(第四版)课后习题及答案 波动之欧阳体创编
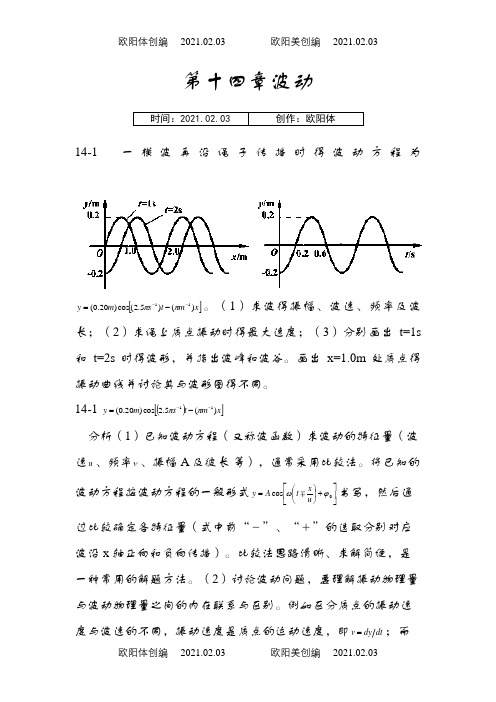
第十四章波动时间:2021.02.03 创作:欧阳体14-1 一横波再沿绳子传播时得波动方程为[]x m t s m y )()5.2(cos )20.0(11---=ππ。
(1)求波得振幅、波速、频率及波长;(2)求绳上质点振动时得最大速度;(3)分别画出t=1s 和t=2s 时得波形,并指出波峰和波谷。
画出x=1.0m 处质点得振动曲线并讨论其与波形图得不同。
14-1 ()[]x m t s m y )(5.2cos )20.0(11---=ππ 分析(1)已知波动方程(又称波函数)求波动的特征量(波速u 、频率ν、振幅A 及彼长 等),通常采用比较法。
将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y 书写,然后通过比较确定各特征量(式中前“-”、“+”的选取分别对应波沿x 轴正向和负向传播)。
比较法思路清晰、求解简便,是一种常用的解题方法。
(2)讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别。
例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即dt dy v =;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质的性质决定。
介质不变,彼速保持恒定。
(3)将不同时刻的t 值代人已知波动方程,便可以得到不同时刻的波形方程)(x y y =,从而作出波形图。
而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程)(t y y =,从而作出振动图。
解(1)将已知波动方程表示为 与一般表达式()[]0cos ϕω+-=u x t A y 比较,可得 则 m v u Hz v 0.2,25.12====λπω(2)绳上质点的振动速度则1max 57.1-⋅=s m v(3) t=1s 和 t =2s 时的波形方程分别为波形图如图14-1(a )所示。
x =1.0m 处质点的运动方程为振动图线如图14-1(b )所示。
大学物理简明教程课后复习题答案(全)

《大学物理简明教程》习题解答习题一1-1 |r ∆|与r ∆有无不同?td d r 和td d r 有无不同? td d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r ϖϖ-=∆;(2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即t v a d d ϖϖ=,t v d d 是加速度a 在切向上的分量.∵有ττϖϖ(v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττϖϖϖ+=式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τϖϖΘ与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =trd d ,及a =22d d t r而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r ϖϖϖ+=,jt y i t x t r a jt y i t x t r v ϖϖϖϖϖϖϖϖ222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x yx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a tr v ==其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
大学物理简明教程习题答案

习题解答 习题一1-1 |r ∆|与r ∆ 有无不同?t d d r 和t d d r 有无不同? t d d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即t d d r ==v ts d d . trd d 只是速度在径向上的分量. ∵有r r ˆr =(式中r ˆ叫做单位矢),则tˆr ˆt r t d d d d d d rrr += 式中trd d 就是速度径向上的分量, ∴tr t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,tv d d 是加速度a 在切向上的分量.∵有ττ(v =v 表轨道节线方向单位矢),所以tvt v t v d d d d d d ττ+= 式中dt dv就是加速度的切向分量. (tt r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =tr d d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分v =22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r +=,jty i t x t r a jty i t x t r v222222d d d d d d d d d d d d +==+==∴ 故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v yxyx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d tr a trv ==其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
大学物理简明教程课后习题加答案

大学物理简明教程习题解答习题一1-1 |r ∆|与r ∆有无不同t d d r 和t d d r 有无不同 t d d v 和t d d v有无不同其不同在哪里试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r ϖϖ-=∆; (2)t d d r 是速度的模,即t d d r ==v tsd d .t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆrˆt r t d d d d d d r r r += 式中t rd d 就是速度径向上的分量, ∴t r td d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d ϖϖ=,t v d d 是加速度a 在切向上的分量. ∵有ττϖϖ(v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττϖϖϖ+=式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τϖϖΘ与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确为什么两者差别何在解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r ϖϖϖ+=,jt y i t x t r a jt y i t x t r v ϖϖϖϖϖϖϖϖ222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a trv ==其二,可能是将22d d d d t r tr 与误作速度与加速度的模。
大学物理简明教程课后题答案

计,F 以 N计。 (1)取 x =0 时EP = 0,试计算与此力相
应的势能; (2)求质点从x = 2m运动到 x =3m时势
能的变化。
目录 结束
(1) ΔE P = x F dx = x( A x +B x 2) dx
0
0
=
A 2
x
2
B 3
x
3
(2) ΔE P = 3( A x +B x 2) dx
2
= 25A
19 3
B
目录 结束
3-8 一弹簧,原长为l0,劲度系数为 k上端 固定,下端挂一质量为m的物体,先用手托 住,使弹簧不伸长。
(1)如将物体托住馒慢放下,达静止(平 衡位置)时,弹簧的最大伸长和弹性力是多 少?
(2)如将物体突然放手,物体到达最低位 置时,弹簧的伸长和弹性力各是多少?物体 经过平衡位置时的速度是多少?
4×10 3
5
t
其中 F 以N为单位,t 以s为单位。 (1)画出 F~t 图。
(2)计算子弹行经枪管长度所花费的时 间,假定子弹到枪口时所受的力变为零。
(3)求该力冲量的大小。 (4)求子弹的质量。
结束 目录
已知:F = 400 解:
4×10 3
5
t
F/N
400
(1)
(2) F = 400
4×10 5 3
v
v
v
结束 目录
u
u
1
v m2 m v 3 v
M
M
M
解:设船的质量为M,沿 x 方向前进
(第二艘船的质量M中包括两抛出物的质量2m) 设第二艘船抛出物体m后的速度为v2, 以第二艘船和抛出物为系统,则抛出物体
大学物理简明教程课后答案

《大学物理简明教程》课后答案习题11-1 |r ∆|与r ∆ 有无不同?t d d r 和t d d r 有无不同? t d d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即t d d r ==v ts d d . trd d 只是速度在径向上的分量. ∵有r r ˆr =(式中r ˆ叫做单位矢),则tˆr ˆt r t d d d d d d rr r +=式中trd d 就是速度径向上的分量, ∴trt d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,tv d d 是加速度a 在切向上的分量.∵有ττ(v =v 表轨道节线方向单位矢),所以式中dt dv就是加速度的切向分量. (tt r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-5 质点沿x 轴运动,其加速度和位置的关系为 a =2+62x ,a 的单位为2s m -⋅,x 的单位为 m. 质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值. 解: ∵ xvv t x x v t v a d d d d d d d d ===分离变量: x x adx d )62(d 2+==υυ 两边积分得由题知,0=x 时,100=v ,∴50=c∴ 13s m 252-⋅++=x x v1-7 一质点沿半径为1 m 的圆周运动,运动方程为 θ=2+33t ,θ式中以弧度计,t 以秒计,求:(1) t =2 s 时,质点的切向和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少?解: t tt t 18d d ,9d d 2====ωβθω (1)s 2=t 时, 2s m 362181-⋅=⨯⨯==βτR a(2)当加速度方向与半径成ο45角时,有即 βωR R =2亦即 t t 18)9(22= 则解得 923=t 于是角位移为习题22-3 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t m k ev )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m k e )(-];(3)停止运动前经过的距离为)(0kmv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量. 答: (1)∵ tvm kv a d d =-= 分离变量,得即⎰⎰-=vv t m t k v v 00d d ∴ tm ke v v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d(3)质点停止运动时速度为零,即t →∞, 故有 ⎰∞-=='00d kmv t ev x tm k (4)当t=km时,其速度为即速度减至0v 的e1. 2-6 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量 将bat =代入,得 (3)由动量定理可求得子弹的质量2-7 设N 67j i F -=合.(1) 当一质点从原点运动到m 1643k j i r++-=时,求F 所作的功.(2)如果质点到r 处时需0.6s ,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化.解: (1)由题知,合F为恒力,∴ )1643()67(k j i j i r F A++-⋅-=⋅=合(2) w 756.045==∆=t A P (3)由动能定理,J 45-==∆A E k2-8 如题2-18图所示,一物体质量为2kg ,以初速度0v =3m ·s -1从斜面A 点处下滑,它与斜面的摩擦力为8N ,到达B 点后压缩弹簧20cm 后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度.解: 取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原 长处为弹性势能零点。
《大学物理简明教程》课后习题答案(全)之欧阳文创编

《大学物理简明教程》习题解答时间:2021.03.12创作:欧阳文习题一1-1|r ∆|与r ∆有无不同?td d r 和td d r 有无不同?td d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即tv a d d =,t vd d 是加速度a 在切向上的分量.∵有ττ (v =v 表轨道节线方向单位矢),所以 式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =trd d ,及a =22d d t r而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在? 解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=, 故它们的模即为而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
在1-1题中已说明trd d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r 也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《大学物理简明教程》习题解答欧阳光明(2021.03.07)习题一1-1|r ∆|与r ∆有无不同?td d r 和td d r 有无不同?td d v和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)td d r 是速度的模,即t d d r ==v ts d d .tr d d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中trd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)td d v 表示加速度的模,即t v a d d=,t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢),所以 式中dt dv就是加速度的切向分量.(t t r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =trd d ,及a =22d d tr 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=, 故它们的模即为而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作其二,可能是将22d d d d tr t r 与误作速度与加速度的模。
在1-1题中已说明trd d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
或者概括性地说,前一种方法只考虑了位矢r在径向(即量值)方面随时间的变化率,而没有考虑位矢r及速度v的方向随间的变化率对速度、加速度的贡献。
1-3 一质点在xOy 平面上运动,运动方程为x =3t +5, y =21t 2+3t -4.式中t 以 s 计,x ,y 以m 计.(1)以时间t 为变量,写出质点位置矢量的表示式;(2)求出t =1 s 时刻和t =2s 时刻的位置矢量,计算这1秒内质点的位移;(3)计算t =0 s 时刻到t =4s 时刻内的平均速度;(4)求出质点速度矢量表示式,计算t =4 s 时质点的速度;(5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算t =4s 时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).解:(1)jt t i t r)4321()53(2-+++=m (2)将1=t ,2=t 代入上式即有(3)∵j i r j j r 1617,4540+=-= ∴104s m 534201204-⋅+=+=--=∆∆=j i ji r r t r v (4) 1s m )3(3d d -⋅++==j t i t r v 则j i v 734+=1s m -⋅(5)∵j i v j i v73,3340+=+=(6) 2s m 1d d -⋅==j t v a这说明该点只有y 方向的加速度,且为恒量。
1-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.图1-4解:设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知 将上式对时间t 求导,得ts s t l ld d 2d d 2=题1-4图根据速度的定义,并注意到l ,s 是随t 减少的, ∴t sv v t l v d d ,d d 0-==-=船绳 即θcos d d d d 00v v s l t l s l t s v ==-=-=船或sv s h s lv v 02/1220)(+==船将船v 再对t 求导,即得船的加速度1-5 质点沿x 轴运动,其加速度和位置的关系为a =2+62x ,a 的单位为2s m -⋅,x 的单位为 m.质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值.解:∵xv v t x x v t v a d d d d d d d d ===分离变量:x x adx d )62(d 2+==υυ两边积分得cx x v ++=322221由题知,0=x 时,100=v ,∴50=c∴13s m 252-⋅++=x x v1-6 已知一质点作直线运动,其加速度为a =4+3t 2s m -⋅,开始运动时,x =5 m ,v =0,求该质点在t =10s 时的速度和位置.解:∵t t va 34d d +==分离变量,得t t v d )34(d +=积分,得12234c t t v ++=由题知,0=t ,00=v ,∴01=c故2234t t v += 又因为2234d d t t t x v +==分离变量,tt t x d )234(d 2+= 积分得232212c t t x ++=由题知0=t ,50=x ,∴52=c故521232++=t t x所以s 10=t 时1-7 一质点沿半径为1 m 的圆周运动,运动方程为θ=2+33t ,θ式中以弧度计,t 以秒计,求:(1) t =2 s 时,质点的切向和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少? 解:t t t t 18d d ,9d d 2====ωβθω(1)s 2=t 时,2s m 362181-⋅=⨯⨯==βτR a(2)当加速度方向与半径成ο45角时,有145tan ==︒na a τ即βωR R =2亦即t t 18)9(22=则解得923=t 于是角位移为rad67.29232323=⨯+=+=t θ1-8 质点沿半径为R 的圆周按s =2021bt t v -的规律运动,式中s 为质点离圆周上某点的弧长,0v ,b 都是常量,求:(1)t 时刻质点的加速度;(2) t 为何值时,加速度在数值上等于b . 解:(1)bt v t sv -==0d d则240222)(R bt v b a a a n-+=+=τ加速度与半径的夹角为(2)由题意应有即0)(,)(4024022=-⇒-+=bt v R bt v b b∴当bv t 0=时,b a =1-9 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔60°的夹角,求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R . (提示:利用曲率半径与法向加速度之间的关系) 解:设小球所作抛物线轨道如题1-10图所示. 题1-9图(1)在最高点, 又∵1211ρv a n =∴m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点,2002==v v 1s m -⋅,而o60cos 2⨯=g a n∴m8060cos 10)20(22222=︒⨯==n a v ρ1-10飞轮半径为0.4 m ,自静止启动,其角加速度为β=0.2rad ·2s -,求t =2s 时边缘上各点的速度、法向加速度、切向加速度和合加速度.解:当s 2=t 时,4.022.0=⨯==t βω1s rad -⋅则16.04.04.0=⨯==ωR v 1s m -⋅1-11 一船以速率1v =30km ·h -1沿直线向东行驶,另一小艇在其前方以速率2v =40km ·h -1沿直线向北行驶,问在船上看小艇的速度为何?在艇上看船的速度又为何?解:(1)大船看小艇,则有1221v v v -=,依题意作速度矢量图如题1-13图(a)题1-11图由图可知1222121h km 50-⋅=+=v v v方向北偏西︒===87.3643arctan arctan21v v θ(2)小船看大船,则有2112v v v-=,依题意作出速度矢量图如题1-13图(b),同上法,得 方向南偏东o87.36习题二2-1 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB 平行,如图所示,求这质点的运动轨道.解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v 方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2. 题2-1图X 方向:0=x F t v x 0=①Y方向:yy ma mg F ==αsin ②0=t 时0=y 0=y v由①、②式消去t ,得2-2 质量为16 kg 的质点在xOy 平面内运动,受一恒力作用,力的分量为x f =6 N ,y f =-7 N ,当t =0时,==y x 0,x v =-2 m ·s -1,y v =0.求当t =2 s 时质点的 (1)位矢;(2)速度.解:2s m 83166-⋅===m f a x x(1)于是质点在s 2时的速度 (2)2-3 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk e v )(0-;(2) 由0到t 的时间内经过的距离为x =(kmv 0)[1-t mke)(-];(3)停止运动前经过的距离为)(0k m v ;(4)证明当k m t =时速度减至0v 的e 1,式中m 为质点的质量.答: (1)∵t vm kv a d d =-=分离变量,得即⎰⎰-=vv t mt k v v 00d d∴tm k ev v -=0(2)⎰⎰---===tttm k m ke k mv t ev t v x 000)1(d d(3)质点停止运动时速度为零,即t →∞,故有⎰∞-=='00d kmv t ev x tm k(4)当t=km 时,其速度为即速度减至0v 的e 1.2-4一质量为m 的质点以与地的仰角θ=30°的初速0v 从地面抛出,若忽略空气阻力,求质点落地时相对抛射时的动量的增量.解: 依题意作出示意图如题2-6图 题2-4图在忽略空气阻力情况下,抛体落地瞬时的末速度大小与初速度大小相同,与轨道相切斜向下,而抛物线具有对y 轴对称性,故末速度与x 轴夹角亦为o30,则动量的增量为由矢量图知,动量增量大小为0v m ,方向竖直向下.2-5 作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化,以及力给予物体的冲量.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则it i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是 ⎰∆==-=∆t p t F p p p 0102d, 同理,12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理.(2)同上理,两种情况中的作用时间相同,即亦即0200102=-+t t解得s 10=t ,(s 20='t 舍去)2-6 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得b a t =(2)子弹所受的冲量将b at =代入,得(3)由动量定理可求得子弹的质量2-7设N 67j i F -=合.(1)当一质点从原点运动到m 1643k j i r ++-=时,求F 所作的功.(2)如果质点到r 处时需0.6s ,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化.解: (1)由题知,合F为恒力,∴)1643()67(k j i j i r F A++-⋅-=⋅=合(2) w 756.045==∆=t A P(3)由动能定理,J 45-==∆A E k2-8 如题2-18图所示,一物体质量为2kg ,以初速度0v =3m ·s -1从斜面A 点处下滑,它与斜面的摩擦力为8N ,到达B 点后压缩弹簧20cm 后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度.解: 取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原 长处为弹性势能零点。
