2010年考研试题

合集下载

2010考研数三真题及解析

2010年全国硕士研究生入学统一考试数学三试题一、选择题(1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸．．．指定位置上.)1 1 x ,则a等于( )(1)若limx0 x x a e1(A)0. (B) 1. (C) 2. (D) 3.(2)设y1, y2 是一阶非齐次微分方程y p x y q x的两个特解,若常数，使y1 y2 是该方程的解,y1 y2 是该方程对应的齐次方程的解,则( )1(A),(B) .(C) ,. (D) .【答案解析】见真题理论验证强化指导部分数二试题一(2).(3)设函数f x , g x具有二阶导数,且g x 0 ,若g x0a 是g x 的极值,则f g x 在x0 取极大值的一个充分条件是( )(A) f a 0. (B) f a 0 . (C) f a 0 . (D)f a 0 .x(4) 设 f xln 10 x g x , x h x ,e 10 ,则当 x 充分大时有( ) (A) g xh xf x. (B) hxg xf x.(C) fx g xh x.(D) g x f x h x .(5) 设向量组 I :1, 2,r 可由向量组II :1,2,s 线性表示,下列命题正确的是( )(A) 若向量组I 线性无关,则rs .(B) 若向量组I 线性相关,则r s . (C) 若向量组II 线性无关,则r s . (D) 若向量组II 线性相关,则r s .(6) 设 A 为4阶实对称矩阵,且 A 2A O ,若 A 的秩为3,则 A 相似于 ()1 1(A)1 .(B)1 .1 11 1(C) 1.(D)1.110, x 01(A) 0.(B).(C)e1.(D) 1e1.为1,3上均匀分布(8) 设 f 1(x ) 为标准正态分布的概率密度, f 2 (x ) 的概率密度,若af x 1( )x 0 f x( )( a 0, b 0)bf 2( )x x 0为概率密度,则a ,b 应满足 ( )(A) 2a3b 4. (B) 3a2b 4. (C) a b 1.(D) ab 2.二、填空题(9~14小题,每小题4分,共24分.请将答案写在答题纸．．．指定位置上.)x yt 2 x2 确定,则dy. (9) 设可导函数 yy x ( )由方程e dtx sin t dt dxx 01 (10)设位于曲线 y( e x ) 下方, x 轴上方的无界区域为G ,则G 绕 x轴旋转一周所得空间区域的体积是.(11) 设某商品的收益函数为R (p ),收益弹性为1p 3 ,其中 p 为价格,且R (1) 1 ,则R (p ) =.(7) 设随机变量 X 的分布函数 F x ( ) 2 1e x ,( )0 x 1 ,则 PX1=x1(12) 若曲线 y x 3 ax 2 bx 1有拐点(1,0) ,则b.(13) 设 A ,B 为3阶矩阵,且 A 3, B 2 , A1B 2 ,则A B1.n212(14)设X X 1, 2, ,X n是来自总体N (,) (0) 的简单随机样本,统计量TXi ,n i 1则ET .三、解答题(15~23小题,共94分.请将解答写在答题纸．．．指定位置上.解答应写出文字说明、证明过程或演算步骤.) (15) (本题满分10分)求极限 lim (xx 11)ln 1x .(16) (本题满分10分)计算二重积分(x y dxdy )由曲线 x 1y 2 与直线 x2y 0 及Dx 2y 0围成.(17) (本题满分10分) 求函数uxy2yz 在约束条件x 2y 2z 210 下的最大值和最小值.(18)(本题满分10分)(I ) 比较1ln tln 1tndt与1t nln t dt n 1,2,的大小,说明理由．1n( II ) 记u nln t ln 1t dt n 1,2,,求极限nli m u n ．(19) (本题满分10分)设函数 f (x ) 在0,3上连续 , 在0,3内存在二阶导数 , 且22f (0)f x dx ( ) f (2) f (3),( I ) 证明存在(0,2) ,使 f ()f (0); ; ( II ) 证明存在(0,3) ,使 f()0 ．(20)(本题满分11分)11 a设A1 ， b11已知线性方程组Ax b 存在2个不同的解． ( I ) 求,a ;( II ) 求方程组Ax b 的通解. (21)(本题满分11 分) 1 (1,2,1)T,求a ,Q ．(22) (本题满分11分) 设二维随机变量(X Y , ) 的概率密度为2f x y ( , )Ae 2x 2xy y2,x,y ,求常数 A 及条件概率密度 f Y X |(y x | ) ．(23)(本题满分11分) 箱中装有6个球,其中红、白、黑球的个数分别为1,2,3 个,现从箱中随机取出2个球, 记 X 为取出的红球个数,Y 为取出的白球个数.( I ) 求随机变量 (X Y ,) 的概率分布；0 设A 141 43a ,正交矩阵 Q 使得 Q T AQ 为对角矩阵,若 Q 的第 1 列为 a( II ) 求Cov X Y( , ) .2010年全国硕士研究生入学统一考试数学三试题参考答案一、选择题(1)【答案】 (C). 【解析】limx1 1 a exlim x1 1e x1axlimx11e xaxe xlim x1e x axe xx x xx x x1e x axe x lim lim 1 a 1x 0 x x 0 x所以a 2.(2) 【答案】 (A)．【解析】因y 1 y 2 是 y P x y 0 的解,故y 1 y 2 P xy 1y 20,所以y 1P x y1y 2p x y ( ) 20 ,而由已知 y 1P x y1q x, y 2P x y2q x,所以q x0,①又由于一阶次微分方程 ypx yq x是非齐的,由此可知 qx0 ,所以0．由于y 1y 2 是非齐次微分方程 yPx yq x的解,所以y 1 y 2 P x y 1 y 2q x,整理得y 1P x y1y 2P x y2q x ,即q xq x,由q x 0 可知1,②由①②求解得,故应选(A)．(3)【答案】 (B).【解析】f g x ( ) f g x ( )g x ( ) ,f g x( ) fg x ( )g x ( ) fg x ( )g x ( )2fg x ( )g x( )由于g (x 0 ) a 是g (x ) 的极值,所以g x ( 0)0 .所以f g x ( 0 )f gx ( 0 )g x( 0 )fa gx ( 0 )由于g x ( 0 ) 0,要使f g x( )0,必须有f a ( ) 0 ,故答案为B.(4)【答案】 (C).x【解析】因为 lim ( ) lim e 10 lim 10x 1 ,所以,当 x 充分大时,h x ( )g x ( ) .xg x ( )xxx1091又因为 limf x ( ) lim ln 10 xlim 10 ln x x 10 lim ln 9xxg x ( ) xxx1 xx81ln x10 9lim x 10 92 lim l x 10! lim 10 .x1xxxx 所以当 x 充分大时, f x ( ) g x ( ) ,故当 x 充分大, f x ( ) g x ( )h x ( ) .(5) 【答案】 (A)．【解析】由于向量组 I 能由向量组 II 线性表示,所以r (I) r (II) ,即r (1, ,r) r (1, , s ) s 若向量组 I 线性无关,则 r (1, ,r) r ,所以 rr (1, ,r )r (1, ,s )s ,即r s ,选(A).(6) 【答案】 (D). 【解析】设为 A 的特征值,由于 A 2A O ,所以20 ,即 (1)0 ,这样 A 的特征值只能为 -1 或 0. 由于 A 为实对称矩阵 , 故 A 可相似对角化 , 即11A,r A ()r ()3,因此,1,即 A1.11(7) 【答案】 (C).【解析】离散型随机变量的分布函数是跳跃的阶梯形分段函数,连续型随机变量的分布函数是连续函数.观察本题中F (x ) 的形式,得到随机变量 X 既不是离散型随机变量,也不是连续型随机变量,所以求随机变量在一点处的概率,只能利用分布函数的定义.根据分布函数的定义,函数在某一点的概率可以写成两个区间内概率的差,即P X 1P X1P X 1 F1 F11 e1e1,故本题选(C).(8) 【答案】 (A).x 21 ,1x 3【解析】根据题意知, f 1x(x),f 2x2 140,其它利用概率密度的性质:f x dx1,故a31 a 3f x dx af 1x dxbf 2 x dx2f 1x dxb4 dx24 b1所以整理得到2a 3b 4,故本题应选(A).二、填空题 (9)【答案】1.x y2x2【解析】e t dtxsin t dt ,令x 0,得 y 0,等式两端对 x 求导：e(x y )2(1dydx ) 0xsin t dt 2x sin x 2 ．dydy将x0, y 0代入上式,得10 .所以1.dxxdx x 02(10)【答案】4【解析】根据绕 x 轴旋转公式, 有2dxVey dxe1ln 2 xe1d ln ln 2x xarctan lnxe2442 .1 33P1.(11)【答案】 pedR p 3dR 1212【解析】由弹性的定义,得1 p ,所以pdp ,即 ln Rln p pC , dp R R p313又R11,所以 C1 .故ln Rln p 1 p 1 ,因此 R p e 3p1.3 33(12)【答案】b3.【解析】函数为 yx 3ax 2bx 1 ,它的一阶导数为 y 3x 2 2ax b ; 二阶导数为ay6x 2a,又因为1,0是拐点,所以 yx10 ,得3过点1,0,所以将x1,y 0 代入曲线方程,得b 3.(13) 【答案】3. A A (1B B )【解析】由于1( E AB B )1B1A ,所以1 1 11B B )A AB B因为 B2 ,所以 B1 B B1321 3 .2(14)【答案】22.1 ( B AA A111 2B,因此1 A BAA【解析】 E T EnXi2 1EnXi21nEX2E X222.n i1n i 1n 三、解答题11ln x1 lnx x 1ln x x1ln e x11lnxlimlim(15)【解析】 lim x x 1lim e ln xe xln xexln xxx其中 ln x xln x x1ln x x ln x xln( e 1) (e 1) e 1ln x e 1ln x ln x1 lim lim limlim e x ( 1)1.xln xx 1xx ln x x x故原式e1.(16)【解析】积分区域 DD 1 D 2 ,1 x y ,0 y1,2y x1y 2D 2x y , 1y 0,2y x1y 2xy3dxdyx 33x y 2 3xy 2y 3 dxdyDD因为区域 D 关于 x 轴对称 , 被积函数 3x 2 y y 3 是 y 的奇函数 ,所以3x 2y y dxdy30．Dx y dxdy3x 3 3xy dxdy 22x 3 3xy dxdy 221DDD 12xln xx211 x 43 x y 22dy2019 4 y 42y 2 1 4 dy 1415 .42(17)【解析】令 F x y z,, ,xy 2yz x 2 y 2 z 2 10,用拉格朗日乘数法得F xy 2x 0,F yx 2z2y0,F z2y 2z 0, F x 2y 2z 2100,又因为该问题必存在最值,并且不可能在其它点处,所以u m ax5 ,u m in5 5 ．(18) 【解析】 (I)当0x 1时0 ln(1x )x,故ln(1t )nt n ,所以ln tln(1t )nln t t n ,则01ln t ln(1t )ndt1ln t t dt n n 1,2, .(II)1 ln t t dt n1ln t t dtnn 111ln td tn1n112 ,故由1n1求解得六个点：152,1, B A1 , , 21CD0,, E F由于在点A 与B 点处,u ；在点C与 D 处, u；在点E 与F 处, 0u ． 1 2 y y0 u n 0 ln n1 2 ,1根据夹逼定理得0 lim u n lim0 ,所以lim u n 0 .n n n1n2(19)【解析】(I) 因为2 f (0) 0 f x dx( ) ,又因为f x 在0,2上连续,所以由积分中值定理得,至少有一点0,2,使得20 f x dx f 20即2 f 0 2 f ,所以存在0,2,使得f f0 .f 2 f 3(Ⅱ)因为f 2 f 3 2 f 0 ,即 f 0 ,又因为f x 在2,3上连2续,由介值定理知,至少存在一点 1 2,3使得f 1 f 0 .因为f x 在0,2上连续,在0,2上可导,且f 0 f 2 ,所以由罗尔中值定数学(三)试题第15页 (共4页)微信公众号：考研研学姐答疑资讯QQ 群：451613025理知,Ｃ存在10,2,有f10. 又因为 f x 在2,1上连续,在2,1上可导,且f 2 ff1 ,所以由罗尔中值定理知,存在22,1,有 f20 . 又因为 fx在1,2上二阶可导,且f1f20 ,所以由罗尔中值定理,至少有一点 Ax b 0,3,使得f0 .(20) 【解析】因为方程组有两个不同的解,所以可以判断方程组增广矩阵的秩小于3,进而可以通过秩的关系求解方程组中未知参数,有以下两种方法.方法1：(I)已知Ax b 有2个不同的解,故r A ( ) r A ( ) 3 ,对增广矩阵进行初等行变换,得11 a 1 1 1A1 0 101 01 1 1 11 1a1 111 1 10 10 1 01010112a0 012a 11 1 1 11 111当1时,A0 00 10 01,此时,r A ( ) r A ( ),故Ax b 无解(舍00 0 a00 001 1 1 1微信公众号：考研研学姐答疑资讯QQ 群：451613025当1时, A 0 2 0 1 ,由于r A ( )0 0 0 a 2方法2：已知Axb 有2个不同的解,故r A ()r A () 3 ,因此 A 0,即11A0 10(1) (21)0 ,11知1或-1.当1时,r A () 1 r A () 2 ,此时,Ax b 无解,因此1.由r A () r A ( ) ,得a2.( II ) 对增广矩阵做初等行变换31121 11211 12A0 201 0 2 010 1 0121 1110 0000 0 003x x3x 1 1232微信公众号：考研研学姐答疑资讯QQ群：451613025x 21x 3 231 21因此Ax b的通解为x k 0 ,其中k为任意常数.10 10 1 4(21)【解析】由于A 1 3 a4 a 01 1微信公众号：考研研学姐答疑资讯QQ 群：45161302513 可知原方程组等价为2 ,写成向量的形式,即x 2x 0 1 .列为(1,2,1)T ,故 A 对应于1 的特征向量为1(1,2,1)T .12,即根据特征值和特征向量的定义,有A116141 3 a 41 1a2 12 ,由此可得a 1,12 .故A10 1 141 31 41.微信公众号：考研研学姐答疑资讯QQ 群：45161302514 由EA1 3 1 (4)( 2)(5) 0 ,41可得 A 的特征值为12,24, 35 . 4 由 (2E A x ) 0,即14特征向量为2(1,0,1)T .17 1 4x 11x 20 ,可解得对应于 24 的线性无关的4x 35 由 (3E A x )0 ,即 143(1,1,1)T .1 2 1 4x 11x 2 0 ,可解得对应于35 的特征向量为5 x 3由于 A 为实对称矩阵,1,2,3 为对应于不同特征值的特征向量,所以1,2,3相互正交,只需单位化：111(1,2,1) ,T2( 1,0,1) ,T3(1,1,1)T ,123163取,则Q T AQQ 1,2,351112微信公众号：考研研学姐答疑资讯QQ 群：451613025(22) 【解析】当给出二维正态随机变量的的概率密度 fx , y 后,要求条件概率密度f x y ( ,)f Y X | (y x | ) ,可以根据条件概率公式 f Y X | (y x | )来进行计算.本题中还有待定参 f X ( )x数, A 要根据概率密度的性质求解,具体方法如下.2 22 2 22x f x y dy, A e2x 2xy ydy A e(y x ) xdyf XAexe(y x )dyx 2A e ,x .根据概率密度性质有1f X x dx A ex2dxA,即 A1,1x 2故 f Xx e ,x. 当x时,有条件概率密度f x y ,Ae x 22xy y21x 2 2 21(x y )2 f YXy xf XxAex 2ee ,x ,y.(23)【解析】(I) X 的所有可能取值为 0,1 ,Y 的所有可能取值为 0,1,2 ．C 323 1,其中X 0,Y 0 表示取到的两个球都是黑球；P X0,Y2C 615 5P X 0,Y 1C C 21231 6 2,其中 X 0,Y 1表示取到的一个是白球,一个是C6 15 5黑球；C22 1 ,其中X 0,Y 2 表示取到的两个球都是白球；P X0,Y 22 C6 15P X 1,YC C112313 1,其中X 1,Y 0 表示取到的一个是红球,一个是C6 15 5黑球；P X 1,Y 1C C112212,其中X 1,Y 1表示取到的一个是红球,一个是白球；C6 15 0P X1,Y20 , C6因此二维离散型随机变量X ,Y 的概率分布为2 2 2 1 1E XY 1 1 ,E X0 1 ,I(I),C o v EXYXY EXEY,33 3E Y 012Cov X Y, E XYE X E Y.。

2010年考研真题和详细解析

1. 1984年1月3日，意大利人卡内帕给恩格斯写信，请求他为即将在日内瓦出版的饿《新纪元》周刊的创刊号题词，而且要求尽量用简短的字句来表述未来的社会主义纪元的基本思想，以区别于伟大诗人但丁的对旧纪元所作的“一些人统治，另一些人受苦难”的界定。

恩格斯回答说，这就是：“代替那存在着阶级和阶级对立的资产阶级旧社会的，将是这样一个联合体，在那里，每个人的自由发展是一切人的自由发展的条件。

”这段话表明，马克思主义追求的根本价值目标是（）A．实现人的自由而全面的发展B．实现人类永恒不变的普适价值C．建立一个四海之内皆兄弟的大同世界D．建立一个自由，平等，博爱的理性王国【答案】A【解析】本题考查的考点是马克思主义最崇高的社会理想，即马克思追求的根本价值目标，进入共产主义社会，实现人的自由而全面的发展，所以，正确答案是A选项。

2.有一则箴言：“在溪水和岩石的斗争中，胜利的总是溪水，不是因为力量，而是因为坚持。

”“坚持就是胜利”的哲理在于（）A．必然性通过偶然性开辟道路B．肯定中包含着否定的因素C．量变必然引起质变D．有其因必有其果【答案】C【解析】坚持就是胜利，体现了事物量变发展到一定阶段必然会引起质变，达到事物根本性质的变化，所以，本题体现的是量变必然引起质变，正确答案是选项C。

3. 右边这张照片反映出由于气候变暖，北极冰盖融化，致使北极熊无处可去的场景，颇具震撼力。

它给我们地球上的人类发出的警示是（）A．人与自然的关系成为人与人之间一切社会关系的核心B．生态失衡已成为自然界自身周期演化不可逆转的趋势C．自然地理环境已成为人类社会发展的根本决定力量D．生态环境已日益成为人类反思自身活动的重要前提【答案】D【解析】本题考查人与自然的关系，气候变暖给人类发出的警示是人在对于自然的作用过程中，生态环境已日益成为人类反思自身活动的重要前提，保护自然，协调人和自然的关系是大势所趋，所以，正确答案是选项D。

4. 劳动力成为商品是货币转化为资本的前提条件，这是因为（）A．资本家购买的是劳动力的价值B．劳动力商品具有价值和使用价值C．货币所有者购买的劳动力能够带来剩余价值D．劳动力自身的价值能够在消费过程中转移到新的商品中去【答案】C【解析】劳动力商品的最主要特点，表现在它的使用价值上。

2010年考研数学一真题及解析(公式及答案修正版)

2010年全国硕士研究生入学统一考试数学试题详解及评分参考数学（一）一．选择题：1 - 8小题，每小题4分，共32分.下列每题给出的四个选项中，只有一个是符合题目要求的，请将所选项前的字母填在答题纸指定的位置上.(1)极限2lim ()()()x x x x a x b ®¥=-+(A)1(B)e(C)a be -(D)b ae -【答】应选 (C) .【解】因22ln ln()ln()lim ln()lim()()1/x x x x x x a x b x a x b x®¥®¥---+=-+()()()3222112=lim lim 1x x a b x abx x x a x b a b x x a x b x ®¥®¥---+-+==--+-，所以2lim (()()x a x b x x a x b e ®¥-=-+，故选 (C) .(2)设函数(,)z z x y =由方程(,0y zF x x=确定，其中F 为可微函数，且20F ¢¹，则z z x y x y ¶¶+=¶¶(A)x (B)z (C)x -(D)z-【答】应选 (B) .【解】在方程两边分别对x 和对y 求偏导，得122211()0y z F z F x x x x ¶¢¢-+-=¶，12110z F F x x y¶¢¢+=¶于是有 22()z z x y F zF x y ¶¶¢¢+=¶¶，即z zx y z x y ¶¶+=¶¶，故选 (B) .(3)设,m n均是正整数，则反常积分ò的收敛性(A)仅与m 的取值有关(B)仅与n 的取值有关(C)与,m n 的取值都有关(D)与,m n 的取值都无关【答】应选 (D) .【解】显然该反常积分有且仅有两个瑕点0,1x x ==，于是需分成两个积分加以考察：dx =+ò(1)对于，易见被积函数非负，且只在0x +®时无界，于是当1n >时，由+0lim 0x®=及120ò收敛，知收敛；当1n=时12/1mx-:及212101mdx x-ò收敛，知收敛；(2)对于，易见被积函数非负，且只在1x -®时无界，于是当1m >时，由11lim lim 0x x --®®==及1收敛，知收敛；当1m =时，由21/211ln (1)lim lim 0(1)x x x x ---®®-==-及212101m dx x -ò收敛，知收敛；由此可见，无论正整数,m n如何取值，0ò都是收敛的，故选 (D) .(4) 2211lim()()n nn i j nn i n j ®¥===++åå (A) 12001(1)(1)x dx dy x y ++òò(B)1001(1)(1)xdx dy x y ++òò(C) 11001(1)(1)dx dyx y ++òò(D) 112001(1)(1)dx dyx y ++òò【答】应选 (D) .【解】记21(,)(1)(1)f x y x y =++，(){},y 01,01D x x y =££££，知(,)f x y 在D 上可积. 用直线()0,1,2,,i i x x i n n ===L 与()0,1,2,,j j y y j n n===L 将D 分成2n等份，可见22221111211()()(1)(1)n n n ni j i j n i j n i n j n n n=====×++++åååå是(,)f x y 在D 上的二重积分的一个和式，于是112222001111lim ()()(1)(1)(1)(1)nnn i j Dn dxdy dx dy n i n j x y x y ®¥====++++++ååòòòò.故选 (D) . (5)设A 为m n ´矩阵，B 为n m ´矩阵，E 为m 阶单位矩阵. 若AB E =，则(A)秩()r A m =，秩()r B m =(B)秩()r A m =，秩()r B n =(C)秩()r A n =，秩()r B m =(D)秩()r A n =，秩()r B n=【答】应选 (A) .【解】因A 是m n ´矩阵，故()r A m £，又()()()r A r AB r E m ³==，故()r A m =. 同理，可得()r B m =，故选 (A) .(6)设A 为4阶实对称矩阵，且2A A O +=. 若A 的秩为3，则A 相似于(A) 1110æöç÷ç÷ç÷ç÷èø(B) 1110æöç÷ç÷ç÷-ç÷èø(C) 1110æöç÷-ç÷ç÷-ç÷èø(D) 1110-æöç÷-ç÷ç÷-ç÷èø【答】应选 (D) .【解】设l 为A 的特征值，则由2A A O +=知2+=0l l ，即=0l 或1-. 又因A 是实对称矩阵，故A 必相似于对角矩阵L ，其中L 的对角线上的元素为特征值1-或0. 再由()3r A =可知()3r L =，故选 (D) .(7)设随机变量X 的分布函数0,0,1(),01,21,1xx F x x e x -<ìïï=£<íï-³ïî则{1}P X ==(A)0 (B)12(C)112e --(D)11e--【答】应选 (C) .【解】由分布函数的用途，知{1}(1)(1)P X F F -==-1111122e e --=--=-. (8)设1()f x 为标准正态分布的概率密度，2()f x 为[1,3]-上均匀分布的概率密度，若12(),0()(0,0)(),0af x x f x a b bf x x £ì=>>í>î为概率密度，则,a b 应满足(A)234a b +=(B)324a b +=(C)1a b +=(D)2a b +=【答】应选 (C) .【解】由题意，有221()x f x -=，21/4,(1,3)()0x f x Î-ì=íî，其他，()1f x dx +¥-¥=ò而0120()()()f x dx af x dx bf x dx +¥+¥-¥-¥=+òòò()3201=2a b f x dx +ò13=24a b +，于是有13124a b +=，即234a b +=. 故选 (C) .二、填空题：9:14小题，每小题4分，共24分. 请将答案写在答题纸．．．指定位置上. (9)设20,ln(1),t tx e y u du -ì=ïí=+ïîò则220t d y dx == .【答】应填 0.【解】因2/ln(1)=/t dy dy dt t dx dx dt e -+=-, 22222ln(1+)12=[][ln(1)]/1t td y d t te t dx dt e dx dt t -=++-+，故2020t d ydx==.(10)2p =ò.【答】应填 4p -.【解】t =，则2dx tdt =，于是有2220002cos 2sin 4sin 4cos 4cos 4.t tdt t tt tdt t tdt p pppp p p ==-=-=-òòòò(11)已知曲线L 的方程为1||([1,1])y x x =-Î-，起点是(1,0)-，终点为(1,0)，则曲线积分2Lxydx x dy +=ò.【答】应填 0.【解法一】补有向线段:0([1,1])L y x =Î-，起点为(1,0)，终点为(1,0)-，设由L 与L 围成的平面区域为D ，则利用格林公式及区域D 关于y 轴的对称性，得222(2)00LDL LLxydx x dy xydx x dy xydx x dy x x dxdy ++=+-+=---=òòòòò【解法二】记1:1([1,0])L y x x =+Î-，起点是(1,0)-，终点是(0,1)；2:1([0,1])L y x x =-Î，起点为(0,1)，终点为(1,0)有12222+LL L xydx x dy xydx x dy xydx x dy+=++òòò 012210=[(1)][(1)]x x x dx x x x dx -+++--òò1212=()(02323-++-=.(12)设22{(,,)|1}x y z x y z W =+££，则W 的形心的竖坐标z = .【答】应填23.【解】记(){}22,y 1D x x y =+£，有221x y Ddxdydz dxdy dz +W=òòòòòò22=(1)Dx y dxdy --òò212=(1)d r rdr p q -òò=2p，2212122240011[1()]=(1)223x yDD zdxdydz dxdy zdz x y dxdy d r rdr p p q +W==-+-=òòòòòòòòòò，从而W 的形心的竖坐标为23DDzdxdydzz dxdydz==òòòòòò. (13)设1(1,2,1,0)Ta =-，2(1,1,0,2)Ta =，3(2,1,1,)Ta a =. 若由123,,a a a 生成的向量空间的维数为2，则a = .【答】应填 6.【解】因由123,,a a a 生成的向量空间的维数为2，故矩阵()123,,a a a 的秩为2，而()123112112211013,,=101006020000a a a a æöæöç÷ç÷ç÷ç÷®ç÷ç÷--ç÷ç÷èøèø，故6a =.(14)设随机变量X 的概率分布为{},0,1,2,!CP X k k k ===L ，则2EX =.【答】应填 2.【解】由概率分布的性质，有{}01k k P X x ¥===å，即01!k Ck ¥==å，亦即1Ce =，1C e -=.由此可见，X 服从参数为1的泊松分布，于是22()112EX DX EX =+=+=.三、解答题（ 15 ～ 23小题，共94分.）(15)（本题满分10分）求微分方程322xy y y xe ¢¢¢-+=的通解.解：对应齐次方程320y y y ¢¢¢-+=的两个特征根为121,2r r ==，其通解为212x x Y C e C e =+.……4分设原方程的特解形式为*()x y x ax b e =+，则*2((2))xy ax a b x b e ¢=+++，*2((4)22)x y ax a b x a b e ¢¢=++++，代入原方程解得1,2a b =-=-，……8分故所求通解为212(2)x x xy C e C e x x e=+-+ ……10分(16)（本题满分10分）求函数2221()()x t f x x t e dt -=-ò的单调区间与极值.解： ()f x 的定义域为(,)-¥+¥，由于2222211()x x t t f x xe dt te dt --=-òò，2224423311()2222xxt x x t f x x e dt x ex ex e dt ----¢=+-=òò，所以()f x 的驻点为0,1x =± ……3分列表讨论如下：x (,1)-¥-1-(1,0)-0 (0,1) 1 (1,)+¥()f x ¢-0 +0 -0 +()f x ↘极小↗极大↘极小↗……6分因此，()f x 的单调增加区间为(1,0)-及(1,)+¥，单调减少区间为(,1)-¥-及(0,1)；极小值为(1)0f ±=，极大值为21101(0)(1)2t f te dt e --==-ò……10分(17)（本题满分10分） (I)比较1|ln |[ln(1)]nt t dt +ò与1|ln |(1,2,)ntt dt n =òL 的大小，说明理由；(II)记1|ln |[ln(1)](1,2,)n n u t t dt n =+=òL ，求极限lim n n u ®¥.解：（I ）当01t ££时，因为ln(1)t t +£，所以|ln |[ln(1)]|ln |n n t t t t +£，因此11|ln |[ln(1)]|ln |n n t t dt t t dt+£òò ……4分（II ）由 (I) 知，110|ln |[ln(1)]|ln |n n n u t t dt t t dt £=+£òò.因为1112011|ln |ln 1(1)n n n t t dt t tdt t dt n n =-==++òòò，所以1lim|ln |0nn tt dt ®¥=ò ……8分从而 lim 0n n u ®¥=……10分(18)（本题满分10分）求幂级数121(1)21n nn x n -¥=--å的收敛域及和函数. 解：记12(1)()21n nn u x x n --=-，由于221()21lim lim ()21n n n nu x n x x u x n +®¥®¥-==+，所以当21x <，即||1x <时，1()n u x ¥=å绝对收敛，当||1x >时，1()n u x ¥=å发散，因此幂级数的收敛半径1R =……3分当1x =±时，原级数为11(1)21n n n -¥=--å，由莱布尼茨判别法知此级数收敛，因此幂级数的收敛域为[1,1]-……5分设1211(1)()(11)21n n n S x x x n -¥-=-=-££-å，则122211()(1)1n n n S x x x ¥--=¢=-=+å，又(0)0S =，故201()arctan 1xS x dt x t==+óôõ， ……8分于是121(1)()arctan ,[1,1]21n nn x xS x x x x n -¥=-==Î--å ……10分(19)（本题满分10分）设P 为椭球面222:1S x y z yz ++-=的动点，若S 在点P 处的切平面与xOy 面垂直，求点P 的轨迹C ，并计算曲面积分I S=，其中S 是椭球面S 位于曲线C 上方的部分.解：椭球面S 上点(,,)P x y z 处的法向量是{2,2,2}n x y z z y =--r， ……2分点P 处的切平面与xOy 面垂直的充要条件是0({0,0,1})n k k ×==r r r，即20z y -=所以点P 的轨迹C 的方程为222201z y x y z yz -=ìí++-=î，即2220314z y x y -=ìïí+=ïî ……5分取223{(,)|1}4D x y x y =+£，记S 的方程为(,),(,)z z x y x y D =Î，==，所以DI =óóôôôôõõ(D x dxdy =+òò ……8分2Ddxdy p== ……10分(20)（本题满分11分）设1101011A l l l æöç÷=-ç÷ç÷èø，11a b æöç÷=ç÷ç÷èø. 已知线性方程组Ax b =存在2个不同的解，（I ）求,a l ；（II ）求方程组Ax b =的通解.解：（I ）设12,h h 为Ax b =的2个不同的解，则12h h -是0Ax =的一个非零解，故2||(1)(1)0l l =-+=A ，于是1l =或1l =- ……4分当1l =时，因为()()r A r A b ¹M ，所以Ax b =无解，舍去. 当1l =-时，对Ax b =的增广矩阵施以初等行变换，有1111013/2()02010101/211110002a A b B a æ-öæ-öç÷ç÷=-=-=ç÷ç÷ç÷ç÷-+èøèøM .因为Ax b =有解，所以2a =- ……8分（II ）当1l =-，2a =-时，1013/20101/20000B æ-öç÷=-ç÷ç÷èø，所以x =A b 的通解为31110201x k æöæöç÷ç÷=-+ç÷ç÷ç÷ç÷èøèø，其中k 为任意常数. ……11分(21)（本题满分11分）已知二次型123(,,)Tf x x x x Ax =在正交变换x Qy =下的标准形为2212y y +，且Q 的第3列为,0,22T. （I ）求矩阵A ；（II ）证明A E +为正定矩阵，其中E 为3阶单位矩阵.解：（I ）由题设，A 的特征值为1,1,0,且(1,0,1)T为A 的属于特征值0的一个特征向量.……3分设123(,,)Tx x x 为A 的属于特征值1的一个特征向量，因为A 的属于不同特征值的特征向量正交，所以1231(,,)001x x x æöç÷=ç÷ç÷èø，即130x x +=.取,0,22T æö-ç÷ç÷èø，(0,1,0)T 为A 的属于特征值1的两个正交的单位特征向量 ……6分令022010022Q æöç÷ç÷=ç÷ç÷ç÷-ç÷èø，则有110T Q AQ æöç÷=ç÷ç÷èø，故1101112020101T -æöæöç÷ç÷==ç÷ç÷ç÷ç÷-èøèøA Q Q . ……9分评分说明：求出满足条件的一个矩阵A ，即可给9分.（II ）由（I ）知A 的特征值为1,1,0，于是A E +的特征值为2，2，1，又A E +为实对称矩阵，故A E +为正定矩阵.……11分(22)（本题满分11分）设二维随机变量(,)X Y 的概率密度为2222(,),,x xy y f x y Ae x y -+-=-¥<<+¥-¥<<+¥，求常数A 及条件概率密度|(|)Y X f y x .解：因2222()(,)x xy y X f x f x y dy A edy +¥+¥-+--¥-¥==òò22()y x x A e dy+¥----¥=ò222(),x y x x Aeedy x +¥-----¥==-¥<<+¥ò，……4分所以21()x X f x dx e dx A p +¥+¥--¥-¥===ò，从而 1A p=……7分当(,)x Î-¥+¥时，22222|1(,)(|)1()x xy y Y X x X ef x y f y x f x p-+--==222x xy y -+-=2(),x y y --=-¥<<+¥ ……11分(23)（本题满分11分）设总体X 的概率分布为X 1 2 3p1q-2q q -2q其中参数(0,1)q Î未知.以i N 表示来自总体X 的简单随机样本（样本容量为n ）中等于i 的个数（1,2,3i =）.试求常数123,,a a a ，使31i ii T a N==å为q 的无偏估计量，并求T 的方差.解: 记11p q =-，22p q q =-，23p q =. 由于(,),1,2,3i i N B n p i =:，故i iEN np = ……4分于是22112233123[(1)()]ET a EN a EN a EN n a a a q q q q =++=-+-+ ……6分为使T 是q 的无偏估计量，必有22123[(1)()]n a a a q q q q q -+-+=，因此12132010a a a n a a =ìïï-=íï-=ïî，……8分由此得 12310,a a a n===……9分由于123N N N n ++=，故123111()()1N T N N n N n n n =+=-=-.注意到1~(,1)N B n q -，故1221(1)(1)n DT DN n n nq q q q --=== ……11分。

2010年考研数学(二)试题

(D) e.
1 m ln2 (1− x)
∫ (4) 设 m, n 是正整数,则反常积分 0
dx 的收敛性 ( ) nx
(A) 仅与 m 的取值有关.
(B) 仅与 n 的取值有关.
(C) 与 m, n 取值都有关.
(D) 与 m, n 取值都无关.
(5) 设函数
z
=
z(x, y)
,由方程
F(y , x
(23) 设
A
=
⎜ ⎜
−1
3
a
⎟ ⎟
,正交矩阵
Q
使得
QT
AQ
为对角矩阵,若
Q
的第
1
列为
⎜⎝ 4 a 0 ⎟⎠
1 (1, 2,1)T ,求 a,Q 6
参考答案
一、选择题 (1)【答案】 (B).
【解析】因为
f
(x)
=
x2 − x x2 −1
1+
1 x2
有间断点 x = 0, ±1 ,又因为
数学（二）试题第 3页（共 3 页）
(5) 【答案】 (B).
【解析】
∂z
=
−
Fx′
=
−
F1′
⎛ ⎜
−
⎝
y x2
⎞ ⎟⎠
+
F2′
⎛ ⎜
−
⎝
z x2
⎞ ⎟⎠
=
F1′ ⋅
y x
+ F2′ ⋅
z x
=
yF1′
+
zF2′
,
∂x Fz′
F2′
⋅
1 x
F2′
xF2′
∂z
=−

2010年考研数一试题及答案

2010年全国硕士研究生入学统一考试数学（一）试题及参考答案一、选择题：1~8小题，每小题4分，共32分。

1、222ln 1()()()()lim lime lime()()xx x xx x a x b x a x b x x x xx a x b ⎛⎫⎛⎫-⎪ ⎪ ⎪ ⎪-+-+⎝⎭⎝⎭→∞→∞→∞⎛⎫==⎪-+⎝⎭()()2()()()()lim elim e a b x ab a b x abxx x a x b x a x b x x -+⎛⎫-+ ⎪ ⎪-+-+⎝⎭→∞→∞==e a b -=方法二22()()lim lim 1()()()()xxx x x x x a x b x a x b x a x b →∞→∞⎛⎫⎛⎫--+=+ ⎪ ⎪-+-+⎝⎭⎝⎭()()()()()()()()lim 1lim 1()()()()x a x b a b x abxxa b x ab x a x b x x a b x ab a b x ab x a x b x a x b -+-+⋅-+-+→∞→∞⎛⎫⎛⎫-+-+=+=+ ⎪ ⎪-+-+⎝⎭⎝⎭()lim()()()ee x a b x abxa b x a x b →∞-+--+==（2）等式两边求全微分得：12d d 0y z F F x x ⎛⎫⎛⎫''⋅+⋅= ⎪ ⎪⎝⎭⎝⎭，即 1222d d dz d 0x y y x x z xF F x x --''+=12(d d )(dz d )0F x y y x F x z x ''⇒⋅-+⋅-= 12122dz d d yF zF F x y xF F '''+∴=-'' 所以有，1212222yF zF F zF z z xy x y z u y xF F F ''''+∂∂+=-==∂∂'''（3）、【解析与点评】：显然0,1x x ==是两个瑕点，有=+⎰对于的瑕点0x =，当0x +→21ln (1)mnx x -=-等价于221(1)mm nx--，而21120m nxdx -⎰收敛（因,m n 是正整数211m n⇒->-），故收敛；对于的瑕点1x =，当1(1,1)(0)2x δδ∈-<<12122ln (1)2(1)n m n mx x <-<-，而2112(1)m x dx -⎰显然收敛，故收敛。

2010年考研数一试题及答案

(6) 设 A 为 4 阶实对称矩阵，且 A2 + A = 0 ，若 A 的秩为 3 ，则 A 相似于
（D）
⎛1
⎞
⎜ A、 ⎜
1
⎟ ⎟
⎜
1⎟
⎜
⎟
⎝
0⎠
⎛1
⎞
⎜ B、 ⎜
1
⎟ ⎟
⎜
−1 ⎟
⎜
⎟
⎝
0⎠
⎛1
⎞
⎜ C、 ⎜
−1
⎟ ⎟
⎜
−1 ⎟
⎜
⎟
⎝
0⎠
⎛ −1
⎞
⎜ D、 ⎜
⎜
−1
⎟ ⎟
−1 ⎟
⎜
⎟
⎝
0⎠
【解析与点评】本题考查的知识点是矩阵的相似的性质，实对称矩阵可对角化的性质，矩阵
1 2 −1
2 xm n dx 收敛（因 m, n 是正整数 ⇒
2
−1
> −1），故
1 m ln2 (1− x)
2
dx
0
mn
0
nx
∫ 收敛；对于
1 m ln2 (1− x)
1 2
dx nx
的瑕点
x =1
，当
x ∈ (1− δ ,1)(0 < δ < 1) 2
时
m ln2 (1− x) 1 2
A、秩 r( A) = m , 秩 r(B) = m
B、秩 r(A) = m , 秩 r(B) = n
2
C、秩 r( A) = n , 秩 r(B) = m
D、秩 r( A) = n , 秩 r(B) = n
【解析与点评】本题主要考查的知识点是矩阵的秩的性质

【数学二】2010年全国考研研究生入学考试真题及答案答案解析

2010年全国硕士研究生入学统一考试数学二试题一、选择题(1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸．．．指定位置上.) (1) 函数()f x =( ) (A) 0. (B) 1. (C) 2. (D) 3.(2) 设12,y y 是一阶线性非齐次微分方程()()y p x y q x '+=的两个特解,若常数λμ，使12y y λμ+是该方程的解,12y y λμ-是该方程对应的齐次方程的解,则( ) (A) 11,22λμ==. (B) 11,22λμ=-=-. (C) 21,33λμ==. (D) 22,33λμ==. (3) 曲线2y x =与曲线ln (0)y a x a =≠相切,则a = ( )(A) 4e. (B) 3e. (C) 2e. (D) e.(4) 设,m n 是正整数,则反常积分⎰的收敛性 ( )(A) 仅与m 的取值有关. (B) 仅与n 的取值有关.(C) 与,m n 取值都有关. (D) 与,m n 取值都无关.(5)设函数(,)z z x y =,由方程(,)0y zF x x=确定,其中F 为可微函数,且20F '≠,则z z x y x y∂∂+=∂∂( ) (A) x . (B) z . (C) x -. (D) z -.(6) ()()2211lim n nn i j n n i n j →∞===++∑∑ ( ) (A) ()()1200111x dx dy x y ++⎰⎰. (B) ()()100111x dx dy x y ++⎰⎰. (C) ()()1100111dx dy x y ++⎰⎰. (D) ()()11200111dx dy x y ++⎰⎰. (7) 设向量组12I :,,,r ααα可由向量组12II :,,,s βββ线性表示,下列命题正确的是( )(A) 若向量组I 线性无关,则r s ≤. (B) 若向量组I 线性相关,则r s >.(C) 若向量组II 线性无关,则r s ≤. (D) 若向量组II 线性相关,则r s >.(8) 设A 为4阶实对称矩阵,且2A A O +=,若A 的秩为3,则A 相似于 ( ) (A) 1110⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭. (B) 1110⎛⎫ ⎪ ⎪ ⎪- ⎪⎝⎭. (C) 1110⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (D) 1110-⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. 二、填空题(9~14小题,每小题4分,共24分.请将答案写在答题纸．．．指定位置上.) (9) 3阶常系数线性齐次微分方程220y y y y ''''''-+-=的通解为y = .(10) 曲线3221x y x =+的渐近线方程为 . (11) 函数()ln 120y x x =-=在处的n 阶导数()()0n y = . (12) 当0θπ≤≤时,对数螺线r e θ=的弧长为 .(13) 已知一个长方形的长l 以2cm/s 的速率增加,宽w 以3cm/s 的速率增加.则当cm 12l = ,cm 5w =时,它的对角线增加的速率为 .(14)设,A B 为3阶矩阵,且132,2A B A B -==+=，,则1A B -+= .三、解答题(15~23小题,共94分.请将解答写在答题纸．．．指定位置上.解答应写出文字说明、证明过程或演算步骤.)(15)(本题满分11分)求函数2221()()x t f x x t e d -=-⎰的单调区间与极值.(16)(本题满分10分) ( I ) 比较()10ln ln 1n t t dt +⎡⎤⎣⎦⎰与10ln n t t dt ⎰()1,2,n =的大小,说明理由；( II ) 记()10ln ln 1n n u t t dt =+⎡⎤⎣⎦⎰()1,2,n =,求极限lim n n u →∞. (17)(本题满分10分)设函数()y f x =由参数方程22,(1)()x t t t y t ψ⎧=+>-⎨=⎩所确定,其中()t ψ具有2阶导数,且5(1)(1) 6.2ψψ'==，已知223,4(1)d y dx t =+求函数()t ψ. (18)(本题满分10分)一个高为l 的柱体形贮油罐,底面是长轴为2a ,短轴为2b 的椭圆.现将贮油罐平放,当油罐中油面高度为32b 时(如图),计算油的质量.(长度单位为m,质量单位为kg,油的密度为常数ρkg/m 3) (19) (本题满分11分)设函数(,)u f x y =具有二阶连续偏导数,且满足等式2222241250u u u x x y y∂∂∂++=∂∂∂∂,确定a ,b 的值,使等式在变换,x ay x by ξη=+=+下化简为20u ξη∂=∂∂. (20)(本题满分10分)计算二重积分2 sin D I r θ=⎰⎰,其中(),|0sec ,04D r r πθθθ⎧⎫=≤≤≤≤⎨⎬⎩⎭. (21) (本题满分10分)设函数()f x 在闭区间[]0,1上连续,在开区间()0,1内可导,且(0)0f =,1(1)3f =,证明：存在1(0,)2ξ∈,1(,1)2η∈,使得22()()=.f f ξηξη''++(22)(本题满分11分) 设110111a A b λλλ ⎛⎫⎛⎫ ⎪ ⎪= - 0= ⎪ ⎪ ⎪ ⎪1 1 ⎝⎭⎝⎭，,已知线性方程组Ax b =存在两个不同的解．( I ) 求λ,a ;( II ) 求方程组Ax b =的通解.(23)(本题满分11 分)设0141340A a a -⎛⎫ ⎪=- ⎪ ⎪⎝⎭,正交矩阵Q 使得T Q AQ 为对角矩阵,若Q 的第1列为2,1)T ,求,a Q .。

2010考研数学一真题答案

2010年全国硕士研究生入学统一考试数学一试题参考答案一、选择题(1)【答案】 (C).【解析】本题属于未定式求极限,极限为1∞型,故可以用“e 的抬起法”求解．()()2lim xx xx a x b →∞⎡⎤⎢⎥-+⎣⎦()()2lnlim x x x a x b x e ⋅-+→∞=()()2lim lnx x x x a x b e→∞⋅-+=,其中又因为()()2222()()lim ln lim ln 1()()()()lim()()()lim()()x x x x x x x a x b x x x a x b x a x b x x x a x b x a x b a b x abxx a x b a b→∞→∞→∞→∞--+⋅=+-+-+⎡⎤--+⎣⎦=-+-+=-+=-⎡⎤⎣⎦故原式极限为a b e -,所以应该选择(C). (2)【答案】 (B).【解析】122212122221x z y z y zF F F F F yF zF zx x x x x F F xF F x⎛⎫⎛⎫''''-+-⋅+⋅ ⎪ ⎪'''+∂⎝⎭⎝⎭=-=-==∂''''⋅, 112211y z F F F z x y F F F x'⋅''∂=-=-=-∂'''⋅, 1212222yF zF yF F z z z xy z x y F F F ''''+⋅∂∂+=-==∂∂'''． (3) 【答案】 (D).【解析】0x =与1x =都是瑕点.应分成=+⎰,用比较判别法的极限形式,对于,由于121012[ln (1)]lim 11mnx n mx xx+→--=.显然,当1201n m<-<,则该反常积分收敛. 当120n m -≤,1210[ln (1)]lim mx nx x+→-存在,此时实际上不是反常积分,故收敛.故不论,m n 是什么正整数,总收敛.对于,取01δ<<,不论,m n 是什么正整数,1211211[ln (1)]lim lim ln (1)(1)01(1)mnmx x x xx x x δδ--→→-=--=-,所以收敛,故选(D).(4)【答案】 (D). 【解析】()()222211111()nnn n i j i j n n n i n j n i n j =====++++∑∑∑∑22111()()n nj i n n j n i ===++∑∑ 12220211111lim lim ,11()nn n n j j n dy j n jn y n →∞→∞====+++∑∑⎰ 1011111lim lim ,11()n n n n i i n dx i n i n x n→∞→∞====+++∑∑⎰()()2222111111lim lim()()n nn nn n i j j i n n j n i n i n j →∞→∞=====++++∑∑∑∑ 221(lim )nn j n n j →∞==+∑1(lim )nn i nn i→∞=+∑1120011()()11dx dy x y =++⎰⎰()()11200111dx dy x y =++⎰⎰. (5)【答案】 (A).【解析】由于AB E =,故()()r AB r E m ==.又由于()(),()()r AB r A r AB r B ≤≤,故(),()m r A m r B ≤≤ ①由于A 为m n ⨯矩阵,B 为n m ⨯矩阵,故(),()r A m r B m ≤≤ ②由①、②可得(),()r A m r B m ==,故选A. (6)【答案】 (D).【解析】设λ为A 的特征值,由于2A A O +=,所以20λλ+=,即(1)0λλ+=,这样A 的特征值只能为-1或0. 由于A 为实对称矩阵,故A 可相似对角化,即AΛ,()()3r A r =Λ=,因此,1110-⎛⎫ ⎪- ⎪Λ= ⎪- ⎪⎝⎭,即1110A -⎛⎫⎪- ⎪Λ= ⎪- ⎪⎝⎭. (7) 【答案】 (C).【解析】离散型随机变量的分布函数是跳跃的阶梯形分段函数,连续型随机变量的分布函数是连续函数.观察本题中()F x 的形式,得到随机变量X 既不是离散型随机变量,也不是连续型随机变量,所以求随机变量在一点处的概率,只能利用分布函数的定义.根据分布函数的定义,函数在某一点的概率可以写成两个区间内概率的差,即{}{}{}()()1111111110122P X P X P X F F e e --==≤-<=--=--=-,故本题选(C).(8)【答案】 (A).【解析】根据题意知,()221x f x e-=(x -∞<<+∞),()21,1340,x f x ⎧ -≤≤⎪=⎨⎪ ⎩其它利用概率密度的性质:()1f x dx +∞-∞=⎰,故()()()()03121001312424a a f x dx af x dx bf x dx f x dxb dx b +∞+∞+∞-∞-∞-∞=+=+=+=⎰⎰⎰⎰⎰ 所以整理得到234a b +=,故本题应选(A).二、填空题 (9) 【答案】0.【解析】因为 ()()22ln 1ln 1tttdy t e dx e -+==-+-,()()()()22222ln 12ln 11tt t td te d y dt t e t e e dx dt dx t -+⎡⎤=⋅=-⋅-+⋅-⎢⎥+⎣⎦,所以220t d y dx ==. (10)【答案】 4π-.t =,2x t =,2dx tdt =,利用分部积分法, 原式220cos 22cos 2sin t t tdt t tdt t d t πππ=⋅==⎰⎰⎰20002sin 2sin 4cos t t t tdt td t πππ⎡⎤=-=⎢⎥⎣⎦⎰⎰0004cos cos 4cos 4sin 4t t tdt t ππππππ⎡⎤=-=-=-⎢⎥⎣⎦⎰. (11) 【答案】0.【解析】12222LL L xydx x dy xydx x dy xydx x dy +=+++⎰⎰⎰()()()01221011x x dx x dx x x dx x dx -=+++-+-⎰⎰()()0122122xx dx x x dx -=++-⎰⎰1322310223223x x x x -⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭211203223⎛⎫⎛⎫=--++-= ⎪ ⎪⎝⎭⎝⎭(12) 【答案】23. 【解析】 ()2221221211000211212021r rrz d rdr zdxdydz d rdr zdz dxdydz d rdr dz d r rdrππππθθθθΩΩ⎛⎫⎪⋅ ⎪⎝⎭==-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰4211222r d r dr πθπ⎛⎫-⎪⎝⎭=⎰⎰126204122r r d πθπ⎛⎫- ⎪⎝⎭=⎰20112266322d πθπππ⋅===⎰.(13)【答案】6a =.【解析】因为由123,,ααα生成的向量空间维数为2,所以123(,,)2r ααα=. 对123(,,)ααα进行初等行变换：123112112112211013013(,,)1010130060202000a a a ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪=→→ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以6a =.(14) 【答案】2.【解析】利用离散型随机变量概率分布的性质,知{}001!k k CP X k Ce k ∞∞======∑∑,整理得到1C e -=,即 {}111!!k e P X k e k k --===.故X 服从参数为1的泊松分布,则()()1,1E X D X ==,根据方差的计算公式有()()()222112E X D X E X =+=+=⎡⎤⎣⎦.三、解答题(15)【解析】对应齐次方程的特征方程为2320λλ-+=,解得特征根121,2λλ==,所以对应齐次方程的通解为212x x c y C e C e =+．设原方程的一个特解为*()xy x ax b e =+,则()()*22x y axax bx b e '=+++,()()*2422x y axax bx a b e ''=++++,代入原方程,解得1,2a b =-=-,故特解为*(2)xy x x e =--．故方程的通解为*212(2)x x x c y y y C e C e x x e =+=+-+． (16)【解析】因为22222222111()()x x x t t t f x x t e dt xe dt te dt ---=-=-⎰⎰⎰,所以2224423311()2222x x t x x t f x x e dt x ex ex e dt----'=+-=⎰⎰,令()0f x '=,则0,1x x ==±.又22421()24x t x f x e dt x e --''=+⎰,则21(0)20t f e dt -''=<⎰,所以2211111(0)(0)(1)22t t f t e dt e e ---=-=-=-⎰是极大值.而1(1)40f e-''±=>,所以(1)0f ±=为极小值.又因为当1x ≥时,()0f x '>；01x ≤<时,()0f x '<；10x -≤<时,()0f x '>；1x <-时,()0f x '<,所以()f x 的单调递减区间为(,1)(0,1)-∞-,()f x 的单调递增区间为(1,0)(1,)-+∞.(17)【解析】 (I)当01x <<时0ln(1)x x <+<,故[]ln(1)nn t t +<,所以[]ln ln(1)ln nn t t t t +<,则[]11ln ln(1)ln nn t t dt t t dt +<⎰⎰()1,2,n =.(II)()111101ln ln ln 1n n n t t dt t t dt td t n +=-⋅=-+⎰⎰⎰ ()211n =+,故由 ()1210ln 1n n u t t dt n <<=+⎰,根据夹逼定理得()210lim lim01n n n u n →∞→∞≤≤=+,所以lim 0n n u →∞=.(18)【解析】(I) (1)1222(1)1122(1)(1)2(1)121lim lim (1)(1)2121n n n n n n n n n nx x n n xx n n +-++--→∞→∞--⋅+-+=--⋅--222(21)21lim lim 2121n n n x n x x n n →∞→∞--==⋅=++, 所以,当21x <,即11x -<<时,原级数绝对收敛.当21x >时,原级数发散,因此幂级数的收敛半径1R =.当1x =±时,11211(1)(1)2121n n n n n x n n --∞∞==--⋅=--∑∑,由莱布尼兹判别法知,此级数收敛,故原级数的收敛域为[]1,1-.(II) 设1122111(1)(1)()2121n n nn n n S x x x x n n --∞∞-==⎛⎫--=⋅=⋅⋅ ⎪--⎝⎭∑∑,其中令 12111(1)()21n n n S x xn -∞-=-=⋅-∑()1,1x ∈-, 所以有 12221111()(1)()n n n n n S x xx ∞∞---=='=-⋅=-∑∑ ()1,1x ∈-,从而有 12211()1()1S x x x '==--+ ()1,1x ∈-, 故 11201()(0)arctan 1xS x dx S x x =+=+⎰,()1,1x ∈-.1()S x 在1,1x =-上是连续的,所以()S x 在收敛域[]1,1-上是连续的.所以()arctan S x x x =⋅,[]1,1x ∈-.(19)【解析】 ( I )令()222,,1F x y z x y z yz =++--,故动点(),,P x y z 的切平面的法向量为()2,2,2x y z zy --,由切平面垂直xOy ,故所求曲线C 的方程为222120x y z yz z y ⎧++-=⎨-=⎩. ( II ) 由⎩⎨⎧=-=-++,02,1222y z yz z y x 消去z ,可得曲线C 在xOy 平面上的投影曲线所围成的xOy 上的区域223:{(,)|1}4D x y x y +≤,由()()x x yz z y x '='-++1222,由 dxdy zy yzz y dxdy y z x z dS 24412222--++=⎪⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+=,故(2DDDx y zI x dxdy xdxdy ∑-==+=+⎰⎰⎰⎰⎰⎰12Dπ==⋅=. (20)【解析】因为方程组有两个不同的解,所以可以判断方程组增广矩阵的秩小于3,进而可以通过秩的关系求解方程组中未知参数,有以下两种方法.方法1：( I )已知Ax b =有2个不同的解,故()()3r A r A =<,对增广矩阵进行初等行变换,得111110101010111111a A a λλλλλλ⎛⎫⎛⎫ ⎪ ⎪=-→- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭22111111010101010110011a a λλλλλλλλλ⎛⎫⎛⎫⎪⎪→-→- ⎪ ⎪ ⎪ ⎪-----+⎝⎭⎝⎭ 当1λ=时,11111111000100010000000A a ⎛⎫⎛⎫⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,此时,()()r A r A ≠,故Ax b =无解(舍去)．当1λ=-时,111102010002A a -⎛⎫ ⎪→- ⎪ ⎪+⎝⎭,由于()()3r A r A =<,所以2a =-,故1λ=- ,2a =-.方法2：已知Ax b =有2个不同的解,故()()3r A r A =<,因此0A =,即211010(1)(1)011A λλλλλ=-=-+=,知1λ=或-1.当1λ=时,()1()2r A r A =≠=,此时,Ax b =无解,因此1λ=-.由()()r A r A =,得2a =-.( II ) 对增广矩阵做初等行变换31012111211121020102010102111100000000A ⎛⎫- ⎪----⎛⎫⎛⎫ ⎪⎪ ⎪⎪=-→-→- ⎪ ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭可知原方程组等价为1323212x x x ⎧-=⎪⎪⎨⎪=-⎪⎩,写成向量的形式,即123332110210x x x x ⎛⎫⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪=+- ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭.因此Ax b =的通解为32110210x k ⎛⎫ ⎪⎛⎫ ⎪⎪⎪=+- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭,其中k 为任意常数.(21)【解析】 ( I )由于二次型在正交变换x Qy =下的标准形为2212y y +,所以A 的特征值为1231,0λλλ===.由于Q 的第3列为22T ⎛ ⎝⎭,所以A 对应于30λ=的特征向量为22T⎛ ⎝⎭,记为3α. 由于A 是实对称矩阵,所以对应于不同特征值的特征向量是相互正交的,设属于121λλ==的特征向量为()123,,Tx x x α=,则30T αα=,即13022x x +=. 求得该方程组的基础解系为()()120,1,0,1,0,1TTαα==-,因此12,αα为属于特征值1λ=的两个线性无关的特征向量.由于12,αα是相互正交的,所以只需单位化：())1212120,1,0,1,0,1T Tααββαα====-. 取()12302,,10002Q ββα⎛⎪⎪==⎝⎭,则110T Q AQ ⎛⎫ ⎪=Λ= ⎪ ⎪⎝⎭,且1T Q Q -=, 故 1102201011022TA Q Q ⎛⎫- ⎪ ⎪=Λ= ⎪ ⎪- ⎪⎝⎭. ( II )A E +也是实对称矩阵,A 的特征值为1,1,0,所以A E +的特征值为2,2,1,由于A E +的特征值全大于零,故A E +是正定矩阵.(22)【解析】当给出二维正态随机变量的的概率密度(),f x y 后,要求条件概率密度|(|)Y X f y x ,可以根据条件概率公式|(,)(|)()Y X X f x y f y x f x =来进行计算.本题中还有待定参数,A 要根据概率密度的性质求解,具体方法如下.()()22222222()(),xxy y y x x xy x X f x f x y dy A e dy A e dy Ae e dy +∞+∞+∞+∞-+--------∞-∞-∞-∞====⎰⎰⎰⎰2,x x -=-∞<<+∞.根据概率密度性质有()21x X f x dx edx A π+∞+∞--∞-∞===⎰,即1A π-=,故()2x X f x -=,x -∞<<+∞.当x -∞<<+∞时,有条件概率密度()()()22222222(),,,x xy y x xy y x y Y X X f x y f y x x y f x -+--+---==-∞<<+∞-∞<<+∞.(23)【解析】()()()22123~,1,~,,~,N B n N B n N B n θθθθ--()()()()31122331i i i E T E a N a E N a E N a E N =⎛⎫==++ ⎪⎝⎭∑()()221231a n a n a n θθθθ=-+-+()()212132na n a a n a a θθ=+-+-.因为T 是θ的无偏估计量,所以()E T θ=,即得()()12132010na n a a n a a =⎧⎪-=⎨⎪-=⎩,整理得到10a =,21,a n =31a n=.所以统计量 ()()12323111110T N N N N N n N n n n n=⨯+⨯+⨯=⨯+=⨯-.注意到1(,1)N B n θ-,故()()()11211D T D n N D N n n⎡⎤=⨯-=⨯⎢⎥⎣⎦()11n θθ=-.。

2010年考研英语真题及答案完整解析

2010年考研英语真题与答案解析从2010年开始，全国硕士研究生入学考试的英语试卷分为了英语（一）和英语（二）。

英语（一）即原统考“英语”。

英语（二）主要是为高等院校和科研院所招收专业学位硕士研究生而设置的具有选拔性质的统考科目。

英语一考试形式、考试内容与试卷结构（一）考试形式考试形式为笔试。

考试时间为180分钟。

满分为100分。

试卷包括试题册和答题卡。

答题卡分为答题卡1和答题卡2。

考生应将1~45题的答案按要求填涂在答题卡1上，将46~52题的答案写在答题卡2上。

（二）考试内容试题分三部分，共52题，包括英语知识运用、阅读理解和写作。

第一部分英语知识运用该部分不仅考查考生对不同语境中规范的语言要素（包括词汇、表达方式和结构）的掌握程度，而且还考查考生对语段特征（如连贯性和一致性等）的辨识能力等。

共20小题，每小题0.5分，共10分。

在一篇240~280词的文章中留出20个空白，要求考生从每题给出的4个选项中选出最佳答案，使补全后的文章意思通顺、前后连贯、结构完整。

考生在答题卡1上作答。

第二部分阅读理解该部分由A、B、C三节组成，考查考生理解书面英语的能力。

共30小题，每小题2分，共60分。

A节（20小题）：主要考查考生理解主旨要义、具体信息、概念性含义，进行有关的判断、推理和引申，根据上下文推测生词的词义等能力。

要求考生根据所提供的4篇（总长度约为1600词）文章的内容，从每题所给出的4个选项中选出最佳答案。

考生在答题卡1上作答。

B节（5小题）：主要考查考生对诸如连贯性、一致性等语段特征以及文章结构的理解。

本部分有3种备选题型。

每次考试从这3种备选题型中选择一种进行考查。

考生在答题卡1上作答。

备选题型有：1）本部分的内容是一篇总长度为500~600词的文章，其中有5段空白，文章后有6~7段文字。

要求考生根据文章内容从这6~7段文字中选择能分别放进文章中5个空白处的5段。

2）在一篇长度约500~600词的文章中，各段落的原有顺序已被打乱，要求考生根据文章的内容和结构将所列段落（7~8个）重新排序，其中有2~3个段落在文章中的位置已给出。

2010年全国考研数三试题及解析

2010年全国研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上. （1）若1)1(1lim =⎥⎦⎤⎢⎣⎡--x e a x x ，则a 等于（C ）（A ）0 （B ）1 （C ）2 （D ）3【解析】=⎥⎦⎤⎢⎣⎡--→x x e a x x )1(1lim 0⎥⎦⎤⎢⎣⎡+-→x x x ae e x )1(1lim 0=111lim00=+-=+-→→a e im al xe x x x x ，因此a =2（2）设21y y ，是一阶线性非齐次微分方程)()('x q y x p y =+的两个特解，若常数λ，程的解，则是该方程对应的齐次方是该方程的解，使2121y y y y μλμλμ-+（A ）（Ａ）λ＝，21μ＝，21 （Ｂ）λ＝－，21μ＝－，21（Ｃ）λ＝32，μ＝31 （Ｄ）λ＝32，μ＝32【解析】根据已知有)()(),()(2211x q x p y y x q x p y y =+"=+"λλ。

于是将2121y y y y μλμλ-+和分别代入方程左边得)(21''+y y μλ+))((21y y x p μλ+)()(x q μλ+= )(21''-y y μλ+))((21y y x p μλ-)()(x q μλ-=21y y μλ+为方程解1=+⇒μλ，21y y μλ-为齐次方程解0=-⇒μλ，解得21==μλ （３）设函数)(x f ，)(x g 具有二阶导数，且0)(<''x g ，若a x g =)(0是)(x g 的极值，则))((x g f 在0x 取极大值的一个充分条件是（B ）（Ａ）)(a f '＜０（Ｂ）)(a f '＞０（Ｃ）)(a f ''＜０（Ｄ）)(a f ''＞０【解析】根据已知得0)(0='x g ，0)(0<''x g 。

2010年考研数学三真题及答案解析

(D) 1 e1 .
(8) 设 f1(x) 为标准正态分布的概率密度, f2 (x) 为1, 3 上均匀分布的概率密度,若
f
(
x)
baff21
(x) (x)
x 0 (a 0,b 0) x0
为概率密度,则 a, b 应满足 ( )
(A) 2a 3b 4 .
(B) 3a 2b 4 .
(C) a b 1.
(D) 3.
(2)
设 y1, y2 是一阶非齐次微分方程 y p x y q x 的两个特解,若常数，使
y1 y2 是该方程的解, y1 y2 是该方程对应的齐次方程的解,则( )
(A) 1 , 1 . 22
(B) 1 , 1 .
2
2
(C) 2 , 1 . 33
y2
P
x
y2
q
x
,
q x q x ,由 q x 0 可知 1 ,
②
由①②求解得 1 ,故应选(A)． 2
(3)【答案】 (B).
【解析】 f g(x) f g(x) g(x) ,
f g(x) f g(x) g(x) f g(x)g(x)2 f g(x) g(x)
2010
2010 年全国硕士研究生入学统一考试
数学三试题
一、选择题(1~8 小题,每小题 4 分,共 32 分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.)
(1)
1
若
lim
x0
x
1 x
a
e
x
1,则 a 等于(
)
(A) 0.
(B) 1.
(C) 2.
(D) 2 , 2 . 33

2010考研数一真题及解析

2010年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸．．．指定位置上.) (1) 极限2lim ()()xx x x a x b →∞⎡⎤=⎢⎥-+⎣⎦( ) (A) 1. (B) e . (C) a be -. (D) b ae-.(2) 设函数(,)z z x y =,由方程,0y z F x x ⎛⎫=⎪⎝⎭确定,其中F 为可微函数,且20F '≠,则z zxy x y∂∂+=∂∂( ) (A) x . (B) z . (C) x -. (D) z -.(3) 设,m n 是正整数,则反常积分⎰的收敛性 ( )(A) 仅与m 的取值有关. (B)仅与n 的取值有关. (C) 与,m n 取值都有关. (D) 与,m n 取值都无关. (4) ()()2211limn nn i j nn i n j →∞===++∑∑ ( ) (A)()()120111xdx dy x y ++⎰⎰. (B) ()()100111x dx dy x y ++⎰⎰. (C)()()11111dx dy x y ++⎰⎰. (D) ()()1120111dx dy x y ++⎰⎰. (5) 设A 为m n ⨯矩阵,B 为n m ⨯矩阵,E 为m 阶单位矩阵,若AB E =,则 ( )(A) 秩()r A m =,秩()r B m =. (B) 秩()r A m =,秩()r B n =. (C) 秩()r A n =,秩()r B m =. (D) 秩()r A n =,秩()r B n =. (6) 设A 为4阶实对称矩阵,且2A A O +=,若A 的秩为3,则A 相似于 ( )(A) 1110⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭. (B) 1110⎛⎫ ⎪⎪ ⎪- ⎪⎝⎭.(C) 1110⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (D) 1110-⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (7) 设随机变量X 的分布函数0,1(),0121,1x x F x x e x -<⎧⎪⎪=≤<⎨⎪-≥⎪⎩,则{}1P X == ( ) (A) 0. (B)12. (C) 112e --. (D) 11e --. (8) 设1()f x 为标准正态分布的概率密度,2()f x 为[]1,3-上均匀分布的概率密度,若12(),0()(),0af x x f x bf x x ≤⎧=⎨>⎩,(0,0)a b >>为概率密度,则,a b 应满足 ( ) (A) 234a b +=. (B) 324a b +=. (C) 1a b +=. (D) 2a b +=.二、填空题(9 14小题,每小题4分,共24分.请将答案写在答题纸．．．指定位置上.) (9) 设()20,ln 1,t tx e y u du -⎧=⎪⎨=+⎪⎩⎰ 求220t d y dx == .(10)2π=⎰.(11) 已知曲线L 的方程为[]{}11,1y x x =- ∈-,起点是()1.0-,终点是()1,0,则曲线积分2Lxydx x dy +=⎰.(12) 设(){}22,,1x y z xy z Ω=+≤≤,则Ω的形心的竖坐标z = .(13) 设()()()1231,2,1,0,1,1,0,2,2,1,1,TTTa ααα=-==,若由123,,ααα生成的向量空间的维数是2,则a = .(14) 设随机变量X 的概率分布为{}!C P X k k ==,0,1,2,k = ,则()2E X = .三、解答题(15～23小题,共94分.请将解答写在答题纸．．．指定位置上.解答应写出文字说明、证明过程或演算步骤.)求微分方程322x y y y xe '''-+=的通解． (16)(本题满分10分)求函数()()2221x t f x xt e dt -=-⎰的单调区间与极值.(17)(本题满分10分)(I)比较()1ln ln 1n t t dt +⎡⎤⎣⎦⎰与10ln nt t dt ⎰()1,2,n = 的大小,说明理由；(II)记()1ln ln 1nn u t t dt =+⎡⎤⎣⎦⎰()1,2,n = ,求极限lim n n u →∞. (18)(本题满分10分)求幂级数()121121n n n x n -∞=--∑的收敛域及和函数.(19)(本题满分10分)设P 为椭球面222:1S x y z yz ++-=上的动点,若S 在点P 处的切平面与xOy 面垂直,求点P 的轨迹C ,并计算曲面积分2x y zI ∑-=,其中∑是椭球面S 位于曲线C 上方的部分.(20)(本题满分11分)设110111a A b λλλ ⎛⎫⎛⎫ ⎪ ⎪= - 0= ⎪ ⎪ ⎪ ⎪1 1 ⎝⎭⎝⎭，,已知线性方程组Ax b =存在两个不同的解.( I ) 求λ,a ；( II ) 求方程组Ax b =的通解. (21)(本题满分11 分)已知二次型123(,,)T f x x x x Ax =在正交变换x Qy =下的标准形为2212y y +,且Q 的第三列为T. ( I ) 求矩阵A ；( II ) 证明A E +为正定矩阵,其中E 为3阶单位矩阵. (22)(本题满分11分)设二维随机变量(,)X Y 的概率密度为2222(,)x xy y f x y Ae -+-=,x -∞<<+∞,y -∞<<+∞,求常数A 及条件概率密度|(|)Y X f y x ．设总体X其中参数()0,1θ∈未知,以i N 表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3i =).试求常数123,,a a a ,使31iii T a N ==∑为θ的无偏估计量,并求T 的方差.2010年全国硕士研究生入学统一考试数学一试题参考答案一、选择题(1)【答案】 (C).【解析】本题属于未定式求极限,极限为1∞型,故可以用“e 的抬起法”求解．()()2lim xx x x a x b →∞⎡⎤⎢⎥-+⎣⎦()()2ln lim x x x a x b x e ⋅-+→∞=()()2lim ln x x x x a x b e →∞⋅-+=, 其中又因为()()2222()()lim ln lim ln 1()()()()lim()()()lim()()x x x x x x x a x b x x x a x b x a x b x x x a x b x a x b a b x abxx a x b a b→∞→∞→∞→∞--+⋅=+-+-+⎡⎤--+⎣⎦=-+-+=-+=-⎡⎤⎣⎦故原式极限为a be-,所以应该选择(C).(2)【答案】 (B).【解析】12221212222x z y z y zF F F F F yF zF zx x x x x F F xF F x⎛⎫⎛⎫''''-+-⋅+⋅ ⎪ ⎪'''+∂⎝⎭⎝⎭=-=-==∂''''⋅, 112211y z F F F z x y F F F x'⋅''∂=-=-=-∂'''⋅, 1212222yF zF yF F z z z x y z x y F F F ''''+⋅∂∂+=-==∂∂'''． (3) 【答案】 (D).【解析】0x =与1x =都是瑕点.应分成dx dx =+⎰,用比较判别法的极限形式,对于,由于121012[ln (1)]lim 11mnx n mx xx+→--=.显然,当1201n m<-<,则该反常积分收敛. 当120n m -≤,1210[ln (1)]lim mx nx x+→-存在,此时实际上不是反常积分,故收敛.故不论,m n 是什么正整数,总收敛.对于,取01δ<<,不论,m n 是什么正整数,1211211[ln (1)]lim lim ln (1)(1)01(1)mnmx x x xx x x δδ--→→-=--=-,所以收敛,故选(D).(4)【答案】 (D). 【解析】()()222211111()nnnn i j i j n nn i n j n i n j =====++++∑∑∑∑22111()()n n j i n n j n i ===++∑∑ 12220211111lim lim ,11()nn n n j j n dy j n jn y n→∞→∞====+++∑∑⎰ 1011111lim lim ,11()nn n n i i n dx i n i n x n→∞→∞====+++∑∑⎰()()2222111111lim lim()()n nn nn n i j j i n n j n i n i n j →∞→∞=====++++∑∑∑∑ 221(lim )nn j n n j→∞==+∑1(lim )nn i nn i →∞=+∑ 1120011()()11dx dy x y =++⎰⎰()()11200111dx dy x y =++⎰⎰. (5)【答案】 (A).【解析】由于AB E =,故()()r AB r E m ==.又由于()(),()()r AB r A r AB r B ≤≤,故(),()m r A m r B ≤≤ ①由于A 为m n ⨯矩阵,B 为n m ⨯矩阵,故(),()r A m r B m ≤≤ ②由①、②可得(),()r A m r B m ==,故选A. (6)【答案】 (D).【解析】设λ为A 的特征值,由于2A A O +=,所以20λλ+=,即(1)0λλ+=,这样A 的特征值只能为-1或0. 由于A 为实对称矩阵,故A 可相似对角化,即A Λ ,()()3r A r =Λ=,因此,1110-⎛⎫ ⎪- ⎪Λ= ⎪- ⎪⎝⎭,即1110A -⎛⎫ ⎪- ⎪Λ= ⎪- ⎪⎝⎭. (7) 【答案】 (C).【解析】离散型随机变量的分布函数是跳跃的阶梯形分段函数,连续型随机变量的分布函数是连续函数.观察本题中()F x 的形式,得到随机变量X 既不是离散型随机变量,也不是连续型随机变量,所以求随机变量在一点处的概率,只能利用分布函数的定义.根据分布函数的定义,函数在某一点的概率可以写成两个区间内概率的差,即{}{}{}()()1111111110122P X P X P X F F e e --==≤-<=--=--=-,故本题选(C).(8)【答案】 (A).【解析】根据题意知,()221x f x -=(x -∞<<+∞),()21,1340,x f x ⎧ -≤≤⎪=⎨⎪ ⎩其它利用概率密度的性质:()1f x dx +∞-∞=⎰,故()()()()03121001312424a a f x dx af x dx bf x dx f x dxb dx b +∞+∞+∞-∞-∞-∞=+=+=+=⎰⎰⎰⎰⎰所以整理得到234a b +=,故本题应选(A).二、填空题 (9) 【答案】0.【解析】因为 ()()22ln 1ln 1ttt dy t e dx e-+==-+-, ()()()()22222ln 12ln 11tt t td te d y dt t e t e e dx dt dx t -+⎡⎤=⋅=-⋅-+⋅-⎢⎥+⎣⎦,所以220t d y dx ==. (10)【答案】 4π-.t =,2x t =,2dx tdt =,利用分部积分法, 原式220cos 22cos 2sin t t tdt t tdt t d t πππ=⋅==⎰⎰⎰20002sin 2sin 4cos t t t tdt td t πππ⎡⎤=-=⎢⎥⎣⎦⎰⎰0004cos cos 4cos 4sin 4t t tdt t ππππππ⎡⎤=-=-=-⎢⎥⎣⎦⎰.(11) 【答案】0.【解析】12222LL L xydx x dy xydx x dy xydx x dy +=+++⎰⎰⎰()()()0122111x x dx x dx x x dx x dx -=+++-+-⎰⎰()()0122122xx dx x x dx -=++-⎰⎰1322310223223x x x x -⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭211203223⎛⎫⎛⎫=--++-= ⎪ ⎪⎝⎭⎝⎭(12) 【答案】23. 【解析】 ()2221221211000211212021r rrz d rdr zdxdydz d rdr zdz dxdydz d rdr dz d r rdrππππθθθθΩΩ⎛⎫⎪⋅ ⎪⎝⎭==-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰4211222r d r dr πθπ⎛⎫-⎪⎝⎭=⎰⎰126204122r r d πθ⎛⎫- ⎪⎝⎭=⎰20112266322d πθπππ⋅===⎰. (13)【答案】6a =.【解析】因为由123,,ααα生成的向量空间维数为2,所以123(,,)2r ααα=. 对123(,,)ααα进行初等行变换：123112112112211013013(,,)1010130060202000a a a ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--⎪ ⎪ ⎪=→→⎪ ⎪ ⎪-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以6a =.(14) 【答案】2.【解析】利用离散型随机变量概率分布的性质,知{}001!k k CP X k Ce k ∞∞======∑∑,整理得到1C e -=,即 {}111!!k e P X k e k k --===.故X 服从参数为1的泊松分布,则()()1,1E X D X ==,根据方差的计算公式有()()()222112E X D X E X =+=+=⎡⎤⎣⎦. 三、解答题(15)【解析】对应齐次方程的特征方程为2320λλ-+=,解得特征根121,2λλ==,所以对应齐次方程的通解为212x x c y C e C e =+．设原方程的一个特解为*()x y x ax b e =+,则()()*22x y axax bx b e '=+++,()()*2422x y axax bx a b e ''=++++,代入原方程,解得1,2a b =-=-,故特解为*(2)xy x x e =--．故方程的通解为*212(2)x x x c y y y C e C e x x e =+=+-+． (16)【解析】因为22222222111()()x x x t t t f x x t e dt xe dt te dt ---=-=-⎰⎰⎰,所以2224423311()2222x x t x x t f x x e dt x ex ex e dt----'=+-=⎰⎰,令()0f x '=,则0,1x x ==±.又22421()24x t x f x e dt x e --''=+⎰,则21(0)20t f e dt -''=<⎰,所以2211111(0)(0)(1)22t t f t e dt e e ---=-=-=-⎰是极大值.而1(1)40f e -''±=>,所以(1)0f ±=为极小值.又因为当1x ≥时,()0f x '>；01x ≤<时,()0f x '<；10x -≤<时,()0f x '>；1x <-时,()0f x '<,所以()f x 的单调递减区间为(,1)(0,1)-∞- ,()f x 的单调递增区间为(1,0)(1,)-+∞ .(17)【解析】 (I)当01x <<时0ln(1)x x <+<,故[]ln(1)nnt t +<,所以[]ln ln(1)ln nn t t t t +<,则[]11ln ln(1)ln nn t t dt t t dt +<⎰⎰()1,2,n = .(II)()111101ln ln ln 1n n n t t dt t t dt td t n +=-⋅=-+⎰⎰⎰ ()211n =+,故由 ()1210ln 1n n u t t dt n <<=+⎰,根据夹逼定理得()210lim lim01n n n u n →∞→∞≤≤=+,所以lim 0n n u →∞=.(18)【解析】(I) (1)1222(1)1122(1)(1)2(1)121lim lim (1)(1)2121n n n n n n n n n nx x n n xx n n +-++--→∞→∞--⋅+-+=--⋅--222(21)21lim lim 2121n n n x n x x n n →∞→∞--==⋅=++, 所以,当21x <,即11x -<<时,原级数绝对收敛.当21x >时,原级数发散,因此幂级数的收敛半径1R =.当1x =±时,11211(1)(1)2121n n n n n x n n --∞∞==--⋅=--∑∑,由莱布尼兹判别法知,此级数收敛,故原级数的收敛域为[]1,1-.(II) 设1122111(1)(1)()2121n n nn n n S x x x x n n --∞∞-==⎛⎫--=⋅=⋅⋅ ⎪--⎝⎭∑∑,其中令12111(1)()21n n n S x x n -∞-=-=⋅-∑()1,1x ∈-,所以有 12221111()(1)()n n n n n S x xx ∞∞---=='=-⋅=-∑∑ ()1,1x ∈-,从而有 12211()1()1S x x x '==--+ ()1,1x ∈-, 故 11201()(0)arctan 1xS x dx S x x =+=+⎰,()1,1x ∈-.1()S x 在1,1x =-上是连续的,所以()S x 在收敛域[]1,1-上是连续的.所以()arctan S x x x =⋅,[]1,1x ∈-.(19)【解析】 ( I )令()222,,1F x y z x y z yz =++--,故动点(),,P x y z 的切平面的法向量为()2,2,2x y z zy --,由切平面垂直xOy ,故所求曲线C 的方程为222120x y z yz z y ⎧++-=⎨-=⎩. ( II ) 由⎩⎨⎧=-=-++,02,1222y z yz z y x 消去z ,可得曲线C 在xOy 平面上的投影曲线所围成的xOy 上的区域223:{(,)|1}4D x y x y +≤,由()()x x yz z y x '='-++1222,由dxdy zy yzz y dxdy y z x z dS 24412222--++=⎪⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+=,故(2DDDx y zI x dxdy xdxdy ∑-==+=+⎰⎰⎰⎰⎰⎰12Dπ==⋅=. (20)【解析】因为方程组有两个不同的解,所以可以判断方程组增广矩阵的秩小于3,进而可以通过秩的关系求解方程组中未知参数,有以下两种方法.方法1：( I )已知Ax b =有2个不同的解,故()()3r A r A =<,对增广矩阵进行初等行变换,得111110101010111111a A a λλλλλλ⎛⎫⎛⎫⎪⎪=-→- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭22111111010101010110011a a λλλλλλλλλ⎛⎫⎛⎫⎪⎪→-→- ⎪ ⎪ ⎪ ⎪-----+⎝⎭⎝⎭当1λ=时,11111111000100010000000A a ⎛⎫⎛⎫⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,此时,()()r A r A ≠,故Ax b =无解(舍去)．当1λ=-时,111102010002A a -⎛⎫ ⎪→- ⎪ ⎪+⎝⎭,由于()()3r A r A =<,所以2a =-,故1λ=- ,2a =-. 方法2：已知Ax b =有2个不同的解,故()()3r A r A =<,因此0A =,即211010(1)(1)011A λλλλλ=-=-+=,知1λ=或-1.当1λ=时,()1()2r A r A =≠=,此时,Ax b =无解,因此1λ=-.由()()r A r A =,得2a =-.( II ) 对增广矩阵做初等行变换31012111211121020102010102111100000000A ⎛⎫- ⎪----⎛⎫⎛⎫ ⎪⎪ ⎪⎪=-→-→-⎪ ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭可知原方程组等价为1323212x x x ⎧-=⎪⎪⎨⎪=-⎪⎩,写成向量的形式,即123332110210x x x x ⎛⎫⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭.因此Ax b =的通解为32110210x k ⎛⎫⎪⎛⎫ ⎪ ⎪ ⎪=+- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭,其中k 为任意常数.(21)【解析】 ( I )由于二次型在正交变换x Qy =下的标准形为2212y y +,所以A 的特征值为1231,0λλλ===.由于Q 的第3列为,0,22T ⎛ ⎝⎭,所以A 对应于30λ=的特征向量为22T⎛ ⎝⎭,记为3α. 由于A 是实对称矩阵,所以对应于不同特征值的特征向量是相互正交的,设属于121λλ==的特征向量为()123,,Tx x x α=,则30T αα=,130x =. 求得该方程组的基础解系为()()120,1,0,1,0,1TTαα==-,因此12,αα为属于特征值1λ=的两个线性无关的特征向量.由于12,αα是相互正交的,所以只需单位化：())1212120,1,0,1,0,1T Tααββαα====-. 取()1230,,10002Q ββα⎛⎪⎪==⎝⎭,则110T Q AQ ⎛⎫ ⎪=Λ= ⎪ ⎪⎝⎭,且1T Q Q -=, 故 1102201011022TA Q Q ⎛⎫- ⎪ ⎪=Λ= ⎪ ⎪- ⎪⎝⎭. ( II )A E +也是实对称矩阵,A 的特征值为1,1,0,所以A E +的特征值为2,2,1,由于A E +的特征值全大于零,故A E +是正定矩阵.(22)【解析】当给出二维正态随机变量的的概率密度(),f x y 后,要求条件概率密度|(|)Y X f y x ,可以根据条件概率公式|(,)(|)()Y X X f x y f y x f x =来进行计算.本题中还有待定参数,A 要根据概率密度的性质求解,具体方法如下.()()22222222()(),xxy y y x x xy x X f x f x y dy A e dy A e dy Ae e dy +∞+∞+∞+∞-+--------∞-∞-∞-∞====⎰⎰⎰⎰2,x x -=-∞<<+∞.根据概率密度性质有()21x X f x dx e dx A π+∞+∞--∞-∞===⎰,即1A π-=,故()2x X f x -=,x -∞<<+∞.当x -∞<<+∞时,有条件概率密度()()()22222222(),,,x xy y x xy y x y Y X X f x y f y x x y f x -+--+---==-∞<<+∞-∞<<+∞.(23)【解析】()()()22123~,1,~,,~,N B n N B n N B n θθθθ--()()()()31122331i i i E T E a N a E N a E N a E N =⎛⎫==++ ⎪⎝⎭∑()()221231a n a n a n θθθθ=-+-+()()212132na n a a n a a θθ=+-+-.因为T 是θ的无偏估计量,所以()E T θ=,即得()()12132010na n a a n a a =⎧⎪-=⎨⎪-=⎩,整理得到10a =,21,a n = 31a n=.所以统计量()()12323111110T N N N N N n N n n n n=⨯+⨯+⨯=⨯+=⨯-.注意到1(,1)N B n θ- ,故()()()11211D T D n N D N n n⎡⎤=⨯-=⨯⎢⎥⎣⎦()11n θθ=-.。

2010年考研数学一真题及解析

2010年全国硕士研究生入学统一考试数学一试题一、选择题：1~8小题，每小题4分，共32分，下列每题给出的四个选项中，只有一个选项符合题目要求，请将所选项前的字母填在答题纸．．．指定位置上. (1)极限2lim ( )()()xx x x a x b →∞⎡⎤=⎢⎥-+⎣⎦(A)1 (B)e(C)a be-(D)b ae-答案：C 详解：2lim ()()xx x x a x b →∞⎡⎤⎢⎥-+⎣⎦=2233221ln ()()()()lim lim lim xxx x bx abxx x x a x b a bx a x b x ax bx abx x x e e ee⎛⎫-+-- ⎪⋅ ⎪-+--+⎝⎭-+-→∞→∞→∞===(2)设函数(),z z x y =，由方程(,)0y zF x x=确定，其中F 为可微函数，且20F '=，则x z x y u y ∂∂+∂∂=( ) (A)x (B)z (C)x - (D)z -答案：B详解：12221222,1x z y z y zF F F F F z x x x x x F F F x⎛⎫⎛⎫''-+-''⋅+⋅⎪ ⎪'∂⎝⎭⎝⎭=-=-=''∂'⋅112211y x F F F z x xF F F x'⋅''∂=-=-=-''∂'⋅1212222yF zF yF F z z z xyz xxF F F ''''+⋅∂∂+=-=='''∂∂(3)设,m n是正整数，则反常积分0⎰的收敛性(A)仅与m 的取值有关 (B)仅与n 取值有关 (C)与,m n 取值都有关 (D)与,m n 取值都无关答案：C 详解：11222111111111ln 1(ln (1))1111mmn mm np p p nnx p p m dx p x p np -∞∞∞⋅⋅⋅⎛⎫⎛⎫⎛⎫- ⎪⎪ ⎪-⎛⎫⎝⎭⎝⎭⎝⎭==-= ⎪⎛⎫⎝⎭⎛⎫ ⎪ ⎪⎝⎭⎝⎭∑∑∑⎰⎰2121121n mm np n m m nn m p m n -∞--⎧>⎪⎛⎫⎪=⎨⎪-⎝⎭⎪≤⎪⎩∑收敛，发散， (4)()()2211limnnx i j nn i n j→∞--=++∑∑(A)()()12111x dx dy x y++⎰⎰(B)()()10111x dx dy x y ++⎰⎰(C)()()1100111dx dy x y ++⎰⎰(D)()()112111dx dy x y++⎰⎰答案：D详解：()()22211112limlim11nnnnx x i j i j nnn i nji j n n n n →∞→∞----=⎛⎫++⎛⎫⎛⎫+⋅⋅+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑∑2211111lim11n nx i j inj n n →∞--=⋅⋅⎛⎫++ ⎪⎝⎭∑∑()()112111dx dy x y=++⎰⎰(5)设A 为m n ⨯型矩阵，B 为n m ⨯型矩阵，E 为m 阶单位矩阵，若AB =E ，则( ) (A)秩(),r A m =秩()r B m =(B)秩(),r A m =秩()r B n = (C)秩(),r A n =秩()r B m = (D)秩(),r A n =秩()r B n =答案：A解析：由于A B E =，故()()r A B r E m ==，又由于()(),()()r A B r A r A B r B ≤≤，故(),()m r A m r B ≤≤ ①由于A 为m n ⨯矩阵，B 为n m ⨯矩阵，故(),()r A m r B m ≤≤ ②由①、②可得(),()r A m r B m ==，故选A 。

2010年计算机考研真题及答案

2010年全国研究生考试计算机统考试题及答案一、单选题1、若元素a,b,c,d,e,f依次进栈，允许进栈、退栈操作交替进行。

但不允许连续三次进行退栈工作，则不可能得到的出栈序列是（ D ）A：dcebfa B：cbdaef C：dbcaef D：afedcb2、某队列允许在其两端进行入队操作，但仅允许在一端进行出队操作，则不可能得到的顺序是（ C ）A：bacde B：dbace C：dbcae D：ecbad3、下列线索二叉树中（用虚线表示线索），符合后序线索树定义的是（ B ）4、在下列所示的平衡二叉树中插入关键字48后得到一棵新平衡二叉树，在新平衡二叉树中，关键字37所在结点的左、右子结点中保存的关键字分别是（C ）A：13，48 B：24，48 C：24，53 D：24，905、在一棵度为4的树T中，若有20个度为4的结点，10个度为3的结点，1个度为2的结点，10个度为1的结点，则树T的叶节点个数是（B）A：41 B：82 C：113 D：1226、对n(n大于等于2)个权值均不相同的字符构成哈夫曼树，关于该树的叙述中，错误的是（B）A：该树一定是一棵完全二叉树B：树中一定没有度为1的结点C：树中两个权值最小的结点一定是兄弟结点D：树中任一非叶结点的权值一定不小于下一任一结点的权值7、若无向图G-（V.E）中含7个顶点，则保证图G在任何情况下都是连通的，则需要的边数最少是（A）A ：6 B：15 C：16 D：218、对下图进行拓补排序，可以得到不同的拓补序列的个数是（B ）A：4 B：3 C：2 D：19、已知一个长度为16的顺序表L，其元素按关键字有序排列，若采用折半查找法查找一个不存在的元素，则比较次数最多是（A）A：4 B：5 C：6 D：710、采用递归方式对顺序表进行快速排序，下列关于递归次数的叙述中，正确的是（D）A：递归次数与初始数据的排列次序无关B：每次划分后，先处理较长的分区可以减少递归次数C：每次划分后，先处理较短的分区可以减少递归次数D：递归次数与每次划分后得到的分区处理顺序无关11、对一组数据（2，12，16，88，5，10）进行排序，若前三趟排序结果如下（A）第一趟：2，12，16，5，10，88第二趟：2，12，5，10，16，88第三趟：2，5，10，12，16，88则采用的排序方法可能是：A：起泡排序B：希尔排序C：归并排序D：基数排序12、下列选项中，能缩短程序执行时间的措施是（D）I 提高CPU时钟频率，II优化数据通过结构，III对程序进行编译优化A：仅I和II B：仅I和III C：仅II和III D：I，II，III 13、假定有4个整数用8位补码分别表示r1=FEH ,r2=F2H ,r3=90H,r4=F8H,若将运算结果存放在一个8位的寄存器中，则下列运算会发生溢出的是（C）A：r1*r2 B ：r2*r3 C：r1*r4 D：r2*r414、假定变量I,f,d数据类型分别为int,float和double(int用补码表示，float和double分别用IEEE754单精度和双精度浮点数据格式表示)，已知i=785,f=1.5678,d=1.5若在32位机器中执行下列关系表达式，则结果为真是（C）（I）f=(int)(float)I (II)f=(float)(int)f (III)f=(float)(double) (IV)=(d+f)-d=fA：仅I和II B：仅I和III C：仅II和III D：仅III和IV 15、假定用若干个2k*4位芯片组成一个8*8位存储器，则地址0B1FH所在芯片的最小地址是（D）A：0000H B：0600H C：0700H D：0800H16、下列有关RAM和ROM的叙述中，正确的是（A）I、RAM是易失性存储器，ROM是非易失性存储器II、RAM和ROM都是采用随机存取的方式进行信息访问III、RAM和ROM都可用作CacheIV、RAM和ROM都需要进行刷新A：仅I和II B：仅II和III C：仅I,II，III D：仅II，III，IV 17、下列命令组合情况中，一次访存过程中，不可能发生的是（D）A：TLB未命中，Cache未命中，Page未命中B：TLB未命中，Cache命中，Page命中C：TLB命中，Cache未命中，Page命中D：TLB命中，Cache命中，Page未命中18、下列存储器中，汇编语言程序员可见的是（B）A：存储器地址寄存器（MAR）B：程序计数器（PC）C：存储器数据寄存器（MDR）D：指令寄存器（IR）19、下列不会引起指令流水阻塞的是（A）A：数据旁路B：数据相关C：条件转移D：资源冲突20、下列选项中的英文缩写均为总线标准的是（D）A：PCI、CRT、USB、EISA B：ISA、CPI、VESA、EISAC：ISA、SCSI、RAM、MIPS D：ISA、EISA、PCI、PCI-Express21、单级中断系统中，中断服务程序执行顺序是（A）I、保护现场II、开中断III、关中断IV、保存断点V、中断事件处理VI、恢复现场VII、中断返回A：I、V、VI、II、VII B：III、I、V、VIIC：III、IV、V、VI、VII D：IV、I、V、VI、VII 22、假定一台计算机的显示存储器用DRAM芯片实现，若要求显示分辨率为1600*1200，颜色深度为24位，帧频为85Hz，显示总带宽的50% 用来刷新屏幕，则需要的显存总带宽至少约为（D）A ：245 Mbps B：979 MbpsC：1958 Mbps D：7834Mbps23、下列选项中，操作S提供的给应用程序的接口是（A）A：系统调用B：中断C：库函数D：原语24、下列选项中，导致创进新进程的操作是（C）I用户成功登陆II设备分配III启动程序执行A：仅I和II B：仅II和IIIC：仅I和III D：I，II，III25、设与某资源相关联的信号量初值为3，当前值为1，若M表示该资源的可用个数，N表示等待资源的进程数，则M,N分别是（B ）A：0，1 B：1，0 C：1，2D：2，026、下列选项中，降低进程优先权级的合理时机是（A ）A：进程的时间片用完B：进程刚完成Z/O，进入就绪队列C：进程长期处于就绪队列中D：就绪从就绪状态转为运行态27、进行P0和P1的共享变量定义及其初值为（A ）boolean flag[2]；int turn=0；flag[0]=faulse；flag[1]=faulse；若进行P0和P1访问临界资源的类C代码实现如下：Void p0（）// 进程p0 Void p1（）// 进程p1{while（TURE）} {while（TURE）}Flag[0]=TURE;ture=1 Flag[1]=TURE; ture=1While （flag[1]&&（turn==1））While （flag[0]&&（turn==0））临界区：Flag[0]=FALSE; Flag[1]=FALSE;} }} }则并发执行进程P0和P1时产生的情况是：A：不能保证进程互斥进入临界区，会出现“饥饿”现象B：不能保证进程互斥进入临界区，不会出现“饥饿”现象C：能保证进程互斥进入临界区，会出现“饥饿”现象D：能保证进程互斥进入临界区，不会出现“饥饿”现象28、某基于动态分区存储管理的计算机，其主存容量为55mb（初试为空间），采用最佳适配（Best fit）算法，分配和释放的顺序为：分配15mb，分配30mb，释放15mb，分配8mb，此时主存中最大空闲分区的大小是（ B ）A：7mb B：9mb C：10mb D：15mb29、某计算机采用二级页表的分页存储管理方式，按字节编制，页大小为216字节，页表项大小为2字节，逻辑地址结构为页目编号页号页内偏移量逻辑地址空间大小为216页，则表示整个逻辑地址空间的页目录表中包含表项的个数至少是（B ）A：64 B：128 C：256 D：51230、设文件索引节点中有7个地址项，其中4个地址项为直接地址索引，2个地址项是一级间接地址索引，1个地址项是二级间接地址索引，每个地址项大小为4字节，若磁盘索引块和磁盘数据块大小均为256字节，则可表示的单个文件的最大长度是（C ）A：33kb B：519kb C：1057kb D：16513kb 31、设置当前工作目录的主要目的是（C ）A：节省外存空间B：节省内容空间C：加快文件的检索速度D：加快文件的读写速度32、本地用户通过键盘登录系统时，首先获得键盘输入信息的程序是（B ）A：命令解释程序B：中断处理程序C：系统调用程序D：用户登录程序33、下列选项中，不属于网络体系结构中所描述的内容是（C ）A：网络的层次B：每一层使用的协议C：协议的内部实现细节D：每一层必须完成的功能34、在下图所示的采用“存储-转发”方式分组的交换网络中，所有链路的数据传输速度为100mbps，分组大小为1000B，其中分组头大小20B，若主机H1向主机H2发送一个大小为980000B的文件，则在不考虑分组拆装时间和传播延迟的情况下，从H1发送到H2接收完为止，需要的时间至少是（ A ）A：80ms B：80.08ms C：80.16ms D：80.24ms35、某自治系统采用RIP协议，若该自治系统内的路由器R1收到其邻居路由器R2的距离矢量中包含信息＜net1，16＞，则可能得出的结论是（ A ）A：R2可以经过R1到达net1，跳数为17B：R2可以到达net1，跳数为16C：R1可以经过R2到达net1，跳数为17D：R1不能进过R2到达net136、若路由器R因为拥塞丢弃IP分组，则此时R可以向发出该IP分组的源主机发送的ICMP报文件类型是（C ）A：路由重定向B：目的不可达C：源抑制D：超时37、某网络的IP地址为192.168.5.0/24采用长子网划分，子网掩码为255.255.255.248，则该网络的最大子网个数，每个子网内的最大可分配地址个数为（ B ）A：32，8 B：32，6C：8，32 D：8，3038、下列网络设备中，能够抑制网络风暴的是（C ）Ⅰ中继器Ⅱ集线器Ⅲ网桥Ⅳ路由器A：仅Ⅰ和ⅡB：仅ⅢC：仅Ⅲ和ⅣD：仅Ⅳ39、主机甲和主机乙之间已建立一个TCP连接，TCP最大段长度为1000字节，若主机甲的当前拥塞窗口为4000字节，在主机甲向主机乙连接发送2个最大段后，成功收到主机乙发送的第一段的确认段，确认段中通告的接收窗口大小为2000字节，则此时主机甲还可以向主机乙发送的最大字节数是（ A ）A：1000 B：2000C：3000 D：400040、如果本地域名服务无缓存，当采用递归方法解析另一网络某主机域名时，用户主机本地域名服务器发送的域名请求条数分别为（A ）A：1条，1条B：1条，多条C：多条，1条D：多条，多条二、综合应用题：41-47小题，共计70分41.（10分）将关键字序列（7、8、11、18、9、14）散列存储到散列列表中，散列表的存储空间是一个下标从0开始的一个一维数组散列函数维：H（key）=（key×3）MODT，处理冲突采用线性探测再散列法，要求装填（载）因子为0.7问题：（1）请画出所构造的散列表；（2）分别计算等概率情况下，查找成功和查找不成功的平均查找长度。

2010年全国硕士研究生入学统一考试西医综合试题、答案与解析

2010 年全国硕士研究生入学统一考试西医综合试题A1.单句型最佳选择题。

每一道试题由一个题干和四个备选答案组成，题干在前，选项在后。

选项A、B、C、D中只有一个为正确答案，其余均为干扰答案。

考生在回答本题型时需对备选答案进行比较，找出最佳的备选答案。

1. 下列关于体液的叙述，正确的是A. 分布在各部分的体液量大体相等B. 各部分体液彼此隔开又相互沟通C. 各部分体液的成分几乎没有差别D. 各部分体液中最活跃的是细胞内液答案解析：本题考点为人体体液的分布及其特点。

人体的体液包括细胞内液和细胞外液两大部分，细胞外液又包括组织液和血浆。

各部分的体液彼此隔开，但又相互沟通。

不同部位的体液量和成分的差距均很大，其中细胞外液相对比较活跃。

所以答案B 是正确的。

2. 需要依靠细胞内CAMP来完成跨膜信号转导的膜受体是A. G蛋白偶联受体B. 离子通道型受体C. 酪氨酸激酶受体D. 鸟苷酸环化酶受体答案解析：本题考点为细胞信号转导的细胞内途径。

细胞的信号转导分为离子通道介导的信号传导、G蛋白偶联受体介导的信号转导和酶联型受体介导的信号转导三种方式。

其中cAMPf乍为G蛋白偶联受体介导的信号转导途径中的第二信使，在该转导方式中发挥重要作用，因此选A。

3. 外加刺激引起细胞兴奋的必要条件是A. 刺激达到一定的强度B. 刺激达到一定的持续时间C .膜去极化达到阈电位D. 局部兴奋必须发生总和答案解析：本题考点为细胞兴奋的条件。

细胞兴奋即产生动乍电位。

动乍电位产生的必要条件是细胞膜去极化达到阈值，也就是电压依赖性N6通道开放形成正反馈。

因此C为最恰当的选择。

4. 发生巨幼红细胞贫血的原因是A. 缺铁B. 蛋白质摄入不足C. 缺乏维生素B12 和叶酸D. EPO生成不足答案解析：本题考点为不同类型贫血的原因。

在红细胞生成过程中，需要有足够的蛋白质、铁、叶酸和维生素B2的供应。

蛋白质和铁是合成血红蛋白的重要原料，而叶酸和维生素B2是红细胞成熟所必需的物质。

2010年考研数三试题及答案

2010年全国硕士研究生入学统一考试数学（三）试题及参考答案一、选择题（1~8小题，每小题4分，共32分，下列每题给出的四个选项中，只有一项符合题目要求的，把所选项前的字母填在答题纸指定的位置上）（1）若011lim e 1x x a x x →⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦，则a =（ C ）（A ）0 （B ）1 （C ） 2 （D ）3【详解】方法一()000111(1)e lim e 1lim 1lim 1(1)e 1x x x x x x ax a ax x x x →→→⎡⎤--⎛⎫'--=⇒=⇒---= ⎪⎢⎥⎝⎭⎣⎦ ()0lim 1e 1112x x ax a a a →⇒--=-⇒-=-⇒=方法二()111111()e 1()1(1())x o x a a x o x a x o x x x x x x x x ⎛⎫⎛⎫⎛⎫--=--++=-++-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()1(1())o x a x o x x ⎛⎫=-+-++ ⎪⎝⎭0011()lim e 1lim 1(1())1x x x o x a a x o x a x x x →→⎡⎤⎛⎫⎛⎫--==-+-++=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，2a ∴= （2）设函数1y ，2y 是一阶非齐次微分方程()()y p x y q x '+=的两个特解，若常数λ，μ使得12y y λμ+是该方程的解，12y y λμ-是该方程对应的齐次方程的解，则（ A ）（A ）12λ=，12μ= （B ）12λ=-，12μ=- （C ）23λ=，13μ= （D ）23λ=，23μ= 【详解】12y y λμ+是()()y p x y q x '+=的解1λμ⇒+=；12y y λμ-是()0y p x y '+=的解0λμ⇒-=，112λμλμλμ+=⎧⇒⇒==⎨-=⎩（3）设函数()f x 、()g x 具有二阶导数，且0()g x a =，0()g x a =是()g x 的极值，则[()]f g x 在0x 处取得极大值的一个充分条件是（ B ）（A ）()0f a '< （B ）()0f a '> （C ）()0f a ''< （D ）()0f a ''>【详解】记()(())h x f g x =，在0x 处取得极大值的一个充分条件：000200000()(())()0()(())(())(())()0h x f g x g x h x f g x g x f g x g x '''=⋅=⎧⎪⎨''''''''=⋅+⋅≠⎪⎩ 因为0()g x a =，又有00000()()()0()0,()0()()()0h x f a g x g x g x h x f a g x '''=⋅=⎧'''=<⇒⎨'''''=⋅<⎩必有()0f a '>.（4）设10()ln f x x =，()g x x =，10()e x h x =，则当x 充分大时有（ C ）（A ）()()()g x h x f x << （B ）()()()h x g x f x << （C ）()()()f x g x h x << （D ）()()()g x f x h x <<【详解】当x →∞时，1010()ln ()()e xf x xg x xh x =<=<=0,,()()()M x M f x g x h x ∃>∀><<本题属于初等函数性质的运用（5）设向量组12:,,...,r I ααα可由向量组12:,,...,s II βββ线性表示，下列命题正确的是（ A ）（A ）若向量组I 线性无关，则r s ≤ （B ）若向量组I 线性相关，则r s >（C ）若向量组II 线性无关，则r s ≤ （D ）若向量组II 线性相关，则r s >【详解】本题考察的知识点是向量组的线性相关性的性质以及向量组的线性表示。

2010年考研计算机统考真题及答案解析

A ．网络的层次 C．协议的内部实现细节 B．每一层使用的协议 D．每一层必须完成的功能
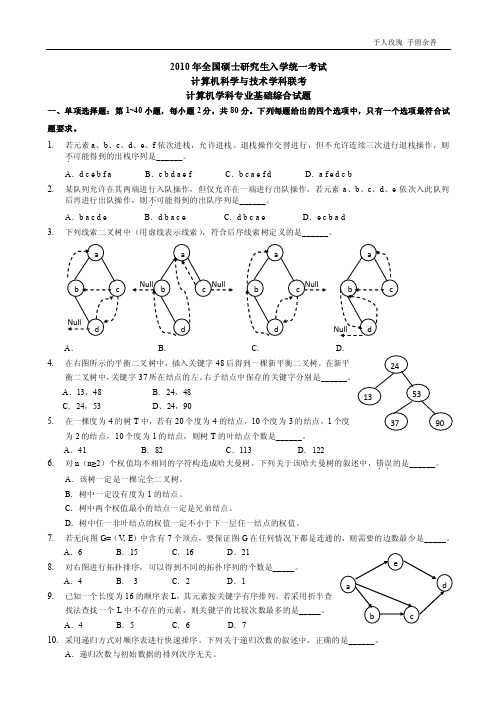
34. 在下图所示的采用“存储 -转发” 方式的分组交换网络中，所有链路的数据传输速率为 100Mbps ，分组大小为
1000B，其中分组头大小为 20B。若主机 H1 向主机 H2 发送一个大小为 980 000B 的文件，则在不考虑分组拆装时间和传播延迟的情况下，从 H1 发送开始到 H2 接收完为止，需要的时间至少．．是______ 。
7. 8. 9.
若无向图 G=（ V, E）中含有 7 个顶点，要保证图 G 在任何情况下都是连通的，则需要的边数最少是_____ 。 A ．6 A ．4 B． 15 B． 3 C． 16 C． 2 D ．21
对右图进行拓扑排序，可以得到不同的拓扑序列的个数是_____ 。 D ．1
e a d
已知一个长度为 16 的顺序表 L，其元素按关键字有序排列。若采用折半查找法查找一个 L 中不存在的元素，则关键字的比较次数最多的是_____ 。 A ．4 B． 5 C． 6 D． 7
寄存器中，则下列运算中会发生溢出的是 A ．r1 x r2 C． r1 x r4 B ．r2 x r3 D ．r2 x r4
14. 假定变量 i、f 和 d 的数据类型分别为 int,float 和 double（int 用补码表示，float 和 double 分别用 IEEE754
单精度和双精度浮点数格式表示），已知 i=785,f=1.5678e3,d=1.5e100 。若在 32 位机器中执行下列关系表达式，则结果为“真” 的是。（I） i == (int)(float)i (II)f == (float)(int)f (III)f == (float)(double)f (IV)(d +f)-d == f A ．仅 I 和 II B．仅 I 和 III C．仅 II 和 III D ．仅 III 和 IV

2010年考研真题数学二试题及参考答案

2010年考研真题：数学二试题及参考答案2010年考研数学二试题及参考答案一、选择题（本大题共12小题，每小题5分，共60分）1.选出下列不等式的解集： (A) x^2 - 3x + 2 > 0 (B) x^2 - 3x + 2 ≥ 0(C) x^2 - 3x + 2 < 0 (D) x^2 - 3x + 2 ≤ 0 正确答案：(A)2.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 的单调增区间为： (A) (-∞, 1) (B) (1, +∞) (C) (-∞, 1]∪[2, +∞) (D) (1, 2) 正确答案：(C) 3.若 a, b, c 均为正整数，且 a + b + c = 11，则 a, b, c 的取值个数为： (A) 45 (B) 55 (C) 66 (D) 77 正确答案：(B)4.已知函数 f(x) = x^3 - 3x^2 + 2x - 1，则 f(x) 有重根的条件是： (A)f(1) = 0 (B) f'(1) = 0 (C) f''(1) = 0 (D) f'''(1) = 0 正确答案：(C) 5.设 a, b, c 均为正整数，且 a + b + c = 12，则 a, b, c 的不等式约束条件个数为： (A) 55 (B) 66 (C) 77 (D) 78 正确答案：(D)6.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 的极值点个数为： (A) 0(B) 1 (C) 2 (D) 3 正确答案：(A)7.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 在(0, +∞) 上的最大值为： (A) 2 (B) 3 (C) 4 (D) 5 正确答案：(D)8.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 在 (-∞, 0) 上的最小值为： (A) -2 (B) -3 (C) -4 (D) -5 正确答案：(A)9.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 的单调减区间为： (A) (0,1) (B) (1, +∞) (C) (-∞, 1]∪[2, +∞) (D) (1, 2) 正确答案：(B) 10.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 在(0, +∞) 上的最小值为： (A) -2 (B) -3 (C) -4 (D) -5 正确答案：(C)11.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 的零点个数为： (A) 0 (B)1 (C)2 (D)3 正确答案：(C)12.设函数 f(x) = x^3 - 3x^2 + 2x - 1, 则 f(x) 在 (-∞, 0) 上的最大值为： (A) 2 (B) 3 (C) 4 (D) 5 正确答案：(B)二、解答题（本大题共7小题，每小题10分，共70分）13.已知函数 f(x) = x^3 - 3x^2 + 2x - 1，求 f(x) 的极值点。

2010年考研英语真题(含答案解析)

2010年全国硕士研究生入学统一考试英语试题Section I Use of EnglishDirections:Read the following text. Choose the best word(s) for each numbered blank and mark [A], [B], [C] or [D] on ANSWER SHEET 1. (10 points)In 1924 America's National Research Council sent two engineers to supervise a series of industrial experiments at a large telephone-parts factory called the Hawthorne Plant near Chicago. It hoped they would learn how stop-floor lighting大1家workers' productivity. Instead, the studies ended 大2家giving their name to the "Hawthorneeffect", the extremely influential idea that the very 大3家to being experimented upon changed subjects' behavior.The idea arose because of the 大4家behavior of the women in the Hawthorne plant. According to 大5家of the experiments, their hourly output rose when lighting was increased, but also when it was dimmed. It did not 大6家what was done in the experiment; 大7家something was changed, productivity rose. A(n) 大8家that they were being experimented upon seemed to be 大9家to alter workers' behavior 大10家itself.After several decades, the same data were 大11家to econometric the analysis. Hawthorne experiments hasanother surprise store 大12家the descriptions on record, no systematic 大13家was found that levels of productivity were related to changes in lighting.It turns out that peculiar way of conducting the experiments may be have let to 大14家interpretation of whathapped. 大15家, lighting was always changed on a Sunday. When work started again on Monday, output大16家rose compared with the previous Saturday and 17 to rise for the next couple of days. 大18家, a comparison with data for weeks when there was no experimentation showed that output always went up on Monday, workers 大19家to be diligent for the first few days of the week in any case, before 大20家 a plateau and then slackening off. This suggests that the alleged "Hawthorne effect" is hard to pin down.1. [A] affected [B] achieved [C] extracted [D] restored2. [A] at [B] up [C] with [D] off3. [A] truth [B] sight [C] act [D] proof4. [A] controversial [B] perplexing [C] mischievous [D] ambiguous5. [A] requirements [B] explanations [C] accounts [D] assessments6. [A] conclude [B] matter [C] indicate [D] work7. [A] as far as [B] for fear that [C] in case that [D] so long as8. [A] awareness [B] expectation [C] sentiment [D] illusion9. [A] suitable [B] excessive [C] enough [D] abundant10. [A] about [B] for [C] on [D] by11. [A] compared [B] shown [C] subjected [D] conveyed12. [A] contrary to [B] consistent with [C] parallel with [D] peculiar to13. [A] evidence [B] guidance [C] implication [D] source14. [A] disputable [B] enlightening [C] reliable [D] misleading15. [A] In contrast [B] For example [C] In consequence [D] As usual16. [A] duly [B] accidentally [C] unpredictably [D] suddenly17. [A] failed [B] ceased [C] started [D] continued18. [A] Therefore [B] Furthermore [C] However [D] Meanwhile19. [A] attempted [B] tended [C] chose [D]intended20. [A] breaking [B] climbing [C] surpassing [D] hittingSection II Reading ComprehensionPart ADirections:Read the following four texts. Answer the questions below each text by choosing [A], [B], [C] or [D]. Mark your answers on ANSWER SHEET 1. (40 points)Text 1Of all the changes that have taken place in English-language newspapers during the past quarter-century, perhaps the most far-reaching has been the inexorable decline in the scope and seriousness of their arts coverage.It is difficult to the point of impossibility for the average reader under the age of forty to imagine a time when high-quality arts criticism could be found in most big-city newspapers. Yet a considerable number of the most significant collections of criticism published in the 20th century consisted in large part of newspaper reviews. To read such books today is to marvel at the fact that their learned contents were once deemed suitable for publication in general-circulation dailies.We are even farther removed from the unfocused newspaper reviews published in England between the turn of the 20th century and the eve of World War II, at a time when newsprint was dirt-cheap and stylish arts criticism was considered an ornament to the publications in which it appeared. In those far-off days, it was taken for granted that the critics of major papers would write in detail and at length about the events they covered. Theirs was a serious business, and even those reviewers who wore their learning lightly, like George Bernard Shaw and Ernest Newman, could be trusted to know what they were about. These men believed in journalism as a calling, and were proud to be published in the daily press. “So few authors have brains enough or literary gift enough to keep their own end up in journalism,” Newman wrote, “that I am tempted to define ‘journalism’ as ‘a term of contempt applied by writers who are not read to w riters who are.’”Unfortunately, these critics are virtually forgotten. Neville Cardus, who wrote for the Manchester Guardian from 1917 until shortly before his death in 1975, is now known solely as a writer of essays on the game of cricket. During his lif etime, though, he was also one of England’s foremost classical-music critics, a stylist so widely admired that his Autobiography (1947) became a best-seller. He was knighted in 1967, the first music critic to be so honored. Yet only one of his books is now in print, and his vast body of writings on music is unknown save to specialists.Is there any chance that Cardus’s criticism will enjoy a revival? The prospect seems remote. Journalistic tastes had changed long before his death, and postmodern readers have little use for the richly upholstered Vicwardian prose in which he specialized. Moreover, the amateur tradition in music criticism has been in headlong retreat.21. It is indicated in Paragraphs 1 and 2 that[A] arts criticism has disappeared from big-city newspapers.[B] English-language newspapers used to carry more arts reviews.[C] high-quality newspapers retain a large body of readers.[D] young readers doubt the suitability of criticism on dailies.22. Newspaper reviews in England before World War II were characterized by[A] free themes.[B] casual style.[C] elaborate layout.[D] radical viewpoints.23. Which of the following would Shaw and Newman most probably agree on?[A] It is writers' duty to fulfill journalistic goals.[B] It is contemptible for writers to be journalists.[C] Writers are likely to be tempted into journalism.[D] Not all writers are capable of journalistic writing.24. What can be learned about Cardus according to the last two paragraphs?[A] His music criticism may not appeal to readers today.[B] His reputation as a music critic has long been in dispute.[C] His style caters largely to modern specialists.[D] His writings fail to follow the amateur tradition.25. What would be the best title for the text?[A] Newspapers of the Good Old Days[B] The Lost Horizon in Newspapers[C] Mournful Decline of Journalism[D] Prominent Critics in MemoryText 2Over the past decade, thousands of patents have been granted for what are called business methods. received one for its "one-click" online payment system. Merrill Lynch got legal protection for an asset allocation strategy. One inventor patented a technique for lifting a box.Now the nation's top patent court appears completely ready to scale back on business-method patents, which have been controversial ever since they were first authorized 10 years ago. In a move that has intellectual-property lawyers abuzz the U.S. court of Appeals for the federal circuit said it would use a particular case to conduct a broad review of business-method patents. In re Bilski, as the case is known , is "a very big deal", says Dennis D. Crouch of the University of Missouri School of law. It "has the potential to eliminate an entire class of patents." Curbs on business-method claims would be a dramatic about-face, because it was the federal circuit itself that introduced such patents with is 1998 decision in the so-called state Street Bank case, approving a patent on a way of pooling mutual-fund assets. That ruling produced an explosion in business-method patent filings, initially by emerging internet companies trying to stake out exclusive rights to specific types of online transactions. Later, move established companies raced to add such patents to their files, if only as a defensive move against rivals that might beat them to the punch. In 2005, IBM noted in a court filing that it had been issued more than 300 business-method patents despite the fact that it questioned the legal basis for granting them. Similarly, some Wall Street investment films armed themselves with patents for financial products, even as they took positions in court cases opposing the practice.The Bilski case involves a claimed patent on a method for hedging risk in the energy market. The Federal circuit issued an unusual order stating that the case would be heard by all 12 of the court's judges, rather than a typical panel of three, and that one issue it wants to evaluate is whether it should "reconsider" its state street Bank ruling. The Federal Circuit's action comes in the wake of a series of recent decisions by the supreme Court that has narrowed the scope of protections for patent holders. Last April, for example the justices signaled that too manypatents were being upheld for "inventions" that are obvious. The judges on the Federal circuit are "reacting to the anti-patent trend at the Supreme Court", says Harold C. Wegner, a patent attorney and professor at George Washington University Law School.26. Business-method patents have recently aroused concern because of[A] their limited value to business[B] their connection with asset allocation[C] the possible restriction on their granting[D] the controversy over authorization27. Which of the following is true of the Bilski case?[A] Its ruling complies with the court decisions[B] It involves a very big business transaction[C] It has been dismissed by the Federal Circuit[D] It may change the legal practices in the U.S.28. The word "about-face" (Line 1, Para 3) most probably means[A] loss of good will[B] increase of hostility[C] change of attitude[D] enhancement of dignity29. We learn from the last two paragraphs that business-method patents[A] are immune to legal challenges[B] are often unnecessarily issued[C] lower the esteem for patent holders[D] increase the incidence of risks30. Which of the following would be the subject of the text?[A] A looming threat to business-method patents[B] Protection for business-method patent holders[C] A legal case regarding business-method patents[D] A prevailing trend against business-method patentsText 3In his book The Tipping Point, Malcolm Gladwell argues that social epidemics are driven in large part by the acting of a tiny minority of special individuals, often called influentials, who are unusually informed, persuasive, or well-connected. The idea is intuitively compelling, but it doesn't explain how ideas actually spread.The supposed importance of influentials derives from a plausible sounding but largely untested theory called the "two step flow of communication": Information flows from the media to the influentials and from them to everyone else. Marketers have embraced the two-step flow because it suggests that if they can just find and influence the influentials, those selected people will do most of the work for them. The theory also seems to explain the sudden and unexpected popularity of certain looks, brands, or neighborhoods. In many such cases, a cursory search for causes finds that some small group of people was wearing, promoting, or developing whatever it is before anyone else paid attention. Anecdotal evidence of this kind fits nicely with the idea that only certain special people can drive trendsIn their recent work, however, some researchers have come up with the finding that influentials have far less impact on social epidemics than is generally supposed. In fact, they don't seem to be required of all.The researchers' argument stems from a simple observing about social influence, with the exception of a few celebrities like Oprah Winfrey—whose outsize presence is primarily a function of media, not interpersonal, influence—even the most influential members of a population simply don't interact with that many others. Yet it is precisely these non-celebrity influentials who, according to the two-step-flow theory, are supposed to drive social epidemics by influencing their friends and colleagues directly. For a social epidemic to occur, however, each person so affected, must then influence his or her own acquaintances, who must in turn influence theirs, and so on; and just how many others pay attention to each of these people has little to do with the initial influential. If people in the network just two degrees removed from the initial influential prove resistant, for example from the initial influential prove resistant, for example the cascade of change won't propagate very far or affect many people. Building on the basic truth about interpersonal influence, the researchers studied the dynamics of populations manipulating a number of variables relating of populations, manipulating a number of variables relating to people's ability to influence others and their tendency to be influenced. Our work shows that the principal requirement for what we call "global cascades"– the widespread propagation of influence through networks – is the presence not of a few influentials but, rather, of a critical mass of easily influenced people, each of whom adopts, say, a look or a brand after being exposed to a single adopting neighbor. Regardless of how influential an individual is locally, he or she can exert global influence only if this critical mass is available to propagate a chain reaction.31. By citing the book The Tipping Point, the author intends to[A] analyze the consequences of social epidemics[B] discuss influentials' function in spreading ideas[C] exemplify people's intuitive response to social epidemics[D] describe the essential characteristics of influentials.32. The author suggests that the "two-step-flow theory"[A] serves as a solution to marketing problems[B] has helped explain certain prevalent trends[C] has won support from influentials[D] requires solid evidence for its validity33. What the researchers have observed recently shows that[A] the power of influence goes with social interactions[B] interpersonal links can be enhanced through the media[C] influentials have more channels to reach the public[D] most celebrities enjoy wide media attention34. The underlined phrase "these people" in paragraph 4 refers to the ones who[A] stay outside the network of social influence[B] have little contact with the source of influence[C] are influenced and then influence others[D] are influenced by the initial influential35. what is the essential element in the dynamics of social influence?[A] The eagerness to be accepted[B] The impulse to influence others[C] The readiness to be influenced[D] The inclination to rely on othersText 4Bankers have been blaming themselves for their troubles in public. Behind the scenes, they have been taking aim at someone else: the accounting standard-setters. Their rules, moan the banks, have forced them to report enormous losses, and it's just not fair. These rules say they must value some assets at the price a third party would pay, not the price managers and regulators would like them to fetch.Unfortunately, banks' lobbying now seems to be working. The details may be unknowable, but the independence of standard-setters, essential to the proper functioning of capital markets, is being compromised. And, unless banks carry toxic assets at prices that attract buyers, reviving the banking system will be difficult.After a bruising encounter with Congress, America's Financial Accounting Standards Board (FASB) rushed through rule changes. These gave banks more freedom to use models to value illiquid assets and more flexibility in recognizing losses on long-term assets in their income statement. Bob Herz, the FASB's chairman, cried out against those who "question our motives." Yet bank shares rose and the changes enhance what one lobby group politely calls "the use of judgment by management."European ministers instantly demanded that the International Accounting Standards Board (IASB) do likewise. The IASB says it does not want to act without overall planning, but the pressure to fold when it completes it reconstruction of rules later this year is strong. Charlie McCreevy, a European commissioner, warned the IASB that it did "not live in a political vacuum" but "in the real word" and that Europe could yet develop different rules. It was banks that were on the wrong planet, with accounts that vastly overvalued assets. Today they argue that market prices overstate losses, because they largely reflect the temporary illiquidity of markets, not the likely extent of bad debts. The truth will not be known for years. But bank's shares trade below their book value, suggesting that investors are skeptical. And dead markets partly reflect the paralysis of banks which will not sell assets for fear of booking losses, yet are reluctant to buy all those supposed bargains.To get the system working again, losses must be recognized and dealt with. America's new plan to buy up toxic assets will not work unless banks mark assets to levels which buyers find attractive. Successful markets require independent and even combative standard-setters. The FASB and IASB have been exactly that, cleaning up rules on stock options and pensions, for example, against hostility from special interests. But by giving in to critics now they are inviting pressure to make more concessions.36. Bankers complained that they were forced to[A] follow unfavorable asset evaluation rules[B] collect payments from third parties[C] cooperate with the price managers[D] reevaluate some of their assets.37. According to the author , the rule changes of the FASB may result in[A] the diminishing role of management[B] the revival of the banking system[C] the banks' long-term asset losses[D] the weakening of its independence38. According to Paragraph 4, McCreevy objects to the IASB's attempt to[A] keep away from political influences.[B] evade the pressure from their peers.[C] act on their own in rule-setting.[D] take gradual measures in reform.39. The author thinks the banks were "on the wrong planet" in that they[A] misinterpreted market price indicators[B] exaggerated the real value of their assets[C] neglected the likely existence of bad debts.[D] denied booking losses in their sale of assets.40. The author's attitude towards standard-setters is one of[A] satisfaction.[B] skepticism.[C] objectiveness[D] sympathyPart BDirections:For Questions 41-45, choose the most suitable paragraphs from the list A-G and fill them into the numbered boxes to form a coherent text. Paragraph E has been correctly placed. There is one paragraph which does not fit in with the text. Mark your answers on ANSWER SHEET1. (10 points)[A] The first and more important is the consumer's growing preference for eating out; the consumption of food and drink in places other than homes has risen from about 32 percent of total consumption in 1995 to 35 percent in 2000 and is expected to approach 38 percent by 2005. This development is boosting wholesale demand from the food service segment by 4 to 5 percent a year across Europe, compared with growth in retail demand of 1 to 2 percent. Meanwhile, as the recession is looming large, people are getting anxious. They tend to keep a tighter hold on their purse and consider eating at home a realistic alternative.[B] Retail sales of food and drink in Europe's largest markets are at a standstill, leaving European grocery retailers hungry for opportunities to grow. Most leading retailers have already tried e-commerce, with limited success, and expansion abroad. But almost all have ignored the big, profitable opportunity in their own backyard: the wholesale food and drink trade, which appears to be just the kind of market retailers need.[C] Will such variations bring about a change in the overall structure of the food and drink market? Definitely not. The functioning of the market is based on flexible trends dominated by potential buyers. In other words, it is up to the buyer, rather than the seller, to decide what to buy .At any rate, this change will ultimately be acclaimed by an ever-growing number of both domestic and international consumers, regardless of how long the current consumer pattern will take hold.[D] All in all, this clearly seems to be a market in which big retailers could profitably apply their scale, existing infrastructure and proven skills in the management of product ranges, logistics, and marketing intelligence. Retailers that master the intricacies of wholesaling in Europe may well expect to rake in substantial profits thereby. At least, that is how it looks as a whole. Closer inspection reveals important differences among the biggest national markets, especially in their customer segments and wholesale structures, as well as the competitive dynamics of individual food and drink categories. Big retailers must understand these differences before they can identify the segments of European wholesaling in which their particular abilities might unseat smaller but entrenched competitors. New skills and unfamiliar business models are needed too.[E] Despite variations in detail, wholesale markets in the countries that have been closely examined—France, Germany, Italy, and Spain—are made out of the same building blocks. Demand comes mainly from two sources: independent mom-and-pop grocery stores which, unlike large retail chains, are two small to buy straight from producers, and food service operators that cater to consumers when they don't eat at home. Such food service operators range from snack machines to large institutional catering ventures, but most of these businesses are known in the trade as "horeca": hotels, restaurants, and cafes. Overall, Europe's wholesale market for food and drink is growing at the same sluggish pace as the retail market, but the figures, when added together, mask two opposing trends.[F] For example, wholesale food and drink sales come to $268 billion in France, Germany, Italy, Spain, and the United Kingdom in 2000—more than 40 percent of retail sales. Moreover, average overall margins are higher in wholesale than in retail; wholesale demand from the food service sector is growing quickly as more Europeans eat out more often; and changes in the competitive dynamics of this fragmented industry are at last making it feasible for wholesalers to consolidate.[G] However, none of these requirements should deter large retailers (and even some large good producers and existing wholesalers) from trying their hand, for those that master the intricacies of wholesaling in Europe stand to reap considerable gains.41→42→43→44→E→45Part CDirections:Read the following text carefully and then translate the underlined segments into Chinese. Your translation should be written carefully on ANSWER SHEET 2. (10 points)One basic weakness in a conservation system based wholly on economic motives is that most members of the land community have no economic value. Yet these creatures are members of the biotic community and, if its stability depends on its integrity, they are entitled to continuance.When one of these noneconomic categories is threatened and, if we happen to love it .We invert excuses to give it economic importance. At the beginning of century songbirds were supposed to be disappearing. (46) Scientists jumped to the rescue with some distinctly shaky evidence to the effect that insects would eat us up if birds failed to control them. the evidence had to be economic in order to be valid.It is painful to read these round about accounts today. We have no land ethic yet, (47) but we have at least drawn near the point of admitting that birds should continue as a matter of intrinsic right, regardless of the presence or absence of economic advantage to us.A parallel situation exists in respect of predatory mammals and fish-eating birds. (48) Time was when biologists somewhat over worded the evidence that these creatures preserve the health of game by killing the physically weak, or that they prey only on "worthless" species.Some species of tree have been read out of the party by economics-minded foresters because they grow too slowly, or have too low a sale vale to pay as timber crops. (49) In Europe, where forestry is ecologically more advanced, the non-commercial tree species are recognized as members of native forest community, to be preserved as such,within reason.To sum up: a system of conservation based solely on economic self-interest is hopelessly lopsided. (50) It tends to ignore, and thus eventually to eliminate, many elements in the land community that lack commercial value, but that are essential to its healthy functioning. It assumes, falsely, I think, that the economic parts of the biotic clock will function without the uneconomic parts.Section Ⅲ WritingPart A51. Directions:You are supposed to write for the postgraduate association a notice to recruit volunteers for an international conference on globalization, you should conclude the basic qualification of applicant and the other information you think relative.You should write about 100 words. Do not sign your own name at the end of the letter. Use "postgraduate association" instead.Part B52. Directions:Write an essay of 160-200 words based on the following drawing. In your essay, you should1) describe the drawing briefly,2) explain its intended meaning, and then3) give your comments.You should write neatly on ANSHWER SHEET 2. (20 points)2010年全国硕士研究生入学统一考试英语试题答案46.科学家们提出一些明显站不住脚的证据迅速来拯救，其大意是：如果鸟类无法控制害虫，那么这些害虫就会吃光我们人类。