工程力学答案解析-压杆稳定
工程力学-26压杆稳定11-2

Pcr2
=σcr ⋅ A= 200.9×106
(3)、d=63.8mm
×3.2×10−3 = 644KN
i = 1 d =15.95mm
3m
Pcr 3
λ3 =
= σ cr
μ
i
⋅
l
A
=
=
94 (λs≤ λ< λ4p)中柔度杆 (304 −1.12 × 94) ×106 × 2.3
×10
−3
= 635KN
1
1
5 Pa 3 − N (2 a ) 3 = Na
1 6 EI
3 EI
EA
(1) BC杆的稳定: C
λ = μl = 4 ×1 = 66.6
N = 0.312 P
(λ0≤ λ< λp)中柔度杆
i 0.06
Pcrσ=crσ=c3r ⋅3A8-=12.1528λ×1=036 3×8π-1×.610242××1606−.66=258MPa
8
四、中小柔度压杆的临界力
1. 直线型经验公式
σ
σs σcr=σs A
σp
σcr=a−bλ
B
σ cr
=
π 2E λ2
O
λO
λp
λ
10
中长杆: σcr= a - bλ
λo≤ λ< λp
a , b 查表 11-2
粗短杆: σcr= σs (σb)
λ< λo
11
λo 的计算
σs = a-bλo
σ
σs σcr=σs A
=
353.5 105
=
3.367 >[nw]
满足稳定条件
22
例题10:图示结构用低碳钢A5制成,求:[P]。已知:E=
工程力学——压杆稳定

欧拉公 式
其中:i
I — 截面的惯性半径;为截 面的几何性质; A
=
l
i
称为压杆的柔度(长细 比);反映压杆的柔软 程度。
15N
32 mm
1mm
第一节
压杆稳定的概念
FP<FPcr :直线平衡形式(稳定平衡)
在扰动作用下,直线平衡形式转为弯曲平衡形式,扰动除 去后,能够恢复到直线平衡形式,则称原来的直线平衡构形是 稳定的。 FP>FPcr :弯曲平衡形式(不稳定平衡) 在扰动作用下,直线平衡形式转为弯曲平衡形式,扰动除去 后,不能恢复到直线平衡形式,则称原来的直线平衡形式是不稳 定的。
F
F
1.
计算柔度判断两杆的临界荷载
5m
d
9m
d
d 4 64 d I i 4 d 2 4 A 1 5 L a 125 d i 0 .5 9 4 112.5 b d 4
(a)
(b )
a b
1
0.5
2. 计算各杆的临界荷载
b a P 101
(n ) EI Fcr 2 L Fcr
n 1
kL sin 2
A
适用条件: •理想压杆(轴线为直线,压力 与轴线重合,材料均匀) •线弹性,小变形 •两端为铰支座
y sin
x 挠曲线中点的挠度 l
挠曲线为半波正弦曲线
由此得到两个重要结果:
临界载荷
(a)
z
b
h
正视图:
专升本工程力学压杆稳定

计算杆在不同方向失稳时的临界力。I 为其相应的对
中性轴的惯性矩。
12
例题 2: 图示各杆材料和截面均相同,试问哪一根杆能承 受的压力最大, 哪一根的最小?
F F
F 因为 l1 l2 l3
又
2 EI
Fcr l 2
可知
0 < p
因此
可用直线公式.
Fcr cr A (a b )A
(304 1.12 77) 106 d 2
4
462KN
37
例4
解: CD梁 M C 0
F 2000 FN sin 30 1500
得 FN 26.6kN
AB杆 l
i
1
1.5
l cos 30 1.732m
2
Pc
r
2 一端固定另端绞支
A
l
0.7l
C
B
C为拐点
Fcr
2EI
(0.7l)
2
7
3 两端固定
Pcr
C,D为拐点
AD
Fcr
2EI
(0.5l)
2
l
C
B
8
4 一端固定,另端自由
Fcr
2EI
(2l)2
l 2l
9
10
欧拉公式 的统一形式
F
cr
2 EI (l)2
为压杆的长度系数; l 为相当长度。
讨论:
(1)相当长度 l 的物理意义
1 压杆失稳时,挠曲线上两拐点间的长度就是压杆的相当
长度 l 。
2 l 是各种支承条件下,细长压杆失稳时,挠曲线中相当于
材料力学答案- 压杆稳定
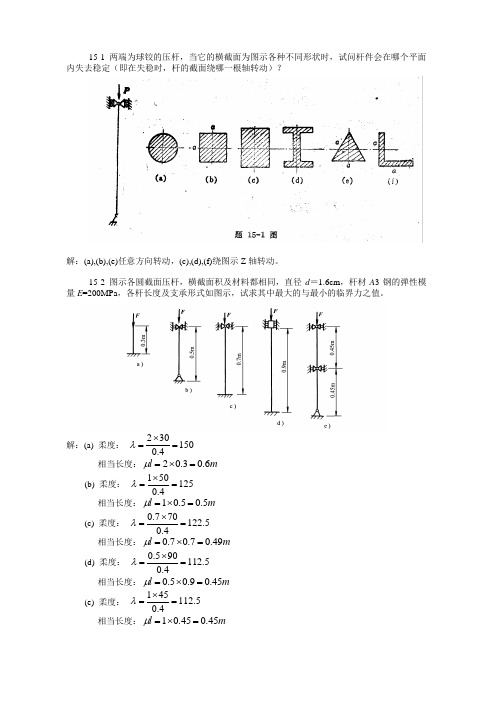
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。
2020年材料力学习题册答案-第9章 压杆稳定

作者:非成败作品编号:92032155GZ5702241547853215475102时间:2020.12.13第九章压杆稳定一、选择题1、一理想均匀直杆受轴向压力P=P Q时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( A )。
A、弯曲变形消失,恢复直线形状;B、弯曲变形减少,不能恢复直线形状;C、微弯状态不变;D、弯曲变形继续增大。
2、一细长压杆当轴向力P=P Q时发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形( C )A、完全消失B、有所缓和C、保持不变D、继续增大3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( D )来判断的。
A、长度B、横截面尺寸C、临界应力D、柔度4、压杆的柔度集中地反映了压杆的( A )对临界应力的影响。
A、长度,约束条件,截面尺寸和形状;B、材料,长度和约束条件;C、材料,约束条件,截面尺寸和形状;D、材料,长度,截面尺寸和形状;5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( C )A.60;B.66.7;C.80;D.507、在横截面积等其它条件均相同的条件下,压杆采用图( D )所示截面形状,其稳定性最好。
8、细长压杆的( A ),则其临界应力σ越大。
A 、弹性模量E 越大或柔度λ越小;B 、弹性模量E 越大或柔度λ越大;C 、弹性模量E 越小或柔度λ越大;D 、弹性模量E 越小或柔度λ越小; 9、欧拉公式适用的条件是,压杆的柔度( C )A 、λ≤、λ≤C 、λ≥π D、λ≥10、在材料相同的条件下,随着柔度的增大( C )A 、细长杆的临界应力是减小的,中长杆不是;B 、中长杆的临界应力是减小的,细长杆不是;C 、细长杆和中长杆的临界应力均是减小的;D 、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( A )A. 临界应力一定相等,临界压力不一定相等;B. 临界应力不一定相等,临界压力一定相等;C. 临界应力和临界压力一定相等;D. 临界应力和临界压力不一定相等;12、在下列有关压杆临界应力σe 的结论中,( D )是正确的。
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题

角钢(连结成一整体)。试确定梁与柱的工作安全因 数。
解:1.查型钢表得
习题 11-12 图
No.16aI:Iz = 1130cm4,Wz = 141cm3 2No. 63×63×5: A = 2 × 6.143 = 12.286 cm2
i y = 1.94cm I y = 2 × 23.17 = 46.34 cm
采用,欧拉公式计算临界力
FPcr = σ cr A =
轴的工作安全因数
2 π E
λ2
=
所以,轴不安全。
11-11 图示正方形桁架结构,由五根圆截面钢杆组成,
连接处均为铰链,各杆直径均为 d=40 mm,a=1 m。材料 均为 Q235 钢,E=200 GPa,[n]st=1.8。试;
网
ww w
.k hd 案
μ =1
co
界力。
m
11-5
图示 a、b、c、d 四桁架的几何尺寸、圆杆的横截面直径、材料、加力点及加力
方向均相同。关于四桁架所能承受的最大外力 FPmax 有如下四种结论,试判断哪一种是正确 的。 (A)FPmax(a)=FPmax(c)<FPmax(b)=FPmax(d); (B)FPmax(a)=FPmax(c)=FPmax(b)=FPmax(d); (C)FPmax(a)=FPmax(d)<FPmax(b)=FPmax(c);
案
对于 A3 钢, λ P = 102,
λs = 61.6 。因此,第一杆为大柔度杆,第二杆为中柔度杆,
网
i μl λ2 = 2 i μl λ3 = 3 i
λ1 =
=
ww w
FPcr = ( a − bλ ) A = (304 − 1.12 × 62.5) × 10 3 ×
《工程力学》第六章 压杆的稳定性计算

x
Fcr
图示两端铰支(球铰)的细长压杆,当压力
B
F达到临界力FCr时,压杆在FCr作用下处于
微弯的平衡状态,
考察微弯状态下局部压杆的平衡
M (x) Fcr w
d 2w dx2
M (x) EI
d 2w Fcr w
w
dx2
EI
x
FCr
M
w
x
根据杆端边界条件,求解上述微分方程 可得两端铰支细长压杆的临界力
FCr
2EI (l)2
Cr
FCr A
Cr
FCr A
2EI (l)2 A
2E (l / i)2
2E 2
Cr
2E 2
——临界应力的欧拉公式
柔度(长细比): L
i
i I A
——截面对失稳时转动
轴的惯性半径。
——表示压杆的长度、横截面形状和尺寸、杆端的约束 情况对压杆稳定性的综合影响。
200
2.中柔度杆(中长压杆)及其临界应力
工程实际中常见压杆的柔度往往小于p,其临界应力超过材料的
比例极限,属于非弹性稳定问题。这类压杆的临界应力通常采用直线 经验公式计算, 即
Cr a b ——直线型经验公式
式中,a、b为与材料有关的常数,单位为MPa。
由于当应力达到压缩极限应力时,压杆已因强度问题而失效,因此
12 h
1 2300 60
12 133
在xz平面内,压杆两端为固定端,=0.5,则
iy
Iy A
b 12
y
l
iy
l 12
b
0.5 2300 40
12 100
因为 z>y,连杆将在xy平面内失稳(绕z轴弯曲),因 此应按 =z=133计算连杆的临界应力。
工程力学上册15压杆稳定

压杆的稳定性直接关系到这些结构物的安全性和可靠性,一旦发生失稳,可能会导致结构物的破坏和倒塌,造成严重的人员伤亡和财产损失。
因此,对压杆稳定性的研究和分析是工程力学中非常重要的一个方面,也是工程设计和安全评估的重要依据。
压杆稳定的重要性
02
压杆的分类与特性
总结词
长细比是描述压杆细长程度的重要参数,对临界力的影响显著。
工程力学上册15压杆稳定
目录
压杆稳定概述 压杆的分类与特性 压杆稳定的影响因素 压杆稳定的计算方法 压杆稳定的实验研究 工程实例分析
01
压杆稳定概述
01
02
压杆稳定的定义
当压杆受到的力小于其临界力时,压杆保持稳定平衡;当压杆受到的力大于其临界力时,压杆将发生屈曲失稳。
压杆稳定是指压杆在受到外力作用时,能够保持其原有平衡状态的能力。
03
压杆稳定的影响因素
压杆在制造过程中可能会产生弯曲,这种弯曲在受力时会进一步发展,导致压杆失稳。
为了提高压杆的稳定性,应尽量减小初始弯曲,可以通过提高制造精度和选用合适的材料来实现。
初始弯曲的影响
减小初始弯曲
初始弯曲
材料在加工过程中会形成残余应力,这些应力会在受力时对压杆的稳定性产生影响。
残余应力
结论应用
将实验结论应用于实际工程中,指导压杆结构的合理设计和应用。
实验结果与分析
06
工程实例分析
桥梁结构的压杆稳定分析
总结词:桥梁结构的压杆稳定分析是确保桥梁安全的重要环节,需要考虑多种因素,如材料特性、载荷分布和支撑条件等。
高层建筑的压杆稳定分析
总结词:高层建筑的压杆稳定分析是确保高层建筑安全的重要环节,需要考虑多种因素,如建筑高度、材料特性、风载荷和地震载荷等。
第十一章压杆的稳定_工程力学

第十一章 压杆的稳定承受轴向压力的杆,称为压杆。
如前所述,直杆在轴向压力的作用下,发生的是沿轴向的缩短,杆的轴线仍然保持为直线,直至压力增大到由于强度不足而发生屈服或破坏。
直杆在轴向压力的作用下,是否发生屈服或破坏,由强度条件确定,这是我们已熟知的。
然而,对于一些受轴向压力作用的细长杆,在满足强度条件的情况下,却会出现弯曲变形。
杆在轴向载荷作用下发生的弯曲,称为屈曲,构件由屈曲引起的失效,称为失稳(丧失稳定性)。
本章研究细长压杆的稳定。
§11.1 稳定的概念物体的平衡存在有稳定与不稳定的问题。
物体的平衡受到外界干扰后,将会偏离平衡状态。
若在外界的微小干扰消除后,物体能恢复原来的平衡状态,则称该平衡是稳定的;若在外界的微小干扰消除后物体仍不能恢复原来的平衡状态,则称该平衡是不稳定。
如图11.1所示,小球在凹弧面中的平衡是稳定的,因为虚箭头所示的干扰(如微小的力或位移)消除后,小球会回到其原来的平衡位置;反之,小球在凸弧面上的平衡,受到干扰后将不能回复,故其平衡是不稳定的。
上述小球是作为未完全约束的刚体讨论的。
对于受到完全约束的变形体,平衡状态也有稳定与不稳定的问题。
如二端铰支的受压直杆,如图11.2(a )所示。
当杆受到水平方向的微小扰动(力或位移)时,杆的轴线将偏离铅垂位置而发生微小的弯曲,如图11.2(b)所示。
若轴向压力F 较小,横向的微小扰动消除后,杆的轴线可恢复原来的铅垂平衡位置,即图11.2(a ),平衡是稳定的;若轴向压力F 足够大,即使(a ) 稳定平衡 图11.1 稳定平衡与不稳定平衡微小扰动已消除,在力F 作用下,杆轴线的弯曲挠度也仍将越来越大,如图11.2(c)所示,直至完全丧失承载能力。
在F =F cr 的临界状态下,压杆不能恢复原来的铅垂平衡位置,扰动引起的微小弯曲也不继续增大,保持微弯状态的平衡,如图11.2(b)所示,这是不稳定的平衡。
如前所述,直杆在轴向载荷作用下发生的弯曲称为屈曲,发生了屈曲就意味着构件失去稳定(失稳)。
压杆稳定习题及答案

压杆稳定习题及答案【篇一:材料力学习题册答案-第9章压杆稳定】xt>一、选择题1、一理想均匀直杆受轴向压力p=pq时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( a )。
a、弯曲变形消失,恢复直线形状;b、弯曲变形减少,不能恢复直线形状; c、微弯状态不变; d、弯曲变形继续增大。
2、一细长压杆当轴向力p=pq时发生失稳而处于微弯平衡状态,此时若解除压力p,则压杆的微弯变形( c )a、完全消失b、有所缓和c、保持不变d、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( d)来判断的。
a、长度b、横截面尺寸c、临界应力d、柔度 4、压杆的柔度集中地反映了压杆的( a)对临界应力的影响。
a、长度,约束条件,截面尺寸和形状;b、材料,长度和约束条件;c、材料,约束条件,截面尺寸和形状;d、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( c )a.60;b.66.7;c.80;d.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( d )所示截面形状,其稳定性最好。
≤?≥?- 1 -10、在材料相同的条件下,随着柔度的增大( c)a、细长杆的临界应力是减小的,中长杆不是;b、中长杆的临界应力是减小的,细长杆不是; c、细长杆和中长杆的临界应力均是减小的; d、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( a )a. 临界应力一定相等,临界压力不一定相等;b. 临界应力不一定相等,临界压力一定相等;c. 临界应力和临界压力一定相等;d. 临界应力和临界压力不一定相等;a、杆的材质b、杆的长度c、杆承受压力的大小d、杆的横截面形状和尺寸二、计算题1、有一长l=300 mm,截面宽b=6 mm、高h=10 mm的压杆。
工程力学-细长压杆稳定性分析

E为材料的弹性模量,常用单位GPa
I
为横截面的轴惯性矩,常用单位 m 4或m m4
l
为压杆长度,常用单位m或mm
μ为压杆的长度因数,反映压杆两端支承对临界力的影响。
由欧拉公式
cr
得到
Fcr 2 EI A (l ) 2 A
令
2 i I/A 令
2E cr ( l / i) 2
10 22 3 Iz 8873.3mm 4 12
I y I z 压杆截面必绕y轴转动而失稳,因此将Iy代入公式,计算
截面对y轴的惯性半径。
iy
Iy A
1833.3 2.89mm 22 10
0.5 800 138.4 2.89
得到矩形截面柔度为
y
l
iy
y 138.4 101 采用欧拉公式计算临界应力
cr s
s
几种材料的相应数值。
例一矩形截面压杆,两端固定,已知b=10mm,h=22mm,l=800mm,
材料为Q235钢,弹性模量E=206GPa,试计算此压杆的临界力和临界
应力。
22
10
解:1)计算压杆的柔度
压杆两端固定,μ =0.5,截面对y轴和z轴的惯性矩为:
22 10 3 Iy 1833.3mm 4 12
d0=50mm ,最大起重量 F = 90kN ,材料为 Q235 钢,规定稳定安全因 数 nw 4 ,试校核该螺旋杆稳定性。
解: 1 )螺旋杆可以简化为下端固定,上端自由的杆,长度因数
μ =2。
2)计算柔度
i
I d 0 50 12.5mm A 4 4
《工程力学》第十六章 压杆稳定
• 式中:I和A都是与截面有关的几何量,如果将 惯性矩写成横截面面积与某一距离平方的乘积, 即I=Ai2。i称为此横截面面积对于某一轴的惯性 半径。如果截面对y轴或z轴的惯性半径分别为
• 其量纲为长度一次方。常见图形的惯性半径 可从有关手册中查到。将I=Ai2代入(a)式得
•或
• 式中 P——工作压力; • Plj——压杆临界压力; • nw——压杆工作时实际具有的稳定安全
系数; • [nw]——规定的稳定安全系数。 • 也可采用应力形式表示压杆稳定性条件,
将式(16-10)及式(16-11),同除以压杆 的横截面面积A得
•或
• 式中[σw]——稳定许用应力。
• 二、折减系数法 • 由式(16-12)可知,压杆的稳定条件为
• 一、减小压杆的支承长度
• 由大柔度杆的临界应力公式
可
知在压杆材料一定的条件下,临界应力与
柔度的平方成反比,压杆的柔度愈小,相
应的临界应力愈高。而柔度
与压
杆长
• 度l成正比,减小压杆支承长度是降低柔度的方 法之一,在条件允许的情况下,应尽可能地减 小压杆的长度。例如,钢铁厂无缝钢管车间的 穿孔机的顶杆(图16-14),为了提高其稳定性, 在顶杆中段增加一个抱辊装置,这就达到了提 高顶杆稳定性的目的。
于是,压杆稳定性条件可以写成
• 对于已有压杆,其λ已知,可直接查表163得φ,代入式(16-14)进行稳定性校核。至
于设计截面尺寸,可采用逐次逼近法,即先
设定一个φ值,由式(16-14)计算出A值,然
后进行验算、调整,使杆件的工作应力逐渐 靠近许用应力。
表16-3.tif
工程力学11-压杆的稳定性分析与设计解析

11.1.3 三种类型压杆的临界状态 压杆的分类:
细长杆 ——当F >Fcr时容易发生弹性屈曲 当F≤Fcr时不发生屈曲
中长杆 ——当F >Fcr时发生屈曲,但不再是弹性的
粗短杆 ——不会发生屈曲,失效属于强度破坏
《工程力学》
11.2
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
长细比概念三类不同压杆判断
11.3.2 三类不同压杆的区分
ห้องสมุดไป่ตู้
因,屈曲在弹性范围内导出
故有:
scr =
Fcr A
≤[sp]
在比例极限内有效
稳定平衡构形到屈曲(不稳定平衡构形)是一个 过程。
介于这个过程之间的平衡构形——临界平衡构形
或称:“临界状态” 临界载荷
处于临界状态时,杆件所受的施压载荷
称:“临界载荷”,或临界力,Fcr
《工程力学》
11.1
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
令:当材料达到比例极限时的长细比为“lp” 当材料屈服极限时的长细比为“ls”
细长杆 中长杆 粗短杆
—— l ≥ lp —— lp >l ≥ ls —— l < ls
细长压杆的临界载荷
工程力学课后答案第8章

第8章 压杆稳定习题:1.【解】d 图临界力最大,b 图临界力最小。
2.【解】σBC =11.25MPa <[σst ]=16.83MPa ,BC 杆满足稳定性要求3.【解】最合理的情况为AB 、BC 两杆同时失稳,此时F 最大。
()βθ22222cr cos ππcos AC AB AB l EI l EI F F === ()βθ22222cr sin ππsin AC BC BCl EI l EI F F === 两式相除得到βθ2cot tan =即()βθ2cot arctan = 4. 【解】由于杆端的约束在各个方向相同,因此,压杆将在抗弯刚度最小的平面内失稳,即杆件横截面将绕其惯性矩为最小的形心主惯性轴转动。
32123min min b bh hb AI i === 欧拉公式适用于λ≥p λ,即min i l μ≥p2πσE 由此得到 l ≥m 76.1m 10200102105.032π103032π693p =⨯⨯⨯⨯⨯=-σμE b 故此压杆适用于欧拉公式时的最小长度为1.76m 。
5. 【解】(1)F cr =329.64kN(2)n =2.29<[n st ]=2.5,结构不安全6. 【解】(1)求挺杆的柔度挺杆的横截面为圆形,两端可简化为铰支座,μ=1,i=d/4计算柔度λ=μli=4μld=4×1×0.2570.008=128.5λ1=π√EσP =π√210×109240×106=92.9挺杆是细长压杆,使用欧拉公式计算临界压力(2)校核挺杆的稳定性I=πd464=π×0.008464=2.01×10−10m4P cr=π2EI(μl)2=π2×210×109×2.01×10−10(1×0.257)2=6.31kN工作安全系数n=P crP max=6.311.76=3.59所以挺杆满足稳定性要求7. 【解】[F]=53.31kN8. 【解】(1)F cr=355.31kN(2)bℎ=0.525。
工程力学课后单选题100道及答案解析

工程力学课后单选题100道及答案解析1. 力的三要素是()A. 大小、方向、作用点B. 大小、方向、作用线C. 大小、作用点、作用线D. 方向、作用点、作用线答案:A解析:力的三要素是大小、方向、作用点。
2. 两个力大小相等、方向相反、作用在同一直线上,则这两个力()A. 平衡B. 不平衡C. 不一定平衡D. 无法确定答案:C解析:这两个力作用在同一物体上时平衡,作用在不同物体上时不平衡。
3. 作用在刚体上的力可以()A. 沿作用线移动B. 任意移动C. 平行移动D. 不能移动答案:A解析:作用在刚体上的力可以沿其作用线移动,不改变其对刚体的作用效果。
4. 约束反力的方向总是与约束所能阻止的物体的运动趋势的方向()A. 相同B. 相反C. 垂直D. 成一定角度答案:B解析:约束反力的方向总是与约束所能阻止的物体的运动趋势的方向相反。
5. 光滑接触面的约束反力总是沿接触面的()指向被约束物体。
A. 切线B. 法线C. 任意方向D. 无法确定答案:B解析:光滑接触面的约束反力总是沿接触面的法线指向被约束物体。
6. 平面汇交力系合成的结果是()A. 一个力B. 一个力偶C. 一个合力偶和一个合力D. 不能确定答案:A解析:平面汇交力系合成的结果是一个合力。
7. 平面汇交力系平衡的必要和充分条件是该力系的()为零。
A. 合力B. 合力偶C. 主矢D. 主矩答案:A解析:平面汇交力系平衡的必要和充分条件是该力系的合力为零。
8. 平面力偶系平衡的必要和充分条件是()A. 各力偶矩的代数和为零B. 各力偶矩相等C. 各力偶矩的矢量和为零D. 各力偶在同一平面内答案:A解析:平面力偶系平衡的必要和充分条件是各力偶矩的代数和为零。
9. 平面一般力系向作用面内一点简化,得到一个主矢和一个主矩。
当主矢为零,主矩不为零时,该力系简化的结果为()A. 合力B. 合力偶C. 平衡D. 无法确定答案:B解析:主矢为零,主矩不为零时,简化结果为合力偶。
工程力学29-压杆稳定计算

1.压杆的稳定校核
F
[F ]
Fcr nst
nst:稳定安全系数
工作安全系数 n
Fcr F
cr
nst
9-
2 目录
n st
解:
CD梁 MC 0
F 2000 FN sin 30 1500
得 FN 26.6kN
3 目录
P 时称为大柔度杆(或长细杆),用欧拉公式求临界力;
P 时称为中、小柔度杆,不能用ns欧t 拉公式求临界力。
已求得FN 26.6kN
32m
l i
1
i
I A
D4 d4 4 64 D 2 d 2
D2 d2
4
16mm
得
1 1.732 16 103
108
P
AB为大柔度杆
Fcr
2EI l 2
制宜根据压杆稳定要求选取最优截面
难点
法三:增大截面惯性矩 I(合理选择截面形状)
法四:增大弹性模量 E(合理选择材料)
大柔度杆
Fcr
2EI (l)2
中柔度杆 cr a b
表 10.2
6 目录
小结:
• 了解:压杆稳定校核公式的适用范围 重点 • 理解:各截面参数对于压杆稳定的影响 • 掌握:压杆稳定校核公式计算与应用,会因地
118kN
n
Fcr FN
118 26.6
4.42
nst
3
AB杆满足稳定性要求
4
2.提高压杆稳定性的措施
Fcr
2EI (l)2
欧拉公式
Fcr 越大越稳定
•减小压杆长度 l •减小长度系数μ(增强约束) •增大截面惯性矩 I(合理选择截面形状) •增大弹性模量 E(合理选择材料)
工程力学第14章答案

习题14-2图习题14-3图P F P F P F P F 0PF P -F 2F -2F 2F -2F 0000000P F P F PF P -F P-F P -F P F P F P F P F 0P F P -F 2F -2F 2F -2F 0000P F PF P F P-F P -F P -F 00习题11-2解图 第14章 压杆的平衡稳定性分析与压杆设计14-1 关于钢制细长压杆受力达到分叉载荷之后,还能不能继续承载,有如下四种答案,试判断哪一种是正确的。
(A )不能,因为载荷达到临界值时,屈曲位移将无限制地增加; (B )能,压杆一直到折断时为止都有承载能力; (C )能,只要横截面上的最大应力不超过一定限度; (D )不能,因为超过分叉载荷后变形不再是弹性的。
正确答案是 C 。
14-2 图示a 、b 、c 、d 四桁架的几何尺寸、杆的横截面直径、材料、加力点及加力方向均相同。
关于四桁架所能承受的最大外力F Pmax 有如下四种结论,试判断哪一种是正确的。
(A ))d ()b ()c ()a (max P max P max P max P F F F F =<=; (B ))d ()b ()c ()a (max P max P max P max P F F F F ===; (C ))c ()b ()d ()a (max P max P max P max P F F F F =<=;(D ))d ()c ()()a (max P max P max P max P F F b F F =<=。
正确答案是 A 。
解:各杆内力如解图所示,由各受杆内力情况可知,应选答案(A )。
14-3 图示四压杆均为圆截面直杆,杆长相同,且均为轴向加载。
关于四者分叉载荷大小有四种解答,试判断哪一种是正确的(其中弹簧的刚度较大)。
(A ))d ()c ()b ()a (Pcr Pcr Pcr Pcr F F F F <<<; (B ))d ()c ()b ()a (Pcr Pcr Pcr Pcr F F F F >>>; (C ))a ()d ()c ()b (Pcr Pcr Pcr Pcr F F F F >>>;(D ))d ()c ()a ()b (Pcr Pcr Pcr Pcr F F F F >>>。
工程力学十压杆的稳定性课后习题答案

图示作用下,四杆受压,(压),受拉.
,即
12-10图示结构中,为铸铁圆杆,直径,许用应力,弹性模量.为钢圆杆,直径,许用应力,若横梁可视为刚性,试用折减系数法求载荷地许用值.
题12-10图
解:问题是一次超静定地,设杆中拉力为,杆中压力为
有平衡条件:,且有变形条件:
虎克定律代入得:(公共项消掉未写)
段:,(与方向无关)
,即,段安全
段,(与方向无关)
,即,段安全
综上分析,结构安全.
12-9四根等长杆相互铰接成正方形,并与杆铰接如图所示.各杆地弹性模量、截面积极惯性矩均相等.当(1)两点处受一对拉力,图();(2)两点处受一对压力,图(),分别求达到临界状态地最小载荷.
题12-9图
解:图示作用下,四杆受拉,受压,若按受压失稳与否确定值,只需考查杆:(压)
第十二章压杆地稳定性
12-1图示细长压杆,两端为球形铰支,弹性模量,对下面三种截面用欧拉公式计算其临界压力.(1)圆截面,;(2)矩形截面,,(3)16号工字钢,.
解:结构为两端铰支,则有
圆截面杆,
矩形截面杆,
16号工字查型钢表知
题12-1图题12-2图
12-2图示为下端固定,上端自由并在自由端受轴向力作用地等直压杆.杆长为,在临界力作用下杆失稳时有可能在平面内维持微弯曲状态下地平衡.杆横截面积对轴地惯性矩为,试推导其临界压力地欧拉公式,并求出压杆地挠曲线方程.
得到.工作应力为
,不合理,所设过大,再取时,减小,取
,则,
选取工字钢,,
,安全.所以,经计算校核,应选用号工字钢.
12-12两端铰支地等截面圆杆,杆长直径,材料地比例极限,弹性模量,线膨胀系数.设安装时地温度为,求温度升高到多少度时此圆杆将失稳.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11-1 两端为铰支座的细长压杆,如图所示,弹性模量E=200GPa,试计算其临界荷载。
(1)圆形截面,25,1d l==mm m;(2)矩形截面2400,1h b l===m m;(3)16号工字钢,2l=ml解:三根压杆均为两端铰支的细长压杆,故采用欧拉公式计算其临界力:(1)圆形截面,25,1d l==mm m:2292220.025200106437.81crEIPlπππ⨯⨯⨯⨯===N kN (2)矩形截面2400,1h b l===m m当压杆在不同平面约束相同即长度系数相同均为1μ=时,矩形截面总是绕垂直短边的轴先失稳20.040.02min(,)12y z yI I I I⨯===,故:2292220.040.02200101252.71crEIPlππ⨯⨯⨯⨯===N kN (3)16号工字钢,2l=m查表知:4493.1,1130y zI I==cm cm,当压杆在不同平面约束相同即长度系数相同均为1μ=时4min(,)93.1y z yI I I I===cm,故:2298222001093.110459.42crEIPlππ-⨯⨯⨯⨯===N kN 11-3 有一根30mm×50mm的矩形截面压杆,一端固定,另一端铰支,试问压杆多长时可以用欧拉公式计算临界荷载?已知材料的弹性模量E=200GPa,比例极限σP=200MPa。
解:(1)计算压杆能采用欧拉公式所对应的Pλ2299.35P PPEπσλλ=→===(2)矩形截面压杆总是绕垂直于短边的轴先失稳,当其柔度大于Pλ可采用欧拉公式计算临界力。
故0.780.83 1.2290.0399.35x P y zlll l i μλλ⋅===>>=→mm , 即 1.229l >mm 为细长杆,可采用欧拉公式计算临界力。
11-6 某钢材的比例极限230P σ=MPa ,屈服极限274s σ=MPa ,弹性模量E=200GPa ,331 1.09cr σλ=-。
试求P s λλ和,并绘制临界应力总图(0150λ≤≤)。
解:(1)计算此钢材的判别柔度①将230P σ=MPa 代入欧拉公式22Eπσλ=可以计算此钢材细长压杆的判别柔度P λ:92.64P λ=== ②由经验公式331 1.09cr σλ=-知:此钢材的331, 1.09a b ==MPa MPa ,将274s σ=MPa 代入中柔度杆的公式可以此钢材中柔度杆的判别柔度s λ:33127452.291.09s s a b σλ--=== (2)绘制临界应力总图如图:σ(MPa)cr11-7 b=40mm,h=60mm 的矩形截面压杆如图所示,在在平面内,两端铰支,出平面内两端固定。
材料为Q 235钢,其弹性模量210E G =Pa ,比例极限σP =200MPa 。
试求(1)压杆的临界荷载P cr ,(2)若[]3st n =,压杆所承受的最大轴向压力为多大?(3)从稳定性考虑b/h 为何值时最佳?习题11-7图解:(1)计算柔度:①当压杆在在平面内xoy 内失稳,为z 中性轴。
1 2.4138.560.060xy xy zli μλ⋅⨯=== ②当压杆在出平面内xoz 内失稳,为y 中性轴。
0.5 2.4103.920.04xz xz yli μλ⋅⨯===③λ越大,压杆越容易失稳,故此压杆将在在平面内先失稳。
max(,)138.56xz xy λλλ==④计算压杆能采用欧拉公式所对应的P λ22101.8P P P E πσλλ=→===⑤101.8138.56P λ=<,故采用欧拉公式计算P cr222362(2101010)(0.0600.040)259.10138.56cr cr E P A Aπσλπ=⋅=⋅⨯⨯⨯=⨯⨯=N kN(2) 由压杆稳定条件求压杆所承受的最大轴向压力[P ]若[]3st n =,[][]259.1086.373cr cr w w w P P n n P P n =≥→≤==kNb(3)求稳定性最佳的b/h当压杆在不同方向的柔度相等时,才不会在某平面内先失稳。
故1 2.41 2.40.5 2.40.50.5 2.4xyxyzxzxzylhibh b hlbiμλμλ⋅⎧⨯==⎪⎪⨯⨯⎪→=→=⎨⋅⨯⎪==⎪⎪⎩补充1 图示边长为a的正方形铰接结构,各杆的E、I、A均相同,且为细长杆。
试求达到临界状态时相应的力P等于多少?若力改为相反方向,其值又应为多少?F BC F N N BCN CD解:(1)各杆的临界力222..222cr BDcrEI EIPPa aππ===外(2)求各杆的轴力与P的关系。
由对称性可知,外围的四个杆轴力相同,NAB NBC NCD NDAF F F F===。
研究C、B结点,设各杆都是受拉的二力杆,则与结点相联系的杆施与背离结点指向杆内的拉力,C、B结点受力如图所示。
第一种情况:C:)02450x NCB NCBF P F cos F=→--=→=∑压杆B:()02450Y NBD NBC NBD NBCF F F cos F P=→--=→==∑拉杆令2,.2=NCB cr CB crEIF P P Paπ===↔外第二种情况:)NCBF=拉杆()-NBD NBCF P==压杆22.22-==22NBD NBC cr BDEI EIF P P Pa aππ===↔补充2 图示矩形截面松木柱,其两端约束情况为:在纸平面内失稳时,可视为两端固定;在出平面内失稳时,可视为上端自由下端固定。
试求该木柱的临界力.解:(1)计算柔度:①当压杆在在平面内xoz内失稳,y为中性轴。
0.57101.040.120xzxzyliμλ⋅⨯===②当压杆在出平面内xoy内失稳,z为中性轴。
27242.490.200xyxyzliμλ⋅⨯===③λ越大,压杆越容易失稳,故此压杆将在在平面内先失稳。
max(.)242.49xz xyλλλ==(2)松木75242.49Pλ=<,故采用欧拉公式计算P cr222112(0.110)(0.1200.200)40.28242.49cr crEP A Aπσλπ=⋅=⋅⨯⨯=⨯⨯=N kN补充3 图示压杆,材料为Q235钢,横截面有四种形式,其面积均为23102.3mm ⨯,试计算其临界力.解:(1)矩形:①计算柔度:23632 3.210103.2100.04b b --=⨯⨯=⨯→=0.530.53129.90.04xz xz ylb i μλ⋅⨯⨯==== 129.9>123=xz P λλ=矩形截面压杆属于细长压杆,采用欧拉公式计算其临界力 ②计算其临界力22113222103,210N 374.34kN 129.9cr E P A ππλ-⨯⨯=⋅=⨯⨯= (2)正方形截面:①计算柔度:23633.210103.2100.057a a --=⨯⨯=⨯→=0.530.5391.860.057xz xz ylb i μλ⋅⨯⨯==== 06091.86<123=xz P λλλ=<=正方形截面压杆属于中柔度杆,采用经验公式计算其临界力 ②采用直线经验公式计算其临界力63()(304 1.1291.86)10 3.210N 643.57kN cr cr P A a b A σλ-=⋅=-⋅=-⨯⨯⨯⨯=(3)圆形截面: ①计算柔度:23633.21010 3.2100.0644d d π--=⨯⨯=⨯→=0.530.5394.000.06444xz xz yld i μλ⋅⨯⨯==== 0=6094<123xz P λλλ<==圆形截面压杆属于中柔度杆,采用经验公式计算其临界力 ②采用直线经验公式计算其临界力63()(304 1.1294)10 3.210N 635.9kN cr cr P A a b A σλ-=⋅=-⋅=-⨯⨯⨯⨯=(3)圆环形截面: ①计算柔度:2222363(1)(10.7) 3.21010 3.2100.0894m 44D D D ππα---=-=⨯⨯=⨯→=0.530.5354.990.0894xz xz ylD i μλ⋅⨯⨯====054.99<60=xz λλ=圆环形截面压杆属于粗短杆,临界应力为屈服极限 ②计算其临界力()()6323510 3.210N 752kN cr cr s P A A σσ-=⋅=⋅=⨯⨯⨯=补充4 图示结构中,横梁AB 由14号工字钢制成,材料许用应力[]160MPa σ=,CD 杆为Q235轧制钢管,2636d D ==mm,mm 。
其弹性模量210E G =Pa 。
若[] 1.5st n =,试对结构进行强度与稳定校核。
F N 图(kN )M 图(kN m )+2412-解:(1)求反力:取ABC 杆为研究对象,受力如图所示。
()0sin 45122033.941kN ANDCNDC m FF =→-+⨯=→==∑F(2)内力分析:ABC杆的AC段发生拉弯组合变形,CB段发生弯曲;CD杆为轴向压缩杆件。
内力图如图所示。
(3)对压杆进行稳定性校核。
①求压杆的柔度127.39liμλ===②求压杆临界力对于Q235钢材料为100Pλ=,127.39>100Pλλ==,采用欧拉公式计算压杆临界应力2292221010Pa127.72MPa127.39crEππσλ⨯⨯===③校核压杆的稳定性[][]666322127.7210127.72101.83 1.526/69.701033.9410/{0.036[1()]}436cr crw w w w NDCn n nF Aσσπσ⨯⨯=≥→===≥=⨯⨯⨯⨯-故,压杆的稳定性足够。
(4)对梁ABC进行强度计算梁的C的左截面为拉弯组合变形的危险面,其上距中性轴最远的上边缘点位危险点。
查表可知14号工字钢的2321.516cm,102cmzA W==。
则梁的最大拉应力为:33maxmax4624101210Pa11.154117.647MPa128.8MPa21.5161010210NzF MA Wσ--⨯⨯=+=+=+=⨯⨯故,ABC梁的的强度足够。
